MAA3 Geometria

Tervetuloa lukion pitkän matematiikan geometria-kurssille! Tämä materiaali sisältää sekä teoriatietoa että tehtäviä, joista suurin osa suoritetaan sähköisesti suoraan oppimateriaaliin. Materiaali on tuotettu lisenssillä Nimeä-JaaSamoin 4.0 Kansainvälinen (CC BY-SA 4.0)

# kuvioiden_yhdenmuotoisuus

1. Kuvioiden yhdenmuotoisuus

Tässä kappaleessa käsitellään kuvioiden ja kappaleiden yhdenmuotoisuutta. Lisäksi puhutaan mittakaavasta eli yhdenmuotoisuussuhteesta. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

# yhdenmuotoisuus

1.1 Yhdenmuotoisuus

Kaksi kuviota on yhdenmuotoisia, kun toinen kuvio saadaan siirtämällä, kiertämällä, peilaamalla, suurentamalla tai pienentämällä kuvio.

Yhdenmuotoisuus

Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat samat riippumatta siitä, mitä sivuja tarkastellaan. Yhdenmuotoisissa kuvioissa vastinkulmat ovat aina yhtä suuret.

1.1.1 Esimerkki: yhdenmuotoiset kuviot GeoGebralla

# yhdenmuotoisuus-geo

Yllä olevassa GeoGebra-appletissa oranssi nelikulmio on ns. vertailukuvio, joka pysyy koko ajan samana. Sen sijaan vihreää nelikulmiota pystyy muokkaamaan.

Kierrä vihreää nelikulmiota vetämällä “kierto”-liukusäädintä ja huomaa, että vihreä nelikulmio on silti yhdenmuotoinen oranssin nelikulmion kanssa.

Muuta seuraavaksi vihreän nelikulmion kokoa raahaamalla “koko”-liukusäädintä. Huomaa, että vihreän nelikulmion kulmien suuruudet pysyvät samoina kuin oranssissa nelikulmiossa, vaikka viheän nelikulmion koko muuttuisi.

Siirrä vihreää nelikulmiota eri suuntiin raahaamalla “siirto”-liukusäädintä. Vihreän nelikulmion muoto pysyy samana, vaikka se olisi eri paikassa. Se on siis edelleen yhdenmuotoinen oranssin nelikulmion kanssa.

Lopuksi lisää valinta kohtaan “peilaus”, jolloin vihreä nelikulmio peilataan pystysuoran akselin suhteen. Huomaa jälleen, että nelikulmioiden vastinkulmat pysyvät yhtä suurina, vaikka vihreä nelikulmio peilataan.

Näiden kohtien perusteella voidaan todeta, että jos kuviota kiertää, siirtää, peilaa tai sen kokoa muuttaa joka suunnassa, kuvio säilyy yhdenmuotoisena alkuperäisen kuvion kanssa.

Kokeile lopuksi muuttaa oranssin nelikulmion kärkipisteiden paikkoja raahamalla sinisiä kärkipisteitä eri paikkoihin. Huomaa, että vihreä ja oranssi nelikulmio pysyvät koko ajan yhdenmuotoisina.

Tähän kappaleeseen liittyvät tehtävät.

# mittakaava

1.2 Mittakaava eli yhdenmuotoisuussuhde

Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat siis vakioita. Vastinsivut määritellään vastinpisteiden avulla. Alla olevassa kuvassa vastinpisteitä ovat ja , ja sekä ja . Näiden avulla voidaan määrittää vastisivut: ja , ja sekä ja . Lasketaan jokaisen vastisivuparin suhde, ja huomataan, että se on jokaisen vastinsivuparin tapauksessa 1,5 .

Tätä suhdetta kutsutaan yhdenmuotoisuussuhteeksi ja se määritellään alla.

Yhdenmuotoisuussuhde eli mittakaava

Jos kuviot ovat yhdenmuotoiset, yhdenmuotoisuussuhde tarkoittaa suhdetta $\frac{s_1}{s_2},$ missä s_1 on sivun pituus ensimmäisessä kuviossa ja s_2 sitä vastaavan sivun pituus toisessa kuviossa.

1.2.1 Esimerkki: yhdenmuotoisuussuhde GeoGebralla

# yhdenmuotoisuussuhde-geo

Yllä olevassa GeoGebra-appletissa on korostettu vastinpisteet ja vastinsivut samoilla väreillä. Lisäksi vasemmalla olevassa CAS-ikkunassa on laskettu kunkin vastinsivuparin suhde.

Kokeile siitää kolmioiden ABC ja DEF kärkipisteitä ja huomaa, että vastinsivujen suhteet pysyvät koko ajan samoina. Tuota suhdetta kutsutaan siis mittakaavaksi tai yhdenmuotoisuussuhteeksi.

Tähän kappaleeseen liittyvät tehtävät.

# kolmiot

1.3 Kolmiot

Kolmioiden yhdenmuotoisuudesta voit lukea myös M niinkuin matematiikka -teoksesta, joka on lukiotason matematiikan tietosanakirja.

Kolmiot ovat yhdenmuotoisia, jos niillä on kaksi yhtä suurta kulmaa. Kahdesta yhtä suuresta kulmastahan seuraa myös, että kolmioiden kolmas kulma on yhtä suuri.

Kolmioiden yhdenmuotoisuuslause KK

Jos kolmion kaksi kulmaa ovat yhtä suuria kuin vastinkulmat toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.

1.3.1 Esimerkki: yhdenmuotoiset kolmiot GeoGebralla

# kk-geo

Kun siirrät yllä olevassa GeoGebra-appletissa kolmion ABC kärkipisteitä, huomaat, että kolmio DEF muuttuu samalla. Voit muuttaa kolmion DEF kokoa raahamalla pistettä E ja siirtää sitä raahaamalla pistettä D.

Koska kolmioiden vastinkulmat ovat koko ajan yhtä suuret, ovat kolmiot yhdenmuotoisia. Riittää, että kolmioissa on kaksi yhtä suurta vastinkulmaa, koska tällöin kolmioiden kolmannetkin vastinkulmat ovat välttämättä yhtä suuria.

1.3.2 Esimerkki: kolmion sivu KK-lauseella

Määritä alla olevan kuvion janan pituus, joka on merkitty kuvioon kirjaimella . Janat ja ovat yhdensuuntaisia.

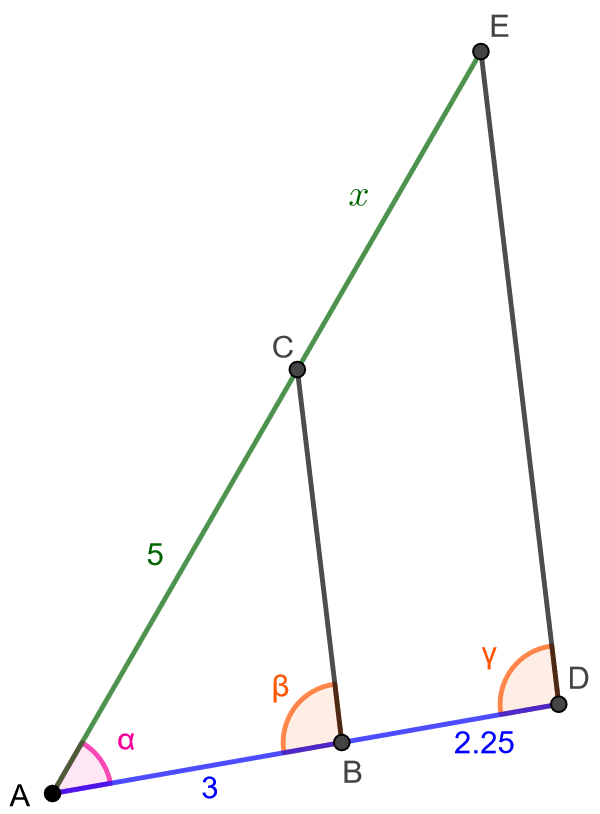
Huomataan, että kuviossa on oikeastaan kaksi päällekkäistä kolmiota: ABC ja ADE . Kolmioilla on yksi yhteinen kulma $\alpha$ joka on siis molemmissa kolmioissa yhtä suuri. Tarkastellaan seuraavaksi kulmia $\beta$ ja $\gamma$ . Koska janat ja ovat yhdensuuntaisia, ja jana on molempien kulmien vasempana kylkenä, kulmat $\beta$ ja $\gamma$ ovat samankohtaisia. Tämä tarkoittaa, että kulmat $\beta$ ja $\gamma$ ovat yhtä suuria. Koska kolmioissa ABC ja ADE on kaksi yhtä suurta vastinkulmaparia, voidaan yhdenmuotoisuuslauseen KK perusteella sanoa, että kolmiot ABC ja ADE ovat yhdenmuotoiset.

Koska kolmiot ovat yhdenmuotoisia, sivun pituuden määittämiseen voidaan käyttää yhdenmuotoisuussuhdetta. Vastinsivuparit ovat nyt ja sekä ja . Näiden parien suhteet ovat yhtä suuret, joten saadaan yhtälö $\frac{AD}{AB}=\frac{AE}{AC},$ johon sijoitetaan kunkin sivun pituus: $\frac{3+2,25}{3}=\frac{5+x}{5}.$ Sievennetään yhtälöä, kerrotaan se ristiin ja ratkaistaan siitä : $\begin{aligned} \frac{5,25}{3} &= \frac{5+x}{5}& \quad &| \text{ kerrotaan ristiin} \\ 5,25 \cdot 5 &= 3 \cdot (5+x)& \quad &| \text{ sievennetään} \\ 26,25 &= 15 + 3x& \quad &| -15 \\ 11,25 &= 3x &\quad &| :3 \\ 3,75 &= x & \quad &| \text{ vaihdetaan yhtälön puolia} \\ x & = 3,75 \end{aligned}$

Vastaukseksi saadaan, että janan pituus on 3,75 .

Jos kolmion kulmien suuruuksia ei tiedetä, voidaan kolmioiden yhdenmuotoisuus päätellä myös niiden sivujen pituuksien avulla. Kuten aiemmin olet opiskellut, yhdenmuotoisissa kuvioissa niiden vastinsivujen suhteet ovat vakioita. Tätä ominaisuutta käytetään hyväksi yhdenmuotoisuuslauseessa SSS.

Kolmioiden yhdenmuotoisuuslause SSS

Jos kolmion kaikki sivut ovat verrannolliset vastinsivuihin toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.

1.3.3 Esimerkki: kulman suuruus SSS-lauseella

Määritä kuvaan merkityn kulman $\beta$ suuruus.

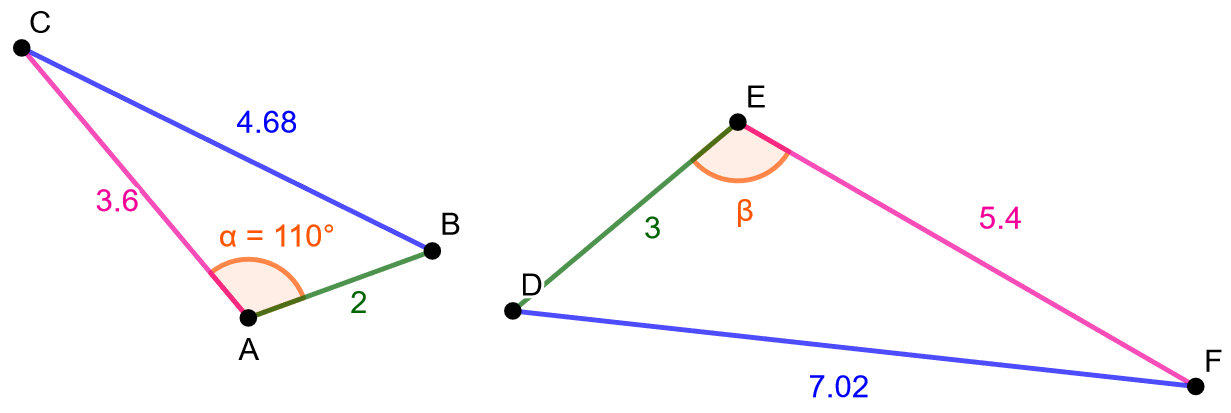
Tutkitaan ensin, ovatko kolmiot yhdenmuotoisia. Koska molemmista kolmioista on tiedossa vain sivujen pituuksia, lasketaan kunkin vastinsivuparin suhde. Jos suhteet ovat samoja, voidaan käyttää kolmioiden yhdenmuotoisuuslausetta SSS. Sinisellä merkittyjen vastinsivujen suhde on $\frac{7,02}{4,68}=1,5.$ Pinkillä merkittyjen vastinsivujen suhde on $\frac{5,4}{3,6}=1,5.$ Vihreällä merkittyjen vastinsivujen suhde on $\frac{3}{2}=1,5.$ Koska kaikkien vastisivuparien suhteet ovat samoja, yhdenmuotoisuuslauseen SSS mukaan kolmiot ovat yhdenmuotoisia. Koska kulmat $\alpha$ ja $\beta$ ovat vastinkulmia, ne ovat yhtä suuret. Kulma $\beta$ on siis $110^{\circ}$ .

Jos kahdesta kolmiosta tiedetään, että vain kaksi vastinsivua on verrannollisia keskenään, ei vielä voida päätellä, ovatko kolmiot yhdenmuotoisia. Jos lisäksi tiedetään vielä, että kahden verrannollisen vastinsivun välissä olevat kulmat ovat molemmissa kolmioissa yhtä suuret, voidaan sanoa, että kolmiot ovat yhdenmuotoisia.

Kolmioiden yhdenmuotoisuuslause SKS

Jos kolmion kaksi sivua ovat verrannolliset vastinsivuihin toisessa kolmiossa ja niiden välinen kulma on yhtä suuri kuin vastinkulma toisessa kolmiossa, niin kolmiot ovat yhdenmuotoiset.

1.3.4 Esimerkki: kolmion sivu SKS-lauseella

Määritä alla olevan kuvion sivun pituus, joka on merkitty kuvaan kirjaimella .

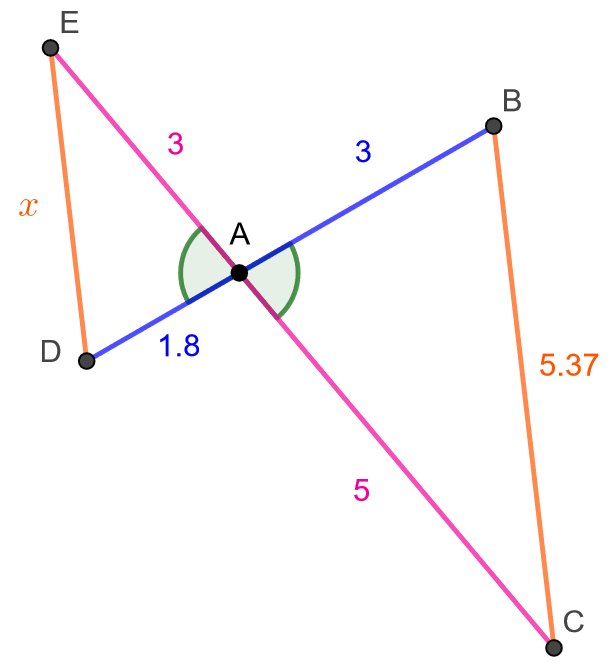
Sivun pituus saadaan helpoiten määritettyä, jos tiedetään, että kuviossa olevat kolmiot ABC ja ADE ovat yhdenmuotoiset. Kuvioon merkityt kulmat $\angle EAD$ ja $\angle CAB$ ovat toistensa ristikulmia ja siten yhtä suuria. Sinisellä mekittyjen vastinsivujen suhde on $\frac{1,8}{3}=0,6$ ja pinkillä merkittyjen vastinsivujen suhde on $\frac{3}{5}=0,6.$ Koska kahden vastinsivun suhteet ovat samat ja lisäksi näiden sivujen välinen kulma on kummassakin kolmiossa yhtä suuri, kolmiot ovat yhdenmuotoiset kolmioiden yhdenmuotoisuuslauseen SSS mukaan.

Oranssilla merkittyjen vastinsivujen suhteen tulee olla sama kuin muidenkin sivujen suhteet, joten saadaan seuraava yhtälö, joka ratkaistaan $\begin{aligned} \frac{x}{5,37}&=0,6 &\quad &|\cdot 5,37 \\ x &= 5,37 \cdot 0,6 &\quad &| \text{ sievennetään} \\ x &= 3,222 & \quad &| \text{ pyöristetään kahden desimaalin tarkkuudelle} \\ x &\approx 3,22 \end{aligned}$

Kuvion sivun pituus on noin 3,22 .

1.3.5 Esimerkki: yhdenmuotoisten kolmioiden piirtäminen GeoGebralla

# yhdenmuotoisten-kolmioiden-piirto

Yllä olevassa GeoGebra-appletissa on esimerkki siitä, kuinka voit muodostaa yhdenmuotoiset dynaamiset kolmiot GeoGebralla. Raahaa liukusäädintä ja lue ohjeet. Harjoittele piirtämistä itse tyhjässä GeoGebra-ikkunassa.

Tähän kappaleeseen liittyvät tehtävät.

# pinta-ala

1.4 Pinta-ala

Aiemmin tarkastelit vain kuvioiden vastinkulmien suuruuksia (jotka olivat samoja) sekä vastisivujen pituuksien suhteita (jotka pysyivät vakioina riippumatta siitä mitä sivupareja tarkasteltiin). Yhdenmuotoisuuden avulla voidaan päätellä lisäksi myös kuvioiden pinta-aloihin liittyviä suhteita.

Yhdenmuotoisten kuvioiden pinta-alalause

Jos kuviot ovat yhdenmuotoiset yhdenmuotoisuussuhteessa s_1 : s_2 , niiden pinta-alojen suhde on $\frac{A_1}{A_2} =\left(\frac{s_1}{s_2}\right)^2.$

1.4.1 Esimerkki: pinta-alojen suhde GeoGebralla

# pinta-alat-geo

Tutki yllä olevaa GeoGebra-applettia siirtämällä suorakulmion ABCD kärkipisteitä sekä raahaamalla yhdenmuotoisuussuhde-liukusäädintä. Vasemmalla olevaan CAS-ikkunaan lasketaan vastinsivujen ja sekä ja väliset suhteet sekä suorakulmioiden pinta-alojen ja välinen suhde. Lisäksi lasketaan yhdenmuotoisuussuhteen neliön lukuarvo. Huomaa, että pinta-alojen suhde ja yhdenmuotoisuussuhteen neliö ovat koko ajan yhtä suuria.

1.4.2 Esimerkki: pinta-alan laskeminen

Laske alla olevan kuvan isomman tähden pinta-ala, kun tiedetään, että tähdet ovat yhdenmuotoiset.

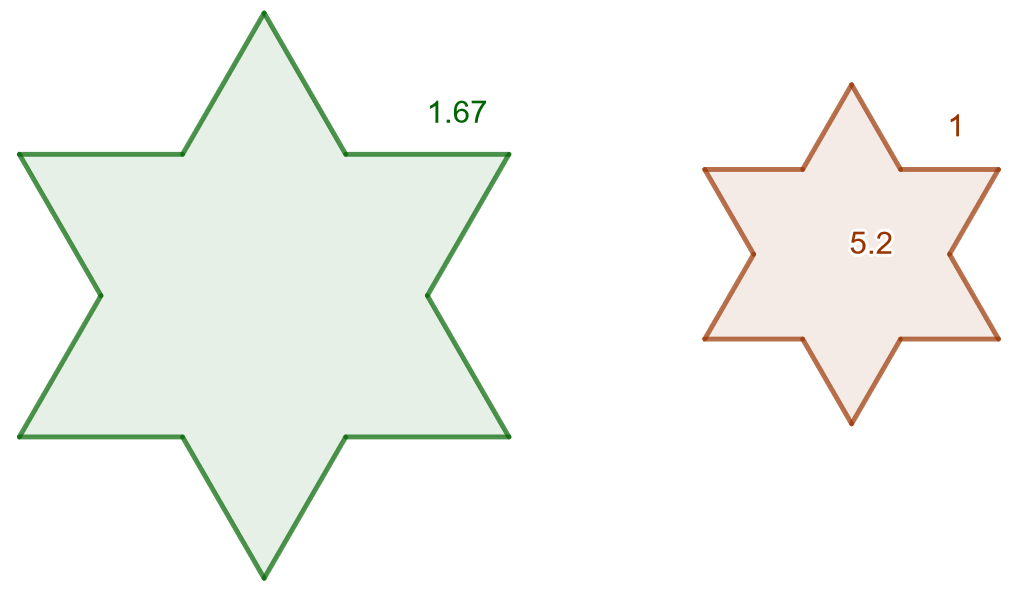
Koska kuviot ovat yhdenmuotoisia, voidaan käyttää yhdenmuotoisten kuvioiden pinta-alalausetta. Kuvioiden yhdenmuotoisuussuhde on $\frac{1,67}{1}=1,67.$ Merkitään kysyttyä isomman tähden pinta-alaa kirjaimella . Tehdään verranto yhdenmuotoisten kuvioiden pinta-alalauseen avulla ja ratkaistaan siitä : $\begin{aligned} \frac{x}{5,2}&=1,67^2 &\quad &| \cdot 5,2 \\ x &= 5,2 \cdot 1,67^2 &\quad &| \text{ sievennetään lauseke} \\ x &= 14,50228 &\quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x & \approx 14,5 \end{aligned}$ Isomman tähden pinta-ala on noin 14,5 .

Tähän kappaleeseen liittyvät tehtävät.

# tilavuus

1.5 Tilavuus

Samoin kuin aiemmin pinta-alan suhteen, yhdenmuotoisuus auttaa päättelemään jotakin myös kappaleiden tilavuuksista. Pinta-alan kohdalla yhdenmuotoisuussuhde korotettiin toiseen potenssiin, mutta tilavuuden kohdalla yhdenmuotoisuussuhde koroteteaankin kolmanteen potenssiin.

Yhdenmuotoisten kappaleiden tilavuuslause

Jos kappaleet ovat yhdenmuotoiset yhdenmuotoisuussuhteessa s_1 : s_2 , niiden tilavuuksien suhde on $\frac{V_1}{V_2} =\left(\frac{s_1}{s_2}\right)^3.$

1.5.1 Esimerkki: tilavuuksien suhde GeoGebralla

# tilavuudet-geo

Yllä olevassa GeoGebra-appletissa voit tutkia yhdenmuotoisten kappaleiden tilavuuksien suhteita. Raahaa liukusäädintä, joka kuvaa yhdenmuotoisuussuhdetta. Kokeile myös raahata punaisen särmiön sinisiä kärkipisteitä ja tutki, miten kappaleet ja tilavuuksien suhde muuttuvat. Kuviot ovat koko ajan yhdenmuotoisia, joten tilavuuksien suhde ja särmien kuutioiden suhde pysyvät koko ajan samoina.

Tähän kappaleeseen liittyvät tehtävät.

1. Kurssin tavoitteet ja keskeiset sisällöt

Geometrian kurssin tavoitteet ja sisällöt löytyvät Lukion opetussuunnitelman sivulta 132.

Kurssin tavoitteena on, että opiskelija

harjaantuu hahmottamaan ja kuvaamaan tilaa sekä muotoa koskevaa tietoa sekä kaksi- että kolmiulotteisissa tilanteissa
harjaantuu muotoilemaan, perustelemaan ja käyttämään geometrista tietoa käsitteleviä lauseita
osaa ratkaista geometrisia ongelmia käyttäen hyväksi kuvioiden ja kappaleiden ominaisuuksia, yhdenmuotoisuutta, Pythagoraan lausetta sekä suora- ja vinokulmaisen kolmion trigonometriaa
osaa käyttää teknisiä apuvälineitä kuvioiden ja kappaleiden tutkimisessa ja geometriaan liittyvien sovellusongelmien ratkaisussa.

Keskeiset sisällöt

kuvioiden ja kappaleiden yhdenmuotoisuus
sini- ja kosinilause
ympyrän, sen osien ja siihen liittyvien suorien geometria
kuvioihin ja kappaleisiin liittyvien pituuksien, kulmien, pinta-alojen ja tilavuuksien laskeminen

2. Teoria

Seuraavilla sivuilla on käyty läpi kurssiin liittyvä asiasisältö. Tärkeimmät lauseet ja kaavat on korostettu harmailla laatikoilla. Joitakin lauseita todistetaan eli perustellaan, mistä lauseet tulevat. Esimerkit ja todistukset eivät oletuksena näy sivulla, vaan ne saa näkyviin painamalla todistuksen tai esimerkin otsikon edessä olevaa -merkkiä. Esimerkit ovat pääosin joko perinteisiä laskuesimerkkejä tai sitten havainnollistuksia GeoGebralla.

Kaikki teoria löytyy yhdeltä sivulta.

MAA3-teoria

Teorian voi avata myös luku kerrallaan omille sivuilleen.

1. Kuvioiden yhdenmuotoisuus

2. Kolmioiden geometriaa

3. Monikulmioiden pinta-aloja

4. Ympyrä

5. Avaruusgeometria

3. Tehtävät

Seuraavilla sivuilla on eri teoriakappaleisiin liittyviä tehtäviä. Tehtävät on jaoteltu sivuille ja sivuilla kappaleisiin samalla tavalla kuin teoriakappaleissakin.

3.1 MathCheck-tehtävät

Suurin osa tehtävistä tuottaa vastaukseksin jonkin lukuarvon. Sen tarkistamiseksi tällaisissa tehtävissä on alla olevan esimerkin näköinen MathCheck-laatikko. Jos laatikossa on valmiina =-merkki, kirjoita vastauksesi suoraan sen perään. Voit kirjoittaa ensin vastauksesi sieventämättömässä muodossa ja sieventää sitä lisämällä ketjuun =-merkkejä. MathCheck osaa kertoa, jos sieventämisesi menee jossakin kohdassa pieleen. Kopioi alla oleva teksti MathCheck-kenttään ja katso mitä tapahtuu, kun painat Tarkista. Korjaa virheellinen kohta ja katso, mitä silloin tapahtuu, kun painat Tarkista.

4^2-1^3 = 16-3 = 13

# esim1

Joissakin tapauksissa vastaus halutaan tallentaa tietyn nimiseksi. Tällöin vastauskentässä on valmiiksi haluttu vastauksen nimi. Jos esimerkiksi neliön pinta-ala halutaan tallentaa muuttujaan A, lukee vastauskentässä valmiiksi <=> A=. Kokeile tätäkin tapaa alla olevaan vastauskenttään kopioimalla alla oleva teksti siinä valmiiksi olevan tekstin perään ja painamalla Tarkista.

3^2 <=> A=9

# esim2

Huomaa, että MathCheck-laatikoissa tulee käyttää desimaalipistettä eikä -pilkkua! Eli desimaaliluku "nolla pilkku viisi" kirjoitetaan MathCheckiin 0.5.

MathCheck ei ymmärrä kulmia asteina vaan radiaaneina (toinen kulman yksikkö). Jotta tämä "ongelma" voidaan kiertää laittamalla asteina olevan kulman suuruuden perään kerroin pi/180. Jos siis haluat laskea MathChekillä laskun $\sin (60^{\circ})$ , sinun tulee kirjoittaa MathCheck-kenttään sin(60*pi/180).

# asteet

3.2 GeoGebra-tehtävät

Joissakin tehtävissä sinun tulee tuottaa vastaus GeoGebralla. Seuraa tarkasti ohjeita. Jos ohjeissa käsketään nimeämään esimerkiksi jokin kulma tietyllä tavalla, se johtuu tehtävän pisteytyksestä. Ohjelma osaa tarkistaa tehtävän vain, jos olet nimennyt kerrotut pisteet, kulmat tms. oikein.

GeoGebra on hyödyllinen väline geometrian opiskelussa, ja se on myös sallittu ohjelma ylioppilaskirjoituksissa. Siksi kannattaa harjoitella sen käyttöä myös sellaisissa tehtävissä, joiden kohdalle GeoGebraa ei ole valmiiksi laitettu. Sillä voit piirtää esimerkiksi mallikuvat tehtävien tilanteista helposti ja tarkasti.

3.3 Monivalintatehtävät

Monivalintatehtävissä on usein vain yksi vastauskerta johtuen siitä, ettei oikeaa vastausta ja täten pisteitä voi saada arvaamalla. Vastaamisen jälkeen tehtävä kertoo malliratkaisun. Jos malliratkaisu näyttää koodikieleltä, kokeile päivittää sivu (esimerkiksi Windows-koneissa F5-painikkeella), jolloin tekstin pitäisi muuttua ymmärrettävämmäksi.

3.4 Ylioppilaskoetehtävät

Osa tehtävistä on vanhoja pitkän matematiikan ylioppilaskoetehtäviä. Nämä tehtävät tunnistat siitä, että tehtäväotsikon perään on suluissa merkitty kokeen tutkintokerta ja tehtävänumero. Esimerkiksi (S2014/5) tarkoittaa syksyn 2014 ylioppilaskokeen tehtävää numero 5. Ylioppilaskoetehtävien malliratkaisut löydät tarvittaessa myös täältä.