1. Kuvioiden yhdenmuotoisuus: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät lukuun Kuvioiden yhdenmuotoisuus. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa luvussakin.

# yhdenmuotoisuus-teht

1.1 Yhdenmuotoisuus

Tämän kappaleen teoria on kappaleessa Yhdenmuotoisuus.

# teht_onko_yhdenmutoinen

1.1.1 Tehtävä

# onko_yhdenmuotoinen

# mittakaava-teht

1.2 Mittakaava eli yhdenmuotoisuussuhde

Tämän kappaleen teoria on kappaleessa Mittakaava eli yhdenmuotoisuussuhde.

# teht_mittakaava1

1.2.1 Tehtävä

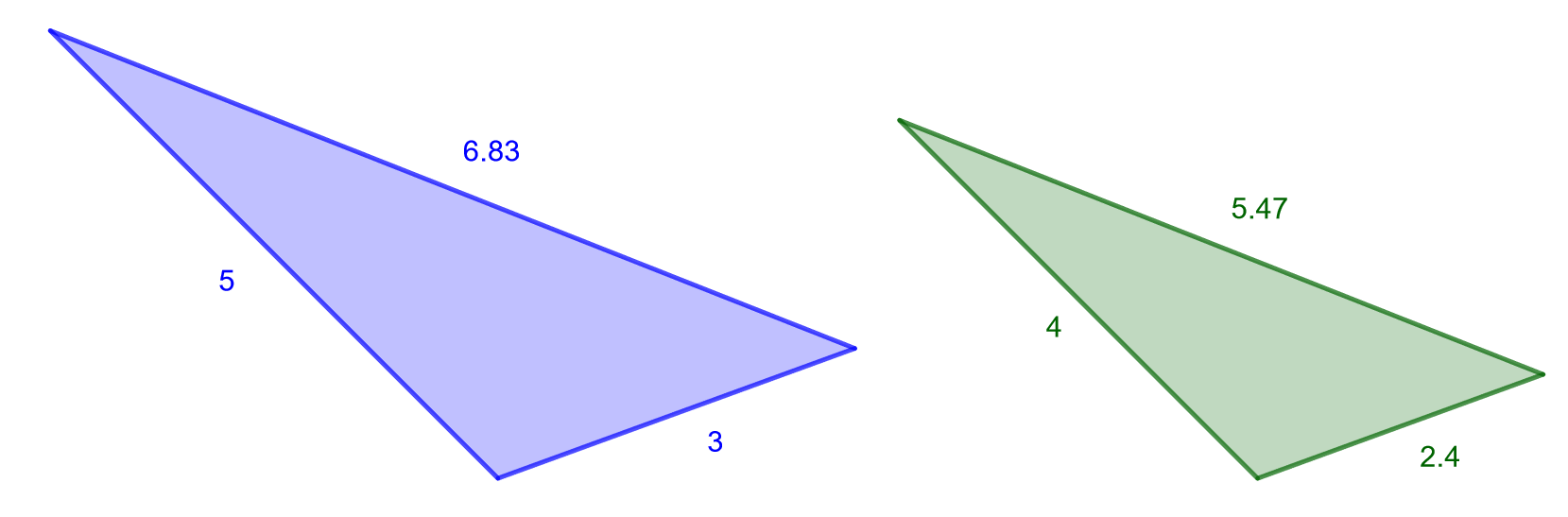
Määritä alla olevan kuvan kolmioiden mittakaava, kun oikeanpuoleinen kolmio on saatu pienentämällä vasemmanpuoleinen kolmio.

# mittakaava1a

# teht_S15T3a

1.2.2 Tehtävä (S2015/3a)

Kuntopolun pituus kartalla on $17,5 \text{ cm}$ . Mikä on polun pituus maastossa, kun kartan mittakaava on $1:20 \, 000$ ? Anna vastaus 100 metrin tarkkuudella.

# mittakaava1

# teht_tyopaikan_etaisyys

1.2.3 Tehtävä

Kartan mittakaava on $1:80 \, 000$ . Kallen työpaikan ja keskustan välimatka kartalla on $24,5 \text{ cm}$ . Kuinka paljon välimatka on luonnossa?

# mittakaava2

# teht_suomineito

1.2.4 Tehtävä

Mikä on kartan mittakaava, kun $1 \, 200 \text{ km}$ pitkä Suomineito on kartalla $25 \text{ cm}$ mittainen?

# mittakaava3

# teht_kukan_suurennos

1.2.5 Tehtävä

Biologian kirjassa on suurennos kukasta mittakaavassa 3:1 . Jos kirjassa olevan kukan leveys on $45 \text{ mm}$ , kuinka leveä on alkuperäinen kukka?

# mittakaava4

# teht_muurahaisen_suurennos

1.2.6 Tehtävä

Seuraavalla sivulla biologian kirjassa on suurennos muurahaisesta. Suurennoksen pituus on $12 \text{ mm}$ . Tekstissä kerrotaan muurahaisen pituuden luonnossa olevan $3 \text{ mm}$ . Mikä on suurennoksen mittakaava?

# mittakaava5

# kolmiot-teht

1.3 Kolmiot

Tämän kappaleen teoria on kappaleessa Kolmiot.

# teht_yhdenmuotoiset_kolmiot

1.3.1 Tehtävä

# kolmio_yhdenmuotoisuus

# teht_yhdenmuotoiset_kolmiot1

1.3.2 Tehtävä

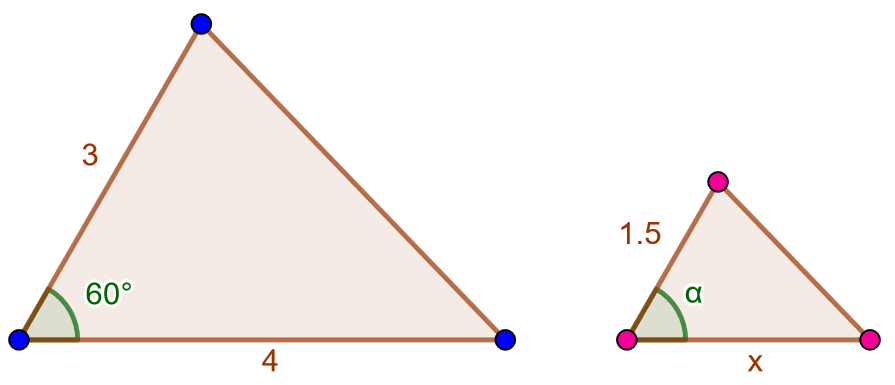
Alla olevassa kuvassa on kaksi yhdenmuotoista kolmiota. Päättele sivun pituus ja kulman $\alpha$ suuruus.

# yhdenmuotoisuus1a

# yhdenmuotoisuus1b

# teht_yhdenmuotoiset_kolmiot2

1.3.3 Tehtävä

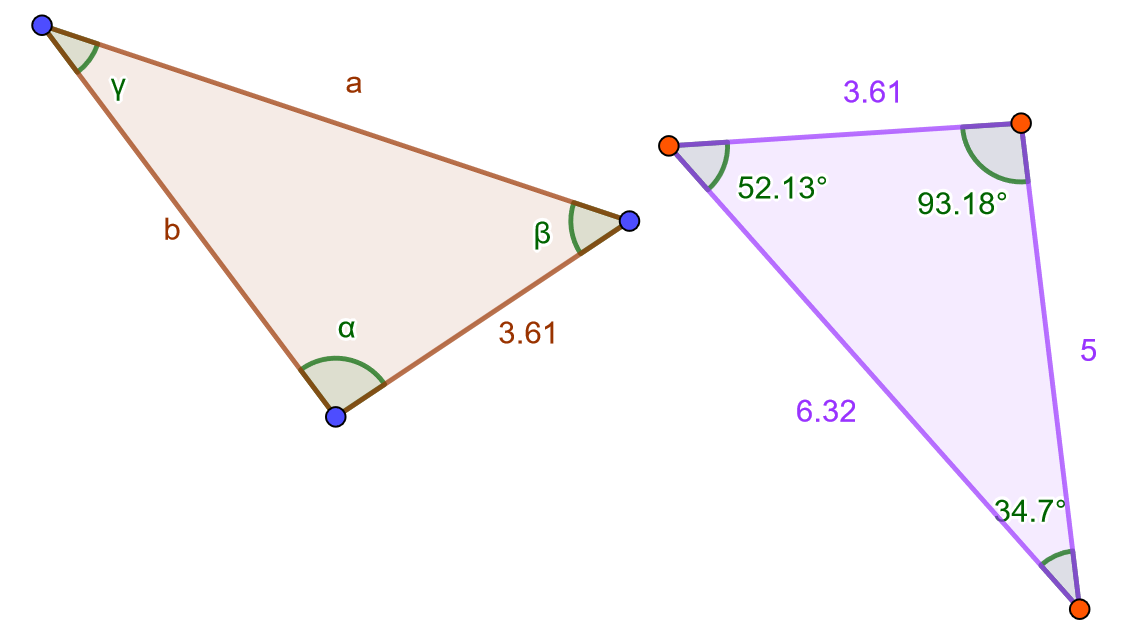
Yllä olevat kolmiot ovat yhdenmuotoisia. Päättele puuttuvat sivujen pituudet ja kulmien suuruudet. Huom! Käytä desimaalipistettä! Älä laita kulmien suuruuksiin astemerkkiä.

# yhdenmuotoisuus2a

# yhdenmuotoisuus2b

# yhdenmuotoisuus2alfa

# yhdenmuotoisuus2beta

# yhdenmuotoisuus2gamma

# teht_lipputanko

1.3.4 Tehtävä

Talon pihalla on lipputanko ja $0,9 \text{ m}$ mittainen pystysuora keppi. Eräänä päivänä kepin varjon pituudeksi mitattiin $1,3 \text{ m}$ ja lipputangon varjon pituudeksi $11,6 \text{ m}$ . Kuinka korkea lipputanko on?

# lipputanko

# teht_geogebra_taydennys

1.3.5 Tehtävä

Täydennä alla olevaa GeoGebra-appletti niin, että siinä on kaksi yhdenmuotoista kolmiota. Käytä hyväksesi valmiina appletissa olevaa kolmion sivua.

Tarkista lopuksi, että piirtämäsi kolmion kulmien nimet ovat D, E ja F.

# geo-kolmioiden-piirto1

Vinkkejä GeoGebran käyttöön

Jana ED voi vastata mitä tahansa sivua kolmiossa ABC.
Syöttökentän avulla voit lisätä uuden pisteen esimerkiksi kohtaan (0,0) yksinkertaisesti kirjoittamalla syöttökenttään (0,0).
Kokeile kirjoittaa syöttökenttään D+(2;90°) (astemerkin saat painamalla ALT + o). Huomaa, että sulkeissa on pilkun sijaan puolipiste. Pohdi, miten voisit tätä tietoa käyttää yllä olevassa tehtävässä.

# teht_kolmion_korkeus

1.3.6 Tehtävä

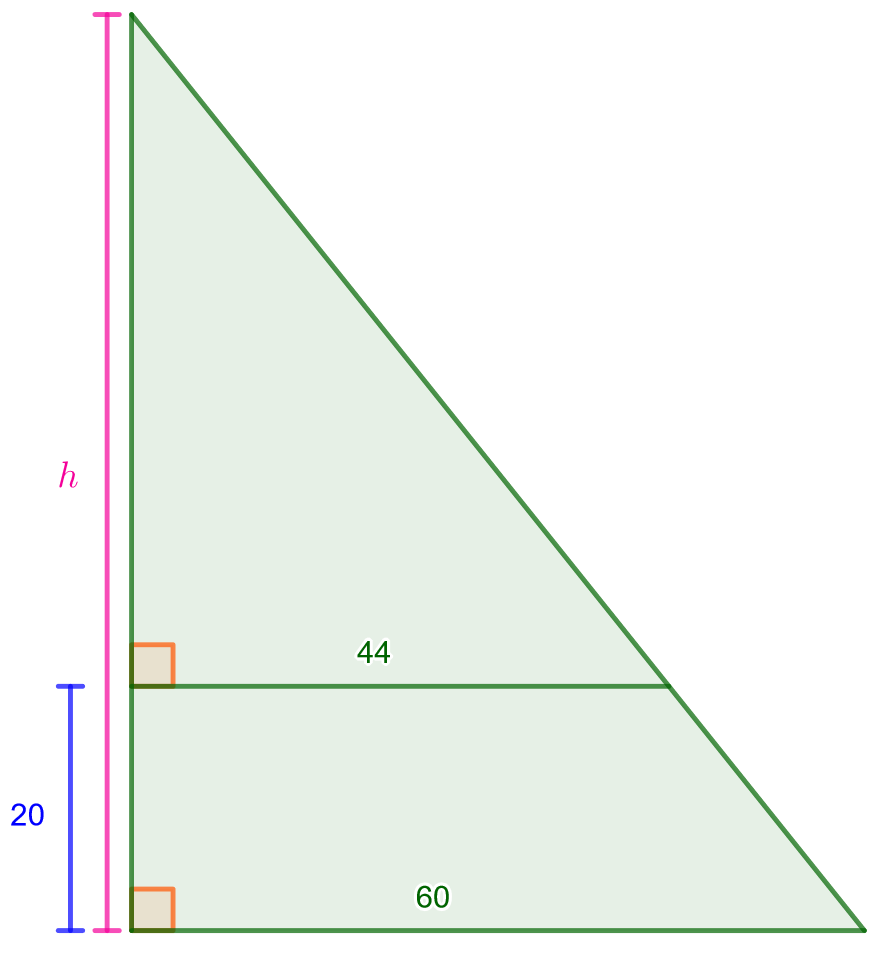
Laske alla olevan kuvan ison kolmion korkeus.

# yhdenmuotoisuus3

# teht_keskijana_osoitus

1.3.7 Tehtävä

Osoita, että tasakylkisen kolmion kannalle piirretty keskijana on huippukulman puolittaja.

Ratkaisu

Alla olevassa kuvassa on tasakylkinen kolmio ABC . Kuvaan on lisäksi piirretty kolmion kannan keskijana , eli jana joka yhdistää kannan keskipisteen kolmion vastakkaiseen kärkeen.

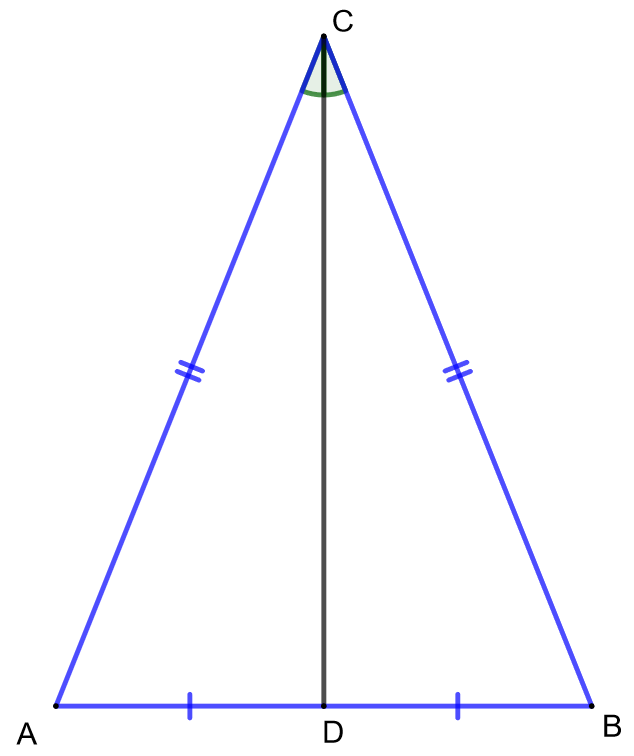
Koska kolmio on tasakylkinen, ovat sen kyljet ja yhtä pitkät. Koska keskijana jakaa kannan kahteen yhtä pitkään osaan, ovat ja yhtä pitkiä. Kolmiot ACD ja BCD ovat yhteneviä yhtenevyyslauseen SSS mukaan, koska AC=BC , AD=BD ja jana on yhtenevä molemmissa kolmioissa.

Koska kolmiot ovat yhdenmuotoisia, niiden vastinkulmat ovat yhtä suuret. Tämä tarkoittaa, että kulmat $\angle ACD$ ja $\angle DCB$ eli kuvaan vihreällä merkityt kulmat ovat yhtä suuria. Jana jakaa siis puolittaa huippukulman.

# pinta-ala-teht

1.4 Pinta-ala

Tämän kappaleen teoria on kappaleessa Pinta-ala.

# teht_lampi

1.4.1 Tehtävä

Maastossa olevan lammen pinta-ala on $2,8 \text{ ha}$ . Maastosta piirretään kartta, jonka mittakaava on $1 : 20 \, 000$ . Mikä on lammen pinta-ala kartalla?

# pintaala1

# teht_pelto

1.4.2 Tehtävä

Kartan mittakaava on $1 : 15 \, 000$ . Kartalla olevan pellon pinta-ala on $25 \text{ cm}^2$ . Mikä on pellon pinta-ala hehtaareissa?

# pintaala2

# teht_suorakulmainen_kolmio

1.4.3 Tehtävä

Kahden suorakulmaisen kolmion mittakaava on 2 : 5 . Suuremman kolmion kannat ovat pituudeltaan ja . Määritä pienemmän kolmion pinta-ala.

# pintaala3

# teht_kolmion_jako

1.4.4 Tehtävä

Kolmio ABC leikataan kahteen osaan kannan suuntaisella suoralla siten, että AP:PC=2:3 . Missä suhteessa suora jakaa kolmion alan?

# pintaala4

Vihje

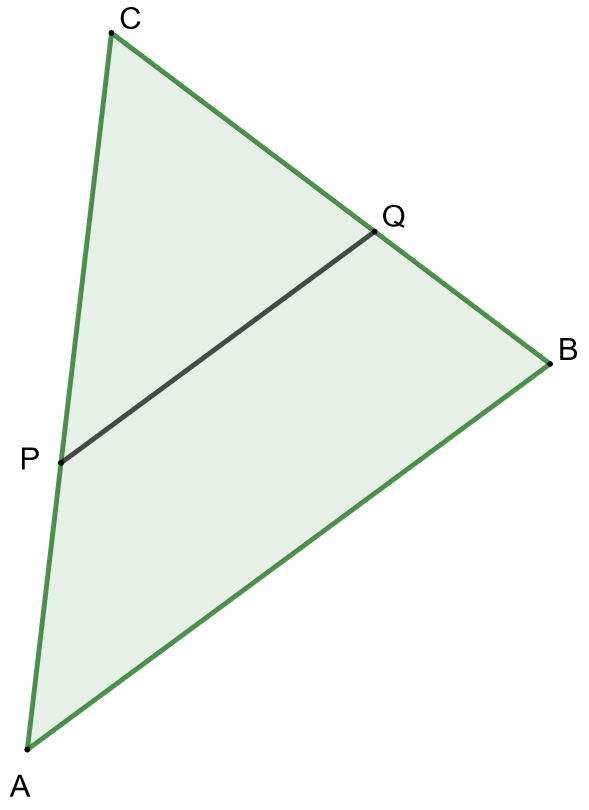
Osoita ensin, että kolmiot ABC ja CPQ ovat yhdenmuotoisia, minkä jälkeen voit ratkaista yhdenmuotoisuussuhteen.

# tilavuus-teht

1.5 Tilavuus

Tämän kappaleen teoria on kappaleessa Tilavuus.

# teht_kuutiot

1.5.1 Tehtävä

Pienemmän kuution sivun pituus on ja suuremman kuution sivun pituus on . Määritä kuutioiden tilavuuksien suhde.

# tilavuus1

# teht_ilmapallot

1.5.2 Tehtävä

Kahteen yhdenmuotoiseen ilmapalloon puhalletaan ilmaa. Pienemmän ilmapallon pituus on $15 \text{ cm}$ ja suuremman $30 \text{ cm}$ .

Mikä on pallojen yhdenmuotoisuussuhde?

# tilavuus2a

Jos pienemmän pallon tilavuus on litraa, mikä on suuremman pallon tilavuus?

# tilavuus2b

# teht_jalkapallo1

1.5.3 Tehtävä

Jalkapallon ympärysmitta on $70 \text{ cm}$ ja tennispallon $20 \text{ cm}$ . Määritä jalkapallon ja tennispallon tilavuuksien suhde.

# tilavuus3

# teht_jalkapallo2

1.5.4 Tehtävä

Käytetään edellisen tehtävän jalkapalloa ja tennispalloa. Mikä on jalkapallon tilavuus, jos tennispallon tilavuus on $135 \text{ cm}^3$ ?

# tilavuus4