4. Ympyrä: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Ympyrä. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

# sade-teht

4.1 Säde, halkaisija, piiri

Tämän kappaleen teoria on kappaleessa Säde, halkaisija, piiri.

# teht_puhelinlinja

4.1.1 Tehtävä

Oleletaan, että maapallo on täysin pyöreä. Eräs puhelinyhtiö on vetänyt puhelinlinjan päiväntasaajaa pitkin maapallon ympäri. Kuinka paljon linjaa tarvitaan lisää, jos se halutaan nostaa $10 \text{ m}$ korkeille tolpille. Anna vastaus metreinä ja yhden desimaalin tarkkuudella.

# puhelinlinja

# teht_S18T8

4.1.2 Tehtävä (S2018/8)

Yksikköympyrän kehän pituus on $2 \pi$ . Arvioi tätä lukua approksimoimalla ympyrää sen sisään piirretyllä säännöllisellä kuusikulmiolla ja laskemalla kuusikulmion piirin pituus. Muodosta toinen arvio säännöllisen 12-kulmion avulla ja määritä kummankin approksimaation suhteellinen virhe vertaamalla tuloksia laskimen antamaan lukun $2 \pi$ likiarvoon.

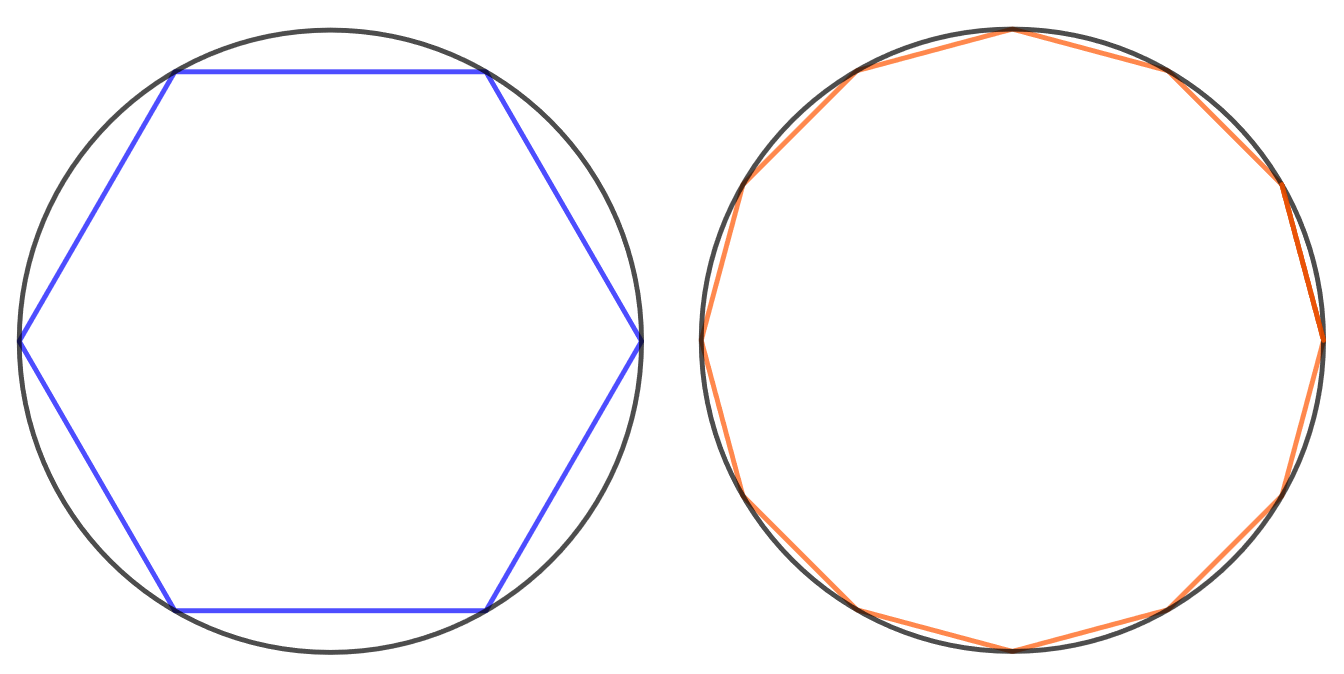
Huomautus: Yksikköympyrä tarkoittaa ympyrää, jonka säde on .

# S18T8a

# S18T8b

# teht_polkupyora

4.1.3 Tehtävä

Polkupyörän renkaan koko on 28" eli sen halkaisija on tuumaa. Pyörään halutaan laittaa matkamittari, jota varten tarvitaan yhdellä renkaan pyörähdyksellä kuljettu matka. Laske pyörän yhden renkaan täydellä pyörähdyksellä kulkema matka ja ilmoita vastaus yhden desimaalin tarkkuudella senttimetreinä.

# polkupyörä

# teht_pyora

4.1.4 Tehtävä

Halkaisijaltaan $60 \text{ cm}$ pyörä pyörähtää kertaa. Kuinka pitkän matkan pyörä etenee?

# pyoriva_pyora_1

Kuinka monta pyörähdystä pyörä etenee $200 \text{ m}$ matkalla?

# pyoriva_pyora_2

# teht_kukkaympyra

4.1.5 Tehtävä

Mari haluaa laittaa kukkia kasvamaan täsmälleen ympyrän muotoon. Hänellä on kukkaa ja hän haluaa, että kukkien välinen etäisyys ympyrän kaarta pitkin mitattuna on tasan $20 \text{ cm}$ . Mikä on tällaisen ympyrän halkaisija?

# kukkaympyra

# teht_keskinormaali

4.1.6 Tehtävä

Osoita, että kahden leikkaavan ympyrän keskipisteiden välinen jana on ympyröiden leikkauspisteiden välisen janan keskinormaali.

Alla olevan kuvan merkinnöillä, sinun tulee osoittaa, että kuvaan punaisella merkittyjen janojen ja OO' välinen kulma on $90^{\circ}$ ja että janat ja ovat keskenään yhtä pitkiä.

Ratkaisu

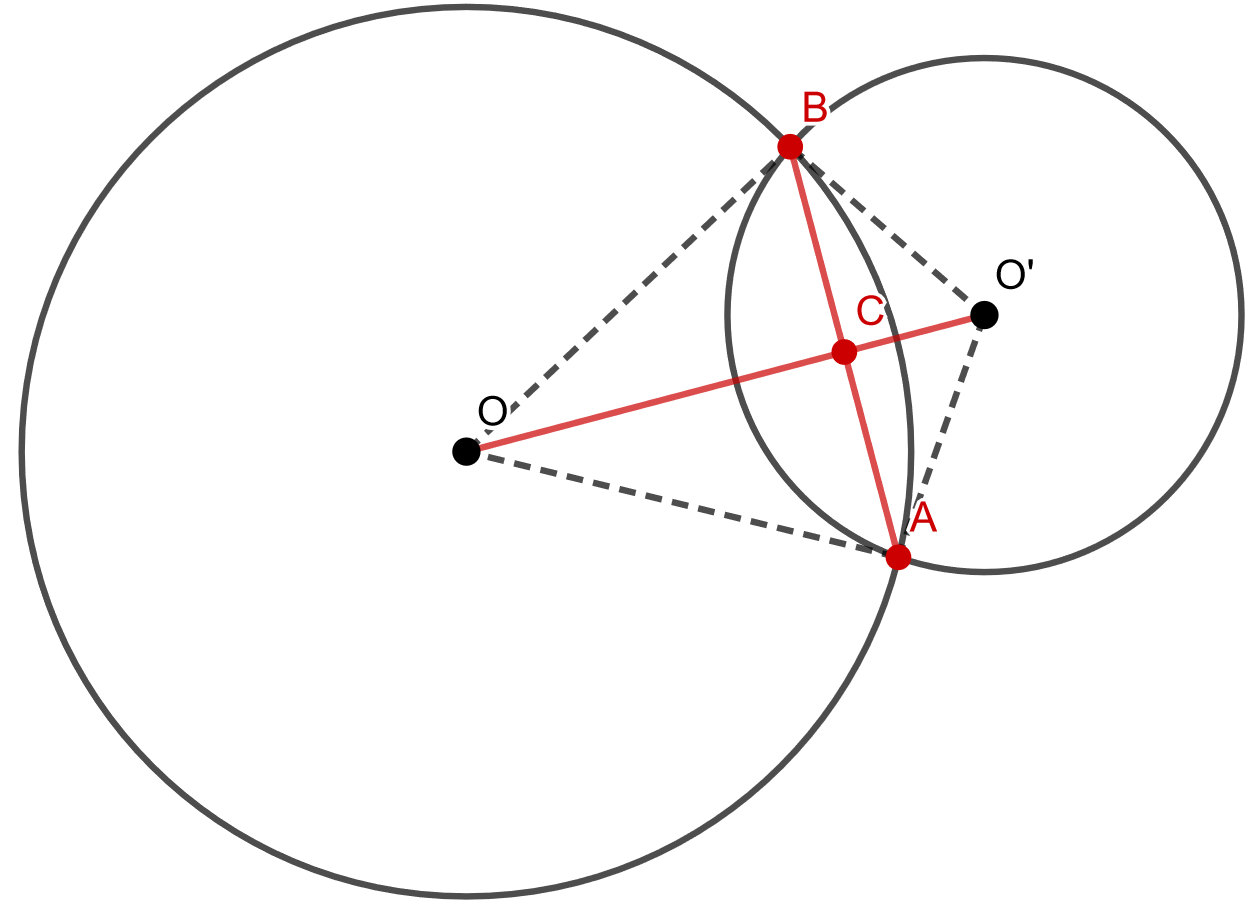
Tarkastellaan ensin kolmioita OO'B ja OO'A . Kolmioiden sivut ja ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Samoin sivut O'B ja O'A ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Sivu OO' on molemmissa kolmioissa sama, joten kolmiot ovat yhteneviä (eli niiden kaikki mitat ovat yhtä suuria). Tällöin myös janat ja ovat keskenään yhtä pitkiä.

Kuvassa piste on janojen ja OO' leikkauspiste, jolloin kulmat BCO ja OCA muodostavat oikokulman. Tarkastellaan seuraavaksi kolmioita BCO ja ACO . Sivut ja ovat yhteneviä (kuten aiemmin todettiin). Lisäksi sivu on yhteinen kummallekin kolmiolle. Lisäksi kulmat COB ja AOC ovat yhteneviä, sillä kolmiot OO'B ja OO'A ovat yhteneviä (kuten aiemmin todettiin). Näin ollen kolmioiden BCO ja ACO on oltava yhtenevät ja kulmien BCO ja OCA on myös oltava yhtenevät. Tällöin $BCO=OCA = \frac{180^{\circ}}{2}=90^{\circ}$ .

# pinta-ala-teht

4.2 Pinta-ala

Tämän kappaleen teoria on kappaleessa Pinta-ala.

# teht_koydella_rajataan_alue

4.2.1 Tehtävä

150 metrin köydellä rajataan alue. Laske alueen pinta-ala, kun se on muodoltaan

neliön muotoinen.

# koysi_nelio

ympyrän muotoinen.

# koysi_ympyra

# teht_ympyra_arkilla

4.2.2 Tehtävä

Piirretään A4-arkille ( $210 \text{ mm} \times 297 \text{ mm}$ ) mahdollisimman suuri ympyrä. Mikä on tämän ympyrän pinta-ala?

# a4

# keskuskulma

4.3 Keskuskulma, kaaren pituus, sektorin pinta-ala

Tämän kappaleen teoria on kappaleessa Keskuskulma, kaaren pituus, sektorin pinta-ala.

# teht_sektorin_ala

4.3.1 Tehtävä

# sektori1

# teht_sektorin_keskuskulma

4.3.2 Tehtävä

Ympyräsektorin pinta-ala on 52,9 ja sen säde on 5,4 . Kuinka suuri on sektorin keskuskulma?

# sektori2

# teht_pizzapalat

4.3.3 Tehtävä

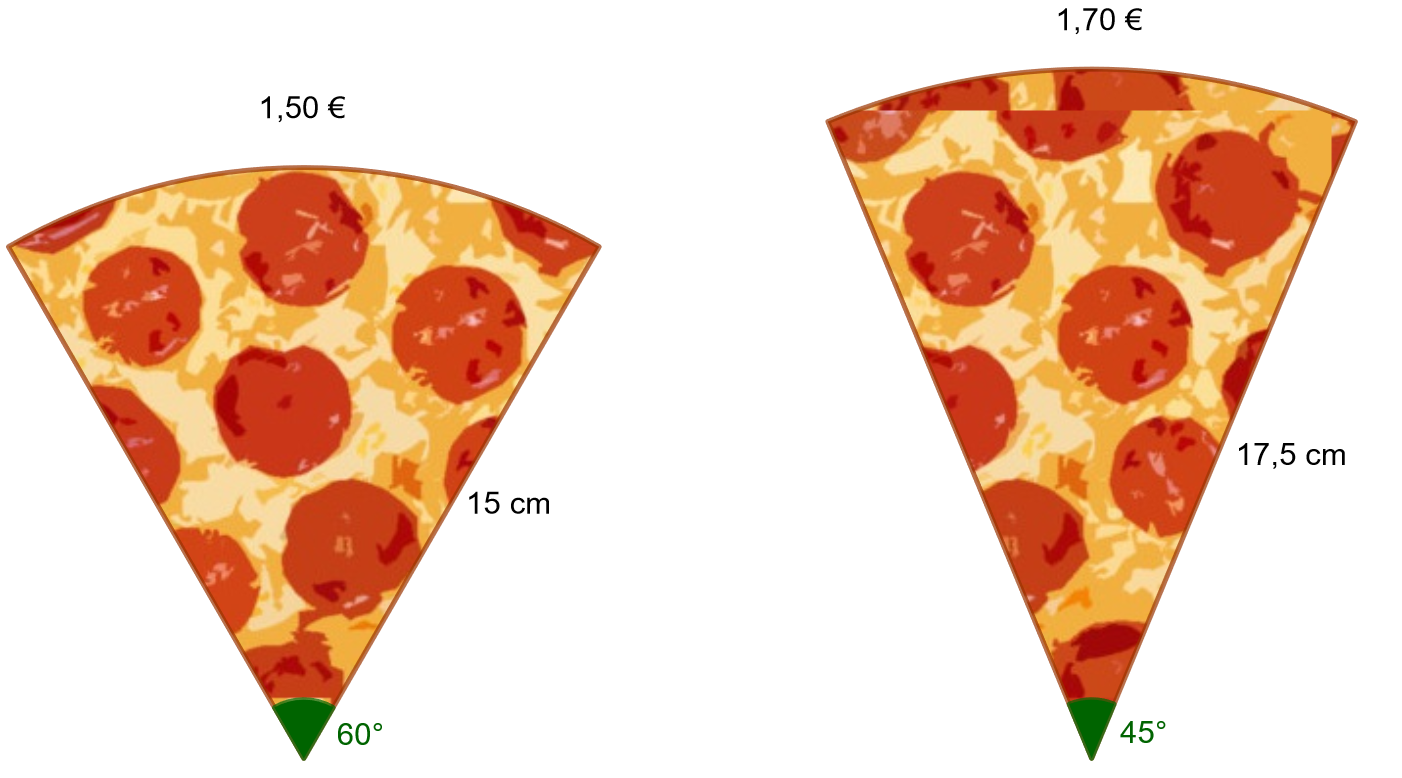
Kumpi alla olevista pizzapaloista kannattaa ottaa, jos haluaa rahalleen eniten vastinetta?

# pizzapalat

# teht_kuulantyonto

4.3.4 Tehtävä

Alla on kuva kuulantyöntöringistä ja -sektorista. Ringin halkaisija on jalkaa eli $2,135 \text{ m}$ .

Kuulantyöntösektori peitetään hiekalla. Kuinka suuri pinta-ala peitetään? Rinkiin ei laiteta hiekkaa.

# kuulantyonto_a

Sektori ja rinki ympäröidään ulkoreunoja pitkin merkintänauhalla. Kuinka paljon nauhaa tarvitaan?

# kuulantyonto_b

# teht_lammas

4.3.5 Tehtävä

Lammas on kiinnitetty $10 \text{ m}$ pitkällä hihnalla aidoitetun alueen kulmaan. Laske, kuinka suurelta alueelta lammas voi syödä ruohoa.

# lammas

# teht_ark11T3

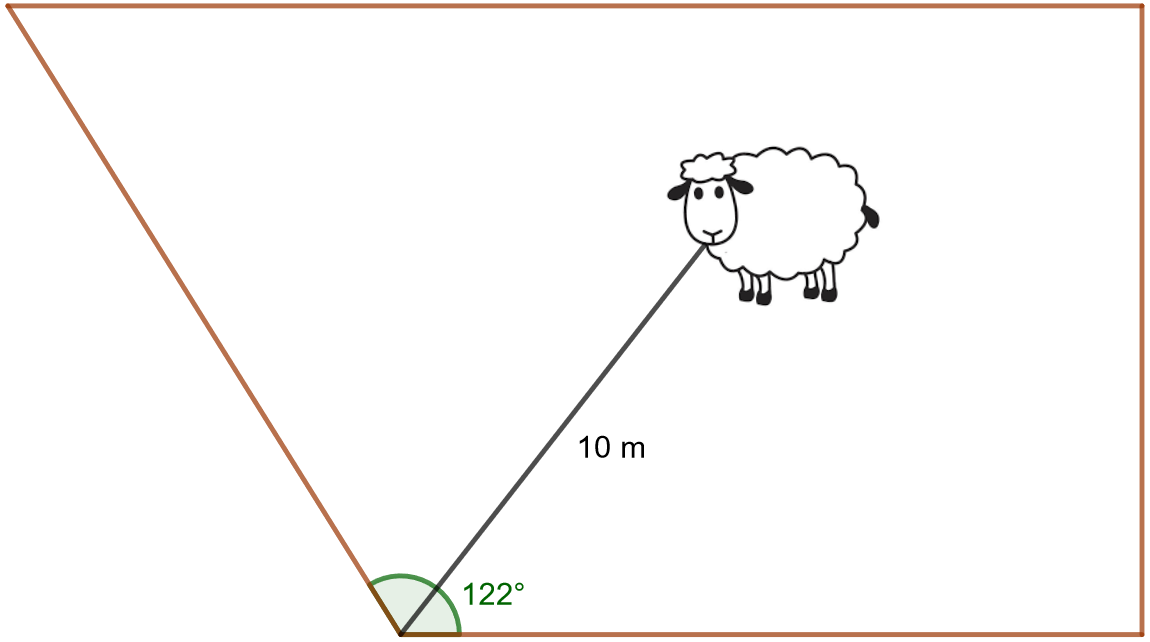
4.3.6 Tehtävä (Arkkitehtivalinnan koe 2011, 3)

Sata metriä pitkä köysi katkaistaan kahteen osaan. Toisesta osasta muodostetaan ympyrän ja toisesta neliön piiri. Kuvioiden pinta-alojen halutaan olevan samat. Miten naru on katkaistava?

Vihje

Tee yhtälöryhmä, jossa tuntemattomat muuttujat ovat neliön sivun pituus a ja ympyrän säde r.

# sadan_metrin_koysi

# teht_S18T11

4.3.7 Tehtävä (S2018/11)

Alla olevien kuvioiden kaksi tilannetta ovat syntyneet erään abiturientin harjoitellessa dynaamisen matematiikkaohjelman käyttöä. Tehtävänä on auttaa häntä viemään tarkastelu loppuun molemmissa tapauksissa.

Mitä ympyrään liittyvää lausetta abiturientti tutkii kuvassa 1? Kirjoita lause mahdollisimman täsmällisiä termejä käyttämällä.
Abiturientti tarkastelee kuvassa 2 näkyvän kolmion merkillistä pistettä . Mikä tämä piste on? Minkä pisteeseen liittyvän geometrisen ominaisuuden abiturientti voi todentaa, jos hän piirtää ympyrän, jonka keskipisteenä on ja jonka säde on sopivan mittainen?
Perustele joko a-kohdan lause, kun pisteet , ja ovat samalla suoralla, tai b-kohdan ominaisuus.

Ratkaisu

# janne-teht

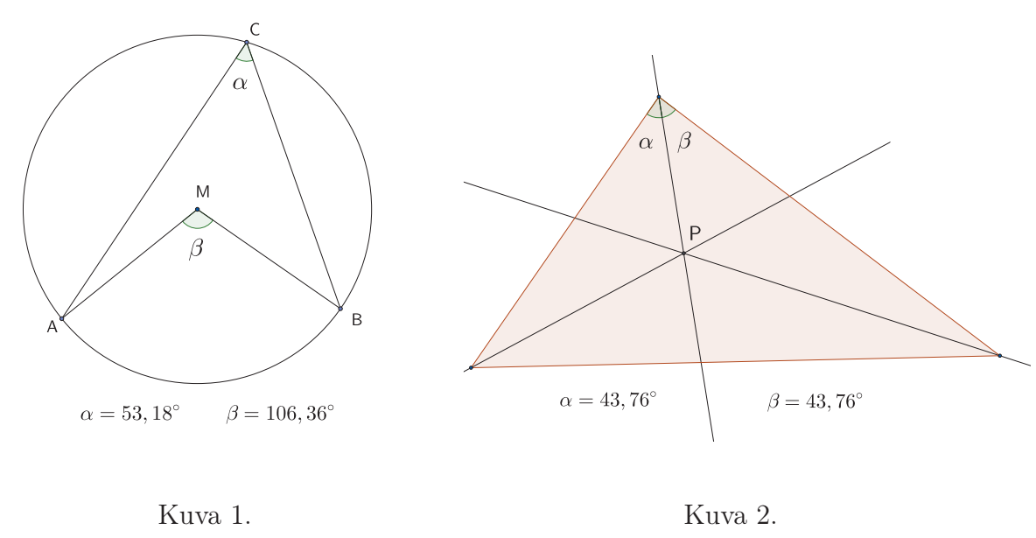
4.4 Jänne, segmentti

Tämän kappaleen teoria on kappaleessa Jänne, segmentti.

# teht_segmentin_ala

4.4.1 Tehtävä

Ympyrän säde on ja segmentin keskuskulman suuruus on $138^{\circ}$ . Mikä on pienemmän muodostuvan segmentin pinta-ala?

# segmentti1

# teht_suuremman_segmentin_ala

4.4.2 Tehtävä

Ympyrän säde on ja segmentin keskuskulman suuruus on $300^{\circ}$ . Mikä on suuremman muodostuvan segmentin pinta-ala?

# segmentti2

# teht_segmentin_ala2

4.4.3 Tehtävä

Ympyrän halkaisija on . Ympyrään on piirretty segmentti, jota vastaavan kaaren pituus on . Kuinka suuri on pienemmän segmentin pinta-ala?

# segmentti3

# teht_ympyraneljannes

4.4.4 Tehtävä

Kuinka monta prosenttia ympyräneljännekseen piirretyn segmentin pinta-ala on koko ympyrän pinta-alasta? Ympyrän säde on .

# ympyraneljannes

# teht_ark15T4

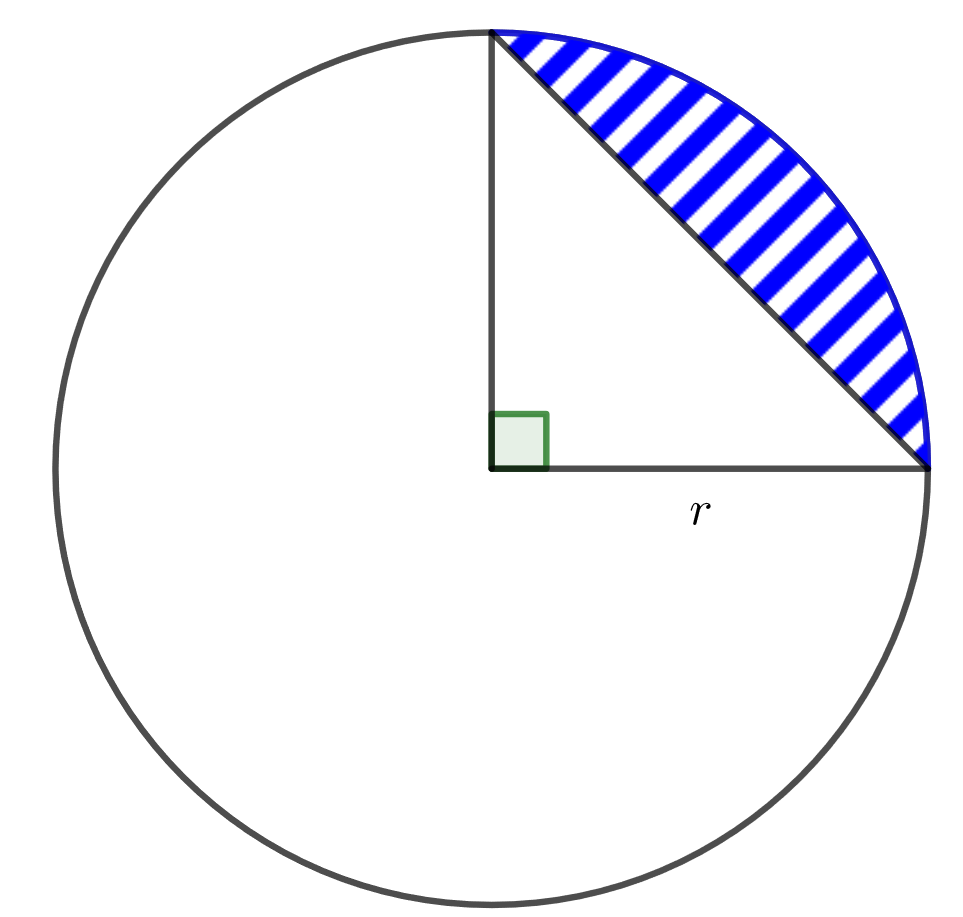
4.4.5 Tehtävä (Arkkitehtivalinnan koe 2015/4)

Kaksi majakkaa sijaitsee kilometrin etäisyydellä toisistaan. Veneen etäisyys merellä (tasopinta) on korkeintaan kilometriä kummastakin majakasta. Laske sen alueen pinta-ala neliökilometreissä, jolla vene voi olla.

Vihje

# majakat

# tangentti-teht

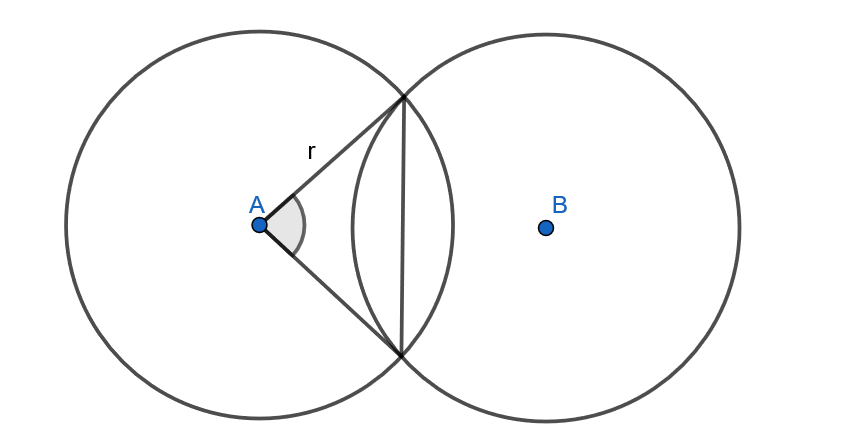
4.5 Tangentti, tangenttikulma

Tämän kappaleen teoria on kappaleessa Tangentti, tangenttikulma.

# teht_tangenttikulma1

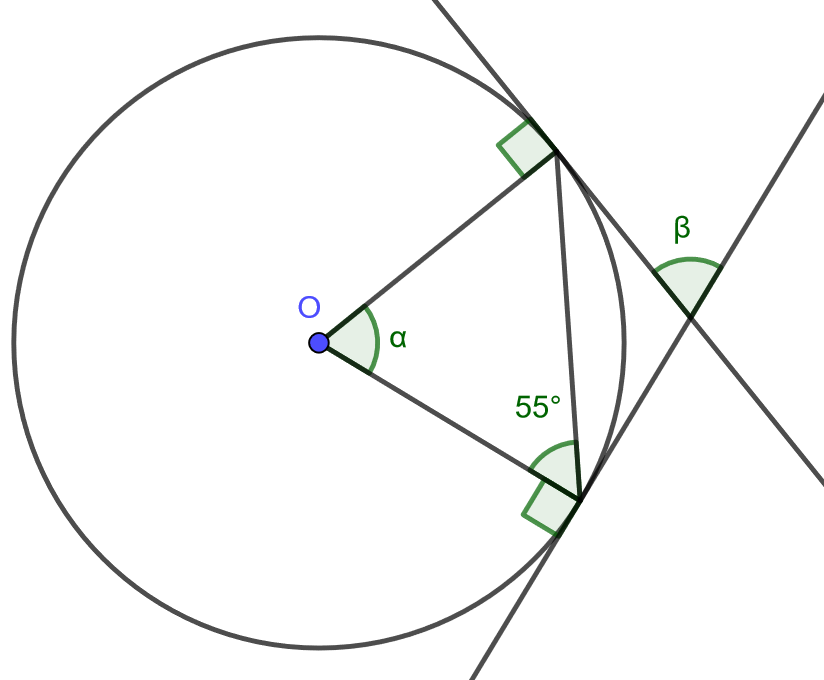
4.5.1 Tehtävä

Ratkaise alla olevasta kuvasta $\alpha$ ja $\beta$ .

# tangenttikulmat1

# tangenttikulmat2

# teht_vesitorni

4.5.2 Tehtävä

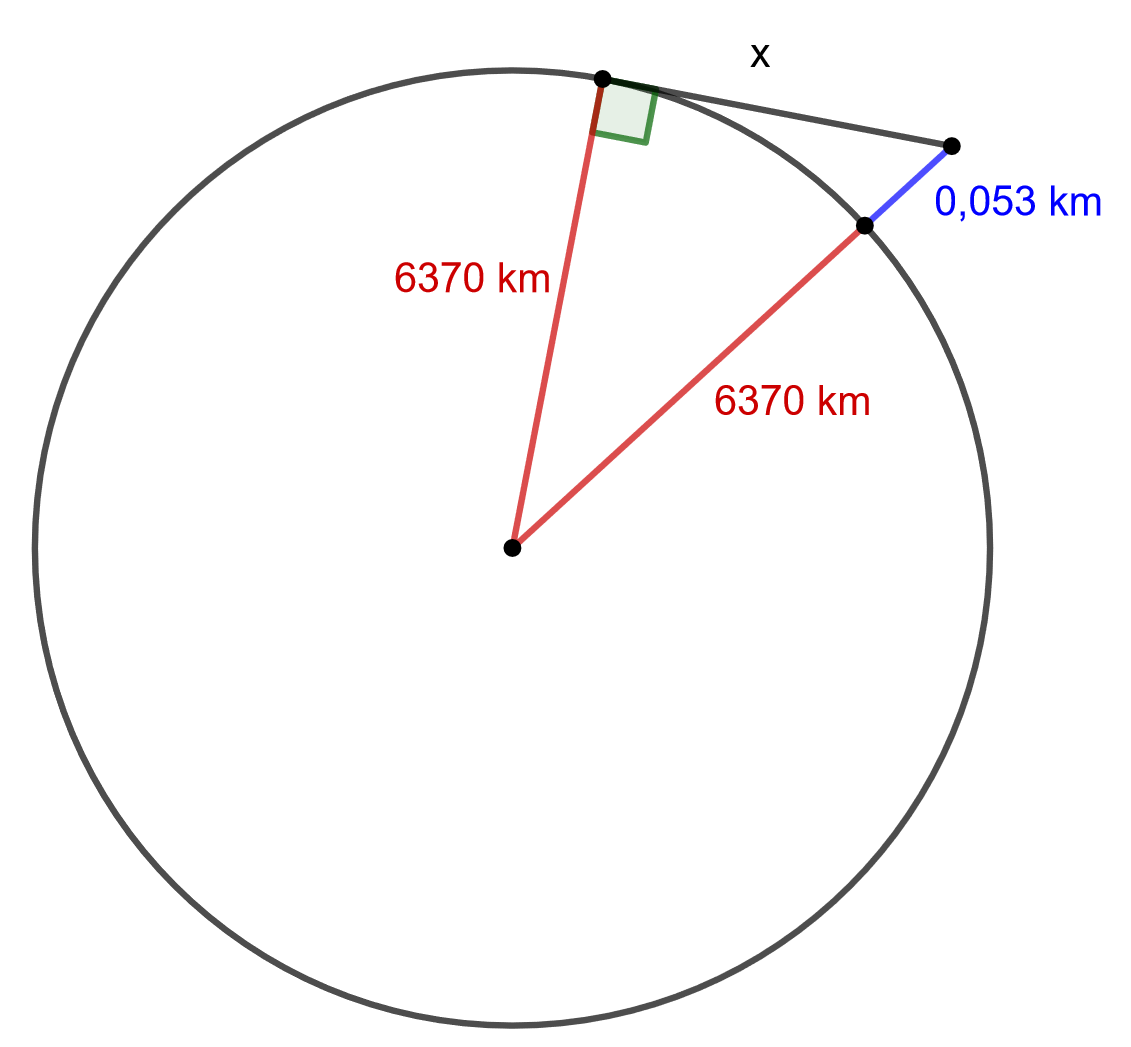
Kuinka pitkälle $53 \text{ m}$ korkeasta vesitornista voi nähdä? Maapallon säde on $6370 \text{ km}$ . Oletetaan, että katsojan silmät ovat myös $53 \text{ m}$ korkeudella maan pinnasta. Piirrä ensin mallikuva tilanteesta.

Mallikuva

Huom! Mallikuva ei ole mittakaavassa!

Tehtävässä tulee ratkaista kuvaan merkitty pituus .

# vesitorni

# teht_tangenttikulma2

4.5.3 Tehtävä

Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä . Tangenttien sivuamispisteet ja ovat etäisyydellä pisteestä . Piirretään ympyrälle vielä yksi tangentti pisteen kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet ja . Laske kolmion ABC piiri. [H]

Vihje

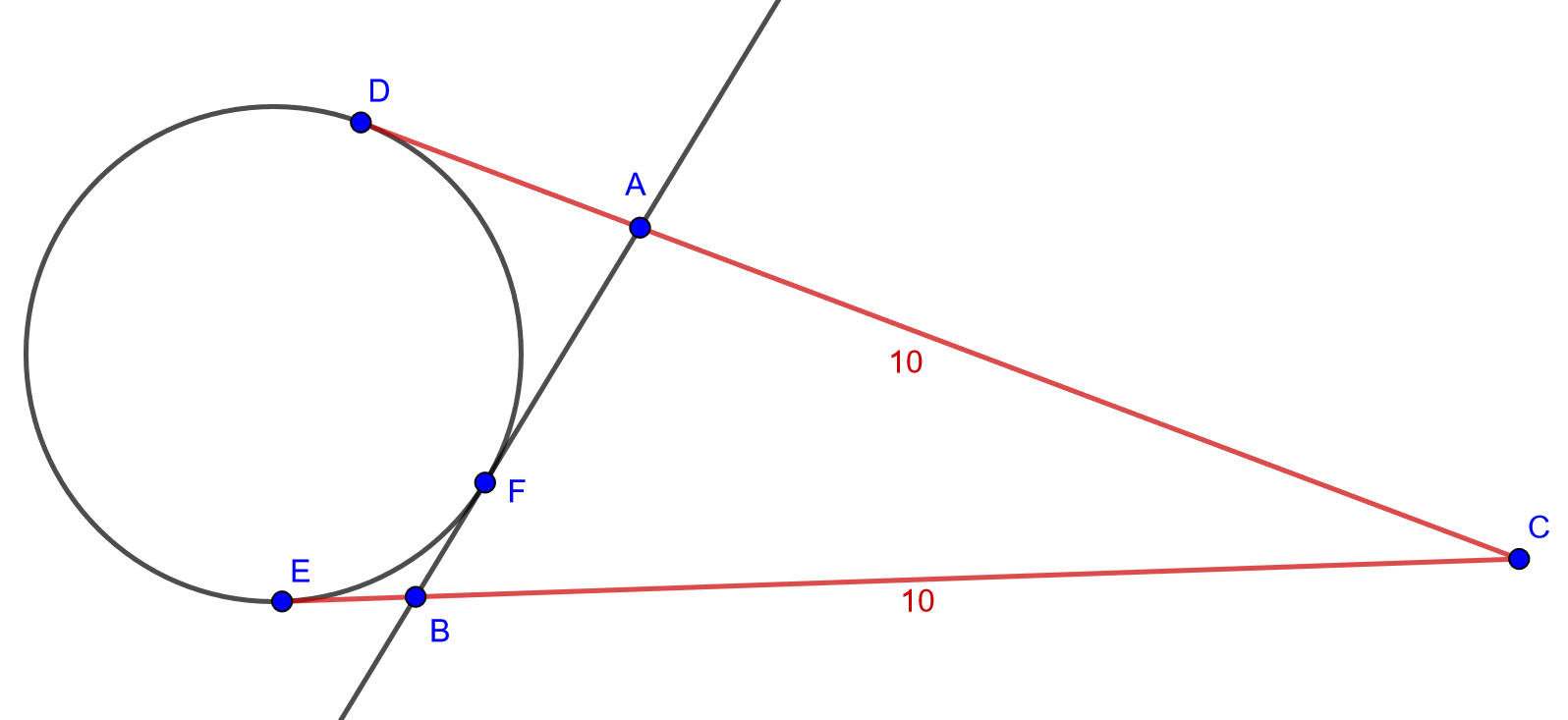
Pisteet A, B ja C ovat tangenttikulmien kärkiä, eli ne ovat yhtä etäällä molemmista tangenttipisteistään.

# tangenttikolmio

# keskuskulma-teht

4.6 Keskuskulma, kehäkulma

Tämän kappaleen teoria on kappaleessa Keskuskulma, kehäkulma.

# teht_kehakulma1

4.6.1 Tehtävä

Määritä kulman $\alpha$ suuruus.

# kehakulma

# teht_kehakulma2

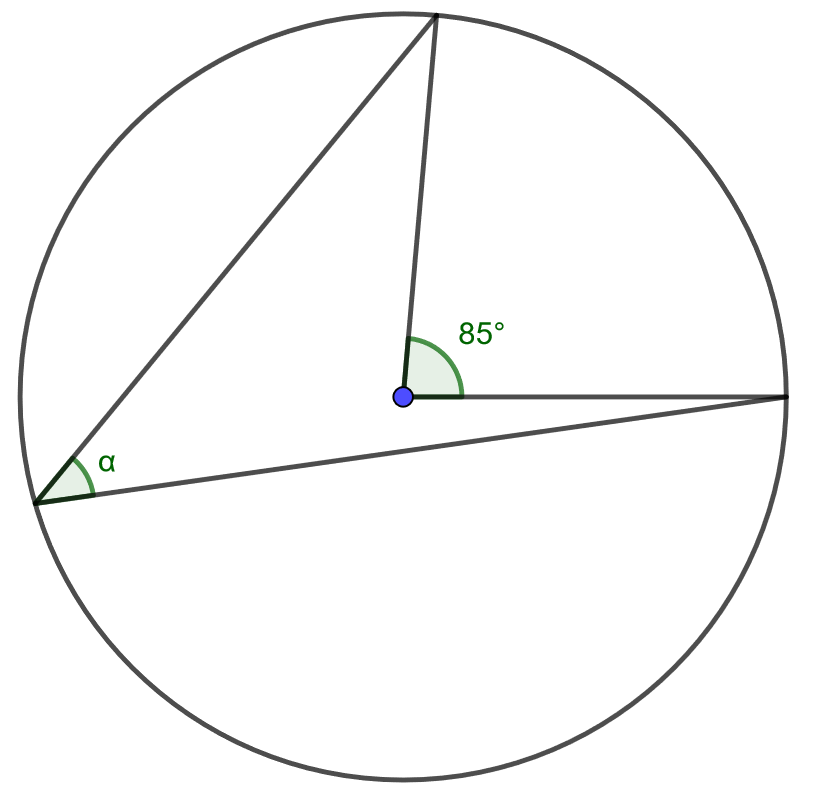
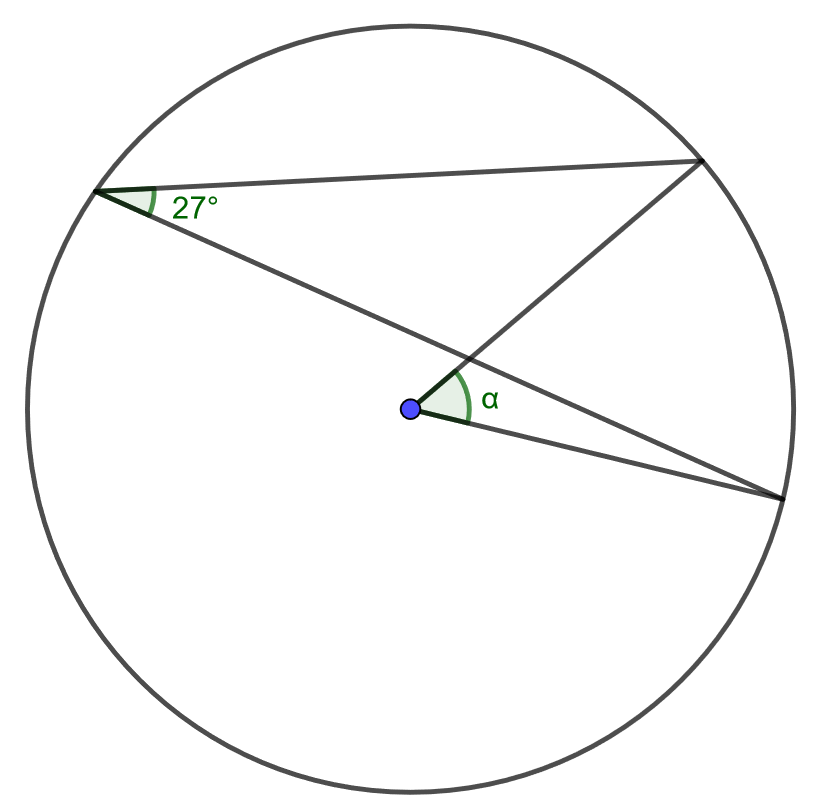
4.6.2 Tehtävä

Määritä kulman $\alpha$ suuruus.

# kehakulma_2

# teht_kehakulma3

4.6.3 Tehtävä

Ratkaise alla olevasta kuvasta kulmat $\alpha$ ja $\beta$ .

# kehakulma_3a

# kehakulma_3b

# teht_jannenelikulmio

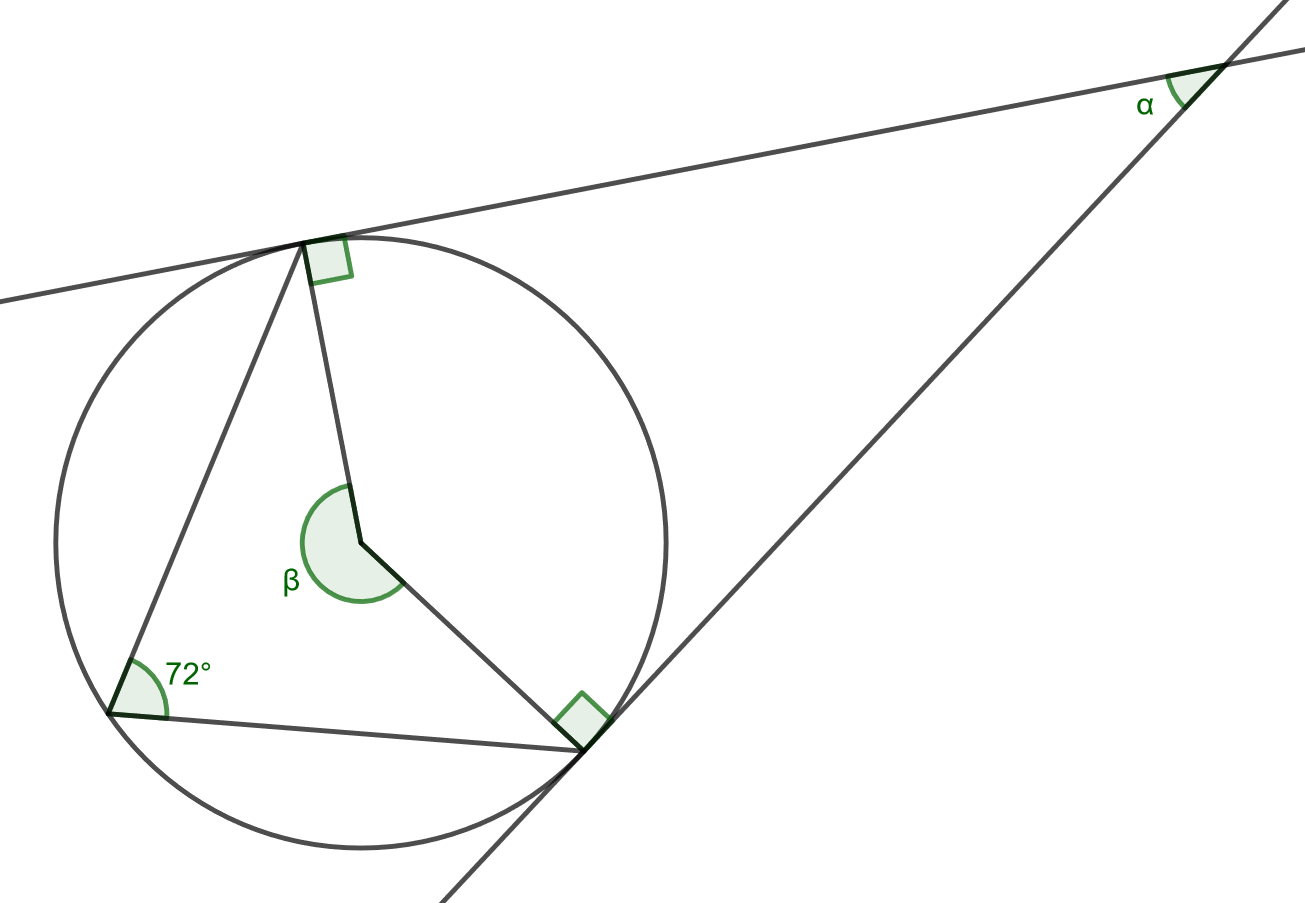
4.6.4 Tehtävä

Jos nelikulmion kaikki kulmat ovat saman ympyrän kaarella, nelikulmiota kutsutaan jännenelikulmioksi. Osoita, että jännenelikulmiossa vastakkaisten kulmien summa on aina $180 ^{\circ}$ .

Vihje

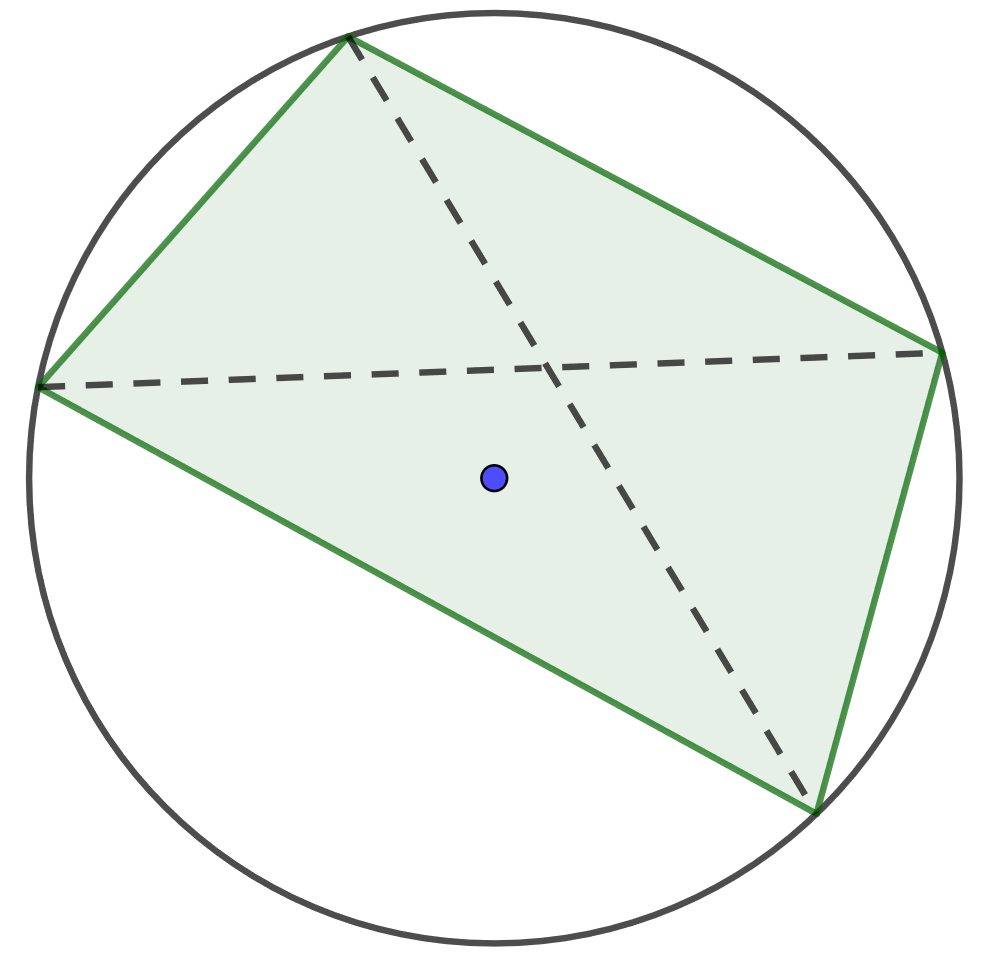
Kokeile käyttää kehäkulmalausetta.

Ratkaisu

Käytetään alla olevan kuvan merkintöjä.

Kulmat ABD ja ACD ovat yhtä suuria, sillä ne ovat samaa kaarta vastaavia kehäkulmia.

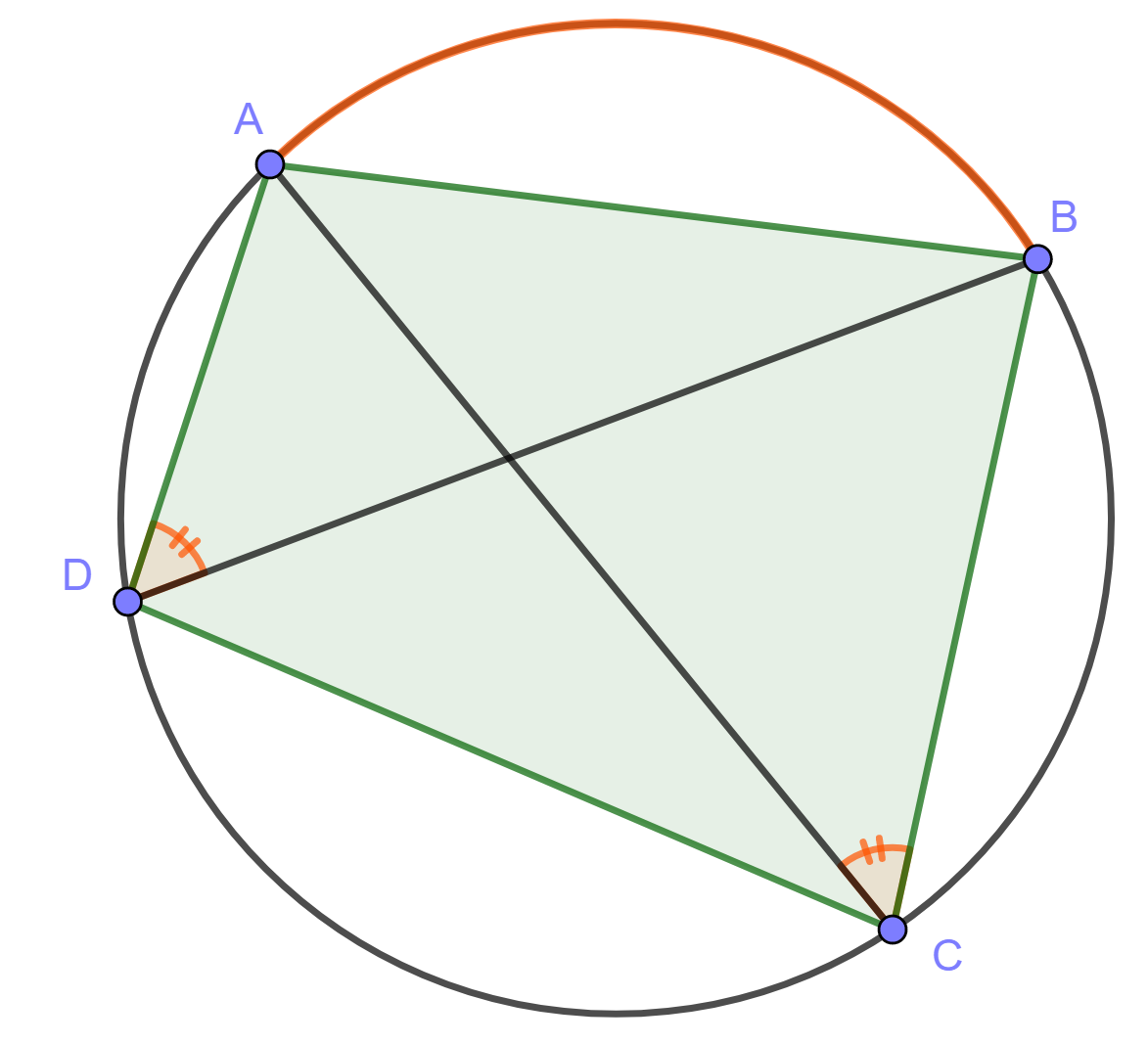
Vastaavasti kulmat BDA ja BCA ovat yhtä suuria, sillä ne ovat samaa kaarta vastaavia kehäkulmia.

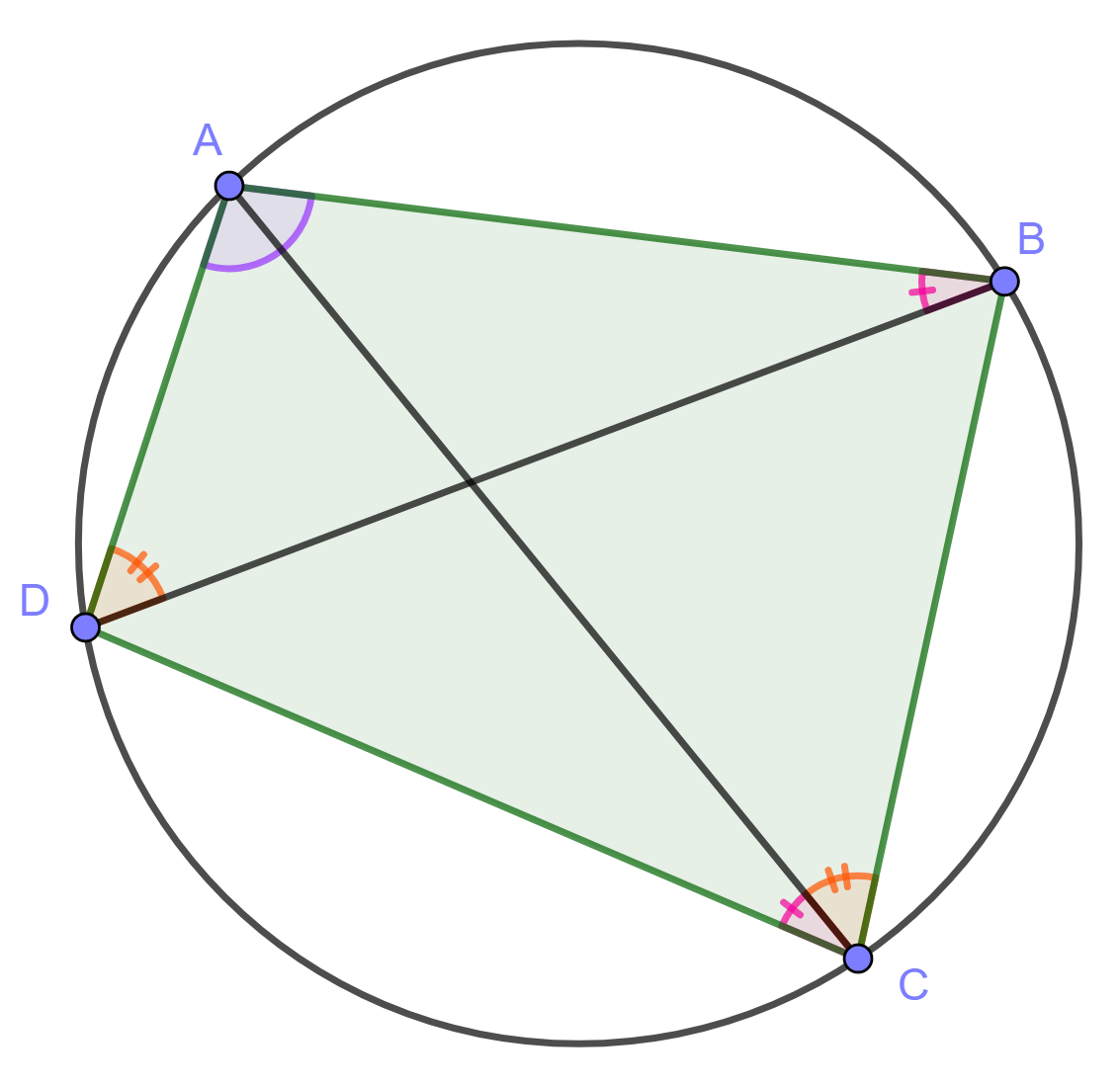
Kolmiosta ABD huomataan, että $DAB=180^{\circ}-(BDA+ABD)$ . Aiemmista kohdista tiedetään, että BCD=ACD+BCA=ABD+BDA . Sijoitetaan tämä aiempaan yhtälöön, jolloin saadaan $DAB = 180^{\circ} - BCD$ $\Leftrightarrow DAB + BCD = 180^{\circ}$ . Eli jännenelikulmion vastakkaisten kulmien summa on $180^{\circ}$ .

4.7 Sekalaisia tehtäviä

Tässä kappaleessa on kaikkiin tämän luvun aiheisiin liittyviä tehtäviä.

# teht_tukkikasa

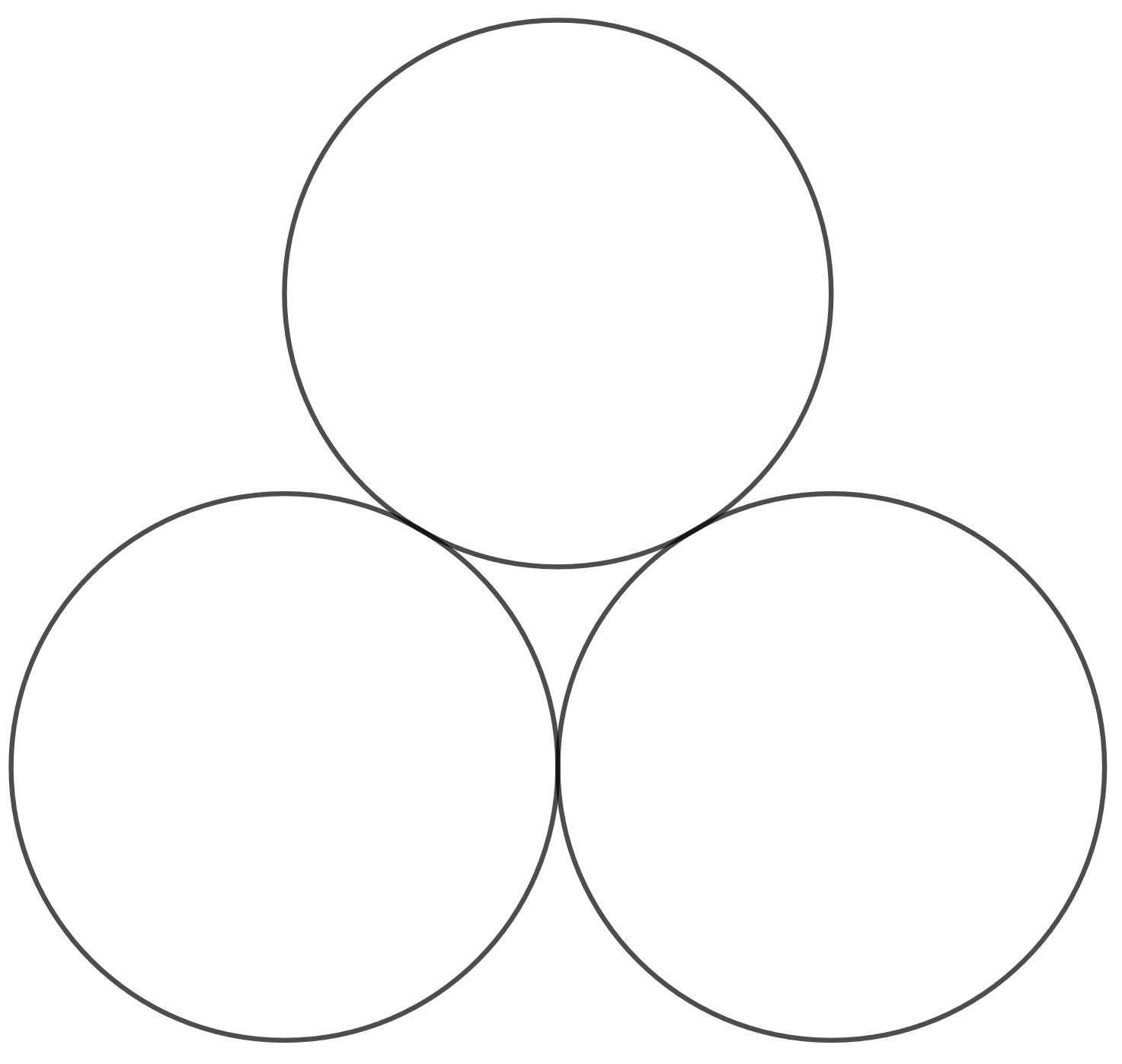
4.7.1 Tehtävä

Laske tukkikasan korkeus, kun tukin säde on $40,0 \text{ cm}$ . Oletetaan tukkien poikkileikkaukset ympyröiksi. Ympyrät sivuavat toisiaan.

# tukkikasa

# teht_ympyrat_neliossa

4.7.2 Tehtävä

Ratkaise alla olevan kuvan pienemmän ympyrän halkaisija isomman ympyrän säteen avulla.

Vihje

Verranto: $\dfrac{d}{k}=\dfrac{2a}{2a+k}$

# iso_pieni_ympyra

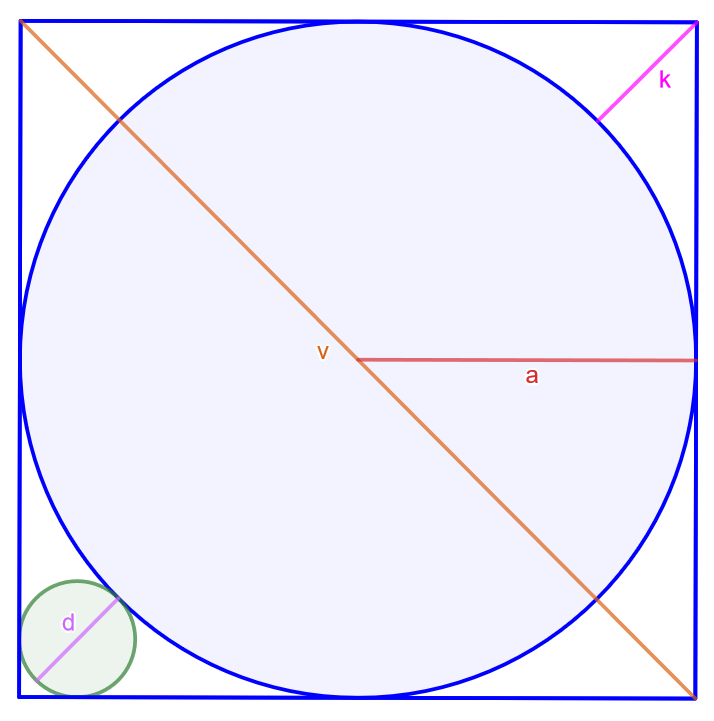
# teht_venalainen_kolmio

4.7.3 Tehtävä

Valitaan mielivaltaisesti piste positiiviselta -akselilta väliltä ]0,1[ ja piste positiiviselta -akselilta väliltä ]0,1[ . Valitaan piste origokeskeisen yksikköympyrän kehältä koordinaatiston ensimmäisestä neljänneksestä. Osoita, että kolmion ABC piiri on enemmän kuin 2. [H]

Voit käyttää hahmottamisessa apuna alla olevaa GeoGebra-applettia. Huomaa kuitenkin, että appletissa voit raahata pisteet janojen päätepisteisiin asti, mikä ei tehtävänannossa ole sallittua.

# venalainen-kolmio-geo

Ratkaisu

Tehtävän voi ratkaista monella eri tavalla, joista tässä on vain yksi. Käytetään alla olevan kuvan merkintöjä.

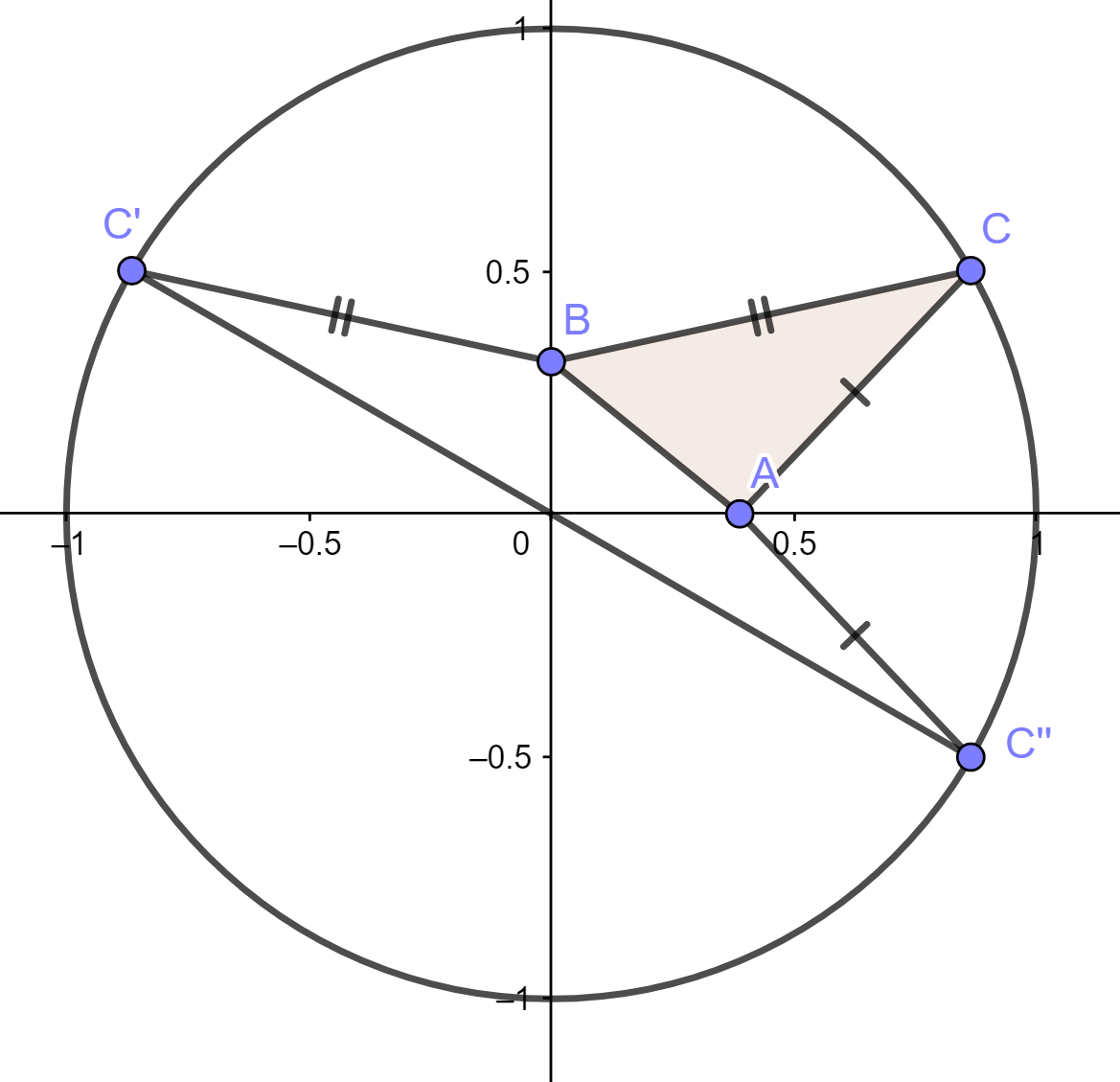
Peilataan piste -akselin suhteen, jolloin saadaan piste . Tehdään samoin -akselin suhteen, jolloin saadaan piste C'' . Symmetrian vuoksi BC=BC' ja samoin AC=AC'' . Kolmion ABC piiri on siis sama kuin murtoviivan C'BAC'' pituus.

Huomataan, että janan C'C'' pituus on , sillä se on ympyrän halkaisija. Murtoviiva pisteiden ja C'' välillä on välttämättä pidempi kuin pisteiden välinen suora etäisyys eli . Kolmion ABC piirin on siis pakko olla suurempi kuin .

# teht_kulma

4.7.4 Tehtävä

Alla olevassa kuvassa piste on ympyrän keskipiste ja pisteet , ja ovat ympyrän kehän pisteitä. Piste on suorien ja leikkauspiste ja janat ja ovat yhtä pitkät. Kulman $\angle BPA$ suuruus on $69^{\circ}$ . Kuinka suuri on kulma $\alpha$ ? [H]

# vieruskulmat

# teht_suorakulmio_neljannesympyra

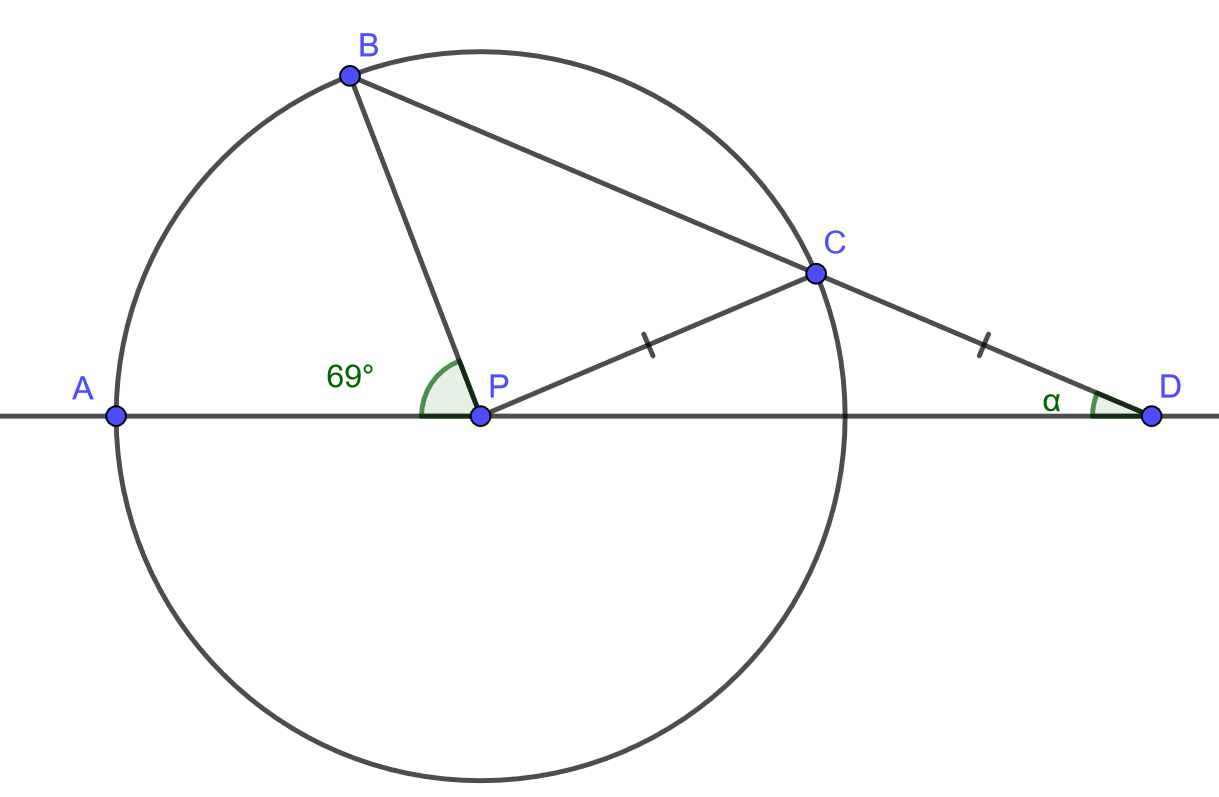
4.7.5 Tehtävä

Neliön sisään piirretään neljännesympyrä siten, että neliön ylänurkasta voidaan erottaa neljännesympyrää koskettava suorakulmio, jonka sivujen pituudet ovat ja . Kuinka pitkä on neliön sivu?

# suorakaide-neljannesympyralla-geo

# suorakaide_neljannesympyralla

# teht_kaarien_rajaama_alue

4.7.6 Tehtävä

Ympyränkaaret, joiden säteet ovat ja , leikkaavat alla olevan GeoGebra-appletin mukaisesti. Mikä on kaarien rajaaman alueen pinta-ala? [T]

# kaarien-rajaama-ala-geo

Vihje 2

Alue voidaan laskea kahden segmentin pinta-alojen summana.

# kaarien_rajaama_alue

# teht_suurempi_piiri

4.7.7 Tehtävä

Neliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä.
Kummalla on suurempi piiri, neliöllä vai ympyrällä? [H]

Vihje

# nelion-ja-ympyran-piirit

# teht_K16T7

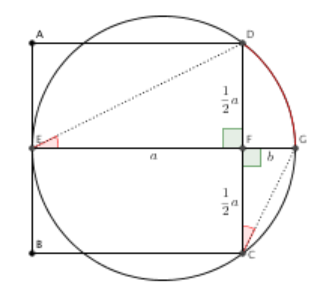
4.7.8 Tehtävä (K2016/7)

Kolme ympyrää sivuaa toisiaan oheisen kuvion mukaisesti. Ympyröiden keskipisteet ovat , ja ja niiden säteet samassa järjestyksessä , ja . Kuinka suuri ympyrä mahtuu näiden kolmen ympyrän väliin jäävään alueeseen?

# K16T7

# teht_S14T14

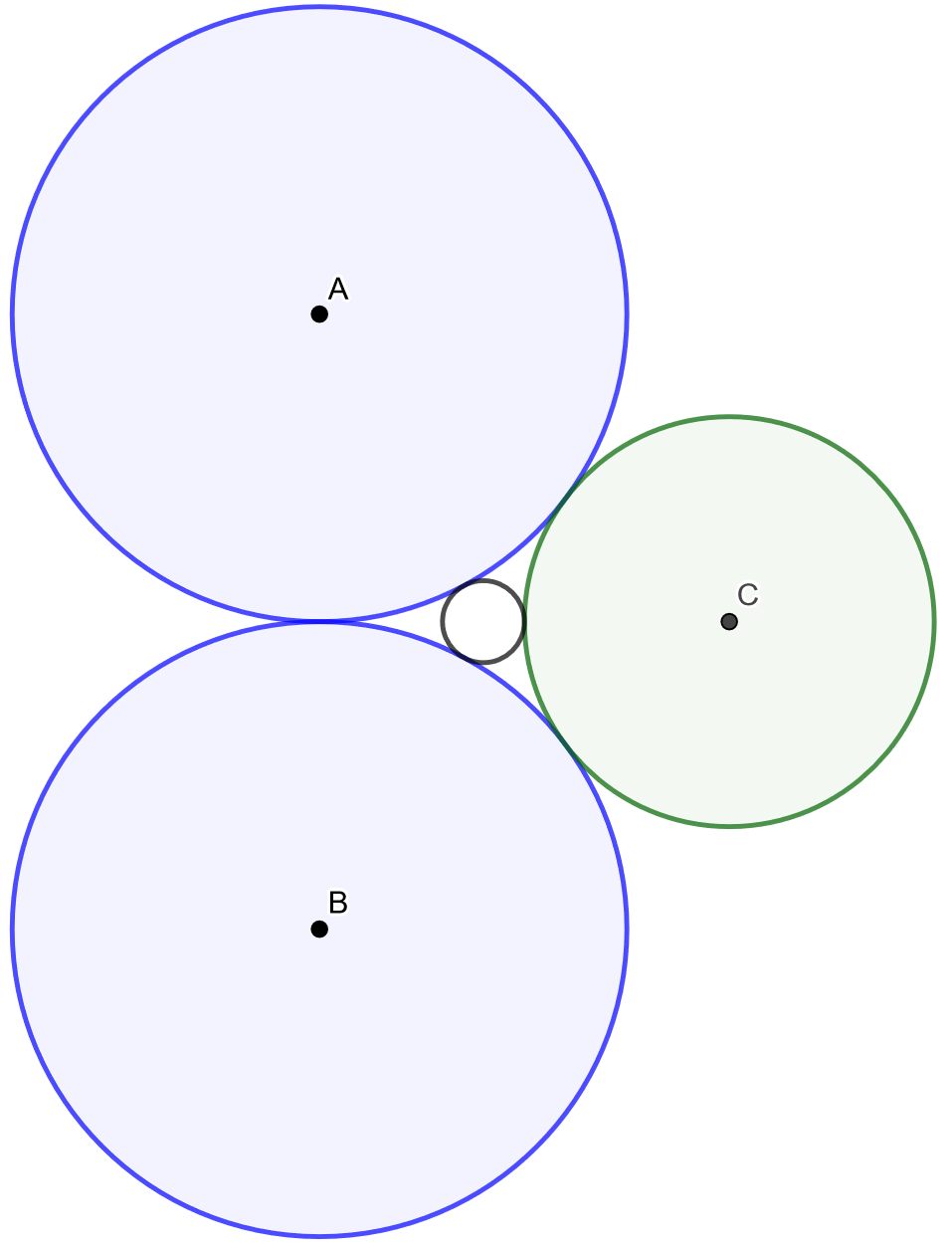
4.7.9 Tehtävä (S2014/14)

Tarkastellaan ympyrää ja sen ulkopuolella olevaa pistettä .

Pisteestä piirretään kaksi suoraa, jotka leikkaavat ympyrän neljässä eri pisteessä , , ja kuvion mukaisesti. Osoita, että kolmiot ja ovat yhdenmuotoiset.

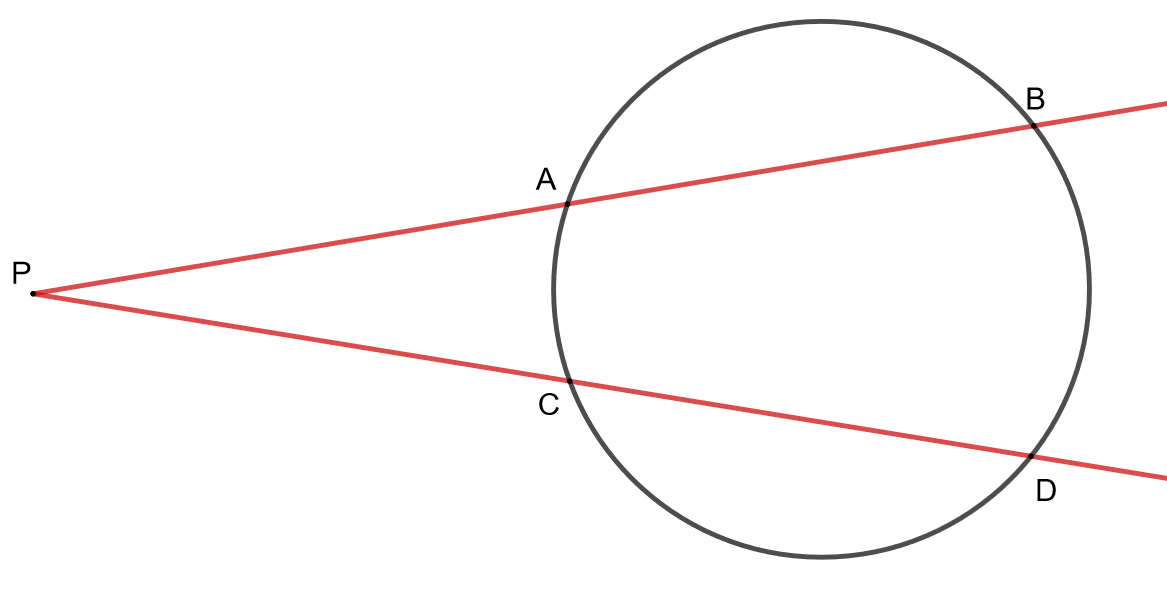
Osoita, että $PA \cdot PB = PC \cdot PD$ .
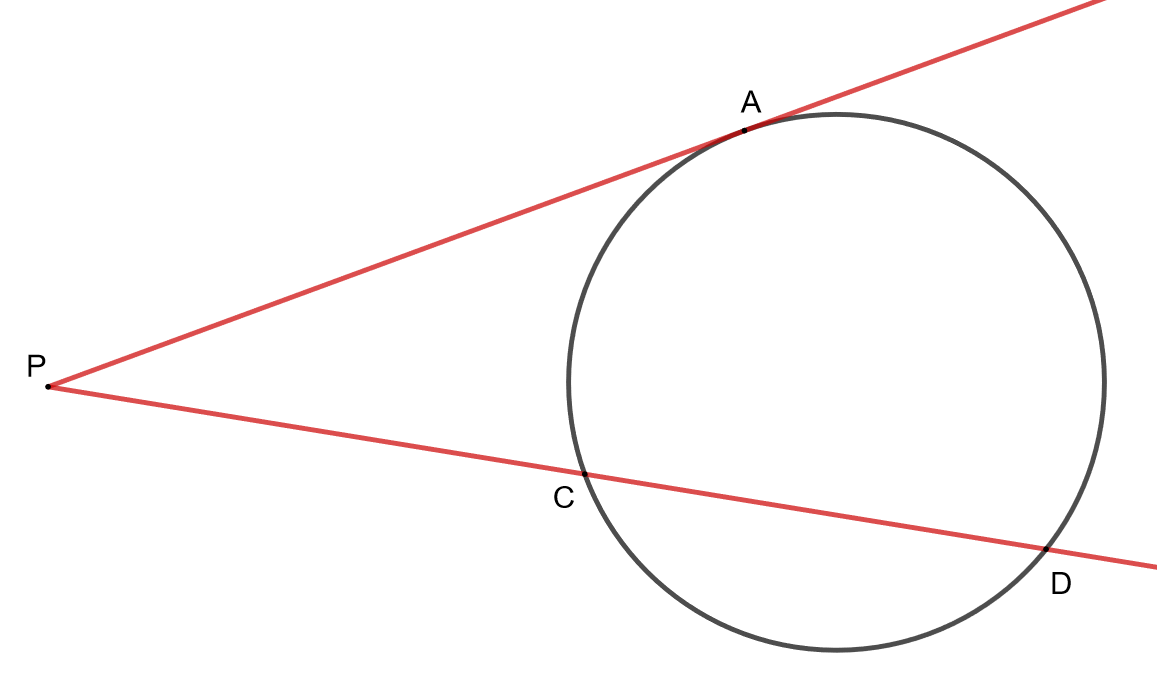
Erikoistapauksessa toinen suorista sivuaa ympyrää. Osoita, että tällöin pätee $(PA)^2=PC \cdot PD$ .

Todista edellisten kohtien avulla Pythagoraan lause tutkimalla alla olevan kuvion kolmiota, jonka kärki on ympyän keskipisteessä ja kärki on ympyrän kehällä.

Ratkaisu

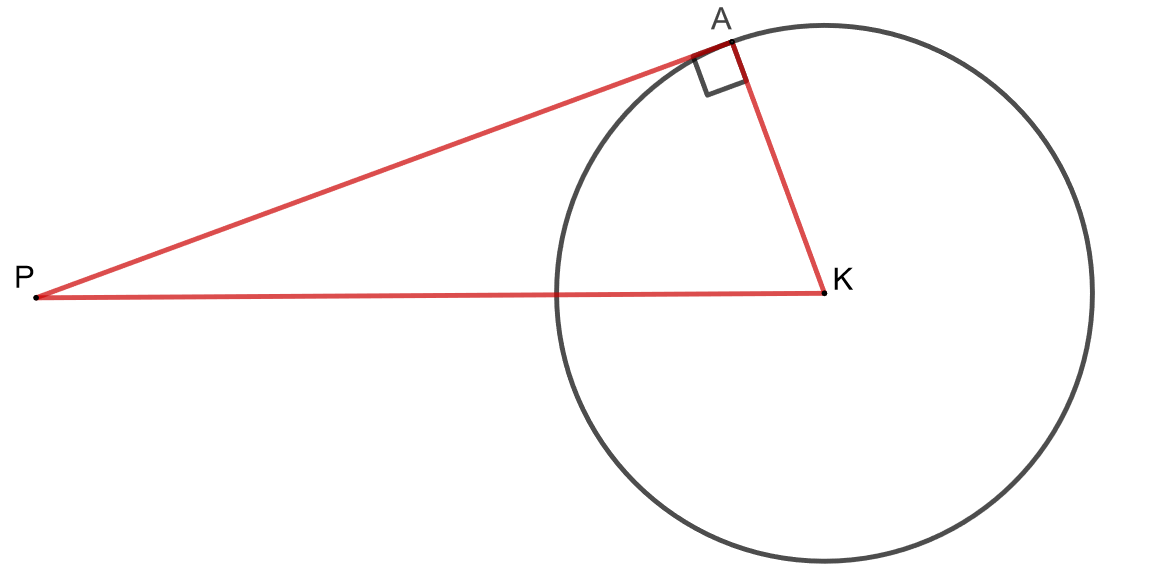
Piirretään janat ja . Tällöin $\angle CBA = \angle CDA$ samaa kaarta vastaavina kehäkulmina. Lisäksi kolmioilla on yhteinen kulma $\angle APC$ . Täten yhdenmuotoisuuslauseen KK mukaan kolmiot ovat yhdenmuotoisia.

Yhdenmuotoisuuden nojalla $\frac{PA}{PD} = \frac{PC}{PB}$ , josta saadaan ristiin kertomalla $PA \cdot PB = PC \cdot PD$ .

Olkoon ympyrän keskipiste. Piirretään janat ja ja merkitään $\angle CDA = \alpha$ . Tällöin $\angle CKA = 2 \alpha$ , koska se on samaa ympyrän kaarta vastaava keskuskulma. Tasakylkisen kolmion kulmille pätee $\angle KCA = \angle CAK=90^{\circ}-\alpha$ . Koska $\angle KAP = 90^{\circ}$ , niin $\angle CAP = 90^{\circ}-(90^{\circ}-\alpha)=\alpha$ . Kolmioissa ja on kaksi yhtä suurta kulmaa, joten ne ovat yhdenmuotoiset, mistä seuraa $(PA)^2=PC \cdot PD$ .

Merkitään kolmion kärkiä , ja . Hypotenuusa leikkaa ympyrää pisteessä . Jatketaan hypotenuusaa säteellä , jolloin jatke kohtaa ympyrän pisteessä . B-kohdan nojalla pätee $PA^2=PE \cdot PD$ . Merkitään ja , jolloin , josta Pythagoraan lause seuraa.

# teht_K14T14

4.7.10 Tehtävä (K2014/14)

Erään tarinan mukaan ihmiskunta kokeili liikkumista säännöllisten monikulmioiden avulla, ennen kuin pyörä keksittiin.

Tasasivuinen kolmio kiertyy oikealle kuvion mukaisesti, kunnes kärki osuu uudelleen alustaan. Kärki piirtää kuvion mukaisen käyrän. Laske käyrän pituus, kun kolmion piiri on .

# K14T14a

Hahmottele vastaavat käyrät neliön ja kuusikulmion tapauksessa. Kummassakin tapauksessa monikulmio kiertyy niin monta kertaa, että vasemmalla alhaalla oleva kärki osuu uudelleen alustaan.

Ratkaisu

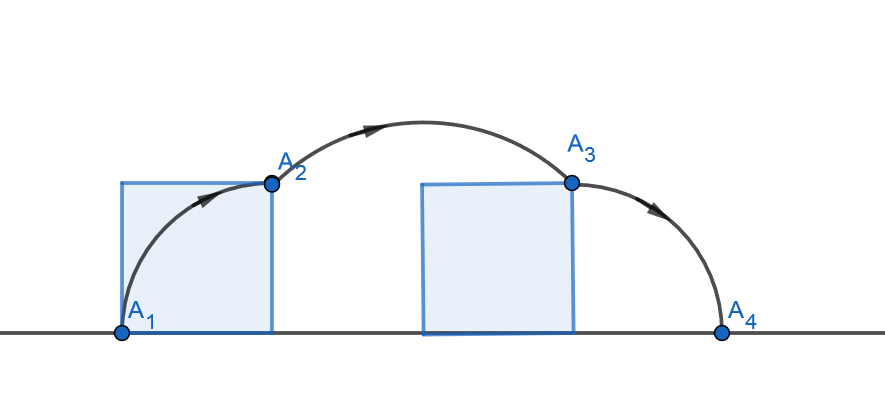
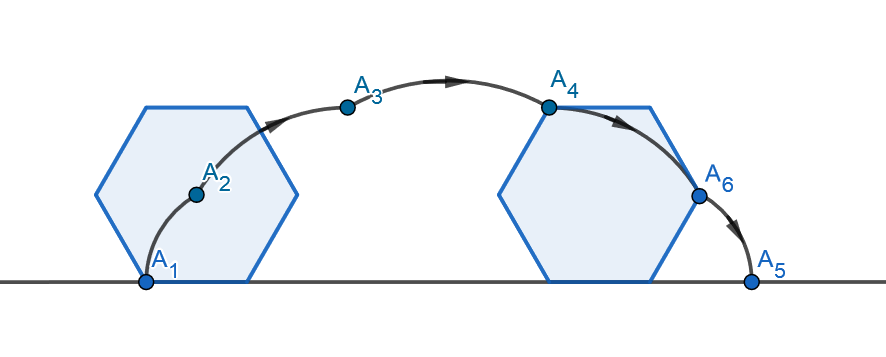
Laske b-kohdan käyrän pituus neliölle, jonka piiri on .

# K14T14c

Laske b-kohdan käyrän pituus kuusikulmiolle, jonka piiri on .

# K14T14d

# teht_monikulmio_ympyrassa

4.7.11 Tehtävä

Mikä on suurimman mahdollisen -säteisen ympyrän sisään mahtuvan säännöllisen -kulmion pinta-ala?

Ratkaisu

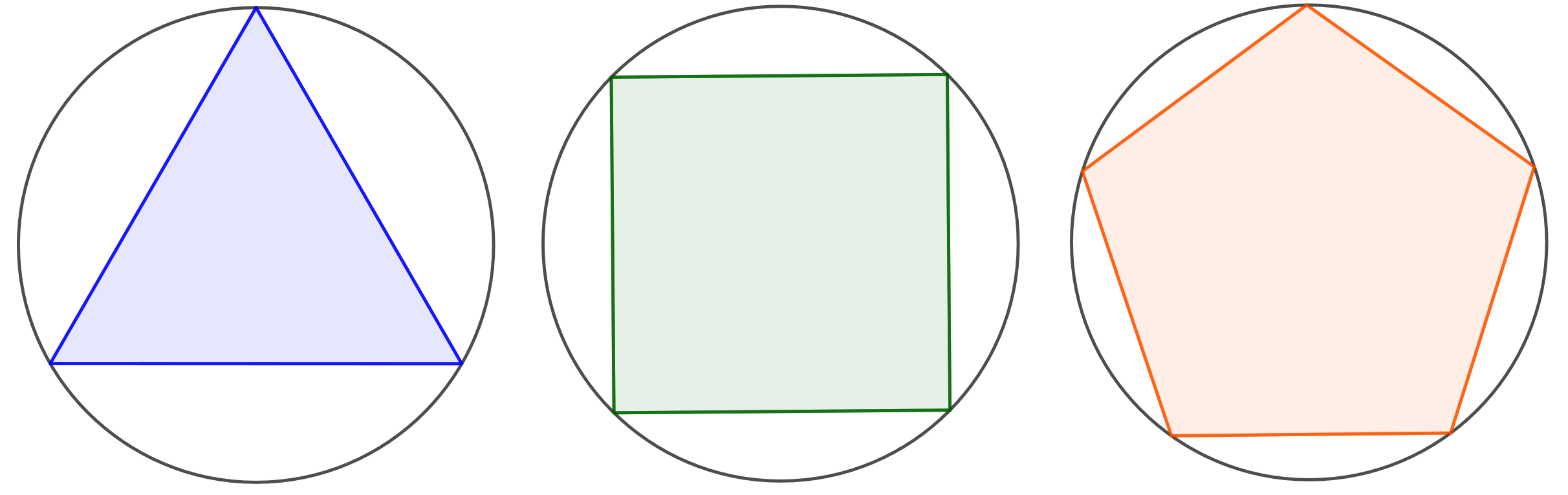
Tehtävän voi ratkaista monilla eri tavoilla, joista tässä esitetään vain yksi. Käytetään hyväksi alla olevaa kuvaa.

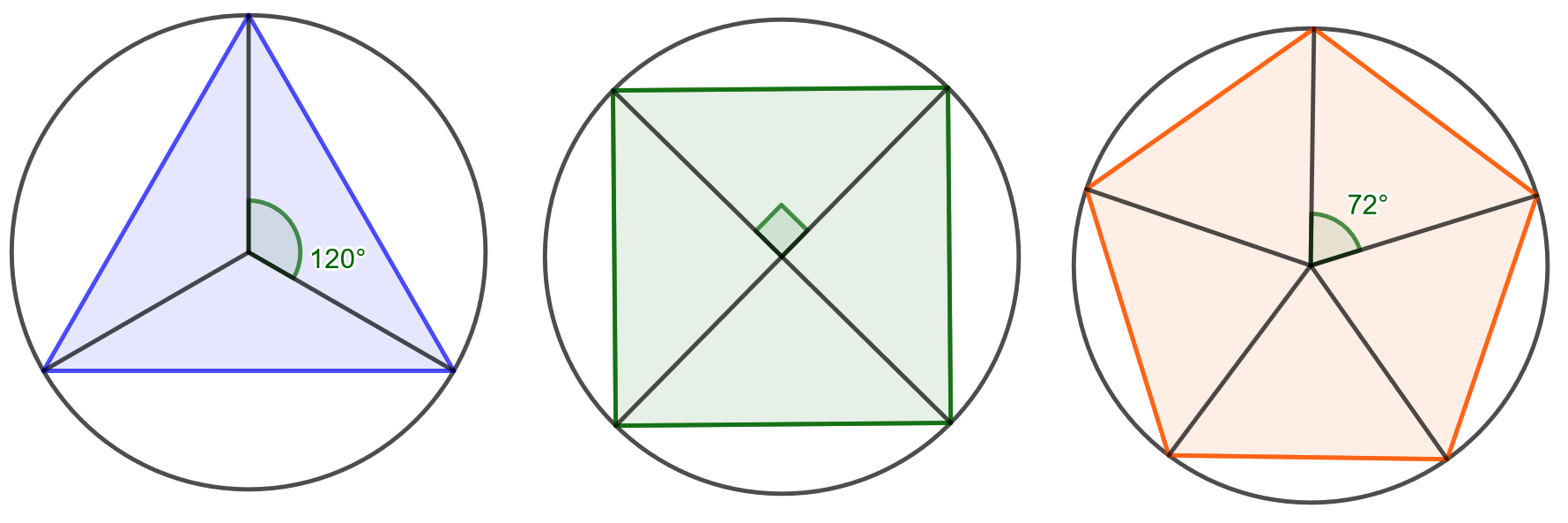
Jos monikulmiossa on kulmaa, jaetaan monikulmio kolmioon. Kolmiot muodostetaan piirtämällä janat ympyrän keskipisteestä monikulmion jokaiseen kulmaan. Kolmion kulma, jonka kärki on ympyrän keskipisteessä, on $\frac{360^{\circ}}{n}$ . Tämän kulman viereiset sivut ovat ympyrän säteen mittaisia. Kolmion pinta-alan trigonometrisella kaavalla saadaan yhden kolmion alaksi $A_k = \frac{r^2}{2} \cos \left( \frac{360^{\circ}}{n} \right).$ Koska kolmioita muodostuu monikulmion sisään kappaletta, on koko monikulmion pinta-ala $A=n \cdot A_k = \frac{r^2n}{2} \cos \left( \frac{360^{\circ}}{n} \right).$

# teht_ympyrat_ympyrassa

4.7.12 Tehtävä

Alla olevassa GeoGebra-appletissa on isompi -säteinen ympyrä, jonka sisällä on kolme pienempää -säteistä ympyrää. Määritä pienempi säde isomman säteen avulla.

# kolme-ympyraa-ympyrassa-geo

# kolme-ympyraa-ympyrassa

# teht_K12T11

4.7.13 Tehtävä (K2012/11)

Tasasivuisen kolmion K_1 sivun pituus on . Sen sisään asetetaan ympyrä Y_1 , joka sivuaa kolmion kylkiä. Tämän ympyrän Y_1 sisään asetetaan tasasivuinen kolmio K_2 , jonka kärjet ovat ympyrällä Y_1 . Jatkamalla näin saadaan oheisen kuvan mukainen päättymätön jono ympyröitä $Y_1,Y_2,\ldots$ Laske ympyröiden pinta-alojen summa.

# ympyra_kolmiossa

Ratkaisu

# teht_K12T15

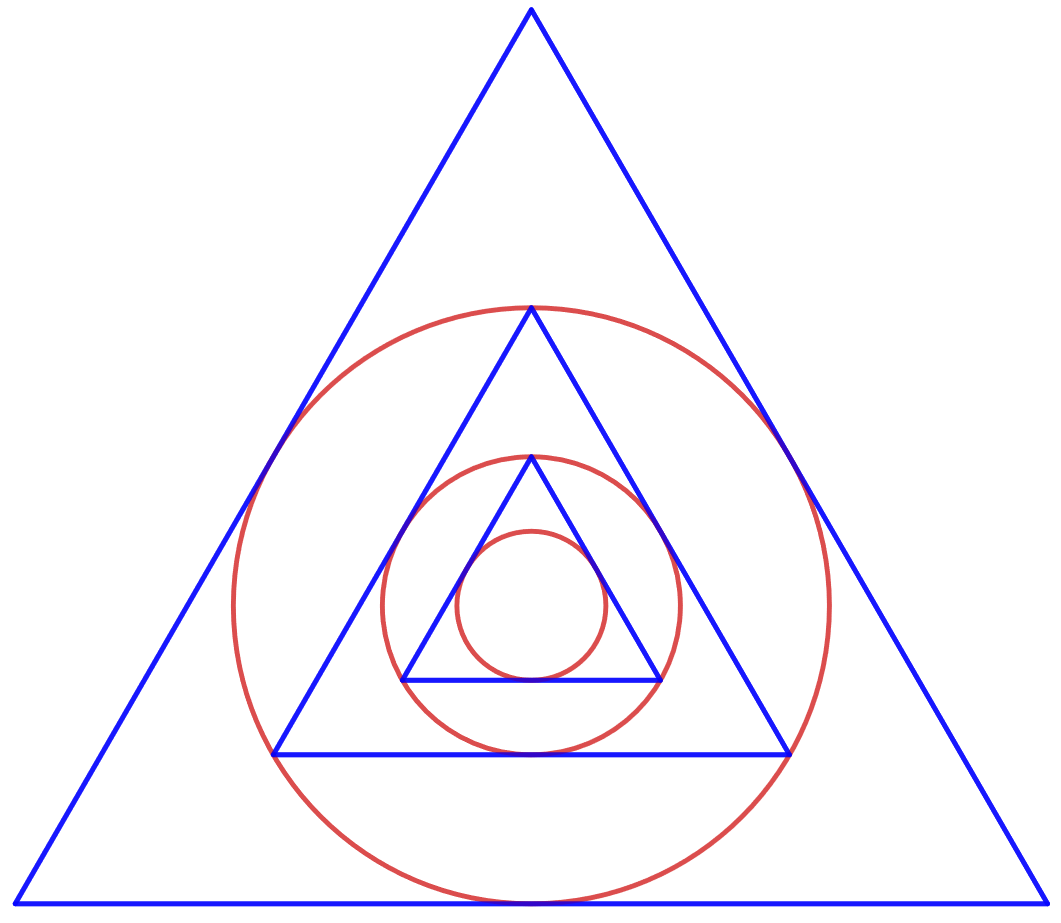
4.7.14 Tehtävä (K2012/15)

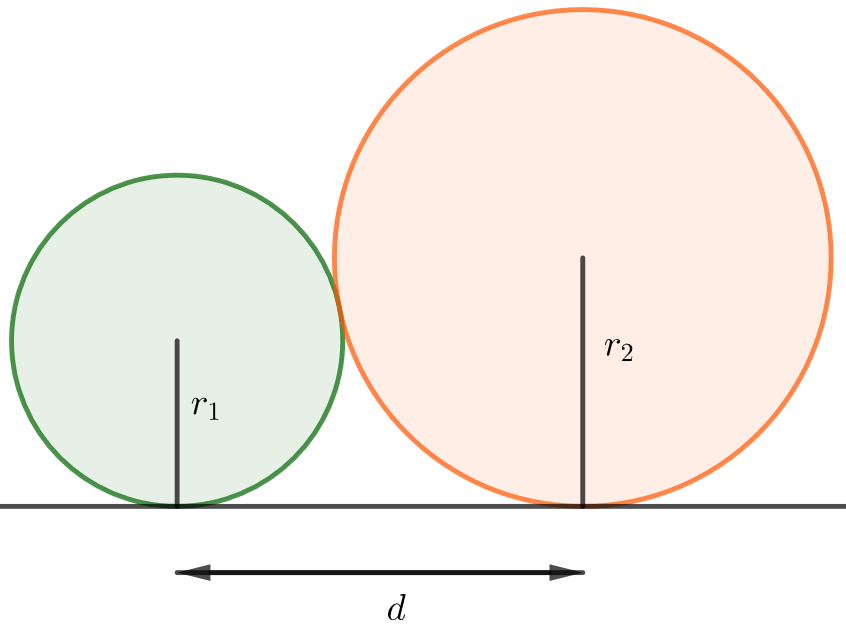
Kaksi ympyrää sivuaa toisiaan ja -akselia alla olevan kuvan mukaisesti. Määritä ympyröiden keskipisteiden vaakaruoda etäisyys d niiden säteiden avulla lausuttuna.

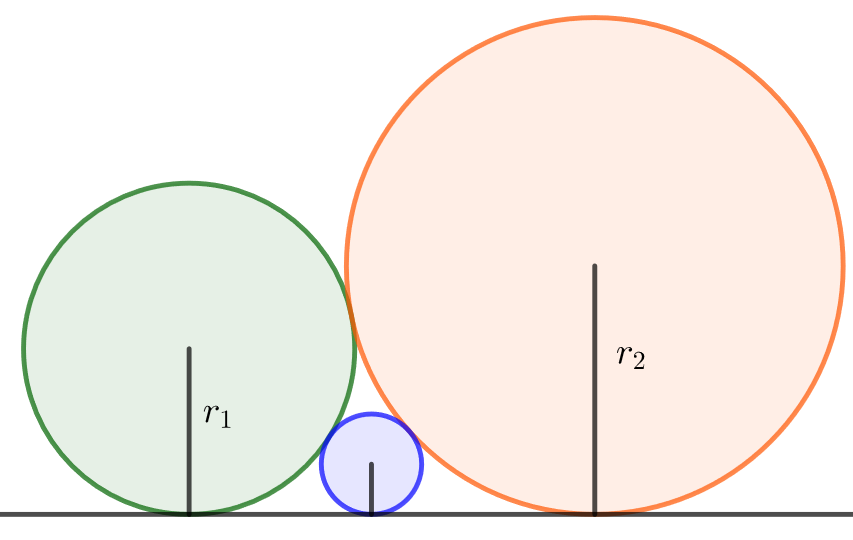
Kolme ympyrää sivuaa toisiaan ja -akselia alla olevan kuvan mukaisesti. Määritä keskimmäisen ympyrän säde kahden reunimmalisen ympyrän säteiden avulla lausuttuna.

Todista René Descartesin (1596-1650) keksimä b-kohdan ympyröihin liittyvä kaava jossa $k_i=\frac{1}{r_i}, \, i=1,2,3.$

Ratkaisu

Yhdistetään ympyröiden keskipisteet janalla, jonka pituus on ja lisäksi piirretään -säteisen ympyrän keskipisteestä -akselin suuntainen jana -säteisen ympyrän säteelle.

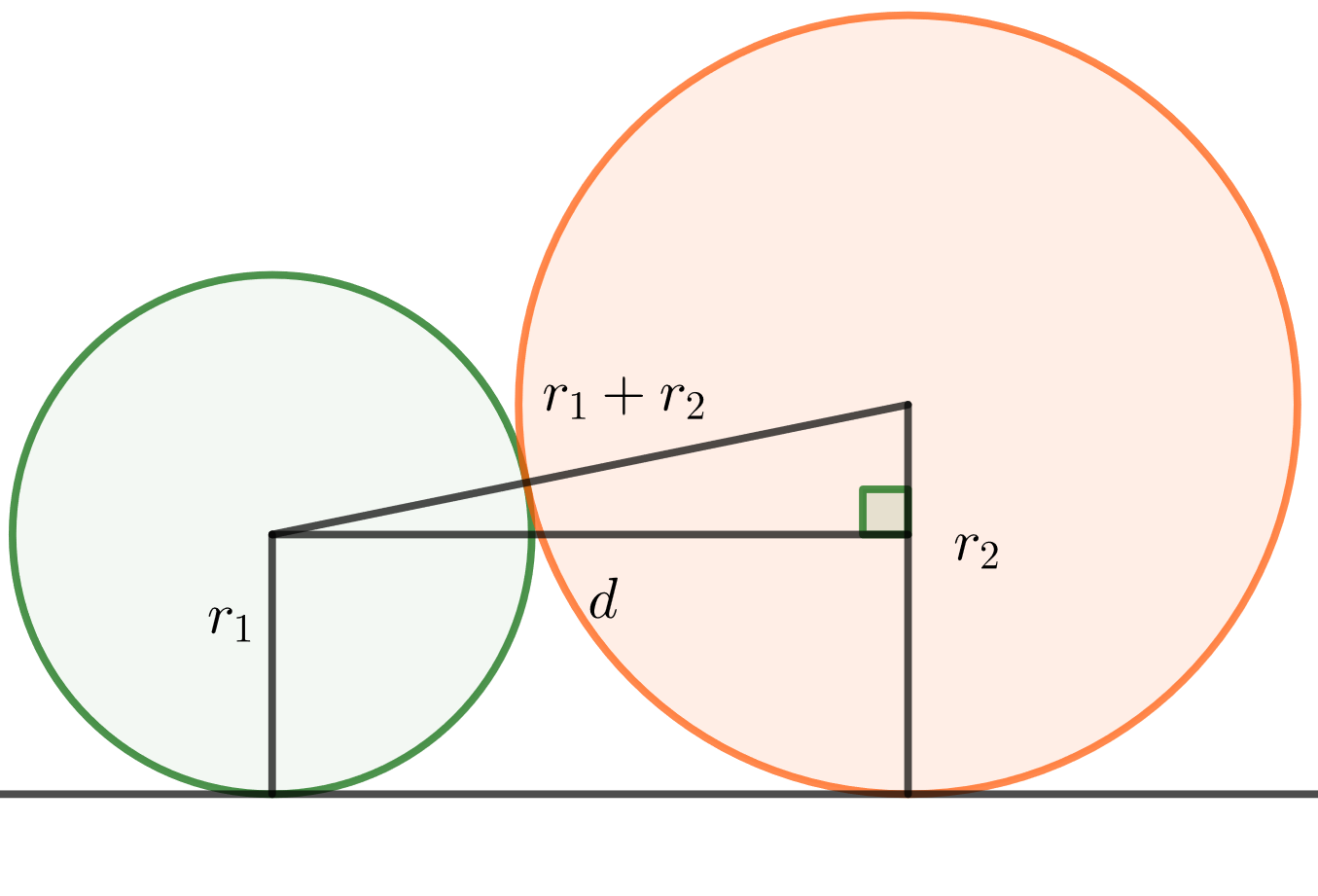
Suorakulmaisen kolmion kateettien pituudet ovat ja r_2-r_1 ja hypotenuusan pituus on r_1+r_2 . Pythagoraan lauseen avulla saadaan $\begin{aligned} d^2+(r_2-r_1)^2 &= (r_1+r_2)^2 \\ d^2+r_2^2-2r_1r_2+r_1^2 &= r_1^2+2r_1r_2+r_2^2 \\ d^2 &= 4r_1r_2 \\ d &= 2 \sqrt{r_1r_2} \end{aligned}$

Piirretään -säteisen ympyrän keskipisteestä -akselin suuntainen jana -säteisen ympyrän säteelle ja yhdistetään - ja -säteisten ympyröiden keskipisteet. Saadaan alla olevan kuvan mukainen suorakulmainen kolmio.

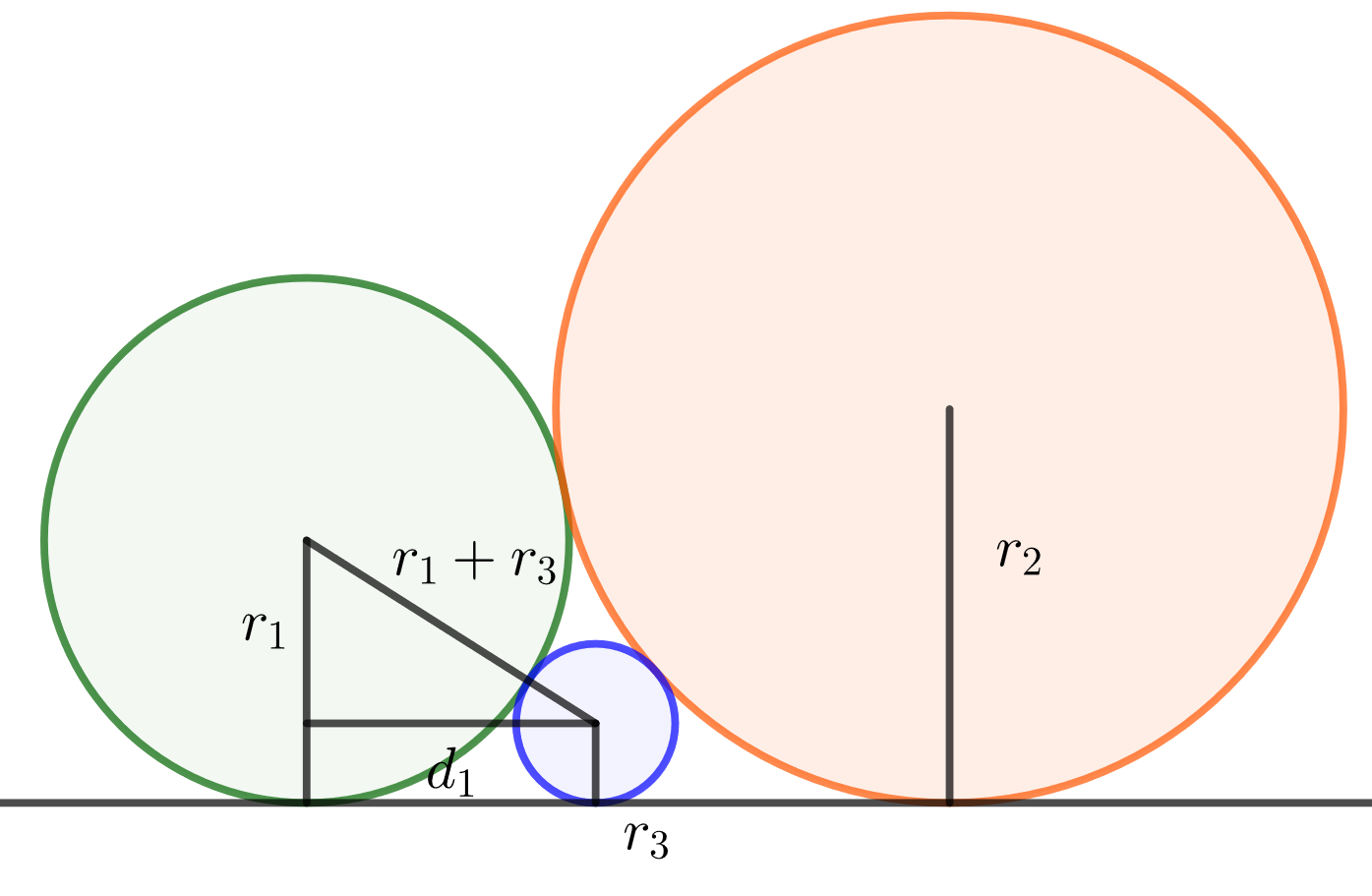
Ratkaistaan Pythagoraan lauseella d_1 $\begin{aligned} d_1^2+(r_1-r_3)^2 &= (r_1+r_3)^2 \\ d_1^2 + r_1^2-2r_1r_3+r_3^2 &= r_1^2+2r_1r_3+r_3^2 \\ d_1 &= 2 \sqrt{r_1r_3} \end{aligned}$

Vastaavasti saadaan toiselle puolelle suorakulmainen kolmio, josta r_3 - ja r_2 -säteisten ympyröiden keskipisteiden välinen etäisyys $d_2=2 \sqrt{r_2r_3}$ . Edellisen kohdan mukaan d=d_1+d_2 eli $2 \sqrt{r_1r_2} = 2 \sqrt{r_1r_3}+2 \sqrt{r_2r_3}$ josta saadaan $r_3=\frac{r_1r_2}{(\sqrt{r_1}+\sqrt{r_2})^2}.$

Avataan annetun lausekkeen sulkeita $\begin{aligned} (k_1+k_2+k_3)^2 &= 2(k_1^2+k_2^2+k_3^2) \\ k_1^2+k_2^2+k_3^2+2k_1k_2+2k_1k_3+2k_2k_3 &= 2k_1^2+2k_2^2+2k_3^2 \\ k_1^2+k_2^2+k_3^2 &= 2k_1k_2+2k_1k_3+2k_2k_3 \end{aligned}$ Nyt $k_1=\frac{1}{r_1}$ , $k_2=\frac{1}{r_2}$ ja $k_3=\frac{(\sqrt{r_1}+\sqrt{r_2})^2}{r_1r_2}$ . Sijoitetaan nämä aiempaan yhtälöön ja sievennetään, jolloin vasen puoli on $k_1^2+k_2^2+k_3^2 = \frac{2}{r_1^2}+\frac{2}{r_2^2}+\frac{6}{r_1r_2}+\frac{4}{r_1 \sqrt{r_1r_2}}+\frac{4}{r_2 \sqrt{r_1r_2}}$ ja oikea puoli $2k_1k_2+2k_1k_3+2k_2k_3 = \frac{2}{r_1^2}+\frac{2}{r_2^2}+\frac{6}{r_1r_2}+\frac{4}{r_1 \sqrt{r_1r_2}}+\frac{4}{r_2 \sqrt{r_1r_2}}.$ Koska lausekkeet ovat yhtä suuret, on kaava oikea.

# teht_viisikulmio_ympyrassa

4.7.15 Tehtävä

Ympyrän, jonka halkaisija on $5,0 \text{ cm}$ sisälle piirretään mahdollisimman suuri viisikulmio. Määritä viisikulmion pinta-ala yhden desimaalin tarkkuudella.

# viisikulmio_ympyrassa

# teht_lehma

4.7.16 Tehtävä

Kuinka suurella alueella lehmä voi laiduntaa, kun sen kaulassa oleva köysi on kytketty kuvan mukaisesti ladon seinustalle pisteeseen ja köyden pituus on $4 \text{ m}$ ?

# lehmalato

# teht_reuleaux

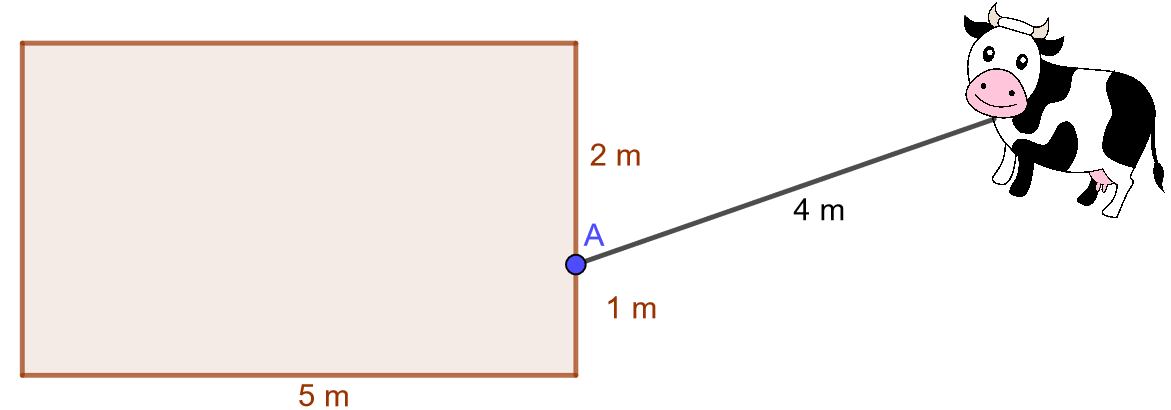
4.7.17 Tehtävä

Piirrä GeoGebralla Reuleaux'n kolmio alla olevilla ohjeilla.

Piirrä GeoGebralla tasasivuinen kolmio. Valitse aluksi työkalun alta lisää ja uudelleen lisää, jolloin saat kaikki työkalut näkyviin.
Valitse Ympyrät-otsikon alta Ympyränkaari-työkalu ja valitse kolmion kärkipisteet vastapäivään kiertäen.
Toista sama vielä kaksi kertaa niin, että aloitat joka kerta eri kärjestä.
Piilota alkuperäinen kolmio. Valitse Muokkaus-otsikon alta Näytä/piilota objekti. Tämän jälkeen valitse piilotettavat kohteet piirtoalueelta.
Lopuksi kokeile siirtää kolmion kärkipisteitä. Pysyykö konstruktiosi kasassa?

# releaux_piirto

# teht_reuleaux_ala

4.7.18 Tehtävä

Jos tasasivuisen kolmion sivun pituus on , mikä on sen ympärille piirretyn Reuleaux'n kolmion pinta-ala?

# reuleaux

# releaux_pinta-ala

Lisätietoa

Mielenkiinnosta voit tutkia myös alla olevaa GeoGebra-applettia. Kokeile muuttaa

ympyrän säde
kolmion "sisäsäde"
kiertosuunta

liukusäätimiä ja katso, miten Reuleaux'n kolmion kärkipisteiden muodostama punaisella merkitty ura muuttuu. Paina Aloita animaatio, jolloin saat kolmion pyörimään.

# pyoriva_reuleaux

# teht_reuleaux_kukka

4.7.19 Tehtävä

Laske varjostetun alueen pinta-ala. Ympyröiden keskipisteet ovat toistensa kehillä, eli jokaisen ympyrän säde on .

# geo_reuleaux_kukka

# releaux_kukka

# teht_kolme_ympyraa

4.7.20 Tehtävä

Samasta keskipisteestä piirretään kolme ympyrää joiden säteet ovat , ja . Tasasivuisen kolmion kärjet ovat näillä ympyröillä. Määritä kolmion sivun pituus.

Vihje 1

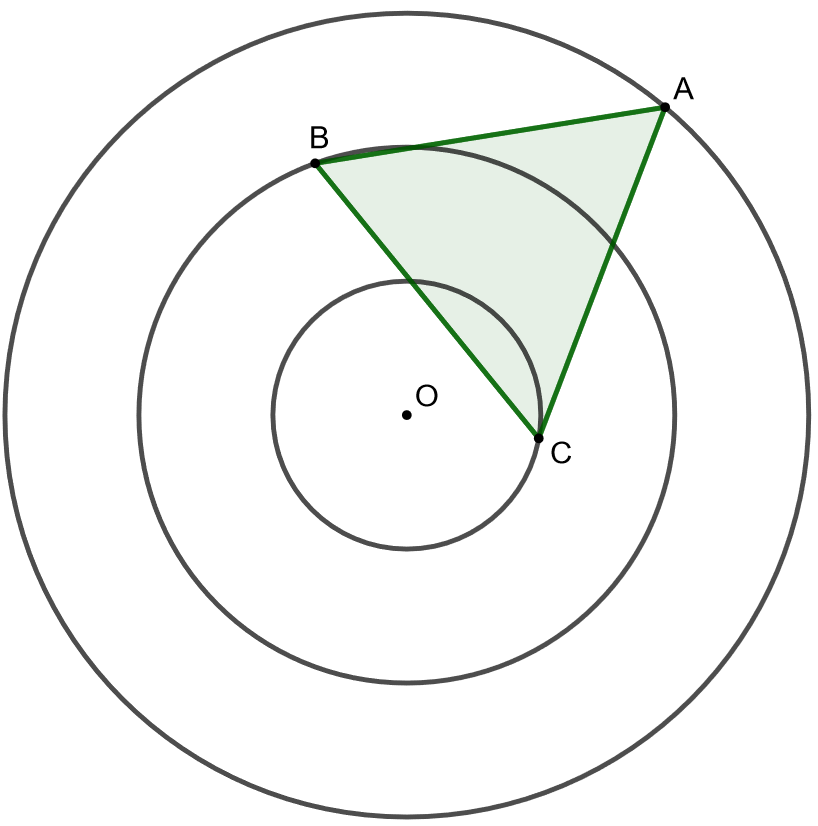
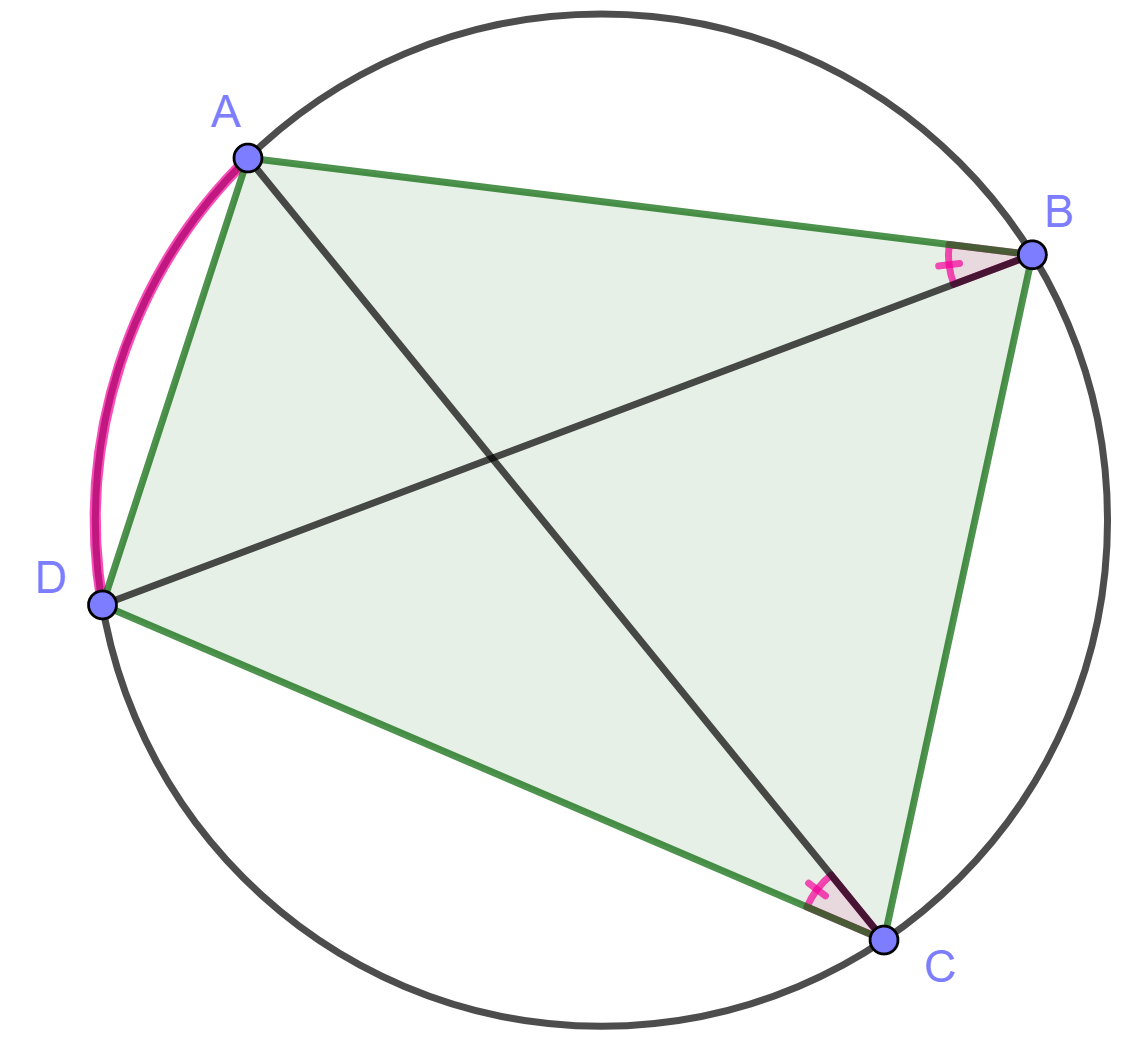
Osoita, että ABOC on jännenelikulmio. Jännenelikulmiossa lävistäjien tulo on yhtä suuri kuin vastakkaisten sivujen tulojen summa.

Vihje 2

Jännenelikulmiossa vastakkaisten kulmien summa on $180^{\circ}$ .

# kolmoisympyrat