# kolmioiden_geometriaa

2. Kolmioiden geometriaa

Tässä kappaleessa käsitellään kolmioiden geometriaa, mikä tarkoittaa esimerkiksi kolmion pinta-alan laskemista sekä sen sivujen pituuksien ja kulmien suuruuksien ratkaisua erilaisten lauseiden avulla. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

# pythagoras

2.1 Suorakulmainen kolmio, Pythagoraan lause

Suorakulmainen kolmio on sellainen kolmio, jonka yksi kulma on suorakulma eli $90^{\circ}$ . Suoran kulman kylkinä olevia sivuja kutsutaan kateeteiksi ja suoran kulman vastaista sivua hypotenuusaksi.

Suorakulmaiseen kolmioon liittyy oleellisesti Pythagoraan lause, jonka mukaan suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin kolmion hypotenuusan neliö. Jos siis tiedetään kolmion kahden sivun pituudet, voidaan kolmannen sivun pituus ratkaista. Voit lukea lisää Pythagoaan lauseen historiasta.

Pythagoraan lause

Suorakulmaisen kolmion kateettien ja neliöiden summa on yhtä suuri kuin sen hypotenuusan neliö, eli a^2+b^2=c^2.

2.1.1 Esimerkki: suorakulmainen kolmio GeoGebralla.

# suorakulmainen-kolmio-geo

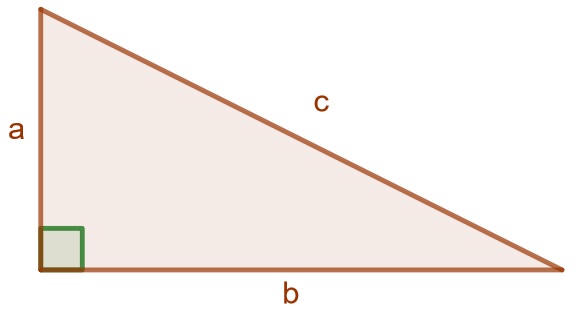
Siirrä kolmion kärkipisteitä ja huomaa, että kolmio säilyy koko ajan suorakulmaisena. Välillä kateettien neliöiden summa voi GeoGebran mukaan olla hieman eri kuin hypotenuusan neliö. Tämä johtuu siitä, että GeoGebra toteuttaa kaikki laskelmansa numeerisesti ja pyöristäen, joten pieniä virheitä saattaa esiintyä.

2.1.2 Todistus

# pythagoras-todistus-geo

Kaikki kuviossa esiintyvät oranssit kolmiot ovat suorakulmaisia, sillä ne ovat neliön sisällä, ja neliön kaikki kulmat ovat $90^{\circ}$ . Kolmiot ovat samanlaisia, sillä jokaisen kolmion kateetit ovat pituuksiltaan ja , ja jokaisen kolmion hypotenuusan pituus on .

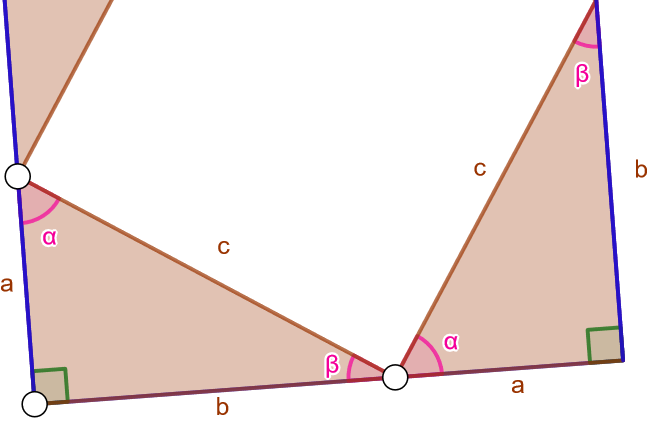
Entä onko alkutilanteessa kolmioiden keskelle jäävä valkoinen alue neliö? Olkoon suorakulmaisen kolmion kulmat $\alpha$ ja $\beta$ kuten alla olevassa kuvassa. Kolmion kulmien summa on $180^{\circ}$ , joten saadaan seuraavat yhtälöt: $\begin{aligned} \alpha + \beta + 90^{\circ} &= 180^{\circ} \quad |-90^{\circ} \\ \alpha + \beta &= 90^{\circ}. \end{aligned}$ Kuvion alareunassa kulmat $\alpha$ , $\beta$ ja keskellä olevan valkoisen alueen muodostama kulma muodostavat oikokulman eli ovat yhteensä $180^{\circ}$ . Koska tiedetään, että $\alpha + \beta = 90^{\circ}$ , on valkoisen alueen muodostaman kulman oltava $90^{\circ}$ eli suora kulma. Koska kolmiot ovat samanlaisia, ovat myös valkoisen alueen muodostamat kulmat yhtä suuria, joten valkoinen alue on neliö.

Alkutilanteessa valkoisen neliön pinta-ala on c^2 . Kun liukusäädin vedetään aivan oikeaan laitaan, kolmiot siirtyvät eri paikoille. Koska ne eivät mene päällekkäin, on valkoisen alueen pinta-ala nyt yhtä suuri kuin alussa. Nyt valkoinen alue muodostuu kahdesta pienestä neliöstä, joiden yhteenlaskettu pinta-ala on a^2+b^2 . Voidaan siis sanoa, että a^2+b^2=c^2 .

Tähän kappaleeseen liittyvät tehtävät.

# trig

2.2 Trigonometriset funktiot

Suorakulmaisen kolmion terävien kulmien suuruudet voidaan ratkaista, jos tiedetään kolmion kateettien tai kateetin ja hypotenuusan pituudet. Tämä on mahdollista, sillä kolmion sivujen suhteet ovat tietyillä kulmilla aina vakioita. Näitä suhteita kutsutaan trigonometrisiksi funktioiksi.

Suorakulmaisen kolmion sini, kosini ja tangentti

Suorakulmaisessa kolmiossa kulman $\alpha$ sini, kosini ja tangentti tarkoittavat seuraavia suhteita: $\sin(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{hypotenuusa}}=\frac{a}{c}$ $\cos(\alpha)=\frac{\text{kulman viereinen kateetti}}{\text{hypotenuusa}}=\frac{b}{c}$ $\tan(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{kulman viereinen kateetti}}=\frac{a}{b}$

2.2.1 Esimerkki: trigonometrisia funktioita GeoGebralla

# trig-geo

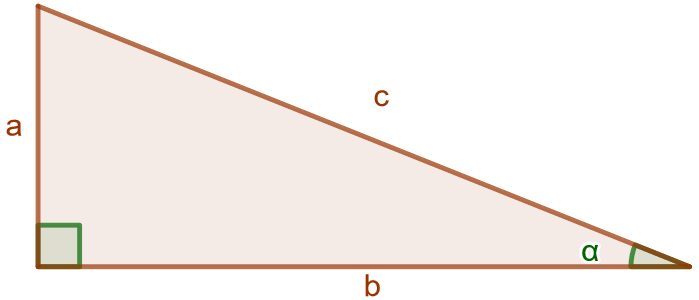
Kokeile laskea eri kulmien sini, kosini ja tangentti sekä sivujen suhteet vasemmalla olevassa cas-ikkunassa. Voit syöttää uuden komennon napauttamalla hiirellä rivinumeron 3 vieressä. Voit käyttää kuvassa näkyviä muuttujien nimiä. Kokeile myös raahata kolmion kärkipisteitä ja tutki, miten lukuarvot muuttuvat.

Muutama ohje cas-laskimen käyttöön:

Jos haluat laskea kuvan $\gamma$ -kulman sinin, kirjoita riville suoraan $\sin(\gamma)$ .
Kreikkalaiset kirjaimet saat näppäimistöltä:
- Alt + a = $\alpha$
- Alt + b = $\beta$
- Alt + g = $\gamma$
Jos laskin antaa vastauksen, kirjoita komento Lukuarvona(()$).
Kokeile ensin laskea jonkin kulman sini ja sen jälkeen muuttaa pisteiden paikkaa kuvaajassa. Mitä sinin arvolle tapahtuu?

Tähän kappaleeseen liittyvät tehtävät.

# muistikolmiot

2.3 Muistikolmiot

Muistikolmioiden avulla voidaan ratkaista tiettyjen usein esiintyvien kulmien sini, kosini ja tangentti. Tällaisia kulmia ovat $30^{\circ}$ , $45^{\circ}$ ja $60^{\circ}$ . Muistikolmiot täytyy niiden nimen mukaisesti muistaa ulkoa, mutta ne löytyvät myös esimerkiksi MAOL-taulukoista.

2.3.1 Esimerkki: trigonometrisia suhteita

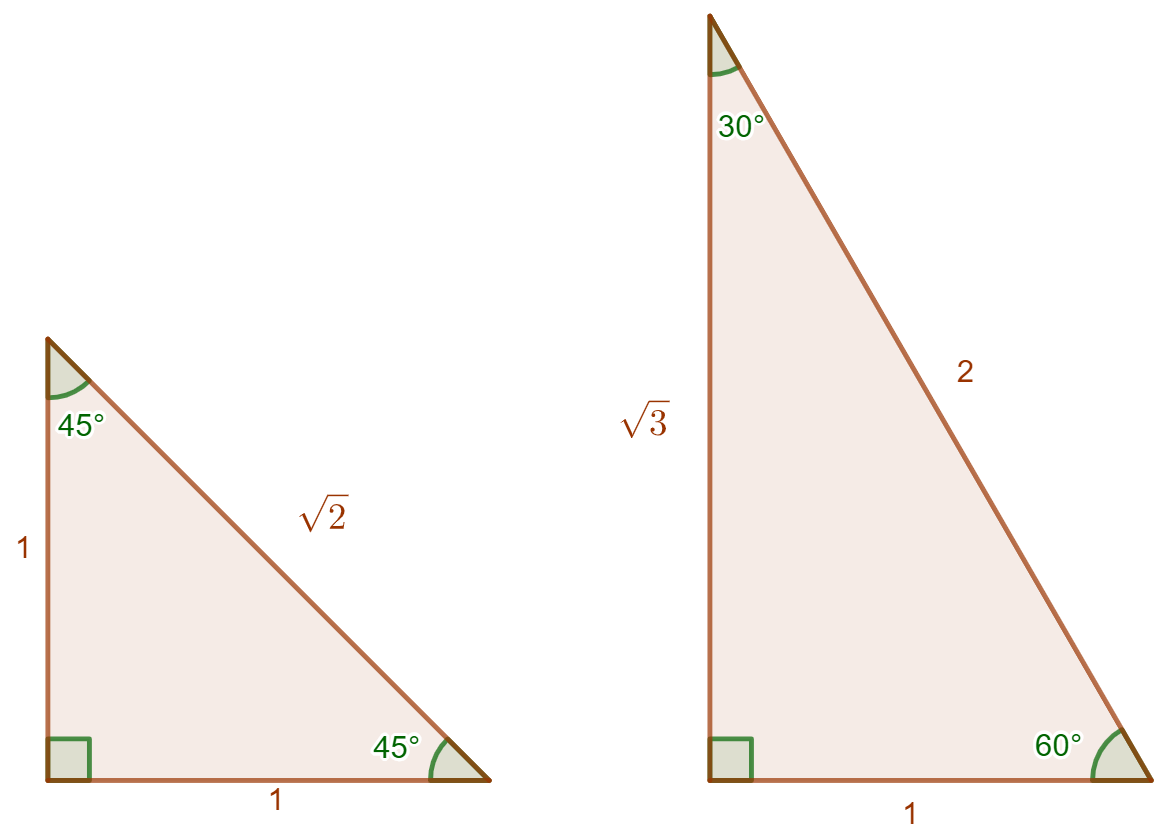
Esimerkkejä muistikolmioiden avulla ratkaistavista trigonometrisista suhteista.

$\sin(45^{\circ})=\frac{1}{\sqrt{2}}$ $\cos(60^{\circ})=\frac{1}{2}$ $\sin(30^{\circ})=\frac{1}{2}$ $\tan(45^{\circ})=\frac{1}{1}=1$

2.3.2 Esimerkki: kolmion sivujen ratkaiseminen

Ratkaistaan alla olevasta kuvasta sivujen ja pituudet.

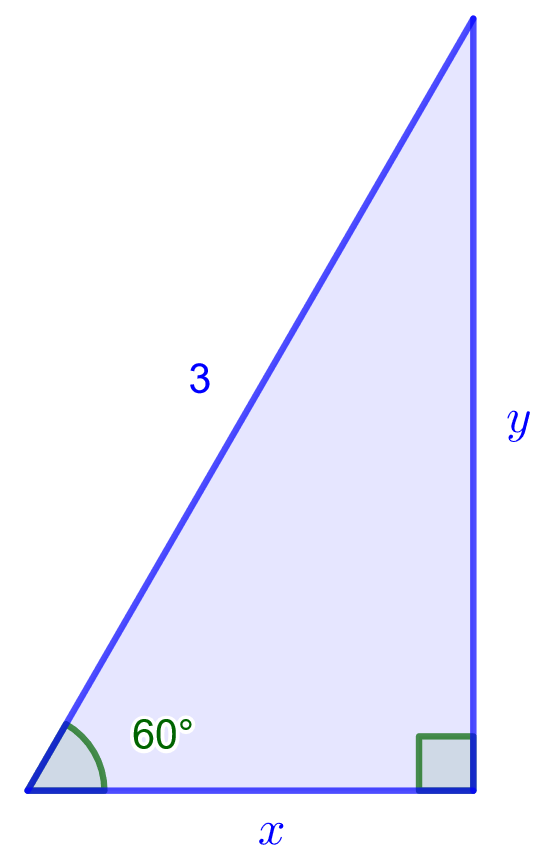
Oikeanpuoleisesta muistikolmiosta tiedetään, että $\cos 60^{\circ}=\frac{1}{2}.$ Annetusta kuvasta taas saadaan, että $\cos 60^{\circ} = \frac{x}{3}.$ Merkitään nämä yhtä suuriksi, jolloin saadaan $\frac{1}{2} = \frac{x}{3}.$ Kerrotaan ristiin ja ratkaistaan , jolloin saadaan $x=\frac{3}{2}.$

Sivun pituus saadaan vastaavasti sinin avulla, sillä $\sin 60^{\circ} = \frac{\sqrt{3}}{2} = \frac{y}{3}$ josta saadaan $y = \frac{3 \sqrt{3}}{2}.$

Tähän kappaleeseen liittyvät tehtävät.

# tylpat-kulmat

2.4 Tylpän kulman sini ja kosini

Aiemmin tigonometriset suhteet määriteltiin vain suorakulmaisessa kolmiossa eli käytännössä vain teräville kulmille. Myöhemmin kurssilla MAA5 Transkendenttiset funktiot ja yhtälöt (vanhassa opsissa MAA7 Trigonometriset funktiot) opit lisää trigonometrisista funktioista, jotka määritellään ilman suorakulmaista kolmiota.

Määritellään nyt kuitenkin tylpän kulman eli suoran kulman ja oikokulman välillä olevalle kulmalle sini ja kosini laskukaavojen avulla. Alla olevissa esimerkeissä havainnollistetaan sitä, mistä laskukaavat tulevat.

Tylpän kulman sini ja kosini

Tylpän kulman ( $90^{\circ} \leq \alpha \leq 180^{\circ}$ ) sini ja kosini voidaan laskea seuraavilla kaavoilla: $\sin (180^{\circ} -\alpha) = \sin (\alpha)$ $\cos(180^{\circ}-\alpha)=-\cos (\alpha).$

2.4.1 Esimerkki: tylpän kulman sini GeoGebralla

# tylppa-sini-geo

Otetaan esimerkiksi GeoGebra-appletissa näkyvä alkutilanne, jossa halutaan selvittää kulman $\alpha=140^{\circ}$ sini. Äsken esitellyn kaavan mukaisesti $\begin{aligned} \sin(140^{\circ}) &= \sin(180^{\circ}-140^{\circ}) \\ &= \sin(40^{\circ}) \\ &= 0,64. \end{aligned}$ GeoGebra-appletissa sekä kulman $140^{\circ}$ että $40^{\circ}$ oikea kylki on x-akselilla, ja vasen kylki on yhden mittainen jana. Huomataan, että kummankin kulman tapauksessa tämän janan päätepisteen y-koordinaatti on 0,64 .

2.4.2 Esimerkki: tylpän kulman kosini GeoGebralla

# tylppa-kosini-geo

Otetaan esimerkiksi GeoGebra-appletissa näkyvä alkutilanne, jossa halutaan selvittää kulman $\alpha=140^{\circ}$ kosini. Äsken esitellyn kaavan mukaisesti $\begin{aligned} \cos(140^{\circ}) &= -\cos(180^{\circ}-140^{\circ}) \\ &= -\cos(40^{\circ}) \\ &= -0,77. \end{aligned}$ GeoGebra-appletissa sekä kulman $140^{\circ}$ että $40^{\circ}$ oikea kylki on x-akselilla, ja vasen kylki on yhden mittainen jana. Huomataan, että kummankin kulman tapauksessa tämän janan päätepisteen x-koordinaatti on 0,77 . Tylpän kulman kosinin arvo on negatiivinen, kun taas vastaavan terävän kulman kosini on positiivinen.

Tähän kappaleeseen liittyvät tehtävät.

# kolmion-ala

2.5 Kolmion pinta-ala

Kolmion pinta-ala voidaan laskea tutulla tavalla, eli kerrotaan kolmion kanta ja korkeus keskenään ja jaetaan tulos kahdella. Joskus kolmion korkeus on kuitenkin vaikea määrittää. Yleisemmässä tapauksessa kolmion pinta-ala voidaan määrittää vain, kun tiedetään kahden kolmion sivun pituudet ja niiden sivujen välisen kulman suuruus.

Kolmion pinta-ala

Jos kolmion kannan pituus on ja korkeus , kolmion pinta-ala on $A=\frac{1}{2} ah.$ Jos kolmion kahden sivun pituudet ovat ja ja näiden välisen kulman suuruus $\alpha$ , voidaan kolmion pinta-ala ilmaista lausekkeella $A=\frac{1}{2} ab \sin \alpha.$

2.5.1 Todistus

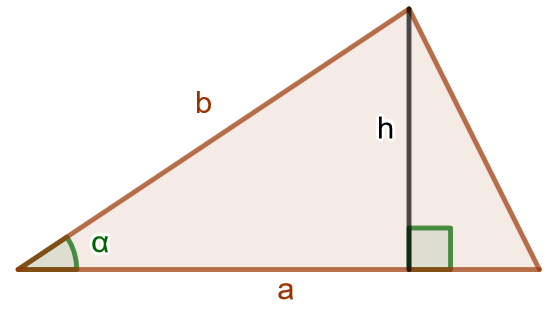
Todistetaan kolmion pinta-alan trigonometrinen kaava kolmessa tapauksessa:

kulma $\alpha$ on suora,
kulma $\alpha$ on terävä ja
kulma $\alpha$ on tylppä.

Jos kulma $\alpha$ on suora, muodostuu alla olevan kuvion mukainen kolmio.

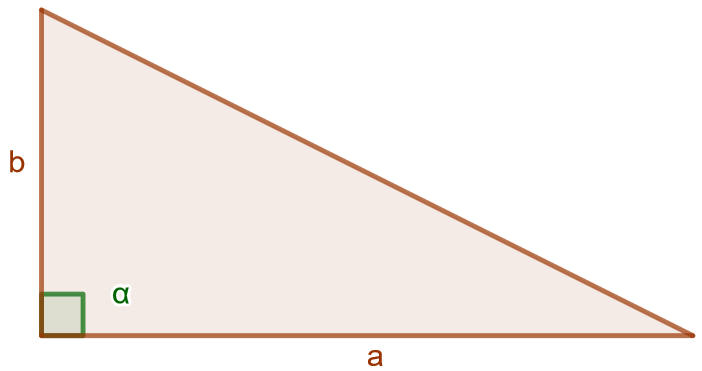
Tämän kolmion pinta-ala saadaan laskettua suoraan perinteisellä pinta-alan kaavalla, sillä kolmion pinta-ala on puolet sellaisen suorakulmion, jonka sivujen pituudet ovat ja , pinta-alasta. Koska $\sin 90^{\circ}=1$ , voidaan kyseinen termi lisätä pinta-alan arvoa muuttamatta. Kolmion pinta-ala on siis

$A=\frac{1}{2} ab = \frac{1}{2}ab \sin \alpha.$

Jos kulma $\alpha$ on terävä, muodostuu alla olevan kuvan mukainen kuvio. Siihen on merkitty kolmion korkeusjana , joka on kohtisuorassa kolmion kantaa vasten.

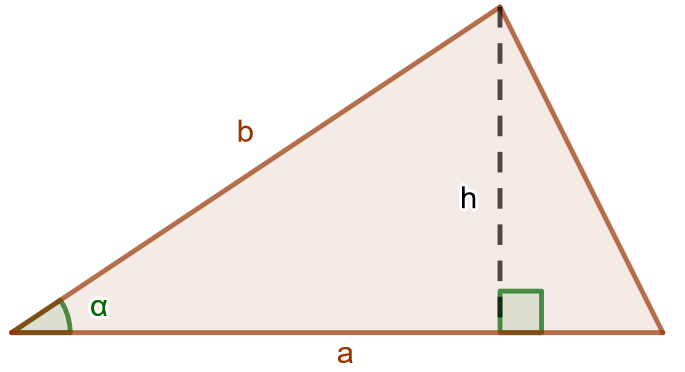
Kolmion pinta-ala saadaan perinteisen kaavan mukaisesti kertomalla kanta ja korkeus keskenään sekä jakamalla saatu tulo kahdella. Nyt kolmion korkeus on , joka voidaan ilmaista sivun sekä kulman $\alpha$ avulla $\sin \alpha = \frac{h}{b} \quad \Leftrightarrow \quad h = b \sin \alpha.$ Sijoitetaan tämä kolmion pinta-alan lausekkeeseen, jolloin saadaan $A=\frac{1}{2} ah = \frac{1}{2} a b \sin \alpha$ mikä on haluttu tulos.

Jos kulma $\alpha$ on tylppä, saadaan alla olevan kuvan kaltainen kolmio.

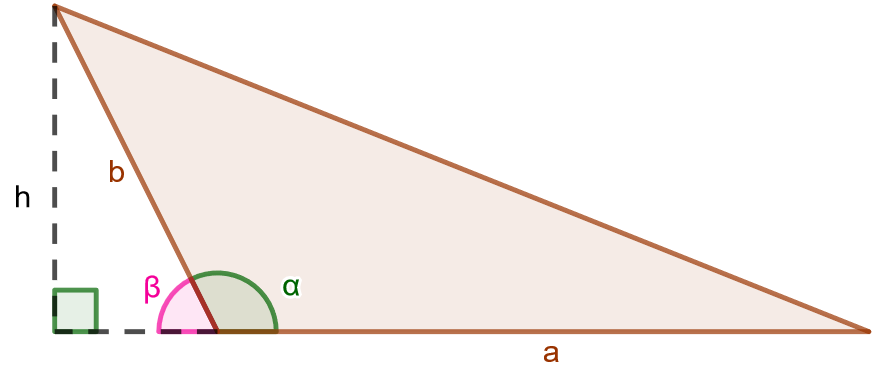
Nyt kolmion korkeusjana on kolmion ulkopuolella. Se voidaan ilmaista sivun ja kulman $\beta$ avulla seuraavasti: $\sin \beta = \frac{h}{b} \quad \Leftrightarrow \quad h = b \sin \beta.$ Haluaisimme ilmaista pinta-alan lausekkeen sivujen ja sekä kulman $\alpha$ avulla. Siksi meidän pitäisi löytää keino kuvata $\sin \beta$ kulman $\alpha$ avulla.

Huomataan, että $\alpha + \beta = 180^{\circ} \quad \Leftrightarrow \quad \beta = 180 ^{\circ} - \alpha$ jolloin $\sin \beta = \sin (180^{\circ}-\alpha)=\sin \alpha.$ Viimeinen yhtäsuuruus saadaan tylpän kulman sinin lausekkeesta. Nyt siis $h = b \sin \alpha$ . Sijoitetaan korkeuden lauseke kolmion pinta-alan lausekkeeseen: $A= \frac{1}{2} ah = \frac{1}{2} a b \sin \alpha$ joka on siinä muodossa kuin sen halusimme.

2.5.2 Esimerkki: kolmion pinta-alan lauseke GeoGebralla

# kolmio-ala-geo

Yllä olevassa GeoGebra-appletissa käydään läpi kolmion pinta-alan trigonometrisen laskukaavan johtaminen. Alussa johdetaan suorakulmaisen kolmion pinta-alan laskukaava lähtien suorakulmion pinta-alan laskukaavasta. Suorakulmion, jonka sivujen pituudet ovat ja , pinta-ala on A_s=ah . Kun suorakulmio puolitetaan lävistäjän kohdalta, saadaan kaksi yhtä suurta kolmiota, jolloin yhden kolmion pinta-ala on puolet suorakulmion pinta-alasta, eli $A_k=\frac{1}{2}A_s=\frac{1}{2}ah$ .

Tarkastellaan yleisesti kolmiota, jonka kanta on sama kuin suorakulmiossa eli , toinen sivu on ja korkeus on . Kolmio ei nyt kuitenkaan ole suorakulmainen. Lisäksi tiedetään, että sivujen ja välinen kulma on $\alpha$ . Kuvioon muodostuu suorakulmainen kolmio, koska korkeusjana on aina kohtisuorassa kolmion kantaan . Näillä merkinnöillä voidaan siis laskea $\sin(\alpha)=\frac{h}{b}$ . Ratkaistaan tästä yhtälöstä $h=b \sin(\alpha)$ . Sijoitetaan tämä :n lauseke nyt tunnettuun kolmion pinta-alan laskukaavaan $A=\frac{1}{2}ah=\frac{1}{2}ab \sin(\alpha).$ Näin saatiin johdettua kolmion pinta-alan trigonometrinen laskukaava.

Tähän kappaleeseen liittyvät tehtävät.

# kosinilause

2.6 Kosinilause

Kolmiomittaus on yksi tärkeimmistä maanmittausmenetelmistä, ja sen avulla on esimerkiksi piirretty Suomen peruskartat. Kolmiomittaus perustuu tunnettuihin pisteisiin ja niistä määritettävien kolmioiden sivujen ja kulmien mittaamiseen ja laskemiseen. Kolmion tuntemattomia sivuja ja kulmia voidaan määrittää kosinilauseen ja sinilauseen avulla.

Kosinilause

Jos ja ovat kolmion sivuja ja $\gamma$ niiden välinen kulma, voidaan kolmion kolmas sivu laskea seruraavasti: $c^2=a^2+b^2-2ab \cos \gamma.$

2.6.1 Todistus

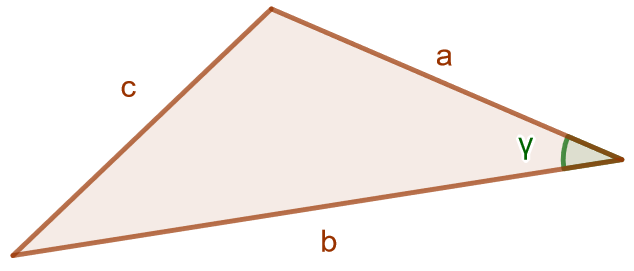
Todistetaan kosinilause kolmessa eri tapauksessa:

kulma $\gamma$ on terävä,
kulma $\gamma$ on suora ja
kulma $\gamma$ on tylppä.

Jos kulma $\gamma$ on terävä, muodostuu alla olevan kuvan kaltainen kolmio.

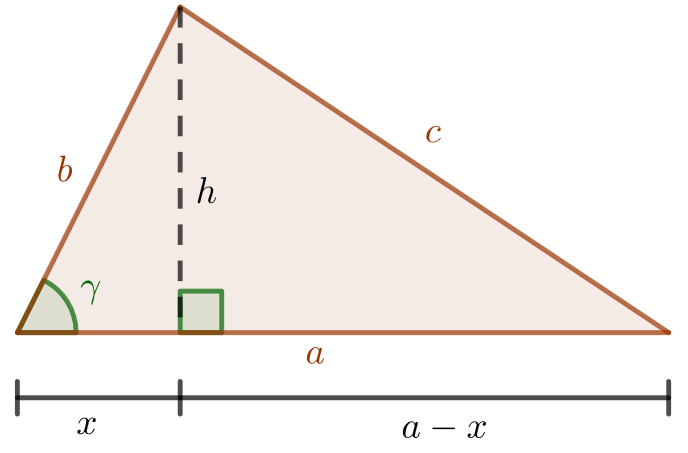
Kolmiossa sivu on jaettu kahteen osaan, joiden pituudet ovat ja a-x . Kolmion korkeusjana on kohtisuorassa kolmion kantaa vastaan.

Jos tarkastellaan vasemmanpuoleista suorakulmaista kolmiota, saadaan Pythagoraan lauseen avulla yhtälö h^2=b^2-x^2 . Toisaalta, jos tarkastellaan oikeanpuoleista suorakulmaista kolmiota, saadaan h^2=c^2-(a-x)^2 . Yhdistetään nämä kaksi lauseketta ja avataan jälkimmäisen lausekkeen sulut, jolloin saadaan b^2-x^2=c^2-a^2+2ax-x^2 . Sievennetään lauseketta, jolloin se saa muodon c^2=a^2+b^2-2ax .

Nyt pitäisi vielä ilmaista kolmion sivujen ja kulman $\gamma$ avulla. Huomataan, että $\cos \gamma = \frac{x}{b}$ eli $x=b \cos \gamma$ . Sijoitetaan tämä aiemmin saatuun yhtälöön, jolloin saadaan tuttu kosinilauseen lauseke $c^2=a^2+b^2-2ab \cos \gamma.$

Jos kulma $\gamma$ on suora, saadaan alla olevan kuvan kaltainen kolmio.

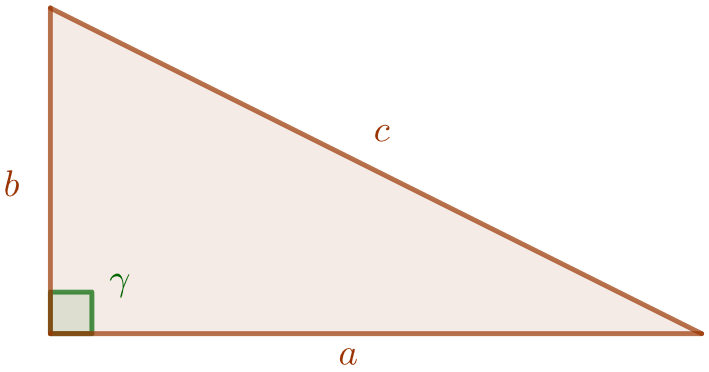
Tutkitaan, päteekö kosinilauseen kaava $c^2=a^2+b^2-2ab \cos \gamma$ suorakulmaisen kolmion tapauksessa. Tiedetään, että $\cos 90^{\circ}=0$ . Tällöin kosinilause sievenee muotoon , mikä on Pythagoraan lause. Koska kyseessä on suorakulmainen kolmio, Pythagoraan lause on varmasti voimassa, ja samoin kosinilause on voimassa suorakulmaisille kolmioille.

Jos kulma $\gamma$ on tylppä, saadaan alla olevan kuvan kaltainen kolmio.

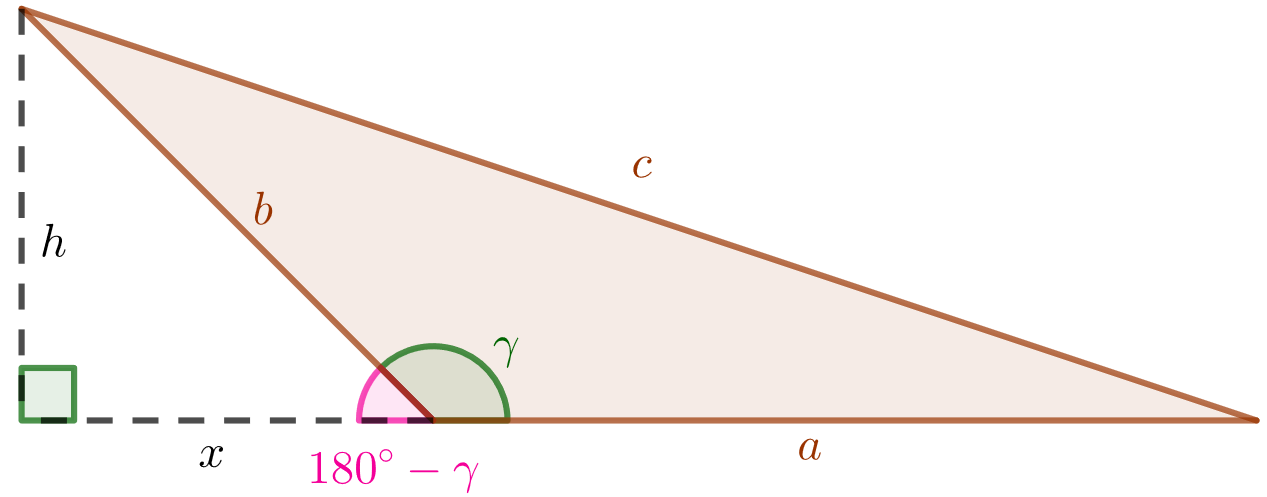
Kuvaan on merkitty kolmion korkeusjana ja sivun jatke, jota merkitään kirjaimella . Nyt kolmion vasemmalle puolelle muodostuu suorakulmainen kolmio, josta saadaan Pythagoraan lauseella h^2=b^2-x^2 . Lisäksi jos tarkastellaan vasemmanpuoleisen kolmion ja alkuperäisen kolmion yhdessä muodostamaa suorakulmaista kolmiota, saadaan h^2=c^2-(x+a)^2 . Yhdistetään nämä kaksi lauseketta ja avataan jälkimmäisen lausekkeen sulut, jolloin saadaan b^2-x^2=c^2-a^2-2ax-x^2 . Kun tätä sievennetään ja järjestellään uudestaan, saadaan c^2=a^2+b^2+2ax .

Kolmion vasemmalle puolelle muodostuvasta kolmiosta saadaan $\cos (180^{\circ}-\gamma)=\frac{x}{b}$ . Tylpän kulman kosinin kaavan avulla saadaan $\cos (180^{\circ}-\gamma)=-\cos \gamma=\frac{x}{b}$ eli $x = - b \cos \gamma$ . Sijoitetaan tämä aiemmin ratkaistuun :n neliön lausekkeeseen: $c^2=a^2+b^2-2ab \cos \gamma$ mikä on kosinilause siinä muodossa kuin sen halusimme.

2.6.2 Esimerkki: kosinilause GeoGebralla

# kosinilause-geo

Yllä olevassa GeoGebra-appletissa on piirretty kolmio, joka ei välttämättä ole suorakulmainen. Vasemmalla olevalla cas-laskimella voidaan varmistaa, että pisimmän sivun neliö on koko ajan yhtä suuri kuin kosinilauseessa väitetään eli $a^2+b^2-2ab \cos(\gamma)$ .

2.6.3 Esimerkki: kulmaa vastakkaisen sivun pituuden ratkaiseminen

Määritä alla olevasta kolmiosta sivun pituus.

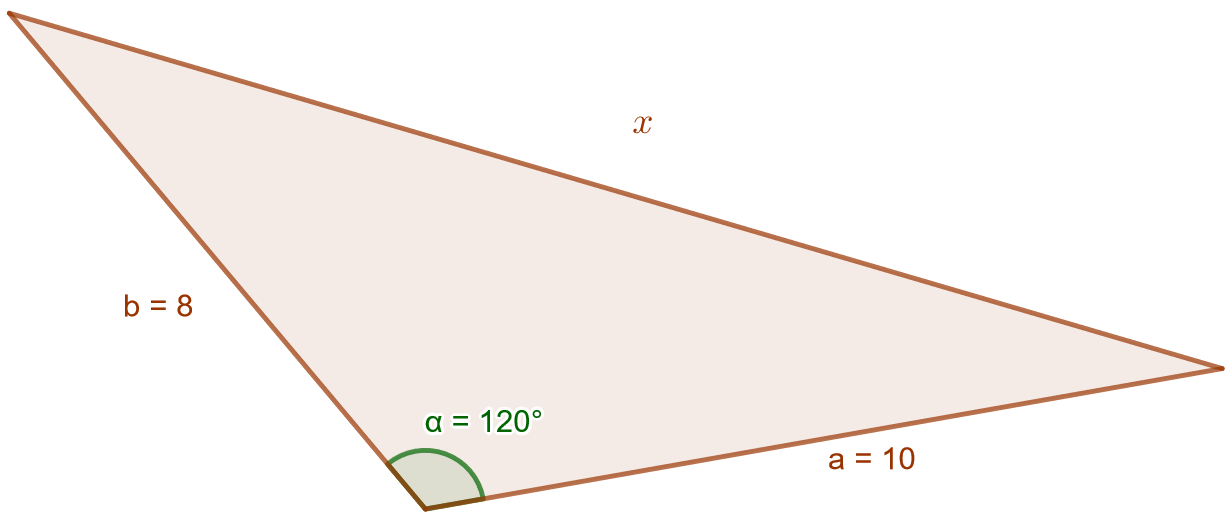
Tiedetään siis sivujen ja pituudet, sekä niiden välisen kulman $\alpha$ suuruus. Voidaan siis käyttää kosinilausetta. Nyt kosinilause tulee muotoon $x^2=a^2+b^2-2ab\cos(\alpha).$ Sijoitetaan sivujen pituudet ja kulman suuruus yhtälöön ja ratkaistaan . $\begin{aligned} x^2 &= 10^2+8^2-2 \cdot 10\cdot 8 \cdot \cos(120^{\circ}) &\quad &| \text{ sievennetään} \\ x^2 &= 244 &\quad &| \sqrt{\text{ }} \\ x &= \sqrt{244} &\quad &| \text{ sievennetään} \\ x &\approx 15,6205 &\quad &| \text{ pyöristetään} \\ x &\approx 15,62 \end{aligned}$ Kolmion sivun pituus on noin 15,62 .

2.6.4 Esimerkki: kulman viereisen sivun ratkaiseminen

Ratkaise alla olevan kolmion sivun pituus.

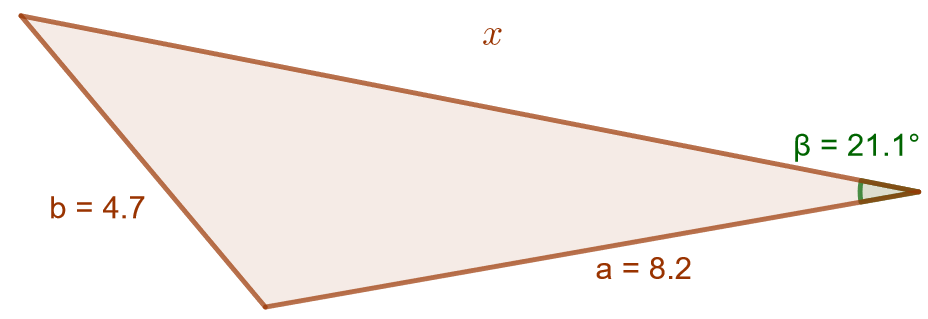
Nyt tiedetään kolmion sivujen ja pituudet, mutta tunnettu kulma $\alpha$ ei olekaan sivujen ja välissä. Käytetään silti kosinilausetta, sillä sitä voidaan käyttää aina, kun tiedetään kaksi kolmion sivua ja yksi kolmion kulma.

Muodostetaan kuvassa olevien tietojen avulla kosinilauseen kaava. Huomaa nyt, että kosinilauseen ja viittaavat tunnetun kulman viereisiin sivuihin, jotka tässä tapauksessa ovat ja . $b^2=a^2+x^2-2ax\cos(\beta)$ Sijoitetaan nyt tähän kaavaan lukuarvot kuvasta ja ratkaistaan . $\begin{aligned} 4,7^2 &= 8,2^2+x^2-2\cdot 8,2 \cdot x \cdot \cos(21,1^{\circ}) &\quad &| \text{ sievennetään} \\ 22,09 &= 67,24 + x^2 - 15,3x &\quad &|-22,09 \\ 0 &= x^2 -15,3x+45,15 &\quad &| \text{ toisen asteen yhtälö} \\ x &= \frac{15,3 \pm \sqrt{(-15,3)^2-4\cdot 1 \cdot 45,15}}{2 \cdot 1} \\ x &\approx 11,068 \qquad x \approx 3,99316 \end{aligned}$ Saatiin kaksi vastausta, joista molemmat ovat positiivisia ja sinällään sopivia vastaukseksi. Todellisuudessa molemmat vastaukset myös sopivat vastaukseksi, sillä kolmiosta ei ole määritelty kuin yksi kulma. Sivujen ja sekä sivujen ja väliset kulmat voivat olla minkä suuruisia tahansa. Tarkastele alla olevia kuvia.

Kolmion sivu on siis noin 11,1 tai noin 3,99 .

Tähän kappaleeseen liittyvät tehtävät.

# sinilause

2.7 Sinilause

Jos kolmiosta tiedetään kahden kulman suuruus sekä yhden sivun pituus, kosinilausetta ei voida käyttää. Tällöin käytetään sinilausetta.

Sinilause

Jos kolmiosta valitaan mikä tahansa sivu ja sitä vastaava kulma, sivun pituuden ja kulman sinin suhde eli suhde $\frac{\text{kolmion sivu}}{\text{vastaisen kulman sini}}$ on vakio. Alla olevan kuvan merkinnöillä saadaan
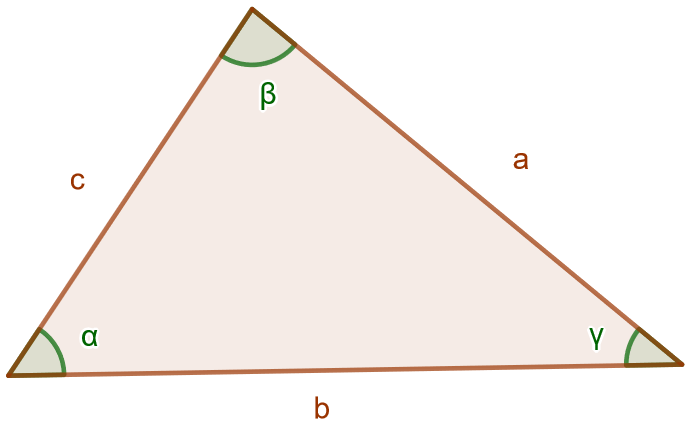
$\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.$

2.7.1 Todistus

Todistetaan sinilause käyttämällä kolmion pinta-alan trigonometrista laskukaavaa. Käytetään alla olevan kuvan merkintöjä.

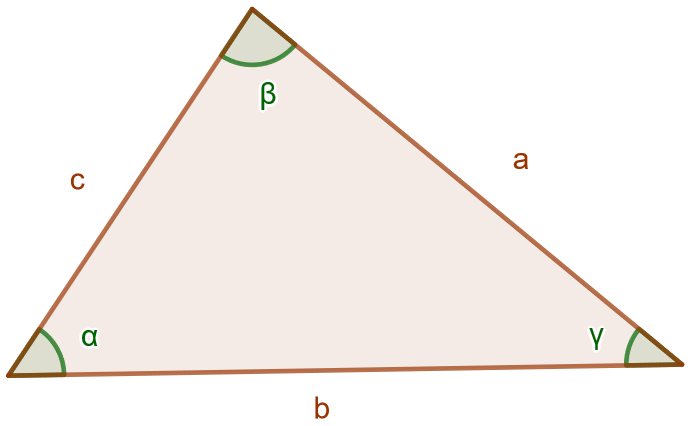
Kolmion pinta-ala voidaan laskea tarkastelemalla kulmaa $\alpha$ tai kulmaa $\beta$ , jolloin saadaan $A=\frac{1}{2}bc \sin \alpha = \frac{1}{2} ac \sin \beta.$ Supistetaan lausekkeista temit $\frac{1}{2}c$ pois ja järjestellään uudelleen, jolloin saadaan $\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}.$

Tehdään sama tarkastelu kulmille $\beta$ ja $\gamma$ , jolloin saadaan $\frac{1}{2} ac \sin \beta = \frac{1}{2} ab \sin \gamma \Leftrightarrow \frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.$

Yhdistämällä nämä kaksi saatua lauseketta, saadaan sinilause $\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}.$

2.7.2 Esimerkki: sinilause GeoGebralla

# sinilause-geo

Yllä olevassa GeoGebra-appletissa lasketaan jokaisen sivun ja sivua vastaan olevan kulman sinin suhde. Huomaa, että kun siirrät kolmion kärkipisteitä, suhteet pysyvät samoina.

2.7.3 Esimerkki: kulman ratkaiseminen

Ratkaise alla olevan kolmion kulma $\beta$ .

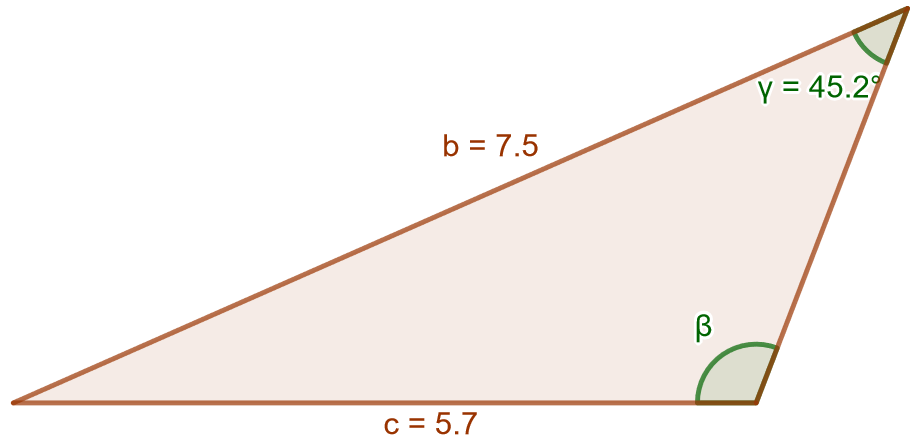
Jos kosinilauseella halutaan ratkaista kulma, tulisi tietää kaikkien kolmion sivujen pituudet. Koska nyt tiedetään vain kahden sivun pituudet ja kysytty kulma sekä tunnettu kulma ovat tunnettujen sivujen vastaisia kulmia, voidaan käyttää sinilausetta. Muotoillaan sinilauseen mukainen yhtälö ensin muuttujilla, ratkaistaan $\beta$ ja lopuksi sijoitetaan lukuarvot muuttujien paikalle. $\begin{aligned} \frac{b}{\sin(\beta)} &= \frac{c}{\sin(\gamma)} &\quad &| \text{ kerrotaan ristiin} \\ c \sin(\beta) &= b \sin(\gamma) &\quad &|:c \\ \sin(\beta) &= \frac{b \sin(\gamma)}{c} &\quad &| \sin^{-1}() \\ \beta &= \sin^{-1}\left( \frac{b \sin(\gamma)}{c} \right) \\ \beta &= \sin^{-1}\left( \frac{7,5 \cdot \sin(45,2^{\circ})}{5,7} \right) \\ \beta &= 69,01^{\circ} \end{aligned}$ Kuvasta huomataan, että kulman $\beta$ tulisi olla tylppä kulma, eikä $69,01^{\circ}$ ole tylppä. Muistetaan kuitenkin aiemmin käsitelty tylpän kulman sini. Sen mukaan $\sin(180^{\circ}-\alpha)=\sin(\alpha).$ Joten haluttu tylppä kulma saadaan laskemalla $\beta=180^{\circ}-69,01^{\circ}=110,99^{\circ}\approx 111^{\circ}.$ Alla olevaan kuvaan on piirretty molemmat tapaukset, ja huomataan, että sekä $69^{\circ}$ että $111^{\circ}$ toteuttavat kolmion muut annetut mitat.

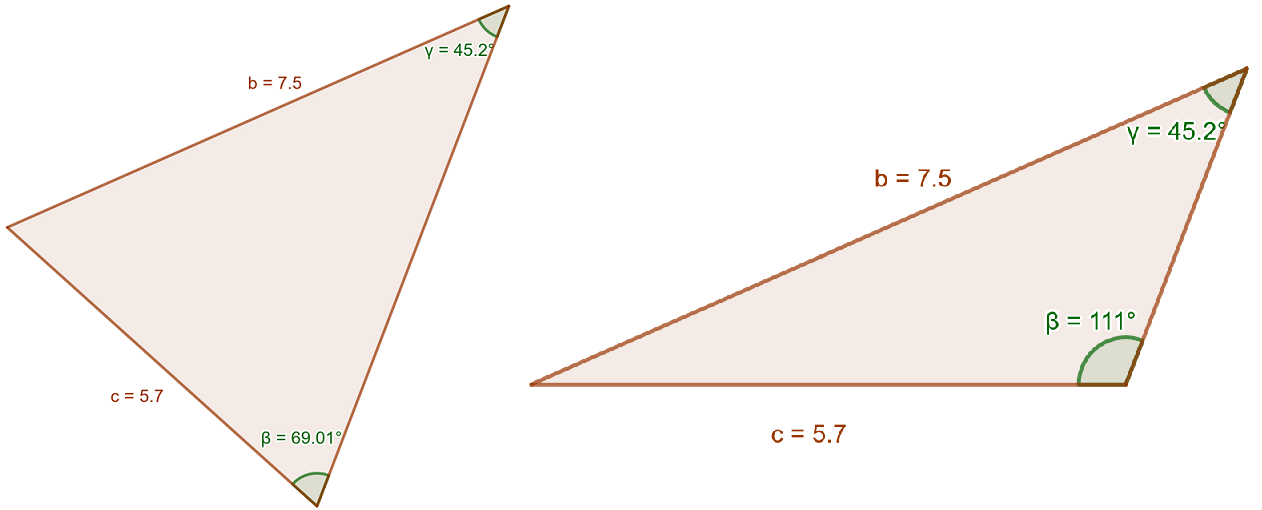
Tässä tapauksessa kysytty kulma $\beta$ on siis noin $111^{\circ}$ .

Sinilauseen avulla voidaan todistaa seuraava lause, jota usein kutsutaan kulmanpuolittajalauseeksi. Alla olevalla videolla on esitelty kulmanpuolittajalause ja käyty läpi kaksi esimerkkiä siihen liittyen.

Kulmanpuolittajalause

Kolmion kulman puolittava jana jakaa kulmaa vastapäätä olevan sivun kulman kylkien pituuksien suhteessa. Alla olevan kuvan merkinnöillä tämä tarkoittaa $\frac{a_1}{a_2} = \frac{x}{y}.$

2.7.4 Todistus

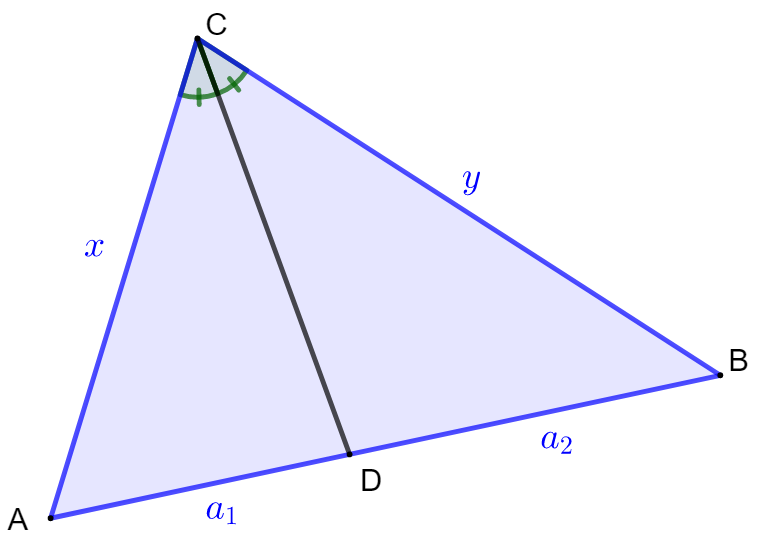
Käytetään alla olevan kuvan merkintöjä.

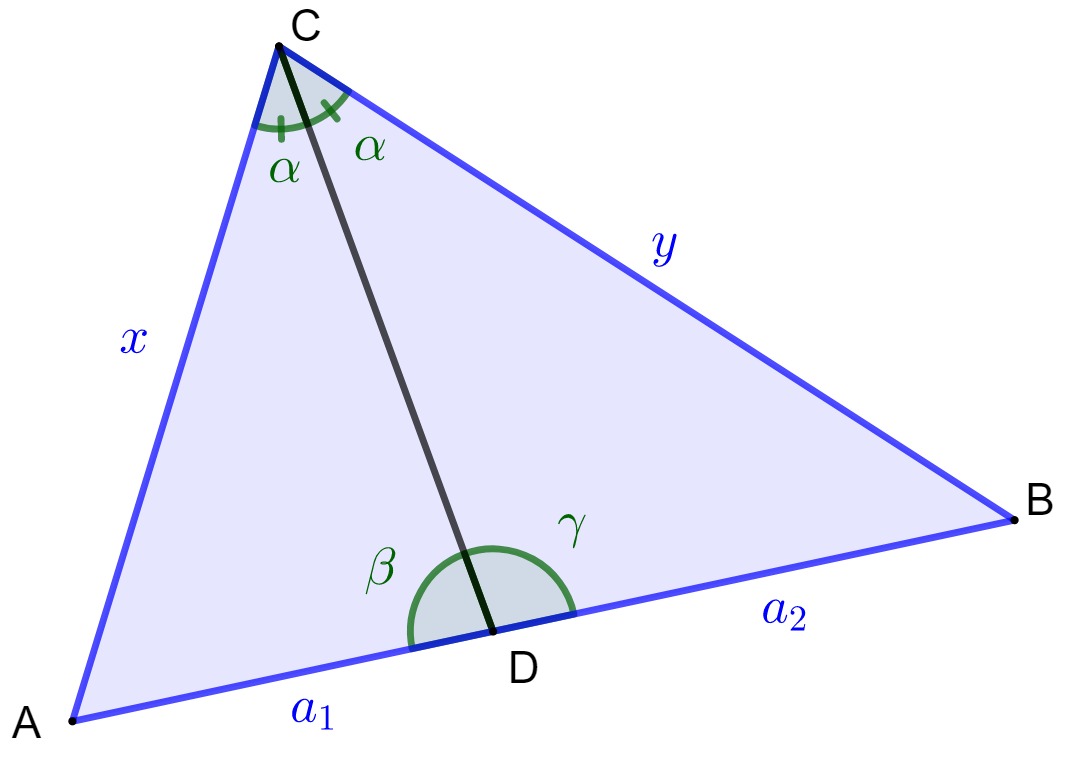
Koska kulmat $\beta$ ja $ muodostavat oikokulman, on oltava $\begin{aligned} \beta + \gamma &= 180^{\circ} \\ \beta &= 180^{\circ} - \gamma. \end{aligned}$

Otetaan puolittain sini ja muistetaan tylpän kulman sinin laskusääntö, jolloin saadaan $\begin{aligned} \sin \beta &= \sin ( 180^{\circ} - \gamma) \\ \sin \beta &= \sin \gamma. \end{aligned}$

Käytetään sinilausetta ensin kolmioon ACD , jolloin saadaan $\frac{a_1}{\sin \alpha} = \frac{x}{\sin \beta} \quad \Leftrightarrow \quad \sin \beta = \frac{x \sin \alpha}{a_1}$ ja seuraavaksi kolmioon BCD , jolloin saadaan $\frac{a_2}{\sin \alpha} = \frac{y}{\sin \gamma} \quad \Leftrightarrow \quad \sin \gamma = \frac{y \sin \alpha}{a_2}.$ Koska $\sin \beta = \sin \gamma$ , merkitään nämä lausekkeet yhtä suuriksi $\frac{x \sin \alpha}{a_1} = \frac{y \sin \alpha}{a_2},$ jaetaan puolittain termillä $\sin \alpha$ $\frac{x}{a_1} = \frac{y}{a_2},$ ja järjestellään termejä uudelleen, jolloin saadaan haluttu tulos $\frac{x}{y} = \frac{a_1}{a_2}.$

2.7.5 Esimerkki: kulmanpuolittajalause GeoGebralla

# geo_kulmanpuolittajalause

Yllä olevassa GeoGebra-appletissa voit siirtää kolmion punaisia kärkipisteitä ja tarkkailla suhteiden $\frac{a_1}{a_2}$ ja $\frac{x}{y}$ arvoja. Jana on aina kulman $\angle ACB$ puolittaja.

2.7.6 Esimerkki: kolmion sivun pituuden ratkaiseminen

Ratkaistaan alla olevaan kuvaan sinisellä merkityn janan pituus.

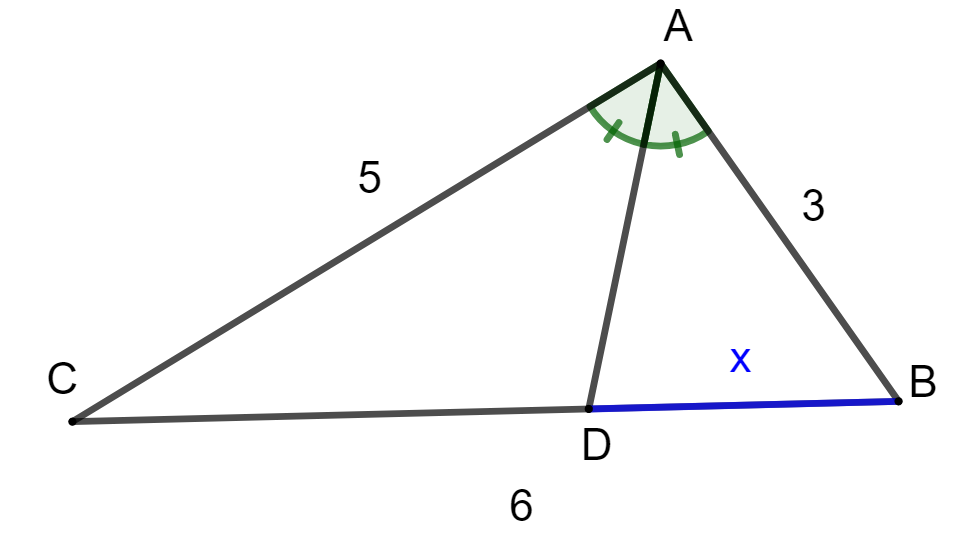
Merkitään kysyttyä janan pituutta kirjaimella . Tällöin janan pituus on 6-x . Käytetään kulmanpuolittajalausetta ja ratkaistaan $\begin{aligned} \frac{6-x}{x} &= \frac{5}{3} &\quad &| \text{ kerrotaan ristiin} \\ 5x &= 3 \cdot (6-x) &\quad &| \text{ kerrotaan sulut auki} \\ 5x &= 18-3x &\quad &| +3x \\ 8x &= 18 &\quad &| :8 \\ x &= \frac{18}{8} = \frac{9}{4} \end{aligned}$ Janan pituus on $\frac{9}{4}$ eli 2,25 .

Tähän kappaleeseen liittyvät tehtävät.

# kaant-pythagoras

2.8 Käänteinen Pythagoraan lause

Pythagoraan lauseen kohdalla todettiin, että se pätee vain suorakulmaisille kolmioille. Eli jos kolmio on suorakulmainen, sen kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö. Sama päättely voidaan kääntää toisinpäin. Jos kolmion kahden lyhyemmän sivun neliön summa on yhtä suuri kuin pisimmän sivun neliö, kyseessä on suorakulmainen kolmio. Jos suoraa kulmaa ei ole merkitty kuvaan tai sitä ei ole kerrottu erikseen, tulee aina tarkistaa, onko kolmio suorakulmainen, vaikka se saattaisi näyttää siltä.

Käänteinen Pythagoraan lause

Jos kolmion pisin sivu on , kaksi muuta sivua ja ja kolmiolle pätee yhtälö a^2+b^2=c^2 , kolmio on suorakulmainen.

2.8.1 Esimerkki: onko kolmio suorakulmainen?

Ovatko seuraavat kuvissa olevat kolmiot suorakulmaisia?

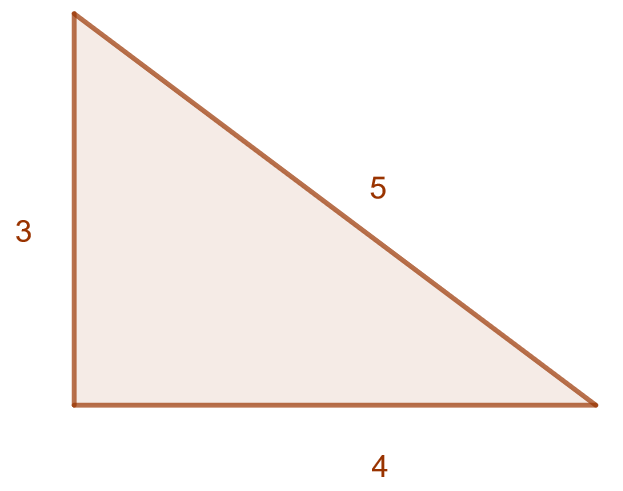
Kolmion pisin sivu on , ja sen neliö on 5^2=25 . Kolmion lyhyemmät sivut ovat ja , ja niiden neliöiden summa on 3^2+4^2=9+16=25 . Koska nämä ovat yhtä suuret, kolmio on suorakulmainen.

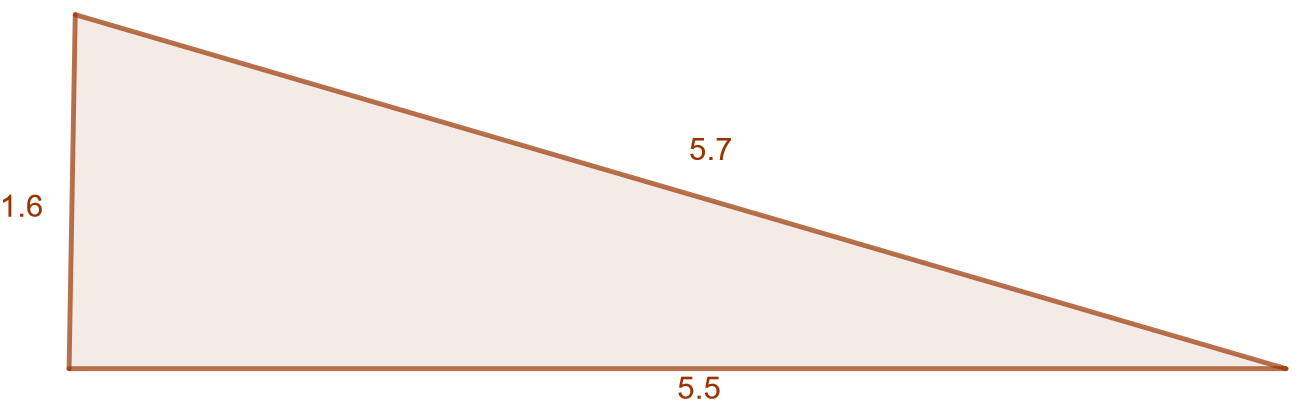
Pisin sivu on 5,7 , ja sen neliö on 5,7^2=32,49 . Kolmion lyhyemmät sivut ovat 1,6 ja 5,5 , ja niiden neliöiden summa on 1,6^2+5,5^2=2,56+30,25=32,81 . Koska tulokset ovat eri suuria, kolmio ei ole suorakulmainen.

Tähän kappaleeseen liittyvät tehtävät.

# merkilliset-pisteet

2.9 Kolmion merkilliset pisteet

Kolmioihin liittyy paljon mielenkiintoisia kaikkia kolmioita koskevia tuloksia. Seuraavaksi esitellään tuloksia liittyen kolmion kulmanpuolittajiin, keskijanoihin ja keskinormaaleihin. Kokeile kaikissa GeoGebra-havainnollistuksissa raahata kolmion kärkipisteitä ja tutkia, mitä kuvassa tapahtuu.

2.9.1 Kulmanpuolittajalause

Kolmion jokaisen kulman kulmanpuolittajat leikkaavat yhdessä pisteessä, joka on aina kolmion sisällä. Tämä piste on myös suurimman mahdollisen kolmion sisään piirretyn ympyrän keskipiste. Ympyrän säde voidaan laskea kaavalla $r=\sqrt{\frac{(s-a)(s-b)(s-c)}{s}},$ missä , ja ovat kolmion sivujen pituudet ja on kolmion piirin puolikas $s=\frac{1}{2}(a+b+c).$

# kulmanpuolittajat-geo

2.9.2 Keskijanalause

Kun kolmion sivujen keskipisteet yhdistetään vastakkaisiin kulmiin, saadaan kolme keskijanaa. Nämä keskijanat leikkaavat yhdessä pisteessä, joka jakaa jokaisen keskijanan suhteessa 2:1 . Leikkauspiste on aina kolmion sisällä ja sitä kutsutaan myös kolmion painopisteeksi.

# keskijanat-geo

2.9.3 Keskinormaalilause

Kolmion sivujen keskinormaalit leikkaavat yhdessä pisteessä, joka on kolmion ympäri piirretyn ympyrän keskipiste. Teräväkulmaisen kolmion tapauksessa piste on kolmion sisäpuolella ja tylppäkulmaisella kolmiolla se on kolmion ulkopuolella. Suorakulmaisella kolmiolla leikkauspiste on täsmälleen hypotenuusan keskipisteessä.

# keskinormaali-geo

Tähän kappaleeseen liittyvät tehtävät.