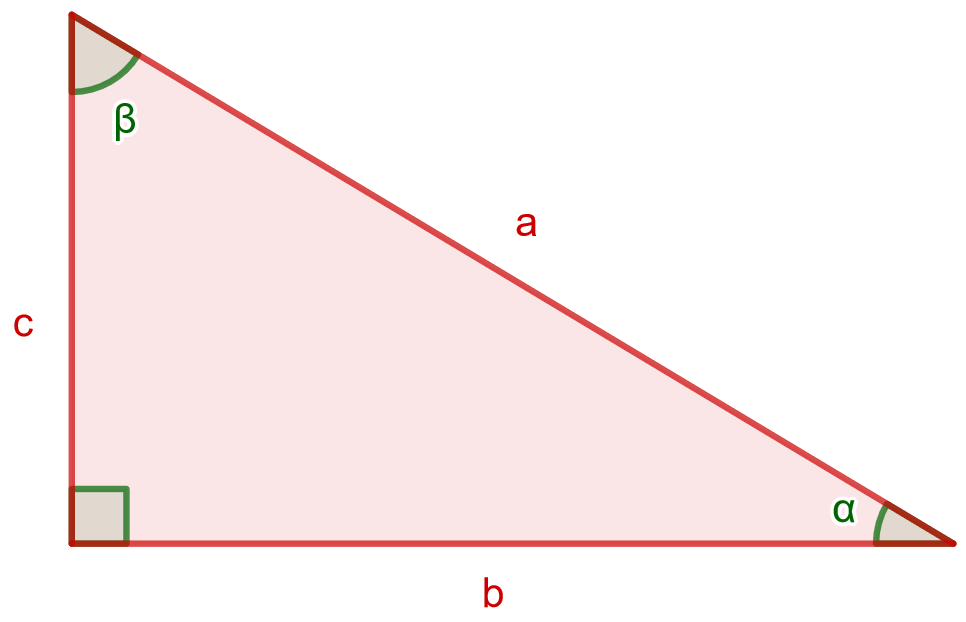
2. Kolmioiden geometriaa: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät lukuun Kolmioiden geometriaa Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa luvussakin.

# pythagoras-teht

2.1 Suorakulmainen kolmio, Pythagoraan lause

Tämän kappaleen teoria on kappaleessa Suorakulmainen kolmio, Pythagoraan lause.

# teht_suorakulmaisen_hypotenuusa

2.1.1 Tehtävä

# pythagoras1

# teht_S11T1b

2.1.2 Tehtävä (S2011/1b)

Suorakulmaisen kolmion hypotenuusan pituus on ja toisen kateetin pituus . Laske toisen kateetin pituus.

# pythagoras2

# teht_S15T10

2.1.3 Tehtävä (S2015/10)

Suorakulmaisen kolmion kateettien ja hypotenuusan pituudet muodostavat geometrisen jonon. Määritä suhdeluku .

# s15t10a

Suorakulmaisen kolmion kateettien ja hypotenuusan pituudet muodostavat aritmeettisen jonon. Määritä suhde .

# s15t10b_a

# s15t10b_b

# s15t10b_c

# teht_geogebra_puu

2.1.4 Tehtävä

Seitsemän metriä korkea puu kasvaa kohtisuoraan maan pintaa vastaan. Puu taittuu kahden metrin korkeudelta niin, että puun latvaosa osuu maahan. Latva ja tyviosa eivät irtoa toisistaan. Piirrä tilanteesta mallikuva oikeanpuoleiselle piirtoalueelle (ei vaikuta tehtävän pisteytykseen) ja laske vasemmanpuoleiselle CAS-alueelle, kuinka suuri kulma on maanpinnan ja taittuneen latvan välillä.

Anna vastaus vasemmanpuoleisella CAS-alueella tallentamalla se muuttujaan nimeltä v. Pyöristä vastaus kokonaislukujen tarkkuudelle käyttämällä komentoa round.

# puu-kaatuu

Vinkkejä GeoGebran käyttöön

Tekstin lisääminen

Monesti on hyödyllistä lisätä tehtävän ratkaisuun tekstiä, jossa selität, miten teit tehtävän. Valitse CAS-alueen oikeassa yläkulmassa oleva valikko ja valitse sieltä teksti . Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.

Muuttujan tallentaminen

Joskus on hyödyllistä tallentaa lukuarvo tai vastaus muuttujaan. Tällöin lukuarvon käyttäminen myöhemmin on kätevää. Jos haluat sijoittaa muuttujaan a arvon 4, kirjoita komento a := 4. Jos myöhemmin haluat laskea laskun , kirjoita komento 5*a, jolloin saat vastaukseksi 20.

Yhtälön ratkaiseminen

Jos haluat ratkaista muuttujan yhtälöstä a^2+3a-4=0 , syötä CAS-laskimeen komento Ratkaisut(a^2+3a-4,a). Vastaukseksi saat listan {-4,1}. Helpoiten ratkaisuihin pääsee käsiksi, kun tallentaa ne muuttujaan: vastaukset := Ratkaisut(a^2+3a-4,a). Tällöin komento vastaukset(1) tuottaa luvun -4, ja komento vastaukset(2) tuottaa luvun 1.

Lukuarvon näyttäminen

Joskus GeoGebra näyttää vastauksen hyvinkin monimutkaisessa muodossa. Käytä tällöin komentoa Lukuarvona(). Jos kirjoitat esimerkiksi komennon a:=sin^(-1)(1/2), GeoGebra tulostaa vastaukseksi saman eli a:=sin^(-1)(1/2). Jos haluat vastauksen lukuarvona, kirjoita komento Lukuarvona(a), jolloin GeoGebra tulostaa 60°.

# trig-teht

2.2 Trigonometriset funktiot

Tämän kappaleen teoria on kappaleessa Trigonometriset funktiot.

# teht_trig1

2.2.1 Tehtävä

Tehtävien 3.2.1-3.2.6 merkinnät vastaavat alla olevan kolmion merkintöjä.

# trig1

# teht_trig2

2.2.2 Tehtävä

# trig2

# teht_trig3

2.2.3 Tehtävä

# trig3

# teht_trig4

2.2.4 Tehtävä

# trig4

# teht_trig5

2.2.5 Tehtävä

# trig5

# teht_trig6

2.2.6 Tehtävä

# trig6

# teht_s96T3b

2.2.7 Tehtävä (s1996/3b)

Katuvalaisimen kannatinvaijeri on kiinnitetty $34,50 \text{ m}$ leveän kadun vastakkaisilla puolilla olevien talojen seiniin $6,50 \text{ m}$ korkeudelle maasta. Lamppu riippuu vaijerista sen keskikohdalta, joka on $1,10 \text{ m}$ vaijerin päitä alempana, ja vetää vaijerin puolikkaat likimain janoiksi. Kuinka pitkä vaijeri on, ja kuinka suuren kulman vaijerin puoliskot muodostavat keskenään?

# lamppua

# lamppualfa

# teht_K17T6

2.2.8 Tehtävä (K2017/6)

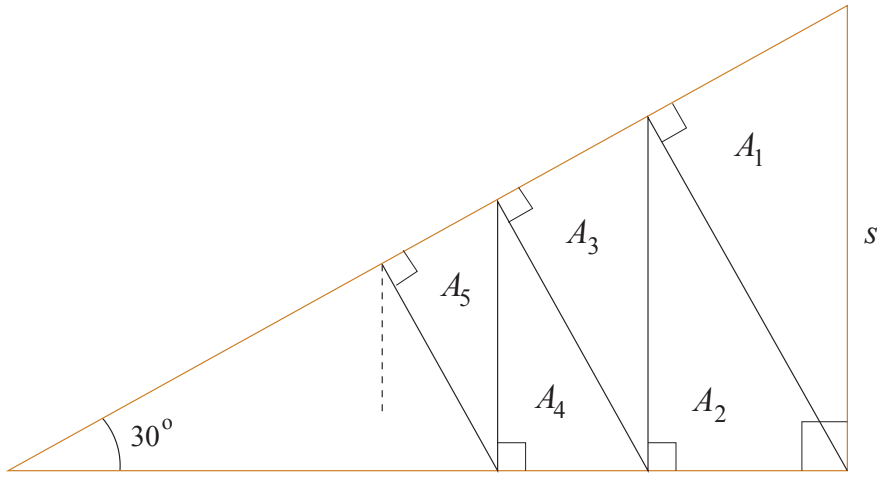
Suorakulmaisen kolmion muotoisesta suklaalevystä lohkotaan alla olevan kuvion mukaisesti kappaletta yhdenmuotoisia paloja, joiden pinta-alat ovat $A_1,A_2,A_3,\ldots,A_n$ . Kuinka monta palaa suklaasta täyty lohkaista, jotta palojen yhteenlasketut pinta-alat muodostavat vähintään $97 \%$ suklaalevyn alkuperäisestä pinta-alasta?

# suklaalevy

# teht_sin18

2.2.9 Tehtävä

Määritä lausekkeen $\sin(18^{\circ})$ tarkka arvo käyttämällä alla olevaa tasakylkistä kolmiota.

# geo_sin18

Vihje 1

Ratkaise alkuperäisen kolmion kolmannen sivun pituus.

Vihje 2

Lisää valinta kohtaan "vihje 1". Millainen kolmio muodostuu mustan janan oikealle puolelle? Voiko sitä verrata alkuperäiseen kolmioon? Saatko ratkaistua mustan janan pituuden?

Vihje 3

Pidä edelleen valinta kohdassa "Vihje 1". Mustan janan oikealle puolelle muodostuu kolmio, joka on yhdenmuotoinen alkuperäisen kolmion kanssa (perustele tämä kulmien suuruuksien avulla). Käytä verrantoa ratkaistaksesi kolmion kolmannen sivun (ja samalla mustan janan) pituus.

Vihje 4

Lisää valinta kohtaan "Vihje 2" ja huomaa, että $\frac{36^{\circ}}{2}=18^{\circ}$ .

# sin18

# muistikolmiot-teht

2.3 Muistikolmiot

Tämän kappaleen teoria on kappaleessa Muistikolmiot.

# teht_muistikolmio1

2.3.1 Tehtävä

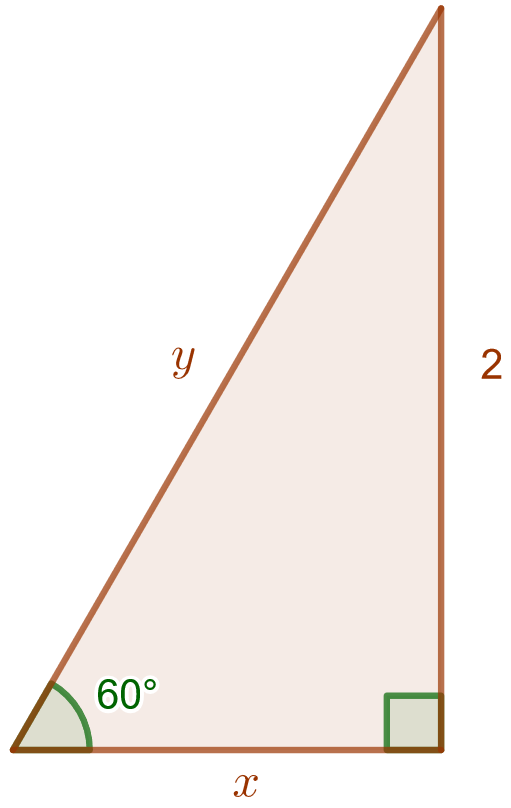
Laske muistikolmion avulla alla olevan kolmion kateetin pituus sekä hypotenuusan pituus.

# muistikolmio1x

# muistikolmio1y

# teht_muistikolmio2

2.3.2 Tehtävä

Määritä kulman $\alpha$ suuruus muistikolmioiden avulla ilman laskinta, kun $\alpha \in [0,90^{\circ}]$ .

# muistikolmio2a

# muistikolmio2b

# muistikolmio2c

# teht_K18T6

2.3.3 Tehtävä (K2018/6)

Suorakulmaisen kolmion toinen terävä kulma on astetta. Kolmion hypotenuusan keskipisteeseen piirretään kuvion mukaisesti kohtisuora jana, jonka toinen päätepiste sijaitsee kolmion kateetilla. Laske niiden kahden osan pituuksien suhde, joihin kohtisuora jakaa kateetin.

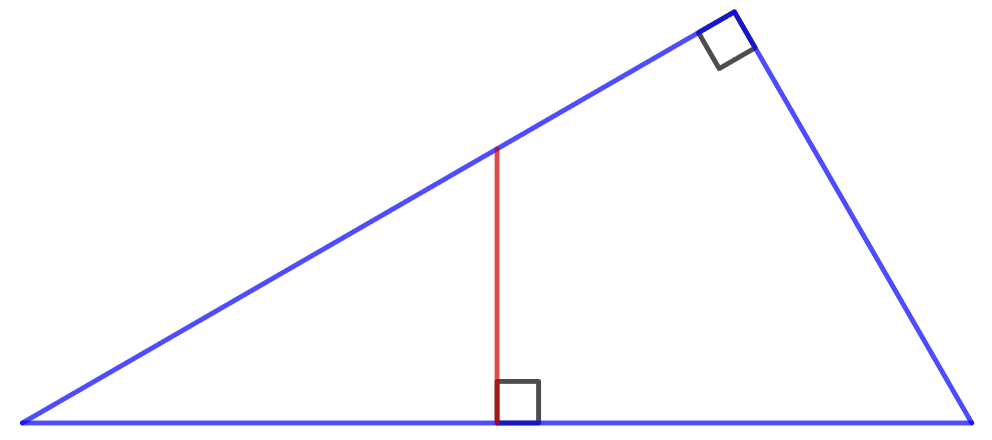
Anna vastaus murtolukuna ja ilmoita suhde suorasta kulmasta lähtien.

# K2018T10

# tylpat-kulmat-teht

2.4 Tylpän kulman sini ja kosini

Tämän kappaleen teoria on kappaleessa Tylpän kulman sini ja kosini.

# teht_tylppa_sini

2.4.1 Tehtävä

Laske ilman laskinta.

# tylppa1

# teht_tylppa_cos

2.4.2 Tehtävä

Laske ilman laskinta.

# tylppa2

# teht_tylpat_selitys

2.4.3 Tehtävä

Käytä alla olevaa GeoGebra-applettia ja määritä, mitä tehtävissä 2.4.4-2.4.7 tulee vastaukseksi.

# puoliympyra2

# sanallinen1a

# teht_tylpat1

2.4.4 Tehtävä

# tylppa3

# teht_tylpat2

2.4.5 Tehtävä

# tylppa4

# teht_tylpat3

2.4.6 Tehtävä

# tylppa5

# teht_tylpat4

2.4.7 Tehtävä

# tylppa6

# kolmion-ala-teht

2.5 Kolmion pinta-ala

Tämän kappaleen teoria on kappaleessa Kolmion pinta-ala.

# teht_kolmion_ala

2.5.1 Tehtävä

# kolmion_ala1

# teht_kolmion_korkeus

2.5.2 Tehtävä

# kolmion_ala2

# teht_kolmion_kanta

2.5.3 Tehtävä

# kolmion_ala3

# teht_kolmion_ala2

2.5.4 Tehtävä

MathCheck laskee kulmia aina radiaaneina. Jos haluat kirjoittaa sin(60°), sinun on kirjoitettava sen sijaan sin(60 * pi/180).

# kolmion_ala4

# teht_kolmion_ala3

2.5.5 Tehtävä

Kolmion kantasivun pituus on $2 \sqrt{2}$ ja kolmion korkeus on $\sqrt{2}$ . Laske kolmion pinta-ala.

# kolmion_ala

# teht_tasasivuinen_ala

2.5.6 Tehtävä

Tasasivuisen kolmion sivun pituus on 3. Mikä on kolmion pinta-ala?

# tasasivuisen_kolmion_ala

# teht_K13T4

2.5.7 Tehtävä (K2013/4)

Laske alla olevan kuvan suorakulmaisen kolmion ABC pinta-alan tarkka arvo.

# K2013T4

# kosinilause-teht

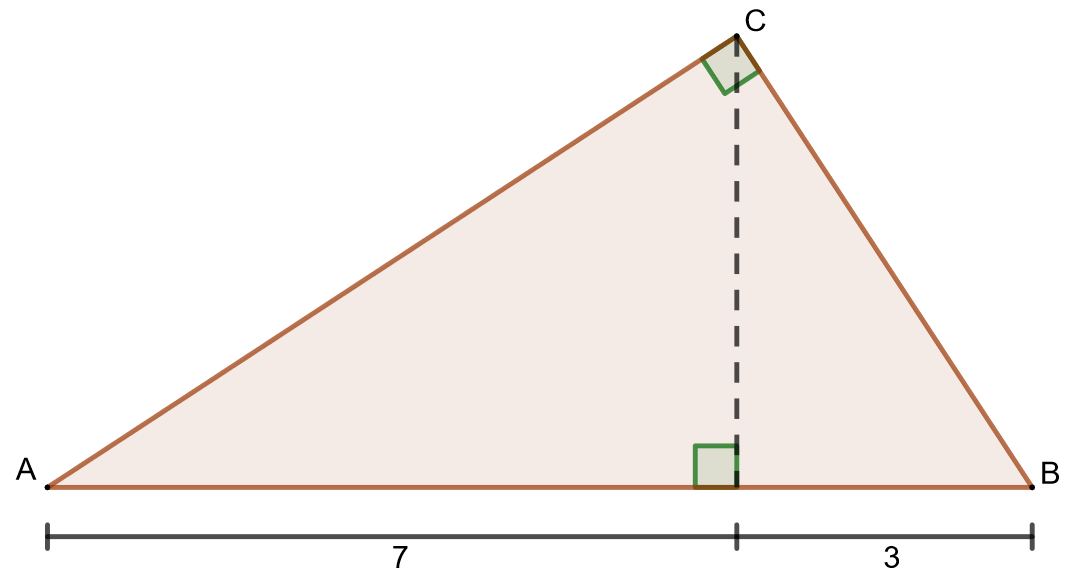
2.6 Kosinilause

Tämän kappaleen teoria on kappaleessa Kosinilause.

# teht_maanmittari

2.6.1 Tehtävä

Maanmittarin tehtävänä on määrittää pisteiden ja välimatka. Pisteiden välissä on vaara, joka kierretään pisteen kautta, josta on näköyhteys pisteisiin ja . Kuvassa olevat etäisyydet ovat metreinä.

# kosinilause1

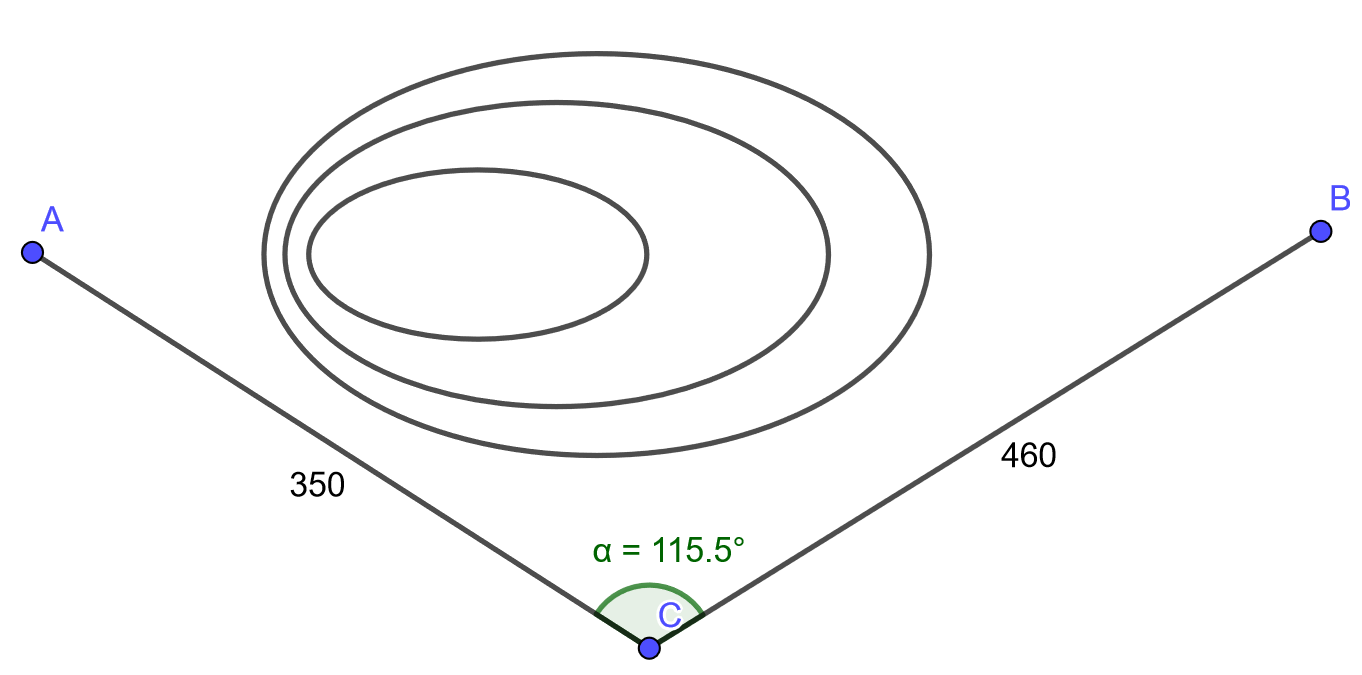
Kokeile myös luoda kuvan mukainen konstruktio (ilman mäen käyriä) GeoGebralla. Saatko selvitettyä pisteiden ja välisen etäisyyden ilman laskemista?

# teht_pelto

2.6.2 Tehtävä

Alla olevassa kuvassa on kolmion muotoinen pelto. Laske pellon pinta-ala hehtaareina. Anna vastaus yhden desimaalin tarkkudella ilman yksikköä ja muista käyttää desimaalipistettä.

# kosinilause2

# teht_S12T4b

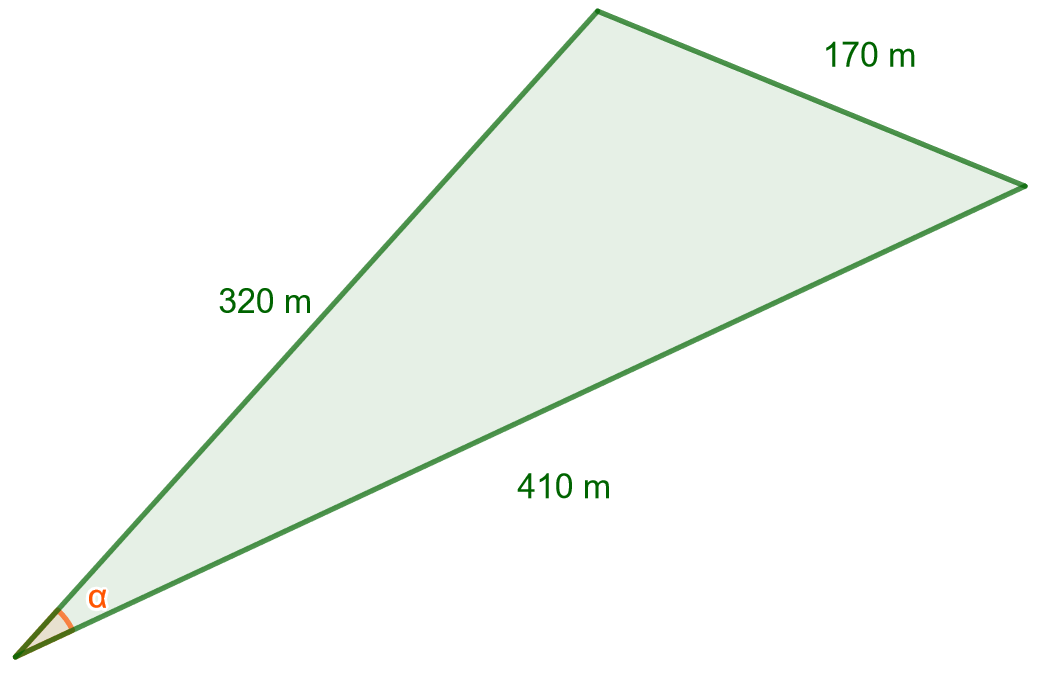
2.6.3 Tehtävä (S2012/4b)

Laske oheisessa kuvassa olevan kolmion sivun pituuden tarkka arvo ja kaksidesimaalinen likiarvo.

# kosinilause3a

# kosinilause3b

# teht_kalle_suunnistaa

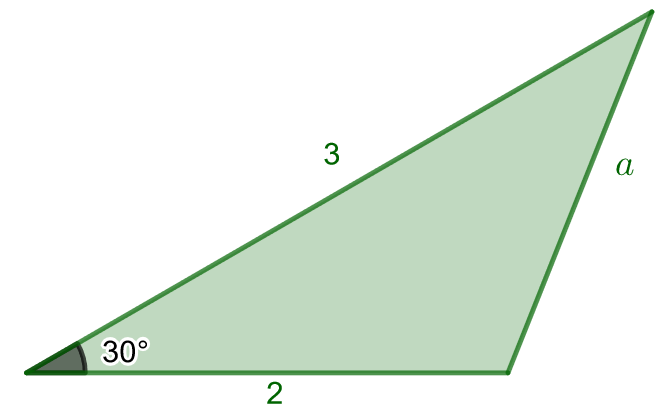
2.6.4 Tehtävä

Kalle kulkee kompassin kanssa ensin $1 \, 500 \text{ m}$ etelään ja sitten $1 \, 100 \text{ m}$ kaakkoon. Kuinka kaukana lähtöpaikastaan Kalle on? Piirrä ensin mallikuvio.

# kosinilause5

# sinilause-teht

2.7 Sinilause

Tämän kappaleen teoria on kappaleessa Sinilause.

# teht_sinilause1

2.7.1 Tehtävä

Kolmion sivun pituus on a=4 ja sen vastaisen kulman suuruus on $\alpha=62^{\circ}$ . Merkitään kolmion toista sivua kirjaimella ja sen vastaista kulmaa $\beta = 112^{\circ}$ . Ratkaise sivun pituus.

# sinilause2a

# teht_sinilause2

2.7.2 Tehtävä

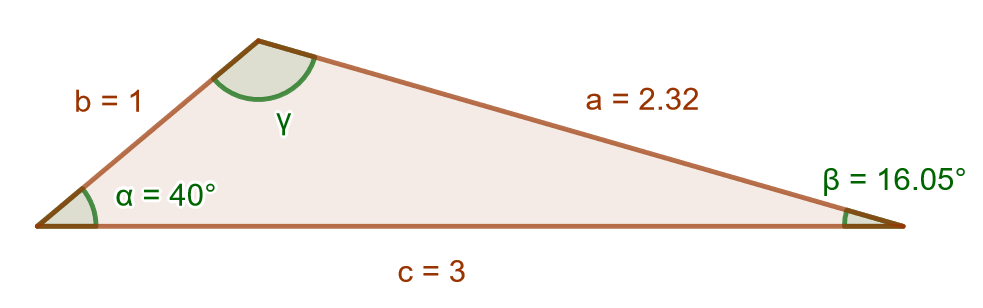
Ratkaise alla olevaan kuvaan merkitty tylppä kulma $\gamma$ .

# sinilause2

# teht_sinilause_kosinilause

2.7.3 Tehtävä

Ratkaise alla olevan kuvion sivun pituus. Anna vastaus kahden desimaalin tarkkuudella.

Vihje

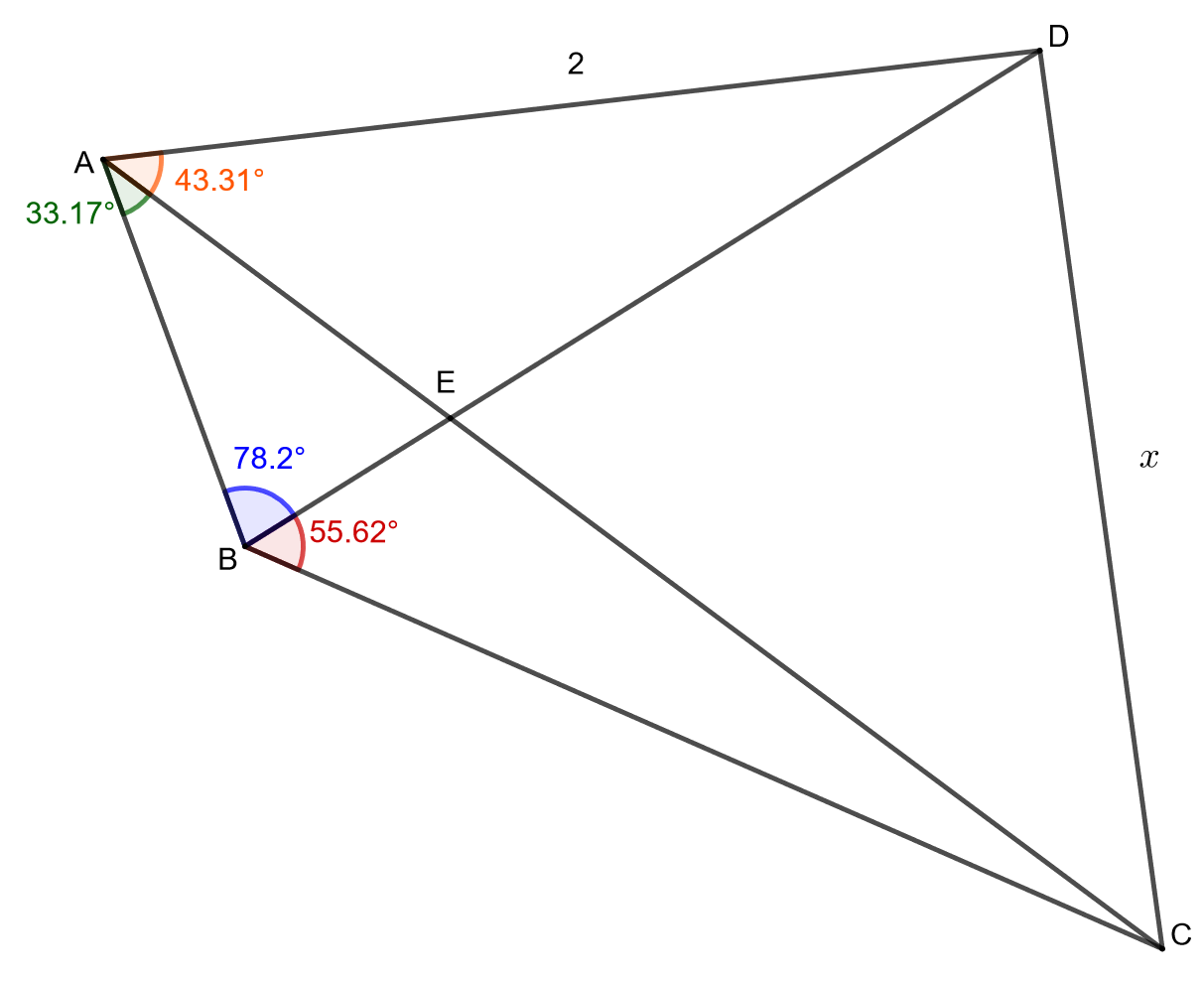
Päättele ensin pisteen E ympärillä olevat kulmat ja laske sinilauseen avulla sivujen , , ja pituudet. Sovella lopuksi kosinilausetta pituuden ratkaisemiseksi.

# sinilause3

# teht_kulmanpuolittajalause

2.7.4 Tehtävä

Ratkaise alla olevaan kuvaan merkityn janan pituus.

# kulmanpuolittajalause

# teht_S13T6

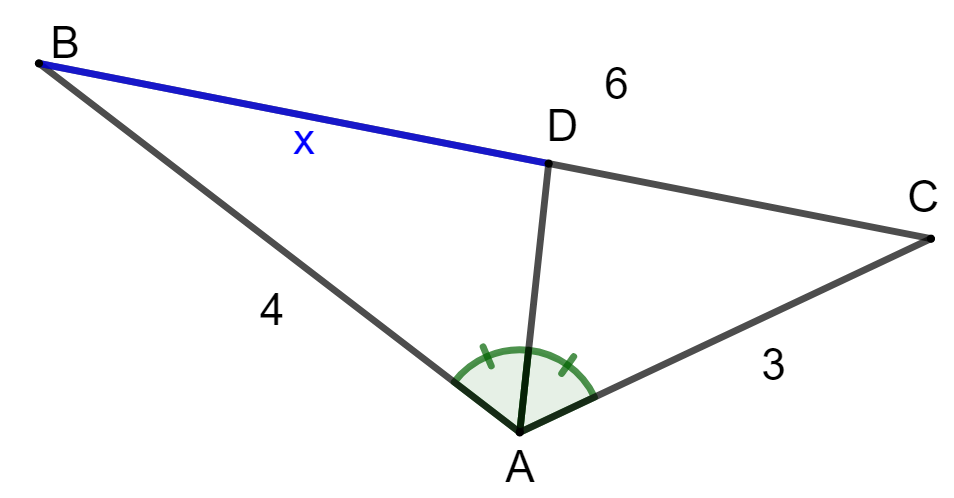
2.7.5 Tehtävä (S2013/6)

Kolmion ABC kulman puolittaja leikkaa sivun pisteessä . Pisteiden välisille etäisyyksille on voimassa CD=6 , AD=4 ja DB=3 . Määritä kolmion sivujen ja pituuksien tarkat arvot.

Vihje

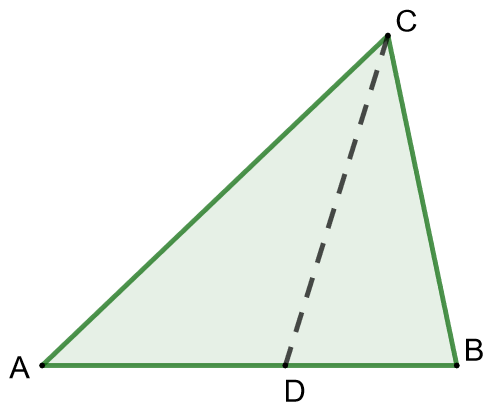
Käytä ensin kulmanpuolittajalausetta ja sen jälkeen kosinilausetta.

# kosinilause4ac

# kosinilause4bc

# teht_kolmion_sivun_pituus

2.7.6 Tehtävä

Kolmiosta ABC tiedetään seuraavaa. Sivun pituus on 4,8 , kulman suuruus on $70^{\circ}$ ja kulman suuruus $77 ^{\circ}$ . Piirrä tilanteesta mallikuvio ja laske sivun pituus. Anna vastaus yhden desimaalin tarkkuudella.

# sinilause4

# kaant-pythagoras-teht

2.8 Käänteinen Pythagoraan lause

Tämän kappaleen teoria on kappaleessa Käänteinen Pythagoraan lause.

# teht_onko_suorakulmainen1

2.8.1 Tehtävä

Kolmion sivujen pituudet ovat , ja . Onko kolmio suorakulmainen?

# kaantpyhtagoras2

# teht_onko_suorakulmainen2

2.8.2 Tehtävä

Kolmion sivujen pituudet ovat $3 \sqrt{2}$ , $4 \sqrt{2}$ ja $5 \sqrt{2}$ . Onko kolmio suorakulmainen?

# kaantpythagoras3

# teht_K17T12

2.8.3 Tehtävä (K2017/12)

Neliöiden N_1 , N_2 ja N_3 pinta-alojen suhde on 9:2:11 . Kolmion yhtenä sivuna on neliön N_1 sivu, toisena sivuna neliön N_2 sivu ja kolmantena sivuna neliön N_3 sivu. Laske kolmion ja neliön N_2 pinta-alojen suhteen tarkka arvo.

Vihje

Onko kolmio suorakulmainen?

# kaantpythagoras1

# merkilliset-pisteet-teht

2.9 Kolmion merkilliset pisteet

Tämän kappaleen teoria on kappaleessa Kolmion merkilliset pisteet.

# teht_suorakulmainen_puolittaja

2.9.1 Tehtävä

Kuinka suuressa kulmassa suorakulmaisen kolmion terävien kulmien puolittajat leikkaavat? Kokeile tehdä tehtävänannosta dynaaminen kuva GeoGebralla.

# merkilliset1

Voidaanko tulos yleistää myös muihin kolmioihin?

[H]

# teht_denny

2.9.2 Tehtävä

Seattlessa on alue, jota kutsutaan 'Denny triangle'ksi sen kolmiomaisen muodon vuoksi. Määritä piste, joka on yhtä kaukana jokaisesta Dennyn kolmion kärkipisteestä.

Kun olet määrittänyt pisteen, joka on yhtä kaukana kärkipisteitä, käytä Mittaa etäisyys -toimintoa ja mittaa pisteen etäisyys kaikista kärkipisteistä. Tehtävän pisteytys perustuu tähän etäisyyteen. Varmista siis, ettet siirrä valmiiksi annettuja punaisia pisteitä ja nimeät määrittämäsi pisteen F:ksi.

Vihje

Käytä keskinormaalilausetta.

# denny

# teht_poyta

2.9.3 Tehtävä

Alla on kuva kolmion muotoisesta pöydästä. Pöytä halutaan seisomaan vain yhden jalan varassa, jolloin jalka pitäisi sijoittaa pöytälevyn painopisteeseen. Määritä pöytälevyn painopiste alla olevalla GeoGebra-appletilla. Varmista, että nimeät painopisteen kirjaimella G.

# kolmio_poyta

2.10 Sekalaisia tehtäviä

Tässä kappaleessa on kaikkiin tämän luvun kappaleisiin liittyviä tehtäviä.

# teht_suunnistaja

2.10.1 Tehtävä

Lähtiessään rastilta suunnistaja tietää, että seuraavalle rastille on matkaa $600 \text{ m}$ , mutta ottaa kompassilla suunnan huolimattomasti ja lähtee kulkemaan $9 ^{\circ}$ väärään suuntaan. Kuinka kaukana suunnistaja on oikeasta rastista, kun hän on kulkenut $600 \text{ m}$ matkan?

# suunnistus

# teht_geogebra_kolmio

2.10.2 Tehtävä

Piirrä teräväkulmainen kolmio, jonka kahden sivun pituudet ovat ja ja näiden sivujen välinen kulma on $72^{\circ}$ . Määritä kolmion kolmannen sivun pituus. Tallenna sivun pituus muuttujaan nimeltä a.

# kolmion_sivu

# teht_S16T5

2.10.3 Tehtävä (S2016/5)

Kolmion kulmat muodostavat aritmeettisen jonon, ja yhden kulman suuruus on $103^{\circ}$ . Määritä kulmien suuruudet asteina.

# kulmajono1

Kolmion kulmat muodostavat geometrisen jonon, ja yhden kulman suuruus on $\frac{\pi}{7}$ radiaania. Määritä kulmien suuruudet radiaaneina.

# kulmajono2

# kulmajono3

# teht_kolmioilla_sama_ala

2.10.4 Tehtävä

Alla olevassa kuvassa ABCD ja AEFG ovat neliöitä. Osoita, että kolmioilla ABG ja ADE on sama pinta-ala. [H]

Ratkaisu

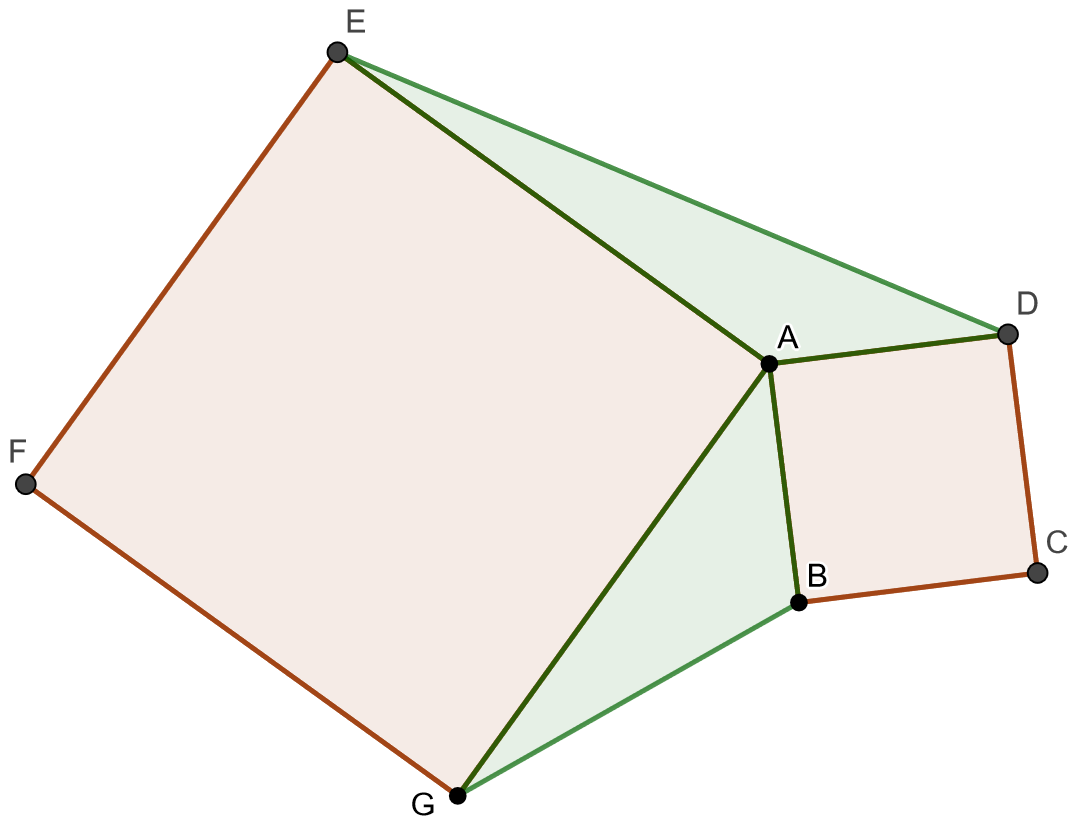
Merkitään |AB|=a ja |AG|=b . Lisäksi merkitään $\angle GAB=\alpha$ . Nyt alemman kolmion pinta-ala on $A_1=\frac{1}{2}ab \sin(\alpha)$ . Merkitään $\angle DAE=\beta$ . Tiedetään, että $\beta=180^{\circ}-\alpha$ . Nyt toisen kolmion pinta-ala on $A_2=\frac{1}{2}ab \sin(\beta) = \frac{1}{2}ab \sin(180^{\circ}-\alpha)$ . Tylpän kulman sinistä tiedetään $\sin(180^{\circ}-\alpha)=\sin(\alpha)$ . Joten $A_2=\frac{1}{2}ab \sin(\alpha)=A_1$ eli kolmioiden pinta-alat ovat samat.

# teht_hoikka_kolmio

2.10.5 Tehtävä

Alla olevassa kuvassa on neljä neliötä, ja vasemmassa alakulmassa olevan neliön pinta-ala on . Mikä on tummanvihreän kolmion pinta-ala? [H]

# hoikkakolmio_geo

Vihje

Kahden kolmion pinta-alat ovat samoja, jos niiden kannat ovat yhtä pitkät ja niiden korkeudet ovat yhtä pitkät. Paina "Näytä korkeusjanaa" -nappia, jolloin voit siirtää tummanvihreän kolmion kärkipistettä.

# hoikkakolmio_ratk

# teht_S15T15

2.10.6 Tehtävä (S2015/15)

Kolmion kahden sivun pituudet ovat CA=a ja CB=b . Näiden sivujen välisen kulman puolittajasta kolmion sisälle jäävän osan pituus on . Puolittaja jakaa kolmannen sivun kahteen osaan, joiden pituudet ovat AD=x ja DB=y . Osoita, että $k=\sqrt{ab-xy}$ ,

kun .
kun $a \neq b$ .

Ratkaisu

Jos , niin kolmio on tasakylkinen ja tällöin myös . Pythagoraan mukaan . Kun tässä toinen korvataan :llä ja toinen korvataan :llä, saadaan , josta väite seuraa.

Olkoon kulman puolikas $\varphi$ . Kosinilauseesta ja kulmanpuolittajalauseesta saadaan ehdot $\left\{ \begin{array}{rcl} x^2 &=& a^2+k^2-2ak \cos \varphi \\ y^2 &=& b^2+k^2-2bk \cos \varphi \\ \frac{x}{y} &=& \frac{a}{b} \end{array} \right.$

Ratkaistaan kahdesta ensimmäisestä yhtälöstä $2 k \cos \varphi$ ja merkitään tulokset samoiksi: $2k \cos \varphi=\frac{a^2+k^2-x^2}{a}=\frac{b^2+k^2-y^2}{b}.$ Kerrotaan puolittain :lla: $\frac{a}{b}(b^2+k^2-y^2)=a^2+k^2-x^2.$

Korvataan $\frac{a}{b} \rightarrow \frac{x}{y}$ ja kerrotaan puolittain :llä xb^2+xk^2-xy^2=ya^2+yk^2-yx^2. Ratkaistaan k^2 : $k^2=\frac{ya^2-yx^2+y^2x-xb^2}{x-y}.$

Sijoitetaan ya=bx : $k^2=\frac{abx-x^2y-aby+xy^2}{x-y}$ ja ryhmitellään $k^2=\frac{abx-aby-x^2y+xy^2}{x-y}=\frac{ab(x-y)-xy(x-y)}{x-y}=ab-xy,$ josta väite seuraa. Ratkaisu edellyttää, että $x-y \neq 0$ , mutta ehto on voimassa, koska oletettiin, että $a \neq b$ , jolloin myös $x \neq y$ .

# teht_napoleon

2.10.7 Tehtävä

Piirrä GeoGebralla Napoleonin lausetta vastaava konstruktio alla olevia ohjeita seuraamalla.

Valitse GeoGebran Monikulmio-työkalu (klikkaa LISÄÄ, jos ei ole näkyvissä työkaluissa) ja piirrä jonkin muotoinen kolmio k1.
Valitse GeoGebran Säännöllinen monikulmio -työkalu, ja piirrä tasasivuiset kolmiot kolmion k1 jokaiselle sivulle (kuvio1, kuvio2 ja kuvio3). Tämä tapahtuu valitsemalla kolmion k1 kaksi kärkipistettä ja syöttämällä kulmien lukumääräksi 3.
- Huomaa, että tasasivuisten kolmioiden tulee olla kolmion k1 ulkopuolella. Jos kolmiot syntyvät alkuperäisen kolmion k1 päälle, kokeile valita kärkipisteet eri järjestyksessä.
Valitse Keskipiste-työkalu ja luo jokaiselle kolmiolle kuvio1, kuvio2 ja kuvio3 keskipiste napsauttamalla kyseistä kolmiota.
Yhdistä äsken luodut keskipisteet käyttämällä Monikulmio-työkalua, jolloin syntyy kolmio k2.
Mittaa kolmion k2 kulmien suuruudet. Helpoiten tämä käy, kun valitset Kulma-työkalun ja napsautat kolmiota k2, jolloin GeoGebra mittaa kolmion k2 kaikkien sisäkulmien (α, β ja γ) suuruudet samalla kertaa.
Kokeile siirtää alkuperäisen kolmion k1 kärkipisteitä. Mitä huomaat?
Halutessasi voit muokata kolmioiden ja pisteiden värejä ja nimien näkyvyyttä.

# napoleon3