Tämä materiaali on tehty Tampereen yliopiston koordinoimassa hankkeessa “Matemaattisten aineiden verkkokurssit lukioon ja ammatilliseen koulutukseen”. Hankkeen ideana on toteuttaa kaikille avoimia verkkomateriaaleja toisen asteen koulutukseen. Hankkeen on rahoittanut Opetushallitus.

Materiaali sisältää lukion matematiikan MAA3 Geometria -kurssin teoriasisällön. Kirja on tehty noudattaen vuonna 2021 käyttöön otettavan lukion opetussuunnitelman perusteiden luonnosta. Kirja kokonaisuudessaan löytyy osoitteesta:

https://tim.jyu.fi/view/tau/toisen-asteen-materiaalit/matematiikka/geometria/maa3

Materiaali on tuotettu lisenssillä CC BY-SA 4.0.

# kuvioiden_yhdenmuotoisuus

1. Kuvioiden yhdenmuotoisuus

Tässä kappaleessa käsitellään kuvioiden ja kappaleiden yhdenmuotoisuutta. Lisäksi puhutaan mittakaavasta eli yhdenmuotoisuussuhteesta. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

# yhdenmuotoisuus

1.1 Yhdenmuotoisuus

Kaksi kuviota on yhdenmuotoisia, kun toinen kuvio saadaan siirtämällä, kiertämällä, peilaamalla, suurentamalla tai pienentämällä kuvio.

Matikkamatskujen video yhdenmuotoisuudesta

Yhdenmuotoisuus

Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat samat riippumatta siitä, mitä sivuja tarkastellaan. Yhdenmuotoisissa kuvioissa vastinkulmat ovat aina yhtä suuret.

1.1.1 Esimerkki: yhdenmuotoiset kuviot GeoGebralla

# yhdenmuotoisuus-geo

Yllä olevassa GeoGebra-appletissa oranssi nelikulmio on ns. vertailukuvio, joka pysyy koko ajan samana. Sen sijaan vihreää nelikulmiota pystyy muokkaamaan.

Kierrä vihreää nelikulmiota vetämällä “kierto”-liukusäädintä ja huomaa, että vihreä nelikulmio on silti yhdenmuotoinen oranssin nelikulmion kanssa.

Muuta seuraavaksi vihreän nelikulmion kokoa raahaamalla “koko”-liukusäädintä. Huomaa, että vihreän nelikulmion kulmien suuruudet pysyvät samoina kuin oranssissa nelikulmiossa, vaikka viheän nelikulmion koko muuttuisi.

Siirrä vihreää nelikulmiota eri suuntiin raahaamalla “siirto”-liukusäädintä. Vihreän nelikulmion muoto pysyy samana, vaikka se olisi eri paikassa. Se on siis edelleen yhdenmuotoinen oranssin nelikulmion kanssa.

Lopuksi lisää valinta kohtaan “peilaus”, jolloin vihreä nelikulmio peilataan pystysuoran akselin suhteen. Huomaa jälleen, että nelikulmioiden vastinkulmat pysyvät yhtä suurina, vaikka vihreä nelikulmio peilataan.

Näiden kohtien perusteella voidaan todeta, että jos kuviota kiertää, siirtää, peilaa tai sen kokoa muuttaa joka suunnassa, kuvio säilyy yhdenmuotoisena alkuperäisen kuvion kanssa.

Kokeile lopuksi muuttaa oranssin nelikulmion kärkipisteiden paikkoja raahamalla sinisiä kärkipisteitä eri paikkoihin. Huomaa, että vihreä ja oranssi nelikulmio pysyvät koko ajan yhdenmuotoisina.

Tähän kappaleeseen liittyvät tehtävät.

# mittakaava

1.2 Mittakaava eli yhdenmuotoisuussuhde

Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat siis vakioita. Vastinsivut määritellään vastinpisteiden avulla. Alla olevassa kuvassa vastinpisteitä ovat ja , ja sekä ja . Näiden avulla voidaan määrittää vastisivut: ja , ja sekä ja . Lasketaan jokaisen vastisivuparin suhde, ja huomataan, että se on jokaisen vastinsivuparin tapauksessa 1,5 .

Tätä suhdetta kutsutaan yhdenmuotoisuussuhteeksi ja se määritellään alla.

Yhdenmuotoisuussuhde eli mittakaava

Jos kuviot ovat yhdenmuotoiset, yhdenmuotoisuussuhde tarkoittaa suhdetta $\frac{s_1}{s_2},$ missä s_1 on sivun pituus ensimmäisessä kuviossa ja s_2 sitä vastaavan sivun pituus toisessa kuviossa.

1.2.1 Esimerkki: yhdenmuotoisuussuhde GeoGebralla

# yhdenmuotoisuussuhde-geo

Yllä olevassa GeoGebra-appletissa on korostettu vastinpisteet ja vastinsivut samoilla väreillä. Lisäksi vasemmalla olevassa CAS-ikkunassa on laskettu kunkin vastinsivuparin suhde.

Kokeile siitää kolmioiden ABC ja DEF kärkipisteitä ja huomaa, että vastinsivujen suhteet pysyvät koko ajan samoina. Tuota suhdetta kutsutaan siis mittakaavaksi tai yhdenmuotoisuussuhteeksi.

Tähän kappaleeseen liittyvät tehtävät.

# kolmiot

1.3 Kolmiot

Kolmioiden yhdenmuotoisuudesta voit lukea myös M niinkuin matematiikka -teoksesta, joka on lukiotason matematiikan tietosanakirja.

Kolmiot ovat yhdenmuotoisia, jos niillä on kaksi yhtä suurta kulmaa. Kahdesta yhtä suuresta kulmastahan seuraa myös, että kolmioiden kolmas kulma on yhtä suuri.

Kolmioiden yhdenmuotoisuuslause KK Matikkamatskuissa

Kolmioiden yhdenmuotoisuuslause KK

Jos kolmion kaksi kulmaa ovat yhtä suuria kuin vastinkulmat toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.

1.3.1 Esimerkki: yhdenmuotoiset kolmiot GeoGebralla

# kk-geo

Kun siirrät yllä olevassa GeoGebra-appletissa kolmion ABC kärkipisteitä, huomaat, että kolmio DEF muuttuu samalla. Voit muuttaa kolmion DEF kokoa raahamalla pistettä E ja siirtää sitä raahaamalla pistettä D.

Koska kolmioiden vastinkulmat ovat koko ajan yhtä suuret, ovat kolmiot yhdenmuotoisia. Riittää, että kolmioissa on kaksi yhtä suurta vastinkulmaa, koska tällöin kolmioiden kolmannetkin vastinkulmat ovat välttämättä yhtä suuria.

1.3.2 Esimerkki: kolmion sivu KK-lauseella

Määritä alla olevan kuvion janan pituus, joka on merkitty kuvioon kirjaimella . Janat ja ovat yhdensuuntaisia.

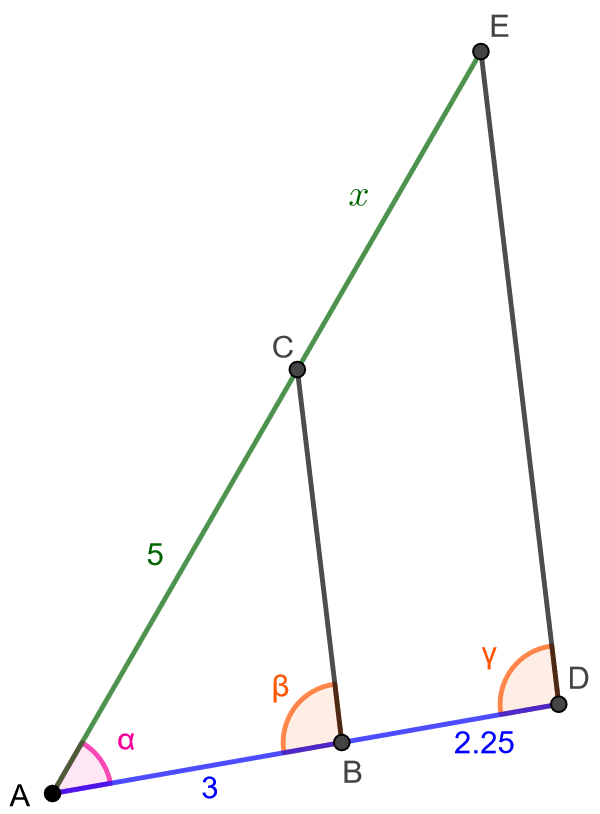
Huomataan, että kuviossa on oikeastaan kaksi päällekkäistä kolmiota: ABC ja ADE . Kolmioilla on yksi yhteinen kulma $\alpha$ joka on siis molemmissa kolmioissa yhtä suuri. Tarkastellaan seuraavaksi kulmia $\beta$ ja $\gamma$ . Koska janat ja ovat yhdensuuntaisia, ja jana on molempien kulmien vasempana kylkenä, kulmat $\beta$ ja $\gamma$ ovat samankohtaisia. Tämä tarkoittaa, että kulmat $\beta$ ja $\gamma$ ovat yhtä suuria. Koska kolmioissa ABC ja ADE on kaksi yhtä suurta vastinkulmaparia, voidaan yhdenmuotoisuuslauseen KK perusteella sanoa, että kolmiot ABC ja ADE ovat yhdenmuotoiset.

Koska kolmiot ovat yhdenmuotoisia, sivun pituuden määittämiseen voidaan käyttää yhdenmuotoisuussuhdetta. Vastinsivuparit ovat nyt ja sekä ja . Näiden parien suhteet ovat yhtä suuret, joten saadaan yhtälö $\frac{AD}{AB}=\frac{AE}{AC},$ johon sijoitetaan kunkin sivun pituus: $\frac{3+2,25}{3}=\frac{5+x}{5}.$ Sievennetään yhtälöä, kerrotaan se ristiin ja ratkaistaan siitä : $\begin{aligned} \frac{5,25}{3} &= \frac{5+x}{5}& \quad &| \text{ kerrotaan ristiin} \\ 5,25 \cdot 5 &= 3 \cdot (5+x)& \quad &| \text{ sievennetään} \\ 26,25 &= 15 + 3x& \quad &| -15 \\ 11,25 &= 3x &\quad &| :3 \\ 3,75 &= x & \quad &| \text{ vaihdetaan yhtälön puolia} \\ x & = 3,75 \end{aligned}$

Vastaukseksi saadaan, että janan pituus on 3,75 .

Jos kolmion kulmien suuruuksia ei tiedetä, voidaan kolmioiden yhdenmuotoisuus päätellä myös niiden sivujen pituuksien avulla. Kuten aiemmin olet opiskellut, yhdenmuotoisissa kuvioissa niiden vastinsivujen suhteet ovat vakioita. Tätä ominaisuutta käytetään hyväksi yhdenmuotoisuuslauseessa SSS.

Kolmioiden yhdenmuotoisuuslause SSS

Jos kolmion kaikki sivut ovat verrannolliset vastinsivuihin toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.

1.3.3 Esimerkki: kulman suuruus SSS-lauseella

Määritä kuvaan merkityn kulman $\beta$ suuruus.

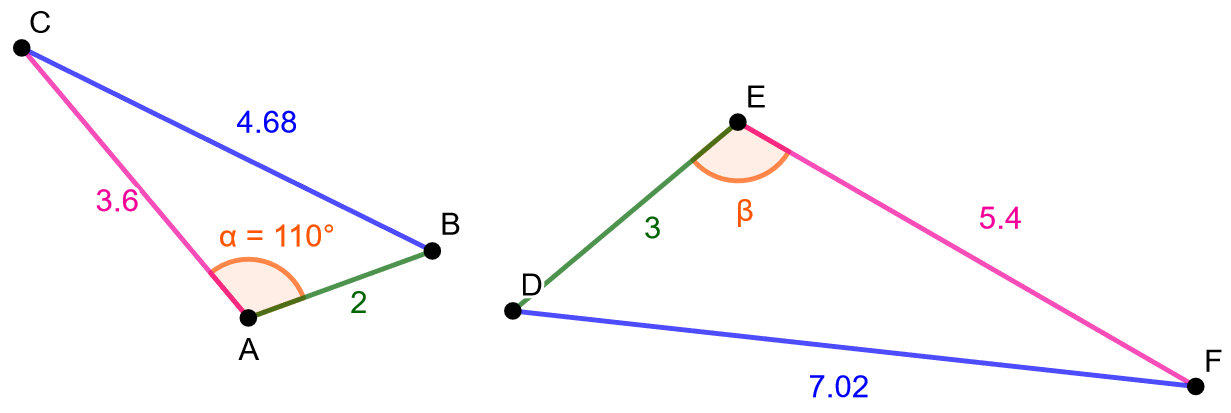
Tutkitaan ensin, ovatko kolmiot yhdenmuotoisia. Koska molemmista kolmioista on tiedossa vain sivujen pituuksia, lasketaan kunkin vastinsivuparin suhde. Jos suhteet ovat samoja, voidaan käyttää kolmioiden yhdenmuotoisuuslausetta SSS. Sinisellä merkittyjen vastinsivujen suhde on $\frac{7,02}{4,68}=1,5.$ Pinkillä merkittyjen vastinsivujen suhde on $\frac{5,4}{3,6}=1,5.$ Vihreällä merkittyjen vastinsivujen suhde on $\frac{3}{2}=1,5.$ Koska kaikkien vastisivuparien suhteet ovat samoja, yhdenmuotoisuuslauseen SSS mukaan kolmiot ovat yhdenmuotoisia. Koska kulmat $\alpha$ ja $\beta$ ovat vastinkulmia, ne ovat yhtä suuret. Kulma $\beta$ on siis $110^{\circ}$ .

Jos kahdesta kolmiosta tiedetään, että vain kaksi vastinsivua on verrannollisia keskenään, ei vielä voida päätellä, ovatko kolmiot yhdenmuotoisia. Jos lisäksi tiedetään vielä, että kahden verrannollisen vastinsivun välissä olevat kulmat ovat molemmissa kolmioissa yhtä suuret, voidaan sanoa, että kolmiot ovat yhdenmuotoisia.

Kolmioiden yhdenmuotoisuuslause SKS

Jos kolmion kaksi sivua ovat verrannolliset vastinsivuihin toisessa kolmiossa ja niiden välinen kulma on yhtä suuri kuin vastinkulma toisessa kolmiossa, niin kolmiot ovat yhdenmuotoiset.

1.3.4 Esimerkki: kolmion sivu SKS-lauseella

Määritä alla olevan kuvion sivun pituus, joka on merkitty kuvaan kirjaimella .

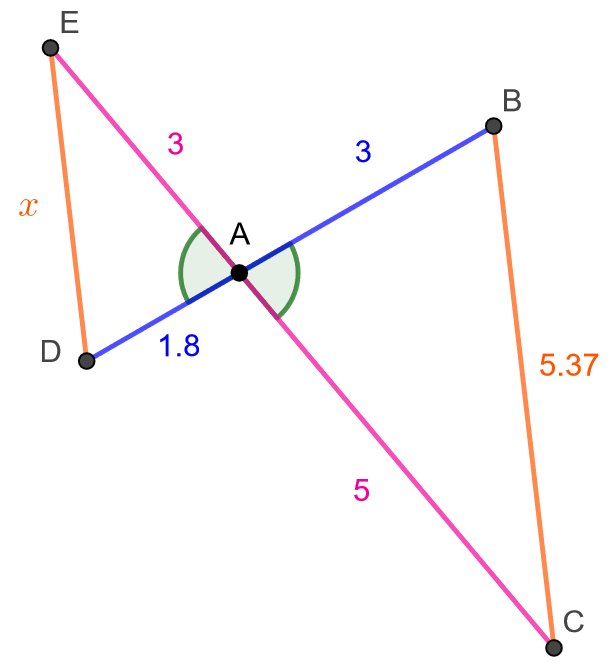
Sivun pituus saadaan helpoiten määritettyä, jos tiedetään, että kuviossa olevat kolmiot ABC ja ADE ovat yhdenmuotoiset. Kuvioon merkityt kulmat $\angle EAD$ ja $\angle CAB$ ovat toistensa ristikulmia ja siten yhtä suuria. Sinisellä mekittyjen vastinsivujen suhde on $\frac{1,8}{3}=0,6$ ja pinkillä merkittyjen vastinsivujen suhde on $\frac{3}{5}=0,6.$ Koska kahden vastinsivun suhteet ovat samat ja lisäksi näiden sivujen välinen kulma on kummassakin kolmiossa yhtä suuri, kolmiot ovat yhdenmuotoiset kolmioiden yhdenmuotoisuuslauseen SSS mukaan.

Oranssilla merkittyjen vastinsivujen suhteen tulee olla sama kuin muidenkin sivujen suhteet, joten saadaan seuraava yhtälö, joka ratkaistaan $\begin{aligned} \frac{x}{5,37}&=0,6 &\quad &|\cdot 5,37 \\ x &= 5,37 \cdot 0,6 &\quad &| \text{ sievennetään} \\ x &= 3,222 & \quad &| \text{ pyöristetään kahden desimaalin tarkkuudelle} \\ x &\approx 3,22 \end{aligned}$

Kuvion sivun pituus on noin 3,22 .

1.3.5 Esimerkki: yhdenmuotoisten kolmioiden piirtäminen GeoGebralla

# yhdenmuotoisten-kolmioiden-piirto

Yllä olevassa GeoGebra-appletissa on esimerkki siitä, kuinka voit muodostaa yhdenmuotoiset dynaamiset kolmiot GeoGebralla. Raahaa liukusäädintä ja lue ohjeet. Harjoittele piirtämistä itse tyhjässä GeoGebra-ikkunassa.

Tähän kappaleeseen liittyvät tehtävät.

# pinta-ala

1.4 Pinta-ala

Aiemmin tarkastelit vain kuvioiden vastinkulmien suuruuksia (jotka olivat samoja) sekä vastisivujen pituuksien suhteita (jotka pysyivät vakioina riippumatta siitä mitä sivupareja tarkasteltiin). Yhdenmuotoisuuden avulla voidaan päätellä lisäksi myös kuvioiden pinta-aloihin liittyviä suhteita.

Yhdenmuotoisten kuvioiden alojen suhde Matikkamatskuissa

Yhdenmuotoisten kuvioiden pinta-alalause

Jos kuviot ovat yhdenmuotoiset yhdenmuotoisuussuhteessa s_1 : s_2 , niiden pinta-alojen suhde on $\frac{A_1}{A_2} =\left(\frac{s_1}{s_2}\right)^2.$

1.4.1 Esimerkki: pinta-alojen suhde GeoGebralla

# pinta-alat-geo

Tutki yllä olevaa GeoGebra-applettia siirtämällä suorakulmion ABCD kärkipisteitä sekä raahaamalla yhdenmuotoisuussuhde-liukusäädintä. Vasemmalla olevaan CAS-ikkunaan lasketaan vastinsivujen ja sekä ja väliset suhteet sekä suorakulmioiden pinta-alojen ja välinen suhde. Lisäksi lasketaan yhdenmuotoisuussuhteen neliön lukuarvo. Huomaa, että pinta-alojen suhde ja yhdenmuotoisuussuhteen neliö ovat koko ajan yhtä suuria.

1.4.2 Esimerkki: pinta-alan laskeminen

Laske alla olevan kuvan isomman tähden pinta-ala, kun tiedetään, että tähdet ovat yhdenmuotoiset.

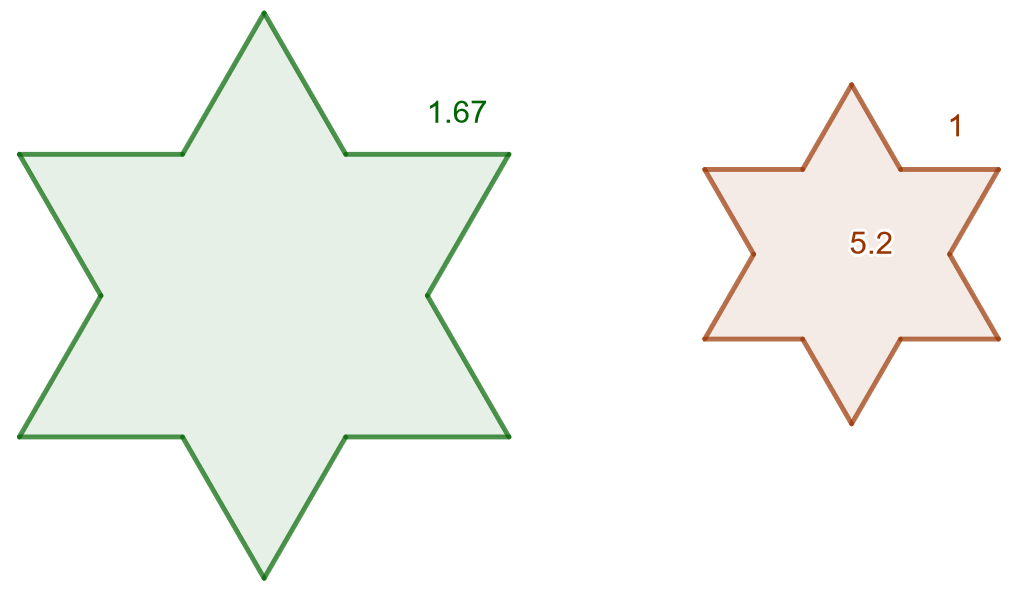
Koska kuviot ovat yhdenmuotoisia, voidaan käyttää yhdenmuotoisten kuvioiden pinta-alalausetta. Kuvioiden yhdenmuotoisuussuhde on $\frac{1,67}{1}=1,67.$ Merkitään kysyttyä isomman tähden pinta-alaa kirjaimella . Tehdään verranto yhdenmuotoisten kuvioiden pinta-alalauseen avulla ja ratkaistaan siitä : $\begin{aligned} \frac{x}{5,2}&=1,67^2 &\quad &| \cdot 5,2 \\ x &= 5,2 \cdot 1,67^2 &\quad &| \text{ sievennetään lauseke} \\ x &= 14,50228 &\quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x & \approx 14,5 \end{aligned}$ Isomman tähden pinta-ala on noin 14,5 .

Tähän kappaleeseen liittyvät tehtävät.

# tilavuus

1.5 Tilavuus

Samoin kuin aiemmin pinta-alan suhteen, yhdenmuotoisuus auttaa päättelemään jotakin myös kappaleiden tilavuuksista. Pinta-alan kohdalla yhdenmuotoisuussuhde korotettiin toiseen potenssiin, mutta tilavuuden kohdalla yhdenmuotoisuussuhde koroteteaankin kolmanteen potenssiin.

Yhdenmuotoisten kappaleiden tilavuuksien suhde Matikkamatskuissa

Yhdenmuotoisten kappaleiden tilavuuslause

Jos kappaleet ovat yhdenmuotoiset yhdenmuotoisuussuhteessa s_1 : s_2 , niiden tilavuuksien suhde on $\frac{V_1}{V_2} =\left(\frac{s_1}{s_2}\right)^3.$

1.5.1 Esimerkki: tilavuuksien suhde GeoGebralla

# tilavuudet-geo

Yllä olevassa GeoGebra-appletissa voit tutkia yhdenmuotoisten kappaleiden tilavuuksien suhteita. Raahaa liukusäädintä, joka kuvaa yhdenmuotoisuussuhdetta. Kokeile myös raahata punaisen särmiön sinisiä kärkipisteitä ja tutki, miten kappaleet ja tilavuuksien suhde muuttuvat. Kuviot ovat koko ajan yhdenmuotoisia, joten tilavuuksien suhde ja särmien kuutioiden suhde pysyvät koko ajan samoina.

Tähän kappaleeseen liittyvät tehtävät.

# kolmioiden_geometriaa

2. Kolmioiden geometriaa

Tässä kappaleessa käsitellään kolmioiden geometriaa, mikä tarkoittaa esimerkiksi kolmion pinta-alan laskemista sekä sen sivujen pituuksien ja kulmien suuruuksien ratkaisua erilaisten lauseiden avulla. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

# pythagoras

2.1 Suorakulmainen kolmio, Pythagoraan lause

Suorakulmainen kolmio on sellainen kolmio, jonka yksi kulma on suorakulma eli $90^{\circ}$ . Suoran kulman kylkinä olevia sivuja kutsutaan kateeteiksi ja suoran kulman vastaista sivua hypotenuusaksi.

Suorakulmaiseen kolmioon liittyy oleellisesti Pythagoraan lause, jonka mukaan suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin kolmion hypotenuusan neliö. Jos siis tiedetään kolmion kahden sivun pituudet, voidaan kolmannen sivun pituus ratkaista. Voit lukea lisää Pythagoaan lauseen historiasta.

Pythagoraan lause Matikkamatskuissa

Pythagoraan lause

Suorakulmaisen kolmion kateettien ja neliöiden summa on yhtä suuri kuin sen hypotenuusan neliö, eli a^2+b^2=c^2.

2.1.1 Esimerkki: suorakulmainen kolmio GeoGebralla.

# suorakulmainen-kolmio-geo

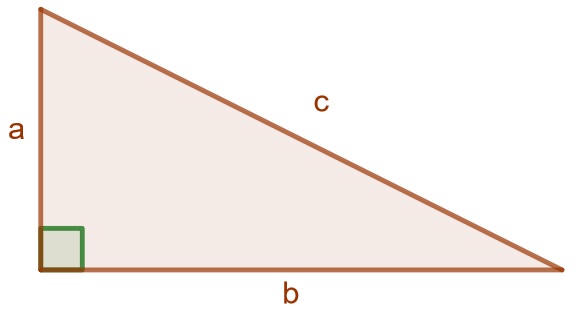
Siirrä kolmion kärkipisteitä ja huomaa, että kolmio säilyy koko ajan suorakulmaisena. Välillä kateettien neliöiden summa voi GeoGebran mukaan olla hieman eri kuin hypotenuusan neliö. Tämä johtuu siitä, että GeoGebra toteuttaa kaikki laskelmansa numeerisesti ja pyöristäen, joten pieniä virheitä saattaa esiintyä.

2.1.2 Todistus

# pythagoras-todistus-geo

Kaikki kuviossa esiintyvät oranssit kolmiot ovat suorakulmaisia, sillä ne ovat neliön sisällä, ja neliön kaikki kulmat ovat $90^{\circ}$ . Kolmiot ovat samanlaisia, sillä jokaisen kolmion kateetit ovat pituuksiltaan ja , ja jokaisen kolmion hypotenuusan pituus on .

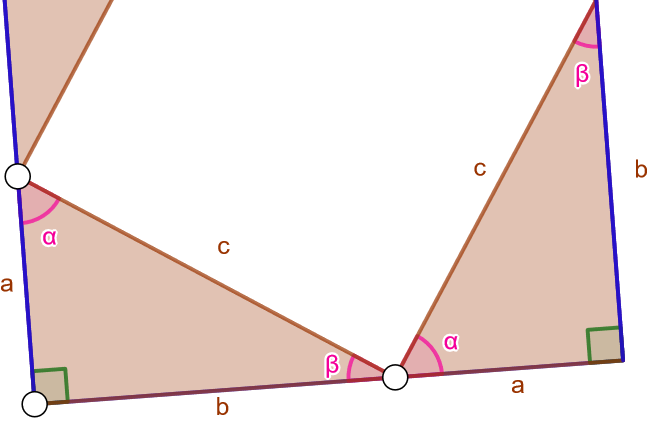
Entä onko alkutilanteessa kolmioiden keskelle jäävä valkoinen alue neliö? Olkoon suorakulmaisen kolmion kulmat $\alpha$ ja $\beta$ kuten alla olevassa kuvassa. Kolmion kulmien summa on $180^{\circ}$ , joten saadaan seuraavat yhtälöt: $\begin{aligned} \alpha + \beta + 90^{\circ} &= 180^{\circ} \quad |-90^{\circ} \\ \alpha + \beta &= 90^{\circ}. \end{aligned}$ Kuvion alareunassa kulmat $\alpha$ , $\beta$ ja keskellä olevan valkoisen alueen muodostama kulma muodostavat oikokulman eli ovat yhteensä $180^{\circ}$ . Koska tiedetään, että $\alpha + \beta = 90^{\circ}$ , on valkoisen alueen muodostaman kulman oltava $90^{\circ}$ eli suora kulma. Koska kolmiot ovat samanlaisia, ovat myös valkoisen alueen muodostamat kulmat yhtä suuria, joten valkoinen alue on neliö.

Alkutilanteessa valkoisen neliön pinta-ala on c^2 . Kun liukusäädin vedetään aivan oikeaan laitaan, kolmiot siirtyvät eri paikoille. Koska ne eivät mene päällekkäin, on valkoisen alueen pinta-ala nyt yhtä suuri kuin alussa. Nyt valkoinen alue muodostuu kahdesta pienestä neliöstä, joiden yhteenlaskettu pinta-ala on a^2+b^2 . Voidaan siis sanoa, että a^2+b^2=c^2 .

Tähän kappaleeseen liittyvät tehtävät.

# trig

2.2 Trigonometriset funktiot

Suorakulmaisen kolmion terävien kulmien suuruudet voidaan ratkaista, jos tiedetään kolmion kateettien tai kateetin ja hypotenuusan pituudet. Tämä on mahdollista, sillä kolmion sivujen suhteet ovat tietyillä kulmilla aina vakioita. Näitä suhteita kutsutaan trigonometrisiksi funktioiksi.

Trigonometriset funktiot Matikkamatskuissa

Suorakulmaisen kolmion sini, kosini ja tangentti

Suorakulmaisessa kolmiossa kulman $\alpha$ sini, kosini ja tangentti tarkoittavat seuraavia suhteita: $\sin(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{hypotenuusa}}=\frac{a}{c}$ $\cos(\alpha)=\frac{\text{kulman viereinen kateetti}}{\text{hypotenuusa}}=\frac{b}{c}$ $\tan(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{kulman viereinen kateetti}}=\frac{a}{b}$

2.2.1 Esimerkki: trigonometrisia funktioita GeoGebralla

# trig-geo

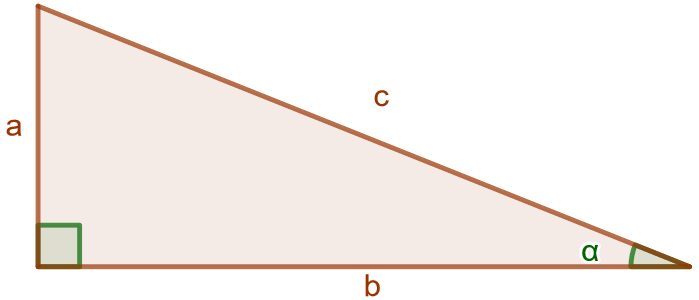
Kokeile laskea eri kulmien sini, kosini ja tangentti sekä sivujen suhteet vasemmalla olevassa cas-ikkunassa. Voit syöttää uuden komennon napauttamalla hiirellä rivinumeron 3 vieressä. Voit käyttää kuvassa näkyviä muuttujien nimiä. Kokeile myös raahata kolmion kärkipisteitä ja tutki, miten lukuarvot muuttuvat.

Muutama ohje cas-laskimen käyttöön:

Jos haluat laskea kuvan $\gamma$ -kulman sinin, kirjoita riville suoraan $\sin(\gamma)$ .
Kreikkalaiset kirjaimet saat näppäimistöltä:
- Alt + a = $\alpha$
- Alt + b = $\beta$
- Alt + g = $\gamma$
Jos laskin antaa vastauksen, kirjoita komento Lukuarvona(()$).
Kokeile ensin laskea jonkin kulman sini ja sen jälkeen muuttaa pisteiden paikkaa kuvaajassa. Mitä sinin arvolle tapahtuu?

Tähän kappaleeseen liittyvät tehtävät.

# muistikolmiot

2.3 Muistikolmiot

Muistikolmioiden avulla voidaan ratkaista tiettyjen usein esiintyvien kulmien sini, kosini ja tangentti. Tällaisia kulmia ovat $30^{\circ}$ , $45^{\circ}$ ja $60^{\circ}$ . Muistikolmiot täytyy niiden nimen mukaisesti muistaa ulkoa, mutta ne löytyvät myös esimerkiksi MAOL-taulukoista.

2.3.1 Esimerkki: trigonometrisia suhteita

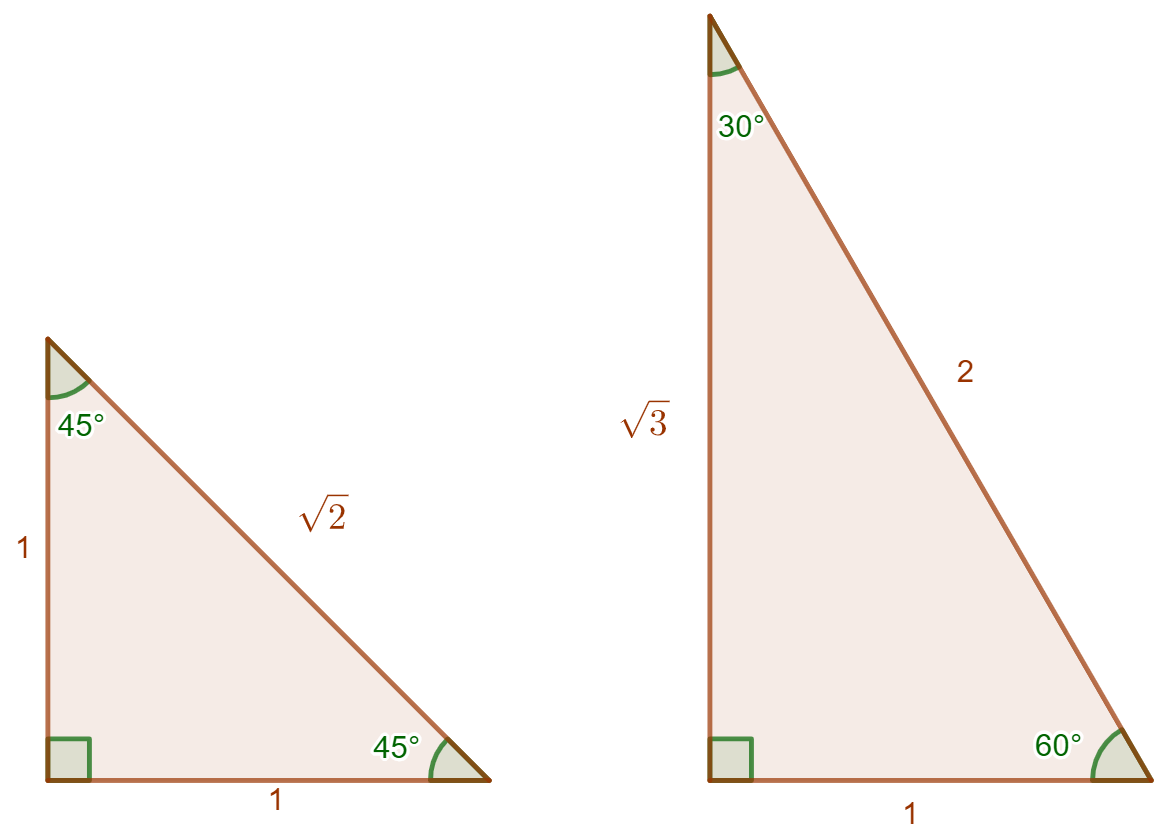
Esimerkkejä muistikolmioiden avulla ratkaistavista trigonometrisista suhteista.

$\sin(45^{\circ})=\frac{1}{\sqrt{2}}$ $\cos(60^{\circ})=\frac{1}{2}$ $\sin(30^{\circ})=\frac{1}{2}$ $\tan(45^{\circ})=\frac{1}{1}=1$

2.3.2 Esimerkki: kolmion sivujen ratkaiseminen

Ratkaistaan alla olevasta kuvasta sivujen ja pituudet.

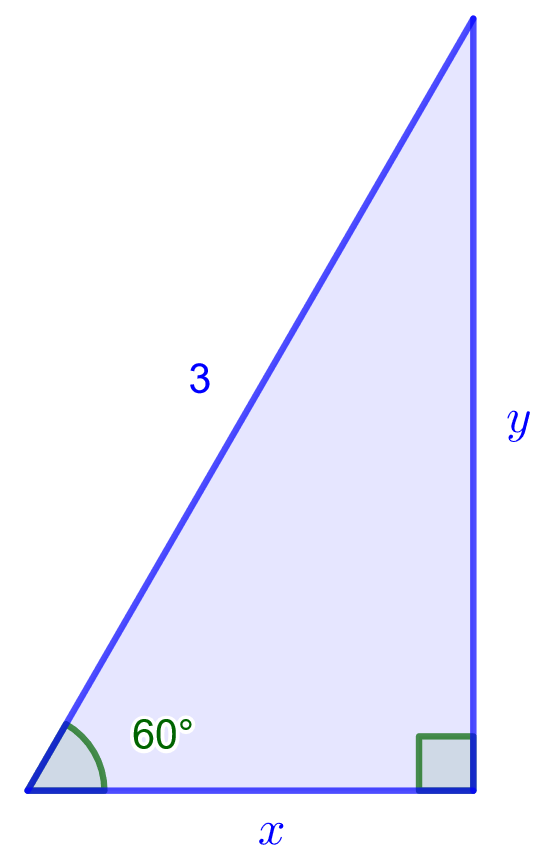
Oikeanpuoleisesta muistikolmiosta tiedetään, että $\cos 60^{\circ}=\frac{1}{2}.$ Annetusta kuvasta taas saadaan, että $\cos 60^{\circ} = \frac{x}{3}.$ Merkitään nämä yhtä suuriksi, jolloin saadaan $\frac{1}{2} = \frac{x}{3}.$ Kerrotaan ristiin ja ratkaistaan , jolloin saadaan $x=\frac{3}{2}.$

Sivun pituus saadaan vastaavasti sinin avulla, sillä $\sin 60^{\circ} = \frac{\sqrt{3}}{2} = \frac{y}{3}$ josta saadaan $y = \frac{3 \sqrt{3}}{2}.$

Tähän kappaleeseen liittyvät tehtävät.

# tylpat-kulmat

2.4 Tylpän kulman sini ja kosini

Aiemmin tigonometriset suhteet määriteltiin vain suorakulmaisessa kolmiossa eli käytännössä vain teräville kulmille. Myöhemmin kurssilla MAA5 Transkendenttiset funktiot ja yhtälöt (vanhassa opsissa MAA7 Trigonometriset funktiot) opit lisää trigonometrisista funktioista, jotka määritellään ilman suorakulmaista kolmiota.

Määritellään nyt kuitenkin tylpän kulman eli suoran kulman ja oikokulman välillä olevalle kulmalle sini ja kosini laskukaavojen avulla. Alla olevissa esimerkeissä havainnollistetaan sitä, mistä laskukaavat tulevat.

Tylpän kulman sini ja kosini

Tylpän kulman ( $90^{\circ} \leq \alpha \leq 180^{\circ}$ ) sini ja kosini voidaan laskea seuraavilla kaavoilla: $\sin (180^{\circ} -\alpha) = \sin (\alpha)$ $\cos(180^{\circ}-\alpha)=-\cos (\alpha).$

2.4.1 Esimerkki: tylpän kulman sini GeoGebralla

# tylppa-sini-geo

Otetaan esimerkiksi GeoGebra-appletissa näkyvä alkutilanne, jossa halutaan selvittää kulman $\alpha=140^{\circ}$ sini. Äsken esitellyn kaavan mukaisesti $\begin{aligned} \sin(140^{\circ}) &= \sin(180^{\circ}-140^{\circ}) \\ &= \sin(40^{\circ}) \\ &= 0,64. \end{aligned}$ GeoGebra-appletissa sekä kulman $140^{\circ}$ että $40^{\circ}$ oikea kylki on x-akselilla, ja vasen kylki on yhden mittainen jana. Huomataan, että kummankin kulman tapauksessa tämän janan päätepisteen y-koordinaatti on 0,64 .

2.4.2 Esimerkki: tylpän kulman kosini GeoGebralla

# tylppa-kosini-geo

Otetaan esimerkiksi GeoGebra-appletissa näkyvä alkutilanne, jossa halutaan selvittää kulman $\alpha=140^{\circ}$ kosini. Äsken esitellyn kaavan mukaisesti $\begin{aligned} \cos(140^{\circ}) &= -\cos(180^{\circ}-140^{\circ}) \\ &= -\cos(40^{\circ}) \\ &= -0,77. \end{aligned}$ GeoGebra-appletissa sekä kulman $140^{\circ}$ että $40^{\circ}$ oikea kylki on x-akselilla, ja vasen kylki on yhden mittainen jana. Huomataan, että kummankin kulman tapauksessa tämän janan päätepisteen x-koordinaatti on 0,77 . Tylpän kulman kosinin arvo on negatiivinen, kun taas vastaavan terävän kulman kosini on positiivinen.

Tähän kappaleeseen liittyvät tehtävät.

# kolmion-ala

2.5 Kolmion pinta-ala

Kolmion pinta-ala voidaan laskea tutulla tavalla, eli kerrotaan kolmion kanta ja korkeus keskenään ja jaetaan tulos kahdella. Joskus kolmion korkeus on kuitenkin vaikea määrittää. Yleisemmässä tapauksessa kolmion pinta-ala voidaan määrittää vain, kun tiedetään kahden kolmion sivun pituudet ja niiden sivujen välisen kulman suuruus.

Kolmion alan trigonometrinen laskukaava Matikkamatskuissa

Kolmion pinta-ala

Jos kolmion kannan pituus on ja korkeus , kolmion pinta-ala on $A=\frac{1}{2} ah.$ Jos kolmion kahden sivun pituudet ovat ja ja näiden välisen kulman suuruus $\alpha$ , voidaan kolmion pinta-ala ilmaista lausekkeella $A=\frac{1}{2} ab \sin \alpha.$

2.5.1 Todistus

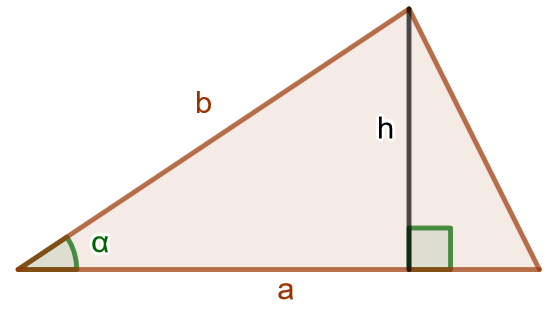
Todistetaan kolmion pinta-alan trigonometrinen kaava kolmessa tapauksessa:

kulma $\alpha$ on suora,
kulma $\alpha$ on terävä ja
kulma $\alpha$ on tylppä.

Jos kulma $\alpha$ on suora, muodostuu alla olevan kuvion mukainen kolmio.

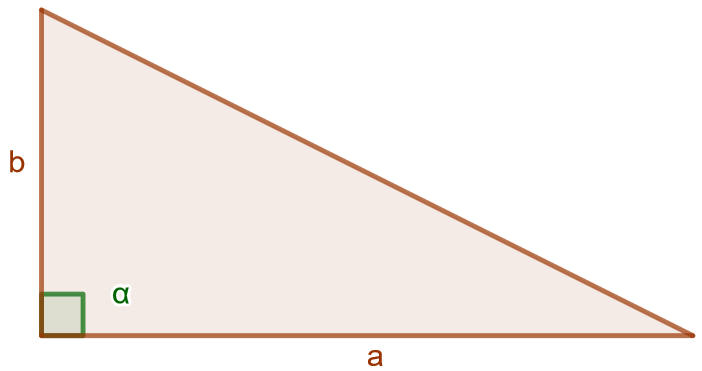
Tämän kolmion pinta-ala saadaan laskettua suoraan perinteisellä pinta-alan kaavalla, sillä kolmion pinta-ala on puolet sellaisen suorakulmion, jonka sivujen pituudet ovat ja , pinta-alasta. Koska $\sin 90^{\circ}=1$ , voidaan kyseinen termi lisätä pinta-alan arvoa muuttamatta. Kolmion pinta-ala on siis

$A=\frac{1}{2} ab = \frac{1}{2}ab \sin \alpha.$

Jos kulma $\alpha$ on terävä, muodostuu alla olevan kuvan mukainen kuvio. Siihen on merkitty kolmion korkeusjana , joka on kohtisuorassa kolmion kantaa vasten.

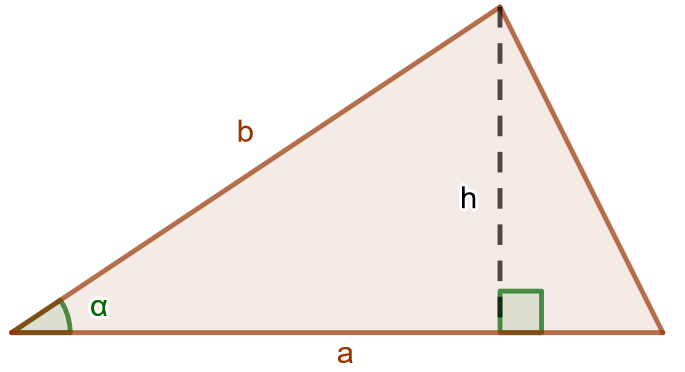
Kolmion pinta-ala saadaan perinteisen kaavan mukaisesti kertomalla kanta ja korkeus keskenään sekä jakamalla saatu tulo kahdella. Nyt kolmion korkeus on , joka voidaan ilmaista sivun sekä kulman $\alpha$ avulla $\sin \alpha = \frac{h}{b} \quad \Leftrightarrow \quad h = b \sin \alpha.$ Sijoitetaan tämä kolmion pinta-alan lausekkeeseen, jolloin saadaan $A=\frac{1}{2} ah = \frac{1}{2} a b \sin \alpha$ mikä on haluttu tulos.

Jos kulma $\alpha$ on tylppä, saadaan alla olevan kuvan kaltainen kolmio.

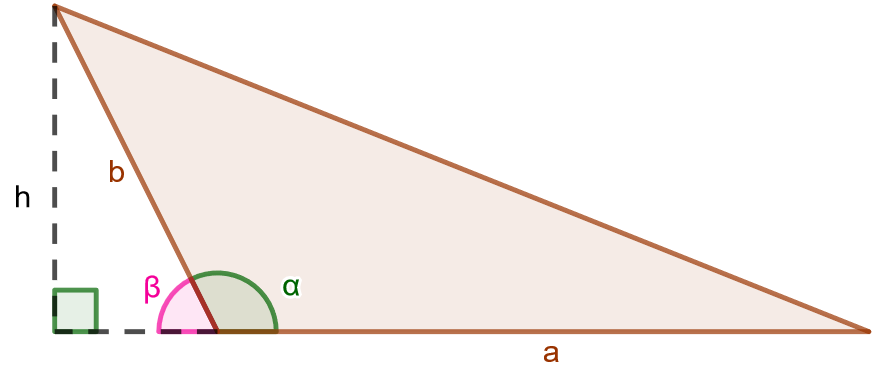
Nyt kolmion korkeusjana on kolmion ulkopuolella. Se voidaan ilmaista sivun ja kulman $\beta$ avulla seuraavasti: $\sin \beta = \frac{h}{b} \quad \Leftrightarrow \quad h = b \sin \beta.$ Haluaisimme ilmaista pinta-alan lausekkeen sivujen ja sekä kulman $\alpha$ avulla. Siksi meidän pitäisi löytää keino kuvata $\sin \beta$ kulman $\alpha$ avulla.

Huomataan, että $\alpha + \beta = 180^{\circ} \quad \Leftrightarrow \quad \beta = 180 ^{\circ} - \alpha$ jolloin $\sin \beta = \sin (180^{\circ}-\alpha)=\sin \alpha.$ Viimeinen yhtäsuuruus saadaan tylpän kulman sinin lausekkeesta. Nyt siis $h = b \sin \alpha$ . Sijoitetaan korkeuden lauseke kolmion pinta-alan lausekkeeseen: $A= \frac{1}{2} ah = \frac{1}{2} a b \sin \alpha$ joka on siinä muodossa kuin sen halusimme.

2.5.2 Esimerkki: kolmion pinta-alan lauseke GeoGebralla

# kolmio-ala-geo

Yllä olevassa GeoGebra-appletissa käydään läpi kolmion pinta-alan trigonometrisen laskukaavan johtaminen. Alussa johdetaan suorakulmaisen kolmion pinta-alan laskukaava lähtien suorakulmion pinta-alan laskukaavasta. Suorakulmion, jonka sivujen pituudet ovat ja , pinta-ala on A_s=ah . Kun suorakulmio puolitetaan lävistäjän kohdalta, saadaan kaksi yhtä suurta kolmiota, jolloin yhden kolmion pinta-ala on puolet suorakulmion pinta-alasta, eli $A_k=\frac{1}{2}A_s=\frac{1}{2}ah$ .

Tarkastellaan yleisesti kolmiota, jonka kanta on sama kuin suorakulmiossa eli , toinen sivu on ja korkeus on . Kolmio ei nyt kuitenkaan ole suorakulmainen. Lisäksi tiedetään, että sivujen ja välinen kulma on $\alpha$ . Kuvioon muodostuu suorakulmainen kolmio, koska korkeusjana on aina kohtisuorassa kolmion kantaan . Näillä merkinnöillä voidaan siis laskea $\sin(\alpha)=\frac{h}{b}$ . Ratkaistaan tästä yhtälöstä $h=b \sin(\alpha)$ . Sijoitetaan tämä :n lauseke nyt tunnettuun kolmion pinta-alan laskukaavaan $A=\frac{1}{2}ah=\frac{1}{2}ab \sin(\alpha).$ Näin saatiin johdettua kolmion pinta-alan trigonometrinen laskukaava.

Tähän kappaleeseen liittyvät tehtävät.

# kosinilause

2.6 Kosinilause

Kolmiomittaus on yksi tärkeimmistä maanmittausmenetelmistä, ja sen avulla on esimerkiksi piirretty Suomen peruskartat. Kolmiomittaus perustuu tunnettuihin pisteisiin ja niistä määritettävien kolmioiden sivujen ja kulmien mittaamiseen ja laskemiseen. Kolmion tuntemattomia sivuja ja kulmia voidaan määrittää kosinilauseen ja sinilauseen avulla.

Kosinilause Opetus.tv:ssä

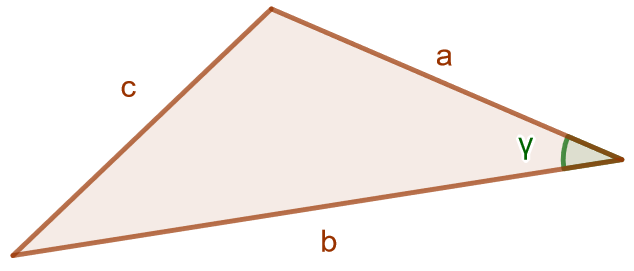
Kosinilause

Jos ja ovat kolmion sivuja ja $\gamma$ niiden välinen kulma, voidaan kolmion kolmas sivu laskea seruraavasti: $c^2=a^2+b^2-2ab \cos \gamma.$

2.6.1 Todistus

Todistetaan kosinilause kolmessa eri tapauksessa:

kulma $\gamma$ on terävä,
kulma $\gamma$ on suora ja
kulma $\gamma$ on tylppä.

Jos kulma $\gamma$ on terävä, muodostuu alla olevan kuvan kaltainen kolmio.

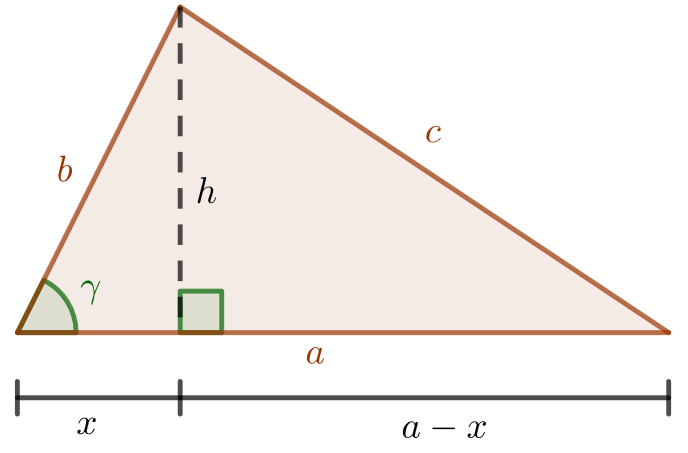
Kolmiossa sivu on jaettu kahteen osaan, joiden pituudet ovat ja a-x . Kolmion korkeusjana on kohtisuorassa kolmion kantaa vastaan.

Jos tarkastellaan vasemmanpuoleista suorakulmaista kolmiota, saadaan Pythagoraan lauseen avulla yhtälö h^2=b^2-x^2 . Toisaalta, jos tarkastellaan oikeanpuoleista suorakulmaista kolmiota, saadaan h^2=c^2-(a-x)^2 . Yhdistetään nämä kaksi lauseketta ja avataan jälkimmäisen lausekkeen sulut, jolloin saadaan b^2-x^2=c^2-a^2+2ax-x^2 . Sievennetään lauseketta, jolloin se saa muodon c^2=a^2+b^2-2ax .

Nyt pitäisi vielä ilmaista kolmion sivujen ja kulman $\gamma$ avulla. Huomataan, että $\cos \gamma = \frac{x}{b}$ eli $x=b \cos \gamma$ . Sijoitetaan tämä aiemmin saatuun yhtälöön, jolloin saadaan tuttu kosinilauseen lauseke $c^2=a^2+b^2-2ab \cos \gamma.$

Jos kulma $\gamma$ on suora, saadaan alla olevan kuvan kaltainen kolmio.

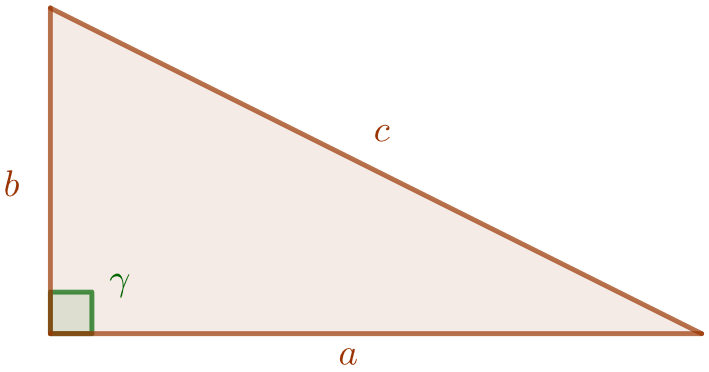
Tutkitaan, päteekö kosinilauseen kaava $c^2=a^2+b^2-2ab \cos \gamma$ suorakulmaisen kolmion tapauksessa. Tiedetään, että $\cos 90^{\circ}=0$ . Tällöin kosinilause sievenee muotoon , mikä on Pythagoraan lause. Koska kyseessä on suorakulmainen kolmio, Pythagoraan lause on varmasti voimassa, ja samoin kosinilause on voimassa suorakulmaisille kolmioille.

Jos kulma $\gamma$ on tylppä, saadaan alla olevan kuvan kaltainen kolmio.

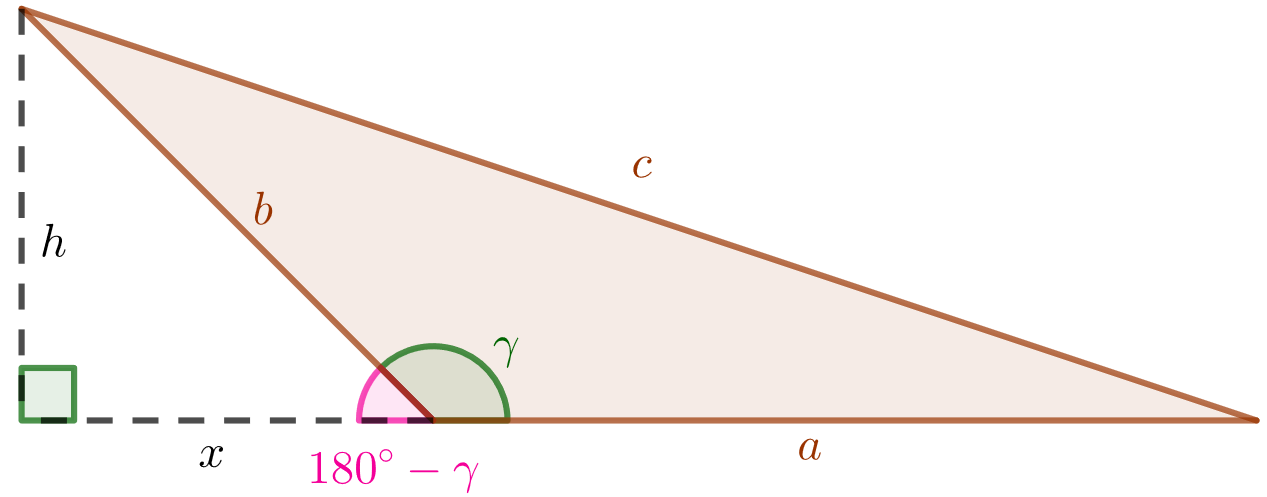
Kuvaan on merkitty kolmion korkeusjana ja sivun jatke, jota merkitään kirjaimella . Nyt kolmion vasemmalle puolelle muodostuu suorakulmainen kolmio, josta saadaan Pythagoraan lauseella h^2=b^2-x^2 . Lisäksi jos tarkastellaan vasemmanpuoleisen kolmion ja alkuperäisen kolmion yhdessä muodostamaa suorakulmaista kolmiota, saadaan h^2=c^2-(x+a)^2 . Yhdistetään nämä kaksi lauseketta ja avataan jälkimmäisen lausekkeen sulut, jolloin saadaan b^2-x^2=c^2-a^2-2ax-x^2 . Kun tätä sievennetään ja järjestellään uudestaan, saadaan c^2=a^2+b^2+2ax .

Kolmion vasemmalle puolelle muodostuvasta kolmiosta saadaan $\cos (180^{\circ}-\gamma)=\frac{x}{b}$ . Tylpän kulman kosinin kaavan avulla saadaan $\cos (180^{\circ}-\gamma)=-\cos \gamma=\frac{x}{b}$ eli $x = - b \cos \gamma$ . Sijoitetaan tämä aiemmin ratkaistuun :n neliön lausekkeeseen: $c^2=a^2+b^2-2ab \cos \gamma$ mikä on kosinilause siinä muodossa kuin sen halusimme.

2.6.2 Esimerkki: kosinilause GeoGebralla

# kosinilause-geo

Yllä olevassa GeoGebra-appletissa on piirretty kolmio, joka ei välttämättä ole suorakulmainen. Vasemmalla olevalla cas-laskimella voidaan varmistaa, että pisimmän sivun neliö on koko ajan yhtä suuri kuin kosinilauseessa väitetään eli $a^2+b^2-2ab \cos(\gamma)$ .

2.6.3 Esimerkki: kulmaa vastakkaisen sivun pituuden ratkaiseminen

Määritä alla olevasta kolmiosta sivun pituus.

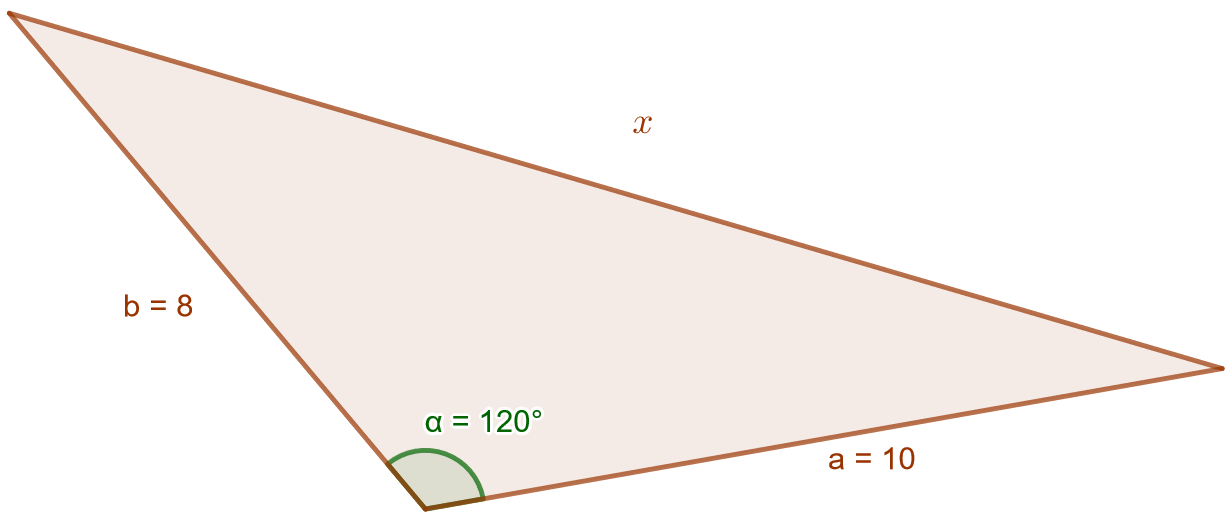
Tiedetään siis sivujen ja pituudet, sekä niiden välisen kulman $\alpha$ suuruus. Voidaan siis käyttää kosinilausetta. Nyt kosinilause tulee muotoon $x^2=a^2+b^2-2ab\cos(\alpha).$ Sijoitetaan sivujen pituudet ja kulman suuruus yhtälöön ja ratkaistaan . $\begin{aligned} x^2 &= 10^2+8^2-2 \cdot 10\cdot 8 \cdot \cos(120^{\circ}) &\quad &| \text{ sievennetään} \\ x^2 &= 244 &\quad &| \sqrt{\text{ }} \\ x &= \sqrt{244} &\quad &| \text{ sievennetään} \\ x &\approx 15,6205 &\quad &| \text{ pyöristetään} \\ x &\approx 15,62 \end{aligned}$ Kolmion sivun pituus on noin 15,62 .

2.6.4 Esimerkki: kulman viereisen sivun ratkaiseminen

Ratkaise alla olevan kolmion sivun pituus.

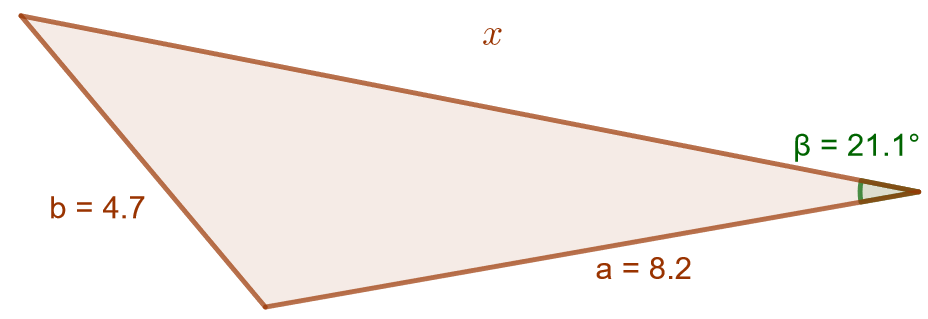
Nyt tiedetään kolmion sivujen ja pituudet, mutta tunnettu kulma $\alpha$ ei olekaan sivujen ja välissä. Käytetään silti kosinilausetta, sillä sitä voidaan käyttää aina, kun tiedetään kaksi kolmion sivua ja yksi kolmion kulma.

Muodostetaan kuvassa olevien tietojen avulla kosinilauseen kaava. Huomaa nyt, että kosinilauseen ja viittaavat tunnetun kulman viereisiin sivuihin, jotka tässä tapauksessa ovat ja . $b^2=a^2+x^2-2ax\cos(\beta)$ Sijoitetaan nyt tähän kaavaan lukuarvot kuvasta ja ratkaistaan . $\begin{aligned} 4,7^2 &= 8,2^2+x^2-2\cdot 8,2 \cdot x \cdot \cos(21,1^{\circ}) &\quad &| \text{ sievennetään} \\ 22,09 &= 67,24 + x^2 - 15,3x &\quad &|-22,09 \\ 0 &= x^2 -15,3x+45,15 &\quad &| \text{ toisen asteen yhtälö} \\ x &= \frac{15,3 \pm \sqrt{(-15,3)^2-4\cdot 1 \cdot 45,15}}{2 \cdot 1} \\ x &\approx 11,068 \qquad x \approx 3,99316 \end{aligned}$ Saatiin kaksi vastausta, joista molemmat ovat positiivisia ja sinällään sopivia vastaukseksi. Todellisuudessa molemmat vastaukset myös sopivat vastaukseksi, sillä kolmiosta ei ole määritelty kuin yksi kulma. Sivujen ja sekä sivujen ja väliset kulmat voivat olla minkä suuruisia tahansa. Tarkastele alla olevia kuvia.

Kolmion sivu on siis noin 11,1 tai noin 3,99 .

Tähän kappaleeseen liittyvät tehtävät.

# sinilause

2.7 Sinilause

Jos kolmiosta tiedetään kahden kulman suuruus sekä yhden sivun pituus, kosinilausetta ei voida käyttää. Tällöin käytetään sinilausetta.

Sinilause Opetus.tv:ssä

Sinilause

Jos kolmiosta valitaan mikä tahansa sivu ja sitä vastaava kulma, sivun pituuden ja kulman sinin suhde eli suhde $\frac{\text{kolmion sivu}}{\text{vastaisen kulman sini}}$ on vakio. Alla olevan kuvan merkinnöillä saadaan
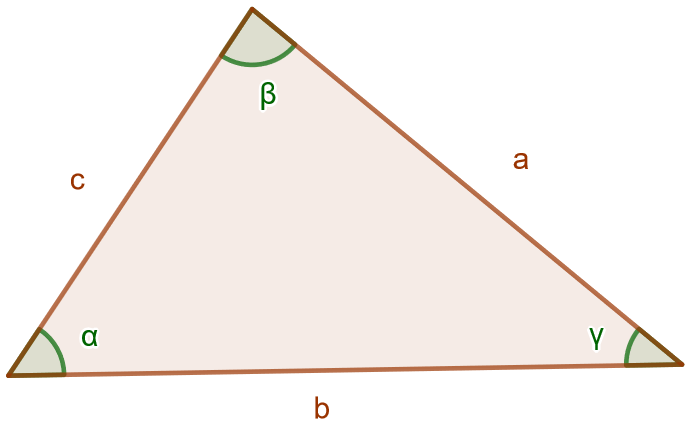
$\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.$

2.7.1 Todistus

Todistetaan sinilause käyttämällä kolmion pinta-alan trigonometrista laskukaavaa. Käytetään alla olevan kuvan merkintöjä.

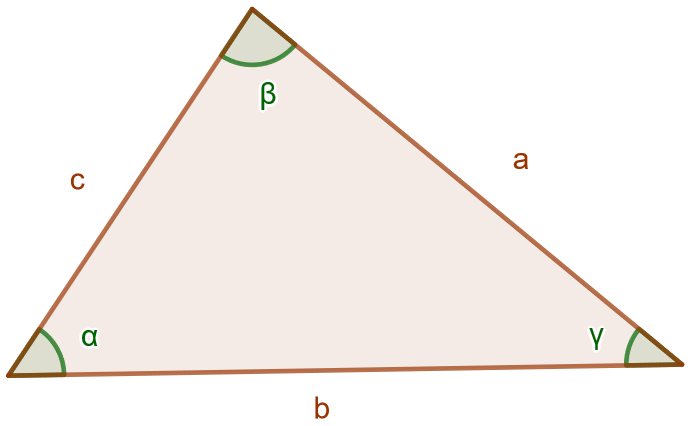
Kolmion pinta-ala voidaan laskea tarkastelemalla kulmaa $\alpha$ tai kulmaa $\beta$ , jolloin saadaan $A=\frac{1}{2}bc \sin \alpha = \frac{1}{2} ac \sin \beta.$ Supistetaan lausekkeista temit $\frac{1}{2}c$ pois ja järjestellään uudelleen, jolloin saadaan $\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}.$

Tehdään sama tarkastelu kulmille $\beta$ ja $\gamma$ , jolloin saadaan $\frac{1}{2} ac \sin \beta = \frac{1}{2} ab \sin \gamma \Leftrightarrow \frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.$

Yhdistämällä nämä kaksi saatua lauseketta, saadaan sinilause $\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}.$

2.7.2 Esimerkki: sinilause GeoGebralla

# sinilause-geo

Yllä olevassa GeoGebra-appletissa lasketaan jokaisen sivun ja sivua vastaan olevan kulman sinin suhde. Huomaa, että kun siirrät kolmion kärkipisteitä, suhteet pysyvät samoina.

2.7.3 Esimerkki: kulman ratkaiseminen

Ratkaise alla olevan kolmion kulma $\beta$ .

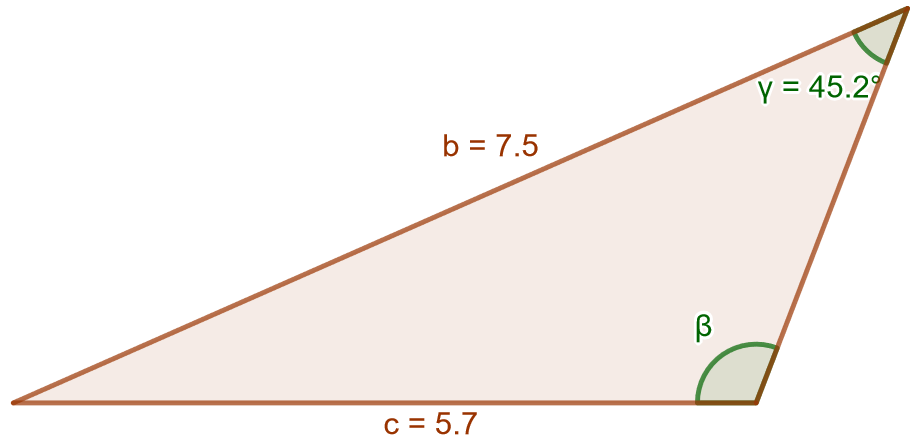
Jos kosinilauseella halutaan ratkaista kulma, tulisi tietää kaikkien kolmion sivujen pituudet. Koska nyt tiedetään vain kahden sivun pituudet ja kysytty kulma sekä tunnettu kulma ovat tunnettujen sivujen vastaisia kulmia, voidaan käyttää sinilausetta. Muotoillaan sinilauseen mukainen yhtälö ensin muuttujilla, ratkaistaan $\beta$ ja lopuksi sijoitetaan lukuarvot muuttujien paikalle. $\begin{aligned} \frac{b}{\sin(\beta)} &= \frac{c}{\sin(\gamma)} &\quad &| \text{ kerrotaan ristiin} \\ c \sin(\beta) &= b \sin(\gamma) &\quad &|:c \\ \sin(\beta) &= \frac{b \sin(\gamma)}{c} &\quad &| \sin^{-1}() \\ \beta &= \sin^{-1}\left( \frac{b \sin(\gamma)}{c} \right) \\ \beta &= \sin^{-1}\left( \frac{7,5 \cdot \sin(45,2^{\circ})}{5,7} \right) \\ \beta &= 69,01^{\circ} \end{aligned}$ Kuvasta huomataan, että kulman $\beta$ tulisi olla tylppä kulma, eikä $69,01^{\circ}$ ole tylppä. Muistetaan kuitenkin aiemmin käsitelty tylpän kulman sini. Sen mukaan $\sin(180^{\circ}-\alpha)=\sin(\alpha).$ Joten haluttu tylppä kulma saadaan laskemalla $\beta=180^{\circ}-69,01^{\circ}=110,99^{\circ}\approx 111^{\circ}.$ Alla olevaan kuvaan on piirretty molemmat tapaukset, ja huomataan, että sekä $69^{\circ}$ että $111^{\circ}$ toteuttavat kolmion muut annetut mitat.

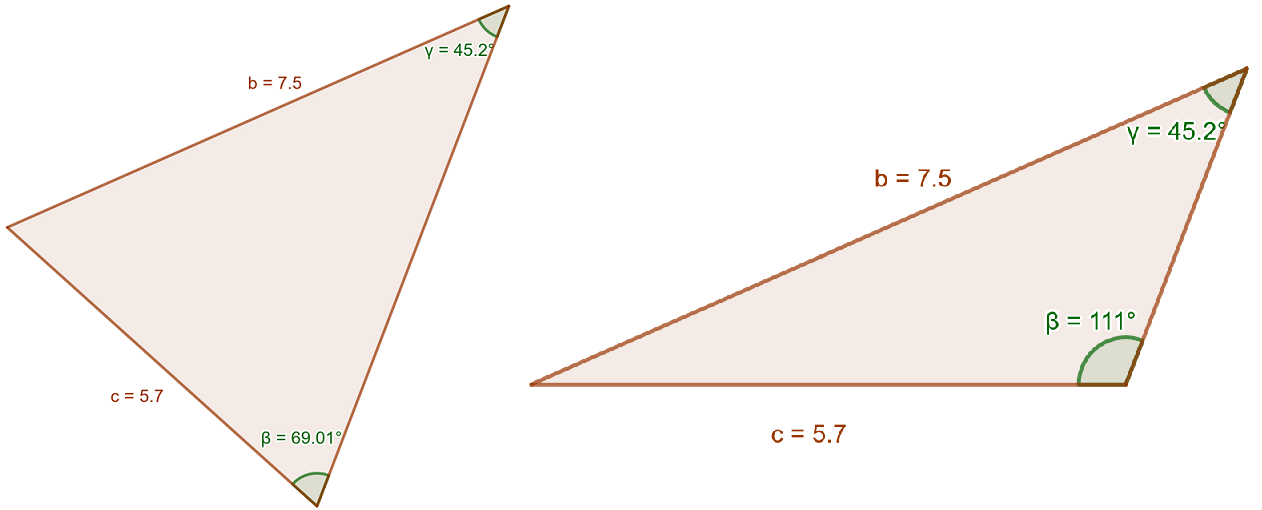
Tässä tapauksessa kysytty kulma $\beta$ on siis noin $111^{\circ}$ .

Sinilauseen avulla voidaan todistaa seuraava lause, jota usein kutsutaan kulmanpuolittajalauseeksi. Alla olevalla videolla on esitelty kulmanpuolittajalause ja käyty läpi kaksi esimerkkiä siihen liittyen.

Kulmanpuolittajalause Opetus.tv:ssä

Kulmanpuolittajalause

Kolmion kulman puolittava jana jakaa kulmaa vastapäätä olevan sivun kulman kylkien pituuksien suhteessa. Alla olevan kuvan merkinnöillä tämä tarkoittaa $\frac{a_1}{a_2} = \frac{x}{y}.$

2.7.4 Todistus

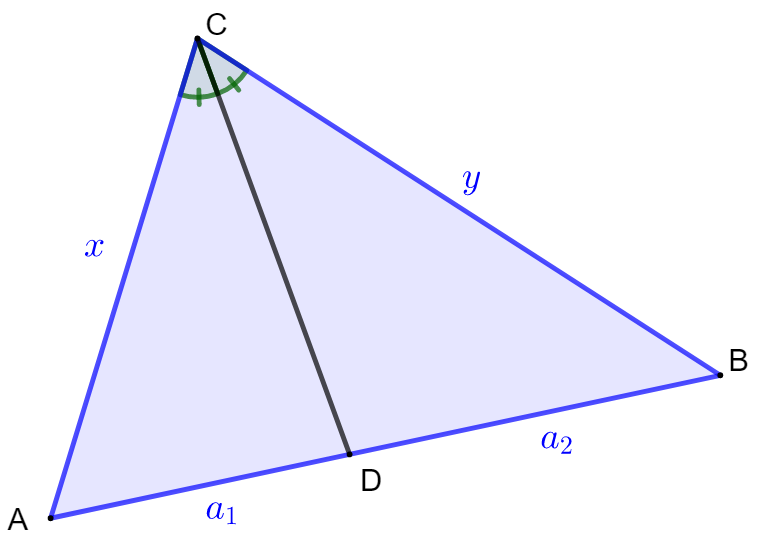
Käytetään alla olevan kuvan merkintöjä.

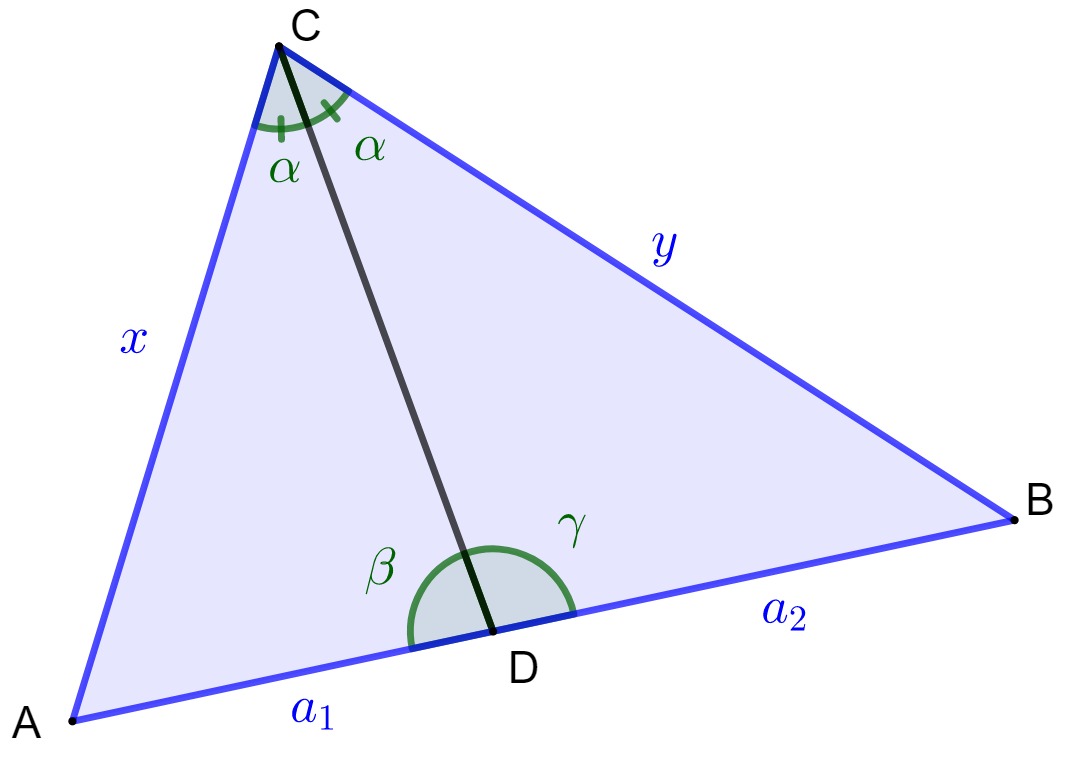
Koska kulmat $\beta$ ja $ muodostavat oikokulman, on oltava $\begin{aligned} \beta + \gamma &= 180^{\circ} \\ \beta &= 180^{\circ} - \gamma. \end{aligned}$

Otetaan puolittain sini ja muistetaan tylpän kulman sinin laskusääntö, jolloin saadaan $\begin{aligned} \sin \beta &= \sin ( 180^{\circ} - \gamma) \\ \sin \beta &= \sin \gamma. \end{aligned}$

Käytetään sinilausetta ensin kolmioon ACD , jolloin saadaan $\frac{a_1}{\sin \alpha} = \frac{x}{\sin \beta} \quad \Leftrightarrow \quad \sin \beta = \frac{x \sin \alpha}{a_1}$ ja seuraavaksi kolmioon BCD , jolloin saadaan $\frac{a_2}{\sin \alpha} = \frac{y}{\sin \gamma} \quad \Leftrightarrow \quad \sin \gamma = \frac{y \sin \alpha}{a_2}.$ Koska $\sin \beta = \sin \gamma$ , merkitään nämä lausekkeet yhtä suuriksi $\frac{x \sin \alpha}{a_1} = \frac{y \sin \alpha}{a_2},$ jaetaan puolittain termillä $\sin \alpha$ $\frac{x}{a_1} = \frac{y}{a_2},$ ja järjestellään termejä uudelleen, jolloin saadaan haluttu tulos $\frac{x}{y} = \frac{a_1}{a_2}.$

2.7.5 Esimerkki: kulmanpuolittajalause GeoGebralla

# geo_kulmanpuolittajalause

Yllä olevassa GeoGebra-appletissa voit siirtää kolmion punaisia kärkipisteitä ja tarkkailla suhteiden $\frac{a_1}{a_2}$ ja $\frac{x}{y}$ arvoja. Jana on aina kulman $\angle ACB$ puolittaja.

2.7.6 Esimerkki: kolmion sivun pituuden ratkaiseminen

Ratkaistaan alla olevaan kuvaan sinisellä merkityn janan pituus.

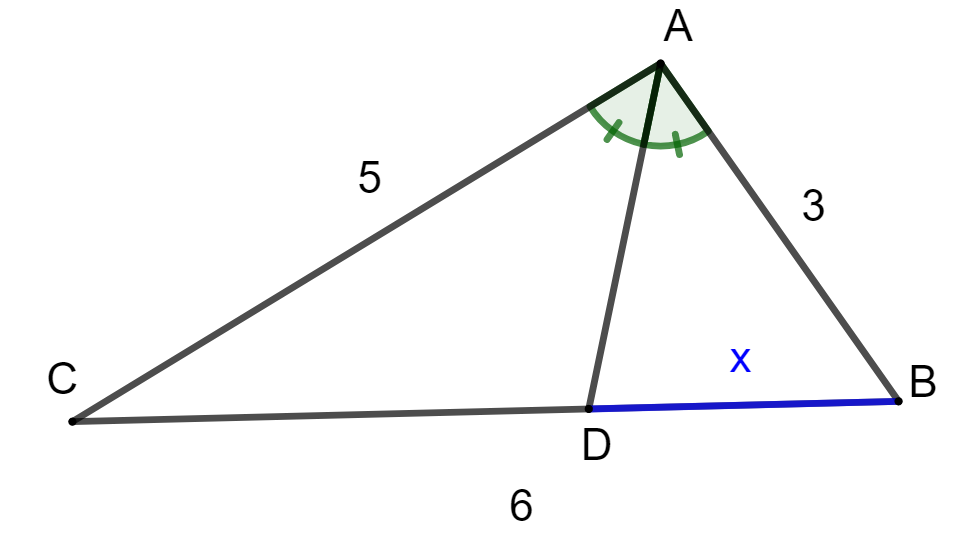
Merkitään kysyttyä janan pituutta kirjaimella . Tällöin janan pituus on 6-x . Käytetään kulmanpuolittajalausetta ja ratkaistaan $\begin{aligned} \frac{6-x}{x} &= \frac{5}{3} &\quad &| \text{ kerrotaan ristiin} \\ 5x &= 3 \cdot (6-x) &\quad &| \text{ kerrotaan sulut auki} \\ 5x &= 18-3x &\quad &| +3x \\ 8x &= 18 &\quad &| :8 \\ x &= \frac{18}{8} = \frac{9}{4} \end{aligned}$ Janan pituus on $\frac{9}{4}$ eli 2,25 .

Tähän kappaleeseen liittyvät tehtävät.

# kaant-pythagoras

2.8 Käänteinen Pythagoraan lause

Pythagoraan lauseen kohdalla todettiin, että se pätee vain suorakulmaisille kolmioille. Eli jos kolmio on suorakulmainen, sen kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö. Sama päättely voidaan kääntää toisinpäin. Jos kolmion kahden lyhyemmän sivun neliön summa on yhtä suuri kuin pisimmän sivun neliö, kyseessä on suorakulmainen kolmio. Jos suoraa kulmaa ei ole merkitty kuvaan tai sitä ei ole kerrottu erikseen, tulee aina tarkistaa, onko kolmio suorakulmainen, vaikka se saattaisi näyttää siltä.

Käänteinen Pythagoraan lause

Jos kolmion pisin sivu on , kaksi muuta sivua ja ja kolmiolle pätee yhtälö a^2+b^2=c^2 , kolmio on suorakulmainen.

2.8.1 Esimerkki: onko kolmio suorakulmainen?

Ovatko seuraavat kuvissa olevat kolmiot suorakulmaisia?

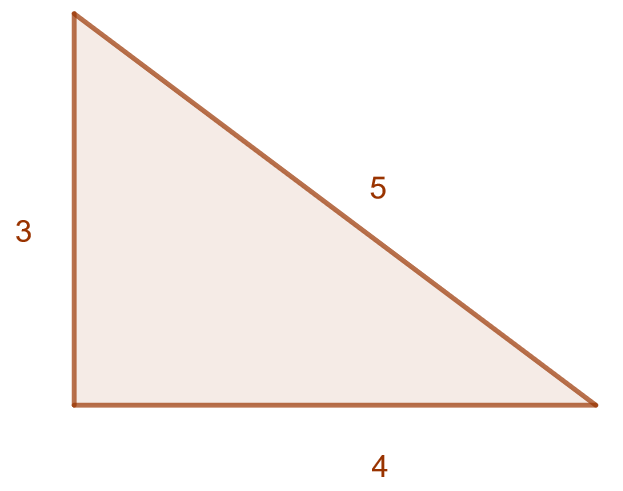
Kolmion pisin sivu on , ja sen neliö on 5^2=25 . Kolmion lyhyemmät sivut ovat ja , ja niiden neliöiden summa on 3^2+4^2=9+16=25 . Koska nämä ovat yhtä suuret, kolmio on suorakulmainen.

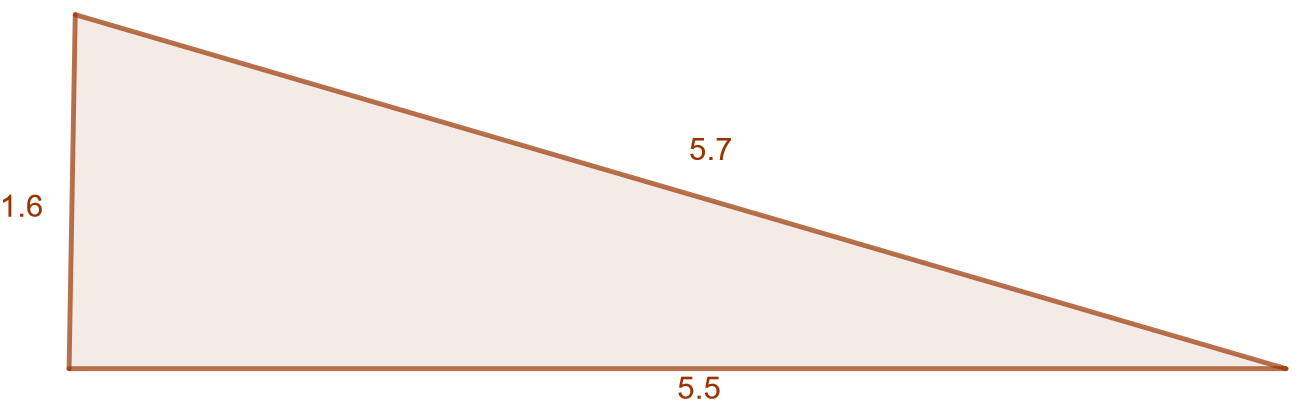
Pisin sivu on 5,7 , ja sen neliö on 5,7^2=32,49 . Kolmion lyhyemmät sivut ovat 1,6 ja 5,5 , ja niiden neliöiden summa on 1,6^2+5,5^2=2,56+30,25=32,81 . Koska tulokset ovat eri suuria, kolmio ei ole suorakulmainen.

Tähän kappaleeseen liittyvät tehtävät.

# merkilliset-pisteet

2.9 Kolmion merkilliset pisteet

Kolmioihin liittyy paljon mielenkiintoisia kaikkia kolmioita koskevia tuloksia. Seuraavaksi esitellään tuloksia liittyen kolmion kulmanpuolittajiin, keskijanoihin ja keskinormaaleihin. Kokeile kaikissa GeoGebra-havainnollistuksissa raahata kolmion kärkipisteitä ja tutkia, mitä kuvassa tapahtuu.

Kulmanpuolittajalause ja kolmion merkilliset pisteet Matikkamatskuissa

2.9.1 Kulmanpuolittajalause

Kolmion jokaisen kulman kulmanpuolittajat leikkaavat yhdessä pisteessä, joka on aina kolmion sisällä. Tämä piste on myös suurimman mahdollisen kolmion sisään piirretyn ympyrän keskipiste. Ympyrän säde voidaan laskea kaavalla $r=\sqrt{\frac{(s-a)(s-b)(s-c)}{s}},$ missä , ja ovat kolmion sivujen pituudet ja on kolmion piirin puolikas $s=\frac{1}{2}(a+b+c).$

# kulmanpuolittajat-geo

2.9.2 Keskijanalause

Kun kolmion sivujen keskipisteet yhdistetään vastakkaisiin kulmiin, saadaan kolme keskijanaa. Nämä keskijanat leikkaavat yhdessä pisteessä, joka jakaa jokaisen keskijanan suhteessa 2:1 . Leikkauspiste on aina kolmion sisällä ja sitä kutsutaan myös kolmion painopisteeksi.

# keskijanat-geo

2.9.3 Keskinormaalilause

Kolmion sivujen keskinormaalit leikkaavat yhdessä pisteessä, joka on kolmion ympäri piirretyn ympyrän keskipiste. Teräväkulmaisen kolmion tapauksessa piste on kolmion sisäpuolella ja tylppäkulmaisella kolmiolla se on kolmion ulkopuolella. Suorakulmaisella kolmiolla leikkauspiste on täsmälleen hypotenuusan keskipisteessä.

# keskinormaali-geo

Tähän kappaleeseen liittyvät tehtävät.

# monikulmioiden_pinta-aloja

3. Monikulmioiden pinta-aloja

Tässä kappaleessa tutustutaan erilaisiin monikulmioihin ja niiden pinta-alojen laskemiseen. Huomataan, että monet monikulmioihin liittyvät ongelmat voidaan yksinkertaistaa kolmioihin liittyviksi ongelmiksi. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

Nelikulmiot muodostavat sarjan, jossa lähdetään liikkeelle "epäsäännöllisestä" nelikulmiosta epäkkäästä, ja ehtoja lisäämällä päädytään lopulta neliöön. Nelikulmiot käsitellään nyt tuossa järjestyksessä.

# puolisuunnikas

3.1 Puolisuunnikas

Puolisuunnikas on ensimmäinen jossain määrin säännöllinen nelikulmio. Sen kaksi vastakkaista sivua ovat keskenään yhdensuuntaiset. Näitä sivuja kutsutaan kannoiksi. Puolisuunnikkaan kahta muuta sivua kutsutaan kyljiksi. Jos kyljet ovat yhtä pitkiä, puolisuunnikasta kutsutaan tasakylkiseksi puolisuunnikkaaksi.

Puolisuunnikkaan pinta-ala

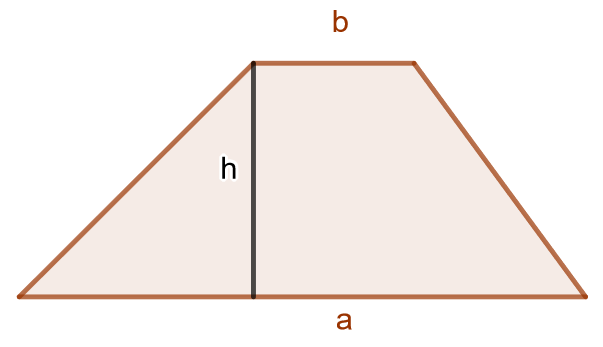
Puolisuunnikas on nelikulmio, jonka kaksi vastakkaista sivua ovat yhdensuuntaiset. Näitä sivuja kutsutaan puolisuunnikkaan kannoiksi. Jos puolisuunnikkaan kannat ovat ja ja sen korkeus on , sen pinta-ala on $A= \frac{a+b}{2}h.$

3.1.1 Esimerkki: pinta-alan laskeminen

Laske puolisuunnikkaan pinta-ala, kun sen kannat ovat $4,0 \text{ cm}$ ja $6,0 \text{ cm}$ , ja kantojen välinen etäisyys on $3,0 \text{ cm}$ .

Aloitetaan tehtävän ratkaiseminen piirtämällä mallikuva tilanteesta. Niin kannattaa tehdä kaikissa geometrian sanallisissa tehtävissä.

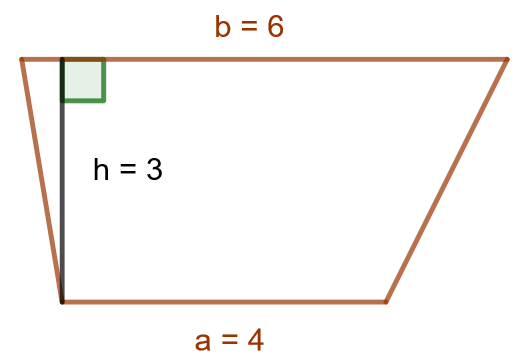
Sijoitetaan annetut arvot puolisuunnikkaan pinta-alan lausekkeeseen. Laskuissa ei ole välttämätöntä käyttää yksiköitä, jos muistaa lisätä ne vastausta annettaessa. $\begin{aligned} A&=\frac{a+b}{2}h \\ &= \frac{4+6}{2}\cdot 3 \\ &= 15 \end{aligned}$ Lopputuloksessa muistetaan käytetyt yksiköt. Koska puolisuunnikkaan sivujen pituudet on ilmoitettu senttimetreinä, on vastaus neliösenttimetreinä. Kysytyn puolisuunnikkaan pinta-ala on $15 \text{ cm}^2$ .

Tähän kappaleeseen liittyvät tehtävät.

# suunnikas

3.2 Suunnikas

Lisätään puolisuunnikkaaseen yksi lisäehto. Sen sijaan, että vain yksi vastakkaisten sivujen muodostama pari olisi yhdensuuntainen, vaaditaankin, että molemmat vastakkaisten sivujen muodostamat parit ovat yhdensuuntaisia. Tällöin saadaan suunnikas.

Suunnikkaan pinta-ala

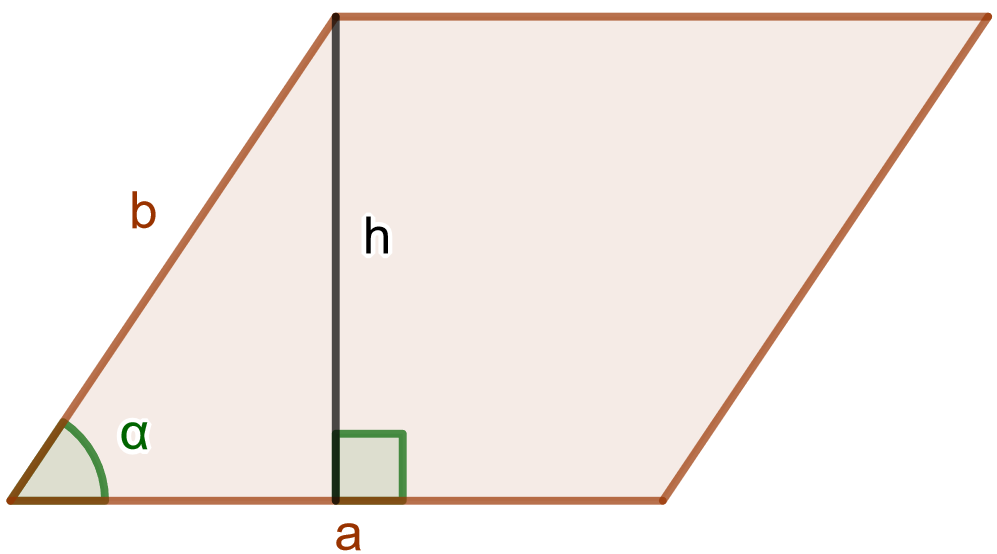
Suunnikas on nelikulmio, jonka molemmat vastakkaiset sivut ovat yhtä pitkiä ja yhdensuuntaisia. Jos suunnikkaan sivujen pituudet ovat ja ja näiden sivujen välinen kulma on $\alpha$ , voidaan suunnikkaan pinta-ala laskea seuraavasti $A=ah=ab \sin \alpha,$ missä on suunnikkaan korkeus.

3.2.1 Esimerkki: suunnikkaan pinta-ala GeoGebralla

# suunnikkaan-ala-geo

Kokeile siirtää liukusäädintä yllä olevassa GeoGebra-appletissa. Huomaa, että molemmilla suunnikkaan pinta-alan laskukaavoilla tulee luonnollisesti sama tulos, mutta tilanteesta riippuu, kumpaa laskukaavaa on helpompi käyttää.

3.2.2 Esimerkki: suunnikkaan piirtäminen GeoGebralla

Harjoittele suunnikkaan muodostamista GeoGebralla.

Piirrä kolme pistettä , ja .
Yhdistä pisteet ja suoralla.
Yhdistä pisteet ja suoralla.
Luo suora, joka on yhdensuuntainen suoran kanssa ja joka kulkee pisteen kautta.
Luo suora, joka on yhdensuuntainen suoran kanssa ja joka kulkee pisteen kautta.
Lisää kohdissa 4 ja 5 luotujen suorien leikkauspiste .
Luo monikulmio , joka on suunnikas.
Piilota ylimääräiset suorat. Kokeile siirtää pisteitä ja varmista, että kuviosi todella on suunnikas.

# suunnikas-geo

Jos suunnikkaan kaikki sivut ovat yhtä pitkiä, puhutaan neljäkkäästä eli vinoneliöstä. Joskus neljäkästä kutsutaan myös nimellä rombi.

3.2.3 Esimerkki: lävistäjän pituuden laskeminen

Ratkaise alla olevan kuvan janan pituus, kun neljäkkään pinta-ala on 33,7 .

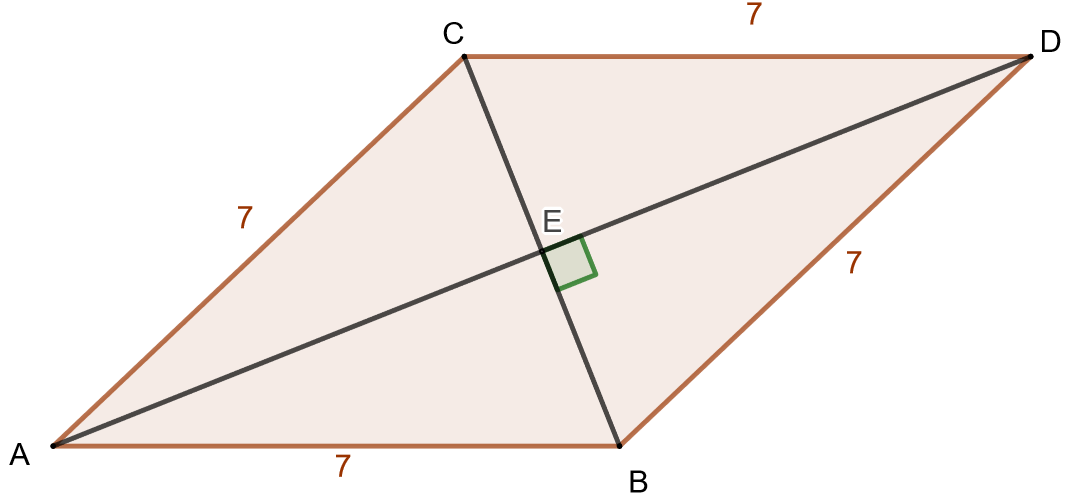
Pinta-alan ja sivun pituuden avulla voidaan laskea kulman $\angle CDB$ suuruus. Merkitään kulmaa $\angle CDB$ kreikkalaisella kirjaimella $\alpha$ ja neljäkkään sivua kirjaimella . Käytetään suunnikkaan pinta-alan kaavaa $\begin{aligned} A&=a^2 \sin(\alpha) &\quad &|:a^2 \\ \sin(\alpha) &= \frac{A}{a^2} &\quad &|\sin^{-1}() \\ \alpha &= \sin^{-1}\left( \frac{A}{a^2} \right) \end{aligned}$ Jana on osa suorakulmaista kolmiota CDE . Merkitään tämän kolmion kulmaa $\angle CDE$ kreikkalaisella kirjaimella $\beta$ . Nyt kulma $\beta$ on puolet kulmasta $\alpha$ . Käytetään trigonometrisista suhteista siniä, jotta saadaan ratkaistua kysytyn janan pituus $\begin{aligned} \sin(\beta) &= \frac{CE}{a} &\quad &|\cdot a \\ CE &= a \sin(\beta) &\quad &|\beta = \frac{\alpha}{2} \\ CE &= a \sin \left( \frac{\alpha}{2} \right) &\quad &|\alpha = \sin^{-1}\left( \frac{A}{a^2} \right) \\ CE &= a \sin \left( \frac{\sin^{-1}\left( \frac{A}{a^2} \right)}{2} \right) \\ CE &= 7 \cdot \sin \left( \frac{\sin^{-1}\left( \frac{33,7}{7^2} \right)}{2} \right) \\ CE &\approx 2,5912 \end{aligned}$ Janan pituus on siis noin 2,59.

Tähän kappaleeseen liittyvät tehtävät.

# suorakulmio

3.3 Suorakulmio

Suorakulmio on suunnikas, jonka kaikki kulmat ovat yhtä suuria. Suorakulmion jokainen kulma on $90^{\circ}$ .

Suorakulmion pinta-ala

Suorakulmio on monikulmio, jolla on neljä kulmaa ja jonka jokainen kulma on suora. Jos suorakulmion eripituisten sivujen pituudet ovat ja , voidaan suorakulmion pinta-ala laskea seuraavasti A=ab.

Tähän kappaleeseen liittyvät tehtävät.

# nelio

3.4 Neliö

Neliö on suunnikas, jonka kaikki sivut ovat yhtä pitkiä. Neliö on siis säännöllinen nelikulmio, sillä kaikki sen sivut ovat yhtä pitkiä ja kaikki sen kulmat ovat yhtä suuria.

Neliön pinta-ala

Neliö on monikulmio, jolla on neljä kulmaa, jonka sivut ovat yhtä pitkiä keskenään ja jonka jokainen kulma on suora. Jos neliön sivun pituus on , sen pinta-ala on A=a^2.

3.4.1 Esimerkki: monikulmion pinta-ala

Laske alla olevan monikulmion pinta-ala.

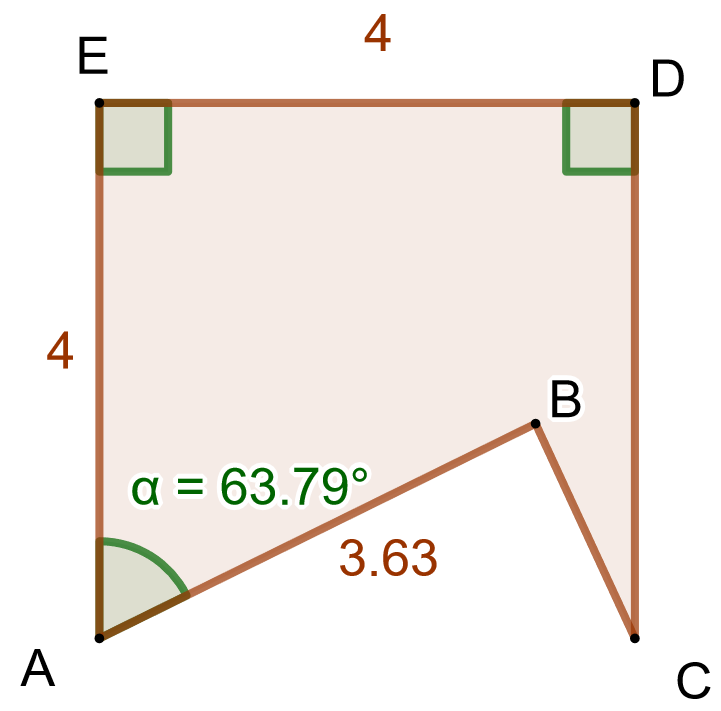
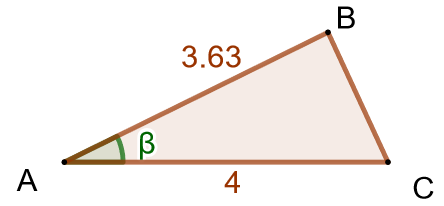
Huomataan, että kuvio koostuu neliöstä ACDE , josta on poistettu kolmio ABC . Kuvion pinta-ala voidaan laskea vähentämällä neliön pinta-alasta kolmion pinta-ala. Neliön pinta-ala on A_n=4^2=16. Alla on pelkän kolmion kuva. Kulman $\beta$ suuruus voidaan päätellä, sillä yhdessä kulmat $\alpha$ ja $\beta$ muodostavat suoran kulman: $\beta = 90^{\circ}- \alpha = 90^{\circ}-63,79^{\circ}=26,21^{\circ}.$

Kun tiedetään yksi kolmion kulma ja kulman viereisten sivujen pituudet, kolmion pinta-ala voidaan laskea trigonometrisella pinta-alakaavalla. $\begin{aligned} A_k&=\frac{1}{2}AC \cdot AB \cdot \sin(\beta) \\ A_k &= \frac{1}{2} \cdot 4 \cdot 3,63 \cdot \sin(26,21^{\circ}) \\ A_k &= 3,21 \end{aligned}$

Koko kuvion pinta-ala voidaan laskea vähennyslaskulla A=A_n - A_k = 16-3,21 = 12,79. Monikulmion ABCDE pinta-ala on 12,79 .

Tähän kappaleeseen liittyvät tehtävät.

# muut-monikulmiot

3.5 Muut monikulmiot

Kaikki monikulmiot voidaan jakaa kolmioiksi, jolloin niiden käsittely helpottuu. Erityisen helppoa tämä on, jos monikulmio on säännöllinen.

3.5.1 Esimerkki: kuusikulmion pinta-ala

Ratkaise alla olevan kuusikulmion pinta-ala.

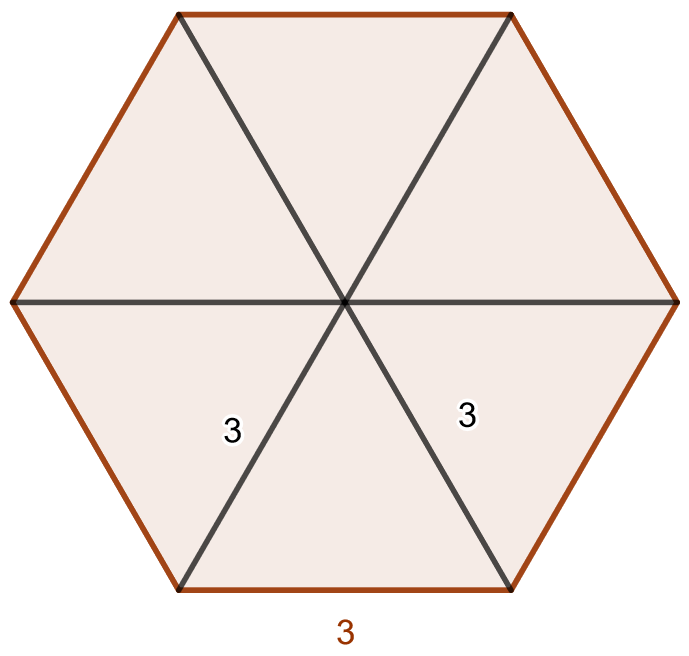
Huomataan, että kuusikulmio on säännöllinen ja se muodostuu kuudesta tasasivuisesta kolmiosta. Lasketaan ensin yhden tasasivuisen kolmion pinta-ala. Se voidaan tehdä kahdella tavalla: perinteisellä kaavalla $A=\frac{ah}{2}$ tai trigonometrisesti $A=\frac{ab \sin(\alpha)}{2}$ . Kolmion korkeuden laskeminen ei ole vaikeaa, mutta jos käytetään trigonometrista kaavaa, ei tarvitse laskea mitään ylimääräistä. Tiedetään, että tasasivuisen kolmion jokainen kulma on $60^{\circ}$ . Yhden tasasivuisen kolmion pinta-ala on $A_{\text{kolmio}}=\frac{ab\sin(\alpha)}{2}=\frac{3 \cdot 3 \cdot \sin(60^{\circ})}{2}=\frac{9 \sqrt{3}}{4}.$ Kerrotaan se kuudella, jotta saadaan kuusikulmion pinta-ala $A=6A_{\text{kolmio}}=6 \cdot \frac{9 \sqrt{3}}{4}=\frac{27 \sqrt{3}}{2} \approx 23,38.$ Kuusikulmion pinta-ala on $\frac{27 \sqrt{3}}{2}$ .

Tähän kappaleeseen liittyvät tehtävät.

4. Ympyrä

Tason pisteet, jotka ovat kiinteällä etäisyydellä pisteestä, muodostavat ympyrän eli ympyräviivan. Ympyröihin liittyy paljon mielenkiintoisia ominaisuuksia, laskuja ja lukuja, kuten irrationaaliluku pii $\pi$ . Lue myös luvun $\pi$ historiasta. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

Alla olevalla videolla on esitelty ympyään liittyviä käsitteitä. Ne käydään myöhemmin läpi yksityiskohtaisemmin.

Ympyrään liittyviä käsitteitä Opetus.tv:ssä

# ympyran-osat-geo

Käytä yllä olevaa GeoGebra-applettia tutkiaksesi videolla esiintyviä ympyrän osia. Muista kokeilla raahata kehällä olevia pisteitä.

# sade

4.1 Säde, halkaisija, piiri

Ympyrän tärkein ja sen määrittävä ominaisuus on ympyrän säde, jota merkitään usein kirjaimella (englannin kielen sanasta radius). Joskus puhutaan myös ympyrän halkaisijasta, jota merkitään kirjaimella (englannin kielen sanasta diameter).

Ympyrän piirin kaavan johtaminen Opetus.tv:ssä.

Ympyrän säde, halkaisija ja piiri

Ympyrän säde on ympyrän keskipisteen etäisyys sen kehältä. Ympyrän halkaisija on jana, joka kulkee ympyrän kehältä kehälle sen keskipisteen kautta. Halkaisijan pituus on d=2r . Ympyrän piiri on sen kehän pituus, ja se lasketaan $p=2 \pi r = \pi d$ .

4.1.1 Esimerkki: ympyrän piiri GeoGebralla

# piiri-geo

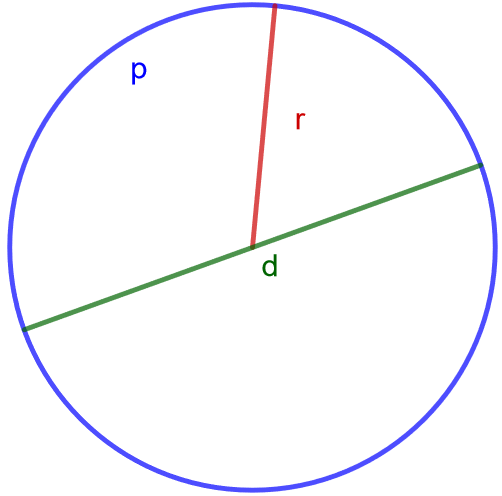
Yllä olevalla GeoGebra-appletilla voit tutkia ympyrän halkaisijan ja piirin suhdetta. Muuta ympyrän halkaisijaa raahaamalla vihreää pistettä, joka on ympyrän päällä. Siirrä ympyrää raahaamalla sen sinistä keskipistettä. Tutki ilmestyvää liukusäädintä ja valintaruutua. Huomaa, että ympyrän halkaisija mahtuu piiriin kolme kertaa, ja piiristä jää vielä hieman yli.

4.1.2 Esimerkki: monikulmion ja ympyrän piirit GeoGebralla

# monikulmio-piiri-geo

Yllä olevassa GeoGebra-appletissa on ympyrä, jonka sisään piirretyn säännöllisen monikulmion kulmien määrää voit muuttaa liukusäätimellä. Vasemmalla olevaan CAS-ikkunaan on laskettu monikulmion piirin suhde ympyrän piiriin. Koska ympyrän säde on , on sen piiri $2 \pi$ . Lisäksi CAS-ikkunassa on laskettu monikulmion piirin ero ympyrän piiristä (muuttujan nimi on virhe) sekä suhteellinen virhe piirien välillä (muuttuja suhtvirhe). Tutki virheiden suuruutta, kun muutat monikulmion kulmien määrää.

Monikulmion sivun pituus ja siten sen piiri on helpompi mitata kuin ympyrän piiri. Siksi lukua $\pi$ voidaankin arvioida tällä menetelmällä.

Tähän kappaleeseen liittyvät tehtävät.

# pinta-ala

4.2 Pinta-ala

Alla olevassa Opetus-tv:n videossa johdetaan ympyrän pinta-alan tuttu laskukaava. Videon täysi ymmärtäminen ei ole edellytys tehtävien osaamiselle, mutta se voi avata hieman paremmin, mistä ympyrän pinta-alan laskukaava tulee.

Ympyrän pinta-ala Opetus.tv:ssä.

Ympyrän pinta-ala

Ympyrän pinta-ala lasketaan sen säteen avulla seuraavasti $A=\pi r^2.$

4.2.1 Esimerkki: uima-altaan pinta-ala

Pihalle halutaan rakentaa ympyrän muotoinen uima-allas. Sille on varattu neliön muotoinen alue, jonka sivun pituus on $2,5 \text{ m}$ . Kuinka suuri on suurimman mahdollisen uima-altaan pinta-ala?

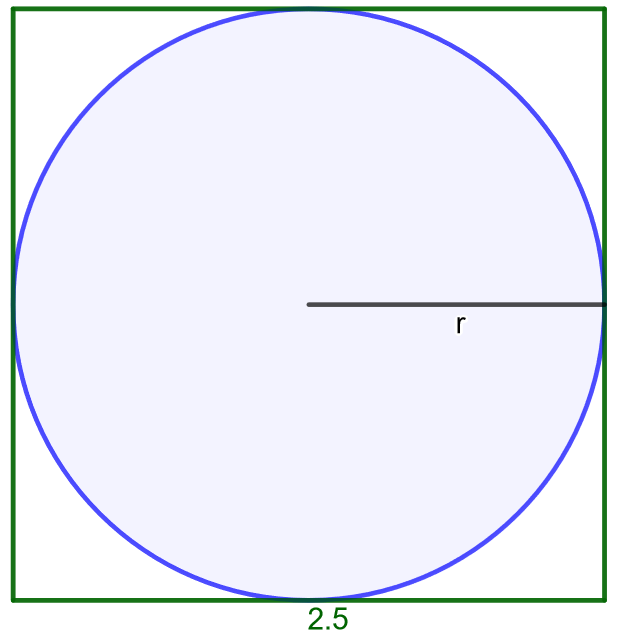
Yllä olevassa kuvassa on piirretty mallikuva tilanteesta. Jotta voitaisi laskea ympyrän pinta-ala, tulee selvittää neliöön mahtuvan ympyrän säde. Koska neliön sivun pituus on $2,5 \text{ m}$ , se on samalla ympyrän halkaisija. Ympyrän säde on puolet sen halkaisijasta, jolloin se on $r=1,25 \text{ m}$ .

Nyt ympyrän pinta-ala lasketaan $\begin{aligned} A&=\pi r^2 \\ A&= \pi \cdot 1,25^2 \\ A&\approx 4,90874 \end{aligned}$ Vastausta annettaessa muistetaan lisätä tarvittava yksikkö. Eli alueelle mahtuvan suurimman mahdollisen uima-altaan pinta-ala on noin $4,9 \text{ m}^2$ .

Tähän kappaleeseen liittyvät tehtävät.

# keskuskulma_kaaren_pituus

4.3 Keskuskulma, kaaren pituus, sektorin pinta-ala

Keskuskulma

Kulma, jonka kärki on ympyrän keskipisteessä, on keskuskulma.

Ympyrän kaaren pituuden kaavan johtaminen Opetus.tv:ssä.

Ympyrän kaaren pituus

Keskuskulman $\alpha$ kyljet rajaavat ympyrän kehältä kaaren, jonka pituus voidaan laskea seuraavasti $b = \frac{\alpha}{360 ^{\circ}} 2\pi r.$

4.3.1 Todistus

Perustellaan ympyrän kaaren pituuden laskukaava $b=\frac{\alpha}{360^{\circ}} 2 \pi r.$ Laskukaavan jälkimmäinen termi $2 \pi r$ on sama kuin koko ympyrän piiri. Laskukaavan ensimmäinen termi $\frac{\alpha}{360^{\circ}}$ kuvaa sitä, kuinka suuri osa kokonaisen ympyrän piiristä otetaan.

Jos kaarta vastaavan keskuskulman suuruus on esimerkiksi $180^{\circ}$ , on kyseisen kaaren pituus luonnollisesti puolet kokonaisen ympyrän kehän pituudesta, sillä $\frac{180^{\circ}}{360^{\circ}}=\frac{1}{2}$ .

4.3.2 Esimerkki: kaaren pituuden laskeminen

Tarkastellaan alla olevan kuvan kaltaista sektoria.

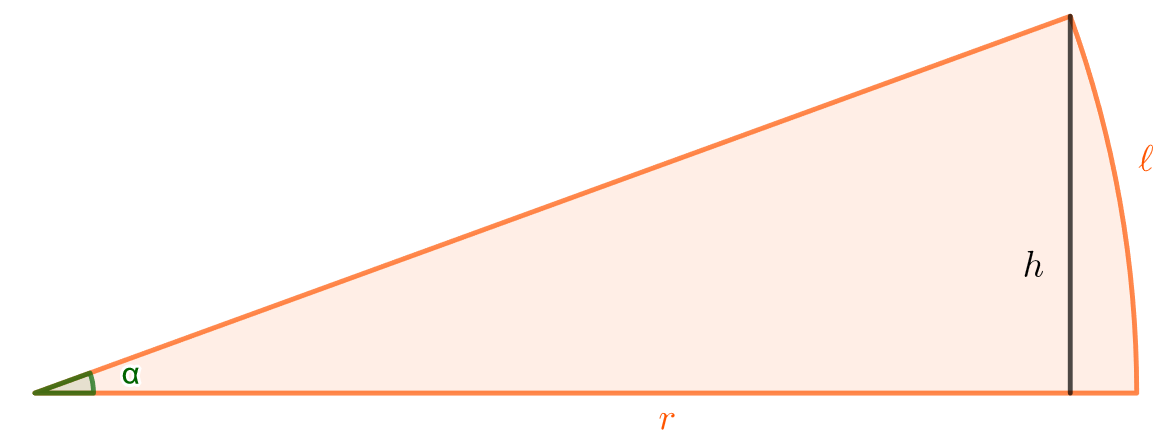
Ratkaistaan kaaren $\ell$ pituus. Jos kulma $\alpha$ on ilmaistu radiaaneissa, edellinen kaava muuttuu muotoon

$b=\frac{\alpha}{2 \pi} 2 \pi r = \alpha r.$

Nyt siis kaarelle $\ell=\alpha r$ . Pystysuoran pituuden suuruus voidaan määrittää sinin avulla:

$\sin \alpha= \frac{h}{r} \quad \Leftrightarrow \quad h = r \sin \alpha.$

Kun kulmaa $\alpha$ pienennetään, janan ja kaaren $\ell$ pituudet lähestyvät toisiaan. Voidaan siis merkitä, että kun $\alpha$ on pieni,

$\begin{aligned} h & \approx \ell \\ r \sin \alpha & \approx \alpha r \quad |:r \\ \sin \alpha & \approx \alpha \end{aligned}$

Eli kun kulma $\alpha$ on pieni, sen siniä voidaan approksimoida kulman arvolla (radiaaneina).

Ympyräsektorin pinta-alan kaavan johtaminen Opetus.tv:ssä.

Ympyrän sektorin pinta-ala

Keskuskulman $\alpha$ kyljet rajaavat ympyrän sisältä sektorin, jonka pinta-ala $A_{SEK}$ voidaan laskea seuraavasti: $A_{SEK}= \frac{\alpha}{360 ^{\circ}} \pi r^2.$ Jos tiedetään keskuskulmaa vastaavan kaaren pituus , voidaan sektorin pinta-ala laskea myös kaavalla $A_{SEK}=\frac{br}{2}.$

4.3.3 Todistus

Sektorin pinta-alan ylempi kaava voidaan perustella samalla tavalla kuin ympyrän kaaren pituuden kaava perusteltiin aiemmin. Toinen kaava voidaan perustella sijoittamalla siihen $b=\frac{\alpha}{360^{\circ}} 2 \pi r$ , jolloin saadaan $A_{SEK}=\frac{\alpha}{360^{\circ}} 2 \pi r \cdot \frac{r}{2}=\frac{\alpha}{360^{\circ}} \pi r^2$ joka on sama kuin sektorin pinta-alan ylempi kaava.

4.3.4 Esimerkki: ympyräsektorin pinta-alan ja keskuskulman laskeminen

Laske alla olevan ympyräsektorin pinta-ala. Kuinka suuri keskuskulma $\alpha$ on?

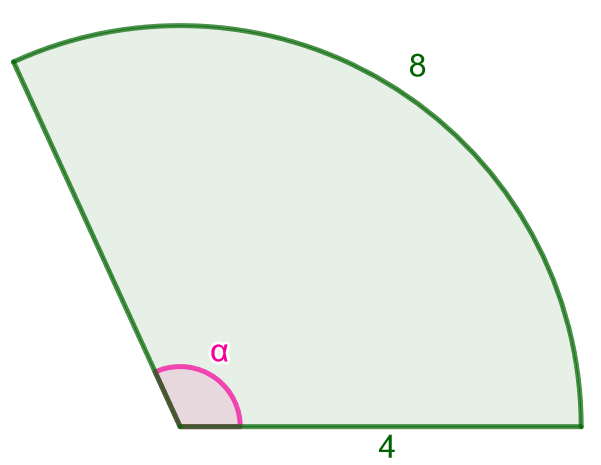
Nyt kaaren pituus on b=8 ja säde r=4 . Sektorin pinta-ala saadaan laskettua näiden tietojen avulla: $A=\frac{br}{2}=\frac{8 \cdot 4}{2}=16.$

Nyt kysytyn keskuskulman suuruus voidaan ratkaista sektorin pinta-alan toisesta kaavasta tai kaaren pituuden kaavan avulla. Ratkaistaan tässä keskuskulma ensimmäisellä tavalla. Ratkaistaan $\alpha$ sektorin pinta-alan kaavasta ja sijoitetaan arvot kaavaan $\begin{aligned} A&=\frac{\alpha}{360^{\circ}} \pi r^2 &\quad &|\cdot 360^{\circ} \\ 360 ^{\circ} A&= \alpha \pi r^2 &\quad &|:\pi r^2 \\ \alpha &= \frac{360^{\circ} A}{\pi r^2} \\ \alpha &= \frac{360^{\circ} \cdot 16}{\pi \cdot 4^2} \\ \alpha &\approx 114,591559 ^{\circ} \\ \alpha &\approx 114,6 ^{\circ} \end{aligned}$

Sektorin pinta-ala on siis ja sen keskuskulman suuruus on noin $114,6^{\circ}$ .

Tähän kappaleeseen liittyvät tehtävät.

# janne

4.4 Jänne, segmentti

Jänne

Ympyrän kehällä olevan kaaren päätepisteet yhdistää jänne.

Segmentin pinta-ala Opetus.tv:ssä.

Segmentin pinta-ala

Jänne jakaa ympyrän kahdeksi segmentiksi, joiden pinta-ala $A_{SEG}$ saadaan laskettua kaavalla $A_{SEG}=A_{SEK} \pm A_{keskuskolmio}.$ Kaavassa käytetään yhteenlaskua, jos keskuskulma $\alpha$ on suurempi kuin $180^{\circ}$ , ja vähennyslaskua, jos keskuskulma $\alpha$ on pienempi kuin $180^{\circ}$ .

4.4.1 Esimerkki: segmentin pinta-alan laskeminen 1

Laske alla olevaan kuvaan sinisellä merkityn segmentin pinta-ala.

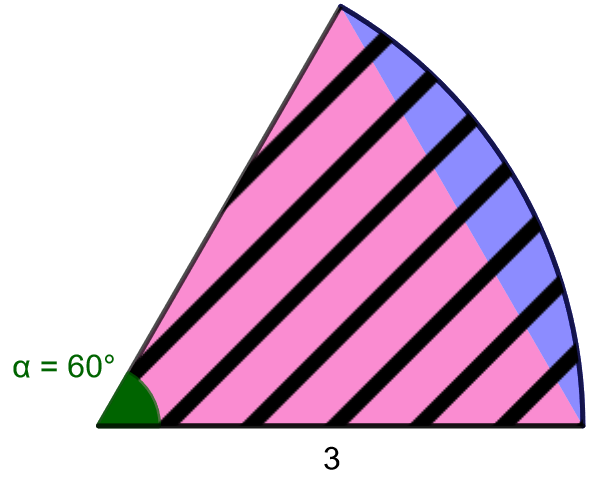
Koska keskuskulma $\alpha$ on pienempi kuin $180^{\circ}$ , käytetään kaavaa $A_{SEG}=A_{SEK}-A_{\text{keskuskolmio}}.$ Lasketaan ensin kuvaan mustalla vinoviivoituksella merkityn sektorin pinta-ala. Sektorin säde r=3 ja keskuskulma $\alpha=60^{\circ}$ , joten sektorin pinta-ala on $\begin{aligned} A_{SEK}&=\frac{\alpha}{360^{\circ}} \pi r^2 \\ &=\frac{60^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 \\ &=\frac{3\pi}{2} \end{aligned}$

Lasketaan sitten kuvaan pinkillä merkityn keskuskolmion pinta-ala. Kolmion kahden sivun pituudet ovat säteen mittaiset eli , ja näiden sivujen välinen kulma on $\alpha=60^{\circ}$ . Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla, jossa a=b=r=3 . $\begin{aligned} A_{\text{keskuskolmio}}&=\frac{ab}{2} \sin(\alpha) \\ &=\frac{r^2}{2} \sin(\alpha) \\ &=\frac{3^2}{2} \sin(60^{\circ}) \\ &=\frac{9\sqrt{3}}{4} \end{aligned}$

Lopuksi lasketaan segmentin pinta-ala vähennyslaskulla $\begin{aligned} A_{SEG}&=A_{SEK}-A_{\text{keskuskolmio}} \\ &= \frac{3 \pi}{2} - \frac{9 \sqrt{3}}{4} \\ &= \frac{6 \pi}{4} - \frac{9 \sqrt{3}}{4} \\ &= \frac{6 \pi - 9 \sqrt{3}}{4} \\ &\approx 0,81527 \\ &\approx 0,82 \end{aligned}$ Kysytyn segmentin pinta-ala on siis noin 0,82 .

4.4.2 Esimerkki: segmentin pinta-alan laskeminen 2

Ratkaise alla olevaan kuvaan sinisellä rajatun segmentin pinta-ala.

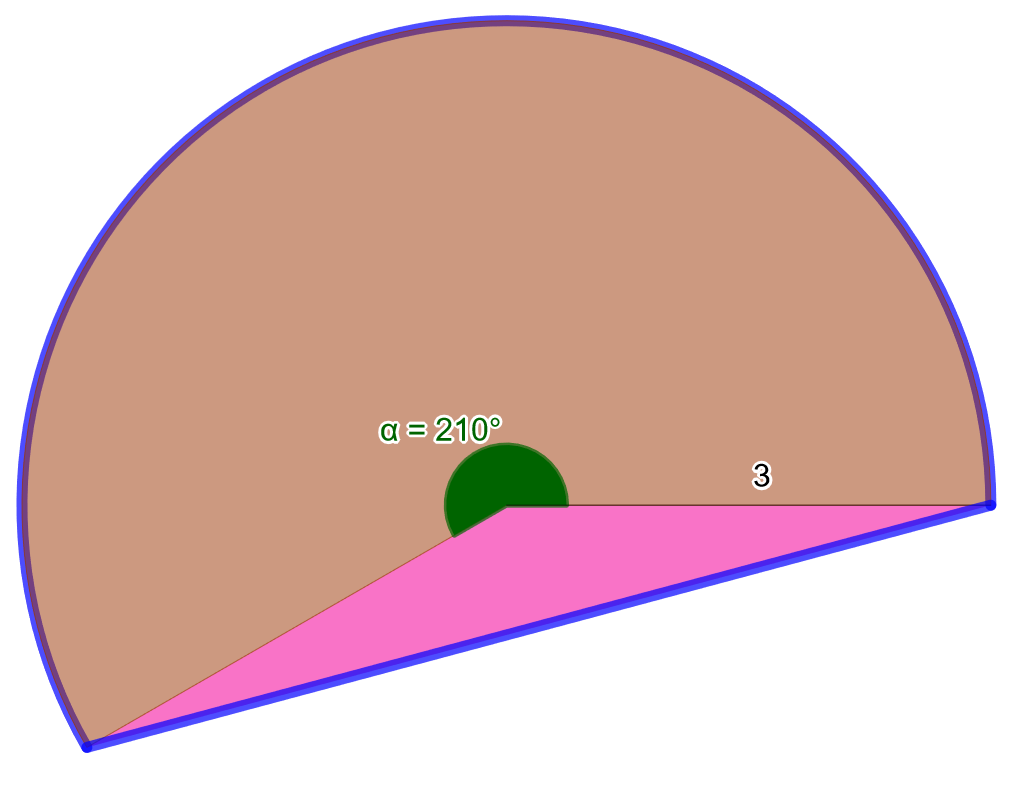
Koska keskuskulma $\alpha=210^{\circ}$ on suurempi kuin $180^{\circ}$ , käytetään laskukaavaa $A_{SEG}=A_{SEK}+A_{\text{keskuskolmio}}.$

Lasketaan ensin kuvaan ruskealla merkityn sektorin pinta-ala. Nyt säde r=3 ja keskuskulma $\alpha=210^{\circ}$ , joten sektorin pinta-ala on $\begin{aligned} A_{SEK} &= \frac{\alpha}{360^{\circ}}\pi r^2 \\ &= \frac{210^{\circ}}{360^{\circ}} \pi \cdot 3^2 \\ &= \frac{21 \pi}{4} \end{aligned}$

Seuraavaksi lasketaan keskuskolmion pinta-ala. Kolmion kahden sivun pituus on a=b=r=3 ja näiden sivujen välisen kulman suuruus on $\beta=360^{\circ}-210^{\circ}=150^{\circ}$ . Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla. $\begin{aligned} A_{\text{keskuskolmio}}&= \frac{r^2}{2} \sin(\beta) \\ &= \frac{3^2}{2} \sin(150^{\circ}) \\ &= \frac{9}{4} \end{aligned}$

Lopuksi lasketaan segmentin pinta-ala yhteenlaskulla $\begin{aligned} A_{SEG} &= A_{SEK} + A_{\text{keskuskolmio}} \\ &= \frac{21 \pi}{4} + \frac{9}{4} \\ &= \frac{21\pi +9}{4} \\ & \approx 18,7436 \\ &\approx 18,74 \end{aligned}$

Kuvaan sinisillä ääriviivoilla piirretyn segmentin pinta-ala on noin 18,74 .

Tähän kappaleeseen liittyvät tehtävät.

# tangentti

4.5 Tangentti, tangenttikulma

Sanalla tangentti voidaan matematiikassa tarkoittaa kahta asiaa, ja ne molemmat liittyvät geometriaan. Yleensä asiayhteydestä selviää, puhutaanko trigonometrisesta funktiosta nimeltä tangentti vai käyrää tasan yhdessä pisteessä sivuava suora. Tässä luvussa puhutaan tangentista sen jälkimmäisessä merkityksessä.

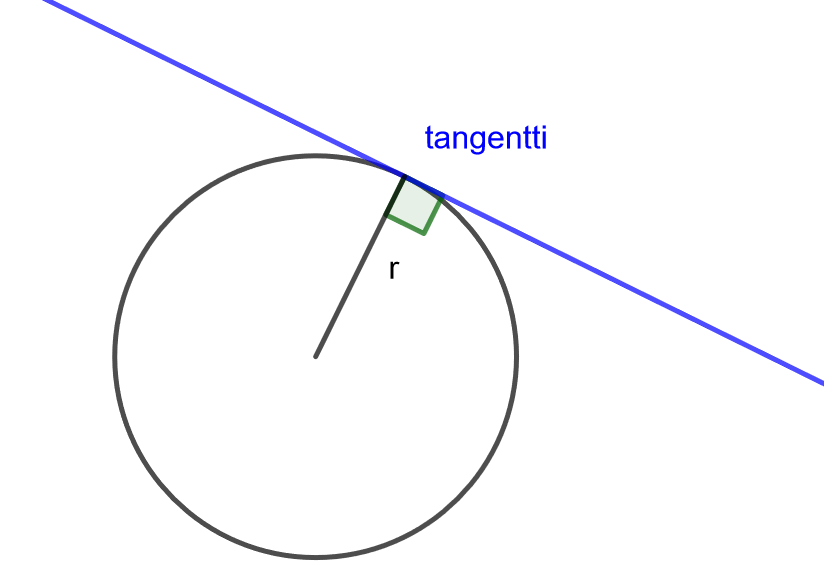
Tangentti

Tangentti on suora, joka kohtaa ympyrän vain yhdessä pisteessä. Ympyrän tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan.

Tangenttikulma Opetus.tv:ssä.

Tangenttikulma

Tangenttikulma on kahden ympyrän tangentin leikkauspisteeseen muodostuva kulma, jonka aukeamassa ympyrä on. Tangenttikulman ja sitä vastaavan keskuskulman summa on aina $180^{\circ}$ .

4.5.1 Todistus

Todistetaan tangenttikulmalause, jonka mukaan tangenttikulman ja sitä vastaavan keskuskulman summa on aina $180^{\circ}$ . Käytetään alla olevan kuvan merkintöjä.

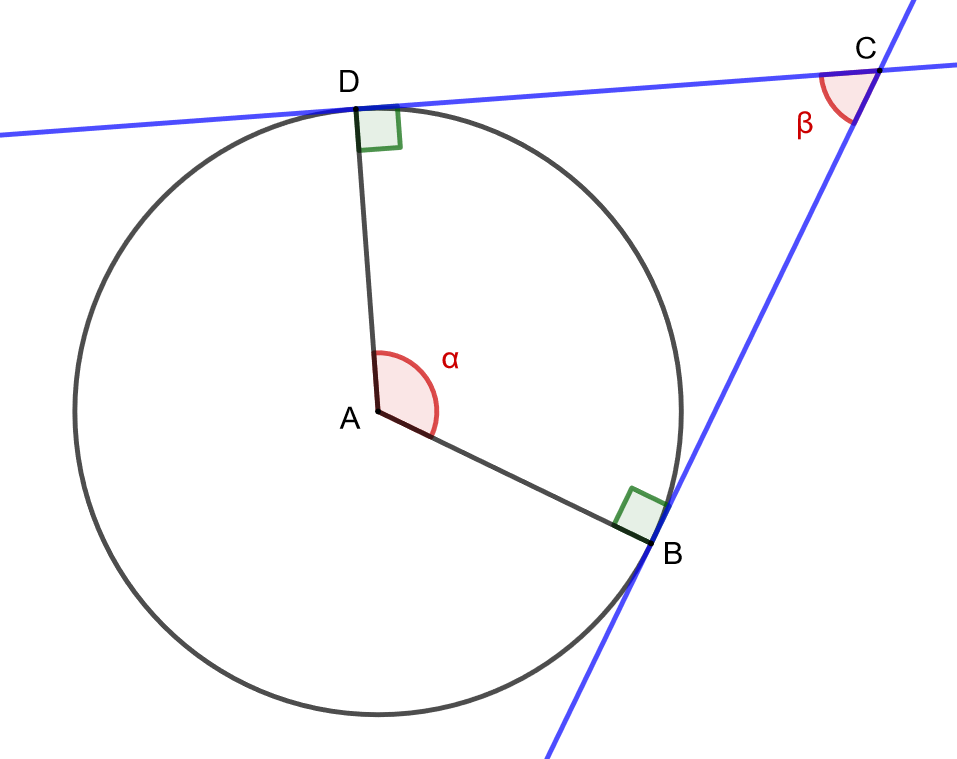
Ympyrän keskipiste , sen kehän pisteet ja sekä näiden kehän pisteiden kautta piirrettyjen tangenttien leikkauspiste muodostavat nelikulmion ABCD . Nelikulmion kulmien summa on aina $360^{\circ}$ . Ympyrän säteen sekä tangentin välinen kulma on aina suora. Samoin säteen ja tangentin välinen kulma on aina suora. Tästä saadaan, että on oltava $\alpha + \beta = 360^{\circ} - 2 \cdot 90^{\circ} = 180^{\circ}.$ Toisin sanoen, tangenttikulman ja sitä vastaavan keskuskulman summan on oltava $180^{\circ}$ .

4.5.2 Esimerkki: tangenttikulma GeoGebralla

# tangenttikulma-geo

Yllä olevalla GeoGebra-appletilla voit tutkia tangenttikulman ja sitä vastaavan keskuskulman suuruuksia. Huomaa, että tangenttien ja ympyrän säteiden väliset kulmat ovat koko ajan suoria kulmia, vaikka sinisiä pisteitä siirtäisikin.

Tähän kappaleeseen liittyvät tehtävät.

# keskuskulma

4.6 Keskuskulma, kehäkulma

Kehäkulma

Kehäkulma on kulma, jonka kärki on ympyrän kehällä ja jonka kylkinä on kaksi jännettä tai jänne ja tangentti. Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta. Samaa kaarta vastaavat kehäkulmat ovat aina yhtä suuria.

4.6.1 Todistus

Todistetaan kehäkulmalause eli lause "Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta". Tehdään todistus kolmessa vaiheessa:

ympyrän keskipiste on kehäkulman $\beta$ kyljellä,
ympyrän keskipiste on kehäkulman $\beta$ aukeamassa ja
ympyrän keskipiste ei ole kehäkulman $\beta$ aukeamassa.

Tarkastellaan ensin tapausta, jossa jänne kulkee ympyrän keskisteen kautta. Käytetään alla olevan kuvan merkintöjä.

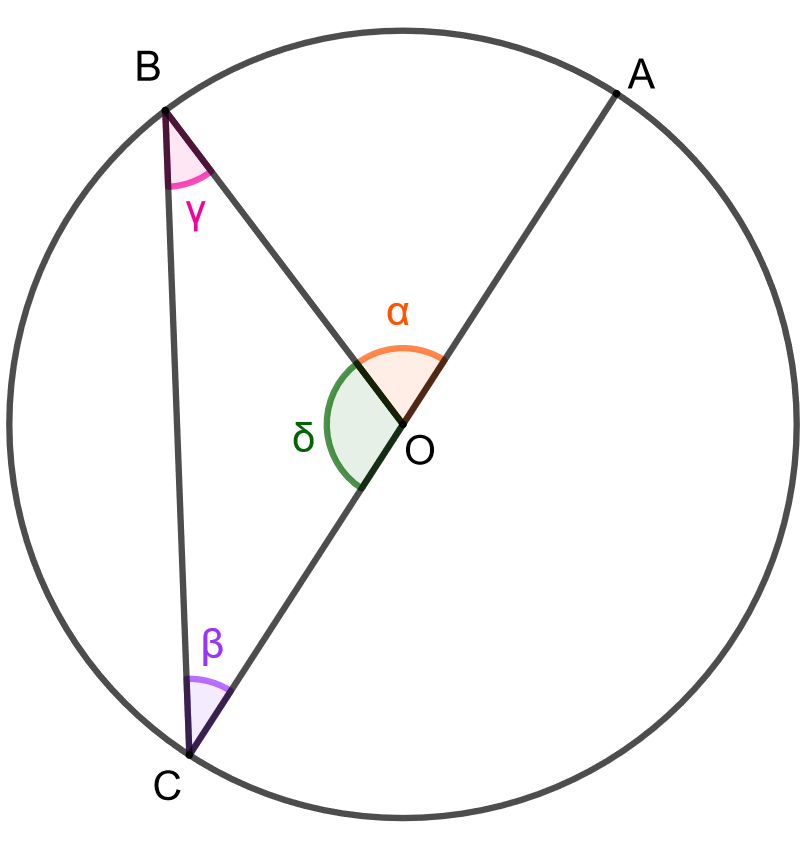
Huomataan, että pisteet , ja muodostavat tasakylkisen kolmion, jonka kantana on jänne ja kylkinä janat sekä . Kyljet ovat keskenään yhtä pitkiä, koska molemmat ovat ympyrän säteitä. Tasakylkisen kolmion kantakulmat ovat keskenään yhtä suuria, joten $\beta = \gamma$ . Koska kolmion kulmien summa on $180^{\circ}$ , saadaan yhtälö $\beta + \gamma + \delta = 180^{\circ}.$ Lisäksi huomataan, että kulmat $\alpha$ ja $\delta$ ovat vieruskulmia, jolloin niiden summa on $180^{\circ}$ eli $\alpha + \delta = 180^{\circ}$ . Ratkaistaan tästä kulma $\delta$ , jolloin saadaan $\delta = 180^{\circ} - \alpha$ . Sijoitetaan tämä sekä $\gamma = \beta$ kolmion kulmien summan lausekkeeseen, jolloin saadaan $\beta + \beta + 180^{\circ} - \alpha = 180^{\circ} \Leftrightarrow \beta = \frac{\alpha}{2}.$ Eli kehäkulma on puolet vastaavasta keskuskulmasta.

Tarkastellaan seuraavaksi tapausta, jossa ympyrän keskipiste on kehäkulman $\beta$ aukeamassa. Käytetään alla olevan kuvan merkintöjä.

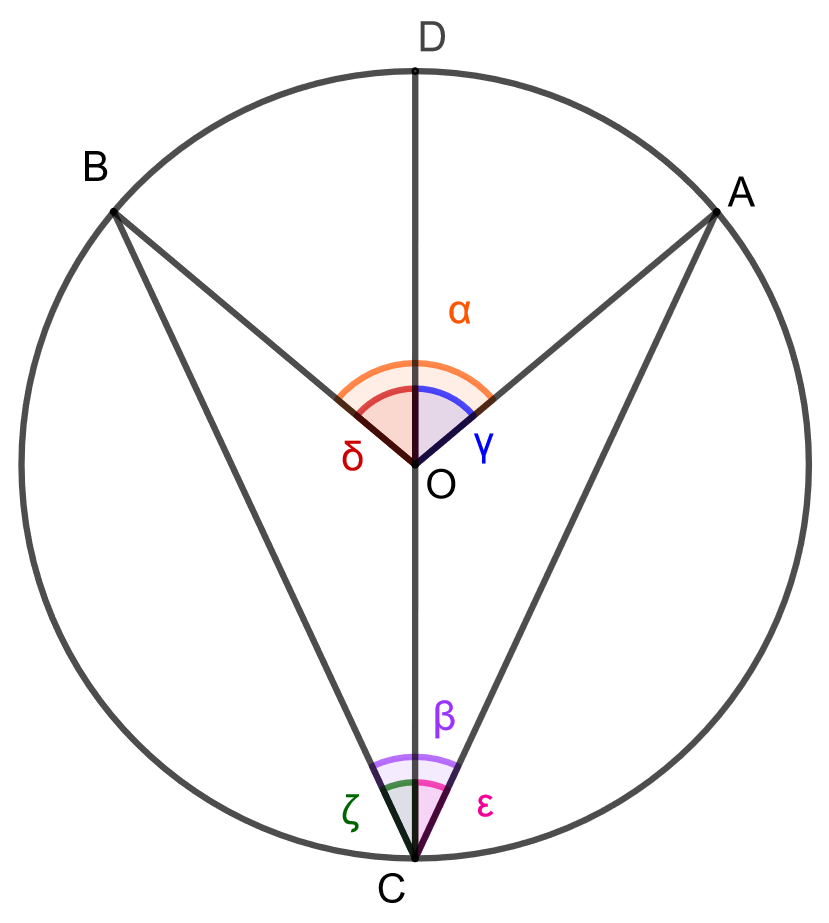
Jaetaan kulma $\alpha$ kahdeksi kulmaksi $\gamma$ ja $\delta$ janalla , joka kulkee ympyrän keskipisteen kautta. Sama jana jakaa kehäkulman $\beta$ kulmiksi $\epsilon$ ja $\zeta$ . Voimme tarkastella ensin pelkästään janan oikealla puolella olevia kulmia ja sitten sen vasemmalla puolella olevia. Tällöin todistuksen edellisen kohdan perusteella saadaan $\epsilon = \frac{\gamma}{2}$ ja $\zeta=\frac{\delta}{2}$ .

Tiedetään, että $\alpha = \gamma + \delta$ . Lisäksi tiedetään, että $\beta = \epsilon + \zeta$ . Sijoitetaan tähän aiemmat yhtälöt, jolloin saadaan $\beta = \frac{\gamma}{2} + \frac{\delta}{2} = \frac{\gamma + \delta}{2} = \frac{\alpha}{2}.$ Eli kehäkulma $\beta$ on puolet vastaavasta keskuskulmasta $\alpha$ .

Tarkastellaan lopuksi tapausta, jossa ympyrän keskipiste ei ole kehäkulman $\beta$ aukeamassa. Käytetään alla olevan kuvan merkintöjä.

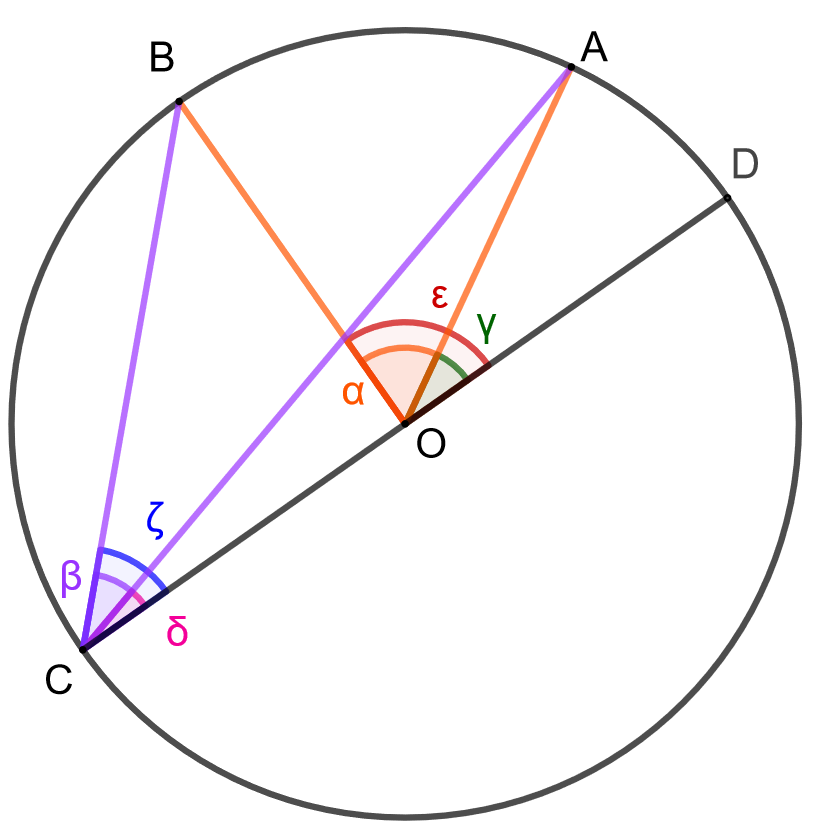
Huomataan, että $\alpha = \epsilon - \gamma$ ja että $\beta = \zeta - \delta$ . Todistuksen ensimmäisen kohdan perusteella voidaan kirjoittaa $\beta = \zeta - \delta = \frac{\epsilon}{2} - \frac{\gamma}{2} = \frac{\epsilon - \gamma}{2} = \frac{\alpha}{2}.$ Kehäkulma $\beta$ on siis puolet keskuskulmasta $\alpha$ .

4.6.2 Esimerkki: kehäkulma GeoGebralla

# kehakulma-geo

Yllä olevassa GeoGebra-appletissa on merkitty vihreällä keskuskulma ja pinkillä samoja pisteitä vastaava kehäkulma. Kokeile muuttaa kulmien suuruuksia, ja huomaa, että kehäkulma on aina puolet vastaavan keskuskulman suuruudesta.

4.6.3 Esimerkki: kaksi kehäkulmaa GeoGebralla

# tupla-kehakulma-geo

Yllä olevassa GeoGebra-appletissa on piirretty kaksi samaa ympyrän kaarta vastaavaa kehäkulmaa. Kokeile siirtää kuvion pisteitä ja huomaa, että kehäkulmat pysyvät koko ajan yhtä suurina keskenään.

Kehäkulmalauseen erityistapauksena on Thaleen lause. Sen mukaan puoliympyrän sisältämä kehäkulma on suora. Kehäkulmalauseen perusteella tämä on selvä asia, sillä puoliympyrän rajaava keskuskulma on $180^{\circ}$ , jolloin kehäkulman on oltava puolet siitä eli $90^{\circ}$ .

4.6.4 Esimerkki: Thaleen lause GeoGebralla

# thaleen-lause-geo

Yllä olevassa GeoGebra-appletissa voit kokeilla siirtää sinisiä pisteitä, jotka kuitenkin pysyvät koko ajan ympyrän vastakkaisilla reunoilla. Kokeile lisäksi siirtää oranssia pistettä ja huomaa, että $180^{\circ}$ kulmaa vastaava kehäkulma on aina suora kulma.

Tähän kappaleeseen liittyvät tehtävät.

5. Avaruusgeometria

Tässä luvussa siirrytään tasosta kolmiulotteiseen avaruuteen. Kuitenkin monia tasogeometriassa opittuja lauseita ja ominaisuuksia voi hyödyntää myös avaruusgeometriassa. Tähän kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

# monitahokas-kasitteet-geo

Yllä olevassa GeoGebra-appletissa on käyty läpi monitahokkaan osia ja niiden nimityksiä. Monitahokas on mikä tahansa monikulmioista koostuva suljettu pinta. Jos kaikki monitahokkaan tahkot ovat samanlaisia säännöllisiä monikulmioita, kyseessä on säännöllinen monitahokas. Tällaisia ovat esimerkiksi kuutio, säännöllinen tetraedri ja oktaedri.

# kulmia-avaruudessa

5.1 Kulmia avaruudessa

Kolmiulotteisessa avaruudessa voidaan laskea muun muassa kahden suoran välinen kulma, kahden tason välinen kulma tai tason ja suoran välinen kulma. Seuraavissa esimerkeissä lasketaan suorakulmaisen särmiön avauuslävistäjän pituus sekä sen ja pohjan välisen kulman suuruus.

5.1.1 Esimerkki: avaruuslävistäjän pituuden laskeminen

Laske suorakulmaisen särmiön avaruuslävistäjän pituus, kun sen sivujen pituudet ovat , ja .

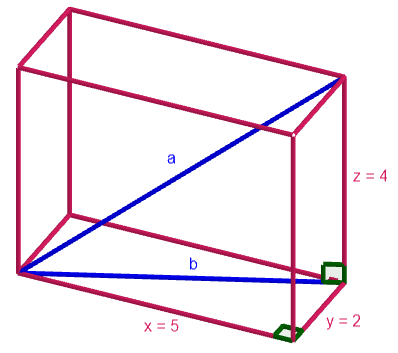
Tehtävässä kysytään siis yllä olevan kuvan avaruuslävistäjän pituutta. Jotta se voitaisi ratkaista, selvitetään ensin, kuinka pitkä lävistäjä on.

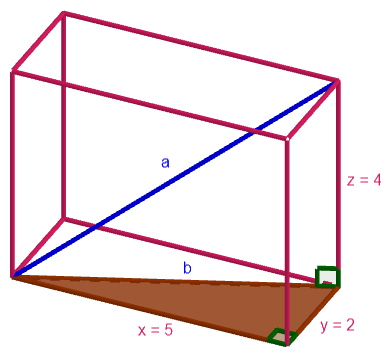
Yllä olevaan kuvaan on korostettu suorakulmaisen särmiön pohjassa oleva suorakulmainen kolmio, jonka hypotenuusa pitäisi ratkaista. Se onnistuu esimerkiksi Pythagoraan lauseella: $\begin{aligned} b^2 &= x^2+y^2 \\ b &= \pm \sqrt{x^2+y^2} \\ b &= \pm \sqrt{5^2+2^2} \\ b &= \pm \sqrt{29} \end{aligned}$ Koska lävistäjän pituus ei voi olla negatiivinen, valitaan vastaukseksi $b=\sqrt{29}$ .

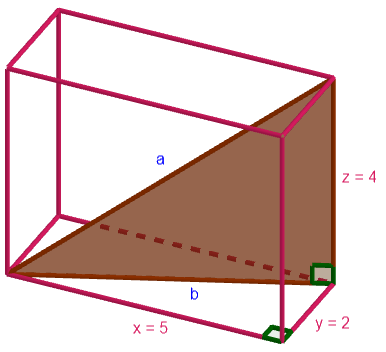
Nyt yllä olevaan kuvaan on korostettu lävistäjän , monitahokkaan särmän ja avaruuslävistäjän muodostama suorakulmainen kolmio. Tästä saadaan ratkaistua hypotenuusa jälleen Pythagoraan lauseella.

$\begin{aligned} a^2 &= b^2+z^2 \\ a &= \pm \sqrt{b^2+z^2} \\ a &= \pm \sqrt{(\sqrt{29})^2+4^2} \\ a &= \pm \sqrt{45} \\ a &= \pm 3 \sqrt{5} \end{aligned}$ Koska avaruuslävistäjän pituus on positiivinen, vastaus on siis $3 \sqrt{5}$ .

5.1.2 Esimerkki: avaruuslävistäjän ja pohjan välinen kulma

Lasketaan seuraavaksi avaruuslävistäjän ja suorakulmaisen särmiön pohjan välinen kulma $\alpha$ .

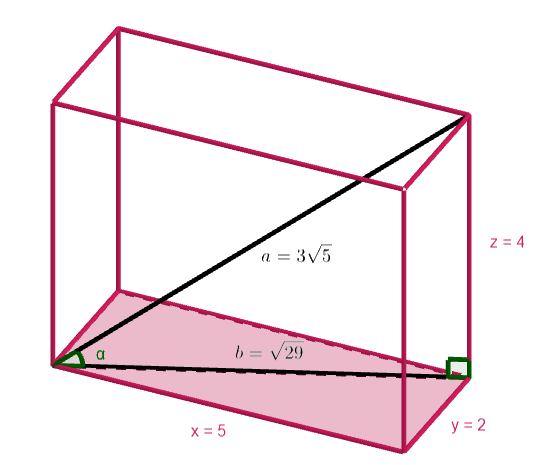
Kulma saadaan ratkaistua trigonometristen funktioiden avulla, esimerkiksi käyttämällä siniä:

$\begin{aligned} \sin ( \alpha) &= \frac{z}{a} \\ \alpha &= \sin ^{-1} \left(\frac{z}{a}\right) \\ \alpha &= \sin ^{-1} \left( \frac{4}{3 \sqrt{5}} \right) \\ \alpha &= 36,6 ^{\circ} \end{aligned}$ Särmiön avaruuslävistäjän ja pohjan välinen kulma on noin $37^{\circ}$ .

Tähän kappaleeseen liittyvät tehtävät.

5.2 Pallo

Pallon pinta-ala ja tilavuus

Pallon muodostavat ne pisteet, jotka ovat säteen etäisyydellä pallon keskipisteestä. Pallon pinta-ala ja tilavuus lasketaan sen säteen avulla $A=4 \pi r^2$ ja $V=\frac{4\pi r^3}{3}.$

5.2.1 Esimerkki: maapallon pinta-ala ja tilavuus

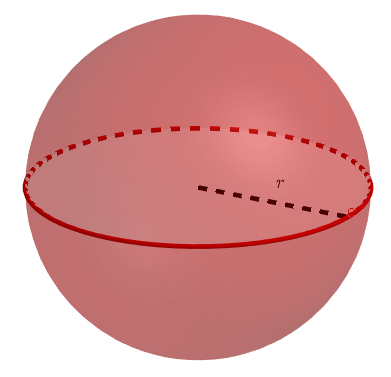
Laske maapallon pinta-ala ja tilavuus, kun sen säde on $6378 \text{ km}$ .

Koska maapallon säde on $r=6378 \text{ km}$ , sen pinta-ala on $A=4 \pi r^2=4 \pi \cdot (6378 \text{ km})^2= 511 \, 185 \, 932,523 \text{ km}^2$

ja tilavuus on $V=\frac{4 \pi r^3}{3}=\frac{4 \pi \cdot (6378 \text{ km})^3}{3} =1 \, 086 \, 781 \, 292 \, 542,889 \text{ km}^3$ Eli maapallon pinta-ala on noin $5,11 \cdot 10^8 \text{ km}^2$ ja tilavuus on noin $1,09 \cdot 10^{12} \text{ km}^3$ .

Segmentti

Taso leikkaa pallon kahteen osaan, joita kutsutaan segmenteiksi. Segmentin tilavuus saadaan sen korkeuden avulla $V_{\text{segmentti}} = \pi h^2 \left(r -− \frac{h}{3} \right).$ Pallon pinnasta taso rajaa kalotin, jonka pinta-ala saadaan segmentin korkeuden avulla $A_{\text{kalotti}}=2 \pi rh.$

5.2.2 Esimerkki: napapiirien rajaama pinta-ala

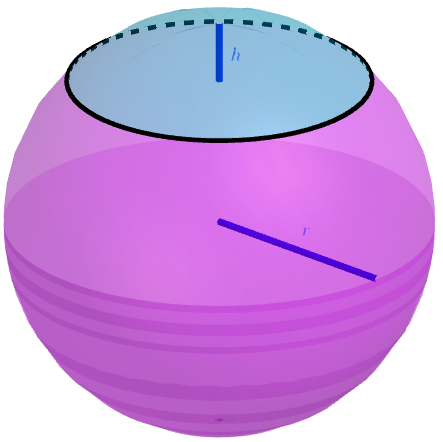
Napapiirit ovat maapallon pohjois- ja eteläosissa sijaitsevat kaksi leveyspiiriä, joiden pohjois- ja eteläpuolilla on mahdollista kokea kaamos ja yötön yö. Napapiirien leveysaste on $66,5^{\circ}$ . Kuinka suuri osa maapallon pinta-alasta on pohjoisen napapiirin pohjoispuolella tai eteläisen napapiirin eteläpuolella?

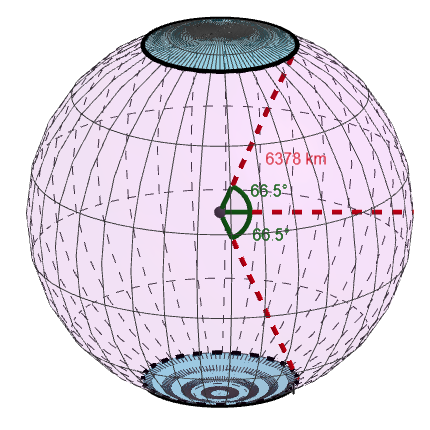
Jotta napapiirien rajaamien kalottien pinta-alat voitaisi laskea, tulee tietää kalotin korkeus. Huomataan, että pallon sisään muodostuu alla olevan kuvan mukainen kolmio, josta voidaan ratkaista kalotin korkeus .

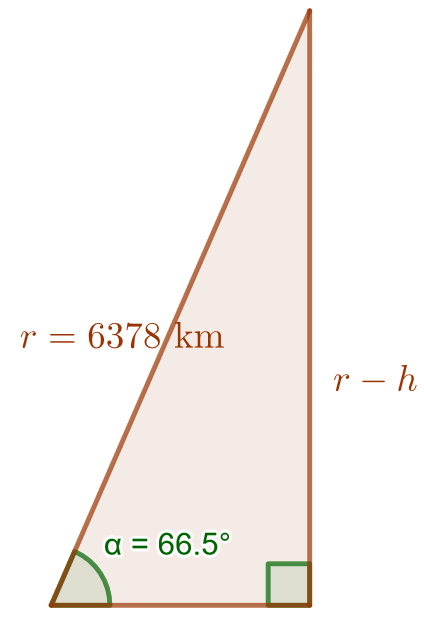
Ratkaistaan kalotin korkeus

$\begin{aligned} \sin(\alpha) &= \frac{r-h}{r} \\ h &= r- r \sin(\alpha) \\ h &= r \cdot (1- \sin(\alpha) ) \end{aligned}$

Yhden kalotin pinta-ala on siis kaavan mukaisesti $\begin{aligned} A_{\text{kalotti}} &= 2 \pi r h \end{aligned}$ jolloin kahden kalotin osuus koko maapallon pinta-alasta voidaan laskea $\begin{aligned} \frac{A_{\text{kalotit}}}{A_{\text{pallo}}} &= \frac{2 \cdot 2 \pi r h}{4 \pi r^2} \\ &= \frac{4 \pi r h}{4 \pi r r} \\ &= \frac{h}{r} \\ &= \frac{r (1-\sin(\alpha))}{r} \\ &= 1-\sin(\alpha) \\ &= 1-\sin(66,5^{\circ}) \\ &= 0,0829 \end{aligned}$

Maapallon pinta-alasta noin $8,3 \%$ on pohjoisen napapiirin pohjoispuolella tai eteläisen napapiirin eteläpuolella.

Tähän kappaleeseen liittyvät tehtävät.

# lierio

5.3 Lieriö

Lieriön pinta-ala ja tilavuus

Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa, muodostuu lieriöpinta. Kun lieriöpinta leikataan kahdella tasolla, syntyy lieriö. Lieriön vaipan pinta-ala saadaan laskettua sen pohjan piirin ja lieriön korkeuden avulla A_v=ph. Lieriön tilavuus saadaan laskettua pohjan pinta-alan A_p ja lieriön korkeuden avulla V=A_p h.

Erityistapaus lieriöstä on suora ympyrälieriö, jota kutsutaan myös sylinteriksi. Suoran ympyrälieriön pohja on ympyrän muotoinen ja sen korkeusjana sekä pohjan säde ovat kohtisuorassa toisiaan vastaan. Lieriö, jonka pohja on muodoltaan monikulmio, on särmiö. Erikoistapaus särmiöstä on esimerkiksi suorakulmainen särmiö.

5.3.1 Esimerkki: suoran ympyrälieriön vaipan aukilevitys GeoGebralla

# aukilevitys-geo

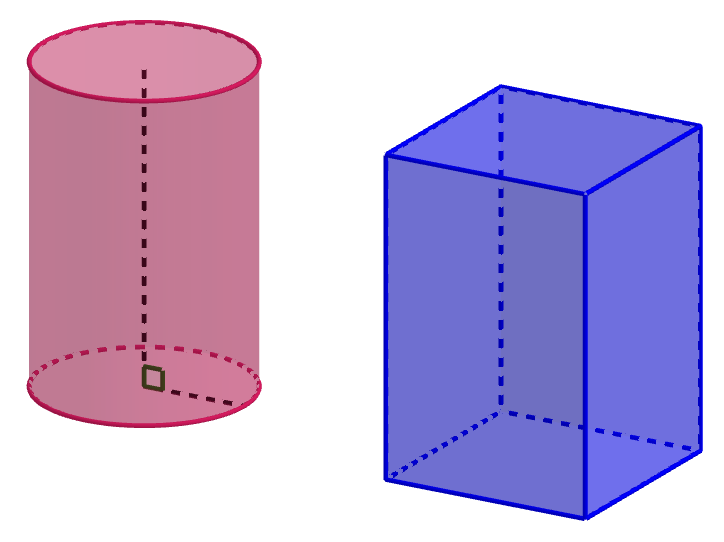
Kokeile vetää suoran ympyrälieriön vaippa auki yllä olevassa GeoGebra-appletissa vetämällä punaista "vedä!"-pistettä hiirellä oikealle. Mitkä ovat syntyvän suorakulmion mitat?

5.3.2 Esimerkki: vinon ympyrälieriön tilavuus

Laske alla olevan lieriön tilavuus.

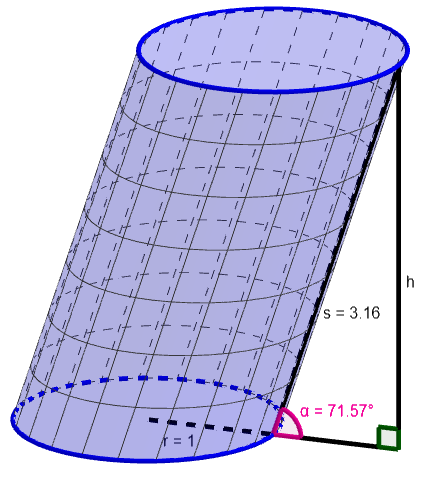
Aluksi pitää ratkaista lieriön korkeus . Se saadaan selville kuvaan piirretyn suorakulmaisen kolmion ja trigonometristen funktioiden avulla. $\begin{aligned} \sin(\alpha) &= \frac{h}{s} \\ h &= s \cdot \sin(\alpha) \end{aligned}$ Tämän jälkeen ratkaistaan tilavuus $\begin{aligned} V&= A_p h \\ &= \pi s r^2 \sin(\alpha) \\ &= \pi \cdot 3,16 \cdot 1^2\cdot \sin (71,57^{\circ}) \\ &= 9,418 \end{aligned}$ Lieriön tilavuus on siis noin 9,4 .

Tähän kappaleeseen liittyvät tehtävät.

# kartio

5.4 Kartio

Kartion tilavuus

Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa ja lisäksi suora kulkee koko ajan saman pisteen kautta, syntyy kartiopinta. Kun kartiopinta leikataan tasolla, syntyy kartio. Kartion tilavuus lasketaan sen pohjan pinta-alan A_p ja korkeuden avulla $V = \frac{A_p h}{3}.$

Erikoistapauksia kartiosta ovat ympyräkartio ja pyramidi eli särmäkartio. Ympyräkartion pohjana on ympyrä ja särmäkartion pohjana on monikulmio. Jos ympyräkartion kokeusjana on kohtisuorassa pohjaympyrän sädettä vastaan, kyseessä on suora ympyräkartio.

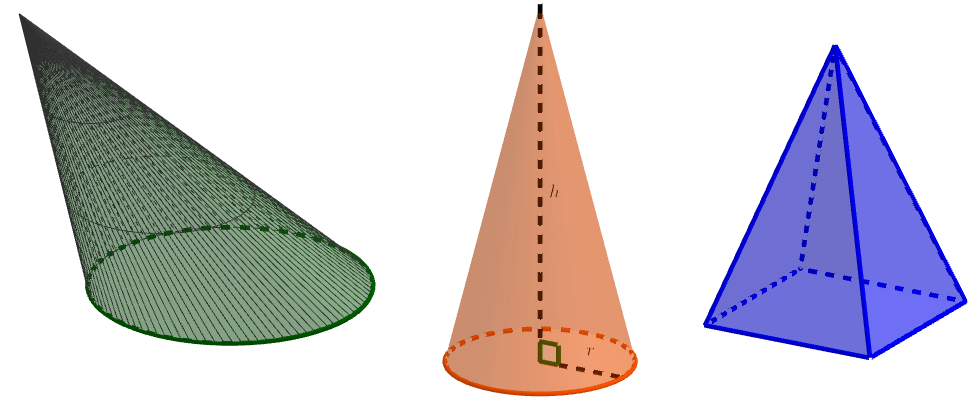
Ympyräkartio, suora ympyräkartio ja pyramidi

5.4.1 Esimerkki: vinon ympyräkartion tilavuus

Laske alla olevan ympyräkartion tilavuus.

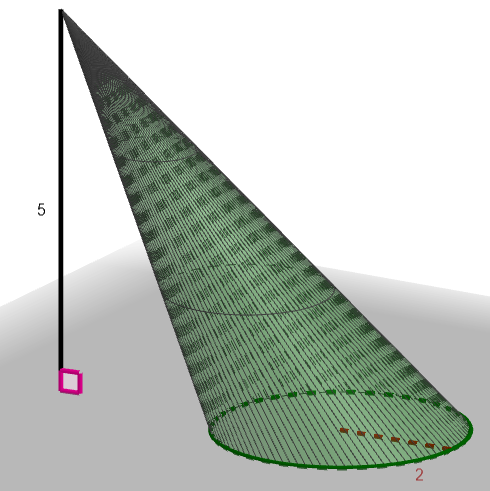
Lasketaan ensin kartion pohjan pinta-ala. Koska pohja on ympyrä, pinta-ala saadaan laskettua $\begin{aligned} A_p &= \pi r^2. \end{aligned}$

Nyt säde r=2 ja kartion korkeus h=5 , jolloin kartion tilavuus on $\begin{aligned} V&=\frac{A_p h}{3} \\ &= \frac{\pi r^2 h}{3} \\ &= \frac{\pi \cdot 2^2 \cdot 5}{3} \\ &= 20,943951 \end{aligned}$ Kartion tilavuus on siis noin 20,9 .

Suoran ympyräkartion vaipan pinta-ala

Suoran ympyräkartion vaipan pinta-ala voidaan laskea pohjaympyrän säteen ja kartion sivujanan avulla $A_v=\pi rs.$

5.4.2 Esimerkki: sirkusteltan pinta-ala

Sirkusteltta muodostuu suorasta ympyrälieriöstä, jonka korkeus on $3 \text{ m}$ ja jonka pohjan säde on $6 \text{ m}$ , sekä suorasta ympyräkartiosta, jonka korkeus on $3 \text{ m}$ ja jonka pohjan säde on $6\text{ m}$ . Kuinka monta neliömetriä tarvitaan telttakangasta?

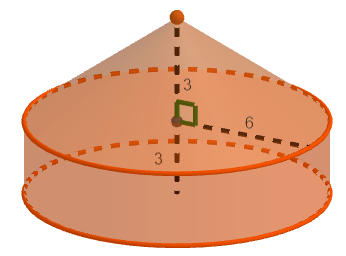
Piirretään ensin yllä olevan kuvan mukainen mallikuva, johon merkitään tunnetut pituudet. Lasketaan ensin pohjalla olevan lieriön vaipan pinta-ala. Se lasketaan pohjaympyrän piirin ja lieriön korkeuden h_1 avulla $\begin{aligned} A_\ell &= ph_1 \\ &= 2 \pi r h_1 \\ \end{aligned}$

Kattona olevan kartion pinta-ala saadaan laskettua sen pohjaympyrän säteen ja kartion sivujanan avulla. Ratkaistaan sivujanan pituus suorakulmaisesta kolmiosta Pythagoraan lauseen avulla.

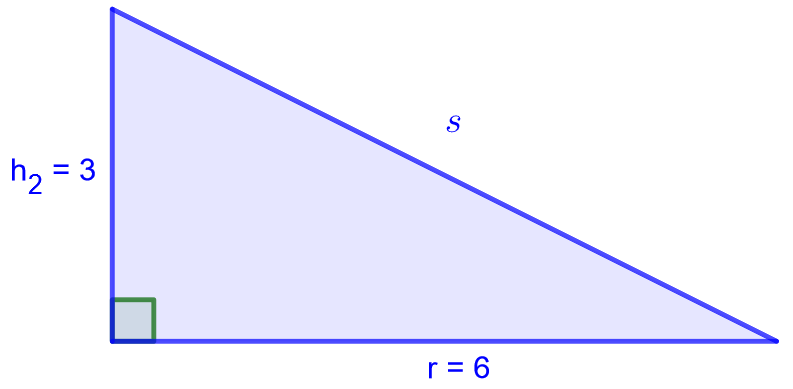
$\begin{aligned} h_2^2+r^2 &= s^2 \\ s &= \sqrt{h_2^2+r^2} \end{aligned}$

Tämän jälkeen lasketaan kartion vaipan pinta-ala $\begin{aligned} A_k &= \pi r s \\ &= \pi r \sqrt{h_2^2+r^2} \end{aligned}$

Lopuksi lasketaan kummankin kappaleen vaippojen alat yhteen. $\begin{aligned} A &= A_\ell + A_k \\ &= 2\pi r h_1 + \pi r \sqrt{h_2^2+r^2} \\ &= 2 \pi \cdot 6 \cdot 3 + 6 \pi \sqrt{3^2+6^2} \\ &= 239,544 \end{aligned}$

Sirkustelttaan tarvitaan telttakangasta noin $240 \text{ m}^2$ .

Tähän kappaleeseen liittyvät tehtävät.