5. Avaruusgeometria: tehtäviä

Tällä sivulla on tehtäviä kappaleeseen Avaruusgeometria liittyen.

# kulmia-avaruudessa

5.1 Kulmia avaruudessa

Tämän kappaleen teoria on kappaleessa Kulmia avaruudessa.

# teht_avaruuslavistaja

5.1.1 Tehtävä

# avaruuslavistaja

# teht_avaruuskulma

5.1.2 Tehtävä

Suorakulmaisen särmiön muotoisen laatikon sivujen pituudet ovat x=10 , y=3 ja z=8 . Laatikon sisään asetetaan lauta kuvan mukaisesti. Kuinka suuri on laatikon pohjan ja laudan välinen kulma?

# avaruuslavistaja_kulma

# teht_pahvikuutio

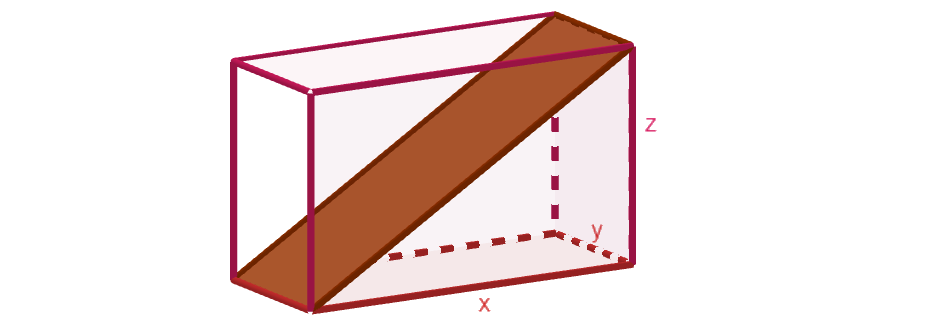
5.1.3 Tehtävä

Matti valmistaa pahvista kuution, jonka sivun pituus on $20 \text{ cm}$ .

Kuinka paljon pahvia tarvitaan kuution tekoon?

# pahvikuutio_1

Matti haluaa asettaa kuution sisään mahdollisimman pitkän ohuen riman. Kuinka pitkä rima kuutioon mahtuu?

# pahvikuutio_2

# pallo-teht

5.2 Pallo

Tämän kappaleen teoria on kappaleessa Pallo.

# teht_auringonpimennys

5.2.1 Tehtävä

Täydellisessä auringonpimennyksessä kuu peittää maasta katsottuna auringon kokonaan. Jos auringon etäisyys maasta on 387 -kertainen kuun etäisyyteen maasta, kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna?

# auringonpimennys

# teht_K16T6

5.2.2 Tehtävä (K2016/6)

Maapallon säde on $6371 \text{ km}$ , ja sen pohjoisen napapiirin leveysaste on 66,5 . Pohjoiselta napapiiriltä valitaan pisteet ja , joiden pituusasteiden erotus on astetta.

Määritä pisteiden ja välisen viivasuoran tunnelin pituus.

# K16T6a

Määritä pisteiden ja välisen lyhimmän napapiirin kaaren pituus.

# K16T6b

# teht_puolipallon_tilavuus

5.2.3 Tehtävä

Pallon pinta-ala on $2,5 \text{ m}^2$ . Pallo jaetaan kahteen yhtä suureen osaan. Laske muodostuvan puolipallon tilavuus.

# puolipallon_tilavuus

# teht_maapallon_vesi

5.2.4 Tehtävä

Vesi peittää noin $70 \%$ maapallon pinnasta. Jos maapallon säde on noin $6 370 \text{ km}$ , kuinka suuren pinta-alan vesi peittää?

# veden_pinta_ala

# teht_maapallon_vedet2

5.2.5 Tehtävä

Maapallon vesien yhteenlaskettu määrä on noin $1,386 \cdot 10^9 \text{ km}^3$ . Oletetaan, että maapallon säde on noin $6370 \text{ km}$ ja että maapallo on täydellinen pallo. Jos kaikki vesi levittäytyisi maapallon pinnalle tasaisesti, kuinka syvä vesikerros olisi?

# maapallon_vedet2

# lierio-teht

5.3 Lieriö

Tämän kappaleen teoria on kappaleessa Lieriö.

# teht_aakkoskarkki

5.3.1 Tehtävä

Palaa tehtävään, jossa laskettiin aakkoskarkin pinta-alaa. Jos aakkoskarkin paksuus on $0,7 \text{ cm}$ , mikä on yhden karkin tilavuus?

# aakkostilavuus

Jos karkin tiheys on $1,5 \text{ g/cm}^3$ ja yksi pussi painaa $315 \text{ g}$ , kuinka monta karkkia yhdessä pussissa on?

# aakkostilavuus2

# teht_vesitorni

5.3.2 Tehtävä

Vesitornin sylinterin muotoiseen säiliöön mahtuu vettä $4000 \text{ m}^3$ ja säiliön korkeus on metriä. Mikä on säiliön halkaisija?

# vesitorni

# teht_maitotolkki

5.3.3 Tehtävä

Alla olevassa kuvassa on havainnekuva maitotölkistä sekä tölkin mitat (senttimetreinä). Laske koko tölkin tilavuus.

# maitotolkki

# teht_muurahainen

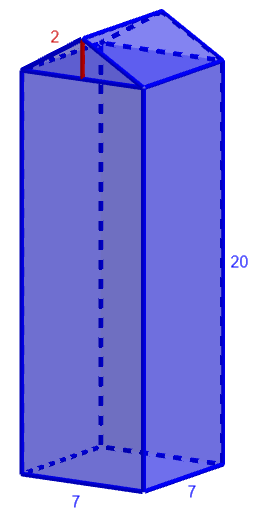
5.3.4 Tehtävä

Muurahainen aloittaa kulkunsa kuution kulmasta. Kuution särmän pituus on . Mikä on lyhin matka, jonka kulkemalla muurahainen pääsee kuution vastakkaiseen kulmaan?

# muurahainen-geo

# muurahaisen_matka

# teht_kuutio_pallossa

5.3.5 Tehtävä

Jos pallon tilavuus on , mikä suurimman sen sisään mahtuvan kuution tilavuus?

# kuutio_pallossa

# teht_pallo_lieriossa

5.3.6 Tehtävä

Mahdollisimman pienen ympyräpohjaisen lieriön sisälle laitetaan mahdollisimman suuri pallo. Määritä pallon tilavuuden suhde lieriön tilavuuteen.

# pallo_lieriossa

# teht_preliK17T5

5.3.7 Tehtävä (Pitkän matematiikan preli K2017/5)

Yritys lähettää tuotteitaan asiakkaille suorakulmaisen särmiön muotoisessa laatikossa, jossa sivujen suhteet ovat laatikon sisällä 1 : 3 : 6 .

Erääseen lähetykseen pakataan kolme suoraa ympyräpohjaista metallilieriötä, joiden korkeus on sama kuin laatikon pisimmän sivun pituus ja pohjan halkaisija on yhtä pitkä kuin laatikon lyhin sivu. Tyhjä tila täytetään styroksilla. Mikä on lieriöiden täyttämän tilan ja laatikon tilavuuksien suhde?

# sarmio_1

Kuinka monta prosenttia laatikon tilavuudesta on styroksia?

# sarmio_2

Jos laatikon tilavuus on litraa, niin mahtuuko laatikkoon metallipallo, jonka säde on $5,0 \text{ cm}$ ?

# sarmio_3

# teht_S15T3b

5.3.8 Tehtävä (S2015/3b)

Laske kuution yhden sivutahkon pinta-ala neliösenttimetrin tarkkuudella, kun kuution tilavuus on 7,0 litraa.

# S15T3b

# teht_S15T9

5.3.9 Tehtävä (S2015/9)

Täysin pyöreän geenimanipuloidun omenan säde on $5,0 \text{ cm}$ . Omenan läpi porataan sen keskeltä kulkeva reikä, jonka säde on $1,0 \text{ cm}$ . Kuinka monta prosenttia omenan tilavuudesta tällöin häviää? Anna vastaus posenttiyksikön kymmenesosan tarkkuudella.

Vihje

# S15T9

# teht_K15T8

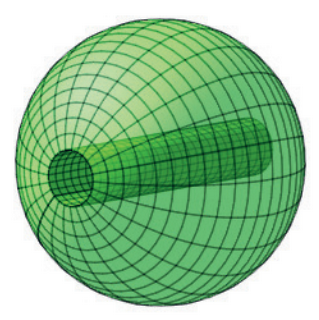
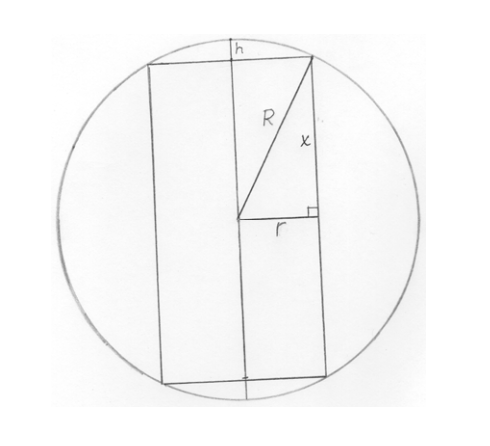
5.3.10 Tehtävä (K2015/8)

Öljysäiliö on suoran ympyrälieriön muotoinen, ja sen akseli on vaakasuorassa. Akselia vastaan kohtisuoran poikkileikkauksen halkaisija on 1,3 metriä.

Määritä säiliön pituus, kun sen tilavuus on $3 \, 000$ litraa.

# S15T8

Öljyn korkeudeksi syvimmässä kohdassa mitataan senttimetriä. Kuinka monta litraa öljyä on jäljellä säiliössä?

Vihje

# K15T8b

# teht_K13T10

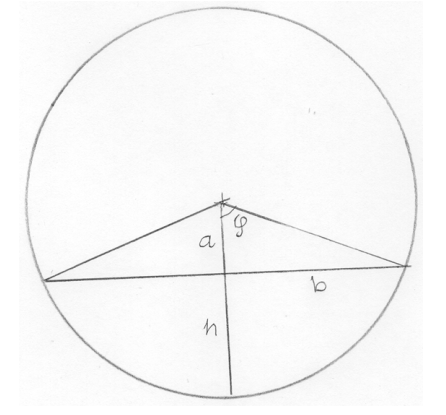
5.3.11 Tehtävä (K2013/10)

Oheisen kuution särmän pituus on . Sen sisällä on punainen pallo, joka sivuaa jokaista kuution tahkoa. Kuution yhdessä kulmassa on pienempi sininen pallo, joka sivuaa suurta palloa ja kolmea kuution tahkoa kuvion mukaisesti. Laske sinisen pallon säteen tarkka arvo.

Vihje

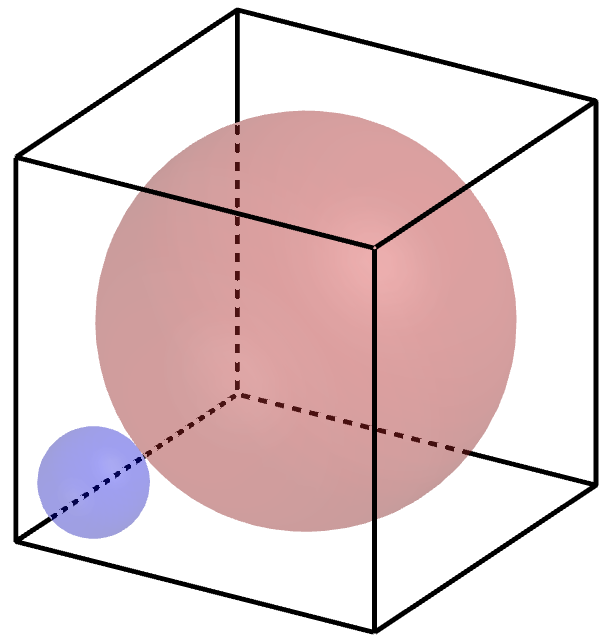
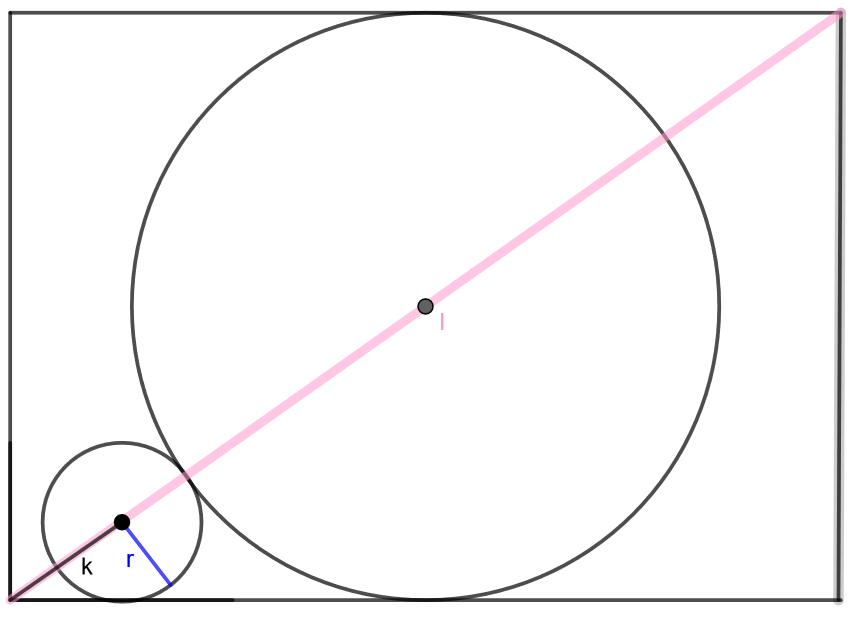
Kuution poikkileikkaus pohjan lävistäjän mukaisesti, eli l on kuution avaruuslävistäjä.

# sininen_pallo

# kartio-teht

5.4 Kartio

Tämän kappaleen teoria on kappaleessa Kartio.

# teht_kartion_tilavuus

5.4.1 Tehtävä

# kartio1

# teht_suoran_ympyrakartion_tilavuus

5.4.2 Tehtävä

# kartio2

# teht_katkaistu_kartio1

5.4.3 Tehtävä

Suoran ympyräkartion pohjan säde on ja sen korkeus on . Kartion huipusta katkaistaan pienempi suora ympyräkartio. Tämän pienemmän kartion pohjan säde on . Kuinka korkea pienempi kartio on?

# katkaistu_kartio

# kartio_yhdenmuotoisuus

# teht_katkaistu_kartio2

5.4.4 Tehtävä

Olkoon edelleen kartion pohjan säde ja korkeus . Sen huipusta leikataan pois pienempi kartio, jonka pohjan säde on . Mikä on jäljelle jäävän osan tilavuus?

# katkaistu_kartio_tilavuus

# teht_suoran_ympyrakartion_tilavuus2

5.4.5 Tehtävä

Suoran ympyräkartion korkeus on ja pohjan säde . Kartion huipulta katkaistaan pienempi kartio, jonka korkeus on $\frac{1}{4}h$ . Kuinka moninkertainen ison kartion tilavuus on verrattuna pienempään kartioon?

# katkaistu_kartio_tilavuus2

# teht_suoran_ympyrakartion_vaippa

5.4.6 Tehtävä

# kartio_sivutahko

# teht_kheopsi

5.4.7 Tehtävä

Kheopsin pyramidin muoto on lähellä neliöpohjaista kartiota. Matti mittaa pyramidin pohjan sivun pituudeksi $230 \text{ m}$ ja kuulee oppaalta pyramidin korkeuden olevan $137 \text{ m}$ . Laske annettujen tietojen avulla arvio pyramidin tilavuudelle.

# kheopsi

# teht_kartion_pohja

5.4.8 Tehtävä

$3,0 \text{ m}$ korkean kartion pohja muodostuu tasasivuisesta kolmiosta. Kartion tilavuus on $150 \, \ell$ . Määritä pohjakolmion sivun pituus.

# kartion_pohjan_sivun_pituus

# teht_jaatelotottero

5.4.9 Tehtävä

Kartion muotoisen jäätelötötterön sivun pituus on $15 \text{ cm}$ ja sen suuaukon halkaisija on $8 \text{ cm}$ . Jäätelötötteröön asestetaan täsmälleen pallon muotoinen jäätelöpallo, jonka halkaisija on $8 \text{ cm}$ . Jos pallon annetaan sulaa kokonaan, mahtuuko se jäätelötötterön sisään?

# jaatelo

# teht_K12T9

5.4.10 Tehtävä (K2012/9)

Suoran ympyräkartion korkeus on $5,0 \text{ cm}$ , ja sen pohjan säde on $2,0 \text{ cm}$ . Kartio katkaistaan niin, että yläreunan säde on $1,0 \text{ cm}$ . Tämän jälkeen katkaistun kartion vaippa maalataan siniseksi ja sitä pyöritellään kyljellään paperilla. Määritä näin saadun sinisen rengasalueen pinta-ala yhden neliösenttimetrin tarkkuudella.

Vihje

# K12T9

# teht_K16T13

5.4.11 Tehtävä (K2016/13)

Olkoon , ja positiivisia reaalilukuja. Tetraedrin kolme kärkeä ovat koordinaattiakseleiden pisteissä (a,0,0) , (0,b,0) ja (0,0,c) , ja neljäs kärki on origossa (0,0,0) . Kärkien vastaisten tetraedrin tahkojen pinta-aloja merkitään samassa järjestyksessä kirjaimilla , , ja , jossa tarkoittaa origon vastaisen tahkon pinta-alaa. Osoita, että A^2+B^2+C^2=D^2.

Vinkki: Luo GeoGebralla liukusäätimet , ja ja luo tarvittavat pisteet niiden avulla. Tarkastele syntyvää kappaletta ja lue ohjeet tarkasti.

Ratkaisu

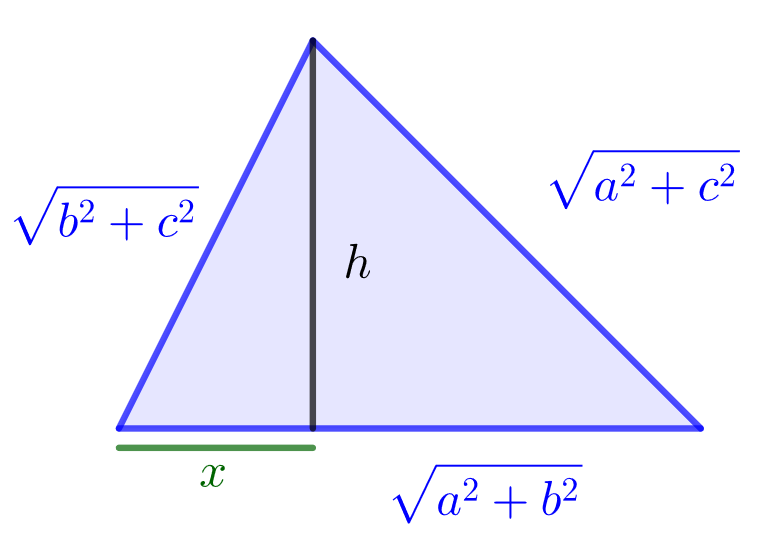
Tetraedrin pohjakolmion sivut ovat $\sqrt{a^2+b^2}$ , $\sqrt{b^2+c^2}$ ja $\sqrt{a^2+c^2}$ . Alla olevan kuvan merkinnöin saadaan $\left\{ \begin{aligned} x^2+h^2 &= b^2+c^2 \\ (\sqrt{a^2+b^2}-x)^2 + h^2 &= a^2+c^2 \end{aligned} \right.$

Vähennetään yhtälöt puolittain, jolloin saadaan $x^2-a^2-b^2+2x \sqrt{a^2+b^2}-x^2 = b^2-a^2$ josta saadaan $x=\frac{b^2}{\sqrt{a^2+b^2}}.$ Tällöin $\begin{aligned} h &= \sqrt{b^2+c^2-x^2} \\ &= \sqrt{b^2+c^2-\frac{b^4}{a^2+b^2}} \\ &= \sqrt{\frac{(a^2+b^2)(b^2+c^2)-b^4}{a^2+b^2}} \\ &= \sqrt{\frac{a^2b^2+b^2c^2+a^2c^2}{a^2+b^2}}. \end{aligned}$ Saadaan siis $D=\frac{1}{2} \sqrt{a^2+b^2}h$ $=\frac{1}{2} \sqrt{a^2b^2+b^2c^2+a^2c^2}$ . Koska akselitasossa olevien kolmioiden alat ovat $A=\frac{1}{2}bc$ , $B=\frac{1}{2}ac$ ja $C=\frac{1}{2}ab$ , niin $A^2+B^2+C^2=\frac{1}{4}(b^2c^2+a^2c^2+a^2b^2)=D^2$ .

5.5 Sekalaisia tehtäviä

Tässä kappaleessa on kaikkiin tämän luvun aiheisiin liittyviä tehtäviä.

# teht_S16T6

5.5.1 Tehtävä (S2016/6)

Vesikaukalon päädyt ovat tasasivuisen kolmion muotoiset, ja kolmion sivujen pituus on . Kaukalon pohja muodostuu kahdesta suorakulmion muotoisesta levystä, joiden pituus on .

Vaakasuorassa oleva kaukalo on aluksi täynnä vettä. Sitä kallistetaan pituussuunnassa niin, että vedenpinta ulottuu vasemmanpuoleisen päätykolmion alakulmaan alla olevan kuvion mukaisesti. Kuinka monta prosenttia vedestä valuu pois kallistuksen aikana?

# S16T6a

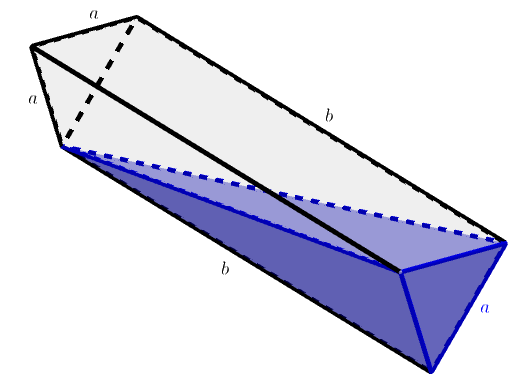
Tämän jälkeen kaukalo palautetaan takaisin vaakasuoraan asentoon. Kuinka korkealla vedenpinta on kaukalon syvimmästä kohdasta mitattuna?

Vihje

Vesi muodostaa nyt särmiön, jonka pohjana on tasakylkinen kolmio. Muodosta lauseke vesisärmiön tilavuudelle ja vertaa sitä a-kohtaan.

# S16T6b