3. Monikulmioiden pinta-aloja: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Monikulmioiden pinta-aloja. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

# puolisuunnikas-teht

3.1 Puolisuunnikas

Tämän kappaleen teoria on kappaleessa Puolisuunnikas.

# teht_puolisuunnikkaan_ala

3.1.1 Tehtävä

# puolisuunnikas1

# teht_puolisuunnikkaan_kanta

3.1.2 Tehtävä

# puolisuunnikas2

# teht_puolisuunnikkaan_korkeus

3.1.3 Tehtävä

# puolisuunnikas3

# suunnikas-teht

3.2 Suunnikas

Tämän kappaleen teoria on kappaleessa Suunnikas.

# teht_suunnikkaan_ala1

3.2.1 Tehtävä

# suunnikas1

# teht_suunnikkaan_ala2

3.2.2 Tehtävä

# suunnikas2

# teht_suunnikkaan_kulma

3.2.3 Tehtävä

Suunnikkaan sivujen pituudet ovat ja , ja sen pinta-ala on . Kuinka suuri kulma sivujen välissä on?

# suunnikas3

# teht_suunnikkaan_ala3

3.2.4 Tehtävä

Suunnikkaan sivujen välinen kulma on $45^{\circ}$ . Lyhyempi sivuista on pituudeltaan ja pidempi . Määritä suunnikkaan ala.

# s98T8a

# aakkostehtava

3.2.5 Tehtävä

Aakkoskarkkien sivujen pituudet ovat $2 \text{ cm}$ ja sen lyhyempi halkaisija on $2,3 \text{ cm}$ . Laske yhden karkin pinta-ala.

# aakkonen

# teht_S11T15

3.2.6 Tehtävä (S2011/15)

Merkitään kolmion ABC keskijanojen ja leikkauspistettä kirjaimella .

Jos on janan keskipiste ja janan keskipiste, niin osoita, että janan pituus on puolet janan pituudesta.
Osoita, että nelikulmio on suunnikas
Osoita, että janan pituus on kolmasosa janan pituudesta.
Todista edellisten kohtien perusteella seuraava lause: Kolmion keskijanat leikkaavat toisensa samassa pisteessä, joka jakaa jokaisen keskijanan siten, että sivun puoleisen osan pituus on kolmasosa koko keskijanan pituudesta.

Ratkaisu

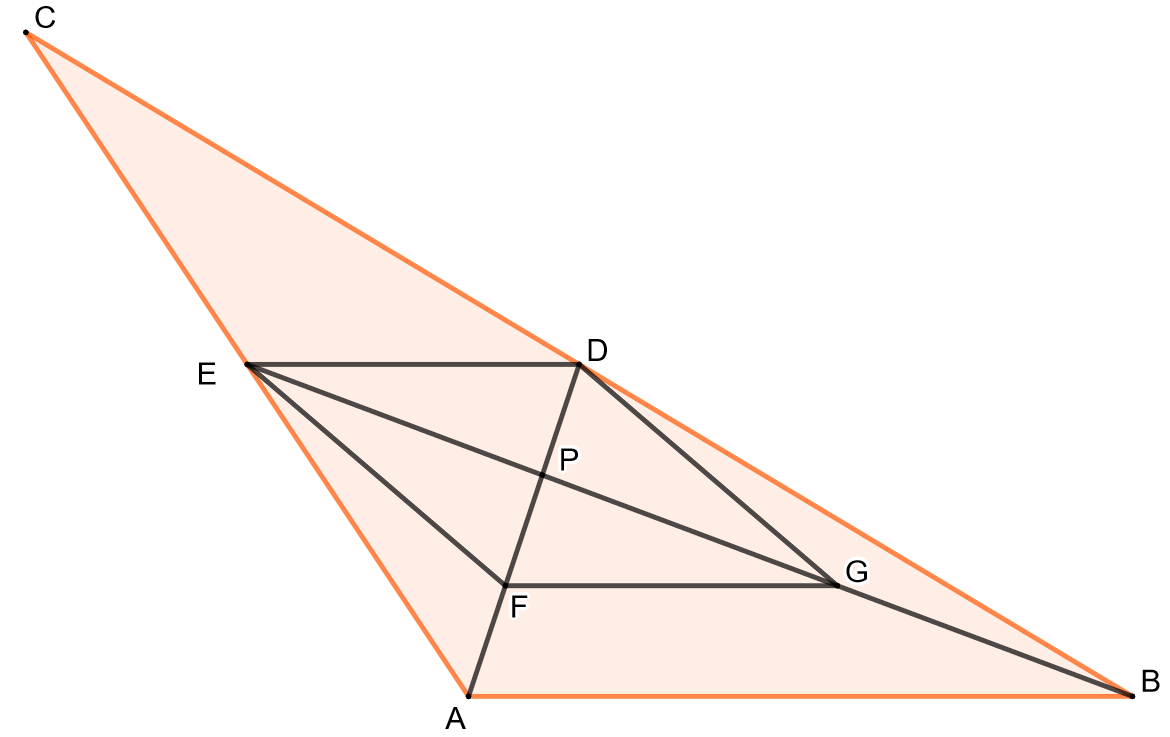
Kolmiot ja ovat yhdenmuotoiset (SKS) yhdenmuotoisuussuhteen ollessa . Näin ollen vastinsivuina $FG=\frac{1}{2} AB$ .

Pisteestä piirretty janan suuntainen suora puolittaa janan eli kulkee pisteen kautta. Tämä johtuu siitä, että kolmiot ja ovat yhdenmuotoisia (SKS). Näin ollen sivut ja ovat yhdensuuntaiset. Vastaavasti nähdään, että sivut ja ovat yhdensuuntaiset, eli sivut ja ovat yhdensuuntaiset. Edelleen, kolmiot ja ovat yhdenmuotoiset (SKS) yhdenmuotoisuussuhteen ollessa . Näin ollen $ED=\frac{1}{2} AB$ eli . Koska sivut ja ovat yhtä pitkiät ja yhdensuuntaiset, nelikulmio on suunnikas.

Suunnikkaan lävistäjät puolittavat toisensa, joten eli $DP=\frac{1}{3} AD$ .

Edellisen mukaan pisteestä piirretty keskijana leikkaa pisteestä piirretyn keskijanan pisteessä, jonka etäisyys pisteestä on $\frac{1}{3}AD$ . Vastaavasti nähdään, että sama pätee pisteestä piirretylle keskijanalle: sekin leikkaa pisteestä piirretyn keskijanan pisteessä, jonka etäisyys pisteestä on $\frac{1}{3} AD$ . Näin ollen myös pisteestä piirretty keskijana kulkee pisteen kautta. Edellisen mukaan nähdään, että piste jakaa kaikki keskijanat suhteessa .

# teht_suunnikkaan_lavistajat

3.2.7 Tehtävä

Osoita, että suunnikkaan lävistäjien $\ell_1$ ja $\ell_2$ neliöiden summa on yhtä suuri kuin suunnikkaan sivujen ja neliöiden summa, eli että $\ell_1^2 + \ell_2^2 = 2a^2+2b^2.$

Ratkaisu

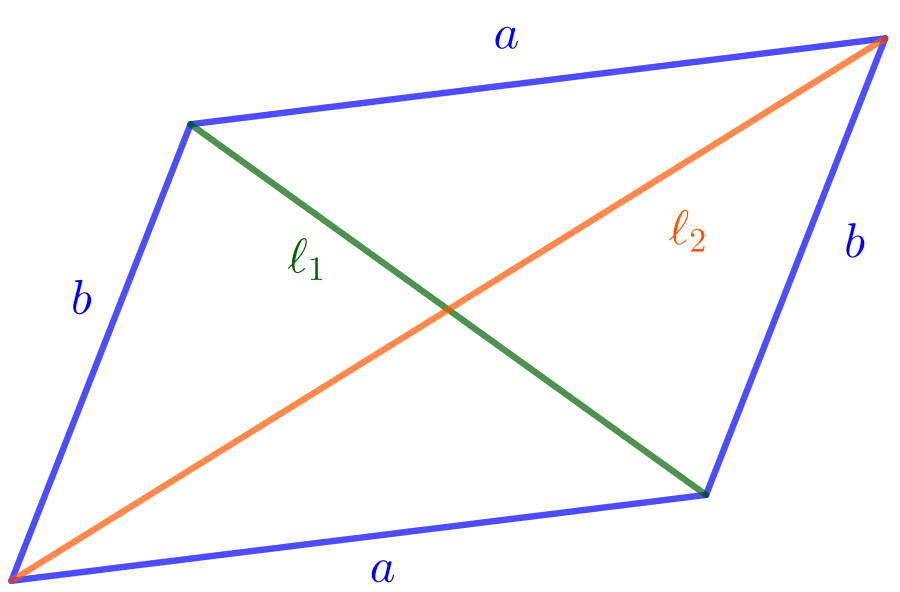
Merkitään suunnikkaan pienempää kulmaa kirjaimella $\alpha$ ja suurempaa kulmaa kirjaimella $\beta$ . Jaetaan suunnikas ensin lävistäjän $\ell_2$ mukaisesti kahdeksi kolmioksi ja muodostetaan tälle kolmiolle kosinilause: $\ell_2^2=a^2+b^2-2ab \cos \beta$ . Koska nelikulmion kulmien summa on $360^{\circ}$ , saadaan yhtälö $2\alpha + 2\beta = 360^{\circ}$ $\Leftrightarrow \alpha + \beta = 180^{\circ}$ . Sijoitetaan $\beta = 180^{\circ}-\alpha$ ja muistetaan tylpän kulman kosinin laskusääntö, jolloin saadaan $\ell_2^2=a^2+b^2-2ab \cos(180^{\circ}-\alpha)$ $=a^2+b^2+2ab \cos \alpha$ .

Jaetaan seuraavaksi suunnikas lyhyemmän lävistäjän $\ell_1$ mukaisesti kahdeksi kolmioksi ja sovelletaan kosinilausetta, jolloin saadaan $\ell_1^2=a^2+b^2-2ab \cos \alpha$ .

Lasketaan seuraavaksi lävistäjien neliöt yhteen, jolloin saadaan $\begin{aligned} \ell_1^2 + \ell_2^2 &= a^2+b^2 -2ab \cos \alpha + a^2+b^2+2ab \cos \alpha \\ \Leftrightarrow \ell_1^2 + \ell_2^2 &= 2a^2+2b^2 \end{aligned}$

# suorakulmio-teht

3.3 Suorakulmio

Tämän kappaleen teoria on kappaleessa Suorakulmio.

# teht_suunnikkaan_osuus

3.3.1 Tehtävä

Määritä alla olevan kuvan suunnikkaan pinta-alan osuus suorakulmion pinta-alasta.

# suunnikas_suorakulmiossa

# teht_suorakulmio_kolmiossa

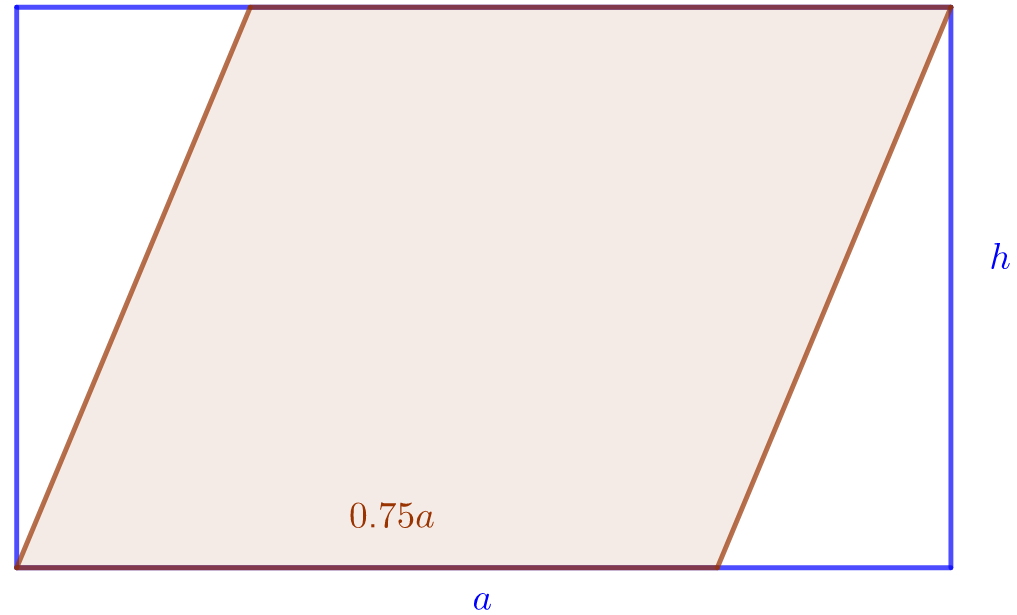
3.3.2 Tehtävä

Laske alla olevaan kuvaan sinisellä merkityn alueen pinta-ala.

# suorakulmio_kolmiossa

# teht_suorakulmion_lavistajat

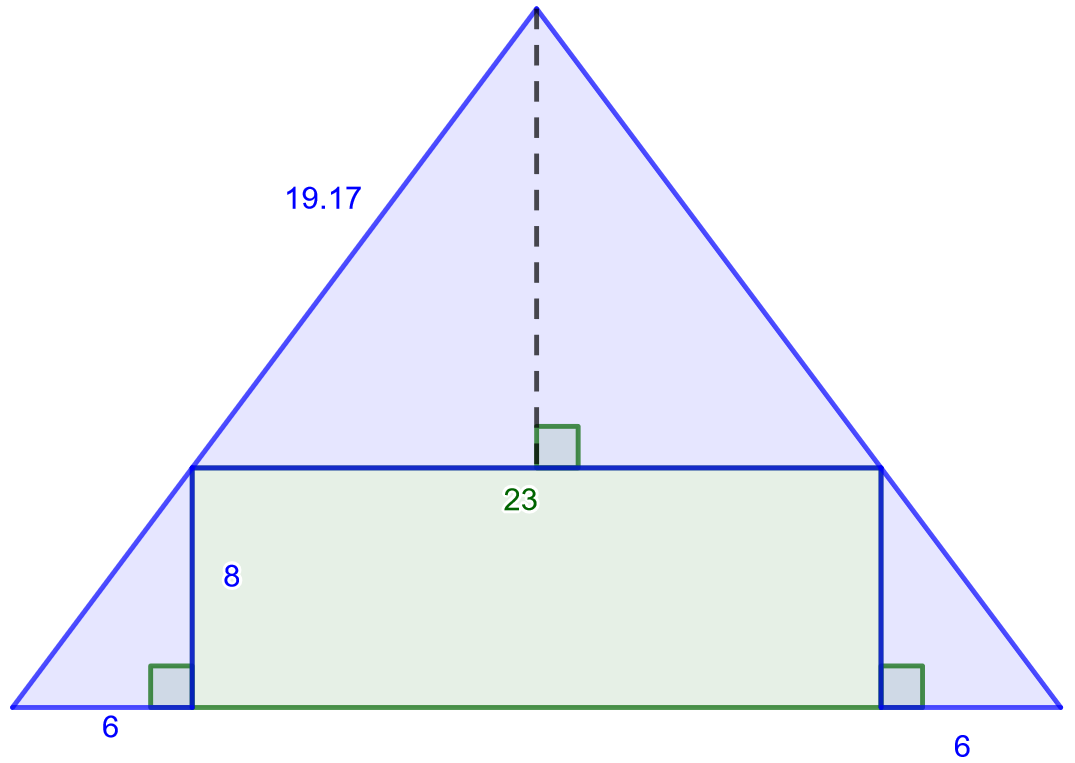
3.3.3 Tehtävä

Olkoot d_1 ja d_2 suorakulmion ABCD piirillä olevan pisteen etäisyydet lävistäjistä ja .

Piirrä annettuja tietoja vastaava dynaaminen kuvio, jossa voit liikuttaa pistettä suorakulmion ympäri pitkin suorakulmion piiriä.
Mitä voit todeta summan arvosta?
Miten arvo riippuu suorakulmion koosta?
Perustele havaintosi matemaattisesti.

Ratkaisu

# geo_suorakulmion_reunat

Tutkitaan yllä olevaa GeoGebra-applettia siirtämällä punaista pistettä suorakulmion reunalla. Huomataan, että summa pysyy koko ajan samana.

Muutetaan suorakulmion kokoa raahaamalla pisteitä ja . Huomataan, että summan arvo muuttuu, mutta jos pistettä liikuttaa, se pysyy edelleen samana. Summa on siis sitä suurempi, mitä suurempi suorakulmio on.

Lisätään valinta GeoGebra-appletin kohtaan "Matemaattinen perustelu", jolloin kuvioon ilmestyy kulmia. (Huom! kulmat toimivat GeoGebrassa oikein vain, jos piste on pisteiden ja välissä.) Merkitään kulmaa $\angle BAC$ kirjaimella $\alpha$ ja kulmaa $\angle CAD$ kirjaimella $\beta$ . Koska suorakulmion kaikki kulmat ovat suoria, saadaan $\alpha + \beta = 90^{\circ}$ . Merkitään vihreää lävistäjää kirjaimella $\ell$ . Sen pituus voidaan ratkaista Pythagoraan lauseella: $\begin{aligned} \ell^2 &= a^2+b^2 \\ \ell &= \sqrt{a^2+b^2}. \end{aligned}$ Nyt voidaan merkitä $\cos \alpha = \frac{a}{\ell} = \frac{a}{\sqrt{a^2+b^2}}.$ Merkitään etäisyyttä kirjaimella , jolloin etäisyys on . Pienistä suorakulmaisista kolmioista saadaan $\cos \alpha = \frac{d_1}{b-x} \quad \Leftrightarrow \quad d_1 = (b-x) \cdot \cos \alpha$ ja $\cos \alpha = \frac{d_2}{x} \quad \Leftrightarrow \quad d_2 = x \cdot \cos \alpha$ jolloin summa saa arvon $\begin{aligned} d_1 + d_2 &= (b-x) \cdot \cos \alpha + x \cdot \cos \alpha \\ &= (b-x+x) \cdot \cos \alpha \\ &= b \cdot \frac{a}{\sqrt{a^2+b^2}} \\ &= \frac{ab}{\sqrt{a^2+b^2}}. \end{aligned}$ Tästä voidaan päätellä, että jos suorakulmion koko pysyy samana, summa pysyy myös vakiona. Toisaalta jos suorakulmion koko kasvaa, myös summa kasvaa.

# nelio-teht

3.4 Neliö

Tämän kappaleen teoria on kappaleessa Neliö.

# teht_nelio_suorakulmainen_kolmio

3.4.1 Tehtävä

Neliöllä ja suorakulmaisella kolmiolla on sama pinta-ala. Kumman piiri on pidempi?

# Plugin1

# teht_S17T5

3.4.2 Tehtävä (S2017/5)

Kuinka monta prosenttia kuvassa olevan pienemmän neliön sivun pituus on suuremman neliön sivun pituudesta?

Suuremman neliön sivun pituus on 1.

# S2017T5a

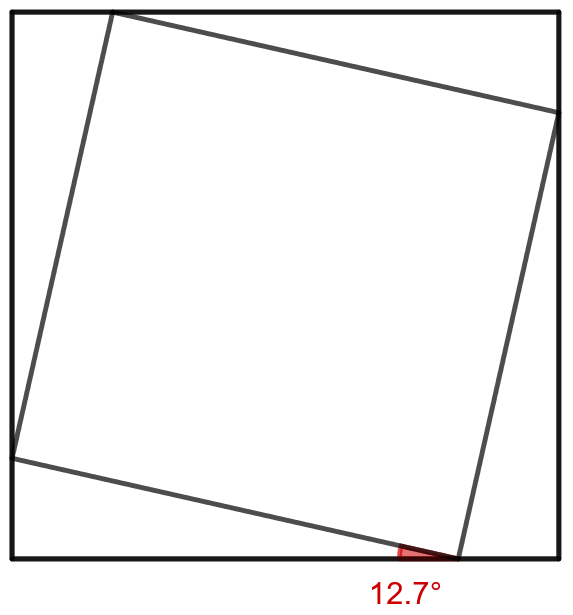
Kuinka monta prosenttia pienemmän neliön pinta-ala on suuremman neliön pinta-alasta?

# S2017T5b

# teht_tahtinelikulmio

3.4.3 Tehtävä

Alla olevassa kuvassa on neliö, jonka pinta-ala on . Sen jokaiselle sivulle on piirretty tasasivuinen kolmio. Mikä on punaisella merkityn alueen pinta-ala?

# tahtinelikulmio

# muut-monikulmiot-teht

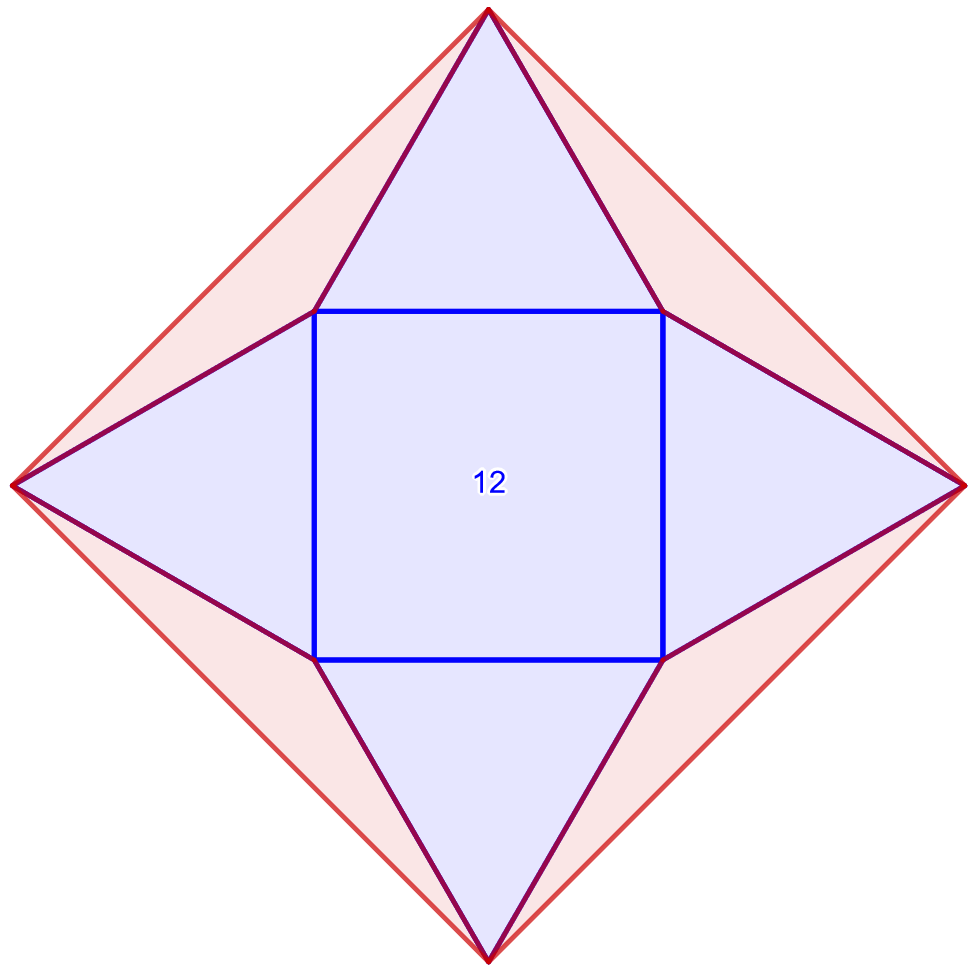
3.5 Muut monikulmiot

Tämän kappaleen teoria on kappaleessa Muut monikulmiot.

# teht_kulmien_summa

3.5.1 Tehtävä

Johda kaava kulmien summalle monikulmiossa, jossa on kulmaa.

Ratkaisu

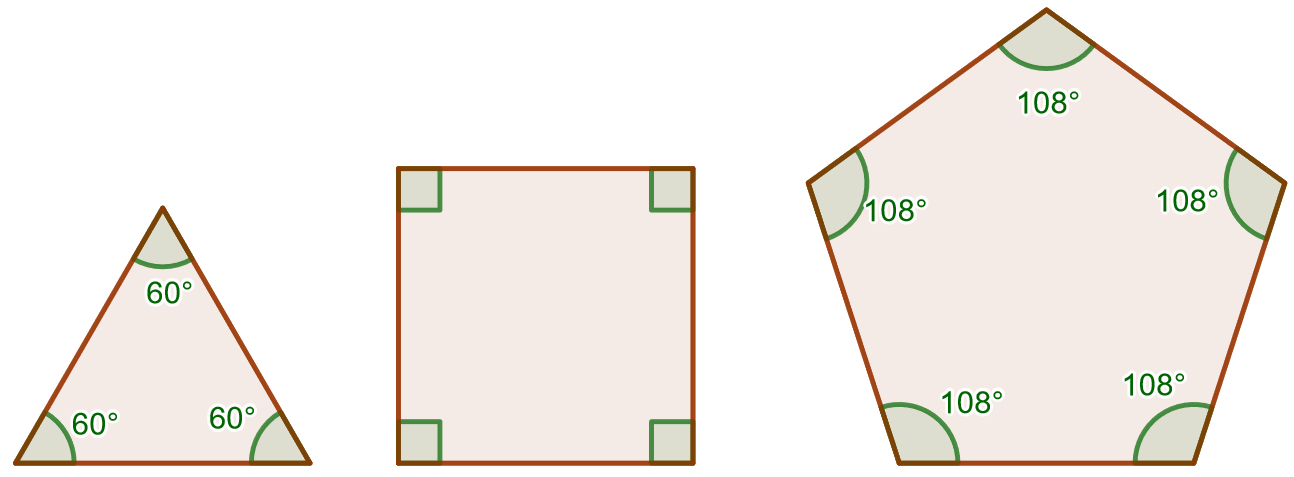
Kun monikulmiossa on kolme kulmaa, niin n=3 ja kyseessä on kolmio. Tällöin kulmien summa on $3 \cdot 60 ^{\circ}=180^{\circ}$ . Kun monikulmiossa on neljä kulmaa, niin n=4 ja kyseessä on nelikulmio. Sen kulmien summa on $4 \cdot 90 ^{\circ}=360 ^{\circ}$ . Kun monikulmiossa on viisi kulmaa, niin n=5 ja kyseessä on viisikulmio. Sen kulmien summa on $5 \cdot 108 ^{\circ}=540^{\circ}$ .

Kun tarkastellaan kulmien summasta muodostuvaa sarjaa $180^{\circ}, 360^{\circ}, 540^{\circ} \ldots$ huomataan, että kulmien summa kasvaa aina $180^{\circ}$ :lla kun kulmien määrä kasvaa yhdellä. Kaava on siis muotoa $x \cdot 180^{\circ}$ . Nyt pitää enää päätellä .

Huomataan, että kaava toimii, jos x=n-2 . Tällöin kolmion kulmien summa on $(3-2) \cdot 180^{\circ} = 180^{\circ}$ , nelikulmion kulmien summa on $(4-2) \cdot 180^{\circ}$ $= 2 \cdot 180^{\circ} =360^{\circ}$ ja viisikulmion kulmien summa on $(5-2) \cdot 180^{\circ}$ $= 3 \cdot 180^{\circ} =540^{\circ}$ . Monikulmion kulmien summa on siis $(n-2) \cdot 180 ^{\circ}$ , missä on monikulmion kulmien määrä.

# teht_halkaisijoiden_lukumaara

3.5.2 Tehtävä

Johda kaava halkaisijoiden lukumäärälle monikulmiossa, jossa on kulmaa.

Ratkaisu

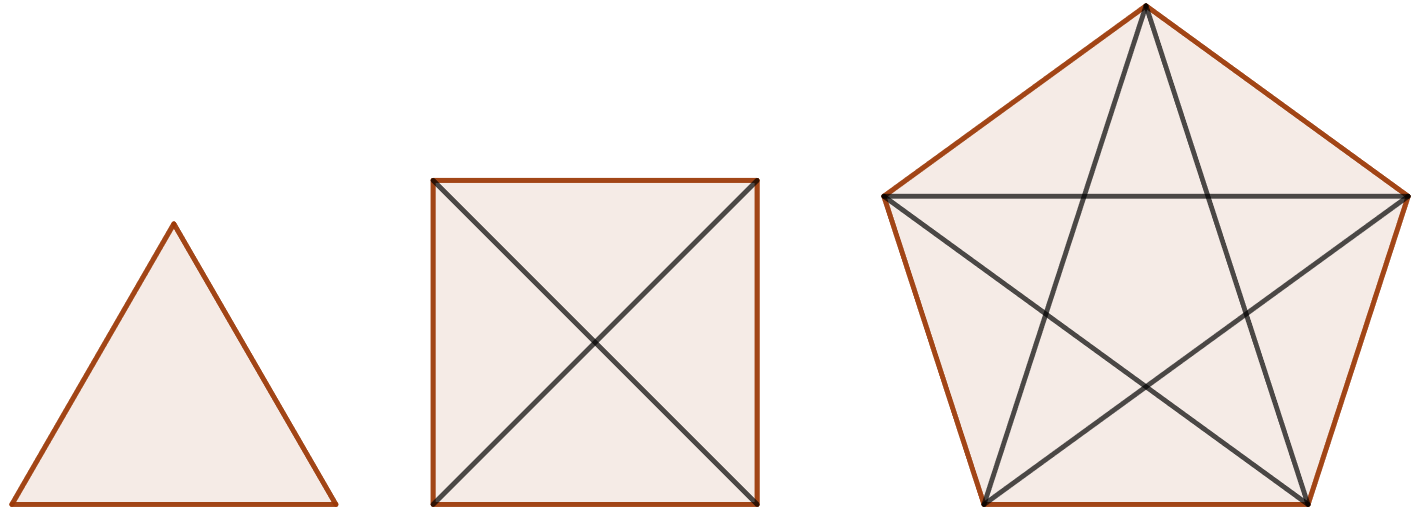
Kolmiossa ( n=3 ) halkaisijoita on . Nelikulmiossa ( n=4 ) halkaisijoita on . Viisikulmiossa ( n=5 ) halkaisijoita on .

Jokaisesta monikulmion kärjestä lähtee halkaisija jokaiseen muuhun kärkeen paitsi niihin kahteen, jotka ovat kärjen vieressä. Jokaisesta kärjestä lähtee siis (n-3) halkaisijaa (termi tulee juuri siitä, ettei halkaisijaa voi piirtää kärkeen itseensä eikä kahteen sen viereisistä kärjistä). Koska kärkiä on kappaletta, on halkaisijoita n(n-3) kappaletta. Jokaisella halkaisijalla on kuitenkin kaksi päätepistettä, eli se tulee laskettu kahteen kertaan. Siksi jaetaan lauseke vielä kahdella. Eli monikulmion halkaisijoiden määrä on $\frac{n (n-3)}{2}$ .

Tarkistetaan vielä, että kaava toimii. Kolmion halkaisijoiden määrä on $\frac{3 \cdot (3-3)}{2} = 0$ . Nelikulmion halkaisijoiden määrä on $\frac{4 \cdot (4-3)}{2} = 2$ . Viisikulmion halkaisijoiden määrä on $\frac{5 \cdot (5-3)}{2} = 5$ . Eli kaava toimii.

# teht_viisikulmion_pinta-ala

3.5.3 Tehtävä

Säännöllisen viisikulmion sivun pituus on . Laske viisikulmion pinta-ala.

# viisikulmion_ala

3.6 Sekalaisia tehtäviä

Tässä kappaleessa on kaikkiin tämän luvun aiheisiin liittyviä tehtäviä.

# teht_K11T7

3.6.1 Tehtävä (K2011/7)

Osa Helsingin keskuskatua muutettiin kävelykaduksi ja päällystettiin Penrosen laatoilla, jotka keksi englantilainen matemaatikko Roger Penrose 1970-luvulla. Niiden avulla taso voidaan laatoittaa äärettömän monella eri tavalla niin, ettei laatoitus ole jaksollinen. Laattoja on kahta eri muotoa, leija ja nuoli. Molemmat ovat nelikulmioita, joiden kulmien suuruudet ja osa sivujen pituuksista on mekitty kuvioon.

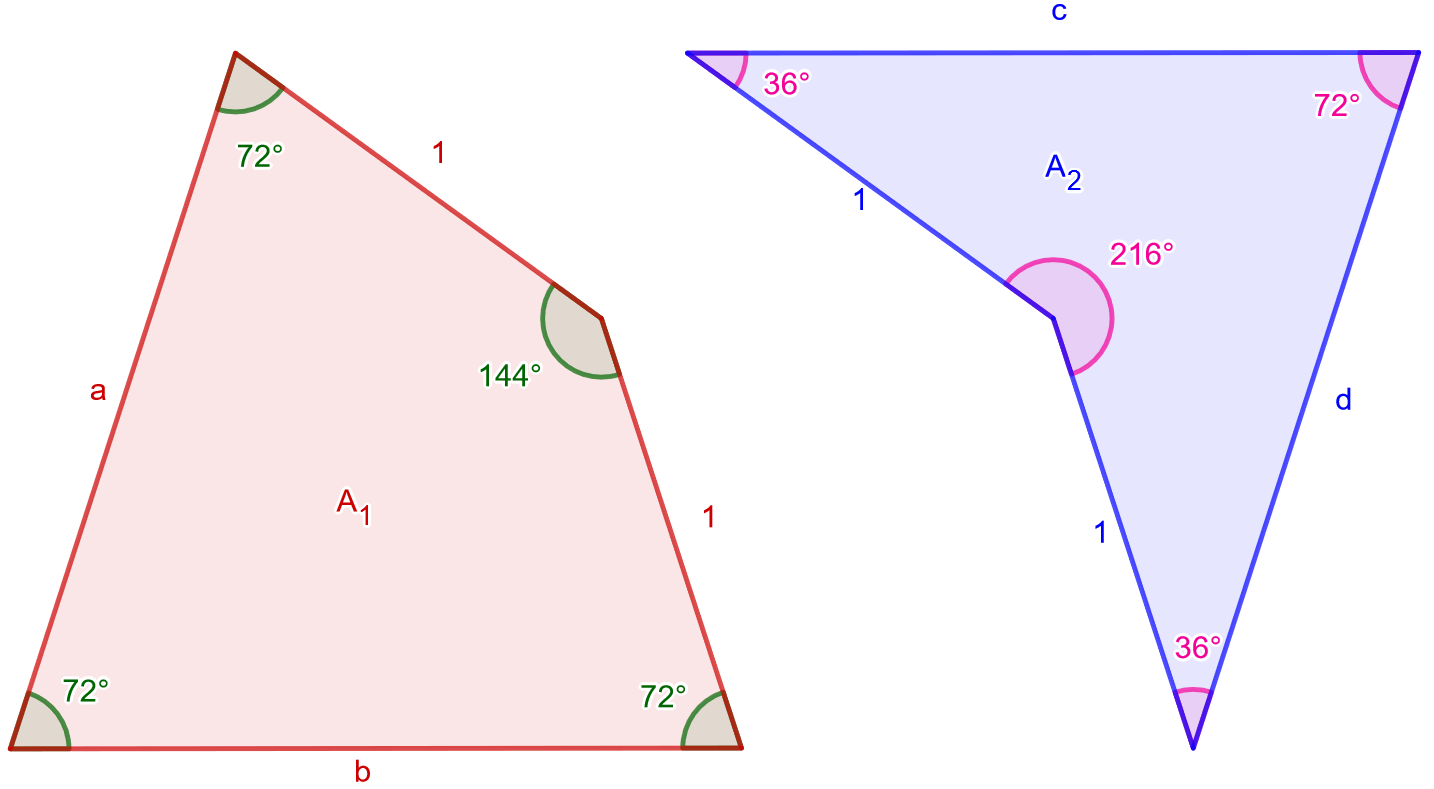
Laske muiden sivujen pituuksien likiarvot kolmen desimaalin tarkkuudella.

Vihje

Jaa kuvio kahdeksi yhteneväksi kolmioksi.

# K2011T7a

# K2011T7b

# K2011T7c

# K2011T7d

Laske laattojen pinta-alojen likiarvot kolmen desimaalin tarkkuudella.

# K2011T7A1

# K2011T7A2