# monikulmioiden_pinta-aloja

3. Monikulmioiden pinta-aloja

Tässä kappaleessa tutustutaan erilaisiin monikulmioihin ja niiden pinta-alojen laskemiseen. Huomataan, että monet monikulmioihin liittyvät ongelmat voidaan yksinkertaistaa kolmioihin liittyviksi ongelmiksi. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

Nelikulmiot muodostavat sarjan, jossa lähdetään liikkeelle "epäsäännöllisestä" nelikulmiosta epäkkäästä, ja ehtoja lisäämällä päädytään lopulta neliöön. Nelikulmiot käsitellään nyt tuossa järjestyksessä.

# puolisuunnikas

3.1 Puolisuunnikas

Puolisuunnikas on ensimmäinen jossain määrin säännöllinen nelikulmio. Sen kaksi vastakkaista sivua ovat keskenään yhdensuuntaiset. Näitä sivuja kutsutaan kannoiksi. Puolisuunnikkaan kahta muuta sivua kutsutaan kyljiksi. Jos kyljet ovat yhtä pitkiä, puolisuunnikasta kutsutaan tasakylkiseksi puolisuunnikkaaksi.

Puolisuunnikkaan pinta-ala

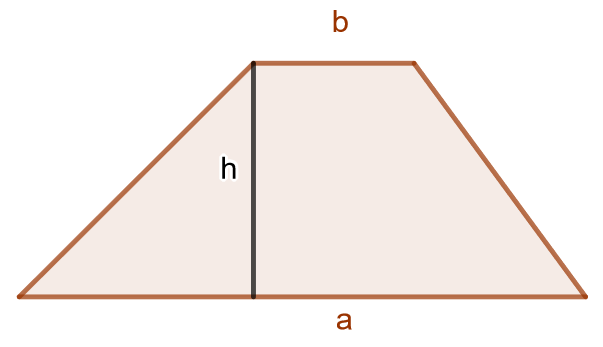
Puolisuunnikas on nelikulmio, jonka kaksi vastakkaista sivua ovat yhdensuuntaiset. Näitä sivuja kutsutaan puolisuunnikkaan kannoiksi. Jos puolisuunnikkaan kannat ovat ja ja sen korkeus on , sen pinta-ala on $A= \frac{a+b}{2}h.$

3.1.1 Esimerkki: pinta-alan laskeminen

Laske puolisuunnikkaan pinta-ala, kun sen kannat ovat $4,0 \text{ cm}$ ja $6,0 \text{ cm}$ , ja kantojen välinen etäisyys on $3,0 \text{ cm}$ .

Aloitetaan tehtävän ratkaiseminen piirtämällä mallikuva tilanteesta. Niin kannattaa tehdä kaikissa geometrian sanallisissa tehtävissä.

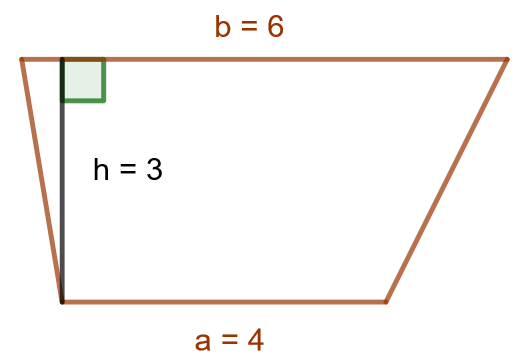
Sijoitetaan annetut arvot puolisuunnikkaan pinta-alan lausekkeeseen. Laskuissa ei ole välttämätöntä käyttää yksiköitä, jos muistaa lisätä ne vastausta annettaessa. $\begin{aligned} A&=\frac{a+b}{2}h \\ &= \frac{4+6}{2}\cdot 3 \\ &= 15 \end{aligned}$ Lopputuloksessa muistetaan käytetyt yksiköt. Koska puolisuunnikkaan sivujen pituudet on ilmoitettu senttimetreinä, on vastaus neliösenttimetreinä. Kysytyn puolisuunnikkaan pinta-ala on $15 \text{ cm}^2$ .

Tähän kappaleeseen liittyvät tehtävät.

# suunnikas

3.2 Suunnikas

Lisätään puolisuunnikkaaseen yksi lisäehto. Sen sijaan, että vain yksi vastakkaisten sivujen muodostama pari olisi yhdensuuntainen, vaaditaankin, että molemmat vastakkaisten sivujen muodostamat parit ovat yhdensuuntaisia. Tällöin saadaan suunnikas.

Suunnikkaan pinta-ala

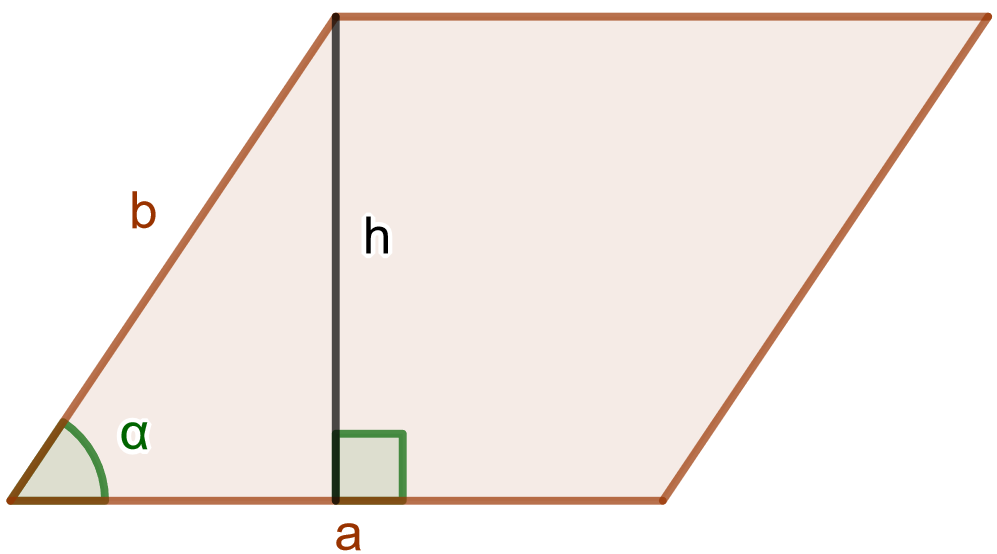
Suunnikas on nelikulmio, jonka molemmat vastakkaiset sivut ovat yhtä pitkiä ja yhdensuuntaisia. Jos suunnikkaan sivujen pituudet ovat ja ja näiden sivujen välinen kulma on $\alpha$ , voidaan suunnikkaan pinta-ala laskea seuraavasti $A=ah=ab \sin \alpha,$ missä on suunnikkaan korkeus.

3.2.1 Esimerkki: suunnikkaan pinta-ala GeoGebralla

# suunnikkaan-ala-geo

Kokeile siirtää liukusäädintä yllä olevassa GeoGebra-appletissa. Huomaa, että molemmilla suunnikkaan pinta-alan laskukaavoilla tulee luonnollisesti sama tulos, mutta tilanteesta riippuu, kumpaa laskukaavaa on helpompi käyttää.

3.2.2 Esimerkki: suunnikkaan piirtäminen GeoGebralla

Harjoittele suunnikkaan muodostamista GeoGebralla.

Piirrä kolme pistettä , ja .
Yhdistä pisteet ja suoralla.
Yhdistä pisteet ja suoralla.
Luo suora, joka on yhdensuuntainen suoran kanssa ja joka kulkee pisteen kautta.
Luo suora, joka on yhdensuuntainen suoran kanssa ja joka kulkee pisteen kautta.
Lisää kohdissa 4 ja 5 luotujen suorien leikkauspiste .
Luo monikulmio , joka on suunnikas.
Piilota ylimääräiset suorat. Kokeile siirtää pisteitä ja varmista, että kuviosi todella on suunnikas.

# suunnikas-geo

Jos suunnikkaan kaikki sivut ovat yhtä pitkiä, puhutaan neljäkkäästä eli vinoneliöstä. Joskus neljäkästä kutsutaan myös nimellä rombi.

3.2.3 Esimerkki: lävistäjän pituuden laskeminen

Ratkaise alla olevan kuvan janan pituus, kun neljäkkään pinta-ala on 33,7 .

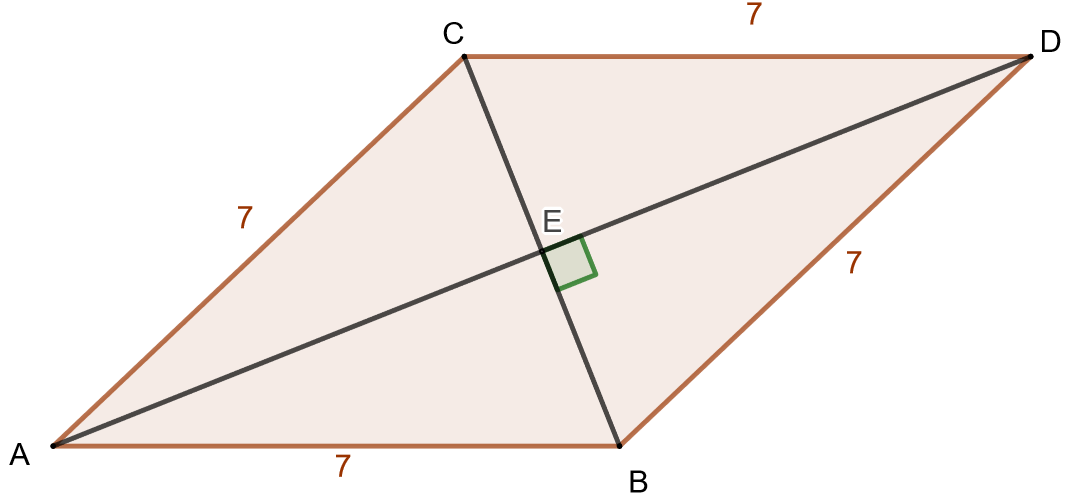
Pinta-alan ja sivun pituuden avulla voidaan laskea kulman $\angle CDB$ suuruus. Merkitään kulmaa $\angle CDB$ kreikkalaisella kirjaimella $\alpha$ ja neljäkkään sivua kirjaimella . Käytetään suunnikkaan pinta-alan kaavaa $\begin{aligned} A&=a^2 \sin(\alpha) &\quad &|:a^2 \\ \sin(\alpha) &= \frac{A}{a^2} &\quad &|\sin^{-1}() \\ \alpha &= \sin^{-1}\left( \frac{A}{a^2} \right) \end{aligned}$ Jana on osa suorakulmaista kolmiota CDE . Merkitään tämän kolmion kulmaa $\angle CDE$ kreikkalaisella kirjaimella $\beta$ . Nyt kulma $\beta$ on puolet kulmasta $\alpha$ . Käytetään trigonometrisista suhteista siniä, jotta saadaan ratkaistua kysytyn janan pituus $\begin{aligned} \sin(\beta) &= \frac{CE}{a} &\quad &|\cdot a \\ CE &= a \sin(\beta) &\quad &|\beta = \frac{\alpha}{2} \\ CE &= a \sin \left( \frac{\alpha}{2} \right) &\quad &|\alpha = \sin^{-1}\left( \frac{A}{a^2} \right) \\ CE &= a \sin \left( \frac{\sin^{-1}\left( \frac{A}{a^2} \right)}{2} \right) \\ CE &= 7 \cdot \sin \left( \frac{\sin^{-1}\left( \frac{33,7}{7^2} \right)}{2} \right) \\ CE &\approx 2,5912 \end{aligned}$ Janan pituus on siis noin 2,59.

Tähän kappaleeseen liittyvät tehtävät.

# suorakulmio

3.3 Suorakulmio

Suorakulmio on suunnikas, jonka kaikki kulmat ovat yhtä suuria. Suorakulmion jokainen kulma on $90^{\circ}$ .

Suorakulmion pinta-ala

Suorakulmio on monikulmio, jolla on neljä kulmaa ja jonka jokainen kulma on suora. Jos suorakulmion eripituisten sivujen pituudet ovat ja , voidaan suorakulmion pinta-ala laskea seuraavasti A=ab.

Tähän kappaleeseen liittyvät tehtävät.

# nelio

3.4 Neliö

Neliö on suunnikas, jonka kaikki sivut ovat yhtä pitkiä. Neliö on siis säännöllinen nelikulmio, sillä kaikki sen sivut ovat yhtä pitkiä ja kaikki sen kulmat ovat yhtä suuria.

Neliön pinta-ala

Neliö on monikulmio, jolla on neljä kulmaa, jonka sivut ovat yhtä pitkiä keskenään ja jonka jokainen kulma on suora. Jos neliön sivun pituus on , sen pinta-ala on A=a^2.

3.4.1 Esimerkki: monikulmion pinta-ala

Laske alla olevan monikulmion pinta-ala.

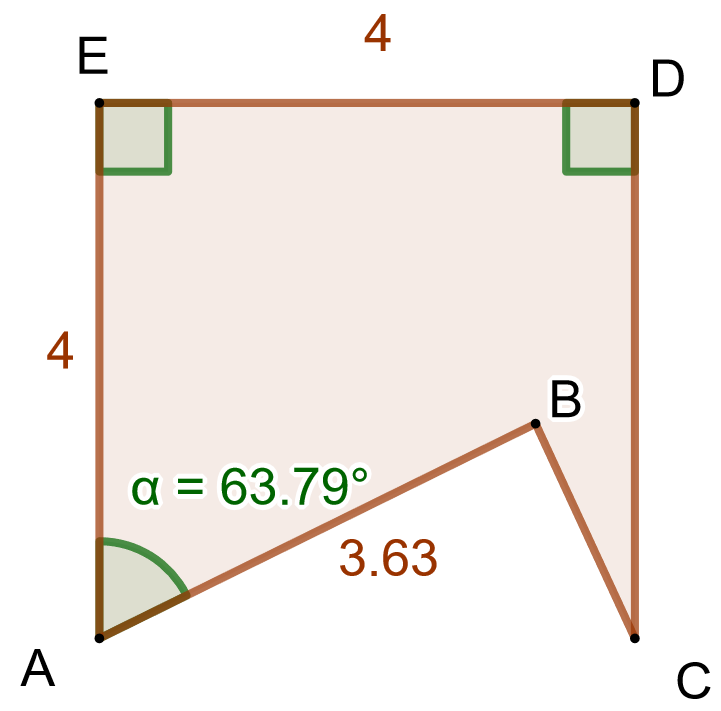
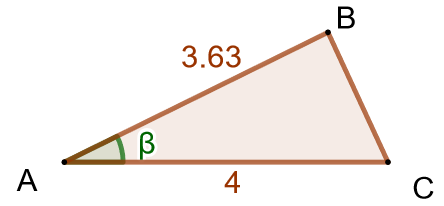
Huomataan, että kuvio koostuu neliöstä ACDE , josta on poistettu kolmio ABC . Kuvion pinta-ala voidaan laskea vähentämällä neliön pinta-alasta kolmion pinta-ala. Neliön pinta-ala on A_n=4^2=16. Alla on pelkän kolmion kuva. Kulman $\beta$ suuruus voidaan päätellä, sillä yhdessä kulmat $\alpha$ ja $\beta$ muodostavat suoran kulman: $\beta = 90^{\circ}- \alpha = 90^{\circ}-63,79^{\circ}=26,21^{\circ}.$

Kun tiedetään yksi kolmion kulma ja kulman viereisten sivujen pituudet, kolmion pinta-ala voidaan laskea trigonometrisella pinta-alakaavalla. $\begin{aligned} A_k&=\frac{1}{2}AC \cdot AB \cdot \sin(\beta) \\ A_k &= \frac{1}{2} \cdot 4 \cdot 3,63 \cdot \sin(26,21^{\circ}) \\ A_k &= 3,21 \end{aligned}$

Koko kuvion pinta-ala voidaan laskea vähennyslaskulla A=A_n - A_k = 16-3,21 = 12,79. Monikulmion ABCDE pinta-ala on 12,79 .

Tähän kappaleeseen liittyvät tehtävät.

# muut-monikulmiot

3.5 Muut monikulmiot

Kaikki monikulmiot voidaan jakaa kolmioiksi, jolloin niiden käsittely helpottuu. Erityisen helppoa tämä on, jos monikulmio on säännöllinen.

3.5.1 Esimerkki: kuusikulmion pinta-ala

Ratkaise alla olevan kuusikulmion pinta-ala.

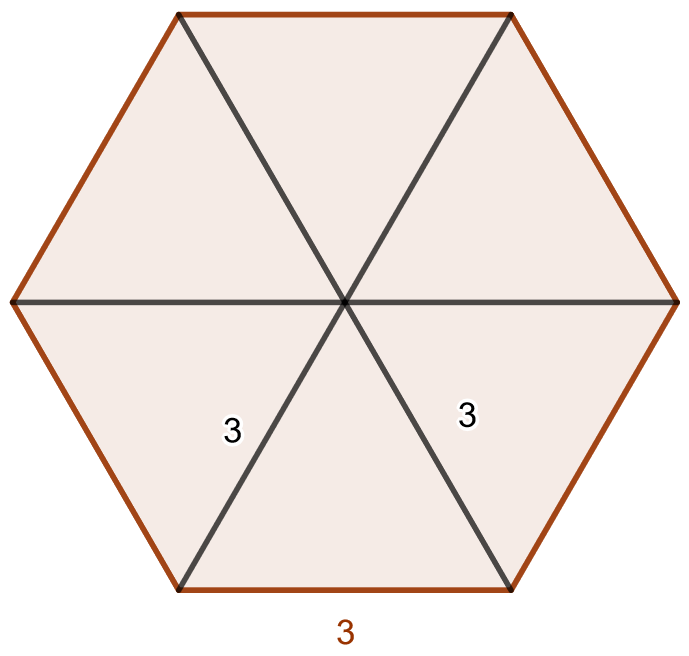
Huomataan, että kuusikulmio on säännöllinen ja se muodostuu kuudesta tasasivuisesta kolmiosta. Lasketaan ensin yhden tasasivuisen kolmion pinta-ala. Se voidaan tehdä kahdella tavalla: perinteisellä kaavalla $A=\frac{ah}{2}$ tai trigonometrisesti $A=\frac{ab \sin(\alpha)}{2}$ . Kolmion korkeuden laskeminen ei ole vaikeaa, mutta jos käytetään trigonometrista kaavaa, ei tarvitse laskea mitään ylimääräistä. Tiedetään, että tasasivuisen kolmion jokainen kulma on $60^{\circ}$ . Yhden tasasivuisen kolmion pinta-ala on $A_{\text{kolmio}}=\frac{ab\sin(\alpha)}{2}=\frac{3 \cdot 3 \cdot \sin(60^{\circ})}{2}=\frac{9 \sqrt{3}}{4}.$ Kerrotaan se kuudella, jotta saadaan kuusikulmion pinta-ala $A=6A_{\text{kolmio}}=6 \cdot \frac{9 \sqrt{3}}{4}=\frac{27 \sqrt{3}}{2} \approx 23,38.$ Kuusikulmion pinta-ala on $\frac{27 \sqrt{3}}{2}$ .

Tähän kappaleeseen liittyvät tehtävät.