5. Avaruusgeometria

Tässä luvussa siirrytään tasosta kolmiulotteiseen avaruuteen. Kuitenkin monia tasogeometriassa opittuja lauseita ja ominaisuuksia voi hyödyntää myös avaruusgeometriassa. Tähän kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

# monitahokas-kasitteet-geo

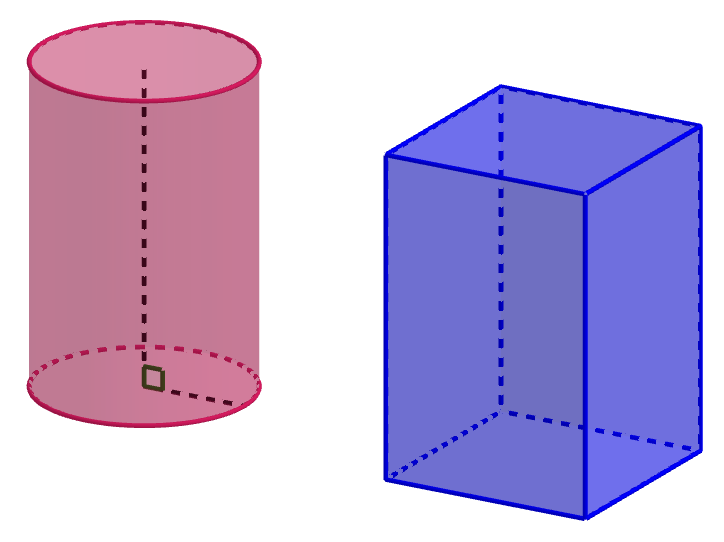
Yllä olevassa GeoGebra-appletissa on käyty läpi monitahokkaan osia ja niiden nimityksiä. Monitahokas on mikä tahansa monikulmioista koostuva suljettu pinta. Jos kaikki monitahokkaan tahkot ovat samanlaisia säännöllisiä monikulmioita, kyseessä on säännöllinen monitahokas. Tällaisia ovat esimerkiksi kuutio, säännöllinen tetraedri ja oktaedri.

# kulmia-avaruudessa

5.1 Kulmia avaruudessa

Kolmiulotteisessa avaruudessa voidaan laskea muun muassa kahden suoran välinen kulma, kahden tason välinen kulma tai tason ja suoran välinen kulma. Seuraavissa esimerkeissä lasketaan suorakulmaisen särmiön avauuslävistäjän pituus sekä sen ja pohjan välisen kulman suuruus.

5.1.1 Esimerkki: avaruuslävistäjän pituuden laskeminen

Laske suorakulmaisen särmiön avaruuslävistäjän pituus, kun sen sivujen pituudet ovat , ja .

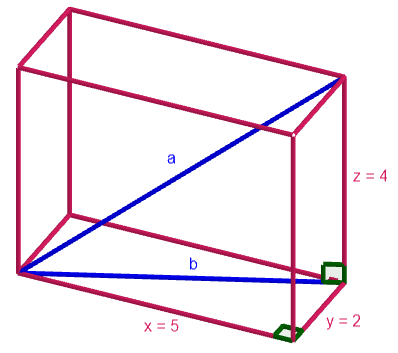
Tehtävässä kysytään siis yllä olevan kuvan avaruuslävistäjän pituutta. Jotta se voitaisi ratkaista, selvitetään ensin, kuinka pitkä lävistäjä on.

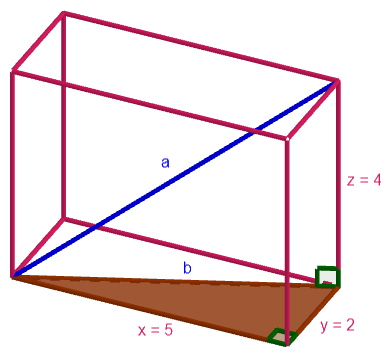
Yllä olevaan kuvaan on korostettu suorakulmaisen särmiön pohjassa oleva suorakulmainen kolmio, jonka hypotenuusa pitäisi ratkaista. Se onnistuu esimerkiksi Pythagoraan lauseella: $\begin{aligned} b^2 &= x^2+y^2 \\ b &= \pm \sqrt{x^2+y^2} \\ b &= \pm \sqrt{5^2+2^2} \\ b &= \pm \sqrt{29} \end{aligned}$ Koska lävistäjän pituus ei voi olla negatiivinen, valitaan vastaukseksi $b=\sqrt{29}$ .

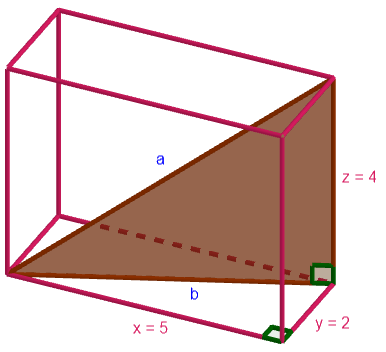
Nyt yllä olevaan kuvaan on korostettu lävistäjän , monitahokkaan särmän ja avaruuslävistäjän muodostama suorakulmainen kolmio. Tästä saadaan ratkaistua hypotenuusa jälleen Pythagoraan lauseella.

$\begin{aligned} a^2 &= b^2+z^2 \\ a &= \pm \sqrt{b^2+z^2} \\ a &= \pm \sqrt{(\sqrt{29})^2+4^2} \\ a &= \pm \sqrt{45} \\ a &= \pm 3 \sqrt{5} \end{aligned}$ Koska avaruuslävistäjän pituus on positiivinen, vastaus on siis $3 \sqrt{5}$ .

5.1.2 Esimerkki: avaruuslävistäjän ja pohjan välinen kulma

Lasketaan seuraavaksi avaruuslävistäjän ja suorakulmaisen särmiön pohjan välinen kulma $\alpha$ .

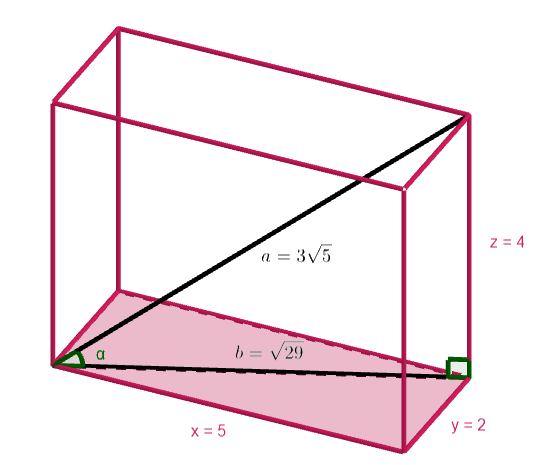
Kulma saadaan ratkaistua trigonometristen funktioiden avulla, esimerkiksi käyttämällä siniä:

$\begin{aligned} \sin ( \alpha) &= \frac{z}{a} \\ \alpha &= \sin ^{-1} \left(\frac{z}{a}\right) \\ \alpha &= \sin ^{-1} \left( \frac{4}{3 \sqrt{5}} \right) \\ \alpha &= 36,6 ^{\circ} \end{aligned}$ Särmiön avaruuslävistäjän ja pohjan välinen kulma on noin $37^{\circ}$ .

Tähän kappaleeseen liittyvät tehtävät.

5.2 Pallo

Pallon pinta-ala ja tilavuus

Pallon muodostavat ne pisteet, jotka ovat säteen etäisyydellä pallon keskipisteestä. Pallon pinta-ala ja tilavuus lasketaan sen säteen avulla $A=4 \pi r^2$ ja $V=\frac{4\pi r^3}{3}.$

5.2.1 Esimerkki: maapallon pinta-ala ja tilavuus

Laske maapallon pinta-ala ja tilavuus, kun sen säde on $6378 \text{ km}$ .

Koska maapallon säde on $r=6378 \text{ km}$ , sen pinta-ala on $A=4 \pi r^2=4 \pi \cdot (6378 \text{ km})^2= 511 \, 185 \, 932,523 \text{ km}^2$

ja tilavuus on $V=\frac{4 \pi r^3}{3}=\frac{4 \pi \cdot (6378 \text{ km})^3}{3} =1 \, 086 \, 781 \, 292 \, 542,889 \text{ km}^3$ Eli maapallon pinta-ala on noin $5,11 \cdot 10^8 \text{ km}^2$ ja tilavuus on noin $1,09 \cdot 10^{12} \text{ km}^3$ .

Segmentti

Taso leikkaa pallon kahteen osaan, joita kutsutaan segmenteiksi. Segmentin tilavuus saadaan sen korkeuden avulla $V_{\text{segmentti}} = \pi h^2 \left(r -− \frac{h}{3} \right).$ Pallon pinnasta taso rajaa kalotin, jonka pinta-ala saadaan segmentin korkeuden avulla $A_{\text{kalotti}}=2 \pi rh.$

5.2.2 Esimerkki: napapiirien rajaama pinta-ala

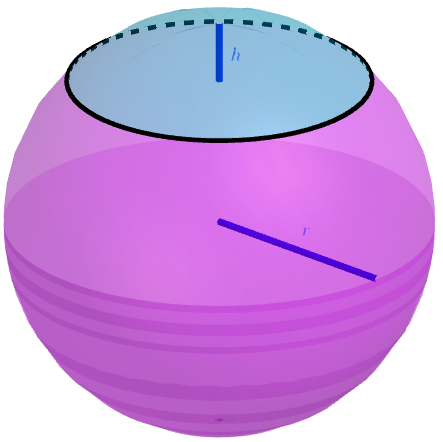
Napapiirit ovat maapallon pohjois- ja eteläosissa sijaitsevat kaksi leveyspiiriä, joiden pohjois- ja eteläpuolilla on mahdollista kokea kaamos ja yötön yö. Napapiirien leveysaste on $66,5^{\circ}$ . Kuinka suuri osa maapallon pinta-alasta on pohjoisen napapiirin pohjoispuolella tai eteläisen napapiirin eteläpuolella?

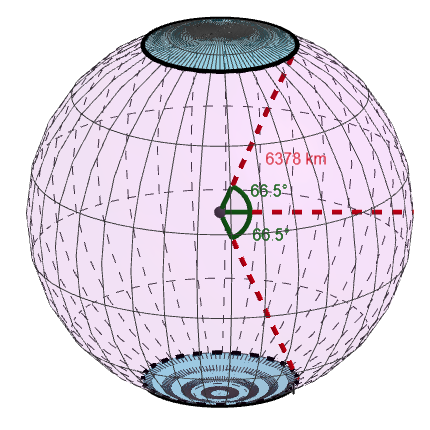
Jotta napapiirien rajaamien kalottien pinta-alat voitaisi laskea, tulee tietää kalotin korkeus. Huomataan, että pallon sisään muodostuu alla olevan kuvan mukainen kolmio, josta voidaan ratkaista kalotin korkeus .

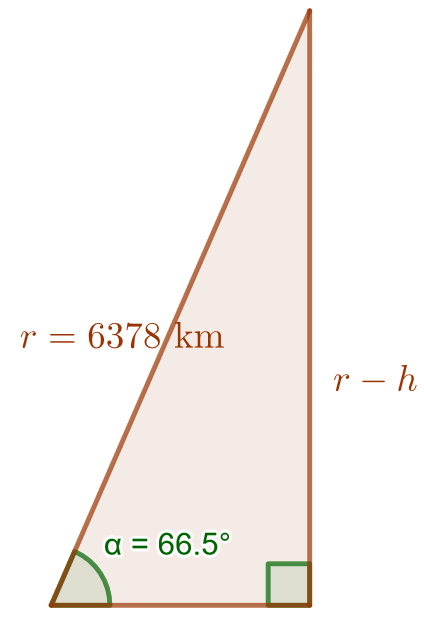
Ratkaistaan kalotin korkeus

$\begin{aligned} \sin(\alpha) &= \frac{r-h}{r} \\ h &= r- r \sin(\alpha) \\ h &= r \cdot (1- \sin(\alpha) ) \end{aligned}$

Yhden kalotin pinta-ala on siis kaavan mukaisesti $\begin{aligned} A_{\text{kalotti}} &= 2 \pi r h \end{aligned}$ jolloin kahden kalotin osuus koko maapallon pinta-alasta voidaan laskea $\begin{aligned} \frac{A_{\text{kalotit}}}{A_{\text{pallo}}} &= \frac{2 \cdot 2 \pi r h}{4 \pi r^2} \\ &= \frac{4 \pi r h}{4 \pi r r} \\ &= \frac{h}{r} \\ &= \frac{r (1-\sin(\alpha))}{r} \\ &= 1-\sin(\alpha) \\ &= 1-\sin(66,5^{\circ}) \\ &= 0,0829 \end{aligned}$

Maapallon pinta-alasta noin $8,3 \%$ on pohjoisen napapiirin pohjoispuolella tai eteläisen napapiirin eteläpuolella.

Tähän kappaleeseen liittyvät tehtävät.

# lierio

5.3 Lieriö

Lieriön pinta-ala ja tilavuus

Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa, muodostuu lieriöpinta. Kun lieriöpinta leikataan kahdella tasolla, syntyy lieriö. Lieriön vaipan pinta-ala saadaan laskettua sen pohjan piirin ja lieriön korkeuden avulla A_v=ph. Lieriön tilavuus saadaan laskettua pohjan pinta-alan A_p ja lieriön korkeuden avulla V=A_p h.

Erityistapaus lieriöstä on suora ympyrälieriö, jota kutsutaan myös sylinteriksi. Suoran ympyrälieriön pohja on ympyrän muotoinen ja sen korkeusjana sekä pohjan säde ovat kohtisuorassa toisiaan vastaan. Lieriö, jonka pohja on muodoltaan monikulmio, on särmiö. Erikoistapaus särmiöstä on esimerkiksi suorakulmainen särmiö.

5.3.1 Esimerkki: suoran ympyrälieriön vaipan aukilevitys GeoGebralla

# aukilevitys-geo

Kokeile vetää suoran ympyrälieriön vaippa auki yllä olevassa GeoGebra-appletissa vetämällä punaista "vedä!"-pistettä hiirellä oikealle. Mitkä ovat syntyvän suorakulmion mitat?

5.3.2 Esimerkki: vinon ympyrälieriön tilavuus

Laske alla olevan lieriön tilavuus.

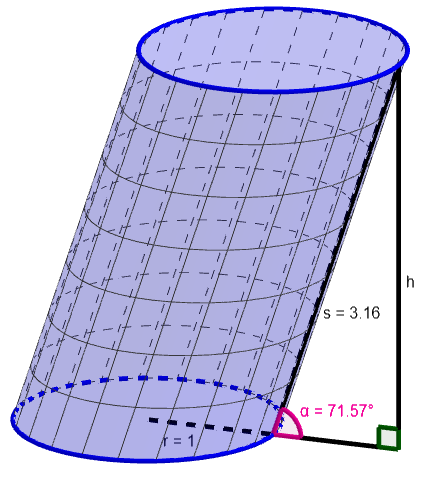
Aluksi pitää ratkaista lieriön korkeus . Se saadaan selville kuvaan piirretyn suorakulmaisen kolmion ja trigonometristen funktioiden avulla. $\begin{aligned} \sin(\alpha) &= \frac{h}{s} \\ h &= s \cdot \sin(\alpha) \end{aligned}$ Tämän jälkeen ratkaistaan tilavuus $\begin{aligned} V&= A_p h \\ &= \pi s r^2 \sin(\alpha) \\ &= \pi \cdot 3,16 \cdot 1^2\cdot \sin (71,57^{\circ}) \\ &= 9,418 \end{aligned}$ Lieriön tilavuus on siis noin 9,4 .

Tähän kappaleeseen liittyvät tehtävät.

# kartio

5.4 Kartio

Kartion tilavuus

Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa ja lisäksi suora kulkee koko ajan saman pisteen kautta, syntyy kartiopinta. Kun kartiopinta leikataan tasolla, syntyy kartio. Kartion tilavuus lasketaan sen pohjan pinta-alan A_p ja korkeuden avulla $V = \frac{A_p h}{3}.$

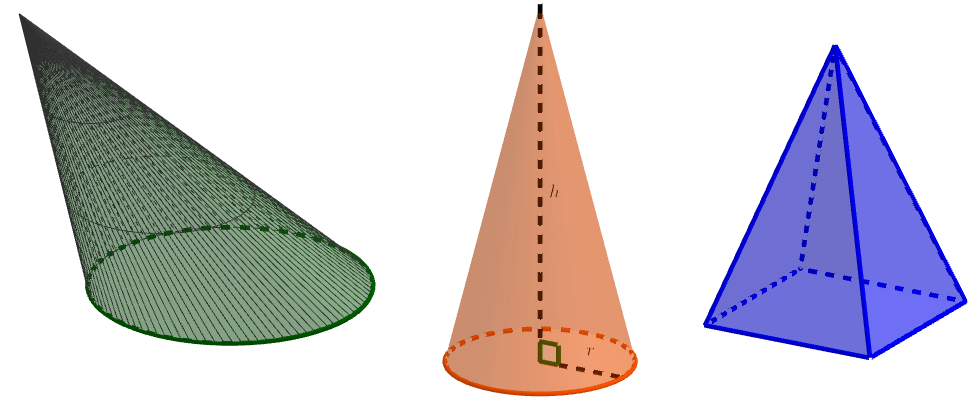
Erikoistapauksia kartiosta ovat ympyräkartio ja pyramidi eli särmäkartio. Ympyräkartion pohjana on ympyrä ja särmäkartion pohjana on monikulmio. Jos ympyräkartion kokeusjana on kohtisuorassa pohjaympyrän sädettä vastaan, kyseessä on suora ympyräkartio.

Ympyräkartio, suora ympyräkartio ja pyramidi

5.4.1 Esimerkki: vinon ympyräkartion tilavuus

Laske alla olevan ympyräkartion tilavuus.

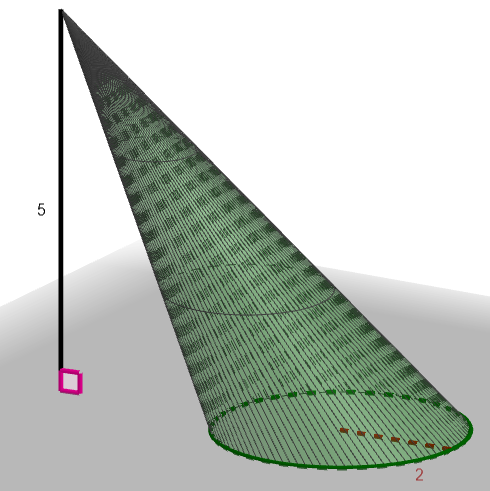
Lasketaan ensin kartion pohjan pinta-ala. Koska pohja on ympyrä, pinta-ala saadaan laskettua $\begin{aligned} A_p &= \pi r^2. \end{aligned}$

Nyt säde r=2 ja kartion korkeus h=5 , jolloin kartion tilavuus on $\begin{aligned} V&=\frac{A_p h}{3} \\ &= \frac{\pi r^2 h}{3} \\ &= \frac{\pi \cdot 2^2 \cdot 5}{3} \\ &= 20,943951 \end{aligned}$ Kartion tilavuus on siis noin 20,9 .

Suoran ympyräkartion vaipan pinta-ala

Suoran ympyräkartion vaipan pinta-ala voidaan laskea pohjaympyrän säteen ja kartion sivujanan avulla $A_v=\pi rs.$

5.4.2 Esimerkki: sirkusteltan pinta-ala

Sirkusteltta muodostuu suorasta ympyrälieriöstä, jonka korkeus on $3 \text{ m}$ ja jonka pohjan säde on $6 \text{ m}$ , sekä suorasta ympyräkartiosta, jonka korkeus on $3 \text{ m}$ ja jonka pohjan säde on $6\text{ m}$ . Kuinka monta neliömetriä tarvitaan telttakangasta?

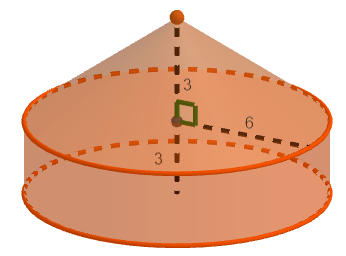
Piirretään ensin yllä olevan kuvan mukainen mallikuva, johon merkitään tunnetut pituudet. Lasketaan ensin pohjalla olevan lieriön vaipan pinta-ala. Se lasketaan pohjaympyrän piirin ja lieriön korkeuden h_1 avulla $\begin{aligned} A_\ell &= ph_1 \\ &= 2 \pi r h_1 \\ \end{aligned}$

Kattona olevan kartion pinta-ala saadaan laskettua sen pohjaympyrän säteen ja kartion sivujanan avulla. Ratkaistaan sivujanan pituus suorakulmaisesta kolmiosta Pythagoraan lauseen avulla.

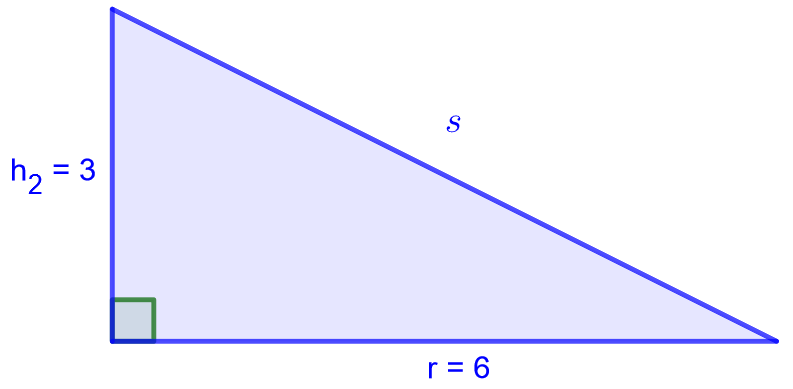
$\begin{aligned} h_2^2+r^2 &= s^2 \\ s &= \sqrt{h_2^2+r^2} \end{aligned}$

Tämän jälkeen lasketaan kartion vaipan pinta-ala $\begin{aligned} A_k &= \pi r s \\ &= \pi r \sqrt{h_2^2+r^2} \end{aligned}$

Lopuksi lasketaan kummankin kappaleen vaippojen alat yhteen. $\begin{aligned} A &= A_\ell + A_k \\ &= 2\pi r h_1 + \pi r \sqrt{h_2^2+r^2} \\ &= 2 \pi \cdot 6 \cdot 3 + 6 \pi \sqrt{3^2+6^2} \\ &= 239,544 \end{aligned}$

Sirkustelttaan tarvitaan telttakangasta noin $240 \text{ m}^2$ .

Tähän kappaleeseen liittyvät tehtävät.