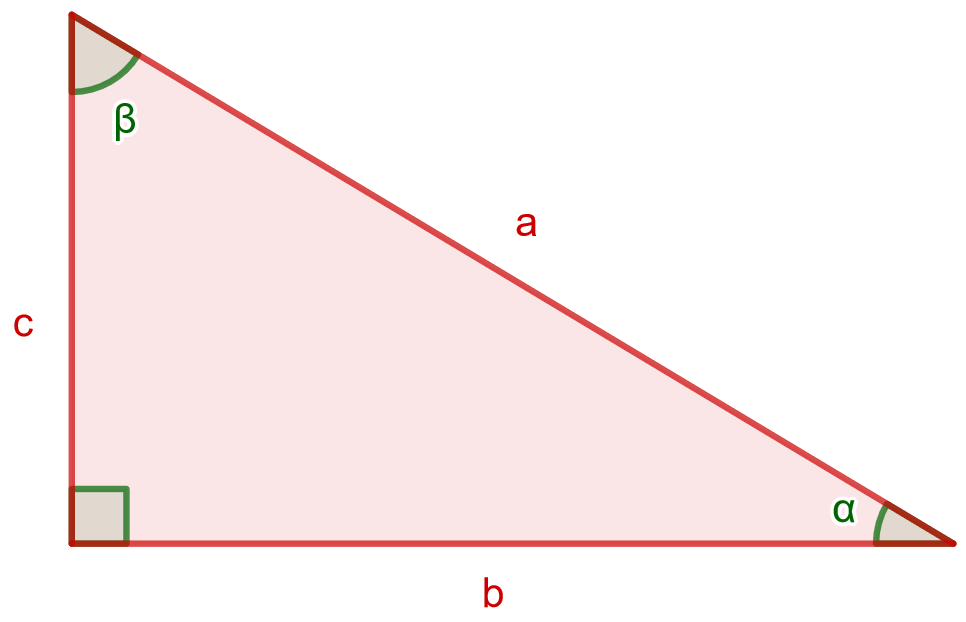
1. Kuvioiden yhdenmuotoisuus: tehtäviä
Tällä sivulla on tehtäviä, jotka liittyvät lukuun Kuvioiden yhdenmuotoisuus. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa luvussakin.
1.1 Yhdenmuotoisuus
Tämän kappaleen teoria on kappaleessa Yhdenmuotoisuus.
1.1.1 Tehtävä
1.2 Mittakaava eli yhdenmuotoisuussuhde
Tämän kappaleen teoria on kappaleessa Mittakaava eli yhdenmuotoisuussuhde.
1.2.1 Tehtävä
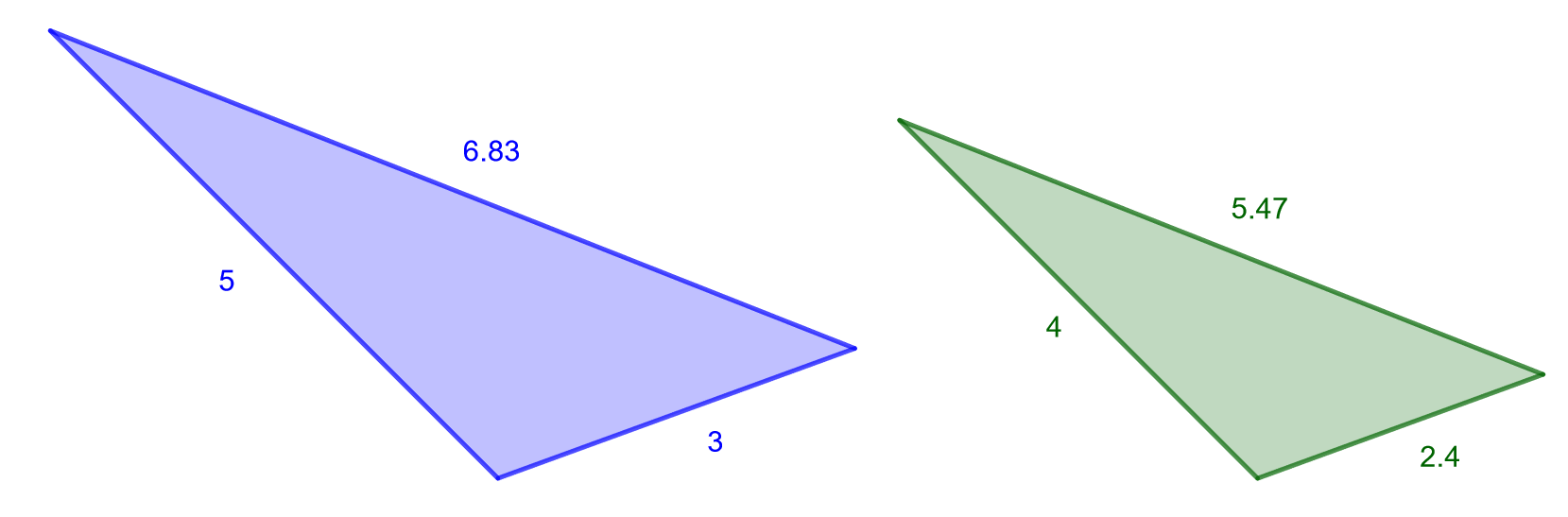
Määritä alla olevan kuvan kolmioiden mittakaava, kun oikeanpuoleinen kolmio on saatu pienentämällä vasemmanpuoleinen kolmio.
1.2.2 Tehtävä (S2015/3a)
Kuntopolun pituus kartalla on . Mikä on polun pituus maastossa, kun kartan mittakaava on
? Anna vastaus
metrin tarkkuudella.
1.2.3 Tehtävä
Kartan mittakaava on . Kallen työpaikan ja keskustan välimatka kartalla on
. Kuinka paljon välimatka on luonnossa?
1.2.4 Tehtävä
Mikä on kartan mittakaava, kun pitkä Suomineito on kartalla
mittainen?
1.2.5 Tehtävä
Biologian kirjassa on suurennos kukasta mittakaavassa . Jos kirjassa olevan kukan leveys on
, kuinka leveä on alkuperäinen kukka?
1.2.6 Tehtävä
Seuraavalla sivulla biologian kirjassa on suurennos muurahaisesta. Suurennoksen pituus on . Tekstissä kerrotaan muurahaisen pituuden luonnossa olevan
. Mikä on suurennoksen mittakaava?
1.3.1 Tehtävä
1.3.2 Tehtävä
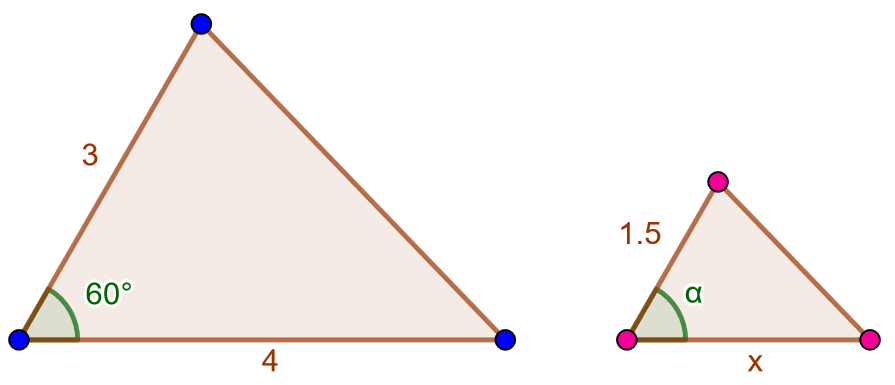
Alla olevassa kuvassa on kaksi yhdenmuotoista kolmiota. Päättele sivun pituus ja kulman
suuruus.
1.3.3 Tehtävä
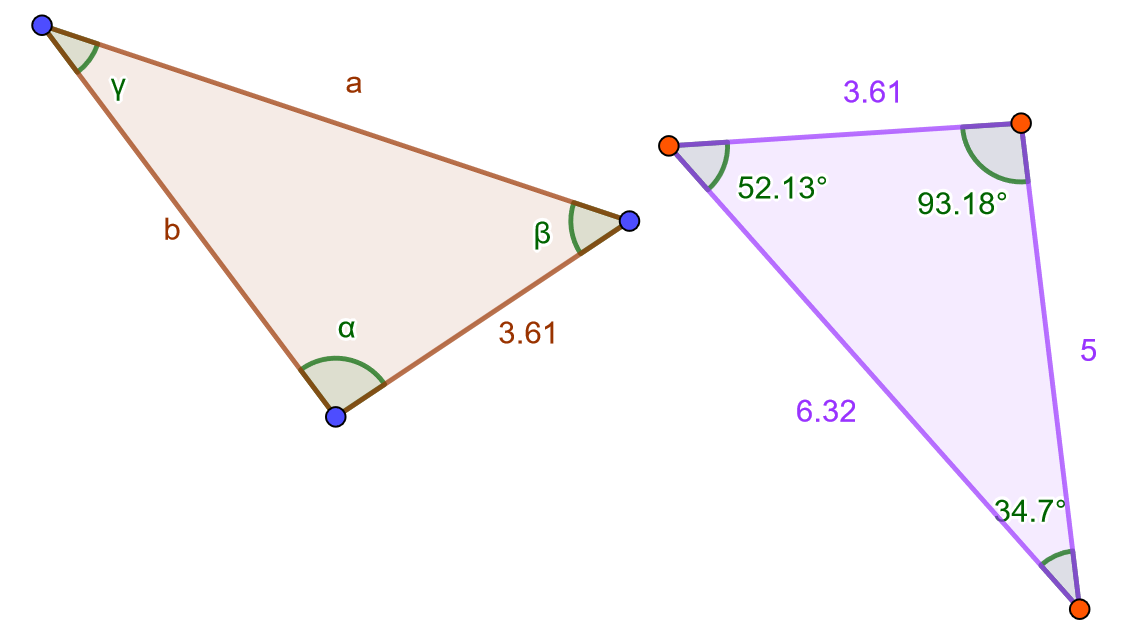
Yllä olevat kolmiot ovat yhdenmuotoisia. Päättele puuttuvat sivujen pituudet ja kulmien suuruudet. Huom! Käytä desimaalipistettä! Älä laita kulmien suuruuksiin astemerkkiä.
1.3.4 Tehtävä
Talon pihalla on lipputanko ja mittainen pystysuora keppi. Eräänä päivänä kepin varjon pituudeksi mitattiin
ja lipputangon varjon pituudeksi
. Kuinka korkea lipputanko on?
1.3.5 Tehtävä
Täydennä alla olevaa GeoGebra-appletti niin, että siinä on kaksi yhdenmuotoista kolmiota. Käytä hyväksesi valmiina appletissa olevaa kolmion sivua.
Tarkista lopuksi, että piirtämäsi kolmion kulmien nimet ovat D, E ja F.
- Jana ED voi vastata mitä tahansa sivua kolmiossa ABC.
- Syöttökentän avulla voit lisätä uuden pisteen esimerkiksi kohtaan (0,0) yksinkertaisesti kirjoittamalla syöttökenttään
(0,0). - Kokeile kirjoittaa syöttökenttään
D+(2;90°)(astemerkin saat painamalla ALT + o). Huomaa, että sulkeissa on pilkun sijaan puolipiste. Pohdi, miten voisit tätä tietoa käyttää yllä olevassa tehtävässä.
Merkitään jonon erotuslukua, eli peräkkäisten jäsenten erotusta kirjaimella , jolloin jonon jäseniä voidaan merkitä
,
ja
.
2. Kolmioiden geometriaa: tehtäviä
Tällä sivulla on tehtäviä, jotka liittyvät lukuun Kolmioiden geometriaa Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa luvussakin.
2.1 Suorakulmainen kolmio, Pythagoraan lause
Tämän kappaleen teoria on kappaleessa Suorakulmainen kolmio, Pythagoraan lause.
2.1.1 Tehtävä
2.1.2 Tehtävä (S2011/1b)
Suorakulmaisen kolmion hypotenuusan pituus on ja toisen kateetin pituus
. Laske toisen kateetin pituus.
2.1.3 Tehtävä (S2015/10)
- Suorakulmaisen kolmion kateettien ja hypotenuusan pituudet
muodostavat geometrisen jonon. Määritä suhdeluku
.
- Suorakulmaisen kolmion kateettien ja hypotenuusan pituudet
muodostavat aritmeettisen jonon. Määritä suhde
.
2.1.4 Tehtävä
Seitsemän metriä korkea puu kasvaa kohtisuoraan maan pintaa vastaan. Puu taittuu kahden metrin korkeudelta niin, että puun latvaosa osuu maahan. Latva ja tyviosa eivät irtoa toisistaan. Piirrä tilanteesta mallikuva oikeanpuoleiselle piirtoalueelle (ei vaikuta tehtävän pisteytykseen) ja laske vasemmanpuoleiselle CAS-alueelle, kuinka suuri kulma on maanpinnan ja taittuneen latvan välillä.
Anna vastaus vasemmanpuoleisella CAS-alueella tallentamalla se muuttujaan nimeltä v. Pyöristä vastaus kokonaislukujen tarkkuudelle käyttämällä komentoa round.
- Tekstin lisääminen
Monesti on hyödyllistä lisätä tehtävän ratkaisuun tekstiä, jossa selität, miten teit tehtävän. Valitse CAS-alueen oikeassa yläkulmassa oleva valikko  ja valitse sieltä teksti
ja valitse sieltä teksti  . Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.
. Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.
- Muuttujan tallentaminen
Joskus on hyödyllistä tallentaa lukuarvo tai vastaus muuttujaan. Tällöin lukuarvon käyttäminen myöhemmin on kätevää. Jos haluat sijoittaa muuttujaan a arvon 4, kirjoita komento a := 4. Jos myöhemmin haluat laskea laskun , kirjoita komento
5*a, jolloin saat vastaukseksi 20.
- Yhtälön ratkaiseminen
Jos haluat ratkaista muuttujan yhtälöstä
, syötä CAS-laskimeen komento
Ratkaisut(a^2+3a-4,a). Vastaukseksi saat listan {-4,1}. Helpoiten ratkaisuihin pääsee käsiksi, kun tallentaa ne muuttujaan: vastaukset := Ratkaisut(a^2+3a-4,a). Tällöin komento vastaukset(1) tuottaa luvun -4, ja komento vastaukset(2) tuottaa luvun 1.
- Lukuarvon näyttäminen
Joskus GeoGebra näyttää vastauksen hyvinkin monimutkaisessa muodossa. Käytä tällöin komentoa Lukuarvona(). Jos kirjoitat esimerkiksi komennon a:=sin^(-1)(1/2), GeoGebra tulostaa vastaukseksi saman eli a:=sin^(-1)(1/2). Jos haluat vastauksen lukuarvona, kirjoita komento Lukuarvona(a), jolloin GeoGebra tulostaa 60°.
2.2 Trigonometriset funktiot
Tämän kappaleen teoria on kappaleessa Trigonometriset funktiot.
2.2.2 Tehtävä
2.2.3 Tehtävä
2.2.4 Tehtävä
2.2.5 Tehtävä
2.2.6 Tehtävä
2.2.7 Tehtävä (s1996/3b)
Katuvalaisimen kannatinvaijeri on kiinnitetty leveän kadun vastakkaisilla puolilla olevien talojen seiniin
korkeudelle maasta. Lamppu riippuu vaijerista sen keskikohdalta, joka on
vaijerin päitä alempana, ja vetää vaijerin puolikkaat likimain janoiksi. Kuinka pitkä vaijeri on, ja kuinka suuren kulman vaijerin puoliskot muodostavat keskenään?
2.2.8 Tehtävä (K2017/6)
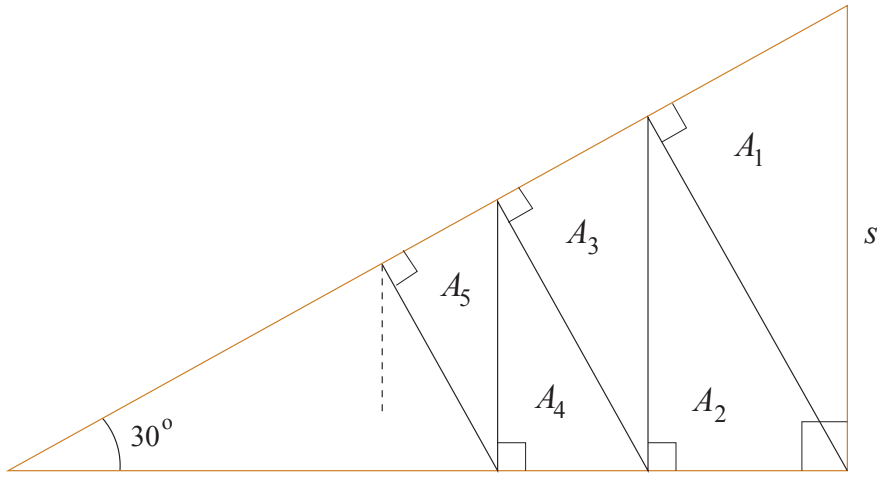
Suorakulmaisen kolmion muotoisesta suklaalevystä lohkotaan alla olevan kuvion mukaisesti kappaletta yhdenmuotoisia paloja, joiden pinta-alat ovat
. Kuinka monta palaa suklaasta täyty lohkaista, jotta palojen yhteenlasketut pinta-alat muodostavat vähintään
suklaalevyn alkuperäisestä pinta-alasta?
2.2.9 Tehtävä
Määritä lausekkeen tarkka arvo käyttämällä alla olevaa tasakylkistä kolmiota.
Ratkaise alkuperäisen kolmion kolmannen sivun pituus.
Lisää valinta kohtaan "vihje 1". Millainen kolmio muodostuu mustan janan oikealle puolelle? Voiko sitä verrata alkuperäiseen kolmioon? Saatko ratkaistua mustan janan pituuden?
Pidä edelleen valinta kohdassa "Vihje 1". Mustan janan oikealle puolelle muodostuu kolmio, joka on yhdenmuotoinen alkuperäisen kolmion kanssa (perustele tämä kulmien suuruuksien avulla). Käytä verrantoa ratkaistaksesi kolmion kolmannen sivun (ja samalla mustan janan) pituus.
Lisää valinta kohtaan "Vihje 2" ja huomaa, että .
2.3 Muistikolmiot
Tämän kappaleen teoria on kappaleessa Muistikolmiot.
2.3.1 Tehtävä
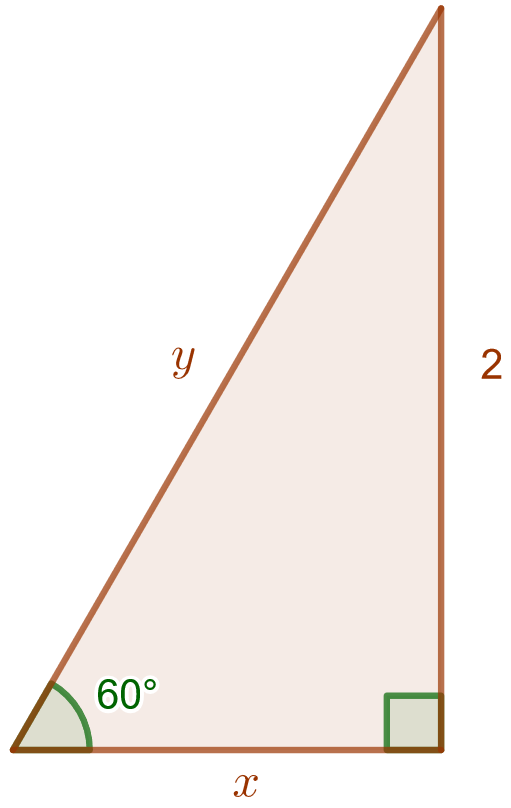
Laske muistikolmion avulla alla olevan kolmion kateetin pituus sekä hypotenuusan
pituus.
2.3.2 Tehtävä
Määritä kulman suuruus muistikolmioiden avulla ilman laskinta, kun
.
2.3.3 Tehtävä (K2018/6)
Suorakulmaisen kolmion toinen terävä kulma on astetta. Kolmion hypotenuusan keskipisteeseen piirretään kuvion mukaisesti kohtisuora jana, jonka toinen päätepiste sijaitsee kolmion kateetilla. Laske niiden kahden osan pituuksien suhde, joihin kohtisuora jakaa kateetin.
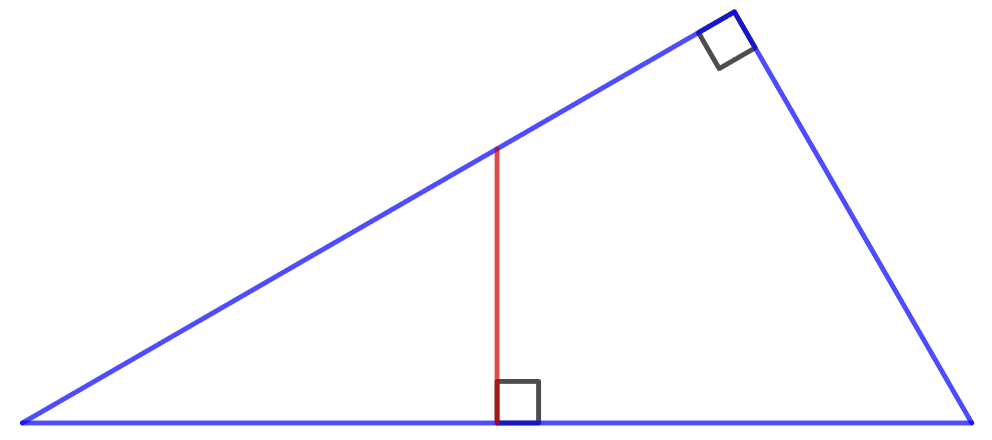
Anna vastaus murtolukuna ja ilmoita suhde suorasta kulmasta lähtien.
2.4 Tylpän kulman sini ja kosini
Tämän kappaleen teoria on kappaleessa Tylpän kulman sini ja kosini.
2.4.1 Tehtävä
Laske ilman laskinta.
2.4.2 Tehtävä
Laske ilman laskinta.
2.4.4 Tehtävä
2.4.5 Tehtävä
2.4.6 Tehtävä
2.4.7 Tehtävä
2.5 Kolmion pinta-ala
Tämän kappaleen teoria on kappaleessa Kolmion pinta-ala.
2.5.1 Tehtävä
2.5.2 Tehtävä
2.5.3 Tehtävä
2.5.4 Tehtävä
MathCheck laskee kulmia aina radiaaneina. Jos haluat kirjoittaa sin(60°), sinun on kirjoitettava sen sijaan sin(60 * pi/180).
2.5.5 Tehtävä
Kolmion kantasivun pituus on ja kolmion korkeus on
. Laske kolmion pinta-ala.
2.5.6 Tehtävä
Tasasivuisen kolmion sivun pituus on 3. Mikä on kolmion pinta-ala?
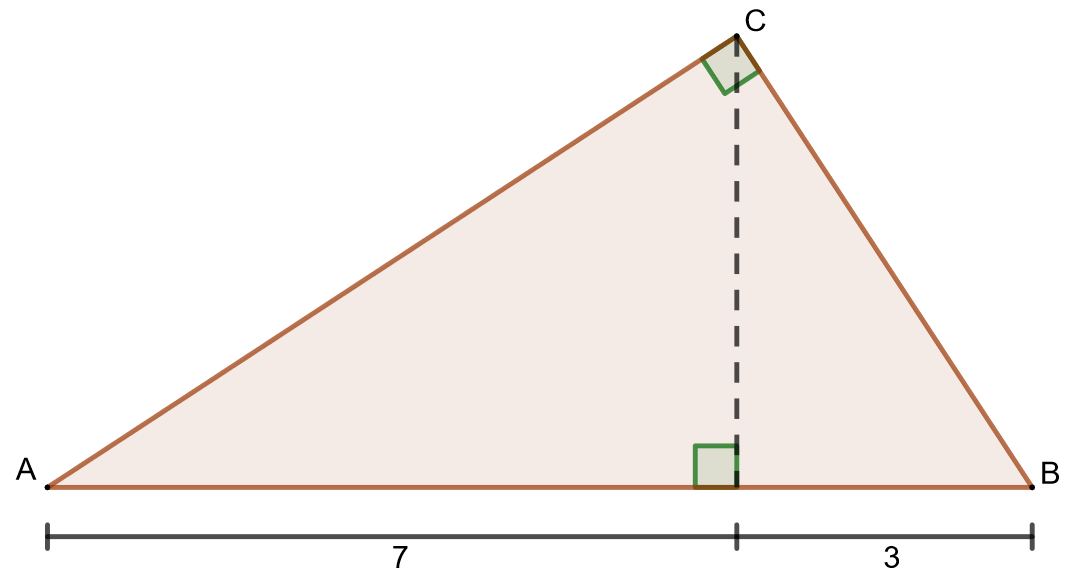
2.5.7 Tehtävä (K2013/4)
Laske alla olevan kuvan suorakulmaisen kolmion pinta-alan tarkka arvo.
2.6 Kosinilause
Tämän kappaleen teoria on kappaleessa Kosinilause.
2.6.1 Tehtävä
Maanmittarin tehtävänä on määrittää pisteiden ja
välimatka. Pisteiden välissä on vaara, joka kierretään pisteen
kautta, josta on näköyhteys pisteisiin
ja
. Kuvassa olevat etäisyydet ovat metreinä.
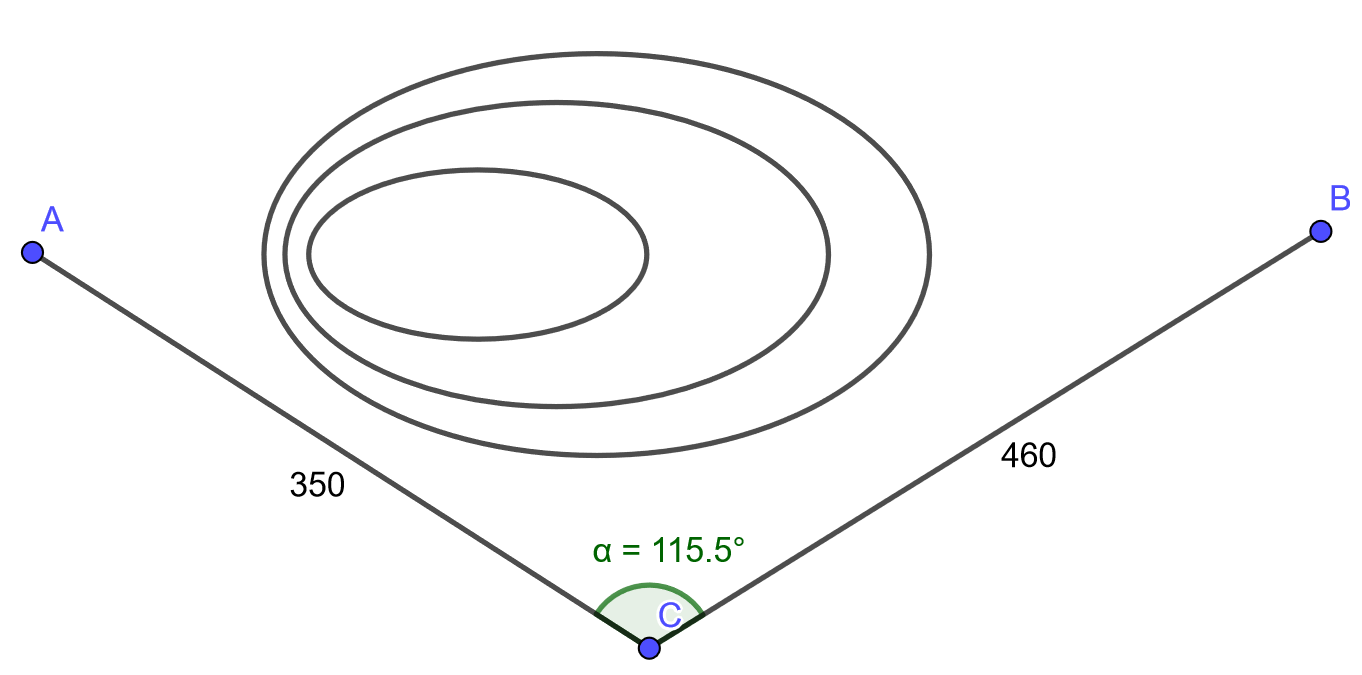
Kokeile myös luoda kuvan mukainen konstruktio (ilman mäen käyriä) GeoGebralla. Saatko selvitettyä pisteiden ja
välisen etäisyyden ilman laskemista?
2.6.2 Tehtävä
Alla olevassa kuvassa on kolmion muotoinen pelto. Laske pellon pinta-ala hehtaareina. Anna vastaus yhden desimaalin tarkkudella ilman yksikköä ja muista käyttää desimaalipistettä.
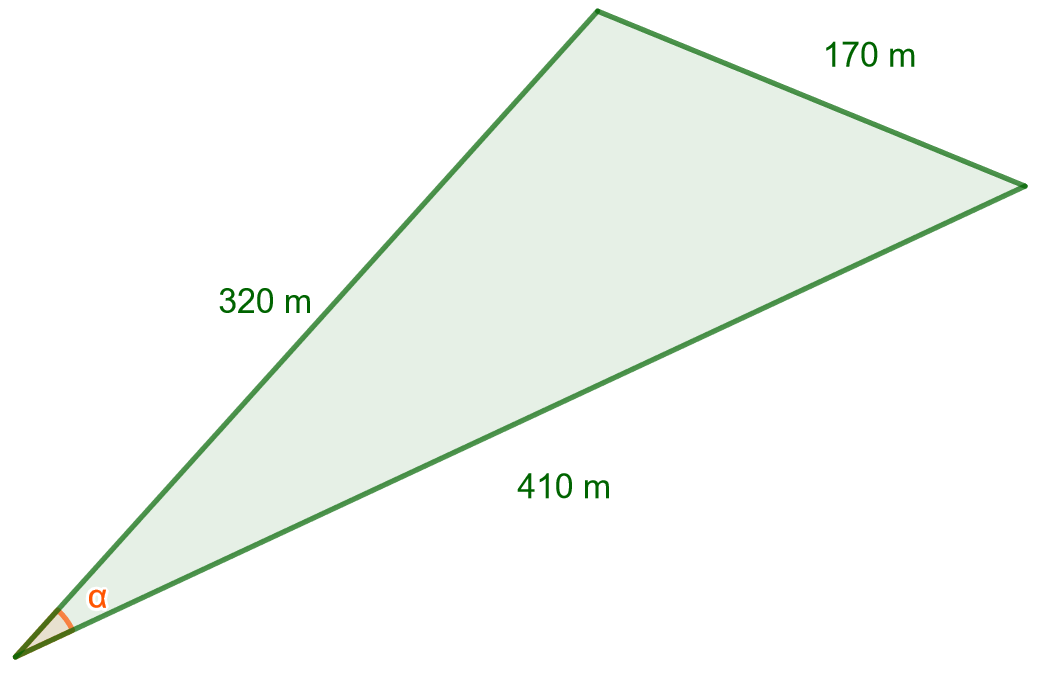
2.6.3 Tehtävä (S2012/4b)
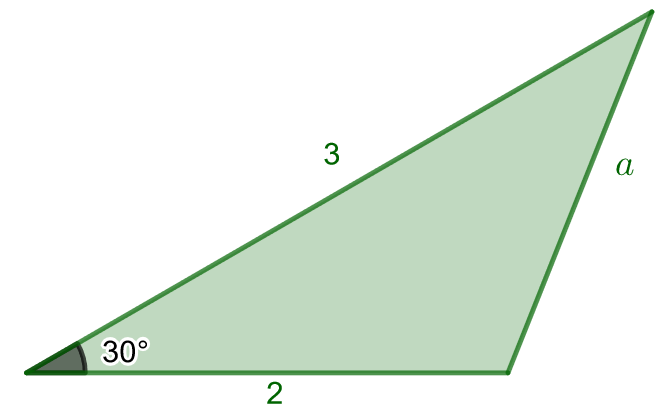
Laske oheisessa kuvassa olevan kolmion sivun pituuden tarkka arvo ja kaksidesimaalinen likiarvo.
2.6.4 Tehtävä
Kalle kulkee kompassin kanssa ensin etelään ja sitten
kaakkoon. Kuinka kaukana lähtöpaikastaan Kalle on? Piirrä ensin mallikuvio.
2.7.1 Tehtävä
Kolmion sivun pituus on ja sen vastaisen kulman suuruus on
. Merkitään kolmion toista sivua kirjaimella
ja sen vastaista kulmaa
. Ratkaise sivun
pituus.
2.7.2 Tehtävä
Ratkaise alla olevaan kuvaan merkitty tylppä kulma .
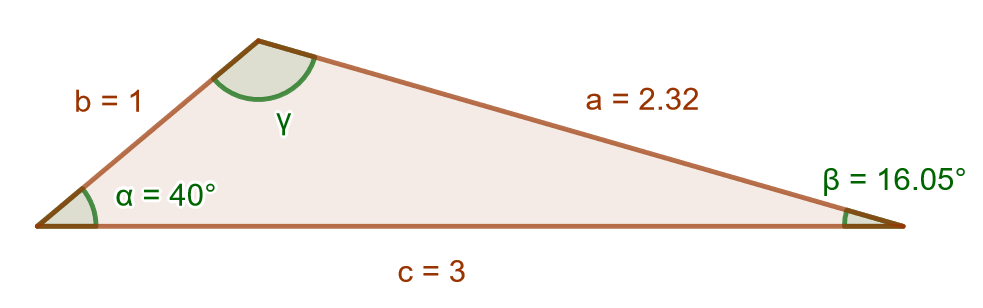
2.7.3 Tehtävä
Ratkaise alla olevan kuvion sivun pituus. Anna vastaus kahden desimaalin tarkkuudella.
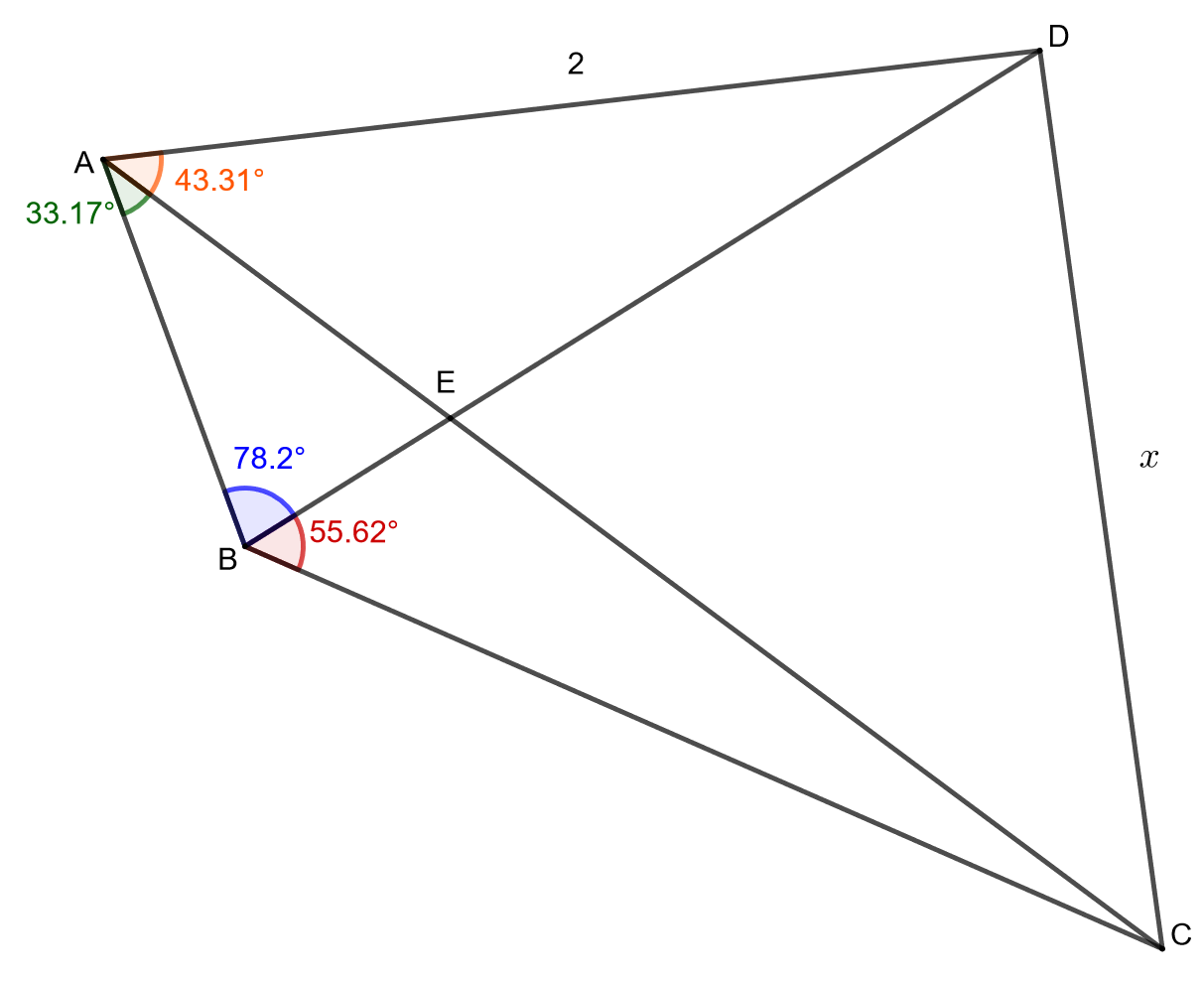
Päättele ensin pisteen E ympärillä olevat kulmat ja laske sinilauseen avulla sivujen ,
,
ja
pituudet. Sovella lopuksi kosinilausetta pituuden
ratkaisemiseksi.
2.7.4 Tehtävä
Ratkaise alla olevaan kuvaan merkityn janan pituus.
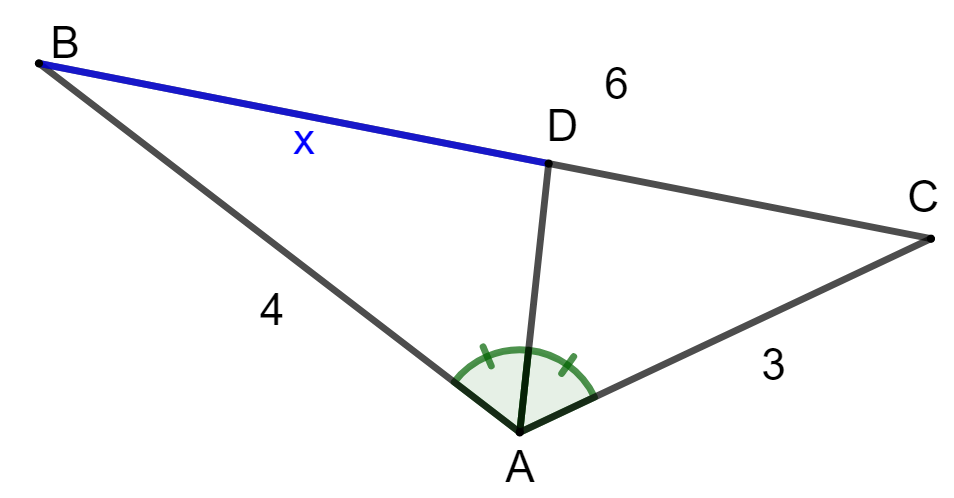
2.7.5 Tehtävä (S2013/6)
Kolmion kulman
puolittaja leikkaa sivun
pisteessä
. Pisteiden välisille etäisyyksille on voimassa
,
ja
. Määritä kolmion sivujen
ja
pituuksien tarkat arvot.
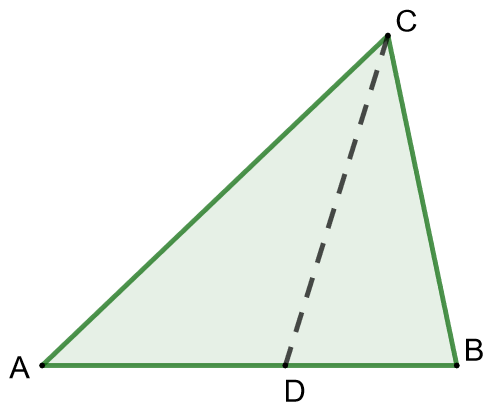
Käytä ensin kulmanpuolittajalausetta ja sen jälkeen kosinilausetta.
2.7.6 Tehtävä
Kolmiosta tiedetään seuraavaa. Sivun
pituus on
, kulman
suuruus on
ja kulman
suuruus
. Piirrä tilanteesta mallikuvio ja laske sivun
pituus. Anna vastaus yhden desimaalin tarkkuudella.
2.8 Käänteinen Pythagoraan lause
Tämän kappaleen teoria on kappaleessa Käänteinen Pythagoraan lause.
2.8.1 Tehtävä
Kolmion sivujen pituudet ovat ,
ja
. Onko kolmio suorakulmainen?
2.8.2 Tehtävä
Kolmion sivujen pituudet ovat ,
ja
. Onko kolmio suorakulmainen?
2.8.3 Tehtävä (K2017/12)
Neliöiden ,
ja
pinta-alojen suhde on
. Kolmion
yhtenä sivuna on neliön
sivu, toisena sivuna neliön
sivu ja kolmantena sivuna neliön
sivu. Laske kolmion
ja neliön
pinta-alojen suhteen tarkka arvo.
Onko kolmio suorakulmainen?
2.9 Kolmion merkilliset pisteet
Tämän kappaleen teoria on kappaleessa Kolmion merkilliset pisteet.
2.9.1 Tehtävä
Kuinka suuressa kulmassa suorakulmaisen kolmion terävien kulmien puolittajat leikkaavat? Kokeile tehdä tehtävänannosta dynaaminen kuva GeoGebralla.
Voidaanko tulos yleistää myös muihin kolmioihin?
[H]
2.9.2 Tehtävä
Seattlessa on alue, jota kutsutaan 'Denny triangle'ksi sen kolmiomaisen muodon vuoksi. Määritä piste, joka on yhtä kaukana jokaisesta Dennyn kolmion kärkipisteestä.
Kun olet määrittänyt pisteen, joka on yhtä kaukana kärkipisteitä, käytä Mittaa etäisyys -toimintoa ja mittaa pisteen etäisyys kaikista kärkipisteistä. Tehtävän pisteytys perustuu tähän etäisyyteen. Varmista siis, ettet siirrä valmiiksi annettuja punaisia pisteitä ja nimeät määrittämäsi pisteen F:ksi.
Käytä keskinormaalilausetta.
2.9.3 Tehtävä
Alla on kuva kolmion muotoisesta pöydästä. Pöytä halutaan seisomaan vain yhden jalan varassa, jolloin jalka pitäisi sijoittaa pöytälevyn painopisteeseen. Määritä pöytälevyn painopiste alla olevalla GeoGebra-appletilla. Varmista, että nimeät painopisteen kirjaimella G.
2.10 Sekalaisia tehtäviä
Tässä kappaleessa on kaikkiin tämän luvun kappaleisiin liittyviä tehtäviä.
2.10.1 Tehtävä
Lähtiessään rastilta suunnistaja tietää, että seuraavalle rastille on matkaa , mutta ottaa kompassilla suunnan huolimattomasti ja lähtee kulkemaan
väärään suuntaan. Kuinka kaukana suunnistaja on oikeasta rastista, kun hän on kulkenut
matkan?
2.10.2 Tehtävä
Piirrä teräväkulmainen kolmio, jonka kahden sivun pituudet ovat ja
ja näiden sivujen välinen kulma on
. Määritä kolmion kolmannen sivun pituus. Tallenna sivun pituus muuttujaan nimeltä
a.
2.10.3 Tehtävä (S2016/5)
- Kolmion kulmat muodostavat aritmeettisen jonon, ja yhden kulman suuruus on
. Määritä kulmien suuruudet asteina.
- Kolmion kulmat muodostavat geometrisen jonon, ja yhden kulman suuruus on
radiaania. Määritä kulmien suuruudet radiaaneina.
2.10.4 Tehtävä
Alla olevassa kuvassa ja
ovat neliöitä. Osoita, että kolmioilla
ja
on sama pinta-ala. [H]
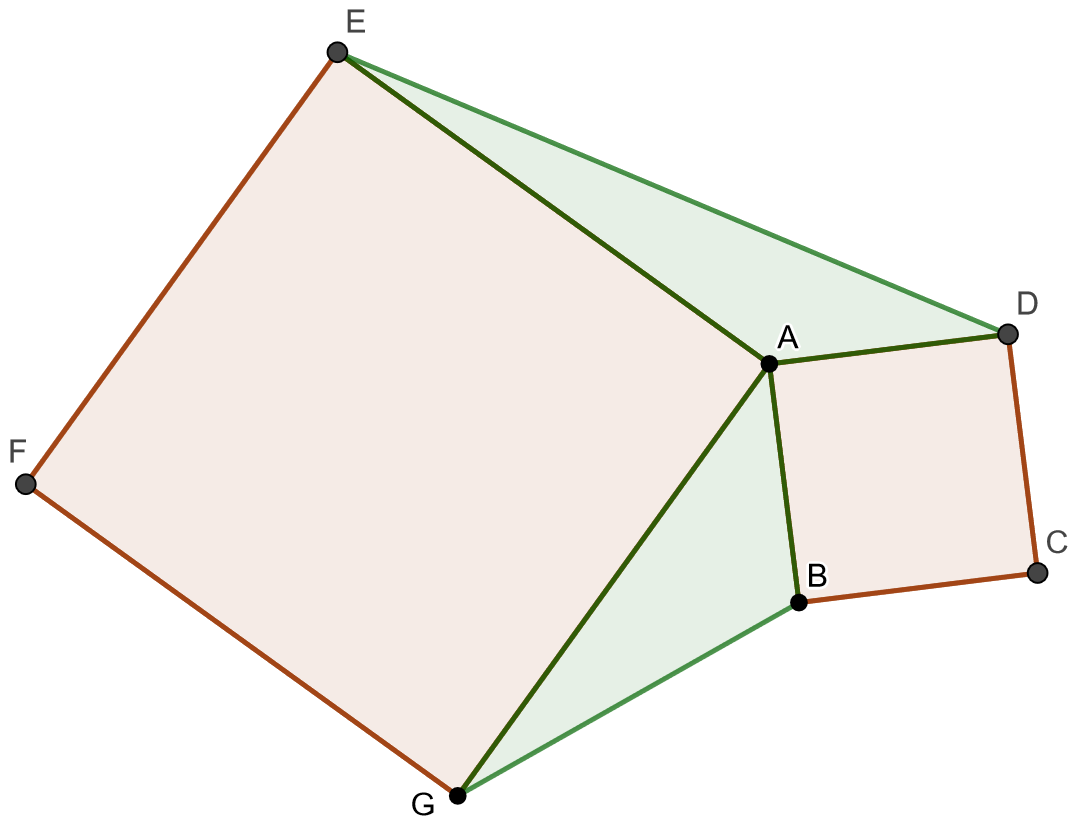
Merkitään ja
. Lisäksi merkitään
. Nyt alemman kolmion pinta-ala on
. Merkitään
. Tiedetään, että
. Nyt toisen kolmion pinta-ala on
. Tylpän kulman sinistä tiedetään
. Joten
eli kolmioiden pinta-alat ovat samat.
2.10.5 Tehtävä
Alla olevassa kuvassa on neljä neliötä, ja vasemmassa alakulmassa olevan neliön pinta-ala on . Mikä on tummanvihreän kolmion pinta-ala? [H]
Kahden kolmion pinta-alat ovat samoja, jos niiden kannat ovat yhtä pitkät ja niiden korkeudet ovat yhtä pitkät. Paina "Näytä korkeusjanaa" -nappia, jolloin voit siirtää tummanvihreän kolmion kärkipistettä.
2.10.6 Tehtävä (S2015/15)
Kolmion kahden sivun pituudet ovat ja
. Näiden sivujen välisen kulman puolittajasta kolmion sisälle jäävän osan pituus on
. Puolittaja jakaa kolmannen sivun kahteen osaan, joiden pituudet ovat
ja
. Osoita, että
,
kun
.
kun
.
- Jos
, niin kolmio on tasakylkinen ja tällöin myös
. Pythagoraan mukaan
. Kun tässä toinen
korvataan
:llä ja toinen
korvataan
:llä, saadaan
, josta väite seuraa.
- Olkoon kulman puolikas
. Kosinilauseesta ja kulmanpuolittajalauseesta saadaan ehdot
Ratkaistaan kahdesta ensimmäisestä yhtälöstä ja merkitään tulokset samoiksi:
Kerrotaan puolittain
:lla:
Korvataan ja kerrotaan puolittain
:llä
Ratkaistaan
:
Sijoitetaan :
ja ryhmitellään
josta väite seuraa. Ratkaisu edellyttää, että
, mutta ehto on voimassa, koska oletettiin, että
, jolloin myös
.
2.10.7 Tehtävä
Piirrä GeoGebralla Napoleonin lausetta vastaava konstruktio alla olevia ohjeita seuraamalla.
- Valitse GeoGebran Monikulmio-työkalu (klikkaa
LISÄÄ, jos ei ole näkyvissä työkaluissa) ja piirrä jonkin muotoinen kolmiok1. - Valitse GeoGebran Säännöllinen monikulmio -työkalu, ja piirrä tasasivuiset kolmiot kolmion
k1jokaiselle sivulle (kuvio1,kuvio2jakuvio3). Tämä tapahtuu valitsemalla kolmionk1kaksi kärkipistettä ja syöttämällä kulmien lukumääräksi 3.- Huomaa, että tasasivuisten kolmioiden tulee olla kolmion
k1ulkopuolella. Jos kolmiot syntyvät alkuperäisen kolmionk1päälle, kokeile valita kärkipisteet eri järjestyksessä.
- Huomaa, että tasasivuisten kolmioiden tulee olla kolmion
- Valitse Keskipiste-työkalu ja luo jokaiselle kolmiolle
kuvio1,kuvio2jakuvio3keskipiste napsauttamalla kyseistä kolmiota. - Yhdistä äsken luodut keskipisteet käyttämällä Monikulmio-työkalua, jolloin syntyy kolmio
k2. - Mittaa kolmion
k2kulmien suuruudet. Helpoiten tämä käy, kun valitset Kulma-työkalun ja napsautat kolmiotak2, jolloin GeoGebra mittaa kolmionk2kaikkien sisäkulmien (α,βjaγ) suuruudet samalla kertaa. - Kokeile siirtää alkuperäisen kolmion
k1kärkipisteitä. Mitä huomaat? - Halutessasi voit muokata kolmioiden ja pisteiden värejä ja nimien näkyvyyttä.
3. Monikulmioiden pinta-aloja: tehtäviä
Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Monikulmioiden pinta-aloja. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.
3.1 Puolisuunnikas
Tämän kappaleen teoria on kappaleessa Puolisuunnikas.
3.1.1 Tehtävä
3.1.2 Tehtävä
3.1.3 Tehtävä
3.2.1 Tehtävä
3.2.2 Tehtävä
3.2.3 Tehtävä
Suunnikkaan sivujen pituudet ovat ja
, ja sen pinta-ala on
. Kuinka suuri kulma sivujen välissä on?
3.2.4 Tehtävä
Suunnikkaan sivujen välinen kulma on . Lyhyempi sivuista on pituudeltaan
ja pidempi
. Määritä suunnikkaan ala.
3.2.5 Tehtävä
Aakkoskarkkien sivujen pituudet ovat ja sen lyhyempi halkaisija on
. Laske yhden karkin pinta-ala.

3.2.6 Tehtävä (S2011/15)
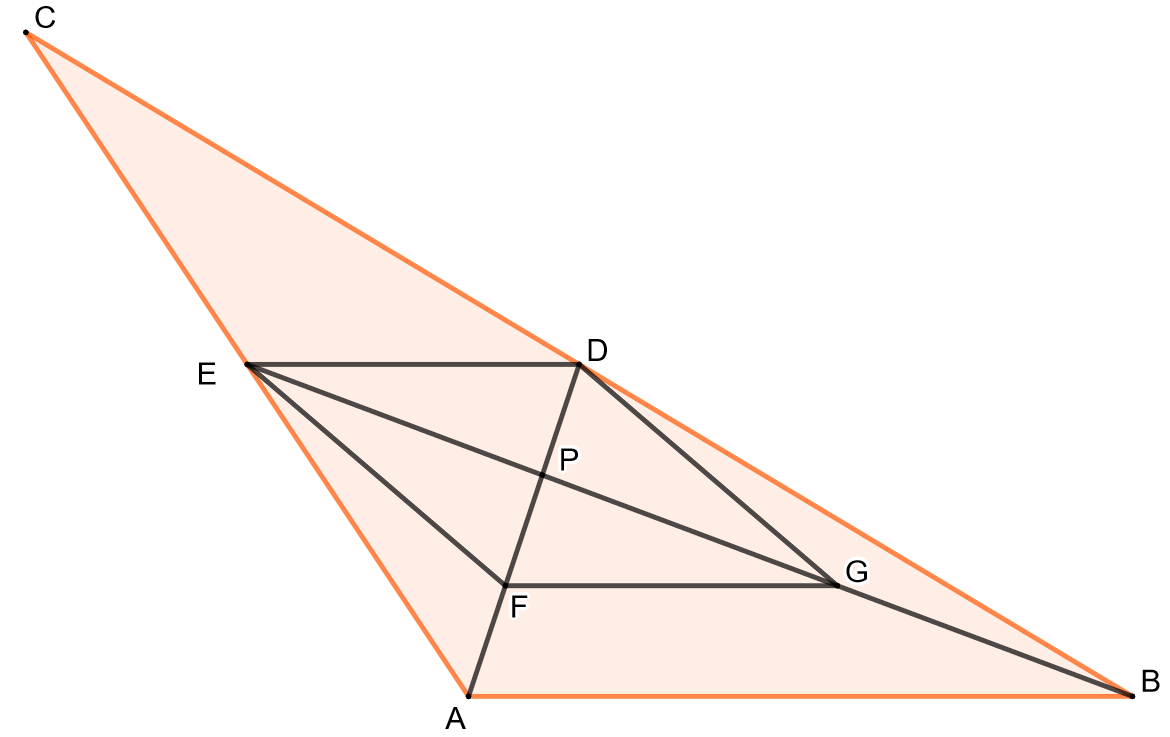
Merkitään kolmion keskijanojen
ja
leikkauspistettä kirjaimella
.
Jos
on janan
keskipiste ja
janan
keskipiste, niin osoita, että janan
pituus on puolet janan
pituudesta.
Osoita, että nelikulmio
on suunnikas
Osoita, että janan
pituus on kolmasosa janan
pituudesta.
Todista edellisten kohtien perusteella seuraava lause: Kolmion keskijanat leikkaavat toisensa samassa pisteessä, joka jakaa jokaisen keskijanan siten, että sivun puoleisen osan pituus on kolmasosa koko keskijanan pituudesta.
- Kolmiot
ja
ovat yhdenmuotoiset (SKS) yhdenmuotoisuussuhteen ollessa
. Näin ollen vastinsivuina
.
- Pisteestä
piirretty janan
suuntainen suora puolittaa janan
eli kulkee pisteen
kautta. Tämä johtuu siitä, että kolmiot
ja
ovat yhdenmuotoisia (SKS). Näin ollen sivut
ja
ovat yhdensuuntaiset. Vastaavasti nähdään, että sivut
ja
ovat yhdensuuntaiset, eli sivut
ja
ovat yhdensuuntaiset. Edelleen, kolmiot
ja
ovat yhdenmuotoiset (SKS) yhdenmuotoisuussuhteen ollessa
. Näin ollen
eli
. Koska sivut
ja
ovat yhtä pitkiät ja yhdensuuntaiset, nelikulmio
on suunnikas.
- Suunnikkaan lävistäjät puolittavat toisensa, joten
eli
.
- Edellisen mukaan pisteestä
piirretty keskijana leikkaa pisteestä
piirretyn keskijanan pisteessä, jonka etäisyys pisteestä
on
. Vastaavasti nähdään, että sama pätee pisteestä
piirretylle keskijanalle: sekin leikkaa pisteestä
piirretyn keskijanan pisteessä, jonka etäisyys pisteestä
on
. Näin ollen myös pisteestä
piirretty keskijana kulkee pisteen
kautta. Edellisen mukaan nähdään, että piste
jakaa kaikki keskijanat suhteessa
.
4. Ympyrä: tehtäviä
Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Ympyrä. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.
4.1 Säde, halkaisija, piiri
Tämän kappaleen teoria on kappaleessa Säde, halkaisija, piiri.
4.1.1 Tehtävä
Oleletaan, että maapallo on täysin pyöreä. Eräs puhelinyhtiö on vetänyt puhelinlinjan päiväntasaajaa pitkin maapallon ympäri. Kuinka paljon linjaa tarvitaan lisää, jos se halutaan nostaa korkeille tolpille. Anna vastaus metreinä ja yhden desimaalin tarkkuudella.
4.1.2 Tehtävä (S2018/8)
Yksikköympyrän kehän pituus on . Arvioi tätä lukua approksimoimalla ympyrää sen sisään piirretyllä säännöllisellä kuusikulmiolla ja laskemalla kuusikulmion piirin pituus. Muodosta toinen arvio säännöllisen 12-kulmion avulla ja määritä kummankin approksimaation suhteellinen virhe vertaamalla tuloksia laskimen antamaan lukun
likiarvoon.
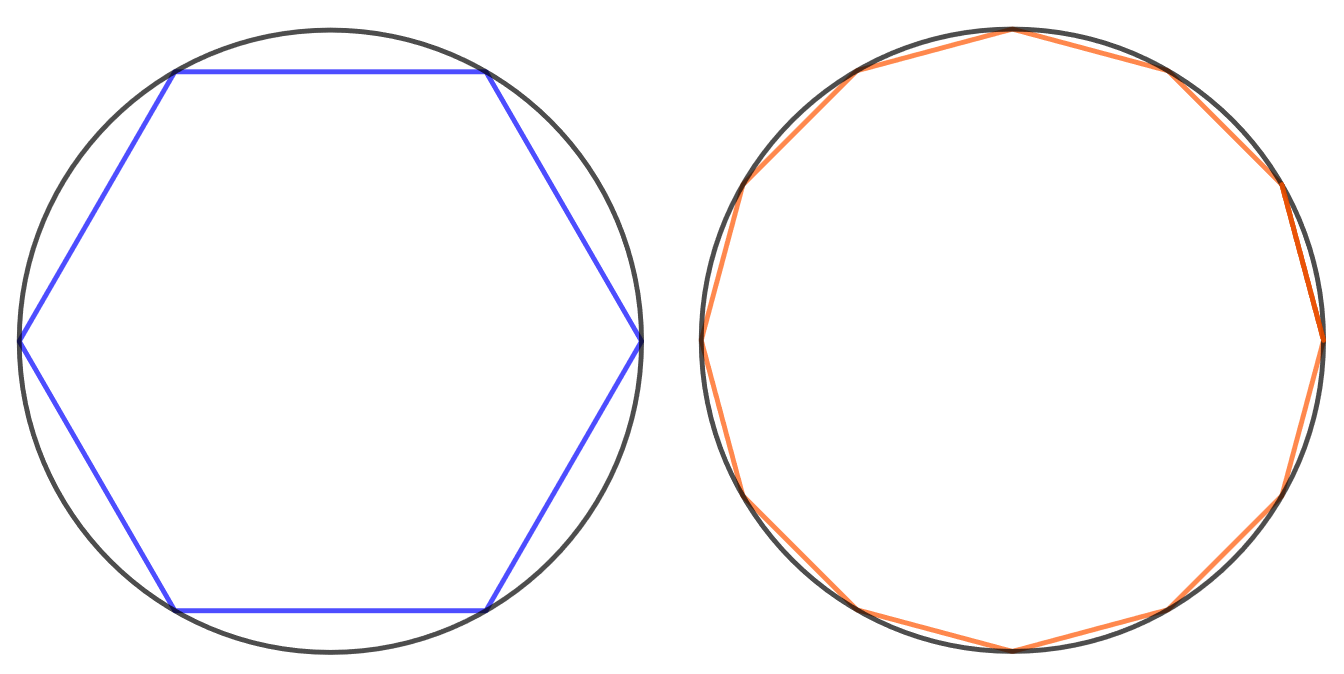
Huomautus: Yksikköympyrä tarkoittaa ympyrää, jonka säde on .
4.1.3 Tehtävä
Polkupyörän renkaan koko on eli sen halkaisija on
tuumaa. Pyörään halutaan laittaa matkamittari, jota varten tarvitaan yhdellä renkaan pyörähdyksellä kuljettu matka. Laske pyörän yhden renkaan täydellä pyörähdyksellä kulkema matka ja ilmoita vastaus yhden desimaalin tarkkuudella senttimetreinä.
4.1.4 Tehtävä
Halkaisijaltaan pyörä pyörähtää
kertaa. Kuinka pitkän matkan pyörä etenee?
Kuinka monta pyörähdystä pyörä etenee matkalla?
4.1.5 Tehtävä
Mari haluaa laittaa kukkia kasvamaan täsmälleen ympyrän muotoon. Hänellä on kukkaa ja hän haluaa, että kukkien välinen etäisyys ympyrän kaarta pitkin mitattuna on tasan
. Mikä on tällaisen ympyrän halkaisija?
4.1.6 Tehtävä
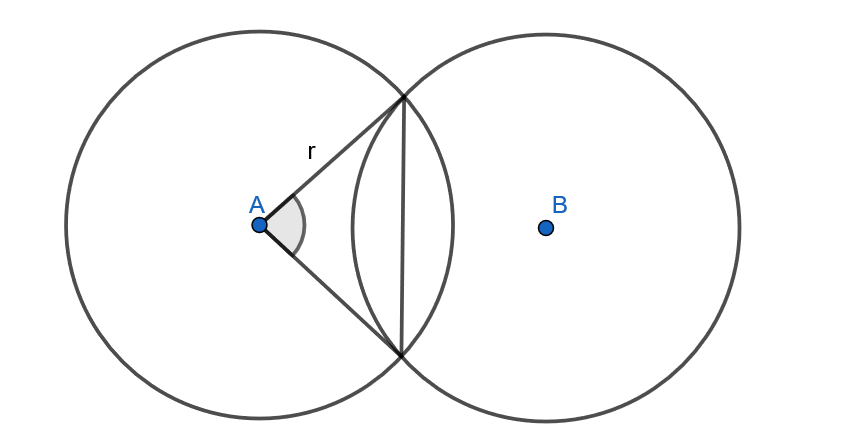
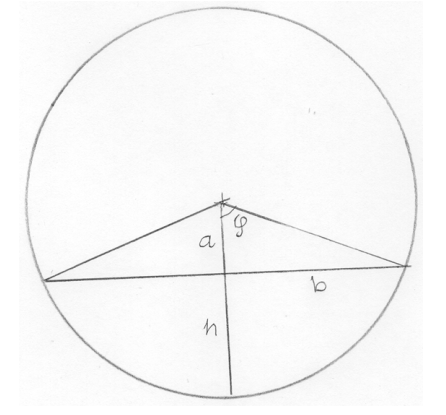
Osoita, että kahden leikkaavan ympyrän keskipisteiden välinen jana on ympyröiden leikkauspisteiden välisen janan keskinormaali.
Alla olevan kuvan merkinnöillä, sinun tulee osoittaa, että kuvaan punaisella merkittyjen janojen ja
välinen kulma on
ja että janat
ja
ovat keskenään yhtä pitkiä.
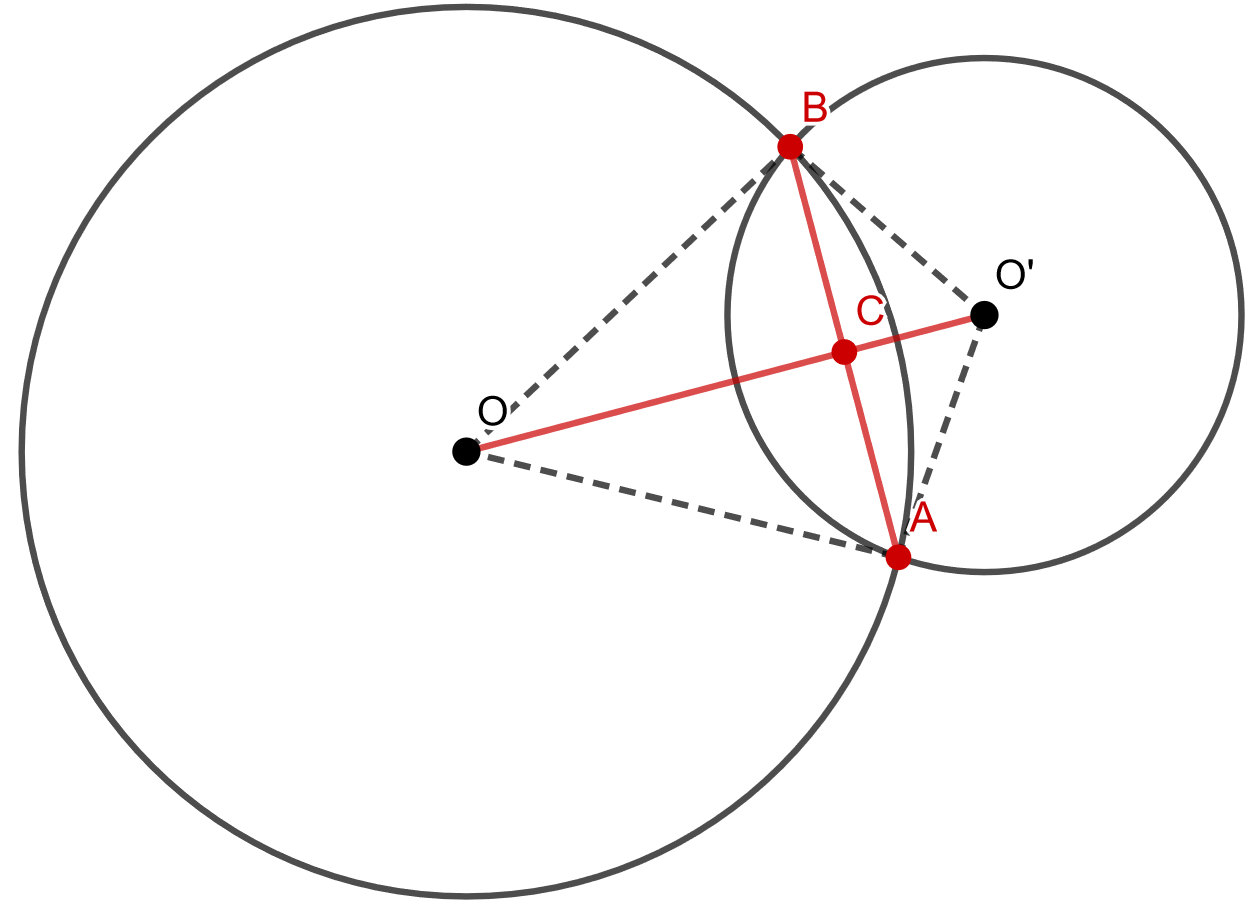
Tarkastellaan ensin kolmioita ja
. Kolmioiden sivut
ja
ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Samoin sivut
ja
ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Sivu
on molemmissa kolmioissa sama, joten kolmiot ovat yhteneviä (eli niiden kaikki mitat ovat yhtä suuria). Tällöin myös janat
ja
ovat keskenään yhtä pitkiä.
Kuvassa piste on janojen
ja
leikkauspiste, jolloin kulmat
ja
muodostavat oikokulman. Tarkastellaan seuraavaksi kolmioita
ja
. Sivut
ja
ovat yhteneviä (kuten aiemmin todettiin). Lisäksi sivu
on yhteinen kummallekin kolmiolle. Lisäksi kulmat
ja
ovat yhteneviä, sillä kolmiot
ja
ovat yhteneviä (kuten aiemmin todettiin). Näin ollen kolmioiden
ja
on oltava yhtenevät ja kulmien
ja
on myös oltava yhtenevät. Tällöin
.
4.2.1 Tehtävä
metrin köydellä rajataan alue. Laske alueen pinta-ala, kun se on muodoltaan
- neliön muotoinen.
- ympyrän muotoinen.
4.2.2 Tehtävä
Piirretään A4-arkille () mahdollisimman suuri ympyrä. Mikä on tämän ympyrän pinta-ala?
4.3 Keskuskulma, kaaren pituus, sektorin pinta-ala
Tämän kappaleen teoria on kappaleessa Keskuskulma, kaaren pituus, sektorin pinta-ala.
4.3.1 Tehtävä
4.3.2 Tehtävä
Ympyräsektorin pinta-ala on ja sen säde on
. Kuinka suuri on sektorin keskuskulma?
4.3.3 Tehtävä
Kumpi alla olevista pizzapaloista kannattaa ottaa, jos haluaa rahalleen eniten vastinetta?
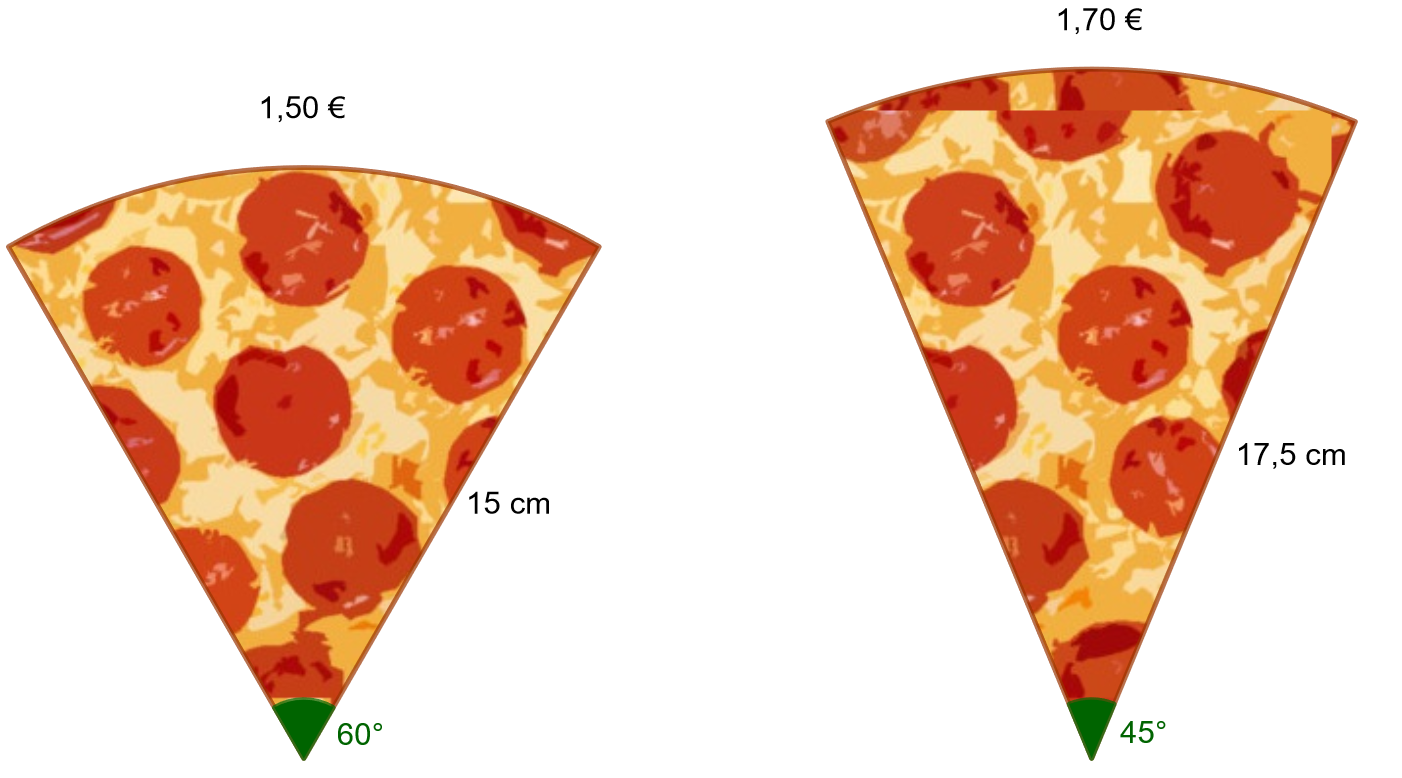
4.3.4 Tehtävä
Alla on kuva kuulantyöntöringistä ja -sektorista. Ringin halkaisija on jalkaa eli
.
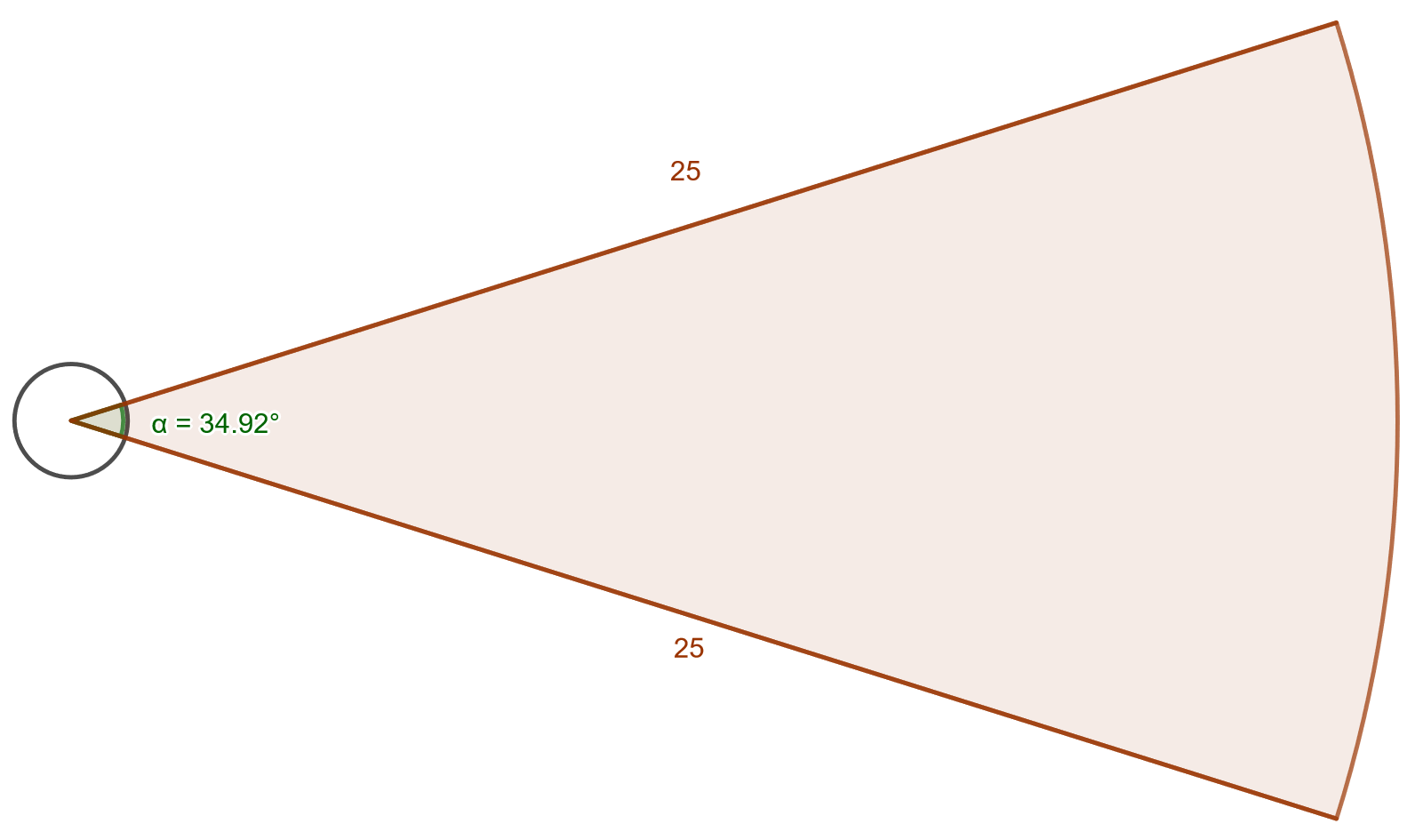
- Kuulantyöntösektori peitetään hiekalla. Kuinka suuri pinta-ala peitetään? Rinkiin ei laiteta hiekkaa.
- Sektori ja rinki ympäröidään ulkoreunoja pitkin merkintänauhalla. Kuinka paljon nauhaa tarvitaan?
4.3.5 Tehtävä
Lammas on kiinnitetty pitkällä hihnalla aidoitetun alueen kulmaan. Laske, kuinka suurelta alueelta lammas voi syödä ruohoa.
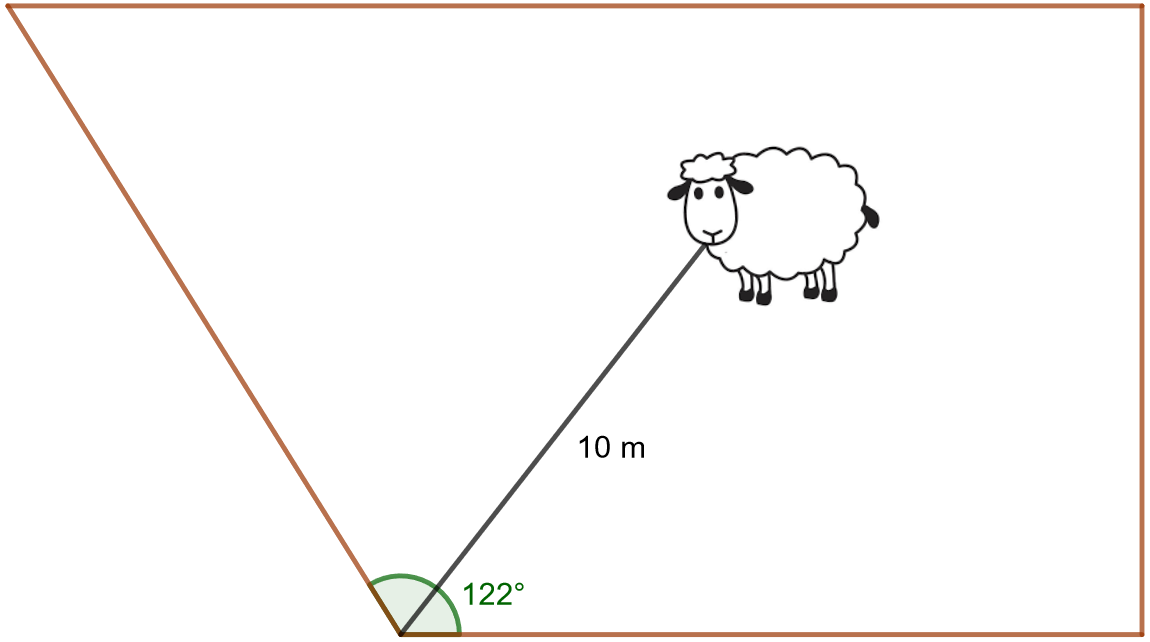
4.3.6 Tehtävä (Arkkitehtivalinnan koe 2011, 3)
Sata metriä pitkä köysi katkaistaan kahteen osaan. Toisesta osasta muodostetaan ympyrän ja toisesta neliön piiri. Kuvioiden pinta-alojen halutaan olevan samat. Miten naru on katkaistava?
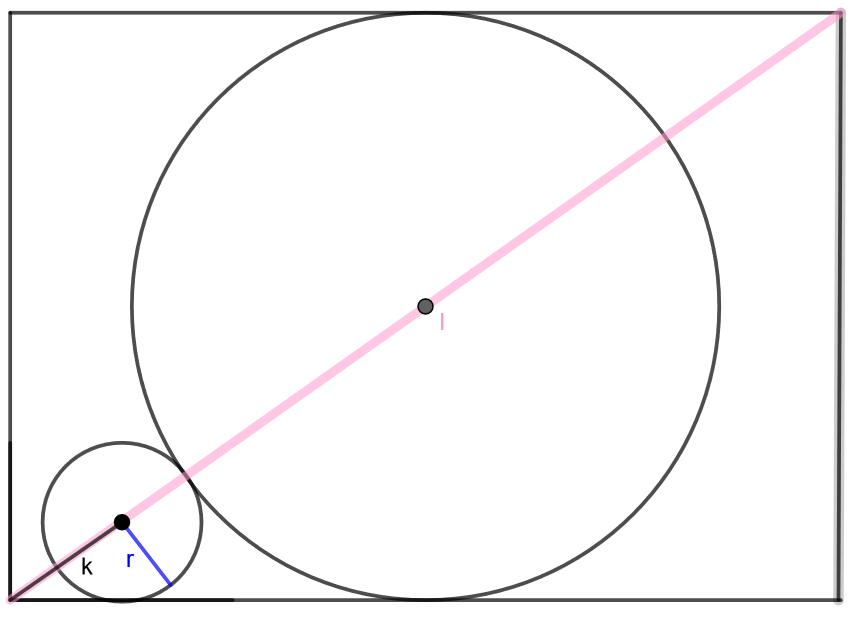
Tee yhtälöryhmä, jossa tuntemattomat muuttujat ovat neliön sivun pituus a ja ympyrän säde r.
4.3.7 Tehtävä (S2018/11)
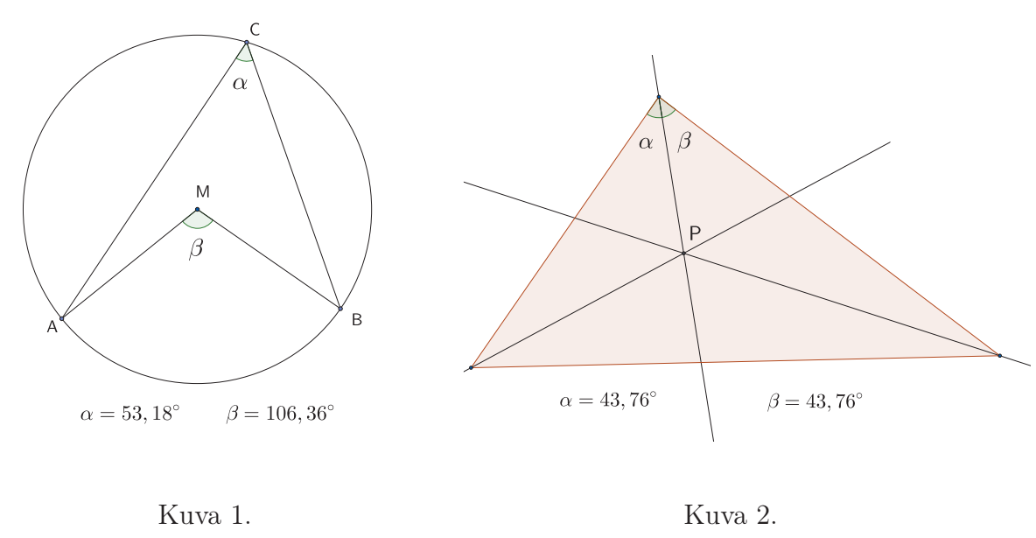
Alla olevien kuvioiden kaksi tilannetta ovat syntyneet erään abiturientin harjoitellessa dynaamisen matematiikkaohjelman käyttöä. Tehtävänä on auttaa häntä viemään tarkastelu loppuun molemmissa tapauksissa.
Mitä ympyrään liittyvää lausetta abiturientti tutkii kuvassa 1? Kirjoita lause mahdollisimman täsmällisiä termejä käyttämällä.
Abiturientti tarkastelee kuvassa 2 näkyvän kolmion merkillistä pistettä
. Mikä tämä piste on? Minkä pisteeseen
liittyvän geometrisen ominaisuuden abiturientti voi todentaa, jos hän piirtää ympyrän, jonka keskipisteenä on
ja jonka säde on sopivan mittainen?
Perustele joko a-kohdan lause, kun pisteet
,
ja
ovat samalla suoralla, tai b-kohdan ominaisuus.

4.4 Jänne, segmentti
Tämän kappaleen teoria on kappaleessa Jänne, segmentti.
4.4.1 Tehtävä
Ympyrän säde on ja segmentin keskuskulman suuruus on
. Mikä on pienemmän muodostuvan segmentin pinta-ala?
4.4.2 Tehtävä
Ympyrän säde on ja segmentin keskuskulman suuruus on
. Mikä on suuremman muodostuvan segmentin pinta-ala?
4.4.3 Tehtävä
Ympyrän halkaisija on . Ympyrään on piirretty segmentti, jota vastaavan kaaren pituus on
. Kuinka suuri on pienemmän segmentin pinta-ala?
4.4.4 Tehtävä
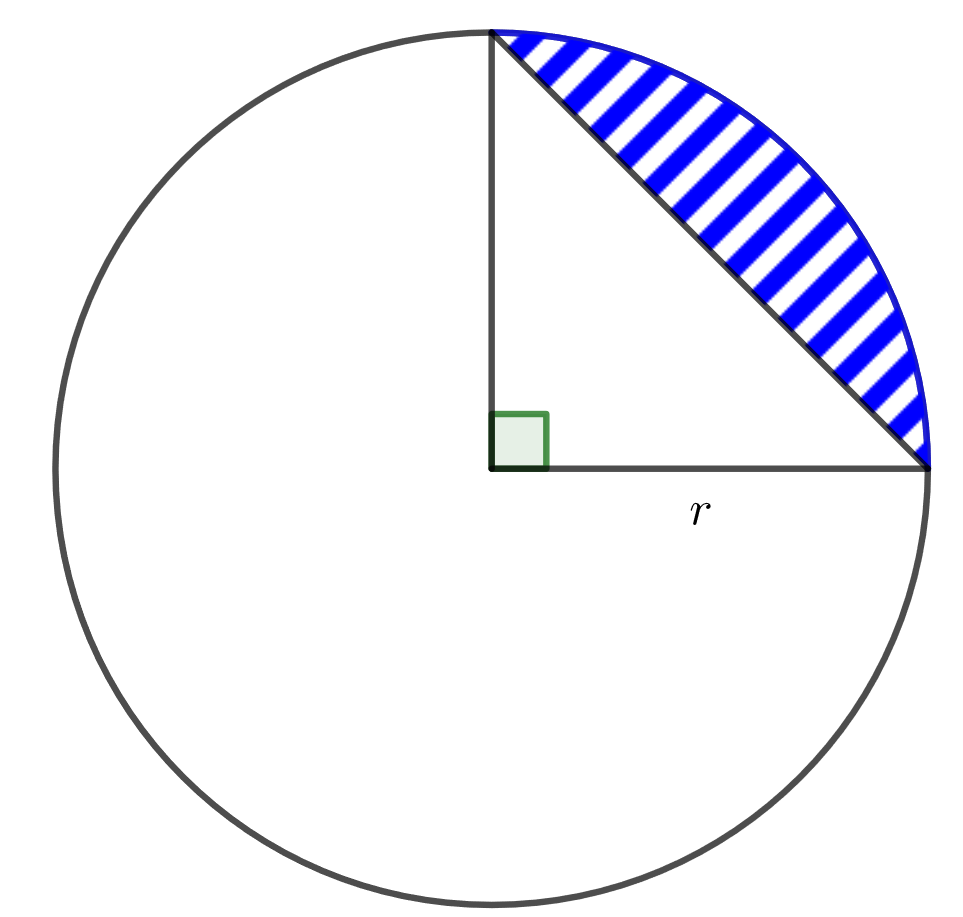
Kuinka monta prosenttia ympyräneljännekseen piirretyn segmentin pinta-ala on koko ympyrän pinta-alasta? Ympyrän säde on .
4.4.5 Tehtävä (Arkkitehtivalinnan koe 2015/4)
Kaksi majakkaa sijaitsee kilometrin etäisyydellä toisistaan. Veneen etäisyys merellä (tasopinta) on korkeintaan
kilometriä kummastakin majakasta. Laske sen alueen pinta-ala neliökilometreissä, jolla vene voi olla.
4.5 Tangentti, tangenttikulma
Tämän kappaleen teoria on kappaleessa Tangentti, tangenttikulma.
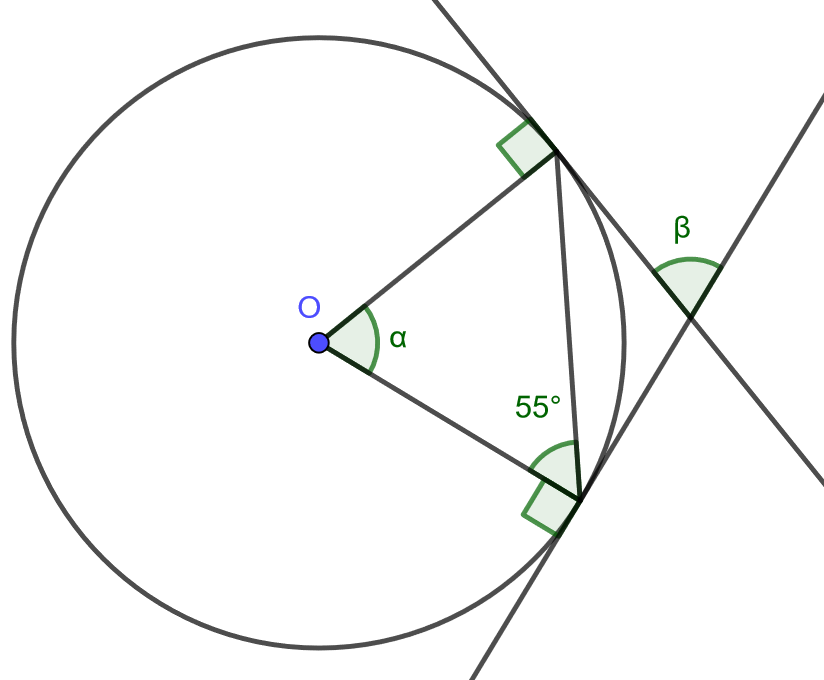
4.5.1 Tehtävä
Ratkaise alla olevasta kuvasta ja
.
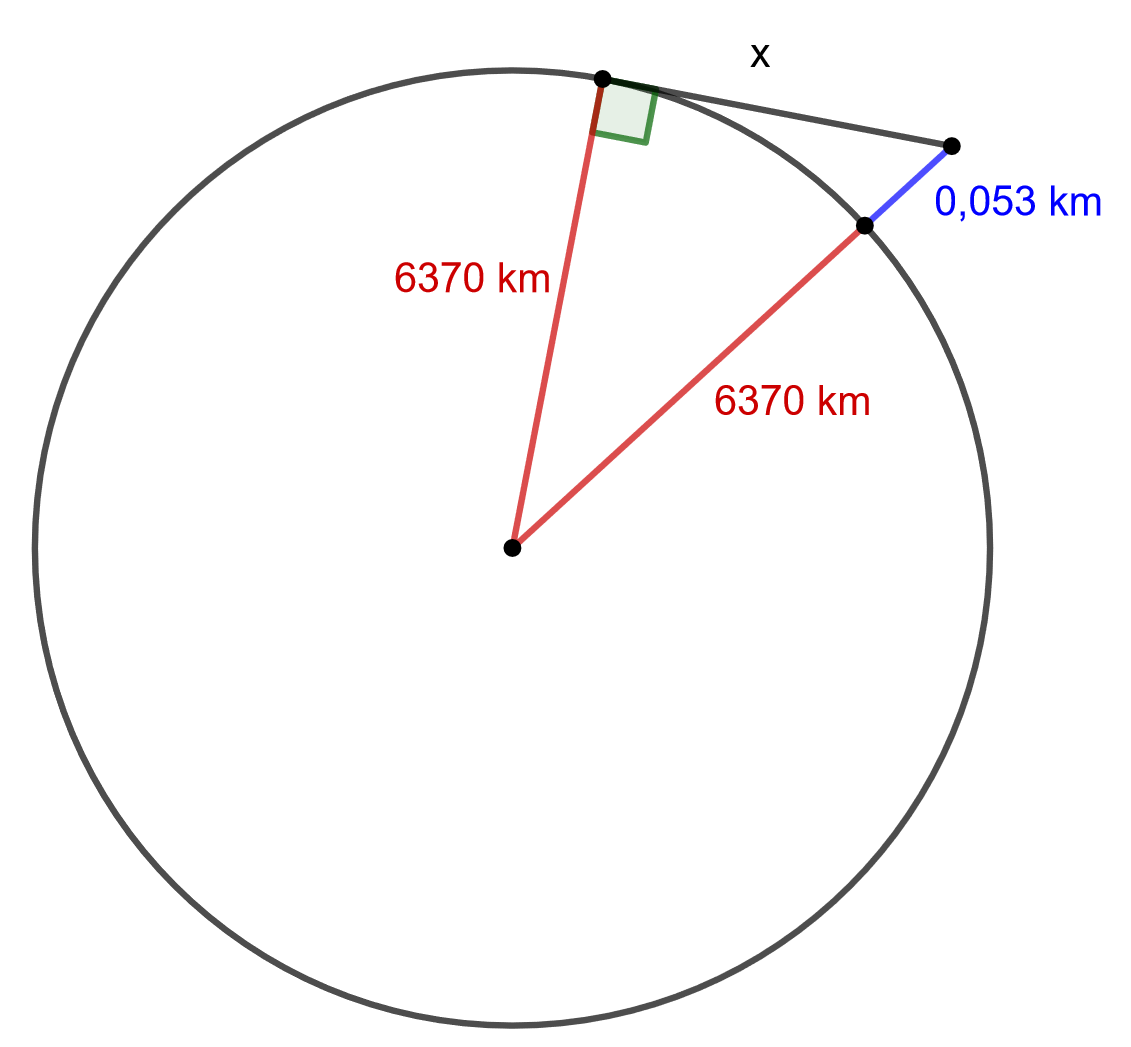
4.5.2 Tehtävä
Kuinka pitkälle korkeasta vesitornista voi nähdä? Maapallon säde on
. Oletetaan, että katsojan silmät ovat myös
korkeudella maan pinnasta. Piirrä ensin mallikuva tilanteesta.
Huom! Mallikuva ei ole mittakaavassa!
Tehtävässä tulee ratkaista kuvaan merkitty pituus .
4.5.3 Tehtävä
Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä . Tangenttien sivuamispisteet
ja
ovat etäisyydellä
pisteestä
. Piirretään ympyrälle vielä yksi tangentti pisteen
kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet
ja
. Laske kolmion
piiri. [H]
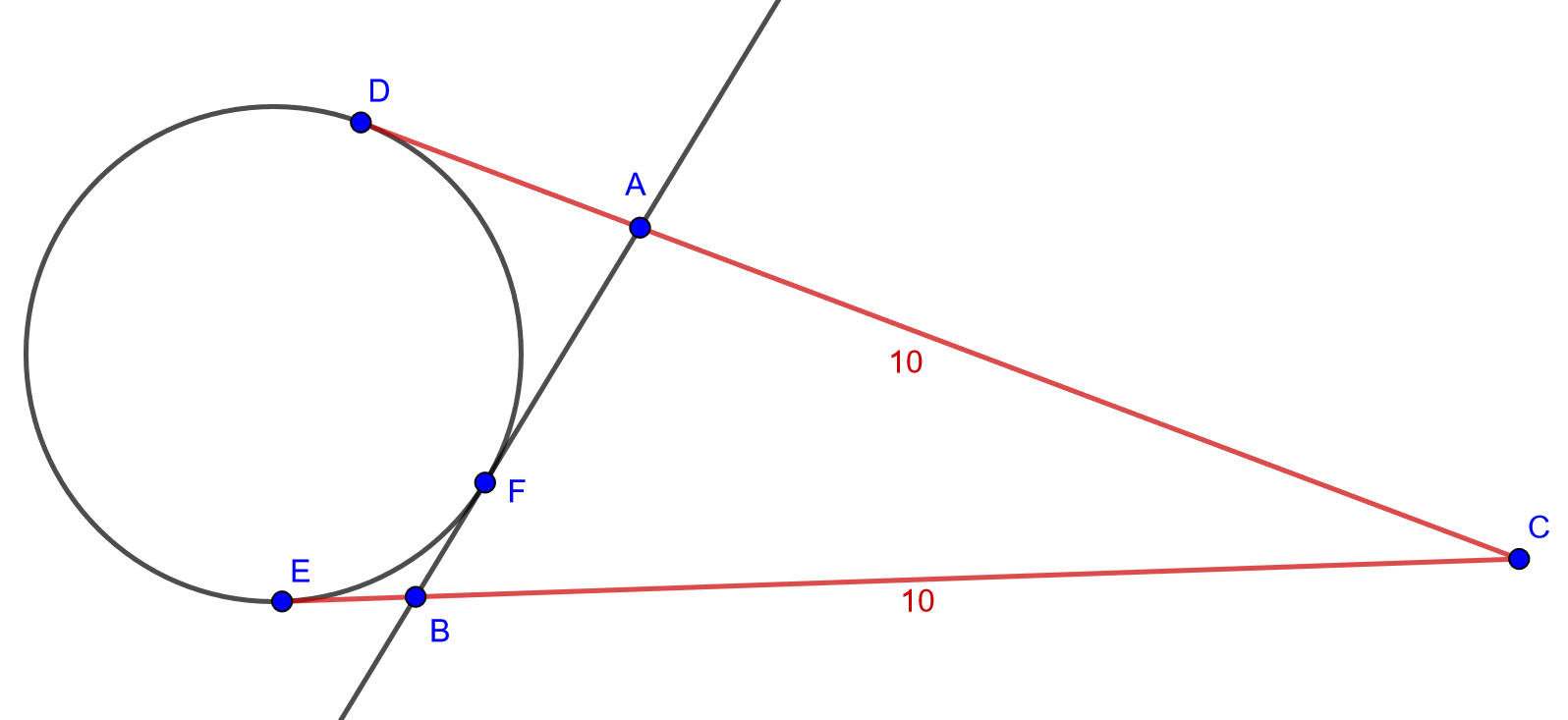
Pisteet A, B ja C ovat tangenttikulmien kärkiä, eli ne ovat yhtä etäällä molemmista tangenttipisteistään.
4.6 Keskuskulma, kehäkulma
Tämän kappaleen teoria on kappaleessa Keskuskulma, kehäkulma.
4.6.1 Tehtävä
Määritä kulman suuruus.
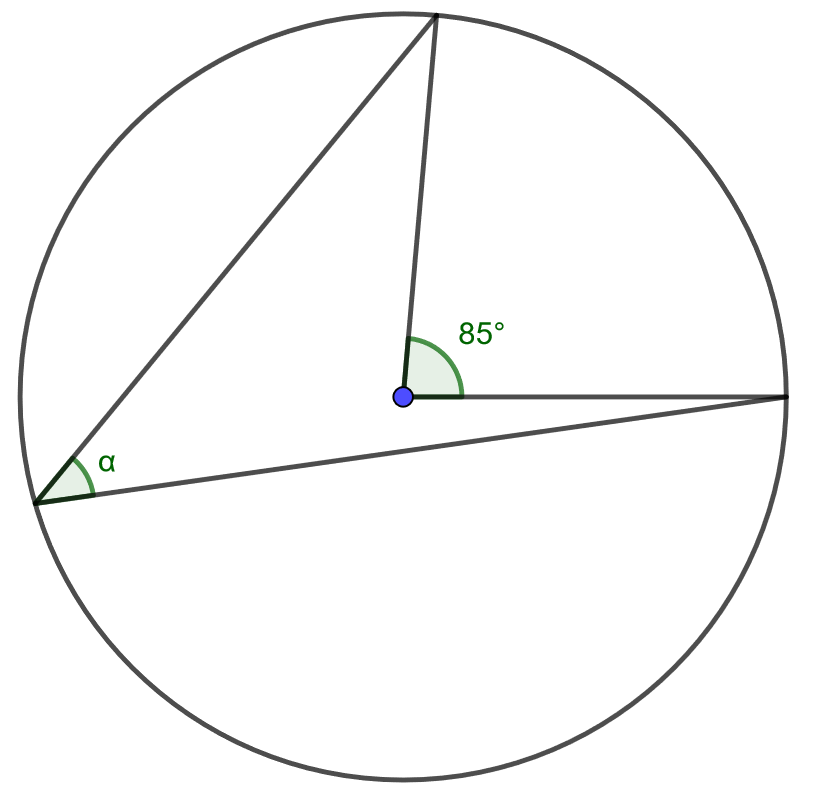
4.6.2 Tehtävä
Määritä kulman suuruus.
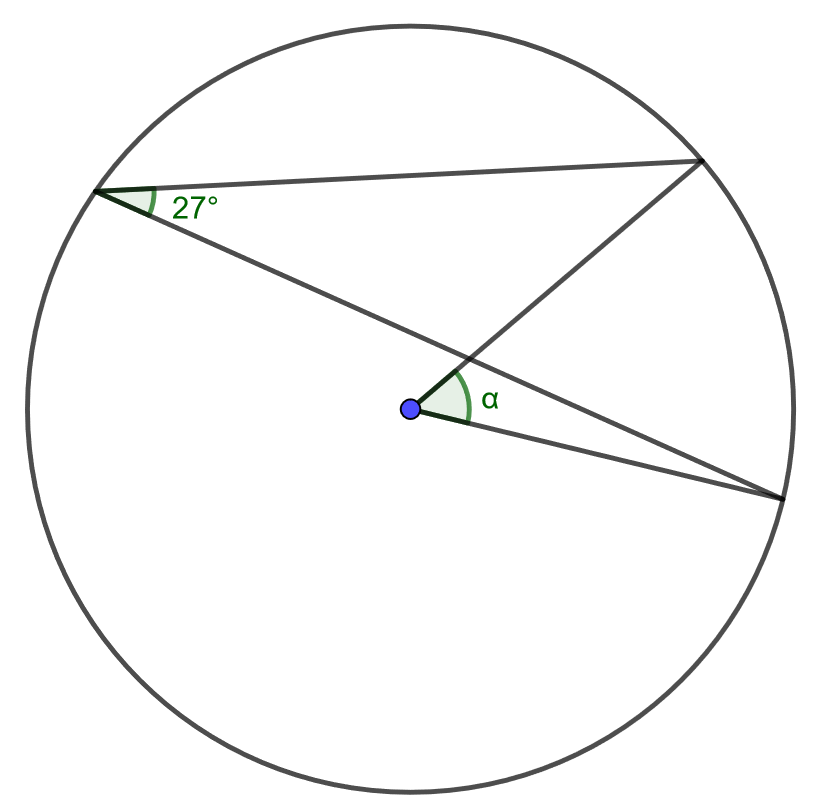
4.6.3 Tehtävä
Ratkaise alla olevasta kuvasta kulmat ja
.
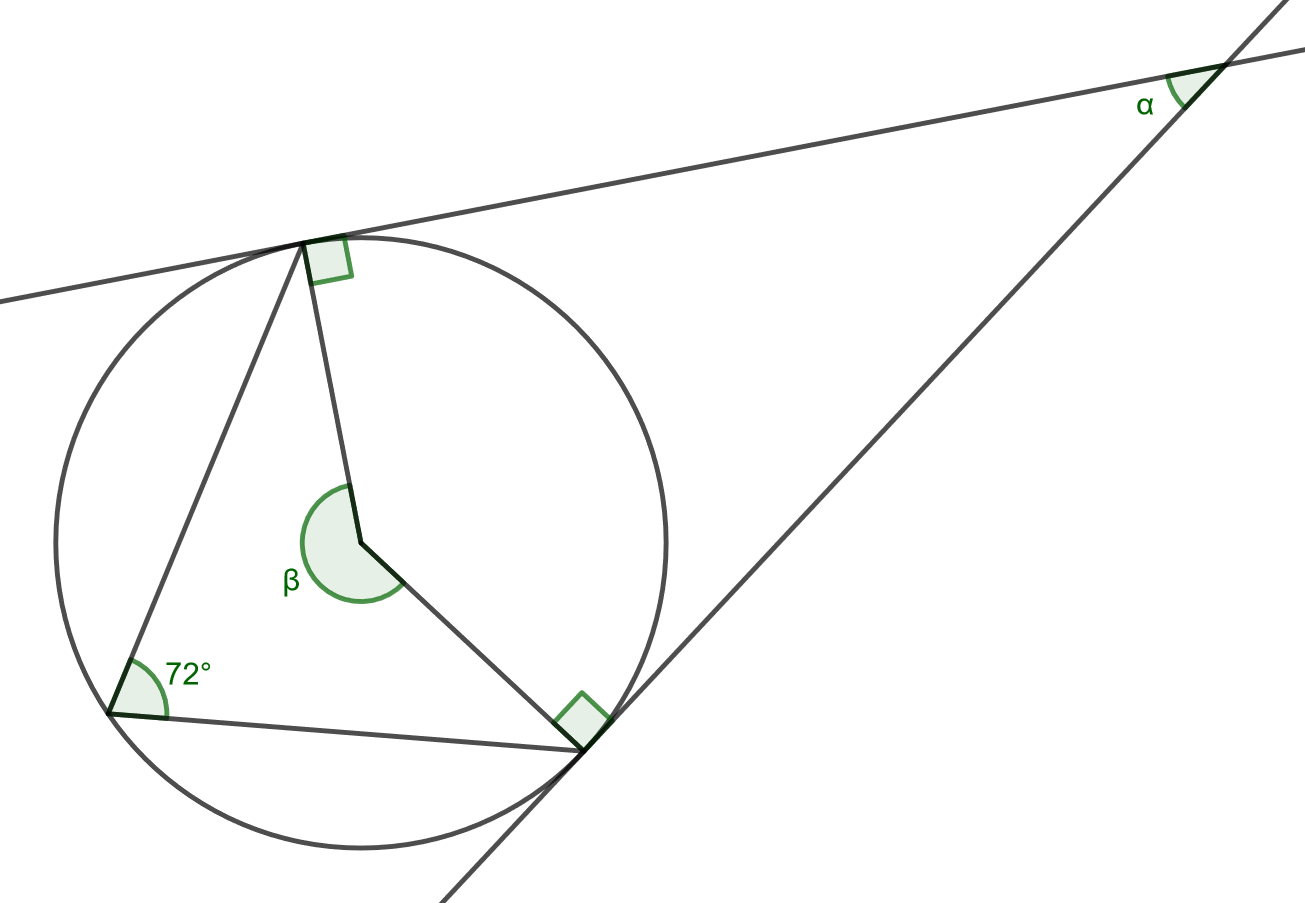
4.6.4 Tehtävä
Jos nelikulmion kaikki kulmat ovat saman ympyrän kaarella, nelikulmiota kutsutaan jännenelikulmioksi. Osoita, että jännenelikulmiossa vastakkaisten kulmien summa on aina .
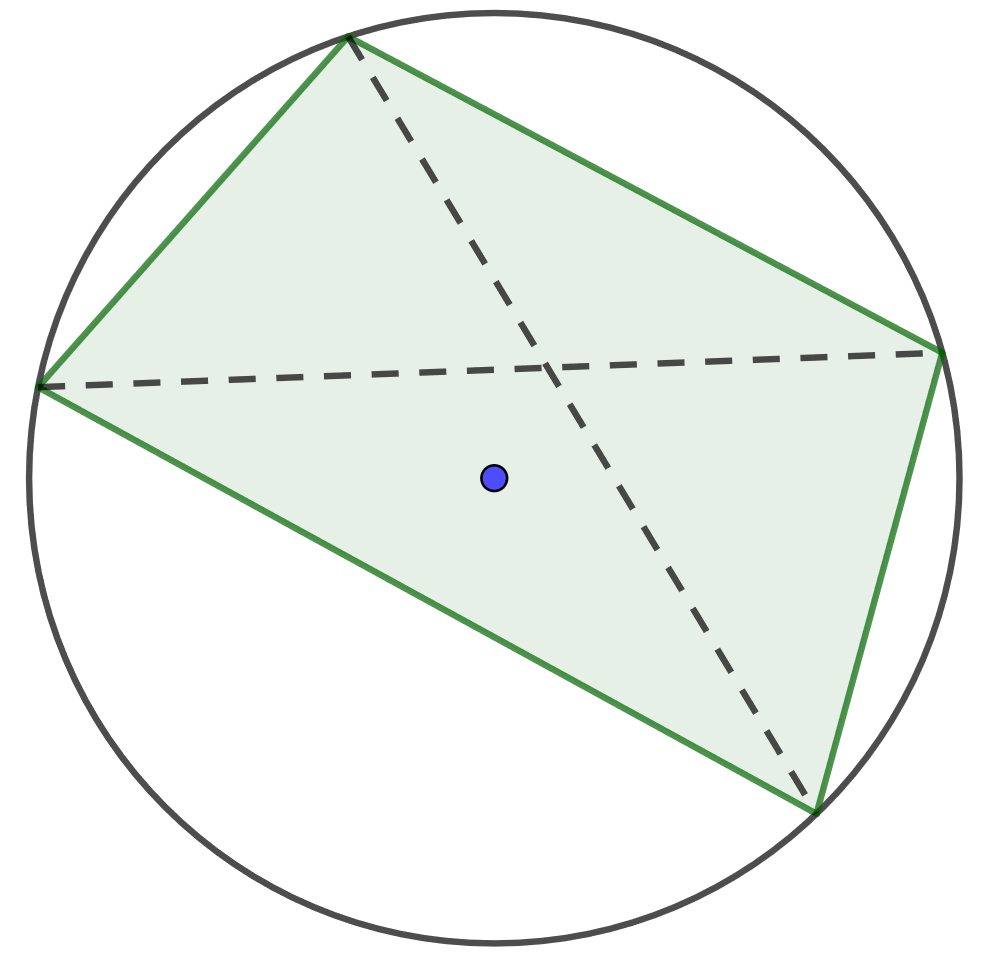
Kokeile käyttää kehäkulmalausetta.
Käytetään alla olevan kuvan merkintöjä.
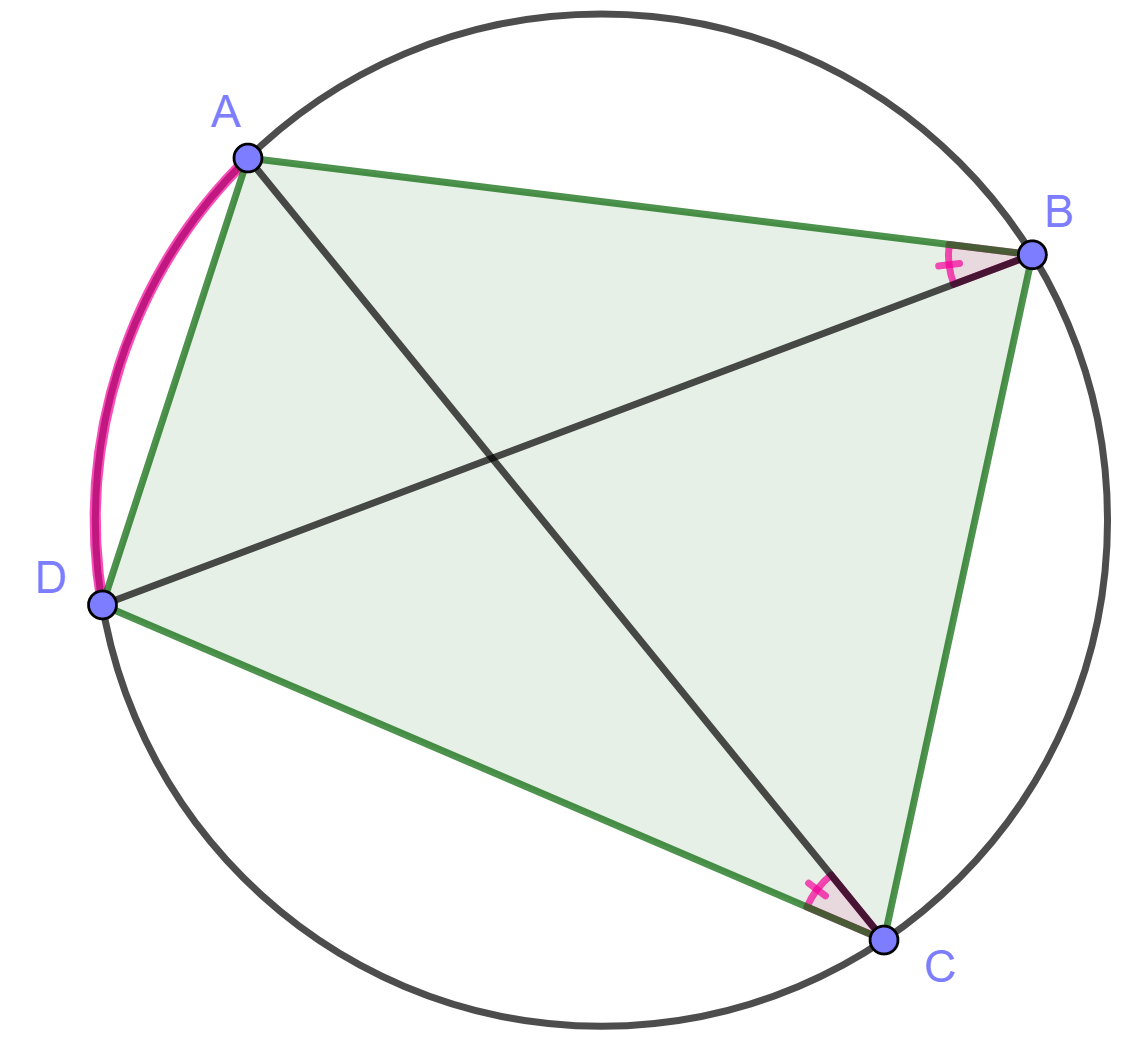
Kulmat ja
ovat yhtä suuria, sillä ne ovat samaa kaarta
vastaavia kehäkulmia.
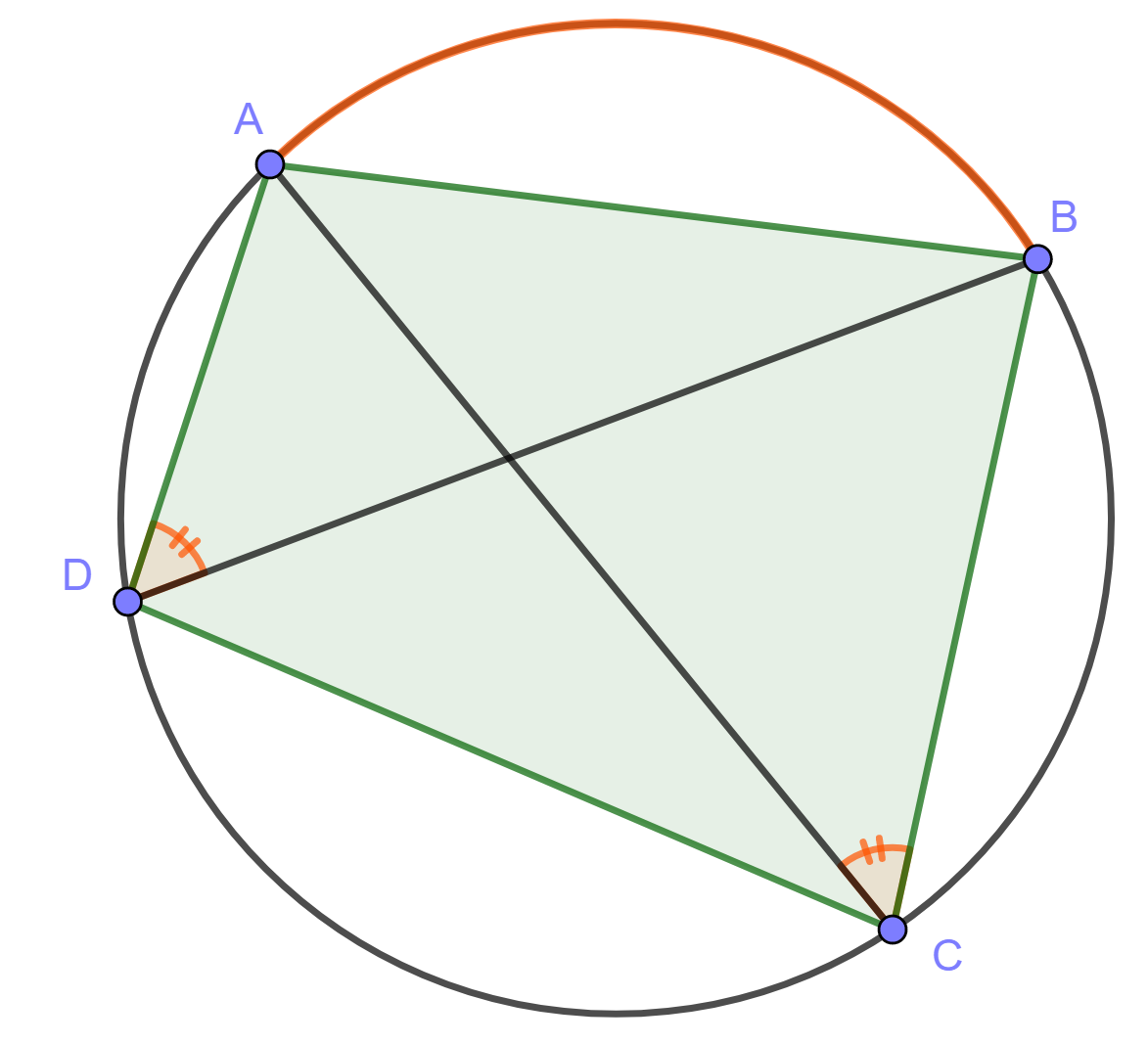
Vastaavasti kulmat ja
ovat yhtä suuria, sillä ne ovat samaa kaarta
vastaavia kehäkulmia.
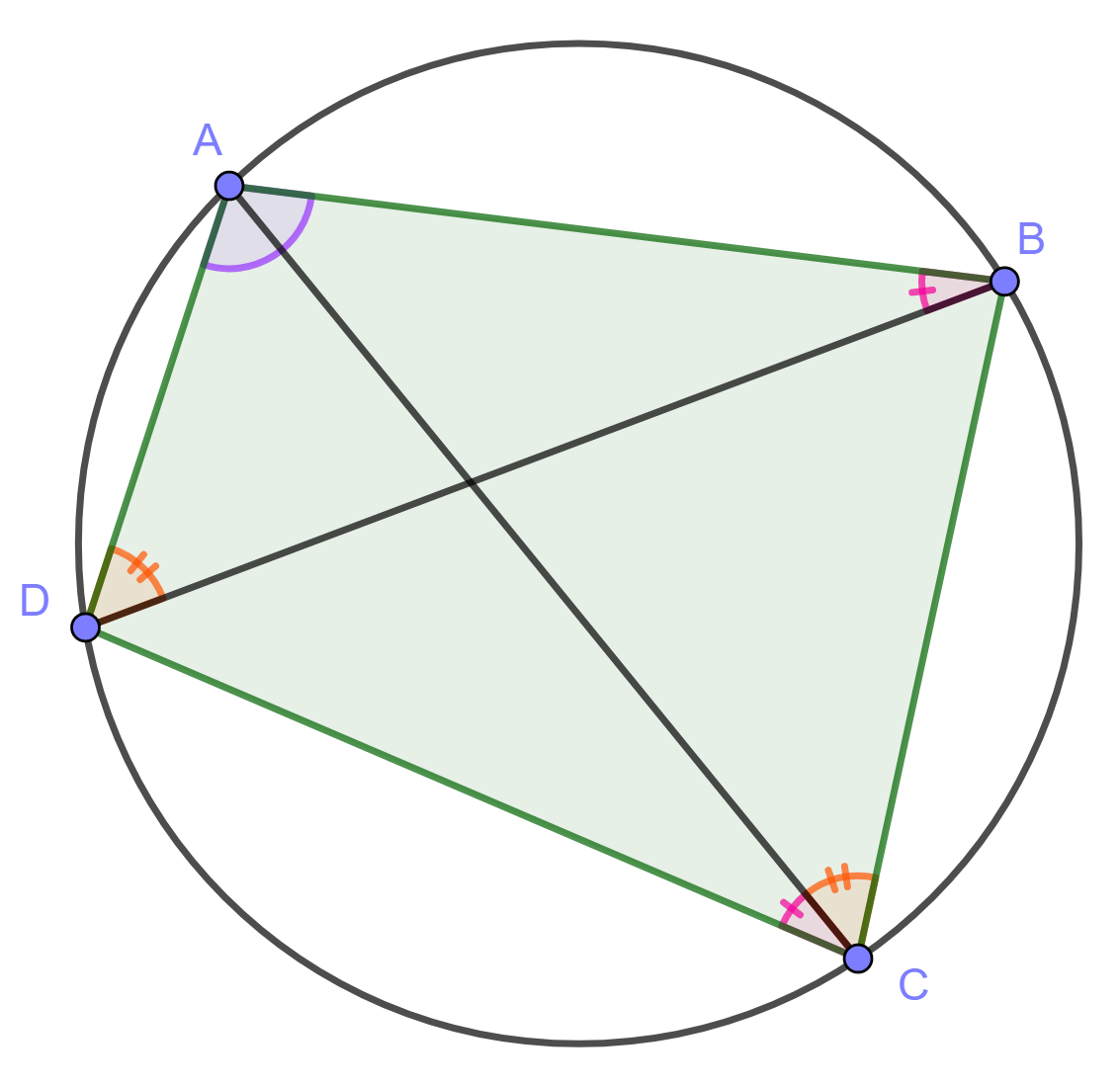
Kolmiosta huomataan, että
. Aiemmista kohdista tiedetään, että
. Sijoitetaan tämä aiempaan yhtälöön, jolloin saadaan
. Eli jännenelikulmion vastakkaisten kulmien summa on
.
4.7 Sekalaisia tehtäviä
Tässä kappaleessa on kaikkiin tämän luvun aiheisiin liittyviä tehtäviä.
4.7.1 Tehtävä
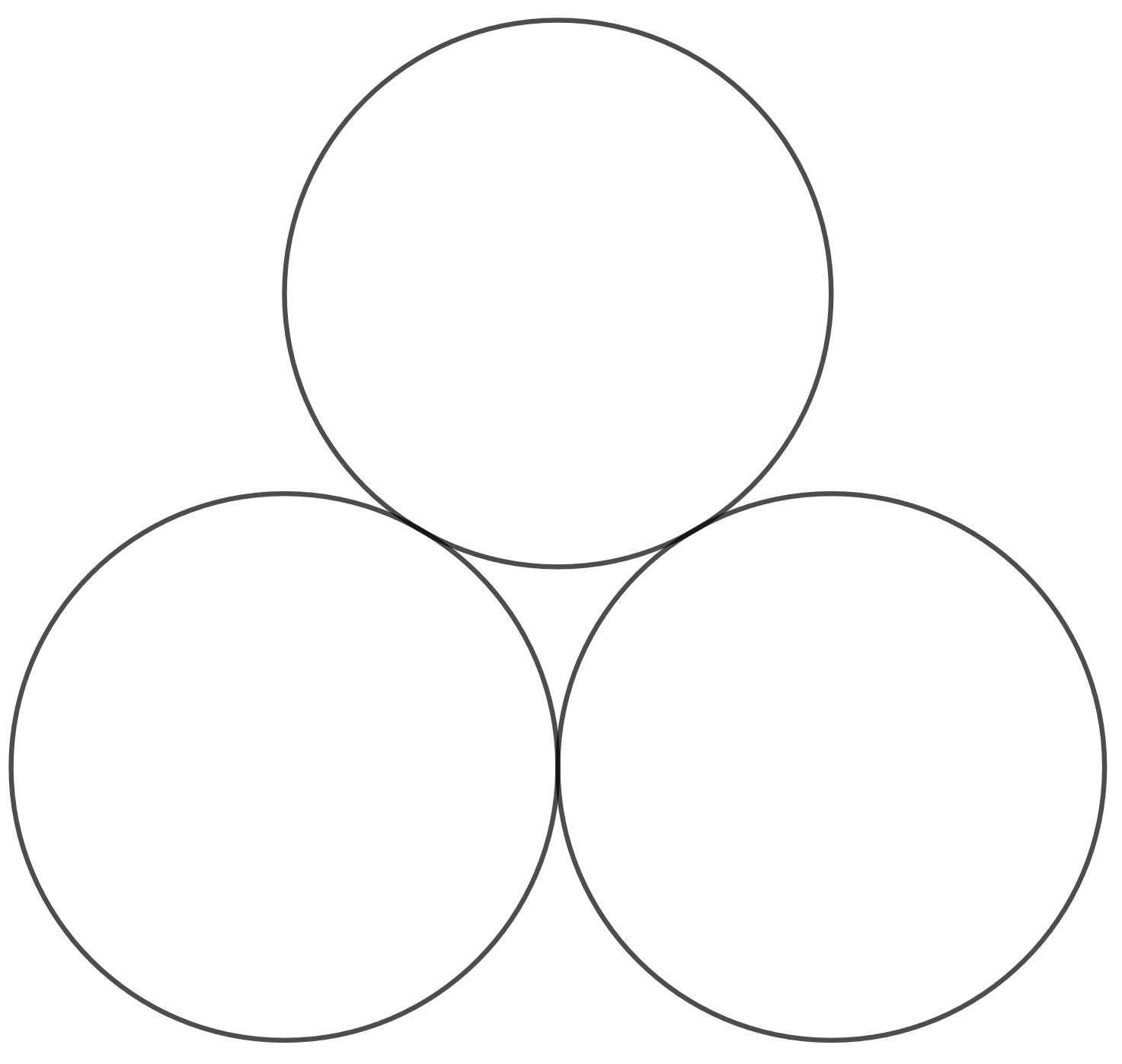
Laske tukkikasan korkeus, kun tukin säde on . Oletetaan tukkien poikkileikkaukset ympyröiksi. Ympyrät sivuavat toisiaan.
4.7.2 Tehtävä
Ratkaise alla olevan kuvan pienemmän ympyrän halkaisija isomman ympyrän säteen avulla.
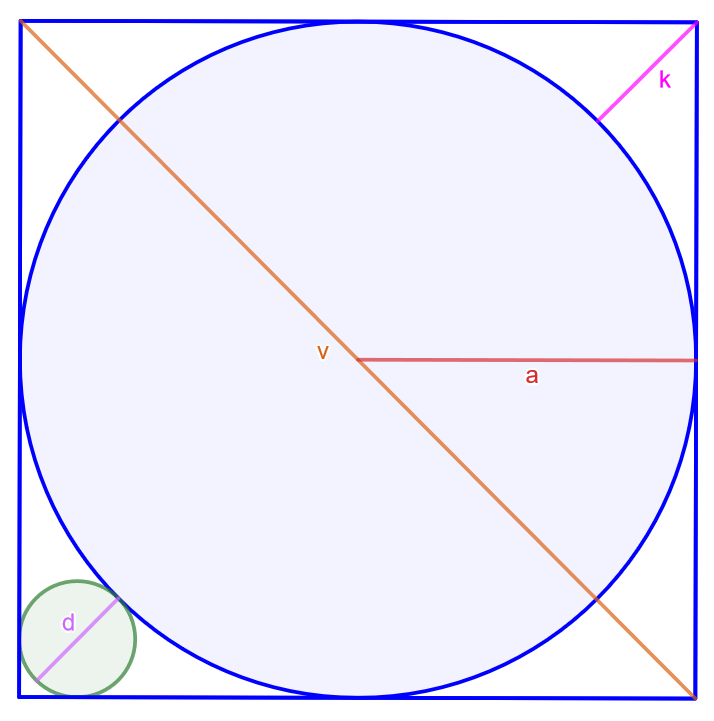
Verranto:
4.7.3 Tehtävä
Valitaan mielivaltaisesti piste positiiviselta
-akselilta väliltä
ja piste
positiiviselta
-akselilta väliltä
. Valitaan piste
origokeskeisen yksikköympyrän kehältä koordinaatiston ensimmäisestä neljänneksestä. Osoita, että kolmion
piiri on enemmän kuin 2. [H]
Voit käyttää hahmottamisessa apuna alla olevaa GeoGebra-applettia. Huomaa kuitenkin, että appletissa voit raahata pisteet janojen päätepisteisiin asti, mikä ei tehtävänannossa ole sallittua.
Tehtävän voi ratkaista monella eri tavalla, joista tässä on vain yksi. Käytetään alla olevan kuvan merkintöjä.
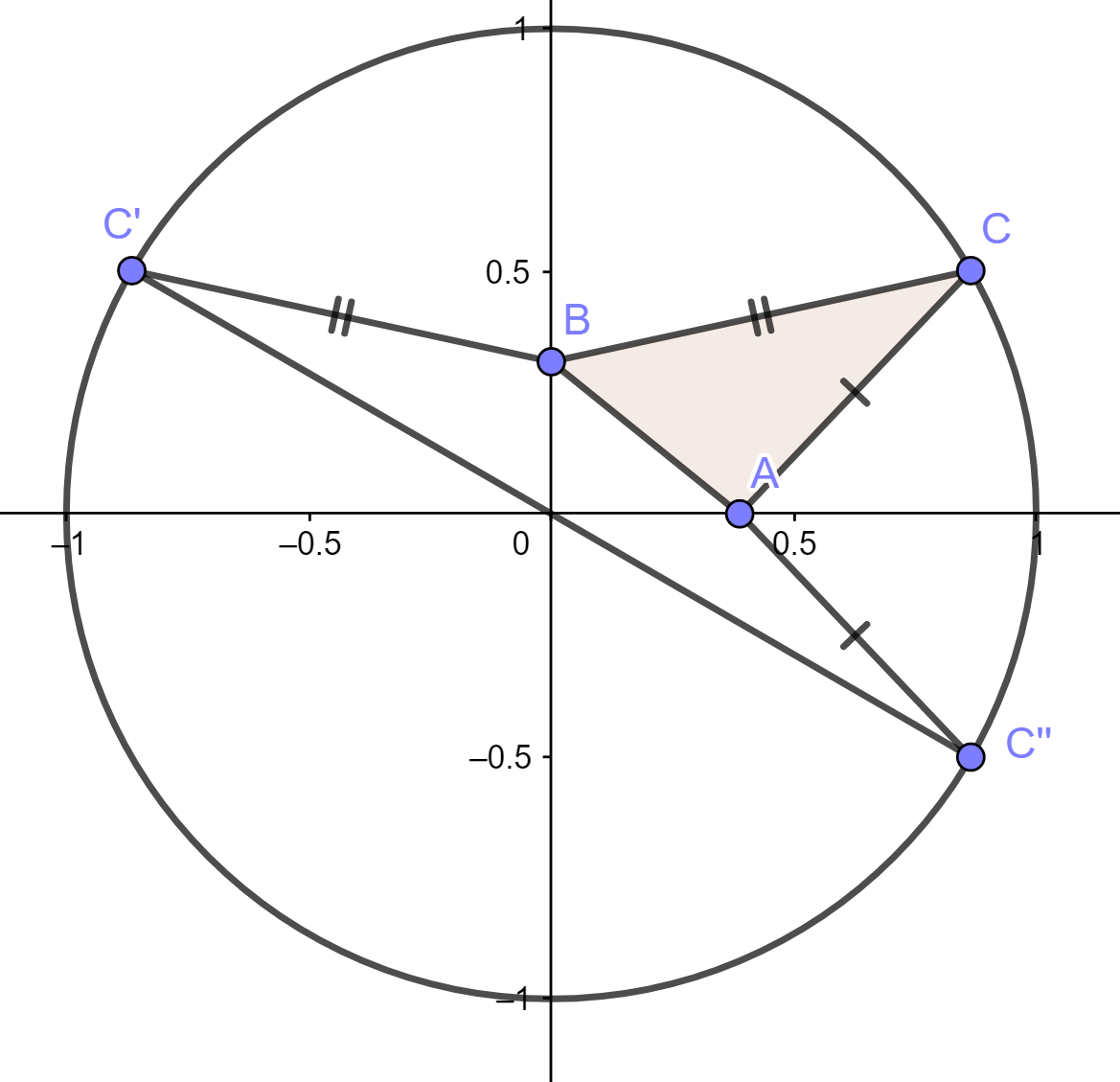
Peilataan piste
-akselin suhteen, jolloin saadaan piste
. Tehdään samoin
-akselin suhteen, jolloin saadaan piste
. Symmetrian vuoksi
ja samoin
. Kolmion
piiri on siis sama kuin murtoviivan
pituus.
Huomataan, että janan pituus on
, sillä se on ympyrän halkaisija. Murtoviiva pisteiden
ja
välillä on välttämättä pidempi kuin pisteiden välinen suora etäisyys eli
. Kolmion
piirin on siis pakko olla suurempi kuin
.
4.7.4 Tehtävä
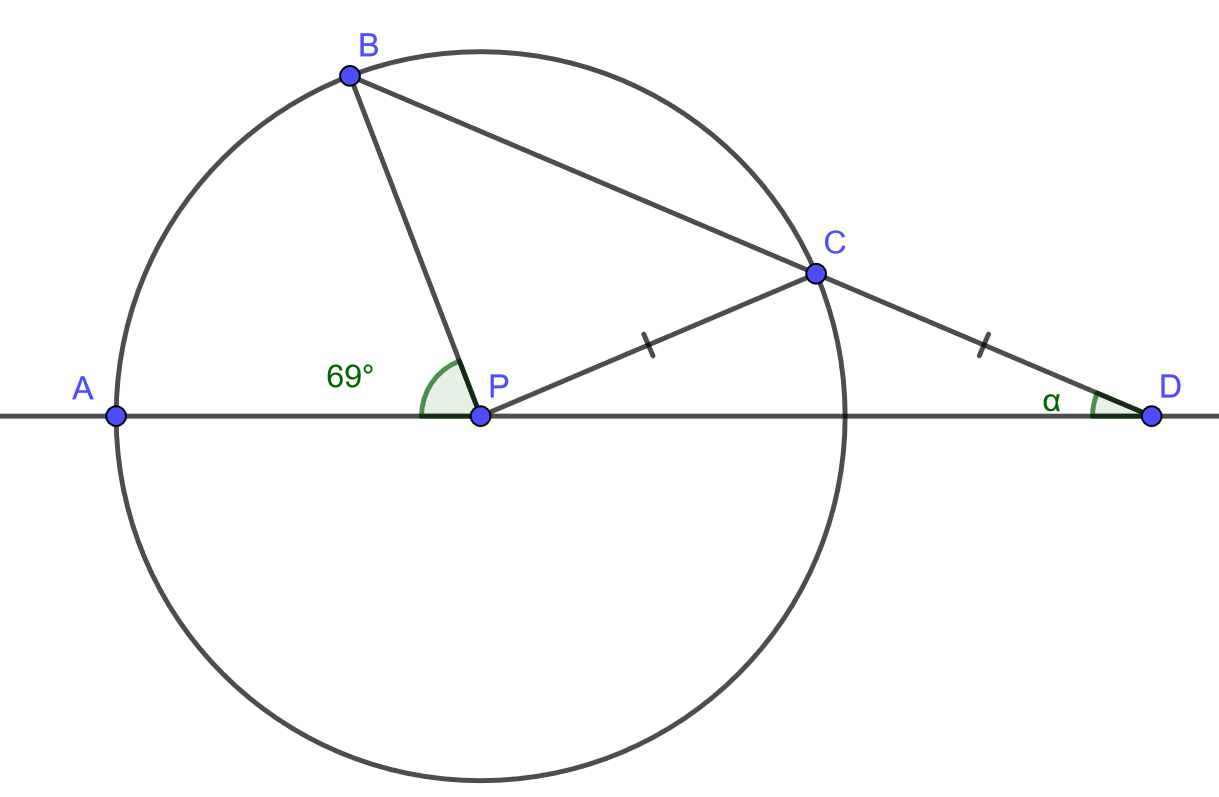
Alla olevassa kuvassa piste on ympyrän keskipiste ja pisteet
,
ja
ovat ympyrän kehän pisteitä. Piste
on suorien
ja
leikkauspiste ja janat
ja
ovat yhtä pitkät. Kulman
suuruus on
. Kuinka suuri on kulma
? [H]
4.7.5 Tehtävä
Neliön sisään piirretään neljännesympyrä siten, että neliön ylänurkasta voidaan erottaa neljännesympyrää koskettava suorakulmio, jonka sivujen pituudet ovat ja
. Kuinka pitkä on neliön sivu?
4.7.6 Tehtävä
Ympyränkaaret, joiden säteet ovat ja
, leikkaavat alla olevan GeoGebra-appletin mukaisesti. Mikä on kaarien rajaaman alueen pinta-ala? [T]
Alue voidaan laskea kahden segmentin pinta-alojen summana.
4.7.7 Tehtävä
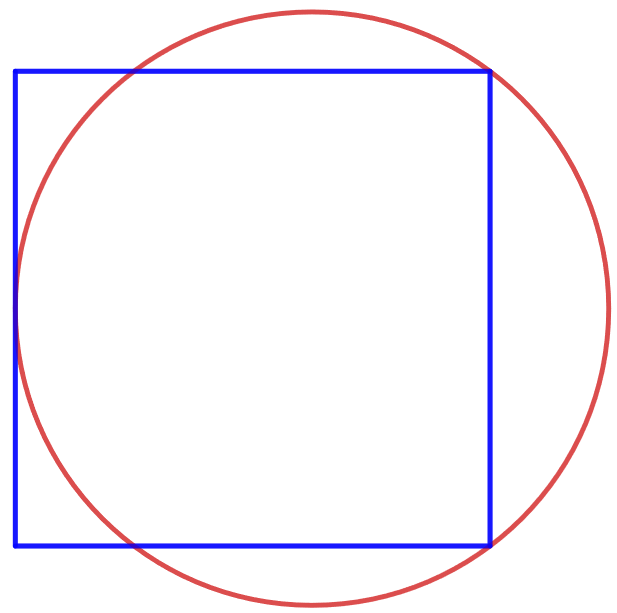
Neliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä.
Kummalla on suurempi piiri, neliöllä vai ympyrällä? [H]
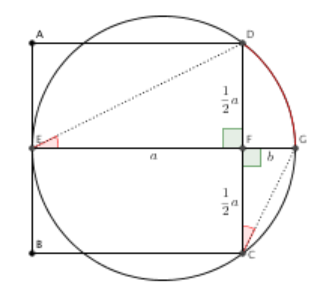
4.7.8 Tehtävä (K2016/7)
Kolme ympyrää sivuaa toisiaan oheisen kuvion mukaisesti. Ympyröiden keskipisteet ovat ,
ja
ja niiden säteet samassa järjestyksessä
,
ja
. Kuinka suuri ympyrä mahtuu näiden kolmen ympyrän väliin jäävään alueeseen?
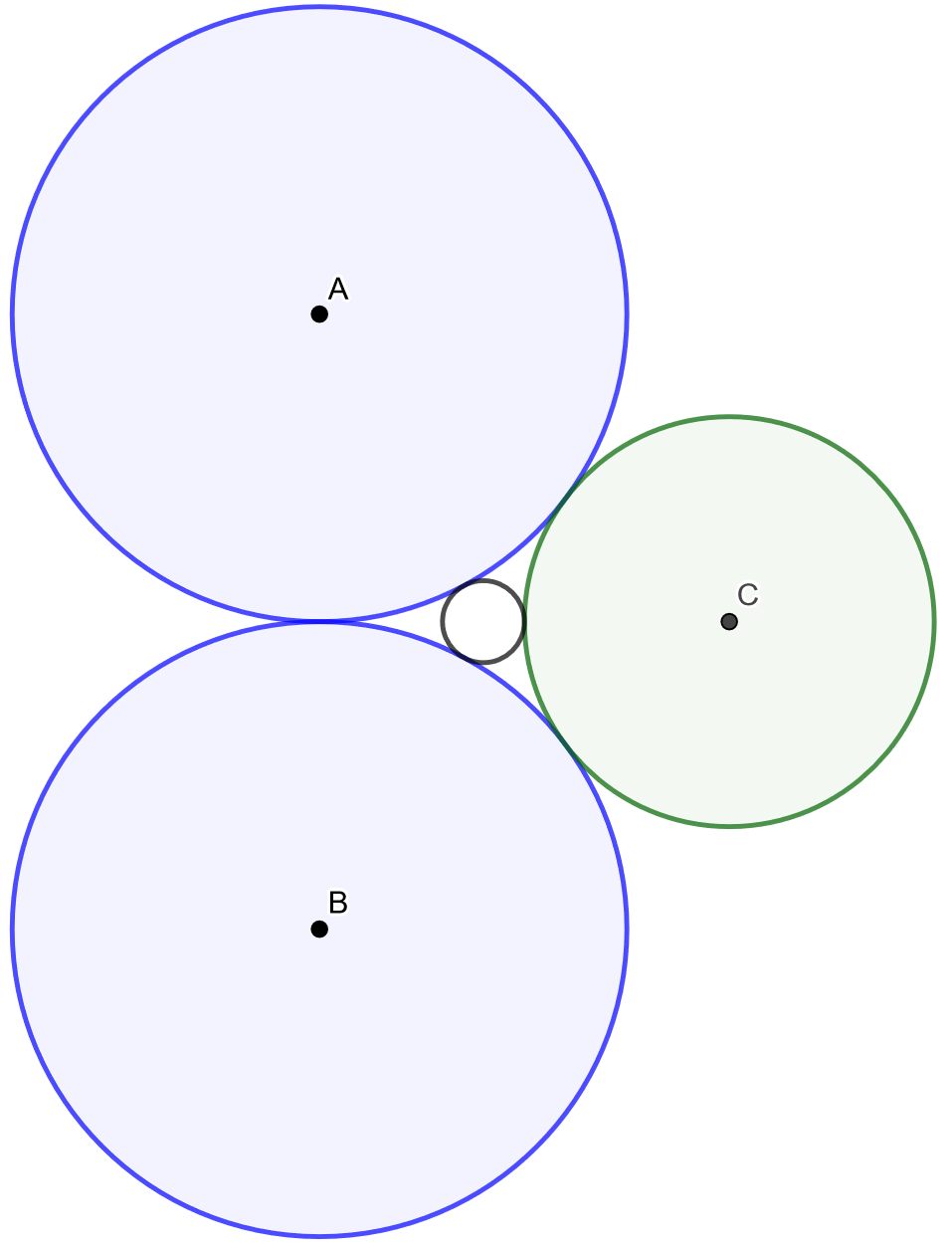
4.7.9 Tehtävä (S2014/14)
Tarkastellaan ympyrää ja sen ulkopuolella olevaa pistettä .
- Pisteestä
piirretään kaksi suoraa, jotka leikkaavat ympyrän neljässä eri pisteessä
,
,
ja
kuvion mukaisesti. Osoita, että kolmiot
ja
ovat yhdenmuotoiset.
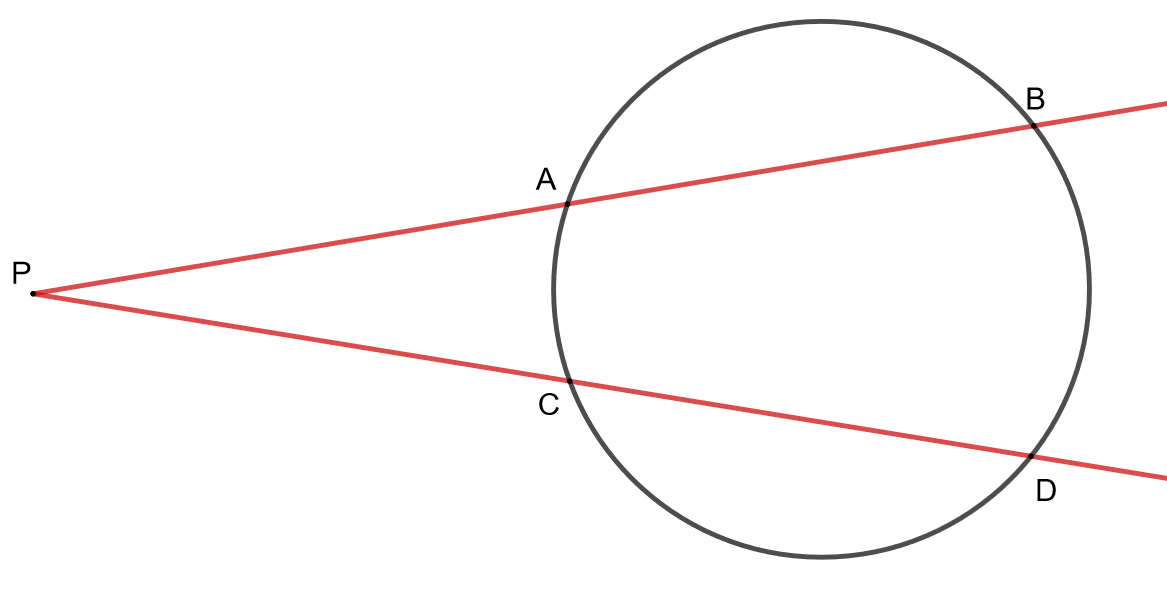
Osoita, että
.
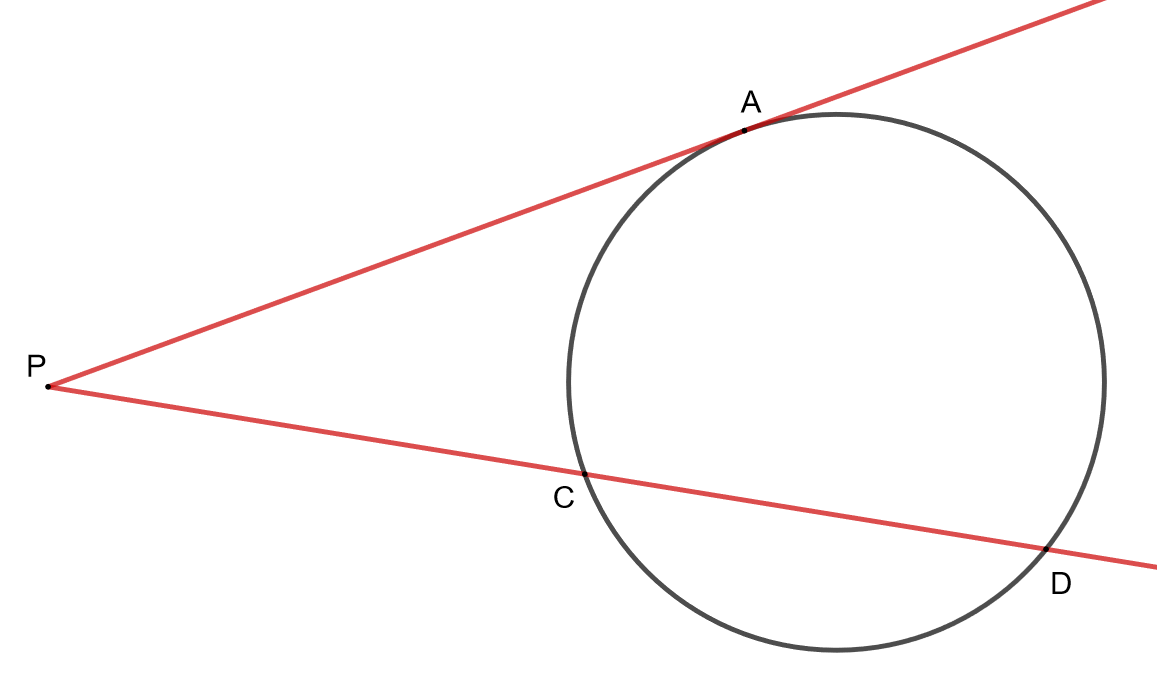
Erikoistapauksessa
toinen suorista sivuaa ympyrää. Osoita, että tällöin pätee
.
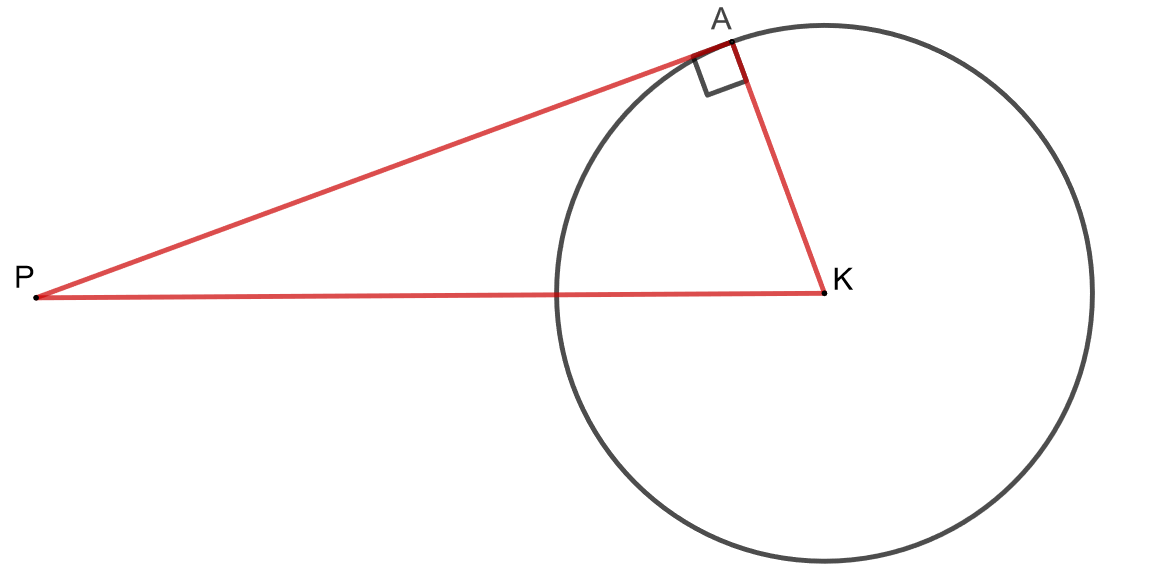
- Todista edellisten kohtien avulla Pythagoraan lause tutkimalla alla olevan kuvion kolmiota, jonka kärki
on ympyän keskipisteessä ja kärki
on ympyrän kehällä.
- Piirretään janat
ja
. Tällöin
samaa kaarta
vastaavina kehäkulmina. Lisäksi kolmioilla on yhteinen kulma
. Täten yhdenmuotoisuuslauseen KK mukaan kolmiot ovat yhdenmuotoisia.
- Yhdenmuotoisuuden nojalla
, josta saadaan ristiin kertomalla
.
- Olkoon
ympyrän keskipiste. Piirretään janat
ja
ja merkitään
. Tällöin
, koska se on samaa ympyrän kaarta
vastaava keskuskulma. Tasakylkisen kolmion
kulmille pätee
. Koska
, niin
. Kolmioissa
ja
on kaksi yhtä suurta kulmaa, joten ne ovat yhdenmuotoiset, mistä seuraa
.
- Merkitään kolmion kärkiä
,
ja
. Hypotenuusa leikkaa ympyrää pisteessä
. Jatketaan hypotenuusaa
säteellä
, jolloin jatke kohtaa ympyrän pisteessä
. B-kohdan nojalla pätee
. Merkitään
ja
, jolloin
, josta Pythagoraan lause
seuraa.
4.7.10 Tehtävä (K2014/14)
Erään tarinan mukaan ihmiskunta kokeili liikkumista säännöllisten monikulmioiden avulla, ennen kuin pyörä keksittiin.
- Tasasivuinen kolmio kiertyy oikealle kuvion mukaisesti, kunnes kärki
osuu uudelleen alustaan. Kärki
piirtää kuvion mukaisen käyrän. Laske käyrän pituus, kun kolmion piiri on
.

- Hahmottele vastaavat käyrät neliön ja kuusikulmion tapauksessa. Kummassakin tapauksessa monikulmio kiertyy niin monta kertaa, että vasemmalla alhaalla oleva kärki osuu uudelleen alustaan.
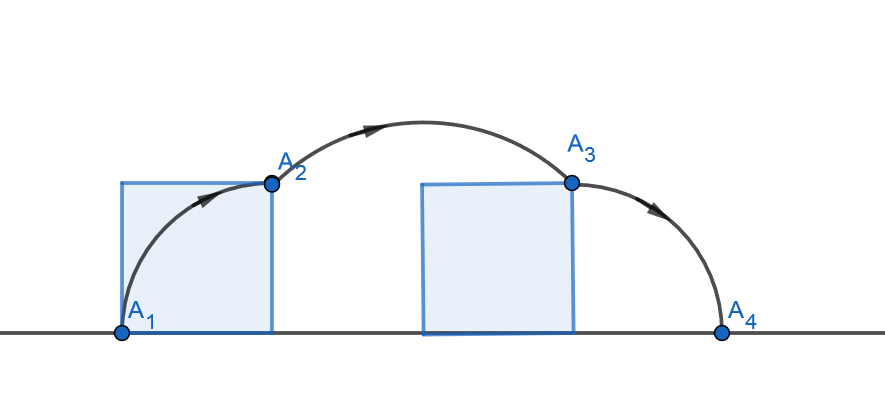
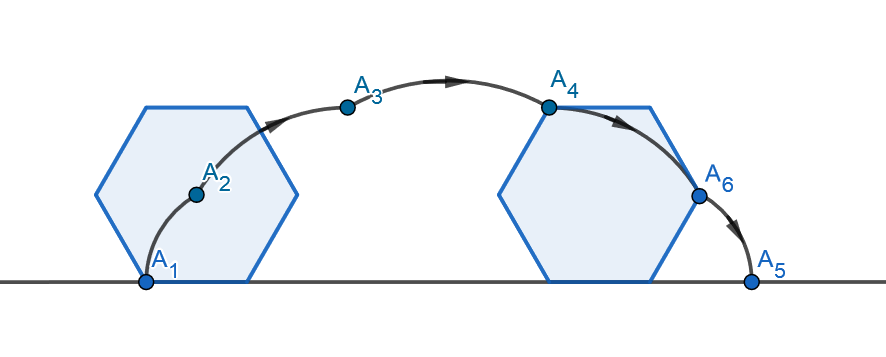
- Laske b-kohdan käyrän pituus neliölle, jonka piiri on
.
- Laske b-kohdan käyrän pituus kuusikulmiolle, jonka piiri on
.
4.7.11 Tehtävä
Mikä on suurimman mahdollisen -säteisen ympyrän sisään mahtuvan säännöllisen
-kulmion pinta-ala?
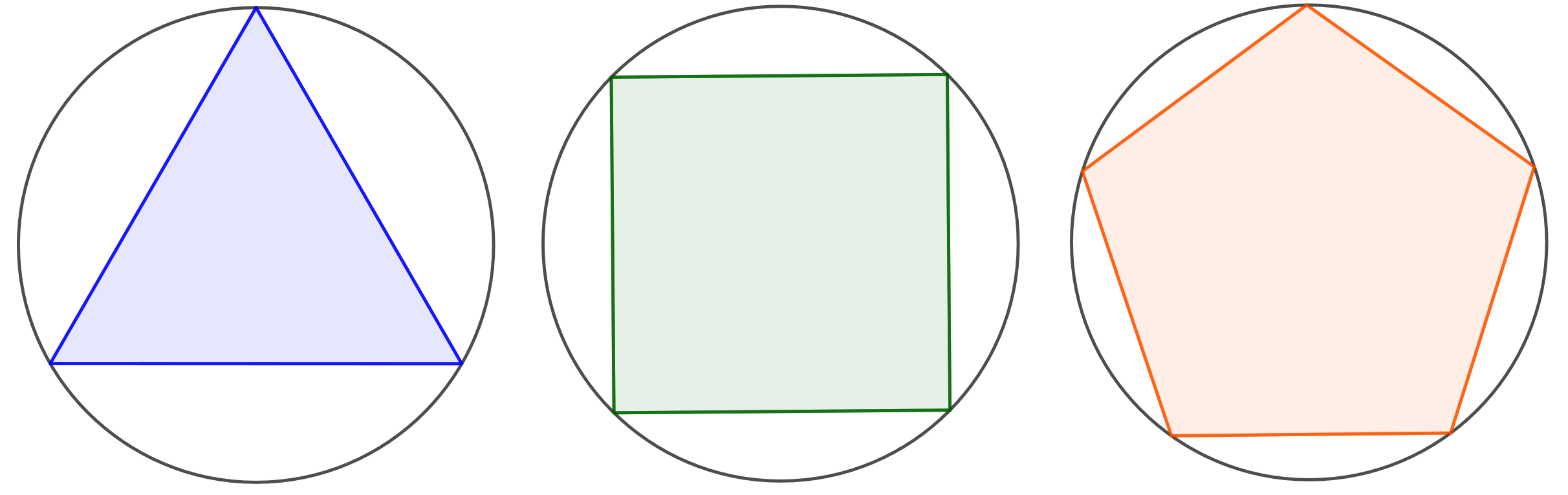
Tehtävän voi ratkaista monilla eri tavoilla, joista tässä esitetään vain yksi. Käytetään hyväksi alla olevaa kuvaa.
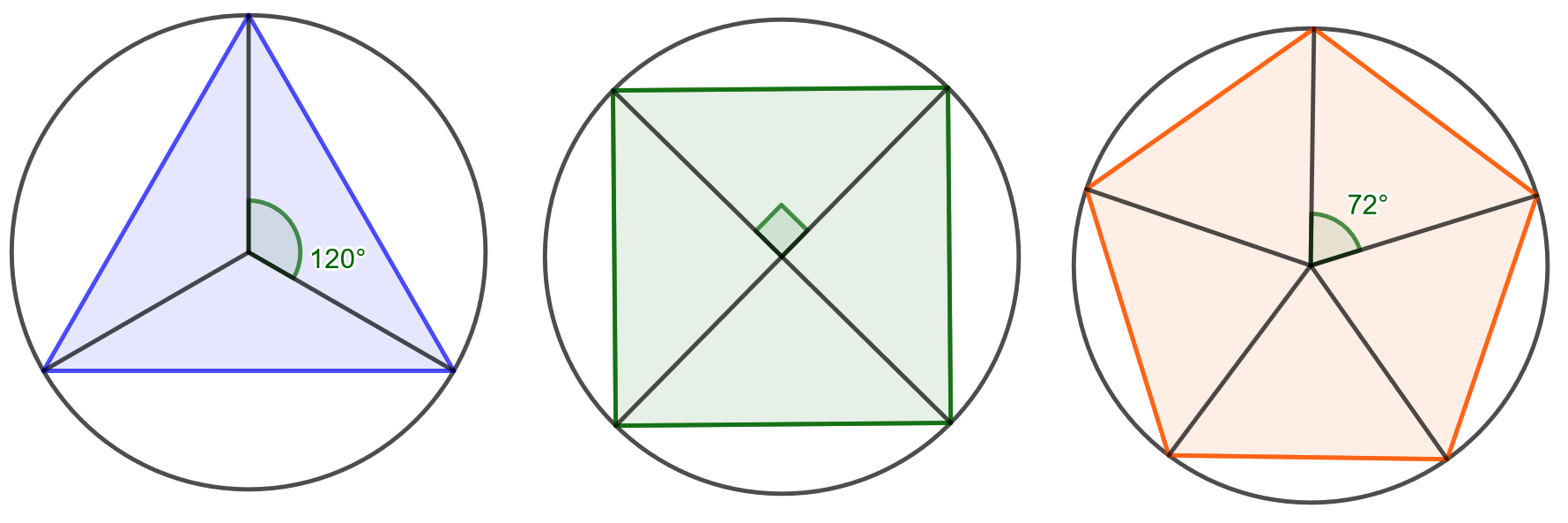
Jos monikulmiossa on kulmaa, jaetaan monikulmio
kolmioon. Kolmiot muodostetaan piirtämällä janat ympyrän keskipisteestä monikulmion jokaiseen kulmaan. Kolmion kulma, jonka kärki on ympyrän keskipisteessä, on
. Tämän kulman viereiset sivut ovat ympyrän säteen
mittaisia. Kolmion pinta-alan trigonometrisella kaavalla saadaan yhden kolmion alaksi
Koska kolmioita muodostuu monikulmion sisään
kappaletta, on koko monikulmion pinta-ala
4.7.12 Tehtävä
Alla olevassa GeoGebra-appletissa on isompi -säteinen ympyrä, jonka sisällä on kolme pienempää
-säteistä ympyrää. Määritä pienempi säde
isomman säteen
avulla.
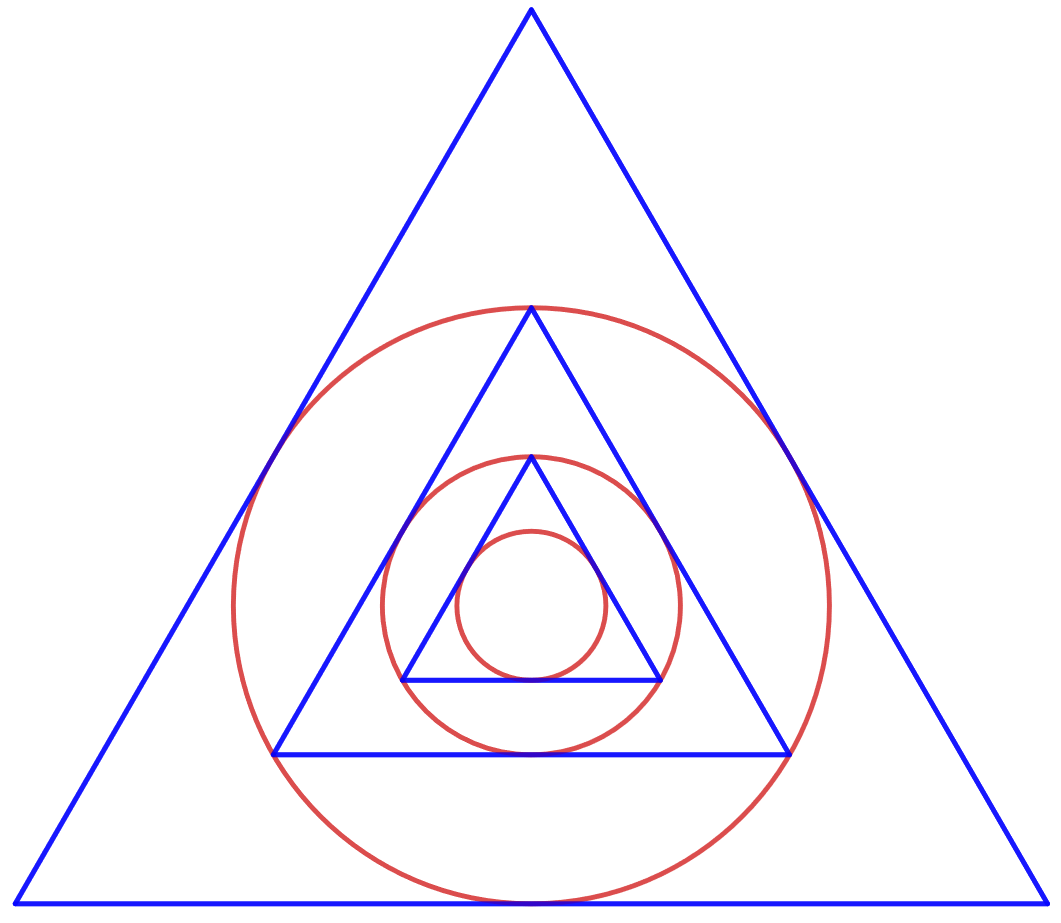
4.7.13 Tehtävä (K2012/11)
Tasasivuisen kolmion sivun pituus on
. Sen sisään asetetaan ympyrä
, joka sivuaa kolmion kylkiä. Tämän ympyrän
sisään asetetaan tasasivuinen kolmio
, jonka kärjet ovat ympyrällä
. Jatkamalla näin saadaan oheisen kuvan mukainen päättymätön jono ympyröitä
Laske ympyröiden pinta-alojen summa.

4.7.14 Tehtävä (K2012/15)
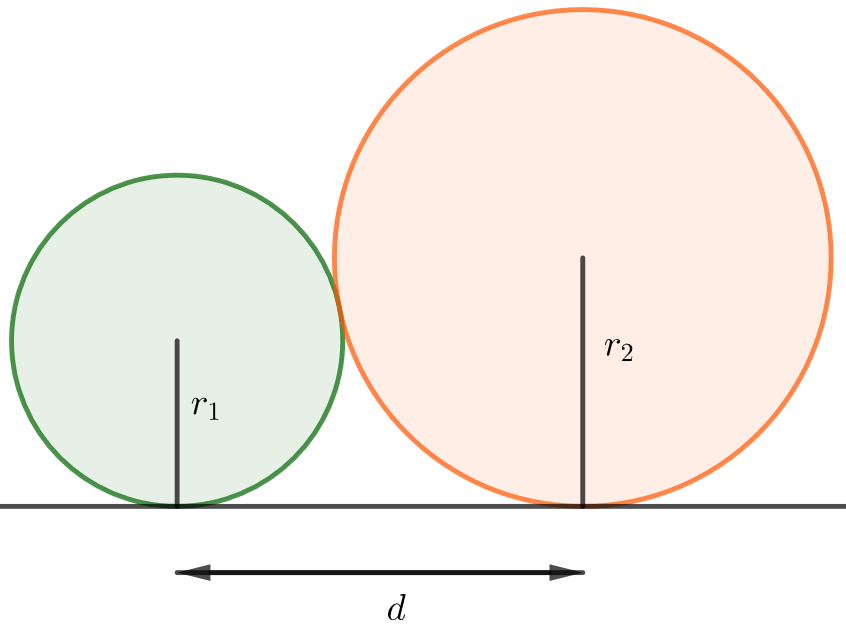
- Kaksi ympyrää sivuaa toisiaan ja
-akselia alla olevan kuvan mukaisesti. Määritä ympyröiden keskipisteiden vaakaruoda etäisyys d niiden säteiden avulla lausuttuna.
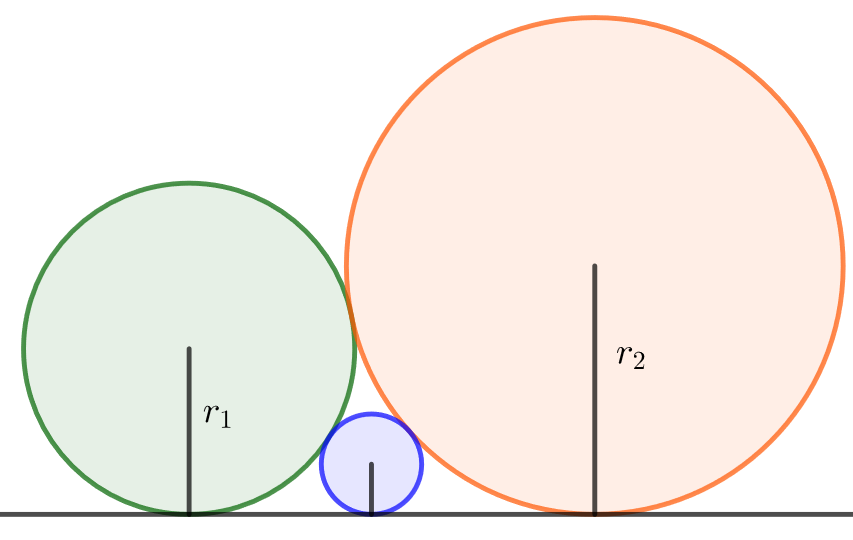
- Kolme ympyrää sivuaa toisiaan ja
-akselia alla olevan kuvan mukaisesti. Määritä keskimmäisen ympyrän säde
kahden reunimmalisen ympyrän säteiden avulla lausuttuna.
- Todista René Descartesin (1596-1650) keksimä b-kohdan ympyröihin liittyvä kaava
jossa
- Yhdistetään ympyröiden keskipisteet janalla, jonka pituus on
ja lisäksi piirretään
-säteisen ympyrän keskipisteestä
-akselin suuntainen jana
-säteisen ympyrän säteelle.
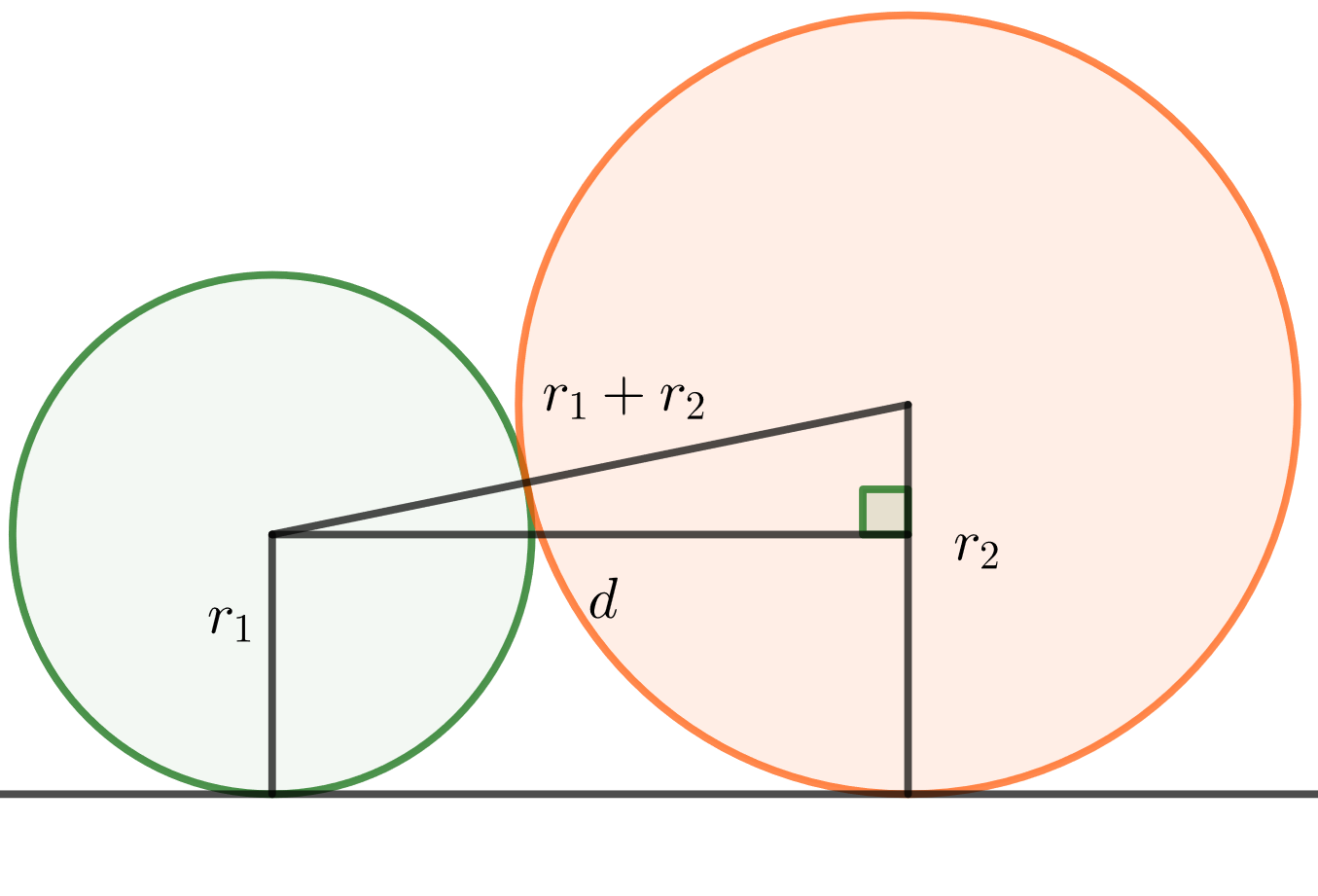
Suorakulmaisen kolmion kateettien pituudet ovat ja
ja hypotenuusan pituus on
. Pythagoraan lauseen avulla saadaan
- Piirretään
-säteisen ympyrän keskipisteestä
-akselin suuntainen jana
-säteisen ympyrän säteelle ja yhdistetään
- ja
-säteisten ympyröiden keskipisteet. Saadaan alla olevan kuvan mukainen suorakulmainen kolmio.
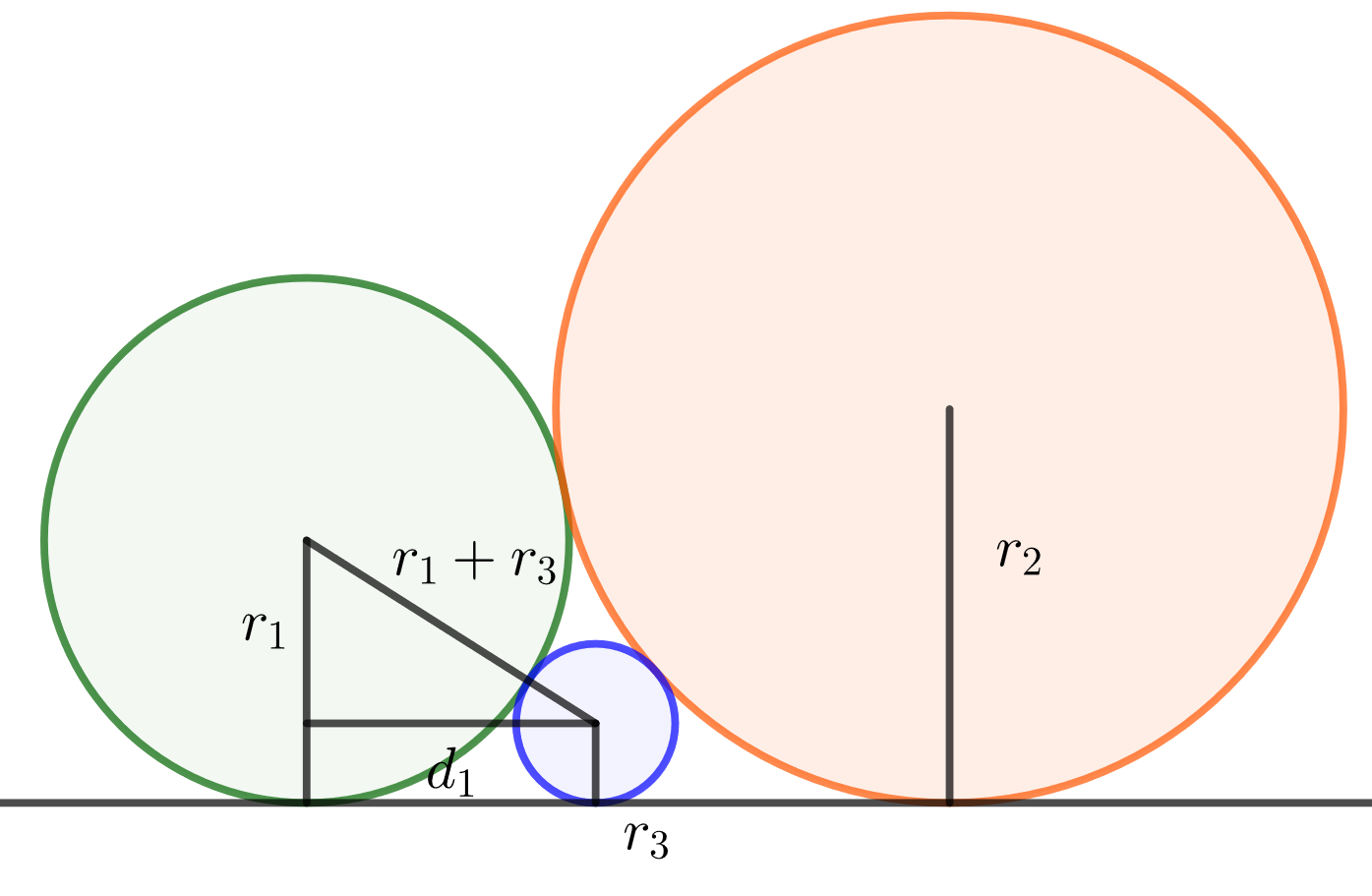
Ratkaistaan Pythagoraan lauseella
Vastaavasti saadaan toiselle puolelle suorakulmainen kolmio, josta - ja
-säteisten ympyröiden keskipisteiden välinen etäisyys
. Edellisen kohdan mukaan
eli
josta saadaan
- Avataan annetun lausekkeen sulkeita
Nyt
,
ja
. Sijoitetaan nämä aiempaan yhtälöön ja sievennetään, jolloin vasen puoli on
ja oikea puoli
Koska lausekkeet ovat yhtä suuret, on kaava oikea.
4.7.15 Tehtävä
Ympyrän, jonka halkaisija on sisälle piirretään mahdollisimman suuri viisikulmio. Määritä viisikulmion pinta-ala yhden desimaalin tarkkuudella.
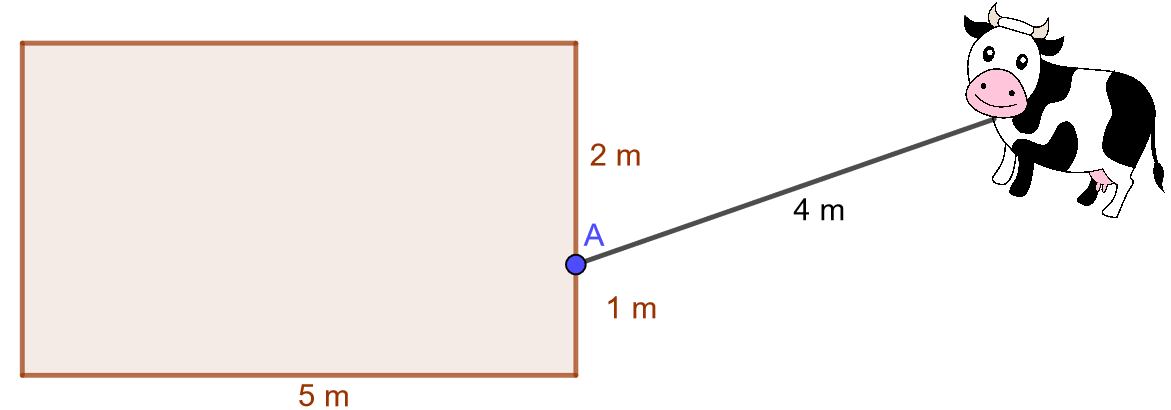
4.7.16 Tehtävä
Kuinka suurella alueella lehmä voi laiduntaa, kun sen kaulassa oleva köysi on kytketty kuvan mukaisesti ladon seinustalle pisteeseen ja köyden pituus on
?
4.7.17 Tehtävä
Piirrä GeoGebralla Reuleaux'n kolmio alla olevilla ohjeilla.
- Piirrä GeoGebralla tasasivuinen kolmio. Valitse aluksi työkalun alta lisää ja uudelleen lisää, jolloin saat kaikki työkalut näkyviin.
- Valitse Ympyrät-otsikon alta Ympyränkaari-työkalu ja valitse kolmion kärkipisteet vastapäivään kiertäen.
- Toista sama vielä kaksi kertaa niin, että aloitat joka kerta eri kärjestä.
- Piilota alkuperäinen kolmio. Valitse Muokkaus-otsikon alta Näytä/piilota objekti. Tämän jälkeen valitse piilotettavat kohteet piirtoalueelta.
- Lopuksi kokeile siirtää kolmion kärkipisteitä. Pysyykö konstruktiosi kasassa?
4.7.18 Tehtävä
Jos tasasivuisen kolmion sivun pituus on , mikä on sen ympärille piirretyn Reuleaux'n kolmion pinta-ala?
Mielenkiinnosta voit tutkia myös alla olevaa GeoGebra-applettia. Kokeile muuttaa
- ympyrän säde
- kolmion "sisäsäde"
- kiertosuunta
liukusäätimiä ja katso, miten Reuleaux'n kolmion kärkipisteiden muodostama punaisella merkitty ura muuttuu. Paina Aloita animaatio, jolloin saat kolmion pyörimään.
4.7.19 Tehtävä
Laske varjostetun alueen pinta-ala. Ympyröiden keskipisteet ovat toistensa kehillä, eli jokaisen ympyrän säde on .
4.7.20 Tehtävä
Samasta keskipisteestä piirretään kolme ympyrää joiden säteet ovat ,
ja
. Tasasivuisen kolmion kärjet ovat näillä ympyröillä. Määritä kolmion sivun pituus.
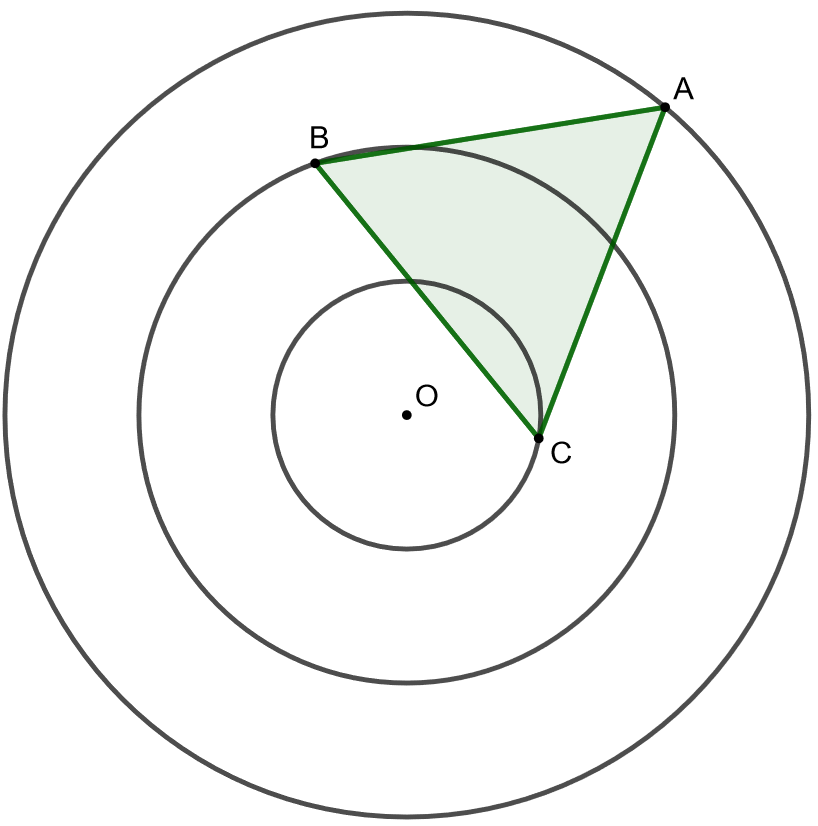
Osoita, että on jännenelikulmio. Jännenelikulmiossa lävistäjien tulo on yhtä suuri kuin vastakkaisten sivujen tulojen summa.
Jännenelikulmiossa vastakkaisten kulmien summa on .
5. Avaruusgeometria: tehtäviä
Tällä sivulla on tehtäviä kappaleeseen Avaruusgeometria liittyen.
5.1 Kulmia avaruudessa
Tämän kappaleen teoria on kappaleessa Kulmia avaruudessa.
5.1.1 Tehtävä
5.1.2 Tehtävä
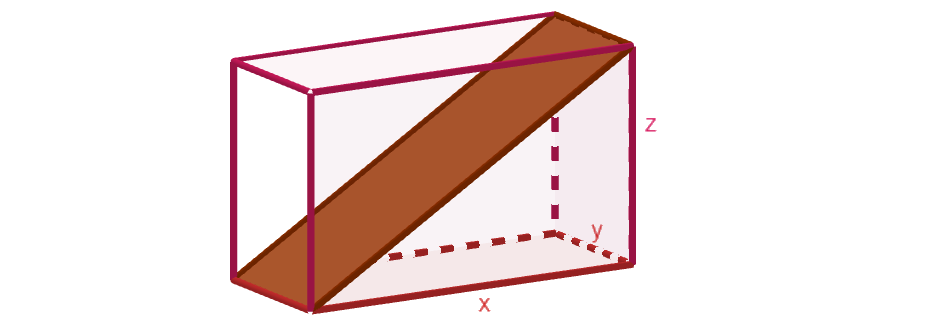
Suorakulmaisen särmiön muotoisen laatikon sivujen pituudet ovat ,
ja
. Laatikon sisään asetetaan lauta kuvan mukaisesti. Kuinka suuri on laatikon pohjan ja laudan välinen kulma?
5.1.3 Tehtävä
Matti valmistaa pahvista kuution, jonka sivun pituus on .
- Kuinka paljon pahvia tarvitaan kuution tekoon?
- Matti haluaa asettaa kuution sisään mahdollisimman pitkän ohuen riman. Kuinka pitkä rima kuutioon mahtuu?
5.2.1 Tehtävä
Täydellisessä auringonpimennyksessä kuu peittää maasta katsottuna auringon kokonaan. Jos auringon etäisyys maasta on -kertainen kuun etäisyyteen maasta, kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna?
5.2.2 Tehtävä (K2016/6)
Maapallon säde on , ja sen pohjoisen napapiirin leveysaste on
. Pohjoiselta napapiiriltä valitaan pisteet
ja
, joiden pituusasteiden erotus on
astetta.
- Määritä pisteiden
ja
välisen viivasuoran tunnelin pituus.
- Määritä pisteiden
ja
välisen lyhimmän napapiirin kaaren pituus.
5.2.3 Tehtävä
Pallon pinta-ala on . Pallo jaetaan kahteen yhtä suureen osaan. Laske muodostuvan puolipallon tilavuus.
5.2.4 Tehtävä
Vesi peittää noin maapallon pinnasta. Jos maapallon säde on noin
, kuinka suuren pinta-alan vesi peittää?
5.2.5 Tehtävä
Maapallon vesien yhteenlaskettu määrä on noin . Oletetaan, että maapallon säde on noin
ja että maapallo on täydellinen pallo. Jos kaikki vesi levittäytyisi maapallon pinnalle tasaisesti, kuinka syvä vesikerros olisi?
5.3.1 Tehtävä
Palaa tehtävään, jossa laskettiin aakkoskarkin pinta-alaa. Jos aakkoskarkin paksuus on , mikä on yhden karkin tilavuus?
Jos karkin tiheys on ja yksi pussi painaa
, kuinka monta karkkia yhdessä pussissa on?
5.3.2 Tehtävä
Vesitornin sylinterin muotoiseen säiliöön mahtuu vettä ja säiliön korkeus on
metriä. Mikä on säiliön halkaisija?
5.3.3 Tehtävä
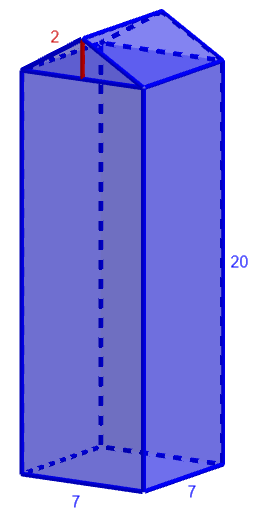
Alla olevassa kuvassa on havainnekuva maitotölkistä sekä tölkin mitat (senttimetreinä). Laske koko tölkin tilavuus.
5.3.4 Tehtävä
Muurahainen aloittaa kulkunsa kuution kulmasta. Kuution särmän pituus on . Mikä on lyhin matka, jonka kulkemalla muurahainen pääsee kuution vastakkaiseen kulmaan?
5.3.5 Tehtävä
Jos pallon tilavuus on , mikä suurimman sen sisään mahtuvan kuution tilavuus?
5.3.6 Tehtävä
Mahdollisimman pienen ympyräpohjaisen lieriön sisälle laitetaan mahdollisimman suuri pallo. Määritä pallon tilavuuden suhde lieriön tilavuuteen.
5.3.7 Tehtävä (Pitkän matematiikan preli K2017/5)
Yritys lähettää tuotteitaan asiakkaille suorakulmaisen särmiön muotoisessa laatikossa, jossa sivujen suhteet ovat laatikon sisällä .
- Erääseen lähetykseen pakataan kolme suoraa ympyräpohjaista metallilieriötä, joiden korkeus on sama kuin laatikon pisimmän sivun pituus ja pohjan halkaisija on yhtä pitkä kuin laatikon lyhin sivu. Tyhjä tila täytetään styroksilla. Mikä on lieriöiden täyttämän tilan ja laatikon tilavuuksien suhde?
- Kuinka monta prosenttia laatikon tilavuudesta on styroksia?
- Jos laatikon tilavuus on
litraa, niin mahtuuko laatikkoon metallipallo, jonka säde on
?
5.3.8 Tehtävä (S2015/3b)
Laske kuution yhden sivutahkon pinta-ala neliösenttimetrin tarkkuudella, kun kuution tilavuus on litraa.
5.3.9 Tehtävä (S2015/9)
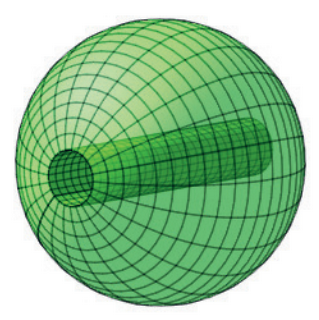
Täysin pyöreän geenimanipuloidun omenan säde on . Omenan läpi porataan sen keskeltä kulkeva reikä, jonka säde on
. Kuinka monta prosenttia omenan tilavuudesta tällöin häviää? Anna vastaus posenttiyksikön kymmenesosan tarkkuudella.
5.3.10 Tehtävä (K2015/8)
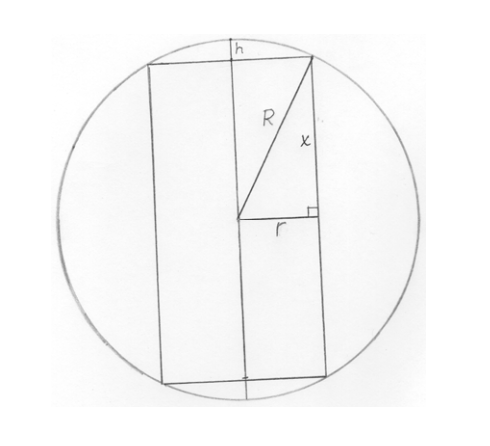
Öljysäiliö on suoran ympyrälieriön muotoinen, ja sen akseli on vaakasuorassa. Akselia vastaan kohtisuoran poikkileikkauksen halkaisija on metriä.
- Määritä säiliön pituus, kun sen tilavuus on
litraa.
- Öljyn korkeudeksi syvimmässä kohdassa mitataan
senttimetriä. Kuinka monta litraa öljyä on jäljellä säiliössä?
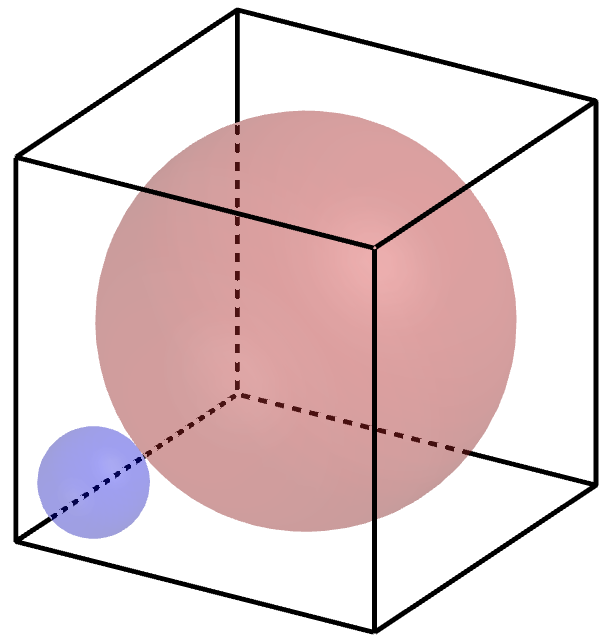
5.3.11 Tehtävä (K2013/10)
Oheisen kuution särmän pituus on . Sen sisällä on punainen pallo, joka sivuaa jokaista kuution tahkoa. Kuution yhdessä kulmassa on pienempi sininen pallo, joka sivuaa suurta palloa ja kolmea kuution tahkoa kuvion mukaisesti. Laske sinisen pallon säteen tarkka arvo.
5.4.1 Tehtävä
5.4.2 Tehtävä
5.4.3 Tehtävä
Suoran ympyräkartion pohjan säde on ja sen korkeus on
. Kartion huipusta katkaistaan pienempi suora ympyräkartio. Tämän pienemmän kartion pohjan säde on
. Kuinka korkea pienempi kartio on?
5.4.4 Tehtävä
Olkoon edelleen kartion pohjan säde ja korkeus
. Sen huipusta leikataan pois pienempi kartio, jonka pohjan säde on
. Mikä on jäljelle jäävän osan tilavuus?
5.4.5 Tehtävä
Suoran ympyräkartion korkeus on ja pohjan säde
. Kartion huipulta katkaistaan pienempi kartio, jonka korkeus on
. Kuinka moninkertainen ison kartion tilavuus on verrattuna pienempään kartioon?
5.4.6 Tehtävä
5.4.7 Tehtävä
Kheopsin pyramidin muoto on lähellä neliöpohjaista kartiota. Matti mittaa pyramidin pohjan sivun pituudeksi ja kuulee oppaalta pyramidin korkeuden olevan
. Laske annettujen tietojen avulla arvio pyramidin tilavuudelle.
5.4.8 Tehtävä
korkean kartion pohja muodostuu tasasivuisesta kolmiosta. Kartion tilavuus on
. Määritä pohjakolmion sivun pituus.
5.4.9 Tehtävä
Kartion muotoisen jäätelötötterön sivun pituus on ja sen suuaukon halkaisija on
. Jäätelötötteröön asestetaan täsmälleen pallon muotoinen jäätelöpallo, jonka halkaisija on
. Jos pallon annetaan sulaa kokonaan, mahtuuko se jäätelötötterön sisään?
5.4.10 Tehtävä (K2012/9)
Suoran ympyräkartion korkeus on , ja sen pohjan säde on
. Kartio katkaistaan niin, että yläreunan säde on
. Tämän jälkeen katkaistun kartion vaippa maalataan siniseksi ja sitä pyöritellään kyljellään paperilla. Määritä näin saadun sinisen rengasalueen pinta-ala yhden neliösenttimetrin tarkkuudella.


5.4.11 Tehtävä (K2016/13)
Olkoon ,
ja
positiivisia reaalilukuja. Tetraedrin kolme kärkeä ovat koordinaattiakseleiden pisteissä
,
ja
, ja neljäs kärki on origossa
. Kärkien vastaisten tetraedrin tahkojen pinta-aloja merkitään samassa järjestyksessä kirjaimilla
,
,
ja
, jossa
tarkoittaa origon vastaisen tahkon pinta-alaa. Osoita, että
Vinkki: Luo GeoGebralla liukusäätimet ,
ja
ja luo tarvittavat pisteet niiden avulla. Tarkastele syntyvää kappaletta ja lue ohjeet tarkasti.
Tetraedrin pohjakolmion sivut ovat ,
ja
. Alla olevan kuvan merkinnöin saadaan
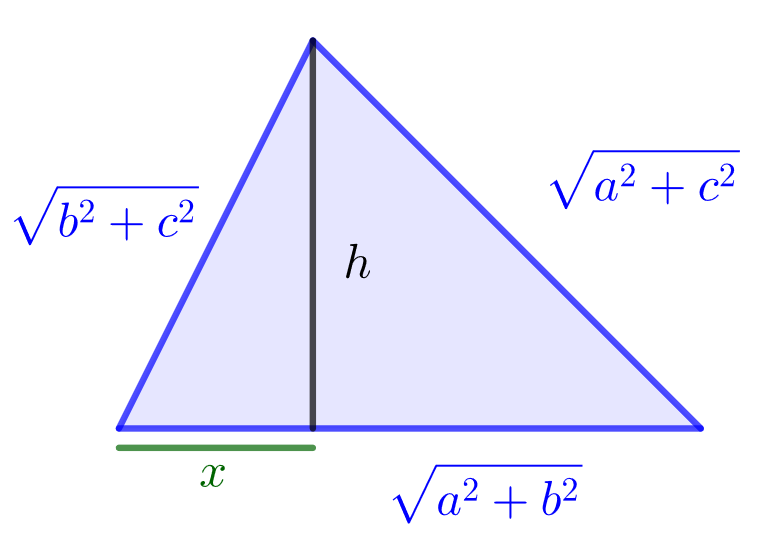
Vähennetään yhtälöt puolittain, jolloin saadaan josta saadaan
Tällöin
Saadaan siis
. Koska akselitasossa olevien kolmioiden alat ovat
,
ja
, niin
.
5.5 Sekalaisia tehtäviä
Tässä kappaleessa on kaikkiin tämän luvun aiheisiin liittyviä tehtäviä.
5.5.1 Tehtävä (S2016/6)
Vesikaukalon päädyt ovat tasasivuisen kolmion muotoiset, ja kolmion sivujen pituus on . Kaukalon pohja muodostuu kahdesta suorakulmion muotoisesta levystä, joiden pituus on
.
- Vaakasuorassa oleva kaukalo on aluksi täynnä vettä. Sitä kallistetaan pituussuunnassa niin, että vedenpinta ulottuu vasemmanpuoleisen päätykolmion alakulmaan alla olevan kuvion mukaisesti. Kuinka monta prosenttia vedestä valuu pois kallistuksen aikana?
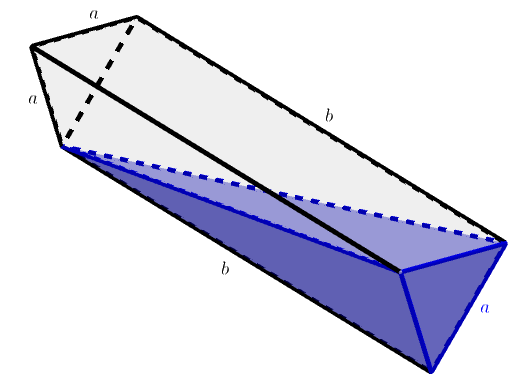
- Tämän jälkeen kaukalo palautetaan takaisin vaakasuoraan asentoon. Kuinka korkealla vedenpinta on kaukalon syvimmästä kohdasta mitattuna?
Vesi muodostaa nyt särmiön, jonka pohjana on tasakylkinen kolmio. Muodosta lauseke vesisärmiön tilavuudelle ja vertaa sitä a-kohtaan.
6. Harjoituskoe MAA3
Tällä sivulla on harjoituskoe MAA3-kurssille. Jokaisesta tehtävästä saa tässä kokeessa vain yhden pisteen oikeasta vastauksesta, mutta oikeassa kurssikokeessa ja ylioppilaskirjoituksissa tehtävän välivaiheet huomioidaan myös pisteytyksessä.
6.1 Tehtävä
Joni vetää pulkkaa pitkällä narulla ja Jonin käsi on
korkeudella maasta. Kuinka kaukana Jonin takana on pulkan etureuna?
6.2 Tehtävä
Määritä alla olevan kolmion sivun pituus kertoimen
avulla lausuttuna.
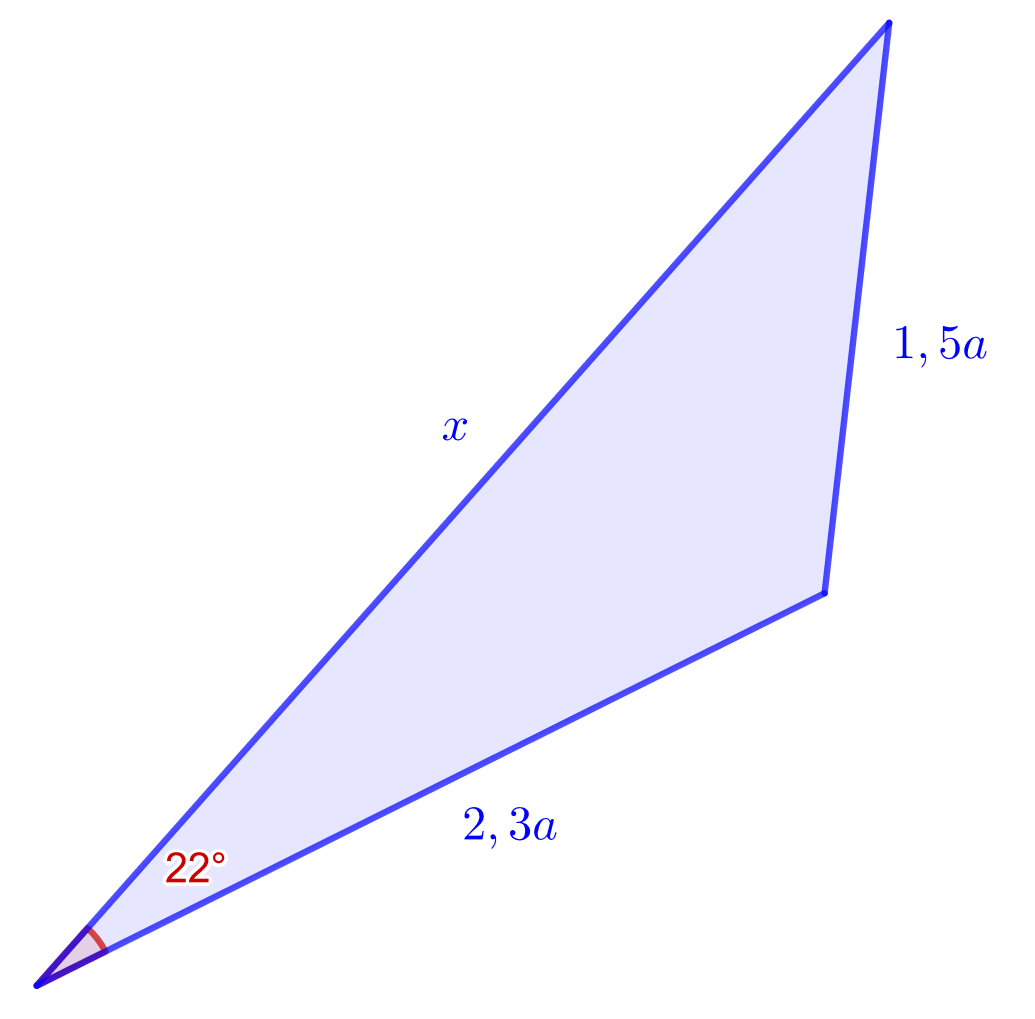
6.3 Tehtävä
Laske edellisen tehtävän kolmion pinta-ala, kun .
6.4 Tehtävä
Tasaisella maalla pituinen keppi astetaan
päähän puusta, jolloin kepin kärki yhtyy puun latvaan, kun niitä katsotaan maan pinnasta
kulmassa. Kuinka korkea puu on?
6.5 Tehtävä
Ympyrän säde on ja sektoria vastaava keskuskulma on
. Tasakylkisen kolmion huippukulma on myös
ja sen kylkien pituudet ovat
. Sektorin ja tasakylkisen kolmion pinta-alat ovat samat. Määritä
.
6.6 Tehtävä
Ratkaise alla olevaan kuvaan oranssilla merkityn kolmion pinta-ala.
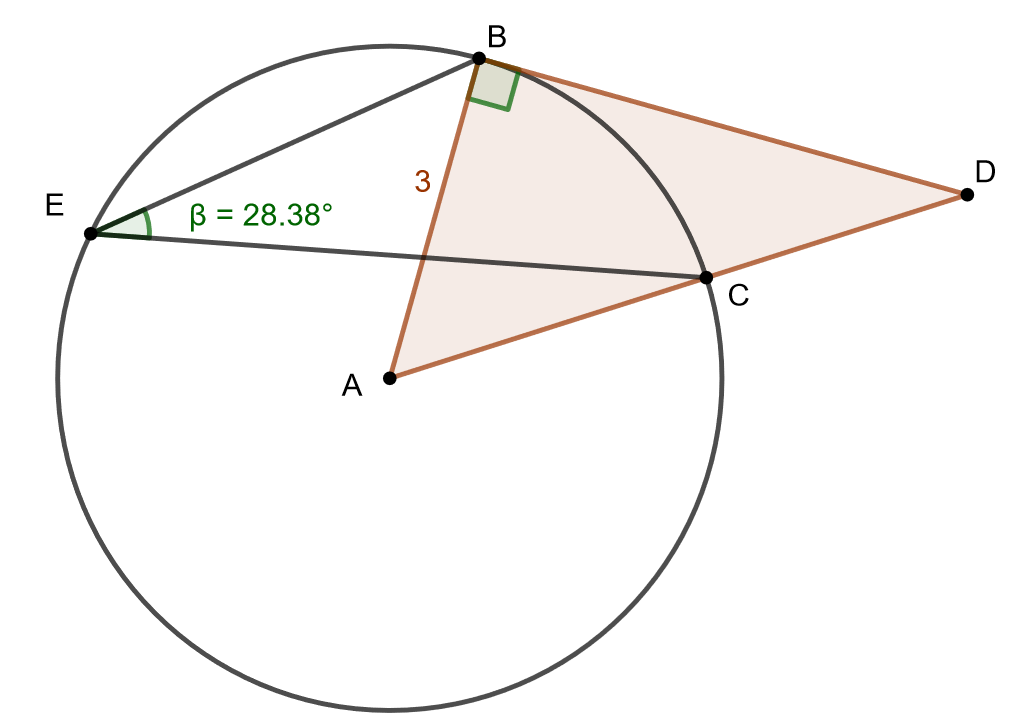
6.7 Tehtävä
Vinon ympyrälieriön sivun pituus on ja pohjaympyrän halkaisija
. Lieriön sivun ja pohjan välinen kulma on
. Mikä on lieriön tilavuus?
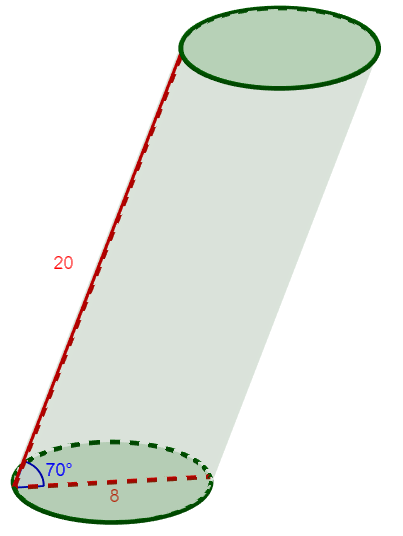
6.8 Tehtävä
Kolmion kärjet ovat pisteissä ,
ja
. Kuinka suuri on suurimman mahdollisen kolmion sisään piirretyn ympyrän säde? Määritä se alla olevan GeoGebra-appletin avulla. Tallenna säde muuttujaan nimeltä r.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.