MAA - Pitkän matematiikan kertauskurssi

Tämän TIM-sivuston tarkoituksena on toimia lukion pitkän matematiikan (MAA) pakollisten kurssien kattavana ja riittävänä kertausmateriaalina ja -ympäristönä.

Sivusto ei kuitenkaan ole kurssin keskeisin asia. Uuden oppiminen ja vanhojen tietojen vahvistaminen sen sijaan ovat. Siksi toivomme ja pyydämme, että jokainen sivustoa opiskellut osallistuu kykyjensä mukaan virheiden ja puutteiden ilmoittamiseen. Myös rakentavat kommentit vievät yhteistä oppimisasiaa eteenpäin.

Tekijät

Henri Jaakkola (040 341 6093)

Petri Luoma (040 341 4774)

etunimi.sukunimi(at)gradia.fi

Johdanto

Kurssin materiaali on luotu TASE-hankkeessa avoimeksi ja saavutettavaksi. Sen tarkoituksena on auttaa pitkän matematiikan itsenäiseen kertaukseen. Materiaali on laadittu siten, ettei varsinaista teoriaa ole erikseen luotu, vaan kaikki tarvittava tieto ja hyvän ratkaisun piirteet käyvät ilmi tehdyistä esimerkeistä.

Materiaalin rakenne on sellainen, että jokaisessa luvussa on aluksi H5P-tekniikalla tehtyjä yksinkertaisia pelejä. Tämän jälkeen on videoita esimerkkitehtävistä ratkaisuineen. Luvun lopussa on aina pieniin paloihin järjestetty yo-tehtäväratkaisu sekä linkkejä itsenäiseen itseopiskeluun ja vanhoihin yo-tehtäviin.

TASE-hanke on vuoden 2019 toisen asteen oppimateriaalikustannusten verkostomainen alentamishanke. Yhtenä sen tavoitteen mukaisena pilottina on toteuttaa toimintakokonaisuus, jossa koostetaan mm. digitaalisia oppimateriaaleja. Hanketta rahoittaa Opetushallitus ja sen hallinnoinnista vastaa Turun kaupungin sivistystoimiala.

Lue lisää osoitteessa koulutustakuu.fi/hankkeet/tase.

MAY1 - Luvut ja lukujonot

Opetussuunnitelman keskeiset sisällöt

reaaliluvut, peruslaskutoimitukset ja prosenttilaskenta
funktio, kuvaajan piirto ja tulkinta
lukujono
rekursiivinen lukujono
aritmeettinen jono ja summa
logaritmi ja potenssi sekä niiden välinen yhteys
muotoa , $x \in \mathbb{N}$ olevien yhtälöiden ratkaiseminen
geometrinen jono ja summa

H5P-peli 1.1

Prosenttikerroinharjoitus

H5P-peli 1.2

Jonojen ja summien laskukaavat

H5P-peli 1.3

Jonot ja summat -harjoitus

H5P-peli 1.4

Sanallisen tehtävän ratkaisuvaiheet

H5P-peli 1.5

Ensimmäisen asteen yhtälönratkaisu

H5P-video 1.6

Makkaran rasvapitoisuus on 36 painoprosenttia. Kuinka monta prosenttia rasvaa makkarasta pitäisi vähentää, jotta makkaran uudeksi rasvaprosentiksi tulee 30 %?

# H5PV16

Prosenttilaskuja

H5P-video 1.7

Kuutio pienennetään toiseksi kuutioksi niin, että sen kokonaispinta-ala pienenee 36 %. Kuinka monta prosenttia tilavuus pienenee?

# H5PV17

Muutosprosentti ja -kerroin

H5P-video 1.8

Osoita, että lukujono

a) a_n = 2n - 3 on aritmeettinen

b) $b_n = \frac{3}{2^{n - 1}}$ on geometrinen.

# H5PV18

Aritmeettinen ja geometrinen jono

H5P-video 1.9

Salissa on istumapaikkoja 1000:lle katsojalle 25 rivissä. Jokaisella rivillä on kaksi paikkaa enemmän kuin edellisellä rivillä. Kuinka monta paikkaa on ensimmäisellä ja viimeisellä rivillä?

# H5PV19

Aritmeettinen summa

H5P-video 1.10

Tietyn alueen turpeen määrä riittää nykyisellä vuotuisella kulutuksella turvevoimalan käyttöön 60 vuodeksi. Jos kulutus kasvaa 3 % vuodessa, niin miten pitkäksi ajaksi turve riittää?

# H5PV110

Geometrinen summa

Videoesimerkki 1.1

Kiinan väkiluku kasvaa 0,6 % ja Intian 1,1 % vuodessa. Vuonna 2017 Kiinassa oli 1,386 miljardia asukasta. Intiassa vastaava lukumäärä oli 1,356 miljardia. Ratkaise vuosi, jolloin Intia ohittaa Kiinan, jos kasvu jatkuu samanlaisena.

# VE11

Videoesimerkin 1.1 ratkaisu

Videoesimerkki 1.2

Potilaalle määrätään lääkettä leikkauksen jälkeisenä aamuna 500 mg. Ratkaise kuukaudessa kuluvan lääkkeen kokonaismäärä, kun lääkkeen määrää pienennetään joka aamu

a) 5 mg

b) 2 %.

# VE12

Videoesimerkin 1.2 ratkaisu

Yo-tehtävä 1.1

Harjoitellaan kevään 2003 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Geometrisen jonon kolmen ensimmäisen termin summa on 3 ja kuuden ensimmäisen termin summa 12. Laske yhdeksän ensimmäisen termin summa. Vastaa, suppeneeko vastaava geometrinen sarja.

Ratkaisu

# YT11_T1

Kirjoitetaan kolmen ensimmäisen jäsenen summa ja otetaan yhteinen tekijä.

a + aq + aq^2 = 3

# YT11_R1

Valitse edellä oleva summa yhteisen tekijän avulla kirjoitettuna.

# YT11_R2

Valitse paras tapa kirjoittaa kuuden ensimmäisen jäsenen summa yhteisen tekijän avulla kirjoitettuna.

Edellä kirjoitettu summa voidaan kirjoittaa vielä uudessa muodossa.

a + aq + aq^2 + aq^3 + aq^4 + aq^5 = 3 + 3q^3 = 12

# YT11_T2

Ratkaistaan .

$\begin{align*} 3q^3 &= 9 \\ q^3 &= 3 \\ q &= \sqrt[3]{3} \end{align*}$

# YT11_R3

Suppeneeko annettu geometrinen sarja?

Kirjoitetaan yhdeksän ensimmäisen jäsenen summa.

S_9 = S_6 + aq^6(1 + q + q^2) = 12 + 3q^6

# YT11_T3

Lasketaan summa.

$S_9 = 12 + 3q^6 = 12 + 3 \cdot (\sqrt[3]{3})^6 = 12 + 3 \cdot 3^2 = 12 + 3^3 = 12 + 27 = 39$

Jälkipohdinta

# YT11_T4

Edellisen tapainen tehtävä voi sähköisissä yo-kokeissa olla A-osassa, joka tehdään ilman teknisiä apuvälineitä. Tässä mielessä tehtäväratkaisun kirjoittamista kannattaa harjoitella koeympäristön vastauskenttää vastaavassa Matikkaeditorissa.

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/may

matikkamatskut.com/may1

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAY1-sisältöjä peilata tehtyyn toteutukseen. Lukujonoja ja summia ei ole uusissa keskeisissä sisällöissä.

TAU/MAY1

Yo-tehtäviä harjoiteltaviksi

Prosentit

S13/2c, K09/3b, K07/3a, K00/4, S16/1, K02/3, S02/2, K03/5, K04/3, K05/3, K06/4, S06/5, S07/4, K08/4

Geometrinen ja aritmeettinen jono ja summa

K03/12, S03/12, S16/5b, S15/8, S14/8, S16/5a, S19/1

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA2 - Polynomifunktiot ja yhtälöt

Opetussuunnitelman keskeiset sisällöt

polynomien tulo ja muotoa , $n \leq 3$ , $n \in \mathbb{N}$ olevat binomikaavat
toisen asteen yhtälö ja ratkaisukaava sekä juurten lukumäärän tutkiminen
toisen asteen polynomin jakaminen tekijöihin
polynomifunktio
polynomiyhtälöitä
polynomiepäyhtälön ratkaiseminen

H5P-peli 2.1

Yhdistä oikea yhtälö

H5P-peli 2.2

Epäyhtälön ratkaisuvaiheet

H5P-peli 2.3

Diskriminantti ja ratkaisujen lukumäärä

Videoesimerkki 2.1

Millä vakion arvolla jakolasku $\dfrac{x^2 + 2x^2 + ax}{x - 3}$ menee tasan? Määritä saadulla vakion arvolla polynomin kaikki nollakohdat. (K80/3)

# VE21

Videoesimerkin 2.1 ratkaisu

Videoesimerkki 2.2

Millä vakion arvolla yhtälöllä x^2 - ax + a = -1 ei ole ratkaisuja?

# VE22

Videoesimerkin 2.2 ratkaisu

Videoesimerkki 2.3

Ratkaise epäyhtälö x - 1 > 2(x - 1)^2 .

# VE23

Videoesimerkin 2.3 ratkaisu

Videoesimerkki 2.4

Olkoon f(x) = -x + 3 ja g(x) = x^2 - x - 5 .

a) Muodosta funktioiden erotus f(x) - g(x) ja tulo $f(x) \cdot g(x)$ .

b) Määritä funktioiden leikkauspisteet sekä piirtämällä että laskemalla.

# VE24

Videoesimerkin 2.4 ratkaisu

Videoesimerkki 2.5

Olkoon $f(x) = 3 - \frac{x}{2}$ .

a) Piirrä funktioiden f(x) ja |f(x)| kuvaajat.

b) Ratkaise yhtälö |f(x)| = 2 ja epäyhtälö |f(x)| < 2 .

# VE25

Videoesimerkin 2.5 ratkaisu

Yo-tehtävä 2.1

Harjoitellaan kevään 2018 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Toisen asteen polynomifunktiolle voidaan käyttää kahta erilaista esitystapaa.

Summamuoto .

Tulomuoto .

a) Muokkaa polynomi summamuotoon.

b) Muokkaa polynomi tulomuotoon.

c) Osoita, että $x_1 x_2 = \frac{c}{a}$ , jos ja ovat polynomin nollakohdat.

Ratkaisu

# YT21_T1

a) Kirjoitetaan polynomi 2(x - 6)(x - 9) summamuotoon.

# YT21_R1

Polynomi summamuodossa?

b) Kirjoitetaan polynomi x^2 + x - 12 tulomuotoon.

Muodostetaan polynomista yhtälö x^2 + x - 12 = 0 .

# YT21_R2

Ratkaisukaavan kertoimet?

Ratkaistaan nollakohdat toisen asteen yhtälön ratkaisukaavalla.

$\begin{align*} x^2 + x - 12 &= 0 \\ x &= \frac{-1 \pm \sqrt{1^2 - 4 \cdot 1 \cdot (-12)}}{2 \cdot 1} \\ x &= \frac{-1 \pm \sqrt{1 + 48}}{2} \\ x &= \frac{-1 \pm 7}{2} \\ x &= 3 \qquad \text{tai} \qquad x = -4 \end{align*}$

# YT21_R3

Nollakohtien merkitys tehtävän kannalta?

c) Osoitetaan, että $x_1 x_2 = \frac{c}{a}$ , jos x_1 ja x_2 ovat polynomin ax^2 + bx + c nollakohdat.

# YT21_R4

Polynomi aukikirjoitettuna?

Vertaillaan vakiotermejä.

$c = ax_1 x_2 \qquad \text{eli} \qquad x_1 x_2 = \frac{c}{a}$

# YT21_T2

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa2

matikkamatskut.com/maa2

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA2-sisältöjä peilata tehtyyn toteutukseen.

TAU/MAA2

Yo-tehtäviä harjoiteltaviksi

Ensimmäisen asteen yhtälö ja epäyhtälö

K12/1b, S11/1c, K13/1b, S10/2a, K17/1c, K09/1

Toisen asteen yhtälö ja epäyhtälö

K10/1a, S10/2c, K11/1b, K10/3b, K18/2, S18/1, K19/7

Itseisarvoyhtälö

S12/1b, S11/6b, K17/5a

Yleinen polynomiyhtälö Ja epäyhtälö

S19/5

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA3 - Geometria

Opetussuunnitelman keskeiset sisällöt

kuvioiden ja kappaleiden yhdenmuotoisuus
sini- ja kosinilause
ympyrän, sen osien ja siihen liittyvien suorien geometria
kuvioihin ja kappaleisiin liittyvien pituuksien, kulmien, pinta-alojen ja tilavuuksien laskeminen

H5P-peli 3.1

$\begin{tikzpicture}[thick, font=\footnotesize] % HENRI JAAKKOLA % Suorakulmainen kolmio \draw [red] (0,0) -- node [below] {$b$} (4,0) -- node [above] {$c$} (0,3) -- node [left] {$a$} cycle; % Kulmat \draw [thin] (0.35,0) -- ++(0,0.35) -- ++(-0.35,0); \draw [thin] (3.5,0) arc (180:143.130:0.5); \draw [thin] (0,2.5) arc (-90:-36.870:0.5); \node at (3.25,0.2) {$\beta$}; \node at (0.35,2.35) {$\alpha$}; \end{tikzpicture}$

Trigonometriaharjoitus

H5P-peli 3.2

Sini- ja kosinilauseharjoitus

H5P-peli 3.3

Pythagorasharjoitus

Videoesimerkki 3.1

Lintutorni on 10 metrin korkuinen. Kuinka kauas merelle sieltä voi kirkkaana päivänä nähdä. Maapallon ympärysmitta on noin 40000 km.

# VE31

Videoesimerkin 3.1 ratkaisu

Videoesimerkki 3.2

Kaksi samankokoista ympyrää, joiden säde on 1, sivuavat toisiaan ja niiden ympärille piirretyn mahdollisimman pienen neliön sivua.

Piirrä kuvio.
Laske neliön sivun pituus.

# VE32

Videoesimerkin 3.2 ratkaisu

Videoesimerkki 3.3

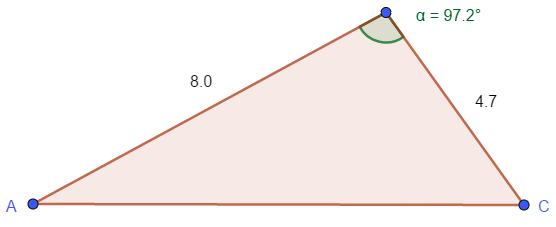
Teräväkulmaisen kolmion kaksi sivua ovat 11 ja 7 ruudun pituiset, ja jälkimmäisen sivun vastainen kulma on 30 astetta. Laske kolmion

muut kulmat
kolmannen sivun pituus.

# VE33

Videoesimerkin 3.3 ratkaisu

Yo-tehtävä 3.1

Harjoitellaan kevään 2012 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Näytä, että pisteet , ja ovat suorakulmaisen kolmion kärjissä.

Ratkaisu

# YT31_T1

Koordinaatistoon piirretyt pisteet , ja muodostavat suorakulmaisen kolmion, jos kahden muodostetun, lyhimmän janan pituuksien neliöiden summa on kolmannen, pisimmän sivun neliö.

Lasketaan janan pituus Pythagoraan lauseella.

$AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

# YT31_R1

Janan $AB$ pituus?

Lasketaan janan pituus Pythagoraan lauseella.

# YT31_R2

Janan $AC$ pituus?

Lasketaan janan pituus Pythagoraan lauseella.

$\begin{align*} BC &= \sqrt{(5 - 4)^2 + (7 - 0)^2} \\ BC &= \sqrt{1^2 + 7^2} \\ BC &= \sqrt{50} \end{align*}$

# YT31_R3

Mikä on pisin sivu?

Tutkitaan vielä Pythagoraan lauseella, muodostavatko janat , ja suorakulmaisen kolmion.

$\begin{align*} AB^2 + AC^2 &= BC^2 \\ (\sqrt{5})^2 + (\sqrt{45})^2 &= (\sqrt{50})^2 \\ 5 + 45 &= 50 \\ 50 &= 50 \end{align*}$

Koska kahden lyhyemmän sivun pituuksien neliöiden summa on pisimmän sivun neliön summa, on janoista muodostuva kolmio suorakulmainen ja pisteet sijaitsevat suorakulmaisen kolmion kärjissä.

# YT31_T2

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa3

matikkamatskut.com/maa3

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA3-sisältöjä peilata tehtyyn toteutukseen.

TAU/MAA3

Yo-tehtäviä harjoiteltaviksi

Kolmio

K99/3, S99/1, K00/5, S00/4, K04/6, S04/2, S05/2, K06/3, S07/6, K10/3a, K12/3, K16/6-7, S17/5, S18/8, S19/1

Sini- ja kosinilause

S02/6, S06/7, K08/8, K11/7, S12/4b, S13/6, K19/12

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA4 - Vektorit

Opetussuunnitelman keskeiset sisällöt

vektoreiden perusominaisuudet
vektoreiden yhteen- ja vähennyslasku ja vektorin kertominen luvulla
koordinaatiston vektoreiden skalaaritulo
yhtälöryhmän ratkaiseminen
suorat ja tasot avaruudessa

H5P-peli 4.1

Vektorit esitetään usein (x,y) -koordinaatistossa ns. $(\overline{i},\overline{j})$ -muodossa, missä $\overline{i}$ ja ovat -tason kantavektorit.

Vektorin $\overline{i}$ suunta on -akselin positiivinen suunta ja pituus 1.

Vektorin $\overline{j}$ suunta on -akselin positiivinen suunta ja pituus 1.

Kokeile alla olevan appletin avulla, miten mikä tahansa -tason vektori voidaan lausua :n ja :n summana.

Huomaa, että GeoGebra ei näytä algebra-ikkunassa summaa, vaan $\overline{i}$ :n ja $\overline{j}$ :n kertoimet ovat allekkain matriisimuodossa siten, että $\overline{i}$ :n kerroin on ylempi luku ja $\overline{j}$ :n kerroin on alempi luku.

Tason vektori kantavektoreiden summana

H5P-peli 4.2

Piste-paikkavektori-peli.

H5P-peli 4.3

Vektorit ovat $\begin{align*} \overline{a} &= 2\overline{i} - 3\overline{j} + \overline{k} \\ \overline{b} &= 4\overline{i} + \overline{k} \\ \overline{c} &= 5\overline{k} - \overline{j} \\ \overline{d} &= \overline{i} - 2\overline{j} - 8\overline{k} \end{align*}$

Pistetulopeli.

Videoesimerkki 4.1

Olkoon A = (3,4) , B = (4,0) ja C = (-1;-1,5) .

Muodosta vektorin ja .
Laske niiden erotus ja kaikkien kolmen pituudet.
Muodosta paikkavektori .
Muodosta yksikkövektori .
Laske pistetulo $AB \cdot AC$ .

# VE41

Videoesimerkin 4.1 ratkaisu

Videoesimerkki 4.2

Onko piste C = (-9,-21,26) pisteiden A = (3,3,2) ja B = (4,5,0) kautta kulkevalla suoralla?

# VE42

Videoesimerkin 4.2 ratkaisu - osa 1

Videoesimerkin 4.2 ratkaisu - osa 2

Videoesimerkki 4.3

Suorakulmaisen särmiön sivut ovat pituudeltaan 1 : 2 : 3 suhteessa toisiina. Laske avaruuslävistäjien välinen kulma.

Pistetulo ja ijk-vektorit

Yo-tehtävä 4.1

Harjoitellaan kevään 2019 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Määritä sellainen vektori $\overline{c} = a\overline{i} + b\overline{j}$ , että $\overline{c} \cdot (\overline{i} + \overline{j}) = 2$ ja $\overline{c} \cdot (\overline{i} - \overline{j}) = 3$ .

Ratkaisu

# YT41_T1

Lasketaan ensimmäinen pistetulo.

$\overline{c} \cdot (\overline{i} + \overline{j}) = (a\overline{i} + b\overline{j}) \cdot (\overline{i} + \overline{j})$

# YT41_R1

Valitse edellä olevan ensimmäisen pistetulon oikea ratkaisu.

Lasketaan toinen pistetulo.

$\overline{c} \cdot (\overline{i} - \overline{j}) = (a\overline{i} + b\overline{j}) \cdot (\overline{i} - \overline{j})$

# YT41_R2

Valitse edellä olevan toisen pistetulon oikea ratkaisu.

Pistetulot on nyt tehty.

# YT41_T2

Muodostetaan ja ratkaistaan yhtälöpari.

\[\begin{cases} a + b &= 2 \\ a - b &= 3 \end{cases}\]

# YT41_T3

Lasketaan puolittain yhteen ja ratkaistaan .

$\begin{align*} 2a &= 5 \\ a &= \frac{5}{2} \end{align*}$

Ratkaistaan $b = 2 - \dfrac{5}{2} = -\dfrac{1}{2}$ .

# YT41_T4

Kysytty vektori on siis $\overline{c} = \dfrac{5}{2}\overline{i} - \dfrac{1}{2}\overline{j}$ .

Jälkipohdinta

# YT41_T5

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa4

matikkamatskut.com/maa4

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA4-sisältöjä peilata tehtyyn toteutukseen.

TAU/MAA4

Yo-tehtäviä harjoiteltaviksi

Vektorit i, j ja k sekä pistetulo

K01/3, S02/5, S03/4, K04/4, S04/4, S05/3, S06/4, K08/6, S09/5, K10/5, K11/8, K12/3, K13/2b, S13/3+5, S14/4, K16/3a, K17/3, K18/10, S18/5, K19/2, S19/3

Suora ja taso

S01/7, K07/4, K03/7, K06/6, K09/8, S10/3a, K12/4, K13/7, K14/8, K16/8, S17/11

Yhtälöryhmä

K11/4, S10/4

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA5 - Analyyttinen geometria

Opetussuunnitelman keskeiset sisällöt

pistejoukon yhtälö
suoran, ympyrän ja paraabelin yhtälöt
itseisarvoyhtälön ja epäyhtälön ratkaiseminen
pisteen etäisyys suorasta

H5P-peli 5.1

Yhdistä oikea kuvaaja ja yhtälö

H5P-peli 5.2

Ympyrän yhtälö keskipistemuodossa

Videoesimerkki 5.1

Suora kulkee pisteen (-1,2) kautta ja on kohtisuorassa suoraa 3x + 7y + 17 = 0 vastaan. Määritä suoran yhtälö.

# VE51

Videoesimerkin 5.1 ratkaisu

Videoesimerkki 5.2

Millä vakion arvolla yhtälö x^2 + y^2 + 12x - 8y = 0 esittää ympyrää?

# VE52

Videoesimerkin 5.2 ratkaisu

Videoesimerkki 5.3

Paraabelin akseli on -akselin suuntainen, ja paraabeli kulkee pisteiden (-3,0) , (-2,-2) ja (1,4) kautta. Määritä paraabelin yhtälö.

# VE53

Videoesimerkin 5.3 ratkaisu

Yo-tehtävä 5.1

Harjoitellaan kevään 2017 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Tarkastellaan ensimmäisen asteen polynomifunktiota p(x) = cx + d , jolle p(4) = 1 ja p(7) = 3 . Ratkaise yhtälö p(x) = 0 .

Ratkaisu

# YT51_T1

Lasketaan funktion arvo p(4) .

$p(4) = c \cdot 4 + d = 4c + d = 1$

Lasketaan funktion arvo p(7) .

$p(7) = c \cdot 7 + d = 7c + d = 3$

# YT51_T2

Muodostetaan ja ratkaistaan yhtälöpari.

\[\begin{cases} 4c + d &= 1 \\ 7c + d &= 3 \end{cases}\]

# YT51_T3

Kerrotaan ylempi yhtälö luvulla ja lasketaan yhtälöt puolittain yhteen.

3c = 2

Sijoitetaan saatu arvo $c = \frac{2}{3}$ ensimmäiseen yhtälöön.

$d = 1 - 4 \cdot \frac{2}{3} = -\frac{5}{3}$

# YT51_T4

Muodostetaan ja ratkaistaan yhtälö.

$\begin{align*} p(x) = cx + d &= 0 \\ \frac{2}{3}x - \frac{5}{3} &= 0 \\ \frac{2}{3}x &= \frac{5}{3} \\ x &= \frac{5}{3} \cdot \frac{3}{2} \\ x &= \frac{5}{2} \end{align*}$

Yhtälö toteutuu, kun $x = \frac{5}{2}$ .

Jälkipohdinta

# YT51_T5

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa5

matikkamatskut.com/maa5

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA5-sisältöjä peilata tehtyyn toteutukseen.

TAU/MAA4

Yo-tehtäviä harjoiteltaviksi

Suora

K02/1, S08/1c, K11/2b, S11/3c, K13/1c, S14/2a, S15/2a, S18/6, K17/1c

Ympyrä

K03/11, K04/8, K06/7, K14/5, S14/10, S15/2b, S15/5, K18/5

Paraabeli

K08/7, K10/8, K11/4, S15/2c

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA6 - Derivaatta

Opetussuunnitelman keskeiset sisällöt

rationaaliyhtälö ja -epäyhtälö
funktion raja-arvo, jatkuvuus ja derivaatta
polynomifunktion, funktioiden tulon ja osamäärän derivoiminen
polynomifunktion kulun tutkiminen ja ääriarvojen määrittäminen

H5P-peli 6.1

Etsi funktio-derivaatta-pari.

H5P-peli 6.2

Kaavapeli

H5P-peli 6.3

Funktion f(x) raja-arvo kohdassa x = a on olemassa, jos toispuoleiset raja-arvot ovat olemassa ja yhtä suuret. Funktio f(x) on jatkuva kohdassa x = a , jos funktion raja-arvo kohdassa x = a on yhtä kuin f(a) .

Alla olevan GeoGebra-appletin syöttäkenttään voit kirjoittaa funktion muodossa $f(x) = \ldots$

a) Tutki, onko funktiolla f(x) = x^2 - 2x + 1 vasemman- ja oikeanpuoleiset raja-arvot kohdassa x = 3 ja ovatko ne samat? Jos ovat, niin funktiolla on raja-arvo kohdassa x = 3 .

b) Tutki, onko funktiolla $f(x) = \dfrac{x}{x + 1}$ raja-arvoa kohdassa x = -1 . Muuta x_0 :n arvo miinus yhdeksi syöttökentän komennolla x_0 = -1 .

c) Tutki, onko funktiolla f(x) = abs(x + 1) raja-arvoa kohdassa x = -1 . Muuta x_0 :n arvo miinus yhdeksi syöttökentän komennolla x_0 = -1 .

Geogebra-appletti

Videoesimerkki 6.1

Määritä funktion $f(x) = \dfrac{1}{x + 1}$ derivaatta kohdassa 1 erotusosamäärän raja-arvon avulla.

# VE61

Videoesimerkin 6.1 ratkaisu

Videoesimerkki 6.2

Mikä paraabelin y = x^2 piste on lähinnä pistettä (0,3) ?

# VE62

Videoesimerkin 6.2 ratkaisu

Videoesimerkki 6.3

Huonetta valaisee kaksi valonlähdettä, valaistusteholtaan 1 ja 4 yksikköä. Valonlähteiden etäisyys toisistaan on 8,0 metriä. Määritä valonlähteiden väliseltä linjalta kohta, jossa valaistusteho on kaikkein heikoin. Valaistusteho on kääntäen verrannollinen valonlähteestä mitatun etäisyyden neliöön.

# VE63

Videoesimerkin 6.3 ratkaisu

Yo-tehtävä 6.1

Harjoitellaan kevään 2018 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

a) Anna esimerkki rationaalifunktiosta f(x) , jolle epäyhtälö $f(x) \geq 2$ toteutuu täsmälleen silloin, kun $-1 \leq x \leq 0$ tai $1 \leq x \leq 2$ .

b) Anna esimerkki funktiosta $g(x) \geq 0$ , joka on määritelty kaikilla reaaliluvuilla ja jonka derivaatalla on täsmälleen kaksi nollakohtaa.

Ratkaisu

# YT61_T1

a) Rationaalifunktiot ymmärretään tässä siten, että siihen kuuluvat myös polynomifunktiotkin.

# YT61_T2

Tehtävänannon perusteella kysytyn rationaalifunktion nollakohdat ovat , , ja .

# YT61_T3

Kysytty rationaalilauseke voi olla esimerkiksi muotoa $(x - (-1)) \cdot (x - 0) \cdot (x - 1) \cdot (x - 2)$ .

Sievennettynä edellinen lauseke on muotoa x(x + 1)(x - 1)(x - 2) + 2 .

Edellä oleva lauseke on neljännen asteen polynomilauseke, joka muistuttaa W-kirjainta ja joka aukeaa ylöspäin.

# YT61_T4

Koska tehtävässä funktio on annetuilla väleillä lukua 2 suurempi, pitää polynomifunktio kertoa luvulla , jotta sen aukeamissuunta muuttuisi.

Kirjoitetaan kysytyn funktion mahdollinen lauseke.

-x(x + 1)(x - 1)(x - 2)

Muodostetaan edellisestä rationaalilausekkeesta epäyhtälö.

$-x(x + 1)(x - 1)(x - 2) \geq 0$

# YT61_T5

Rationaalilausekkeen pitää olla yhtä suuri tai suurempi kuin luku 2, joten lisätään edellisen epäyhtälön molemmille puolille luku 2.

$-x(x + 1)(x - 1)(x - 2) + 2 \geq 2$

Pyydetty rationaalifunktio on siis f(x) = -x(x + 1)(x - 1)(x - 2) + 2 , koska sille on voimassa ehto $f(x) \geq 2$ , kun $-1 \leq x \leq 0$ tai $1 \leq x \leq 2$ .

Edellistä asiaa voi kvalitatiivisesti tutkia esim. sopivien testipisteiden avulla.

Jälkipohdinta

# YT61_T6

b) Etsitään polynomifunktio, jolla on mimini ja terassikohta.

# YT61_T7

Mahdollisen derivaattafunktion nollakohdat voivat olla esimerkiksi x = 0 ja x = 1 . Huomioidaan vielä, että derivaattafunktio saa negatiivisia arvoja vain esimerkiksi toista nollakohtaa pienemmillä arvoilla.

# YT61_T8

Kirjoitetaan mahdollinen derivaattafunktio edellä valittujen nollakohtien avulla.

g'(x) = x(x-1)^2

Muodostetaan derivaattafunktiosta vielä polynomilauseke.

g'(x) = x(x - 1)^2 = x(x^2 - 2x + 1) = x^3 - 2x^2 + x

# YT61_T9

Kysytty funktio saadaan MAA6-kurssin tiedoin päättelemällä alkuperäinen funktio, josta derivointisäännöillä saadaan muodostettua kyseinen derivaattafunktio.

$g(x) = \frac{1}{4}x^4 - \frac{2}{3}x^3 + \frac{1}{2}x^2$

# YT61_T10

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa6

matikkamatskut.com/maa6

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA6-sisältöjä peilata tehtyihin toteutuksiin.

TAU/MAA2 TAU/MAA6

Yo-tehtäviä harjoiteltaviksi

Derivaatan määritelmä ja raja-arvo

S10/1c, K16/4, S16/9.2

Polynomimifunktio

K03/8, K05/5, S06/11, S08/10, K09/7, S12/5, S13/4, K13/5, K14/2+3, S14/6, S15/7, K16/11, S16/4, S17/ 1a+6, K18/1b+11, S19/6

Rationaalifunktio

K02/10, S05/7, K06/10, S16/2b, K18/11, S18/2a, K19/4

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA7 - Trigonometriset funktiot

Opetussuunnitelman keskeiset sisällöt

suunnattu kulma ja radiaani
trigonometriset funktiot symmetria- ja jaksollisuusominaisuuksineen
trigonometristen yhtälöiden ratkaiseminen
yhdistetyn funktion derivaatta
trigonometristen funktioiden derivaatat

H5P-peli 7.1

Etsi funktio-derivaatta-pari.

H5P-peli 7.2

a) Etsi liukusäätimillä sellaiset arvot että punainen kuvaaja f(x) = A sin(Bx + C) osuu täysin sinisen kuvaajan g(x) = a cos(bx + c) päälle.

b) Etsi toinen A, B, C yhdistelmä, joka tuottaa saman kuvaajan.

Trigonometriaan liittyvä Geogebra-appletti.

Videoesimerkki 7.1

Määrittele yksikköympyrän avulla trigonometriset funktiot $\sin(x)$ , $\cos(x)$ ja $\tan(x)$ .

# VE71

Videoesimerkin 7.1 ratkaisu

Videoesimerkki 7.2

Ratkaise

GeoGebralla $2\cos(x) - 1 = 0$
GeoGebralla $2\sin(2x+1) = \sqrt{3}$
kaavaeditorilla $\sin(x) - \cos(x) = 0$ .

# VE72

Videoesimerkin 7.2 ratkaisu

Videoesimerkki 7.3

Syksyn 2000 yo-koetehtävä.

Ympyrän muotoisen suon halkaisija on 1 km. Suunnistaja haluaa päästä mahdollisimman lyhyessä ajassa kohdasta kohtaan . Miten hänen on valittava reittinsä, jos hän juoksee kovalla maalla 10 km/h ja suolla 5 km/h?

# VE73

Videoesimerkin 7.3 ratkaisu - osa 1

Videoesimerkin 7.3 ratkaisu - osa 2

Yo-tehtävä 7.1

Harjoitellaan kevään 2018 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Määritä funktion $f(x) = \sin(x) + \sqrt{3}\cos(x)$ suurin ja pienin arvo välillä $0 \leq x \leq 2\pi$ .

Ratkaisu

# YT71_T1

# YT71_R1

md:Muodosta funktiosta $f(x) = \sin(x) + \sqrt{3}\cos(x)$ derivaattafunktio.

Annettu funktio on jatkuva annetulla välillä. Se saa ääriarvonsa suljetun välin päätepisteissä tai välille kuuluvassa derivaattafunktion nollakohdassa.

# YT71_T2

Muodostetaan funktiosta derivaattafunktio.

$f'(x) = \cos(x) - \sqrt{3}\sin(x)$

Ratkaistaan derivaattafunktion nollakohdat.

$\begin{align*} f'(x) &= 0 \\ \cos(x) - \sqrt{3}\sin(x) &= 0 \\ \cos(x) &= \sqrt{3}\sin(x) \\ 1 &= \sqrt{3}\tan(x) \\ \tan(x) &= \frac{1}{\sqrt{3}} \end{align*}$

# YT71_T3

Luetaan taulukkokirjasta (MAOL, s. 54), että $\tan(x) = \frac{1}{\sqrt{3}}$ , kun $x = \frac{\pi}{6} + \pi n$ .

Edellisistä annetulle välille $0 \leq x \leq 2\pi$ kuuluvat $\frac{\pi}{6}$ ja $\frac{7\pi}{6}$ .

# YT71_T4

Lasketaan funktion arvot välin päätepisteissä ja derivaattafunktion nollakohdissa.

$\begin{align*} f(x) &= \sin(x) + \sqrt{3}\cos(x) \\ f(0) &= \sin(0) + \sqrt{3}\cos(0) = \sqrt{3} \\ f(2\pi) &= \sin(2\pi) + \sqrt{3}\cos(2\pi) = \sqrt{3} \\ f(\pi/6) &= \sin(\pi/6) + \sqrt{3}\cos(\pi/6) = 2 \\ f(7\pi/6) &= \sin(7\pi/6) + \sqrt{3}\cos(7\pi/6) = -2 \end{align*}$

Huomaa edellä, että laskimessa kulmat ovat radiaaneina.

Valitaan saaduista funktion arvoista ääriarvot, jotka ovat siis $\pm 2$ .

Jälkipohdinta

# YT71_T5

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa7

matikkamatskut.com/maa7

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA7-sisältöjä peilata tehtyihin toteutuksiin.

TAU/MAA5 TAU/MAA6

Yo-tehtäviä harjoiteltaviksi

Trigonometrisiin funktioihin liittyviä tehtäviä

K01/6, S04/8, K08/3b, S09/2c, K10/2b+9, S10/1b+7, S11/10, K12/2d+10, S12/4a, K13/2c+9, K14/12, K15/1, S17/1b+4a, K18/3, S18/4, K19/11, S19/7

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA8 - Juuri- ja logaritmifunktiot

Opetussuunnitelman keskeiset sisällöt

potenssien laskusäännöt
juurifunktiot ja -yhtälöt
eksponenttifunktiot ja -yhtälöt
logaritmifunktiot ja -yhtälöt
juuri-, eksponentti- ja logaritmifunktioiden derivaatat

H5P-peli 8.1

Kertaa logaritmeihin liittyviä kaavoja.

H5P-peli 8.2

Käy läpi syksyn 2016 yo-tehtävävaiheet.

Videoesimerkki 8.1

Ratkaise kevään 1983 yo-tehtävä.

$\left\{ \begin{array}{l} x^{\frac{1}{y}} = 27 \\ \left(\frac{x^2}{3}\right)^y = 3 \end{array} \right.$

# VE81

Videoesimerkin 8.1 ratkaisu

Videoesimerkki 8.2

Derivoi $f(x) = x^{-x}$ , x > 0 ja määritä derivaatan nollakohdat.

# VE82

Videoesimerkin 8.2 ratkaisu

Videoesimerkki 8.3

Ratkaise kevään 1991 yo-tehtävä.

Ratkaise yhtälö $x - \sqrt{43 - 3x} = 11$ .

# VE83

Videoesimerkin 8.3 ratkaisu

Videoesimerkki 8.4

Videon idea Yo-kevät 1991.

Yhtälössä

$\ln y = \frac{x}{2} + 10^5$

kasvaa yhdellä. Kuinka monta prosenttia kasvaa tällöin ?

# VE84

Videoesimerkin 8.4 ratkaisu

Videoesimerkki 8.5

Vanhan, suosta nostetun puunäytteen C-14-aktiivisuus on 32 prosenttia vastaavan elävän puun C-14-aktiivisuudesta. Kuinka vanha näyte on? C-14-isotoopin puoliintumisaika on noin 5700 a.

Lue myös https://fi.wikipedia.org/wiki/Radiohiiliajoitus

# VE85

Videoesimerkin 8.5 ratkaisu

Videoesimerkki 8.6

Ratkaise epäyhtälö $\log_2(x^2 - 1) \leq 3$ .

# VE86

Videoesimerkin 8.6 ratkaisu

Yo-tehtävä 8.1

Harjoitellaan syksyn 2018 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Aseta luvut $\sqrt{2}$ , $\sqrt[3]{3}$ ja $\sqrt[5]{5}$ suuruusjärjestykseen ja perustele vastauksesi.

Ratkaisu

# YT81_T1

Koska lukujen suuruuseroa ei voi ilman teknisiä apuvälineitä tietää, tutkitaan ja perustellaan ensin lukujen $\sqrt{2}$ ja $\sqrt[3]{3}$ suuruusero.

# YT81_T2

Juuret tarkoittavat murtolukupotensseja, joten korotetaan molemmat luvut sellaiseen yhtä korkeaan potenssiin, joka hävittää kyseiset potenssit.

$(\sqrt[2]{2})^6 = 2^3 = 8 < (\sqrt[3]{3})^6 = 3^2 = 9$

Luku $\sqrt{2} < \sqrt[3]{3}$ .

Tutkitaan seuraavaksi lukujen $\sqrt{2}$ ja $\sqrt[5]{5}$ suuruuseroa. Työjärjestys ei välttämättä ratkaise lopullista suuruuseroa, ja kolmantena vertailuna voi olla vielä luvut $\sqrt[3]{3}$ ja $\sqrt[5]{5}$ .

$(\sqrt[2]{2})^{10} = 2^5 = 32 > (\sqrt[5]{5})^{10} = 5^2 = 25$

Luku $\sqrt[5]{5} < \sqrt{2}$ .

Kolmatta vertailua ei siis tarvitse tehdä.

# YT81_T3

Lopullinen suuruusjärjestys on siten $\sqrt[5]{5} < \sqrt{2} < \sqrt[3]{3}$ .

Jälkipohdinta

# YT81_T4

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa8

matikkamatskut.com/maa8

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA8-sisältöjä peilata tehtyihin toteutuksiin.

TAU/MAA2 TAU/MAA5

Yo-tehtäviä harjoiteltaviksi

Juuri- ja logaritmifunktioihin liittyviä tehtäviä

S00/2, K03/5a, K08/2a+9+10, S08/7, K09/2b+5, S09/1c+2b+3a, K10/1b+2c, K11/2c+3ab, S11/3a, K12/2bcf+5+8, S12/2c+10, K13/3+5, S13/9, S14/2c+9+11, K15/2+3+7, K16/2c, S16/3+10, K17/4+10, S17/1c+4b+8, S18/2b+7, K19/3, S19/4

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA9 - Integraalilaskenta

Opetussuunnitelman keskeiset sisällöt

integraalifunktio
alkeisfunktioiden integraalifunktiot
määrätty integraali
pinta-alan ja tilavuuden laskeminen

H5P-peli 9.1

Yo-tehtäväratkaisun askeleet.

H5P-peli 9.2

Tutki GeoGebra-appletin avulla määrätyn integraalin käyttäytymistä.

Videoesimerkki 9.1

Olkoon f(x) = 2x + 1 . Määritä se f(x) :n integraalifunktio, joka kulkee pisteen (0,1) kautta.

# VE91

Videoesimerkin 9.1 ratkaisu

Videoesimerkki 9.2

Harjoittele yhdistetyn funktion integrointia.

a) $\int 6x^2 \cdot (x^3 + 1)^{10} dx$

b) $\int \dfrac{5x}{4x^2 + 1} dx$

# VE92

Videoesimerkin 9.2 ratkaisu

Videoesimerkki 9.3

Harjoittele kahden käyrän y = sin(x) ja y = cos(x) rajaaman pinta-alan laskemista.

a) Laske käyrien leikkausten ja -akselin rajaama pinta-ala, kun $0 \leq x \leq \pi/2$ .

b) Laske käyrien leikkausten ja -akselin rajaama pinta-ala, kun $0 \leq x \leq \pi/4$ .

# VE93

Videoesimerkin 9.3 ratkaisu

Videoesimerkki 9.4

Kerrataan ensin määrätty integraali.

Harjoitellaan toiseksi alla olevan määrätyn integraalin ratkaisu.

$\int_1^2 \left(\frac{1}{2}x^2 + xe^{x^2}\right) dx$

# VE94

Videoesimerkin 9.4 ratkaisu

Yo-tehtävä 9.1

Harjoitellaan syksyn 2002 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Nykytaiteen museorakennuksen pohja on ympyrä, jonka halkaisija on 19,7 metriä. Jos rakennus leikataan pohjaympyrän tietyn halkaisijan suuntaisella pystysuoralla tasolla, leikkauskuvio on aina suorakulmio, jonka korkeus on puolet kannasta. Määritä rakennuksen tilavuus.

$\begin{tikzpicture}[scale=2, thin] % HENRI JAAKKOLA % Pohjaympyra \foreach \k in { 0.5,1,...,360 } { \pgfmathparse{cos(\k)} \tikzmath{ real \x; \x = \pgfmathresult; } \pgfmathparse{sin(\k)} \tikzmath{ real \z; \z = \pgfmathresult; } \fill [red] (\x,0,\z) circle (0.25pt); } % Rakennus \foreach \k in { 5,10,...,175 } { \pgfmathparse{cos(\k)} \tikzmath{ real \x; \x = \pgfmathresult; } \pgfmathparse{sin(\k)} \tikzmath{ real \z; \z = \pgfmathresult; } \draw (\x,0,\z) -- ++(0,\z,0) -- ++(0,0,-2*\z) -- ++(0,-1*\z,0); } % Silhuetti \foreach \k in { 0.5,1,...,180 } { \pgfmathparse{cos(\k)} \tikzmath{ real \x; \x = \pgfmathresult; } \pgfmathparse{sin(\k)} \tikzmath{ real \z; \z = \pgfmathresult; } \fill (\x,\z,\z) circle (0.15pt); \fill (\x,\z,-1*\z) circle (0.15pt); } \end{tikzpicture}$

Ratkaisu

# YT91_T1

Olkoon pohjaympyrän keskipiste, pystysuoran tason ja pohjaympyrän leikkaus sekä janan keskipiste.

Piirretään apukuva ja lisätään siihen vielä pohjaympyrän säde sekä mitat x = CO sekä $d_x = \sqrt{r^2 - x^2}$ , $0 \leq x \leq r$ .

$\begin{tikzpicture}[thick, font=\footnotesize] % HENRI JAAKKOLA % Pohjaympyra ja keskipiste \draw [red] (0,0) circle (2); \fill (0,0) circle (1pt); \node at (0,0) [left] {$O$}; % Sade, sekantti, jana ja mitat \draw [semithick] (0,0) -- node [sloped, above] {$r$} (60:2) -- node [right, pos=0.25] {$d_x$} (-60:2); \draw [semithick] (0,0) -- node [below] {$x$} (1,0); \fill (60:2) circle (1pt); \fill (-60:2) circle (1pt); \fill (1,0) circle (1pt); \node at (60:2) [above right] {$A$}; \node at (-60:2) [below right] {$B$}; \node at (1,0) [right] {$C$}; % Suora kulma \draw [thin] (0.65,0) -- ++(0,0.35) -- ++(0.35,0); \end{tikzpicture}$

Kirjoitetaan nyt tason ja rakennuksen leikkauskuvion pinta-ala.

A_x = 2d_x d_ x = 2(r^2 - x^2)

Kirjoitetaan rakennuksen tilavuus.

$\begin{align*} V &= 2 \int_0^r A_x dx \\ V &= 4 \int_0^r (r^2 - x^2) dx \\ V &= 4 \left[r^2 x - \frac{1}{3} x^3\right]_0^r \\ V &= 4r^3 - \frac{4}{3}r^3 \\ V &= \frac{8}{3} r^3 \end{align*}$

Lasketaan lopuksi vielä rakennuksen tilavuus, kun sen halkaisija $2r = 19{,}7\;\text{m}$ .

$V = \frac{8}{3} \cdot \left(\frac{19{,}7\;\text{m}}{2}\right)^3 = 2\,548{,}457667\;\text{m}^3 \approx 2\,550\;\text{m}^3$

Vastaus

Rakennuksen tilavuus on noin $2\,550\;\text{m}^3$ .

Jälkipohdinta

# YT91_T4

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa9

matikkamatskut.com/maa9

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA9-sisältöjä peilata tehtyyn toteutukseen.

TAU/MAA7

Yo-tehtäviä harjoiteltaviksi

Integraalilaskentaan liittyviä tehtäviä

S02/12, K04/10, K08/3a+7+14c, S08/2b+3a+6, K09/2ac+9, S09/3b+10+14, K10/2a, S10/2b+3b, K11/3c+10, S11/ 4, K12/2e+7, S12/3a+6, K13/8, S13/2b+7, K14/3a+10+11, K16/3b+12, S16/2c, S17/9+13, K18/1c, S18/3+9, K19/5, S19/2

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

MAA10 - Todennäköisyys ja tilastot

Opetussuunnitelman keskeiset sisällöt

diskreetti ja jatkuva tilastollinen jakauma
jakauman tunnusluvut
klassinen ja tilastollinen todennäköisyys
kombinatoriikka
todennäköisyyksien laskusäännöt
diskreetti ja jatkuva todennäköisyysjakauma
diskreetin jakauman odotusarvo
normaalijakauma

H5P-peli 10.1

Etsi oikea pari.

H5P-peli 10.2

Ratkaise alla olevat tehtävät GeoGebra-appletin avulla.

a) Etsi kuvion avulla se kohta, jonka vasemmalle puolelle jäävä pinta-ala on 0,885. Siirrä siis a ensin -5:een ja liikuta vain b:tä.

b) Etsi kuvion avulla se kohta, jonka oikealle puolelle jäävä pinta-ala on 0,382. Siirrä siis b ensin 5:een ja liikuta vain a:ta.

c) Etsi a:ta ja b:tä liikuttamalla se y-akselin suhteen symmetrinen väli, jonka ala on 0,500.

d) Makeispussin paino on jakautunut normaalisti keskiarvon ollessa 251 g ja keskihajonnan 12 g.

1 Kuinka monta prosenttia pusseista painaa alle 270 g?

2 Kuinka monta prosenttia pusseista painaa yli 245 g?

3 Kuinka monta prosenttia pusseista painaa 245… 255 g?

Ohje

Muuta tutkittava kohta x normitetun kuvaajan arvoksi z kaavalla z = (x-ka)/s, missä ka = keskiarvo ja s = keskihajonta. Säädä z:n arvo kohdilleen liukusäätimiä liikuttamalla.

Vastaukset

a) x = 1,2

b) x = 0,3

c) noin -1,6-1,6

d) / 1 noin 95 %

d) / 2 noin 69 %

d) / 3 noin 31 %

Videoesimerkki 10.1

Pekan koulumatkalla on kolmet toisistaan riippumattomat liikennevalot, jotka ovat punaisella 75 %, 65 % ja 60 % ajasta. Millä todennäköisyydellä Pekka joutuu koulumatkallaan pysähtymään valoihin vain yhden kerran?

# VE101

Videoesimerkin 10.1 ratkaisu

Videoesimerkki 10.2

Arpajaisissa, jossa arpojen lukumäärä on suuri, 35 % arvoista voittaa. Ostetaan kymmenen arpaa. Millä todennäköisyydellä sadaan vähintään kolme voittoa?

# VE102

Videoesimerkin 10.2 ratkaisu

Videoesimerkki 10.3

Ratkaise kevään 2001 yo-tehtävä.

Tutkimuksessa todettiin, että 200 gramman keksipakkausten massan keskiarvo oli 204 g ja keskihajonta 6 g. Oletetaan, että massa on normaalisti jakautunut. Kuinka monella prosentilla pakkauksista massa oli alle 200 g? Kuinka monella prosentilla pakkauksista massa oli välillä 200 g - 210 g?

# VE103

Videoesimerkin 10.3 ratkaisu

Videoesimerkki 10.4

Kerrataan normaalijakauman käytön perusteet.

Videoesimerkin 10.4 ratkaisu

Videoesimerkki 10.5

a) Seitsemän veljestä menee joka aamu erilaiseen ruokajonoon. Kuinka monta päivää kestää ennen kuin kaikki jonot on käyty läpi?

b) Seitsemästä veljeksestä valitaan kolme niin, että 1. valittu tiskaa astiat, 2. valittu lakaisee lattiat ja 3. valittu pesee pyykit. Kuinka monella tavalla valinta voidaan tehdä?

c) Seitsemästä veljeksestä valitaan kolme veljestä auttamaan peltotöissä. Kuinka monella tavalla valinta voidaan tehdä?

# VE105

Videoesimerkin 10.5 ratkaisu

Yo-tehtävä 10.1

Harjoitellaan kevään 2018 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Lotto-peli alkoi Suomessa vuonna 1971, ja sen sääntöjä on muutettu useita kertoja vuosien varrella. Viimeisin sääntöuudistus tehtiin vuoden 2016 lopussa.

Ennen uudistusta arvottiin 7 varsinaista ja 2 lisänumeroa 39 numerosta. Uudistuksen jälkeen arvotaan 7 varsinaista ja vain 1 lisänumero 40 numerosta. Seuraavassa loton pelaaja täyttää yhden lottorivin eli käytännössä valitsee 7 numeroa.

Laske tuloksen ''6 + 1'' todennäköisyys ennen uudistusta ja sen jälkeen. Tässä ''6 + 1'' tarkoittaa tulosta, jossa kuusi varsinaista ja yksi lisänumero oikein.

Ratkaisu

# YT101_T1

Lasketaan todennäköisyys ennen sääntöuudistusta.

# YT101_R1

Kuusi oikeaa seitsemästä?

Kuusi oikeaa numeroa voidaan saada seitsemällä eri tavalla. Vastaavasti kahdesta lisänumerosta yksi oikea voidaan saada kahdella tavalla.

Kirjoitetaan ja lasketaan erilaisten lotto-rivien lukumäärä, kun arvotaan 7 numeroa.

$\binom{39}{7} = \frac{39!}{7!(39 - 7)!} = \frac{39 \cdot 38 \cdot 37 \cdot 36 \cdot 35 \cdot 34 \cdot 33}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 15\,380\,937$

Nykyisessä sähköisen matematiikan kokeen A-osassa tekniset työvälineet ovat poissa käytössä, mutta SpeedCrunch-laskin on silti käytettävissä. Edellisen laskun ja sen vastauksen saa erittäin helposti seuraavalla komennolla.

ncr(39;7) = 15380937

# YT101_R2

Erilaisten "6 + 1" -rivien lukumäärä?

Yhteensä erilaisia toivottuja ''6 + 1'' ratkaisuja on $\binom{7}{6} \cdot \binom{2}{1} = 7 \cdot 2 = 14$ .

Lasketaan ''6 + 1'' tilanteen todennäköisyys.

$P = \frac{\binom{7}{6} \cdot \binom{2}{1}}{\binom{39}{7}} = 9{,}102176 \cdot 10^{-7} \approx 9{,}10 \cdot 10^{-7}$

Kirjoitetaan edellinen vielä SpeedCrunch-laskimella.

14 / ncr(39;7) = 0,00000091021762848388

# YT101_T2

Lasketaan todennäköisyys sääntöuudistuksen jälkeen, kun kuusi oikeaa numeroa voidaan valita seitsemällä eri tavalla ja yksi lisänumero yhdellä eri tavalla.

Yhteensä erilaisia toivottuja ''6 + 1'' ratkaisuja on $\binom{7}{6} \cdot \binom{1}{1} = 7 \cdot 1 = 7$ .

Lasketaan todennäköisyys suoraan SpeedCrunch-laskimella.

7 / ncr(40;7) = 0,0000003754647717496

Kysytty todennäköisyys on siis noin $3{,}75 \cdot 10^{-7}$ .

Jälkipohdinta

# YT101_T4

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

omaantahtiin.com/pitkamatikka/maa10

matikkamatskut.com/maa10

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi lisätä ja nykyisiä MAA10-sisältöjä peilata tehtyyn toteutukseen.

TAU/MAA8

Yo-tehtäviä harjoiteltaviksi

Todennäköisyyden peruskaavat

K03/4, S07/8, K08/5, S08/8, K09/6, K10/6, S10/6, K11/6, K13/6, S13/8, S17/7, K18/7, S18/12, K19/6, S19/7

Odotusarvo

S09/7, S11/8, K12/6, S12/8, K14/7, S15/6, K16/5

Normaalijakauma

S14/7, K15/6

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

LOPS2021 --- MAA9

LOPS2021-opetussuunnitelmaluonnoksen keskeiset sisällöt

aritmeettinen ja geometrinen lukujono ja niiden summat
korkolaskut: koronkorko, talletukset ja lainat
taloudellisiin tilanteisiin soveltuvia matemaattisia malleja, joissa hyödynnetään lukujonoja ja summia

GeoGebra-appletti LOPS2021 - 9.1

Diskonttausharjoitus

Harjoittele ja tutkit GeoGebra-appletin avulla seuraavia tehtäviä.

a) Kuinka paljon tilille pitää tallettaa vuoden 2019 alussa, jotta tilillä olisi vuoden 2030 lopussa 25 000 €? Tilin vuosikorkokanta on 2,7 %.

b) Maansiirtoyrittäjä aikoo hankkia kaivinkoneen. Hän saa tarvitsemalleen lainalle kaksi rahoitusvaihtoehtoa.

Hän maksaa heti 40 000 € ja kahden vuoden kuluttua 60 000 €.
Hän maksaa heti 30 000 €, vuoden kuluttua 30 000 € ja kahden vuoden kuluttua 40 000 €.

Kumpi vaihtoehto on yrittäjän kannalta halvempi, kun vuosikorkokanta on 5,00 %.

c) Vastaa, miten tällä appletilla lasketaan koronkorkolaskuja? Laske 5 000 €:n suuruisen talletuksen arvo 12 vuoden kuluttua, kun tilin vuosikorkokanta on 1,25 %.

Videoesimerkki LOPS2021 - 9.1

Määritä KHI:n avulla inflaatio 2008-2018.

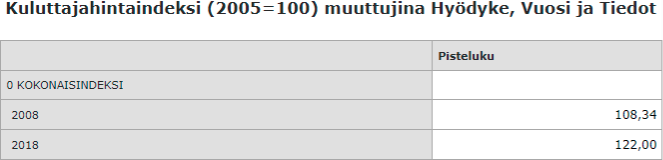
Tiedot löytyvät Tilastokeskuksen sivuilta.

stat.fi

# LOPS2021VE1

Videoesimerkin LOPS2021-9.1 ratkaisu

Videoesimerkki LOPS2021 - 9.2

Matti ja Maija ottavat 50 000 €:n asuntolainan neljän vuoden maksuajalla, korkokanta on 1,8 %. Lainaa lyhennetään joka kuukausi. Laske

a) tasaerän (annuiteetin) suuruus

b) tasalyhennyslainan erät.

c) Vertaa maksutapojen kokonaiskustannuksia toisiinsa.

# LOPS2021VE2

Videoesimerkin LOPS2021-9.2 ratkaisu - osa 1

Videoesimerkin LOPS2021-9.2 ratkaisu - osa 2

Videoesimerkki LOPS2021 - 9.3

Ratkaise talousmatematiikan termeistä K(n) , , ja symbolisesti GeoGebralla. Käytä apunasi MAOL-taulukkokirjan s. 22.

# LOPS2021VE3

Videoesimerkin LOPS2021-9.3 ratkaisu

Tehtäväesimerkki LOPS2021-9.1

Tasaerälyhenteinen asuntolaina on 141 600 €, laina-aika on kymmenen vuotta ja lainan korkokanta kokonaisuudessaan on 2,28 %. Lainaa lyhennetään kuukausittain. Laske

a) lainan tasaerän suuruus

b) ensimmäisen lyhennyksen suuruus

c) kokonaisuudessaan maksettujen korkojen summa

d) lainan määrä kahden vuoden jälkeen.

Ratkaisu

# LOPS2021T1_1

a) Lasketaan lainan kuukausikorko.

$\frac{2{,}28\;\%}{12} = 0{,}19\;\%$

Lasketaan tasaerän eli annuiteetin suuruus, kun lainapääoma $K = 141\,600\;\text{\texteuro}$ , korkotekijä q = 1,0019 ja maksukertojen lukumäärä n = 120 .

$\begin{align*} A &= Kq^n \frac{1 - q}{1 - q^n} \\ A &= 141\,600\;\text{\texteuro} \cdot 1{,}0019^{120} \cdot \frac{1 - 1{,}0019}{1 - 1{,}0019^{120}} \\ A &= 1\,320{,}743144538\;\text{\texteuro} \\ A &\approx 1\,320{,}74\;\text{\texteuro} \end{align*}$

b) Lasketaan ensimmäisen lyhennyksen suuruus ensimmäisen tasaerän avulla, kun siinä maksetaan korkoa koko lainamäärästä.

$\begin{align*} 1\,320{,}743144538\;\text{\texteuro} - 0{,}0019 \cdot 141\,600\;\text{\texteuro} &= 1\,051{,}703144538\;\text{\texteuro} \\ &\approx 1\,051{,}70\;\text{\texteuro} \end{align*}$

c) Lasketaan tasaerien ja lainan avulla maksettujen korkojen kokonaissumma.

$\begin{align*} 120 \cdot 1\,320{,}743144538\;\text{\texteuro} - 141\,600\;\text{\texteuro} &= 16\,889{,}177344545\;\text{\texteuro} \\ &\approx 16\,889{,}18\;\text{\texteuro} \end{align*}$

d) Lasketaan lainan määrä kahden vuoden kuluttua, kun lainan lyhennyksiä on tehty $2 \cdot 12 = 24$ .

$\begin{align*} V_k &= Kq^k - A \frac{1 - q^k}{1 - q} \\ V_{24} &= 141\,600\;\text{\texteuro} \cdot 1{,}0019^{24} - 1\,320{,}743144538\;\text{\texteuro} \cdot \frac{1 - 1{,}0019^{24}}{1 - 1{,}0019} \\ V_{24} &= 115\,799{,}849747698\;\text{\texteuro} \\ V_{24} &\approx 115\,799{,}85\;\text{\texteuro} \end{align*}$

Jälkipohdinta

# LOPS2021T1_4

Yo-tehtävä LOPS2021 - 9.1

Harjoitellaan syksyn 2019 yo-koetehtävän ratkaisu ilman teknisiä apuvälineitä.

Vaikka aineisto on annettu sähköisesti, ei tehtävän ratkaisussa tarvita tavallista nelilaskinta monimutkaisempaa välinettä.

Tehtäväratkaisu antaa valmiuksia matematiikan yo-kokeen A-osaan, jossa ei ole käytössä teknisiä apuvälineitä.

Tehtävänanto

Aineistossa 7.A on Helsingin pörssin kolmen eri osakkeen osakekurssit, joiden mukaisin hinnoin Roope osti ja myi osakkeita. Hän ostaa 1.2.2018 klo 14.00 osaketta B yhteensä 1 000 eurolla. Hän vaihtaa 2.2.2018 klo 10.00 kaiken osakkeeseen C, ja samana päivänä klo 18.00 hän vaihtaa edelleen kaiken osakkeeseen A. Hän myy kaiken 3.2.2018 klo 16.00. Jokaisesta osto- ja myyntitoimeksiannosta Roope maksaa 4,00 euroa välityspalkkiota. Vaihdon yhteydessä tapahtuu sekä myynti- että ostotoimeksianto. Kuinka paljon Roopella on rahaa osakkeet myytyään?

Aineisto Ylen Abitreeneissä

Ratkaisu

# LOPS2021YO1_1

# YTfas_R2

Valitse Roopen saamien osakkeiden lukumäärä.

Lasketaan ensin Roopen ostamien B-osakkeiden lukumäärä. Huomioidaan välityspalkkio ja osakkeen hinta.

$\frac{1\,000\;\text{\texteuro} - 4{,}00\;\text{\texteuro}}{3{,}00\;\text{\texteuro/kpl}} = 332\;\text{kpl}$

Lasketaan seuraavaksi Roopen vaihtamien C-osakkeiden lukumäärä. Huomioidaan välityspalkkiot ja osakkeiden hinnat.

$\frac{332\;\text{kpl} \cdot 2{,}50\;\text{\texteuro/kpl} - 2 \cdot 4{,}00\;\text{\texteuro}}{6{,}00\;\text{\texteuro/kpl}} = 137\;\text{kpl}$

Lasketaan vielä Roopen vaihtamien A-osakkeiden lukumäärä. Huomioidaan välityspalkkiot ja osakkeiden hinnat.

$\frac{137\;\text{kpl} \cdot 7{,}00\;\text{\texteuro/kpl} - 2 \cdot 4{,}00\;\text{\texteuro}}{3{,}00\;\text{\texteuro/kpl}} = 317\;\text{kpl}$

Lasketaan lopuksi Roopen myymien A-osakkeiden arvo. Huomioidaan välityspalkkio ja osakkeen hinta.

$317\;\text{kpl} \cdot 2{,}80\;\text{\texteuro/kpl} - 4{,}00\;\text{\texteuro} = 883{,}60\;\text{\texteuro}$

Roopella on lopuksi rahaa 883,60 €. Osakekaupat eivät olleet ainakaan hänelle taloudellisesti kannattavia.

# LOPS2021YO1_4

Linkkejä

Vahvista keskeisten sisältöjen osaamistasi.

Tampereen yliopisto (TAU) on tehnyt LOPS2021-sisältöisen pitkän matematiikan kertauskurssin. Osaamistaan voi jo ennakkoon petrata tehdyn toteutuksen avulla. toteutukseen.

TAU/MAA9

Yo-tehtäviä harjoiteltaviksi

Listaus perustuu lyhyen matematiikan yo-tehtäviin, koska pitkässä matematiikassa talousmatematiikkaa ei ole lähihistoriassa ollut.

S19/7, K19/7, S18/6, K18/8, S17/5, K17/5+10, S16/11, K16/5+10, S15/14, K15/14, S14/14, S13/14, S12/13, K12/13, S11/5+14, K11/14, S10/5+14, K10/5+14, S09/4+15, K09/8, S08/4+14, K08/11+14, S07/14, K07/4, S06/13, K06/5+14, S05/15, K05/8+14, S04/7+14, K04/8+15, S03/8+14, K03/4+12+14, S02/7+14, K02/14

Voit etsiä edellä listattuja ja paljon muita yo-tehtäviä alla olevista linkeistä.

matemaattinenyhdistys.fi/yo

matta.hut.fi/matta/yoteht/index.html

Ohjelmia avuksi matematiikkaan

Alla on muutamia ohjelmia, joista on apua ja hyötyä varsinkin matematiikan yo-kokeen B-osan tehtävissä, joissa kaikki sähköisen Abitti-järjestelmän ohjelmat on käytettävissä.

Ohjelmat on listattu aakkosjärjestyksessä.

GeoGebra

GeoGebra on hyvä ja toimiva kompromissi lähes kaikkiin lukion pitkän matematiikan virittämiin tarpeisiin.

Ohjelman voi ladata osoitteesta

geogebra.org

GeoGebraa voi käyttää myös suoraan selaimessa, mutta on huomattava mahdolliset eroavaisuudet työpöytäsovellukseen verrattuna.

GeoGebran perusasetukset

GeoGebralla funktion määrittely

LibreOffice Calc

LibreOffice Calc hyvä ja helposti opittava ohjelma taulukkolaskentaan ja tilastollisen aineiston piirtoon. Calcilla voi kirjoittaa soluihin funktioita, tehdä viittauksia toisiin soluihin, laskea solualueista tilastollisia tunnuslukuja ja piirtää tilastokuvaajia. Ohjelmalla onnistuu myös erilaisten käyrien sovittaminen annettuun pistejoukkoon. Se ei kuitenkaan ole ns. raskaan sarjan plottausohjelma.

Tämän avoimen lähdekoodin ja ilmaisen ohjelman voi ladata osoitteesta

fi.libreoffice.org

LoggerPro

LoggerPro on erittäin hyvä ohjelma numeerisen aineiston käsittelyyn. Toisin kuin LibreOffice Calc, on LoggerPro vaativampiin tarpeisiin soveltuva plottausohjelma.

Tämän maksullisen ohjelman voi ostaa osoitteesta

vernier.com/products/software/lp

Tiedustele opettajaltasi mahdollisuutta mahdollisesti ilmaiseen oppilaitoslisenssiin.

LoggerPron peruskäyttö

LoggerPron jatkokäyttö

Pinta

Pinta ei ole pelkkää liitoa, vaan yksinkertainen Abitti-koejärjestelmästä löytyvä rasterigrafiikan piirto-ohjelma.

Tämän avoimen lähdekoodin ja ilmaisen ohjelman voi ladata osoitteesta

pinta-project.com/pintaproject/pinta

Pinta-ohjelman peruskäyttö

SpeedCrunch

SpeedCrunch on erittäin monipuolinen, kustomoitava ja käyttöhistorialtaan muokattava laskinohjelma. Laskin on käytettävissä myös matematiikan yo-kokeen A-osassa.

Tämän avoimen lähdekoodin ja ilmaisen ohjelman voi ladata osoitteesta

speedcrunch.org

SpeedCrunchin peruskäyttö