MAA3 Geometria
Kurssin tavoitteena on, että opiskelija
- harjaantuu hahmottamaan ja kuvaamaan tilaa ja muotoa koskevaa tietoa sekä kaksi- että kolmiulotteisissa tilanteissa
- osaa ratkaista geometrisia ongelmia käyttäen hyväksi yhdenmuotoisuutta, Pythagoraan lausetta sekä suora- ja vinokulmaisen kolmion trigonometriaa
- harjaantuu muotoilemaan, perustelemaan ja käyttämään geometrista tietoa sisältäviä lauseita
- osaa käyttää ohjelmistoja tutkiessaan kuvioita ja kappaleita sekä niihin liittyvää geometriaa sekä ratkaistessaan niihin liittyviä sovellusongelmia.
Keskeiset sisällöt
- kuvioiden ja kappaleiden yhdenmuotoisuus
- sini- ja kosinilause: ympyrän ja sen osien ja siihen liittyvien suorien geometriaa; tasokuvioihin liittyvien pituuksien, kulmien ja pinta-alojen laskeminen; kappaleisiin liittyvien pituuksien, pinta-alojen ja tilavuuksien laskeminen
1.Tasogeometrian peruskäsitteitä
Kulmat nimetään usein käyttämällä kreikkalaisia pieniä aakkosia: \(\alpha\) (alfa), \(\beta\) (beeta), \(\gamma\) (gamma) ...
1.1 Erilaisia kulmia
Vieruskulmat
Vieruskulmien \(\alpha\) ja \(\beta\) summa on \(180^{°}\).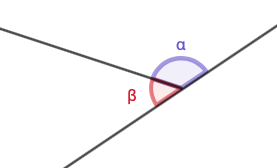 
Ristikulmat
Ristikulmat \(\alpha\) ja \(\beta\) ovat yhtä suuret.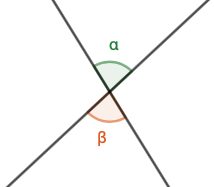 
Samankohtaiset kulmat
Jos suorat \(a\) ja \(b\) ovat yhdensuuntaiset, kulmat \(\alpha\) ja \(\beta\) ovat yhtä suuret.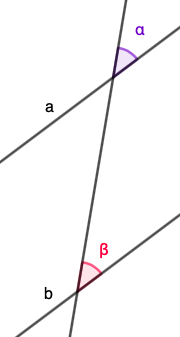 
Kolmion kulmien summa on \(180^{°}\).
Jos kolmiossa on kolme yhtä suurta kulmaa, tällöin kolmion kaikki sivut ovat yhtä pitkiä. Tällainen kolmio on tasasivuinen kolmio. Jos kolmion kaksi sivua ovat yhtä pitkät, niiden kantakulmatkin ovat yhtä suuret. Tällaista kolmiota kutsutaan tasakylkiseksi kolmioksi.
Monikulmion kulmien summa on \((n-2)\cdot 180\), missä \(n\) on monikulmion kärkien lukumäärä.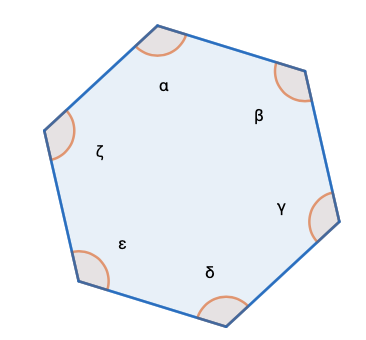 
Säännöllisen monikulmion kaikki sivut ovat yhtä pitkiä ja kulmat yhtä suuria.
1.2 Kuvioiden yhdenmuotoisuus
Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat samat riippumatta siitä, mitä sivuja tarkastellaan. Yhdenmuotoisissa kuvioissa vastinkulmat ovat aina yhtä suuret.
Yhdenmuotoisuussuhde eli mittakaava
Jos kuviot ovat yhdenmuotoiset, yhdenmuotoisuussuhde tarkoittaa suhdetta \[\frac{s_1}{s_2},\] missä \(s_1\) on sivun pituus ensimmäisessä kuviossa ja \(s_2\) sitä vastaavan sivun pituus toisessa kuviossa.
Kolmiot ovat yhdenmuotoisia, jos niillä on kaksi yhtä suurta kulmaa. Kahdesta yhtä suuresta kulmastahan seuraa myös, että kolmioiden kolmas kulma on yhtä suuri.
Yhdenmuotoisuuden avulla voidaan päätellä lisäksi myös kuvioiden pinta-aloihin liittyviä suhteita.
Kolmioiden yhdenmuotoisuuslause KK
Jos kolmion kaksi kulmaa ovat yhtä suuria kuin vastinkulmat toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.
Kolmioiden yhdenmuotoisuuslause SSS
Jos kolmion kaikki sivut ovat verrannolliset vastinsivuihin toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.
Kolmioiden yhdenmuotoisuuslause SKS
Jos kolmion kaksi sivua ovat verrannollista vastinsivuihin toisessa kolmiossa ja niiden välinen kulma on yhtä suuri kuin vastinkulma toisessa kolmiossa, niin kolmiot ovat yhdenmuotoiset.
1.2.1 Esimerkki
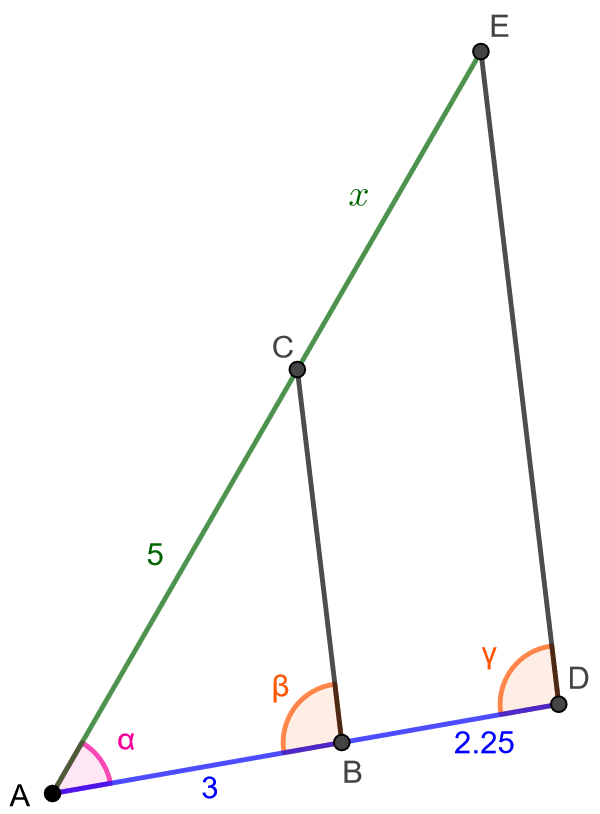
Määritä alla olevan kuvion sivun \(DE\) pituus, joka on merkitty kuvaan kirjaimella \(x\).
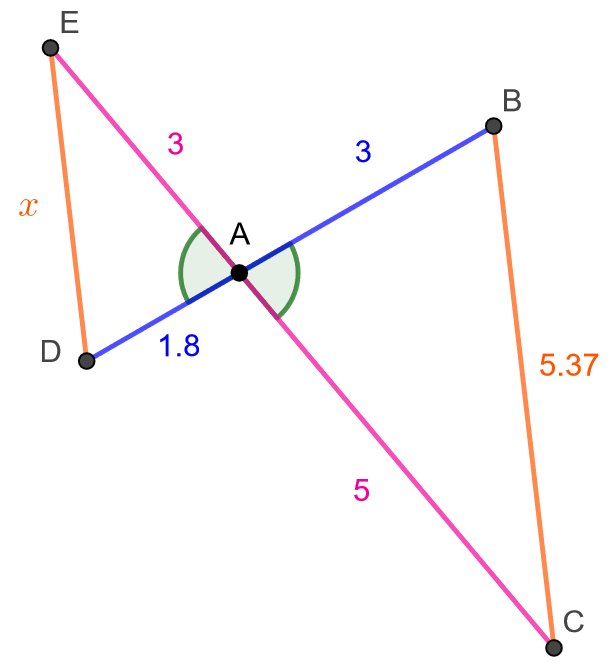
Sivun \(DE\) pituus saadaan helpoiten määritettyä, jos tiedetään, että kuviossa olevat kolmiot \(ABC\) ja \(ADE\) ovat yhdenmuotoiset. Kuvioon merkityt kulmat \(\angle EAD\) ja \(\angle CAB\) ovat toistensa ristikulmia ja siten yhtä suuria. Sinisellä mekittyjen vastinsivujen suhde on \[\frac{1,8}{3}=0,6\] ja pinkillä merkittyjen vastinsivujen suhde on \[\frac{3}{5}=0,6.\] Koska kahden vastinsivun suhteet ovat samat ja lisäksi näiden sivujen välinen kulma on kummassakin kolmiossa yhtä suuri, kolmiot ovat yhdenmuotoiset kolmioiden yhdenmuotoisuuslauseen SSS mukaan.
Oranssilla merkittyjen vastinsivujen suhteen tulee olla sama kuin muidenkin sivujen suhteet, joten saadaan seuraava yhtälö, joka ratkaistaan \[ \begin{aligned} \frac{x}{5,37}&=0,6 &\quad &|\cdot 5,37 \\ x &= 5,37 \cdot 0,6 &\quad &| \text{ sievennetään} \\ x &= 3,222 & \quad &| \text{ pyöristetään kahden desimaalin tarkkuudelle} \\ x &\approx 3,22 \end{aligned} \]
Kuvion sivun \(DE\) pituus on noin \(3,22\).
Yhdenmuotoisten kuvioiden pinta-alalause
Jos kuviot ovat yhdenmuotoiset yhdenmuotoisuussuhteessa \(s_1 : s_2\), niiden pinta-alojen suhde on \[\frac{A_1}{A_2} =\left(\frac{s_1}{s_2}\right)^2.\]
Laske alla olevan kuvan isomman tähden pinta-ala, kun tiedetään, että tähdet ovat yhdenmuotoiset.
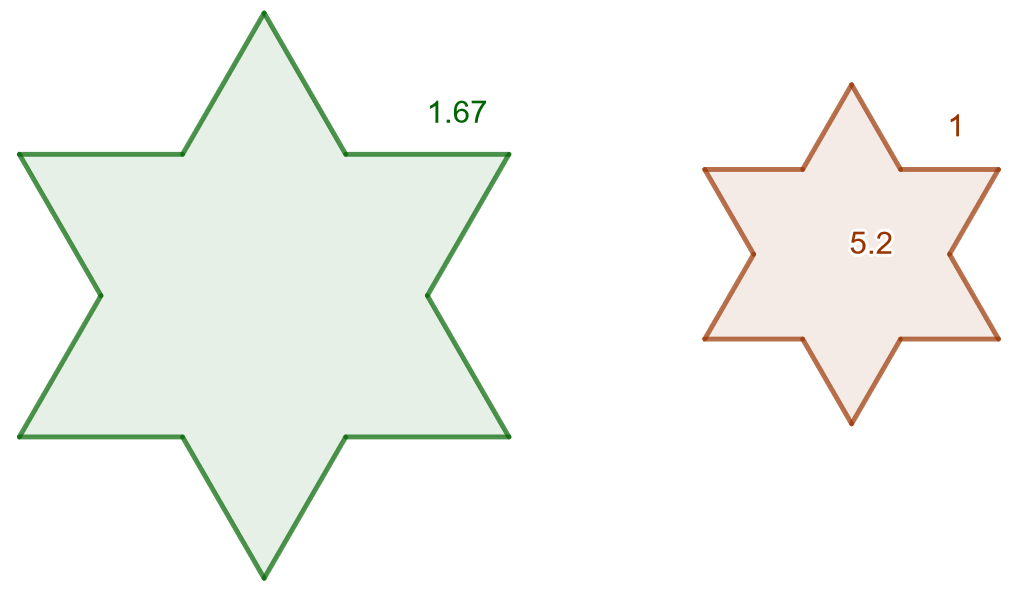
Koska kuviot ovat yhdenmuotoisia, voidaan käyttää yhdenmuotoisten kuvioiden pinta-alalausetta. Kuvioiden yhdenmuotoisuussuhde on \[\frac{1,67}{1}=1,67.\] Merkitään kysyttyä isomman tähden pinta-alaa kirjaimella \(x\). Tehdään verranto yhdenmuotoisten kuvioiden pinta-alalauseen avulla ja ratkaistaan siitä \(x\): \[ \begin{aligned} \frac{x}{5,2}&=1,67^2 &\quad &| \cdot 5,2 \\ x &= 5,2 \cdot 1,67^2 &\quad &| \text{ sievennetään lauseke} \\ x &= 14,50228 &\quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x & \approx 14,5 \end{aligned} \] Isomman tähden pinta-ala on noin \(14,5\).
1.2.2 Esimerkki
Pinta-alan kohdalla yhdenmuotoisuussuhde korotettiin toiseen potenssiin, mutta tilavuuden kohdalla yhdenmuotoisuussuhde korotetaankin kolmanteen potenssiin.
Yhdenmuotoisten kappaleiden tilavuuslause
Jos kappaleet ovat yhdenmuotoiset yhdenmuotoisuussuhteessa \(s_1 : s_2\), niiden tilavuuksien suhde on \[\frac{V_1}{V_2} =\left(\frac{s_1}{s_2}\right)^3.\]
2. Kolmioiden geometriaa
2.1 Pythagoraan lause
Suorakulmainen kolmio on sellainen kolmio, jonka yksi kulma on suorakulma eli \(90^{\circ}\). Suoran kulman kylkinä olevia sivuja kutsutaan kateeteiksi ja suoran kulman vastaista sivua hypotenuusaksi.
Jos suorakulmaisen kolmion kahden sivun pituus tiedetään, kolmannen sivun pituus voidaan selvittää Pythagoraan lauseen avulla:
Pythagoraan lause
Suorakulmaisen kolmion kateettien \(a\) ja \(b\) neliöiden summa on yhtä suuri kuin sen hypotenuusan \(c\) neliö, eli \[a^2+b^2=c^2.\]
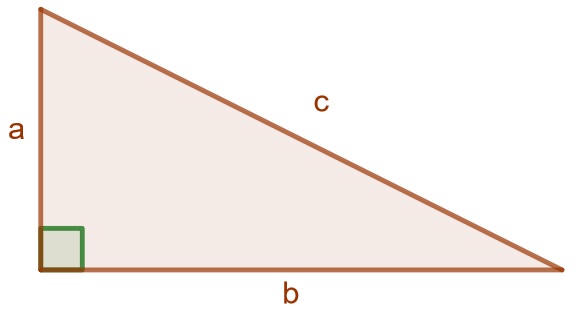
Pythagoraan lausetta voidaan käyttää myös käänteisesti: jos kolmion kateettien neliöiden summa \(a^{2}+b^{2}\) on yhtä suuri kuin hypotenuusan neliö \(c^{2}\), on kyseessä tällöin suorakulmainen kolmio.
Jos suoraa kulmaa ei ole erikseen mainittu tai merkitty, tulee aina tarkistaa, onko kolmio suorakulmainen.
2.2 Trigonometriset funktiot ja muistikolmiot
Kolmion sivujen suhteet ovat aina vakioita tietyillä kulman suuruuksilla. Näitä suhteita kutsutaan trigonometrisiksi funktioiksi.
Kolmion kulmien suuruudet voidaan ratkaista, jos tiedetään kolmion kateettien pituudet tai kateetin ja hypotenuusan pituus.
Suorakulmaisen kolmion sini, kosini ja tangentti
Suorakulmaisessa kolmiossa kulman \(\alpha\) sini, kosini ja tangentti tarkoittavat seuraavia suhteita: \[\sin(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{hypotenuusa}}=\frac{a}{c}\] \[\cos(\alpha)=\frac{\text{kulman viereinen kateetti}}{\text{hypotenuusa}}=\frac{b}{c}\] \[\tan(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{kulman viereinen kateetti}}=\frac{a}{b}\]
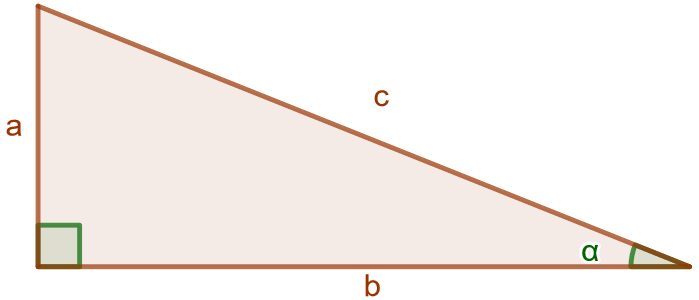
Ylläolevat trigonometriset funktiot pätevät ainoastaan suorakulmaiselle kolmiolle. Mille tahansa kolmiolle pätevät seuraavat sini- ja kosinilauseet:
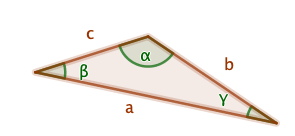
Sinilause: \(\displaystyle\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}\) eli \(\dfrac{\text{kolmion sivu}}{\text{vastaisen kulman sini}}\)
Kosinilause: \(c^{2}=a^{2}+b^{2}-2ab\cos\gamma\)
Määritä alla olevasta kolmiosta sivun \(x\) pituus.
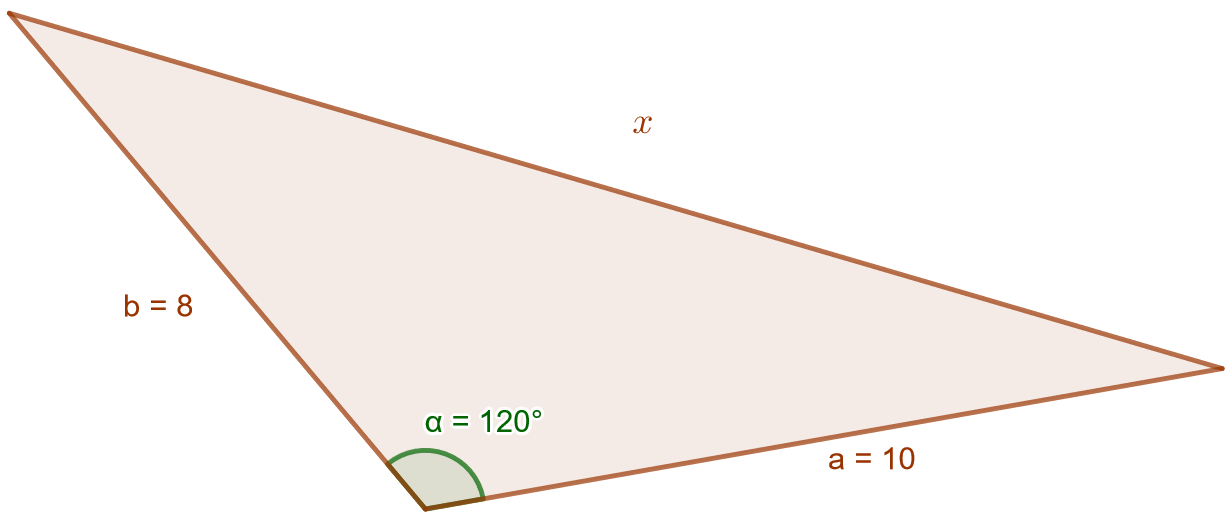
Tiedetään siis sivujen \(a\) ja \(b\) pituudet, sekä niiden välisen kulman \(\alpha\) suuruus. Voidaan siis käyttää kosinilausetta. Nyt kosinilause tulee muotoon \[x^2=a^2+b^2-2ab\cos(\alpha).\] Sijoitetaan sivujen pituudet ja kulman suuruus yhtälöön ja ratkaistaan \(x\). \[ \begin{aligned} x^2 &= 10^2+8^2-2 \cdot 10\cdot 8 \cdot \cos(120^{\circ}) &\quad &| \text{ sievennetään} \\ x^2 &= 244 &\quad &| \sqrt{\text{ }} \\ x &= \sqrt{244} &\quad &| \text{ sievennetään} \\ x &\approx 15,6205 &\quad &| \text{ pyöristetään} \\ x &\approx 15,62 \end{aligned} \] Kolmion sivun \(x\) pituus on noin \(15,62\).
Jos kolmiosta tiedetään kahden kulman suuruus sekä yhden sivun pituus, kosinilausetta ei voida käyttää. Tällöin käytetään sinilausetta.
Muistikolmioiden avulla voidaan ratkaista tietyille usein esiintyville kulmille sini, kosini ja tangentti. Tällaisia kulmia ovat \(30^{\circ}\), \(45^{\circ}\) ja \(60^{\circ}\).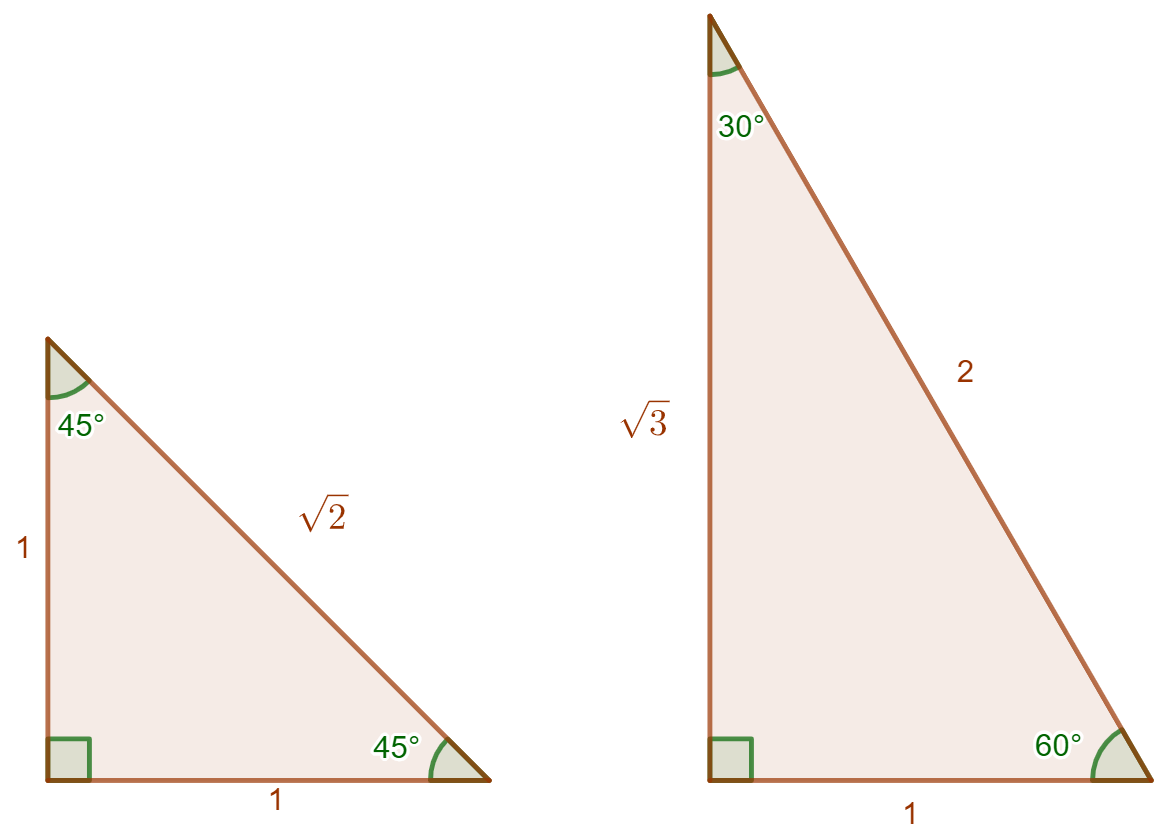 
2.3 Kolmioiden pinta-ala
Kolmion pinta-ala
Jos kolmion kannan pituus on \(a\) ja korkeus \(h\), kolmion pinta-ala on \[A=\frac{1}{2} ah.\] Jos kolmion kahden sivun pituudet ovat \(a\) ja \(b\) ja näiden välisen kulman suuruus \(\alpha\), voidaan kolmion pinta-ala ilmaista lausekkeella \[A=\frac{1}{2} ab \sin \alpha.\]
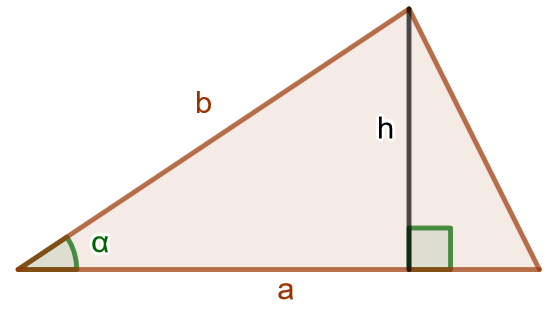
Kolmion korkeusjana merkitään aina kohtisuoraksi kantaa tai sen jatketta vastaan.
2.4 Kolmion merkilliset pisteet
Kulmanpuolittajalause 1
Kolmion jokaisen kulman kulmanpuolittajat leikkaavat yhdessä pisteessä, joka on aina kolmion sisällä. Tämä piste on myös suurimman mahdollisen kolmion sisään piirretyn ympyrän keskipiste
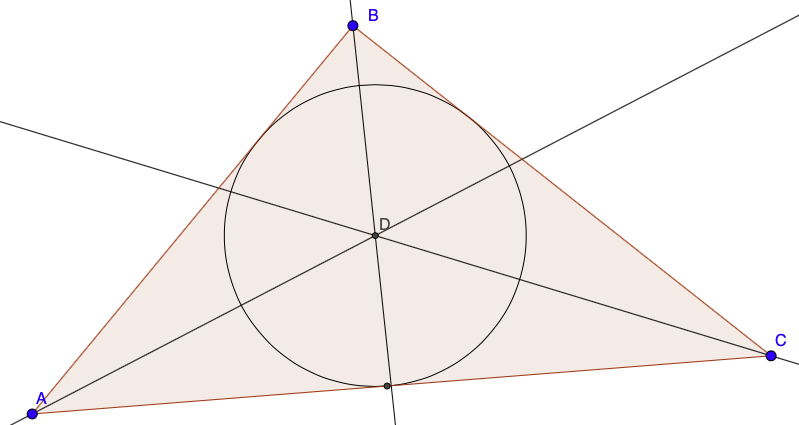
Ympyrän säde voidaan laskea kaavalla \(r=\displaystyle\sqrt{\frac{(s-a)(s-b)(s-c)}{s}}\), missä \(a,b\) ja \(c\) ovat kolmion sivujen pituudet ja \(s\) on kolmion piirin puolikas
\(s=\frac{1}{2}(a+b+c)\).
Kulmanpuolittajalause 2
Kolmion yhden kulman kulmanpuolittaja jakaa vastaisen sivun viereisten sivujen suhteessa: \(\displaystyle\frac{x}{y}=\frac{a}{b}\)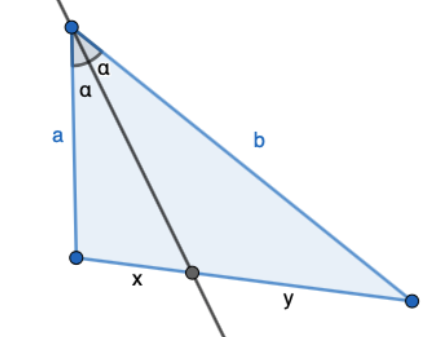 
Keskijanalause (mediaanilause)
Kun kolmion sivujen keskipisteet yhdistetään vastakkaisiin kulmiin, saadaan kolme keskijanaa. Nämä keskijanat leikkaavat yhdessä pisteessä, joka jakaa jokaisen keskijanan suhteessa 2:1. Leikkauspiste on aina kolmion sisällä ja sitä kutsutaan myös kolmion painopisteeksi.
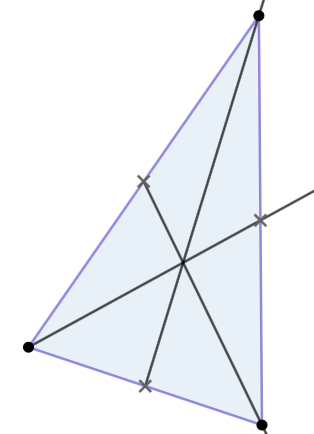
Keskinormaalilause
Kolmion sivujen keskinormaalit leikkaavat yhdessä pisteessä, joka on kolmion ympäri piirretyn ympyrän keskipiste.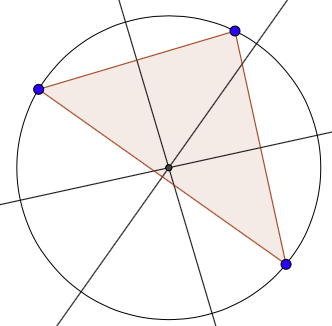 
Teräväkulmaisen kolmion tapauksessa piste on kolmion sisäpuolella ja tylppäkulmaisella kolmiolla se on kolmion ulkopuolella. Suorakulmaisella kolmiolla leikkauspiste on täsmälleen hypotenuusan keskipisteessä.
2.5 Tylppäkulmainen kolmio
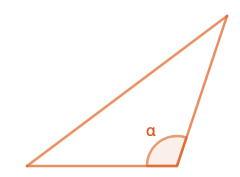
Tylpän kulman sini ja kosini
Tylpän kulman (\(90^{\circ} \leq \alpha \leq 180^{\circ}\)) sini ja kosini voidaan laskea seuraavilla kaavoilla: \[\sin (180^{\circ} -\alpha) = \sin (\alpha)\] \[\cos(180^{\circ}-\alpha)=-\cos (\alpha).\]
Määritellään nyt tylpän kulman eli suoran kulman ja oikokulman välillä olevalle kulmalle sini ja kosini laskukaavojen avulla. Alla olevissa esimerkeissä havainnollistetaan sitä, mistä laskukaavat tulevat.
Otetaan esimerkiksi GeoGeba-appletissa näkyvä alkutilanne, jossa halutaan selvittää kulman \(\alpha=140^{\circ}\) sini. Äsken esitellyn kaavan mukaisesti \[ \begin{aligned} \sin(140^{\circ}) &= \sin(180^{\circ}-140^{\circ}) \\ &= \sin(40^{\circ}) \\ &= 0,64. \end{aligned} \] GeoGebra-appletissa sekä kulman \(140^{\circ}\) että \(40^{\circ}\) oikea kylki on x-akselilla, ja vasen kylki on yhden mittainen jana. Huomataan, että kummankin kulman tapauksessa tämän janan päätepisteen y-koordinaatti on \(0,64\).
Otetaan esimerkiksi GeoGebra-appletissa näkyvä alkutilanne, jossa halutaan selvittää kulman \(\alpha=140^{\circ}\) kosini. Äsken esitellyn kaavan mukaisesti \[ \begin{aligned} \cos(140^{\circ}) &= -\cos(180^{\circ}-140^{\circ}) \\ &= -\cos(40^{\circ}) \\ &= -0,77. \end{aligned} \] GeoGebra-appletissa sekä kulman \(140^{\circ}\) että \(40^{\circ}\) oikea kylki on x-akselilla, ja vasen kylki on yhden mittainen jana. Huomataan, että kummankin kulman tapauksessa tämän janan päätepisteen x-koordinaatti on \(0,77\). Tylpän kulman kosinin arvo on negatiivinen, kun taas vastaavan terävän kulman kosini on positiivinen.
3. Monikulmioiden pinta-aloja
Monet monikulmioihin liittyvät ongelmat voidaan yksinkertaistaa kolmioihin liittyviksi ongelmiksi. Jos monikulmio on säännöllinen, sitä yksinkertaisempaa sen pinta-alan laskeminen on.
3.1 Puolisuunnikas
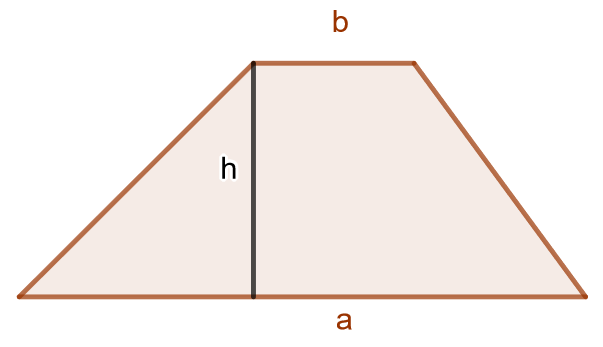
Puolisuunnikkaan pinta-ala
Puolisuunnikas on nelikulmio, jonka kaksi vastakkaista sivua ovat yhdensuuntaiset. Näitä sivuja kutsutaan puolisuunnikkaan kannoiksi. Jos puolisuunnikkaan kannat ovat \(a\) ja \(b\) ja sen korkeus on \(h\), sen pinta-ala on \[A= \frac{a+b}{2}h.\]
3.2 Suunnikas
Jos suunnikkaan kaikki sivut ovat yhtä pitkiä, puhutaan neljäkkäästä eli vinoneliöstä. Joskus neljäkästä kutsutaan myös nimellä rombi.
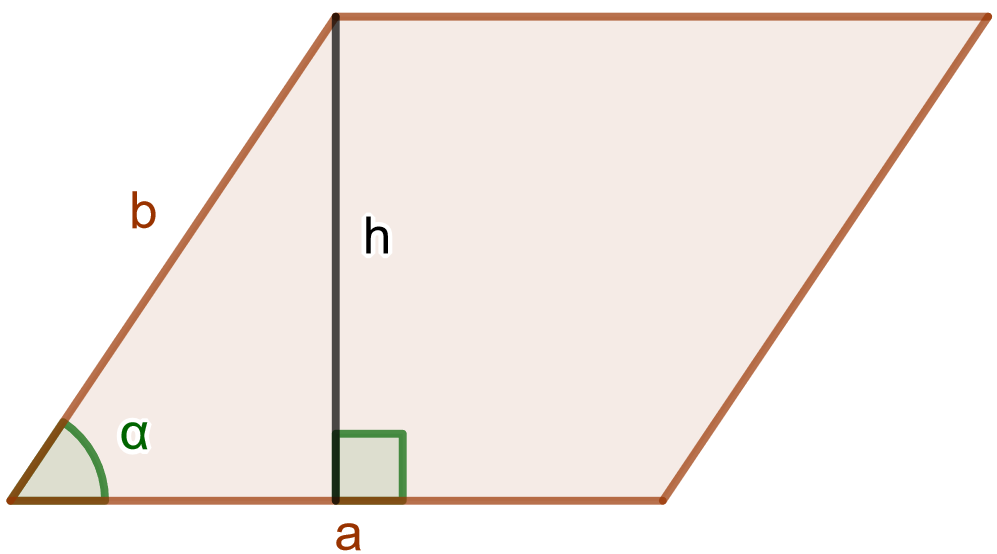
Suunnikkaan pinta-ala
Suunnikas on nelikulmio, jonka molemmat vastakkaiset sivut ovat yhtä pitkiä ja yhdensuuntaisia. Jos suunnikkaan sivujen pituudet ovat \(a\) ja \(b\) ja näiden sivujen välinen kulma on \(\alpha\), voidaan suunnikkaan pinta-ala laskea seuraavasti \[A=ah=ab \sin \alpha,\] missä \(h\) on suunnikkaan korkeus.
3.3 Suorakulmio
Suorakulmion pinta-ala
Suorakulmio on monikulmio, jolla on neljä kulmaa ja jonka jokainen kulma on suora. Jos suorakulmion eripituisten sivujen pituudet ovat \(a\) ja \(b\), voidaan suorakulmion pinta-ala laskea seuraavasti \[A=ab.\]
Neliö on suunnikas, jonka kaikki neljä kulmaa ovat \(90^{\circ}\) ja sen kaikki sivut ovat yhtäpitkiä. Tällöin neliön pinta-alaksi \(A\) saadaan \(A=a\cdot a=a^{2}\).
4. Ympyrä
Tutki alla olevan piirroksen avulla ympyrän eri osia.
4.1 Säde, halkaisija ja piiri
Ympyrän säde, halkaisija ja piiri
Säde: \(r\)
Halkaisija: \(d=2r\)
Piiri: \(p=2\pi r=\pi d\)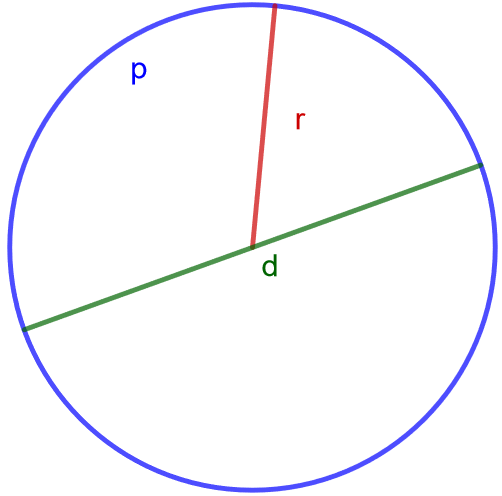 
Ympyrän pinta-ala
Ympyrän pinta-ala lasketaan sen säteen \(r\) avulla seuraavasti \[A=\pi r^2.\]
Keskuskulma on se kulma, jonka kärki on ympyrän keskipisteessä.
Ympyrän kaaren pituus
Keskuskulman 
kyljet rajaavat ympyrän kehältä kaaren, jonka pituus 
voidaan laskea seuraavasti 
Tarkastellaan alla olevan kuvan kaltaista sektoria.
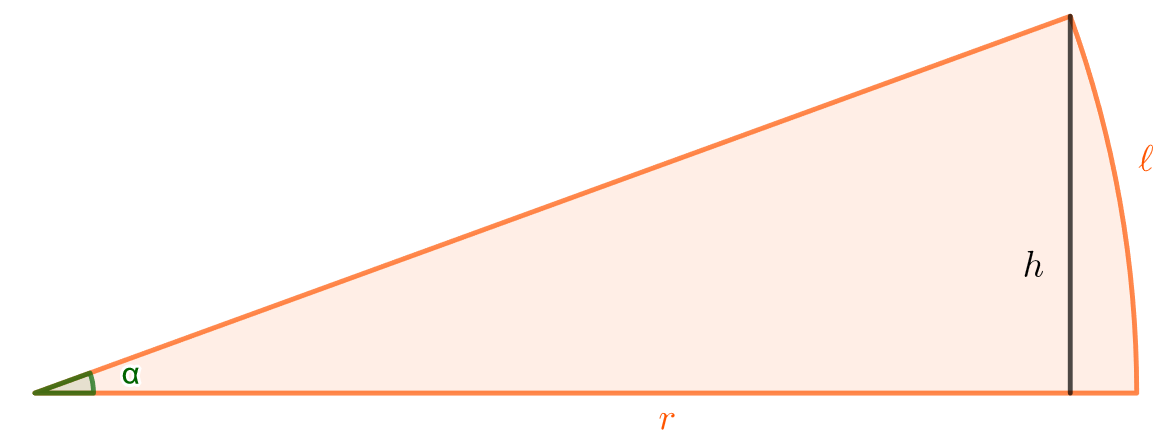
Ratkaistaan kaaren \(\ell\) pituus. Jos kulma \(\alpha\) on ilmaistu radiaaneissa, edellinen kaava muuttuu muotoon
\[b=\frac{\alpha}{2 \pi} 2 \pi r = \alpha r.\]
Nyt siis kaarelle \(\ell=\alpha r\). Pystysuoan pituuden \(h\) suuruus voidaan määrittää sinin avulla:
\[\sin \alpha= \frac{h}{r} \quad \Leftrightarrow \quad h = r \sin \alpha.\]
Kun kulmaa \(\alpha\) pienennetään, janan \(h\) ja kaaren \(\ell\) pituudet lähestyvät toisiaan. Voidaan siis merkitä, että kun \(\alpha\) on pieni,
\[ \begin{aligned} h & \approx \ell \\ r \sin \alpha & \approx \alpha r \quad |:r \\ \sin \alpha & \approx \alpha \end{aligned} \]
Eli kun kulma \(\alpha\) on pieni, sen siniä voidaan approksimoida kulman arvolla (radiaaneina).
4.2 Sektori ja segmentti
Ympyrän sektorin pinta-ala
Keskuskulman \(\alpha\) kyljet rajaavat ympyrän sisältä sektorin, jonka pinta-ala \(A_{SEK}\) voidaan laskea seuraavasti: \[A_{SEK}= \frac{\alpha}{360 ^{\circ}} \pi r^2.\] Jos tiedetään keskuskulmaa vastaavan kaaren pituus \(b\), voidaan sektorin pinta-ala laskea myös kaavalla \[A_{SEK}=\frac{br}{2}.\]
Jänne on jana, joka yhdistään ympyrän kehällä olevan kaaren päätepisteet.
Segmentin pinta-ala
Jänne jakaa ympyrän kahdeksi segmentiksi, joiden pinta-ala \(A_{SEG}\) saadaan laskettua kaavalla \[A_{SEG}=A_{SEK} \pm A_{keskuskolmio}.\] Kaavassa käytetään yhteenlaskua, jos keskuskulma \(\alpha\) on suurempi kuin \(180^{\circ}\), ja vähennyslaskua, jos keskuskulma \(\alpha\) on pienempi kuin \(180^{\circ}\).
Laske alla olevaan kuvaan sinisellä merkityn segmentin pinta-ala.
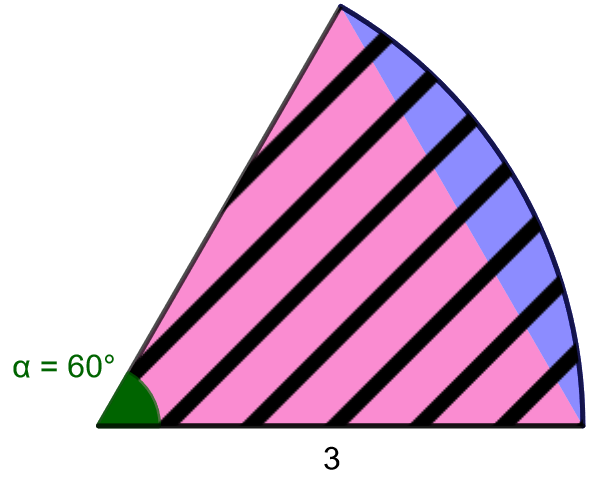
Koska keskuskulma \(\alpha\) on pienempi kuin \(180^{\circ}\), käytetään kaavaa \[A_{SEG}=A_{SEK}-A_{\text{keskuskolmio}}.\] Lasketaan ensin kuvaan mustalla vinoviivoituksella merkityn sektorin pinta-ala. Sektorin säde \(r=3\) ja keskuskulma \(\alpha=60^{\circ}\), joten sektorin pinta-ala on \[ \begin{align} A_{SEK}&=\frac{\alpha}{360^{\circ}} \pi r^2 \\ &=\frac{60^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 \\ &=\frac{3\pi}{2} \end{align} \]
Lasketaan sitten kuvaan pinkillä merkityn keskuskolmion pinta-ala. Kolmion kahden sivun pituudet ovat säteen mittaiset eli \(3\), ja näiden sivujen välinen kulma on \(\alpha=60^{\circ}\). Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla, jossa \(a=b=r=3\). \[ \begin{align} A_{\text{keskuskolmio}}&=\frac{ab}{2} \sin(\alpha) \\ &=\frac{r^2}{2} \sin(\alpha) \\ &=\frac{3^2}{2} \sin(60^{\circ}) \\ &=\frac{9\sqrt{3}}{4} \end{align} \]
Lopuksi lasketaan segmentin pinta-ala vähennyslaskulla \[ \begin{align} A_{SEG}&=A_{SEK}-A_{\text{keskuskolmio}} \\ &= \frac{3 \pi}{2} - \frac{9 \sqrt{3}}{4} \\ &= \frac{6 \pi}{4} - \frac{9 \sqrt{3}}{4} \\ &= \frac{6 \pi - 9 \sqrt{3}}{4} \\ &\approx 0,81527 \\ &\approx 0,82 \end{align} \] Kysytyn segmentin pinta-ala on siis noin \(0,82\).
4.3 Tangentti
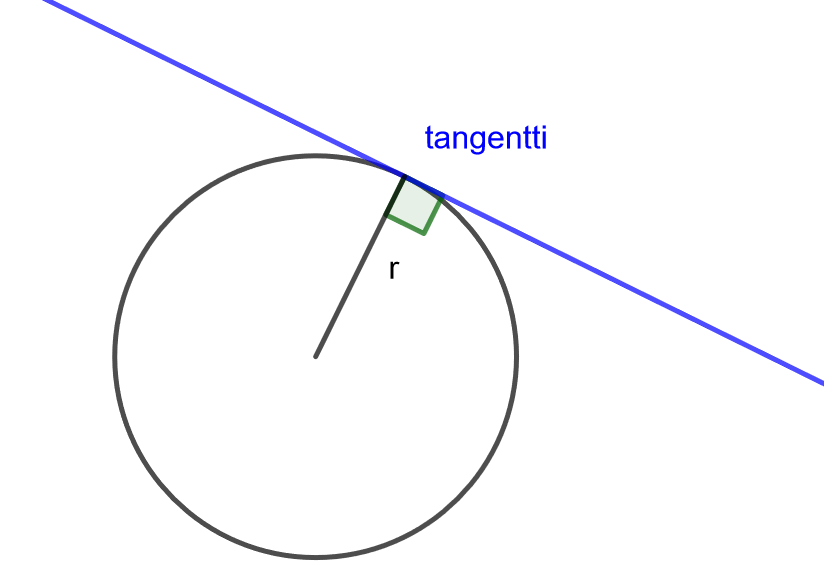
Tangentti
Tangentti on suora, joka kohtaa ympyrän vain yhdessä pisteessä. Ympyrän tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan.
4.4 Ympyrään liittyviä kulmia
Kehäkulma on kulma, jonka kärki on ympyrän kehällä ja jonka kylkinä on kaksi jännettä tai jänne ja tangentti. Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta. Samaa kaarta vastaavat kehäkulmat ovat aina yhtä suuria.
Kehäkulman lause 1
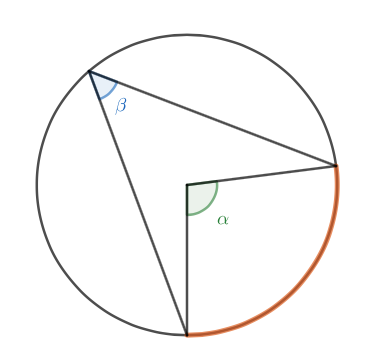
Kehäkulma \(\beta\) on puolet samaa kaarta vastaavasta keskuskulmasta \(\alpha\), eli \[\begin{align*} \beta=\frac{\alpha}{2} \end{align*}\]
Kehäkulman lause 2
Samaa kaarta vastaavat kehäkulmat ovat yhtä suuria.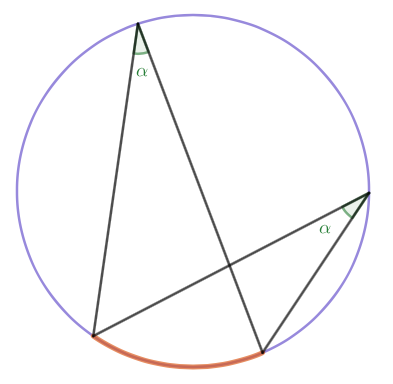 
Kehäkulman lause 3
Puoliympyrän sisältämä kehäkulma on suora.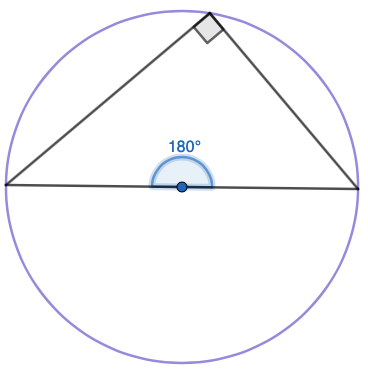 
Tangenttikulma on kahden ympyrän tangentin leikkauspisteeseen muodostuva kulma, jonka aukeamassa ympyrä on. Tangenttikulman ja sitä vastaavan keskuskulman summa on aina \(180^{\circ}\)
Tangenttikulman lause
Tangenttikulman \(\beta\) ja sitä vastaavan keskuskuman \(\alpha\) summa on \(180°\), eli \(\alpha+\beta=180°\).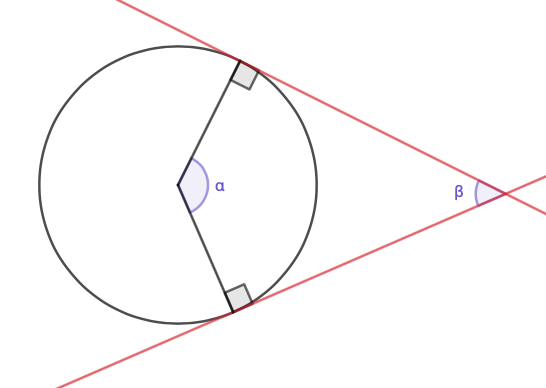 
Kehäkulmalauseen erityistapauksena on Thaleen lause. Sen mukaan puoliympyrän sisältämä kehäkulma on suora. Kehäkulmalauseen perusteella tämä on selvä asia, sillä puoliympyrän rajaava keskuskulma on \(180^{\circ}\), jolloin kehäkulman on oltava puolet siitä eli \(90^{\circ}\).
5. Avaruusgeometria
Monia tasogeometriassa hyödynnettyjä lauseita ja ominaisuuksia voi hyödyntää myös kolmiulotteisessa, eli avaruusgeometriassa. Suorien välinen kulma on suorien leikkauspisteeseen muodostuneista kulmista pienempi.
5.1 Kulmat avaruudessa
Kolmiulotteisessa avaruudessa voidaan laskea muun muassa kahden suoran välinen kulma, kahden tason välinen kulma tai tason ja suoran välinen kulma. Usein tilanne voidaan yksinkertaistaa kaksiulotteiseksi.
Avaruuslävistäjän pituus
Suorakulmaisen särmiön särmien pituudet ovat \(a\),\(b\) ja \(c\). Avaruuslävistäjän \(d\) pituus on \[\begin{align*} d^{2}=a^{2}+b^{2}+c^{2} \end{align*}\]
Laske suorakulmaisen särmiön avaruuslävistäjän pituus, kun sen sivujen pituudet ovat \(2\), \(5\) ja \(4\).
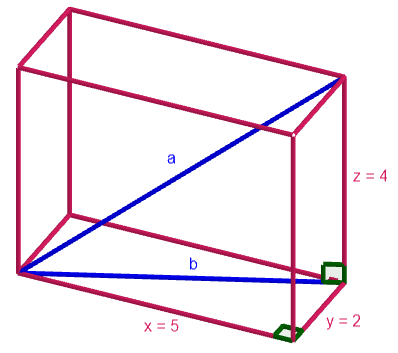
Tehtävässä kysytään siis yllä olevan kuvan avaruuslävistäjän \(a\) pituutta. Jotta se voitaisiin ratkaista, on ensin selvitettävä, kuinka pitkä lävistäjä \(b\) on.
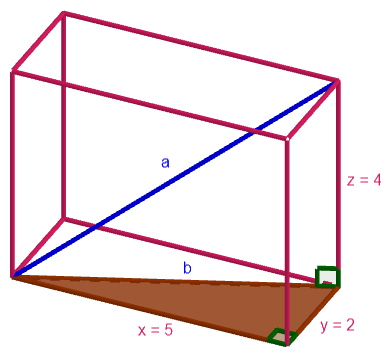
Yllä olevaan kuvaan on korostettu suorakulmaisen särmiön pohjassa oleva suorakulmainen kolmio, jonka hypotenuusa \(b\) pitäisi ratkaista. Se onnistuu esimerkiksi Pythagoraan lauseella: \[ \begin{aligned} b^2 &= x^2+y^2 \\ b &= \pm \sqrt{x^2+y^2} \\ b &= \pm \sqrt{5^2+2^2} \\ b &= \pm \sqrt{29} \end{aligned} \] Koska lävistäjän \(b\) pituus ei voi olla negatiivinen, valitaan vastaukseksi \(b=\sqrt{29}\).
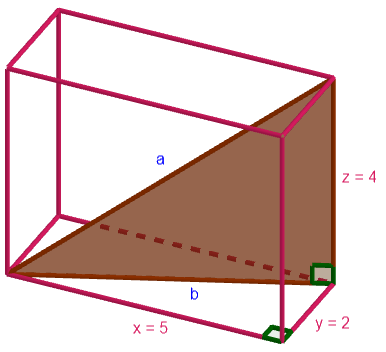
Nyt yllä olevaan kuvaan on korostettu lävistäjän \(b\), monitahokkaan särmän \(z\) ja avaruuslävistäjän \(a\) muodostama suorakulmainen kolmio. Tästä saadaan ratkaistua hypotenuusa \(a\) jälleen Pythagoraan lauseella.
\[ \begin{aligned} a^2 &= b^2+z^2 \\ a &= \pm \sqrt{b^2+z^2} \\ a &= \pm \sqrt{(\sqrt{29})^2+4^2} \\ a &= \pm \sqrt{45} \\ a &= \pm 3 \sqrt{5} \end{aligned} \] Koska avaruuslävistäjän pituus on positiivinen, vastaus on siis \(3 \sqrt{5}\).
5.2 Pallo
Pallon pinta-ala ja tilavuus
Pallon muodostavat ne pisteet, jotka ovat säteen 
etäisyydellä pallon keskipisteestä. Pallon pinta-ala ja tilavuus lasketaan sen säteen avulla 
ja 
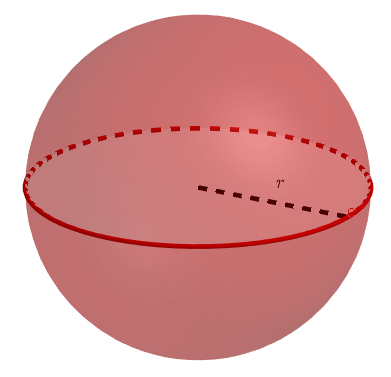
Jos pallo leikataan keksipisteen kautta, leikkausta kutsutaan isoympyräksi. Jos leikkaus ei kulje pallon keksipisteen kautta, leikkauksen nimi on pikkuympyrä.
Suoran ympyrälieriön sisään asetetaan mahdollisimman suuri pallo. Lasketaan lieriön ja pallon tilavuuksien suhde. 
Merkitään pallon sädettä kirjaimella \(r\). Koska ympyrä on mahdollisimman suuri, pallon pinta koskettaa ympyrälieriötä.
Pallon tilavuus on \(V_{pallo}=\frac{4}{3}\pi r^{3}\).
Ympyrälieriön pohjan säde on sama kuin sisällä olevalla pallolla. Pallo koskettaa myös ympyrälieriön pohjaa sekä kantta, joten ympyrälieriön korkeus on myös \(2r\).
Ympyrälieriön tilavuus on \(V_{lieriö}=A_{p}\cdot h=\pi r^{2}\cdot 2r=2\pi r^{3}\).
Lasketaan seuraavaksi tilavuuksien suhde, eli \[\begin{align*} \frac{V_{pallo}}{V_{lieriö}}=\frac{\frac{4}{3}\cancel{\pi r^{3}}}{2\cancel{\pi r^{3}}}=\frac{4}{3}:2=\frac{4}{3}\cdot\frac{1}{2}=\frac{2}{3}=2:3 \end{align*}\]
Lieriön ja pallon tilavuuksien suhde on \(2:3\) huolimatta siitä, minkä kokoisia kappaleet ovat.
Segmentti
Taso leikkaa pallon kahteen osaan, joita kutsutaan segmenteiksi. Segmentin tilavuus saadaan sen korkeuden 
avulla 
Pallon pinnasta taso rajaa kalotin, jonka pinta-ala saadaan segmentin korkeuden avulla 
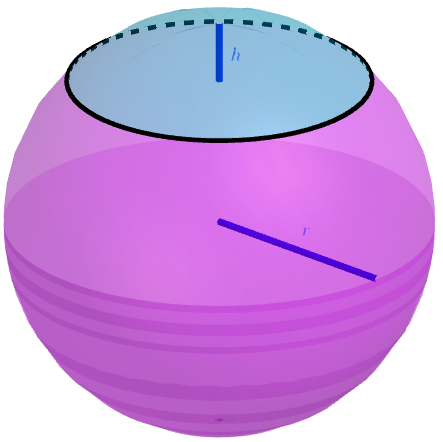
Pallosektorin tilavuus
\[\begin{align*} V=\frac{2}{3}\pi r^{2}h, \end{align*}\] missä \(r\) on pallon säde ja \(h\) segmentin korkeus
Ympyräsektori pyörähtää toisen säteensä ympäri. Määritetään syntyvän pallosektorin tilavuus ja kalotin pinta-ala. Sektorin keskuskulma on \(60°\) ja säde \(5,0 \text{ cm}\). Ratkaistaan ensin pallosektorin tilavuus. Jotta tilavuus voidaan ratkaista, tarvitaan segmentin korkeus \(h\). Piirretään tilanteesta kaksiulotteinen kuva: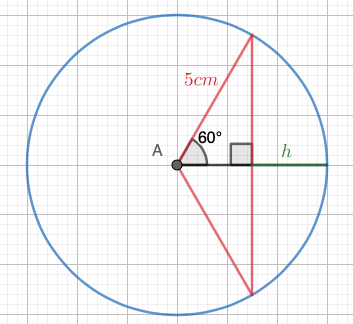 
\[\begin{align*} \cos{60°}&=\frac{5,0-h}{5,0}\\ \frac{1}{2}&=\frac{5,0-h}{5,0}\\ 10,0-2h&=5,0\\ h&=2,5 \end{align*}\] Segmentin korkeus on \(2,5 \text{ cm}\).
Nyt voidaan laskea pallosektorin tilavuus \[\begin{align*} V&=\frac{2}{3}\pi r^{2}h\;\;\;\;\;\;\;\;\;\;\;\;\;\;|r=5,0 \text{ cm}, h=2,5 \text{ cm}\\ V&=\frac{2}{3}\pi ({5,0 \text{ cm}})^{2}\cdot (2,5 \text{ cm})\\ V&=\frac{125}{3}\pi \text{ cm}^{3}\\ V&≈131 \text{ cm}^{3} \end{align*}\]
Lasketaan vielä kalotin pinta-ala \[\begin{align*} A&=2\pi rh\;\;\;\;\;\;\;\;\;\;\;\;\;\;|r=5,0 \text{ cm}, h=2,5 \text{ cm}\\ A&=2\pi\cdot(5,0 \text{ cm})\cdot(h=2,5 \text{ cm})\\ A&=25\pi \text{ cm}^{2}≈79\text{ cm}^{2} \end{align*}\]
Vastaus: Pallosektorin tilavuus on \(131 \text{ cm}^{3}\) ja kalotin pinta-ala on \(79\text{ cm}^{2}\).
5.3 Lieriö
Lieriön erityistapaus on suora ympyrälieriö, jota kutsutaan myös sylinteriksi. Lieriö, jonka pohja on muodoltaan monikulmio on särmiö.
Lieriön pinta-ala ja tilavuus
Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa, muodostuu lieriöpinta. Kun lieriöpinta leikataan kahdella tasolla, syntyy lieriö. Lieriön vaipan pinta-ala saadaan laskettua sen pohjan piirin 
ja lieriön korkeuden avulla 
Lieriön tilavuus saadaan laskettua pohjan pinta-alan 
ja lieriön korkeuden avulla 
5.4 Kartio
Kartion tilavuus
Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa ja lisäksi suora kulkee koko ajan saman pisteen kautta, syntyy kartiopinta. Kun kartiopinta leikataan tasolla, syntyy kartio. Kartion tilavuus lasketaan sen pohjan pinta-alan \(A_p\) ja korkeuden \(h\) avulla \[V = \frac{A_p h}{3}.\]
Erikoistapauksia kartiolle ovat ympyräkartio ja pyramidi, eli särmäkartio. Jos ympyräkartion korkeusjana on kohtisuorassa pohjaa vastaan, kyseessä on suora ympyräkartio.
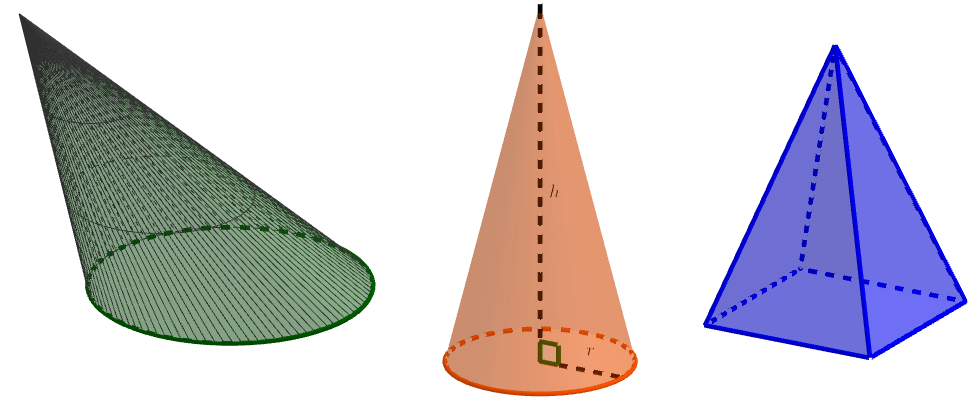
Suoran ympyräkartion vaipan pinta-ala
Suoran ympyräkartion vaipan pinta-ala voidaan laskea pohjaympyrän säteen ja kartion sivujanan 
avulla 
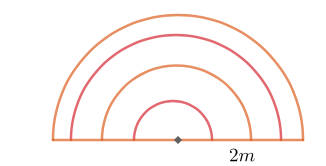Puoliympyrän muotoisesta kankaanpalasta tehdään ympyräkartion muotoinen teltta. Puoliympyrän säde on \(2,0 \text{ m}\). Mahtuuko \(180\text{ cm}\) pitkä henkilö seisomaan ja makaamaan teltassa?
Hahmotellaan teltasta piirros: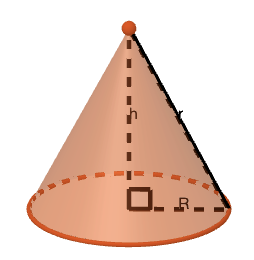 
Teltan pohjan säde on \(R\) ja korkeus \(h\). Teltan ulkosivu on \(r\).
Ratkaistaan ensin, pystyykö henkilö makaamaan teltassa, eli onko teltan pohjan halkaisija pitempi kuin \(180\text{ cm}\).
Kartion pohjaympyrän kehän pituus on yhtä suuri kuin puoliympyrän kaaren pituus: \[\begin{align*} 2\pi R&= \frac{1}{2}2\pi r\\ R&=\frac{r}{2}\;\;\;\;\;\;\;\;\;\;| r=2,0\text{ m}\\ R&=1,0\text{ m} \end{align*}\] Edelleen pohjaympyrän halkaisija on \(2R=2,0\text{ m}\). Henkilö pystyy siis makaamaan teltassa.
Ratkaistaan seuraavaksi teltan korkeus ja pystyykö henkilö seisomaan sen sisällä. Teltan korkeus saadaan ratkaistua Pythagoraan lauseen avulla. \[\begin{align*} r^{2}&=h^{2}+R^{2}\\ h&=\sqrt{r^{2}-R^{2}}\\ h&=\sqrt{(2,0 \text{ m})^{2}-(1,0\text{ m})^{2}}=\sqrt{3}≈1,73\text{ m} \end{align*}\]
Henkilö ei siis pysty seisomaan suorassa teltassa.
Vastaus: Henkilö pystyy makaamaan teltassa, mutta ei seisomaan.
Tehtäviä
Tehtävä 1
Tekokuut A ja B kiertävät Maata ympyränmuotoisilla radoilla. Tekokuun A rata on \(50 \text{ km}\) pitempi kuin tekokuun B rata. Kuinka paljon korkeammalla tekokuu A on? [S94/2]
mikäb ittu tää o
—wtf voiko joku kertoo vastauksen?
—Tee yhtälö jossa on tuntemattomana ratojen korkeusero. Tai aloita miettimällä paljonko enemmän narua tarvitaan maapallon päivantasaajan kohdalla jos naru nostetaan metrin irti maasta.
—joo en osaa
—
Tehtävä 2
Helikopteri tekee turistilentoja etelämantereen ympäri lentokorkeutenaan 500 metriä. Kuinka pitkän matkan helikopteri lentää kiertäessään koko mantereen? Voit olettaa etelämantereen sijaitsevan kokonaisuudessaan Eteläisen napapiirin sisäpuolella. Eteläinen napapiiri sijaitsee \(66^{°}\) etelään päiväntasaajasta. Maapallon säde on 6370 kilometriä.
Tehtävä 3
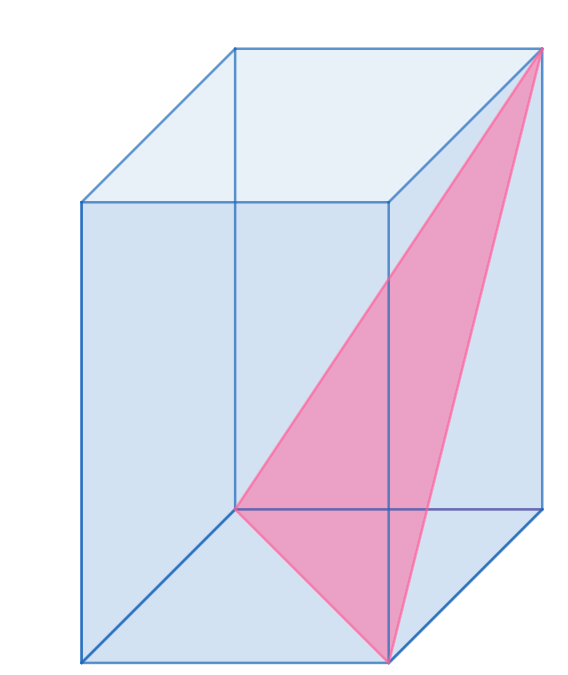Laatikossa, jonka pohja on neliö, on kolmio asetettu siten, että kolmion kantakulmat ovat laatikon pohjan vastakkaisissa kulmissa. Kolmion kärki on laatikon yläkulmassa. Laske kolmion pinta-ala, kun laatikon kannan pituus on 3 ja tilavuus on 45.
Tehtävä 4
Jäätyneen kuplan säde on 3 cm. Kuplan pinnasta \(\frac{2}{3}\) on jäässä.
- Kuinka suuren pinta-alan jää peittää?
Approksimoidaan jään raja siten, että se on taso, joka jakaa kuplan kahteen pallosegmenttiin: 
- Laske jäätymättömän alueen (pienemmän kalotin) korkeus
- Laske jäätymättömän segmentin tilavuus.
Tehtävä 5
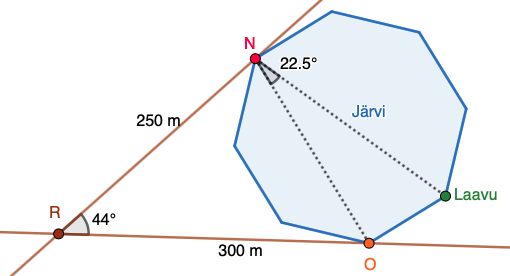Kaksi mökkiä, N ja O, sijaitsevat säännöllisen kahdeksankulmion ympärillä. Järven rannalla on myös laavu. Järven ympäri kulkee kaksi tietä, joiden risteyksestä R etäisyys mökille N on 250 m ja mökille O 300 m.
- Kuinka pitkä matka on soudettava, jotta päästään mökiltä N mökille O?
- Kuinka pitkä matka mökiltä N on laavulle?
Tehtävä 6
Syntymäpäiväpallot on puhallettu siten, että isomman pallon sisällä on pienempi pallo. Pienempi pallo vie neljänneksen suuremman pallon tilavuudesta. Suuremmassa pallossa on materiaalia \(450\text{ cm}^{2}\). Laske, paljonko materiaalia on pienemmässä pallossa.
Tehtävä 7
Faaraon hautapaikka on kullalla vuoratussa kuution muotoisessa kammiossa pyramidin sisällä. Pyramidin särmä on 50 m ja sen neliön muotoisen pohjan kannan pituus on 30 m. Kammio on 2% koko pyramidin tilavuudesta.
- Laske kammion tilavuus.
- Muumion kammio vuorataan kullalla. Yhdelle neliömetrille valetaan yhden senttimetrin paksuinen kerros kultaa. Montako kiloa kultaa kammion seinissä on yhteensä? Kullan tiheys on 19,32 \(\frac{g}{cm^{3}}\)
Tehtävä 8
Liisalla on symmetrinen maljakko, jossa on kaarevat kulmat. Maljakon pohjapiirrustus on alla olevassa kuvassa. Kapeimmillaan maljakko on 10 cm leveä. Maljakon korkeus on 12 cm.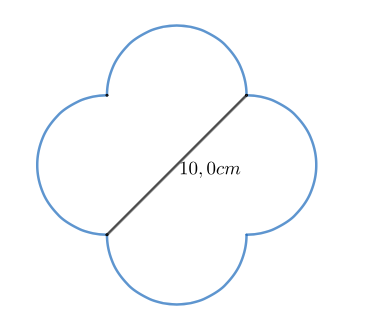 
Mikä on maljakon tilavuus desilitroina?
Vanhoja YO-tehtäviä
1.
Tasaisella maanpinnalla sijaitsevan tornin huippu näkyy eräästä paikasta katsottuna 3,5 asteen kulmassa vaakasuoraan tasoon nähden. Tasan puoli kilometriä kauempaa katsottuna kulma on 2,5 astetta. Mikä on tornin korkeus, ja mitkä ovat katseluetäisyydet? [S00/04]
VASTAUS: Tornin korkeus on 76,3 m ja katseluetäisyydet 1250 m ja 1750 m.
RATKAISU:
Jos tornin korkeus on \(h\) m ja katseluetäisyydet \(x\) m ja \(x+500 m\), saadaan suorakulmaisista kolmioista sekä \(h=x\tan3,5°\) että \(h=(x+500)\tan2,5°\). Siis \(x\tan3,5°=(x+500)\tan2,5°\), josta \(x=\dfrac{500\tan2,5°}{\tan3,2°-\tan2,5°}≈1247,3\) ja \(h=x\tan3,5°≈76,29\).
2.
Kuutio pienennetään toiseksi kuutioksi siten, että sen kokonaispinta-ala pienenee \(36\%\). Kuinka monta prosenttia tilavuus pienenee? [S04/3]
VASTAUS: Tilavuus pieneni \(48,8\%\).
RATKAISU:
Jos kuution svun pituus on \(a\), on kuution pinta-ala \(6a^{2}\) ja tilavuus \(a^{3}\). Pienennetyn kuution pinta-ala on \(0,64\cdot6a^{2}=6(0,8a)^{2}\), joten sen kuution sivun pituus on \(0,8a\) ja tilavuus \((0,8a)^{3}=0,512a^{3}\). Tilavuuksien suhde on 0,512, joten tilavuus on pienentynyt \(100(1-0,512)\%=48,8\%\)
3.
Kolmion \(ABC\) kulman \(C\) puolittaja leikkaa sivun \(AB\) pisteessä \(D\). Pisteiden välisille etäisyyksille on voimassa \(CD=6\), \(AD=4\) ja \(DB=3\). Määritä kolmion sivujen \(AC\) ja \(BC\) pituuksien tarkat arvot. [S13/6]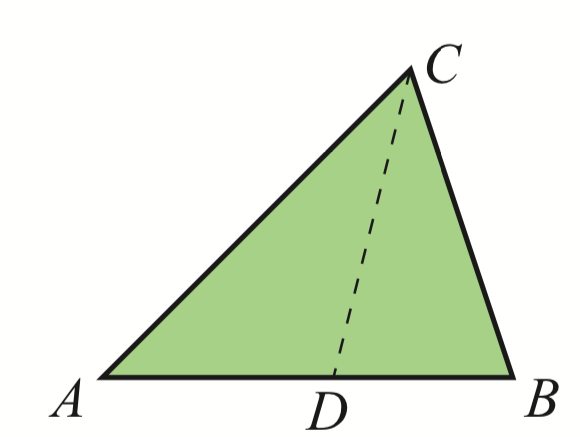 
VASTAUS: Sivu \(AC=4x=8\) ja sivu \(BC=3x=6\).
RATKAISU:
Kulmanpuolittajalauseen nojalla saadaan \(CA=4x\) ja \(CB=3x\). Olkoon \(\alpha\) puolet kulmasta \(BCA\). Kosinilauseen nojalla \[\begin{align*} \begin{cases} 4^{2}=(4x)^{2}+6^{2}-2\cdot4x\cdot6\cos\alpha\\ 3^{2}=(3x)^{2}+6^{2}-2\cdot3x\cdot6\cos\alpha. \end{cases} \end{align*}\] Kerrotaan ylempi yhtälö 3:lla ja alempi -4:llä ja lasketaan puolittain yhteen.
Näin saadaan \(12=12x^{2}-36\Leftrightarrow x^{2}=4\Leftrightarrow x=\pm2.\) Vain \(x=2\) kelpaa, joten \(AC=4x=8\) ja \(BC=3x=6\).
4.
Kuvion suorakulmaisessa kolmiossa on toisen kateetin projektio hypotenuusalle yhtä pitkä kuin toinen kateetti: \(AD=BC=a\). Määritä kolmion kulmat asteen tarkkuudella. [K05/6]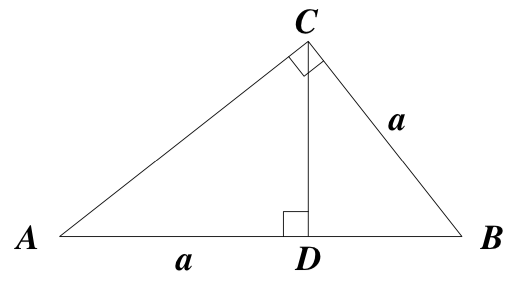 
VASTAUS: Kulmat ovat 38°, 52° ja 90°.
RATKAISU:
Kolmiot \(ABC\) ja \(CBD\) ovat yhdenmuotoiset. Jos \(BD=b\), on \(\dfrac{a}{a+b}=\dfrac{a}{b}\), josta \(a^{2}=b(a+b)\) eli \(b^{2}+ab-a^{2}=0\). Tästä saadaan, koska \(b>0\), \(b=\frac{1}{2}(-1+\sqrt{1+4})a\).
Kulmalle \(\angle CBD=\beta\) saadaan tästä \(\cos\beta=\frac{b}{a}=\frac{1}{2}(-1+\sqrt{5})\), josta \(\alpha≈51,83°\).
Edelleen kulmalle \(\angle BAC=90°-\beta≈38,17°\).
5.
Talosta 4 metrin korkeudelta katsottaessa linkkimaston huippu näkyy 25 asteen korkeuskulmassa ja 12 metriä korkeammalta katsottaessa 22,5 asteen korkeuskulmassa vaakatasoon nähden. Maston perusta on 21 metriä korkeammalla kuin talon perusta. Määritä maston korkeus 0,1 metrin tarkkuudella. [K04/6]
VASTAUS: 90,4 m.
RATKAISU:
Olkoon \(s\) maston huipun \(H\) ja perusta \(P\) määräämä suora ja kohdatkoon \(s\) talon perustan tason pisteessä \(T\). Olkoon \(d\) talon vaakasuora etäisyys suorasta \(s\) ja \(x\) maston korkeus \(PH\). Olkoon vielä \(A\) ja \(B\) suoran \(s\) pisteitä siten, että \(AT=4\)m ja \(BT=16\)m .
Suorakulmaisesta kolmiosta, jonka muodostavat 4 metrin korkeudelta katsova, \(H\) ja \(A\), saadaan \(\tan25°=\dfrac{x+17}{d}\) ja kolmiosta, jonka muodostavat 12 metriä korkeammalta katsova, \(H\) ja \(B\), saadaan \(\tan22,5°=\dfrac{x+5}{d}\). Näin ollen \(\dfrac{x+17}{\tan25°}=d=\dfrac{x+5}{\tan22,5°}\).
Tästä voidaan ratkaista \(x=\dfrac{17\tan22,5°-5\tan25°}{\tan25°-\tan22,5°}≈90,4151\).
6.
Kuinka monta prosenttia kuvassa olevan pienemmän neliön sivun pituus on suuremman neliön sivun pituudesta? Kuinka monta prosenttia pienemmän neliön pinta-ala on suuremman neliön pinta-alasta? Suuremman neliön sivun pituus on 1. [S17/5 (B-osa)]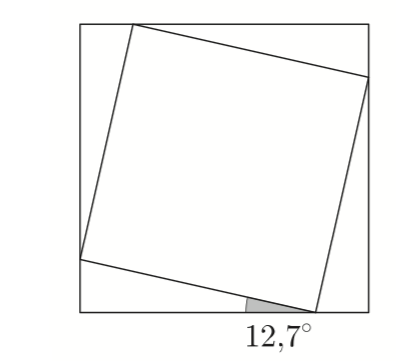 
VASTAUS: Pienemmän pinta-ala on n.70 prosenttia suuremmasta pinta-alasta.
RATKAISU:
Merkitään annetun kulman vastaista kateettia \(b\) ja viereistä kateettia \(a\) sekä pienemmän neliön sivua \(c\).
\(a+b=1\) on ison neliön sivun pituus.
Kolmiosta \(\tan(12,7°)=\frac{b}{a} \Rightarrow a≈0,184\) ja \(b≈0,816\).
Pythagoraan lauseesta \(c^{2}=a^{2}+b^{2}\) saadaan ratkaistua \(c≈0,837\) eli sivu on noin 84 prosenttia suuremmasta sivusta. \(c^{2}≈0,700\) eli pinta-ala on noin 70 prosenttia suuremmasta pinta-alasta.
7.
Suorakulmaisen kolmion toinen terävä kulma on 30 astetta. Kolmion hypotenuusan keskipisteeseen piirretään kuvion mukaisesti kohtisuora jana, jonka toinen päätepiste sijaitsee kolmion kateetilla. Laske niiden kahden osan pituuksien suhde, joihin kohtisuora jakaa kateetin. [K18/6 (B-osa)]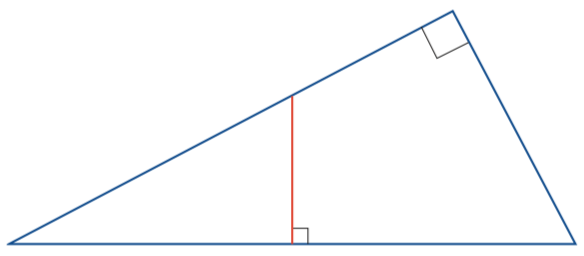 
VASTAUS: \(\dfrac{1}{2}\).
RATKAISU:
Suhde säilyy mittakaavan muutoksissa, joten voimme olettaa, että hypotenuusan pituus on 2.
Terävän kulman viereisen kateetin osan pituus on silloin \(\dfrac{1}{\cos30°}=\dfrac{2}{\sqrt{3}}\).
Koko kateetin pituus on \(2\cos30°=\sqrt{3}\).
Kateetin toisen osan pituus on siten \(\sqrt{3}-\dfrac{2}{\sqrt{3}}=\sqrt{3}(1-\dfrac{2}{3})=\dfrac{1}{\sqrt{3}}\). Kysytty suhde on siis \(\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{1}{\sqrt{3}}}=2\).
8.
Suoran ympyräkartion korkeus on \(5,0\) cm ja sen pohjan säde on \(2,0\) cm. Kartio katkaistaan niin, että yläreunan säde on \(1,0\) cm. Tämän jälkeen katkaistun kartion vaippa maalataan siniseksi ja sitä pyöritetään kyljellään paperilla. Määritä näin saadun sinisen rengasalueen pinta-ala yhden neliösenttimetrin tarkkuudella. [K12/9] 
VASTAUS: 68 \(cm^{2}\)
RATKAISU:
Leikataan kartiota sen akselin kautta kulkevalla tasolla.
Olkoon leikkauskuviossa \(A\) pohjan keskipiste, \(AB\) pohjan säde, \(C\) kartion huippu, \(D\) katkaistun kartion yläympyrän keskipiste ja \(DE\) yläympyrän säde.
Suorakulmaisesta kolmiosta \(ABC\) saadaan, että reunaviiva \(CB=\sqrt{2^{2}+5^{2}}=\sqrt{29}\). Yhdenmuotoisuuden perusteella \(\dfrac{CE}{CB}=\dfrac{DE}{AB}=\dfrac{1}{2}\), josta saadaan \(CE=\dfrac{1}{2}CB=\dfrac{1}{2}\sqrt{29}\).
Tämä on rengasalueen sisäympyrän säde. Ulkoympyrän säde on \(CB=\sqrt{29}\). Rengasalueen pinta-ala on siten \(\pi(\sqrt{29})^{2}-\pi(\dfrac{1}{2}\sqrt{29})^{2}=\dfrac{3}{4}\cdot29\pi≈68,3296 (cm^{2}).\)
9.
Vesikaukalon päädyt ovat tasasivuisen kolmion mauotoiset, ja kolmion sivujen pituus on \(a\). Kaukalon pohja koostuu kahdesta suorakulmion muotoisesta levystä, joiden pituus on \(b\).
Vaakasuorassa oleva kaukalo on aluksi täynnä vettä. Sitä kallistetaan pituussuunnassa niin, että vedenpinta ulottuu vasemmanpuoleisen päätykolmion alakulmaan alla olevan kuvion mukaisesti. Kuinka monta prosenttia vedestä valuu pois kallistuksen aikana?
Tämän jälkeen kaukalo palautetaan takaisin vaakasuoraan asentoon. Kuinka korkealla vedenpinta on kaukalon syvimmästä kohdasta mitattuna? [S16/6]
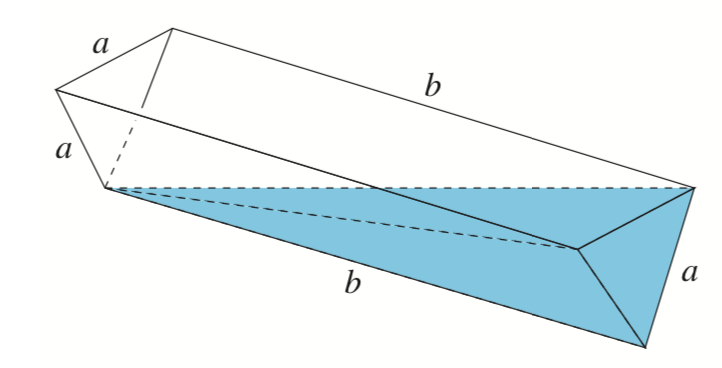
VASTAUS: a. \(≈67\%\) b.\(\dfrac{a}{2}\)
RATKAISU:
a.
Kaukalo on suora särmiö. Jos päätykolmion pinta-ala on \(A\), niin kaukalon tilavuus on \(V_{k}=Ab\).
Jäljelle jäänyt vesi muodostaa kolmisivuisen pyramidin, jonka tilavuus on \(V_{v}=\dfrac{1}{3}Ab\). Poistuneen veden tilavuus on siten \(V=\dfrac{2}{3}Ab=\dfrac{2}{3}V_{k}\).
Vettä on valunut pois \(\dfrac{2}{3}\) koko määrästä, eli \(\dfrac{200}{3}\%=66\dfrac{2}{3}\%≈67\%\).
b.
Päätykolmion korkeus \(H=\dfrac{a\sqrt{3}}{2}\) ja pinta-ala \(A_{1}=\dfrac{a^{2}\sqrt{3}}{4}\).
Päätykolmioiden pinta-aloja vertaamalla \(\dfrac{d^{2}}{a^{2}}=\dfrac{1}{3}\) tai yhtälöstä \(\dfrac{1}{3}A_{1}b=\dfrac{\sqrt{3}}{4}d^{2}b\) saadaan \(d=\dfrac{a}{\sqrt{3}}\).
Veden korkeus on siten \(\dfrac{d\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{\sqrt{3}\cdot2}=\dfrac{a}{2}\).
10.
Pöydällä on kolme samankokoista palloa, joista kukin koskettaa kahta muuta. Niiden päälle asetetaan neljäs samanlainen pallo, joka koskettaa kaikkia kolmea alkuperäistä palloa. Mikä on rakennelman korkeus? Anna vastauksena tarkka arvo pallojen säteen avulla lausuttuna.[S13/10] 
VASTAUS: Rakennelman korkeus on \(h+2r=\left(\sqrt{\frac{8}{3}}+2\right)r\).
RATKAISU:
Olkoon pallojen säde \(r\). Niiden keskipisteet ovat säännöllisen tetraedrin kärjissä. Tetraedrin särmän pituus on \(2r\), joten jokainen tahdo on tasasivuinen kolmio, jonka korkeus on \(\sqrt{3}r\).
Tetraedrin korkeusjana leikkaa pohjakolmion mediaanien leikkauspisteessä, jonka etäisyys pohjakolmion kärjestä on \(\frac{2}{3}\sqrt{3}r\).
Pythagoraan lauseen nojalla tetraedrin korkeus \(h\) toteuttaa yhtälön \[\begin{align*} h^{2}+\left(\frac{2}{3}\sqrt{3}r\right)^{2}=(2r)^{2}\Leftrightarrow h^{2}=\frac{8}{3}r^{2}. \end{align*}\] Rakennelman korkeus on \(h+2r=\left(\sqrt{\frac{8}{3}}+2\right)r\).
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.