MAA8 Tilastot ja todennäköisyys
Kurssin tavoitteena on, että opiskelija
- osaa havainnollistaa diskreettiä tilastollista jakaumaa sekä määrittää ja tulkita jakauman tunnuslukuja
- osaa määrittää korrelaatiokertoimen ja lineaarisen regressiokäyrän
- perehtyy kombinatorisiin menetelmiin
- perehtyy todennäköisyyden käsitteeseen ja todennäköisyyksien laskusääntöihin
- ymmärtää diskreetin todennäköisyysjakauman käsitteen ja oppii määrittämään jakauman odotusarvon ja soveltamaan sitä
- osaa käyttää ohjelmistoja digitaalisessa muodossa olevan datan hakemisessa, käsittelyssä ja tutkimisessa sekä tilastollisen tiedon esittämisessä
- osaa hyödyntää ohjelmistoja jakaumien tunnuslukujen määrittämisessä sekä todennäköisyyksien laskemisessa annetun jakauman ja parametrien avulla.
Keskeiset sisällöt
- keskiluvut ja keskihajonta
- korrelaatio ja lineaarinen regressio
- klassinen ja tilastollinen todennäköisyys
- permutaatiot ja kombinaatiot
- todennäköisyyksien laskusäännöt
- binomijakauma
- diskreetti todennäköisyysjakauma
- diskreetin jakauman odotusarvo
1. Tilastot
Tilastoitavat suureet voivat olla joko diskreettejä tai jatkuvia. Diskreetit muuttuja voi olla numeerinen, esimerkiksi yksilöiden lukumäärä, tai ei-numeerinen, esimerkiksi vaatekoko.
Jatkuva muuttuja voi saada ainakin teoriassa minkä tahansa lukuarvon tietyltä välilä. Vaikkapa tutkittaessa suomalaisten ikää muuttuja voi saada minkä tahansa arvon esim. väliltä \([0,100]\).
Joissain tutkimuksissa ei ole mahdollista asettaa havaintoja suuruusjärjestykseen. Tällöin muuttujia tarkastellaan vain laatuasteikolla, jolloin mediaania tai keskiarvoa ei voida laskea.
1.1 Keskiluvut
Tilastoaineistot ovat usein erittäin laajoja, jonka vuoksi niiden tiivistäminen on tarpeellista. Tilastoaineistoja voidaan tiivistää esimerkiksi erilaisten tunnuslukujen avulla, joita ovat mm. keski- ja hajontaluvut.
Tilastoaineistoissa tiettyjen arvojen lukumäärää kutsutaan frekvensseiksi. Esimerkiksi, kuinka moni oppilas luokassa sai arvosanan 8.
Frekvenssin lisäksi tilastoista voidaan laskea myös summafrekvenssit, suhteelliset frekvenssit ja suhteelliset summafrekvenssit.
Summafrekvenssit kuvaavat tiettyyna arvoon mennessä kertyneitä lukumääriä ja suhteelliset frekvenssit lukumäärien prosenttiosuuksia kokonaisuudesta.
Keskiarvo
Olkoon luvut \(x_1, x_2, x_3, ..., x_n\). Näiden lukujen keskiarvo on \[\begin{align*} \overline{x}=\dfrac{x_1+x_2+x_3+...+x_n}{n}=\dfrac{\displaystyle\sum_{i=1}^{n}x_i}{n} \end{align*}\]
Moodi ja mediaani
Moodi, eli tyyppiarvo, on aineistossa eniten esiintyvä luku tai luvut.
Mediaani on suuruusjärjestyksessä keskimmäinen luku. Jos lukuja on parillinen määrä, mediaani on kahden keskimmäisen luvun keskiarvo.
Tilastoaineistoa voi olla tarpeen luokitella, eli tiivistää. Tämä parantaa luettavuutta, mutta sen jälkeen yksittäiset havainnot eivät ole enää näkyvissä lukijalle.
Luokitellussa aineistossa voi olla mediaaniluokka, johon mediaani kuuluu. Mediaaniluokka määritetään suhteellisten frekvenssien avulla.
Tyyppiarvoluokka on vastaavasti se luokka, johon kuuluvia havaintoja on eniten.
1.2 Hajontaluvut
Tilastoaineiston havaintoarvot voivat vaihdella toisistaan paljon. Tätä kutsutaan hajonnaksi. Vaihteluväli on se väli, joka on pienimmän ja suurimman arvon välillä.
Keskihajonta
Olkoon luvut \(x_1, x_2, x_3,...x_n\). Näiden lukujen keskihajonta \(s\) on \[\begin{align*} s&=\sqrt{\dfrac{(x_1-\overline{x})^{2}+(x_2-\overline{x})^{2}+(x_3-\overline{x})^{2}+...+(x_n-\overline{x})^{2}}{n}}\\ &=\sqrt{\dfrac{\displaystyle\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n}}, \end{align*}\] tässä \(\overline{x}\) on lukujen \(x_1,x_2,x_3,...,x_n\) keskiarvo.
Keskihajonta voidaan myös merkitä sigmalla \(\sigma\).
Keskihajonta kuvaa, kuinka paljon tilaston yksittäiset havaintoarvot poikkeavat tilaston keskiarvosta.
Poikkeamien keskiarvoa \(\dfrac{\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})^{2}}{n}\) kutsutaan varianssiksi.
Jos tutkittavana on jokin suuri joukko, esim. kaikki ihmiset Suomessa, ei ole järkevää suorittaa tutkimusta kaikille vaan ottaa tästä perusjoukosta pienempi joukko, eli otos, jolle tutkimus suoritetaan.
Otoksesta saaduista tuloksista tehdään oletukset liittyen koko perusjoukkoon.
Otoskeskihajonta
Otoskeskihajonta poikkeaa keskihajonnasta ainoastaan otoksen koossa: otoksen koko ei ole \(n\) vaan \(n-1\). \[\begin{align*} s_{n-1}=\sqrt{\dfrac{\displaystyle\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n-1}} \end{align*}\]
Normitettu arvo
\[\begin{align*} z=\dfrac{x-\overline{x}}{s}, \end{align*}\] tässä \(\overline{x}\) on tilaston keskiarvo ja \(s\) keskihajonta.
Normitetun arvon avulla voidaan tarkastella sitä, kuinka monen keskihajonnan päässä keskiarvosta muuttujan arvo on. Tätä voidaan hyödyntää esimerkiksi kahden eri muuttujan vertailussa: kumpi poikkeaa enemmän keskiarvosta?
Leikkipuistossa on eri ikäisiä lapsia. Lasten iät on lueteltu oheisessa taulukossa
| Ikä (v) | f |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 4 |
| 6 | 4 |
Lasketaan
a. Keskiarvo
\[\begin{align*} \mu&=\frac{f_1\cdot x_1+f_2\cdot x_2+...+f_n\cdot x_n}{N}\\&=\frac{0\cdot0+1\cdot2+2\cdot1+3\cdot3+4\cdot6+5\cdot4+6\cdot4}{2+1+3+6+4+4}\\&=\frac{81}{20}\\&=4,05 \end{align*}\]
Leikkipuistossa olevien lasten iän keskiarvo on \(4,05\).
b. varianssi ja keskihajonta
\[\begin{align*} \sigma^{2}&=\dfrac{\displaystyle\sum_{i=1}^{N}(x_i-\mu)^{2}}{N}\\ &=\dfrac{(1-4,05)^{2}+(1-4,05)^{2}+(2-4,05)^{2}+...+(6-4,05)^{2}}{20}\\ &=\dfrac{2\cdot(1-4,05)^{2}+(2-4,05)^{2}+3\cdot(3-4,05)^{2}+6\cdot(4-4,05)^{2}+4\cdot(5-4,05)^{2}+4\cdot(6-4,05)^{2}}{20}\\ &=2,2475\\ &≈2,25 \end{align*}\]
Varianssi on keskihajonnan neliö, eli \[\begin{align*} \sigma&=\sqrt{2,2475}\\&=1,49917\\&≈1,50 \end{align*}\]
Leikkipuistossa olevien lasten iän keskihajonta on \(1,5\).
1.2 Tilastojen havainnollistaminen
Tilastoja voidaan havainnollistaa erilaisten diagrammien avulla. Diagrammityyppi valitaan sen mukaan, mihin lukijan tulisi kiinnittää tuloksissa huomio.
- Pylväsdiagrammi soveltuu hyvin frekvenssien havainnollistamiseen
- Viivakuviolla havainnollstetaan kehityssuuntaa sekä vaihtelua esim. ajan suhteen
- Ympyräkuviota voidaan hyödyntää eri kokonaisuuksien havainnollistamiseen
Kertymäkuvaajaa hyödynnetään summafrekvenssin ja suhteellisen summafrekvenssin havainnollistamiseen. Jatkuvan muuttujan kuvaaja on murtoviiva, ja diskreetin muuttujan kuvaaja on porrastettu.
1.3 Korrelaatio ja lineaarinen regressio
Useimpiin tutkimuksiin sisältyy kysymys siitä, miten kaksi tai useampi eri asia on riippuvainen toisistaan. Tällaista kahden ilmiön välistä tilastollista riippuvuutta kutsutaan korrelaatioksi.
Riippuvuuden selvittäminen auttaa ennustamaan sekäa arvioimaan toisen tilastomuuttujan suuruutta.
Kun tilastomuuttujien välillä on lineaarista riippuvuutta, puhutaan tällöin lineaarisesta regressiosta.
Olkoon tilastomuuttujat \(x\) ja \(y\). Näiden tilastomuuttujien vastinparit \((x_iy_i)\), \(i=1,2,...,n\).
Arvoparien joukkoa approksimoivaa suoraa kutsutaan regressiosuoraksi, jonka yhtälö on \(y=ax+b\). \[\begin{align*} a=\frac{\sum y_i-b\sum x_i}{n}\;\;\;\;\;\;\text{ ja }\;\;\;\;\;\;b=\frac{n\sum x_{i}y_{i}-(\sum x_i)(\sum y_i)}{n\sum x^{2}_{i}-(\sum x_{i})^{2}} \end{align*}\]
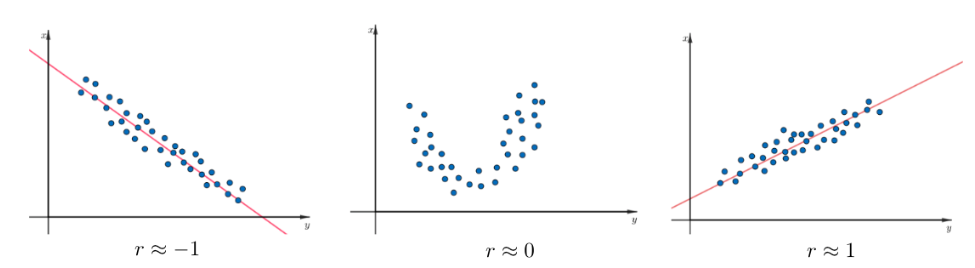
Kahden tilastomuuttujan välistä tilastollisen riippuvuuden suuruutta kuvaa korrelaatiokerroin \(r\). Mitä suurempi korrelaatokerroin, sitä vahvempi on tilastollinen riippuvuus.
Korrelaatiokerroin
\[\begin{align*} r=\dfrac{\sum(x_i-\overline{x}(y_i-\overline{y})}{\sqrt{\sum(x_i-\overline{x})^{2}\sum(y_i-\overline{y})^{2}}} \end{align*}\]
Korrelaatiokerroin \(r\) on aina välillä \([-1,1]\), ja mitä lähempänä korrelaatiokerroin \(r\) on lukua 1, sitä suurempi korrelaatio on.
Korrelaatiokerroin voi olla negatiivista tai positiivista. Negatiivinen korrelaatio tarkoittaa sitä, että muuttujan \(x\) kasvaessa muuttuja \(y\) vähenee. Vastaavasti positiivisen korrelaation tilanteessa muuttujan \(x\) kasvaessa myös muuttuja \(y\) kasvaa.
Esimerkki
Open plugin
Muodostetaan väliaikojen regressiosuora sekä lasketaan sen korrelaatiokerroin.
RATKAISU:
Taulukosta pisteparit ovat \((10;0,68),(20;1,48),...,(100;7,70)\).
Kirjataan nämä taulukkosovellukseen ja saadaan
2. Todennäköisyys
- klassinen todnäk ja tilastollinen todnäk
- laskusäännöt
- kertolaskusääntö ja tapahtumien riippumattomuus
- yhteenlaskusääntö
2.1 Tilastollinen todennäköisyys
Frekvenssi ilmoitti tietyn havainnon lukumäärän tutkimuksessa. Kun tätä samaa tutkimusta toistetaan useasti, huomataan suhteelisen frekvenssin keskittyvän tietyn luvun läheisyyteen. Tätä tapahtuman suhteellista frekvenssiä kutsutaan tilastolliseksi todennäköisyydeksi.
Tilastollinen todennäköisyys
\[\begin{align*} P(A)=\dfrac{f}{n}, \end{align*}\] jossa \(A\) on tapahtuma, \(f\) on frekvenssi (eli tapahtuman \(A\) esiintymiskertojen lukumäärä) ja \(n\) on koko aineiston lukumäärä.
Kirjain \(P\) tulee englannin kielen sanasta probability eli todennäköisyys.
Varman tapahtuman todennäköisyys on \(100\%=1\) ja mahdottoman tapahtuman todennäköisyys on vastaavasti \(0\%=0\).
2.2 Klassinen todennäköisyys
Tapahtuma \(A\) voi olla yksi mahdollisista tapauksista. Esimerkiksi nopassa on kuusi tahkoa, joten on mahdollista heittää mikä tahansa luvuista \(1-6\).
Nämä yksittäiset tapaukset: \(P(\)Nopan heitolla saadaan silmäluvuksi 1\()\), \(P(\)Nopan heitolla saadaan silmäluvuksi 2\()\),... ovat nimeltään alkeistapauksia.
Suotuisaksi alkeistapaukseksi kutsutaan sitä tulosta, jolla saadaan haluttu tapahtuma. Esimerkiksi tapahtuman \(P(\)Nopan heitolla saadaan silmäluvuksi 2\()\) suotuisa alkeistapaus on heittää silmäluku 2. Tämän tapahtuman todennäköisyys on \(\frac{1}{6}\).
Klassinen todennäköisyys
Tapahtuman \(A\) klassinen todennäköisyys on \[\begin{align*} P(A)=\dfrac{\text{Suotuisten alkeistapausten lukumäärä}}{\text{Kaikkien alkeistapausten lukumäärä}}=\dfrac{k}{n} \end{align*}\]
Geometrinen todennäköisyys
Myös geometrisia ominaisuuksia voidaan pitää alkeistapauksina. Tällöin puhutaan geometrisesta todennäköisyydestä: \[\begin{align*} P(A)=\dfrac{\text{Suotuisa mitta}}{\text{Koko mitta}}=\dfrac{k}{n} \end{align*}\]
Vinkki: Merkintään \(P(A)\) kannattaa kirjoittaa \(A\):n tilalle jokin tarkentavampi nimi jos tehtävässä on kyse jostain tietystä ilmiöstä, tämä helpottaa muistamista. (Esim. Jos tehtävässä nostetaan mustia, punaisia ja vihreitä sukkia, mustan sukan nostamisen alkeistapauksen nimi voisi olla \(P(musta)\). )
Linja-auto pysähtyy pysäkille 15 minuutin välein. Lilja kävelee pysäkille kelloa katsomatta. Kuinka suurella todennäköisyydellä Lilja joutuu odottamaan linja-autoa vähintään 8 minuuttia?
RATKAISU:
Piirretään linja-auton aikataulusta aikajana: 
Odotus "vähintään 8 minuuttia" tarkoittaa, että bussi saapu tasan 8 minuutin kuluttua saapumisesta, tai myöhemmin.
Olkoon \(A\)="Odotusaika on vähintään 8 minuuttia". \[\begin{align*} P(A)=\frac{m(A)}{m(E)}=\frac{(15-8)\text{ min}}{15\text{ min}}=\frac{7\text{ min}}{15\text{ min}}=0,4667≈0,47 \end{align*}\]
2.3 Kertolaskusääntö
Tutkittavat tapaukset voivat olla toisistaan riippuvaisia tai riippumattomia. Esimerkiksi heitettäessä nopalla kaksi kertaa, peräkkäisten heittojen tulokset ovat toisistaan riippumattomia.
Riippumattomien tapahtumien kertolaskusääntö
Olkoon tapahtumat \(A\) ja \(B\), näille tapahtumille \[\begin{align*} P(A \text{ ja }B)=P(A)\cdot P(B) \end{align*}\]
Joko tai -tilanne on esimerkki toisistaan riippuvaisista tapahtumista: joko ihminen elää tai on kuollut.
Toinen mahdollisuus toisistaan riippuvista tapahtumista on se, ettei tapahtumaa \(B\) voi tapahtua ellei myös tapahtuma \(A\) tapahdu. Esimerkiksi kahden marmorikuulan nostaminen maljasta peräjälkeen palauttamatta ensimmäistä marmorikuulaa takaisin maljaan.
Yleinen kertolaskusääntö
Olkoon tapahtumat \(A\) ja \(B\), näille tapahtumille \[\begin{align*} P(A\text{ ja }B)=P(A)\cdot P(B|A) \end{align*}\]
Kertolaskusäännössä ei ole väliä tapahtumien järjestyksellä: \[\begin{align*} P(A\text{ ja }B)=P(A)\cdot P(B|A) \Leftrightarrow P(B\text{ ja }A)=P(B)\cdot P(A|B) \end{align*}\]
Tapahtumat \(A\) ja \(B\) ovat riippumattomia täsmälleen silloin, kun \(P(A\text{ ja }B)=P(A)\cdot P(B)\).
2.4 Yhteenlaskusääntö
Yhteenlaskusääntö
Olkoon tapahtumat \(A\) ja \(B\), näille tapahtumille \[\begin{align*} P(A\text{ tai }B)=P(A)+P(B)-P(A\text{ ja }B) \end{align*}\]
a
—Yhteenlaskusäännössä \(P(A\text{ tai }B)\) tarkoittaa siis "Joko A tai B tai molemmat".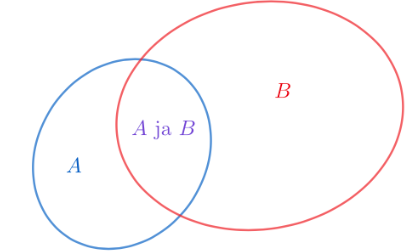 
Yhteenlaskusääntö erillisille tapahtumille
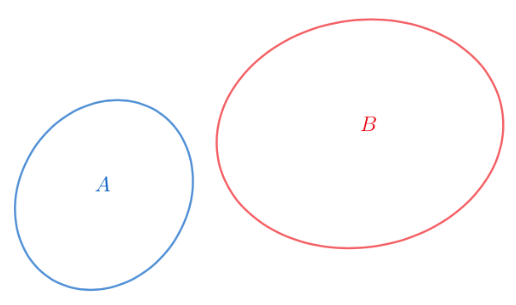
Tapahtumat \(A\) ja \(B\) ovat erilliset tapahtumat, niille \[\begin{align*} P(A\text{ tai }B)=P(A)+P(B) \end{align*}\]
Karkkipussissa on hedelmä- ja lakritsikarkkeja. Karkit ovat muodoltaan joko neliöitä tai ympyröitä.
Hedelmäkarkkeja on yhteensä 17, joista 7 on neliön muotoisia ja loput ympyröitä.
Lakritsikarkkeja on yhteensä 13, joista 9 on neliöitä ja loput ympyröitä.
Millä todennäköisyydellä karkkipussista satunnaisesti otettu karkki on ympyrän muotoinen lakritsikarkki tai neliön mallinen hedelmäkarkki?
Ratkaisu:
Merkitään erilaisia tilanteita hieman lyhyemmin:
Olkoon
\(L\)="lakritsikarkki"
\(H\)="hedelmäkarkki"
\(N\)="neliö"
\(Y\)="ympyrä"
Nyt siis etsitään yhdistelmiä \(LY\) tai \(HN\), eli merkitään \(P(LY\text{ tai }HN)\).
Yhteenlaskusäännön perusteella \[\begin{align*} P(LY\text{ tai }HN)&=P(LY)+P(HN)-P(LY\text{ ja }HN)\\ &=\frac{4}{30}+\frac{7}{30}+0\\ &=\frac{11}{30}\\ &≈0,3667 \end{align*}\]
Todennäköisyys nostaa pussista joko neliön muotoinen hedelmäkarkki tai ympyrän muotoinen lakritsikarkki on \(36,7\%\).
Nää laskut ei näy mulla
—3. Kombinatoriikka
Kombinatoriikassa tutkimuksen kohteena on se, kuinka monella eri tavalla jokin joukko voidaan jakaa osiin. Tähän vaikuttaa se, onko järjestyksellä väliä vai ei.
3.1 Tuloperiaate
Kun useasta vaihtoehdoista valitaan aina yksi useassa eri vaiheessa. Esimerkiksi asukokonaisuuden valitseminen.
Tuloperiaate
Vaiheessa \(i\) on vaihtoehtoja \(n_i\) kappaletta. Yhteensä valintoja tehdään \(k\) kappaletta, tällöin mahdollisia lopputuloksia on yhteensä \(n_1\cdot n_2\cdot n_3\cdot ... n_k\) kappaletta.
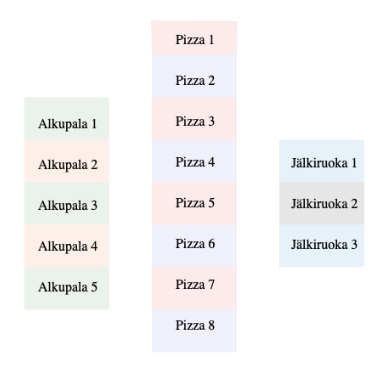Ruokalistalla on 5 erilaista alkupala vaihtoehtoa, 8 eri pääruokavaihtoehtoa ja 3 erilaista jälkiruoka vaihtoehtoa. Kuinka monta eri kolmen ruokalajin kokonaisuutta ruokalistasta voi valita?
Kaikkien yhdistelmien lukumäärä saadaan, kun vaihtoehtojen lukumäärät valintatilanteissa kerrotaan keskenään.
Tässä siis \(5\cdot8\cdot3=120\).
Asiakas voi siis valita 120 erilaista kolmen ruokalajin kokonaisuutta.
3.2 Permutaatio
Tuloperiaatetta hyödynnetään esimerkiksi erilaisten permutaatioiden lukumäärän laskemiseen. Permutaatio tarkoittaa joukon alkioista muodostettua jonoa.
Permutaatioiden lukumäärä
Joukossa on \(n\) alkiota. Tämän joukon permutaatioiden lukumäärä on \[\begin{align*} n!=n\cdot(n-1)\cdot(n-2)\cdot...\cdot2\cdot1 \end{align*}\]
Joukosta voidaan tehdä myös osajoukko, jossa ei ole kaikkia joukon alkioita, vaan ainoastaan \(k\) alkiota. Tällöin puhutaan joukon \(k\)-permutaatiosta (tai \(k\)-variaatioksi).
\(k\)-permutaatioiden lukumäärä
Joukossa on \(n\) alkiota ja \(k\leq n\). Joukon \(k\)-permutaatioiden lukumäärä on \[\begin{align*} (n)_k=n\cdot(n-1)\cdot...\cdot(n-k+1)=\dfrac{n!}{(n-k)!} \end{align*}\]
Erään metallimusiikkia soittavan bändin CD:llä on 12 eri kappaletta. Niistä kuunnellaan viisi kappaletta satunnaisessa järjeystyksessä. Kuinka monessa järjestyksessä kappaleet voidaan kuunnella?
RATKAISU: Erilaisia metallikappaleiden 5-permutaatioita on \[\begin{align*} (12)_{5}=12\cdot11\cdot10\cdot9\cdot8=95040. \end{align*}\]
Lasku voidaan suorittaa myös \[\begin{align*} (12)_{5}=\dfrac{12!}{(12-5)!}=\dfrac{12!}{7!}=95040. \end{align*}\]
3.3 Kombinaatio
Jos joukosta, jossa on \(n\) yksilöä, valitaan \(k\) yksilöä ja muodostetaan osajoukko, puhutaan \(k\)-kombinaatiosta.
\(k\)-kombinaatio
Joukossa on \(n\) alkiota, ja \(k\leq n\). Joukosta tehtyjen eri kombinaatioiden lukumäärä on \[\begin{align*} {{n}\choose{k}}=\dfrac{n!}{k!\cdot(n-k)!} \end{align*}\]
Lukua \({n}\choose{k}\) kutsutaan binomikertoimeksi, ja se kertoo, kunka monella erilaisella tavalla \(n\):stä alkiosta voidaan valita \(k\) alkiota.
Lotto-pelissä valitaan seitsemän numeroa 39 numerosta. Kuinka monella tavalla voit valita seitsemän numeroa?
Ratkaistaan siis kuinka monta erilaista 7-numeroista kombinaatiota 39 numerosta voidaan muodostaa. \[\begin{align*} {{39}\choose{7}}=\dfrac{39!}{7!\cdot(39-7)!}=15380937 \end{align*}\]
Erilaisia lottorivejä voidaan muodostaa 15380937 kappaletta.
3.4 Toistokoe
Nopanheitto usesasti peräkkäin on esimerkki toistokokeesta. Kun koetta toistetaan \(n\) kertaa, voidaan laskea todennäköisyys \(k\) onnistumiselle, jos jokaisen onnistumisen todennäköisyys on \(p\).
Binomitodennäköisyys
\[\begin{align*} P(k\text{ onnistumista})={{n}\choose{k}}p^{k}(1-p)^{n-k} \end{align*}\]
Kauran siemenistä \(82\%\) menestyy. Voidaan olettaa, että siemenien menestyminen on toisistaan riippumatonta. Kuinka monta kauransiementä tulee istuttaa, jotta todennäköisyys sille, että ainakin 2 kauran siementä menestyy ja kasvaa, on yli \(98\%\).
Merkitään siemenien lukumäärää kirjaimella \(n\).
Tapahtuma A="ainakin 2 kauran siementä menestyy" tarkoittaa samaa kuin "3 tai 4 tai 5 tai... \(n\) siementä menestyy".
Vastatapahtuma olisi tällöin \(\overline{A}\)="0 tai 1 siemen menestyy".
Jokaisen siemenen menestymisen todennäköisyys on \(0,85\), joten ei menestymisen todennäköisyys on \(1-0,85=0,15\).
Kyseessä on toistokoe. Lasketaan tapahtuman \(A\) komplementin \(\overline{A}\) todennäköisyys. \[\begin{align*} P(\overline{A})&=P(\text{0 menestyy})+P(\text{1 menestyy})\\ &={{n}\choose{0}}\cdot0,85^{0}\cdot0,15^{n-0}+{{n}\choose{1}}\cdot0,85^{1}\cdot0,15^{n-1}\\ &=\underbrace{\frac{n!}{0!(n-0)!}}_{\text{1}}\cdot\underbrace{0,85^{0}}_{\text{1}}\cdot0,15^{n-0}+\frac{n!}{1!(n-1)!}\cdot0,85^{1}\cdot0,15^{n-1}\\ &=0,15^{n}+\frac{n!}{(n-1)!}\cdot0,85\cdot0,15^{n-1}\\ &=0,15^{n}+\frac{\cancel{1\cdot2\cdot...\cdot(n-1)\cdot} n}{\cancel{1\cdot2\cdot...\cdot(n-1)}}\cdot0,85\cdot0,15^{n-1}\\ &=0,15^{n}+n\cdot0,85\cdot\frac{0,15^{n}}{0,15}\\ &=0,15^{n}\left(1+\frac{0,85}{0,15}n\right) \end{align*}\] Nyt halutaan, että \(P(A)>0,98\), eli \(1-P(\overline{A})>0,98\).
Edelleen siis komplementtitapahtumalle \(P(\overline{A})<0,02\).
Ratkaistaan laskimella yhtälö \[\begin{align*} &0,15^{n}\left(1+\frac{0,85}{0,15}n\right)=0,02\\ &\Leftrightarrow n=-0,173933\;\;\;\;\text{ tai }n=3,68914 \end{align*}\]
Tulkitaan saatua tulosta. Mitä enemmän siemeniä istutetaan, sitä todennäköisempää useamman siemenen menestyminen on.
Laskusta \(n=3,68914\) on siis se arvo, jolla ei menestyminen tapahtuu \(2\%\) todennäköisyydellä. Eli menestyminen tapahtuu \(98\%\) todennäköisyydellä.
Siemeniä tulee siis istuttaa vähintään 4 kappaletta.
4. Todennäköisyysjakauma
- diskreetin jakauman odotusasrvo
Jakauma on helpointa havainnollistaa taulukoimalla kaikki eri arvot, joita satunnaismuuttuja voi saada. Taulukkoon kirjoitetaan jokaisen arvon todennäköisyys. Satunnaismuuttujan jakauma muodostuu siis eri satunnaismuuttujan arvojen todennäiköisyyksistä.
Tutki erilaisia jakaumia GeoGebralla
https://www.geogebra.org/m/fusDCEhh
4.1 Diskreetti todennäköisyysjakauma
Satunnaismuuttuja on diskreetti, jos se saa ainoastaan yksittäisiä arvoja, esim. 0,1,2. Satunnaismuuttujan yksittäisten arvojen \(x_i\) todennäköisyyksiä \(p_i\) kutsutaan pistetodennäköisyyksiksi.
Pistetodennäköisyys
Olkoon satunnaismuuttuja \(X\) ja sen eri mahdolliset arvot ovat \(x_1,x_2,x_3,...,x_n\).
Nyt satunnaismuuttujan jakauman muodostavien pistetodennäköisyyksien \(p_1,p_2,p_3,...,p_n\)(järjestyksessä) summa on 1. \[\begin{align*} p_1+p_2+p_3+...+p_n=1 \end{align*}\]
Satunnaismuuttujalle \(X\) voidaan määrittää odotusarvo, eli minkä arvon satunnaismuuttuja todennäköisimmin saa. Tämä määritetään laskemalla todennäköisyysjakauman keskiarvo.
Diskreetin satunnaismuuttujan odotusarvo
Olkoon satunnaismuuttuja \(X\), tietyn arvon \(x_{i}\) saamisen todennäköisyys \(p_i\). Nyt odotusarvo on \[\begin{align*} E(X)=\sum_{i=1}^{n}p_{i}x_{i} \end{align*}\] Odotusarvoa voidaan myös merkitä kreikkalaisella kirjaimella myy, \(\mu\).
Satunnaismuuttujan saamat arvot voivat vaihdella, eli jakaumassa voi olla hajontaa.
Diskreetin satunnaismuuttujan keksihajonta
Olkoon satunnaismuuttuja \(X\) ja sen saaman arvon \(x_i\) todennäköisyys \(p_i\). Nyt satunnaismuuttujan keskihajonnalle \[\begin{align*} D(X)=\sqrt{\sum_{i=1}^{n}p_i(x_i-E(X))^{2}} \end{align*}\] Keskihajontaa voidaan merkitä myös kirjaimella sigma, \(\sigma\).
Kertymäfunktio voidaan laskea, jos tiedetään satunnaismuuttujan \(X\) arvojen pistetodennäköisyydet.
Diskreetin satunnaismuuttujan pistetodennäköisyydet vastaavat diskreetin tilastomuuttujan suhteellisia frekvenssejä. Edelleen satunnaismuuttujan kertymäfunktion arvot vastaavat tilastomuuttujan suhteellisia summafrekvenssejä.
Diskreetin satunnaismuuttujan kertymäfunktio
Jos satunnaismuuttuja on \(X\) ja se saa arvot \(x_i\) todennäköisyyksillä \(p_i\), niin sen kertymäfunktio on \[\begin{align*} F(x)=P(X\leq x), \end{align*}\] jossa \(x\in\R\).
Toisin sanoen funktion \(F\) arvo kohdassa \(x\) on todennäköisyys sille, että satunnaismuuttuja \(X\) saa korkeintaan arvon \(x\).
Kaverukset Johannes, Veeti ja Viljo pelaavat erästä korttipeliä.
Jokainen pelaaja nostaa korttipakasta yhden korttin ja riippuen minkä kortin tämä nostaa, saa tietyn summan rahaa. Säännöt ovat seuraavat:
- Korteilla 1-7 saa \(1€\)
- Korteilla 8-11 saa \(5€\)
- Kuvakorteilla (12-13) saa \(10€\)
Satunnaismuuttuja \(X\) on voitettu rahasumma yhdellä kortilla. Muodostetaan satunnaismuuttujalle jakauma.
RATKAISU:
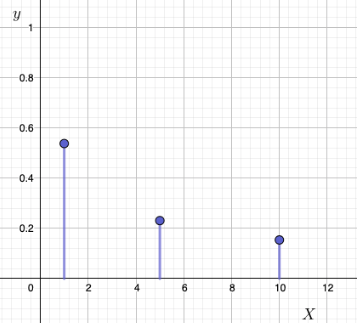
Mahdolliset rahasummat, jotka pelaaja voi voittaa on \(1€\), \(5€\) ja \(10€\). Eli satunnaismuuttuja \(X\) voi saada arvot \(1,5,10\).
Jakauman määrittämiseksi tarvitaan mahdollisten arvojen todennäköisyydet.
\[\begin{align*} P(X=1)&=P(\text{kortti }1-7)=\frac{4\cdot7}{52}=\frac{7}{13}\\ P(X=5)&=P(\text{kortti }8-11)=\frac{4\cdot3}{52}=\frac{3}{13}\\ P(X=10)&=P(\text{kortti }12-13)=\frac{4\cdot2}{52}=\frac{2}{13}\\ \end{align*}\] Ilmoitetaan jakauma taulukkona:
| \(x\) | \(P(X=x)\) |
|---|---|
| 1 | \(\frac{7}{13}\) |
| 5 | \(\frac{3}{13}\) |
| 10 | \(\frac{2}{13}\) |
4.2 Binomijakauma
Kun koetta toistetaan \(n\) kertaa ja onnistumisen mahdollisuus jokaisella kerralla on \(p\), niin satunnaismuuttujan \(X\) (onnistumisien lukumäärä) voi saada arvot \(0,1,2,...,n\).
Jokaiselle arvolle voidaan laskea todennäköisyys binomitodennäköisyyden avulla, ja sanotaan satunnaismuuttujan \(X\) noudattavan binomitodennäköisyysjakaumaa parametrein \(n\) ja \(p\).
Tästä käytetään merkintää \(X\sim \text{Bin}(n,p)\).
Jos satunnaismuuttuja \(X\) noudattaa binomijakaumaa \(X\sim\text{Bin}(n,p)\), niin sen odotusarvo on satunnaismuuttujan arvo kerrottuna sen todennäköisyydellä.
Binomijakauman odotusarvo ja keskihajonta
Jos satunnaismuuttuja \(X\) noudattaa binomijakaumaa, niin tällöin sen odotusarvo on \[\begin{align*} E(X)=np. \end{align*}\] Jakauman keskihajonta on tällöin \[\begin{align*} D(X)=\sqrt{np(1-p)} \end{align*}\]
Binomijakauman kertymäfunktio voidaan laskea:
Binomijakauman kertymäfunktio
\[\begin{align*} F(k)=P(X\leq k)=\sum_{i=1}^{n}{{n}\choose{i}}p^{i}(1-p)^{n-1} \end{align*}\]
Korttipakasta nostetaan sattumanvaraisesti yksi kortti neljä kertaa. Jokaisen noston välillä kortti palautetaan takaisin pakkaan.
Olkoon satunnaismuuttuja \(X\)="patojen lukumäärä". Mikä on satunnaismuuttujan todennäköisin arvo?
RATKAISU: Koska kortti palautetaan aina takaisin pakkaan, on kyseessä toistokoe, jonka toistojen lukumäärä \(n=4\).
Todennäköisyys, että korttipakasta saadaan pata, on \(\frac{13}{52}=\frac{1}{4}\).
Satunnaismuuttuja noudattaa binomijakaumaa parametrein \(4\) ja \(\frac{1}{4}\). Merkitään \(X\sim\text{Bin}(4,\frac{1}{4})\).
Lasketaan seuraavaksi pistetodennäköisyydet hyödyntäen binomitodennäköisyyttä \(P(k\text{ onnistumista})={{n}\choose{k}}p^{k}(1-p)^{n-k}\). \[\begin{align*}
P(X=0)&={{4}\choose{0}}\left(\frac{1}{4}\right)^{0}\left(\frac{3}{4}\right)^4= 1\cdot1\cdot\frac{81}{256}≈0,316\\
P(X=1)&={{4}\choose{1}}\left(\frac{1}{4}\right)^{1}\left(\frac{3}{4}\right)^3= 4\cdot\left(\frac{1}{4}\right)\cdot\frac{27}{64}≈0,422\\
P(X=2)&={{4}\choose{2}}\left(\frac{1}{4}\right)^{2}\left(\frac{3}{4}\right)^2= 12\cdot\left(\frac{1}{16}\right)\cdot\frac{9}{16}≈0,422\\
P(X=3)&={{4}\choose{3}}\left(\frac{1}{4}\right)^{3}\left(\frac{3}{4}\right)^1= 24\cdot\left(\frac{1}{64}\right)\cdot\frac{3}{4}≈0,281\\
P(X=4)&={{4}\choose{4}}\left(\frac{1}{4}\right)^{4}\left(\frac{3}{4}\right)^0= 24\cdot\left(\frac{1}{256}\right)\cdot1≈0,094\\
\end{align*}\]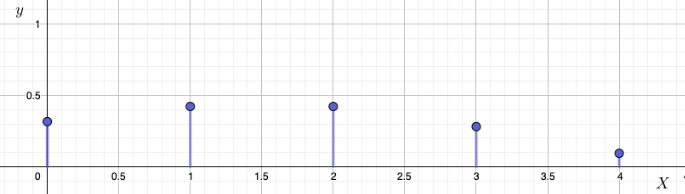 
Satunnaismuuttujan todennäköisimmät arvot ovat \(1\) ja \(2\). Tämä tarkoittaa, että neljällä toistolla on todennäköisintä saada joko yksi pata tai kaksi pataa.
4.3 Jatkuva todennäköisyysjakauma
Tutkittaessa esimerikiksi ihmisen pituutta satunnaismuuttuja voi saada reaaliluvun eri arvoja tietyltä väliltä. Tällaista tilannetta mallinnetaan jatkuvasti jakautuneiden satunnaismuuttujien avulla.
Toisin kuin diskreetissä jakaumassa, jatkuvassa jakaumassa satunnaismuuttujan eri arvojen todennäköisyyksiä ei voida esittää pistetodennäköisyyksien avulla.
Satunnaismuuttujan yksittäisen arvon todennäköisyys on nolla.
Jakautumisen kuvaamiseen käytetään tiheysfunktiota.
Jatkuva jakauma
Olkoon satunnaismuuttuja \(X\) ja funktio \(f\) sen tiheysfunktio. Tällöin kaikilla luvuilla \(a<b\) tapahtuman \(a\leq X\leq b\) todennäköisyys on sama kuin funktion \(f\) kuvaajan ja \(x\)-akselin välin \(a\leq x\leq b\) väliin jäävä pinta-ala.
Jos tiheysfunktio \(f\) on jatkuva kyseisellä välillä, voidaan pinta-ala laskea integroimalla. Jos välillä on epäjatkuvuuskohtia, pinta-ala tulee laskea erillisissä osissa.
Kertymäfunktio siis osoittaa nimensä mukaisesti, paljonko todennäköisyyttä "on kertynyt" tiettyyn kohtaan \(x=a\) mennessä.
Kertymäfunktion määritelmä
Olkoon satunnaismuuttuja \(X\), jolle kertymäfunktio on \[\begin{align*} F(x)=P(X\leq x), \end{align*}\] jossa \(x\in\R\).
Jatkuvan satunnaismuuttujan \(X\) kertymäfunktio on \[\begin{align*} F(x)= \begin{cases} 0,\;\;\;\;\;\;\;\; \text{kun }x<1\\ 1-\frac{1}{x},\;\text{kun } x\geq1 \end{cases} \end{align*}\] Määritetään todennäköisyys \(P(4<X<6)\).
RATKAISU:
Piirretään kertymäfunktio.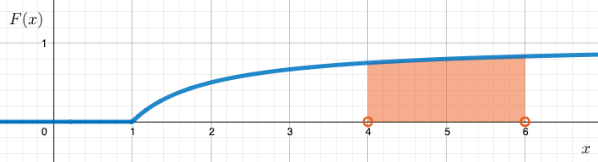 
Kyseessä on jatkuva jakauma. Todennäköisyys saadaan, kun lasketaan kertynyt todennäköisyys aina kohtaan \(x=6\) asti, jonka jälkeen alueesta vähennetään alue \(x\leq4\). \[\begin{align*} &P(4<X<6)\\ &=P(X<6)-P(\leq4)\;\;\;\;\;\;\;\;\;\;|\text{ jatkuva jakauma}\\ &=P(X\leq6)-P(\leq4)\\ &=F(6)-F(4)\\ &=\left(1-\frac{1}{6}\right)-\left(1-\frac{1}{4}\right)\\ &=\frac{5}{6}-\frac{3}{4}\\ &=\frac{1}{12}\\ &≈0,0833 \end{align*}\]
Kysytty todennäköisyys on \(0,083\).
4.4 Normaali todennäköisyysjakauma
Tähän
Normaalijakauma on jatkuva jakauma, mutta se on tilastotieteen ja todennäköisyyslaskennan kannalta niin oleellinen, että se on eritelty omaksi luvukseen. Normaalijakaumaa kutsutaan myös Gaussin jakaumaksi tai Gaussin kellokäyräksi.
Normaalijakauman määritelmä
Jos satunnaismuuttujan tiheysfunktio on \[\begin{align*} f(x)=\dfrac{1}{\sigma\sqrt{2\pi}}e^{-\dfrac{(x-\mu)^{2}}{2\sigma^{2}}}, \end{align*}\] jossa \(\mu\) on satunnaismuuttujan \(X\) odotusarvo ja \(\sigma\) keskihajonta, niin satunnaismuuttuja \(X\) on normaalisti jakautunut.
Tällöin merkitään \(X\sim N(\mu,\sigma)\)
Jatkuvan jakauman keskihajonta ja odotusarvo määräävät tiheysfunktion \(f\) muodon ja sijainnin. Jakauma on symmetrinen odotusarvon \(\mu\) suhteen ja keskihajonta \(\sigma\) kuvaa jakauman leveyttä.
Standardinormaalijakauma \(N(0,1)\)
Olkoon satunnaismuuttuja \(X\), joka on normaalisti jakautunu parametrein \(\mu\) ja \(\sigma\). Nyt normitettu satunnaismuuttuja \[\begin{align*} Z=\dfrac{X-\mu}{\sigma} \end{align*}\] noudattaa standardi normaalijakaumaa. Merkintä on \(Z\sim N(0,1)\).
Standardinormaalijakaun ominaisuuksille käytettään kreikkalaista kirjainta fii: tiheysfunktiota merkitään fiillä \(\varphi\) ja kertymäfunktiota isolla fiillä \(\Phi\).
Tietokoneen akunkesto on aktiivisella käytöllä 12 tuntia. Keskihajonta akun kestolle on 4 tuntia.
Millä todennäköisyydellä tietokoneen akku kestää yli 10 tuntia?
Akun kesto on normaalisti jakautunut.
RATKAISU: 
Varianssi on keskihajonnan neliö, eli varianssi \(\sigma^{2}=(4h)^{2}\).
Nyt voidaan merkitä akun kestolle \(X\sim\text{N}\left(12h,(16h)^{2}\right)\).
Normitettu satunnaismuuttuja \(Z\) on tällöin \[\begin{align*} Z=\dfrac{X-12h}{4h}\sim\text{N}(0,1). \end{align*}\]
Todennäköisyys akun kestolle yli 10 tuntia on siis \[\begin{align*} &P(\text{akku kestää yli 10 h})\\ &=P(X>10h)\\ &=P(Z>\dfrac{10h-12h}{4h})\\ &=P(Z>-0,5)\\ &=1-\Phi(-0,5)\\ &=1-[1-\Phi(0,5)]\\ &=1-1+\Phi(0,5)\\ &≈0,6915\\ \end{align*}\]
Tietokoneen akku kestä yli 10 tuntia \(69\%\) todennäköisyydellä.
Tehtäviä
1. Tehtävä
Niklas ajatteli tehdä tutkimuksen siitä, paljonko muut 17-vuotiaat tienaavat kesätöiden aikana. Hän toteuttaa tutkimuksensa kyselemällä muutamalta ystäviltään heidän palkkatietojaan ja listaamalla ne. Tämän jälkeen Niklas laskee palkkojen keskiarvon.
Pohdi tutkimuksen asetelmaa ja vastaa kysymyksiin.
a.
b.
Onko Niklaksen tutkimus pätevä? Perustele vastauksesi.
2. Tehtävä
a.
Montako mökkiä on yllä olevan taulukon kaupungeissa keskimäärin?
b.
Mikä on tilaston moodi?
c.
Millä todennäköisyydellä sijaitsee kaupungissa, jossa on yli 8000 mökkiä?
d.
Millä todennäköisyydell mökki sijaitsee joko Kuusamossa tai Raaseporissa?
3. Tehtävä
Kala ui kohti verkon reunaa. Verkko näyttää kalasta katsottuna pelkältä kaarevalta narulta, sillä se ui kohtisuorassa verkon reunaa vastaan.
Verkon alareuan on kiinni pohjassa ja kohoaa hieman kaarevasti kohti pintaa.
Jos kala oletetaan niin pieneksi, ettei sillä ole itsessään pinta-alaa ja verkon nousevan funktion \(y=x^{2}\) mukaisesti.
Kala ui silmät kiinni kohti verkkoa, millä todennäköisyydellä se väistää verkon ja ui sen ali?
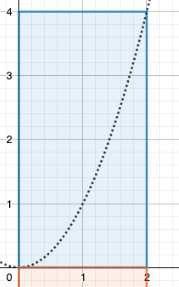
4. Tehtävä
a.
b.
Markuksen kesätyömatkalla on kolmet liikennevalot, jotka toimivat toisistaan riippumattomasti. Ensimmäiset valot ovat punaiset 10 sekuntia minuutissa, toiset valot 8 sekuntia ja kolmannet 20 sekuntia.
Millä todennäköisyydellä markus joutuu pysähtymään punaisiin valoihin täsmälleen kerran?
5. Tehtävä
Todennäköisyyslaskennan käsitteet perustuvat joukko-oppiin. Esimerkiksi tuttu reaalilukujen joukko \(\R\) on joukko, jonka alkiona ovat kaikki reaaliluvut. Joukon koko voi olla äärellinen tai ääretön.
Eräs abiluokka jakautuu seuraavasti joukkoihin. Yhteensä oppilaita luokalla on 8.
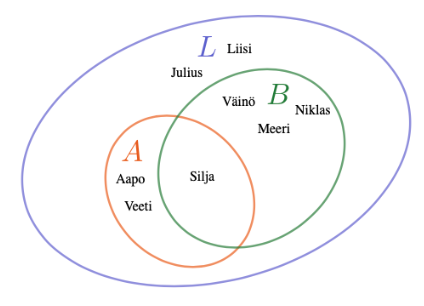
a.
b.
Eräät joukko-opin peruslait ovat de Morganin lait: \[\begin{align*} \overline{A\cap B}=\overline{A}\cup\overline{B}\;\;\;\;\;\;\; \text{ja}\;\;\;\;\;\;\; \overline{A\cup B}=\overline{A}\cap\overline{B}. \end{align*}\]
Olkoon \(M\) perusjoukko sekä lisäksi \(A\subset M\) ja \(B\subset M\).
Todista de Morganin lait hyödyntämällä Venn-diagrammia.
6. Tehtävä
Lotto-pelissä pelaaja valitsee \(1-40\) numerosta seitsemän. Viikottain suoritetaan arvonta, jossa kone arpoo seitsemän lukua ja jos omat valintasi täsmäävät arvottujen lukujen kanssa, voitat pääpalkinnon.
a.
Montako erilaista 7-kombinaatiota luvuista voidaan muodostaa?
b.
Mikä on todennäköisyys "Kaikki seitsemän oikein"-riville?
c.
Mikä on todennäköisyys, että saat 5 numeroa ja yhden lisänumeron oikein?
7. Tehtävä
a. Pascalin kolmio
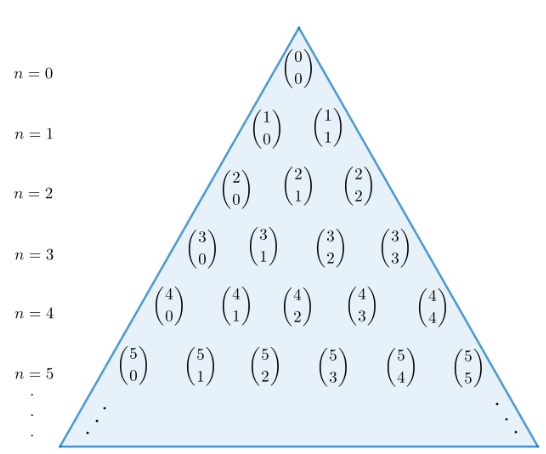Pascalin kolmio voidaan kirjoittaa kokonaislukuina tai binomikertoimien avulla. Ylläolevassa kuvassa kolmio on täytetty binomikertoimien avulla.
Binomin potenssin \((a+b)^{n}\) kertoimet saadaan Pascalin kolmion riviltä \(n\).
Täydennä taulukkoon binomikerrointa vastaava lukuarvo.
Open plugin
Kirjoita auki lauseke \((3x+2)^{4}\).
Olkoon binomi \((x+1)^{3}\). Tässä tapauksessa binomin \((a+b)^{n}\) \(a=x\) ja \(b=1\). Lausekkeen \(x\) eksponentit pienenevät \(3\):sta nollaan ja vastaavasti lausekkeen \(1\) eksponentit kasvavat nollasta \(3\):een. \[\begin{align*} (x+1)^{3}&=\color{green}{{3}\choose{0}}\color{black}\cdot x^{3}\cdot1^{0}+\color{green}{{3}\choose{1}}\color{black}\cdot x^{2}\cdot1^{1}+\color{green}{{3}\choose{2}}\color{black}\cdot x^{1}\cdot1^{2}+\color{green}{{3}\choose{3}}\color{black}\cdot x^{0}\cdot1^{3}\\ &=1x^{3}+3x^{2}+3x^{1}+1\\ &=x^{3}+3x^{2}+3x+1 \end{align*}\]
Binomi \((x+1)^{3}\) avattuna on \(x^{3}+3x^{2}+3x+1\).
b. Poissonin jakauma
Jos jokin tapahtuma esiintyy useita kertoja toisistaan riippumatta, esiintymisten lukumäärä noudattaa Poissonin jakaumaa parametrilla \(\lambda\). Esiintymisen lukumäärää merkitään lambdalla \(\lambda\).
Satunnaismuuttuja \(X\) noudattaa Poissonin jakaumaa parametrein \(\lambda\), jos sen pistetodennäköisyydet ovat \(P(X=k)=e^{-\lambda}\dfrac{\lambda^{k}}{k!}\), jossa \(k=0,1,2,3...\).
Pankkiin saapuu arkiaamuisin keskimäärin 5 asiakasta yhden tunnin aikana. Henkilökunnan lukumäärä mitoitettiin niin, että yksi työntekijä voi palvella tunnissa 6 asiakasta.
Oletetaan, että asiakkaiden saapuminen pankkiin on toisistaan riippumatonta ja noudattaa Poissonin jakaumaa.
Arvioi Poissonin jakauman avulla riski, että pankkiirien palvelukapasiteetti ylittyy seuraavana arkiaamuna.
8. Tehtävä
Ilmavoimilla on omat vaatimukset näkemiselle, ja kaikki halukkaat eivät välttämättä pääse kouluttautumaan esimerkiksi lentäjiksi. Näön tarkkuuden on oltava vähintään 0,5 ja laseilla korjattuna 1,0. Taittovihrettä saa olla maksimissaan +2,5– -1,5 ja värinäön on oltava virheetön. (Lähde: Piilolinssioptikko)
Yhdeksällä prosentilla miehistä on puna-vihersokeus. Millä todennäköisyydellä 100 sotilaasta ainakin kolmella on puna-vihersokeus?
Vanhoja YO-tehtäviä
1.
Lotto-peli alkoi Suomessa vuonna 1971, ja sen sääntöjä on muutettu useita kertoja vuosien varrella. Viimeisin sääntöuudistus tehtiin vuoden 2016 lopussa.
Ennen uudistusta arvottiin 7 varsinaista ja 2 lisänumeroa 39 numerosta. Uudistuksen jälkeen arvotaan 7 varsinaista ja vain 1 lisänumero 40 numerosta. Seuraavassa loton pelaaja täyttää yhden lottorivin eli käytännössä valitsee 7 numeroa.
Laske tuloksen "\(6+1\)" todennäköisyys ennen uudistusta ja sen jälkeen. Tässä "\(6+1\)" tarkoittaa tulosta, jossa on kuusi varsinaista ja yksi lisänumero oikein. [K18/7]
VASTAUS: Ennen uudistusta \(9,10218...\cdot10^{-7}\) ja \(3,75464...\cdot10^{-7}\) uudistuksen jälkeen.
Ratkaisu: Seitsemästä varsinaisesta numerosta voidaan valita kuusi seitsemällä tavalla:
Kahdesta lisänumerosta voidaan valita yksi kahdella tavalla ja yhdestä lisänumerosta yhdellä tavalla.
Mahdollisia 6+1- rivejä on ennen uudistusta \(7\cdot2\) ja uudistuksen jälkeen \(7\) kappaletta.
Kaikkiaan rivejä on \({39}\choose{7}\) ja \({40}\choose{7}\).
Todennäköisyydet ovat siis
Ennen uudistusta: \[\begin{align*} \dfrac{14}{{{39}\choose{7}}}=\dfrac{14}{15380937}=9,10218...\cdot10^{-7} \end{align*}\]
Uudistuksen jälkeen: \[\begin{align*} \dfrac{7}{{{30}\choose{7}}}=\dfrac{7}{18643560}=3,75464...\cdot10^{-7} \end{align*}\]
2.
Tavallista noppaa heitetään kolme kertaa, jolloin saadaan heittojärjestykseessä luvut \(a,b,c\). Laske seuraavien tapahtumien todennäköisyydet:
- Jono \((a,b,c)\) on aidosti kasvava ja artimeettinen
- Jono \((a,b,c)\) on geometrinen. [S17/7]
VASTAUS: a. \(\frac{1}{36}\) b. \(\frac{1}{27}\)
RATKAISU:
a.
Mahdollisia jonoja kaikkiaan on \(6^{3}=216\) kappaletta.
Nousevia aritmeettisia jonoja niistä ovat \(123, 234, 345, 456, 135, 246\).
Todennäköisyys on siis \(\dfrac{6}{6^{3}}=\dfrac{1}{36}\).
b.
Geometrisia jonoja ovat \(124,421,111,222,333,444,555,666\).
Todennäköisyys on siis \(\dfrac{8}{6^{3}}=\dfrac{1}{27}\)
3.
Arkikielessä keskimääräisyyteen liittyvät käsitteet keskiarvo ja mediaani menevät usein sekaisin. Tässä tehtävässä "keskimääräisellä" tarkoitetaan keskiarvoa.
Valtion liikenneturvallisuuslaitos pyysi taksinkuljettajia arvioimaan ajotaitoaan kouluarvosanoin \(4-10\). Vastaukset tuhannelta kuljettajalta näkyvät oheisessa pylväsdiagrammissa, joka perustuu kiireisen toimittajan hätäisiin muistiinpanoihin. Arvioi kuvion perusteella arvosanan neljäsosan tarkkuudella, mikä oli tutkimuksen mukaan keskimääräisen kuljettajan ajotaidon arvosana.
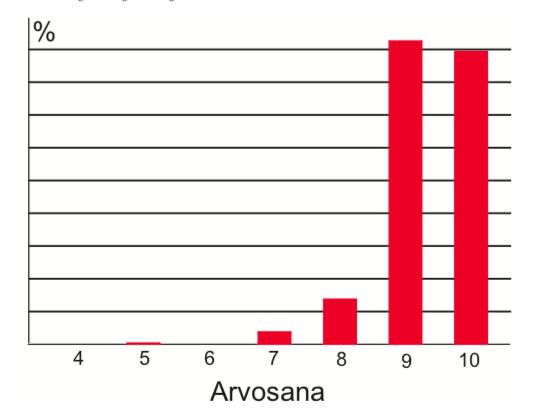
Sama kysely tehtiin tuhannelle tavalliselle autoilijalle. Anna perusteltu esimerkki sellaisesta jakaumasta (mahdollisesta tuloksesta), jossa vähintään \(80\%\) vastaajista arvioi olevansa keskimääräistä parempia kuljettajia. [K17/11]
VASTAUS: a. \(9+\) b. esim. \((5,10,80,5)\) tai \((0,0,1,99)\) prosenttia arvosanoille \(7-10\)
RATKAISU:
a.
TAPA1:
Päättelemällä: koska arvosanan 9 ylittäviä arvosanoja on selvästi enemmän kuin sen alittavia, päätellään keskiarvon olevan yli 9.
Toisaalta arvosana 9 on tavallisempi kuin arvosana 10, keskiarvo on alle 9,5. Arvosanojen 8 painolla keskiarvon pitää siis olla \(9\frac{1}{4}\), eli \(9+\).
TAPA2: Pylväitä mittaamalla: Käytetään prosentteja siten, että kokonaismäärä on alle \(80\%\) tai yli \(120\%\).
b.
Jakauma (jos frekvenssit, niin yhteensä \(≈1000\) vastausta, jos prosentteja niin yhteensä \(≈100\%\).
Lasketaan jakauman keskiarvo, yli \(50\%\) vastaajista on yli keskiarvon ja yli \(80\%\) vastaajista on yli keskiarvon
Jakaumaksi käy esimerkiksi \((5,10,80,5)\) tai \((0,0,1,99)\) prosenttia arvosanoille \(7-10\).
4.
Alla oleva kuvio esittää pienen kaupungin katuverkkoa. Anssi kulkee pisteestä \(A\) pisteeseen \(B\) käyttämällä mahdollisimman lyhyttä reitti, jolloin matkan pituus on neljä korttelinväliä. Sellaisissa risteyksissä, joissa kaksi vaihtoehtoa johtaa lyhimpään reittiin, hän valitsee suunnan kolikkoa heittämällä.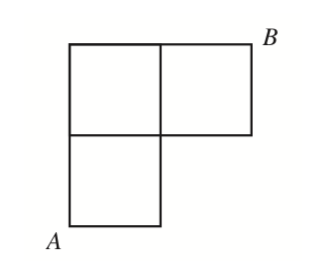 
Piirrä erilliset kuviot kaikista niistä viidestä mahdollisesta reitistä, joiden pituus on neljä korttelinväliä, ja määritä niiden valintatodennäköisyydet.
Birgitta kulkee pisteestä \(B\) pisteeseen \(A\) ja valitsee mahdollisimman lyhyen reitin vastaavalla tavalla. Anssi ja Birgitta lähtevät liikkeelle samanaikaisesti ja kulkevat samaa vauhtia. Kuinka suurella todennäköisyydellä he kohtaavat toisensa matkan puolivälissä? [S16/8]
VASTAUS: a. \(\frac{1}{4}\), \(\frac{1}{8}\), \(\frac{1}{8}\), \(\frac{1}{4}\) ja \(\frac{1}{4}\) b.\(\frac{5}{8}\).
RATKAISU:
a.
Eri reitit: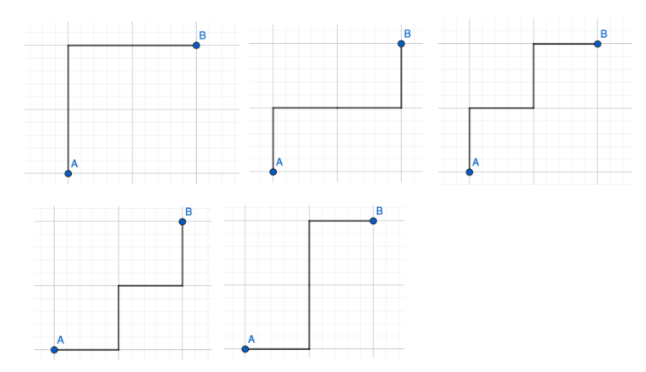 
Lasketaan seuraavaksi yhden kävelyreitin todennäköisyys. Loput reitit lasketaan samalla tavalla.
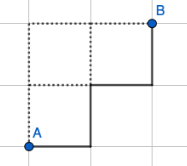Jokaisessa kulmassa pohditaan, valitaanko suunta kolikkoa heittämällä (\(\frac{1}{2}\)) vai onko kyseiseen suuntaan pakko kulkea (\(1\)). Yllä olevan reitin todennäköisyys on \(\frac{1}{2}\cdot1\cdot\frac{1}{2}\cdot1=\frac{1}{4}\).
Reittien todennäköisyydet vasemmalta oikealle ja riveittäin: \(\frac{1}{4}\), \(\frac{1}{8}\), \(\frac{1}{8}\), \(\frac{1}{4}\) ja \(\frac{1}{4}\).
b.
Mahdolliset Anssin ja Birgitan kohtauspaikat reittien puolivälissä ovat seuraavat pisteet \(J\) ja \(K\):
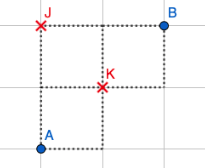
Todennäköisyydet kohtaamispaikoille lasketaan siten, että tarkastellaan eri reittejä lähtöpisteinä sekä \(A\) ja \(B\).
Todennäköisyys kohdata pisteessä \(J\) on:
\[\begin{align*} j=\left(\frac{1}{2}\cdot\frac{1}{2}\right)\left(\frac{1}{2}\cdot\frac{1}{2}\right)=\frac{1}{16} \end{align*}\]
Todennäköisyys kohdata pisteessä \(K\) on:
\[\begin{align*} k=\left(\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot1\right)\left(\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot1\right)=\frac{9}{16} \end{align*}\]
Kysytty todennäköisyys on nyt \(j+k=\frac{1}{16}+\frac{9}{16}=\frac{5}{8}\).
5.
Koirien kaksipäiväiseen HeinäHaukku-tapahtumaan ilmoittaudutaan joko lauantainäyttelyyn, sunnuntainäyttelyyn tai molempiin.
Eräänä vuonna HeinäHaukkuun ilmoitettiin \(1372\) koiraa, joista \(31\) ilmoitettiin vain lauantainäyttelyyn ja \(43\) vain sunnuntainäyttelyyn. Olkoon \(L\) tapahtuma "HeinäHaukkuun ilmoitettu koira ilmoitettiin lauantainäyttelyyn" ja \(S\) tapahtuma "HeinäHaukkuun ilmoitettu koira ilmoitettiin sunnuntainäyttelyyn".
Laske todennäköisyys \(P(L\text{ ja }S)\) kyseisenä vuonna.
Ovatko \(L\) ja \(S\) riippumattomia kyseisenä vuonna?
Olkoot yleisesti \(a\) vain lauantaille ilmoitettujen koirien lukumäärä, \(b\) kummallekin päivälle ilmoitettujen lukumäärä ja \(c\) vain sunnuntaille ilmoitettujen lukumäärä. Millä lukuja \(a,b,c\) koskevalla ehdolla tapahtumat \(L\) ja \(S\) ovat riippumattomia? [K15/14]
VASTAUS: a. \(≈95\%\) b. Tapahtumat eivät ole riippumattomia
RATKAISU:
a.
Ratkaistaan ensin, montako koiraa ilmoitettiin molempiin näyttelyihin. \(1372-31-43=1298\). Merkitään tätä lukumäärää \(x\):llä, eli \(x=1298\).
Nyt todennäköisyys \(P(L\text{ ja }S)=\dfrac{1298}{1372}=0,94606...≈95\%.\)
b.
Tapahtumat ovat riippumattomia, jos niille pätee että \(P(A\text{ ja }B)=P(A)\cdot P(B)\).
\[\begin{align*} P(A\text{ ja }B)&=P(A)\cdot P(B)\\ \dfrac{1298}{1372}&=\frac{1329}{1372}\cdot\frac{1341}{1372}\\ 0,94606...&=0,94677... \end{align*}\] Yhtälö on epätotta, eli tapahtumat \(L\) ja \(S\) eivät ole riippumattomia.
c:
Riippuvuusehto b-kohdatn mukaan on \(P(L\text{ ja }S)=P(L)\cdot P(S)\).
Eli \[\begin{align*} \frac{b}{a+b+c}&=\frac{a+b}{a+b+c}\cdot\frac{b+c}{a+b+c}\\ b(a+b+c)&=(a+b)(b+c)\\ ab+b^{2}+bc&=ab+ac+b^{2}+bc\\ ac&=0 \text{ eli } a=0 \text{ tai }c=0 \end{align*}\]
6.
Laatikossa on kaksi valkoista ja kolme mustaa palloa. Laatikosta otetaan umpimähkää kaksi palloa. Olkoon satunnaismuuttujan \(X\) nostossa saatujen mustien pallojen lukumäärä. Laske todennäköisyydet \(P(X=k),k=0,1,2\). Määritä odotusarvo \(E(X)\). [S08/8]
VASTAUS: \(P(X=0)=\frac{1}{10}\), \(P(X=1)=\frac{6}{10}\), \(P(X=2)=\frac{6}{10}\) ja \(E(X)=1,2\).
RATKAISU:
Lasketaan ensin todennäköisyydet eri kahden pallon nostoille. \(P(v,v)=\frac{2}{5}\cdot\frac{1}{4}=\frac{1}{10}\)
\(P(v,m)=\frac{2}{5}\cdot\frac{3}{4}+\frac{3}{5}\cdot\frac{2}{4}=\frac{6}{10}\)
\(P(m,m)=\frac{3}{5}\cdot\frac{2}{4}=\frac{3}{10}\).
Todennäköisyydet \(P(X=k),k=0,1,2\) ovat siis
\(P(X=0)=\frac{1}{10}\)
\(P(X=1)=\frac{6}{10}\)
\(P(X=2)=\frac{3}{10}\).
Ja odotusarvo on edelleen \(E(X)=\frac{1}{10}\cdot0+\frac{6}{10}\cdot1+\frac{3}{10}\cdot2=\frac{12}{10}=1,2\).
7.
Monivalintatestissä on \(25\) väitettä ja kussakin kaksi vaihtoehtoa. Opiskelija tietää oikean vastauksen \(10\) väitteeseen, mutta joutuu arvaamaan loput. Millä todennäköisyydellä hän läpäisee testin, kun läpipääsyyn vaaditaan \(15\) oikeaa vastausta? [S10/6]
VASTAUS: \(≈0,94\)
RATKAISU:
Todennäköisyys sille, että \(15\):sta on oikein \(n\) kappaletta ja väärin \(15-n\) kappaletta, on \[\begin{align*} p_{n}={{15}\choose {n}}{{1}\choose {2}}^{n}{{1}\choose {2}}^{15-n}. \end{align*}\] Ja edelleen todennäköisyys sille, että oppilas läpäisee on \[\begin{align*} 1-(p_{0}+p_{1}+p_{2}+p_{3}+p_{4})≈0,94. \end{align*}\]
8.
Annin pelaamassa tietokonepelissä on \(90\%\):n todennäköisyys onnistua.
Kuinka suurella todennäköisyydellä neljän pelin sarjassa tulee tarkalleen yksi epäonnistuminen?
Mikä on neljän pelin sarjassa onnistuneiden pelien lukumäärän odotusarvo?
Kuinka monta kertaa Annin täytyy pelata, jotta onnistuneiden pelien lukumäärän odotusarvo olisi vähintään \(10\)? [S15/6]
VASTAUS: a. \(≈29\%\) b. \(3,6\) c. vähintään 12 kertaa.
RATKAISU:
a.
Merkitään onnistumisen todennäköisyyttä \(p_{o}=0,9\), josta saadaan edelleen epäonnistumiselle \(p_{e}=1-0,9=0,1\). Merkitään pelien lukumäärää kirjaimella \(n\). Kyseessä on binomitodennäköisyys.
9.
Todennäköisyys, että erään tulppaanilajikkeen sipuli itää, on \(0,7\). Kuinka monta sipulia on vähintään istutettava, jotta niistä ainakin kaksi itäisi yli \(99\%\) todennäköisyydellä? [S00/7]
VASTAUS: Vähintään 7 sipulia.
RATKAISU:
Koska yksi sipuli itää todennäköisyydellä \(0,7\), joten se on itämättä todennäköisyydellä \(0,3\). Lisäksi kahden sipulin itämisen todennäköisyys pitää olla \(99\%\), joten itämättömyyden todennäköisyys on \(1\%=0,01\).
Istutetaan nyt \(n\) sipulia, jolloin vähintään kaksi sipulia itää todennäköisyydellä \[\begin{align*} p=1-(P(0\text{ itää})+P(1\text{ itää}))=1-(0,3^{n}+n\cdot0,7\cdot0,3^{n-1}). \end{align*}\]
Määritellään nyt funktio \(f(x)=0,3^{x}+n\cdot0,7\cdot0,3^{x-1}\), jonka ehdoksi tulee \(0,01>f(n)\).
Funktion \(f(x)\) derivaatta \(f'(x)=0,3^{x}(\frac{7}{3}+(1+\frac{7x}{3})\ln0,3)<0\) ainakin kun \(x\geq1\).
Funktio \(f(x)\) on siis monotonisesti pienenevä, kun \(x\geq1\). Tarvittava sipulimäärä selviää, kun sijoitetaan funktioon eri lukumäärä sipuleita. Jos funktion arvo on pienempää kuin \(1\%=0,01\), niin se on vähimmäismäärä istutettavia sipuleita.
Tarkastellaan \(x\):n arvoilla \(6\) ja \(7\):
\(f(6)\geq0,0109>0,01\) ja \(f(7)\leq0,004<0,01\). Istutettavana on siis vähintään \(7\) sipulia.
10.
Tiedetään, että eräässä nelilapsisessa perheessä ainakin yksi lapsista on tyttö. Mikä on tällöin todennäköisyys, että kaikki lapset ovat tyttöjä?
Jos tiedetään, että ainakin kaksi lapsista on tyttöjä, mikä on todennäköisyys, että perheessä on kaksi poikaa?
Oletetaan, että poikia ja tyttöjä syntyy yhtä suurella todennäköisyydellä. Millaiset tulokset saadaan, jos käytetäänkin tilastojen antamia todennäköisyyksiä: poikien syntymistodennäköisyys on \(p=0,51\) ja tyttöjen \(t=0,49\)? Sukupuolen määräytymiset oletetaan riippumattomiksi tapahtumiksi. [S06/10]
VASTAUS: \(\frac{1}{15}\), \(\frac{6}{11}\), \(0,06183\) ja \(0,55730\).
RATKAISU:
Syntymistodennäköisyydet ovat nyt \(p\) ja \(t\).
Lasketaan ensin todennäköisyys, että kaikki nelilapsisen perheen lapsista on tyttöjä, kun ainakin yksi on tyttö.
Olkoon nyt tapahtuma \(A\) tapahtuma "Ainakin yksi tyttö" ja \(B\) "neljä tyttöä".
Kysytty tapahtuma on nyt \(P(A\cap B)\), sillä molempien tapahtumien tulee tapahtua.
Voidaan merkitä \(P(A\cap B)=t^{3}\cdot t=t^{4}\) ja \(P(A)=1-p^{4}\).
Jos nyt tiedetään, että ainakin yksi lapsista on tyttö, todennäköisyys sille että kaikki ovat tyttöjä on
\[\begin{align*} \color{green}P(B|A)=\dfrac{P(A\cap B)}{P(A)}. \end{align*}\]
Oletetaan ensin että \(p=t=\frac{1}{2}\). Nyt todennäköisyydeksi \(P(A\cap B)=\frac{1}{16}\) ja \(P(A)=\frac{15}{16}\) ja edelleen nämä sijoittamalla tapahtumaan \(\color{green}{P(A|B)}\color{black}=\frac{1}{16}\cdot\frac{16}{15}=\color{green}\frac{1}{15}\).
Oletetaan sitten, että \(p=0,51\) ja \(t=0,49\). Nyt todennäköisyydeksi \(P(A\cap B)=0,057688\) ja \(P(A)=0,932348\) ja edelleen nämä sijoittamalla tapahtumaan \(\color{green}{P(A|B)}\color{black}=\color{green}{0,061831}\)
Lasketaan seuraavaksi todennäköisyys sille, että nelilapsiseen perheessä on kaksi poikaa kun ainakin kaksi lapsista on tyttöä.
Merkitään nyt tapahtumaa \(C\)("ainakin kaksi tyttöä") ja \(D\)("kaksi poikaa").
Nyt \(P(C\cap D)=6p^{2}t^{2}\) ja \(P(1-p^{4}-4p^{3}t\). Jos tiedetään, että ainakin kaksi lapsista on tyttöjä niin todennäköisyys sille, että perheessä on kaksi poikaa on \[\begin{align*} \color{blue}P(D|C)=\dfrac{P(C\cap D)}{P(C)}. \end{align*}\]
Nyt jos \(p=t=\frac{1}{2}\), niin \(P(C\cap D)=\frac{6}{16}\) ja \(P(C)=\frac{11}{16}\). Nämä sijoittamalla saadaan \(\color{blue}{P(D|C)}=\frac{6}{16}\cdot\frac{16}{11}=\color{blue}{\frac{6}{11}}\).
Nyt jos \(p=0,51\) ja \(t=0,49\), niin \(P(C\cap D)=0,374700\) ja \(P(C)=0,672352\). Nämä sijoittamalla saadaan \(\color{blue}{P(D|C)}=\color{blue}{0,557298}\)
Lisätehtäviä verkossa
Lähteet
- Tilasto 1: Suomen virallinen tilasto (SVT): Väestön koulutusrakenne [verkkojulkaisu]. ISSN=1799-4586. 2017. Helsinki: Tilastokeskus [viitattu: 22.7.2019]. Saantitapa: http://www.stat.fi/til/vkour/2017/vkour_2017_2018-11-02_tie_001_fi.html
- Tilasto 2: Suomen virallinen tilasto (SVT): Koulutukseen hakeutuminen [verkkojulkaisu].ISSN=1799-4500. 2017. Helsinki: Tilastokeskus [viitattu: 22.7.2019]. Saantitapa: http://www.stat.fi/til/khak/2017/khak_2017_2018-12-13_tie_001_fi.html
- Tilasto 3: SVT: Luonnonvarakeskus, Maatilojen sadonkäyttö.
- Tilasto NN: Suomen virallinen tilasto (SVT): Rakennukset ja kesämökit [verkkojulkaisu]. ISSN=1798-677X. 2018. Helsinki: Tilastokeskus [viitattu: 29.7.2019]. Saantitapa: http://www.stat.fi/til/rakke/2018/rakke_2018_2019-05-21_tie_001_fi.html
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.