MAA4 Analyyttinen geometria ja vektorit
Kurssin tavoitteena on, että opiskelija
- ymmärtää, kuinka analyyttinen geometria luo yhteyksiä geometristen ja algebrallisten käsitteiden välille
- ymmärtää käyrän käsitteen ja oppii tutkimaan käyriä tietoteknisesti yhtälöiden avulla
- osaa ratkaista muotoa \(| f(x) | = a\) tai \(| f(x) | = | g(x) |\) olevia itseisarvoyhtälöitä
- ymmärtää vektorikäsitteen ja perehtyy vektorilaskennan perusteisiin
- osaa tutkia kaksiulotteisen koordinaatiston pisteitä, etäisyyksiä ja kulmia vektoreiden avulla
- osaa ratkaista tasogeometrian ongelmia vektoreiden avulla
- osaa käyttää ohjelmistoja käyrien ja vektoreiden tutkimisessa sekä niihin liittyvien sovellusongelmien ratkaisussa.
Keskeiset sisällöt
- käyrän yhtälö
- suoran, ympyrän, paraabelin yhtälöt
- lineaarinen yhtälöryhmä
- suorien yhdensuuntaisuus ja kohtisuoruus
- itseisarvoyhtälö
- pisteen etäisyys suorasta
- vektoreiden perusominaisuudet
- tason vektoreiden yhteen- ja vähennyslasku sekä tason vektorin kertominen luvulla
- tason vektoreiden pistetulo, tason vektoreiden välinen kulma
1. Itseisarvoyhtälöt
1.1 Itseisarvo
Määritelmä
Reaaliluvun \(a\) itseisarvo on \[\begin{align*} |a|=\begin{cases} a,\text{ kun }a\geq0 \\ -a,\text{ kun }a<0. \end{cases} \end{align*}\]
Itseisarvo kertoo luvun etäisyyden nollasta. Esimerkiksi luvut \(2\) ja \(-2\) ovat yhtä etäällä nollasta: \(|2|=|-2|\).
Itseisarvon ominaisuuksia
\(|a|=|b|\text{, jos ja vain jos }a=b\text{ tai }a=-b\)
\(|a|^{2}=a^{2}\)
\(|ab|=|a||b|\)
\(\sqrt{a^{2}}=|a|\)
\(\left|\frac{a}{b}\right|=\frac{|a|}{|b|}\text{, kun }b≠0.\)
Kahden luvun \(a\) ja \(b\) välinen etäisyys on \(|a-b|\).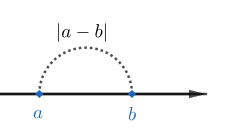 
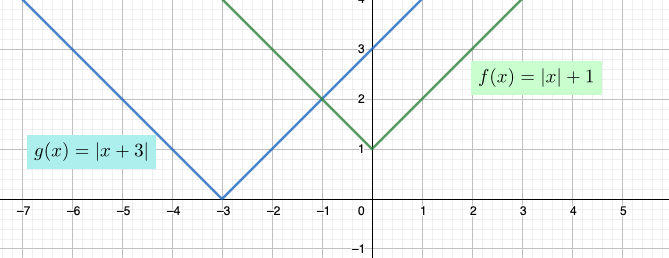
Ratkaistaan itseisarvoyhtälö \(|3-x|=|x+9|\).
Tapa 1: Lukujen \(3-x\) ja \(x+9\) itseisarvot, eli etäisyydet nollasta, ovat yhtäsuuret jos ja vain jos luvut ovat samoja tai toistensa vastalukuja:
\(|a|=|b|\text{, jos ja vain jos }a=b\text{ tai }a=-b\).
\[\begin{align*} |3-x|&=|x+9|\\ 3-x=x+9 &\text{ tai }3-x=-(x+9)\\ 2x=-6 &\text{ tai }3-x=-x-9\\ x=-3 &\text{ tai }3=-9 \end{align*}\] Jälkimmäinen ratkaisu on epätotta, joten yhtälön ainut ratkaisu on \(x=-3\).
Tapa 2: Itseisarvohtälön \(|3-x|=|x+9|\) molemmat puolet ovat ei-negatiivisia (itseisarvo on aina suurempaa tai yhtäsuurta kuin nolla). Nyt voidaan hyödyntää neliöönkorotuslausetta: \[\begin{align*} |3-x|^{2}&=|x+9|^{2}\;\;\;\;\;\;|\text{Jos }a\geq 0 \text{ ja }b\geq 0\text{, niin }a=b\Leftrightarrow a^{2}=b^{2}\\ (3-x)^{2}&=(x+9)^{2}\;\;\;\;\;\;||a|^{2}=a^{2}\\ 9-6x+x^{2}&=x^{2}+18x+81\\ -24x-72&=0\\ x&=-3 \end{align*}\] Itseisarvoyhtälön ratkaisu on \(x=-3\).
1.2 Itseisarvoepäyhtälö
Itseisarvoepäytälön ratkaisemisessa käytetään hyödyksi tietoa, että itseisarvo tarkoittaa luvun etäisyyttä nollasta.
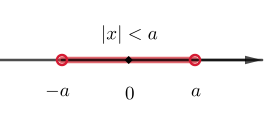
Epäyhtälön \(|x|<a\) ratkaisu
- väli \(-a<x<a\), jos \(a>0\)
- ei ratkaisuja, jos \(a\leq0\)
Yhtäsuuruuden sisältävän epäyhtälön \(|x|\leq a\) ratkaisu on
- \(-a\leq x \leq a\), jos \(a>0\)
- ei ratkaisuja, jos \(a< 0\)
- \(x=0\), jos \(a=0\).
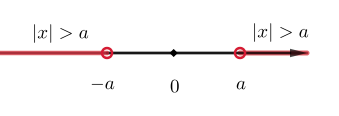
Epäyhtälön \(|x|>a\) ratkaisu
- \(x<-a\) tai \(x>a\), jos \(a\geq0\)
- kaikki luvut \(x\), jos \(a<0\)
Yhtäsuuruuden sisältävän epäyhtälön \(|x|\geq a\) ratkaisu on
- \(x\leq -a\) tai \(x\geq a\), jos \(a>0\)
- kaikki luvut \(x\), jos \(a\leq 0\).
Huomioita itseisarvoepäyhtälön ratkaisemiseen:
- Jos yhtälön molemmat puolet jaetaan negatiivisella luvulla, yhtälömerkin suunta muuttuu
- Yhtälö voidaan myös ratkaista korottamalla yhtälön molemmat puolet neliöön. Näin voi tehdä, jos yhtälön molemmat puolet ovat ei-negatiivisia.
Neliöönkorotuslause
Jos luvut \(a\) ja \(b\) ovat ei-negatiiviisia, niin pätee
- \(a=b\), jos ja vain jos \(a^{2}=b^{2}\)
- \(a<b\), jos ja vain jos \(a^{2}<b^{2}\)
Jos toinen luvuista on ei-negatiivinen, niin neliöönkorotuslause ei päde.
Esim. \((-2)^{2}>1^{2}\), vaikka \(-2<1\).
Ratkaistaan itseisarvoepäyhtälö \(|x+1|<|x-2|\).
Itseisarvohtälön \(|x+1|=|x-2|\) molemmat puolet ovat ei-negatiivisia, sillä itseisarvo on aina suurempaa tai yhtäsuurta kuin nolla. Nyt voidaan hyödyntää neliöönkorotuslausetta:
\[\begin{align*}
|x+1|&<|x-2|\;\;\;\;\;\;|\text{Jos }a\geq 0 \text{ ja }b\geq 0\text{, niin }a=b\Leftrightarrow a^{2}=b^{2}\\
|x+1|^{2}&<|x-2|^{2}\;\;\;\;||a|^{2}=a^{2}\\
(x+1)^{2}&<(x-2)^{2}\\
x^{2}+2x+1&<x^{2}-4x+4\\
x^{2}-x^{2}+2x+4x+1-4&<0\\
6x-3&<0\\
x<\frac{1}{2}
\end{align*}\] 
Itseisarvoepäyhtälön ratkaisu on \(x<\frac{1}{2}\).
2. Pisteitä ja käyriä
Käyrän yhtälöllä tarkoitetaan sellaista yhtälöä, jonka toteuttavat ainoastaan kyseisen käyrän pisteet. Tason käyrä on siis pistejoukko, joka voidaan ajatella radaksi, jota tietty piste kulkee.
Tietty piste \((x,y)\) on käyrällä, jos ja vain jos pisteen koordinaatit toteuttavat käyrän yhtälön.
Kahden pisteen välinen etäisyys
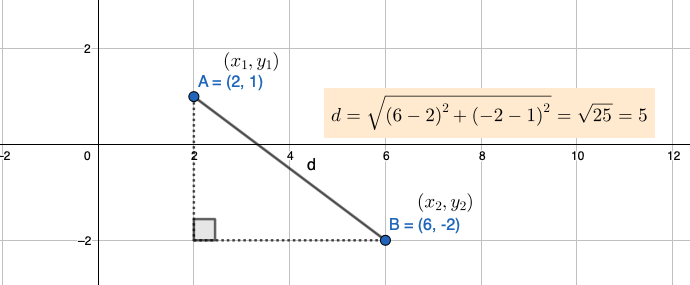
Pisteiden \(A=(x_{1},y_{1})\) ja \(B=(x_{2},y_{2})\) välinen etäisyys \(d\) voidaan laskea hyödyntämällä Pythagoraan lausetta:
\(d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)
3. Suora
Suoran kulmakerroin
Suora kulkee pisteiden \((x_{1},y_{1})\) ja \((x_{2},y_{2})\) kautta. Suoran kulmakerroin on \(k=\displaystyle\frac{\Delta y}{\Delta x}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Kaksi suoraa ovat yhdensuuntaiset, jos ja vain jos niillä on sama kulmakerroin tai ne ovat molemmat y-akselin suuntaisia.
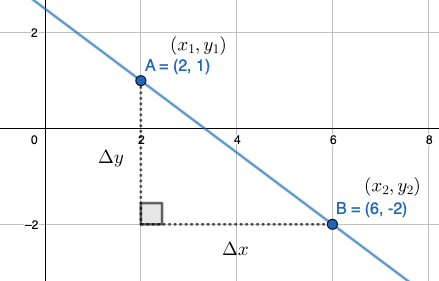
Suoran suunta määräytyy sen kulmakertoimen perusteella. Jos kulmakerroin on negatiivinen, suora on laskeva. Vastaavasti jos kulmakerroin on positiivinen, suora on nouseva. Yllä olevassa kuvassa on laskeva suora.
3.1 Suoran yhtälöt
Pisteen \((x_{0}, y_{0})\) kautta kulkeva suora
\(y-y_{0}=k(x-x_{0})\), jossa suoran kulmakerroin on \(k\).
Ratkaisemalla yllä oleva yhtälö \(y\):n suhteen, saadaan suoran nk. ratkaistu muoto:
Suoran ratkaistu muoto:
\(y=kx+b\)
Kun suoran ratkaistussa muodossa siirretään kaikki termit yhtälön vasemmalle puolelle, saadaan muodostettua suoran yleinen muoto, eli nk. normaalimuoto:
Suoran normaalimuoto
\(ax+by+c=0\), jossa \(a≠0\) ja \(b≠0\).
3.2 Suorien leikkauspiste ja välinen kulma
Kahdella suoralla tasossa voi olla leikkauspisteitä joko yksi, ääretön määrä tai ei yhtään.
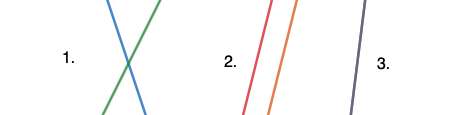Tilanteessa 1. sinisellä sekä vihreällä suoralla on yksi leikkauspiste.
Tilanteessa 2. Oranssilla ja punaisella suoralla ei ole yhtään leikkauspistettä.
Tilanteessa 3. kahdella suoralla on ääretön määrä leikkauspisteitä (suorat ovat päällekkäin).
Suorien välinen leikkauspiste
Suorien leikkauspiste on kahden suoran yhteinen piste. Tämä piste toteuttaa kummankin suoran yhtälöt. Leikkauspiste saadaan selville ratkaisemalla yhtälöpari.
4.2.1 Esimerkki
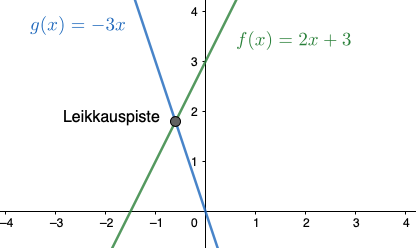
Määritetään suorien \(f(x)\) ja \(g(x)\) leikkauspiste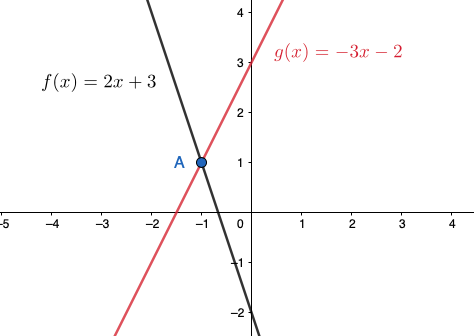 
Muodostetaan ensin suorista yhtälöpari
\[\begin{align*} &\begin{cases} y=2x+3\;\;\;\;\;\;\;\;\;\;\;\;\;\\ y=-3x-2\;\;\;\;\;\;\;\,\\ \end{cases}\\ \end{align*}\]
Koska molemmat yhtälöt on ratkaistu muuttujan \(y\) suhteen, voidaan muodostaa yhtälö
\(2x+3=-3x-2\), josta ratkaistaan leikkauspisteen x-koordinaatti:
\[\begin{align*}
2x+3&=-3x-2\\
5x+3&=-2\\
5x&=-5\\
x&=-1
\end{align*}\]
Nyt sijoittamalla \(x=-1\) kumpaan tahansa yhtälöistä, saadaan ratkaistua leikkauspisteen y-koordinaatti:
\[\begin{align*} y&=2\cdot (-1) +3\\ y&= -2+3\\ y&=1\\ \end{align*}\]
Suorien \(f(x)\) ja \(g(x)\) leikkauspiste on \((-1,1)\).
Suorien välinen kulma on aina se pienempi kulma, joka muodostuu suorien leikatessa toisensa. Täten suorien välinen kulma on aina välillä \([0°,90°]\). Yhdensuuntaisten suorien välinen kulma on \(0°\).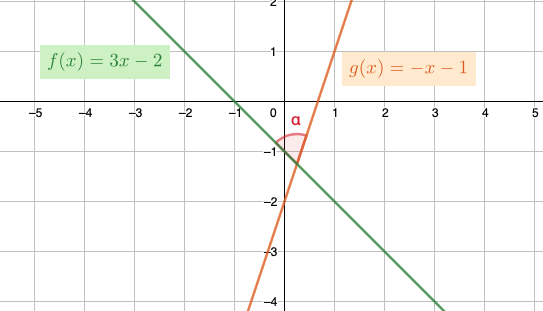 
Suorien välinen kulma
Suorat \(y=k_{1}x+b_{1}\) ja \(y=k_{2}x+b_{2}\) leikkaavat toisensa. Näiden suorien välinen kulma \(\alpha\) toteuttaa yhtälön \[\begin{align*} \tan \alpha=\mid\frac{k_{1}-k_{2}}{1+k_{1}k_{2}}\mid. \end{align*}\]
Suorat eivät saa olla toisiaan kohtisuorassa, koska \(\tan 90°\) ei ole määritelty.
Määritetään suorien \(f(x)=\frac{1}{2}x+1\) ja \(g(x)=-3x\) välinen kulma \(\alpha\).
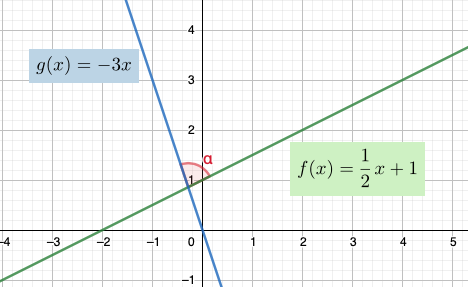
Suorien yhtälöt ovat jo valmiiksi ratkaistussa muodossa, joten lausekkeista voidaan suoraan lukea kulman ratkaisemiseen tarvittavat termit. \(k_{1}=\frac{1}{2}, k_{2}=-3\).
Sijoitetaan arvot yhtälöön \[\begin{align*} \tan \alpha&=\left|\frac{k_{1}-k_{2}}{1+k_{1}k_{2}}\right|\\ \tan\alpha&=\frac{\frac{1}{2}- (-3)}{1+\frac{1}{2}\cdot(-3)}\\ \tan\alpha&=-7\\ \alpha&=\tan^{-1}(-7)=-81,87°≈-81,9° \end{align*}\] Koska kyseessä on kahden suoran välinen kulma, vastaukseksi annetaan positiivinen kulman arvo \(\alpha=81,9°\).
3.3 Suorien kohtisuoruus
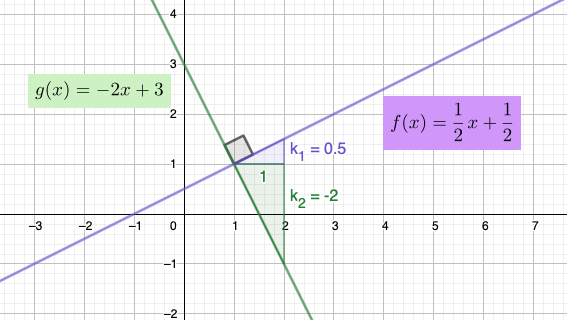
Suorat \(l_{1}\) ja \(l_{2}\) ovat kohtisuorassa toisiaan vastaan, jos ja vain jos niiden kulmakertoimien \(k_{1}\) ja \(k_{2}\) tulo \(k_{1}k_{2}= -1\) tai suorat ovat eri koordinaattiakselien suuntaiset.
Määritetään janan \(AB\) keskinormaalin yhtälö.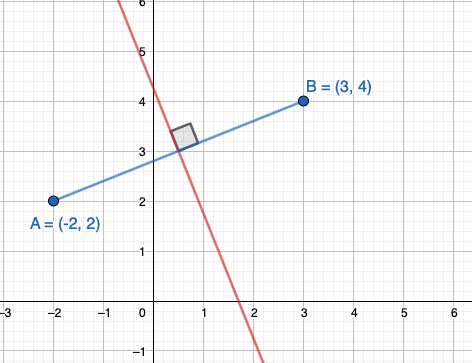 
Janan \(AB\) keskipiste on kohdassa \(P=(\frac{-2+3}{2},\frac{2+4}{2})=(\frac{1}{2},3)\).
Määritetään sen suoran kulmakerroin, joka kulkee pisteiden \(A\) ja \(B\) kautta. \[\begin{align*} k_{AB}&=\frac{4-2}{3-(-2)}\\ k_{AB}&=\frac{2}{5} \end{align*}\]
Kohtisuorien suorien kulmakertoimien tulo on \(-1\), joten nyt voidaan ratkaista normaalin kulmakerroin \(k_n\).
\[\begin{align*} k_{n}\cdot k_{AB}&=-1\\ k_{n}&=\frac{-1}{k_{AB}}\\ k_{n}&=\frac{-1}{\frac{2}{5}}\\ k_{n}&=-\frac{5}{2} \end{align*}\]
Nyt tiedetään normaalin kulmakerroin sekä piste, jonka kautta se kulkee. Näillä tiedoilla voidaan muodostaa keskinormaalin yhtälö.
\[\begin{align*} y-y_{0}&=k(x-x_{0})\\ y-3&=-\frac{5}{2}(x-\frac{1}{2})\\ y&= -\frac{5}{2}x+\frac{5}{4}+3\\ y&=-\frac{5}{2}x+\frac{17}{4} \end{align*}\]
3.4 Pisteen etäisyys suorasta
Pisteen \((x_{0},y_{0})\) etäisyys suorasta \(ax+by+c=0\) on
\[\begin{align*}
\displaystyle\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}.
\end{align*}\]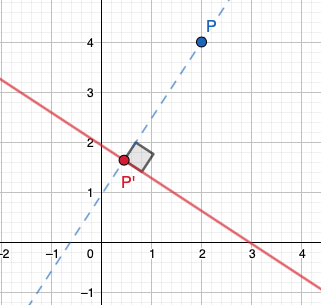 
Suora \(y-x+3\) kulkee ympyrän ohi. Ympyrän keskipiste on \((-2,0)\) ja ympyrän säde on 2. Kuinka kaukana suora on ympyrän kehästä?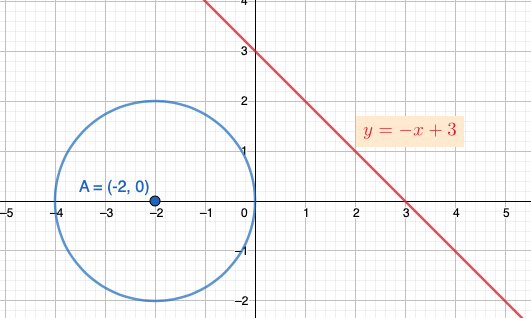 
Ympyrän kehää lähimpänä oleva piste \(P\) sijaitsee siinä kohdassa, jossa suoran normaali kulkee ympyrän keskipisteen kautta.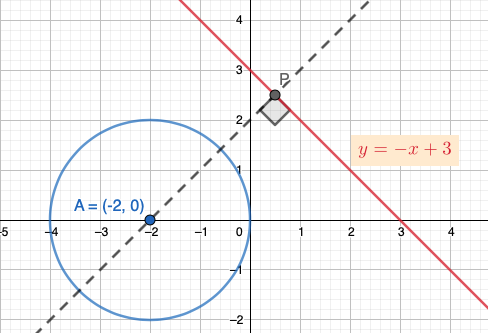 
Suoran yhtälö on nyt ratkaistussa muodossa, joten se täytyy muuntaa suoran normaalimuotoon: \[\begin{align*} y&=-x+3 \;\;\;\;\;\;\;\;&&|\text{ratkaistu muoto}\\ x+y-3&=0 \;\;\;\;\;\;\;&&|\text{normaalimuoto}\\ \end{align*}\]
Sijoitetaan suoran yhtälön termien kertoimet laskukaavaan \[\begin{align*} &\displaystyle\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}\\ &=\displaystyle\frac{|1\cdot -2+1\cdot 0+(-3)|}{\sqrt{1^{2}+1^{2}}}\\ &=\displaystyle\frac{|-4|}{\sqrt{2}}\\ &=2\sqrt{2} \end{align*}\]
Koska kysymyksenä oli suoran etäisyys ympyrän kehästä, pitää pituudesta vielä vähentää ympyrän säteen pituus: \(2\sqrt{2}-2≈0,828\).
4. Paraabeli
4.1 Määritelmä
Paraabelin määritelmä
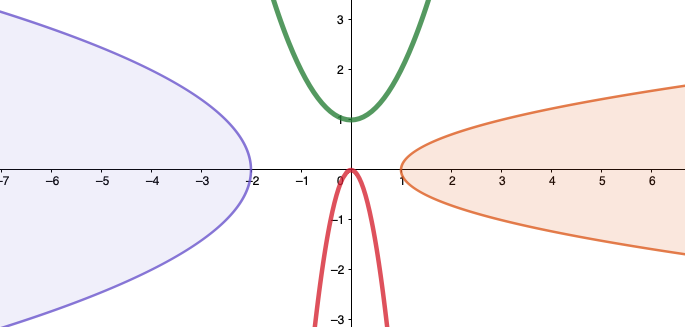
Paraabeli on niiden tason pisteiden joukko, jotka ovat yhtä etäällä kiinteästä suorasta (johtosuora) ja yksittäisestä pisteestä (polttopiste), joka ei ole suoralla.
Paraabelin polttopiste on \((2,1)\) ja johtosuora on \(y=3\). Määritetään paraabelin yhtälö.
Paraabelin määritelmän mukaan paraabelin käyrällä sijaitseva piste \((x,y)\) on yhtä etäällä paraabelin polttopisteestä sekä johtosuorasta.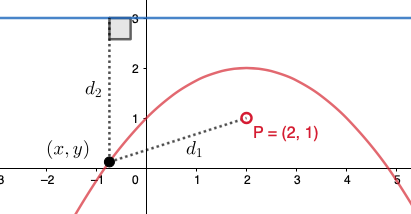 
Ratkaistaan ensin pisteen \((x,y)\) etäisyys \(d_{1}\) polttopisteestä:
\(d_{1}=\sqrt{(x-2)^{2}+(y-1)^{2}}\)
Ratkaistaan seuraavaksi pisteen etäisyys \(d_{2}\) johtosuorasta \(y=3\):
\(d_{2}=|y-3|\). Tässä voidaan hyödyntää myös pisteen \((x,y)\) etäisyyttä suorasta \(y=3\), eli \(y-3=0\)
\[\begin{align*} d_{2}=\frac{|y-3|}{\sqrt{0^{2}+1^{2}}}=|y-3| \;\;\;\;\;\; \big |\frac{|ax_{0}+by_{0}-c|}{\sqrt{a^{2}+b^{2}}} \end{align*}\]
Etäisyydet voidaan nyt asettaa yhtäsuuriksi \(d_{1}=d_{2}\), jolloin
\[\begin{align*} \sqrt{(x-2)^{2}+(y-1)^{2}}&=|y-3|\;\;\;\;\;\;&&|\text{Jos }a\geq 0 \text{ ja }b\geq 0\text{, niin }a=b\Leftrightarrow a^{2}=b^{2}\\ \left(\sqrt{(x-2)^{2}+(y-1)^{2}}\right)^{2}&=|y-3|^{2}\;\;\;\;&&|(\sqrt{a})^{2}=a\\ (x-2)^{2}+(y-1)^{2}&=(y-3)^{2}\;\;\;\;&&||a|^{2}=a^{2}\\ x^{2}-4x+y^{2}-2y+5&=y^{2}-6y+9\\ x^{2}-4x-4&=-4y\\ y=-\frac{1}{4}x^{2}+x+1 \end{align*}\]
Paraabelin perusmuotoinen yhtälö on siis \(y=-\frac{1}{4}x^{2}+x+1\).
4.2 Yhtälö
Yhtälöä \(y=ax^{2}+bx+c\) (\(a≠0\)) vastaava käyrä on ylöspäin aukeava paraabeli, jos \(a>0\). Vastaavasti, jos \(a<0\), paraabeli aukeaa alaspäin.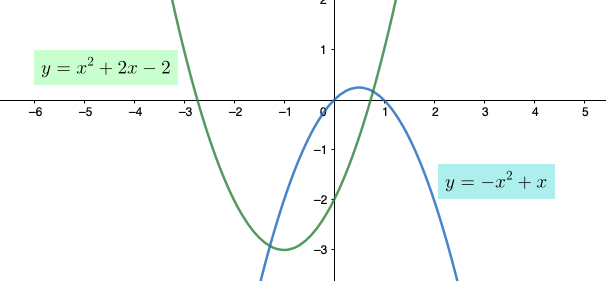 
Jos yhtälössä vaihdetaan muuttujien \(x\) ja \(y\) roolit, saadaan käyrä, joka aukeaa vasemmalle tai oikealle. Yhtälö on tällöin muotoa \(x=ay^{2}+bx+c\) (\(a≠0\)). Jos \(a<0\), niin paraabeli on vasemmalle aukeava, ja vastaavasti kun \(a>0\), paraabeli aukeaa oikealle.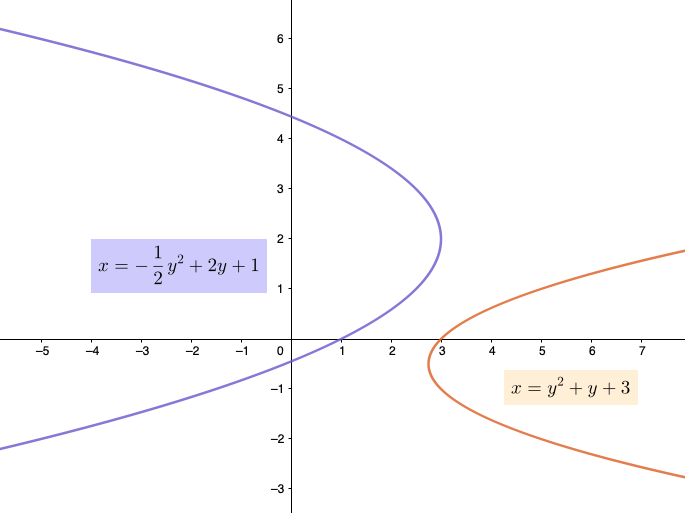 
Paraabelin yhtälö perusmuodossa
\[\begin{align*} y=ax^{2}+bx+c,\;\;\; a≠0 \end{align*}\]
Vastaavasti vaakasuoraan aukeaville paraabeleille pätee \(x=ay^{2}+by+c, a≠0\).
Paraabelin yhtälö huippumuodossa
Paraabelin yhtälö \(y=ax^{2}+bx+c\) voidaan esittää huippumuodossa: \[\begin{align*} y-y_{0}=a(x-x_{0})^2 \end{align*}\] Tässä \((x_{0},y_{0})\) on paraabelin huipun koordinaatit.
Vastaavasti vaakasuoraan aukeaville paraabeleille pätee \(x-x_{0}=a(y-y_{0})^2\).
Paraabelin yhtälö nollakohtamuodossa
\[\begin{align*} y=a(x-x_{1})(x-x_{2}), \;\;\;\;a≠0 \end{align*}\]
Tässä \(x_{1}\) ja \(x_{2}\) ovat paraabelin nollakohdat.
Vastaavasti vaakasuoraan aukeaville paraabeleille pätee \(x=a(y-y_{1})(y-y_{2}), a≠0\).
Paraabelin huipun koordinaatit
Pystysuoraan aukeavan paraabelin huipun \((x_{0},y_{0})\) x-koordinaatti on muotoa \[\begin{align*} x_{0}=\frac{-b}{2a}. \end{align*}\]
Vaakasuoraan aukeavan paraabelin huipun y-koordinaatti on muotoa \[\begin{align*} y_{0}=\frac{-b}{2a}. \end{align*}\]
Määritetään paraabelien \(y=\frac{1}{2}x^{2}\) ja \(x=\frac{1}{2}y^{2}\) leikkauspisteet.
Leikkauspiste toteuttaa aina molemmat yhtälöt. Leikkauspisteet saadaan siis selville ratkaisemalla yhtälöparin \[\begin{cases} y=\frac{1}{2}x^{2} \\ x=\frac{1}{2}y^{2} \end{cases}\]Sijoittamalla ylempi yhtälö alempaan yhtälöön saadaan \[\begin{align*} x&=\frac{1}{2}(\frac{1}{2}x^{2})^{2}\\ x&=\frac{1}{2}\cdot \frac{1}{2}^{2}x^{4}\\ x&=\frac{1}{2}^{3}x^{4}\\ x(1-\frac{1}{2}^{3}x^{3})&=0\\ 1-\frac{1}{2}^{3}x^{3}&=0 \text{ tai } x=0 \\ -\frac{1}{2}^{3}x^{3}&=-1\\ x^{3}&=8\\ x&=2 \end{align*}\]
Paraabeleilla on kaksi leikkauspistettä. Toisen pisteen x-koordinaatti on \(x=0\) ja toisen \(x=2\).
Sijoitetaan leikkauspisteen x-koordinaatti jompaan kumpaan yhtälöistä ja ratkaistaan y-koordinaatti: \[\begin{align*} y&=\frac{1}{2}2^{2}\;\;\;\;\;\;| x=2\\ y&=2 \end{align*}\] Toinen leikkauspiste on \((2,2)\).
Selvitetään vielä toisenkin pisteen y-koordinaatti: \[\begin{align*} y&=\frac{1}{2}0^{2}\;\;\;\;\;\;| x=0\\ y&=0 \end{align*}\] Toinen leikkauspiste on \((0,0)\).
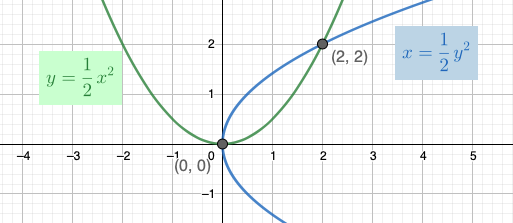
Vastaus: Paraabelit leikkaavat pisteissä \((0,0)\) ja \((2,2)\).
5. Ympyrä
Ympyrän määritelmä
Ympyrä on niiden tason pisteiden joukko, jotka ovat positiivisella vakioetäisyydellä kiinteästä pisteestä.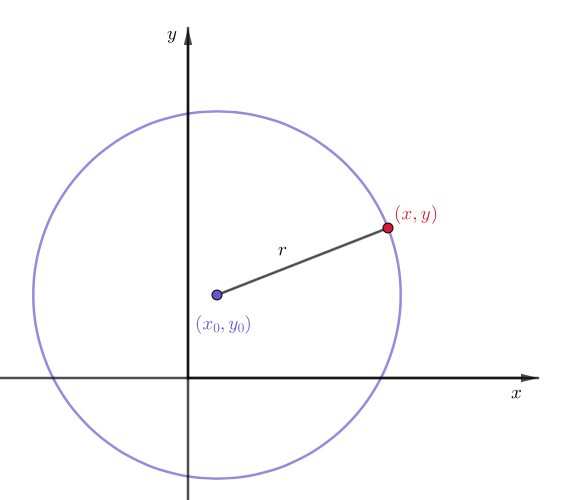 
5.1 Ympyrän yhtälöt
Ympyrän kehällä olevan pisteen \((x,y)\) etäisyys ympyrän keskipisteestä \((x_{0},y_{0})\) on säde \(r\).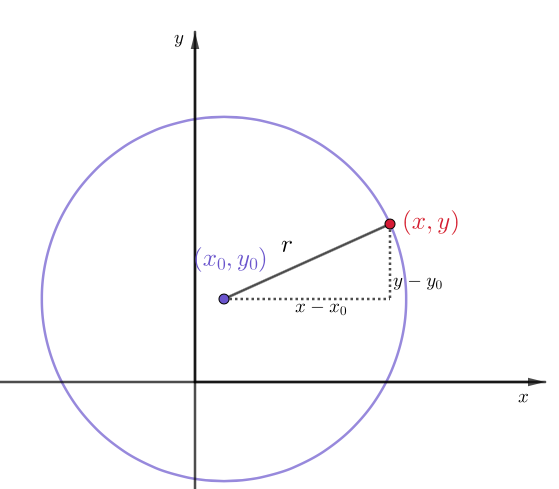 
Säteelle saadaa pituus Pythagoraan lauseen mukaisesti: \[\begin{align*} r&=\sqrt{(x-x_{0})^{2}+(y-y_{0})^2}\\ \text{joka edelleen on muotoa}\\ r^{2}&=(x-x_{0})^{2}+(y-y_{0})^2.\\ \end{align*}\]
Keskipistemuoto
Ympyrän keskipistemuotoinen yhtälö on \[\begin{align*} r^{2}=(x-x_{0})^{2}+(y-y_{0})^2 \end{align*}\]
Sievennetään edelleen saatua keskipistemuotoista yhtälöä: \[\begin{align*} r^{2}&=(x-x_{0})^{2}+(y-y_{0})^2\\ x^{2}-2xx_{0}+x_{0}^{2}+y^{2}-2yy_{0}+y_{0}^{2}&=r^{2}\\ x^{2}+y^{2}-2x_{0}x-2y_{0}y+x_{0}^{2}+y_{0}^{2}-r^{2}&=0 \end{align*}\] Jos nyt merkitään vakioita lyhyemmin: \(a=-2x_{0}\), \(b=-2y_{0}\), \(c=x_{0}^2+y_{0}^2-r^{2}\), saadaan ympyrän yhtälö muotoon \[\begin{align*} x^{2}+y^{2}+ax+by+c=0 \end{align*}\]
Yleinen muoto
Ympyrän yleinen muoto on \[\begin{align*} x^{2}+y^{2}+ax+by+c=0 \end{align*}\]
Kaikki keskipistemuodossa olevat ympyrän yhtälöt voidaan muuttaa yleiseen muotoon, mutta kaikki yleisessä muodossa olevat yhtälöt eivät ole ympyröitä.
Määritetään ympyrän \(x^{2}+y^{2}+3x-2y+2=0\) keskipiste sekä säde.
Keskipiste ja säde ovat luettavissa ympyrän keskipistemuotoisesta yhtälöstä, joten muokataan ympyrän yhtälö tähän muotoon. \[\begin{align*} x^{2}+y^{2}+3x-2y+2&=0\\ x^{2}+y^{2}+3x-2y&=-2\\ x^{2}+3x+y^{2}-2y&=-2\\ \end{align*}\] Muodostetaan seuraavaksi yhtälön vasemmalle puolelle binomin neliöt
\[\begin{align*} x^{2} + 3x + \text{\_\_} + y^{2} - 2y + \text{\_\_} &= -2\\ x^{2}+2\cdot x\cdot\frac{3}{2}+\text{\_\_}+y^{2}-2\cdot y\cdot 1+\text{\_\_}&=-2\\ x^{2}+2\cdot x\cdot\frac{3}{2}+\left(\frac{3}{2}\right)^{2}+y^{2}-2\cdot y\cdot 1+1^{2}&=-2+\left(\frac{3}{2}\right)+1^{2}\\ \left(x+\frac{3}{2}\right)^{2}+\left(y-1\right)^{2}&=\frac{5}{4}\\ \left(x-\left(-\frac{3}{2}\right)\right)^{2}+\left(y-1\right)^{2}&=\left(\frac{\sqrt{5}}{2}\right)^{2} \end{align*}\]
Ympyrän keskipistemuotoisesta yhtälöstä nähdään, että ympyrän keskipisteen koordinaatit ovat \((-\frac{3}{2},1)\) ja säde on \(\frac{\sqrt{5}}{2}\).
5.2 Ympyrä ja suora
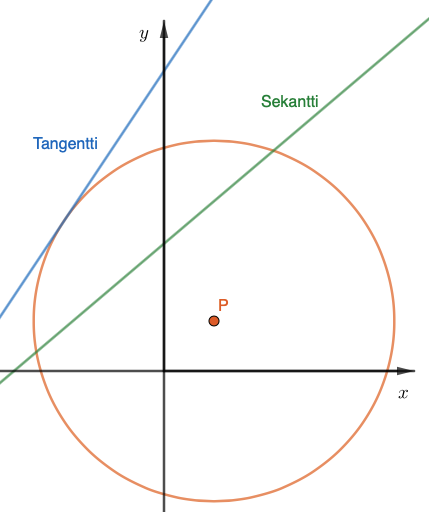
Ympyrällä ja suoralla on maksimissaan kaksi leikkauspistettä. Tällöin suoraa kutsutaan ympyrän sekantiksi. Jos suoralla ja ympyrällä on täsmälleen yksi leikkauspiste, suora on ympyrän tangentti.
Tangentin erityisominaisuuksia
- Tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan
- Tangentti on säteen etäisyydellä ympyrän keskipisteestä
- Tangentilla on tasan yksi leikkauspiste ympyrän kanssa
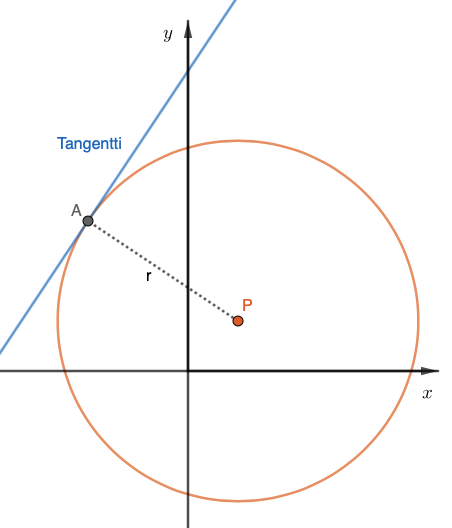Jos suoralla on yksikin yllä luetelluista ominaisuuksista, se on ympyrän tangentti.
Määritetään ympyrän \(x^{2}+y^{2}-2x-4y-20=0\) pisteeseen \((4,6)\) piirretyn tangentin yhtälö.
Selvitetään ensin ympyrän keksipisteen koordinaatit. Muutetaan ympyrän yhtälö keskipistemuotoon. \[\begin{align*} x^{2}+y^{2}-2x-4y-20&=0\\ x^{2}-2x+y^{2}-4y-20&=0\\ \end{align*}\] Muokataan yhtälön vasemmalle puolelle binomin neliöiden summa ja oikealle vakio: \[\begin{align*} x^{2}-2x+\_+y^{2}-4y+\_&=20\\ x^{2}-2x+1+y^{2}-4y+4&=20+1+4\\ (x-1)^{2}+(y-2)^{2}&=25 \end{align*}\]
Tästä muodosta saadaan selville ympyrän keskipiste \((1,2)\).
Piirretään nyt suora kulkemaan ympyrän keskipisteen ja kehän pisteen \((4,6)\) kautta.
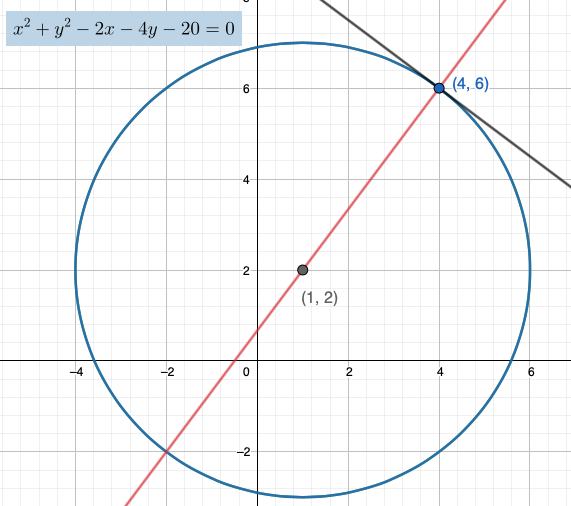
Tangenttia kohtisuorassa olevan suoran yhtälö on muotoa \(y-y_{0}=k_{s}(x-x_{0})\). Selvitetään kulmakerroin \(k_{s}\). \[\begin{align*} k_{s}&=\frac{\Delta y}{\Delta x}\\ k_{s}&=\frac{6-2}{4-1}=\frac{4}{3} \end{align*}\]
Tangentti on kohtisuorassa suoraa vastaan, jolloin kulmakertoimien tulo \(k_{t}k_{s}=-1\). Ratkaistaan tästä tangentin kulmakerroin. \[\begin{align*} k_{t}=\frac{-1}{\frac{4}{3}}=-\frac{3}{4} \end{align*}\]
Tangentin kulmakerroin on \(-\frac{3}{4}\) ja se kulkee pisteen \((4,6)\) kautta. Kirjoitetaan suoralle yhtälö: \[\begin{align*} y-6&=-\frac{3}{4}(x-4)\\ y&=-\frac{3}{4}x+9\\ y&=9-\frac{3}{4}x \end{align*}\]
Ympyrän \(x^{2}+y^{2}-2x-4y-20=0\) tangentin yhtälö on siis \(y=9-\dfrac{3}{4}x\).
6. Vektorit
Tässä luvussa tutustutaan vektoreihin ja niiden perusominaisuuksiin. Käsiteltäviä asioita ovat mm. vektoreiden yhteen- ja vähennyslasku, vektoreiden pistetulo, vektorin kertominen luvulla sekä vektoreiden välinen kulma
6.1 Vektorit tasolla ja avaruudessa
Vektorilla on aina suunta ja pituus. Poikkeuksena on nollavektori \(\overline{0}\), jolla ei ole suuntaa ja jonka pituus on \(0\).
Vektoreiden yhdensuuntaisuus
Vektorit ovat yhdensuuntaiset silloin, kun \(\overline{b}=t\overline{a}\), jollakin \(t≠0\). Tällöin pätee
- \(|\overline{b}|=|t\overline{a}|=|t||\overline{a}|\)
huom. tässä \(|t|\) on luvun \(t\) itseisarvo, ja \(|a|\) on vektorin \(\overline{a}\) pituus.
- \(\overline{b}\uparrow\uparrow\overline{a}\), jos \(t>0\)
- \(\overline{b}\uparrow\downarrow\overline{a}\), jos \(t<0\)
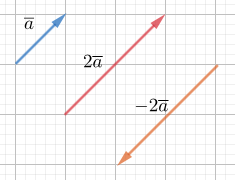
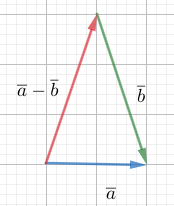
Vektoreiden summa ja erotus
Summavektori \(\overline{a}+\overline{b}\) kulkee vektorin \(\overline{a}\) alkupisteestä vektorin päätepisteeseen.
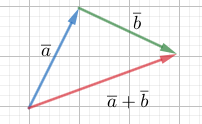
Erotusvektori: \(\overline{a}+(-\overline{b})=\overline{a}-\overline{b}\). Huomioi tässä summavektorin suunta ja vektorin \(\overline{b}\) suunta.
Pisteen paikkavektori
Avaruuden pisteen \(P(x,y,z)\) paikkavektori on \[\begin{align*} \overline{OP}=x\overline{i}+y\overline{j}+z\overline{k} \end{align*}\]
Pisteiden välinen vektori
Avaruuden kahden pisteen \(A=(x_{1},y_{1},z_{1})\) ja \(B=(x_{2},y_{2},z_{2})\) välinen vektori \(\overline{AB}\) on muotoa \[\begin{align*}
\overline{AB}=(x_{2}-x_{1})\overline{i}+(y_{2}-y_{1})\overline{j}+(z_{2}-z_{1})\overline{k}
\end{align*}\]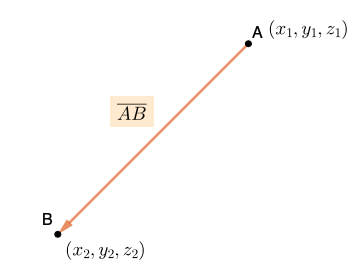 
Vektorin pituus
Avaruuden vektorin \(\overline{v}=x\overline{i}+y\overline{j}+z\overline{k}\) pituus on \[\begin{align*} |\overline{v}|=\sqrt{x^{2}+y^{2}+z^{2}} \end{align*}\]
Yksikkövektori
Vektorin \(\overline{a}\) yksikkövektori \(\overline{a}^{0}\) on vektorin \(\overline{a}\) kanssa samansuuntainen vektori, jonka pituus on 1:
\(\overline{a}^{0}=\displaystyle\frac{\overline{a}}{|\overline{a}|}\)
Vektorit voidaan jakaa osiin, komponentteihin, jotka ovat tason erisuuntaisten vektoreiden \(\overline{v}\) ja \(\overline{u}\) suuntaisia. Tällöin vektori \(\overline{a}\) voidaan esittää muodossa \(\overline{a}=t\overline{u}+s\overline{v}\), jossa \(t\) ja \(s\) ovat reaalilukuja.
Tämä jako on yksikäsitteinen, eli jos vektorille \(\overline{a}\) on kaksi erilaista esitystapaa \(\overline{a}=t\overline{u}+s\overline{v}\) ja \(\overline{a}=p\overline{u}+r\overline{v}\), niin \(t=p\) ja \(s=r\).
Vektorin \(\overline{v}\) alkupiste on pisteessä \(A=(2,4,3)\) ja päätepiste on \(B=(-1,-2,5)\). Vektorin \(\overline{v}\) päätepisteestä lähtee vektori \(\overline{w}\) vastakkaiseen suuntaan pisteeseen \(C\) asti. Vektorin \(\overline{w}\) pituus on 8.
Lasketaan vektorin \(\overline{v}\) pituus sekä pisteen \(C\) koordinaatit.
Hahmotellaan tilanteesta kuva: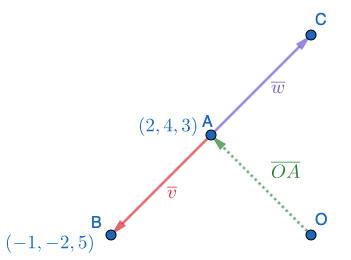 
Ratkaistaan ensin vektorin \(\overline{v}\) pituus: \[\begin{align*} |\overline{v}|=\sqrt{(-1-2)^{2}+(-2-4)^{2}+(5-3)^{2}}=\sqrt{49}=7 \end{align*}\] Vektorin \(\overline{v}\) yhtälö on \[\begin{align*} \overline{v}=\overline{AB}=(-1-2)\overline{i}+(-2-4)\overline{j}+(5-3)\overline{k}=-3\overline{i}-6\overline{j}+2\overline{k} \end{align*}\] Ratkaistaan seuraavaksi pisteen \(C\) koordinaatit:
Koska vektori \(\overline{w}\) on vastakkaissuuntainen kuin vektori \(\overline{v}\), niin vektori \(\overline{w}\) voidaan kirjoittaa muotoon \(\overline{w}=-8\overline{v}^{0}\). Muodostetaan vektorin \(\overline{v}\) suuntaisen yksikkövektorin yhtälö: \[\begin{align*} \overline{v}^{0}&=\frac{\overline{v}}{|\overline{v}|}=\frac{1}{|\overline{v}|}\cdot \overline{v}\\ \overline{v}^{0}&=\frac{1}{7}\cdot (-3\overline{i}-6\overline{j}+2\overline{k})\\ \overline{v}^{0}&=\frac{-3}{7}\overline{i}-\frac{6}{7}\overline{j}+\frac{2}{7}\overline{k} \end{align*}\]
Nyt vektorille \(\overline{w}\) \[\begin{align*} \overline{w}&=-8\overline{v}^{0}=-8\cdot (\frac{-3}{7}\overline{i}-\frac{6}{7}\overline{j}+\frac{2}{7}\overline{k})\\ \overline{w}&=\frac{24}{7}\overline{i}+\frac{48}{7}\overline{j}-\frac{16}{7}\overline{k} \end{align*}\]
Pisteen \(C\) koordinaatit saadaan paikkavektorista \(\overline{OC}\).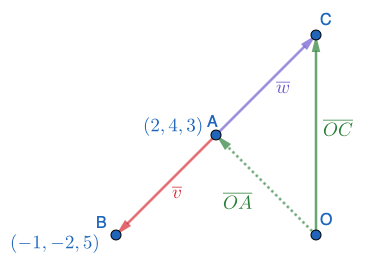 
\[\begin{align*}
\overline{OC}&=\overline{OA}+\overline{w}\\
\overline{OC}&=2\overline{i}+4\overline{j}+3\overline{k}+(\frac{24}{7}\overline{i}+\frac{48}{7}\overline{j}-\frac{16}{7}\overline{k})\\
\overline{OC}&=\frac{38}{7}\overline{i}-\frac{20}{7}\overline{j}+\frac{5}{7}\overline{k}
\end{align*}\]
Vektorin \(\overline{v}\) pituus on \(7\) ja pisteen \(C\) koordinaatit ovat \(\displaystyle(\frac{38}{7},-\frac{20}{7},\frac{5}{7})\).
6.2 Vektoreiden välinen kulma ja pistetulo
Vektoreiden \(\overline{a}\) ja \(\overline{b}\) välinen kulma on pienempi niistä kulmista, jotka muodostuvat kun vektorit piirretään alkamaan samasta pisteestä.
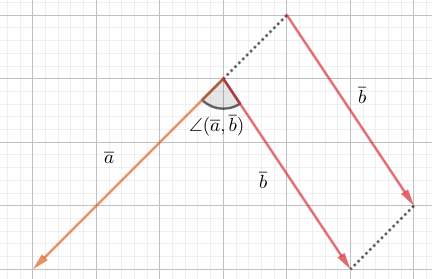
Vektoreiden pistetulo
Tasossa: \[\begin{align*} \overline{a}\cdot\overline{b}=x_{1}x_{2}+y_{1}y_{2}, \end{align*}\] kun \(\overline{a}=x_{1}\overline{i}+y_{1}\overline{j}\) ja \(\overline{b}=x_{2}\overline{i}+y_{2}\overline{j}\)
Avaruudessa: \[\begin{align*} \overline{a}\cdot\overline{b}=x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}, \end{align*}\] kun \(\overline{a}=x_{1}\overline{i}+y_{1}\overline{j}+z_{1}\overline{k}\) ja \(\overline{b}=x_{2}\overline{i}+y_{2}\overline{j}+z_{2}\overline{k}\) ja \(\overline{c}=x_{3}\overline{i}+y_{3}\overline{j}+z_{3}\overline{k}\)
Vektoreiden pistetulolla on yhteys vektoreiden väliseen kulmaan. Jos vektoreiden \(\overline{a}\) ja \(\overline{b}\) pistetulo on 0, niin vektorit ovat kohtisuorassa toisiaan vastaan.
Vektoreiden välinen kulma
Kahden vektorin, jotka eivät ole nollavektoreita, välisen kulman kosini on yhteydessä vektoreiden pistetuloon sekä vektoreiden pituuksiin: \[\begin{align*} &\overline{a}\cdot\overline{b}=|\overline{a}||\overline{b}|\cos{(\overline{a},\overline{b})}\\ &\text{eli}\\ &\cos{(\overline{a},\overline{b})}=\frac{\overline{a}\cdot\overline{b}}{|\overline{a}||\overline{b}|} \end{align*}\]
Määritetään vektoreiden \(\overline{a}=-2\overline{i}+\overline{j}+2\overline{k}\) ja \(\overline{b}=\overline{i}-5\overline{j}-\overline{k}\) välinen kulma.
Jotta kulman suuruus voidaan ratkaista, täytyy määrittää vektoreiden pituudet sekä pistetulo.
Vektorin \(\overline{a}\) pituus on \[\begin{align*} |\overline{a}|=\sqrt{(-2)^{2}+1^{2}+2^{2}}=3 \end{align*}\]
Vektorin \(\overline{b}\) pituus on \[\begin{align*} |\overline{b}|=\sqrt{1^{2}+(-5)^{2}+(-1)^{2}}=3\sqrt{3} \end{align*}\] Vektoreiden pistetulo \[\begin{align*} \overline{a}\cdot\overline{b}=(-2)\cdot1+1\cdot(-5)+2\cdot(-1)=-9 \end{align*}\] Nyt voidaan ratkaista vektoreiden välinen kulma: \[\begin{align*} \cos{(\overline{a},\overline{b})}=\frac{\overline{a}\cdot\overline{b}}{|\overline{a}||\overline{b}|}=\frac{-9}{3\cdot3\sqrt{3}}=\frac{-\sqrt{3}}{3} \end{align*}\] Ja tästä saadaan vektoreiden väliseksi kulmaksi \(125,3°\).
6.3 Vektori ja suora
Avaruuden suora
Suora kulkee avaruudessa pisteen \(A=(x_{0},y_{0},z_{0})\) kautta vektorin \(\overline{s}=s_{x}\overline{i}+s_{y}\overline{j}+s_{z}\overline{k}\) suuntaisesti.
Suoran vektorimuotoinen yhtälö: \[\begin{align*} \overline{OP}&=\overline{OA}+t\overline{s}\\ &=x_{0}\overline{i}+y_{0}\overline{j}+z_{0}\overline{k}+t(s_{x}\overline{i}+s_{y}\overline{j}+s_{z}\overline{k})\;\;\;\;\;(t\in\R) \end{align*}\]
Suoran parametrimuotoinen yhtälö: \[\begin{align*} \begin{cases} x=x_{0}+ts_{x}\\ y=y_{0}+ts_{y}\\ z=z_{0}+ts_{z} \end{cases} \end{align*}\]
Xy-tason suoran kulmakerroin on \(k=\frac{\Delta y}{\Delta x}\) ja suoran eräs suuntavektori on \(\overline{s}=\Delta x\overline{i}+\Delta y\overline{j}\).
Suoran \(ax+by+c=0\) eräs normaalivektori on \(\overline{n}=a\overline{i}+b\overline{j}\).
Johdetaan pisteiden \((2,2,2)\) ja \((-1,-2,-1)\) kautta kulkevan suoran yhtälöt vektori- ja parametrimuodossa.
Olkoon \(A=(2,2,2)\), \(Q=(-1,-2,-1)\) ja \(P=(x,y,z)\)
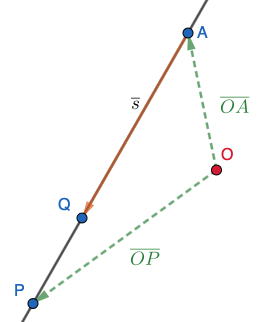Johdetaan ensin vektorimuotoinen yhtälö:
Suoran suuntavektoriksi voidaan valita annettuja pisteitä yhdistävä vektori \(\overline{s}=(-1-2)\overline{i}+(-2-2)\overline{j}+(-1-2)\overline{k}=-3\overline{i}-4\overline{j}-3\overline{k}\).
Nyt suoran vektorimuotoiseksi yhtälöksi saadaan \[\begin{align*} \overline{OP}&=\overline{OA}+t\overline{s}\\ \overline{OP}&=2\overline{i}+2\overline{j}+2\overline{k}+t(-3\overline{i}-4\overline{j}-3\overline{k}) \end{align*}\]
Johdetaan sitten suoralle parametrimuotoinen yhtälö. Tämä yhtälö saadaan kertoimien vertailulla, kun vektoriyhtälö kirjoitetaan muotoon \[\begin{align*} x\overline{i}+y\overline{j}+z\overline{k}=(2-3t)\overline{i}+(2-4t)\overline{j}+(2-3t)\overline{k}. \end{align*}\]
Suoran parametrimuotoinen yhtälö on \[\begin{align*} \begin{cases} x=2-3t\\ y=2-4t\\ z=2-3t.\\ \end{cases} \end{align*}\]
Huomaa, että suoran parametrimuotoinen yhtälö voidaan muodostaa, kun tunnetaan kiinteän pisteen ja suuntavektorin koordinaatit.
6.4 Vektori ja taso
Avaruuden pisteet muodostavat tason, jos ja vain jos ne toteuttavat yhtälön \(ax+by+cz+d=0\), jossa ainakin yksi kertoimista \(a, b, c\) ei ole nolla. Tälle tasolle eräs normaalivektori on \(\overline{n}=a\overline{i}+b\overline{j}+c\overline{k}+d\).
Pisteen kautta kulkevan tason yhtälö
Taso kulkee pisteen \(A=(x_{0},y_{0},z_{0})\) kautta ja on kohtisuorassa vektoria \(\overline{n}=a\overline{i}+b\overline{j}+c\overline{k}\) vastaan. Tason yhtälö on: \[\begin{align*} a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0 \end{align*}\]
Tason normaalimuotoinen yhtälö on: \[\begin{align*} ax+by+cz+d=0 \end{align*}\]
Määritetään, missä kulmassa tasot \(2x+y-z+1=0\) ja \(6x+3y+2z-10=0\) leikkaavat toisensa.
Hahmotellaan piirros tilanteesta.
Muodostetaan nyt näille tasoille normaalit. Normaalien välinen kulma on saman suuruinen kuin tasojen välinen kulma.
Tason \(2x+y-z+1=0\) eräs normaali on muotoa \(\overline{n}=2\overline{i}+\overline{j}-\overline{k}\) ja tasolle \(6x+3y+2z-10=0\) eräs normaalivektori on muotoa \(\overline{m}=6\overline{i}+3\overline{j}+2\overline{k}\).
Jotta kahden vektorin välinen kulma voidaan laskea, tarvitaan näiden vektoreiden pistetulo ja pituudet.
Vektoreiden pistetulo on \[\begin{align*} \overline{n}\cdot\overline{m}=2\cdot6+1\cdot3+(-1)\cdot2=13 \end{align*}\] Ja pituudet \[\begin{align*} &|\overline{n}|=\sqrt{2^{2}+1^{2}+(-1)^{2}}=\sqrt{6}\\ &|\overline{m}|=\sqrt{6^{2}+3^{2}+2^{2}}=7 \end{align*}\]
Nyt voidaan ratkaista normaalien välinen kulma: \[\begin{align*} &\cos{(\overline{n},\overline{m})}=\frac{\overline{n}\cdot\overline{m}}{|\overline{n}||\overline{m}|}=\frac{13}{\sqrt{6}\cdot7} \end{align*}\]
Normaalivektoreiden välinen kulma on \(40,7°\).
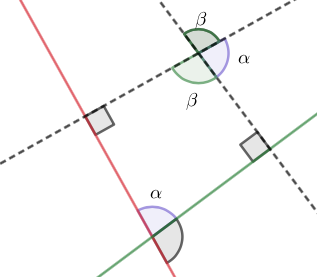
Tasojen välinen kulma on yhtä suuri kuin normaalien välinen kulma, eli \(40,7°\).
Tehtäviä
Tehtävä 1
a.
b.
Tehtävä 2
a.
Siirrä limen siivu koordinaatistopohjaan siten, että sen yhtälö on \((x-\frac{4}{3})^{2}+ (y+\frac{4}{3})^{2}=2\).
b.
Siirrä banaanit koordinaattiruudukon päälle siten, että ne kuvaavat yhtälöitä \(x=\frac{1}{3}y^{2}\) ja \(x=-\frac{1}{3}y^{2}-1\).
Tehtävä 3.
Sijoitetaan kartta koordinaatistoon siten, että asemakatu kulkee suoran \(y=0,14x+4,6\) suuntaisesti ja infopiste on pisteessä \((-4,7;-5)\).
a.
Laske infopisteen etäisyys Asemakadusta (koordinaatistossa etäisyys 1 tarkoittaa noin 56 metriä luonnossa)
Suoran normaalimuoto on \(0,14x-y+4,6=0\). Mikä on infopisteen etäisyys suorasta?
b.
Lilja on eksynyt Kuopion keskustaan ja kiertää kehää Sankaripuiston ympärillä. Kulkureitti on ympyrän \((x+10,4)^{2}+(y+1,6)^{2}=4\) muotoinen. Kuinka lähellä Asemakatua Lilja enimmillään käy?
Ympyrän keskipistemuoto on \((x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}\). Mikä on ympyrän keskipisteen etäisyys suorasta \(y=0,14x+4,6\)?
Tehtävä 4.
Ravirata voidaan muodostaa yhdistämällä kaksi toisensa sivuavaa, yhdenmuotoista ympyrää kahdella tangentilla. Raviradan suoran pituus on 175m ja kaarresäteet ovat 85m.
a.
Hevonen ravaa yhden kierroksen. Kuinka pitkän matkan hevonen ravaa yhteensä kaarteissa?
Ympyrän kaarenpituus saadaan yhtälöstä \(b=\frac{\alpha}{360°}\cdot2\pi\cdot r\), jossa \(r\) on kaarevuussäde, \(\alpha\) on kierrettävä kulma, ja \(b\) on kaaren pituus.
b.
Bruno ravaa raviradan kaarteessa siten, että sillä on kaarretta jäljellä \(\frac{1}{4}\) ennen alkavaa suoraa. Toisella puolella rataa Hillevi on jo ravannut kolmanneksen kaarteesta. Hahmotetaan Bruno sekä Hillevi vektoreina seuraavasti: \(\overline{B}=-\frac{2}{3}\overline{i}+\frac{2}{3}\overline{j}\) ja \(\overline{H}=-\frac{2}{3}\overline{i}-\overline{j}\).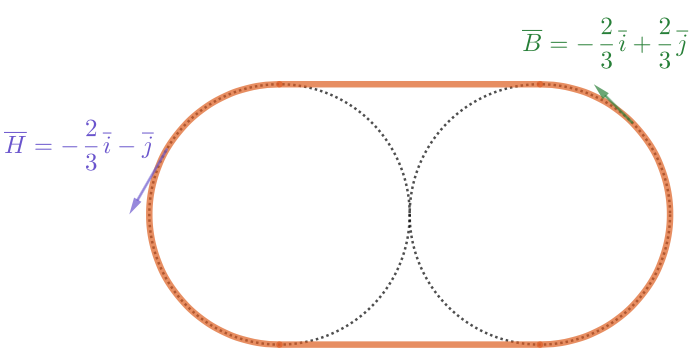 
Kuinka suuri on Brunon ja Hillevin välinen kulma?
Tehtävä 5.
Kuumailmapallo on lähdössä lennolle, mutta 200 m päässä kuumailmapallosta on 20 m korkea radiomasto. Muotoile kuumailmapallon lentoradalle paraabelin yhtälö, jos pallo ainoastaan ylittäisi radiomaston ja laskeutuisi sen toiselle puolelle 200 metrin päähän mastosta. Lentäjä haluaa 5 m turvavälin maston ylityksessä.
Muodosta paraabelin lauseke.
Tehtävä 6.
Komeetta, joka saapuu aurinkokuntaan suurella nopeudella, ohittaa planeetan hyperbelin muotoisella radalla. Planeetan gravitaatiovoima vaikuttaa komeetan liikerataan tehden siitä kaarevan.
Alla olevassa kuvassa on origokeskinen, ylöspäin ja alaspäin aukeava hyberpeli. Hyperbelin yhtälö akselimuodossa on \(\displaystyle\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=-1\). Hyperbelillä on kaksi asymptoottia, eli suoraa, jotka kulkevat hyperbelin kylkien suuntaisesti kuitenkaan leikkaamatta hyperbeliä. Tutki ja päättele, mitä osia hyperbelissä on.
Tehtävä 7.
Navetan katolla istuu 50 cm korkea kukko. Aurinko paistaa vinon katon suuntaisesti. Kuinka kaukana talon seinästä on kukon pään varjo?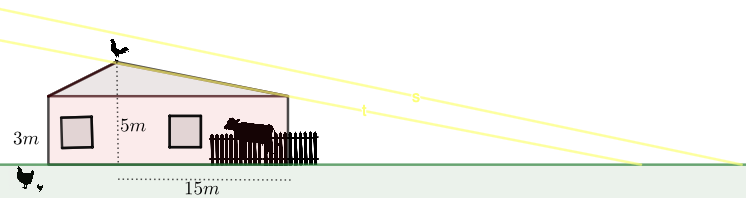 
Tehtävä 8.
Vanhoja YO-tehtäviä
1.
Ympyrän \(x^{2}+y^{2}=16\) jänteen keskipiste on \((2,1)\). Määritä jänteen pituus. [S15/5]
VASTAUS: \(2\sqrt{11}\)
RATKAISU:
TAPA 1:
Jänteen keskipisteen etäisyys origosta on \(a=\sqrt{2^{2}+1^{2}}=\sqrt{5}\).
Jänteen päätepisteen etäisyys origosta on ympyrän säde \(r=4\).
Pythagoraan lauseen mukaan jänteen pituuden puolikas \(b=\sqrt{r^{2}-a^{2}}=\sqrt{16-5}=\sqrt{11}\).
Koko jänteen pituus on siten \(2b=2\sqrt{11}\).
TAPA 2:
Olkoon \(P=(2,1)\). Janan \(OP\) tulee olla kohtisuorassa jännettä vastaan.
Koska janan \(OP\) kulmakerroin on \(\frac{1}{2}\), niin jänteen kulmakertoimen tulee olla \(-2\).
Jänne on siten osa suoraa \(y-1=-2(x-2)\) eli \(y=-2x+5\).
Leikkauspisteet saadaan yhtälöparista \[\begin{align*} \begin{cases} y=-x+5\\ x^{2}+y^{2}=16 \end{cases} \end{align*}\]
josta \[\begin{align*} \begin{cases} x=2+\sqrt{\frac{11}{5}}\\ y=1-2\sqrt{\frac{11}{5}} \end{cases} \text{ tai } \begin{cases} x=2-\sqrt{\frac{11}{5}}\\ y=1+2\sqrt{\frac{11}{5}} \end{cases} \end{align*}\]
Jänteen pituus on \(\sqrt{\left(2-\sqrt{\frac{11}{5}}-2-\sqrt{\frac{11}{5}}\right)^{2}+\left(1+2\sqrt{\frac{11}{2}}-1+2\sqrt{\frac{11}{5}}\right)^{2}}=\sqrt{4\cdot11}=2\sqrt{11}\).
2.
Tasokäyrä kulkee pisteen \((3,4)\) kautta. Määritä käyrän yhtälö, kun kyseessä on
- origon kautta kulkeva suora
- origokeskeinen ympyrä
- ylöspäin aukeava paraabeli, jonka huippu on origossa. [S15/2]
VASTAUS: a. \(y=\frac{4}{3}x\), b. \(x^{2}+y^{2}=r^{2}\), c. \(y=\frac{4}{9}x^{2}\)
RATKAISU:
a.
Suoran kulmakerroin on \(k=\frac{4-0}{3-0}=\frac{4}{3}\), joten sen yhtälö on \(y=\frac{4}{3}x\) tai \(4x-3y=0\).
b.
Ympyrän säde \(r\) on pisteen \((3,4)\) etäisyys origosta, eli \(r=\sqrt{3^{2}+4^{2}}=5\).
Yhtälö on \(x^{2}+y^{2}=r^{2}\) eli \(x^{2}+y^{2}=25\).
c.
Origohuippuisen, ylöspäin aukeavan paraabelin yhtälö on muotoa \(y=ax^{2}\). Koska piste \((3,4)\) on käyrällä, niin on voimassa: \(4=a\cdot3^{2}\Leftrightarrow a=\dfrac{4}{9}\), joten paraabelin yhtälö on \(y=\dfrac{4}{9}x^{2}\).
3.
Määritä se toisen asteen polynomi, joka saa pisteissä \(x=0, x=1\) ja \(x=2\) samat arvot kuin funktio \(f(x)=2^{x}\). [K11/4]
VASTAUS: \(\frac{1}{2}x^{2}+\frac{1}{2}x+1\).
RATKAISU:
Polynomille \(P(x)=ax^{2}+bx+c\) pätee:
\(P(0)=c=2^{0}\Leftrightarrow c=1\).
\(P(1)=a+b+c=2^{1}\leftrightarrow a+b=1\)
\(P(2)=4a+2b+c=2^{2}\Leftrightarrow 4a+2b=3\).
On saatu yhtälöpari \(a+b=1\) ja \(4a+2b=3\), jonka ratkaisu on \(a=\frac{1}{2}, b=\frac{1}{2}\).
4.
Ympyrä sivuaa suoraa \(3x-4y=0\) pisteessä \((8,6)\). Lisäksi se sivuaa positiivista x-akselia. Määritä ympyrän keskipiste ja säde. [K14/5]
VASTAUS: Säde on \(\frac{10}{3}\) ja keskipiste on \((10,\frac{10}{3})\).
RATKAISU:
Pisteen \((8,6)\) kautta kulkevan suoran \(3x-4y=0\) normaalin yhtälö on \(y-6=-\frac{4}{3}(x-8)\Leftrightarrow x=-\frac{3}{4}y+\frac{25}{2}\).
Ympyrän keskipiste sijaitsee normaalilla. Jos ympyrän säde on \(r\), niin keskipisteen \(\left(-\frac{3}{4}r+\frac{25}{2},r\right)\) tulee olla alkuperäisestä suorasta etäisyydellä \(r\).
Näin saadaan ehto
\(\dfrac{|-\frac{9}{4}r+\frac{75}{2}-4r|}{\sqrt{9+16}}=r\Leftrightarrow |-\dfrac{25}{4}r+\dfrac{72}{2}|=5r\Leftrightarrow -25r+150=\pm20r\leftrightarrow r=\dfrac{10}{3}\text{ tai } r=30\).
Tapauksessa \(r=30\) ympyrä sivuaa negatiivista x-akselia. Kysytty säde on siis \(\frac{10}{3}\) ja keskipiste \((10,\frac{10}{3})\).
5.
Olkoon \(A=(1,0), B=(0,-1) ja t>1\). Piste \(T=(t,0)\) keskipisteenä piirretään ympyrä, joka leikkaa yksikköympyrän \(x^{2}+y^{2}=1\) kohtisuorasti kuvion mukaisessa pisteessä \(C\) janan \(=A\) pisteessä \(D\). [S14/10]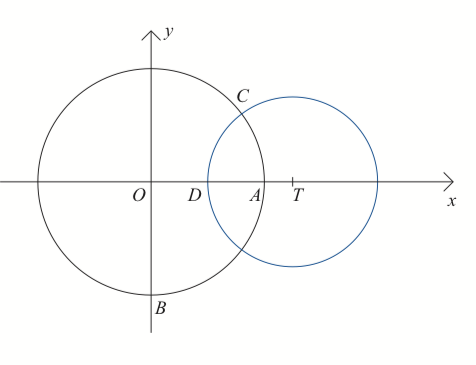 
Määritä pisteen \(C\) koordinaatit parametrin \(t\) avulla lausuttuna.
Osoita, että pisteet \(B,D\) ja \(C\) ovat samalla suoralla.
VASTAUS: a. \(\left(\frac{1}{t},\frac{\sqrt{t^{2}-1}}{t}\right)\)
RATKAISU:
a.
Olkoon piste \(C=(x,y)\) ja \(E=(x,0)\). Tällöin \(\Delta TOC\sim\Delta COE\), joten \[\begin{align*} \dfrac{t}{1}=\dfrac{1}{x}\\ \Leftrightarrow x=\dfrac{1}{t}. \end{align*}\]
Koska \(x^{2}+y^{2}=1\), niin \(y=\sqrt{1-x^{2}}\).
Pisteen \(C\) koordinaatit ovat siten \(\left(\dfrac{1}{t},\sqrt{1-(\frac{1}{t})^{2}}\right)=\left(\dfrac{1}{t},\dfrac{\sqrt{t^{2}-1}}{t}\right)\).
b.
Pienemmän ympyrän säde \(CT=\sqrt{t^{2}-1}\).
Merkitään \(DE=a\).
Jana \(TA=t-1\) ja \(AE=1-\frac{1}{t}\). Saadaan yhtälö \(TA+AE+ED=TD\), eli \[\begin{align*} t-1+1-\frac{1}{t}+a=\sqrt{t^{2}-1} \end{align*}\] josta \(a=\sqrt{t^{2}-1}-t+\frac{1}{t}=\dfrac{1-t^{2}+t\sqrt{t^{2}-1}}{t}\).
Janan \(CD\) kulmakerroin \[\begin{align*} k_{CD}=\dfrac{y}{a}\\ &=\dfrac{\dfrac{\sqrt{1-t^{2}}}{t}}{\dfrac{1-t^{2}+t\sqrt{t^{2}-1}}{t}}\\ &=\dfrac{\sqrt{t^{2}-1}}{t\sqrt{t^{2}-1}-(t^{2}-1)}\\ &=\dfrac{\sqrt{t^{2}-1}}{t\sqrt{t^{2}-1}-(\sqrt{t^{2}-1})^{2}}\\ &=\dfrac{1}{t-\sqrt{t^{2}-1}}. \end{align*}\]
Koska jana \(OD=\frac{1}{t}-a=\frac{1}{t}-\sqrt{t^{2}-1}+t-\frac{1}{t}=t-\sqrt{t^{2}-1}\), niin \(k_{BD}=\dfrac{1}{OD}=\dfrac{1}{t-\sqrt{t^{2}-1}}=k_{CD}.\)
Näin ollen pisteet \(B,D\) ja \(C\) ovat samalla suoralla.
6.
Pisteestä \(A(1,-1,0)\) siirrytään 9 pituusyksikköä vektorin \(\overline{i}-2\overline{j}+2\overline{k}\) suuntaan pisteeseen \(B\) ja siitä edelleen 10 pituusyksikköä vektorin \(3\overline{i}-4\overline{k}\) suuntaan pisteeseen \(C\). Määritä pisteen \(C\) koordinaatit.[S13/5]
VASTAUS: \(C=(10,-7,-2)\)
RATKAISU:
Suuntavektorit ja niiden pituudet ovat \(\overline{a}=\overline{i}-2\overline{j}+2\overline{k}, |\overline{a}|=\sqrt{1+4+4}=3\) ja \(\overline{b}=3\overline{i}-4\overline{k}, |\overline{b}|=\sqrt{9+16}=5\).
Lähtöpisteen paikkavektori on \(\overline{OA}=\overline{i}-\overline{j}\).
Koska \(|\overline{a}|=34\) niin ensimmäinen siirtymävektori on \(3\overline{a}\).
Koska \(|\overline{b}|=5\), niin toinen siirtymäektori on \(2\overline{b}\).
Täten \(\overline{OC}=\overline{OA}+3\overline{a}+2\overline{b}=(\overline{i}-\overline{j})+3(\overline{i}-2\overline{j}+2\overline{k})+2(3\overline{i}-4\overline{k})=10\overline{i}-7\overline{j}-2\overline{k}\), joten \(C=(10,-7,-2)\).
7.
Pisteiden \(A(2,0,1)\) ja \(B(3,1,3)\) yhdysjanan keskipisteen kautta asetetaan taso, joka on kohtisuorassa yhdysjanaa vastaan. Missä pisteessä tämä taso leikkaa y-akselin? [K13/7]
VASTAUS: Leikkauspiste on \((0,7,0)\).
RATKAISU:
Yhdysjanan keskipiste on \(M=(\frac{2+3}{2},\frac{1+0}{2},\frac{3+1}{2})=(\frac{5}{2},\frac{1}{2},2)\).
Tason normaalivektori on
\(\overline{AB}=(3-2)\overline{i}+(1-0)\overline{j}+(3-1)\overline{k}=\overline{i}+\overline{j}+2\overline{k}\),
joten tason yhtälö on muotoa \(x+y+2z+d=0\).
Taso kulkee pisteen \(M\) kautta, joten \[\begin{align*} \frac{5}{2}+\frac{1}{2}+4+d=0\Leftrightarrow d=-7 \end{align*}\]
Sijoittamalla yhtälöön \(x=0\) ja \(z=0\), saadaan \(y=7\).
Leikkauspiste on \((0,7,0)\).
8.
Suoran vektorimuotoinen yhtälö on \(\overline{OP}=\overline{i}+2\overline{j}+2\overline{k}+t(2\overline{i}+\overline{j}+s\overline{k})\), missä \(t\in\R\) on suoran parametri. Märitä sellainen luku \(s\), että suora on tasossa \(3x+4y+5z=21\). [S10/3a]
VASTAUS: \(s=-2\)
RATKAISU:
Suoran piste on \((1+2t,2+t,2+ts)\).
Tämän tulee toteuttaa tason yhtälö kaikilla parametrin \(t\) arvoilla, mistä seuraa \(s=-2\).
9.
Määritä ympyrän \(x^{2}+y^{2}+4x-2y+1=0\) niiden tangenttien yhtälöt, jotka kulkeutuvat pisteen \((1,3)\) kautta. [S07/5]
VASTAUS: \(y=3\) ja \(12x-5y+3=0\)
RATKAISU:
Täydentämällä neliöksi saadaan ympyrän yhtälö muotoon \((x+2)^{2}+(y-1)^{2}=4\).
Ympyrän keskipiste on siis \((-2,1)\) ja säde 2. Piste \((1,3)\) on ympyrän ulkopuolella. Siitä ympyrälle piirretyt tangentit ovat muotoa \(y-3=k(x-1)\).
Keskipisteen etäisyyden tangentista on oltava kaksi.
Tästä saadaan kulmakertoimelle \(k\) ehto \[\begin{align*} \dfrac{|-2k-1-k+3|}{\sqrt{k^{2}+1}}=2 \end{align*}\]
Joka edelleen sievenee muotoon \(5k^{2}-12k=0.\)
ratkaisut ovat \(k=0\) ja \(k=\dfrac{12}{5}.\)
Vastaavat tangentit ovat \(y=3\) ja \(12x-5y+3=0\).
10.
- Muodosta sen tason yhtälö, joka kulkee pisteen \((2,4,6)\) kautta ja leikkaa xy-tason pitkin suoraa \(x+2y=3\).
- Missä pisteissä a-kohdan taso leikkaa koordinaattiakselit? [K16/8]
VASTAUS: a. \(x+2y-\frac{7}{6}z=3\) b. \(x=3\), \(y=\frac{3}{2}\) ja \(z=-\frac{18}{7}\).
RATKAISU:
a.
Koska xy-tasossa \(z=0\), on tason yhtälö muotoa \(x+2y+kz=3\).
Koska taso kulkee pisteen \((2,4,6)\) kautta, niin pisteen koordinaatit toteuttavat sen yhtälön, eli \(2+2\cdot4+6k=3\), josta \(k=-\frac{7}{6}.\)
Yhtälö on siten \(x+2y-\frac{7}{6}z=3\) eli \(6x+12y-7z=18\).
b.
x-akselilla \(y=z=0\), joten \(6x=18\Leftrightarrow x=3\)
y-akselilla \(x=z=0\), joten \(12y=18\Leftrightarrow y=\frac{3}{2}\)
z-akselilla \(y=x=0\), joten \(-7z=18\Leftrightarrow z=-\frac{18}{7}\)
11.
Olkoon \(\overline{a}=4\overline{i}-5\overline{j}+3\overline{k}\) ja \(\overline{b}=2\overline{i}+\overline{j}-2\overline{k}\). Esitä vektori \(\overline{a}\) summana vektoreista \(\overline{u}\) ja \(\overline{v}\), joista \(\overline{u}\) on yhdensuuntainen vektorin \(\overline{b}\) kanssa ja \(\overline{v}\) kohtisuorassa vektoria \(\overline{b}\) vastaan. [K11/8]
VASTAUS: \(\overline{u}=-\frac{2}{3}\overline{i}-\frac{1}{3}\overline{j}+\frac{2}{3}\overline{k}\) ja \(\overline{v}=\frac{14}{3}\overline{i}-\frac{14}{3}\overline{j}+\frac{7}{3}\overline{k}\).
RATKAISU:
On oltava \(\overline{a}=\overline{u}+\overline{v}\), missä \(\overline{u}=t\overline{b}\) ja \(\overline{v}\cdot\overline{b}=0\).
Edelleen \(\overline{v}\cdot\overline{b}=(\overline{a}-t\overline{b})\cdot\overline{b}=\overline{a}\cdot\overline{b}-t\overline{b}\cdot\overline{b}=-3-9t\).
Tämä pistetulo on nolla, kun \(t=-\frac{1}{3}\).
Näin ollen \(\overline{u}=-\frac{1}{3}\overline{b}=-\frac{2}{3}\overline{i}-\frac{1}{3}\overline{j}+\frac{2}{3}\overline{k}\)
ja \(\overline{v}=\overline{a}+\frac{1}{3}\overline{b}=\frac{14}{3}\overline{i}-\frac{14}{3}\overline{j}+\frac{7}{3}\overline{k}\).
12.
Vektoreiden \(\overline{a}\) ja \(\overline{b}\) summa on vektori \(4\overline{i}+\overline{j}\) ja niiden pistetulo on \(\overline{a}\cdot\overline{b}=4\). Vektori \(\overline{b}\) on yhdensuuntainen vektorin \(\overline{i}\) kanssa. Määritä vektorit \(\overline{a}\) ja \(\overline{b}\). [K10/5]
VASTAUS: \(\overline{a}=2\overline{i}+\overline{j}, \overline{b}=2\overline{i}\)
RATKAISU: Tehtävänannon mukaan \(\overline{a}+\overline{b}=4\overline{i}+\overline{j}\) ja \(\overline{a}\cdot\overline{b}=4\). Lisäksi vektori \(\overline{b}\) on vektorin \(\overline{i}\) kanssa yhdensuuntainen, eli voidaan merkitä \(\overline{b}=k\cdot\overline{i}\), jossa \(k\in\Z\).
Olkoon nyt vektori \(\overline{a}\) muotoa \(\overline{a}=m\overline{i}+n\overline{j}\) ja \(\overline{b}=k\overline{i}\).
Summavektori on \(4\overline{i}+\overline{j}=(m+k)\overline{i}+n\overline{j}\) ja pistetulo \(4=m\cdot k+n\cdot0=m\cdot k\).
Summavektorista voidaan päätellä, että \(n=1\).
Ja edelleen vektoreiden summasta ja pistetulosta voidaan muodostaa yhtälöpari: \[\begin{align*} &\begin{cases} 4=m+k\\ 4=m\cdot k \end{cases} \end{align*}\] Tästä voidaan jo päätellä, että luvut, jotka toteuttavat molemmat yhtälöt ovat \(m=2\) ja \(k=2\). Matemaattinen ratkaisu: \[\begin{align*} &\begin{cases} 4=m+k\;\;\;\;\;\;\;\|-k\\ 4=m\cdot k \end{cases} \\ &\begin{cases} 4-k=m\\ 4=m\cdot k\;\;\;\;\;\;\;\;\;\|\text{sij. }m=4-k \end{cases} \\ &4=(4-k)k\\ &4=4k-k^{2}\\ &k^{2}-4k+4=0 \end{align*}\] Ja toisen asteen ratkaisukaavasta saadaan ratkaisuksi \(k=2\).
Sijoitetaan \(k=2\) toiseen yhtälöparin yhtälöistä: \[\begin{align*} 4&=m+k\\ 4&=m+2\;\;\;\|-2\\ m&=2 \end{align*}\]
Ja koska vektorit olivat muotoa \(\overline{a}=m\overline{i}+n\overline{j}\) ja \(\overline{b}=k\overline{i}\), ja sijoittamalla kertoimet saadaan vektorit \(\overline{a}=2\overline{i}+1\overline{j}=2\overline{i}+\overline{j}\) ja \(\overline{b}=2\overline{i}\).
13.
Lasersäteellä osoitetaan pisteestä \(A(1,-2,3)\) vektorin \(\overline{u}=2\overline{i}-\overline{j}-3\overline{k}\) suuntaan. Toisella säteellä osoitetaan pisteestä \(B(9,-1,-12)\) vektorin \(\overline{v}=-\overline{i}-2\overline{j}+3\overline{k}\) suuntaan. Näytä, että säteet leikkaavat toisensa, ja määritä niiden leikkauspiste. [K14/8]
VASTAUS: Leikkauspiste on \((7,-5,-6)\).
RATKAISU:
Säteet leikkaavat toisensa, jos yhtälö \(\overline{OA}+s\overline{u}=\overline{OB}+t\overline{v}\) toteutuu joillain \(s>0,t>0\).
Tällöin \[\begin{align*} (1+2s)\overline{i}+(-2-s)\overline{j}+(3-3s)\overline{k}=(9-t)\overline{i}+(-1-2t)\overline{j}+(-12+3t)\overline{k}. \end{align*}\] Vertaamalla komponentteja saadaan yhtälöryhmä \[\begin{align*} \begin{cases} 1+2s=9-t\\ -2-s=-1-2t\\ 3-3s=-12+3t. \end{cases} \end{align*}\]
Ratkaistaan kahdesta ylimmästä yhtälöstä \(t=2\) ja \(s=3\). Huomataan, että tällöin myös kolmas yhtälö toteutuu.
Näin ollen säteet leikkaavat ja kysytty leikkauspiste on \((7,-5-6)\).
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.