MAA5 Transkendenttiset funktiot ja yhtälöt


Kurssin tavoitteena on, että opiskelija
- tutustuu ilmiöiden matemaattiseen mallintamiseen sini- ja kosinifunktioiden sekä eksponentti- ja logaritmifunktioiden avulla
- tutkii sini- ja kosinifunktioita yksikköympyrän symmetrioiden avulla
- osaa ratkaista sellaisia trigonometrisia yhtälöitä, jotka ovat tyyppiä \(\sin f(x)=a\) tai \(\sin f(x)=\sin g(x)\)
- osaa soveltaa sini- ja kosinifunktioiden yhteyttä \(\sin^2 x + \cos^2 x = 1\)
- tuntee eksponentti- ja logaritmifunktioiden ominaisuudet ja osaa ratkaista niihin liittyviä yh- tälöitä
- osaa käyttää ohjelmistoja sini- ja kosinifunktioiden sekä eksponentti- ja logaritmifunktioiden tutkimisessa sekä sini- ja kosiniyhtälöiden sekä eksponentti- ja logaritmiyhtälöiden ratkaise- misessa sovellusongelmien yhteydessä.
Keskeiset sisällöt
- suunnattu kulma ja radiaani
- yksikköympyrä
- sini- ja kosinifunktiot symmetria- ja jaksollisuusominaisuuksineen
- sini- ja kosiniyhtälöiden ratkaiseminen
- negatiivinen eksponentti ja murtopotenssi
- eksponenttifunktiot ja -yhtälöt
- logaritmi ja logaritmin laskusäännöt
- logaritmifunktiot ja -yhtälöt
1. Trigonometriset funktiot
1.1 Suunnattu kulma ja radiaani
Kulma on samasta pisteestä lähtevän puolisuoran rajaama alue. Kulma voidaan myös ajatella puolisuorana, joka kiertyy tasossa oman alkupisteensä ympäri. On sovittu, että jos kierto on myötäpäivään, se on silloin negatiivista ja vastaavasti vastapäivään kierto on positiivista. Näin syntyy suunnattu kulma, joka on joko positiivinen tai negatiivinen.
Radiaanin määritelmä
Kulman suuruus on 1 radiaani (1 rad), jos sitä vastaava kaari on säteen pituinen.
Edelleen määritelmästä voidaan johtaa kulman suuruudelle \(\alpha=\displaystyle\frac{b}{r}\), jossa \(\alpha\) on mitattu kulma, \(b\) on vastaavan kaaren pituus ja \(r\) on säde. 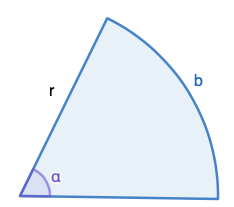
Radiaanin ja asteen vastaavuus
Koko ympyrän kehän pituus on \(2\pi r\), jota vastaava keskuskulma on \(360°\). Radiaaniluvuksi saadaan tällöin \(\displaystyle\frac{2\pi r}{r}=2\pi\).
Tällöin siis \[\begin{align*} 360°=2\pi. \end{align*}\]
1.2 Yksikköympyrä
Tutki yksikköympyrää radiaaneilla ja asteilla.
Yksikköympyrän määritelmä
Yksikköympyrää käyttäen trigonometriset funktiot määritellään kulman \(\alpha\) kehäpisteen \(P(x,y)\) koordinaattien avulla: \[\begin{align*}
\sin\alpha=y\\
\cos\alpha=x\\
\tan\alpha=\frac{y}{x}
\end{align*}\] 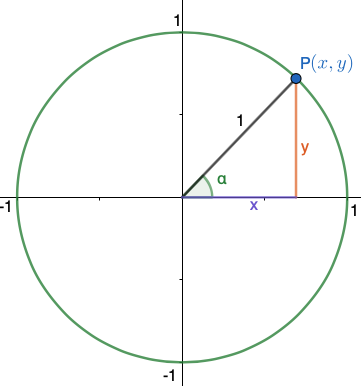
Yksikköympyrän kehäpisteen koordinaatit toteuttavat yhtälön \(x^{2}+y^{2}=1\).
Trigonometristen funktioiden merkit eri neljänneksissä. 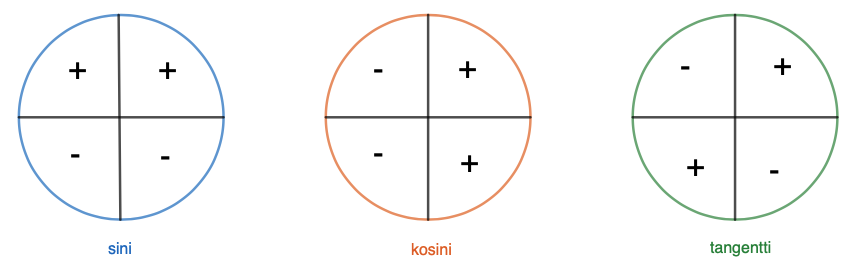
Peruskaavat
\[\begin{align*} \sin^{2}\alpha+\cos^{2}\alpha=1\\ \tan\alpha=\frac{\sin\alpha}{\cos\alpha} \end{align*}\]
Trigonometristen funktioiden arvot voidaan aina lausua terävän kulman avulla, koska yksikköympyrä on symmetrinen.
Palautuskaavat
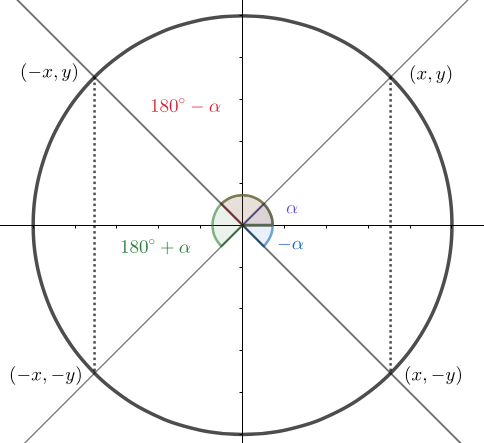
Vastakulmat \(\alpha\) ja \(-\alpha\) \[\begin{align*} \cos(-\alpha)&=\cos\alpha\\ \sin(-\alpha)&=-\sin\alpha\\ \end{align*}\]
Suplementtikulmat \(\alpha\) ja \(\pi-\alpha\) \[\begin{align*} \cos(\pi-\alpha)&=-\cos(\alpha)\\ \sin(\pi-\alpha)&=\sin\alpha\\ \end{align*}\]
Koska kulman ja sen vastakulman sinit ovat toistensa vastalukuja, sinifunktion sanotaan olevan pariton. Vastaavasti koska kosinifunktion kulma ja vastakulma ovat yhtä suuret, kosinifunktio on parillinen.
1.3 Sinin ja kosinin ominaisuuksia
Kun kulman suuruus kasvaa arvosta \(0\) arvoon \(2\pi\), sen sini, eli y-koordinaatti, kasvaa arvosta \(0\) arvoon \(1\). Edelleen sini pienenee arvoon nolla ja edelleen arvoon \(-1\), josta se kasvaa uudelleen arvoon \(0\).
Samanaikaisesti saman kulman kosini, eli x-koordinaatti, vähenee arvosta \(1\) arvoon \(0\). Edelleen kosini vähenee arvoon \(-1\), josta se kasvaa arvoon nolla ja edelleen arvoon \(1\).
Trigonometristen funktioiden saamat arvot toistuvat aina tietyin arvovälein. Tätä ominaisuutta kutsutaan jaksollisuudeksi.
Sinin ja kosinin jaksollisuudesta
\[\begin{align*} \sin(\alpha+n\cdot2\pi)=\sin\alpha\text{, kun }n\in\Z,\\ \cos(\alpha+n\cdot2\pi)=\cos\alpha\text{, kun }n\in\Z. \end{align*}\]
Funktiot \(\sin x\) ja \(\cos x\) ovat jaksollisia ja jatkuvia funktioita. Niiden määrittelyjoukko on \(\R\) ja ne saavat arvoja väliltä \([-1,1]\).
1.4 Sini- ja kosiniyhtälöiden ratkaiseminen
Määritetään \(\cos\displaystyle\frac{13\pi}{4}\).
Kulma \(\frac{13\pi}{4}\) on suurempi kuin yksi kokonainen kierros, eli \(2\pi\). Erotetaan kulmasta täydet kierrokset: \[\begin{align*} \frac{13\pi}{4}=\frac{5\pi+8\pi}{4}=\frac{5\pi}{4}+\frac{8\pi}{4}=\frac{5\pi}{4}+2\pi \end{align*}\]
Nyt jaksollisuuden perusteella \[\begin{align*} \cos\frac{13\pi}{4}=\cos(\frac{5\pi}{4}+2\pi)=\cos\frac{5\pi}{4}=-\frac{1}{\sqrt{2}}. \end{align*}\]
Siis \(\cos\displaystyle\frac{13\pi}{4}=-\frac{1}{\sqrt{2}}\).
1.5 Kulman tangentti
\(\tan\alpha\) on kulman \(\alpha\) tangenttipisteen \(T\) y-koordinaatti, kun \(\alpha≠\frac{\pi}{2}+n\cdot\pi\), kun \(n\in\Z\).
Tangentin arvot toistuvat puolen kierroksen \(\pi\) välein, eli \(\tan(\alpha+n\cdot\pi)=\tan\alpha\), kun \(n\in\Z\). 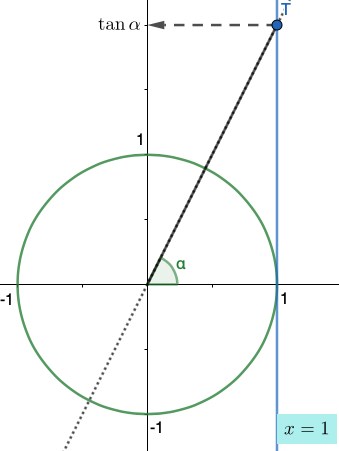
Tangentin ominaisuuksia
Vastakulmat \(\alpha\) ja \(-\alpha\) \[\begin{align*} \tan(\alpha)=-\tan\alpha \end{align*}\] Suplementtikulmat \(\alpha\) ja \(\pi-\alpha\) \[\begin{align*} \tan(\pi-\alpha)=-\tan\alpha \end{align*}\]
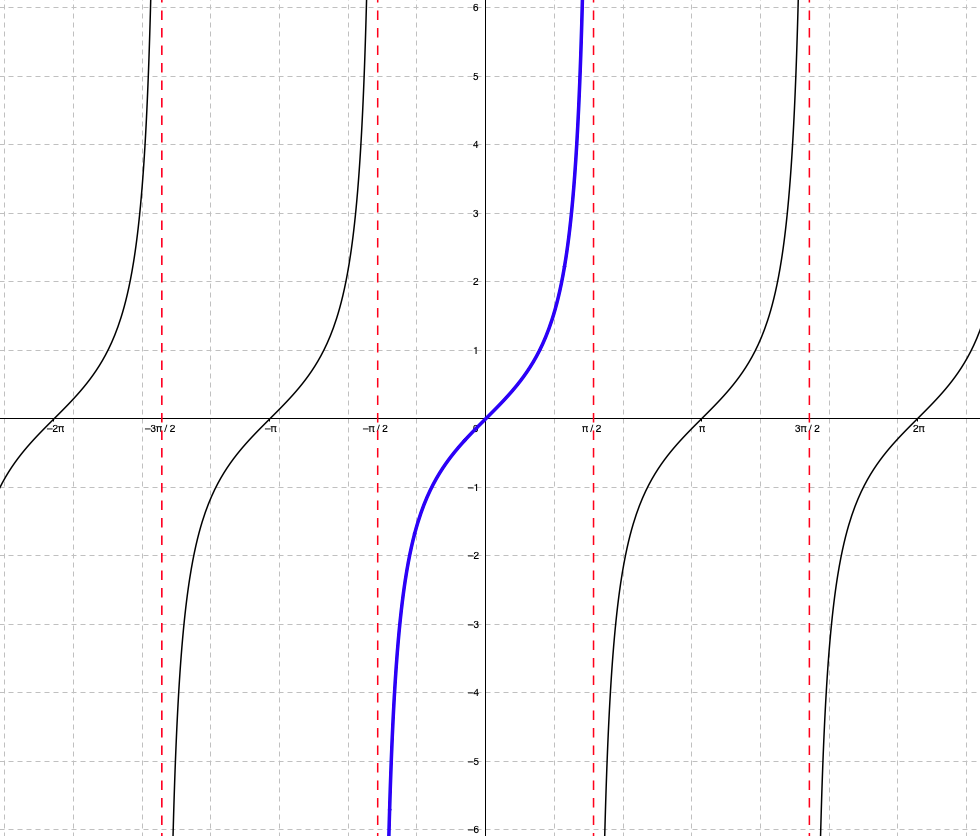
Funktio \(\tan x\) on jatkuva ja jaksollinen funktio. Sen määrittelyjoukko on \(x≠\frac{\pi}{2}+n\cdot\pi\), \(n\in\Z\) ja funktio saa arvoja koko reaalilukujen joukossa \(\R\).
2. Eksponentti- ja logaritmifunktiot
2.1 Eksponenttifunktio
Eksponenttifunktio
Funktio, joka on muotoa \(f(x)=a^{x}\) jossa \(a>0, a≠1\), kutsutaan eksponenttifunktioksi.
- Eksponenttifunktio on jatkuva ja monotoninen, ja se on määritelty koko reaalilukujen joukossa \(\R\).
- Jos \(a>1\), eksponenttifunktio \(a^{x}\) on kasvava
- Jos \(0<a<1\), eksponenttifunktio \(a^{x}\) on vähenevä
2.2 Negatiivinen eksponentti
Luvun \(a\) negatiivinen eksponentti tarkoittaa luvun \(a\) käänteisluvun vastaavaa positiivista potenssia.
Negatiivinen eksponentti
\[\begin{align*} a^{-n}=\left(\frac{1}{a}\right)^{n}=\frac{1^{n}}{a^{n}}=\frac{1}{a^{n}} \end{align*}\]
Sievennetään \(\displaystyle\frac{3^{5}}{3^{7}}\):
\[\begin{align*} \displaystyle\frac{3^{5}}{3^{7}}=3^{5-7}=3^{-2}=\frac{1}{3^{2}}=\frac{1}{9} \end{align*}\]
Vastaus on siis \(\displaystyle\frac{3^{5}}{3^{7}}=\frac{1}{9}\).
2.3 Murtopotenssi
Neliöjuuri luvusta \(a\): \(\sqrt{a}\) voidaan kirjoittaa myös muodossa \(a^{\frac{1}{2}}\). Tällaista eksponenttia kutsutaan murtopotenssiksi.
Murtopotenssi
Jos luvulla \(a\) on eksponenttina rationaalimuotoinen eksponentti, voidaan se tulkita seuraavasti: \[\begin{align*} \sqrt[n]{a^{m}}=\left(a^{\frac{1}{n}}\right)^{m}=\left(a^{m}\right)^{\frac{1}{n}}=a^{\frac{m}{n}},\\ \end{align*}\] kun \(a\in\R_{+}\) ja \(m,n\in\Z_{+}\)
Ratkaistaan, mikä luku on \(a^{\frac{4}{3}}\), kun \(a^{-\frac{1}{3}}=2\).
\[\begin{align*} a^{-\frac{1}{3}}= \left(\frac{1}{a}\right)^{\frac{1}{3}}= \sqrt[3]{\frac{1}{a}}= 2 \end{align*}\] Ratkaistaan tästä \(a\) korottamalla yhtälön molemmat puolet potenssiin \(3\): \[\begin{align*} \frac{1}{a}= 2^{3}\\ a=\frac{1}{8} \end{align*}\] Ratkaistaan seuraavaksi, paljonko on \(a^{\frac{4}{3}}\): \[\begin{align*} a^{\frac{4}{3}}=\left(\frac{1}{8}\right)^{\frac{4}{3}}=\frac{1^{\frac{4}{3}}}{8^{\frac{4}{3}}}=\frac{\sqrt[3]{1^{4}}}{\sqrt[3]{8^{4}}}=\frac{1}{16}. \end{align*}\]
Siis \(a^{\frac{4}{3}}=\frac{1}{16}.\)
2.4 Logaritmifunktio
Logaritmifunktio
Funktiota, joka on muotoa \(f(x)=\log_a(x)\) jossa \(a>0,a≠1\) sanotaan logaritmifunktioksi.
- Logaritmifunktio on jatkuva ja monotoninen, ja se on määritelty kun \(x>0\).
- Jos \(a>1\), logaritmifunktio \(f(x)=\log_a(x)\) on kasvava
- Jos \(0<a<1\), logaritmifunktio \(f(x)=\log_a(x)\) on vähenevä
\(e\)-kantaista logaritmifunktiota \(\ln(x)=\log_e(x)\), kutsutaan luonnolliseksi logaritmiksi. Tässä luku \(e\) on nimeltään Neperin luku, joka on irrationaalinen: \(e=2,71828182845...\)
10-kantainen logaritmi on \(\lg(x)=\log_{10}(x)\).
3. Eksponentti- ja logaritmiyhtälöiden ratkaiseminen
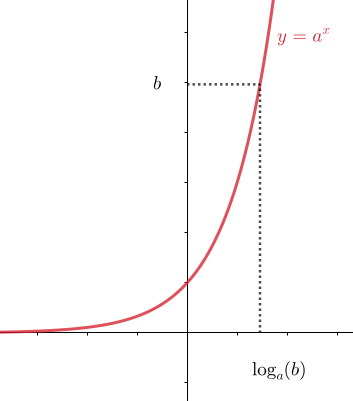
Logaritmi \(\log_a(b)\) on se luku, johon kantaluku \(a\) täytyy korottaa, jotta potenssin arvo on luku \(b\).
3.1 Logaritmi- ja eksponenttiyhtälön ratkaiseminen
logaritmi- ja eksponenttiyhtälön ratkaisu
Luvun \(b\) \(a\)-kantainen logaritmi \(\log_{a}(b)\) on eksponenttiyhtälön \(a^{x}=b\) ratkaisu täsmälleen silloin kun \(x=\log_a(b)\).
Tässä \(a>0, a≠1\) ja \(b>0\).
3.2 Logaritmin laskusääntöjä
Logaritmin laskusääntöjä
\[\begin{align*} \log_a(xy)&=\log_a(x)+\log_a(y)\\ \log_a(\frac{x}{y})&=\log_a(x)-\log_a(y)\\ \log_a(x^{r})&=r\cdot\log_a(x)\\ \log_a(1)&=0\\ \log_a(a)&=1\\ \end{align*}\]
\[\begin{align*} \text{Logaritmin kannan vaihto: } \log_a(x)=\frac{\log_b(x)}{\log_b(a)}\\ \end{align*}\]
Määritetään \(\log_2(\frac{3}{\sqrt[3]{2}})\).
\[\begin{align*} \log_2\left(\frac{2}{\sqrt[3]{2}}\right)=\log_2\left(\frac{2}{2^{\frac{1}{3}}}\right)=\log_2\left({2^{1-\frac{1}{3}}}\right)=\log_2\left({2^{\frac{2}{3}}}\right)=\frac{2}{3}\cdot\log_2\left({2}\right)=\frac{2}{3}\cdot1=\frac{2}{3} \end{align*}\]
Siis \(\log_2(\frac{3}{\sqrt[3]{2}})=\frac{2}{3}\).
Ratkaistaan \(x\) yhtälöstä \(\displaystyle\frac{25^{x}}{5^{3}}=0,2\).
\[\begin{align*} \frac{25^{x}}{5^{3}}&=0,2\\ \frac{(5^{2})^{x}}{5^{3}}&=0,2\\ \frac{5^{2\cdot x}}{5^{3}}&=0,2\\ 5^{2\cdot x-3}&=0,2\\ \end{align*}\] Kun \(a\) ja \(b\) ovat positiivisia, \(a=b\) täsmälleen silloin kun \(\ln a=\ln b\). Nyt siis: \[\begin{align*} \ln5^{2\cdot x-3}&=\ln0,2\\ (2x-3)\ln5&=\ln0,2\\ 2x-3&=\frac{\ln0,2}{\ln5}\\ 2x&=\frac{\ln0,2}{\ln5}+3\\ x&=1 \end{align*}\]
Vastaus: \(x=1\).
Tehtäviä
Tehtävä 1.
a.
b.
Tehtävä 2.

Olkoon eksponenttifunktio \(f(x)=a^{x}+1\), jossa \(a>0,a≠0\). Tämä eksponenttifunktio kulkee pisteen \((4,3)\) kautta. Määritä funktion kantaluku \(a\) ja \(f(8)\).
Tehtävä 3.

Lääketieteessä käytetään jodi-131:stä, jonka puoliintumisaika on noin 8 päivää. Puoliintumisaika tarkoittaa sitä aikaa, joka kuluu atomimäärän vähenemiseen puoleen.
a.
Kuinka monta prosenttia alkuperäisestä määrästä jodia on yhä ihmisen elimistössä yhden päivän jälkeen?
Joka päivä jodin määrä elimistössä \(k\)-kertaistuu. Ensimmäisen päivän jälkeen jodia on elimistössä \(k\cdot M\) verran, toisen päivän jälkeen jodia on elimistössä \(\underbrace{k\cdot k\cdot}_{\text{2 kpl}} M\) verran..
Ratkaise kerroin \(k\), kun tiedetään, että kahdeksantena päivänä jodin määrä on puoliintunut, eli \(k^{8}\cdot M=\frac{1}{2}M\).
b.
Yhdessä joditabletissa on vaikuttavaa ainetta 130 mg. Jos tabletteja ottaa kaksi, kuinka monen päivän kuluttua elimistössä on alle puolikkaan tabletin verran vaikuttavaa ainetta?
Olkoon \(f(t)\) jodin määrä hetkellä \(t\). Samassa ajassa hajoaa aina sama määrä ainetta, joten hajoaminen on eksponentiaalista ja \(f(t)=k\cdot a^t\). Nyt alkuarvo \(k\) on joditablettien määrä alussa eli \(k=2\cdot130\;\text{mg}=260\;\text{mg}\).
Ensin ratkaistaan kerroin \(a\). Koska tiedetään, että \(8\) päivän jälkeen jodista on puolet jäljellä, saadaan yhtälö
\[\frac{1}{2}k=k\cdot a^8,\]
josta \(a=\left(\dfrac{1}{2}\right)^\frac{1}{8}=2^{-\frac{1}{8}}\).
Jodin määrää kuvaava funktio siis \(f(t)=260\cdot\left(2^{-\frac{1}{8}}\right)^t\).
Tästä halutaan selvittää, milloin jodin määrä on pienempää kuin \(\dfrac{130\;\text{mg}}{2}=65\;\text{mg}\dots\)
Tehtävä 4.

Vaihtovirta on sähkövirtaa, joka suunta vaihtuu ajan \(t\) funktiona. Vaihtovirta on sinimuotoista, ja sille käytetään merkintä \(AC\) tai symbolia \(\sim\).
Vaihtovirtapiirissä yhtälö \(i=0,48\cdot\sin(100\pi t)\) esittää sähkövirran voimakkuutta ampeereina, ja yhtälö \(u=50\cdot\sin(100\pi t-0,52)\) esittää sähköpiirin jännitettä voltteina. Yhtälöissä käytetty \(t\) tarkoittaa aikaa sekunteina.
a.
Mikä on sähkövirran sinifunktion amplitudi?
Sinifunktiossa, joka on muotoa \(f(x)=a\cdot \sin(bx+c),\) parametri \(a\) kuvaa aallon amplitudia eli suurinta etäisyyttä \(x-\)akselista.
b.
Mikä on jännitteen ja virran sinifunktioiden vaihe-ero?
Sinifunktiossa, joka on muotoa \(f(x)=a\cdot \sin(bx+c),\) parametri \(b\) kuvaa aallon tiheyttä. Nyt sekä sähkövirran, että jännitteen yhtälöissä \(b=100\pi\) eli siniaallot ovat samantaajuisia.
Parametri \(c\) puolestaan siirtää kuvaajaa vaakasuunnassa, joten parametrien \(c\) erotus kertoo sinifunktioiden vaihe-eron.
c.
Mikä on virran \(i\) suuruus silloin, kun jännite \(u\) on nolla?
Ensin täytyy ratkaista, millä muuttujan \(t\) arvolla jännite on nolla, yhtälöstä
\[50\cdot\sin(100\pi t-0,52)=0\]
ja sen jälkeen laskea sähkövirran arvo saadulla muuttujan \(t\) arvolla.
Voit katsoa lisätietoja sinifunktion kulusta tältä Opetustv:n videolta.
Tehtävä 5.

Ranskassa Normandian rannikolla sijaitsee Unescon perintökohde Mont-St-Michelin luostarisaari. Saarelle on mahdollista kävellä meren pohjaa pitkin laskuveden aikaan.
Merenpinnan korkeus muuttuu ajan funktiona \(h(t)=4.0\text{ m}+3.0\text{ m}\cdot\cos\left(\dfrac{\pi(t-2)}{6}\right)\) vuorovesi-ilmiön takia.
a.
Kuinka matalalla merenpinta voi alimmillaan olla?
Kosinifunktion pienin arvo on \(-1,\) joten funktio \(h(t)\) saa pienimmän arvonsa, kun \(\cos\left(\dfrac{\pi(t-2)}{6}\right)=-1\).
b.
Mihin kellonaikaan iltapäivästä meren pinta on korkeimmillaan?
Funktio \(h(t)\) saa suurimman arvonsa, kun kosinifunktio saa suurimman arvonsa. Kosifunktion suurin arvo \(1\) saavutetaan, kun
\[\cos(2\pi n)=1, \;n\in\mathbb{Z}\]
eli saadaan yhtälö
\[\begin{align*} \cos(2\pi n)&=\cos\left(\dfrac{\pi(t-2)}{6}\right) \\ 2\pi n&=\dfrac{\pi(t-2)}{6} \end{align*}\]
Tästä yhtälöstä ratkaisemalla \(t\) saadaan ajat, jolloin merenpinta on korkeimmillaan\(\dots\)
Tehtävä 6.
Tehtävä 7.
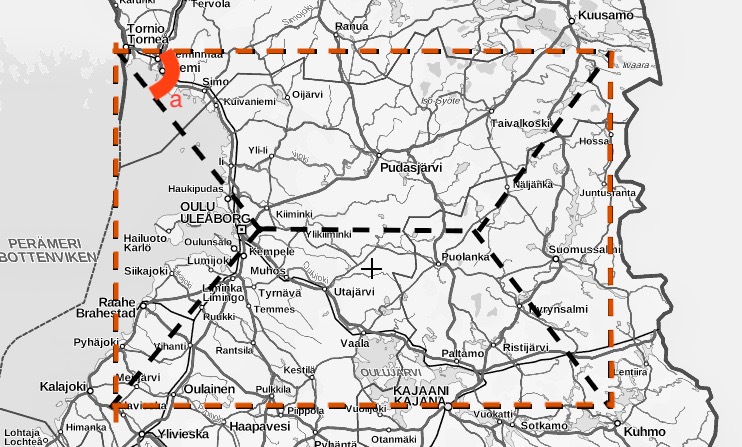
Suomen kaupungit Tornio, Kuusamo, Kuhmo ja Kalajoki sijaitsevat (melkein) suorakaiteen muotoisen alueen reunoilla.
- Jos olisi mahdollista tehdä tieverkosto yllä olevan kuvan mukaisesti, kuinka suuri kulman \(a\) pitäisi olla, jotta tiereitti olisi kaikista lyhin?
- Jos etäisyys Kalajoelta Tornioon on linnuntietä 100 km, kuinka pitkä tie olisi?
Tehtävä 8.
Olkoon funktio \(f(x)=\ln(9-4x^{2})\).
a.
Milloin funktio \(f\) on määritelty?
Logaritmifunktio on määritelty, kun \(9-4x^2>0\). Toisen asteen epäyhtälö ratkaistaan selvittämällä vastaavan yhtälön nollakohdat, hahmottelemalla kuvaaja ja tulkitsemalla kuvasta, milloin funktio on \(x-\)akselin alapuolella.
b.
Mikä on funktion \(f\) suurin arvo?
Logaritmifunktio \(f(x)\) saa suurimman arvonsa, kun lauseke \(9-4x^2\) saa suurimman arvonsa. Päättele a-kohdassa laskettujen nollakohtien ja lausekkeen kulun perusteella\(\dots\)
Vanhoja YO-tehtäviä
1.
Määritä \(\sin(x-y)\), kun \(\sin x=\frac{1}{4}, -\frac{\pi}{2}\leq x\leq\frac{\pi}{2},\) ja \(\cos y=-\frac{1}{3}, \pi\leq y\leq2\pi\). Tarkka arvo ja kaksidesimaalinen likiarvo. [S03/6]
VASTAUS: \(\frac{2\sqrt{30}-1}{12}≈0,83\)
RATKAISU:
Jos \(|x|\leq\frac{\pi}{2}\) ja \(\pi\leq y\leq2\pi\), on \(\cos x=+\sqrt{1-(\sin x)^{2}}\) ja \(\sin y=-\sqrt{1-(\cos y)^{2}}\). Siis \(\sin(x-y)=\sin x\cos y-\cos x\sin y=\frac{1}{4}(-\frac{1}{3})-\sqrt{\frac{15}{16}}\sqrt{\frac{8}{9}}=\frac{2\sqrt{30}-1}{12}≈0,83\).
Vastauksessa virhe. Pitäisi olla: \[\frac{-2\sqrt{30} - 1}{12}\]
—2.
Ratkaise yhtälöryhmä \[\begin{align*} \begin{cases} x+2y=4\\ 2^{x}=8^{y}. \end{cases} \end{align*}\] [K03/5a]
VASTAUS:\(y=\frac{4}{5}\) ja \(x=\frac{12}{5}\)
RATKAISU:
Koska \(2^{x}=8^{y}=2^{3y}\), on \(x=3y\). Sijoitus ensimmäiseen antaa \(3y+2y=4\) eli \(y=\frac{4}{5}\), josta \(x=\frac{12}{5}\).
3.
Määritä funktion \(f(x)=\dfrac{5}{4+3\cos2x}\) suurin ja pienin arvo reaalilukujen joukossa. Millä argumentin arvoilla nämä saadaan? [K01/6]
VASTAUS: suurin arvo on \(5\) ja se saavutetaan kun \(x=\frac{1}{2}\pi+n\pi, n\in\Z\). Pienin arvo on \(\frac{5}{7}\)ja se saavutetaan, kun \(x=n\pi, n\in\Z\).
RATKAISU:
Koska funktio on murtolauseke, jonka osoittaja on vakio, funktio saavuttaa suurimman arvonsa, kun nimittäjä saavuttaa pienimmän arvonsa. Vastaavasti funktio saavuttaa pienimmän arvonsa silloin kun nimittäjä saavuttaa suurimman arvonsa.
Tämä tapahtuu, kun \(\cos2x\) saavuttaa pienimmän (tai suurimman) arvonsa. Tunnetusti \(\cos2x\):n pienin arvo on \(-1\) ja suurin arvo \(1\).
Edelleen arvo \(-1\) saavutetaan kun \(2x=\pi+2n\pi, n\in\Z\) ja jälkimmäinen arvo \(1\), kun \(2x=2n\pi, n\in\Z\). Näin ollen funktion suurin arvo on \(\frac{5}{4-3}=5\) ja se saavutetaan kun \(x=\frac{1}{2}\pi+n\pi, n\in\Z\). Funktion pienin arvo saadaan vastaavasti \(\frac{5}{4+3}=\frac{5}{7}\), ja se saavutetaan, kun \(x=n\pi, n\in\Z\).
4.
Olkoot \[\begin{align*} \overline{a}&=(\cos\varphi-2\sin\varphi)\overline{i}+\overline{j}+(\sin\varphi+2\cos\varphi)\overline{k},\\ \overline{b}&=(\cos\varphi+\sin\varphi)\overline{i}+\overline{j}+(\sin\varphi-\cos\varphi)\overline{k}. \end{align*}\]
Osoita, että vektorit \(\overline{a}\) ja \(\overline{b}\) ovat kohtisuorassa toisiaan vastaan kaikilla \(\varphi\in\R\).
Olkoon \(\varphi=0\). Onko olemassa sellaisia kertoimia \(s,t\in\R\), että \(\overline{i}-\overline{j}=s\overline{a}+t\overline{b}\)? [S12/9]
VASTAUS: b. kertoimia \(s\) ja \(t\) ei ole olemassa.
RATKAISU:
a.
\(\overline{a}\cdot\overline{b}=(\cos\varphi-2\sin\varphi)(\cos\varphi+\sin\varphi)+1+(\sin\varphi+2\cos\varphi)(\sin\varphi-\cos\varphi)=1-(\sin^{2}\varphi+\cos^{2}\varphi)=1-1=0.\) Koska pistetulo on aina nolla, niin vektorit ovat toisiaan vastaan kaikilla \(\varphi\in\R\).
b.
Jos \(\varphi=0\), on \(\overline{a}=\overline{i}+\overline{j}+2\overline{k}\) ja \(\overline{b}=\overline{i}+\overline{j}-\overline{k}\).
Nyt \(s\overline{a}+t\overline{b}=(s+t)\overline{i}+(s+t)\overline{j}+(2s-t)\overline{k}\).
Tämä on \(\overline{i}-\overline{j}\) vain jos \(s+t=1\), \(s+t=-1\) ja \(2s-t=0\). Kaksi ensimmäistä yhtälöä ovat ristiriitaiset, joten tällaisia kertoimia \(s\) ja \(t\) ei ole olemassa.
5.
Olkoon annettuna trigonometrian kaavat \(\sin^{2}\alpha+\cos^{2}\alpha=1\), \(\sin2\alpha=2\sin\alpha\cos\alpha\), \(\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha\) ja \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\). Osoita pelkästään näiden perusteella oikeiksi seuraavat kaavat: \[\begin{align*} \sin x=\dfrac{2\tan\frac{x}{2}}{1+\tan^{2}\frac{x}{2}},\;\;\;\;\;\;\cos x=\dfrac{1-\tan^{2}\frac{x}{2}}{1+\tan^{2}\frac{x}{2}} \end{align*}\] Ilmoita, mitä kaavaa olet missäkin laskun vaiheessa käyttänyt. [S04/8]
RATKAISU:
Ensimmäinen kaava: \[\begin{align*} \frac{2\tan\frac{x}{2}}{1+\tan^{2}\frac{x}{2}}=2\frac{\sin\frac{x}{2}}{\cos\frac{x}{2}}\cdot\frac{1}{1+\frac{\sin^{2}\frac{x}{2}}{\cos^{2}\frac{x}{2}}}=\frac{2\sin\frac{x}{2}\cos\frac{x}{2}}{\cos^{2}\frac{x}{2}+\sin^{2}\frac{x}{2}}=\frac{\sin x}{1}=\sin x \end{align*}\]
Toinen kaava: \[\begin{align*} \frac{1-\tan^{2}\frac{x}{2}}{1+\tan^{2}\frac{x}{2}}=\frac{1-\frac{\sin^{2}\frac{x}{2}}{\cos^{2}\frac{x}{2}}}{1+\frac{\sin^{2}\frac{x}{2}}{\cos^{2}\frac{x}{2}}}=\frac{\cos^{2}\frac{x}{2}-\sin^{2}\frac{x}{2}}{\cos^{2}\frac{x}{2}+\sin^{2}\frac{x}{2}}=\frac{\cos x}{1}=\cos x \end{align*}\]
6.
Ratkaise seuraavat yhtälöt välillä \([0,2\pi]\).
\(\sin x=1\)
\(f'(t)=0\), kun \(f(t)=\cos t\)
\(\sin z=(1+\cos z)(1-\cos z)\). [S18/4]
RATKAISU:
a. \(\sin x=1\Leftrightarrow x=\frac{\pi}{2}+n\cdot2\pi, n\in\Z\)
Välillä \([0,2\pi]\) vain ratkaisu \(x=\frac{\pi}{2}\)
b. \(f'(t)=-\sin t\).
Välillä \([0,2\pi]\) nollakohdat \(t=0, t=\pi\) tai \(t=2\pi\).
c. \(\sin z=1-\cos^{2}z=\sin^{2}z \Leftrightarrow\sin z(1-\sin z)=0 \Leftrightarrow\sin z=0\) tai \(\sin z=1\).
Edellisten kohtien perusteella \(z=0\) tai \(z=\frac{\pi}{2}, z=\pi\) tai \(z=2\pi\).
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.