MAA6 Derivaatta
Kurssin tavoitteena on, että opiskelija
- tutustuu ilmiöiden matemaattisten mallien käyttäytymiseen derivaatan avulla
- omaksuu havainnollisen käsityksen funktion raja-arvosta ja jatkuvuudesta
- ymmärtää derivaatan funktion muutosnopeutena
- kykenee määrittämään yksinkertaisten funktioiden derivaatat
- osaa derivoida yhdistettyjä funktioita
- hallitsee funktioiden kulun tutkimisen derivaatan avulla ja osaa määrittää niiden ääriarvot suljetulla välillä
- osaa käyttää ohjelmistoja raja-arvon, jatkuvuuden ja derivaatan tutkimisessa sovellusongelmien yhteydessä.
Keskeiset sisällöt
- funktion raja-arvo, jatkuvuus ja derivaatta
- polynomi- ja rationaalifunktioiden sekä juurifunktion derivaatat
- sini- ja kosinifunktioiden sekä eksponentti- ja logaritmifunktioiden derivaatat
- funktioiden tulon ja osamäärän derivaatta
- yhdistetyn funktion derivaatta
- funktion kulun tutkiminen ja ääriarvojen määrittäminen
1. Funktion raja-arvo ja jatkuvuus
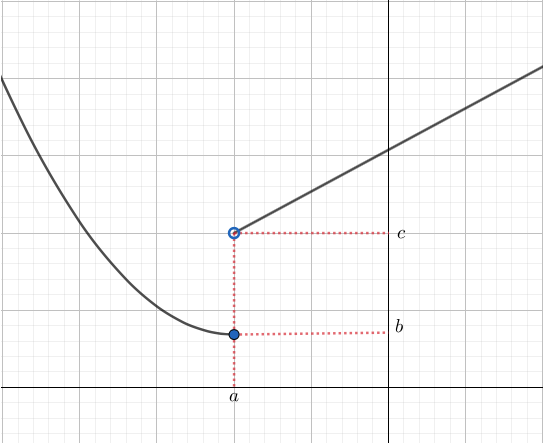
Jos funktion muuttuja \(x\) lähestyy kohtaa \(a\), funktion arvo \(f(x)\) lähestyy arvoa \(b\). Tätä arvoa \(b\) kutsutaan funktion raja-arvoksi.
1.1 Raja-arvo
Funktion raja-arvo
Funktion raja-arvo lähestyy arvoa \(b\), kun muuttuja \(x\) lähestyy kohtaa \(a\). Merkitään tätä \[\begin{align*} \lim_{x \to a} f(x) = b \end{align*}\]
Määritetään raja-arvo \(\lim_{x\rightarrow0}\;\dfrac{e^{2x}-1}{1-e^{x}}\).
Huomataan, että suora sijoitus \(x=0\) johtaa tilanteeseen \(\dfrac{0}{0}\). Lauseketta täytyy siis muokata.
\[\begin{align*} \lim_{x\rightarrow0}\;\dfrac{e^{2x}-1}{1-e^{x}}=\lim_{x\rightarrow0}\;\dfrac{(e^{x})^{2}-1^{2}}{1-e^{x}}=\lim_{x\rightarrow0}\;\dfrac{(e^{x}+1)\cancel{(e^{x}-1)}}{\cancel{1-e^{x}}}=\lim_{x\rightarrow0}\;\dfrac{(e^{x}+1)}{-1} \end{align*}\] Sijoittamalla muokattuun lausekkeeseen \(x=0\) saadaan \[\begin{align*} \dfrac{(e^{0}+1)}{-1}=\dfrac{1+1}{-1}=-2. \end{align*}\] Nyt siis \(\lim_{x\rightarrow0}\;\dfrac{e^{2x}-1}{1-e^{x}}=-2\)
Toispuoleiset raja-arvot Funktion raja-arvo-kohtaa voidaan lähestyä oikealta sekä vasemmalta. Jos funktion muuttuja \(x\) lähestyy kohtaa \(a\) oikealta puolelta, merkitään \[\begin{align*} \lim_{x \to a^{+}} f(x) = b. \end{align*}\] Vastaavasti, jos funktion muuttuja \(x\) lähestyy kohtaa \(a\) vasemmalta, merkitään \[\begin{align*} \lim_{x \to a^{-}} f(x) = b. \end{align*}\]
Funktion raja-arvo
Funktiolla on raja-arvo, jos ja vain jos toispuoleiset raja-arvot ovat yhtä suuret: \[\begin{align*} \text{Jos }\lim_{x \to a^{+}} f(x) = b=\lim_{x \to a^{+}} f(x)\text{, niin }\lim_{x \to a} f(x) = b \end{align*}\]
1.2 Jatkuvuus
Jatkuvalle funktiolle sen raja-arvo \(\lim_{x \to a} f(x) = b\) on sama kuin funktion arvo \(f(a)\) kohdassa \(a\).
Funktion jatkuvuus pisteessä
Kohdassa \(a\) jatkuvalle funktiolle \[\begin{align*} f(a)=\lim_{x \to a} f(x). \end{align*}\]
Funktio on jatkuva, jos se on jatkuva määrittelyjoukkonsa jokaisessa kohdassa.
Jatkuvia funktioita:
polynomi-, rationaali-, potenssi-, juuri-, eksponentti- ja logaritmifunktiot sekä trigonometriset funktiot.
Erilaisten jatkuvien funktioiden summa, erotus, tulo, osamäärä sekä yhdistetty funktio ovat myös jatkuvia funktioita.
Bolzanon lause
Oletetaan, että funktio on jatkuva suljetulla välillä \([a,b]\) ja funktion arvot ovat erimerkkiset välin päätepisteissä. Tällöin Funktiolla on ainakin yksi nollakohta avoimella välillä \(]a,b[\).
![Funktio on jatkuva välillä [a,b] ja sen arvot välin päätepisteissä ovat erimerkkiset. Funktiolla on vähintään yksi nollakohta.](/images/189882/Screenshot_2019-07-01_at_16.10.26.png)
Osoitetaan, että funktiolla \(f(x)=1-2x^{5}-x\) on ainakin yksi nollakohta.
Tarkastellaan funktion arvoja eri kohdissa. \[\begin{align*} &f(-2)=1-2\cdot(-2)^{5}-(-2)=65\\ &f(2)=1-2\cdot2^{5}-2=-65 \end{align*}\] Funktion on polynomifunktiona jatkuva välillä \([-2,2]\).
Nyt Bolzanon lauseen nojalla funktiolla \(f\) on ainakin yksi nollakohta avoimella välillä \(]-2,2[\).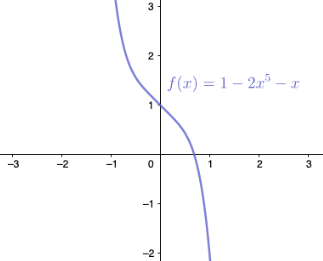 
2. Derivaatta
2.1 Erotusosamäärä
Erotusosamäärä kuvaa funktion keskimääräistä muutosnopeutta kohtien \(x\) ja \(a\) välillä.
Funktion erotusosamäärä
\[\begin{align*} \frac{f(x)-f(a)}{x-a} \end{align*}\] Tämä voidaan kirjoittaa myös muodossa \[\begin{align*} \frac{f(a+h)-f(a)}{h}, \end{align*}\] joka voidaan muodostaa, kun merkitään \(x=a+h\).
Jos tällä erotusosamäärällä on raja-arvo, kun \(x\rightarrow a\), niin keskimääräinen muutosnopeus lähestyy muutosnopeutta \(a\).
Määritetään funktion \(f(x)=x^{2}+1\) derivaatta kohdassa \(x=1\) erotusosamäärän avulla.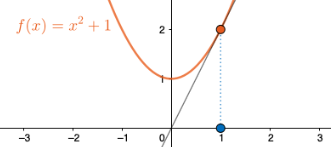 
\[\begin{align*} f'(1)&=\lim_{x\rightarrow1}\dfrac{f(x)-f(1)}{x-1}\\ &=\lim_{x\rightarrow1}\dfrac{(x^{2}+1)-(1^{2}+1)}{x-1}\\ &=\lim_{x\rightarrow1}\dfrac{x^{2}-1}{x-1}\\ &=\lim_{x\rightarrow1}\dfrac{x^{2}-1^{2}}{x-1}\\ &=\lim_{x\rightarrow1}\dfrac{(x+1)\cancel{(x-1)}}{\cancel{x-1}}\\ &=\lim_{x\rightarrow1}{x+1}\\ &=2 \end{align*}\]
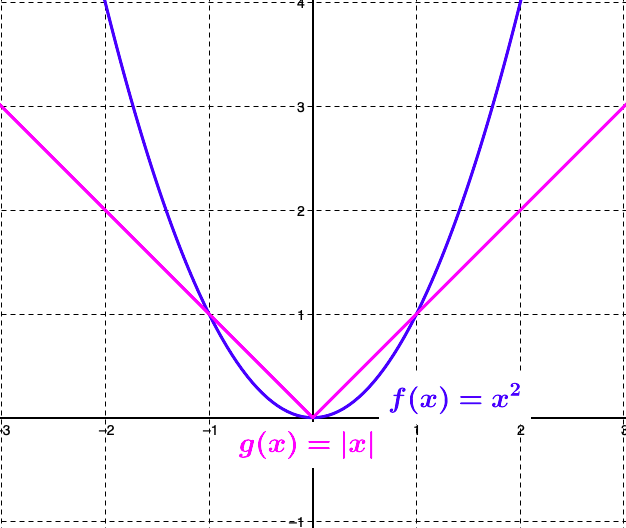
Derivaatta kohdassa \(x=1\) tarkoittaa siis funktion kuvaajan kohtaan \(x=1\) piirretyn tangentin kulmakerrointa. Alla olevassa kuvassa on kirjoitettu näkyviin tangentin yhtälö \(y=2x\), josta huomataan kulmakertoimen olevan myös \(2\).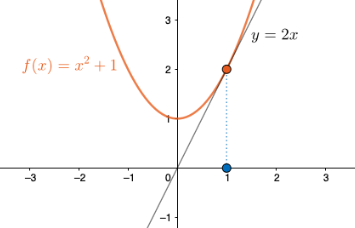 
2.2 Derivoituvuus ja jatkuvuus
Funktio on derivoituva kohdassa \(a\), jos funktion erotusosamäärällä on raja-arvo lähestyttäessä kohtaa \(a\).
Funktion derivoituvuus
Jos raja-arvo \[\begin{align*} \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \end{align*}\] on olemassa, niin funktio on derivoituva pisteessä \(a\).
Jos funktio on derivoituva kohdassa \(x=a\), niin se on myös jatkuva kohdassa \(x=a\).
2.3 Derivaattafunktio ja derivointisääntöjä
Derivaattafunktiota merkitään \(f'\). Funktion \(f\) derivaatta kohdassa \(x\) on tällöin \(f'(x)\).
Derivoimissääntöjä:
\(D(f(x)+g(x))=f'(x)+g'(x)\)
\(Dkf(x)=kf'(x)\)
\(Df(x)g(x)=f'(x)g(x)+f(x)g'(x)\)
\(D\dfrac{f(x)}{g(x)}=\dfrac{f'(x)g(x)-f(x)g'(x)}{(g(x))^{2}}\)
Derivoidaan \(\dfrac{1-x}{x-1}\).
Nyt kyseessä on osamäärä, joten hyödynnetään derivoimissääntöä \[\begin{align*} D\dfrac{f(x)}{g(x)}=\dfrac{f'(x)g(x)-f(x)g'(x)}{(g(x))^{2}} \end{align*}\]
Tässä tehtävässä nyt \(f(x)=\color{orange}{1-x}\) ja \(g(x)=\color{green}{x-1}\).
Derivoimissäännössä \(f'(x)\) tarkoittaa funktion \(f\) derivaattaa. Ratkaistaan \(f'\) ja \(g'\): \[\begin{align*} &f'(x)=0-1=\color{blue}-1\\ &g'(x)=1-0=\color{red}1 \end{align*}\]
Sijoitetaan derivoimissääntöön nyt funktiot \(f\), \(g\), \(f'\) ja \(g'\):
\[\begin{align*} D\dfrac{\color{orange}f(x)}{\color{green}g(x)}&=\dfrac{\color{blue}f'(x)\color{green}g(x)-\color{orange}f(x)\color{red}g'(x)}{(\color{green}g(x)\color{black})^{2}}\\ D\dfrac{\color{orange}{1-x}}{\color{green}{x-1}}&=\dfrac{\color{blue}-1\color{black}\cdot(\color{green}{x-1}\color{black})-(\color{orange}{1-x}\color{black})\color{black}\cdot\color{red}1}{(\color{green}{x-1}\color{black})^{2}}\\ &=\dfrac{(-x+1)-(1-x)}{(x-1)^{2}}\\ &=\dfrac{-x+1-1+x}{(x-1)^{2}}\\ &=\dfrac{0}{(x-1)^{2}}\\&=0,\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{kun }x≠1. \end{align*}\]
3. Funktion derivaatan tulkitseminen
3.1 Funktion kasvaminen ja väheneminen
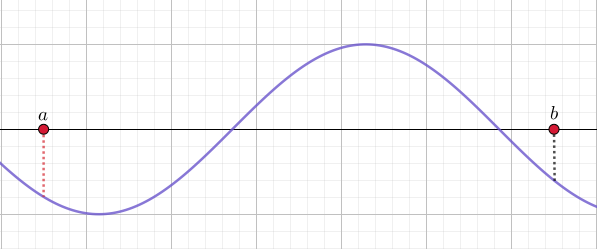
Funktio \(f(x)\) on kasvava annetulla välillä, jos \(f(x_{1})<f(x_{2})\), aina kun \(x_{1}<x_{2}\). Vastaavasti funktio \(f(x)\) on vähenevä annetulla välillä, jos \(f(x_{1})>f(x_{2})\), aina kun \(x_{1}<x_{2}\).
Jos funktio on kasvava tai vähenevä, funktiota kutsutaan monotoniseksi.
Derivaatan yhteys monotonisuuteen
Funktio \(f(x)\) on kasvava, jos funktion derivaatta \(f'(x)\)>0 kaikissa välin kohdissa lukuun ottamatta yksittäisiä kohtia, joissa derivaatta voi olla nolla (\(f'(x)=0\)).
Vastaavasti funktio \(f(x)\) on vähenevä, jos funktion derivaatta \(f'(x)\)<0 kaikissa välin kohdissa lukuun ottamatta yksittäisiä kohtia, joissa derivaatta voi olla nolla (\(f'(x)=0\)).
Funktiot, joiden derivaatta ei saa arvoa nolla missään välin kohdassa, ovat aidosti kasvavia tai aidosti väheneviä.
3.2 Funktion suurin ja pienin arvo
Jos funktio on jatkuva välillä \([a,b]\), niin funktiolla on suurin ja pienin arvo välillä \([a,b]\).
Jos funktio on jatkuva sekä derivoituva avoimella välillä \(]a,b[\), niin funktion suurin ja pienin arvo saavutetaan joko välin päätepisteissä tai välille kuuluvassa derivaattafunktion nollakohdassa.
3.3 Ääriarvot
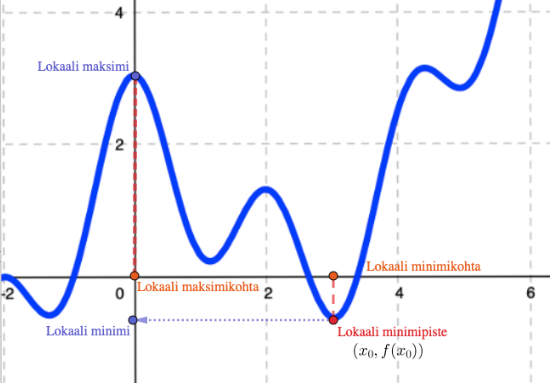
Funktion ääriarvoja ovat lokaalit minimi- ja maksimi-arvot. Nämä saavutetaan minimi- ja maksimikohdissa.
Funktion \(f\) arvo \(f(x_{0})\) on lokaali minimi, jos \(f(x_{0})\) on funktion pienin arvo kohdan \(x_{0}\) lähellä.
Vastaavasti funktion \(f\) arvo \(f(x_{0})\) on lokaali maksimi, jos \(f(x_{0})\) on funktion suurin arvo kohdan \(x_{0}\) lähellä.
Jos funktion minimi- tai maksimiarvo on pienin/suurin arvo, jonka funktio voi saavuttaa, kutsutaan minimiä/maksimia globaaliksi minimiksi/maksimiksi. Globaali ääriarvo on aina myös lokaali ääriarvo.
Määritetään funktion \(f(x)=x^{2}-x^{4}\) ääriarvot.
Funktio \(f\) on polynomifunktiona jatkuva ja derivoituva koko reaalilukujen joukossa \(\R\).
Tarkastellaan funktion \(f\) derivaattafunktion \(f'\) merkkiä, eli määritetään ensin funktion \(f\) derivaattafunktio.
\[\begin{align*}
&f(x)=x^{2}-x^{4}\\
&f'(x)=2x-4x^{3}
\end{align*}\]
Ratkaistaan derivaattafunktion \(f'\) nollakohdat: \[\begin{align*} f'(x)&=0\\ 2x-4x^{3}&=0\\ 2x(1-2x^{2})&=0\\ 1-2x^{2}=0\;\;\;\;\;\; &\text{ tai }\;\;\;\;\;\; x=0\\ x=\pm\frac{\sqrt{2}}{2}\;\;\;\;\;\; &\text{ tai }\;\;\;\;\;\; x=0 \end{align*}\]
Lasketaan derivaattafunktion arvo nollakohtien läheisyydessä.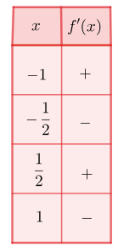 
Muodostetaan seuraavaksi kulkukaavio, johon on merkitty derivaattafunktion \(f'\) nollakohdat.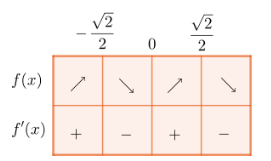 
Kulkukaaviosta voidaan päätellä, että paikalliset maksimikohdat ovat \(x=\pm\frac{\sqrt{2}}{2}\) ja paikallinen minimikohta on \(x=0\).
Funktio saa näissä kohdissa arvot \[\begin{align*} f(0)=0\\ f(\pm\frac{\sqrt{2}}{2})=\frac{1}{4} \end{align*}\] Vastaus: Funktion minimiarvo on \(f(0)=0\) ja maksimiarvot ovat \(f(\pm\frac{\sqrt{2}}{2})=\frac{1}{4}\).
Tehtäviä
Tehtävä 1.
a.
b.
Tehtävä 2.
a.
b.
Tehtävä 3.
Astronautti on laskeutunut Kuuhun ja heittää löytämänsä kiven suoraan ylöspäin. Kiven paikka \(h\) metreinä noudattaa lakia \(h(t)=-0,8t^{2}+6,9t+1,5\), missä \(t\) on aika sekunteina.
a.
Kuinka korkealla kivi on 2 sekunnin kuluttua?
b.
Kuinka korkealla kivi alkaa putoamaan takaisin Kuun pintaa kohti?
c.
Mikä on kiven nopeus neljän sekunnin kuluttua?
Nopeus on paikan derivaatta ajan suhteen.
d.
Mikä on Kuun vetovoiman kiihtyvyys?
Tehtävä 4.
Saimaannorppa on yksi maailman harvinaisimmista hylkeistä, ja niitä elää ainoastaan Suomessa Saimaalla. Saimaannorppien suojelu aloitettiin vuonna 1979, jolloin norppakanta oli sukupuuton partaalla, norppia oli tällöin ainoastaan 120-150 yksilöä. Nykyään norppien määrä on kasvanut hitaasti lähes 400 yksilöön (Lähde: WWF).
Havainnollistetaan norppien kannan vuotuista kasvua funktiolla \(f(t)=\dfrac{4e^{0.065t}}{e^{0.05t}+5}\), jossa \(t\) kuvaa vuosia aloitusajankohdasta 1979 lähtien. (Kun \(t=1\) on kyseessä vuosi 1980 jne.)
a.
Milloin saimaannorppien populaatio oli n. 200?
b.
Millä nopeudella norppakanta kasvaa vuonna 2019?
Tehtävä 5.
a.
Määritä funktion \(f(x)=\dfrac{4x^{2}}{6-x}\) ääriarvokohdat.
b.
Toinen ylläolevan funktion \(f(x)=\dfrac{4x^{2}}{6-x}\) ääriarvoista on \(0\). Mikä on funktion toinen ääriarvo?
Tehtävä 6.
Osoita, että funktio \(f(x)=\dfrac{|x^{2}+3|}{x^{2}+x}+(x+1)^{3}\) on jatkuva.
Tehtävä 7.
Missä pisteessä käyrät \(y=x^{3}-5x^{2}+11x\) ja \(y=3x^{2}-5x\) sivuavat toisiaan?
vastaus?
—Onko tämä tehtävä oikein?
—Tehtävä 8.
Huvipuistossa on laite nimeltään Koskiseikkailu, jossa istutaan kelluvassa lautassa ja kuljetaan erilaisten suihkulähteiden alitse puroa pitkin.
Matkan varrella on kaksi suihkulähdettä 15 m päässä toisistaan ja lautta kulkee näiden välistä. Toinen suihkulähteistä on puolet pienempi kuin toinen.
Vesisuihkun voimakkuus on suoraan verrannollinen suihkun kokoon ja kääntäen verrannollinen lähteestä mitatun etäisyyden kolmanteen potenssiin.
Kuinka kaukaa lautan pitäisi ohittaa suurempi suihkulähde, jotta matkustajat saisivat niskaansa mahdollisimman vähän vettä?
Vanhoja YO-tehtäviä
1.
Suorakulmion yksi kärki on origossa, ja siitä lähtevät kaksi sivua sijaitsevat positiivisilla koordinaattiakseleilla. Neljäs kärki sijaitsee paraabelilla \(y=4-x^{2}\) alueessa \(x\geq0,y\geq0\). Määritä suorakulmion suurimman mahdollisen pinta-alan tarkka arvo. [S16/4]
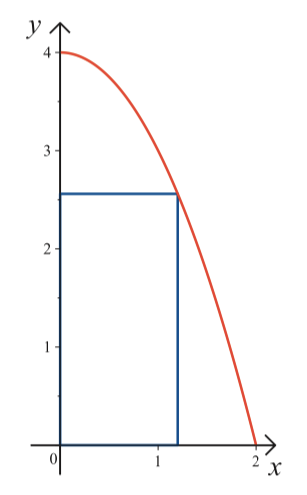
VASTAUS: \(A=\frac{16}{9}\sqrt{3}\)
RATKAISU:
Suorakulmion sivut ovat \(x\) ja \(4-x^{2}\), jolloin suorakulmion pinta-alaksi saadaan \(A(x)=x(4-x^{2})=4x-x^{3}\), kun \((0≤x≤2)\).
Pinta-alafunktion derivaatta \(A'(x)=4-3x^{2}\), ja sen nollakohdat ovat \(x=\pm\dfrac{2}{\sqrt{3}}\), joista vain positiivinen arvo otetaan tarkasteluun.
Koska \(A(x)\) on suljetulla välillä \([0,2]\) määritelty derivoituva funktio ja \(A(0)=A(2)=0\) (myös kulkukaavion avulla),
niin suurin pinta-ala \(A=A\left(\dfrac{2}{\sqrt{3}}\right)=\dfrac{16}{9}\sqrt{3}=\dfrac{16}{3\sqrt{3}}\)
2.
Määritä funktion \(f(x)=\sin x +\sqrt{3}\cos x\) suurin ja pienin arvo välillä \(0\leq x\leq2\pi\). [K18/3]
VASTAUS: Ääriarvot ovat \(\pm2\)
RATKAISU:
Määritetään funktion \(f(x)\) derivaattafunktio
\(f'(x)=\cos x-\sqrt{3}\sin x\) ja asettamalla derivaatan nollaksi: \[\begin{align*} f'(x)&=0\\ &\Rightarrow \cos x=\sqrt{3}\sin x\\ &\Rightarrow \tan x=\dfrac{1}{\sqrt{3}}\\ &\Rightarrow x=\dfrac{\pi}{6}+\pi n \end{align*}\] Ratkaisuista välille kuuluvat vain \(\dfrac{\pi}{6}\) ja \(\dfrac{7\pi}{6}\). Nyt funktion arvot näissä kohdissa ovat \[\begin{align*} &f\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}+\sqrt{3}\dfrac{\sqrt{3}}{2}=2\\ &\text{ ja }\\ &f\left(\dfrac{7\pi}{6}\right)=-\dfrac{1}{2}-\sqrt{3}\dfrac{\sqrt{3}}{2}=-2. \end{align*}\]
3.
Laske ja sievenä derivaatta \(h'(2t)\), kun \(h(x)=\dfrac{\ln{x}}{x}.\) [S17/1c]
VASTAUS: \(h'(x)=\dfrac{1-\ln{x}}{x^{2}}\), \(h'(2t)=\dfrac{1-\ln{2t}}{4t^{2}}\)
4.
Tarkastellaan raja-arvoa \(\lim_{x \to 2} \dfrac{x^{n}-60x-8}{x^{2}-4}\) eksponentin \(n=1,2,3,...\) eri arvoilla. [S16/9.2]
- Osoita, että raja-arvo on olemassa, kun \(n=7\).
- Osoita, että raja-arvoa ei ole olemassa, kun \(n≠7\).
RATKAISU:
a.
Tarkastellaan ensin tilannetta, kun \(x=2\) ja \(n=7\): \[\begin{align*} 2^{7}-60\cdot2-8=0 \end{align*}\]
Osoitetaan seuraavaksi, että raja-arvo on olemassa kohdassa \(n=7\). Jaetaan osoittaja tekijöihin \[\begin{align*} \dfrac{x^{7}-60x-8}{x^{2}-4}&=\dfrac{(x-2)(x^{6}+2x^{5}+4x^{4}+8x^{3}+16x^{2}+32x+4)}{(x-2)(x+2)}\\ &=\dfrac{(x^{6}+2x^{5}+4x^{4}+8x^{3}+16x^{2}+32x+4)}{(x+2)} \end{align*}\] Nyt, jos sijoitetaan raja-arvoon \(x=2\) saadaan raja-arvoksi 0.
Raja-arvo on siis olemassa kohdassa \(n=7\). (huom. Voidaan myös osoittaa perustellen l'Hôspitalin säännöllä)
b.
Koska \(x^{2}-4=(x-2)(x+2)\), niin äärellinen raja-arvo voi olla olemassa vain, jos \(x-2\) on myös osoittajan tekijä. Eli luku 2 on sen nollakohta.
Tästä saadaan ehto \(2^{n}-128=0\), josta edelleen \(2^{n}=2^{7}\), eli \(n=7\). Nyt siis raja-arvo on olemassa ainoastaan arvolla \(n=7\).
5.
Olkoot \(\overline{a}=\overline{i}+2\overline{j}+3\overline{k}\) ja \(\overline{b}=2\overline{i}+5\overline{k}\). Millä parametrin \(-2\leq t \leq 2\) arvolla vektorin \(\overline{c}_{t}=t\overline{a}+(1-t)\overline{b}\) pituus on mahdollisimman pieni? [K17/3]
VASTAUS: \(t=\dfrac{4}{3}\)
RATKAISU:
TAPA 1.
Pituuden minimi saavutetaan pisteessä, jossa \(\overline{c}_t\) on kohtisuorassa vektorin \(\overline{d}=\overline{b}-\overline{a}\) kanssa (tai päätepisteessä). \[\begin{align*} \overline{d}&=\overline{i}-2\overline{j}+2\overline{k}\\ \overline{d}\cdot\overline{a}&=1-4+6=3\\ \overline{d}\cdot\overline{b}&=2+0+10=12 \end{align*}\] Nyt siis \(\overline{c}_t\cdot\overline{d}=3t+12(1-t)\), josta ratkaisemalla nollakohta saadaan \(t=\frac{4}{3}\).
Koska \(-2≤\dfrac{4}{3}≤2\) saavutetaan minimi tällä parametrin arvolla eikä päätepisteessä.
TAPA 2. \[\begin{align*} \overline{c}_t&=(t+2(1-t))\overline{i}+2t\overline{j}+(3t+5(1-t))\overline{k}\\ &=(2-t)\overline{i}+2t\overline{j}+(5-2t)\overline{k}\\ |\overline{c}_t|&=(2-t)^{2}+(2t)^{2}+(5-2t)^{2}=9t^{2}-24t+29 \end{align*}\]
Nyt derivaatta on \(18t-24\) ja sen nollakohdasta \(t=\dfrac{4}{3}\).
Kulkukaaviosta huomataan, että \(-2≤\dfrac{4}{3}≤2\) saavutetaan minimi tällä parametrin arvolla eikä päätepisteessä.
6.
Tiedetään, että \(h(x)=g(f(x))\), \(f(x)=e^{x}\) ja \(g(x)=2x^{2}+1\). Elmeri ja Uolevi laskevat derivaatan \(h'(x)\) seuraavalla tavalla: 
Mari saa laskimella vastaukseksi \(4e^{2x}\). Kenen vastaus on oikein? Etsi väärien ratkaisujen virheet ja esitä korjatut ratkaisut. [K17/10]
VASTAUS: Marin vastaus on oikein.
RATKAISU:
Huomataan, ettei Elmeri ottanut huomioon sisäfunktion derivaattaa.
Oikea kaava on \(h'(x)=g'(f(x))f'(x)=4e^{x}e^{x}=4e^{2x}\).
Huomataan, että Uolevi on laskenut potenssit väärin.
\((e^{x})^{2}=e^{2x}\), joten \(h(x)=2e^{2x}+1\).
Nyt sisäfunktion derivaatan avulla \(h'(x)=4e^{2x}\), eli Marin vastaus on oikein.
7.
Tehtaassa valmistetaan tölkitettyjä säilykehedelmiä. Päärynänpuolikkaita pakataan suoran ympyrälieriön muotoiseen peltitölkkiin. Tölkin pohja- ja kansilevyjen materiaalin hinta on \(2,00\) \(€/m^{2}\) ja vaipan materiaalin hinta \(1,00\) \(€/m^{2}\). Suunnittele materiaalikustannuksiltaan mahdollisimman halpa peltitölkki, jonka tilavuus on \(1000\) \(cm^{2}\). Anna vastauksena tölkin korkeuden ja pohjan halkaisijan suhteen tarkka arvo. [K16/11]
VASTAUS: 2
RATKAISU:
Tölkin pohjaympyrän säde on \(r\) ja korkeus \(h\). Tilavuusehto antaa \(\pi r^{2}h=1000\), josta \(h=\dfrac{1000}{\pi r^{2}}\).
Vaippapellin hinta on \(1€/m^{2}\) ja pohjapellin \(2€/m^{2}\).
Pellin kokonaishinta on \[\begin{align*} H(r)&=2\pi r^{2}\cdot2+2\pi rh\cdot1\\&=4\pi r^{2}+2\pi r\cdot\dfrac{1000}{\pi r^{2}}\\&=4\pi r^{2}+\dfrac{2000}{r} \end{align*}\] Ja tässä \(r>0\).
Pinta-alan derivaatan nollakohta \[\begin{align*} &A'(r)=8\pi r-\dfrac{2000}{r^{2}}=0\\ &\Leftrightarrow 8\pi r^{3}-2000=0\\ &\Leftrightarrow\pi r^{3}=250\\ &\Leftrightarrow r^{3}=\dfrac{250}{\pi}\\ &\Leftrightarrow r=5\cdot\sqrt[3]{\dfrac{2}{\pi}} \end{align*}\] Derivaatan \(H'(r)\) merkkikaavio osoittaa, että saatu \(r\) on minimikohta ja siten myös halvimman tölkin pohjan säde.
Kysytty suhde on \(\dfrac{h}{2r}=\dfrac{1000}{\pi r^{2}\cdot2r}=\dfrac{500}{\pi r^{3}}=\dfrac{500}{250}=2.\)
8.
Ympyräsektorin säde on 3 ja keskuskulman suuruus on \(\alpha\). Sektori taivutetaan ympyräpohjaisen kartion vaipaksi. Mikä on kulman \(\alpha\) tarkka arvo silloin, kun kartion tilavuus on mahdollisimman suuri? [S17/6] 
VASTAUS: \(\alpha=2\pi\sqrt{\dfrac{2}{3}}\)
RATKAISU:
Kartion pohjan ympärysmitta on \(3\alpha\) ja säre \(r=\dfrac{3\alpha}{2\pi}\).
Korkeus saadaan Pythagoraan lauseesta \(h=\sqrt{3^{2}-\left(\dfrac{3\alpha}{2\pi}\right)^{2}}=\dfrac{3}{2\pi}\sqrt{4\pi^{2}-\alpha^{2}}\).
Kartion tilavuus on \(V=\dfrac{\pi}{3}r^{2}h=\dfrac{9}{8\pi^{2}}\alpha^{2}\sqrt{4\pi^{2}-\alpha^{2}}\).
Edelleen muuttujan vaihdolla \((x=a^{2})\) riittää lausekkeen \(x\sqrt{4\pi^{2}-x}\) maksimointi tai sen neliön \(x^{2}(4\pi^{2}-x)\) maksimointi.
Derivaatalla saadaan maksimi kun \(x=\dfrac{8\pi^{2}}{3}\), eli \(\alpha=2\pi\sqrt{\dfrac{2}{3}}\).
9.
- Anna esimerkki rationaalifunktiosta \(f(x)\), jolle epäyhtälö \(f(x)\geq2\) toteutuu täsmälleen silloin, kun \(-1\leq x \leq 0\) tai \(1\leq x \leq 2\).
- Anna esimerkki funktiosta \(g(x)\geq0\), joka on määritelty kaikilla reaaliluvuilla ja jonka derivaatalla on täsmälleen kaksi nollakohtaa. [K18/11]
Esimerkki 1:
Valitaan ensin polynomi, jonka nollakohdat ovat \(-1,0,1\) ja \(2\), eli esimerkiksi \(x(x+1)(x-1)(x-2)\).
Kun \(|x|\) on suuri, tämä on positiivinen, eli polynomin kuvaaja on W-muotoinen, joten kertomalla se luvulla \(-1\) saadaan funktio, joka on positiivinen täsmälleen vaadituilla väleillä.
Lisätään polynomiin \(2\), jolloin saadaan \(f(x)=2-x(x+1)(x-1)(x-2)\).
Esimerkki 2:
Voidaan etsiä ei-negatiivista funktiota, jolla on yksi minimi ja yksi maksimi.
Funktion \(g(x)=x^{2}e^{x}\) derivaatta on \(g'(x)=(x^{2}+2x)e^{2}\), jonka nollakohdat ovat \(x=0\) ja \(x=2\).
Toinen vaihtoehto on etsiä polynomia, jolla on minimi ja terassikohta.
Derivaatta voisi olla esimerkiksi \(12x(x-1)^{2}\), jolloin integroimalla saadaan \(g(x)=3x^{4}-8x^{3}+6x^{2}\).
Lisätehtäviä verkossa
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.