MAY1 Luvut ja yhtälöt
Kurssin tavoitteena on, että opiskelija
- kertaa prosenttilaskennan periaatteet
- osaa käyttää verrannollisuutta ongelmanratkaisussa
- syventää murtolukujen laskutoimitusten osaamistaan
- kertaa potenssien laskusäännöt
- vahvistaa ymmärrystään funktion käsitteestä
- ymmärtää yhtälön ja yhtälöparin ratkaisemisen periaatteet
- oppii käyttämään ohjelmistoja funktion kuvaajan piirtämisessä, havainnoinnissa ja yhtälöiden ratkaisemisessa.
Keskeiset sisällöt
- lukujoukot, peruslaskutoimitukset ja prosenttilaskenta
- potenssin laskusäännöt (eksponenttina luonnollinen luku)
- suoraan ja kääntäen verrannollisuus
- funktio, kuvaajan piirto ja tulkinta
- ensimmäisen asteen yhtälön ratkaiseminen
- yhtälöpari
- neliö- ja kuutiojuuri
- potenssifunktio ja potenssiyhtälö (asteluvut 2 ja 3)
1. Luvut ja laskutoimitukset
1.1 Lukujoukot
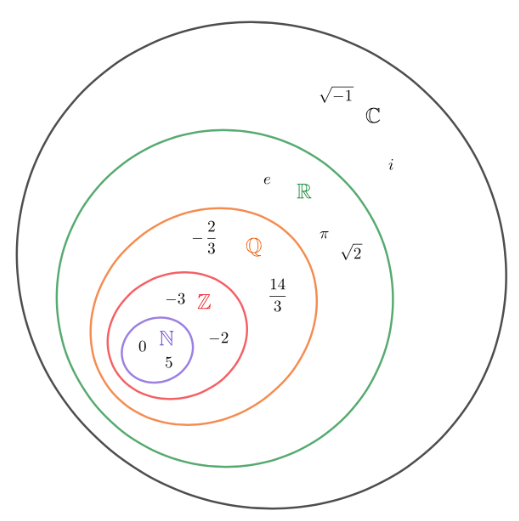Yllä olevassa kuvassa on lukujoukot. Luonnollisten lukujen joukko \(\N\) sisältää kaikki luvut nollasta eteenpäin. Kokonaislukujen joukko \(\Z\) sisältää kaikki positiiviset ja negatiiviset kokonaisluvut. Kokonaislukujen joukkoa voidaan tarkentaa alaindekseillä \(\Z_{+}\) ja \(\Z_{-}\).
Rationaaliluvut ovat lukuja, jotka voidaan esittää murtolukumuodossa \(\frac{m}{n}\), jossa \(n≠0\). Näitä lukuja kutsutaan rationaaliluvuiksi \(\mathbb{Q}\).
Symbolilla \(\R\) kuvataan kaikkia reaalilukuja, joihin sisältyvät kaikki edellä mainitut luvut. Edelleen kaikki reaaliluvut sisältyvät kompleksilukuihin \(\mathbb{C}\), joka on reaalilukujen lukulaajennus. Kompleksilukuihin ei perehdytä lukion oppimäärässä tarkemmin. Lisätietoja saat esimerkiksi tältä sivulta.
1.2 Vastaluku, käänteisluku ja itseisarvo
Jos kahden luvun summa on nolla, luvut ovat toistensa vastalukuja. Esimerkiksi luvun \(5\) vastaluku on \(-5\), koska \(5+(-5)=0\). Yleisemmin siis luvun \(a\) vastaluku on \(-a\), ja \(a+(-a)=0\).
Jos kahden luvun tulo on yksi, luvut ovat toistensa käänteislukuja. Esimerkiksi luvun \(3\) vastaluku on \(\frac{1}{3}\), sillä \(3\cdot\frac{1}{3}=1\). Yleisemmin luvun \(a\) vastaluku on \(\frac{1}{a}\), ja \(a\cdot\frac{1}{a}=1\).
Itseisarvo
Reaaliluvun 
itseisarvo on
Kahden luvun välinen etäisyys on niiden erotuksen itseisarvo.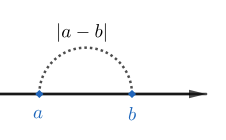 
Itseisarvo ilmaisee, kuinka suuri etäisyys luvulla \(a\) on nollaan. Esim. \(|-2|=|2|\), koska molemmilla luvuilla on sama etäisyys nollaan, eli \(2\).
Hei!
Jyväskylän yliopiston TIM-ympäristö ymmärtää TikZ-vektorigrafiikkakieltä.
Alla oleva koodi piirtää vasemmalla olevan kuvan. Saa testata!
Terv. Henri
#- {math_type=“svg” math_preamble=“\usetikzlibrary{arrows}”} —Tutki itseisarvoa GeoGebran avulla!
- Luvun \(-111\) itseisarvo \(|-111|=111,\) koska \(-111<0.\)
- Luvun \(\pi-2\) itseisarvo \(|\pi-2|=\pi-2,\) koska \(\pi-2>0.\)
- Luvun \(1-\sqrt{2}\) itseisarvo \(|1-\sqrt{2}|=-(1-\sqrt{2})=\sqrt{2}-1,\) koska \(1-\sqrt{2}\approx-0,41<0.\)
1.3 Murtoluvut
Murtoluku on kahden kokonaisluvun osamäärä \(\displaystyle\frac{m}{n}\), missä jaettavaa \((m)\) sanotaan osoittajaksi ja jakajaa \((n)\) nimittäjäksi, ja osoittaja ei ole jaollinen jakajalla. Murtoluku on siis rationaaliluku, joka ei supistu kokonaisluvuksi.
Sekaluvut ovat murtoluvun vaihtoehtoinen esittämistapa, missä murtoluku esitetään Nimittäjän tulee olla suurempi kuin osoittaja. Esimerkiksi murtoluku \(\displaystyle\frac{7}{4}=\frac{4+3}{4}=\frac{4}{4}+\frac{3}{4}=1+\frac{3}{4}\) voidaan esittää sekalukuna \(1\displaystyle\frac{3}{4}\).
Murtolukujen kerto- ja jakolasku
Murtolukujen kertolasku, missä \(b,d\neq0\)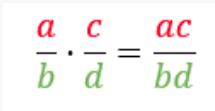 
Murtolukujen jakolasku, missä \(b,c,d\neq0\)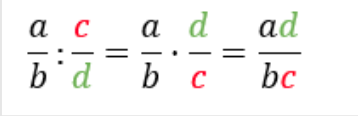 
Ystävykset Aada, Hilda, Iida ja Ville päättivät mennä syömään pizzeriaan. He tilasivat pepperoni- sekä vegepizzan, jotka he jakoivat seuraavasti:
Ville sanoi herrasmiehenä, että hän voi syödä jäljelle jäävät osuudet pizzoista viimeisenä. Aada leikkasi ensimmäisenä itselleen \(\displaystyle\frac{1}{4}\) pepperonipizzaa ja \(\displaystyle\frac{1}{8}\) vegepizzaa. Hilda leikkasi toisena jäljellä olevista pepperonipizzasta \(\displaystyle\frac{4}{5}\) ja vegepizzasta \(\displaystyle\frac{1}{4}\). Iida leikkasi kolmentena jäljellä olevasta vegepizzasta puolet. Paljonko Villelle jäi pizzaa?
Ratkaisu:
Kun Aada leikkasi pepperonipizzaa, niin jäljelle jäi \(^{4)}1-\displaystyle\frac{1}{4}=\frac{4}{4}-\frac{1}{4}=\frac{3}{4}\).
Kun Aada leikkasi vegepizzaa, niin jäljelle jäi \(^{8)}1-\displaystyle\frac{1}{8}=\frac{8}{8}-\frac{1}{8}=\frac{7}{8}\).
Kun Hilda leikkasi pepperonipizzaa, niin jäljelle jäi \((1-\displaystyle\frac{4}{5})\cdot\frac{3}{4}=\frac{1}{5}\cdot\frac{3}{4}=\frac{3}{20}\).
Kun Hilda leikkasi vegepizzaa, niin jäljelle jäi \((1-\displaystyle\frac{1}{4})\cdot\frac{7}{8}=\frac{3}{4}\cdot\frac{7}{8}=\frac{21}{32}\).
Kun Iida leikkasi vegepizzaa, niin jäljelle jäi \((1-\displaystyle\frac{1}{2})\cdot\frac{21}{32}=\frac{1}{2}\cdot\frac{21}{32}=\frac{21}{64}\).
Vastaus:
Villelle jäi siis \(\displaystyle\frac{3}{20}\) pepperonipizzaa ja \(\displaystyle\frac{21}{64}\) vegepizzaa.
1.4 Suoraan ja kääntäen verrannollisuus
Kun työskennellään tuntipalkalla ansaitaan sitä enemmän, mitä useampi tunti työskennellään. Palkka ja tehtyjen tuntien määrä kasvavat siis samassa suhteessa. Kun esimerkiksi työtuntien määrä kasvaa kolminkertaiseksi, myös palkka kolminkertaistuu. Tällaisia suureita, joiden suhde on aina vakio, sanotaan suoraan verrannollisiksi.
Suoraan verrannollisuus
Suureet \(x\) ja \(y\) ovat suoraan verrannolliset, jos \(y\) saadaan kertomalla \(x\) vakiolla \(k\) eli jos \(y=kx.\)
Vakio \(k\) on nimeltään verrannollisuuskerroin.
Yhtälö \(y=kx\) saadaan muotoon \(\dfrac{y}{x}=k,\) josta nähdään että suoraan verrannollisten suureiden suhde on vakio. On siis voimassa verranto \(\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}\) eli \(\dfrac{y_1}{y_2}=\dfrac{x_1}{x_2}.\)
Suoraan verrannollisuutta kuvaa graafisesti origon kautta kulkeva suora.
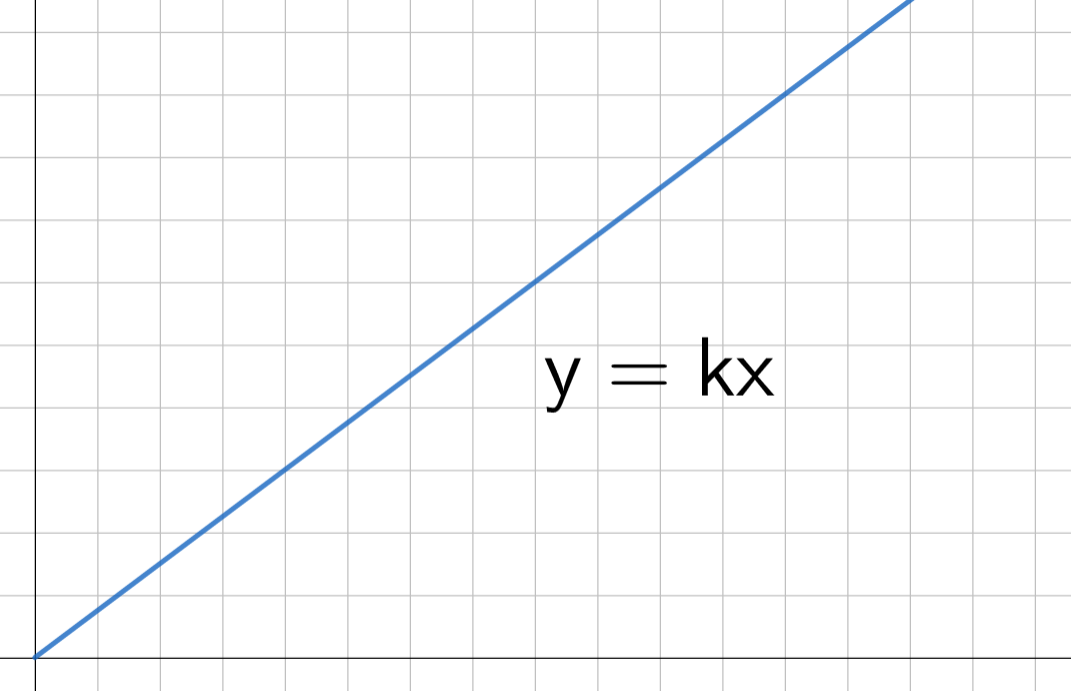
Vuotavasta vesihanasta tippuu tasatahtia \(6\) pisaraa \(10\) sekunnissa. Kuinka monta vesipisaraa hanasta tippuu \(2\) minuutissa?
Ratkaisu:
Olkoon pisaramäärä \(x\) ja aika \(y\). Koska pisaramäärä ja aika ovat suoraan verrannollisia suureita, niin
\[\begin{align*} \frac{y_1}{x_1}=\frac{y_2}{x_2} \end{align*}\]
Merkitään \(x_1=6,\) \(y_1=10\;\text{(s)}\) ja \(y_2=2\cdot 60=120\;\text{(s)}.\) Ratkaistaan \(x_2\), joka kuvaa kysyttyä pisaramäärää.
\[\begin{align*}
\frac{y_1}{x_1}&=\frac{y_2}{x_2} &&|\; \text{kerrotaan ristiin} \\
y_1x_2&=y_2x_1 &&|:y_1\\
x_2&=\frac{y_2 x_1}{y_1}&&|\;\text{sijoitetaan arvot}\\
x_2&=\frac{120\cdot6}{10} \\
x_2&=72
\end{align*}\]
Vastaus: \(72\) pisaraa
Kääntäen verrannollisuus
Suureet \(x\) ja \(y\) ovat kääntäen verrannolliset, jos \(y\) saadaan jakamalla vakio \(k\) suureella \(x\) eli jos \(y=\dfrac{k}{x}.\)
Yhtälo \(y=\dfrac{k}{x}\) saadaan muotoon \(xy=k,\) josta nähdään että kääntäen verrannollisten suureiden tulo on vakio. On siis voimassa myös yhtälö \(x_1y_1=x_2y_2\) eli \(\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}.\)
Kääntäen verrannollisten suureiden kuvaaja on hyperbeli.
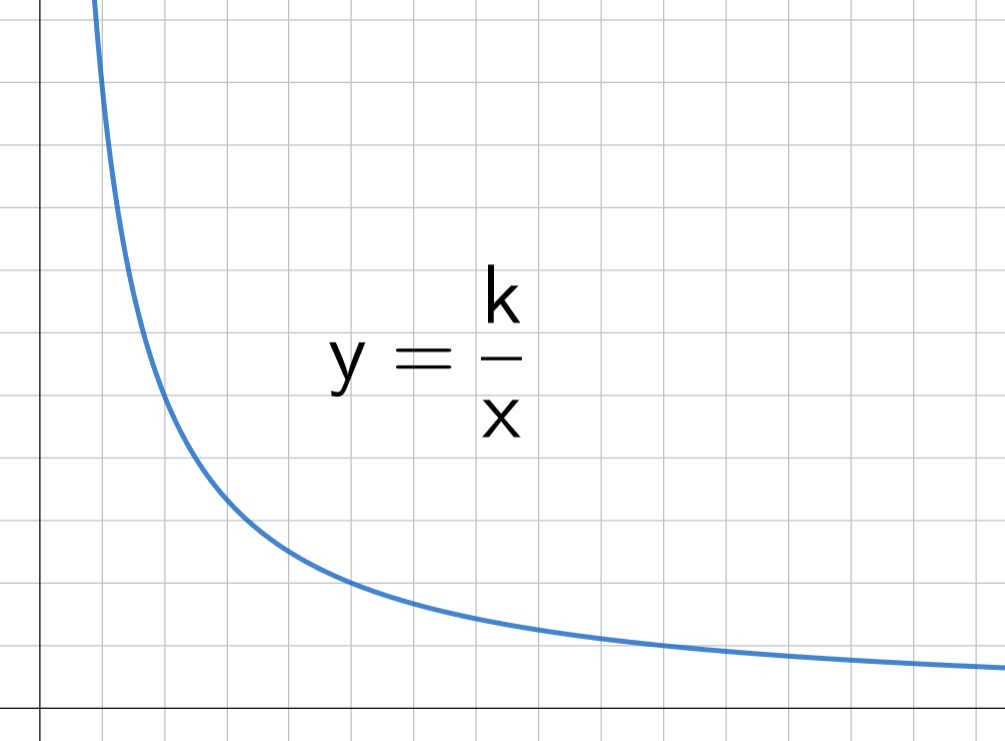
Kylpyhuoneen lattian kaakelointiin tarvitaan \(360\) kappaletta vaaleanpunaisia \(10\;\text{cm}\times10\;\text{cm}\)-kokoisia laattoja. Kuinka paljon laattoja tarvittaisiin, jos niiden koko olisi \(12\;\text{cm}\times12\;\text{cm}\)?
Ratkaisu:
Olkoon \(x\) laattojen määrä ja \(y\) niiden koko. Laattojen määrä ja koko ovat kääntäen verrannollisia suureita, joten
\[\begin{align*} x_1y_1=x_2y_2 \end{align*}\]
Merkitään \(x_1=360,\) \(y_1=10\cdot10=100\;(\text{cm}^2)\) ja \(y_2=12\cdot12=144\;(\text{cm}^2)\). Ratkaistaan \(x_2,\) joka kuvaa kysyttyä laattamäärää.
\[\begin{align*}
x_1y_1&=x_2y_2 && |:y_2\\
x_2&=\frac{x_1y_1}{y_2} &&|\;\text{sijoitetaan arvot}\\
x_2&=\frac{360\cdot100}{144} \\
x_2&=250
\end{align*}\]
Vastaus: \(250\) laattaa
2. Yhtälö
Laskutuoimitusta tai yhtä numeroa kutsutaan lausekkeeksi, esim. \(x+2\), \(a\), \(\frac{x}{2}\), 6,...
Jos kaksi lauseketta merkitään yhtäsuuriksi, on kyseessä yhtälö, esim. \(2x=6\).
2.1 Ensimmäisten asteen yhtälö
Ensimmäisen asteen yhtälö
Ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan saattaa muotoon
jossa 
.
Ensimmäisen asteen epäyhtälö on muotoa \(ax+b>0\), missä \(>\):n tilalla voi olla myös \(<, \geq, \leq\) tai \(\neq\).
Ristiin kertominen
Olkoon 
ja 
. Tällöin voidaan sieventää
Eli voidaan kertoa ristiin tällaista muotoa olevat yhtälöt.
Ratkaise yhtälö \(2x+1=-x+2\).
Ratkaisu:
\[\begin{align*} 2x+1 & = -x+2 \;\;\;\;\;\;\;\;\,\;| +x \\ 3x+1 & = 2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; | -1 \\ 3x & = 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|:3 \\ x &= \frac{1}{3} \end{align*}\]
Vastaus: \(x = \displaystyle\frac{1}{3}\)
Tarkistus:
Ratkaisun voi tarkistaa sijoittamalla vastaus \(x=\dfrac{1}{3}\) yhtälöön:
\[\begin{align*}
2\cdot\frac{1}{3}+1 &=-\frac{1}{3}+2 \\
\frac{2}{3}+\frac{3}{3} &=-\frac{1}{3}+\frac{6}{3} \\
\frac{5}{3}&=\frac{5}{3}\\
\text{}&{\bf{tosi}}
\end{align*}\]
Ratkaisun voi tarkistaa myös hyödyntämällä laskinohjelmistoja. Alla näytetään, miten se onnistuu Geogebran CAS-laskimella.
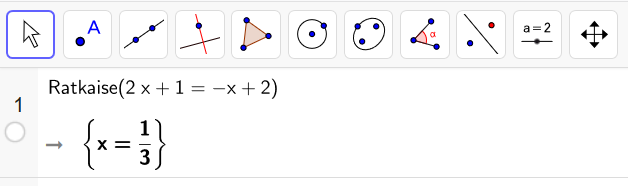
2.2 Yhtälöpari
Yhtälöparin ratkaisu on lukupari \((x,y)\), joka toteuttaa molemmat yhtälöt. Muuttujia voidaan merkitä myös muilla kirjaimilla.
Yhtälöparin ratkaisussa voidaan käyttää joko sijoitus- tai yhteenlaskukeinoa. Nämä menetelmät esitellään seuraavissa esimerkeissä.
Yhtälöpari
Yhtälöpari muodostuu kahdesta yhtälöstä, esimerkiksi
\[\begin{cases} 2x-y+3=0 \\ -4x+2y+1=0 \end{cases}\]Ratkaisu:
\[\begin{cases} 2x+y=6 && (1)\\ 3x+2y=2 && (2) \end{cases}\]Ratkaistaan esimerkiksi yhtälöstä \((1)\) muuttuja \(y\) muuttujan \(x\) suhteen. Saadaan yhtälö
\[y=-2x+6 \;\;\;\;\;\;(3)\]
Sijoitetaan yhtälö \((3)\) yhtälöön \((2)\), jolloin saadaan
\[\begin{align*}
3x+2(-2x+6)&=2 \\
3x-4x+12&=2 \\
-x&=-10 \\
x&=10
\end{align*}\]
Muuttujan \(y\) arvo saadaan sijoittamalla \(x=10\) yhtälöön \((3)\).
\[y=-2\cdot10+6=-20+6=-14\]
Vastaus:
\[\begin{cases} x=10\\ y=-14 \end{cases}\]Ratkaisu:
Kerrotaan ensin yhtälöt luvuilla, jotka tekevät muuttujan \(x\) kertoimet vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.
\[\begin{align*}
&\begin{cases}
2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-3) \\
3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot2\\
\end{cases}\\
+
&\begin{cases}
-6x-3y=-18\\
6x+4y=4\\
\end{cases}\\
&\rule{3cm}{0.4pt}\\
&-3y+4y=-18+4\\
&\;\;\;\;\;\;\;\;\;\;\;\;\;\;y=-14
\end{align*}\]
Tämän jälkeen kerrotaan yhtälöt luvuilla, jotka tekevät muuttujan \(y\) kertoimet vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.
\[\begin{align*} &\begin{cases} 2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-2) \\ 3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot1\\ \end{cases}\\ + &\begin{cases} -4x-2y=-12\\ 3x+2y=2\\ \end{cases}\\ &\rule{3cm}{0.4pt}\\ &-4x+3x=-12+2\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=10 \end{align*}\]
Vastaus:
\[\begin{cases} x=10\\ y=-14 \end{cases}\]dddddd
Ratkaisu:
Kerrotaan ensin yhtälöt luvuilla, jotka tekevät muuttujan \(x\) kertoimet vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.
\[\begin{align*}
&\begin{cases}
2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-3) \\
3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot2\\
\end{cases}\\
+
&\begin{cases}
-6x-3y=-18\\
6x+4y=4\\
\end{cases}\\
&\rule{3cm}{0.4pt}\\
&-3y+4y=-18+4\\
&\;\;\;\;\;\;\;\;\;\;\;\;\;\;y=-14
\end{align*}\]
Tämän jälkeen kerrotaan yhtälöt luvuilla, jotka tekevät muuttujan \(y\) kertoimet vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.
\[\begin{align*} &\begin{cases} 2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-2) \\ 3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot1\\ \end{cases}\\ + &\begin{cases} -4x-2y=-12\\ 3x+2y=2\\ \end{cases}\\ &\rule{3cm}{0.4pt}\\ &-4x+3x=-12+2\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=10 \end{align*}\]
Vastaus:
\[\begin{cases} x=10\\ y=-14 \end{cases}\]3. Prosenttilaskenta
Kuva ei näy.
—Prosentin nimitys tulee latinan kielestä per centum, joka tarkoittaa yksi sadasta. Prosentti siis tarkoittaa sadasosaa, ja sen merkki on \(\%\). Prosenttia käytetään suhteellisen osuuden ilmoittamiseen.
Prosentti
Kuinka paljon on 
prosenttia luvusta ?
Kun kysytään kuinka paljon prosenttia on luvusta , niin tällöin lasketaan tulo 
Tulossa luku ilmaistaan sadasosina tai desimaalilukuna.
Opiskelijaryhmän 32 opiskelijasta \(62,5\;\%\) on tyttöjä. Tällöin tyttöjä on
\[62,5\cdot\displaystyle\frac{1}{100}\cdot32=0,625\cdot32=20.\]
Kun positiivinen luku \(a\) kasvaa \(p\;\%\), saadaan
\[a+\frac{p}{100}\;a=(1+\frac{p}{100})a\]
Samoin kun \(a\) pienenee \(p\;\%\), saadaan
\[a-\frac{p}{100}\;a=(1-\frac{p}{100})a\]
Näin saadaan laskettua muuttunut arvo.
Korotus
Mikä luku on 
suurempi kuin ?
Alennus
Mikä luku on pienempi kuin ?
Nokian osakkeet laskivat aamupäivällä \(10,9\;\%\). Kuinka paljon maksaa aiemmin
- \(1\;000\;\text{euroa}\)
- \(12\;475\;\text{euroa}\)
maksaneet osakkeet?
Ratkaisu:
- Osakkeet laskivat \(10,9\;\%\), joten uusi osakkeiden hinta on \(100\;\%-10,9\;\%=89,1\;\%\) alkuperäisestä. Kerrotaan tällä alkuperäinen hinta:
\[89,1\;\%\cdot1000=0,891\cdot1000=891\;\text{(euroa)}\]
- Osakkeet laskivat \(10,9\;\%\), joten uusi osakkeiden hinta on \(100\;\%-10,9\;\%=89,1\;\%\) alkuperäisestä. Kerrotaan tällä (desimaaliluku) alkuperäinen hinta:
\[0,891\cdot12\;475=11\;115,22500\approx11\;115\;\text{(euroa)}\]
Vastaus:
- \(891\;\text{€}\)
- \(11\;115\;\text{€}\)
Prosenttiluvuilla kuvataan myös suureen muutosta alkuperäisestä arvosta.
Muutosprosentti
Kuinka monta prosenttia muutos on? 
Vuokra nousi \(327\) eurosta \(333\) euroon. Kuinka monta prosenttia vuokra nousi?
Ratkaisu:
Tapa 1:
Lasketaan vuokran muutoksen suuruus: \[333-327=6\;\text{(euroa)}\]
Lasketaan muutoksen suhde alkuperäiseen vuokraan: \[\displaystyle\frac{6}{327}\approx0,018=1,8\;\%\]
Tapa 2:
Lasketaan suoraan uuden vuokran suhde alkuperäiseen vuokraan:
\[\displaystyle\frac{333}{327}\approx1,018=101,8\;\%\]
Lasketaan suhteen ja alkuperäisen vuokran välinen ero, kun alkuperäistä vuokraa vastaava osuus on \(100\;\%\):
\[101,8\;\%-100\;\%=1,8\;\%\]
Vastaus: Vuokra nousi \(1,8\;\%\).
HUOM! Prosenttiyksikkö on absoluuttisen pronsenttimäärän yksikkö. Esimerkiksi koron noustessa 10 prosentista 11 prosenttiin:
- korko kasvaa 10 prosenttia
- korko kasvaa yhden prosenttiyksikön
Vertailuprosentti lasketaan samaan tyyliin kuin muutosprosentti.
Vertailuprosentti
Kuinka monta prosenttia \(a\) on suurempi kuin \(b\)?
\[\displaystyle\frac{a-b}{b}\cdot100\;\%\]
Kuinka monta prosenttia \(b\) on pienempi kuin \(a\)?
\[\displaystyle\frac{a-b}{a}\cdot100\;\%\]
Iltalehden tietojen mukaan Vaasalaisen jääkiekkoseura Sportin pelaajabudjetti kaudella \(2018-2019\) oli \(1,5\) miljoonan euron suuruinen, kun taas Helsinkiläisen HIFK:n budjetti oli \(3,25\) miljoonaa euroa.
- Kuinka monta prosenttia Sportin pelaajabudjetti oli pienempi kuin HIFK:n?
- Kuinka monta prosenttia HIFK:n pelaajabudjetti oli suurempi kuin Sportin?
Ratkaisu:
- Lasketaan, kuinka monta prosenttia budjettien erotus on HIFK:in budjetista.
\[\displaystyle\frac{3,25\;\text{milj. €}-1,5\;\text{milj. €}}{3,25\;\text{milj. €}} \approx 0,538=53,8\%\]
Sportin pelaajabudjetti oli \(53,8\;\%\) pienempi kuin HIFK:n.
- Lasketaan, kuinka monta prosenttia budjettien erotus on Sportin budjetista.
\[\displaystyle\frac{3,25\;\text{milj. €}-1,5\;\text{milj. €}}{1,5\;\text{milj. €}} \approx 1,167=116,7\%\]
HIFK:n pelaajabudjetti oli \(116,7\;\%\) suurempi kuin Sportin.
(Tehtävän olisi voinut ratkaista myös esimerkin 4.2.1 toisella tavalla)
Vastaus:
- \(53,8\;\%\)
- \(116,7\;\%\)
4. Potenssi ja juuri
Jos lukua \(a\) kerrotaan itsellään, voidaan tämä tulo kirjoittaa lyhyemmin potenssimerkintänä.
Jos luvulla \(a\) on eksponenttina nolla, lausekkeen arvo on aina 1: \(a^{0}=1\), missä \(a\neq0\).
Potenssi
Olkoon 
positiivinen kokonaisluku (
). Tällöin luvun :s potenssi on
Erityisesti 
Kymmenpotenssimuoto (suuret luvut)
Suuri luku voidaan merkitä kymmenpotenssimuodossa 
missä 
ja on positiivinen kokonaisluku.
Eetu voitti veikkaamalla \(6\,000\) euroa, jotka hän päätti sijoittaa indeksirahastoihin. Asiantuntija arvioi, että Eetu saisi \(6,5\;\%\):n vuotuisella korolla voittoa. Kuinka paljon Eetun rahaston arvo on \(20\) vuoden kuluttua jos oletetaan, että vuotuinen korko säilyy?
Ratkaisu:
Indeksirahasto tuottaa vuodesa \(6,5\;\%\) pääomasta, joten rahaston arvo kasvaa siis vuodessa \(1,065\)-kertaiseksi. Yhden vuoden kuluttua Eetun pääoman arvo on
\[1,065\cdot6000\;\text{(euroa)}\]
Korkoprosentti säilyy vakiona, joten vastaavasti myös seuraavan vuoden aikana rahaston arvo kasvaa \(1,065\)-kertaiseksi. Kahden vuoden kuluttua rahaston arvo on
\[\underbrace{1,065\cdot 1,065}_{\text{$2$ kappaletta}}\cdot\;6000=1,065^2\cdot6000\]
Vastaavasti kolmen vuoden kuluttua rahaston arvo on
\[\underbrace{1,065\cdot 1,065\cdot1,065}_{\text{$3$ kappaletta}}\cdot\;6000=1,065^3\cdot6000\]
20 vuoden kuluttua rahaston arvo on
\[\underbrace{1,065\cdot 1,065\cdot ... \cdot 1,065}_{\text{20 kappaletta}}\cdot\;6000=1,065^{20}\cdot6000=21141,87038\approx21141,87\]
Vastaus: \(20\) vuoden kuluttua Eetun rahaston arvo on \(21\;141,87\) euroa.
Rahalaskut pyöristetään aina sentin tarkkuudella ellei toisin mainita.
4.1 Potenssien laskusäänöt
Potensseille on omat laskusääntönsä:
Samankantaisten potenssien tulo ja osamäärä
\(a^{m}a^{n}=a^{m+n}\\\) \(\displaystyle\frac{a^{m}}{a^{n}}=a^{m-n}\), missä \(a\neq0\)
Potenssin potenssi
\((a^{m})^{n}=a^{mn}\)
Osamäärän ja tulon potenssit
\((ab)^{n}=a^{n}b^{n}\\\) \(\displaystyle\left(\frac{a}{b}\right) ^{n}=\frac{a^{n}}{b^{n}}\)
Neliöjuurien tulo ja osamäärä
\(\sqrt{a}\sqrt{b}=\sqrt{ab}\), missä \(a\geq0\) ja \(b\geq0\) \(\displaystyle\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\), missä \(a\geq0\) ja \(b>0\)
Sievennä.
- \(\dfrac{2d^7}{d^3}\) b. \(3a^4\cdot(-2a^3)\) c. \((ax^3y)^2\)
Ratkaisu:
- \(d-\)kantaisten potenssien eksponentit vähennetään toisistaan ja luku \(2\) jää eteen kertoimeksi.
\[\dfrac{2d^7}{d^3}=2d^{7-3}=2d^4\]
- \(a-\)kantaisten potenssien eksponentit lisätään yhteen ja luvut \(3\) ja \(-2\) kerrotaan keskenään.
\[3a^4\cdot(-2a^3)=-6a^{4+3}=-6a^7\]
- Jokainen termi korotetaan erikseen toiseen.
\[(ax^3y)^2=a^2(x^3)^2y^2=a^2x^{3\cdot2}y^2=a^2x^{6}y^2\]
Sievennä.
\(\sqrt{9}+\sqrt{16}\)
\(\sqrt{9+16}\)
\(\sqrt{\sqrt{25}+\sqrt{81}-5}\)
\(\sqrt{(x^2+1)^2}\)
Ratkaisu:
- Lasketaan ensin neliöjuuret.
\[\sqrt{9}+\sqrt{16}=3+4=7\]
- Lasketaan ensin yhtenlasku.
\[\sqrt{9+16}=\sqrt{25}=5\]
- Lasketaan ensin sisimmät neliöjuuret.
\[\begin{align*} &\sqrt{\sqrt{25}+\sqrt{81}-5}\\ &=\sqrt{5+9-5}\\ &=\sqrt{9}=3 \end{align*}\]
- Käytetään neliöjuuren kolmatta ominaisuutta.
\[\begin{align*} &\sqrt{(x^2+1)^2} \\ &=|x^2+1| \\ \text{(itseisarvot voidaan }&\text{poistaa, sillä aina}\;x^2+1>0) \\ &=x^2+1 \end{align*}\]
5. Funktio
Funktio liittää jokaiseen muuttujan arvoon tietyn (yhden) luvun, eli funktion arvon.
Usealla eri muuttujan arvolla voi kuitenkin olla sama funktion arvo, esimerkiksi jos \(f(x)=x^{2}\). Tällöin muuttuja arvolla \(-1\) saa funktion arvoksi \(f(-1)=(-1)^{2}=1\) samoin kuin muuttuja arvolla \(1\), jolloin \(f(1)=x^{2}=1\).
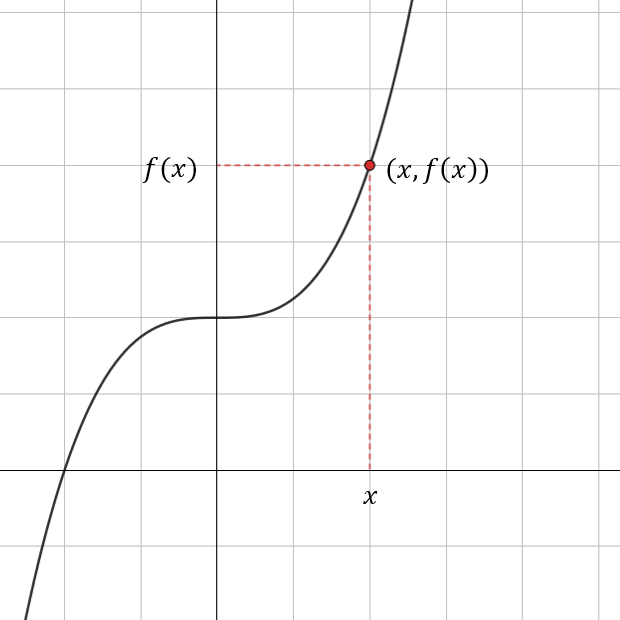
Funktion kuvaaja xy-koordinaatistossa
Funktion 
kuvaaja muodostuu pisteistä 
, joissa 
on muuttujan arvo ja 
funktion arvo kohdassa eli 
.
Tehtäviä
Tehtävä 1.
a.
Sievennä lauseke \((b+5)^{2}-(b-3)^{2}\)
b.
Sievennä lauseke \(\displaystyle \frac{x}{1-x}+\frac{x}{1+x}\) [K05/1a]
c.
Positiivinen luku \(a\) on 25 prosenttia pienempi kuin luku \(b\). Kuinka monta prosenttia luku \(b\) on suurempi kuin \(a\)?
Tehtävä 2.
Matkaa kuljetaan tasaisella nopeudella. Kun matkasta on jäljellä 40\(\%\), nopeutta lisätään 20 \(\%\). Kuinka monta prosenttia koko matkaan kuluva aika tällöin lyhenee? [S00/3]
Tehtävä 3.
a.
Ratkaise yhtälö \(\mid\frac{3}{2}x-6\mid=6\). [K11/1c]
b.
Sievennä lauseke \(\sqrt{a\sqrt{a\sqrt{a^{2}}}}\), kun \(a\geq0\). [S16/2a]
Tehtävä 4.
Pauliinan laskun välivaiheet ovat menneet sekaisin. Tehtävänä on järjestää allekain vaiheet A-G niin, että niistä muodostuu yhtälö \(20+4x=x^2+8\). [S17/3b]
A: \(20+4x=x^{2}+8\)
B: \(x^{2}-4x=12\)
C: \(x-2=\pm 4\)
D: \(x^{2}-4x+4=16\)
E: \((x-2)^{2}=4^{2}\)
F: \(x=-2\) tai \(x=6\)
Tehtävä 5.
a.
Ratkaise \(L\) yhtälöstä \(t=\displaystyle\frac{1}{2\pi \sqrt{LC}}\). [S07/1c]
b.
Sievennä lauseke \(\displaystyle\frac{1}{\sqrt{2}}+\frac{1}{2+\sqrt{2}}\) välivaiheet esittäen. [S11/2a]
Tehtävä 6.
Päärynämehusta ja omenamehusta tehdyn sekamehun sokeripitoisuus on \(11\%\). Määritä mehujen sekoitussuhde, kun päärynämehun sokeripitoisuus on \(14\%\) ja omenamehun \(7\%\).
Tehtävä 7.
Merkitse, onko seuraavat väittämät totta vai tarua [K16/1]
Tehtävä 8.
Vuonna 2007 alennettiin parturimaksujen arvonlisäveroa 22 prosentista 8 prosenttiin. Arvonlisävero ilmoitetaan prosentteina verottomasta hinnasta ja se on osa tuotteen tai palvelun hintaa.
a.
Kuinka monta prosenttiyksikköä alhaisempi uusi arvonlisäveroprosentti on verrattuna alkuperäiseen?
b.
Kuinka monta prosenttia enemmän arvonlisäveroa maksettiin vanhalla arvonlisäveroprosentilla?
vanhoja YO-tehtäviä
1.
- Osoita, että luvut \(\frac{\sqrt{6}}{3}\) ja \(\frac{\sqrt{6}}{2}\) ovat toistensa käänteislukuja. [K16/2b]
- Osoita, että \(\sqrt{a+b}<\sqrt{a}+\sqrt{b}\), kun \(a>0\) ja \(b>0\). [K16/2c]
RATKAISU:
a. Lukujen tulo on 1, joten ne ovat toistensa käänteislukuja
b. Epäyhtälö voidaan neliöidä, koska yhtälön molemmat puolet ovat positiivisia: \[\begin{align*} a+b<a+b+2\sqrt{ab} \end{align*}\] Ja tämä on tosi, koska \(2\sqrt{ab}>0\).
2.
Sievennä lauseke \(\displaystyle\frac{a^{2}-b^{2}}{a-b}+\frac{a^{2}-b^{2}}{a+b}\), kun \(a\neq b\) ja \(a\neq -b\). [K14/1c]
VASTAUS: \(2a\)
RATKAISU:
\[\begin{align*} \frac{a^{2}-b^{2}}{a-b}+\frac{a^{2}-b^{2}}{a+b}=\frac{(a-b)(a+b)}{a-b}+\frac{(a-b)(a+b)}{a+b}=(a+b)+(a-b) =2a \end{align*}\]
3.
Sievennä lausekkeet
\(\displaystyle\frac{\sqrt{3\frac{3}{4}}}{\sqrt{1\frac{2}{3}}}\)
\(\displaystyle\frac{(\frac{x}{y}+\frac{y}{x}-2)}{(\frac{x}{y}-\frac{y}{x})}\). [K03/1]
VASTAUS: a.\(\frac{3}{2}\) b.\(\frac{x-y}{x+y}\)
RATKAISU:
a. \[\begin{align*} \frac{\sqrt{3\frac{3}{4}}}{\sqrt{1\frac{2}{3}}}=\sqrt{\frac{15}{4}\cdot\frac{3}{5}}=\sqrt{\frac{9}{4}}=\frac{3}{2}. \end{align*}\]
b. \[\begin{align*} \frac{(\frac{x}{y}+\frac{y}{x}-2)}{{\frac{x}{y}-\frac{y}{x}}}=\frac{x^{2}+y^{2}-2xy}{x^{2}-y^{2}}=\frac{(x-y)^{2}}{(x+y)(x-y)}=\frac{x-y}{x+y}. \end{align*}\]
4.
Osoita, että \(\sqrt{27-10\sqrt{2}}=5-\sqrt{2}\). [S09/1c]
RATKAISU:
Todistetaan osoittamalla, että yhtälön toisesta puolesta saadaan toinen puoli. Tässä esimerkkinä yhtälön oikea puoli: \[\begin{align*} (5-\sqrt{2})^{2}=25-2\cdot5\cdot\sqrt{2}+(\sqrt{2})^{2}=25-10\sqrt{2}+2=27-10\sqrt{2}=\left(\sqrt{27-10\sqrt{2}}\right)^{2} \end{align*}\] Korotus toiseen potenssiin voidaan tehdä, koska lauseke \(5-\sqrt{2}\) on aina positiivista.
5.
Merivettä, jossa on 4,0 painoprosenttia suolaa, haihdutetaan altaassa, kunnes sen massa on vähentynyt \(28\%\). Mikä on suolapitoisuus haihduttamisen jälkeen? Anna vastaus prosentin kymmenesosan tarkkuudella.
Mikä on vuotuinen korkoprosentti, jos tilille talletettu rahamäärä kasvaa korkoa korolle 1,5-kertaiseksi 10 vuodessa? Lähdeveroa ei oteta huomioon. Anna vastaus prosentin sadasosan tarkkuudella. [K07/3]
VASTAUS: a. \(5,6\%\) b. \(4,14\%\)
RATKAISU:
a. Oletetaan, että merivettä on \(100a\), jolloin siinä on vettä \(96a\) ja \(4a\) suolaa. Haihdutuksen jälkeen jäljellä on vettä \(68a\), ja jäljellä on yhä suolaa \(4a\). Yhteensä merivettä on siis jäljellä \(72a\). Meriveden suolaprosentti on nyt \[\begin{align*} 100\cdot\frac{4a}{72a}=\frac{59}{9}≈5,5556. \end{align*}\]
b. Jos korkoprosentti on \(p\), on korkotekijä \(q=1+\frac{p}{100}\). Tehtävän mukaan rahamäärä \(a\) kasvulle pätee \[\begin{align*} q^{10}a=1,5a \text{ eli } q^{10}=1,5. \end{align*}\] Tästä saadaan edelleen ratkaistua \(q\): \[\begin{align*} q=\sqrt[10]{1,5}≈1,01438, \end{align*}\] josta edelleen \(p=100(q-1)≈4,138.\)
6.
Perheen vuokramenot olivat \(25\%\) tuloista. Vuokramenot nousivat \(15\%\). Montako prosenttia vähemmän rahaa riitti muuhun käyttöön korotuksen jälkeen? [K04/3]
VASTAUS: \(5\%\)
RATKAISU:
Jos tulot olivat \(100a\), olivat vuokramenot \(25a\). Muuhun käyttöön jää tällöin \(75a\). Vuokramenot olivat korotuksen jälkeen \(1,15\cdot25a=28,75a\). Muuhun käyttöön jää enää \(71,25a\), eli \(3,75a\) vähemmän kuin ennen. Prosenteissa vähennys oli \(100\cdot\frac{3,75a}{75a}=5\).
7.
Määrittele, mitä tarkoitetaan reaaliluvun \(x\) itseisarvolla (1p.). Todista, että seuraavat epäyhtälöt ovat voimassa kaikille reaaliluvuille \(x\) ja \(y\).
\(x \leq \mid x\mid\) (1p.)
\(x+y \leq \mid x\mid+\mid y\mid\) (2p.)
\(\mid x+y\mid \leq \mid x\mid+\mid y\mid\) (2p.)
\(\mid\mid x\mid - \mid y\mid \mid \leq \mid x\mid + \mid y\mid\) (3p.) [S08/14]
RATKAISU:
Määrittely: Reaaliluvun \(x\) itseisarvo on \[\begin{align*} \begin{cases} x, &\text{ kun }x\geq0,\\ -x,&\text{ kun }x<0 \end{cases} \end{align*}\]
a. Jos \(x\geq0\), on \(x\leq x=|x|\). Jos \(x<0\), niin \(-x>0\) ja \(x<-x=|x|\).
b. a-kohdan perusteella \(x\leq|x|\) ja \(y\leq|y|\). Näin ollen myös \(x+y\leq|x|+|y|\).
c. Määritelmän ja a-kohdan perusteella \(-|x|\leq x\leq|x|\) ja \(-|y|\leq y\leq|y|\). Siis \[\begin{align*} -(|x|+|y|)\leq x+y\leq|x|+|y|. \\ \text{ Jos } x+y\geq0, \text{ on } |x+y|=x+y\leq|x|+|y|. \end{align*}\] Jos
\[\begin{align*} x+y<0, \text{ on }|x+y|=-(x+y)\leq|x|+|y| \end{align*}\] edellisen epäyhtälön perusteella. Siis aina \(|x+y|\leq|x|+|y|.\)
d. Jos \(|x|-|y|\geq0\), niin \(||x|-|y||=|x|-|y|\leq|x|+|y|.\) Jos \(|x|-|y|<0\), niin \(||x|-|y||=-|x|+|y|\leq|x|+|y|\). Siis aina \(||x|-|y||\leq|x|+|y|.\)
Lisätehtäviä verkossa
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.