MAA2 Algebralliset funktiot ja yhtälöt


Kurssin tavoitteena on, että opiskelija
- tutustuu ilmiöiden matemaattiseen mallintamiseen polynomi-, rationaali ja juurifunktioiden avulla, tuntee polynomi-, rationaali ja juurifunktioiden ominaisuudet ja osaa ratkaista niihin liittyviä yhtälöitä sekä tietää polynomifunktion nollakohtien ja polynomin tekijöiden välisen yhteyden
- osaa ratkaista yksinkertaisia polynomiepäyhtälöitä
- osaa käyttää ohjelmistoja matemaattisessa mallintamisessa, polynomi-, rationaali ja juurifunktioiden tutkimisessa sekä polynomi-, rationaali- ja juuriyhtälöiden ja polynomiepäyhtälöi- den ratkaisemisessa sovellusongelmien yhteydessä.
Keskeiset sisällöt
- polynomifunktio ja -yhtälö sekä polynomiepäyhtälö
- asteen yhtälön ratkaisukaava
- polynomien tulo ja binomikaavat (summan neliö, summan ja erotuksen tulo)
- polynomien tekijät
- potenssifunktio ja potenssiyhtälö
- rationaalifunktiot ja -yhtälöt
- juurifunktiot ja -yhtälöt
1. Polynomifunktiot
Funktiota voidaan ajatella sääntöjä, joka liittää tiettyyn muuttujan arvoon täsmälleen yhden luvun. Tätä lukua kutsutaan funktion arvoksi.
Olkoon funktio \(f(x)=x+2\). Funktio käskee liittämään jokaiseen \(x\):n arvoon luvun, joka on "luku itse + 2".
Lasketaan eri funktion arvot muuttujan \(x\) saadessa arvot \(-2,0\) ja \(5\). \[\begin{align*} f(-2)&=(-2)+2=0\\ f(0)&=0+2=2\\ f(5)&=5+2=7\\ \end{align*}\]
Tässä tilanteessa funktion \(f\) lähtöjoukko on \([-2,0,5]\) ja maalijoukko \([0,2,7]\). Funktio \(f(x)=x+2\) on määritelty koko reaalilukujen joukossa \(\R\), eli se voi teoriassa saada mitä tahansa arvoja väliltä \([-\infty,\infty]\).
Funktion määrittely- ja arvojoukko
Funktion määrittelyjoukko sisältää kaikki ne arvot, joissa funktiolle on asetettu jokin arvo.
Funktion arvojoukko sisältää kaikki ne funktion arvot, jotka funktion on mahdollista saada.
Olkoon funktio \(f(x)=\dfrac{1}{2+x}\).
- Funktio on määritelty kaikilla muilla luvuilla paitsi kun \(x=-2\).
\[\begin{align*} f(-2)=\dfrac{1}{2+(-2)}=\dfrac{1}{\color{red}0} \end{align*}\]
- Funktion määrittelyjoukko on tällöin \(\R\setminus\{-2\}\)
- Funktion arvojoukko on koko \(\R\).
Funktion kattava merkintätapa olisi \(f:\R\setminus\{-2\} \rightarrow\R, f(x)=\dfrac{1}{2+x}\).
Piirrettäessä funktion kuvaaja, funktion kuvaajasta ei voida lukea funktion arvoa kohdassa \(x=-2\). 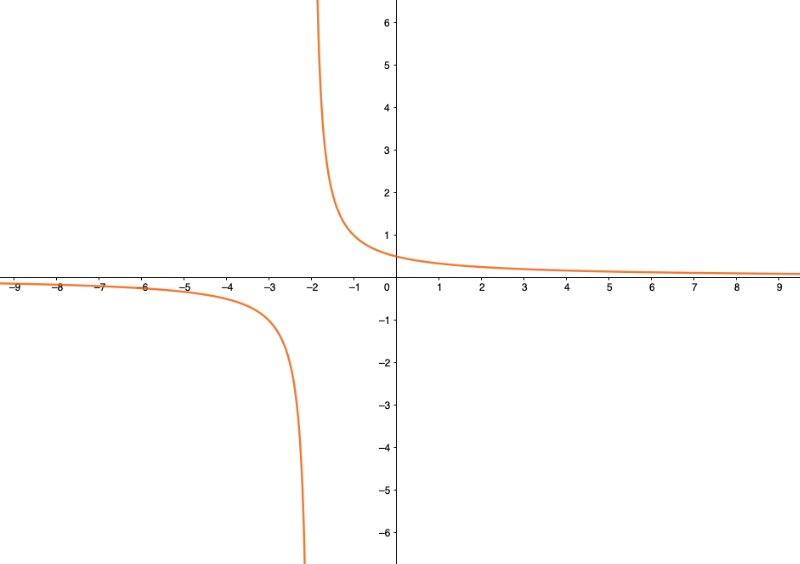
1.1 Ensimmäisen asteen polynomifunktio
Ensimmäisen asteen polynomifunktio
Funktiota \(f\) kutsutaan ensimmäisen asteen polynomifunktioksi, jos se voidaan esittää muodossa \(f=ax+b\), missä \(a\neq0\).
Ensimmäisen polynomifunktion nollakohta saadaan ratkaisemalla ensimmäisen asteen yhtälö \(ax+b=0\).
Olkoon funktio \(g(x)=4x-6\). Ratkaistaan funtkion nollakohta, eli kohta jossa sen kuvaaja leikkaa \(x\)-akselin.
Kun funktion kuvaaja leikkaa \(x\)-akselin, \(y\)-akselin arvo on tällöin 0.
\[\begin{align*} g(x)=4x-6 \end{align*}\] Asetetaan funktion arvo nollaksi: \[\begin{align*} &\;\;\;\;\;\;\;\;\;g(x)=0\\ &\Leftrightarrow 4x-6=0\;\;\;\;\;\;\;\;\;|+6\\ &\Leftrightarrow 4x-6+6=6\\ &\Leftrightarrow 4x=6\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|:4\\ &\Leftrightarrow \frac{\color{red}\cancel{\color{black}4}\color{black}x}{\color{red}\cancel{\color{black}4}}=\frac{6}{4}\\ &\Leftrightarrow x=\frac{6}{4}\\ &\Leftrightarrow x=\frac{3}{2} \end{align*}\]
Funktio saa arvoksi \(0\), kun \(x=\frac{3}{2}\). Graafisesti tarkistettuna funktion kuvaajan tulisi leikata \(x\)-akseli tässä kohdassa. 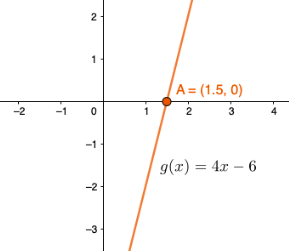
1.2 Toiseen asteen polynomifunktio
Toisen asteen polynomifunktio
Funktiota \(f\) kutsutaan toisen asteen polynomifunktioksi, jos se voidaan esittää muodossa \(f(x)=ax^2 +bx+c\), jossa \(a\neq0\).
Toisen asteen polynomifunktion kuvaaja on ylöspäin aukeava paraabeli, jos \(a>0\). Jos \(a<0\), kuvaaja on alaspäin aukeava paraabeli.
Funktion \(f(x)=x^2+bx+c\) nollakohdat saadaan ratkaisemalla toisen asteen yhtälö \(ax^2+bx+c=0\). Nollakohtien ratkaisemisessa voidaan hyödyntää nollasääntöä, muistikaavoja ja/tai toisen asteen yhtälön ratkaisukaavaa.
Toisen asteen yhtälön ratkaisukaava
Olkoon funktio \(f(x)=ax^{2}+bx+c\). Muuttuja \(x\) voidaan nyt ratkaista kaavalla \[\begin{align*} x=\displaystyle\frac{-b\pm \sqrt{b^2-4ac}}{2a}, \end{align*}\] jossa \(a\neq0\).
Osoittajasta löytyvä \(b^2-4ac\) on nimeltään diskriminantti \(D\). Se kertoo, montako ratkaisua toisen asteen yhtälöllä on.
Reaalijuurien määrä
- Jos \(D>0,\) yhtälöllä on kaksi eri juurta.
- Jos \(D=0,\) yhtälöllä on yksi juuri (kaksoisjuuri).
- Jos \(D<0,\) yhtälöllä ei ole juuria.
Ratkaise yhtälö \(x^2+2x-8=0\).
Ratkaisu:
Yhtälö on valmiiksi muodossa \(ax^2+bx+c=0\). Yhtälön kertoimet ovat
\[a=\textcolor{red}1,\;b=\textcolor{blue}2\;\text{ja}\;c=\textcolor{green}{-8}\]
Sijoitetaan kertoimet ratkaisukaavaan.
\[\begin{align*} x&=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ x&=\frac{-\textcolor{blue}2\pm\sqrt{\textcolor{blue}2^2-4\cdot\textcolor{red}1\cdot (\textcolor{green}{-8})}}{\textcolor{blue}2\cdot \textcolor{red}1} \\ x&=\frac{-2\pm\sqrt{4+32}}{4} \\ x&=\frac{-2\pm\sqrt{36}}{4} \\ x&=\frac{-2\pm6}{4} \end{align*}\]
Kirjoitetaan vastaus kahtena eri lausekkeena.
\[x=\frac{-2-6}{4}=\frac{-8}{4}=-4\;\;\;\;\text{tai}\;\;\;\;\frac{-2+6}{4}=\frac{4}{4}=1\]
Vastaus: \(x=-4\;\;\text{tai}\;\;x=1\)
Tulon nollasääntö
Tulo on nolla vain ja ainoastaan silloin, kun ainakin yksi tulon tekijöistä on nolla.
Ratkaise yhtälö.
- \(2x^2-6x=0\)
- \(x^2=ax\)
Ratkaisu:
\[\begin{align*} 2x^2-6x&=0 \\ x(2x-6)&=0 &&|\;\text{tulon nollasääntö}\\ x=0\;\;&\text{tai}\;\;2x-6=0 \\ &\;\;\;\;\;\;\;\;\;\;\;\;2x=-6 \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=-3 \end{align*}\]
\[\begin{align*} x^2&=ax \\ x^2-ax&=0 \\ x(x-a)&=0 &&|\;\text{tulon nollasääntö}\\ x=0\;\;&\text{tai}\;\;x-a=0 \\ x=0 \;\;&\text{tai}\;\;x=a \end{align*}\]
Vastaus:
- \(x=0\) tai \(x=-3\)
- \(x=0\) tai \(x=a\)
2. Epäyhtälöt
Epäyhtälöissä kyseessä ei ole ainoastaan yhtäsuuruudet, vaan myös "pienempi kuin"- tai "suurempi kuin"-ominaisuudet. Yhtälöiden ratkaisu tapahtuu suurimmaksi osaksi samalla tavalla kuin yhtäsuuruustilanteessa, mutta epäyhtälön muokkausvaiheessa tulee muistaa kiinnittää huomiota yhtälön totuusarvoon.
2.1 Ensimmäisen asteen epäyhtälö
Ensimmäisen asteen epäyhtälö
on muotoa \(ax+b>0\), jossa \(a\neq0\).
Epäyhtälömerkin tilalla voi olla myös \(\leq,\geq,<\) tai \(\neq\).
Ratkaise epäyhtälö
\(2x+1<3\)
\(-3x+8\leq -1\)
\(-\dfrac{2}{3}x+2>-\dfrac{2}{3}x+2\)
\(x-1 \geq x\)
Ratkaisu
\[\begin{align*} 2x+1 & <3 && | -1 \\ 2x & < 2 && | :2 \\ x & < 1 \end{align*}\]
Vastaus: \(x<1\)
\[\begin{align*} -3x+8 & \leq -1 && | -8 \\ -3x & \leq -9 && | :(-3), \textrm{ merkin suunta vaihtuu} \\ x & \geq 3 \end{align*}\]
Vastaus: \(x\geq 3\)
\[\begin{align*} -\dfrac{2}{3}x+2 &> -\dfrac{2}{3}x+1 && | + \dfrac{2}{3}x \\ 2 &> 1 && \\ \text{tosi} \end{align*}\]
Luku \(2\) on suurempi kuin luku \(1\) riippumatta muuttujasta \(x\). Näin ollen epäyhtälön \(-\dfrac{2}{3}x+2 > -\dfrac{2}{3}x+1\) toteuttavat kaikki reaaliluvut.
Vastaus: \(x \in \mathbb{R}\)
\[\begin{align*} x-1 & \geq x && | -x \\ -1 \geq 0 \\ \text{epätosi} \end{align*}\]
\(-1\) ei ole suurempi tai yhtä suuri kuin \(0\). Näin ollen yhtälöllä \(x-1 \geq x\) ei ole olemassa ratkaisua.
Vastaus: Ei ratkaisua
2.2 Toisen asteen epäyhtälö
Toisen asteen epäyhtälö
on muotoa \(ax^2+bx+c<0\), jossa \(a≠0\).
Epäyhtälömerkin tilalla voi olla myös \(\leq,\geq,>\) tai \(≠\).
Toisen asteen epäyhtälö \(ax^2+bx+c<0\) ratkaistaan kirjoittamalla se ensin muotoon, jossa yhtälöä verrataan nollaan. Välit, joissa yhtälö on tosi, voidaan tulkita nollakohtien sekä paraabelin aukeamissuunnan perusteella.
Ratkaise toisen asteen epäyhtälö \(x<x^2+1\).
Ratkaisu:
Muokataan epäyhtälö normaalimuotoon.
\[\begin{align*} x&<x^2+1 \\ -x^2+x-1&<0 \end{align*}\]
Tutkitaan yhtälön \(-x^2+x-1=0\) ratkaisuja. Nyt diskriminantti \[D=1^2-4\cdot(-1)\cdot(-1)=-3<0,\] joten yhtälöllä ei ole reaalisia juuria.
Hahmotellaan funktion \(f(x)=-x^2+x-1\) kuvaaja niiden tietojen perusteella, että
- paraabeli aukeaa alaspäin
- funktiolla ei ole nollakohtia
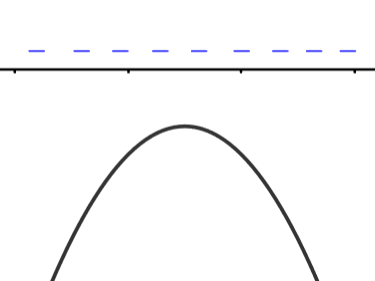
Kuvasta nähdään, että funktion kuvaaja on aina \(x-\)akselin alapuolella, joten funktio saa aina negatiivisia arvoja.
Vastaus: Epäyhtälö toteutuu kaikilla muuttujan \(x\) arvoilla.
Yleisesti toisen asteen epäyhtälön ratkaisu ilman ohjelmistoja etenee seuraavasti:
Saatetaan epäyhtälö normaalimuotoon.
Ratkaistaan vastaavan toisen asteen polynomin nollakohdat.
Hahmotellaan polynomia vastaavan paraabelin kuvaaja. Riittää, että kuvaajasta näkyy paraabelin aukeamissuunta ja nollakohdat.
Ilmoitetaan tulos kuvaajan perusteella.
3. Polynomin jakaminen tekijöihin
Polynomin jakamisella tekijöihin tarkoitetaan sitä kyseisen polynomin esittämistä kahden pienempi asteisen polynomin tulona. Polynomi voidaan jakaa tekijöihin etsimällä yhteinen tekijä, muistikaavojen avulla, ryhmittelyn avulla tai nollakohtien avulla.
Toisen asteen polynomifunktio voidaan jakaa ensimmäisen asteen tekijöihin, vain jos sillä on nollakohtia. Korkeamman asteen polynomi voidaan jakaa tekijöihin, vaikka sillä ei olisikaan nollakohtia.
3.1 Yhteinen tekijä
Lausekeesta voi ottaa yhteisen tekijän erottamalla sen kertoimeksi: \[\begin{align*} 3x^2+9x=\color{green}3\cdot x\color{black}\cdot x+3\cdot\color{green}3\cdot x\color{black}=\color{green}3x\color{black}(x+3) \end{align*}\]
3.2 Muistikaavat
Muistikaavat
\((a+b)^{2} =a^{2} +2ab+b^{2}\\ (a-b)^{2} = a^{2}-2ab+b^2\\ (a+b)(a-b)=a^2-b^2\)
Jaetaan polynomi \(16-x^{4}\) toisen asteen tekijöihin:
\[\begin{align*} 16-x^{4}=4^{2}-(x^{2})^{2}=(4+x^2)(4-x^2) \end{align*}\]
Sievennä
\((x+1)(x-1)\)
\((2a-\sqrt{3}b)(2a+\sqrt{3b})\)
\((\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e)(-\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e)\)
\((\dfrac{1}{3}x+\sqrt{2}y)^2(-\dfrac{1}{3}x+\sqrt{2}y)^2\)
Ratkaisu
Hyödynnetään summan ja erotuksen binomikaavaa \((a+b)(a-b)=a^2-b^2\)
\[\begin{align*} &(x+1)(x-1) && |a=x, b=1 \\ &= x^2-1^2 \\ &= x^2-1 \end{align*}\]
\[\begin{align*} &(2a-\sqrt{3}b)(2a+\sqrt{3b}) && |a=2a, b=\sqrt{3}b \\ &= (2a)^2-(\sqrt{3}b)^2 \\ &= 4a^2-3b^2 \end{align*}\]
\[\begin{align*} &(\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e)(-\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e) \\ &= (\sqrt{9} e+\dfrac{1}{2}\sqrt{\pi})(\sqrt{9}e-\dfrac{1}{2}\sqrt{\pi}) && |a=\sqrt{9} e, b=\dfrac{1}{2}\sqrt{\pi}\\ &= (\sqrt{9}e)^2-(\dfrac{1}{2}\sqrt{\pi})^2\\ &= 9e^2-\dfrac{1}{4}\pi \end{align*}\]
\[\begin{align*} &(\dfrac{1}{3}x+\sqrt{2}y)^2(-\dfrac{1}{3}x+\sqrt{2}y)^2 \\ &=(\sqrt{2}y+\dfrac{1}{3}x)^2(\sqrt{2}y-\dfrac{1}{3}x)^2 \\ &=((\sqrt{2}y+\dfrac{1}{3}x)(\sqrt{2}y-\dfrac{1}{3}x))^2 && |\textrm{summan ja erotuksen tulo: }a=\sqrt{2}y,b=\dfrac{1}{3}x \\ &=((\sqrt{2}y)^2-(\dfrac{1}{3}x)^2)^2 \\ &=(2y^2-\dfrac{1}{9}x^2)^2 && |\textrm{erotuksen neliö: }a=2y^2,b=\dfrac{1}{9}x^2 \\ &= (2y^2)^2-2\cdot2y^2 \cdot \dfrac{1}{9} x^2+(\dfrac{1}{9}x^2)^2 \\ &= 4y^4-\dfrac{4}{9}x^2y^2+\dfrac{1}{81}x^4 \end{align*}\]
3.3 Ryhmittely
Ratkaistaan funktion \(f(x)=3x^{3}+2x^{2}-6x-4\) nollakohdat. \[\begin{align*} 3x^{3}+2x^{2}-6x-4&=0\;\;\;\;\;\;\;\;|\text{yhteinen tekijä}\\ \color{blue}x^{2}\color{black}(3x+2)\color{blue}-2\color{black}(3x+2)&=0\;\;\;\;\;\;\;\;|\text{ryhmittely}\\ (3x+2)(\color{blue}x^{2}-2\color{black})&=0\;\;\;\;\;\;\;\;|\text{tulon nollasääntö}\\ 3x+2=0\;\;\;\;\;\;\;\;\;\;&\text{tai}\;\;\;\;\;\;\;\;\;\;x^{2}-2=0\\ 3x=-2\;\;\;\;\;\;\;&\text{tai}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^{2}=2\\ x=-\frac{2}{3}\;\;\;\;\;\;&\text{tai}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=\pm\sqrt{2} \end{align*}\] Funktion \(f\) nollakohdat ovat siis \(x=-\frac{2}{3}\), \(x=-\sqrt{2}\) tai \(x=\sqrt{2}\).
3.4 Nollakohdat
Toisen asteen polynomin tekijöihin jako tarkoittaa, että polynomi kirjoitetaan kahden ensimmäisen asteen polynomin tuloksi. Kun toisen asteen polynomin nollakohdat ovat tiedossa, tekijöihin jako onnistuu seuraavan teoreeman avulla.
Polynomin jakaminen tekijöihin
Jos \(x_1\) ja \(x_2\) ovat polynomin \(ax^2+bx+c\) nollakohdat, niin
\[ax^2+bx+c=a(x-x_1)(x-x_2).\]
Jos toisen asteen yhtälöllä \(ax^2+bx+c=0\) on vain yksi ratkaisu \(x_1,\) niin
\[ax^2+bx+c=a(x-x_1)^2.\]
Jos yhtälöllä taas ei ole yhtään ratkaisua, niin polynomia ei voi jakaa ensimmäisen asteen tekijöihin.
Jaa polynomi \(9x^2-3x-2\) tekijöihin.
Ratkaisu:
Ratkaistaan ensin yhtälön \(9x^2-3x-2=0\) juuret.
\[\begin{align*} 9x^2-3x-2&=0 \\ x&=\frac{-(-3)\pm\sqrt{(-3)^2-4\cdot 9\cdot(-2)}}{2\cdot9} \\ x&=\frac{3\pm\sqrt{81}}{18} \\ x&=\frac{3\pm9}{18} \\ x&=-\frac{6}{18}=-\frac{1}{3}\;\;\text{tai}\;\;x=\frac{12}{18}=\frac{2}{3} \end{align*}\]
Tekijöihin jako
\[\begin{align*} &9x^2-3x-2 &&|\,a=\textcolor{red}9,\,x_1=\textcolor{blue}{-\frac{1}{3}},\,x_2=\textcolor{green}{\frac{2}{3}}\\ &=\textcolor{red}9\left(x-\left(\textcolor{blue}{-\frac{1}{3}}\right)\left(x-\textcolor{green}{\frac{2}{3}}\right)\right) \\ &=3\left(x+\frac{1}{3}\right)\cdot3\left(x-\frac{2}{3}\right) \\ &=(3x+1)(3x-2) \end{align*}\]
Tarkastetaan tehtävä GeoGebralla. Tekijöihin jako tapahtuu käskyllä JaaTekijöihin().

Vastaus:
\(9x^2-3x-2=(3x+1)(3x-2)\)
4. Potenssi-, rationaali- ja juurifunktiot
4.1 Potenssifunktiot ja -yhtälöt
Potenssiyhtälön \(x^n=a\) ratkaisut
Kun \(n\) on parillinen positiivinen kokonaisluku ja \(a\geq 0\), niin yhtälön \(x^n=a\) ratkaisu on luvun \(a\) \(n\):s juuri tai sen vastaluku.
\[\begin{align*} x^n&=a && |\sqrt[n]{} \\ x&=\sqrt[n]{a} \text{ }\text{ tai } x=-\sqrt[n]{a} \end{align*}\]
Kun \(n\) on pariton positiivinen kokonaisluku ja \(a \in \mathbb{R}\), niin yhtälön \(x^n=a\) ratkaisu on luvun \(a\) \(n\):s juuri.
\[\begin{align*} x^n&=a && |\sqrt[n]{} \\ x&=\sqrt[n]{a} \end{align*}\]
Ratkaise yhtälö
a) \(x^5=32\)
b) \(x^6=4096\)
c) \(-2x^7=4\)
d) \(11x^8-\pi=\dfrac{1}{2}\).
Ratkaisu:
a) Yhtälöllä on täsmälleen yksi ratkaisu, sillä \(n=5\) on pariton.
\[\begin{align*} x^5 &= 32 && |\sqrt[5]{}\\ x &= \sqrt[5]{32} \\ x &= 2 \end{align*}\]
b) Yhtälöllä on kaksi ratkaisua, luvun \(4096\) kuudes juuri ja sen vastaluku, sillä \(n=6\) on parillinen.
\[\begin{align*} x^6 &= 4096 && |\sqrt[6]{}\\ x &=\pm\sqrt[6]{4096} \ \ \text{ tai } x=-\sqrt[6]{4096}\\ x &=4 \ \ \ \ \ \ \ \ \ \ \ \text{ tai } x=-4 \end{align*}\]
c) Yhtälöllä on täsmälleen yksi ratkaisu, sillä \(n=7\) on pariton.
\[\begin{align*} -2x^7 &= 4 && |:(-2)\\ x^7 &= -2 && |\sqrt[7]{} \\ x &= \sqrt[7]{-2} \\ x &= -\sqrt[7]{2} \end{align*}\]
d)
\[\begin{align*} 11x^8-\pi&=\dfrac{1}{2} &&|+\pi\\ 11x^8 &= \pi+\dfrac{1}{2} && |:11 \\ x^8 &=\dfrac{\pi+\dfrac{1}{2}}{11} \\ x^8 &= \dfrac{2\pi+1}{22} && |\sqrt[8]{} \text{ Kaksi ratkaisua, sillä parillinen potenssi} \\ x&= \sqrt[8]{\dfrac{2\pi+1}{22}} \ \text{ tai } x=-\sqrt[8]{\dfrac{2\pi+1}{22}} \end{align*}\]
4.2 Rationaalifunktiot ja -yhtälöt
Rationaalifunktioksi kutsutaan sellaista funktiota joka on kahden funktion \(P(x)\) ja \(Q(x)\) osamäärä.
Rationaalifunktio
Funktio \(f(x)\) on kahden polynomifunktion \(P(x)\) ja \(Q(x)\) osamäärä \[\begin{align*} f(x)=\dfrac{P(x)}{Q(x)}, \end{align*}\] jossa \(Q(x)\) voi olla vakiofunktio, kunhan se ei ole nollafunktio, eli \(Q(x)≠0\).
Sievennetään rationaalifunktiota \(\dfrac{b}{(b^2+b)}(b^{2}-1)\).
\[\begin{align*} \dfrac{b}{(b^2+b)}(b^{2}-1) = \frac{b}{b(b+1)}(b^{2}-1)=\frac{\cancel{b}}{\cancel{b}(b+1)}(b^{2}-1)=\frac{(b^{2}-1)}{(b+1)}=\frac{\cancel{(b+1)}(b-1)}{\cancel{(b+1)}}=(b-1). \end{align*}\]
Eli \(\dfrac{b}{(b^2+b)}(b^{2}-1)=(b-1)\).
4.3 Juurifunktiot ja -yhtälöt
Juuriyhtälön \(\sqrt[n]{x}=a\) ratkaisut
Kun \(n\) on parillinen positiivinen kokonaisluku ja \(a\geq 0\), niin yhtälön \(\sqrt[n]{x}=a\) ratkaisu on luvun \(a\) \(n\):s potenssi.
\[\begin{align*} \sqrt[n]{x}&=a && |()^n \\ (\sqrt[n]{x})^n&=a^n && \\ x&=a^n \end{align*}\]
Kun \(n\) on pariton positiivinen kokonaisluku ja \(a \in \mathbb{R}\), niin yhtälön \(\sqrt[n]{x}=a\) ratkaisu on luvun \(a\) \(n\):s potenssi.
\[\begin{align*} \sqrt[n]{x}&=a && |()^n \\ (\sqrt[n]{x})^n&=a^n && \\ x&=a^n \end{align*}\]
Yhtälö \[\sqrt[n]{x}=a\]
on ratkeamaton, jos \(n\) on parillinen ja \(a<0\). Muussa tapauksessa yhtälöllä on olemassa yksikäsitteinen ratkaisu \(x\). Yksikäsitteisyys on tärkeä huomata, sillä potenssiyhtälöistä poiketen, parillisella juuri yhtälöllä ei ole ratkaisun lisäksi ratkaisun vastaluku ratkaisua.
Mikä reaaliluku on kyseessä, kun luvun ja sitä yhtä isomman luvun osamäärän kuutiojuuri on \(2\)? Ratkaisu:
Olkoon \(x="\text{luku}"\). Muodostetaan ja ratkaistaan tehtävänannon mukainen yhtälö:
\[\begin{align*} \sqrt[3]{\dfrac{x}{x+1}}&= 2 && |()^3 \\ \dfrac{x}{x+1}&= 8 && |\cdot(x+1), \text{ missä } x+1\neq0 \\ x &= 8x + 8 && |-x-8 \\ 7x &= -8 && |:7 \\ x &= -\dfrac{8}{7} \end{align*}\]
Alkuperäisen yhtälön nimittäjän \(x+1\) tulee olla nollasta poikkeava, koska nollalla jakoa ei ole määritelty. Näin ollen saadaan ehto
\[\begin{align*} x+1 \neq 0 && |-1 \\ x \neq -1, \end{align*}\]
jonka ratkaisumme \(x = -\dfrac{8}{7}\) toteuttaa.
Vastaus: Kyseessä on luku \(-\dfrac{8}{7}\)
Ilmaise \(n\):s juuren ja potenssin potenssin laskusäännön avulla
a) \(3^{\frac{5}{7}}\)
b) \(a^{\frac{m}{n}}\), missä \(a>0\) sekä \(m\) ja \(n\) ovat positiivisa kokonaislukuja.
Ratkaisu:
a) Murtoluku \(\frac{5}{7}\) voidaan ilmoittaa myös muodossa \(\frac{5}{7}=5\cdot\frac{1}{7}\). Sievennetään
\[\begin{align*} 3^{\frac{5}{7}} &= 3^{5\cdot\frac{1}{7}} && |\text{ potenssin potenssi } a^{m\cdot n}=(a^m)^n\\ &= (3^5)^{\frac{1}{7}} && |\text{ murtopotenssi } a^{\frac{1}{n}}=\sqrt[n]{a} \\ &= \sqrt[7]{3^5}. \end{align*}\]
Vastaus: \(3^{\frac{5}{7}}=\sqrt[7]{3^5}\)
b) Murtoluku \(\frac{m}{n}\) voidaan ilmoittaa myös muodossa \(\frac{m}{n}=m\cdot\frac{1}{n}\). Sievennetään
\[\begin{align*} a^{\frac{m}{n}} &= a^{m\cdot\frac{1}{n}} && |\text{ potenssin potenssi } \\ &= (a^m)^{\frac{1}{n}} && |\text{ murtopotenssi } \\ &= \sqrt[n]{a^m} \end{align*}\]
Vastaus: \(a^{\frac{m}{n}}=\sqrt[n]{a^m}\)
Tehtäviä
Tehtävä 1
Tehtävä 2
Tehtävä 3
Tehtävä 4
a.
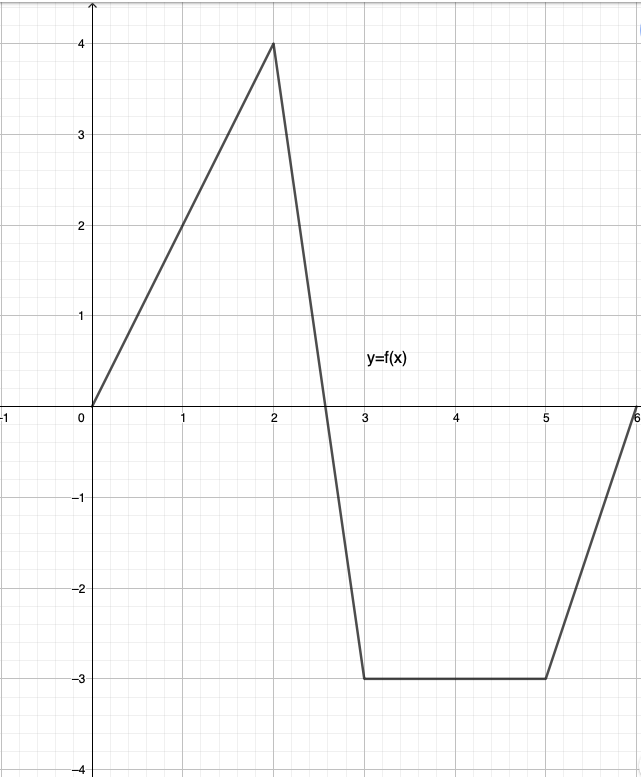
b.
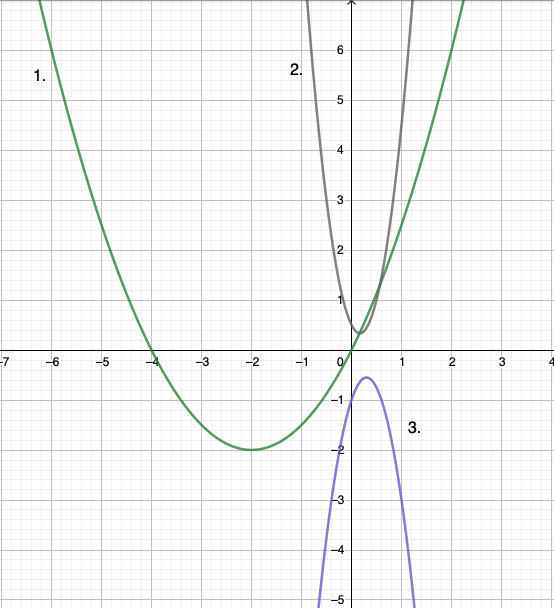
Tehtävä 5
Tehtävä 6
Suorakulmion muotoisessa puistossa on yhteensä 190 ruusupensasta. Pituussuunnassa pensaita on 9 kappaletta enemmän kuin leveyssuunnassa. Montako ruusupensasta on leveyssuunnassa?

Tehtävä 7
a.
Piirrä GeoGebralla funktioiden \(f(x)=\frac{1}{3}x-2\) ja \(g(x)=|\frac{1}{3}x-2|\) kuvaajat.
b.
Yhtälön \(|x-2|=|x^{2}+2|\) toinen ratkaisu on \(0\). Mikä on toinen ratkaisu?
Tehtävä 8
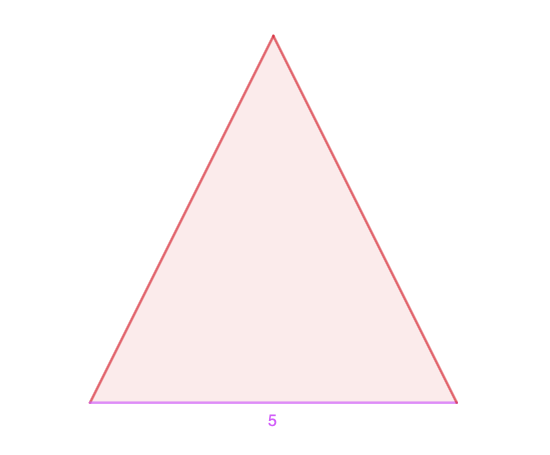
Tasasivuisen kolmion kanta on 5. Kolmion kannan suhde kyljen pituuteen on yhtä suuri kuin kyljen pituuden suhde kyljen ja kannan pituuden summaan. Määritä tasasivuisen kolmion kyljen pituus.
Vanhoja YO-tehtäviä
1.
- Ratkaise yhtälö \(7x^7 + 6x^6 =0\) [K10/1a]
- Millä \(x\):n arvoilla pätee \(\frac{3}{3-2x}<0\) [K10/1c]
VASTAUS:
a. \(x_{1}=0, x_{2}=-\frac{6}{7}\)
b. \(x>\frac{3}{2}\)
2.
Määritä toisen asteen yhtälön \(x^2+px+q=0\) kertoimet \(p\) ja \(q\), kun yhtälön juuret ovat \(-2-\sqrt{6}\) ja \(-2+\sqrt{6}\). [K10/3b]
VASTAUS: \(p=4, q=-2\)
3.
- Sievennä lauseke \((a+b)^2-(a-b)^2\) [S10/1a]
- Ratkaise epäyhtälö \(x\sqrt{7}-3 \leq4x\) [S10/2a]
- Ratkaise yhtälö \(x^4 -3x^2 -4=0\) [S10/2c]
VASTAUS:
a. \(4ab\)
b. \(x\geq\frac{3}{\sqrt{7}-4}\)
c. \(x_{1}=2, x_{2}=-2\)
4.
Ratkaise
yhtälö \(\frac{2}{x}=\frac{3}{x-2}\)
epäyhtälö \(x^2 -2\leq x\).
yhtälö \(\mid\frac{3}{2}x-6\mid=6\) [K11/1]
VASTAUS: a.\(x=-4\), b.\(-1\leq x\leq2\), c.\(x=0\) tai \(x=8\)
RATKAISU:
a. \[\begin{align*} \frac{2}{x}&=\frac{3}{x-2}\\2(x-2)&=3x\\2x-4&=3x\\ x&=-4 \end{align*}\]
b. \[\begin{align*} x^{2}-2&\leq x\\ x^{2}-x-2&\leq0. \end{align*}\] Vasemman puolen kuvaaja on ylöspäin aukeava paraabeli, joka leikkaa x-akselia kohdissa \(x=-1\) tai \(x=2\). Epäyhtälö toteutuu, kun \(-1\leq x\leq2\)
c. \[\begin{align*} &\frac{3}{2}x-6=0 \Leftrightarrow x=4.\\ &\text{Kun } x\leq4,\text{ on }|\frac{3}{2}x-6|=6\Leftrightarrow -\frac{3}{2}x+6=6\Leftrightarrow x=0.\\ &\text{Kun }x>4,\text{ on }|\frac{3}{2}-6=6\Leftrightarrow\frac{3}{2}-6=0\Leftrightarrow x=8. \end{align*}\] Yhtälö toteutuu kun \(x=0\) tai \(x=8\).
5.
Ratkaise yhtälöt
\(\frac{x}{6}-\frac{x-3}{2}-\frac{7}{9}=0\) [K12/1b]
\(\frac{x}{2}-\frac{2}{x}=0\) [K12/1c]
VASTAUS: a. \(x=\frac{13}{6}\) b. \(x=\pm2\)
RATKAISU:
a.
\[\begin{align*} \frac{x}{6}-\frac{x-3}{2}-\frac{7}{9}=0\Leftrightarrow3x-9(x-3)-2\cdot7=0\Leftrightarrow-6x+13=0\Leftrightarrow x=\frac{13}{6} \end{align*}\]
b.
\[\begin{align*} \frac{x}{2}-\frac{2}{x}=0\Leftrightarrow\frac{x^{2}}{2}-2=0\Leftrightarrow x^{2}-4=0\Leftrightarrow x=\pm2 \end{align*}\]
6.
Ratkaise yhtälöt
\(\mid x \mid=1+x\) [S12/1b]
\(1-x=\frac{1}{1-x}\) [s12/1c]
VASTAUS: a. \(x=-\frac{1}{2}\), kun \(x\leq0\) ja ei ratkaisua, kun \(x>0\). b. \(x=0\text{ tai }x=2\)
RATKAISU:
a.
Jos \(x>0\). b., on \(|x|=1+x \Leftrightarrow x=1+x\). Tällä ei ole ratkaisua.
Jos \(x\leq0\), on\(|x|=1+x\Leftrightarrow -x=1+x\Leftrightarrow x=-\frac{1}{2}\)
b.
\[\begin{align*} 1-x=\frac{1}{1-x}\Leftrightarrow(1-x)^{2}=1\Leftrightarrow1-x=\pm1\Leftrightarrow x=0\text{ tai }x=2 \end{align*}\]
7.
Määritä suorien \(\frac{x}{3}+\frac{y}{2}=1\) ja \(3x-2y+3=0\) leikkauspiste. [k09/1c]
VASTAUS: \(x=\frac{3}{13},y=\frac{24}{13}\)
RATKAISU:
Suorien leikkauspisteessä suorien yhtälöt ovat yhtäsuuret. Muokataan ensin suorien lausekkeet niin, että ne ovat molemmat muotoa \(y=ax+b\).
\[\begin{align*} \frac{x}{3}+\frac{y}{2}&=1\;\;\;\;\;\;\;\;\;\;\;\;\|\cdot2\\ 2\cdot\frac{x}{3}+y&=2\;\;\;\;\;\;\;\;\;\;\;\;\|-\frac{2}{3}x\\ y&=-\frac{2}{3}x+2 \end{align*}\] Toisen suoran yhtälö:
\[\begin{align*} 3x-2y+3&=0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\|+2y\\ 3x+3&=2y\;\;\;\;\;\;\;\;\;\;\;\;\|:-2\\ y&=\frac{3}{2}x+\frac{3}{2} \end{align*}\]
Kysytty leikkauspiste saadaan sijoittamalla yhtälöt yhtäsuuriksi ja ratkaistaan tästä \(x\): \[\begin{align*} -\frac{2}{3}x+2&=\frac{3}{2}x+\frac{3}{2} \;\;\;\;\;\;\;\|-\frac{3}{2}\\ -\frac{2}{3}x+2-\frac{3}{2}&=\frac{3}{2}x \;\;\;\;\;\;\;\;\;\;\;\;\;\;\|+(-\frac{2}{3}x)\\ 2-\frac{3}{2}&=\frac{3}{2}x+\frac{2}{3}x\\ \frac{1}{2}&=\frac{13}{6}x\;\;\;\;\;\;\;\;\;\;\;\;\|:\frac{13}{6}\\ x&=\frac{3}{13} \end{align*}\]
Leikkauspisteen \(x\)-koordinaatti on siis \(\frac{3}{13}\). Ratkaistaan vielä \(y\)-koordinaatti sijoittamalla \(x=\frac{3}{13}\) kumpaan tahansa suoran yhtälöistä.
\[\begin{align*} 3x-2y+3&=0\;\;\;\;\;\\ y&=\frac{3}{2}x+\frac{3}{2}\;\;\;\;\;\;\;\;\;\;\;\|\text{sij. }x=\frac{3}{13}\\ y&=\frac{3}{2}\cdot\frac{3}{13}+\frac{3}{2}\\ y&=\frac{9}{26}+\frac{3}{2}\\ y&=\frac{24}{13} \end{align*}\]
Suorien leikkauspiste on \((\frac{3}{13},\frac{24}{13})\).
8.
Toisen asteen polynomifunktiolle voidaan käyttää kahta erilaista esitystapaa. Summamuoto: \(ax^2+bx+c\) ja tulomuoto: \(a(x-x_{1})(x-x_{2})\).
Muokkaa polynomi \(2(x-6)(x-9)\) summamuotoon
Muokkaa polynomi \(x^2+x-12\) tulomuotoon
Osoita, että \(x_{1}x_{2}=\frac{c}{a}\), jos \(x_{1}\) ja \(x_{2}\) ovat polynomin \(ax^2+bx+c\) nollakohdat. [K18/2]
VASTAUS: a.\(2x^{2}-30x+108\) b. \((x-3)(x+4)\)
RATKAISU:
a.
\(2(x-6)(x-9)=2x^{2}-2\cdot6x-2\cdot9x+2\cdot6\cdot9=2x^{2}-30x+108\)
b.
\(x^{2}+x-12=0\Rightarrow x=3\text{ tai }x=-4\)
\(\Rightarrow(x-3)(x+4)\)
c.
\(p(x)=a(x-x_{1})(x-x_{2})\) joillakin \(a\):n arvolla. Kertomalla auki saadaan: \(p(x)=ax^{2}-a(x_{1}+x_{2})x+ax_{1}{x_{2}}\).
Toisaalta \(p(x)=ax^{2}+bx+c\), joten vakiotermejä vertailemalla saadaan \(ax_{1}x_{2}=c\) eli \(x_{1}x_{2}=\frac{c}{a}\).
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.