MAA7 Integraalilaskentaa
Kurssin tavoitteena on, että opiskelija
- ymmärtää integraalifunktion käsitteen ja oppii määrittämään alkeisfunktioiden integraalifunktioita
- ymmärtää määrätyn integraalin käsitteen ja sen yhteyden pinta-alaan sekä tutustuu numeeri- seen menetelmään määrätyn integraalin määrittämisessä
- osaa määrittää pinta-aloja ja tilavuuksia määrätyn integraalin avulla
- perehtyy integraalilaskennan sovelluksiin
- osaa käyttää ohjelmistoja funktion ominaisuuksien tutkimisessa, integraalifunktion määrittämisessä, määrätyn integraalin laskemisessa sovellusongelmien yhteydessä sekä numeerisessa integroinnissa.
Keskeiset sisällöt
- integraalifunktio: alkeisfunktioiden integraalifunktiot, suorakaidesääntö
- määrätty integraali
- pinta-alan ja tilavuuden laskeminen
1. Integraalifunktio
Integroinnin käänteisoperaatio on derivointi, joten integroinnin tulos voidaan aina tarkistaa derivoimalla funktio.
Integraalifunktio on derivoituva, joten se on myös jatkuva.
1.1 Integraalifunktio ja integroimissääntöjä
Integraalifunktion määritelmä
Oletetaan funktiot \(f\) ja \(F\) määritellyiksi avoimella välillä \(I\).
Jos \(F'=f\), eli \(F'(x)=f(x)\) kaikilla \(x\in I\), niin funktiota \(F\) kutsutaan funktion \(f\) integraalifunktioksi.
Jokaisella jatkuvalla funktiolla on integraalifunktio.
Integraalifunktio ei ole yksikäsitteinen, mutta yhden integraalifunktion avulla löydetään kaikki kyseisen funtion integraalifunktiot.
Integroimisvakio
Jos funktiolla \(f\) on integraalifunktio \(F_{0}\), niin kaikki muotoa \(F(x)=F_{0}+C\) olevat funktiot ovat funktion \(f\) integraalifunktioita.
\(C\) on integroimisvakio ja se on mielivaltainen: \(C\in \R\).
Integroinniksi kutsutaan funktion \(f\) integraalifunktioiden \(F\) määrittämistä.
Integroinnin merkintä
Funktion \(f\) integraalifunktiota \(F\) voidaan merkitä \[\begin{align*} F(x)=\int f(x) dx \end{align*}\] Lausutaan: "integraali \(f\) \(x\) \(d\) \(x\)."
Merkintä \(dx\) kertoo, että integrointi tapahtuu muuttujan \(x\) suhteen. Jos funktiossa on useita eri muuttujia, niin merkintä muutetaan kuvaamaan oikeaa termiä.
Integroimissääntöjä
- \(\displaystyle\int kf(x)dx=k\int f(x) dx\), kun \(k\) on vakio
- \(\displaystyle\int(f(x)+g(x))dx=\int f(x)dx+ \int g(x)dx\)
- \(\displaystyle\int s'(x)u(s(x))dx=U(s(x))+C\), jossa \(C\in\R\) ja \(U\) on ulkofunktion \(u\) integraalifunktio.
1.2 Potenssi- ja polynomifunktion integrointi
Potenssifunktion integroimissääntö
\[\begin{align*} \int x^{r}dx=\dfrac{1}{r+1}x^{r+1}+C, \end{align*}\] jossa \(r≠-1\)
Integroidaan \(x^{3}-2x^{2}+2x+1\). \[\begin{align*} \int(x^{3}-2x^{2}+2x+1)dx&=\int x^{3}dx-\int 2x^{2}dx+\int 2xdx+\int1dx\\ &=\frac{1}{4}x^{4}-2\cdot\frac{1}{3}x^{3}+2\cdot\frac{1}{2}x^{2}+x+C\\ &=\frac{x^{4}}{4}-\frac{2x^{3}}{3}+x^{2}+x+C \end{align*}\]
1.3 Sini- ja kosinifunktion integrointi
Sini- ja kosinifunktion integrointi
\[\begin{align*} \int\sin x dx=-\cos x+C\\ \int\cos x dx=\sin x+C \end{align*}\]
Integroidaan \(\tan^{2}x\).
Tiedetään tangentin derivoimiskaava \(D\tan x=1+\tan^{2}x\), ja hyödynnetään sitä integroinnissa.
\[\begin{align*} &\int\tan^{2}x\;dx\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|\text{täydennetään lauseketta sopivasti}\\&=\int(\color{red}1\color{black}+\tan^{2}x\color{red}-1\color{black})dx\\&=\int(1+\tan^{2}x\;dx)dx-\int1\;dx\\&=\tan x-x+C. \end{align*}\]
1.4 Eksponentti- ja logaritmifunktion integrointi
Eksponenttifunktion \(e^{x}\) integrointi
\[\begin{align*} \int e^{x}dx=e^{x}+C \end{align*}\]
Eksponenttifunktion \(a^{x}\) integrointi
\[\begin{align*} \int a^{x}dx=\dfrac{a^{x}}{\ln a}+C, \end{align*}\] \(a>0, a≠1\)
Määritetään \(\displaystyle\int e^{2+x}dx\). \[\begin{align*} \displaystyle\int e^{2+x}dx&=\displaystyle\int e^{2}\cdot e^{x}dx\\ &=e^{2}\displaystyle\int e^{x}dx\\ &=e^{2}\cdot e^{x}+C\\&=e^{2+x}+C. \end{align*}\]
1.5 Murtofunktion integrointi
Rationaalifunktio on muotoa \(\dfrac{P(x)}{Q(x)}\), ja \(P(x)\) ja \(Q(x)\) ovat polynomeja.
Murtofunktion \(\dfrac{1}{x}\) integrointi
kun \(x>0\) \[\begin{align*} \int \dfrac{1}{x}dx=\ln |x|+C=\ln x+C, x>0 \end{align*}\]
kun \(x<0\) \[\begin{align*} \int \dfrac{1}{x}dx=\ln |x|+C=\ln (-x)+C, x<0 \end{align*}\]
Muodostetaan integraali \(\displaystyle\int\dfrac{x^{2}}{1-x^{3}}dx\). \[\begin{align*} &\displaystyle\int\dfrac{x^{2}}{1-x^{3}}dx\\ &=\displaystyle\int\color{red}-\frac{1}{3}\cdot-3\color{black}\frac{x^{2}}{1-x^{3}}\\ &=-\frac{1}{3}\displaystyle\int\overbrace{\underbrace{\frac{-3x^{2}}{1-x^{2}}}}^{\text{$f'(x)$}}_{\text{$f(x)$}}dx\;\;\;\;\;\;\;\;\;\;\;\;|\int\frac{f'(x)}{f(x)}dx=\ln|f(x)|+C\\ &=-\frac{1}{3}\ln|1-x^{3}|+C. \end{align*}\] Ja tässä \(x≠1\).
1.6 Yhdistetyn funktion ja paloittain määritellyn funktion integrointi
Yhdistetyn funktion integroimissääntöä voidaan käyttää, jos integroitava lauseke voidaan tulkita ulkofunktion \(u(s(x))\) ja sisäfunktion derivaatan \(s'(x)\) tuloksi, ja jos ulkofunktion integraalifunktio osataan laskea.
Aina sisäfunktion derivaatta ei ole valmiina lausekkeessa, vaan lauseke pitää täydentää vakiolla sopivaksi.
Yhdistetyn funktion integroimissääntö
\[\begin{align*} \int u(s(x))\cdot s'(x)dx=U(s(x))+C \end{align*}\]
Muodostetaan integraali \(\displaystyle\int3\cos^{2}x\;dx\).
Käytetään integroinnissa hyödyksi taulukkokirjan kaavaa \(\cos^{2}x=\frac{1}{2}(1+\cos2x)=\frac{1}{2}+\frac{1}{2}\cos2x\).
\[\begin{align*} \displaystyle\int3\cos^{2}x\;dx&=\displaystyle\int(\frac{3}{2}+\frac{3}{2}\cos2x)dx\\ &=\frac{3}{2}\displaystyle\int dx+\frac{3}{2}\displaystyle\int\cos2x\;dx\\ &=\frac{3}{2}\displaystyle\int dx+\frac{3}{2}\cdot\frac{1}{2}\displaystyle\int2\cdot\cos2x\; dx\\ &=\frac{3}{2}x+\frac{3}{4}\sin2x+C. \end{align*}\]
2. Määrätty integraali
2.1 Välisumma
Käyrän ja x-akselin väliin jäänyttä pinta-alaa voidaan tutkia välisumman avulla.
Kun väli \([a,b]\) jaetaan yhtä pitkiin osaväleihin ja jokainen osaväli erotellaan piirtämällä suorakulmio jokaiseen osaväliin. Suorakulmion korkeus määräytyy funktiosta, joka kulkee myös välillä \([a,b]\).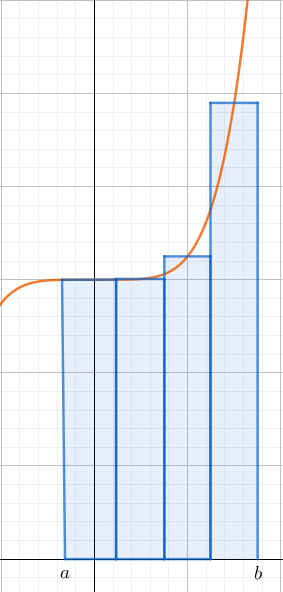 
Nyt funktion ja x-akselin väliin jäävää pinta-alaa voidaan arvioida laskemalla suorakulmioiden pinta-alat yhteen. Tätä suorakulmioiden pinta-alojen summaa kutsutaan Riemann-integraaliksi eli välisummaksi.
Arvio pinta-alan suuruudesta on sitä tarkempi mitä pienempiin osa väleihin väli \([a,b]\) jaetaan.
Välisumman määritelmä
Olkoon funktio \(f:[a,b]\rightarrow\R\). Väli \([a,b]\) jaetaan \(n\):ään yhtä pitkään osaväliin. Nyt jokaisen osavälin pituus on \(\Delta x=\dfrac{b-a}{n}\).
Välisumma on summa \[\begin{align*} S_{f}(x_{1},x_{2},x_{3},...x_{n})&=\sum^{n}_{i=1}f(x_{i})\Delta x\\&=f(x_{1})\Delta x+f(x_{2})\Delta x+f(x_{3})\Delta x+...+f(x_{n})\Delta x \end{align*}\] Pisteet \(x_{1},x_{2},x_{3},...x_{n}\) on valittu kultakin osaväliltä.
Arvioidaan funktion \(f(x)=\ln x\) kuvaajan ja suorien \(y=0\) ja \(x=2\) rajaaman äärellisen alueen alaa käyttämällä jakoa \(n=4\) vastaavaa välisummaa, jossa funktion arvo lasketaan osavälin keskipisteessä.
Piirretään tilanteesta kuva.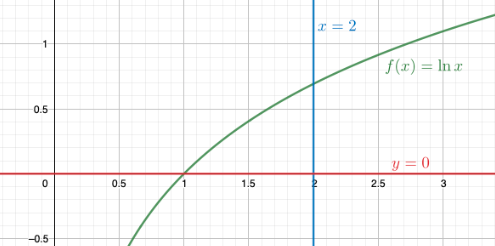 
Jaetaan väli \([1,2]\) neljään osaväliin. Yhden osavälin pituus on tällöin \(\Delta x=\frac{b-a}{n}=\frac{2-1}{4}=\frac{1}{4}\). Osavälit ovat siis \([1,1\frac{1}{4}]\), \([1\frac{1}{4},1\frac{1}{2}]\), \([1,\frac{1}{2},1\frac{3}{4}]\) ja \([1\frac{3}{4},2]\).
Osavälien keskipisteet ovat \(1\frac{1}{8}\), \(1\frac{3}{8}\), \(1\frac{5}{8}\) ja \(1\frac{7}{8}\).
Piirretään nyt kuvaan neljä pylvästä.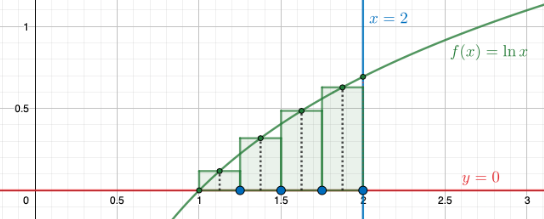 
Nyt arvio pinta-alasta saadaan laskemalla nämä neljän pylvään pinta-alat yhteen.
\[\begin{align*} &S_f\left(1\frac{1}{8}, 1\frac{3}{8}, 1\frac{5}{8}, 1\frac{7}{8}\right)\\ &=f\left(1\frac{1}{8}\right)\cdot\frac{1}{4}+f\left(1\frac{3}{8}\right)\cdot\frac{1}{4}+f\left(1\frac{5}{8}\right)\cdot\frac{1}{4}+f\left(1\frac{7}{8}\right)\cdot\frac{1}{4}\\ &=\ln \left(1\frac{1}{8}\right)\cdot\frac{1}{4}+\ln \left(1\frac{3}{8}\right)\cdot\frac{1}{4}+\ln \left(1\frac{5}{8}\right)\cdot\frac{1}{4}+\ln\left( 1\frac{7}{8}\right)\cdot\frac{1}{4}\\ &≈0,388 \end{align*}\]
Vastaus: Arvio pinta-alalle on \(0,388\).
Mitä useampaan osaväliin väli \([a,b]\) jaetaan, sitä tarkemmaksi pinta-alan arvio muuttuu. Edelleen siis, kun osavälien lukumäärä \(n\) lähestyy ääretöntä \(\infty\), niin päädytään puhumaan määrätystä integraalista yli välin \([a,b]\).
Määrätty integraali
Jos funktio \(f\) on määritelty suljetulla välillä \([a,b]\) ja jos välisumman raja-arvo \[\begin{align*} \lim_{n\to\infty}S_{f}(x_{1},x_{2},...,x_{n})=\lim_{n\to\infty}\sum_{i=1}^{n}f(x_{i})\Delta x \end{align*}\] on olemassa riippumatta siitä mistä välisummat valittiin, niin funktio \(f\) on integroituva välillä \([a,b]\).
Kyseinen raja-arvo \[\begin{align*} \lim_{n\to\infty}\sum_{i=1}^{n}f(x_{i})\Delta x \end{align*}\] on tällöin funktion \(f\) määrätty integraali kohdasta \(a\) kohtaan \(b\). Tätä merkitään \[\begin{align*} \int_{a}^{b}f(x)dx. \end{align*}\] Siis: \[\begin{align*} \int_{a}^{b}f(x)dx=\lim_{n\to\infty}\sum_{i=1}^{n}f(x_{i})\Delta x. \end{align*}\]
Ylläolevassa määritelmässä integraalimerkinnässä olevaa lukua \(a\) kutsutaan alarajaksi ja vastaavasti lukua \(b\) ylärajaksi.
2.2 Integroimissääntöjä
Määrättyyn integraaliin liittyviä sääntöjä
\(\displaystyle\int_{a}^b(f(x)+g(x))dx=\int_{a}^{b}f(x)dx+\int_{a}^{b}g(x)dx\)
\(\displaystyle\int_{a}^{b}kf(x)dx=k\int_{a}^{b}f(x)\), kun \(k\) on vakio.
\(\displaystyle\int_{a}^{b}f(x)dx=\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx\)
\(\displaystyle\int_{a}^{a}f(x)dx=0\)
\(\displaystyle\int_{a}^{b}f(x)dx=-\int_{b}^{a}f(x)dx\)
Lasketaan määrätty integraali \(\displaystyle\int_{-2}^{4}(|x|-2)\;dx\).
Piirretään funktion \(f(x)=|x|-2\) kuvaaja ja merkitään siihen määrätyn integraalin ylä- ja alarajat.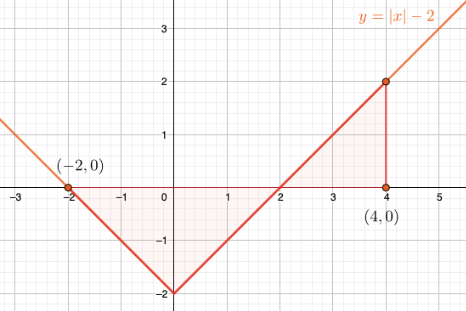 
Huomataan, että \(f(x)<0\) välillä \([-2,2]\), ja \(f(x)>0\) välillä \([2,4]\).
Lasketaan määrättyintegraali osissa.
\(x\)-akselin alapuolelle jäävä osuus: \[\begin{align*} &\displaystyle\int_{-2}^{2}(|x|-2)dx\\ &=\left[\frac{x\cdot|x|}{2}-2x\right]_{-2}^{2}\\ &=\left[\frac{2\cdot|2|}{2}-2\cdot2\right]-\left[\frac{(-2)\cdot|-2|}{2}-2\cdot({-2})\right]\\ &=-2-2\\ &=-4 \end{align*}\]
\(x\)-askelin yläpuolelle jäävä osuus: \[\begin{align*} &\displaystyle\int_{2}^{4}(|x|-2)dx\\ &=\left[\frac{x\cdot|x|}{2}-2x\right]_{2}^{4}\\ &=\left[\frac{4\cdot|4|}{2}-2\cdot4\right]-\left[\frac{2\cdot|2|}{2}-2\cdot{2}\right]\\ &=0-(-2)\\ &=2\\ \end{align*}\]
Ja nyt koska pinta-ala koostuu kahdesta osasta, lasketaan määrätyt integraalit yhteen: \[\begin{align*} -4+2=-2 \end{align*}\]
Vastaus: Määrättyintegraali \(\displaystyle\int_{-2}^{4}(|x|-2)\;dx=-2\)
Analyysin peruslause
Jatkuvan funktion integraalifunktio voidaan määrittää välisumman raja-arvon avulla, mutta se on joskus työläs prosessi. Yleisesti käytetään apuna analyysin peruslausetta, joka yhdistää toisiinsa määrätyn integraalin ja integraalifunktion.
\[\begin{align*} \int_{a}^{b}f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a), \end{align*}\] jossa \(F\) on funktion \(f\) integraalifunktio.
Huom. Hakasulkeet voidaan korvata myös sijoitusviivalla.
2.3 Pinta-ala
2.3.1 Käyrän ja x-akselin rajaama alue
Pinta-ala saadaan laskemalla yhteen sellaisten suorakulmioiden alat, joiden leveys on \(dx\) ja korkeus \(f(x)\). Tällaista yhtä suorakulmiota kutsutaan pinta-alkioksi, joten koko pinta-ala voidaan laskea vain summaamalla nämä pinta-alkiot yhteen.
Yhden pinta-alkion pinta-ala on \[\begin{align*} dA=f(x)dx\;\;\;\;\;\;\;|\text{vrt. kanta}\cdot\text{ korkeus.} \end{align*}\] Tällöin koko alueen pinta-ala on \[\begin{align*} A=\int_{a}^{b}dA=\int_{a}^{b}f(x)dx. \end{align*}\]
Vastaavasti, jos käyrä ja y-akseli rajoittavat pinta-alan, integrointi voidaan tällöin suorittaa muuttujan \(y\) suhteen: \[\begin{align*} A=\int_{a}^{b}dA=\int_{a}^{b}x\;dy \end{align*}\]
2.3.2 Kahden käyrän rajaama pinta-ala
Olkoot \(f\) ja \(g\) jatkuvia funktioita. Näillä funktioilla on kuvaajat \(y_{1}=f(x)\) ja \(y_{2}=g(x)\). Olkoot lisäksi x-akselilla pisteet \(a\) ja \(b\), joiden kautta kulkevat suorat \(x=a\) ja \(x=b\).
Nyt käyrät sekä suorat rajaavat pinta-alan, jonka suuruus on \[\begin{align*} A=\int_{a}^{b}dA=\int_{a}^{b}|y_{1}-y_{2}|dx=\int_{a}^{b}|f(x)-g(x)|dx. \end{align*}\]
Vastaavasti, jos pinta-alan rajaavat käyrät sekä suorat \(y=a\) ja \(y=b\): \[\begin{align*} A=\int_{a}^{b}dA=\int_{a}^{b}(x_{1}-x_{2})dy \end{align*}\]
Käyrä \(y=\cos x\) ja sille pisteiden \(x=0\) ja \(x=\frac{\pi}{2}\) kautta piirretty jänne rajaavat alueen. Lasketaan muodostuneen alan pinta-ala.
Piirretään tilanteesta kuva: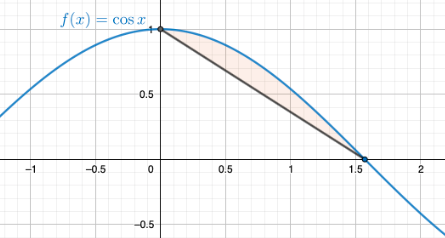 
Pisteiden kautta kulkevan suoran suoran yhtälö on muotoa \(y-y_0=k(x-x_0)\), eli \(y-1=-\frac{2}{\pi}x\), josta saadaan edelleen \(y=-\frac{2}{\pi}x+1\).
Leikkauspisteet ovat \((0,1)\) ja \((\frac{\pi}{2},0)\).
Pinta-ala saadaan laskemalla määrätty integraali \[\begin{align*} A&=\displaystyle\int_0^{\frac{\pi}{2}}\left[(\cos x)-(-\frac{2}{\pi}x+1)\right]dx\\ &=\displaystyle\int_0^{\frac{\pi}{2}}\left[\cos x+\frac{2}{\pi}x-1\right]dx\\ &=\left[\sin x+\frac{x^{2}}{\pi}-x\right]_{0}^{\frac{\pi}{2}}\\ &=\left[\sin (\frac{\pi}{2})+\frac{(\frac{\pi}{2})^{2}}{\pi}-(\frac{\pi}{2})\right]-\left[\sin 0+\frac{0^{2}}{\pi}-0\right]\\ &=1+\frac{\pi}{4}-\frac{\pi}{2}-0\\ &=1-\frac{\pi}{4}\\ &≈0,215 \end{align*}\]
Funktion ja jänteen rajaaman alueen pinta-ala on \(0,215\).
2.4 Tilavuus
Kun jatkuva funktio \(f\) pyörähtää x-akselin tai y-akselin ympäri, syntyy avaruuden pinta. Jos tämä pinta katkaistaan kahden suoran avulla, syntyy avaruuskappale, jolla on tilavuus.
Kappale muodostuu tällöin ohuista ympyrälieriöistä, jotka ovat tilavuusalkioita. Tällaisen tilavuusalkion paksuus on \(dx\) ja pohjan säde on \(r=|y|=f(x)\)
Pyörähdyskappalee tilavuus
Olkoon funktio \(f\) välillä \([a,b]\) jatkuva funktio ja sen kuvaaja on \(y=f(x)\). Kun tämä kuvaaja pyörähtää x-akselin ympäri, muodostuu avaruuden pinta. Tämä pinta rajoittuu kahteen tasoon \(x=a\)ja \(x=b\). Tämän syntyneen kappaleen tilavuus on \[\begin{align*} V=\int_{a}^{b}dV=\int_{a}^{b}\pi r^{2}dx=\int_{a}^{b}\pi y^{2}dx=\int_{a}^{b}\pi f(x)^{2}dx \end{align*}\]
Käyrät \(y=\sqrt{x+1}\), \(y=0\) ja \(x=3\) rajaavat alueen, joka pyörähtää suoran \(x=3\) ympäri. Lasketaan syntyvän pyörähdyskappaleen tilavuus.
Piirretään tilanteesta kuva: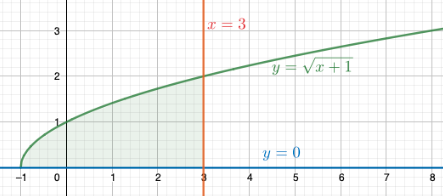 
Suoran \(x=3\) ja käyrän leikkauspiste: \[\begin{align*} y=\sqrt{3+1}=2 \end{align*}\] Leikkauspiste on \((3,2)\). Tilavuutta laskiessa käytetään \(y\)-arvoja määrätyn integraalin ylä- ja alarajoina.
Tilavuus voidaan nyt ajatella eri kokoisina kiekkoina, jotka ovat leveimmillään \(x\)-tason suuntaisena ja kapeimmillaan lähestyessä \(y\)-akselin arvoa \(2\).
Koska lasketaan \(y\)-akselin suuntaista määrättyä integraalia, tilavuus lasketaan määrätyllä integraalilla, joka on muotoa \(\displaystyle\int_{0}^{2}\pi\cdot r^{2}\;dy\).
Määrättyynintegraaliin vaadittu säde \(r\) saadaan kiekon säteestä. Tässä tilanteessa \(r=3-x\).
Määrättyintegraali on nyt muotoa \(\displaystyle\int_{0}^{2}\pi\cdot (3-x)^{2}\;dy\). Tässä muodossa on on vielä muokattavaa, koska integroitavassa funktiossa on muuttujana \(x\), mutta integraali on \(y\):n suhteen.
Hyödynnetään nyt tietoa käyrästä \(y=\sqrt{x+1}\). Tästä voidaan ratkaista \(x\): \[\begin{align*} y&=\sqrt{x+1}\;\;\;\;\;\;\;|(x+1)\geq0\text{ joten korotetaan puolittain toiseen potenssiin }\\ y^{2}&=(\sqrt{x+1})^{2}\\ y^{2}&=x+1\\ x&=y^{2}-1 \end{align*}\]
Nyt määrätty integraali saadaan muotoon \(\displaystyle\int_{0}^{2}\pi\cdot (3-(y^{2}-1))^{2}\;dy\). Lasketaan nyt määrättyintegraali.
\[\begin{align*} &\displaystyle\int_{0}^{2}\pi\cdot (3-(y^{2}-1))^{2}\;dy\\ &=\int_{0}^{2}\pi\cdot (-y^{2}+4)^{2}\;dy\\ &=\pi\cdot\int_{0}^{2} (-y^{2}+4)^{2}\;dy\\ &=\pi\cdot\left[\frac{y^{5}}{5}-\frac{8y^{3}}{3}+16y\right]_{0}^{2}\\ &=\pi\cdot\left[\left(\frac{2^{5}}{5}-\frac{8\cdot2^{3}}{3}+16\cdot2\right)-\left(\frac{0^{5}}{5}-\frac{8\cdot0^{3}}{3}+16\cdot0\right)\right]\\ &=\frac{256\cdot\pi}{15}\\ &≈53,6 \end{align*}\]
Vastaus: Pinta-ala on noin \(53,6\).
Tehtäviä
Tehtävä 1.
Tehtävä 2.
Tehtävä 3.
Määritä \(\int_{0}^{3}|2h-2|dh\)
a.
hyödyntäen geometrista pinta-alatulkintaa
b.
hyödyntämällä integrointia
Tehtävä 4.
Eräs planeetta kiertää aurinkoa hetkellisesti paraabelin \(y=x^{2}+3x-2\) muotoisella radalla. Sen kiertoradan leikkaa suurella nopeudella kiitävä komeetta, joka kulkee suoran \(y=2x\) suuntaisesti.
Laske pinta-ala, joka muodostuu komeetan lentäessä planeetan kiertoradan läpi.
Tehtävä 5.
Lumileopardi on luokiteltu uhanalaisluokituksessa vaaraantuneeksi, ja niitä elää arviolta 4000-6400 yksilöä. Lumileopardit elelevät karuissa olosuhteissa jopa 5400 metrin korkeudessa. Näitä kissaeläimiä voi havaita muun muassa Kiinassa, Intiassa, Venäjällä ja Mongoliassa. (Lähde:WWF).
Lumileopardien yksilöiden lukumäärää tutkittiin 10 vuoden ajan. Yksilöiden lukumäärä noudatti funktiota \(f(x)=21t^{3}+3t+9\), missä \(t\) on aika vuosina.
a.
Laske lumileopardien lukumäärän keskiarvo 10 vuoden aikana
Funktion \(f\) keskiarvo välillä \([a,b]\) on \[\begin{align*} \dfrac{1}{a-b}\int_{a}^{b}f(x)dx. \end{align*}\]
b.
Lumileopardin reviiri kartalla on ympyrän \((x-2)^{2}+(y-2)^{2}=2\) muotoinen. Reviirin läpi kulkee joki, joka on suoran \(y=1\) suuntainen. Kuinka suuri on muodostuneen sektorin pinta-ala? Kartta on mittakaavassa 1:500.
Tehtävä 6.
Shirehevoset voivat kasvaa säkäkorkeudeltaan nopa 200 cm korkeiksi ja kyseinen hevosrotu onkin maailman suurin hevosrotu. Suomen suurin hevonen on säkäkorkeudeltaan 190 cm ja painaa yli 1300 kiloa. (Lähde:Yle.fi)
Varsan kasvamista täysikokoiseksi kuvaa funktio \(f(t)=40e^{-0,2t}\), jossa \(t\) kuvaa kulunutta aikaa kuukausina.
a.
Piirrä funktion kuvaaja välillä \([0,6]\).
b.
Laske kuvaajan ja \(t\)-akselin väliin jäävän pinta-ala välillä \([0,6]\).
c.
Mitä pinta-ala ilmaisee?
Tehtävä 7.
Sepelvaltimotaudin eräs oire on valtimon tukkeutuminen. Valtimo voidaan avata asettamalla valtimoon pallokatetri, joka laajennetaan ahtauman kohdalla palauttaen veren virtauksen. Samaan aikaan ahtaumakohtaan asennetaan metallinen tukiverkko, eli stentti, joka estää suonta ahtautumasta uudelleen. Sepelvaltimotaudin syntyä voi ehkäistä terveellisillä elämäntavoilla. (Lähde:Sydän.fi)
Stentti on ympyrälieriön muotoinen, ja sen halkaisja on 2,8-3,0 mm ja pituus 15-16 mm.
a.
Hahmottele stentti GeoGebralla
b.
Mikä on Stentin tilavuus, jos sen halkaisija on 3,0 mm ja pituus 15 mm?
c.
Suora \(y=\frac{3}{2}\) pyrähtää x-akselin ympäri välillä \([0,15]\). Laske pyörähdyskappaleen tilavuus hyödyntäen määrättyä integraalia.
Tehtävä 8.
a.
Käyrä \(y=\frac{3x}{x^{2}}+\frac{1}{2}\) pyörähtää y-akselin ympäri välillä \([1,6]\). Laske syntyneen pörähdyskappaleen tilavuus.
b.
Käyrä \(y=\cos x\) pyörähtää x-akselin ympäri välillä \([-\frac{\pi}{2},\frac{\pi}{2}]\). Laske syntyneen pyörähdyskappaleen tilavuus.
c.
Maljakko on muodoltaan pyörähdyskappale, joka muodostuu suorien \(y=-5\) ja \(y=5\), paraabelin \(x=2+y^{2}\) sekä y-akselin rajoittaman alueen pyörähtäessä x-akselin ympäri. Maljakon pohjan halkaisija on 10cm. Kuinka paljon maljakko painaa, jos lasin tiheys on \(3600 \frac{kg}{m^{3}}\)?
Vanhoja YO-tehtäviä
1.
Millä vakion \(a\) arvolla suorien \(x=a\), \(x=a+2\) ja \(y=0\) sekä käyrän \(y=(x^{2}+x+1)^{-1}\) rajoittaman alueen pinta-ala on suurin? [S01/11]
VASTAUS: \(a=-\dfrac{3}{2}\)
RATKAISU:
Pinta-ala on \(A(a)=\int_{a}^{a+2}(x^{2}+x+1)^{-1}dx=F(a+2)-F(a)\), missä \(F(x)\) on funktion \((x^{2}+x+1)^{-1}\) integraalifunktio.
Pinta-alan derivaatta on
\(A'(a)=F'(a+2)-F'(a)=((a+2)^{2}+(a+2)+1)^{-1}-(a^{2}+a+1)^{-1}\\=-(4a+6)(a^{2}+5a+7)^{-1}(a^{2}+a+1)^{-1}.\)
Edelleen \(A'(a)=0\), kun \(a=-\dfrac{3}{2}\).
Ja \(A'(a)>0\), kun \(a<-\dfrac{3}{2}\) ja \(A'(a)<0\), kun \(a>-\dfrac{3}{2}\).
Suurin pinta-ala saavutetaan siis kun \(a=-\dfrac{3}{2}\).
2.
Suorat \(y=\dfrac{1}{2}x\) ja \(y=2x\) sekä hyperbeli \(xy=1\) rajaavat kaksiosaisen alueen. Laske sen ala. Ilmoita tarkka arvo ja kaksidesimaalinen likiarvo. [S05/12]
VASTAUS: \(A=2\ln2≈1,3863\).
RATKAISU:
Alueen ensimmäisessä ja kolmannessa koordinaattineljänneksessä olevat osat ovat symmetrisetn, joten riittää määrätä ensimmäisessä neljänneksessä oleva ala.
Suorat \(y=2x\) ja \(y=\dfrac{1}{2}x\) kulkevat origon \(O\) kautta ja leikkaavat hyperbeliä \(xy=1\) pisteissä \(A=(\dfrac{1}{\sqrt{2}},\sqrt{2})\) ja \(B=(\sqrt{2},\dfrac{1}{\sqrt{2}})\).
Nyt ensimmäisessä neljänneksessä oleva ala on \[\begin{align*} \int_{0}^{\frac{1}{\sqrt{2}}}(2x-\frac{1}{2}x)dx+\int_{\frac{1}{\sqrt{2}}}^{\sqrt{2}}(\frac{1}{x}-\frac{1}{2}x)dx\\=\frac{3}{8}+2\ln\sqrt{2}-\frac{3}{8}=\ln 2. \end{align*}\]Nyt kysytty ala on \(2\ln2≈1,3863\)
3.
Käyrän \(y=\ln x\) välillä \(1≤x≤e\) oleva osa pyörähtää x-akselin ympäri. Määritä muodostuneen kappaleen tilavuus. [S03/13]
VASTAUS: Tilavuus on \(\pi(e-2)\)
RATKAISU:
Tilavuus \(V=\pi\int_{1}^{e}(\ln x)^{2}dx\).
Nyt osittaisintegroinnilla \(V=\pi(e-2e+2(e-1))=\pi(e-2).\)
Tilavuus on \(\pi(e-2)\).
4.
Nykytaiteen museorakennuksen pohja on ympyrä, jonka halkaisija on 19,7 metriä. Jos rakennus leikataan pohjaympyrän tietyn halkaisijan suuntaisella pystysuoralla tasolla, leikkauskuvio on aina suorakulmio, jonka korkeus on puolet kannasta. Määritä rakennuksen tilavuus. [S02/12]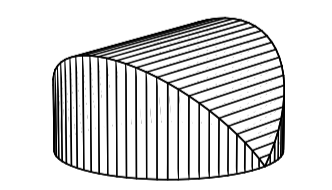 
VASTAUS: \(2550 m^{3}\)
RATKAISU:
Olkoon \(O\) pohjaympyrän keskipiste, \(AB\) pystysuoran tason ja pohjaympyrän leikkaus sekä \(C\) janan \(AB\) keskipiste.
Olkoon \(r\) pohjaympyrän säde ja \(x=CO\) sekä \(d_{x}=\sqrt{r^{2}-x^{2}}, 0≤x≤r\).
Tällöin edellä mainitun tason ja rakennuksen leikkauskuvion ala on \(A_{x}=2d_{x}d_{x}=2(r^{2}-x^{2}).\)
Rakennuksen tilavuus on \(V=2\int_{0}^{r}A_{x}dx=4\int_{0}^{r}r^{2}-x^{2}dx=\frac{8}{3}r^{3}.\)
Kun \(2r=19,7 m\), niin tilavuus \(V=2548,46 m^{3}\).
5.
Näytä, että molemmat funktiot \[\begin{align*} F_{1}(x)=\dfrac{1}{1-x}\text{ ja }F_{2}(x)=\dfrac{x}{1-x} \end{align*}\] ovat funktion \(f(x)=\dfrac{1}{(1-x)^{2}}\) integraalifunktioita, kun \(x>1\).
Sievennä erotus \(F_{1}(x)-F_{2}(x)\).
Laske funktion \(f(x)\) kuvaajan ja x-akselin rajoittaman alueen pinta-ala, kun \(2 \leq x \leq 5\).[S11/4]
VASTAUS: b. 1 c.\(\frac{3}{4}\)
RATKAISU:
a.
Kun \(x>1\), niin \(F_{1}'(x)=\dfrac{1}{(1-x)^{2}}=f(x)\)
ja \(F-{2}'(x)=\dfrac{1-x+x}{(1-x)^{2}}=\dfrac{1}{(1-x)^{2}}=f(x)\).
Näin ollen molemmat ovat funktion \(f(x)\) integraalifunktioita.
b.
\[\begin{align*} F_{1}(x)-F_{2}(x)=\dfrac{1-x}{1-x}=1. \end{align*}\]
c.
Pinta-ala on \[\begin{align*} \int_{2}^{5}\dfrac{1}{(1-x)^{2}}dx=-\frac{1}{4}+1=\frac{3}{4}. \end{align*}\]
6.
Olkoon \(f(x)\) funktio, joka on määritelty välillä \(0≤x≤12\). Alla on esitetty funktion \[\begin{align*} F(x)=\int_{0}^{x}f(t)dt \end{align*}\] kuvaaja välillä \(0\leq x\leq 12\). Arvioi kujaavan perusteella
Määrättyä integraalia \(\int_{1}^{4}f(t)dt\)
Millä väleillä funktio \(f(x)\) on vakio
Millä väleillä funktio \(f(x)\) on aidosti vähenevä. [S17/13]
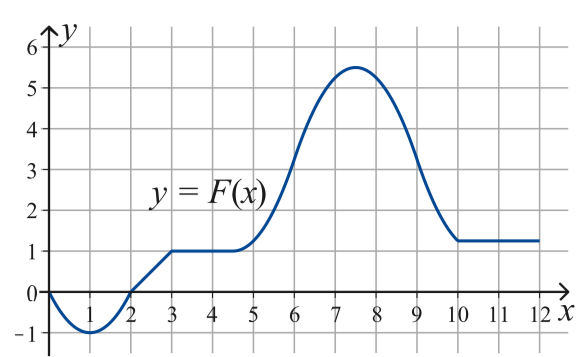
VASTAUS: a. 2, b. väleillä \([2,3], [3;4,5], [10,12]\), c. n.\([6,2;8,8]\)
RATKAISU:
a.
\(\displaystyle\int_{1}^{4}f(t)\;dt=F(4)-F(1)=2\)
b.
\(f\) on vakio, kun integraalifunktio on suora, eli väleillä \([2,3]\), \([3;4,5]\) ja \([10,12]\).
c.
\(f\) on aidosti vähenevä, kun \(F\):n kuvaajan tangentin kulmakerroin vähenee, eli käyrä on ylöspäin kupera. Tämä on noin välillä \([6,2;8,8]\).
7.
Laske integraalit
\(\displaystyle\int_{-1}^{1}\frac{1}{3+x}dx\)
\(\displaystyle\int_{-1}^{1}e^{2|x|}dx\) [S18/3]
VASTAUS: a. \(\ln2\) b.\(e^{2}-1\)
RATKAISU:
a.
\[\begin{align*} \displaystyle\int_{-1}^{1}\frac{dx}{3+x}=\left[\ln(3+x)\right]_{-1}^{1}=\ln4-\ln2=\ln\frac{4}{2}=\ln2 \end{align*}\]
b. \[\begin{align*} \displaystyle\int_{-1}^{1}e^{2|x|}dx=\int_{-1}^{0}e^{-2x}dx+\int_{0}^{1}e^{2x}dx=-\frac{1}{2}\left[e^{-2x}\right]_{-1}^{0}+\frac{1}{2}\left[e^{2x}\right]_{0}^{1}=e^{2}-1 \end{align*}\]
8.
Anna esimerkki rationaalifunktiosta \(f(x)\), jolle epäyhtälö \(f(x)\geq2\) toteutuu täsmälleen silloin, kun \(-1\leq x\leq0\) tai \(1\leq x\leq2\).
Anna esimerkki funktiosta \(g(x)\geq0\), joka on määritelty kaikilla reaaliluvuilla ja jonka derivaatalla on täsmälleen kaksi nollakohtaa. [K18/11]
RATKAISU:
a.
Eräs esimerkki.
Valitaan sellainen polynomi, jonka nollakohdat ovat määrittelyalueen yhtäsuuruuskohdat, eli \(-1,0,1\) ja \(2\). Polynomi voi nyt olla esimerkiksi \(x(x+1)(x-1)(x-2).\)
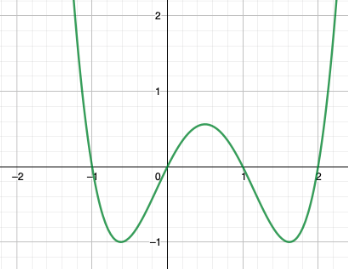
Käännetään funktio nyt "ylösalaisin" kertomalla funktio \(-1\):llä. Polynomi on nyt siis \(-x(x+1)(x-1)(x-2).\)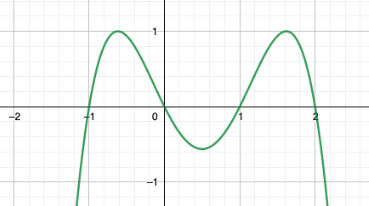 
Koitetaan nyt siirtää tätä M:n muotoista funktiota korkeammalle \(y\)-akselin suhteen, jotta epäyhtälö \(h(x)\geq2\) toteutuu. Funktion kuvaaja saadaan korkeammalle \(y\)-akselilla, kun polynomiin lisätään \(2\): Polynomi on nyt \(2-x(x+1)(x-1)(x-2)\).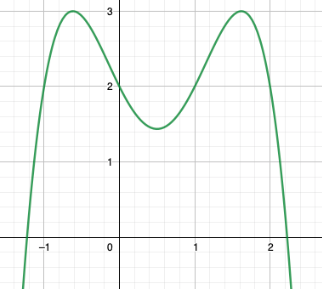 
Nyt kyseisen polynomifunktion kuvaaja on suurempaa kuin \(2\) väleillä \([-1,0]\) ja \([1,2]\).
b.
Tässä voidaan etsiä polynomia, jolla on minimi sekä terassikohta.
Derivaattafunktion kuvaaja voisi olla vaikka tälläinen: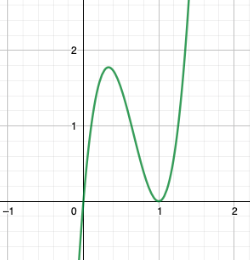 
Tällä derivaattafunktiolla \(g'(x)=12x(x-1)^{2}\) on kaksi nollakohtaa. Itse kysytty funktio saadaan nyt integroimalla tämä funktio \(f'\).
\[\begin{align*} \displaystyle\int g'(x)\;dx=\int 12x(x-1)^{2}\;dx=\int 12x(x^{2}-2x+1)\;dx&=\int 12x^{3}-24x^{2}+12x \;dx\\&=3x^{4}-8x^{3}+6x^{2} \end{align*}\]
Kysytty funktio on siis \(g(x)=3x^{4}-8x^{3}+6x^{2}\).
9.
Olkoon \(a>0\). Määritellään \(a\)-kantainen logaritmi funktion \(f(x)=a^{x}\) käänteisfunktiona, toisin sanoen \(\log_{a}x=f^{-1}(x)\). Kiinnitetään \(x>1\) ja määritellään \(g(a)=\log_{a}x\). Osoita, että funktio \(g(a)\) on vähenevä.
Olkoon \(h(t)\) jatkuva funktio. Osoita että \[\begin{align*} H(x)=\displaystyle\int_{0}^{x}h(t)\;dt \end{align*}\] on kasvava täsmälleen silloin, kun \(h\geq0\) kaikilla \(t\in\R\). [K18/12]
RATKAISU:
a.
Funktio ei ole vähenevä koko määrittelyjoukossa: esimerkiksi \(g(\frac{1}{2})=\log_{\frac{1}{2}}x=\frac{\ln x}{\ln(\frac{1}{2})}=-\frac{\ln x}{\ln 2}=-g(2)<g(2),\) sillä \(g(2)>0\).
b.
Olkoon \(x<y\). Nyt \(H(y)-H(x)=\displaystyle\int_{x}^{y}h(t)dt\).
Jos \(h\geq0\), tästä seuraa että \(H(y)-H(x)\geq0\), eli siis \(H\) on kasvava.
Jos \(h<0\), jollain välillä \([a,b]\), niin \(H(b)-H(a)=\displaystyle\int_{a}^{b}h(t)dt<0\), joten \(H\) ei ole kasvava.
10.
Tarkastellaan funktiota \[\begin{align*} f(x)=\displaystyle\int_{0}^{x}|\sin t|\;dt. \end{align*}\] kun \(0\leq x\leq 2\pi\).
- Perustele geometrisesti kaava \(f(2\pi)=2f(\pi)\).
- Laske \(f(x)\), kun \(0\leq x \leq 2\pi\). [K16/12]
VASTAUS: b. \(f(x)=\begin{cases}1-\cos x,\;0\leq x\leq\pi\\3+\cos x,\; \pi\leq x\leq2\pi\end{cases}\)
RATKAISU:
a.
Sinifunktion kuvaajan perusteella havaitaan, että \[\begin{align*} \displaystyle\int_{0}^{x}\sin t\;dt=-\int_{\pi}^{2\pi}\sin t\;dt. \end{align*}\]
Tällöin \(f(\pi)=\displaystyle\int_{0}^{\pi}|\sin t|dt=\int_{\pi}^{2\pi}|\sin t|dt.\)
Edelleen \(f(2\pi)=\displaystyle\int_{0}^{\pi}|\sin t|dt+\int_{\pi}^{2\pi}|\sin t|dt=2\cdot\int_{0}^{\pi}|\sin t|dt=2f(\pi)\).
b.
Kun \(0\leq t\leq\pi\), niin \(|\sin t|=\sin t\).
Nyt siis \(\displaystyle\int_{0}^{x}|\sin t|dt=\int_{0}^{x}\sin t\;dt=[(-\cos t)]_{0}^{x}=-\cos x+\cos0=1-\cos x\), kun \(0\leq x\leq\pi\).
Kun \(\pi\leq t\leq2\pi\), niin \(|\sin t|=-\sin t\).
Nyt siis \[\begin{align*} \displaystyle\int_{0}^{x}|\sin t|dt&=\displaystyle\int_{0}^{\pi}\sin t\;dt+\displaystyle\int_{\pi}^{x}(-\sin t)dt\\ =&[(-\cos t)]_{0}^{\pi}+[\cos t]_{\pi}^{x}\\=&-\cos\pi+\cos0+\cos x-\cos\pi\\=&3+\cos x,\text{ kun }x\leq2\pi \end{align*}\]
Muotoillaan vielä vastaukseksi, eli \(f(x)=\begin{cases}1-\cos x,\;0\leq x\leq\pi\\3+\cos x,\; \pi\leq x\leq2\pi\end{cases}\).
Lisätehtäviä verkossa
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.