MAA9 Talousmatematiikka
Kurssin tavoitteena on, että opiskelija
- oppii hyödyntämään matemaattisia valmiuksiaan resurssien riittävyyteen, talouden suunnit- teluun, yrittäjyyteen ja kannattavuuden laskentaan
- soveltaa lukujonojen kaavoja talouteen liittyvissä matemaattisissa ongelmissa
- oppii sovittamaan taloudellisiin tilanteisiin matemaattisia malleja ja ymmärtää niiden rajoitukset
Keskeiset sisällöt
- aritmeettinen ja geometrinen lukujono ja niiden summat
- korkolaskut: koronkorko, talletukset ja lainat
- taloudellisiin tilanteisiin soveltuvia matemaattisia malleja, joissa hyödynnetään lukujonoja ja summia
Talousmatematiikassa prosentit ovat tärkeää osata. Kertaa prosentit täältä!
1. Lukujonot ja summat
Kun reaaliluvut järjestellään luetteloksi, syntyy lukujono. Lukujonossa peräkkäiset jäsenet liittyvät toisiinsa jollain säännöllä. Tällä säännöllä voidaan edelleen päätellä kuinka lukujono jatkuisi. Esimerkiksi lukujonosta \((2,4,6,..)\) voidaan nopeasti poimia sääntö vain tarkastelemalla lukujonon ensimmäisiä termejä.
Jos lukujonossa olevat jäsenet lasketaan sen järjestysnumeron \(n\) mukaan, lukujonon sääntö on analyyttinen. Toisaalta, jos jäsenen laskeminen vaatii tiedon aiemmista lukujonon jäsenistä, lukujonon sääntö on rekursiivinen.
Jos lukujonon analyyttinen sääntö on \(a_{n}=n^{2}+3\), ja \(n=1,2,3...\), niin säännön perusteella osataan luoda lukujono.
Ensimmäinen jäsen \(a_1\): \[\begin{align*} a_{1}=1^{2}+3=4 \end{align*}\]
Toinen jäsen \(a_2\): \[\begin{align*} a_{2}=2^{2}+3=7 \end{align*}\]
Kolmas jäsen \(a_3\): \[\begin{align*} a_{3}=3^{2}+3=12 \end{align*}\]
Tällöin lukujono on \((4,7,12,...)\). Jos lukujonon ensimmäinen jäsen \(a_1=5\) ja sääntö on \(a_{n}=2a_{n-1}-2\), kun \(n=2,3,4...\). Tämä kaksiosainen sääntö on rekursiivinen ja sen avulla voidaan luoda lukujono.
Ensimmäinen jäsen \(a_1=5\).
Toinen jäsen \(a_2\): \[\begin{align*} a_{2}=2\cdot a_{2-1}-2=2\cdot a_{1}-2=2\cdot5-2=8 \end{align*}\]
Kolmas jäsen \(a_3\): \[\begin{align*} a_{3}=2\cdot a_{3-1}-2=2\cdot a_{2}-2=2\cdot8-2=14 \end{align*}\]
Tällöin lukujono on \((5,8,14,...)\)
1.1 Aritmeettinen lukujono
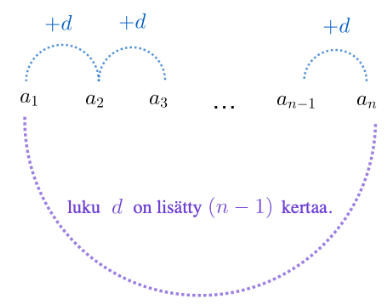
Lukujono on aritmeettinen, jos lukujonon peräkkäisten jäsenten välinen erotus on vakio. Toisin sanoen lukujonon seuraava jäsen saadaan aina lisäämällä edelliseen jäseneen jonkin luvun.
Aritmeettinen lukujono
Jos lukujonon peräkkäisten jäsenten erotus \(a_{n+1}-a_n\) on vakio \(d\), niin lukujono \((a_{n})\) on aritmeettinen.
Aritmeettisen lukujonon \(n\):s jäsen on \(a_n=a_1+(n-1)\cdot d\).
Vakiota \(d\) kutsutaan erotusluvuksi.
1.2 Aritmeettinen summa
Summalla tarkoitetaan lukujen yhteenlaskua. Aritmeettisessa summassa kyse on lukujonon jäsenten laskemisesta yhteen.
Aritmeettinen summa
Olkoon lukujono \((a_n)\) aritmeettinen. Tällöin summa \[\begin{align*} S_{n}=a_1+a_2+a_3+...+a_n=\sum_{i=1}^{n}a_i \end{align*}\] on aritmeettinen summa.
Summa voidaan laskea kaavalla \[\begin{align*} S_n=n\cdot\dfrac{a_1+a_n}{2}, \end{align*}\]
jossa \(n\) on yhteenlaskettavien jäsenten lukuäärä, \(a_1\) on ensimmäinen yhteenlaskettava jäsen ja \(a_n\) on viimeinen yhteenlaskettava jäsen.
Lasketaan aritmeettinen summa \(5+9+13+17+...+81\).
Ratkaistaan ensin, montako yhteenlaskettavaa lukujonossa on. Määritetään lukujonon yleinen jäsen \(a_n\).
Koska kyseessä on aritmeettinen lukujono, niin kahden peräkkäisen jäsenen erotus on vakio \(d\).
\[\begin{align*} &d=9-5=4\\ &a_n=5+(n-1)\cdot4=4n-4+5=4n+1 \end{align*}\]
Lukujonon viimeinen yhteenlaskettava jäsen on \(a_n=81\), mutta myös \(a_n=4n+1\), niin saadaan ratkaistua n: \[\begin{align*} 4n+1=81\\ n=20 \end{align*}\]
Yhteenlaskettavia on siis yhteensä 20 kappaletta.
nyt voidaan hyödyntää aritmeettisen summan kaavaa: \[\begin{align*} S_n&=n\cdot\frac{a_1+a_n}{2}\\&=20\cdot\frac{5+81}{2}\\&=860 \end{align*}\]
Summa on siis 860.
1.3 Geometrinen lukujono
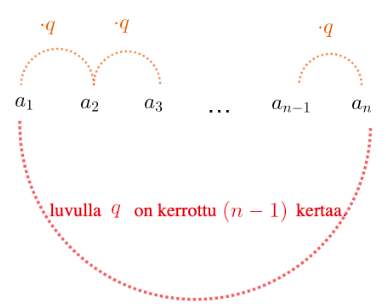
Lukujono on geometrinen, jos lukujonon jäsenet on saatu kertomalla edellinen jäsen jollain luvulla. Toisin sanoen lukujonon peräkkäisten jäsenten suhde on vakio.
Geometrinen lukujono
Jos lukujonon peräkkäisten jäsenten suhde \(\frac{a_{n+1}}{a_n}\) on vakio \(q\), niin lukujono on geometrinen.
Geometrisen lukujonon \(n\):s jäsen on \(a_n=a_1\cdot q^{n-1}\).
Vakiota \(q\) kutsutaan suhdeluvuksi.
1.4 Geometrinen summa
Geometrisessa summassa kaikki geometrisen lukujonon jäsenet lasketaan yhteen.
Geometrinen summa
Olkoon lukujono \((a_n)\) geometrinen. Tällöin summa \[\begin{align*} S_n=a_1+a_2+a_3+...+a_n=\sum_{i=1}^{n}a_i \end{align*}\] on geometrinen summa.
Summa voidaan laskea kaavalla \[\begin{align*} S_n=\dfrac{a_1\cdot(1-q^{n})}{1-q}, \end{align*}\] jossa \(q\) on suhdeluku, \(a_1\) on ensimmäinen yhteenlaskettava jäsen ja \(n\) on yhteenlaskettavien lukumäärä.
Lasketaan geometrinen summa lukujonolle \((2,10,50,...,2\cdot5^{11})\).
Kirjoitetaan lukujono yhtenevään muotoon: \((2\cdot5^0,2\cdot5^1,2\cdot5^2,...,2\cdot5^{11})\). Eksponenteista voidaan päätellä, että yhteenlaskettavia on yhteensä 12 kappaletta. Ensimmäinen yhteenlaskettava jäsen on \(2\), ja suhde \(q=5\).
Nyt voidaan hyödyntää geometrisen summan kaavaa \[\begin{align*} S_n&=\dfrac{a_1\cdot(1-q^n)}{1-q}\\&=\dfrac{2\cdot(1-5^{12})}{1-5}\\&=122070312 \end{align*}\]
Lukujonon geometrinen summa on \(122070312\).
2. Rahan arvo
2.1 Valuutat
Matkustaessa muihin valtioihin voi vastaan tulla ajankohtaiseksi valuutan vaihtaminen. Euro otettiin käyttöön kahdessatoista jäsenmaassa vuonna 2002, ja se on Euroopan unionissa käytetty valuutta. Jos matkustat esimerkiksi Yhdysvaltoihin, täytyy käytettävät eurot vaihtaa Yhdysvaltain dollareiksi.
Esimerkiksi kaupankäynnin kannalta valuuttoja tulee pystyä vaihtaa toisiksi valuutaksi mahdollisimman helposti. Valuuttakurssi ilmoittaa kahden valuutan välistä suhdetta.
Euroopan keskuspankki (EKP) ilmoittaa valuuttakurssit euroalueen ulkopuolella. Tätä kutsutaan epäsuoraksi noteeraukseksi. Vastaavasti suora noteeraus tarkoittaa ulkomaanvaluutan arvoa euroina. Heti kun Euroopan keskuspankki on julkaissut valuuttakurssit, Suomen Pankki julkaisee samat kurssit.
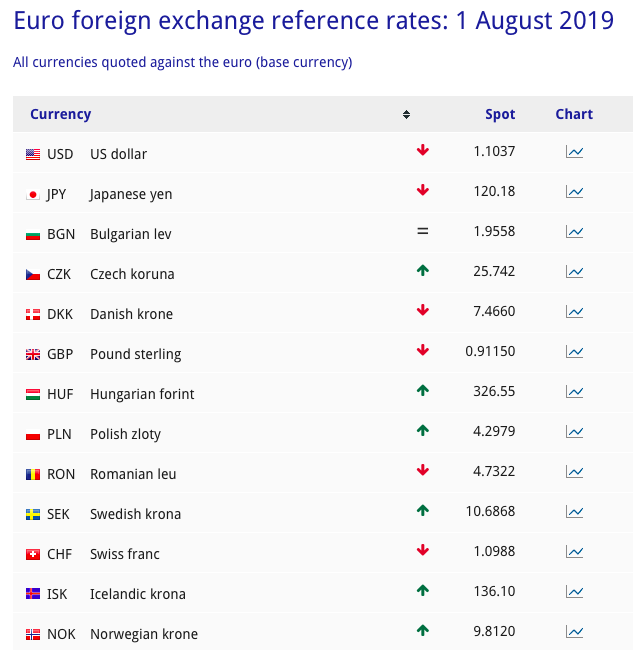
Esimerkiksi dollareiden ja eurojen välinen on \(1€=1,1037\$\).
Rahanvaihto on liiketoimintaa kaikille valuutanvaihtopisteille. Turistin vaihtaessa valuuttaa ulkomaanlomamatkaan varten, valuutanvaihtopiste myy ulkomaan valuutan myyntikurssinmukaisesti. Turistin palatessa lomamatkaltaan ja vaihtaessaan valuutan takaisin kotimaan valuutaksi valuutanvaihtopiste ostaa valuutan ostokurssin mukaisesti.
Myynti- ja ostokurssin hintojen lisäksi eri valuutanvaihtopisteet voivat veloittaa omia valuutanvaihtopalkkioita myyntitapahtumssa.
Euron arvo muuttuu joka päivä suhteessa muiden valtioiden valuuttoihin. Euron arvo voi kasvaa (vahvistua) tai laskea (heikentyä) muihin valuuttoihin nähden ja tätä kutsutaan valuutan ulkoisen arvon muuttumiseksi.
Kun euron arvo suhteessa dollariin heikkenee, puhutaan euron devalvoitumisesta. (Esim. Yhdellä eurolla saa vähemmän dollareita kuin aiemmin)
Vastaavasti, jos euron arvo suhteessa dollariin kasvaa, eli vahvistuu, puhutaan euron revalvoitumisesta. (Esim. Yhdellä eurolla saa enemmän dollareita kuin aiemmin) 
2.2 Indeksit
Jonkin tuotteen hinnan kasvua tai laskua voidaan vertailla saman tuotteen aiempaan hintaan. Sitä vuotta, jonka hintaan nykyistä hintaa verrataan, kutsutaan perusajankohdaksi.
Tuotteen hinnan indeksin pisteluku saadaan, kun taulukoidaan vertailuprosenttiluku ilman prosenttimerkintää.
Kun nämä indeksin pisteluvut taulukoidaan, saadaan hinnan indeksisarja, eli indeksi.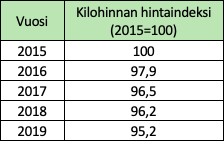 
Ryhmäindeksiksi kutsutaan useamman kuin yhden suureen (vaikkapa tuotteen) yhteisarvon muutosta.
Venla on taulukoinut kolmen eri vakio-ostoksensa hinnat viimeisen kolmen vuoden ajalta. Hän on ostanut yhden paketin kahvia, kaksi pakettia mysliä sekä neljä litraa maitoa.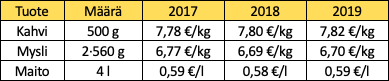 
Muodostetaan Venlan ostosten hintakehitystä kuvaava indeksi. Perusajankohta on vuosi 2017.
Lasketaan Venlan ostosten hinta eri vuosina:
\(\color{green}{2017}:\)
\[\begin{align*} 0,5\text{kg}\cdot7,78\frac{€}{\text{kg}}+2\cdot0,56\text{kg}\cdot6,77\frac{€}{\text{kg}}+4\text{l}\cdot0,59\frac{€}{\text{l}}=\color{green}13,832€ \end{align*}\]
\(\color{green}{2018}:\)
\[\begin{align*} 0,5\text{kg}\cdot7,80\frac{€}{\text{kg}}+2\cdot0,56\text{kg}\cdot6,69\frac{€}{\text{kg}}+4\text{l}\cdot0,58\frac{€}{\text{l}}=\color{green}13,713€ \end{align*}\]
\(\color{green}{2019}:\)
\[\begin{align*} 0,5\text{kg}\cdot7,82\frac{€}{\text{kg}}+2\cdot0,56\text{kg}\cdot6,70\frac{€}{\text{kg}}+4\text{l}\cdot0,59\frac{€}{\text{l}}=\color{green}13,774€ \end{align*}\]
Verrataan nyt ostoskorin kokonaishintaa vuoden 2017 ostoskorin hintaan ja muodostetaan indeksisarja: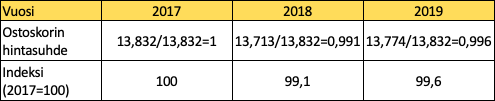 
VASTAUS: Ostosten hinnan kehitystä kuvaava indeksi on 
Eräs tärkein ryhmäindeksi on kuluttajahintaindeksi (KHI). Se kuvaa Suomessa asuvien kotitalouksien Suomesta ostamien palveluiden ja tavaroiden hintakehitystä. Kuluttajahintaindeksi julkaistaan joka kuukausi ja indeksin laskemista varten Tilastokeskus kerää noin 44 000 hintatietoa (2019).
Kuluttajahintaindeksin laskemisessa hyödynnetään Laspeyresin hintaindeksikaavaa . Siinä painotetaan eri hyödykkeiden hintoja niiden kulutuksen määrällä.
Kuluttajaintaindeksin avulla voidaan laskea elinkustannusindeksi (EKI). Esimerkiksi useiden asuntojen vuokrien hinta määräytyy elinkustannusindeksin mukaan.
2.3 Inflaatio ja deflaatio
Rahan määrä ei pysty aina vakiona, vaan se voi kasvaa tai vähentyä riippuen ajasta. Esimerkiksi lama vaikuttaa liikkeellä olevan rahan määrään, jolloin palkat alenevat ja edelleen eri tuotteiden hinnat pienentyvät. Tällöin rahaa liikkuu vähemmän.
Liikkeellä olevan rahan määrän kasvua kutsutaan inflaatioksi. Tällöin tuotteiden hinnat nousevat, jolloin palkkojen suuruus kasvaa. Palkkojen noustessa lainojen ottaminen lisääntyy, joka edelleen kasvattaa liikkeellä olevan rahan määrää.
Hintojen nopeaa nousua estetään mm. korkotason nostolla. Korkojen nouseminen hidastaa kulutusta, jolloin myös tuotteiden hinnat eivät enää nouse niin nopeasti.
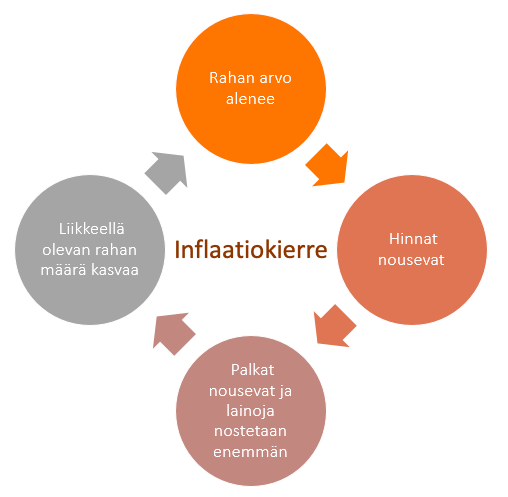
Inflaation vastakohta on deflaatio, jossa rahan arvo kasvaa, mikä edelleen pienentää tuotteiden hintoja ja vaikuttaa palkan pienenemiseen. Koska palkka on pienentynyt, myöskään lainaa ei oteta niin paljoa, mikä vähentää liikkeellä olevan rahan määrää.
Deflaatiota esiintyy lama-aikoina, ja se viittaakin kansantalouden häiriöön. Deflaatiota voi kuitenkin esiintyä myös nousukaudella, jolloin hyödykkeiden tuotanto kasvaa nopeammin kuin liikkeellä olevan rahan määrä.
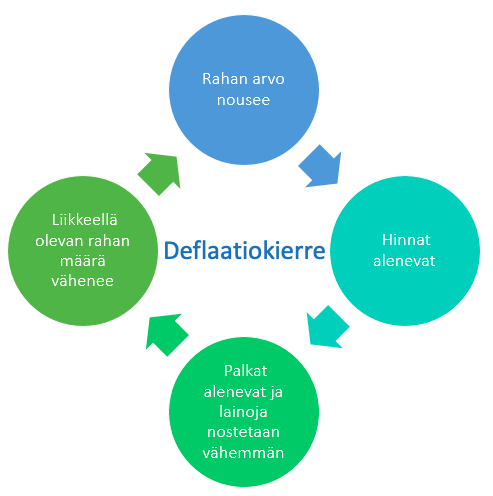
Koska inflaatio ja deflaatio vaikuttaa rahan arvoon, monia hintoja sidotaan indekseihin. Tällä tavoin hintojen muutokset mukautuvat hintojen kehitykseen.
Nimelliset ja reaaliset muutokset tarkoittavat erilaisten rahasummien muutosten tarkastelemista. Nimelliset muutokset eivät ota huomioon inflaation vaikutusta ja vastaavasti reaaliset muutokset ottavat huomioon inflaation vaikutus.
Reaalisella muutoksella voidaan muuttaa esimerkiksi muutaman vuoden takainen rahasumma sitä vastaavaksi tämän hetkiseksi summaksi, johon inflaatio on vaikuttanut.
Rahasumma voidaan joko deflatoida tai inflatoida riippuen siitä halutaanko rahasumma muuttaa aikaisemman ajankohdan rahasummaksi vai myöhäisemmän ajankohdan rahasummaksi.
Tutkitaan, mikä olisi nykyistä \(300€\):a vastaava summa vuonna 2017.
Koska tutkitaan aiemman ajankohdan rahasummaa, on kyseessä deflatointi.
\[\begin{align*} \dfrac{103,6}{105,8}&=\dfrac{x}{300}\\ x&=293,76€ \end{align*}\]
Vuoden 2017 rahassa vastaava rahasumma olisi ollut \(293,76€\).
3. Verotus
Vero on rahasuoritus, jonka verovelvollisen (yksityishenkilö tai yritys) tulee maksaa veronsaajalle (valtio). Kerätyillä verorahoilla valtio pitää yllä julkisyhteisöjen toimintaa, kuten julkista terveydenhuoltoa.
Tutustu Verohallinnon sivustoon tästä!
Kunnalle maksettavat verot voivat olla välillisiä tai välittömiä. Välilliset verot maksetaan palvelun tai tuotteen ostamisen yhteydessä ja esimerkiksi arvonlisävero (ALV) on välillinen vero. Välittömiä veroja ovat kiinteistövero, perintövero sekä tulovero esimerkiksi.
Veroa maksetaan sekä ansiotulosta sekä pääomasta. Tarkastellaan ensin ansiotuloverotusta.
3.1 Ansiotulojen vero
Ansiotuloa ovat palkkatulot, yrittäjätulon ansiotulo-osuus, eläketulo ja esimerkiksi opintoraha tai työttömyyskorvaus. Ansiotuloveroa perivät valtio, kunta sekä eri seurakunnat.
Verokortista käy ilmi ennakonpidätysprosentti, tuloraja sekä lisäprosentti. Ennakonpidätysprosentti pätee niin kauan, kunnes tuloraja ylittyy. Tällöin esimerkiksi palkasta verotetaan lisäprosentin määräämän verran.
Ennakonpidätyksen lisäksi palkasta peritään veroluontoisia maksuja, joita ovat esimerkiksi eläkemaksu ja työttömyysvakuutusmaksu. Lisäksi voidaan periä vapaaehtoisia maksuja, joita ovat erilaiset jäsenmaksut ammattiyhdistyksiin tai työttömyyskassaan.
Vuoden lopussa jokaiselle veronmaksajalle lasketaan lopullinen vero. Jos tämän veron suuruus on pienempi kuin mitä ennakkoverotus on ollut, valtio maksaa veronmaksajalle takaisin veronpalautusta. Toisaalta, jos veronmaksaja on vuoden aikana maksanut liian vähän veroja, tulee hänen maksaa vuoden lopussa jäännösveroa.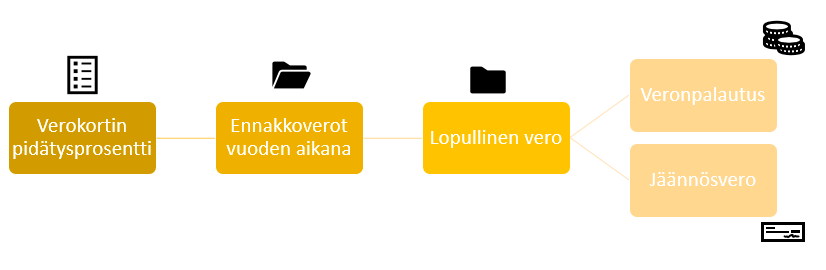 
Se, paljonko veronmaksaja maksaa veroja, riippuu maksajan tuloista. Suurempi tuloinen henkilö maksaa enemmän veroja kuin pienempi tuloinen henkilö.
Tämä johtuu tuloveroasteikon progressiivisuudesta, eli verojen suhteellisuudesta ansiotuloon. Joka vuosi valtio julkaisee tuloveroasteikon, joka määrittää verotuksen.
Ei-progressiivisia veroja ovat esimerkiksi kunnallis- ja kirkollisvero. Kunnallisvero on tulovero, jonka velanmaksaja maksaa kunnalle. Jokainen kunta määrittelee oman kunnallisveronsa joka vuosi. Kirkollisveroa maksavat evankelisluterilaisten sekä ortodoksisten seurakuntien jäsenet. Kirkollisvero määräytyy asuinkunnan mukaan.
3.2 Perintövero
Perintövero on välitön vero, joka maksetaan suoraan verottajalle. Perintöveron suuruuteen vaikuttaa saadun perinnön suuruus. Perintöveroa tulee maksaa, jos perintö on vähintään \(20 000€\). Perinnönjättäjän koti-irtaimisto on verovapaata aina \(4000\) euroon asti.
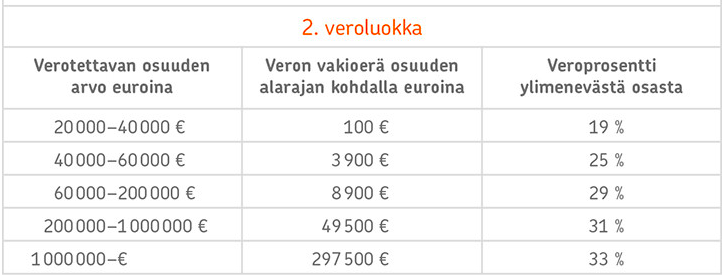
Maksettavan perintöveron suuruus riippuu omaisuuden arvosta sekä sukulaisuussuhteesta. Ensimmäiseen veroluokkaan kuuluvat lähiomaiset, eli aviopuoliso, lapset, vanhemmat ja isovanhemmat. Toiseen veroluokkaan kuuluvat muut sukulaiset ja perheen ulkopuoliset henkilöt.
3.3 Lahjavero
Jos saa lahjaksi rahaa, ja sen määrä ylittää \(5000\) euroa, tulee siitä maksaa lahjavero. Lahjavero koskettaa samalta lahjoittajalta saatuja lahjoja, joiden yhteissumma ylittää \(5000\) euron rajan. Veroilmoituksen lahjasta tekee lahjan saaja viimeistään kolmen kuukauden kuluttua lahjoituksesta.
Maksettavan lahjaveron suuruus riippuu sukukaissuhteesta sekä lahjoitetun omaisuuden arvosta.
Ensimmäiseen veroluokkaan lukeutuvat lähiomaiset, eli aviopuoliso, lapset, vanhemmat ja isovanhemmat. 
Toiseen veroluokkaan lukeutuvat muut sukulaiset sekä perheen ulkopuoliset henkilöt. 
Lilja saa tädiltään ylioppilaslahjaksi \(6000\) euroa lahjarahaa. Kuinka paljon hän maksaa lahjasta veroa?
RATKAISU:
Täti lukeutuu "muiksi sukulaisiksi", eli hän kuuluu 2. veroluokkaan. 
Liljan saama rahasumma lukeutuu verotaulukon ensimmäiseen luokkaan, jossa veron vakioerä on \(\color{green}100€\) alarajalla.
Lasketaan seuraavaksi, paljonko lahjaraha ylittää alarajan: \[\begin{align*} 6000€-5000€=1000€. \end{align*}\] Alarajan ylittäneestä osuudesta maksetaan taulukon mukaan \(19\%\) vero \[\begin{align*} 0,19\cdot1000€=\color{green}190€ \end{align*}\] Yhteensä veroa maksetaan siis \[\begin{align*} \color{green}100€\color{black}+\color{green}190€\color{black}=290€. \end{align*}\]
Lilja maksaa lahjastaan \(290€\) arvoisen lahjaveron.
3.4 Arvonlisävero
Monelle tuttu kulutusvero on arvonlisävero (ALV). Tämä vero maksetaan välillisesti ja se on sisällytetty tuotteen tai palvelun hintaan. Arvonlisävero lasketaan tuotteen (tai palvelun) verottomasta hinnasta, Suomessa tämä lisättävä arvonlisävero on yleisesti \(24\%\), mutta tässä voi olla poikkeuksia.
Suomessa ostettavan tuotteen verollinen hinta tulee olla näkyvissä ostajalle. Yritysten välisessä kaupankäynnissä tuotteiden (tai palveluiden) hinnat esitetään verottomina.
Eri maissa on erisuuruiset arvolisäverot. Katso allaolevat taulukko kokonaisuudessaa täältä!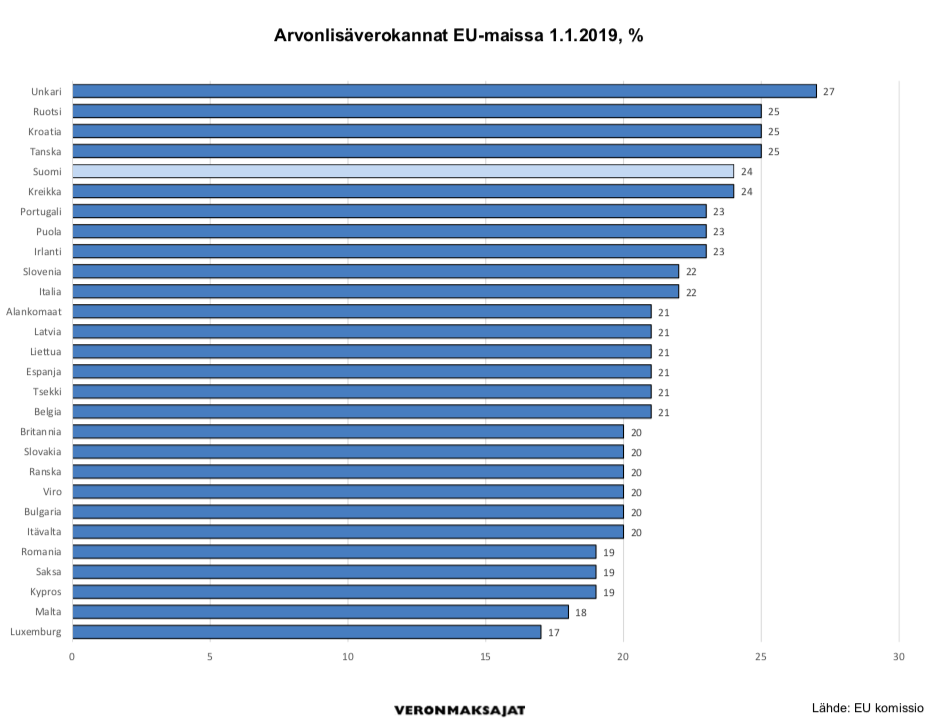 
Veeti etsii itselleen mustaa farkkutakkia. Takin veroton hinta on \(116€\). Paljonko Veeti maksaa farkkutakista
- Suomessa
- Saksassa?
RATKAISU: a.
Vaatteiden ALV Suomessa on \(24\%\). Maksettava summa saadaan lisäämällä takin verottomaan hintaan ALV: \[\begin{align*} 116€+0,24\cdot116€=143,84€. \end{align*}\]
Vastaus: Veeti maksaa takista \(143,84€\) Suomessa.
- Vaatteiden ALV Saksassa on \(19\%\). Maksettava summa on siis \[\begin{align*} 116€+0,19\cdot116€=138,04€. \end{align*}\]
Vastaus: Veeti maksaa takista \(138,04€\) Saksassa.
4. Korko ja laina
Jos henkilö lainaa rahaa esimerkistä, lainattua rahaa ei makseta takaisin saman suuruisena kuin se lainattiin. Lainattuun summaan lisätään korko, joka on lainanantajalle maksettava korvaus. Koron suuruuteen vaikuttaa lainatun rahamäärän suuruus, eli pääoman suuruus, korkoaika sekä korkokanta.
Korkoaika tarkoittaa sitä aikaa, jolloin raha oli lainassa tai talletettuna. Korkokanta kuvaa maksettavan koron suuruutta, eli korkoprosenttia.
Korko
Merkitään korkoa kirjaimmella \(r\). \[\begin{align*} r=k\cdot p\cdot t, \end{align*}\] jossa \(k\) on pääoma, \(p\) on korkokanta ja \(t\) on korkoaika.
Tallettaessa rahaa esimerkiksi pankkiin, tallettaja saa itselleen korkotuottoa. Tämä tuotto on veronalaista tuloa, josta peritään lähdevero. Lähdeveron suuruus on \(30\%\) ja jos pääomatulo ylittää \(30 000\) euron rajan, lähdeveron suuruus on \(34\%\). Tallettaja ei maksa lähdeveroa suoraan valtiolle, vaan lähdeveron perii lainanantajan (esimerkiksi pankki).
Korkokannasta poistettaessa lähdeveron osuus saadaan nettokorkokanta. Vastaavasti nettokorko on se korko, joka todelisuudessa maksetaan talletukselle. Nettokorko saadaan kun pankin maksamasta korosta vähennetään lähdevero.
Kasvanut pääoma
Merkitään kasvanutta pääomaa kirjaimella \(K\). \[\begin{align*} K&=k+r\\&=k+kpt, \end{align*}\] jossa \(k\) on alkuperäinen pääoma ja \(r\) korko.
Pankkiin talletetaan \(\color{green}2500€\) arvoinen pääoma. Korkokanta on \(1,4\%\).
Lasketaan nettokorko erikorkoajoille.
a. Kun korkoaika on \(\color{blue}1\) vuosi
Nettokorkokanta saadaan vähentämällä lähdeveron (\(30\%\)) suuruus korkokannasta: \[\begin{align*} \text{Nettokorko on }100\%-30\%=70\%\text{ korkokannasta} \end{align*}\] \[\begin{align*} \text{Nettokorkokanta on } 0,70\cdot1,4\%=0,98\%=\color{red}0,0098 \end{align*}\]
Nyt yhden vuoden aikana korkoa maksetaan \[\begin{align*} \color{blue}1\color{black}\cdot\color{red}0,0098\color{black}\cdot\color{green}2500€\color{black}=24,50€ \end{align*}\]
Vastaus: Korkoa maksetaan \(24,50€\), kun korkoaika on yksi vuosi.
b. Kun korkoaika on \(\color{blue}2\) kuukautta
Nettokorkokanta on sama kuin a-kohdassa, koska kyseessä on sama pankki ja sama korkokanta. Eli nettokorkokanta on \(\color{red}{0,0098}\).
Nyt yhden vuoden aikana korkoa maksetaan \[\begin{align*} \color{blue}0,1667\color{black}\cdot\color{red}0,0098\color{black}\cdot\color{green}2500€\color{black}=4,08€ \end{align*}\]
Vastaus: Korkoa maksetaan \(4,08€\), kun korkoaika on kaksi kuukautta.
Pikavipeissä korkoaika on todella lyhyt. Tällöin korkolaskussa käytetään todellisten korkopäivien määrä, joihin ei lukeudu lainan nostopäivää.
4.1 Koronkorko
Jos pankissa on talletus useita vuosia, voidaan pääoman kasvua tarkastella koronkoron kautta. Tällöin jokaista vuotta ei tarvitse laskea erikseen, vaan haluttuun lopputulokseen päädytään yksinkertaisella potenssilaskulla.
Jokaisena vuonna pääomalle maksetaan korkoa. Ensimmäisenä vuonna pääomaan \(k\) lisätään korko \(r\). Seuraavana vuonna maksetaan sama korko \(r\), mutta tähän hetkeen mennessä pääoma on jo kasvanut yhden koron verran.
| Ajankohta | Tilillä rahaa ennen koron lisäystä | Tilillä rahaa koronlisäyksen jälkeen |
|---|---|---|
| Talletushetki | \(1000€\) | \(1000€\) |
| 1 vuosi | \(1000€\) | \(1,02\cdot1000€\) |
| 2 vuotta | \(1,02\cdot1000€\) | \(1,02\cdot1,02\cdot1000€=1,02^{\color{red}2\color{black}}\cdot1000€\) |
| 3 vuotta | \(1,02^{\color{red}2\color{black}}\cdot1000€\) | \(1,02^{\color{red}3\color{black}}\cdot1000€\) |
| n vuotta | \(1,02^{\color{red}n-1\color{black}}\cdot1000€\) | \(1,02^{\color{\red}n\color{black}}\cdot1000€\) |
Koronkorko
Merkitään kasvanutta pääomaa kirjaimella \(K\). \[\begin{align*} K=kq^{n}, \end{align*}\] jossa \(k\) on alkuperäinen pääoma, \(q=\left(1+\frac{i}{100}\right)\) on korkotekijä, \(i\) on korkokanta ja \(n\) on korkokausien lukumäärä.
4.2 Laina
Pankin lainatessa rahaa, se määrittää lainatulle rahalle maksettavan koron suuruuden. Käytössä on erilaisia viitekorkoja, esimerkiksi primekorko ja euribor 6kk- viitekorko. Lainan korko muodostuu, kun viitekorkoon lisätään vielä korkomarginaali, joka on asiakaskohtainen.
Primekorko on pankin oma viitekorko. Tämä on yleensä euriborkorkoa vakaampia, sillä niitä tarkistetaan harvemmin. Euriborkorko (Euro Interbank Offered Rate) on euroalueen yhteinen viitekorko, jonka määrittelee Euroopan keskuspankki.
Lainan takaisinmaksu koostuu kahdesta eri osasta, lainan lyhennuksestä sekä lainan korosta. Lainaa voi lyhentää esimerkiksi kerran kuukaudessa, jolloin korkoa laskiessa käytetään kuukausikorkoa.
Tasalyhennyslainassa jokainen lyhennyserä on samansuuruinen ja koron osuus on aluksi suuri, koska takaisin maksettavaa lainaa on enemmän. Mitä vähemmän lainaa on enää jäljellä, sitä pienempi on myös koron osuus takaisinmaksuerässä.
Tasaerälainassa (eli annuiteettilainassa) takaisinmaksuerät pysyvät samansuuruisina niin kauan kunnes korkokanta muuttuu. Koron osuus voi muuttua maksuerissä, koska korko lasketaan lainan suuruuden mukaan. Lyhennyksen osuus riippuu maksettavasta korosta: mitä enemmän lyhennyserässä maksetaan korkoa, sitä vähemmän maksetaan lyhennystä.
Annuiteetin eli yhden maksuerän suuruus voidaan laskea seuraavasti
Annuiteetti
Merkitään annuiteettia kirjaimella \(A\). \[\begin{align*} A=Kq^{n}\dfrac{1-q}{1-q^n}, \end{align*}\] jossa \(K\) on lainapääoma, \(n\) on maksukertojen lukumäärä ja \(q\) korkotekijä.
Jäljellä olevan lainan suuruus voidaan ratkaista seuraavasti:
Jäljellä oleva laina annuiteettilainassa
\[\begin{align*} V_k=Kq^k-A\dfrac{1-q^k}{1-q}, \end{align*}\] jossa \(V_k\) on jäljellä oleva laina, \(K\) on lainapääoma, \(q\) on korkotekijä, \(k\) on lyhennysten määrä ja \(A\) on annuiteetti.
5. Sijoittaminen
Rahaa voi sijoittaa useaan eri kohteeseen. Esimerkiksi vakuutuksen ostaminen on jo sijoitus ja pankkitilillä korkoa kasvava pääoma on sijoitus. Muita sijoituskohteita ovat esimerkiksi asunnot, metsä, taide, rahastot, osakkeet sekä joukkovelkakirjalainat. Toisinsanoen sijoittaminen tarkoittaa sitä, että rahaa ei pidetä itsellä valuuttana, vaan on sidottu johonkin toiseen muotoon.
5.1 Sijoittaminen
Sijoittamisessa pääoma voi kasvaa tai pienentyä. Sijoittamisessa on aina riski, että pääoma ei kasvakaan vaan romahtaa. Tällöin sijoitus ei tuota sitä haluttua tuottoa. Sijoittessa rahaa, pohdi ainakin seuraavia asioita: Kuinka pitkäksi ajaksi olet valmis sijoittamaan rahasi? Kuinka paljon olet valmis sijoittamaan ja kuinka paljon siedät epävarmuutta tuotosta?
Turvallinen sijoitus on pankkitallettaminen. Tällöin pääoma kasvaa korkoa pankkitilillä ja saat rahan käyttöösi milloin vain. Jos pankki joutuisi konkurssiin, talletuksilla on talletussuoja, jonka takia riskit tallettamisessa ovat todella pienet.
Sijoittamalla joukkovelkakirjoihin (eli obligaatioihin) sijoittaja antaa sovitun määrän rahaa sovitulla kiinteällä korolla esimerkiksi valtion käyttöön. Lainanottaja maksaa joka vuosi korkoa lainastaan, joten lainanantajan on maksettava lähdeveroa.
Vakuutukset ovat yksi sijoituskohde. Säästövakuutukseksi kutsutaan vakuutusta, joka säästetään pienissä erissä, esimerkiksi kuukausittain maksettava henkivakuutus. Sijoitusvakuutus ei nimestään huolimatta ole vakuutus vaan se koostuu vaikkapa rahasto-osuuksiin tehdyistä sijoituksista. Sijoittaminen eläkevakuutukseen tarkoittaa joko oman eläkkeen aikaistamista tai eläkkeen suuruudeen kasvattamista.
Eräs sijoitusmuoto on osakkeet. Osake on osuus jostain yhtiöstä, ja osakkeiden arvo vaihtelee ajan mukaan. Jos yhtiö menestyy, se voi maksaa osakkailleen osinkoja, eli voitto-osuuksia. Osingot ovat \(85\%\) veronalaista pääomatuloa ja \(15\%\) verovapaata tuloa. Osingoista maksetaan \(30\%\) suuruinen vero.
Sijoitusrahastot toimivat siten, että rahastot keräävät yksityishenkilöiltä ja yhteisöltä varoja, jotka se edelleen sijoittaa useisiin eri arvopapereihin. Osakerahasto sijoittaa osakkeisiin, korkorahasto sijoittaa korkoa tuottaviin kohteisiin ja yhdistelmärahasto sijoittaa osakkeisiin sekä korkoa tuottaviin kohteisiin.
Erään sijoitusvakuutuksen tuotoksi arvioidaan \(6,2\%\) joka vuosi. Risto sijoittaa joka vuosi tähän kyseiseen vakuutukseen \(1200€\). Lasketaan vakuutuksen nettotuotto 8 vuoden kuluttua.
Sijoittettu summa kerää korkotuottoa, joten mitä kauemmin summa on sijoitettuna, sitä suuremman tuoton se antaa. Taulukoidaan nyt muutaman vuoden sijoituksen korkotuotto:
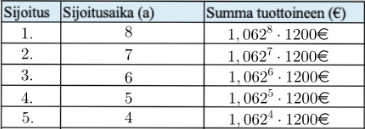
Kyseessä on siis geometrinen summa, jonka suhdeluku \(q=1,062\) ja ensimmäinen termi \(a_{1}=1,062\cdot1200€\). Nettotuotto 8 vuoden päästä saadaan laskemalla yhteen \[\begin{align*} 1,062\cdot1200€+1,062^{2}\cdot1200€+1,062^{3}\cdot1200€+...+1,062^{8}\cdot1200€. \end{align*}\]
Summassa on yhteenlaskettavana 8 termiä, eli \(n=8\). Geometrinen summa saadaan laskettua \[\begin{align*} S=a_{1}\cdot\frac{1-q^{n}}{1-q}=1,062\cdot1200€\cdot\frac{1-1,062^{8}}{1-1,062}=12704,2€. \end{align*}\]
Tuotto on siis \(12704,2€-8\cdot1200€=3104,24€\).
Tuotosta peritään vielä pääomatulovero, joka on \(30\%\).
\(0,7\cdot3104,24€=2172,97€\)
Vastaus: Nettotuotto sijoituksesta on \(2172,97€\).
5.2 Rahoitus
Rahoituksella tarkoitetaan yksityishenkilölle tai yritykselle myönnettyä rahallista apua johonkin investointiin. Rahoitus myönnetään harkinnanvaraisesti ja sen myöntämiseen täytyy olla pätevät syyt. Yritykselle rahoitusta voidaan myöntää, jos rahoituksella edesautetaan esimerkiksi yrityksen kasvua, kansainvälistymistä, teknologiaa tai tuottavuutta.
Yrityksen aloittaessa toimintansa, suurin osa rahoituksesta tulee yrittäjän omasta taskusta. Kuitenkin rahoitusta on mahdollista saada muualtakin, ja ulkopuolelta saatu rahoitus on yleensä lainarahaa.
Yrityksellä tulee olla omaakin pääomaa, jota ei tarvitse maksaa takaisin ja se ei ole lainarahaa. Esimerkiksi aloitavalla yrityksellä voi olla rahastoja tai sijoituspääomaa. Rahoitukseen ei lukeudu niin kutsuttu starttiraha, joka on TE-palveluiden antamaa tukea aloittavalle yritykselle.
6. Yrityksen taloudesta
Yrityksen taloudesta huolehtiminen sisältää paljon tulevaisuuden tapahtumien ennustamista ja rahatilanteen sunnittelua. Tässä kappaleessa tutustutaan diskonttaukseen sekä investointiin liittyviin seikkoihin.
6.1 Diskonttaus
Diskonttaus tarkoittaa tapahtumaa, jossa yritys muuttaa tulevaisuudessa tehtävän maksun arvoa ajassa taaksepäin, eli nykypäivään.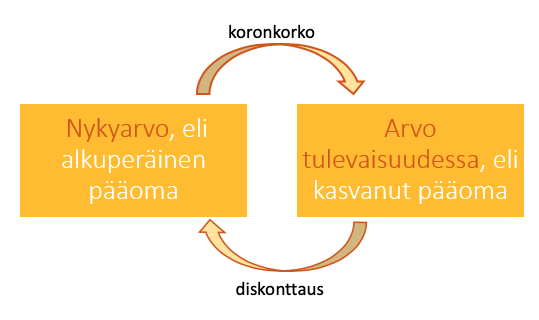 
Koronkorkoa laskettaessa hyödynnettiin tietoa pääomasta \(K\), korkotekijästä \(q\) sekä alkuperäisestä pääomasta \(k\). \[\begin{align*} K=k\cdot q^{n} \end{align*}\]
Diskonttaustilanteessa ratkaistaan ylläoleva yhtälö alkuperäisen pääoman \(k\) suhteen: \[\begin{align*} k=\frac{K}{q^{n}}=K\cdot q^{-1}, \end{align*}\]
jossa termiä \(q^{-1}\) kutsutaan diskonttaustekijäksi.
Diskonttausta hyödynnetään esimerkiksi silloin, kun yritys tekee investointeja, eli sijoittaa johonkin kohteeseen rahasumman pitemmäksi ajaksi. Tällaisia sijoituskohteita ovat esimerkiksi yrityksen toimitilat, laitteet, henkilöstön koulutus jne.
6.2 Yrityksen kannattavuus
Yritykset joko myyvät tuotteita tai tuottavat palveluita. Volyymilla tarkoitetaan esimerkiksi myytyjen tuotteiden lukumäärää. Volyymi vaikuttaa yrityksen myyntituottoon, eli siihen paljonko yritys saa arvonlisäverotonta tuottoa tuotteistaan tai palveluistaan.
Yritys kohtaa erilaisia kustannuksia.** Muuttuvat kustannukset** ovat sellaisia kustannuksia, jotka riippuvat yrityksen toiminnan volyymista. Esimerkiksi raaka-ainekustannukset, toimituskulut, ylityöpalkat, jne. Kiinteitä kustannuksia ovat muuttumattomat kustannukset kuten kuukausipalkat, vakuutukset sekä vuokrat.
Vähentämällä myyntituotosta muuttuvat kustannukset, saadaan laskettua yrityksen katetuotto. Katetuottolaskennan avulla yritys voi arvioida toiminnansa volyymin, tuottojen sekä kustannusten riippuvuuksia.
Katetuottolaskennassa lasketaan usein katetuottoprosentti (KTP), joka saadaan jakamalla katetuotto myyntituotolla. Tämä prosenttiarvo kertoo, paljonko myynnistä on katetuottoa.
Yrityksen tulos on katetuoton ja kiinteiden kustannusten erotus. Yrityksen toiminta on kannattavaa, jos tulos on positiivista.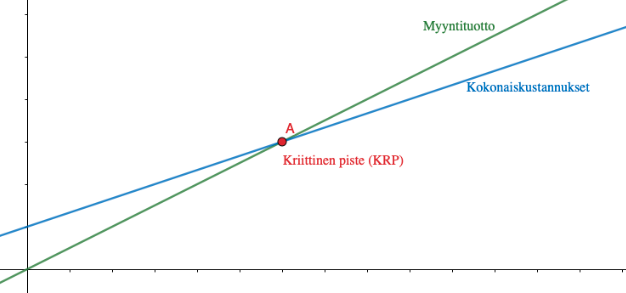 
Kun myyntituotto sekä kokonaiskustannukset muokataan yhtälöiksi, niiden kuvaajat saattavat leikata toisensa. Tämä leikkauspiste on kriittinen piste, joka kertoo milloin yrityksen toiminta on kannattavaa. Jos myyntituoton funktion arvo on suurempaa kuin kokonaiskustannusten funktion arvo, yrityksen tulos jää positiiviselle.
Tehtäviä
1. Tehtävä
Kukkaniitylle on istutettu 1500 neilikkaa siten, etteivät rivit ole tasaiset. Neilikoita istutetaan yhteensä 100 riviin, ja jokaiselle rivistölle istutetaan aina kuusi neilikkaa enemmän kuin edelliselle.
a.
Montako neilikkaa on niityn viimeisellä rivillä?
b.
Neilikoiden kasvua rajoittavat esimerkiksi jänikset ja myyrät. Oletetaan myyrien populaatio kasvavan keväisin 35 yksilöllä, mutta loppusyksystä populaatiosta menehtyy yksi kuudesosa. Eräänä alkuvuonna myyriä on 800 yksilöä, kuinka suuri myyräpopulaatio on viiden vuoden kuluttua?
2. Tehtävä
a.
Venla on heinäkuun kesätöissä marjatilan kahviossa. Hänen tuntipalkkansa on \(10,5€\)/h ja hän tekee viikossa 25 tuntia töitä.
Paljonko on Venlan bruttopalkka heinäkuulta?
b.
Paljonko on Venlan nettopalkka heinäkuulta?
c.
Erään pankin korkokanta on \(3,1\%\). Vilja tallettaa kyseisessä pankissa olevalle säästötililleen \(6500\) euroa. Korosta peritään lähdevero, joka on \(30\%\). Kuinka paljon Viljan pääoma on kasvanut kymmenen vuoden aikana?
3. Tehtävä
Koronkorko ja pikavippi Marjatilalla myydään vadelmakakkupaloja hintaan \(4,50€\). Hinta sisältää arvonlisäveron \(14\%\). Marjatila myy heinäkuun aikana 2000 kakkupalaa. Kiinteät kustannukset kahvilassa ovat \(1900€\) ja muuttuvat kustannukset (esim. raaka-ainekustannukset) ovat \(1,00€\)/kakkupala.
a.
Paljonko Marjatila saa katetuottoa kakkupaloista heinäkuun aikana?
b.
Kuinka suuren tuloksen Marjatila tekee heinäkuun aikana?
4. Tehtävä
Kalle ja Iiro sijoittivat pääomaansa kolmeen erilaiseen yhtiöön. Alla olevassa taulukossa on näkyvissä, kuinka paljon osinkoja yhtiöt maksavat ja montako osaketta Kalle ja Iiro omistavat.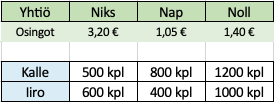 
a.
Paljonko Iiro maksaa veroa osingoistaan?
b.
Kuinka paljon Kalle saa puhdasta osinkotuloa?
5. Tehtävä
a.
Sinulla on käytössäsi 15 000 euroa rahaa. Mihin sijoittaisit rahat?
6. Tehtävä
Veeti päätti ostaa itselleen syntymäpäivälahjaksi uuden auton. Tähän hän tarvitsi 12 000 euron lainan pankista. Lainan takaisinmaksu ajaksi sovittiin 20 vuotta, ja lainaa maksetaan takaisin joka kuukausi.
a.
Kyseessä on annuiteettilaina, jonka korkokanta on \(4,2\%\). Kuinka paljon korkoa Veeti maksaa yhteensä?
b.
Kyseessä on tasalyhenteinen laina, jossa korkokanta on \(2,8\%+2,1\%\). Kuinka suuri on viimeinen maksuerä?
7. Tehtävä
Suomeen tuoduilla kukilla voi olla yllättävän suuri hiilijalanjälki. Osa kukista lennätetään Suomeen esimerkiksi Afrikasta, ja niiden kasvatuksessa voi olla käytetty haitallisia tuholaismyrkkyjä. Kukat saatetaan myös tuoda maista, joissa puhdas vesi on muutenkin vähäistä. Kasvihuoneissa kasvatetut kukat kuluttavat energiaa paljon. Suosi sesonkikukkia sekä Reilun kaupan tuotteita, jos haluat piristää kotiasi kukkasilla!
Uudessa-Seelannissa on käytössä valuutta Uuden-Seelannin dollari, ja sieltä tuodaan Suomeen esimerkiksi tulppaaneja. Tulppaanien myyntihinta nousee Uudessa-Seelannissa \(6,0\%\) ja samaan aikaan euro devalvoituu \(15\%\) Uuden-Seelannin dollariin nähden. Kuinka monta prosenttia tulppaanien hinta muuttuu euroissa?
8. Tehtävä
Sähköpyörien valmistaja myy tuotteitaan hintaan 450€ (veroton myyntihinta). Muuttuvat kustannukset valmistajalle on 120€/pyörä ja kiinteät kustannukset ovat 100 000€ vuodessa.
a.
Muodosta GeoGebralla kuvaajat myyntituoton funktiolle \(M(x)\) ja kokonaiskustannusfunktiolle \(K(x)\). Tässä \(x\) on myytyjen pyörien lukumäärä.
b.
Kuinka monta sähköpyörää valmistajan on myytävä vuodessa, jotta valmistaja jää voitolle?
9. Tehtävä
Elinkustannusindeksi (1951=100) vuonna 2012 oli \(1863\). Vastaava indeksi vuonna 2016 oli \(1913\).
a.
Mitä tarkoittaa inflaatio?
b.
Mikä oli inflaatioprosentti aikavälillä 2012-2016?
c.
Kuinka paljon rahan ostovoima on laskenut?
Vanhoja YO-tehtäviä
1.
Elintarvikkeiden arvonlisävero on 17 prosenttia tuotteen verottomasta hinnasta. Tapio maksoi ruokaostoksistaan 54,35 euroa. Kuinka monta euroa ostoksen hinta alenisi, jos ruoan arvonlisäveroa laskettaisiin 9 prosenttiyksiköllä? Kuinka suuri olisi ostoksen hinnan alennus prosentteina? [S09/4]
VASTAUS: \(4,18€\) ja \(7,7%\)
RATKAISU:
ALV=17% ja yhdeksän prosenttiyksikön alennuksen jälkeen ALV=8%.
Tapion maksama hinta sisältää siis ruokaostosten verottoman hinnan + 17% verottomasta hinnasta:
\[\begin{align*} 54,35€=x+0,17x\\ 54,35€=1,17\cdot x\\ x=\frac{54,35€}{1,17}\\ x=46,453€ \end{align*}\]
Lasketaan nyt, paljonko Tapion pitäisi maksaa silloin, kun ALV=8%. Merkitään uutta hintaa \(a\):lla.
\[\begin{align*} a&=46,453€\cdot1,08\\ a&=50,1692€ \end{align*}\]
Ostosten hinta alenisi siis \[\begin{align*} 54,35€-50,1692€=4,18€ \end{align*}\]
Ja ostoksen hinnan alennus olisi \[\begin{align*} \frac{4,18€}{54,35€}=0,0769=7,7\% \end{align*}\]
2.
Hamamstahnaputkilon tilavuus on \(100\) ml ja hinta \(1,50€\). Putkilon tilavuutta kasvatetaan $25%4, mutta samalla myyntihintaa korotetaan \(40\%\). Kuinka monta prosenttia kalliimpaa hammastahna on uudessa putkilossa millilitraa kohden? [S14/4]
VASTAUS: \(12\%\)
RATKAISU:
Lasketaan aluksi tahnan hinta millilitraa kohden: \[\begin{align*} \frac{1,50€}{100 \text{ ml}}=0,015\text{€/ml} \end{align*}\]
Kun putkilon tilavuutta kasvatetaan \(25\%\), uusi tilavuus on \[\begin{align*} 1,25\cdot100\text{ ml}=125\text{ ml} \end{align*}\]
Ja kun hintaa nostetaan, uusi hinta on \[\begin{align*} 1,40\cdot1,50\text{ €}=2,10\text{ €} \end{align*}\]
Jolloin uusi hinta millilitraa kohden on \[\begin{align*} \frac{2,10€}{125 \text{ ml}}=0,0168\text{€/ml} \end{align*}\]
Ja nyt vertailulla saadaan \[\begin{align*} \frac{0,0168\text{€/ml}}{0,015 \text{ €/ml}}=1,12 \end{align*}\]
Eli tahna on kallistunut \(12\%\).
3.
Eräällä reitillä on 20 matkustajaa. Heistä seitsemän ostaa opiskelijalipun, viisi eläkeläislipun ja loput kahdeksan maksavat täyden hinnan 20 euroa. Opiskelija-alennus on \(50\%\), ja eläkeläisalennus on \(30\%\). Mikä on kaikkien matkustajien maksamien lippujen keskihinta? [K17/2a]
VASTAUS: \(15€\)
RATKAISU:
Täyden lipun hinta on \(20€\), jolloin opiskelijalipun hinnaksi saadaan \(10€\) ja eläkeläislipun hinnaksi saadaan \(14€\).
Lipputuloja saadaan yhteensä: \(7\cdot10€+5\cdot14€+8\cdot20€=300€\)
Edelleen keskihinnaksi saadaan \(\frac{300}{20}=15€\)
4.
Vuonna 2015 helsingin pörssi heilahteli voimakkaasti. OMXH-indeksi, joka kuvaa pörssiyhtiöiden kokonaismarkkina-arvoa, vaihteli vuosineljänneksittäin alla olevan taulukon osoittamalla tavalla. Mikä oli indeksin kokonaismuutos vuoden 2015 aikana, ja mihin suuntaan? [K17/5b]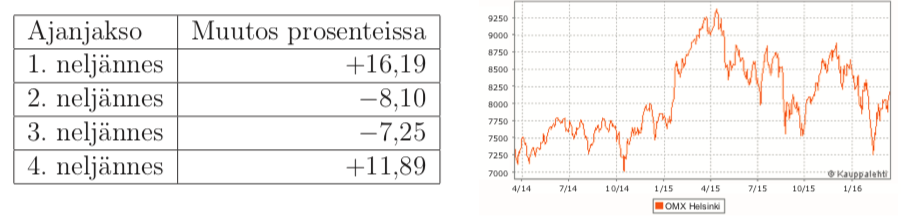 
VASTAUS: Kasvua n. \(10,8\%\)
RATKAISU:
Muutetaan ensin prosentit suhteiksi. \[\begin{align*} +16,19 \rightarrow 1,1619\\ -8,10\rightarrow 0,9190\\ -7,25\rightarrow 0,9275\\ +11,89\rightarrow 1,1189 \end{align*}\]
Kaikkien muutosten tulo: \[\begin{align*} 1,1619\cdot0,9190\cdot0,9275\cdot1,1189=1,10813 \end{align*}\]
Eli kasvua on noin \(10,8\%\).
5.
Tavaratalossa jokainen kanta-asiakas saa alennuskupongin, jonka voi käyttää yhden ostoksen yhteydessä. Ostos voi sisältää useamman tuotteen. Alennus määräytyy ostoksen kokonaissumman perusteella alla olevan taulukon mukaisesti.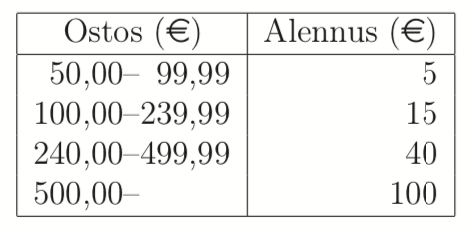 
Tee taulukko alennusprosenteista, kun ostoksen kokonaissumma on 50,100,300 ja 600 euroa.
Risto ostaa vaatteita 80 eurolla ja hänen isänsä 200 eurolla. Kuinka monta prosenttiyksikköä suurempi on isän alennusprosentti verrattuna Riston alennusprosenttiin?
Mikä olisi ollut Riston ja isän yhteinen alennusprosentti, jos he olisivat yhdistäneet ostoksensa? [S17/5]
VASTAUS: b. Maurin alennusprosentti \(1,25\%\) suurempi. c.Alennusprosentti \(14,3\)
RATKAISU:
Kokonaissumma Alennusprosentti 50€ \(\frac{5}{50}=0,10=10%\) 100€ \(\frac{15}{100}=0,15=15%\) 300€ \(\frac{40}{300}=0,133=13%\) 600€ \(\frac{100}{600}=0,1667=17%\)
Riston alennusprosentti on \[\begin{align*} \frac{5}{80}=0,0625=6,25\% \end{align*}\]
Isän alennusprosentti on \[\begin{align*} \frac{15}{200}=0,075=7,5\% \end{align*}\]
Erotusprosenttiyksikköinä on \(7,5-6,25=1,25\). Maurin isällä on \(1,25\) prosenttiyksikköä suurempi alennusprosentti.
- Jos ostokset olisi yhdistetty, kokonaissummaksi olisi tullut \(280€\). Alennusprosentti olisi tällöin \[\begin{align*} \frac{40}{280}=0,1428=14,3\% \end{align*}\]
6.
Vuonna 2014 pääomatulojen veroprosentti on 40 000 euroon saakka 30 ja sen yli menevältä osalta veroprosentti on 32.
Muodosta lauseke \(f(x)\) pääomatuloveron suuruudelle, kun pääomatulo \(x\) on yli 40 000 euroa vuodessa.
Laske veron määrä, kun pääomatuloja on 41 700,23 euroa vuodessa.
Kun yksityihenkilö saa osinkotuloa pörssiyhtiön osakkeista, niin veronalainen osuus on \(85\%\) osinkotuloista. Tästä osuudesta masketaan pääomatuloveroa yllä mainitun säännön mukaisesti. Kuinka monta prosenttia veroa henkilö maksaa osinkotulostaan, kun osingon määrä on 41 700,23 euroa? [S15/14]
VASTAUS: a.\(0,32x-800\), kun \(x>40000\) b.n.\(12544,07€\) c.\(25,5\)
RATKAISU:
Pääomatulojen veroprosentti on \(30\%\), kun pääomatuloja on maksimissaan \(40 000€\). Tämän jälkeen veroprosentti kasvaa \(32\%\):iin.
Tästä saadaan lauseke: \[\begin{align*} f(x)&=0,30\cdot40000+0,32\cdot(x-40000)\\ f(x)&=0,32x-800, \end{align*}\] kun \(x>40000\).
Pääomatuloja on \(41700,23€\)/vuosi. Tällöin veron määrä saadaan laskettu a-kohdassa muodostetulla funktiolla : \[\begin{align*} f(41700,23)&=0,32\cdot41700,23-800\\ &=12544,0736€\\ &≈12544,07€ \end{align*}\]
Osingon määrä on \(41700,23€\), ja tästä veronalainen osuus on
\(0,85\cdot41700,23€≈35445,20\)
Pääomatuloa menee \(30\%\), eli \(0,30\cdot35445,20=10633,56€\).
Edelleen henkilö maksaa veroa osinkotulostaan
\(\frac{10633,56€}{41700,23€}=0,255=25,5\%\)
7.
Kristian aikoo vaihtaa autoa ja hakee pankilta \(8000\) euron lainaa. Pankki tarjoaa hänelle tasaerälainaa, joka maksetaan takaisin kahdessa vuodessa. Lainan vuotuinen korko on \(6,6\%\) koko takaisinmaksukauden ajan. Muita kuluja ei oteta huomioon.
- Määritä lainan kuukausittaisen tasaerän suuruus
- Kuinka paljon lainaa on jäljellä silloin, kun puolet takaisinmaksuajasta on kulunut?
- Kuinka paljon korkoa Kristian maksaa yhteensä koko kahden vuoden laina-aikana? [S14/14]
VASTAUS: a. \(356,73€\) b.\(4131,59€\) c. \(561,52€\)
RATKAISU:
Annuiteettikaava on \[\begin{align*} A=Kq^{n}\frac{1-q}{1-q^{n}}, \end{align*}\] missä \(K=8000€\) eli haettu lainan määrä ja \(n=24\) eli takaisinmaksu kuukausien määrä.
Vuosikorko on \(6,6\%\), eli yhdelle kuukaudelle \(\frac{6,6}{12}=0,55\%\).
Nyt suhdeluku \(q=1+\frac{0,55}{100}=1,0055\).
Sijoitetaan nämä annuiteettikaavaan: \[\begin{align*} A=8000€\cdot q^{24}\frac{1-q}{1-q^{24}}=356,7316..., \end{align*}\] joten kuukausierä on \(356,73€\).
Jäljellä oleva aika on $k=$12 kk. Sijoitetaan tämä ja laskettu \(q\) jäljellä olevan lainan kaavaan: \[\begin{align*} V_{k}=Kq^{k}-A\frac{1-q^{k}}{1-q} \end{align*}\]
Nyt saadaan \[\begin{align*} V_{12}=8000q^{12}-A\frac{1-q^{12}}{1-q}=4131,5908... \end{align*}\] Eli lainaa on jäljellä noin \(4131,59€\).
Kristianin maksama korko saadaan laskulla \[\begin{align*} 24A-8000=24\cdot356,73-8000=561,52€ \end{align*}\]
8.
Sijoitustilin talletukselle lasketaan vuotuinen korko, josta vähennetään lähdevero. Jäljelle jäänyt tuotto lisätään tilille vuoden lopussa. Hannele talletti vuoden 2010 lopussa 1000 euroa säästötilille. Vuoden 2013 lopussa tilillä oli 1086,37 euroa. Kyseisellä aikavälillä kuluttajahintaindeksi nousi arvosta 100,0 arvoon 108,5, toisin sanoen inflaatio oli tällä aikavälillä yhteensä \(8,5\%\).
- Laske talletuksen nimellinen vuosikorkoprosentti näiden kolmen vuoden aikana.
- Mikä on talletuksen todellinen korko euroina näiden kolmen vuoden aikana? [K15/14]
VASTAUS: a. \(2,8\%\) b.\(1,37€\)
RATKAISU:
Merkitään vuotuista korkokerrointa \(x\):llä, ja nyt saadaan ehto \[\begin{align*} 1000\cdot x^{3}&=1086,37\\ x^{3}&=\frac{1086,37}{1000}=1,08637\\ x&=\sqrt[3]{1,08637}\\ &=1,0279\\ &≈1,028 \end{align*}\] Nimellinen vuosikorkoprosentti on siten noin \(2,8\).
Inflaation takia rahan arvo on laskenut, eli nykyhetken raha on ollut suurempi arvoista aiempina vuosina.
Vuonna 2010 rahamäärä \(1000€\) on ollut \(1000\cdot 1,085€=1085€\) vuonna 2013.
Kolmessa vuodessa todellista korkoa talletukselle on kertynyt siten \[\begin{align*} 1086,37-1085=1,37€ \end{align*}\]
9.
Allu haluaa ostaa 1800 euroa maksavan maastopyörän. Mummo antaa hänelle 700 euroa. Allu tallettaa mummolta saamansa rahat 30.12.2014 tilille, jonka vuosittainen korkotuotto on \(0,6\%\). Lisäksi Allu asettaa itselleen kuukausttaisen säästötavoitteen: hän tallettaa jokaisen kuukauden ensimmäisenä päivänä tietyn summan, alkaen helmikuusta 2015. Paljonko Allun tulee kuukausittain säästää, jotta hän saa vuoden 2015 loppuun mennessä kokoon 1800 euroa? Oletetaan, että jokaisessa kuussa on 30 päivää ja että lähdevero on \(30\%\). [S16/13]
VASTAUS: \(99,53€\)
RATKAISU:
Vuoden sisällä korko määräytyy tilin keskimääräisen saldon mukaan. Tammikuussa tilillä on \(700€\). Edelleen helmikuussa tilillä on \(700+x€\), jossa \(x\) on kuukausitalletuksen määrä. Samoin voidaan laskea maaliskuun saldon määrä, kun talletuksia on tehty jo kahdesti, jolloin saldo on \(700€+2x\).
Keskimäärin tilillä on \(\frac{700+(700+x)+(700+2x)+...+(700+11x)}{12}=700+\frac{66}{12}x €\)
Korko lähdeverojen jälkeen on nyt \((700+\frac{66}{12}x)\cdot0,006\cdot0,7\). Pääoma vuoden lopussa on \[\begin{align*} 700+11x \end{align*}\] Saadaan edelleen yhtälö \[\begin{align*} 700+11x+(700+\frac{66}{12}x)\cdot0,0042=1800\\ x=99,53€ \end{align*}\]
10.
Suomalaisten kotitalouksien talletusten kokonaisarvo oli 80 778 000 000 euroa vuoden 2015 lopussa. Näiden talletusten keskimääräinen korko oli \(0,32\%\). Valtiovarainministeriö yrittää arvioida talletusten koroista saatavan vuoden 2017 lähdeveron suuruutta seuraavien oletusten pohjalta: kotitalouksien talletusten arvo noudee vuoden 2016 loppuun mennessä \(1,5\%\) ja edelleen \(1,0\%\) vuoden 2017 loppuun mennessä. Lisäksi arvioidaan, että keskikorko laskee 0,05 prosenttiyksikköä kumpanakin vuonna.
Kuinka paljon Suomen valtio saa tämän arvion perusteella talletusten koroista perittävää lähdeveroa vuodelta 2017, kun lisäksi oletetaan, että lähdeveroprosentti on koko ajan 30? Anna vastaus miljoonan euron tarkkuudella. [K17/10]
VASTAUS: 55 miljoonaa euroa
RATKAISU:
Muunnetaan ensin kotitalousten nousuprosentit: \[\begin{align*} 1,5\%\rightarrow1,015\\ 1,0\%\rightarrow1,01 \end{align*}\]
Vuoden 2017 lopussa talletusten arvioitu kokonaismäärä on \(80778000000\cdot1,015\cdot1,01=82809566700\).
Arvioitu talletusten korko on \(0,32\%-2\cdot0,05\%=0,22\%\) Josta talletuksille maksettu korko on \(82809566700\cdot0,0022≈182181000\).
Verot \(182181000\cdot 0,3≈54654000\)
Eli noin \(55\) miljoonaa euroa.
Lisätehtäviä verkossa
Lähteet
- https://www.kauppalehti.fi/porssi/valuutat/EURUSD
- https://www.ecb.europa.eu/stats/policy_and_exchange_rates/euro_reference_exchange_rates/html/index.en.html
- https://www.vero.fi/contentassets/653c812344f84cd1ab790e899e989305/kunnat2019s.pdf
- https://op.media/talous/raha-ja-arki/%22kaikkien-vahennysten-jalkeen-perintoveron-pienuus-yllatti%22-nain-kiistelty-vero-maaraytyy-da7617f1048540a0a06f344dec9572b6
- https://vm.fi/verotus/henkiloverotus/perinto-ja-lahjaverotus
- https://vm.fi/verotus/henkiloverotus/perinto-ja-lahjaverotus
https://www.geogebra.org/m/bsfvshee
https://www.geogebra.org/m/mmp9ukxf
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.