Osittaisdifferentiaaliyhtälöt
Ennen tähän materiaaliin perehtymistä kertaa tarvittaessa moniulotteinen derivointi.
Merkitys
Tavallisissa DY:issä on vain yksi muuttuja, kuten etäisyys tai aika. Useamman muuttujan tilanteessa päädytään osittaisdifferentiaaliyhtälöihin (ODY).
Esimerkiksi kemiallisessa reaktiossa aineen konsentraatio muuttuu ajan mukaan, ja reaktion nopeus riippuu lämpötilasta
Konsentraatiota voidaan siis kuvata funktiolla
Esimerkiksi elektronin potentiaalienergia epähomogeenisessa sähkökentässä riippuu sen sijainnista, eli potentiaaliernergia on paikan funktio
Tällaisten usean muuttujan funktioiden muutosta voidaan kuvata osittaisderivaattojen avulla. Osittaisderivaattojen vuoksi DY:t ovat osittaisdifferentiaaliyhtälöitä.
Esimerkki: Aaltoyhtälö
Aaltoyhtälö on osittaisdifferentiaaliyhtälö, joka kuvaa aaltojen käyttäytymistä. Aaltoyhtälön ratkaisu on aaltofunktio, joka voi kuvata esimerkiksi viritetyn langan värähtelyä tai paineen vaihtelua ilmassa.
Yhdessä ulottuvuudessa aaltoyhtälö on missä
on aika,
tarkasteltava piste ja
aallon etenemisnopeus. Yhtälön ratkaisulla eli funktiolla
on siis kaksi muuttujaa ja se kertoo aallon aiheuttaman poikkeaman tasapainoasemasta pisteessä
ajanhetkellä
Osoitetaan sijoittamalla, että kyseessä on eräs ODY:n toteuttava funktio. Funktion osittaisderivaatat ovat Tästä näemme, että
joten funktio toteuttaa aaltoyhtälön.
Tässä GeoGebrassa on kuvattuna kolme aaltoyhtälön ratkaisua:
Voit muuttaa aikaa liukusäätimestä tai käynnistää animaation vasemman alakulman painikkeesta.
Aaltoyhtälö voidaan myös laajentaa useampaan ulottuvuuteen. Kaksiulotteisessa yhtälössä aaltofunktio on kolmen muuttujan funktio
joka siis kertoo aallon aiheuttaman poikkeaman pisteessä
ajanhtekellä
Tällä voisimme kuvata vaikka rumpukalvon värähtelyä, jolloin poikkeama on
-suunnassa. Useamman muuttujan tilanteessa aaltoyhtälön ratkaiseminen vaikeutuu huomattavasti.
Erityisesti kvanttimekaniikassa tärkeä käsite on ajasta riippumaton aaltoyhtälö, jossa aaltofunktio ei riipu ajasta, eli Tällöin esimerkiksi kaksiulotteinen aaltofunktio on kahden muuttujan funktio
joka kuvaa stationaarista tilaa.
Aiemmin esitetyt aaltoyhtälöt ovat ajasta riippuvia, eli
Tässä ja
voivat olla mitkä tahansa kahdesti derivoituvat funktiot. Ratkaisujoukko on siis paljon laajempi verrattuna toisen asteen tavalliseen DY:hyn. Luonnollisesti myös ensimmäisenä näyttämämme ratkaisu voidaan esittää tässä muodossa, sillä
ODY:n kaikkien ratkaisujen löytäminen ei yleensä ole niin keskeistä, vaan halutaan löytää ne ratkaisut, jotka toteuttavat tietyt reunaehdot.
Esimerkiksi voisimme etsiä aaltoyhtälölle ratkaisuja reunaehdoilla jolloin ratkaisut olisivat
pituiseen kieleen syntyviä seisovia aaltoja.
ODY:n separointi
Periaate
Periaate osittaisdifferentiaaliyhtälön separoinnissa on samanlainen kuin tavallisessa DY:ssä: erotellaan muuttujat eri puolille yhtälöä.
ODY:n separoinnissa tuntemattoman funktion oletetaan olevan yhden muuttujan funktioiden tulo.
Olkoon tuntematon kahden muuttujan funktio. Tällöin
ODY:yn voidaan tehdä sijoitus
missä
ja
ovat tuntemattomia yhden muuttujan funktioita.
Huomaa, että:
- Separointi toimii vastaavasti myös useamman muuttujan funktioille.
- Uusia funktioita merkitään usein muuttujiensa isommilla symboleilla.
Sijoituksen jälkeen funktiot ja
voidaan erotella eli separoida yhtälön eri puolille.
Separoimalla ODY:stä saadaan jokaiselle muuttujalle oma tavallinen DY. Esimerkiksi 1. kertaluvun kahden muuttujan ODY:stä jää ratkaistavaksi kaksi 1. kl. DY:tä missä
ja
ovat funktioita ja
on separointivakio.
Esimerkkejä separoinnista
Oletetaan, että Tämän osittaisderivaatat ovat
ja
Sijoittamalla saadaan
josta voidaan jakaa puolittain funktiolla
jotta saadaan muuttujat
ja
yhtälön eri puolille
Koska eri puolet riippuvat eri muuttujista, mutta ovat silti yhtäsuuret, niiden täytyy olla vakioita. Merkitään tätä vakiota
jolloin
Tästä saadaan kaksi 1. kertaluvun homogeenista DY:tä
Ratkaisuiksi saadaan eksponenttifunktiot
Separoimalla saatu ratkaisufunktio on siis
Lineaarisille ODY:ille, kuten tämä, saadaan kahdesta ratkaisusta
ja
myös kolmas ratkaisu summaamalla
Näin voimme valita mielivaltaisen määrän
vakioita
ja
sekä rakentaa niistä uuden ratkaisun ODY:lle
Tämä on hyvin samanlainen kuin ensimmäisen kertaluvun tapaus. Ainoana erona on, että saadaan kaksi toisen kertaluvun homogeenista DY:tä ratkaistavaksi.
Oletetaan, että Tämän toisen kertaluvun osittaisderivaatat ovat
ja
Sijoittamalla saadaan
jolloin voidaan jakaa puolittain funktiolla
ja saadaan muuttujat
ja
eri puolille yhtälöä
Merkitsemällä separointivakiota
saadaan
eli kaksi VLHDYVakiokertoiminen Lineaarinen Homogeeninen DY:tä
jotka ratkeavat karakteristisella yhtälöllä. Ratkaisut riippuvat vakiosta
joka voi olla
jolloin
jolloin
- tai
jolloin
Vakiot
ja
voidaan valita vapaasti kullekin ratkaisulle, koska ODY:llä ei ole reunaehtoja.
Saatu ratkaisu on jokin näistä kolmesta parista tulona Jos
jne. ovat ratkaisuja, niin ODY:n lineaarisuuden perusteella myös summa
on ratkaisu.
ODY:n separoinnissa yhtälön eri puolilla olevat muuttujat ja
ovat toisistaan riippumattomat. Saadaan siis differentiaaliyhtälö, joka on muotoa
Oikea puoli ei riipu muuttujasta
jolloin vasemman puolen funktio
ei myöskään voi riippua siitä. Siis funktion
täytyy olla vakio. Vastaavasti funktion
on oltava sama vakio.
Tavallisen DY:n separoinnissa yhtälön eri puolilla on muuttujat ja
jotka kuitenkin riippuvat toisistaan, koska toinen muuttuja on funktio
Reuna-arvotehtävälle separointi ei anna punaisen reunaehdon takia kuin yhden ratkaisun. Jos haluaisimme löytää enemmän ratkaisuja tai toteuttaa useampia reunaehtoja, voisimme lisätä näillä reunaehdoilla saatuun yksittäisratkaisuun kaikki ne ratkaisut, jotka saadaan kun
Sijoittamalla saadaan
eli Koska
ja
saamme DY:t ja reunaehdot
eli
Vakio
tulee lämpöyhtälöstä ja on erisuuri kuin nolla. Vakio
ei myöskään voi olla nolla. Siispä separointivakion
on oltava nolla. Tällöin
ja reunaehtojen takia
Separoinnilla saamme ratkaisuksi
Epähomogeenisen ODY:n pystyy separoimaan vain tilanteessa, jossa
on nollaa kaikkialla, joten tässä tilanteessa olisi tarvetta ylimääräisille työkaluille.
Separointi antaa onnistuessaan yhden vakioista riippuvan ratkaisun. Kuitenkin sopivissa tilanteissa näitä vakioita vaihtelemalla saadaan uusia ratkaisuja, joita voidaan myös laskea yhteen. Tällöin päädytään sarjaratkaisuihin.
Tätä varten ODY:n on oltava homogeeninen ja lineaarinen sekä reunaehtojen sopivia, yleensä nollaa.
Schrödingerin yhtälön separointi
Kvanttimekaaninen aaltofunktio toteuttaa toisen kertaluvun ODY:n, joka tunnetaan nimellä Schrödingerin yhtälö. Ajasta riippumaton Schrödingerin yhtälö on missä kolmiulotteisessa tapauksessa:
on hiukkasen aaltofunktio
on Hamiltonin operaattori
on Planckin vakio ja
hiukkasen massa
on Laplacen operaattori
on potentiaalienergia ja
kokonaisenergia. Termi
vastaa hiukkasen liike-energiaa.
Jos potentiaalienergia on annettu, yhtälö on ominaisarvo-ongelma, jossa ratkaistavana ovat ominaisfunktiot ja niitä vastaavat ominaisarvot eli energiat
Schrödingerin yhtälö yhdessä ulottuvuudessa on missä:
on tuntematon aaltofunktio, joka kuvaa
suuntaista aaltoa
on Planckin vakio ja
hiukkasen massa
on potentiaalienergia.
on kokonaisenergia.
Seuraavissa separoinnin sovellusesimerkeissä Schrödingerin yhtälöä on havainnollisuuden vuoksi yksinkertaistettu.
Kvanttimekaaninen aaltofunktio kuvaa järjestelmän kvanttitilaa. Sen itseisarvon neliö antaa todennäköisyystiheyden
Tästä voidaan laskea todennäköisyys sille, että hiukkanen sijaitsee
-suunnassa välillä
integraalilla
Todennäköisyys, että hiukkanen on jollakin alueella
on vastaavasti tiheysfunktion integraali alueen yli, eli
Moniulotteisen integraalin merkinnöistä voit lukea täältä.
Fysikaaliselle aaltofunktiolle vaaditaan normitus. Tämä tarkoittaa sitä, että on oltava mahdollista määrätä aaltofunktion vapaat vakiot siten, että kun alue
kattaa kaikki hiukkasen mahdolliset sijainnit.
Sovellus: Laatikkopotentiaali
Etsitään separoinnin avulla aaltofunktio hiukkaselle, jonka liike on rajoitettu kuution muotoiseen laatikkoon.
Hiukkasen aaltofunktio noudattaa Schrödingerin yhtälöä, joka on ODY
missä havainnollisuuden vuoksi on jätetty pois vakioita ja muutettu etumerkkejä.
Merkitään laatikon sivun pituudeksi ja valitaan yksi laatikon kulma pisteeksi
siten, että vastakkainen kulma on pisteessä
Koska hiukkanen ei pääse laatikosta ulos, potentiaalienergia on yksinkertaisesti
Kun
Schrödingerin yhtälö toteutuu vain, jos
Aaltofunktion täytyy olla kaikkialla jatkuva, joten potentiaalienergia määrittelee reunaehdon
jos
tai
on
tai
(Ks. kuva.)
Kun hiukkanen on laatikossa, potentiaalienergiatermi häviää. Ratkaistaan jäljelle jäävä yhtälö separoimalla.
Ratkaistavana on yksinkertaistetusta Schrödingerin yhtälöstä saatu ODY
Separoinnin ensimmäinen vaihe on olettaa, että ratkaistava funktio on muuttujiensa suhteen tulomuotoinen, eli Merkitään muuttujat selkeyden vuoksi vain alaindeksillä. Aaltofunktio on siis
, jonka toisen kertaluvun derivaatat ovat
Sijoittamalla nämä saadaan yhtälö
josta voidaan supistaa funktio
jolloin
Yhtälön oikea puoli on vakio, mutta vasemmalla puolella jokainen termi riippuu eri muuttujasta. Tämä tarkoittaa sitä, että termien täytyy olla vakioita
ja
.
Jokaiselle koordinaatille saadaan muista riippumaton tavallinen DY Tämä on ominaisarvotehtävä, jossa ratkaistavana ovat funktiot
ja ominaisarvot eli vakiot
Kaikki kolme yhtälöä ovat samanlaiset, joten tarkastellaan vain -koordinaattia. Ratkaistavana on toisen kertaluvun VLHDY
Tämän ratkaisut saadaan karakteristisen yhtälön
juurista
- Jos
saadaan lineaarinen aaltofunktio
Reunaehtojen perusteella tämä on
kaikilla
Kokonaisaaltofunktio on siis
kaikilla
Tätä ei voida normittaa, joten se ei ole hyväksyttävä ratkaisu.
- Jos
saadaan aaltofunktioksi
Tarkistetaan reunaehdot sijoittamalla
eli
ja edelleen
Tämän perusteella vakiot ovat
jolloin aaltofunktio on jälleen nollafunktio eli ei hyväksyttävä ratkaisu.
- Jos
karakteristisen yhtälön ratkaisut ovat imaginääriset
ja aaltofunktio on
Sijoitetaan tämä reunaehtoihin
Ensimmäisestä saadaan vakio
Nyt halutaan, että
ettei tulos olisi jälleen nollafunktio. Merkitään
Toisesta yhtälöstä saadaan nyt
eli sinin jaksollisuuden mukaan
missä
on kokonaisluku. Näin vakiolle
saadaan ehto
missä uusi vakio
on
-koordinaatin kvanttiluku. (Normittaminen vaatii, että
Sen merkki voidaan jättää vakiolle
)
Muuttujan aaltofunktio on reunaehtojen avulla
Muiden koordinaattien aaltofunktiot saadaan täsmälleen samalla tavalla korvaamalla
koordinaateilla
ja
Hiukkasen aaltofunktio laatikossa on
Vakiot
ja
voidaan määrittää normittamalla aaltofunktio:
Vaaditaan, että hiukkanen on laatikossa todennäköisyydellä Tämä voidaan tehdä yhdessä ulottuvuudessa siten, että todennäköisyys olla laatikossa on kussakin koordinaatissa
Normitus voidaan siis käsitellä yhden muuttujan integraaleina. Otetaan tarkasteluun koordinaatti.
Aaltofunktio on normitettu, jos
Samoin funktioille
ja
Integraali on Oletetaan, että vakiot
ovat positiivisia reaalilukuja, jolloin
Tehdään muuttujanvaihto:
Rajat ovat
ja
Nyt integraalista saadaan trigonometrian kaavoilla
Tästä saadaan
Siis täytyy olla Vakio oletettiin positiiviseksi. Se ei riipu koordinaatista
eli
Normitettu kokonaisaaltofunktio laatikon sisällä on kun
on laatikon tilavuus ja
ja
ovat positiivisia kokonaislukuja
Sovellus: Vetyatomin potentiaali
Schrödingerin yhtälö vetyatomille voidaan ratkaista separoimalla pallokoordinaateissa, jolloin saadaan kolme tavallista toisen kertaluvun DY:tä. Näistä yksi on helposti ratkaistavissa ja kaksi muuta johtavat monimutkaisempiin sarjaratkaisuihin, joita ei tässä käsitellä.
Vetyatomi on atomeista ainoa, jolle Schrödingerin yhtälö on ratkaistu täydellisesti. Useamman elektronin systeemin matemaattinen mallintaminen on erittäin vaikeaa.
Karteesisissa koordinaateissa vetyatomin elektronille Schrödingerin yhtälö on toisen kertaluvun ODY
missä:
Havainnollisuuden vuoksi on jätetty pois vakioita ja muutettu etumerkkejä.
on tuntematon aaltofunktio.
Potentiaalienergiatermin vuoksi separointi koordinaattien
suhteen ei onnistu. Potentiaali riippuu vain etäisyydestä
joten se on pallosymmetrinen. Käytetään siis pallokoordinaatteja
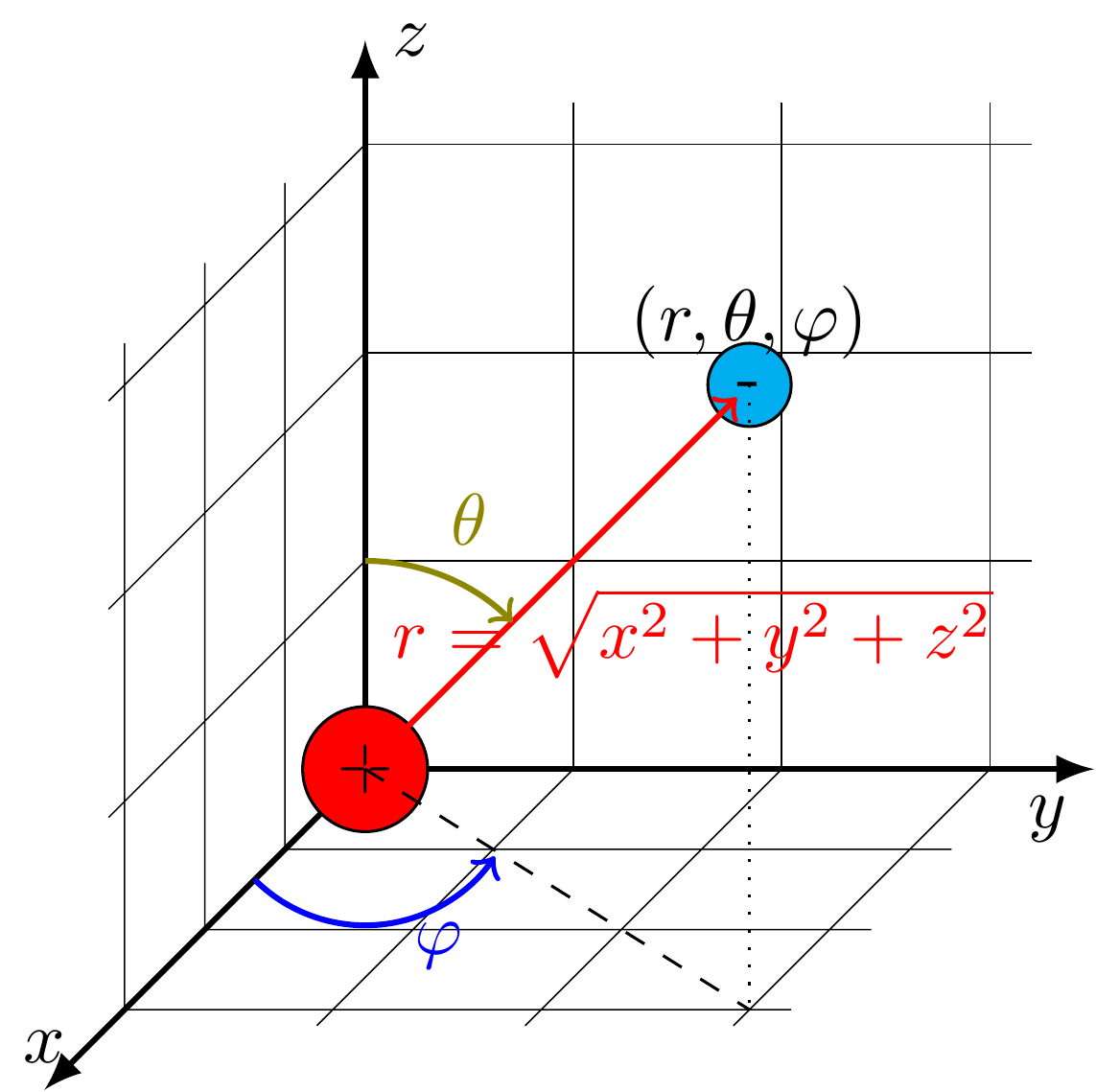
Nyt aaltofunktio on Schrödingerin yhtälö pallokoordinaateissa on monimutkaisempi, mutta voidaan separoida yritteellä
Funktiota
kutsutaan radiaaliosaksi ja funktiota
kulmaosaksi.
Kirjoitetaan yksinkertaistettu Schrödingerin yhtälö muodossa joka on pallokoordinaateissa hieman monimutkainen
Sijoitetaan yhtälöön
jolloin
Separoinnin tavoite on erotella punainen (radiaaliosa) ja sininen (kulmaosa) yhtälön eri puolille. Merkitään kulmaosaa funktiolla
eli
Sijoitetaan
ja kirjoitetaan auki radiaaliosan
derivaattatermi
. Sitten vain sievennetään
Yhtälön termit voidaan jakaa tekijällä
ja saadaan
Tämän termit voidaan kertoa tekijällä
jolloin yhtälö on
Näin saadaan radiaaliosa ja kulmaosa separoitua yhtälön eri puolille:
Tästä voidaan päätellä, että molemmat puolet ovat vakioita. Radiaaliosalle
saadaan differentiaaliyhtälö
Kulmaosalle saadaan yhtälö
Avaamalla funktio
saadaan
Separoidaan nyt kulmat
ja
sijoittamalla
, jolloin yhtälö on
Tästä saamme eroteltua kulmaosat differentiaaliyhtälöiksi: Elevaatiokulmalle
ja atsimuuttikulmalle
Atsimuuttikulman funktion DY on ominaisarvo-ongelma
Tämä ratkeaa sijoituksella
missä
on imaginääriyksikkö, jolle pätee
Atsimuuttikulma
kiertää
-akselin ympäri, eli funktion on oltava
-jaksollinen. Siis
kaikilla
Tästä seuraa, että ratkaisuja on vain ominaisarvoilla
Nämä ratkaisut voidaan esittää muodossa
missä
on imaginääriyksikkö ja
Tästä saimme rajoituksen mahdollisille ominaisarvolle
, kvanttiluvun
Elevaatiokulman DY on
Atsimuuttikulma asetti rajoituksen
Pienellä siirtelyllä saadaan
Tästä saadaan sijoituksella
ja
differentiaaliyhtälö
Tälle saadaan ratkaisu sarjojen avulla, kunhan
ja
Näille ratkaisuille on annettu nimeksi Legendren liittofunktiot. Näin saamme myös rajoituksen lambdalle, eli uuden kvanttiluvun. Sarjaratkaisuja ei käsitellä tässä.
Radiaaliosalle saimme DY:n Elevaatiokulman ratkaisut rajoittivat lambdan arvoiksi
Sijoittamalla ja uudelleenjärjestämällä saamme DY:n muotoon
Tälle saadaan fysikaallisesti järkeviä ratkaisuja sarjojen avulla sopivilla
arvoilla
. Ratkaisut ovat
ja
riippuvia funktioita
Sarjaratkaisuja ei käsitellä tässä.
Radiaaliosan DY on missä
on vakio, kun
Sijoituksella saadaan DY muotoon
joka on yksinkertaistamamme yksiulotteinen Schrödingerin yhtälö, josta potentiaalienergia on korvattu efektiivisellä potentiaalilla
Sijoituksen yksityiskohdat
Sijoituksella radiaalifunktio on
ja sen derivaatta tulosäännöllä
Toinen derivaatta on jälleen tulosäännöllä
Nyt Schrödingerin yhtälön ensimmäinen termi on Sijoittamalla muihin termeihin
saadaan
Tästä voidaan supistaa
jolloin saadaan
Tarkemmalla laskemisella voitaisiin osoittaa, että vetyatomin Schrödingerin yhtälöllä on fysiikan kannalta järkeviä ratkaisuja vain, jos
arvoa vastaava ratkaisu on separoinnilla saatavien ratkaisujen tulo kerrottuna normitusvakiolla
,
Nämä ovat siis tehtävän ominaisarvot sekä ominaisarvoja vastaavat ominaisfunktiot. Luvut
ja
kuvaavat elektronin tilaa, mutta eivät vaikuta sen energiaan.
Muistutus: Yllä oli Schrödingerin yhtälössä merkitty joitakin vakioita ykkösellä, jotta itse separoinnin vaiheet tulisivat paremmin esiin.
Reuna-arvotehtäviä ja sarjaratkaisuja
Tässä kappaleessa tarkastellaan joidenkin ODY-reuna-arvotehtävien ratkaisemista.
Muutamassa esimerkissä sovelletaan sarjaratkaisuja. Nämä on merkitty sinisellä summamerkillä
Laplacen yhtälö
Yleinen fysiikassa esiintyvä ODY on Laplacen yhtälö.
Olkoon funktio Tällöin sen Laplacen yhtälö on
joka voidaan kirjoittaa myös nabla-merkinnällä
Tämä on tärkeä toisen kertaluvun osittaisdifferentiaaliyhtälö, jonka ratkaisuja kutsutaan harmonisiksi funktioiksi.
Laplacen yhtälö ja harmoniset funktiot esiintyvät muun muassa ongelmissa koskien:
- Sähkömagnetismia
- Sähköisiä potentiaaleja
- Magneettisia potentiaaleja
- Tähtitiedettä
- Gravitaatiopotentiaaleja
- Virtausmekaniikkaa
- Termodynamiikkaa
Karteesisessa koordinaatistossa
Käyräviivaiset koordinaatistot
Napakoordinaateissa
Sylinterikoordinaateissa
Pallokoordinaateissa
Katso myös koordinaatistojen sivut.
Seuraavissa esimerkeissä ratkaistaan Laplacen yhtälöä erilaisilla reunaehdoilla.
Aloitetaan ratkaisun etsiminen separoimalla, jolloin Laplacen yhtälöstä saadaan
eli
Koska yhtäsuuruus pätee kaikille
on molempien puolien oltava vakiota
Lisäämällä reunaehdot saadaan
Reuna-arvotehtävä funktiolle
on ratkaistu täällä. Sen ratkaisu on
missä
on kokonaisluku. Näillä vakion
arvoilla funktion
DY:n toteuttaa
Reunaehdosta
saadaan
Merkitään molempia vakiolla
eli
Yhdistämällä
ja
saadaan ratkaisuja Laplacen yhtälöön
Tämä ei täytä viimeistä reunaehtoa
. Sijoittamalla saadaan
joka toteutuu vain jos
ja
Reuna-arvotehtävän ratkaisu on
Ratkaistaan seuraavaksi sarjojen avulla yleisempi tilanne, jossa Edellisessä tehtävässä saimme äärettömästi ratkaisuja
Koska Laplacen yhtälö on lineaarinen ODY, saamme uusia ratkaisuja myös näiden summista. Koska kolmelle sivuista oli asetettuna arvoiksi nollaa, säilyvät myös nämä ominaisuudet ratkaisuja yhdistellessä. Reuna-arvotehtävälle
saadaan siis ratkaisuiksi
Voimme yrittää etsiä sopivat kertoimet
joilla saisimme
Tässä voidaan hyödyntää tietoa, että
Kertomalla molemmat puolet funktiolla
ja integroimalla saadaan
Kertoimet
saadaan siis kaavalla
Reunaehdon takia on selvää, että ratkaisua kannattaa etsiä napakoordinaatistossa funktiolle Tällöin Laplacen yhtälö on muotoa
Separoinnista, eli oletuksella
saadaan
Funktiolle
asetetut reunaehdot tulevat siitä, että atsimuuttikulman funktion on oltava jaksollinen. Ratkaisuksi saadaan
Kun
Muilla lambdan arvoilla saadaan Eulerin DY
Tämä ratkeaa yritteellä
josta saadaan
Kun otetaan huomioon reuna-arvo
saadaan
eli
Yhdistämällä nämä saadaan Laplacen yhtälölle ratkaisuiksi
Joskus tehtävän symmetrioiden perusteella voidaan päätellä, että ratkaisu on joidenkin muuttujien suhteen vakio. Tällöin osittaisderivaatta kyseisen muuttujan suhteen on nolla. Esimerkiksi tilanteessa, jossa tiedetään ratkaisun riippuvan vain etäisyydestä origoon, kannattaa käyttää pallokoordinaatteja, jolloin Tästä voidaan päätellä, että
josta integroimalla saadaan
Tämä voisi kuvastaa esimerkiksi origossa olevan pistevarauksen aiheuttamaa potentiaalikenttää.
Vastaavasti kolmiulotteisen tilanteen ollessa symmetrinen -akselin kierron suhteen saadaan pallokoordinaateissa
Separoinnilla päädyttään DY:ihin
josta edelleen sarjaratkaisujen ja Legendren polynomien
avulla saadaan
Sylinterikoordinaateissa
-akselin kierron suhteen symmetrisessä tilanteissa saadaan
josta separoimalla päädytään DY-pariin
Lämpö- eli diffuusioyhtälö
Tässä kappaleessa käsitellään lämpöyhtälöä eli diffuusioyhtälöä, joka kuvaa lämmön tai aineen diffuusiota. Lämpöyhtälö on toisen kertaluvun ODY, joka on yksiulotteisessa tapauksessa missä
on lämpötilafunktio,
on tarkasteltava piste ja
ajanhetki.
Ajasta riippumaton lämpöyhtälö, eli kun , on Laplacen yhtälö
joka kuvaa lämpöprofiilin stationaarista tilaa.
Sovellus: sauvan lämpöjakauman kehitys
Tässä tutkitaan yksiulotteista lämpöyhtälöä erilaisilla reunaehdoilla.
Tämä ODY kuvaa lämmön jakautumista -pituisessa sauvassa, jonka päät pidetään 0-asteisina. Lämpötila on
missä
on etäisyys sauvan toisesta päästä mitattuna ja
on aika.
Separoidaan ODY, eli etsitään ratkaisua muodossa Tällä yritteellä saadaan
eli
Yhtälön eri puolet riippuvat eri muuttujista, joten niiden täytyy olla vakiot. Saadaan siis kaksi toisistaan riippumatonta DY:tä funktioille
ja
missä
on jokin vakio. Lisäämällä reuna-arvot saadaan
Ratkaistaan ensin funktio
vasemmasta ominaisarvotehtävästä, saadaan
Näitä ominaisarvoja vastaa funktion
DY:n ratkaisu
Ratkaisuiksi kelpaavat siis kaikki funktiot muotoa
Koska alkuperäinen ODY on lineaarinen, voimme myös yhdistellä näitä ratkaisuja ja saamme aina uuden ratkaisun, joka toteuttaa ODY:n.
Tämä ODY kuvaa ympäristöstä eristettyä -pituista sauvaa. Lämpötila on
missä
on etäisyys mitattuna toisesta päästä ja
on aika.
Separoidaan, eli oletetaan, että Tällöin
Jakamalla funktiolla
saadaan
Koska oikea puoli ei riipu ajasta, on sen oltava ajan suhteen vakio eli
Näin ollen myös
Reunaehdoista saamme paikan differentiaaliyhtälölle reuna- ja ominaisarvotehtävän
Tälle saadaan ratkaisuja vain, kun
ja tällöin
Näitä vakion
arvoja vastaa ajan funktiot
Nämä yhdistämällä saadaan ratkaisuiksi
Kaksi sauvaa ovat lämpötiloissa ja
Sauvat tuodaan päistään yhteen, jolloin lämpötilajakaumaa hetkellä
kuvaa yllä esitetty paloittain määritelty funktio
, missä
on etäisyys mitattuna toisen tangon uloimmasta päästä.
Etsitään lämpöyhtälön ratkaisu, joka toteuttaa myös tämän reunaehdon. Edellisessä tehtävässä saimme tuloksen, että on yhtälön ratkaisu kaikilla
Lämpöyhtälön lineaarisuudesta sekä reuna-arvojen homogeenisuudesta
seuraa, että myös
toteuttaa sekä lämpöyhtälön, että edellisen tehtävän reuna-arvot (kunhan sarja suppenee). Etsitään kertoimet
siten, että
Helpointa on määrittää kerroin
koska
kaikilla
Tällöin saadaan
Funktion
integraali voidaan jakaa kahtia, jolloin
Siis
Käytetään muiden kertoimien ratkaisemiseen tietoa, että Tällöin kertomalla funktiolla
missä
ja integroimalla saadaan
Lasketaan tämän avulla kertoimet
kun
Parillisilla
tästä tulee nolla, ja parittomilla
saadaan
missä
Nyt tiedetään kaikki kertoimet, joten tehtävän ratkaisu on
Tarkastellaan edellisen tehtävän ratkaisun kuvaajaa , kun
ja
. Säädettävät muuttujat ovat summan yläraja
sekä aika
. Ajanhetkellä
vakion
kasvattaminen antaa paremman approksimaation lähtötilanteesta. Mustalla piirretty lähtötilanne kuvastaa sauvojen lämpötiloja yhdistämishetkellä. Kasvattamalla
arvoa voit katsoa kuinka tämä lämpöjakauma kehittyy ajan kuluessa.
Lämpötila näyttää asettuvan sauvojen keskilämpötilaan, huomaa kuinka summan sisällä eksponenttifunktio pakottaa kaikki termit kohti nollaa Voit myös todeta, että suuret lämpötilaerot tasaantuvan nopeammin.
 Sovellus: Lämmön johtuminen
Sovellus: Lämmön johtuminen
Tässä tutkitaan lämmön johtumista, kun systeemin reunaehtona on jaksottainen lämpötilan vaihtelu. Systeemi voisi olla esimerkiksi Auringon lämmittämä maaperä, jos Maapallon sisältä tulevaa lämpöä ei huomioida.
- Ensimmäisenä on lämpöyhtälö, jossa
kuvastaa syvyyttä ja
aikaa.
- Seuraavana on reunaehto, joka kertoo, että pinnalla lämpötila vaihtelee jaksollisesti ajan suhteen.
- Viimeinen reunaehto seuraa siitä, että lämpötilan vaihtelu on pientä riittävän syvällä.
Käytetään ratkaisemiseen Fourierin sarjaa ajan suhteen missä
on syvyydestä
riippuva kerroin ja
imaginääriyksikkö. Tehtävän ymmärtämiseksi on osattava laskea kompleksiluvuilla.
Sijoittamalla sarja lämpöyhtälöön saadaan
Kertoimille täytyy siis olla
kaikilla
Syvyydestä riippuvien kerrointen on siis toteutettava DY
kaikilla
Tämän karakteristinen yhtälö on missä imaginääriyksikkö on Eulerin kaavan
mukaan
Yhtälön juuret ovat
Tunkeutumissyvyyden
avulla tämä voidaan kirjoittaa muotoon
Dy:n yleiset ratkaisut ovat siis
Ratkaisuun ei saa jäädä
kerrointa, koska haluamme sen menevän nollaan kun
Näin ollen, kun
saadaan
Kun
neliöjuuressa on negatiivinen luku, joten
Kerroinfunktioiden yleinen ratkaisu on
Toistaiseksi olemme saaneet Pinnalla, eli kun
saamme
Tämän perusteella voimme olettaa, että kaikki termit paitsi
ja
ovat nollaa, siispä
Eulerin kaavalla
saadaan
Saadaan yhtälöryhmä
Sijoittamalla nämä kertoimet saadaan
ja tästä vielä sieventämällä
missä
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.