Derivointi useammassa ulottuvuudessa

# vektorifunktio

Vektorifunktioista

Vektorifunktioksi sanotaan funktiota, joka saa arvoinaan vektoreita.

Kirjallisuudessa käytetään usein lihavoitua vektorimerkintää $\mathbf{v}$ vektorifunktiolle.

Mikä merkintä milloinkin, $\ve v$ vai $\ve v(x,y,z)?$

Vektorifunktioiden yhteydessä on helppo sekaantua siitä, millä merkitään mitäkin. Vektorifunktioihin liittyvät merkinnät voidaan jakaa kolmeen osaan:

funktion nimi, eli millä symbolilla funktio tunnistetaan
funktio, eli sääntö minkä mukaan funktio määritellään
funktion arvo, eli se mitä funktio tuottaa

Seuraavassa taulukossa funktio on reaaliarvoinen yhden muuttujan funktioFunktio, jolla on yksi argumentti. Esim. f(x) = 3x^2-4x ja $\ve v$ vektoriarvoinen kolmen muuttujan funktio:

Viimeisellä rivillä on myös yleinen merkintätapa, jossa jätetään argumentit (x,y,z) näkyvistä funktion säännöstä.

Fysiikassa merkitään lisäksi usein argumentteja (x,y,z) lyhemmin vektorilla $\ve r$ , jolloin esimerkiksi $\begin{aligned} &f(x,y,z) = f(\ve r), \\ &g(x,y,z,t) = g(\ve r, t). \end{aligned}$

# vektorikentta

Vektorikenttä

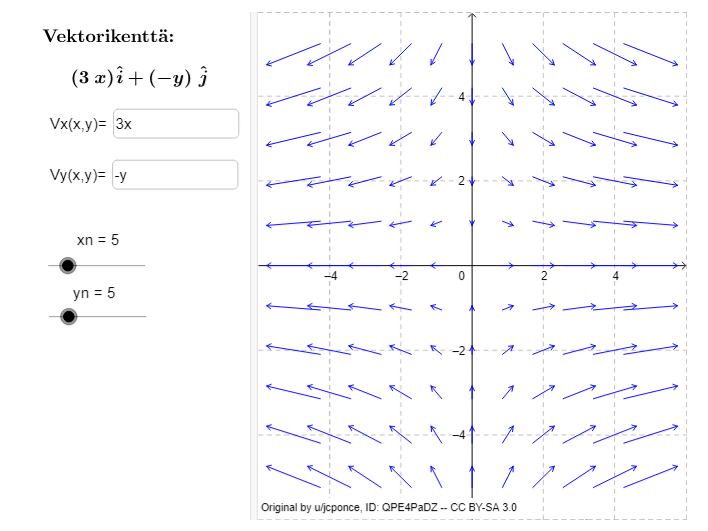
Vektorifunktioita havainnollistetaan vektorikenttien avulla. Jokaiseen vektorikenttään liittyy jokin vektorifunktio. Usein termillä vektorifunktio ja vektorikenttä tarkoitetaan kuitenkin samaa asiaa.

Vektorikenttä piirretään piirtämällä jokaiseen pisteeseen vektorifunktion tuottama vektori (eli arvo) kyseisessä pisteessä. Piirrettyjen vektoreiden pituudet skaalataan mahdollisesti.

Vektorikenttä visuaalisesti Mitä se siis tarkoittaa?

Yllä taulukossa esitellyn vektorifunktion $\ve v$ vektorikenttä on piirretty alle joihinkin pisteisiin.

Tarkista, onko taulukon $\ve v(0, 3)$ piirretty oikein tutkimalla pisteestä (0, 3) lähtevän vektorin suuntaa. Vektorien pituudet eivät ole oikein, mutta suunnat ja suhteelliset pituudet ovat.

Voit vaihtaa liukusäätimistä piirrettyjen vektorien määrää sekä vektorikenttää vaihtamalla syöttökenttien sisältöä.

# geo_vektorikenttä

# laskusääntöjä

Laskusääntöjä derivointiin useammassa ulottuvuudessa

Merkitään

ja reaaliarvoisia kolmen muuttujan funktioita
$\ve v$ ja $\ve u$ vektoriarvoisia kolmen muuttujan funktioita
$\displaystyle \nabla = \i \frac{\partial}{\partial x} + \j \frac{\partial}{\partial y} + \k \frac{\partial}{\partial z}$ (nabla-operaattori).

Tällöin seuraavat säännöt ovat voimassa:

Osittaisderivaattojen ketjusääntö

Jos on reaaliarvoinen kahden muuttujan funktio siten, että sen muuttujat ovat riippuvaisia esimerkiksi ajasta, niin sille voidaan johtaa oma ketjusääntö kun derivoidaan ajan suhteen.

Olkoon siis $g(t)=f\left(u(t),v(t)\right).$ Tällöin

$g'(t)=\osit[f(u(t),v(t))]{u}u'(t)+\osit[f(u(t),v(t))]{v}v'(t).$

Leibnizin merkinnöillä tämä näyttää hieman erilaiselta. Merkitään z=f(u(t),v(t)), x=u(t) ja y=v(t). Tällöin ketjusääntö saa muodon

$\frac{dz}{dt}=\osit[z]{x}\frac{dx}{dt}+\osit[z]{y}\frac{dy}{dt}.$

# gradientti

Gradientti

Funktion gradientti on vektorifunktio, joka määritellään operaatiolla

$\nabla f = \osit[ f]{x}\i + \osit[ f]{y}\j + \osit[ f]{z}\k.$

Gradientti on vastine yksiulotteisen funktion derivaatalle.

Pisteessä (x,y,z) gradientti $\nabla f(x,y,z)$ on vektori, joka osoittaa suunnan, johon funktion arvo kasvaa nopeiten pisteestä (x,y,z) . Gradienttivektorin pituus $|\nabla f|$ on kasvun suuruus.

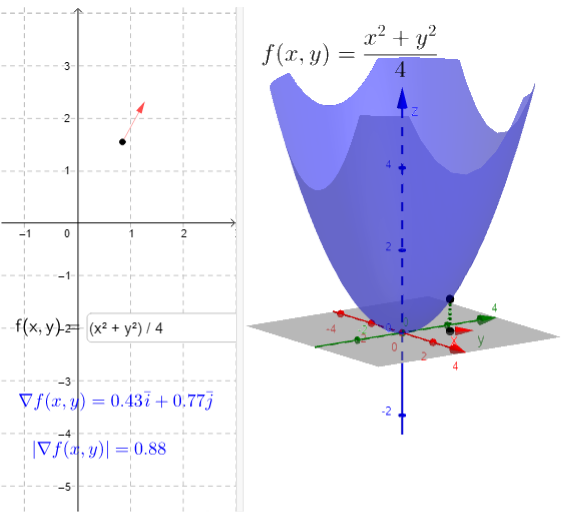
Gradientti visuaalisesti Mitä se siis tarkoittaa?

Appletissa näkyy funktion tietyssä pisteessä oleva gradienttivektori tasossa (vasemmalla) sekä kohta funktion kuvaajalla (oikealla).

Pistettä voi liikuttaa molemmissa kuvissa ja tutkia, miten kuvaajan jyrkkyys vaikuttaa vektorin pituuteen ja mihin suuntaan vektori osoittaa verrattuna kuvaajan muotoon.

Vektorifunktiota voi myös halutessaan muuttaa syöttökentästä.

# geo_gradientti

Esimerkkejä gradientista

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Gradientin laskeminen: Laske $\nabla f$ kun $f(x,y,z) = \sqrt{x^2 + z^2 + y^2}$ .

Lasketaan funktion gradientti määritelmän mukaan. Aloitetaan osittaisderivaattojen laskemisesta.

Laskuissa tulee muistaa, minkä muuttujan suhteen derivoidaan, ja muita muuttujia tulee käsitellä kuin vakioita. Kaikissa :n osittaisderivaatoissa on kyse yhdistetyn funktion derivoinnista, missä "ulkofunktio" on neliöjuuri ja "sisäfunktio" on muuttujan neliö (esim. z^2 ).

$\begin{aligned} \ositx f(x,y,z)=\frac{1}{2}\frac{1}{\sqrt{x^2+y^2+z^2}}2x=\frac{x}{\sqrt{x^2+y^2+z^2}} \end{aligned}$

$\begin{aligned} \osity f(x,y,z)=\frac{1}{2}\frac{1}{\sqrt{x^2+y^2+z^2}}2y=\frac{y}{\sqrt{x^2+y^2+z^2}} \end{aligned}$

$\begin{aligned} \ositz f(x,y,z)=\frac{1}{2}\frac{1}{\sqrt{x^2+y^2+z^2}}2z=\frac{z}{\sqrt{x^2+y^2+z^2}}. \end{aligned}$

Yhdistetään nämä gradienttivektoriksi

$\begin{aligned} \nabla f(x,y,z)&=\frac{x}{\sqrt{x^2+y^2+z^2}}\i+\frac{y}{\sqrt{x^2+y^2+z^2}}\j+\frac{z}{\sqrt{x^2+y^2+z^2}}\k\\ &=\frac{x\i+y\j+z\k}{\sqrt{x^2+y^2+z^2}}. \end{aligned}$

Mitä tämä tarkoittaa: Gradientiksi saatiin siis pisteen (x,y,z) paikkavektorin suuntainen yksikkövektori eli vektorin $x\i+y\j+z\k$ suuntainen yksikkövektori. Funktio siis kasvaa nopeiten aina origosta poispäin, mutta samalla nopeudella joka pisteessä.

Gradientti: Olkoon (x', y', z') jokin piste ja $\ve r(x,y,z)$ vektori pisteestä pisteeseen (x, y, z) ja vektorin $\ve r$ pituus. Osoita, että $\nabla (r^2) = 2\ve r$ .

Aluksi on hyvä huomata, että pisteessä (x',y',z') esiintyvät koordinaatit ovat vakioita ja pisteessä (x,y,z) esiintyvät ovat muuttujia.

Muodostetaan aluksi vektorille $\ve r$ lauseke. Pisteestä pisteeseen oleva vektori saadaan vähentämällä kohdepisteen koordinaateista lähtöpisteen koordinaatit. Tällöin

$\begin{aligned} \ve r(x,y,z)=(x-x')\i+(y-y')\j+(z-z')\k. \end{aligned}$

Lasketaan nyt tämän vektorin pituuden neliö

$\begin{aligned} r^2=|\ve r|^2&=\left(\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}\right)^2\\ &=(x-x')^2+(y-y')^2+(z-z')^2. \end{aligned}$

Muodostetaan r^2 :n gradientti. Lasketaan siis osittaisderivaatat, missä käsitellään muita kuin derivoitavaa muuttujaa vakiona:

$\begin{aligned} \ositx r^2&=\ositx(x-x')^2+\red{\ositx(y-y')^2}+\red{\ositx(z-z')^2} &&\Big|\red{\text{vakio}}\ \text{muuttujan}\ x\ \text{suhteen}\\ &=2(x-x')\cdot 1\\ &=2(x-x') \end{aligned}$

$\begin{aligned} \osity r^2&=\red{\osity(x-x')^2}+\osity(y-y')^2+\red{\osity(z-z')^2} &&\Big|\red{\text{vakio}}\ \text{muuttujan}\ y\ \text{suhteen}\\ &=2(y-y')\cdot 1\\ &=2(y-y') \end{aligned}$

$\begin{aligned} \ositz r^2&=\red{\ositz(x-x')^2}+\red{\ositz(y-y')^2}+\ositz(z-z')^2 &&\Big|\red{\text{vakio}}\ \text{muuttujan}\ z\ \text{suhteen}\\ &=2(z-z')\cdot 1\\ &=2(z-z'). \end{aligned}$

Nyt

$\begin{aligned} \nabla r^2&=2(x-x')\i+2(y-y')\j+2(z-z')\k\\ &=2\left((x-x')\i+(y-y')\j+(z-z')\k\right)\\ &=2\ve r, \end{aligned}$

mikä haluttiinkin osoittaa.

Tulon gradientti: Osoita, että $\nabla(fg) = f \nabla g + g\nabla f$ .

Käytetään tietoa siitä, että tiedämme vastaavan tulon derivointisäännön yhden muuttujan funktioille. Toisin sanoen tiedämme, että osittaisderivaatoille tulon derivointisäännöt pätevät.

Avataan nyt funktion gradientin määritelmä

$\begin{aligned} \nabla(fg)&=\ositx(fg)\i+\osity(fg)\j+\ositz(fg)\k\\ &=\left(g\ositx f+f\ositx g\right)\i+\left(g\osity f+f\osity g\right)\j+\left(g\ositz f+f\ositz g\right)\k\\ &=g\ositx f\i+f\ositx g\i+g\osity f\j+f\osity g\j+g\ositz f\k+f\ositz g\k. \end{aligned}$

Järjestellään seuraavaksi viimeisen rivin termejä

$\begin{aligned} &g\ositx f\i+f\ositx g\i+g\osity f\j+f\osity g\j+g\ositz f\k+f\ositz g\k\\ &=f\left(\ositx g\i+\osity g\j+\ositz g\k\right)+g\left(\ositx f\i+\osity f\j+\ositz f\k\right)\\ &=f\nabla g+g\nabla f. \end{aligned}$

Siispä $\nabla(fg)=f\nabla g+g\nabla f.$

# nabla

$\color{RedOrange}{\nabla}$ -operaattori eli nabla-operaattori

$\nabla$ -operaattori määritellään kantavektorien ja osittaisderivaattojen avulla

$\nabla=\i\ositx+\j\osity+\k\ositz.$

Tämän operaattorin avulla voi helposti määritellä divergenssin, Laplace-operaattorin sekä roottorin.

Huomaa, että $\nabla$ -operaattorilla itsellään ei ole geometrista tulkintaa, vaan sen hyödyllisyys nousee esiin nimenomaan merkintöjen kautta.

# divergenssi

Divergenssi (divergence)

Vektorifunktion $\ve v$ divergenssi on reaaliarvoinen funktio, joka määritellään pistetulona

$\nabla \cdot \ve v=\ositx v_1+\osity v_2+\ositz v_3.$

Pisteessä (x,y,z) divergenssi $\nabla \cdot \ve v(x,y,z)$ on reaaliluku, joka kuvastaa sitä, kuinka paljon vektorifunktion $\ve v$ vektorit loittonevat (diverge) tarkastelupisteestä (x,y,z) .

Huomaa, että $\ \nabla\cdot\ve v\neq\ve v\cdot\nabla$ .

Divergenssi visuaalisesti Mitä se siis tarkoittaa?

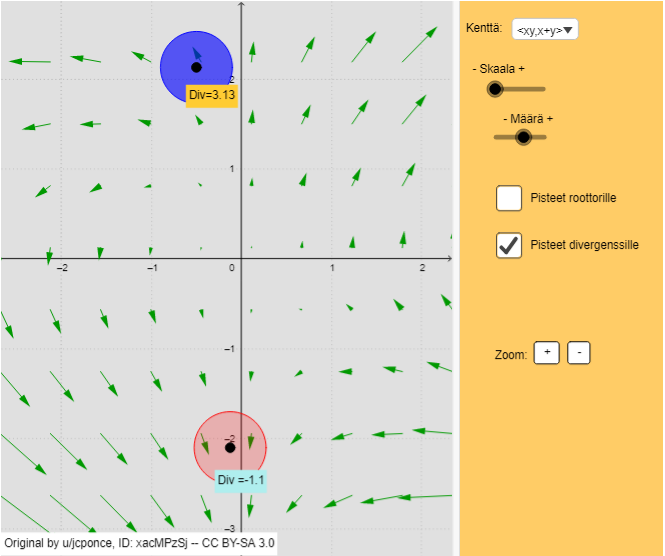
Alla on laskettu divergenssi kahdessa vektorikentän $\ve v(x,y) = xy\, \i + (x+y)\, \j$ pisteessä. Väri kuvastaa, onko divergenssi pisteessä negatiivinen vai positiivinen.

Liikuta pisteitä ja tutki, mitä arvoja divergenssi saa vektorikentässä. Kiinnitä erityisesti huomiota siihen, kuinka paljon ja minkä kokoisia vektoreita "virtaa" tarkastelupisteeseen tai siitä pois.

Kenttää voi myös muuttaa pudotusvalikosta.

# geo_divergenssi

Esimerkkejä divergenssistä

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Käänteisen neliön divergenssi: Osoita, että funktion $\ve v = \frac{\hat r}{|\ve r|^2},$ missä $\ve r=x\i+y\j+z\k,$ divergenssi on nolla.

Aluksi on hyvä huomata, että $\hat{r}=\frac{\ve r}{|\ve r|},$ jolloin

$\begin{aligned} \ve v&=\frac{\hat r}{|\ve r|^2}=\frac{\ve r}{|\ve r|^3}\\ &=\frac{x\i+y\j+z\k}{(x^2+y^2+z^2)^{3/2}}\\ &=\frac{x}{(x^2+y^2+z^2)^{3/2}}\i+\frac{y}{(x^2+y^2+z^2)^{3/2}}\j+\frac{z}{(x^2+y^2+z^2)^{3/2}}\k\\ &=v_1\i+v_2\j+v_3\k. \end{aligned}$

Lasketaan nyt osittaisderivaatat divergenssin määritelmästä, muistaen käsitellä muita kuin derivointimuuttujaa vakioina:

$\begin{aligned} \ositx v_1&=\frac{1\cdot (x^2+y^2+z^2)^{3/2}-x\frac{3}{2}(x^2+y^2+z^2)^{1/2}2x}{(x^2+y^2+z^2)^{3}}\\ &=\frac{(x^2+y^2+z^2)^{3/2}-3x^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}\\ &=\frac{\left((x^2+y^2+z^2)^{2/2}-3x^2\right)(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}\\ &=\frac{x^2+y^2+z^2-3x^2}{(x^2+y^2+z^2)^{5/2}}\\ &=\frac{-2x^2+y^2+z^2}{(x^2+y^2+z^2)^{5/2}}. \end{aligned}$

Vastaavasti saadaan muut osittaisderivaatat

$\begin{aligned} \osity v_2&=\frac{x^2-2y^2+z^2}{(x^2+y^2+z^2)^{5/2}} \end{aligned}$

$\begin{aligned} \ositz v_3&=\frac{x^2+y^2-2z^2}{(x^2+y^2+z^2)^{5/2}}. \end{aligned}$

Summataan nämä, jolloin

$\begin{aligned} \nabla\cdot\ve v&=\ositx v_1+\osity v_2+\ositz v_3\\ &=\frac{-2x^2+y^2+z^2}{(x^2+y^2+z^2)^{5/2}}+\frac{x^2-2y^2+z^2}{(x^2+y^2+z^2)^{5/2}}+\frac{x^2+y^2-2z^2}{(x^2+y^2+z^2)^{5/2}}\\ &=\frac{-2x^2+y^2+z^2+x^2-2y^2+z^2+x^2+y^2-2z^2}{(x^2+y^2+z^2)^{5/2}}\\ &=\frac{-2x^2+2x^2-2y^2+2y^2-2z^2+2z^2}{(x^2+y^2+z^2)^{5/2}}\\ &=\frac{0}{(x^2+y^2+z^2)^{5/2}}\\ &=0. \end{aligned}$

Siispä $\nabla\cdot \ve v=0.$

# roottori

Roottori (curl)

Vektorifunktion $\ve v$ roottori on vektorifunktio, joka määritellään ristitulona

$\begin{aligned}\nabla\times\ve v&=\left(\osit[v_3]{y}-\osit[v_2]{z}\right)\i+\left(\osit[v_1]{z}-\osit[v_3]{x}\right)\j+\left(\osit[v_2]{x}-\osit[v_1]{y}\right)\k\\&=\begin{vmatrix} \i & \j & \k\\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ v_1 & v_2 & v_3 \end{vmatrix}.\end{aligned}$

Pisteessä (x,y,z) roottorivektorin $\nabla\times\ve v(x,y,z)$

pituus mittaa sitä, kuinka suuri osa vektorifunktion $\ve v$ vektoreista kiertää tarkastelupisteen ympäri,
suunta kertoo kierron suunnan, johon vektorifunktion $\ve v$ vektorit kiertävät eniten tarkastelupisteen ympäri. Katso ristitulovektorin suunta.

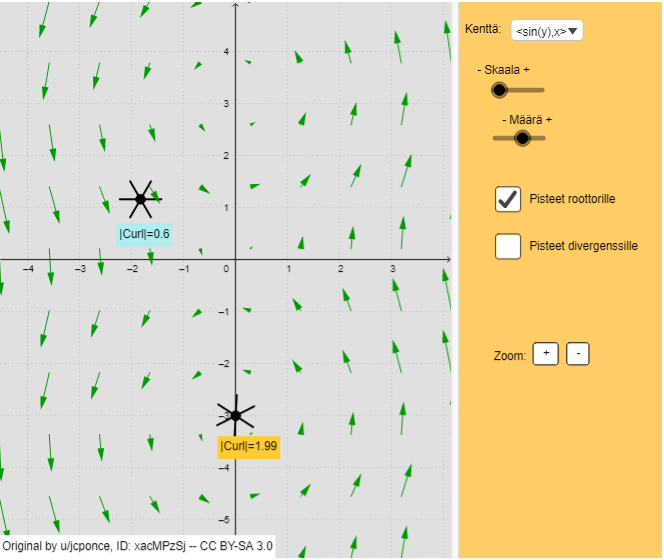
Roottori visuaalisesti Mitä se siis tarkoittaa?

Alla on laskettu roottorivektorin pituus kahdessa vektorikentän $\ve v(x,y) = \sin(y) \, \i + x\, \j$ pisteessä. Vektorifunktio on -tasossa, jolloin roottorivektori on aina vektorin $\k$ suuntainen.

Pisteen rattaiden pyörimissuunta kertoo roottorivektorin suunnan:

myötäpäivään $\to$ roottorivektori ruudusta ulospäin
vastapäivään $\to$ roottorivektori ruutuun päin

Liikuta pisteitä ja tutki, miten roottorin arvo ja suunta muuttuu eri pisteissä.

Kenttää voi myös muuttaa pudotusvalikosta.

# geo_roottori

Esimerkkejä roottorista

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Roottorin laskeminen: Laske roottori $\nabla \times \ve v$ kun $\ve v = x^2 \, \i + 3xz\,\j - 2xz\,\k$ .

Tunnistetaan vektorin $\ve v$ komponentit

$v_1=x^2,\quad v_2=3xz,\quad v_3=-2xz.$

Lasketaan sitten roottorin laskuun tarvittavat osittaisderivaatat:

$\begin{aligned} &\osit[v_3]{y}=\osity(-2xz)=0,&&\quad \osit[v_2]{z}=\ositz(3xz)=3x,\\ &\osit[v_1]{z}=\ositz(x^2)=0,&&\quad \osit[v_3]{x}=\ositx(-2xz)=-2z,\\ &\osit[v_2]{x}=\ositx(3xz)=3z,&&\quad \osit[v_1]{y}=\osity(x^2)=0. \end{aligned}$

Sijoitetaan nämä seuraavaksi roottorin määritelmään

$\begin{aligned} \nabla\times\ve v&=\left(\osit[v_3]{y}-\osit[v_2]{z}\right)\i+\left(\osit[v_1]{z}-\osit[v_3]{x}\right)\j+\left(\osit[v_2]{x}-\osit[v_1]{y}\right)\k\\ &=\left(0-3x\right)\i+\left(0-(-2z)\right)\j+\left(3x-0\right)\k\\ &=-3x\i+2z\j+3x\k. \end{aligned}$

# laplace

$\color{RedOrange}{\nabla ^2}$ -operaattori eli Laplace-operaattori

$\nabla ^2$ -operaattori on toisten (ei sekoitettujen) osittaisderivaattojen summa

$\nabla ^2 =\frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} + \frac{\partial^2 }{\partial z^2}.$

Operoitaessa tällä funktioon saadaan

$\nabla ^2 f=\frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}.$

Laplace-operaattori voidaan esittää myös $\nabla$ -operaattorin avulla

$\nabla^2 f = \nabla\cdot\nabla f.$

Joskus Laplace-operaattorista käytetään myös merkintää $\nabla^2 = \Delta$ .

Esimerkkejä Laplace-operaattorista

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Laplace-operaattori: Laske $\nabla ^2 f$ kun f = x^2 + 2xy + 3z + 4 .

Laplace-operaattorin määritelmästä saadaan $\begin{aligned} \nabla ^2 f &= \left(\frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} + \frac{\partial^2 }{\partial z^2}\right)\left(x^2 + 2xy + 3z + 4\right) \\ &= \frac{\partial^2 }{\partial x^2}\left(x^2 + 2xy + 3z + 4\right) \\ &+ \frac{\partial^2 }{\partial y^2}\left(x^2 + 2xy + 3z + 4\right) \\ &+ \frac{\partial^2 }{\partial z^2}\left(x^2 + 2xy + 3z + 4\right) .\\ \end{aligned}$

Lasketaan toiset osittaisderivaatat erikseen:

$\begin{aligned} \frac{\partial^2 }{\partial x^2}\left(x^2 + 2xy + 3z + 4\right) &= \ositx\left(\ositx \left(x^2 + 2xy + 3z + 4\right)\right) \\ &= \ositx\left(2x + 2y\right) \\ &= 2.\\ \frac{\partial^2 }{\partial y^2}\left(x^2 + 2xy + 3z + 4\right) &= 0 \quad \Big| \text{ vastaavasti} \\ \frac{\partial^2 }{\partial z^2}\left(x^2 + 2xy + 3z + 4\right) &= 0 \quad \Big| \text{ vastaavasti}\\ \end{aligned}$

Sijoitetaan osittaisderivaatat takaisin:

$\begin{aligned} \nabla ^2 f &= \frac{\partial^2 }{\partial x^2}\left(x^2 + 2xy + 3z + 4\right) \\ &+ \frac{\partial^2 }{\partial y^2}\left(x^2 + 2xy + 3z + 4\right) \\ &+ \frac{\partial^2 }{\partial z^2}\left(x^2 + 2xy + 3z + 4\right) \\ &= 2 + 0 + 0 \\ &= 2. \end{aligned}$

# differentiaali

Differentiaali

Useamman muuttujan funktion $f(x_1, x_2,\dots,x_n)$ differentiaalin, jonka voidaan ajatella olevan hyvin pieni muutos funktion arvossa, kun yhden tai useamman muuttujan arvoa muutetaan hyvin vähän. Toisin sanoen, kun merkitään funktion muutosta merkinnällä $\Delta f,$ niin $\Delta f\approx df=\osit[f]{x_1}dx_1+\osit[f]{x_2}dx_2+\dots+\osit[f]{x_n}dx_n.$ Esimerkiksi kolmen muuttujan funktion tapauksessa: $\Delta f\approx df=\osit[f]{x}dx+\osit[f]{y}dy+\osit[f]{z}dz.$ Yhden muuttujan funktion tilanteessa katso derivointityökalut sivua. Muuttujien arvojen muutosten olleessa pieniä, mutta äärellisiä, voidaan approksimoida, että $dx_i\approx\Delta x_i.$ Tällöin $\Delta f\approx \osit[f]{x_1}\Delta x_1+\osit[f]{x_2}\Delta x_2+\dots+\osit[f]{x_n}\Delta x_n.$

Useamman muuttujan funktion differentiaali voidaan esittää myös gradientin avulla:

Olkoon $f:\R^n\rightarrow \R.$ Jos funktiolla on tarkastelupisteessä $x=(x_{1},x_{2},\dots ,x_{n})$ ja sen lähiympäristössä kaikki sen osittaisderivaatat, niin tällöin funktion arvo pisteessä x+h on $f(x+h)=f(x)+\nabla f(x)\cdot h,$ missä $\nabla f(x)$ on funktion gradientti pisteessä ja $h=(h_1,h_2,\dots,h_n)$ on vektori, jolle $||h||\ll 1.$

Esimerkki differentiaalien käytöstä

Arvio funktion f(x{,}y) arvosta pisteessä (0{,}04;0{,}05) saadaan, kun tunnetaan kyseisen funktion arvo ja sen osittaisderivaattojen arvot pisteessä (0{,}0). Kun f(0{,}0)=2, $\osit[f]{x}=5$ ja $\osit[f]{y}=3,$ niin $\begin{align*} f(0{,}07;0{,}05)&=f(0{,}0)+\Delta f\\&\approx f(0{,}0)+\osit[f]{x}\Delta x+\osit[f]{y}\Delta y\\&=2+5\cdot0{,}0+3\cdot0{,}05=2{,}35. \end{align*}$