Vektorien ristitulo

Ristitulo (vektoritulo)

Vektorien $\ve{a}$ ja $\ve{b}$ ristitulo (cross product) $\ve{a}\times\ve{b}$ on vektori, joka on kohtisuorassa vektoreiden $\ve{a}$ ja $\ve{b}$ kanssa. Ristitulovektorin pituus on vektorien $\ve{a}$ ja $\ve{b}$ määräämän suunnikkaan pinta-ala ja suunta saadaan oikean käden säännöllä.

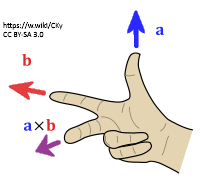Huom: Toisin kuin pistetulo, ristitulo toimii vain kolmiulotteisessa tilanteessa.

Ristitulo visuaalisesti Mitä se siis tarkoittaa?

GeoGebra-havainnollistuksessa näkyy vektorien $\ve a$ ja $\ve b$ määräämä suunnikas, sen pinta-ala sekä ristitulovektorin $\ve a \times \ve b$ pituus.

Voit pyörittää näkymää raahaamalla.

# geoRistitulo

Olkoon vektorit $\ve{a} = a_x\i + a_y\j + a_z\k$ ja $\ve{b} = b_x\i + b_y\j + b_z\k$ .

Vektoreiden ristitulo $\ve a \times \ve b$ ristitulo sovitaan laskettavaksi

komponenttien kertoimilla $\ve a \times \ve b =(a_yb_z-a_zb_y)\i+(a_zb_x-a_xb_z)\j+(a_xb_y-a_yb_x)\k = \begin{vmatrix} \i & \j & \k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}$
vektorien välisen kulman $\theta$ avulla $\ve{a}\times\ve{b}=|\ve{a}||\ve{b}|\sin\theta\,\hat{e}$ missä
- $\theta$ on vektorien $\ve a$ ja $\ve b$ välinen pienin kulma $(0 \le \theta \le 180^\circ)$ ,
- $\hat{e}$ on ristitulon suuntainen yksikkövektori.

Ristitulovektori on vektorien $\ve{a}$ ja $\ve{b}$ virittämää tasoa vastaan kohtisuorassa. Ristitulon suunta saadaan oikean käden säännöllä. Oikean käden sääntö

Muistisääntöjä ristitulon suunnan laskemiseen:

Kantavektorien ristitulo:

Kirjoitetaan kantavektorit vierekkäin ja piirretään nuolet myötäpäivään: $\xymatrix{& \i\ar@/^1.0pc/@[][r]& \j\ar@/^1.0pc/@[][r] & \k\ar@/^1.0pc/@[][ll]}$ Kuvasta luetaan ristitulo: $\i\times\j=\k,\quad \j\times\k=\i,\quad \k\times\i=\j$

Piirretään toinen kuva, nuolet vastapäivään: $\xymatrix{& \i\ar@/^1.0pc/@{<-}@[][r]& \j\ar@/^1.0pc/@{<-}@[][r] & \k\ar@/^1.0pc/@{<-}@[][ll]}$ Kuvasta luetaan ristitulo: $\k\times\j=-\i,\quad \j\times\i=-\k,\quad \i\times\k=-\j$

Ristitulon arvosta voidaan tehdä päätelmiä vektorien suhteesta toisiinsa:

$\quad\ve{a}\times\ve{b}=0,\quad\iff\quad\theta=0^{\circ}\quad\text{tai}\quad\theta=180^{\circ}$	Vektorit samansuuntaisia $(0^{\circ})$ tai vastakkaissuuntaisia $(180^{\circ})$
$\quad\ve{a}\times\ve{b}=\|\ve{a}\|\|\ve{b}\|\ve{e},\quad\iff\quad\theta=90^{\circ}$	Vektorit kohtisuorassa

# laskusaannot

Ristitulon laskusäännöt

Kun $\ve{a}$ , $\ve{b}$ ja $\ve{c}$ ovat vektoreita ja $\theta$ vektorien $\ve{a}$ ja $\ve{b}$ välinen kulma, niin seuraavat säännöt pätevät ristitulolle:

Sääntö	Selitys tai nimi
$\vphantom{\Big\|}\ve{a}\times\ve{a}=0$	Ristitulo itsensä kanssa on nolla.
$\vphantom{\Big\|}\|\ve{a}\times\ve{b}\|=\|\ve{a}\|\|\ve{b}\|\|\sin\theta\|$	Ristitulovektorin pituus.
$\vphantom{\Big\|}\ve{a}\times\ve{b}=\red{-}\ve{b}\times\ve{a}$	Ristitulon järjestyksellä on väliä. Huomaa merkki.
$\vphantom{\Big\|}\ve{a}\times(\ve{b}+\ve{c})=\ve{a}\times\ve{b}+\ve{a}\times\ve{c}$	Osittelulaki.
$\vphantom{\Big\|}(\la\ve{a})\times\ve{b}=\ve{a}\times(\la\ve{b})=\la(\ve{a}\times\ve{b}),\quad\gray{\la\in\R}$	Vakiolla kertominen.

# esimerkkejä

Esimerkkejä ristitulosta

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Vektorien ristitulo, vektorien välinen kulma: Laske vektorien $\ve a =2\i+2\j-4\k$ ja $\ve b =-\i+2\j-\k$ ristitulo sekä vektorien välisen kulman $\theta$ suuruus.

Vektorien ristitulon voi laskea ristitulon kaavalla tai muistisäännöillä:

Vektorien ristitulo ristitulon kaavalla: $\begin{aligned} \ve{a}\times\ve{b}&=\big(2\cdot(-1)-(-4)\cdot2\big)\i+\big((-4)\cdot(-1)-2\cdot(-1)\big)\j\\ &\phantom{==}+\big(2\cdot2-2\cdot(-1)\big)\k\\ &=6\i+6\j+6\k. \end{aligned}$

Vektorien ristitulo muistisäännöillä: Avataan vektorien ristitulo kuten tavallinen tulo, jonka jälkeen käytetään muistisääntöjä kantavektoreille:

$\begin{aligned} \ve{a}\times\ve{b} &= (2\i + 2\j -4 \k) \times (-\i + 2\j - \k) \\ &=\quad 2\i \times (-\i) + 2\i \times 2\j + 2\i \times (-\k) \\ &\quad+ 2\j \times (-\i) + 2\j \times 2\j + 2\j \times (-\k) \\ &\quad+ (-4\k) \times (-\i) + (-4\k) \times 2\j + (-4\k) \times (-\k) \\ &=\quad 0 + 4\k + 2\j \\ &\quad+ 2\k + 0 - 2\i \\ &\quad+ 4\j + 8\i + 0 \\ &= 6\i + 6\j + 6\k. \end{aligned}$

Myötäpäivään, niin ristitulo antaa positiivisena kolmannen kantavektorin:

Vastapäivään, niin ristitulo antaa negatiivisena kolmannen kantavektorin:

Eli: \[\hat{i}\times\hat{j}=\hat{k},\ \hat{j}\times\hat{k}=\hat{i},\ \hat{k}\times\hat{i}=\hat{j}\] \[\hat{k}\times\hat{j}=-\hat{i},\ \hat{j}\times\hat{i}=-\hat{k},\ \hat{i}\times\hat{k}=-\hat{j}\]

— 02 Dec 19 (edited 02 Dec 19)

Vektorien välinen kulma saadaan ristitulovektorin $\ve a \times \ve b$ ja vektorien $\ve a,$ $\ve b$ pituuksien avulla $|\ve a|=\sqrt{2^2+2^2+(-4)^2}=\sqrt{24}=2\sqrt{6}$

$|\ve{b}|=\sqrt{(-1)^2+2^2+(-1)^2}=\sqrt{6}$

$|\ve a \times \ve b|=\sqrt{6^2+6^2+6^2}=\sqrt{3\cdot36}=6\sqrt{3}.$

Ristitulovektorin pituus saadaan myös kaavasta

$|\ve a \times \ve b|=|\ve a||\ve b||\sin\theta|.$ Koska $0^{\circ} \leq \theta \leq 180^{\circ}$ , niin saadaan

$\begin{aligned} \theta&=\sin^{-1}\left(\frac{|\ve a \times \ve b|}{|\ve a||\ve b|}\right)\\ &=\sin^{-1}\left(\frac{6\sqrt{3}}{2\sqrt{6}\cdot\sqrt{6}}\right)\\ &=\sin^{-1}\left(\frac{\sqrt{3}}{2}\right)\\ &=60^{\circ}. \end{aligned}$

Vääntömomentti, oikean käden sääntö: Vääntömomentti $\ve{\tau}$ määritellään ristitulona $\ve{\tau} = \ve{r} \times \ve{F},$ missä $\ve{F}$ on voima ja $\ve{r}$ vektori pyörimisakselista voiman vaikutuspisteeseen. Pulttia väännetään suoraan alaspäin 100 N voimalla 20cm pitkällä jakoavaimella, joka on 30° kulmassa vaakatasoon nähden. Määritä vääntömomenttivektori.

Vääntömomentin määrittämiseksi on määritettävä paikkavektori $\ve{r}$ ja voimavektori $\ve{F}$ , tai vektorien pituudet ja niiden välinen kulma. Käytetään tässä tehtävässä ristitulon laskukaavaa: $\ve{\tau} = |\ve{r}||\ve{F}|\sin\theta\,\hat{e},$ missä $\hat{e}$ on vääntömomentin suunta, joka määritetään myöhemmin oikean käden säännöllä.

Paikkavektori $\ve{r}$ :

Voima kohdistuu jakoavaimen päähän, eli 0,2m päähän pultin pyörimisakselista. Tällöin $|\ve{r}| = 0{,}2$ (m).

Voimavektori $\ve{F}$ :

Voiman suuruus on 100 N, joten voimavektorin pituus on $|\ve{F}| = 100$ (N).

Vääntömomentti $\ve{\tau}$ :

Koska jakoavain on 30° kulmassa, niin paikkavektori ja voimavektori ovat 120° kulmassa. Tällöin vääntömomentti on $\begin{aligned} \ve{\tau} &= |\ve{r}||\ve{F}|\sin\theta\,\hat{e} \\ &= 0,2 \cdot 100 \sin(120^\circ)\,\hat{e} \\ &= 20 \cdot \frac{\sqrt3}{2}\,\hat{e} \\ &\approx 17{,}3 \, \hat{e} \text{ (Nm)}. \end{aligned}$

Asettamalla vektorit lähtemään samasta paikasta, voidaan käyttää oikean käden sääntöä: Peukalo asetetaan paikkavektorin $\ve{r}$ suuntaisesti ja etusormi voimavektorin $\ve{F}$ suuntaisesti. Keskisormi osoittaa tällöin ruutuun päin (katsojasta poispäin). Siispä vääntömomentti on 17,3 Nm ruutuun päin.

Sovitaan koordinaatisto siten, että -akseli on $\ve F$ -vektorin kanssa vastakkaissuuntainen ja -akseli on siitä kohtisuoraan jakovaimen tasossa. Valitaan -akselin suunnaksi ruudusta ulospäin. Kuvakulmaa kääntämällä vektorit ja kantavektorit näyttävät siis seuraavalta.

Vääntömomenttivektori on tällöin tässä koordinaatistossa $\ve \tau = -17{,}3 \, \k \text{ (Nm)}.$

# derivointi

Ristitulon derivointi

Jos $\ve{a}(t)=a_x(t)\i+a_y(t)\j+a_z(t)\k,$ $\ve{b}(t)=b_x(t)\i+b_y(t)\j+b_z(t)\k,$ eli vektorit riippuvat muuttujasta , niin ristituloa voidaan derivoida muuttujan suhteen kaavalla

$\frac{d}{dt}\left(\ve{a}(t)\times\ve{b}(t)\right)=\frac{d\ve{a}(t)}{dt}\times\ve{b}(t)+\ve{a}(t)\times\frac{d\ve{b}(t)}{dt}.$

Tämä muistuttaa tuttua tulon derivointisääntöä, mutta huomioi ristitulon järjestys.

# pistetulo-ja-ristitulo

Pistetulon ja ristitulon välisiä yhteyksiä

Pistetulon ja ristitulon välille saadaan erilaisia kaavoja, joista alla olevassa taulukossa muutama.