Derivaatta

# derivaatan-merkitys

Derivaatan merkitys

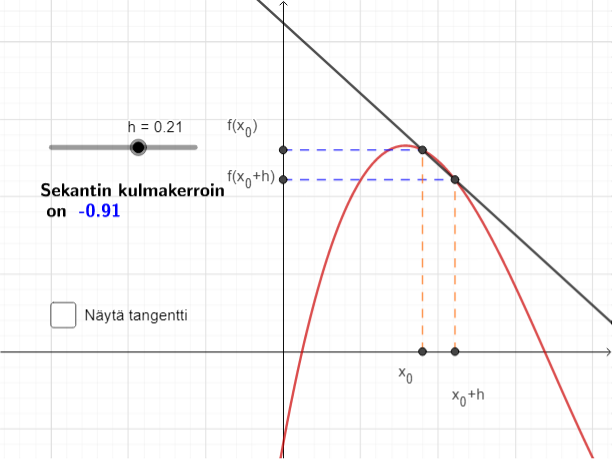
Derivaatta kuvaa funktion "kasvunopeutta" tietyssä pisteessä. Derivaatta määritellään erotusosamäärän (difference quotient) raja-arvon avulla:

Funktion derivaatta pisteessä $x\in\mathbb{R}$ on $f'(x) = \lim_{h\to 0}\frac{f(x+h)-f(x)}{h},$ $h\in\R,$ jos tämä raja-arvo on olemassa. Tällöin sanotaan, että funktio on derivoituva pisteessä .

Derivaatan yksikkö on $[f'(x)] = \frac{[f]}{[x]}.$

Yksikön perustelu

Derivaatalla f'(x) tarkoitetaan pientä funktion muutosta $\text{d}f$ jaettuna pienellä :n muutoksella $\dx$ , eli $\begin{aligned} f'(x) = \frac{\text{d}f}{\dx}. \end{aligned}$

Muutoksen suuruus ei vaikuta suureen yksikköön, joten $[\text{d}f] = [f]$ ja $[\text{d}x] = [x]$ , joten

$\begin{aligned} \left[f'(x)\right] = \frac{[\text{d}f]}{[\dx]} = \frac{[f]}{[x]}. \end{aligned}$

Derivaatta visuaalisesti Mitä se siis tarkoittaa?

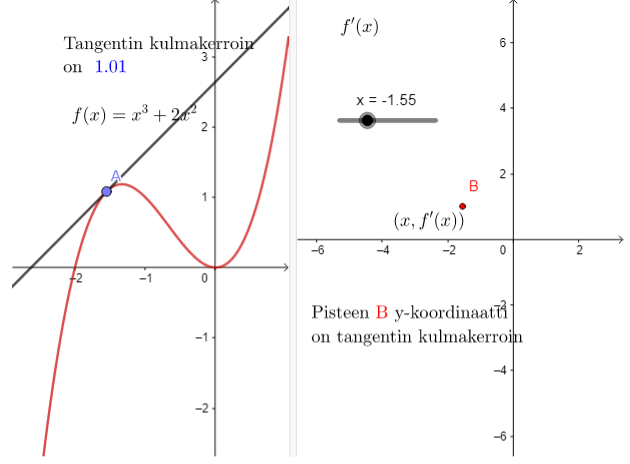
Graafisesti derivaatta pisteessä tarkoittaa funktion kuvaajalle pisteeseen (x, f(x)) piirretyn tangentin kulmakerrointa. Alla olevissa GeoGebra-appleteissa havainnollistetaan derivaatan määritelmää sekä graafista tulkintaa.

Derivaatan määritelmä

Tutki mitä tapahtuu sekantin kulmakertoimelle, kun $h\to 0$ .

# geo_derivaatan_graaf3

Derivaatan graafinen tulkinta

Tutki, mitä arvoja funktiolle piirretyn tangentin kulmakerroin saavuttaa eri :n arvoilla.

# geo_derivaatan_graaf2

Derivaatta ja derivoituvuus fysiikassa ja kemiassa

Fysiikassa ja kemiassa kaikki käsiteltävät funktiot ovat lähtökohtaisesti derivoituvia, jolloin derivoituvuustarkasteluja ei tarvita.

Derivaatta esiintyy mekaniikassa: Nopeus ajanhetkellä määritellään derivaatan tapaan $v = \lim_{\Delta t \to 0}\frac{\Delta s}{\Delta t} = \frac{\text{d}s}{\text{d}t}.$

jolloin nopeus ajanhetkellä saadaan paikan derivaattana.

Vastaavasti kiihtyvyys ajanhetkellä määritellään nopeuden aikaderivaattana $a = \frac{\text{d}v}{\text{d}t}.$

# derivaatan-merkinnöistä

Derivaattaan liittyvistä merkinnöistä

Klikkaa merkintää tai käsitettä , josta haluat lisätietoja.

Derivaattafunktio: $f', \quad \frac{\text d}{\dx}f, \quad \frac{\text df}{\dx}, \quad \text Df, \quad \frac{\text d}{\dx}f(x), \quad \dot f$

Merkinnöillä ilmaistaan funktion derivaattafunktiota, eli funktiota, joka saadaan yleensä derivoimalla funktiota käyttäen derivaatan laskusääntöjä.

Merkinnässä $\frac{\text{d}}{\dx}$ kirjain kuvastaa sitä muuttujaa, jonka suhteen derivoidaan. Esimerkiksi $\frac{\text{d}}{\text{d}t}f$ tarkoittaa funktion derivoimista muuttujan suhteen.

Katso esimerkkejä derivoinnista.

# toinenderivaatta

Toinen derivaatta eli toisen kertaluvun derivaatta: $f'',\quad \frac{\text d^2}{\dx^2}f, \quad\frac{\text d^2f}{\dx^2}$

Merkinnöillä tarkoitetaan funktion derivaattafunktiota, eli funktion toista derivaattafunktiota tai toisen kertaluvun derivaattafunktiota.

Merkintä tarkoittaa käytännössä sitä, että $\frac{\text{d}^2f}{\dx^2}=\frac{\text{d}}{\text{d}x}\left(\frac{\text{d}f}{\dx}\right)$ eli aluksi derivoidaan kerran funktiota muuttujan suhteen ja saatua derivaattaa derivoidaan uudestaan muuttujan suhteen.

Vastaavasti voidaan merkitä $\frac{\text{d}^n}{\dx^n}f$ tai $f^{(n)}$ ilmaisemaan funktion kertaluvun derivaattafunktiota.

Katso esimerkki toisen derivaatan laskemisesta.

# osittaisderiv

Osittaisderivaatta: $\frac{\partial}{\partial x}f, \quad \frac{\partial}{\partial y}f, \quad \frac{\partial^2}{\partial x \partial y}f$

Merkinnällä tarkoitetaan funktion osittaisderivaattaa (partial derivative) jonkin muuttujan suhteen, kun on usean muuttujan funktio. Merkinnöistä viimeinen voidaan purkaa useammaksi osittaisderivaataksi: esimerkiksi kolmen muuttujan , ja funktion tapauksessa $\frac{\partial^2}{\partial x \partial y}f(x, y, z) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}f(x,y,z)\right).$

Osittaisderivaatta voidaan määritellä raja-arvon avulla. Esimerkiksi kahden muuttujan funktion f(x,y) osittaisderivaatta muuttujan suhteen pisteessä (x_0,y_0) on $\dfrac{\partial}{\partial x}f(x_0,y_0)=\lim_{h\to 0} \frac{f(x_0+h,y_0)-f(x_0,y_0)}{h}$

Käytännössä osittaisderivoiminen eli osittaisderivaatan $\frac{\partial}{\partial x}f$ määrittäminen tapahtuu kuitenkin kuten derivaatan $\frac{\text{d}}{\dx}f$ määrittäminen, käsittelemällä muita muuttujia vakiona. Katso esimerkit osittaisderivoinnista.

Useamman muuttujan tapauksessa funktion $f(x_1{,}x_2{,}\dots{,}x_n)$ kertaluvun osittaisderivaatta määräytyy seuraavasti: $\begin{align*}&\dfrac{\partial^m}{\partial x_{k_m} \partial x_{k_{m-1}}\dots\partial x_{k_1}}f(x_1{,}x_2{,}\dots{,}x_n)\\& =\dfrac{\partial}{\partial x_{k_m}}\left(\dfrac{\partial}{\partial x_{k_{m-1}}}\left(\dots\left(\dfrac{\partial}{\partial x_{k_1}} f(x_1{,}x_2{,}\dots{,}x_n)\right)\right)\right),\end{align*}$ missä $k_1, k_2,...,k_m \in \{1,2,...,n\}$ .

Osittaisderivoinnin järjestystä on mahdollista vaihtaa, jos on kertaa jatkuvasti derivoituva eli kaikki sen kertaluvun ja sitä alemman kertaluvun osittaisderivaatat ovat jatkuvia.

Esimerkiksi, jos funktion f(x{,}y) kaikki ensimmäisen kertaluvun osittaisderivaatat eli $\dfrac{\partial}{\partial x}f$ ja $\dfrac{\partial}{\partial x}f$ ja kaikki toisen kertaluvun derivaatat eli $\dfrac{\partial^2}{\partial x\partial y}f$ , $\dfrac{\partial^2}{\partial y\partial x}f$ , $\dfrac{\partial^2}{\partial x\partial x}f$ ja $\dfrac{\partial^2}{\partial y\partial y}f$ ovat jatkuvia, niin silloin toisen kertaluvun osittaisderivaattojen järjestystä voi vaihtaa eli $\dfrac{\partial^2}{\partial x\partial y}f(x{,}y)=\dfrac{\partial^2}{\partial y\partial x}f(x{,}y).$

Differentiaalit: $\dy, \quad f'(x) \, \dx, \quad \text dz$

Merkinnöillä ilmaistaan differentiaaleja.

Kun merkitään y = f(x) , niin differentiaalin $\dy$ voi ajatella lukuna joka kuvastaa sitä, kuinka paljon muuttuu kun muuttuu vähän, eli $\dx$ :n verran. Tällöin $\dy = f'(x)\, \dx.$

# derivaatan-laskusäännöt

Derivaatan laskusäännöt

Merkitään D(f(x)) ja f'(x) tarkoittamaan funktion derivaattaa pisteessä .

Jos funktiot ja ovat derivoituvia, niin seuraavat derivointisäännöt pätevät derivaatalle.

Sääntö	Selitys tai nimi
$\vphantom{\Big\|}D(a)=0$	Vakion derivaatta on nolla.
$\vphantom{\Big\|}D(a\cdot f(x))=a\cdot f'(x)$	Vakio voidaan ottaa ulos derivoitaessa.
$\vphantom{\Big\|}D\left(f(x)+g(x)\right) = f'(x) + g'(x)$	Summan derivaatta on derivaattojen summa.
$\vphantom{\Big\|}D(f(x)\cdot g(x)) = f'(x)g(x) + f(x)g'(x)$	Tulon derivaatta.
$\vphantom{\Big\|}{D\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f'(x)g(x) - f(x) g'(x)}{\left(g(x)\right)^2}}$	Osamäärän derivaatta.
$\vphantom{\Big\|}D\left(\frac{1}{f(x)}\right) = -\frac{f'(x)}{f(x)^2}, \color{gray}\text{ jos } f(x) \ne 0$	Funktion derivaatta.
$\vphantom{\Big\|}D\Big((f(g(x))\Big)=f'(g(x))\cdot g'(x)$	Ketjusääntö, yhdistetyn funktion derivointi.

Derivointisäännöt merkinnällä $\frac{\text{d}}{\dx}$

Derivaattamerkintöjä on lukuisia. Taulukon merkinnän ja pilkkumerkinnän voi aina korvata jollakin muulla, vastaavalla merkinnällä.

Kirjallisuus ja kokeneet luennoitsijat käyttävät joskus nk. Leibnizin merkintää $\dfrac{\dy}{\dx}$ merkitsemällä y = f(x) .

Seuraavissa derivointisäännöissä on merkitty y = f(x) ja u = g(x) .

Sääntö	Selitys tai nimi
$\vphantom{\Bigg\|}\dfrac{\text{d}}{\dx}(a)=0$	Vakion derivaatta on nolla.
$\vphantom{\Bigg\|}\dfrac{\text{d}}{\dx}(a\cdot y)=a\cdot \dfrac{\dy}{\dx}$	Vakio voidaan ottaa ulos derivoitaessa.
$\vphantom{\Bigg\|}\dfrac{\text{d}}{\dx}\left(y+u\right) = \dfrac{\dy}{\dx} + \dfrac{\text{d}u}{\dx}$	Summan derivaatta on derivaattojen summa.
$\vphantom{\Bigg\|}\dfrac{\text{d}}{\dx}(y\cdot u) = \dfrac{\dy}{\dx}u+y\dfrac{\text{d}u}{\dx}$	Tulon derivaatta.
$\vphantom{\Bigg\|}\dfrac{\text{d}}{\dx}\left(\dfrac{y}{u}\right) = \dfrac{\dfrac{\dy}{\dx}u-\dfrac{\text{d}u}{\dx}y}{u^2}$	Osamäärän derivaatta.
$\vphantom{\Bigg\|}\dfrac{\dy}{\dx} =\dfrac{\dy}{\text{d}u}\dfrac{\text{d}u}{\dx}, \color{gray}\text{ kun } y = f(u)$	Ketjusääntö, yhdistetyn funktion derivointi.

Mutta miksi?

Derivointisäännöt voi johtaa derivaatan määritelmästä.

Vakiofunktio:

Olkoon $x_0\in\R.$ Muodostetaan erotusosamäärän raja-arvo funktiolle f(x)=a

$\begin{aligned} \lim_{h\to0}\frac{f(x_0+h)-f(x_0)}{h}&=\lim_{h\to0}\frac{a-a}{h}\\ &=\lim_{h\to0}\frac{0}{h}=0. \end{aligned}$

Koska tämä pätee kaikille pisteille x_0 , on f'(x)=0 kaikilla $x\in\R.$

Vakion ulosottaminen: $D(a\cdot f(x))=a\cdot f'(x)$

Perustellaan esimerkiksi tulon derivointisäännöllä.

Summan derivaatta:

Oletetaan, että funktiot ja ovat derivoituvia. Olkoon $x_0\in\R$ . Käytetään derivaatan määritelmää sekä raja-arvon laskusääntöjä derivointisäännön todistamiseen

$\begin{aligned} \lim_{h\to0}\frac{(f+g)(x_0+h)-(f+g)(x_0)}{h}&=\lim_{h\to0}\frac{f(x_0+h)+g(x_0+h)-f(x_0)-g(x_0)}{h}\\ &=\lim_{h\to0}\frac{f(x_0+h)-f(x_0)+g(x_0+h)-g(x_0)}{h}\\ &=\lim_{h\to0}\frac{f(x_0+h)-f(x_0)}{h}+\lim_{h\to0}\frac{g(x_0+h)-g(x_0)}{h}\\ &=f'(x_0)+g'(x_0). \end{aligned}$

Koska tämä pätee kaikille pisteille x_0, on D(f(x)+g(x))=f'(x)+g'(x) kaikilla $x\in\R.$

Tulon derivaatta: $D(f(x)\cdot g(x))=f'(x)g(x)+f(x)g'(x)$

Oletaan, että funktiot ja ovat derivoituvia. Olkoon $x_0\in\R$ ja merkitään $F(x)=f(x)\cdot g(x).$ Muodostetaan erotusosamäärän raja-arvo tulofunktiolle ja yritetään pakottaa siinä näkyviin funktioiden ja erotusosamäärät.

$\begin{aligned} \lim_{h\to 0}\frac{F(x_0+h)-F(x_0)}{h}&=\lim_{h\to 0}\frac{f(x_0+h)g(x_0+h)-f(x_0)g(x_0)}{h}. \end{aligned}$ Lisätään edellisen osoittajaan muodossa 0=f(x_0)g(x_0+h)-f(x_0)g(x_0+h), jolloin $\begin{aligned} &\lim_{h\to 0}\frac{f(x_0+h)g(x_0+h)-f(x_0)g(x_0)}{h}\\ &=\lim_{h\to 0}\frac{f(x_0+h)g(x_0+h)-f(x_0)g(x_0)+f(x_0)g(x_0+h)-f(x_0)g(x_0+h)}{h}\\ &=\lim_{h\to 0}\frac{(f(x_0+h)-f(x_0))g(x_0+h)+f(x_0)(g(x_0+h)-g(x_0))}{h}\\ &=\lim_{h\to 0}\frac{(f(x_0+h)-f(x_0))g(x_0+h)}{h}+\lim_{h\to 0}\frac{f(x_0)(g(x_0+h)-g(x_0))}{h}\\ &=\lim_{h\to 0}\frac{(f(x_0+h)-f(x_0))}{h}g(x_0+h)+\lim_{h\to 0}\frac{(g(x_0+h)-g(x_0))}{h}f(x_0). \end{aligned}$

Käyttämällä viimeiseen riviin raja-arvon laskusääntöjä sekä funktion jatkuvuutta $\left(\lim_{h\to 0}g(x_0+h)=g(x_0)\right),$ saadaan

$\begin{aligned} &\lim_{h\to 0}\frac{(f(x_0+h)-f(x_0))}{h}g(x_0+h)+\lim_{h\to 0}\frac{(g(x_0+h)-g(x_0))}{h}f(x_0)\\ &=\lim_{h\to 0}\frac{(f(x_0+h)-f(x_0))}{h}\lim_{h\to 0}g(x_0+h)+f(x_0)\lim_{h\to 0}\frac{(g(x_0+h)-g(x_0))}{h}\\ &=f'(x_0)g(x_0)+f(x_0)g'(x_0). \end{aligned}$

Tämä pätee kaikille pisteille x_0, joten $D(f(x)\cdot g(x))=f'(x)g(x)+f(x)g'(x)$ kaikilla $x\in\R.$

Osamäärän derivaatta: $D\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f'(x)g(x) - f(x) g'(x)}{\left(g(x)\right)^2}$

Perustellaan osamäärän derivointisääntö määritelmän avulla. Olkoon $x_0\in\R$ ja merkitään $F(x)=\frac{f(x)}{g(x)}.$ Muodostetaan erotusosamäärän raja-arvo funktiolle

$\begin{aligned} \lim_{h\to 0}\frac{F(x_0+h)-F(x_0)}{h}=\lim_{h\to 0}\frac{\frac{f(x_0+h)}{g(x_0+h)}-\frac{f(x_0)}{g(x_0)}}{h}. \end{aligned}$

Lavennetaan osoittaja samannimiseksi, jolloin

$\begin{aligned} \lim_{h\to 0}\frac{\frac{f(x_0+h)}{g(x_0+h)}-\frac{f(x_0)}{g(x_0)}}{h} &=\lim_{h\to 0}\frac{\frac{f(x_0+h)g(x_0)-f(x_0)g(x_0+h)}{g(x_0+h)g(x_0)}}{h}\\ &=\lim_{h\to 0}\frac{f(x_0+h)g(x_0)-f(x_0)g(x_0+h)}{g(x_0+h)g(x_0)h}. \end{aligned}$

Yritetään pakottaa viimeisen riviin funktioiden ja erotusosamäärän raja-arvot näkyviin. Tämä tehdään lisäämällä sopivassa muodossa. Tässä tapauksessa 0=f(x_0)g(x_0)-f(x_0)g(x_0), jolloin

$\begin{aligned} &\lim_{h\to 0}\frac{f(x_0+h)g(x_0)-f(x_0)g(x_0+h)}{g(x_0+h)g(x_0)h}\\ &=\lim_{h\to 0}\frac{f(x_0+h)g(x_0)-f(x_0)g(x_0+h)+f(x_0)g(x_0)-f(x_0)g(x_0)}{g(x_0+h)g(x_0)h}\\ &=\lim_{h\to 0}\frac{(f(x_0+h)-f(x_0))g(x_0)-f(x_0)(g(x_0+h)-g(x_0))}{g(x_0+h)g(x_0)h}\\ &=\lim_{h\to 0}\left(\frac{(f(x_0+h)-f(x_0))g(x_0)}{g(x_0+h)g(x_0)h}-\frac{f(x_0)(g(x_0+h)-g(x_0))}{g(x_0+h)g(x_0)h}\right)\\ &=\lim_{h\to 0}\left(\frac{f(x_0+h)-f(x_0)}{h}\frac{g(x_0)}{g(x_0+h)g(x_0)}-\frac{f(x_0)}{g(x_0+h)g(x_0)}\frac{g(x_0+h)-g(x_0)}{h}.\right) \end{aligned}$

Ottamalla nyt raja-arvo, saadaan

$\begin{aligned} &\lim_{h\to 0}\left(\frac{f(x_0+h)-f(x_0)}{h}\frac{g(x_0)}{g(x_0+h)g(x_0)}-\frac{f(x_0)}{g(x_0+h)g(x_0)}\frac{g(x_0+h)-g(x_0)}{h}.\right)\\ &=f'(x_0)\frac{g(x_0)}{g(x_0)g(x_0)}-f(x_0)\frac{g'(x_0)}{g(x_0)g(x_0)}\\ &=\dfrac{f'(x_0)g(x_0) - f(x_0) g'(x_0)}{\left(g(x_0)\right)^2}. \end{aligned}$

Koska tämä pätee kaikille pisteille $x_0\in\R,$ on $D\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f'(x)g(x) - f(x) g'(x)}{\left(g(x)\right)^2}$ kaikilla $x\in\R.$

Funktion derivaatta: $D\left(\frac{1}{f(x)}\right) = -\frac{f'(x)}{f(x)^2}$

Tämä on erikoistapaus osamäärän derivaatasta.

Yhdistetyn funktion derivaatta, ketjusääntö: $D\Big((f(g(x))\Big)=f'(g(x))\cdot g'(x)$

Aluksi on hyvä käydä läpi oletukset, millä derivointisääntö on voimassa.

Olkoon $f\colon I\to\R,$ $g\colon J\to\R,$ missä ja ovat avoimia välejä, sekä lisäksi $g(J)\subset I.$ Oletus $g(J)\subset I$ siis takaa, että yhdistetty funktio $f\circ g$ on määritelty.

Olkoon $x_0\in\R.$ Oletetaan, että on derivoituva pisteessä x_0 ja derivoituva pisteessä g(x_0). Merkitään F(x)=f(g(x)). Käytetään perustelussa derivaatan määritelmälle yhtäpitävää määritelmää

$\lim_{x\to x_0}\frac{F(x)-F(x_0)}{x-x_0}.$

Merkitään y=g(x) ja a=g(x_0) ja kirjoitetaan derivaatan määritelmä funktiolle

$\begin{aligned} &\lim_{x\to x_0}\frac{F(x)-F(x_0)}{x-x_0}\\ &=\lim_{x\to x_0}\frac{f(g(x))-f(g(x_0))}{x-x_0}\\ &=\lim_{x\to x_0}\frac{\big(f(g(x))-f(g(x_0))\big)\cdot(g(x)-g(x_0))}{(x-x_0)\cdot(g(x)-g(x_0))}&&\Big|\,y=g(x), a=g(x_0)\\ &=\lim_{x\to x_0}\frac{f(y)-f(a)}{y-a}\cdot \frac{g(x)-g(x_0)}{x-x_0}, \end{aligned}$

olettaen, että $y\neq a$ eli $g(x)\neq g(a).$ Tämä ei kuitenkaan aina päde. Vaikka olisi mielivaltaisen lähellä lukua , niin on olemassa funktioita, joille g(x)=g(a) (esim. $g(x)=x^2\sin(1/x),\, \text{kun}\, x\neq0\,\text{ja}\, g(0)=0).$ Tämän takia tässä kohdassa perustelua tulee olla tarkka.

Määritellään funktio

$h(y)=\left\{\begin{array}{ll} \frac{f(y)-f(a)}{y-a}, & \text{kun} \, y\neq a \\ f'(a), & \text{kun} \, y=a, \end{array} \right.$

välttääksemme ongelmat. Huomaa, että on jatkuva, koska on derivoituva pisteessä a=g(x_0). Tällöin yhdistetty funktio

$h(g(x))=\left\{\begin{array}{ll} \frac{f(g(x))-f(g(x_0))}{g(x)-g(x_0)}, & \text{kun} \, y\neq a \\ f'(g(x_0)), & \text{kun} \, y=a, \end{array} \right.$

on jatkuva pisteessä x_0. Nyt jos $g(x)\neq g(x_0)$ , niin aiemmin käsitelty raja-arvo saadaan muotoon

$\begin{aligned} &\lim_{x\to x_0}\frac{F(x)-F(x_0)}{x-x_0}\\ &=\lim_{x\to x_0}\frac{f(y)-f(a)}{y-a}\cdot \frac{g(x)-g(x_0)}{x-x_0}\\ &=\lim_{x\to x_0}h(g(x))\cdot\frac{g(x)-g(x_0)}{x-x_0}. \end{aligned}$

Lisäksi jos g(x)=g(x_0), niin

$\begin{aligned} 0=\frac{F(x)-F(x_0)}{x-x_0}=h(g(x))\cdot\frac{g(x)-g(x_0)}{x-x_0}=0. \end{aligned}$ Nyt käyttäen yhdistetyn funktion $h\circ g$ jatkuvuutta pisteessä x_0 , saadaan

$\begin{aligned} &\lim_{x\to x_0}\frac{F(x)-F(x_0)}{x-x_0}\\ &=\lim_{x\to x_0}h(g(x))\cdot\frac{g(x)-g(x_0)}{x-x_0}\\ &=f'(g(x_0))\cdot g'(x_0). \end{aligned}$

Tämä pätee kaikille $x_0\in\R,$ joten $D\Big((f(g(x))\Big)=f'(g(x))\cdot g'(x)$ kaikille $x\in\R.$

# funktioiden-derivaattoja

Funktioiden derivaattoja

Merkitään derivointioperaatiota kirjaimella . Yleisimmille funktioille ovat voimassa seuraavat derivointisäännöt:

Sääntö	Funktio
$\displaystyle \vphantom{\Big\|} D(a)=0$	Vakiofunktio
$\displaystyle \vphantom{\Big\|} D(x^{\red{a}}) = {\red{a}}\cdot x^{{\red{a}}-1}, \quad \color{gray}a \ne 0$	Potenssifunktio
$\displaystyle \vphantom{\Big\|} D(e^x) = e^x$	Luonnollinen eksponenttifunktio
$\displaystyle \vphantom{\Big\|} D({\red{a}}^x)={\red{a}}^x\cdot \ln {\red{a}}$	Eksponenttifunktio
$\displaystyle \vphantom{\Big\|} D(\ln x) = \frac{1}{x}, \ \color{gray}x > 0$	Luonnollinen logaritmifunktio
$\displaystyle \vphantom{\Big\|} D(\log_{{\red{a}}}x)=\dfrac{1}{x\cdot \ln {\red{a}}}, \color{gray}\ x > 0$	${\red{a}}$ -kantainen logaritmifunktio
$\displaystyle \vphantom{\Big\|} D(\sin x)=\cos x$	Sinifunktio
$\displaystyle \vphantom{\Big\|} D(\cos x)=-\sin x$	Kosinifunktio
$\begin{align}D(\tan(x))&=\frac{1}{\cos^2(x)}\\&=1+\tan^2(x)\end{align}$	Tangenttifunktio

Mutta miksi?

Osio työn alla. Funktioiden derivointisäännöt voidaan perustella derivaatan määritelmää sekä esiteltyjä yleisiä derivointisääntöjä käyttäen.

Potenssifunktion derivaatta

Perustellaan tämä sääntö kahdessa eri tapauksessa.

1) Oletetaan, että on positiivinen kokonaisluku. Olkoon f(x)=x^a. Tässä tilanteessa käytetään derivaatan määritelmälle yhtäpitävää määritelmää

$\lim_{x\to c}\frac{f(x)-f(c)}{x-c}=\lim_{x\to c}\frac{x^a-c^a}{x-c}.$

Polynomin x^a-c^a nolla kohta on joten

$\begin{aligned} x^a-c^a&=(x-c)(x^{a-1}+c\cdot x^{a-2}+c^2\cdot x^{a-3}+\cdots+c^{a-2}\cdot x+c^{a-1}\cdot x^{0})\\ &=(x-c)(x^{a-1}+c\cdot x^{a-2}+c^2\cdot x^{a-3}+\cdots+c^{a-2}\cdot x+c^{a-1}). \end{aligned}$

Sijoitetaan tämä määritelmään, jolloin

$\begin{aligned} &\lim_{x\to c}\frac{x^a-c^a}{x-c}\\ &=\lim_{x\to c}\frac{(x-c)(x^{a-1}+c\cdot x^{a-2}+c^2\cdot x^{a-3}+\cdots+c^{a-2}\cdot x+c^{a-1})}{x-c}\\ &=\lim_{x\to c}\left(x^{a-1}+c\cdot x^{a-2}+c^2\cdot x^{a-3}+\cdots+c^{a-2}\cdot x+c^{a-1}\right)\\ &=c^{a-1}+c\cdot c^{a-2}+c^2\cdot c^{a-3}+\cdots+c^{a-2}\cdot c+c^{a-1}\\ &=\underbrace{c^{a-1}+c^{a-1}+c^{a-1}+\cdots+c^{a-1}+c^{a-1}}_{a\ \text{kertaa}}\\ &=a\cdot c^{a-1}. \end{aligned}$

Saatiin siis $f'(c)=a\cdot c^{a-1}.$ Koska tämä pätee kaikille $c\in\R,$ on $D(x^a)=a\cdot x^{a-1}$ kaikille $x\in\R.$

2) Oletetaan, että $a\in\R$ ja merkitään f(x)=x^a (huom. x>0 ). Muokataan yhtälöä hieman ottamalla luonnollinen logaritmi puolittain

$\begin{aligned} f(x)&=x^a&&\Big|\ \ln(\,\cdot\,)\\ \ln(f(x))&=\ln(x^a)\\ \ln(f(x))&=a\cdot\ln(x). \end{aligned}$

Derivoidaan yhtälö puolittain ns. implisiittisesti, jolloin

$\begin{aligned} \frac{\text{d}}{\dx}\ln(f(x))&=\frac{\text{d}}{\dx}a\cdot\ln(x)\\ \frac{1}{f(x)}\cdot f'(x)&=a\cdot\frac{1}{x}. \end{aligned}$

Ratkaisemalla saadusta yhtälöstä f'(x), saadaan

$\begin{aligned} \frac{1}{f(x)}\cdot f'(x)&=a\cdot\frac{1}{x}&&\Big| \cdot f(x)\\ f'(x)&=f(x)\cdot\frac{a}{x}. \end{aligned}$

Sijoittamalla f(x)=x^a

$f'(x)=f(x)\cdot\frac{a}{x}=x^a\cdot\frac{a}{x}=a\cdot x^{a-1}.$

Luonnollisen eksponenttifunktion derivaatta

Muodostetaan eksponenttifunktiolle erotusosamäärän raja-arvo.

$\begin{aligned} \lim_{h\to 0}\frac{e^{x+h}-e^x}{h}&=\lim_{h\to 0}\frac{e^xe^h-e^x}{h}\\ &=\lim_{h\to 0}e^x\frac{e^h-1}{h}\\ &=e^x\lim_{h\to 0}\frac{e^h-1}{h}\\ &=e^x, \end{aligned}$

sillä $\lim_{h\to 0}\frac{e^h-1}{h}=1.$ Saatiin siis D(e^x)=e^x.

Luonnollisen logaritmin derivaatta

Perustellaan luonnollisen logaritmin derivaatta käyttäen derivaatan määritelmää logaritmin laskusääntöjä sekä luonnollisen eksponenttifunktion määritelmää.

Aloitetaan kirjoittamalla derivaatan määritelmä funktiolle $f(x)=\ln x$

$\begin{aligned} \lim_{h\to 0}\frac{\ln(x+h)-\ln(x)}{h}&=\lim_{h\to 0}\frac{\ln(\frac{x+h}{x})}{h}\\ &=\lim_{h\to 0}\frac{1}{h}\ln\left(1+\frac{h}{x}\right)\\ &=\lim_{h\to 0}\ln\left(\left(1+\frac{h}{x}\right)^{1/h}\right)\\ &=\ln\left(\lim_{h\to 0}\left(1+\frac{h}{x}\right)^{1/h}\right). \end{aligned}$

Koska $\frac{h}{x}=\frac{1/x}{1/h}$ ja $\lim_{h\to 0}\frac{1}{h}=\infty,$ niin huomataan, että viimeinen raja-arvo luonnollisen eksponenttifunktion määritelmä $e^y=\lim_{n\to\infty}\left(1+\frac{y}{n}\right)^n,$ kun merkitään $y=\frac{1}{x}$ ja $n=\frac{1}{h}.$

Saadaan siis

$\begin{aligned} \lim_{h\to 0}\frac{\ln(x+h)-\ln(x)}{h}&=\ln\left(\lim_{h\to 0}\left(1+\frac{h}{x}\right)^{1/h}\right)\\ &=\ln(e^{1/x})=\frac{1}{x}. \end{aligned}$

-kantaisen logaritmin derivaatta

Luonnollisen logaritmin derivaatta on $D(\ln x)=\frac{1}{x}.$

Yleisen logaritmin derivaatta saadaan tämän avulla käyttämällä kannanvaihtoa

$\log_a x=\frac{\ln x}{\ln a},$

jolloin

$D(\log_a x)=\frac{D(\ln x)}{\ln a}=\frac{1}{x\ln a}$

Logaritmin määritelmän ja laskusäännöt löytyvät täältä.

Sinin derivaatta

Käytetään sinin derivaatan perustelemiseen derivaatan määritelmää. Kirjoitetaan erotusosamäärä funktiolle $f(x)=\sin x$

$\begin{aligned} &\frac{\sin(x+h)-\sin x}{h}. \end{aligned}$

Käytetään sinin summakaavaa $\sin(x+ y)=\sin x \cos y + \cos x \sin y,$ jolloin

$\begin{aligned} \frac{\sin(x+h)-\sin x}{h}&=\frac{\sin x\cos h+\cos x\sin h-\sin x}{h}\\ &=\frac{\sin x(\cos h-1)+\cos x\sin h}{h}\\ &=\sin x\cdot\frac{\cos h-1}{h}+\cos x\cdot\frac{\sin h}{h}\\ &=-\sin x\cdot\frac{1-\cos h}{h}+\cos x\cdot\frac{\sin h}{h}. \end{aligned}$

Ottamalla raja-arvo erotusosamäärästä, saadaan

$\begin{aligned} &\lim_{h\to0}\frac{\sin(x+h)-\sin x}{h}\\ &=\lim_{h\to0}\left(-\sin x\cdot\frac{1-\cos h}{h}+\cos x\cdot\frac{\sin h}{h}\right)\\ &=\cos x, \end{aligned}$

sillä $\lim_{h\to0}\frac{1-\cos h}{h}=0$ ja $\lim_{h\to0}\frac{\sin h}{h}=1.$ Saatiin siis $D(\sin x)=\cos x.$

Kosinin derivaatta

Kosinin derivaatan perustelu noudattelee samoja ideoita kuin sinin derivaatan perustelu.

Tangentin derivaatta

Tangentin derivaatan voi perustella esimerkiksi osamäärän derivointisäännöllä.

Vähemmän käytettyjä derivointisääntöjä (arcsin, arccos, sinh, ...)

Sääntö	Funktio
$D(\arcsin x)=\cfrac{1}{\sqrt{1-x^2}}$	Arkussinifunktio ( $=\sin^{-1}$ )
$D(\arccos x)=\cfrac{-1}{\sqrt{1-x^2}}$	Arkuskosinifunktio ( $=\cos^{-1}$ )
$D(\arctan x)=\cfrac{1}{1+x^2}$	Arkustangenttifunktio ( $=\tan^{-1}$ )
$D(\sinh x)=\cosh x$	Hyperbolinen sinifunktio
$D(\cosh x)=\sinh x$	Hyperbolinen kosinifunktio
$D(\tanh x)=\cfrac{1}{\cosh^2x}$	Hyperbolinen tangenttifunktio

Vielä vähemmän käytettyjä derivointisääntöjä löytyy wikipediasta.

Esimerkkejä derivaatasta ja derivoinnista

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Polynomifunktion derivointi: Määritä $\frac{\text{d}}{\text{d}t}f(t)$ , kun $f(t) = 2t^3+t^{5}$ .

Lyhyesti:

$\begin{aligned} \frac{\text{d}}{\text{d}t}f(t) &= \frac{\text{d}}{\text{d}t}(\green2t^{\red{3}}+t^{\red5}) \\ &=\green2\cdot {\red{3}} t^{{\red{3}}-1} + \red5t^{\red5-1} \\ &= 6t^2 + 5t^4 \end{aligned}$

Pitkästi:

Määritetään derivaatta sääntöjä käyttäen: $\begin{aligned} \frac{\text{d}}{\text{d}t}f(t) &= \frac{\text{d}}{\text{d}t}(2t^{3}\ \textbf{\blue{+}} \ t^5) &&\Big| \text{ \blue{summan} derivointi}\\ &= \frac{\text{d}}{\text{d}t}\green2t^3 + \frac{\text{d}}{\text{d}t}t^5&&\Big| \text{ \green{vakiot} ulos} \\ &= 2\cdot\frac{\text{d}}{\text{d}t}t^{\red3} + \frac{\text{d}}{\text{d}t}t^{\red5} &&\Big| \text{ \red{potenssifunktion derivointi}}\\ &= 2\cdot \red3t^{\red3-1} + \red5t^{\red5-1} \\ &= 6t^2 + 5t^4 \end{aligned}$ Siispä $\frac{\text{d}}{\text{d}t}f(t) = 6t^2 + 5t^4$ .

Eksponenttifunktion derivointi: Määritä f'(x) , kun f(x) = 2^x+4 .

Määritetään derivaatta f'(x) käyttämällä derivointisääntöjä vakion derivoinnille, summan derivoinnille sekä eksponenttifunktion derivoinnille: $\begin{aligned} f'(x)&=D(2^x+4) &&\Big|\text{ summan derivointi}\\ &=D(2^x)+D(4) &&\Big|\text{ eksponentti ja vakio}\\ &=2^x\cdot\ln 2+0\\ &=2^x\cdot\ln 2 \end{aligned}$

Yhdistetyn funktion derivointi, ketjusääntö: Määritä $\frac{\text{d}}{\dx}(2x-3)^4$ .

Lyhyesti:

Derivoidaan funktio käyttäen potenssifunktion derivointisääntöjä, mutta kerrotaan lopuksi sisäfunktion derivaatalla.

$\begin{aligned} \frac{\text{d}}{\dx}(2x-3)^4 &= \color{red}{4(2x-3)^3} \cdot \color{blue}{2} \\ &= 8(2x-3)^3 \end{aligned}$

Pitkästi:

Derivaatta $\frac{\text{d}}{\dx}(2x-3)^4$ voidaan laskea käyttämällä ketjusääntöä: $D(f(g(x)) = f'(g(x))\cdot g'(x).$ Jotta sääntöä voi käyttää, on selvitettävä ensin, mitä funktiot ja ovat.

Derivoitava funktio on yhdistetty funktio. $\begin{aligned} \color{blue}(\color{red}{2x}&\color{red}{-3}\color{blue}{)^4} \\ \swarrow \quad&\quad \ \ \searrow\\ \color{red}{2x-3} \quad & \quad \ \ \ \quad \color{blue}{x^4} \end{aligned}$

Merkitään sisäfunktiota g(x) = 2x-3 ja ulkofunktiota f(x) = x^4 , jolloin f(g(x)) = (2x-3)^4. Ketjusäännön kaavassa tarvitaan derivaattafunktiot ja : $f'(x) = \frac{\text{d}}{\dx}(x^4) = 4x^3$ $g'(x) = \frac{\text{d}}{\dx}(2x-3) = 2$

Sijoitetaan tiedot ketjusäännön kaavaan: $\begin{aligned} D(f(\red{g(x)})) &= f'(\red{g(x)})\cdot \green{g'(x)} &&\Big| \ \red{g(x)} = 2x-3, \green{g'(x)} = 2 \\ &= \blue{f'(}2x-3\blue{)}\cdot 2 &&\Big| \ f(x) = x^4, \blue{f'(x)} = 4x^3\\ &= 4(2x-3)^3 \cdot 2 \\ &= 8(2x-3)^3 \end{aligned}$

Siispä $\frac{\text{d}}{\dx}(2x-3)^4 = 8(2x-3)^3$

Eksponenttifunktion derivointi, ketjusääntö: Määritä derivaatta $\frac{\text{d}}{\text{d}t}(c e^{-kt})$ , kun $c, k \in \mathbb{R}$ .

On hyvä huomata, minkä muuttujan suhteen derivointi tapahtuu, eli tässä tapauksessa muuttujan suhteen. Luvut ja ovat muuttumattomia vakioita.

Lyhyesti:

Derivoidaan funktio käyttäen luonnollisen eksponenttifunktion derivointisääntöä ja kerrotaan lopuksi sisäfunktion derivaatalla: $\begin{align*} \frac{\text{d}}{\text{d}t}(c e^{-kt})=c\textcolor{red}{e^{-kt}}\cdot \textcolor{blue}{(-k)}=-kce^{-kt} \end{align*}$

Pitkästi:

Halutaan käyttää ketjusääntöä. Tunnistetaan ulko- ja sisäfunktiot derivoitavasta funktiosta. Merkitään $ce^{-kt}=f((g(t)),$ missä $f(t)=ce^{t}$ ja g(t)=-kt. Tällöin f'(t)=ce^t vakion derivointisäännön ja luonnollisen eksponentin derivointisäännön nojalla. Lisäksi $g'(t)=-k\cdot D(t)=-k$ vakiolla kertomisen ja potenssin derivaatan laskusääntöjen nojalla. Nyt olemme valmiit käyttämään ketjusääntöä: $\begin{align*} \frac{\text{d}}{\text{d}t}(ce^{-kt})&=f'(g(t))\cdot g'(t)\\ &=f'(-kt)\cdot(-k)\\ &=ce^{-kt}\cdot(-k)\\ &=-kce^{-kt} \end{align*}$

Toinen derivaatta, toisen kertaluvun derivaatta: Laske eksponenttifunktion toinen derivaatta $\frac{\text{d}^2}{\dx^2}e^{ax^2}$ .

Lasketaan derivaatta $\frac{\text{d}^2}{\dx^2}e^{ax^2}$ derivoimalla funktiota $e^{ax^2}$ kahdesti.

$\begin{aligned} \frac{\text{d}^2}{\dx^2}e^{ax^2} &= \frac{\text{d}}{\dx}\left({\color{red}{\frac{\text{d}}{\dx}e^{ax^2}}}\right) &&\Big| \text{ \red{ketjusääntö}} \\ &= \frac{\text{d}}{\dx}(e^{ax^2}\cdot 2ax) &&\Big| \text{ tulon derivaatta}\\ &= \red{\frac{\text{d}}{\dx}\left(e^{ax^2}\right)}\cdot 2ax + e^{ax^2}\cdot \frac{d}{dx}2ax &&\Big| \text{ \red{ketjusääntö}}\\ &= \blue{e^{ax^2}}\cdot 2ax\cdot 2ax + \blue{e^{ax^2}}\cdot 2a &&\Big| \text{ \blue{yhteinen tekijä}}\\ &= e^{ax^2}(4a^2x^2+2a) &&\Big| \text{ yhteinen tekijä}\\ &= 2ae^{ax^2}(2ax^2+1)\\ \end{aligned}$

Tulon derivaatta, ketjusääntö:

Laske derivaatta $\frac{\text{d}\left[f(t)g(t)\right]}{\text{d}t}$ kun $f(t) = A^2\cos(at)$ ja $g(t)=e^{-t/\tau}$ .

Tulon derivointisäännön nojalla $\frac{d[f(t)g(t)]}{dt}=\frac{d}{dt}f(t) \cdot g(t) + f(t) \cdot \frac{d}{dt} g(t).$

Lasketaan tarvittavat derivaatat. Käytetään molemmissa ketjusääntöä. Derivoidaan ensin funktio normaalisti, mutta kerrotaan lopuksi sisäfunktion derivaatalla

$\begin{aligned} \frac{d}{dt}f(t) &= \frac{d}{dt} A^2\cos(at)&&\Big| \text{ ketjusääntö} \\ &=A^2 (\blue{-\sin(at)})\cdot \red a \\ &=-aA^2 \sin(at) \\ \\ \frac{d}{dt}g(t) &= \frac{d}{dt}e^{-t/\tau}&&\Big| \text{ ketjusääntö} \\ &= \blue{e^{-t/\tau}}\cdot \red{(-1/\tau)} \\ &= -\frac{e^{-t/\tau}}{\tau} \end{aligned}$

Sijoitetaan lasketut derivaatat tulon derivointisääntöön:

$\begin{aligned} \frac{d[f(t)g(t)]}{dt} &= \frac{d}{dt}f(t) \cdot g(t) + f(t) \cdot \frac{d}{dt} g(t) \\ &=-aA^2 \sin(at) \cdot e^{-t/\tau} + A^2\cos(at)\cdot \left(-\frac{e^{-t/\tau}}{\tau}\right) &&\Big| \text{ yhteinen tekijä} \\ &= -A^2e^{-t/\tau}\left(a\sin(at) + \frac{\cos(at)}{\tau}\right) \end{aligned}$

Osamäärän derivaatta Laske derivaatta $\frac{d}{dx}\frac{x^2}{x-1}$

Valitaan f(x)=x^2 ja g(x)=x-1 . Soveltamalla osamäärän derivointisääntöä saadaa:

\[\begin{aligned}\frac{d}{dx}\frac{f(x)}{g(x)}=&\frac{f'(x)g(x)-g'(x)f(x)}{(g(x))^2}\\ =&\frac{2x(x-1)-(1-0)(x^2)}{(x-1)^2}\\ =&\frac{2x^2-2x-x^2}{(x-1)^2}\\ =&\frac{x^2-2x}{(x-1)^2}, \;\text{ kun }x\ne 1.\end{aligned}\]

Osittaisderivointi: Laske osittaisderivaatta $\frac{\partial}{\partial y} \left((4\pi ax)^{-1/2}e^{-y^2/4ax}\right)$ .

Merkinnällä $\frac{\partial}{\partial y}$ tarkoitetaan osittaisderivointia muuttujan suhteen. Tällöin derivoidaan normaalisti :n suhteen ja käsitellään kaikkia muita funktion muuttujia vakioina.

Huomataan, että $(4\pi a x)^{-1/2}$ on vakio muuttujan suhteen, joten

$\frac{\partial}{\partial y} \left((4\pi ax)^{-1/2}e^{-y^2/4ax}\right)=(4\pi ax)^{-1/2}\frac{\partial}{\partial y}\left(e^{-y^2/4ax}\right).$

Lasketaan osittaisderivaatta $\frac{\partial}{\partial y}\left(e^{-y^2/4ax}\right)$ :

$\begin{aligned} \frac{\partial}{\partial y}\left(e^{-y^2/4ax}\right) &= e^{-y^2/4ax} \cdot (-2y/4ax) &&\Big| \text{ ketjusääntö}\\ &= e^{-y^2/4ax} \cdot (-y/2ax) \end{aligned}$

Siispä haluttu osittaisderivaatta on $\frac{\partial}{\partial y} \left((4\pi ax)^{-1/2}e^{-y^2/4ax}\right) = (4\pi ax)^{-1/2}e^{-y^2/4ax}(-y/2ax)$

Osittaisderivointi: Määritä $\frac{\partial^2}{\partial x \partial y}f(x, y, z)$ , kun f(x, y, z) = 3xz^2 - 5yx^2.

Osittaisderivaattamerkinnällä tarkoitetaan, että

$\frac{\partial^2}{\partial x \partial y}f(x, y, z) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}f(x, y, z)\right).$

Osittaisderivaatat voidaan nyt laskea yksi kerrallaan. Osittaisderivoidessa muuttujan suhteen voidaan käsitellä kaikkia muita esiintyviä muuttujia vakiona:

$\begin{aligned} \frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}f(x, y, z)\right) &= \frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}(\blue{3xz^2} - 5yx^2)\right) && \Big| \ \text{\blue{vakio} muuttujan } y \text{ suhteen} \\ &= \frac{\partial}{\partial x}\left(-5x^2\right)\\ &= -10x \end{aligned}$

Osittaisderivointi: Miksi osittaisderivoinnin järjestyksellä on merkitystä?

Määritä derivaatan arvo kun $\frac{\partial^2}{\partial x \partial y}f(0{,} 0),$ kun $f(x{,}y)=\left\{\begin{array}{ll} 0 & (x{,}y)=(0{,}0)\\ \dfrac{xy^3}{x^2+y^2} & \mbox{muualla.}\end{array}\right .$ Lasketaan funtion osittaisderivaatat $\dfrac{\partial^2}{\partial y\partial x}f(0{,}0)$ ja $\dfrac{\partial^2}{\partial x\partial y}f(0{,}0)$ :

$\begin{align*} \dfrac{\partial}{\partial x}f(0{,}0)&=\lim_{t\to 0} \frac{f(t{,}0)-f(0{,}0)}{t}\\&=\lim_{t\to 0} \frac{0-0}{t}=0 \end{align*}$ $\begin{align*} \dfrac{\partial}{\partial y}f(0{,}0)&=\lim_{t\to 0} \frac{f(0{,}t)-f(0{,}0)}{t}\\&=\lim_{t\to 0} \frac{0-0}{t}=0 \end{align*}$ $\begin{align*} \dfrac{\partial^2}{\partial x\partial y}f(0{,}0)&=\lim_{t\to 0} \frac{\dfrac{\partial}{\partial y}f(t{,}0)-\dfrac{\partial}{\partial y}f(0{,}0)}{t}\\&=\lim_{t\to 0} \frac{0-0}{t}=0 \end{align*}$ $\begin{align*} \dfrac{\partial^2}{\partial y\partial x}f(0{,}0)&=\lim_{t\to 0} \frac{\dfrac{\partial}{\partial x}f(t{,}0)-\dfrac{\partial}{\partial x}f(0{,}0)}{t}\\&=\lim_{t\to 0} \frac{t-0}{t}=1 \end{align*}$

Tässä tapauksessa kävi niin, että $\dfrac{\partial^2}{\partial y\partial x}f(0{,}0)\ne \dfrac{\partial^2}{\partial x\partial y}f(0{,}0),$ sillä funktion $\text{f}$ toisen kertaluvun osittaisderivaatat eivät ole jatkuvia origossa. Epäjatkuvuuden toteamiseksi lasketaan osittaisderivaatat myös origon ulkopuolella:

$\begin{align*} \dfrac{\partial}{\partial x}f(x{,}y)&=\frac{y^3(x^2+y^2)-2x(xy^3)}{{(x^2+y^2)}^2}\\&=\frac{y^5-x^2y^3}{{(x^2+y^2)}^2} \end{align*}$ $\begin{align*} \dfrac{\partial}{\partial y}f(x{,}y)&=\frac{3xy^2(x^2+y^2)-2y(xy^3)}{{(x^2+y^2)}^2}\\&=\frac{xy^4-3x^2y^2}{{(x^2+y^2)}^2} \end{align*}$ $\begin{align*} \dfrac{\partial^2}{\partial y\partial x}f(x{,}y)&=\frac{5y^4-2x^2y^2}{{(x^2+y^2)}^2}-\frac{4(y^5-x^2y^3)y}{{(x^2+y^2)}^3}\\&=\frac{y^6+6y^4x^2-3y^2x^4}{{(x^2+y^2)}^3} \end{align*}$ $\begin{align*} \dfrac{\partial^2}{\partial x\partial y}f(x{,}y)&=\frac{y^4+6xy^2}{{(x^2+y^2)}^2}-\frac{4(xy^4+3x^2y^2)x}{{(x^2+y^2)}^3}\\&=\frac{y^6+6y^4x^2-3y^2x^4}{{(x^2+y^2)}^3} \end{align*}$

Nyt $\begin{align*} \lim_{x\to 0} \dfrac{\partial^2}{\partial y\partial x}f(x{,}0)&=\lim_{x\to 0} \frac{0}{{(x^2)}^3}=0\\&\neq1=\dfrac{\partial^2}{\partial y\partial x}f(0{,}0) \end{align*}$ ja $\begin{align*} \lim_{y\to 0} \dfrac{\partial^2}{\partial x\partial y}f(0{,}y)&=\lim_{y\to 0} \frac{y^6}{{(y^2)}^3}=\lim_{y\to 0} 1=1\\&\neq0=\dfrac{\partial^2}{\partial x\partial y}f(0{,}0) \end{align*}$

eli toisen kertaluvun osittaisderivaatat eivät ole jatkuvia origossa. Origon ulkopuolella sen sijaan $\dfrac{\partial^2}{\partial y\partial x}f(x{,}y)= \dfrac{\partial^2}{\partial x\partial y}f(x{,}y).$