Koordinaatistot

Ongelmien ratkaisemisessa kannattaa hyödyntää mahdollisia symmetrioita. Esimerkiksi tarkastellessa etäisyyksiä johonkin pisteeseen on laskeminen helpompaa pallokoordinaateissa, joissa etäisyys origoon on koordinaatti $\red r.$ Karteesisessa koordinaatistossa sama etäisyys on $\sqrt{\red x^2+\green y^2+\blue z^2}.$

Yleisesti käytettyjä koordinaattijärjestelmiä ovat

Karteesiset koordinaatit $(\red x,\green y)$ ja $(\red x,\green y,\blue z)$
Käyräviivaiset koordinaatit
- Napakoordinaatit $(\red r,\green \varphi)$
- Sylinterikoordinaatit $(\red r,\green \varphi,\blue z)$ eli napakoordinaatit + $\blue z\text-$ akseli
- Pallokoordinaatit $(\red r,\green \theta,\blue \varphi)$

Ajatusleikki:Kulkija koordinaatistoissa ja teleskooppi.

Kuvitellaan, että seisot origossa katse $x\text-$ akselin suuntaan ja haluat päästä johonkin pisteeseen tasossa. Voit ensin kääntyä paikallasi kohti tätä pistettä ja sitten kävellä suoraan pistettä kohti kunnes olet perillä. Napakoordinaateissa kulma $(\green\varphi)$ kertoo, kuinka paljon käännyit ja säde $(\red r)$ kuinka pitkään kävelit.

Sylinterikoordinaateissa joudut ottamaan mukaan tikapuut. Matkasi alkaa kuten napakoordinaateissa, mutta et kävele suoraan pistettä kohti vaan paikkaan suoraan pisteen alapuolelle (tai yläpuolelle). Vasta kun olet saapunut pisteen kohdalle $xy\text-$ tasossa, otat esiin tikkaasi ja lähdet kiipeämään suoraan ylöspäin. Edelleen kulma $(\green\varphi)$ kertoo paljonko käännyit matkasi alussa ja säde $(\red r)$ kertoo paljonko kävelit. $\blue z$ -koordinaatti kertoo kuinka korkealle kiipesit.

Pallokoordinaatteja varten tarkastelemme pyörivällä jalustalla olevaa teleskooppia, jota voi kallistaa vain yhteen suuntaan. Aivan aluksi teleskooppi osoittaa suoraan ylöspäin ja voimme kallistaa sitä vain positiivisen -akselin suuntaan. Joudumme pyörittämään jalustaa $(\blue\varphi)$ sen verran, että saamme seuraavaksi kallistettua $(\green\theta)$ teleskoopin kohti kohdetta. Sitten tarvitsee enää vain säätää linssit sopivalle etäisyydelle $(\red r)$ .

# napajasylinteri

Napa- ja sylinterikoordinaatit

Napakoordinaateissa pisteen $(\red r,\green\varphi)$ koordinaatit ovat pisteen etäisyys origosta $\red r$ sekä positiivisen $x\text-$ akselin ja paikkavektorin välinen kulma $\green\varphi,$ vastapäivään kierrettynä.

Sylinterikoordinaateissa on otettu napakoordinaatteihin lisäksi mukaan korkeus $\blue z.$ Säde $\red r$ on etäisyys pisteen ja $\blue z$ -akselin välillä ja kulma $\green\varphi$ kertoo paikkavektorin $xy\text-$ tasoon otetun projektion ja positiivisen $x\text-$ akselin välisen kulman.

Karteesisissa koordinaateissa yhdellä pisteellä on vain yksi mahdollinen esitystapa. Tämä ei päde esimerkiksi napakoordinaateissa, joissa (1,0) ja $(1,2\pi)$ ovat sama piste. Tästä ongelmasta voidaan päästä rajoittamalla kulman $\green\varphi$ arvo sopivalle välille, kuten $0\le\green\varphi<2\pi$ tai $-\pi<\green\varphi\leq\pi.$

# pallokoordinaatit

Pallokoordinaatit

Pallokoordinaateissa pisteen koordinaatit määrää etäisyys origosta $\red r$ sekä kaksi kulmaa: elevaatiokulma $\green \theta$ ja atsimuuttikulma $\blue \varphi.$

Elevaatiokulma $\green \theta$ kertoo pisteen paikkavektorin ja positiivisen -akselin välisen kulman ja sen arvo on välillä $[0,\pi].$ Arvo vastaa positiivista -akselia ja $\pi$ negatiivista. Elevaatiokulman eri arvot vastaavat eri leveyspiirejä ja -asteita.

Atsimuuttikulma $\blue\varphi$ saadaan ottamalla paikkavektorin projektio -tasolle ja laskemalla tämän projektion sekä -akselin välinen kulma. Myös napa- ja sylinterikoordinaateissa voidaan puhua atsimuuttikulmasta. Atsimuuttikulman arvo on useimmiten välillä $[0,2\pi)$ tai $[-\pi,\pi).$ Toisin kuin elevaatiokulmalla, määrittelyvälin päätepisteet vastaavat samaa pistettä koordinaatistossa. Atsimuuttikulman eri arvot vastaavat eri pituuspiirejä ja -asteita.

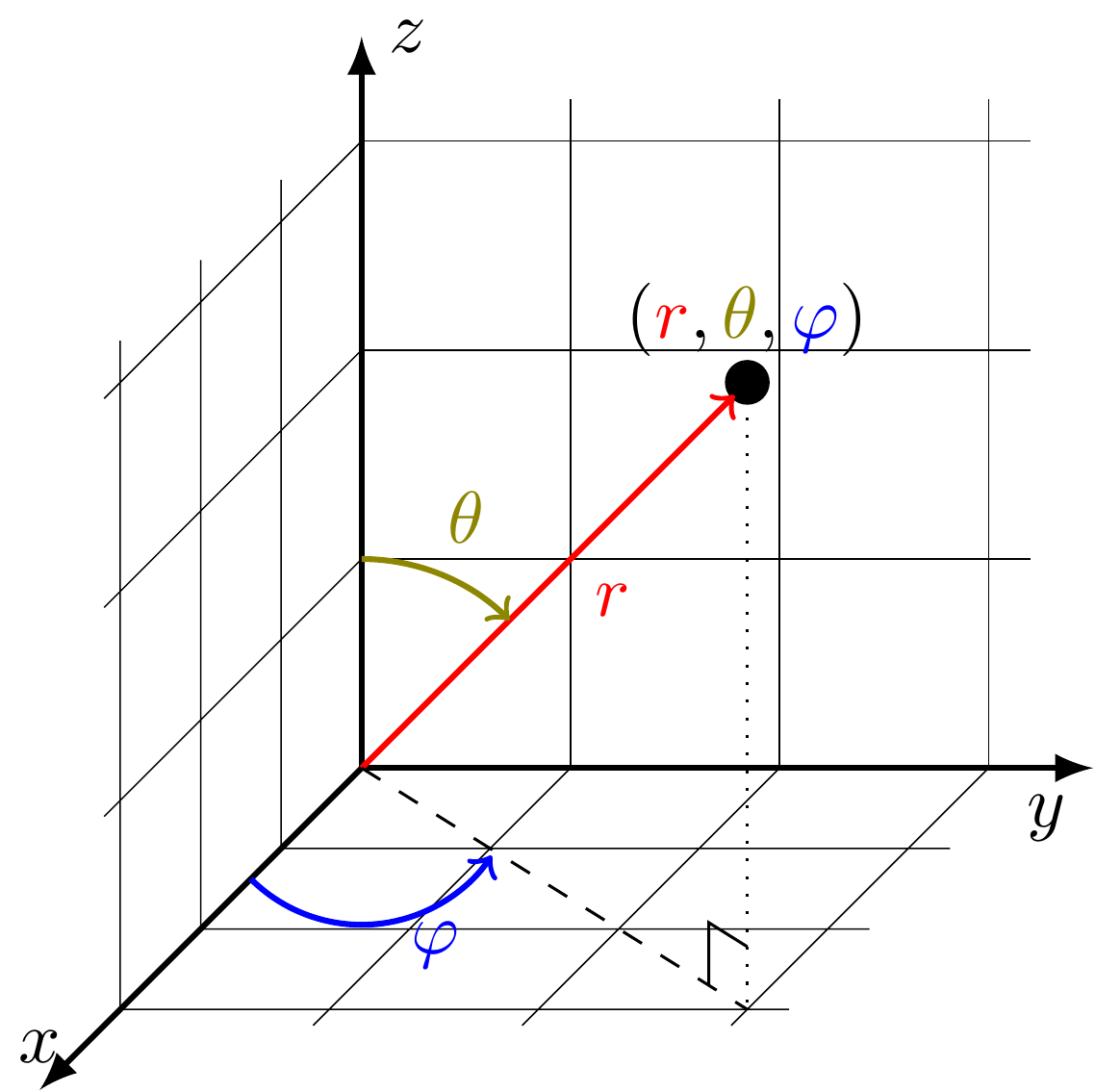
Elevaatio- ja atsimuuttikulman merkitys on hyvin erilainen, eikä näitä tämän takia tulisi sekoittaa keskenään. On hyvä tietää, että matematiikan yhteydessä näiden kulmien merkinnät ovat usein käänteiset, jolloin $\green\theta$ on atsimuuttikulma ja $\blue\varphi$ elevaatiokulma.

# geo363

Muunnoskaavat

Muunnoskaavojen avulla voidaan vaihtaa koordinaatistosta toiseen. Karteesisesta koordinaatistosta pois vaihtaminen on yksinkertaista, mutta muihin suuntiin mentäessä oikean kulman löytäminen on hiukan haastavampaa.

Koordinaattien muunnoskaavat

Karteesisten- ja napa/sylinterikoordinaattien välillä pätevät seuraavat muunnoskaavat $\begin{align*} x&=r\cos(\varphi) & r&=\sqrt{x^2+y^2}\\ y&=r\sin(\varphi). \end{align*}$

$\begin{tikzpicture}[domain=0:4] \draw[very thin,color=gray] (-0.5,-0.5) grid (3.5,3.5); \draw[->] (-0.5,0) -- (3.5,0) node[right] {$x$}; \draw[->] (0,-0.5) -- (0,3.5) node[above] {$y$}; \filldraw[black] (2,3) circle (2pt); \draw[thick,blue] (0,0) -- (2,0); \draw[thick,blue] (2,0) -- (2,3); \node[color=blue] at (1.1,-.3) {$x$}; \node[color=blue] at (2.4,1.7) {$y$}; \draw[thick,red] (0,0) -- (2,3); \node[color=red] at (.7,1.7) {$r$}; \draw[red] (.4,0) to [bend right=20] (.23,.35); \node[color=red] at (.7,.4) {$\varphi$}; \draw[very thin,blue] (2,0) rectangle (1.7,.3); \end{tikzpicture}$

Kulmaa $\varphi$ on hankala määrittää yhdellä yhtälöllä kaikilla ja . Kuvan tilanteessa saataisiin $\varphi=\arctan(\frac{ y}{ x}).$ Huomaa kuitenkin, kuinka tämä kaava antaa saman tuloksen myös, jos ja ovat molemmat negatiivisia. Käytännössä helpointa on päätellä kulman suuruus kuvan avustuksella. Kulman saa myös paloittain määritetyllä funktiolla atan2, jota käytetään lähinnä ohjelmoinnissa.

Karteesisten- ja pallokoordinaattien välillä pätevät muunnoskaavat $\begin{align*} x&=r_p\sin(\theta)\cos(\varphi) & r_p&=\sqrt{x^2+y^2+z^2}\\ y&=r_p\sin(\theta)\sin(\varphi) & \theta&=\arccos(z/r_p)\\ z&=r_p\cos(\theta). \end{align*}$ Kulma $\varphi$ on käsiteltävä samalla tavalla kuin edellä.

Kaavat voi laskea tai päätellä trigonometrian avulla. Kuva on tässä iso apu. (Vinkki: aloita $z\text-$ koordinaatista.)

Esimerkki: piste napakoordinaateissa

$\begin{tikzpicture}[domain=0:4] \draw[very thin,color=gray] (-0.5,-0.5) grid (4.5,4.5); \draw[->] (-0.5,0) -- (4.5,0) node[right] {$x$}; \draw[->] (0,-0.5) -- (0,4.5) node[above] {$y$}; \filldraw[black] (2,3.46) circle (2pt); \draw[thick,blue] (0,0) -- (2,0); \draw[thick,blue] (2,0) -- (2,3.46); \node[color=blue] at (1.1,-.3) {2}; \node[color=blue] at (2.4,1.7) {$2\sqrt 3$}; \draw[thick,red] (0,0) -- (2,3.46); \node[color=red] at (.7,1.7) {4}; \draw[red] (.4,0) to [bend right=20] (.23,.35); \node[color=red] at (.7,.4) {$\pi/3$}; \end{tikzpicture}$

Muutetaan karteesisten koordinaattien piste $(\blue 2,\blue{2\sqrt3})$ napakoordinaatteihin: $\begin{align*} \red r&=\sqrt{\blue 2^2+\blue{(2\sqrt{3})}^2}=\red 4\\ \red \varphi&=\arctan\frac{\blue{2\sqrt3}}{\blue2}=\red{\frac\pi3}. \end{align*}$ Piste on napakoordinaateissa $(\red 4,\red{\frac\pi3}).$ Muutetaan tämä takaisin karteesisiin koordinaatteihin: $\begin{align*} \blue x&=\red 4\cos\red{\frac\pi3}=\blue 2\\ \blue y&=\red 4\sin\red{\frac\pi3}=\blue{2\sqrt3}. \end{align*}$

Esimerkki: piste sylinteri- ja pallokoordinaateissa

$\begin{tikzpicture}[domain=0:4] \draw[->] (-2,0) -- (2,0) node[right] {$x$}; \draw[->] (0,-1) -- (0,2) node[above] {$z$}; \draw[->] (-1,-1) -- (1,1) node[above] {$y$}; \draw[thick,red] (0,0) -- (-1,0); \draw[thick,green] (-1,0) -- (-1.5,-0.5); \draw[thick,blue] (-1.5,1.5) -- (-1.5,-0.5); \filldraw[black] (-1.5,1.5) circle (1pt) node[anchor=west] {$(\textcolor{red}{x},\textcolor{green}{y},\textcolor{blue}z)$}; \end{tikzpicture}$

Muutetaan karteesisten koordinaattien piste $(\red{-\sqrt2},\green{-\sqrt2},\blue{2\sqrt3})$ pallokoordinaatteihin: $\begin{align*} r_p&=\sqrt{(-\sqrt 2)^2+(-\sqrt 2)^2+(2\sqrt 3)^2}=4\\ \varphi&=\pi+\tan\left(\frac{-\sqrt2}{-\sqrt2}\right)=\frac54\pi\\ \theta&=\cos^{-1}\left(\frac{2\sqrt3}{4}\right)=\frac\pi6. \end{align*}$ Piste on pallokoordinaateissa $(r_p,\varphi,\theta)=(\red 4,\green{\frac54\pi},\blue{\frac\pi6}).$

$\begin{tikzpicture}[domain=0:4] \draw[fill=green!15] (.4,0) to[out=90,in=140] (-.45,-.15) -- (0,0); \draw[thick,green] (.4,0) to[out=90,in=140] (-.45,-.15); \draw[thick,blue] (-.3,.3) to [bend left=50] (0,.4); \draw[fill=blue!15] (-.3,.3) to [bend left=50] (0,.4) -- (0,0); \draw[->] (-2,0) -- (2,0) node[right] {$x$}; \draw[->] (-1,-1) -- (1,1) node[above] {$y$}; \draw[->] (0,-1) -- (0,2) node[above] {$z$}; \draw[thick,red,dashed] (0,0) -- (-1.5,-.5); \draw[thick,dashed] (-.9,0) -- (-1.5,-0.5); \draw[thick,dashed] (-1.5,1.5) -- (-1.5,-0.5); \draw[thick,red] (0,0) -- (-1.5,1.5); \filldraw[black] (-1.5,1.5) circle (1pt) node[anchor=west] {$(\textcolor{red}{r_p},\textcolor{green}{\varphi},\textcolor{blue}\theta)$}; \end{tikzpicture}$

Pisteen esittäminen sylinterikoordinaateissa onnistuu nyt helposti, sillä tiedämme jo $\blue z\text-$ koordinaatin ja atsimuuttikulman $\green\varphi.$ lasketaan vielä sylinterin säde $r_s=\sqrt{(-\sqrt 2)^2+(-\sqrt 2)^2}=2.$ Piste on sylinterikoordinaateissa $(r_s,\varphi,z)=(\red 2,\green{\frac54\pi},\blue{2\sqrt3}).$

$\begin{tikzpicture}[domain=0:4] \draw[fill=green!15] (.4,0) to[out=90,in=140] (-.45,-.15) -- (0,0); \draw[thick,green] (.4,0) to[out=90,in=140] (-.45,-.15); \draw[->] (-2,0) -- (2,0) node[right] {$x$}; \draw[->] (-1,-1) -- (1,1) node[above] {$y$}; \draw[->] (0,-1) -- (0,2) node[above] {$z$}; \draw[thick,dashed] (-.9,0) -- (-1.5,-0.5); \draw[thick,blue] (-1.5,1.5) -- (-1.5,-0.5); \draw[thick,red] (0,0) -- (-1.5,-.5); \filldraw[black] (-1.5,1.5) circle (1pt) node[anchor=west] {$(\textcolor{red}{r_s},\textcolor{green}{\varphi},\textcolor{blue}z)$}; \end{tikzpicture}$

Sovellus: suoran yhtälö napakoordinaateissa

Suoran yhtälö muuttujan funktiona on y=f(x)=ax+b. Esitetään tämä napakoordinaateissa atsimuuttikulman $\varphi$ funktiona, $\begin{align*} y&=ax+b\\ r\sin(\varphi)&=ar\cos(\varphi)+b\\ r(\sin(\varphi)-a\cos(\varphi))&=b\\ r=g(\varphi)&=\frac{b}{\sin(\varphi)-a\cos(\varphi)}. \end{align*}$ Funktiot f(x) ja $g(\varphi)$ ovat saman suoran kuvaajia silloin, kun ovat molemmat hyvin määriteltyjä. Huomaa, että napakoordinaateissa funktio on hyvin määritelty vain, jos $r\geq0$ ja nimittäjä ei ole nolla. Origon kautta kulkevia suoria ( b=0 ) ei voi esittää atsimuuttikulman funktiona. Karteesisissa koordinaateissa ei vastaavasti voida esittää $y\text-$ akselin suuntaisia suoria muuttujan funktiona.

Lisää muunnoskaavoja differentiaalilaskentaa varten.

# koordinaatinjoukko

Koordinaatin määräämä joukko

Eri koordinaatteja voi tarkastella myös sen mukaan, minkälainen kuvaaja syntyy kun pidetään yksi koordinaateista vakioina ja annetaan muiden vaihdella vapaasti. Yksinkertaisimpana esimerkkinä $(\red x,\green y)\text-$ koordinaatistossa koordinaatin $\red x$ arvo määrittää $\green y\text-$ akselin suuntaisen suoran. Piste $(\red x,\green y)$ on koordinaattiakselien suuntaisien suorien leikkauspiste. Napakoordinaateissa $\red r$ määrää ympyrän ja $\green\varphi$ origosta lähtevän puolisuoran.

$\begin{tikzpicture}[domain=0:4] \draw[->,thick] (0,-2) -- (0,2) node[right] {$y$}; \draw[->,thick] (-2,0) -- (2,0) node[right] {$x$}; \draw[red] (0.7,-2) -- (0.7,0.5) node[right] {$\textcolor{red}x=1$} --(0.7,2); \draw[green!50!black] (-2,1.4) -- (-1,1.4) node[above] {$\textcolor{green!50!black}y=2$} --(2,1.4); \filldraw[black] (0.7,1.4) circle (1.5pt) node at (1.2,1.7) {$(\textcolor{red}1,\textcolor{green!50!black}2)$}; \draw[->,thick] (5,-2) -- (5,2) node[right] {$y$}; \draw[->,thick] (3,0) -- (7,0) node[right] {$x$}; \draw[red] (5,0) circle (1.4) node at (6.5,-1) {$\textcolor{red}r=2$}; \draw[green!50!black] (5,0) -- (6,2); \draw[green!50!black] (5.4,0) to [bend right=20] (5.2,.4) node[right] {$\textcolor{green!50!black}\varphi=\frac\pi3$}; \filldraw[black] (5.63,1.24) circle (1.5pt) node at (6.2,1.3) {$(\textcolor{red}2,\textcolor{green!50!black}{\frac\pi3})$}; \end{tikzpicture}$

Kolmessa ulottuvuudessa (x,y,z) koordinaatin pitäminen vakiona määrittää $yz\text-$ suuntaisen tason. Koordinaattien määräämä piste on kolmen tason leikkauspiste.

Sylinterikoordinaateissa säde $\red r$ määrittää $\red r\text-$ säteisen sylinterin, $\blue z$ $xy\text-$ suuntaisen tason ja kulma $\green\varphi$ jonkin $\blue z\text-$ akselin suuntaisen puolitason. Koordinaattien määräämä piste on tason, puolitason ja sylinterin leikkauspiste.

$\begin{tikzpicture}[domain=0:4] \fill[fill=red!20] (1.8,2.7) to [bend right=35] (-1.8,2.7) to [bend right=35] (1.8,2.7); \draw[thick] (0,-2.98) -- (0,0); \fill[fill=green!30] (0,2.7) to (4.5,2.7) -- (4.5,-2.7) -- (0,-2.7); \fill[fill=blue!15] (0,-2.7) to (-4.5,0) -- (-1.8,1.5) -- (0,0) -- (4.5,0); \fill[fill=red!30] (1.8,0) to [bend left=35] (-1.8,0) -- (-1.8,2.7) to [bend right=35] (1.8,2.7); \draw[->,thick] (0,2.1) -- (0,3.6) node[right] {$z$}; \filldraw[black] (1.8,0) circle (2pt) node[anchor=north] {$(\textcolor{red}r,\textcolor{green!50!black}\varphi,\textcolor{blue}z)$}; \end{tikzpicture}$

Pallokoordinaateissa säde $\red r$ määrittää $\red r\text-$ säteisen origokeskisen pallon, kulma $\blue\varphi$ puolitason kuten edellä ja $\green\theta$ määrää kartion vaipan, jonka kärki on origossa. Koordinaattien määräämä piste on siis pallokuoren, puolitason ja kartion vaipan leikkauspiste.

$\begin{tikzpicture}[domain=0:4] \fill[fill=green!25] (-3,3) to [bend left = 22] (3,3) to [bend left = 22] (-3,3); \draw[thick] (0,-2.3) -- (0,0); \fill[fill=red!30] (0,0) circle (2.12); \fill[fill=blue!30] (0,3) to (1.5,2.5) -- (0,2); \fill[fill=green!50] (-3,3) to [bend right = 22] (3,3) -- (1.5,1.5) to [bend left = 20] (-1.5,1.5); \fill[fill=blue!30] (1.5,2.5) to (3,2) -- (3,-3) -- (0.7,-2) to [bend right = 30] (0.7,1.25); \draw[->,thick] (0,2.34) -- (0,4) node[right] {$z$}; \filldraw[black] (0.7,1.25) circle (2pt) node[anchor=north] {$(\textcolor{red}r,\textcolor{green!50!black}\theta,\textcolor{blue}\varphi)$}; \end{tikzpicture}$

# geo373