Moniulotteinen integrointi

Moniulotteisen integroinnin keskeisiä aiheita ovat

Kaksois- ja kolmoisintegraalit
Käyräintegraalit
Pintaintegraalit
Tärkeät tulokset: gradienttilause, Greenin lause, divergenssilause ja Stokesin lause.

Tällä sivulla käydään läpi yleisimpiä laskusääntöjä sekä kaksois- ja kolmoisintegraalien laskemista. Käyrä- ja pintaintegraalien laskeminen sekä niitä koskevat tärkeät tulokset käsitellään omalla sivullaan.

Integraaleja voidaan käsitellä vastaavalla tavalla myös useammassa ulottuvuudessa, mutta tässä rajoitutaan kahden ja kolmen muuttujan tapauksiin.

Esimerkit, joissa on käytetty napa-, sylinteri- tai pallokoordinaatteja on merkattu kuvakkein.

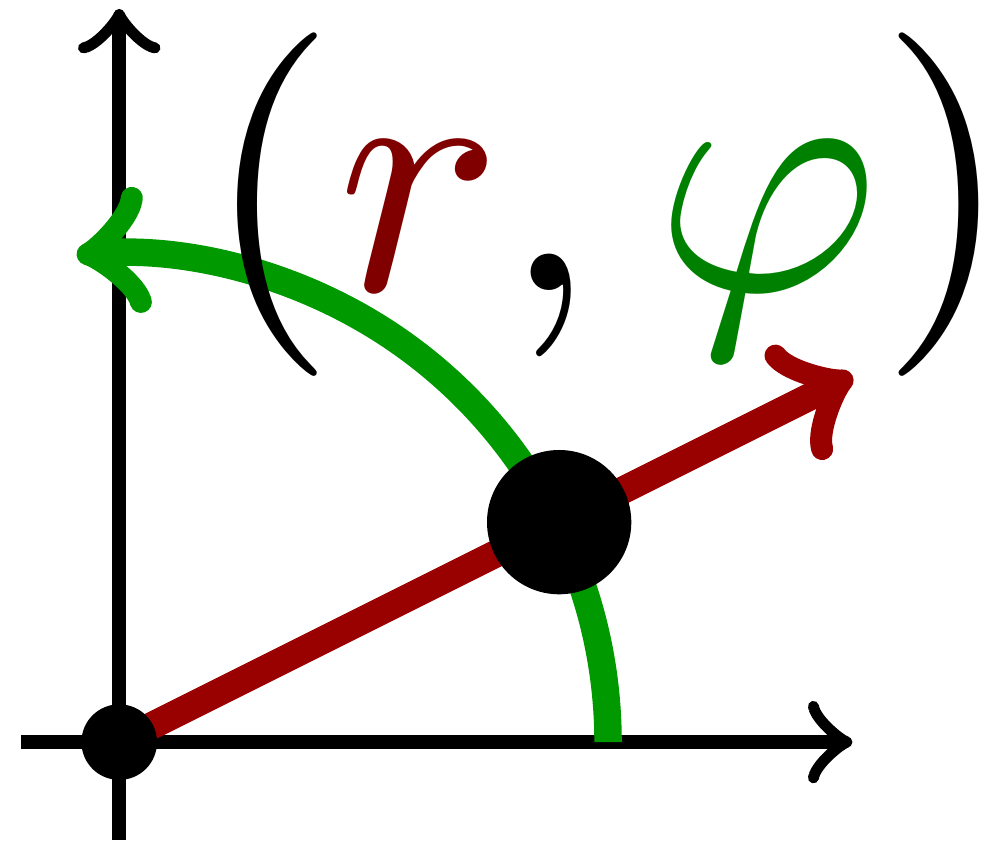
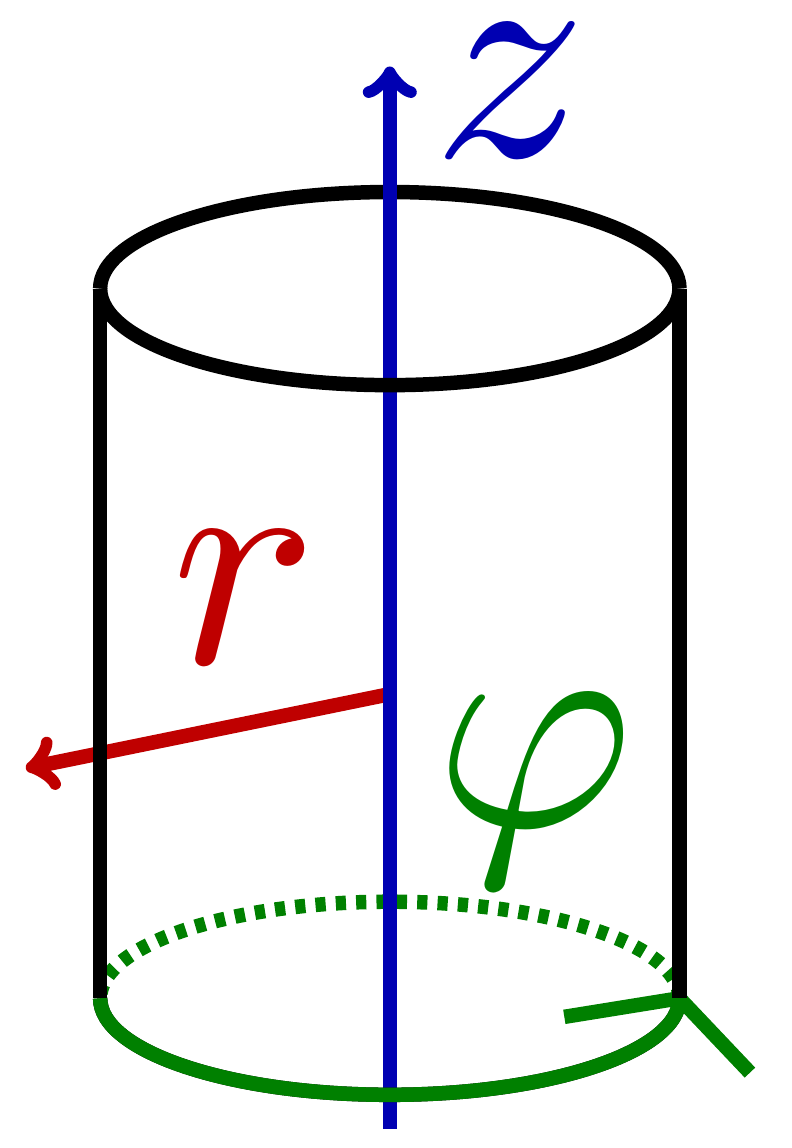
Napa: $\quad$ Sylinteri: $\quad$ Pallo: Pallo

# tasojatilaintegraalit

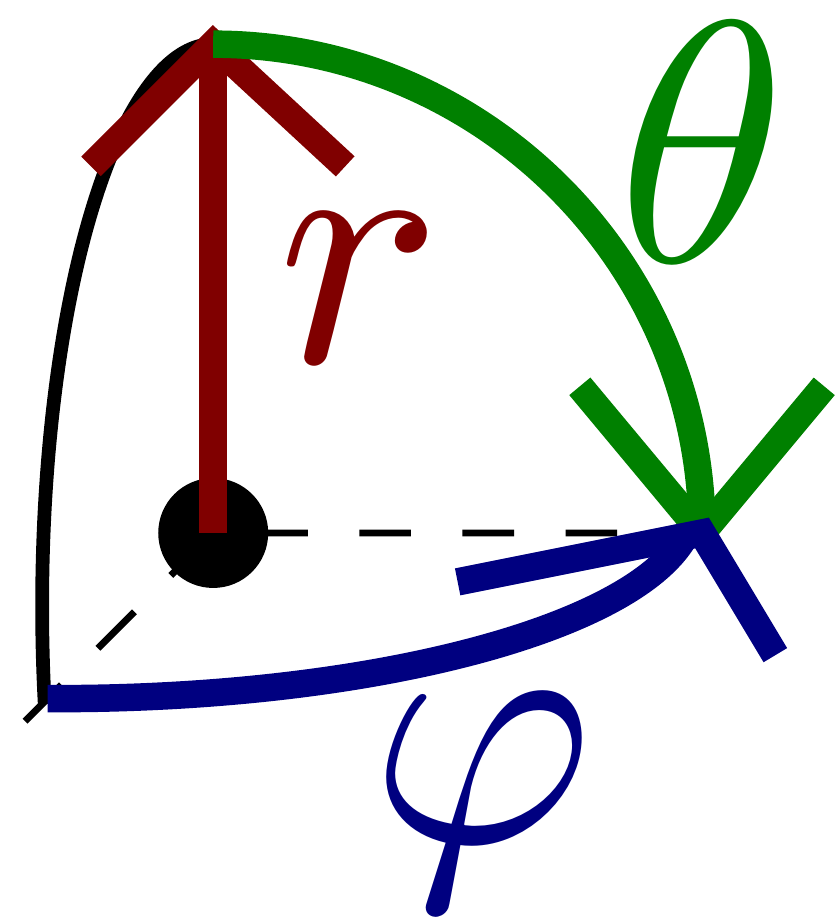
Taso- ja tilavuusintegraalit

# sanastoa

Käsitteistä lyhyesti

Tasoalue $\blue D$ on $(x,y)\text-$ tason kaksiulotteinen osajoukko, jolla on jokin pinta-ala. Kappale $\green E$ on $(x,y,z)\text-$ avaruuden kolmiulotteinen osajoukko, jolla on jokin tilavuus.

Tasoalueen yli integroitaessa käytetään merkintää $\blue{\text dA},$ joka tarkoittaa hyvin pientä pinta-ala-alkiota. Vastaavasti kappaleen yli integroitaessa kirjoitetaan $\green{\text dV},$ joka tarkoittaa hyvin pientä tilavuusalkiota.

$\begin{tikzpicture}[domain=0:4] \draw [thick,blue,fill=blue!30] plot [smooth cycle] coordinates {(0,1) (1,2) (3,2) (2,1) (2,0)}; \draw[->] (-1,0)--(3,0) node[above]{x}; \draw[->] (0,-1)--(0,3) node[above]{y}; \node at (1.4,1.3){D}; \draw (1.75,1.75) -- (2,1.75) --(2,2) -- (1.75,2) -- (1.75,1.75); \draw[dashed] (1.9,1.9) -- (2,2.5); \node at (2,2.65) {$\text dA$}; \draw[->] (6,.5)--(8.5,.5) node[above]{y}; \draw[->] (6.5,0)--(6.5,3) node[above]{z}; \draw[->] (7,1)--(5.5,-.5) node[above]{x}; \draw[thick,green!60!black,fill=green!35] (6,0)--(7,0)--(7,2)--(6,2)--(6,0); \draw[thick,green!60!black,fill=green!35] (6.5,2.5)--(7.5,2.5)--(7,2)--(6,2)--(6.5,2.5); \draw[thick,green!60!black,fill=green!35] (7.5,.5)--(7,0)--(7,2)--(7.5,2.5)--(7.5,.5); \node at (6.5,1){E}; \draw (6.75,0) -- (7,0)-- (7.125,0.125) -- (7.125,0.375) -- (7,0.25) -- (6.75,0.25) -- (6.75,0); \draw[dashed] (6.75,0.25) -- (6.875,0.375) -- (7.125,0.375); \draw[dashed] (7.075,0.15) -- (7.5,-0.05); \node at (7.75,-0.1) {$\text dV$}; \end{tikzpicture}$

# laskusaantoja

Hyödyllisiä laskusääntöjä

Määritelmä	Selitys
$\text dA=\dx\,\dy$	Tason differentiaali.
$A(D)=\iint_D 1\,\text dA$	Tasoalueen pinta-ala.
$m(D)=\iint_D\rho(x,y)\,\text dA$	Tasoalueen massa tai varaus, kun $\rho$ on tiheysfunktio.
$\text{mkp}_x(D)=\dfrac1{m(D)}\iint_Dx\rho(x,y)\,\text dA$	Tasoalueen massakeskipisteen $x\text-$ koordinaatti.
$V=\iint_D f(x,y)\,\text dA$	Funktion kuvaajan ja tasoalueen väliin jäävä tilavuus (kunhan $f(x,y)\geq0$ ).

$\text dV=\dx\,\dy\,\text dz$	Tilavuuden differentiaali.
$V(E)=\iiint_E 1\,\text dV$	Kappaleen tilavuus.
$m(E)=\iiint_E\rho(x,y,z)\,\text dV$	Kappaleen massa tai varaus, kun $\rho$ on tiheysfunktio.

$\text dA=r\,\text dr\,\text d\varphi$	Tason differentiaali napakoordinaateissa.
$\text dV=r\,\text dr\,\text d\varphi\,\text dz$	Tilavuuden differentiaali sylinterikoordinaateissa.
$\text dV=r^2\sin\theta\,\text dr\,\text d\varphi\,\text d\theta$	Tilavuuden differentiaali pallokoordinaateissa.

Napakoordinaatiston differentiaalin muunnoskaavan laskeminen.

Johdetaan [napakoordinaattien]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#napajasylinteri differentiaalin muunnoskaava Jacobin matriisin avulla:

Napakoordinaattien muunnoskaavat ovat (vrt. yksikköympyrä) $\begin{cases} x=r\cos(\varphi),\\ y=r\sin(\varphi). \end{cases}$ Näistä saatavan Jacobin matriisin determinantti antaa koordinaatistojen differentiaalien suhteen, jota kutsutaan Jakobiaaniksi $\begin{align*} \dfrac{\partial(x,y)}{\partial(r,\varphi)}&= \begin{vmatrix} \frac{\partial x}{\partial r} \ \frac{\partial x}{\partial \varphi}\\ \frac{\partial y}{\partial r} \ \frac{\partial y}{\partial \varphi} \end{vmatrix}= \begin{vmatrix} \cos(\varphi) &\ -r\sin(\varphi)\\ \sin(\varphi) &\ r\cos(\varphi) \end{vmatrix}\\ &=r(\cos^2(\varphi)+\sin^2(\varphi))\\ &=r. \end{align*}$ Tällöin $\dx\,\dy=\partial(x,y)=r\partial(r,\varphi)=r\;\text dr\,\text d\varphi.$

Kaavaa havainnollistaa kuva pienestä kiekon palasesta.

Kun kulma $\textcolor{green!50!black} {\text d\varphi}$ on pieni, on palanen lähes suorakaide, jonka leveys on $\textcolor{red}{\text dr}$ ja korkeus $\textcolor{red}r\,\textcolor{green!50!black}{\text d\varphi}.$

$\begin{tikzpicture} % koordinaatisto \filldraw (0,0) circle (1pt); \draw[red, ->, dashed] (0,0) -- (3,0) node[above] {$\textcolor{red}r$}; \draw[green!50!black, ->, dashed] (0.5,0) arc (0:66:0.5) node[above] {$\textcolor{green!50!black}\varphi$}; % pinta-alkio \draw (2,0) arc (0:45:2); \draw (1,0) arc (0:45:1); \draw[dashed] (0,0) -- (0.7,0.7); \draw (0.7,0.7) -- (1.41,1.41); \draw (1,0) -- (2,0); \node at (1.4,0.5) {$\text d A$}; % kanta \draw[red,|-|] (1,-.1)--(2,-.1); \node at (1.5,-.3) {$\textcolor{red}{\text dr}$}; % korkeus \draw[green!50!black, |-|] (2.1,0) arc (0:45:2.1); \node at (2.4,0.5) {$\textcolor{red}r\,\textcolor{green!50!black}{\text d \varphi}$}; \end{tikzpicture}$

Pallokoordinaatiston differentiaalin muunnoskaavan laskeminen.

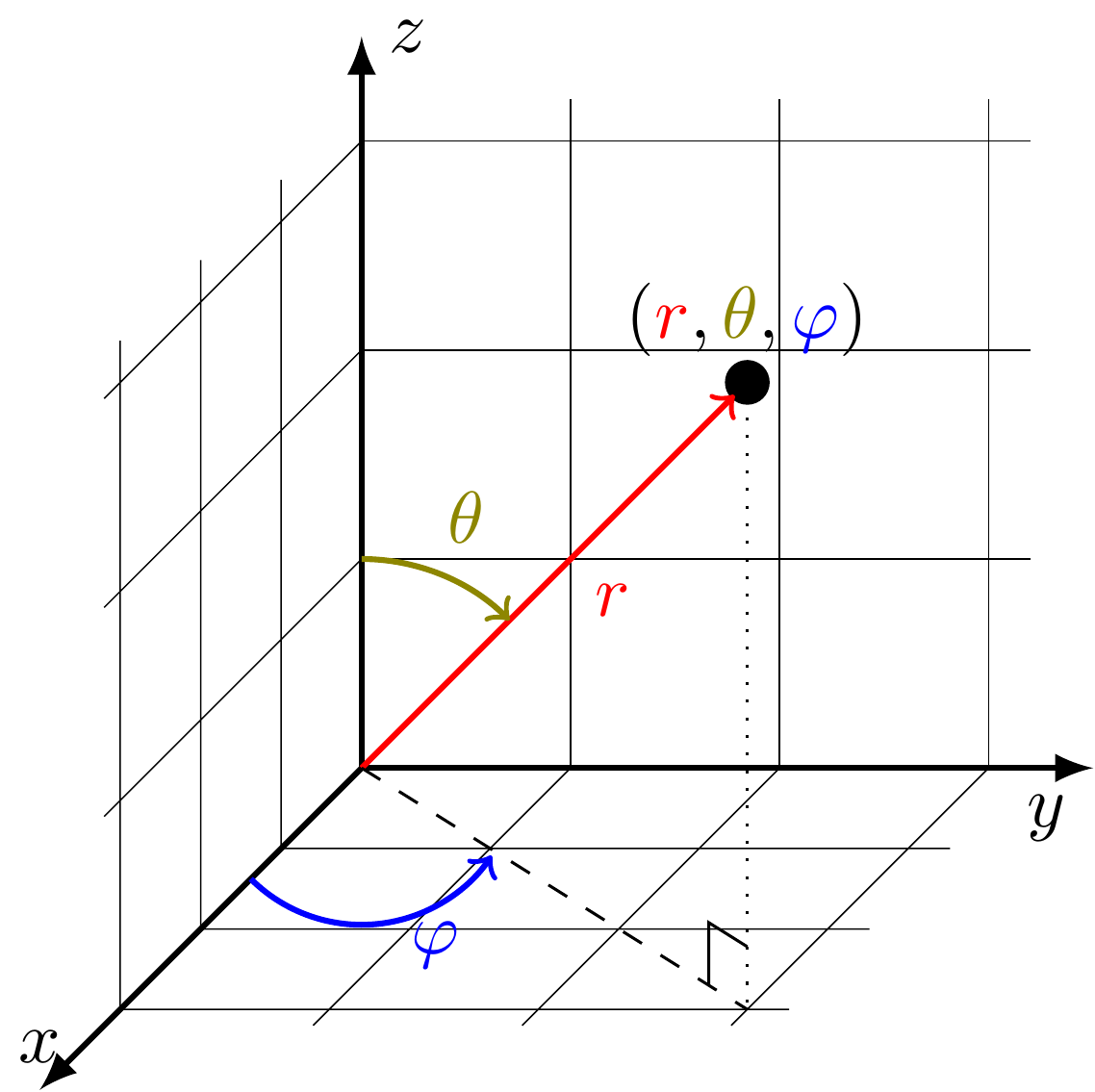
Kolmiulotteinen vastine napakoordinaateille on [pallokoordinaatit]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#pallokoordinaatit. Näille muunnoskaavat ovat $\begin{cases} x=r\sin(\theta)\cos(\varphi),\\ y=r\sin(\theta)\sin(\varphi),\\ z=r\cos(\theta). \end{cases}$

Differentiaalit voidaan muuttaa toisikseen laskemalla Jacobin matriisin $(3\times 3)$ determinantti: $\begin{align*} \dfrac{\partial(x,y,z)}{\partial(r,\theta,\varphi)}&= \begin{vmatrix} \frac{\partial x}{\partial r} \ \frac{\partial x}{\partial \theta} \ \frac{\partial x}{\partial \varphi} \\ \frac{\partial y}{\partial r} \ \frac{\partial y}{\partial \theta} \ \frac{\partial y}{\partial \varphi} \\ \frac{\partial z}{\partial r} \ \frac{\partial z}{\partial \theta} \ \frac{\partial z}{\partial \varphi}\\ \end{vmatrix}\\&= \begin{vmatrix} \sin(\theta)\cos(\varphi) &\ r\cos(\theta)\cos(\varphi) &\ -r\sin(\theta)\sin(\varphi)\\ \sin(\theta)\sin(\varphi) &\ r\cos(\theta)\sin(\varphi) &\ r\sin(\theta)\cos(\varphi)\\ \cos(\theta) &\ -r\sin(\theta) &\ 0 \end{vmatrix}\\ &=\cos^2(\theta)r^2\sin(\theta)(\cos^2(\varphi)+\sin^2(\varphi))\\&+r^2\sin^3(\theta)(\cos^2(\varphi)+\sin^2(\varphi)). \end{align*}$ Tulos on hankalan näköinen, mutta sievenee: $\begin{align*} ...&=\cos^2(\theta)r^2\sin(\theta)+r^2\sin^3(\theta) = r^2\sin(\theta)\left(\cos^2(\theta)+\sin^2(\theta)\right)\\ &=r^2\sin(\theta). \end{align*}$ Tällöin $\dx\,\dy\,\text dz=r^2\sin(\theta)\;\text dr\,\text d\varphi\,\text d\theta.$

# ominaisuuksia

Integraalin ominaisuuksia

Ominaisuus	Selitys tai nimi
$\iint_D f(x,y)\;\red\dx\,\green\dy=\iint_D f(x,y)\;\green\dy\,\red\dx,$ kunhan $\iint_D\|f(x,y)\|\,\dx\,dy<\infty$	Integrointijärjestyksen vaihtaminen. Fubinin lause.
$\iint_{D_1\cup D_2} f(x,y)\;\text dA=\iint_{D_1} f(x,y)\;\text dA+\iint_{D_2} f(x,y)\;\text dA,$	Alueen paloittelu. ja on oltava erilliset.
Jos $f(x,y)\leq g(x,y)$ joukossa niin $\iint_D f(x,y)\;\text dA\leq\iint_D g(x,y)\;\text dA$	Arvioiminen yläpuolelta. Monotonisuus.
$\left\|\iint_D f(x,y)\;\text dA\right\|\leq\iint_D \|f(x,y)\|\text dA$	Kolmioepäyhtälö.
$\frac{\text d}{\red \dx}\int_a^bf(x,y)\;\green\dy=\int_a^b\frac{\partial}{\red{\partial x}}f(x,y)\;\green\dy$	Derivoinnin ja integroinnin järjestyksen vaihtaminen. Leibnizin sääntö.

Vastaavat tulokset pätevät myös kolmoisintegraaleille.

# moniulotteinenintegraali

Moniulotteinen integraali

Moniulotteiset integraalit lasketaan käytännössä niin kutsuttuina iteroituina integraaleina, joissa käsitellään vain yhtä muuttujaa kerrallaan. Tätä voidaan pitää osittaisderivoinnin käänteisoperaationa. Integroitava alue täytyy esittää sopivalla tavalla. Monimutkaisempia tilanteita käsitellään hiukan alempana.

Esimerkiksi suorakaiteen $D=[a,b]\times[c,d]$ voi esittää $(\red x,\green y)\text-$ tasossa joukkona, jossa $a \le \red x \le b$ ja $c \le \green y \le d.$ Tällöin funktion $f(\red x,\green y)$ integraalin yli alueen voi kirjoittaa seuraavasti $\int_D f(\red x,\green y)\, \text dA = \int_a^b \left(\int_c^df(\red x,\green y)\, \green\dy\right)\, \red\dx.$ Tässä $\text dA$ voidaan mieltää pieneksi tasoalkioksi ja differentiaalit $\red \dx$ ja $\green \dy$ puolestaan pieniksi pituusalkoiksi.

Esimerkki: Levyn massan määrittäminen tiheyden avulla.

Tarkastellaan tapausta, jossa metallilevyn $D=\red{[0,2]}\times\green{[0,4]}$ massatiheyttä $\left([\rho]=\frac{\text{massa}}{\text{pinta-ala}}\right)$ kuvaa funktio $\rho(\red x,\green y) = \red x\green y.$ Tiheys siis muuttuu lineaarisesti levyn sivujen suuntaisesti. Miten tiheys muuttuu lävistäjän suuntaisesti? (VastausNeliöllisesti.)

Levyn massa saadaan tiheyden avulla summaamalla pienten pinta-ala-alkioiden $\text dA$ massat $m = A\cdot \rho = \text dA\cdot \rho(\red x,\green y)$ . Levyn massa on siis integraali $m(D) = \int_D\rho(\red x,\green y)\,\text dA.$

Tarkastellaan ensin funktion yksiulotteisia integraaleja. Integroimalla funktio $\rho$ pelkästään muuttujan $\red x$ suhteen saadaan $\begin{aligned} &\int_{ 0}^{2}\red x y\;\red{\dx}=y\int_{ 0}^{2}\red x\;\red{\dx}\\ &=y\intsub 0 2 \frac12\red x^2=\red 2 y. \end{aligned}$

Integroimalla saatu uusi funktio kuvaa levyn pituusmassatiheyttä $\left(\frac{\text{massa}}{\text{pituus}}\right)$ $\green y\text-$ suunnassa. Levyn massa saadaan integroimalla tämä funktio muuttujan $\green y$ suhteen: $\begin{align*} \int_D \rho(\red x,\green y)\, \text dA = &\int_{ 0}^{4}\left(\int_{ 0}^{2}\red x\green y\;\red{\dx}\right)\;\green{\dy} =\int_{ 0}^{4}\left(\green y\int_{0}^{2}\red x\;\red{\dx}\right)\;\green{\dy}\\ &=\int_{ 0}^{4}\red2\green y\;\green{\dy}=\intsub 0 4 y^2=4^2=16. \end{align*}$ Sulkeet jätetään tavallisesti merkitsemättä; integraalien laskujärjestys on aina sisältä ulospäin. Samaan tulokseen päädyttäisiin tässä myös integroimalla ensin muuttujan $\green y$ suhteen, jolloin saadaan

$\int_{ 0}^{4}x\green y\;\green{\dy}=x \intsub 0 4 \frac{1}{2} \green y^2 = \green 8x.$ Integroimalla tämä muuttujan $\red x$ suhteen saadaan levyn massaksi 16.

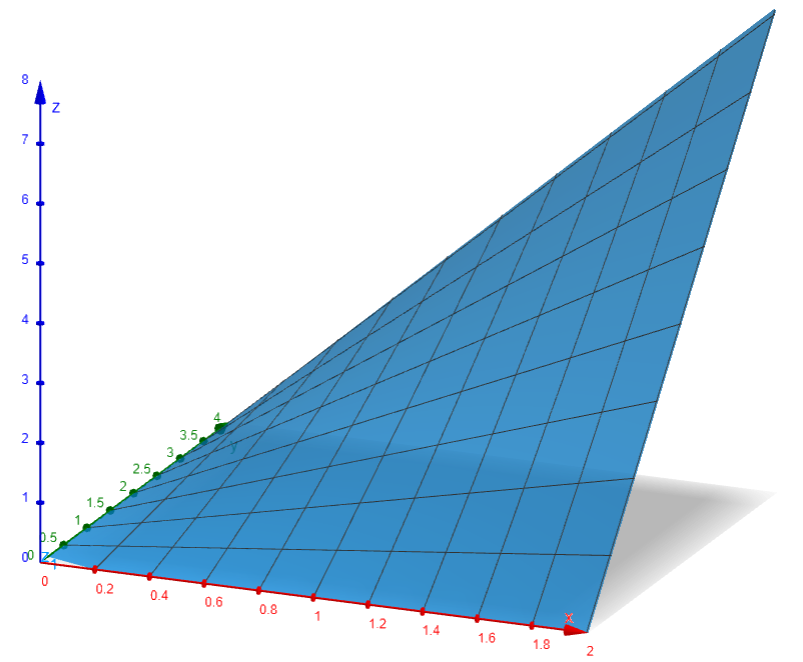
Kaksiulotteisen integraalin visualisoimiseksi yleensä merkitään $\rho(\red x,\green y)=\blue z,$ jolloin funktion kuvaaja voidaan piirtää kolmiulotteiseen $(\red x,\green y,\blue z)$ koordinaatistoon. Integraalin arvo vastaa pinnan $\blue z=\red x\green y$ alle jäävän alueen tilavuutta suorakulmiossa $0<\red x< 2,\quad 0<\green y< 4$ .

Tiheysfunktion graafi piirrettynä GeoGebra 3D:llä. — Tiheysfunktion $\blue z=\rho(\red x,\green y)$ graafi piirrettynä GeoGebra 3D:llä.

Tiheysfunktion $\blue z=\rho(\red x,\green y)$ graafi piirrettynä GeoGebra 3D:llä.

# integrointirajat

Integrointirajojen määrittäminen

Käsitellään integroimisrajojen määrittämistä yleisimmissä tilaintessa ensin parin esimerkin avulla.

Suorien $\green x=0$ , $\green y=2$ ja käyrän $\green y=\green x^2$ rajaaman alueen pinta-ala

Rajoitutaan tarkastelemaan aluetta, jossa $x\ge0.$

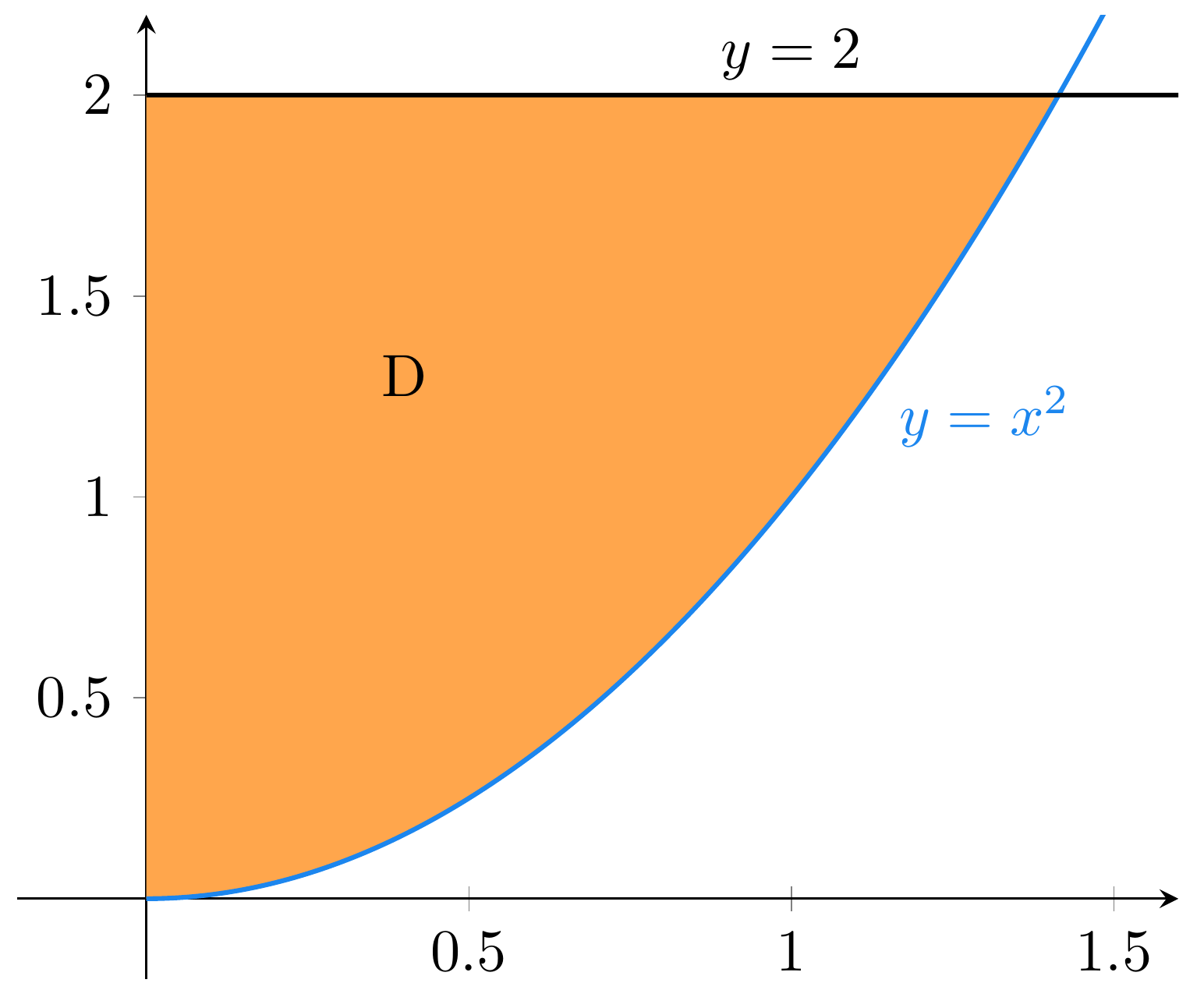
Laskuna tämä on seuraavanlainen:

$\begin{aligned} \text{Pinta-ala}(D)=\iint_D \,\text dA &= \violet{\int_0^2 \green{\int_0^{\sqrt y}\,\text dx}\,\text dy} \\ &= \violet {\int_0^2 \green {\sqrt y} \,\text dy} = \violet {\intsub 0 2 \frac{2}{3} y^{3/2}} \\ &= \frac{2}{3} \sqrt 8 = \frac{4}{3} \sqrt 2. \end{aligned}$

Mutta miksi?

Ensiksi on valittava integrointijärjestys. Tällä ei ole merkitystä lopputuloksen kannalta, mutta hyvä valinta voi helpottaa laskemista. Valitaan ensimmäiseksi integroitavaksi tämä on siis sisempi integraali. Integrointirajat ensimmäiselle integraalille $x\text{:n}$ suhteen täytyy esittää toisen muuttujan avulla.

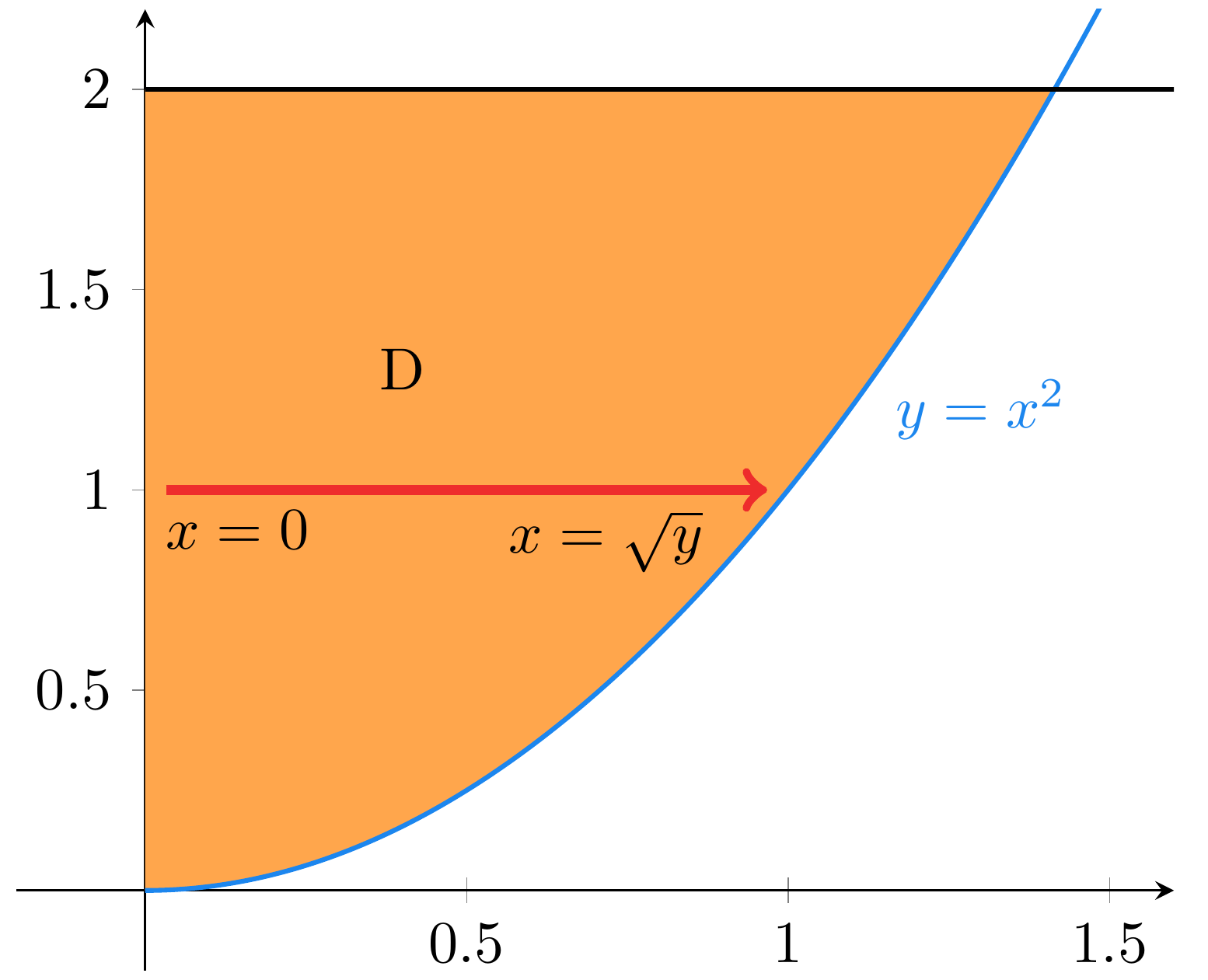
Pienimmän arvon rajaa ja suurimman paraabeli .

x=0 — Pienimmän arvon rajaa ja suurimman paraabeli .

Pienimmillään on x=0. Kuvassa näkyvällä paraabelin y=x^2 osalla on $x=\sqrt y$ . Tällöin on välillä $\blue{[0,\sqrt y]}$ . Nämä ovat rajat sisemmälle integraalille

$\green{\int_0^{\sqrt y}\,\dx =\intsub 0 {\sqrt y} 1 = \sqrt y}.$

Seuraavaksi selvitetään uloimman integraalin rajat, eli mitkä ovat viimeisen muuttujan pienin ja suurin arvo kyseisellä alueella.

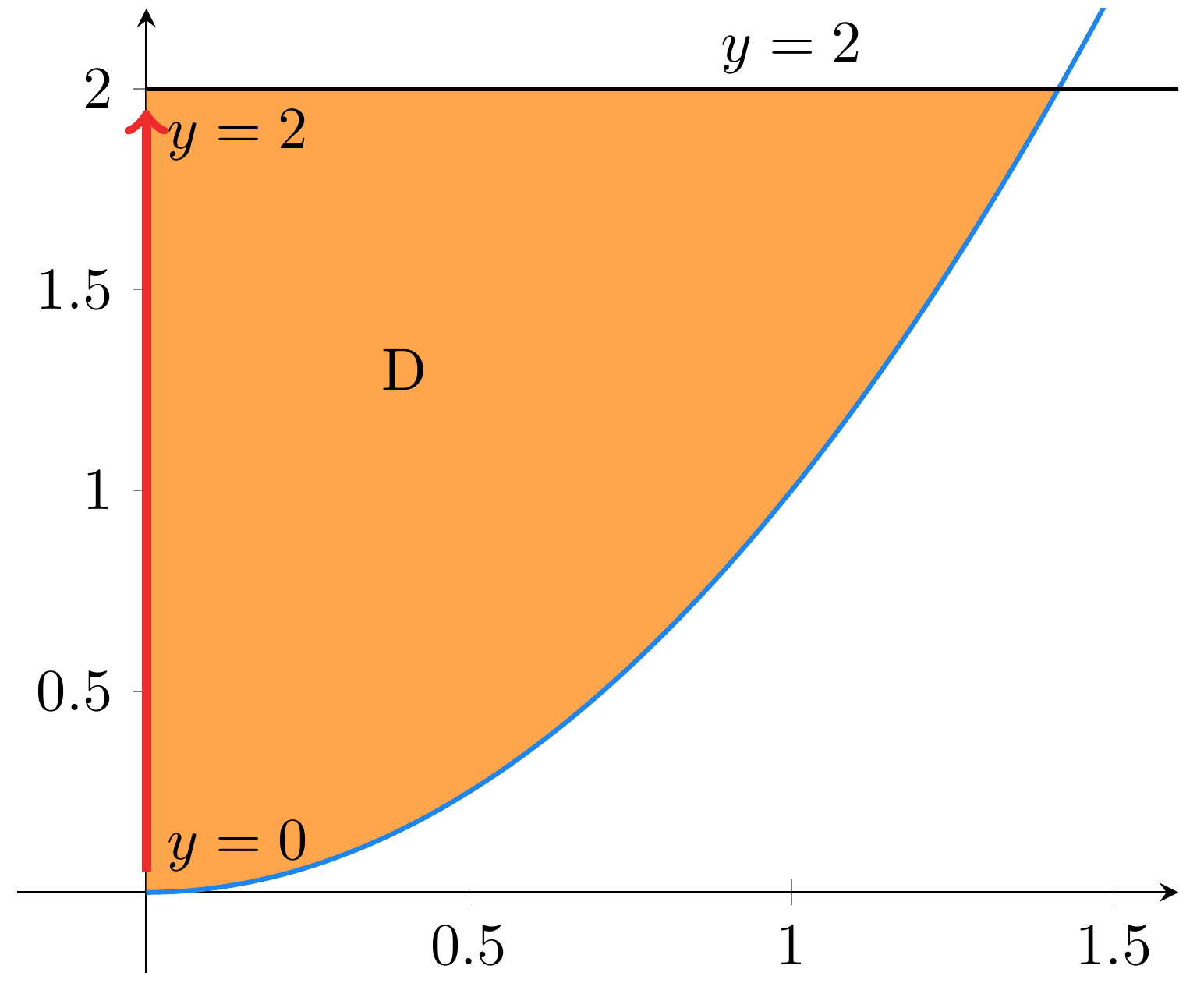
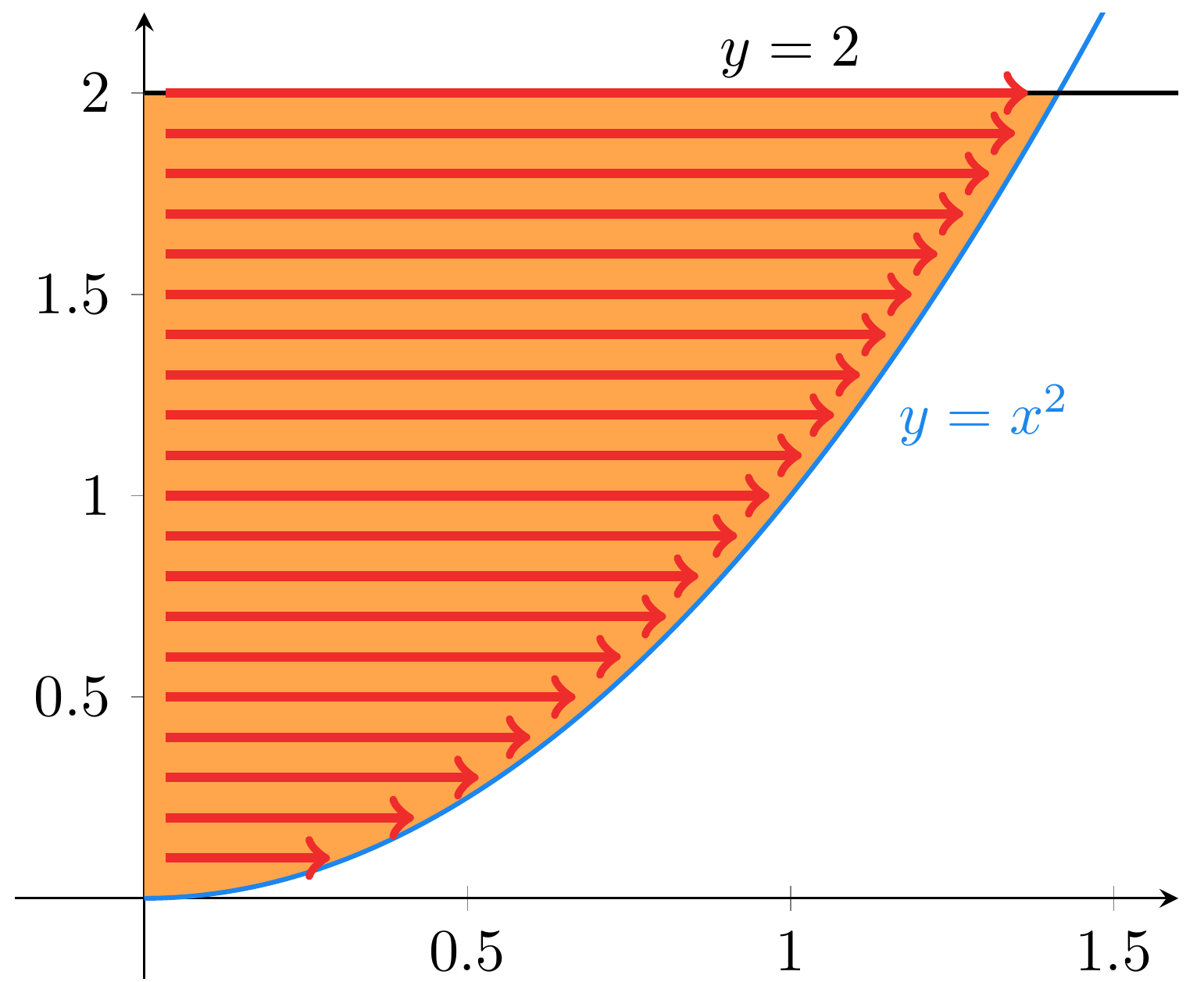
Muuttuja on välillä $\violet{[0,2]}$ . Ulompi integraali on siis $\violet {\int_0^2 \green {\sqrt y} \,\text dy} = \violet {\intsub 0 2 \frac{2}{3} y^{3/2}} = \frac{2}{3} \sqrt 8 = \frac{4}{3} \sqrt 2.$

Tämän alueen pinta-alan saisi myös laskettua tuttuun tapaan kuvaajan alle jäävänä pinta-alana peilaamalla kuva suoran x=y suhteen. Tällöin muodostuisi integraali funktiolle $x=\sqrt y,$ kun on välillä [0,2].

Integrointirajojen etsimisen voi aloittaa myös uloimmasta integraalista, kuten myöhemmissä esimerkeissä tehdään.

Kolmion massa ja massakeskipiste

$\begin{tikzpicture}[domain=0:4] \draw[->] (-0.5,0) -- (4.5,0) node[right] {$x$}; \draw[->] (0,-0.5) -- (0,4.5) node[above] {$y$}; \fill[fill=blue!33] (0,0) -- (3,0) -- (1,4); \draw[thick,blue] (0,0) -- (3,0); \draw[thick,blue] (0,0) -- (1,4); \draw[thick,blue] (3,0) -- (1,4); \draw[dashed] (1,0) -- (1,4); \node at (0.5,0.25) {(0,0)}; \node at (3.3,0.25) {(3,0)}; \node at (1.4,4.2) {(1,4)}; \node at (1.6,1.4) {$D_2$}; \node at (0.7,1.4) {$D_1$}; \draw[very thin,color=gray] (-0.5,-0.5) grid (4.5,4.5); \end{tikzpicture}$

Pisteet (0,0),(1,4),(3,0) rajaavat kolmion muotoisen levyn jonka tiheys on vakio $\rho.$ Levyn massa on $m(D)=\iint_D\rho\;\text dA.$ Jaetaan integrointi kahteen alueeseen: D_1, jossa 0<x<1 ja 0<y<4x ja D_2, jossa 1<x<3 ja 0<y<6-2x. Tällöin $m(D)=\iint_{D_1}\rho\;\text dA+\iint_{D_2}\rho\;\text dA.$ Tiheys $\rho$ on vakio, joten se voidaan ottaa ulos integraaleista. Sijoitetaan alueiden rajat ja differentiaali $\text dA=\dy\,\dx\text:$ $m(D)=\rho\int_0^1\int_0^{4x}\;\dy\;\dx+\rho\int_1^3\int_0^{6-2x}\;\dy\;\dx.$ Sisemmistä integraaleista saadaan tuloksena ylärajat, koska molemmissa on integroitavana ja alarajana Uloimmat integraalit ovat $\begin{align*} m(D)&=\rho\int_0^14x\;\dx+\rho\int_1^36-2x\;\dx\\ &=\rho\intsub 0 1 2x^2+\rho\intsub 1 3 6x-x^2 = \rho\big[ 2+(18-9)-(6-1)\big]=6\rho. \end{align*}$ Samaan tulokseen pääsee myös laskemalla kolmion pinta-alan geometrisesti.

Etsitään seuraavaksi kolmion massakeskipiste. Mkp:n $x\text-$ koordinaatti on $\text{mkp}_{x}(D)=\frac1{m(D)}\left(\int_0^1\green{\int_0^{4x}}\red x\rho\;\green\dy\;\dx+\int_1^3\green{\int_0^{6-2x}}\red x \rho\;\green\dy\;\dx\right).$ Sisemmissä integraaleissa integroidaan $y\text:$ n suhteen vakioita. Saadaan $\text{mkp}_x(D)=\frac{\rho}{m(D)}\left[\int_0^1\red x\,\green{4x}\;\dx+\int_1^3\red x\green{(6-2x)}\;\dx\right]$ ja ulommista integraaleista $\begin{align*} \text{mkp}_x(D)&=\frac{\rho}{m(D)}\left[\intsub01\frac43x^3+\intsub133x^2-\frac23x^3\;\dx\right]\\ &=\frac{\rho}{m(D)}\left[\frac43+(27-18)-\left(3-\frac23\right)\right]\\ &=\frac{8\rho}{m(D)}. \end{align*}$ Toinen koordinaatti saadaan samoin: $\text{mkp}_y(D)=\frac{\rho}{m(D)}\left[\int_0^1\int_0^{4x}\green y\;\dy\;\dx+\int_1^3\int_0^{6-2x}\green y\;\dy\;\dx\right].$ Nyt sisemmät integroitavat eivät olekaan vakioita, vaan $\begin{align*} \text{mkp}_y(D)&=\frac{\rho}{m(D)}\left[\int_0^1\intsub 0{4x}\green{\frac{y^2}2}\;\dx+\int_1^3\intsub0{6-2x}\green{\frac{y^2}2}\;\dx\right]\\ &=\frac{\rho}{m(D)}\left[\int_0^1\green{\frac{(4x)^2}2}\;\dx+\int_1^3\green{\frac{(6-2x)^2}2}\;\dx\right]. \end{align*}$ Neliölliset termit avaamalla tästä saadaan $\text{mkp}_y(D)=\frac{\rho}{m(D)}\left[\intsub01\frac{16x^3}6+\intsub1318x-6x^2+\frac23x^3\;\dx\right]$ ja sijoittamalla $\begin{align*} \text{mkp}_y(D)&=\frac{\rho}{m(D)}\left[\frac83+(54-54+6)-\left(18-6+\frac23\right)\right]\\ &=\frac{8\rho}{m(D)}. \end{align*}$ Massaksi saatiin $m(D)=6\rho,$ joten massakeskipiste on $\text{mkp}(D)=\left(\frac{8\rho}{6\rho},\frac{8\rho}{6\rho}\right)=\left(\dfrac43,\dfrac43\right).$ Koska annoimme kolmiolle vakiotiheyden, massakeskipisteen saisi myös keskijanojen leikkauspisteellä.

$\begin{tikzpicture}[domain=0:4] \draw[->] (-0.5,0) -- (4.5,0) node[right] {$x$}; \draw[->] (0,-0.5) -- (0,4.5) node[above] {$y$}; \fill[fill=blue!33] (0,0) -- (3,0) -- (1,4); \draw[thick,blue] (0,0) -- (3,0); \draw[thick,blue] (0,0) -- (1,4); \draw[thick,blue] (3,0) -- (1,4); \draw (0,0) -- (2,2); \draw (3,0) -- (0.5,2); \draw (1,4) -- (1.5,0); \node at (1.9,1.35) {$(\frac43,\frac43)$}; \draw[very thin,color=gray] (-0.5,-0.5) grid (4.5,4.5); \end{tikzpicture}$

Moniulotteisessa integraalissa sisempien eli laskemisjärjestyksessä ensimmäisten integraalien rajat saadaan "ratkaisemalla" ne toisten muuttujien suhteen. Esimerkiksi integraalissa $\iint_D\,\dy\,\dx$ muuttujan integrointirajat annetaan muuttujan suhteen.

Tarkemmin sanottuna joukko pitää esittää esimerkiksi -yksinkertaisena eli muodossa $D=\{(\red x,\green y): a<\red x< b,\; {c(\red x)}<\green y< {d(\red x)}\}.$ Muuttujan $\green y$ rajat ovat siis muuttujan $\red x$ funktioita.

$\begin{tikzpicture} \begin{axis}[xlabel=$x$, ylabel=$y$, xmin=-0.5, ymin=-0.5, xmax=5.5, ymax=5, axis lines=middle, ticks=none] \addplot[dashed, green!50!black, samples=100, domain=-1:0.9]{sin(deg(x))/5+1}; \addplot[name path=g2, thick, green!50!black, samples=100, domain=0.9:5]{sin(deg(x))/5+1}node at (axis cs:1.7,1.4) {$y=c(x)$}; \addplot[dashed, green!50!black, samples=100, domain=4.9:5.5]{sin(deg(x))/5+1}; \addplot[dashed, green!50!black, samples=100, domain=-1:0.9]{sin(deg(1.4*x))/5+4}; \addplot[name path=g1, thick, green!50!black, samples=100, domain=0.9:5]{sin(deg(1.4*x))/5+4}node[] at (axis cs:4.2,3.6){$y=d(x)$}; \addplot[dashed, green!50!black, samples=100, domain=4.9:5.5]{sin(deg(1.4*x))/5+4}; \addplot[red!90!black,mark=none, ultra thick] coordinates {(1, 4.2) (1, 1.18)}; \addplot[red!90!black,mark=none, ultra thick] coordinates {(4.9, 0.8)(4.9, 4.1)}; \addplot +[red!90!black,mark=none, dashed]coordinates {(1, 1.18) (1, 0)}node[anchor=south west] {$x=a$}; \addplot +[red!90!black,mark=none, dashed]coordinates {(4.9, 0.8) (4.9, 0)}node[anchor=south east] {$x=b$}; \node at (axis cs:2.8,2.4) {$D$}; \addplot [ thick, color=blue, fill=blue, fill opacity=0.03, ] fill between[ of=g1 and g2, soft clip={domain=1:4.9}, ]; \end{axis} \end{tikzpicture}$

Kuvassa näkyy integrointialueen eli joukon rajat. Kuva ei kuitenkaan kerro mitään integroitavasta funktiosta f(x,y).

Tällöin funktion f(x,y) integraali joukon yli on $\int_{\red a}^{\red b}\int_{\green {c(x)}}^{\green {d(x)}}f(x,y)\;\green\dy\,\red\dx.$ Kun integroidaan suorakulmion yli, funktiot $\green{c(x)}$ ja $\green{d(x)}$ ovat vakioita.

Vastaavasti $x\text-$ yksinkertaisessa alueessa esitetään muuttujan $\red x$ rajat muuttujan $\green y$ funktioina. Tällöin integrointijärjestys on vaihdettava.

Rajojen määrittämisessä auttaa kuvan piirtäminen, joidenkin joukon pisteiden laskeminen sekä sopivan koordinaatiston valinta. Esimerkiksi ympyrän kaaren rajaamat alueet kannattaa yleensä esittää napakoordinaateissa $(r,\theta).$ Alueen muodosta riippuen integraali voidaan myös joutua laskemaan useamman integraalin summana.

# esimerkkeja

Esimerkkejä

Kolmio, jonka kärjet ovat pisteissä (0,0),(0,4) ja (2,4).

$\begin{tikzpicture}[domain=0:4] \draw[very thin,color=gray] (-0.5,-0.5) grid (4.5,4.5); \draw[->] (-0.5,0) -- (4.5,0) node[right] {$x$}; \draw[->] (0,-0.5) -- (0,4.5) node[above] {$y$}; \fill[fill=blue!33] (0,0) -- (0,4) -- (2,4); \draw[thick,blue] (0,0) -- (0,4); \draw[thick,blue] (0,4) -- (2,4); \draw[thick,blue] (0,0) -- (2,4); \node at (0.35,-.25) {(0,0)}; \node at (2.35,3.75) {(2,4)}; \node at (0.35,3.75) {(0,4)}; \end{tikzpicture}$

Etsitään joukolle esitystapa -yksinkertaisena:

Muuttujan arvo on välillä 0<y<4, joten tästä saadaan ensimmäinen epäyhtälö.

Muuttujan arvo on välillä 0<x<2, mutta tämä ei riitä joukon määrittämiseen. Pisteet (0,0) ja (2,4) määrittävät suoran y=2x ja kuvasta voi nähdä, että kaikki muuttujan arvot ovat tämän suoran vasemmalla puolella. Siis voimme rajoittaa muuttujan ylhäältä päin funktiolla $x=\frac12y.$

Saatu joukko on $\{(x,y):0<y<4,\;0<x<\frac12y\}.$ Integroinnin kannalta ei ole merkitystä onko rajoissa yhtäsuuruutta $\le$ vai pelkkä

Tason $\red x+2\green y+3\blue z=6$ ja koordinaattiakselien rajaama tetraedri.

$\begin{tikzpicture}[domain=0:4] \draw[->] (0,0) -- (4,0) node[right] {$y$}; \draw[->] (0,0) -- (0,3) node[above] {$z$}; \draw[->] (0,0) -- (-3.5,-3.5) node[above] {$x$}; \node at (3.5,.3) {$(0,3,0)$}; \node at (0.6,2.3) {$(0,0,2)$}; \node at (-2.4,-3.2) {$(6,0,0)$}; \fill[fill=blue!33] (3,0) -- (0,2) -- (-3,-3); \draw[thick,blue] (3,0) -- (0,2); \draw[thick,blue] (0,2) -- (-3,-3); \draw[thick,blue] (-3,-3) -- (3,0); \draw[blue,dashed] (-3,-3) -- (0,0); \draw[blue,dashed] (3,0) -- (0,0); \draw[blue,dashed] (0,2) -- (0,0); \end{tikzpicture}$

Tason ja koordinaattiakselien leikkauspisteet $(0,0,0),\;(6,0,0),\;(0,3,0)$ ja (0,0,2) ovat tetraedrin neljä kulmaa.

Asetetaan aluksi välille $\red {0<x<6}.$

Asettamalla tason yhtälössä z=0 saadaan rajoitettua ylhäältä päin funktiolla x+2y=6. Ratkaisemalla tästä saadaan yläraja, jolloin $\green{0<y<\frac12(6-x)}.$

Viimeisenä rajoitetaan tason yhtälöstä ratkaisemalla välille $\blue{0<z<\frac13(6-2y-x)}.$

Funktion f(x,y,z) integraali tetraedrin yli on siis $\int_{\red 0}^{\red 6}\int_{\green 0}^{\green{\frac12(6-x)}}\int_{\blue 0}^{\blue {\frac13(6-2y-x)}}f(x,y,z)\;\text d\blue z\,\text d\green y\,\text d\red x.$

Integrointijärjestyksen vaihtaminen tasointegraalissa $\int_{\red 0}^{\red 1}\int_{\green {\sqrt x}}^{\green 1}e^{\green y^3}\;\green\dy\,\red\dx.$

Jotkin integrointijärjestykset voivat tehdä integraalin laskemisesta vaikeampaa, kuten tässä tilanteessa. Laskusta tulee huomattavasti yksinkertaisempi, kun etsimme uuden esitysmuodon integrointijoukolle ja vaihdamme järjestyksen.

Integrointijoukko on alue, jossa $0<\red x<1$ ja $\sqrt{\red x}<\green y<1.$ Voimme esittää tämän toisella tavalla rajoittamalla ensin muuttuja $\green y$ välille $0<\green y<1,$ jolloin $0<\red x<y^2.$

$\begin{tikzpicture} \begin{axis}[xlabel=x, ylabel=y, xmin=-0.1, ymin=-0.1, xmax=1.1, ymax=1.1, axis lines=middle, ticks=none] \addplot[name path=g1, thick, green!50!black, samples=100, domain=0:1]{sqrt(x)}node at (axis cs:0.4,0.5) {$y=\sqrt x$}; \addplot[dashed, green!50!black, samples=1000, domain=1:1.25]{sqrt(x)}; \addplot[name path=g2, thick, green!50!black, samples=100, domain=0:1]{1}node[] at (axis cs:0.5,1.05){$y=1$}; \addplot[dashed, green!50!black, samples=100, domain=-0.2:0]{1}; \addplot[dashed, green!50!black, samples=100, domain=1:1.2]{1}; \addplot[red!90!black,mark=none, ultra thick] coordinates {(0, 1) (0, 0)}node[anchor=south west] {$x=0$}; \addplot +[red!90!black,mark=none, dashed]coordinates {(1, 1.2) (1, 0)}node[anchor=south east] {$x=1$}; \node at (axis cs:0.2,0.8) {$D$}; \addplot [ thick, color=blue, fill=blue, fill opacity=0.05, ] fill between[ of=g1 and g2, soft clip={domain=0:1}, ]; \end{axis} \end{tikzpicture}$

$\updownarrow \text{Vaihdetaan integrointijärjestys.}$

$\begin{tikzpicture} \begin{axis}[xlabel=x, ylabel=y, xmin=-0.1, ymin=-0.1, xmax=1.1, ymax=1.1, axis lines=middle, ticks=none] \addplot[name path=g1, thick, red!90!black, samples=100, domain=0:1]{sqrt(x)}node at (axis cs:0.4,0.5) {$x=y^2$}; \addplot[dashed, red!90!black, samples=100, domain=1:1.25]{sqrt(x)}; \addplot[name path=g2, thick, green!50!black, samples=100, domain=0:1]{1}node[] at (axis cs:0.5,1.05){$y=1$}; \addplot[dashed, green!50!black, samples=100, domain=-0.2:0]{1}; \addplot[dashed, green!50!black, samples=100, domain=1:1.2]{1}; \addplot +[green!50!black,mark=none, ultra thick] coordinates {(0, 0) (1, 0)} node at (axis cs:0.5,-0.05) {$y=0$}; \addplot [red!90!black,mark=none, ultra thick]coordinates {(0, 1) (0, 0)}node[anchor=south west] {$x=0$}; \node at (axis cs:0.2,0.8) {$D$}; \addplot [ thick, color=blue, fill=blue, fill opacity=0.05, ] fill between[ of=g1 and g2, soft clip={domain=0:1}, ]; \end{axis} \end{tikzpicture}$

Integrointijärjestystä vaihtamalla saadaan $\begin{align*} \int_{\red 0}^{\red1}\int_{\green{\sqrt x}}^{\green1}e^{\green y^3}\;\green\dy\,\red\dx &=\int_{\green 0}^{\green 1}\int_{\red 0}^{\red {y^2}}e^{\green y^3}\;\red\dx\,\green \dy\quad\text{(vakio $x$:n suhteen)}\\ &=\int_{\green0}^{\green1}\green y^2e^{\green y^3}\;\green\dy\\ &=\intsub{\green 0}{\green 1}\frac13e^{\green y^3}\quad\text{(tarkista edellinen derivoimalla)}\\ &=\frac13. \end{align*}$

Esimerkkejä eri koordinaatistoissa

Useissa sovelluksissa koordinaatiston vaihtaminen helpottaa laskemista. Integraalilaskennassa on oltava tarkkana differentiaalien muuntamisessa (ks. laskusäännöt-taulukko ja muunnoskaavojen johtaminen sen alla).

Tähän on kerätty muutamia esimerkkejä integroinnista napa-, sylinteri- ja pallokoordinaatistoissa. Muista, että kuvien piirtäminen auttaa hahmottamaan tilannetta!

Napakoordinaatisto Ympyrän muotoisen R-säteisen levyn massa.

Levyn massa saadaan integraalista $m(D) = \iint_D\rho(x,y)\,\text dA.$ Jos tiheys $\rho$ on vakio, se voidaan ottaa ulos integraalista. Integrointi ympyrän muotoisen tasoalueen yli on helpointa [napakoordinaateissa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#napajasylinteri $(\red r,\green \varphi).$ Tällöin integroitava alue voidaan esittää säteen ja kulman avulla helposti, kun levyn keskipiste asetetaan origoon: $\red{0\le r\le R}$ ja $\green{0\le\varphi\le2\pi}.$

Nyt integraalin arvo on (huomaa $\text dA=r\,\text dr\,\text d\varphi$ ) $\begin{aligned} m(D)&=\rho\green{\int_0^{2\pi}}\red{\int_0^R}\,\red{r\,\text dr}\,\green{\text d\varphi}\\ &=\rho\green{\int_0^{2\pi}}\red{\frac12 R^2}\,\green{\text d\varphi}\\ &=\rho\,\green{\pi}\red R^2, \end{aligned}$

eli tiheys kertaa pinta-ala. Jos tiheys ei ole vakio, täytyy tiheysfunktio $\rho(x,y)$ kirjoitaa napakoordinaateissa $\rho(r,\varphi).$ Tällöin pitää osata laskea myös tiheysfunktion integraali.

Napakoordinaatisto Origokeskisen ympyräalueen esitys.

-säteinen ympyrä on joukko $D=\{(x,y):x^2+y^2\leq d^2\}.$ Tätä esitysmuotoa ei kuitenkaan voi käyttää integroinnissa, joten etsitään vaihtoehtoisia esitysmuotoa muuttujan suhteen: $\begin{align*} x^2+y^2&\leq d^2\\ y^2&\leq d^2-x^2 \end{align*}$ $\begin{cases} -\sqrt{d^2-x^2}\leq y\leq\sqrt{d^2-x^2},\\ -d\leq x\leq d. \end{cases}$ Joukko $\{(x,y):\red{-\sqrt{d^2-x^2}}\leq y\leq\red{\sqrt{d^2-x^2}},\;\blue{-d}\leq x\leq \blue d\}$ vastaa samaa -säteistä ympyrää ja on lisäksi -yksinkertainen. Näiden rajojen avulla voimme integroida funktiota f(x,y) joukon yli: $\iint_D f(x,y)\;\text dA=\int_{\blue{-d}}^{\blue d}\int_{\red{-\sqrt{d^2-x^2}}}^{\red{\sqrt{d^2-x^2}}}f(x,y)\;\dy\,\dx.$ Alueen voi esittää myös [napakoordinaateissa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#napajasylinteri, jolloin $x^2+y^2 \le d^2\Leftrightarrow r \le d$ ja saamme hyvin yksinkertaiset integrointirajat $0\leq\varphi\leq2\pi$ ja $0\leq r\leq d.$ Näillä integraaliksi saadaan $\iint_D f(x,y)\;\text dA=\int_0^{2\pi}\int_0^d f(r\cos\theta,r\sin\theta)r\;\text dr\text \,d\theta.$

Pallokoordinaatisto Pallon tilavuus

Lasku on helpoin suorittaa pallokoordinaateissa: $V(E)=\iiint_E1~\text dV=\iiint_E \red {r}^2\sin\green\theta~\text d\red {r}\,\text d\blue\varphi\,\text d\green\theta.$ Integrointirajat ovat $0<\red {r}<d,\;0<\green\theta<\pi$ ja $0<\blue\varphi<2\pi,$ $\begin{align*} &\int_0^\pi\int_0^{2\pi}\int_0^d\red {r}^2\sin\green\theta~\text d\red {r}\,\text d\blue\varphi\,\text d\green\theta\\ =&\green{\int_0^\pi\sin\green\theta\,\text d\green\theta}\blue{\int_0^{2\pi}\,\text d\blue\varphi}\red{\int_0^dr^2~\text dr}\\ =&\blue{2\pi}\green{\intsub0\pi-\cos\green\theta~\text d\green\theta\;}\red{\intsub{0}{d}\frac13r^3~\text dr}\\ =&\blue{2\pi}\cdot\green2\cdot\red{\frac13d^3}\\ =&\frac{4\pi}3d^3. \end{align*}$ Tekijä $\green{\int_0^\pi\sin\green\theta\,\text d\green\theta}\blue{\int_0^{2\pi}\,\text d\blue\varphi}=\int d\Omega=4\pi$ on usein fysiikassa vastaan tuleva käsite, ykkösen integraali täyden avaruuskulman yli.

Sylinterikoordinaatisto Pallon hitausmomentti

Kappaleen hitausmomentti voidaan laskea integraalilla $\iiint_E\rho(x,y,z)|\ve r|^2\text dV,$ missä $\rho(x,y,z)$ on tiheys pisteessä (x,y,z) ja $|\ve r|^2$ on neliöity etäisyys pyörimisakselista.

Lasketaan hitausmomentti pallolle, jonka säde on ja tiheys vakio $\rho(x,y,z)=\rho.$ Pyörimisakseli kulkee pallon keskipisteen läpi.

Laskuun kannattaa käyttää [sylinterikoordinaatistoa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#napajasylinteri $(\red r,\green \varphi,\blue z),$ jolloin saamme pisteen etäisyyden pyörimisakselista suoraan ensimmäisestä koordinaatista: $|\ve r| = \red r.$ Pallon integrointirajat ovat $\red {0<r<\sqrt{d^2-\blue z^2}},~~~\green{0<\varphi<2\pi}$ ja $\blue{-d<z<d}.$ Lisäksi sylinterikoordinaateissa $\text dV=\red r \,\text d\red r \, \text d\green \varphi \, \text d\blue z.$ $\begin{align*} &\blue{\int_{-d}^d}\green{\int_0^{2\pi}}\red{\int_0^{\sqrt{d^2-\blue z^2}}}\rho \,\red r^2\red r~\text d\red r\,\text d\green\varphi\,\text d\blue z\\ =&\rho\blue{\int_{-d}^d}\green{\int_0^{2\pi}}\text d\green\varphi\red{\int_0^{\sqrt{d^2-\blue z^2}}} \red r^3~\text d\red r\,\text d\blue z\\ =&\green{2\pi} \rho \blue{\int_{-d}^d} \red {\intsub{0}{\sqrt{d^2-\blue z^2}} \frac{1}{4}} \red r^4 \text{d}\blue z \\ =&\green{2\pi} \rho \blue{\int_{-d}^d}\red{\frac14(d^2-\blue z^2)^2}~\text d\blue z\\ =&\red{\frac12}\pi\rho\blue{\int_{-d}^d}\red{d^4-2d^2\blue z^2+\blue z^4}\;\text d\blue z\\ =&\frac12\pi\rho \blue{d^5 \left( 2-\frac43+\frac25 \right)}\\ =&\frac{8\pi }{15}\rho d^5. \end{align*}$ Pallon massa on $m=\frac43\pi \rho d^3,$ joten -massaisen -säteisen tasa-aineisen pallon hitausmomentti keskiakselin ympäri on $I=\frac25d^2m.$

Sylinterikoordinaatisto Pallon ja sylinterin erotusjoukko.

$\begin{tikzpicture}[domain=0:4] \draw (1.2,1) to [bend left=10] (2.4,1); \draw (1.2,1) to [bend right=10] (2.4,1); \draw (1.2,-1) to [bend right=10] (2.4,-1); \draw[dashed] (1.2,0) to [bend right=10] (2.4,0); \draw[dashed] (1.2,0) to [bend left=10] (2.4,0); \draw[dashed] (1.2,-1) to [bend left=10] (2.4,-1); \draw (1.2,1) to [bend right=65] (1.2,-1); \draw (2.4,1) to [bend left=65] (2.4,-1); \draw[dashed] (2.4,1) -- (2.4,-1); \draw[dashed] (1.2,1) -- (1.2,-1); \draw (-4.1,1) to [bend left=10] (-1.1,1); \draw (-4.1,1) to [bend right=10] (-1.1,1); \draw (-4.1,-1) to [bend right=10] (-1.1,-1); \draw[dashed] (-4.1,0) to [bend right=10] (-1.1,0); \draw[dashed] (-4.1,0) to [bend left=10] (-1.1,0); \draw[dashed] (-4.1,-1) to [bend left=10] (-1.1,-1); \draw (-4.1,1) to [bend right=32] (-4.1,-1); \draw (-1.1,1) to [bend left=32] (-1.1,-1); \draw[dashed] (-1.1,1) -- (-1.1,-1); \draw[dashed] (-4.1,1) -- (-4.1,-1); \draw[red] (-2.6,0) -> (-4.43,0); \node[color=red] at (-3.9,.2) {b}; \draw[blue] (-2.6,0.5) -> (-4.1,0.5); \node[color=blue] at (-3.4,.7) {a}; \end{tikzpicture}$

Määritetään integrointirajat joukolle, joka saadaan kun pallosta x^2+y^2+z^2<2 poistetaan sylinterin x^2+y^2<1 pisteet. Tehtävä kannattaa selvästi tehdä joko [sylinteri- tai pallokoordinaateissa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot. Vaihtamalla sylinterikoordinaatteihin saadaan joukko kirjoitettua muotoon $D=\{(r,\varphi,z):1<r^2<2-z^2\}.$ Epäyhtälöstä 1<2-z^2 saadaan -1<z<1. Edelleen saadaan rajoitettua välille $1<r<\sqrt{2-z^2},$ eli $D=\{(r,\varphi,z):1<r<\sqrt{2-z^2},\;-1<z<1,\;0<\varphi<2\pi\}.$

Otetaan seuraavaksi säteinen pallo ja säteinen sylinteri ( b>a ). Tällöin pallo, josta on poistettu sylinterin pisteet, on joukko $\{(r,\varphi,z):a^2<r^2<b^2-z^2\}.$ Ratkaistaan muuttujan rajat: $\begin{align*} a^2&<b^2-z^2\\ -\sqrt{b^2-a^2}<&z<\sqrt{b^2-a^2}. \end{align*}$ Integrointiin soveltuva esitystapa on $\{(r,\varphi,z):a<r<\sqrt{b^2-z^2},\;-\sqrt{a^2-b^2}<z<\sqrt{a^2-b^2},\;0<\varphi<2\pi\}.$

# sovelluksia

Sovelluksia

Sähkökentän laskeminen

Ympyrän muotoisen $R\text-$ säteisen varatun levyn sähkökenttä symmetria-akselilla.

Piirretään aluksi kuva. Valitaan koordinaatisto siten, että levy on $(x,y)\text-$ tasossa. Tällöin symmetria-akseli on $\blue z\text-$ akselin suuntainen.

$\begin{tikzpicture} % Levy \draw[red!90!black, fill = gray!20] plot [smooth cycle, tension=1] coordinates {(2,0,0) (0,0,2) (-2,0,0) (0,0,-2)}; \node at (-0.5,0,0.5) {$D$}; % Koordinaatisto % x-akseli \draw[gray, dashed,->] (0,0,0) -- (1,0,0) node [below] {$\textcolor{gray}x$}; %y-akseli \draw[gray, dashed,->] (0,0,0) -- (0,0,-1.5) node [right] {$\textcolor{gray}y$}; % z-akseli \draw[blue!75!black,->] (0,0,0) -- (0,3,0) node [right, scale=1.3] {$\textcolor{blue!75!black}z$}; % etäisyys origosta \draw[red, ->] (0,0,0) -- (1,0,-1) node [below, scale=1.3] {$\textcolor{red}r$}; % etäisyys levyltä zetalle \draw[dashed, magenta!80!black] (0,2.5,0) -- (1,0,-1); \node at (1,1.3,-.2) {$\textcolor{magenta!80!black}d$}; \draw[fill] (0,2.5) circle (2pt); % suora kulma \draw (.2,0,-.2) -- (.2,.2,-.2) -- (0,.2,0); \end{tikzpicture}$

Superpositio

Varauksen muodostaman sähkökentän suuruus etäisyydellä $\textcolor{magenta!80!black}d$ on $E(\textcolor{magenta!80!black}d)=\frac1{4\pi\epsilon_0}\frac { q}{\textcolor{magenta!80!black} {d^2}}.$

Olkoon levyn pintavaraustiheys vakio, eli ${\dfrac{q}{A} =\rho}.$ Varaus voidaan ilmaista pintavaraustiheyden $\rho$ avulla: jaetaan levy pieniksi pinta-alkioiksi $\text dA$ jolloin varausalkio ${\text dq} = {\rho}\,\text dA.$

Sähkökenttä saadaan varausalkioista superpositioperiaatteen nojalla summaamalla. Jatkuvalla varausjakaumalla tämä voidaan laskea integraalina, tässä tapauksessa yli levyn $D\text:$ $E(\textcolor{magenta!80!black}d)=\iint_D \frac1{4\pi\epsilon_0}\frac {\rho}{\textcolor{magenta!80!black}{d^2}}\,\text dA.$

Symmetria

Kentän laskeminen helpottuu huomattavasti, kun käytetään hyväksi tilanteen symmetriaa. Mikään ei muutu, jos levyä kierretään $z\text-$ akselin ympäri. Tällöin:

Kentällä on vain $z\text-$ suuntainen komponentti.
- Valittiinpa mikä tahansa piste levyltä, löytyy yhtä kaukaa akselin vastakkaiselta puolelta piste, jolla on samansuuruinen varaus. Tällöin kentän $x\text-$ ja $y\text-$ suuntaiset komponentit häviävät.
Integraali voidaan laskea helpommin [napakoordinaateissa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#napajasylinteri $(\red r,\green \varphi).$
- Huom: Napakoordinaateissa pinta-alkio on $\text dA = \red {r\,\text dr}\,\green {\text d\varphi}.$

Etäisyys $\textcolor{magenta!80!black} d$ joltain levyn pisteeltä $\blue z\text-$ akselille on nyt Pythagoraan lauseen mukaan $\textcolor{magenta!80!black} d= \sqrt{\red{r^2}+\blue{z^2}}.$

Varausalkion muodostaman sähkökentän $z\text-$ komponentti saadaan akselin ja kentän suunnan välisen kulman kosinista.

$\begin{tikzpicture} % z-akseli \draw[blue!50, ->] (0,0) -- (5.2,0); \node at (5.3,-0.1) {$\textcolor{blue!50}z$}; % r \draw[red] (0,0) -- (0,1); \node at (-.15,.4) {$\textcolor{red}r$}; \draw [fill, red] (0,1) circle (2pt); % suora kulma \draw (.3,0) -- (.3,.3) -- (0,.3); %levy \draw[gray] plot [smooth cycle, tension=1] coordinates{(0,0,1)(0,1,0)(0,0,-1) (0,-1,0)}; % etäisyys levyltä zetalle \draw[dashed, magenta!80!black] (0,1) -- (3.333,0); \node at (1.6,.75) {$\textcolor{magenta!80!black}d$}; %akseli-kenttä-kulma \draw (2.5,.25) arc (165:180:1) node [above left] {$\alpha$}; \draw (4.1,-.25) arc (345:360:1) node [below right] {$\alpha$}; %matka z:lla \draw[|-|, blue!80] (0,-0.25) -- (3.333,-0.25); \node at (1.5,-.4) {$\textcolor{blue!80} z$}; %sähkökenttä \draw[->] (3.333,0) -- (5,-.5) node [below left] {$E$}; \draw[dashed] (5,-.5) -- (5,0); \draw (4.8,0) -- (4.8,-.2) -- (5,-.2); %shäkökenttä z-suuntaan \draw[|-|] (3.333,0.25) -- (5,0.25); \node at (4.1,.5) {$E_z$}; %tutkittava piste \draw [fill] (3.333,0) circle (1.5pt); \end{tikzpicture}$

Kentän $z\text-$ komponentti on siis $\begin{aligned} E_{\blue z}(\textcolor{magenta!80!black}d) &= E(\textcolor{magenta!80!black}d)\cdot \cos\alpha= E(d)\, \frac {\blue z} {\textcolor{magenta!80!black}d}\\ &=\frac1{4\pi\epsilon_0}\frac{\rho}{\red{r^2}+\blue{z^2}}\cdot\frac{\blue z} {\sqrt{\red {r^2} +\blue {z^2}}}\\ &=\frac1{4\pi\epsilon_0}\frac{\rho\,{\blue z}}{\left(\red{r^2}+\blue{z^2}\right)^{3/2}}. \end{aligned}$

Integraalissa tuntematon on enää integrointialue Valitussa koordinaatistossa tämä on yksinkertainen: $\red R\text-$ säteinen, pyöreä levy on alue $\red{0\le r\le R},$ $\green{0\le\varphi\le2\pi}.$

Integrointi

Levyn muodostama sähkökenttä on $\blue z\text-$ akselilla $E(\blue z)=\red{\int_0^R}\green{\int_0^{2\pi}}\frac1{4\pi\epsilon_0}\frac{\rho \blue z}{\left(\red{r^2}+\blue{z^2}\right)^{3/2}}\,\green{\text d\varphi}\,\red{ r\,\text dr}.$ Tästä nähdään heti, että integroitava funktio ei riipu kulmasta $\green \varphi$ (tämän vuoksi integroidaan napakoordinaateissa.) Sisemmän integraalin tulos on sama funktio kerrottuna ylärajalla $\green {2\pi}$ $E(\blue z)=\red{\int_0^R}\frac1{\green 2\epsilon_0}\frac{\rho \blue z}{\left(\red{r^2}+\blue{z^2}\right)^{3/2}}\,\red{ r\,\text dr}.$

Tehdään tähän integraaliin muuttujanvaihto. Merkitään $u=\red{r^2}+\blue{z^2}.$ Tällöin $\text du = \red{2r\,\text dr}$ ja edelleen $\red{r\,\text dr} = \red{\frac12}\,\text du.$ Saadaan $E(\blue z)=\red{\int_{\blue{z^2}}^{\red {R^2}\textcolor{black}+\blue {z^2}}}\frac1{2\epsilon_0}\frac{\rho \blue z}{u^{3/2}}\red{\frac12} \,\text du.$ Siirretään vakiot ulos integraalista ja lasketaan $\begin{aligned} E(\blue z)&=\frac{\rho \blue z}{\red 4\epsilon_0}\red{\int_{\blue{z^2}}^{\red {R^2}\textcolor{black}+\blue {z^2}}}u^{-3/2} \,\text du\\ &=\frac{\rho \blue z}{4\epsilon_0} \red {\intsub {\blue{z^2}} {\red {R^2}\textcolor{black}+\blue {z^2}}}-2\,u^{-1/2} \\ &=\frac{\rho \blue z}{2\epsilon_0} \left(-\frac1{\sqrt{\red {R^2}+\blue {z^2}}}-\left(-\sqrt{\blue{z^2}}\right)\right)\\ &=\frac{\rho}{2\epsilon_0} \left(1-\frac {\blue z}{\sqrt{\red {R^2}+\blue {z^2}}}\right). \end{aligned}$ Sähkökentän suuruus $\blue z\text-$ akselilla on $E(\blue z)=\frac{\rho}{2\epsilon_0} \left(1-\frac {\blue z}{\sqrt{\red {R^2}+\blue {z^2}}}\right),\quad\text{kun}\;\blue z\ne0.$ Kun $\blue z = 0,$ sähkökenttä on symmetrian nojalla $E(\blue 0)=0.$ Kentän suunta riippuu levyn varauksen merkistä: positiivinen varaus ( $\rho >0$ ) aiheuttaa kentän poispäin levystä, eli $\ve E(\blue z)= \begin{cases} \frac{\rho}{2\epsilon_0} \left(1-\frac {\blue z}{\sqrt{\red {R^2}+\blue {z^2}}}\right)\hat k, &\quad\text{kun}\;{\blue z>0},\\ -\frac{\rho}{2\epsilon_0} \left(1+\frac {\blue z}{\sqrt{\red {R^2}+\blue {z^2}}}\right)\hat k, &\quad\text{kun}\;{\blue z <0},\\ 0,&\quad\text{kun}\;\blue z=0. \end{cases}$

Aaltofunktion normitus

Aaltofunktiolla on yhteys todennäköisyyteen löytää hiukkanen jostain alueesta. Tarkemmin, todennäköisyys löytää hiukkanen alueesta on hiukkasen aaltofunktion normin neliön integraali alueen yli, eli $P(\text{hiukkanen on alueessa }E)=\iiint_E|\psi|^2\text dV.$ Todennäköisyys löytää hiukkanen edes jostain täytyy olla eli $\iiint_{\R^3}|\psi|^2\text dV=1.$ Tätä kutsutaan aaltofunktion normitukseksi. Normittamattomalla aaltofunktiolla integraali kaikkien pisteiden yli ei välttämättä ole jolloin pitää etsiä aaltofunktiolle sopiva normitusvakio .

Laatikkopotentiaali

Lasketaan normitusvakio hiukkaselle kaksiulotteisessa laatikkopotentiaalissa.

Kaksiulotteisessa laatikkopotentiaalissa jatkuvuusehdot toteuttava aaltofunktio on sinimuotoinen: $\psi(\red x,\green y) = N\sin\left(\frac{n_x\pi \red x}{L_x}\right)\sin\left(\frac{n_y\pi \green y}{L_y}\right),$ missä on normitusvakio, n_x ja n_y ovat kokonaislukuja ja L_x ja L_y ovat laatikon mitat $x\text-$ ja $y\text-$ suunnissa. Näin aaltofunktio on nollaa laatikon reunoilla.

Aaltofunktion normitus tarkoittaa vakion asettamista siten, että $\int_{-\infty}^\infty\int_{-\infty}^\infty |\psi(x,y)|^2\,\dy\,\dx = 1.$

Laatikkopotentiaalissa tiedetään, että aaltofunktio on nolla kaikkialla, paitsi laatikon sisällä. Siis integroinnin rajat voidaan vaihtaa laatikon rajoiksi.

Asettamalla laatikon yksi nurkkaa origoon saadaan integraaliksi $\int_0^{L_x}\int_0^{L_y} N^2\sin^2\left(\frac{n_x\pi \red x}{L_x}\right)\sin^2 \left(\frac{n_y\pi \green y}{L_y}\right)\,\dy\,\dx.$ Tekijä $\sin^2\left(\dfrac{n_x\pi \red x}{L}\right)$ on vakio muuttujan $\green y$ suhteen, joten se voidaan siirtää seuraavaan integraaliin. N^2 on vakio myös muuttujan $\red x$ suhteen, joten se voidaan ottaa ulos molemmista integraaleista. Saadaan $N^2\int_0^{L_x}\sin^2\left(\frac{n_x\pi \red x}{L_x}\right)\int_0^{L_y} \sin^2 \left(\frac{n_y\pi \green y}{L_y}\right)\,\dy\,\dx.$ Integraali ratkeaa pyörittämällä trigonometrian kaavoja, joilla saadaan $\sin^2(\red k x)=\frac12-\frac{\cos(2\red k x)}2.$ Tämän integraali on $\begin{aligned} \int_{\blue a}^{\green b} \sin^2(\red k x)\,\text dx &= \int_{\blue a}^{\green b}\frac12-\frac{\cos(2 \red kx)}2\,\dx \\ &= \intsub {\blue a}{\green b} \frac12 x + \frac{\sin(2\red kx)}{4\red k} = \frac {\green b}2+\frac{\sin(2{\red k\green b})}{4\red k} -\left(\frac {\blue a}2 + \frac{\sin(2{\red k\blue a})}{4\red k}\right). \end{aligned}$

Sijoittamalla sinifunktioihin sisemmän integraalin vakio $\red k_y = \dfrac{n_y\pi}{L_y}$ ja rajat $\blue a_y = 0$ ja $\green b_y=L_y$ sinitermit ovat nollia $\sin(n\pi)=0,$ kun on kokonaisluku.. Saadaan

$N^2\int_0^{L_x}\sin^2\left(\frac{n_x\pi \red x}{L_x}\right)\left(\frac{L_y}2 \right)\,\dx.$

Myös muuttujan $\red x$ integraalista saadaan samoin $\dfrac{L_x}2.$

Integroimisvakion määrittää nyt yhtälö $N^2\frac{L_x}2\frac{L_y}2=1,$ eli $N=\sqrt{\frac{4}{L_xL_y}}=\frac2{\sqrt{L_xL_y}}.$ Jos laatikon sivut ovat yhtä pitkät, on $N=\dfrac 2L.$

Vetyatomi

Lasketaan normitusvakio vetyatomin ominaistilaa kuvaavalle funktiolle $\red\psi_0(\green r)=Ne^{-\green r/a_0}.$

Tapa 1: kolme yksiulotteista integraalia

Tehtävä on helpointa ratkaista [pallokoordinaatistossa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#pallokoordinaatit $(\red r,\green \theta,\blue \phi).$ Aaltofunktio on normitettu, joten $1=\iiint_{\mathbb R^3}\red{|\psi_0(r)|r^2}\green{\sin\theta}\,\red{\text dr}\,\green{\text d\theta}\,\blue{\text d\phi},$ missä integroidaan koko avaruuden $\mathbb R^3$ yli. Pallokoordinaateissa tämä tarkoittaa, että $\red{0\le r<\infty},$ $\green{0\le\theta\le\pi}$ ja $\blue{0\le\phi<2\pi}.$

Integroitaessa muuttujan suhteen, $\sin\theta$ on vakio ja voidaan ottaa ulos omaan integraaliinsa. Kolmoisintegraali voidaan siis kirjoittaa kolmen integraalin tulona $1=\blue{\int_0^{2\pi}\,\text d\phi}\green{\int_0^{\pi}\sin\theta\,\text d\theta}\red{\int_0^\infty\,|\psi_0(r)|^2r^2\,\text dr}.$ Ensimmäisessä integroidaan ykköstä, joten integraali on yläraja $\blue{2\pi}.$ Toinen integraali on helppo $\green{\int_0^\pi \sin \theta\,\text d\theta }= \intsub 0\pi -\cos\theta = -(-1)-(-1) =\green 2.$

Sijoitetaan viimeiseen integraaliin aaltofunktion normin neliö $|Ne^{-r/a_0}|^2=N^2e^{-2r/a_0}.$ Vakio N^2 voidaan ottaa ulos, jolloin integraali on

$\red{N^2\int_0^\infty r^2e^{-2r/a_0}\,\text dr}.$ Tämä epäoleellinen integraaliIntegroimisväli ei ole rajoitettu. voidaan ratkaista osittaisintegroimalla. Yleisemmälle integraalille $\int x^ne^{kx}\,\dx$ saadaan osittaisintegroinnin kaavalla $\dint_a^b \green u\cdot \blue v'\,\dx=\intsub a b\green u\cdot \blue v-\dint_a^b \green u'\cdot \blue v\,\dx$ iteratiivinen kaava $\int_a^b \red x^ne^{k\red x} \,\red{\dx}= \intsub ab\frac{\red x^n}{k}e^{k\red x} - \frac{n}{k}\int_a^b \red x^{n-1}e^{k\red x}\,\red{\dx}.$ Sijoittamalla tähän $\red{x=r},$ n=2 ja rajat a=0 ja $b\to\infty$ saadaan $N^2\int_0^\infty r^2e^{kr}\,\text dr = N^2\left(\red{\intsub 0 \infty\frac{r^2}{k} e^{kr}} - \frac{2}{k}\int_0^\infty re^{kr}\,\text dr\right).$ Ylärajalla $r\to\infty$ eksponenttitekijä $e^{kr},$ missä k=-2/a_0<0 menee nopeasti nollaan. Sijoituksesta saadaan $N^2\left(\red{0} - \frac{2}{k}\int_0^\infty re^{kr}\,\text dr\right).$ Käytetään samaa kaavaa uudestaan, mutta nyt n=1 $\begin{aligned} -\frac{2N^2}{k}\int_0^\infty re^{kr}\,\text dr&= -\frac{2N^2}{k}\left(\green{\intsub 0 \infty \frac{r}{k} e^{kr}} - \frac1{k}\int_0^\infty e^{kr}\,\text dr\right)\\ &=-\frac{2N^2}{k}\left(\green 0-\frac1 k \blue{\intsub 0 \infty \frac1 k e^{kr}}\right) = -\frac{2}{k}\left(-\frac1 k\blue{\left(-\frac1 k\right)}\right)\\ = -\frac{2N^2}{k^3}. \end{aligned}$ Sijoittamalla vakio k=-2/a_0 saadaan $-\frac{2N^2}{k} = -\frac{2N^2}{(-2/a_0)^3} = \frac{a_0^3N^2}{4}.$ Kertomalla kolmen integraalin tulokset keskenään saadaan $1= \green2\cdot \blue{2\pi}\cdot\red{\frac{a_0^3N^2}{4}} = \pi a_0^3N^2$ eli $N=\sqrt{\frac1 {a_0^3\pi}}.$

Tässä on alussa theetan ja fiin rajat väärin päin (“matemaatikkotyyliin”): koordinaatistosivulla annetuilla määritelmillä theeta on välillä [0, pii] ja fii välillä [0, 2*pii[. Virhe toistuu kohdissa “Pallokoordinaateissa tämä tarkoittaa, että…” sekä sitä seuraavassa kolmen integraalin tulossa. Siitä eteenpäin rajat ovatkin taas oikein päin.

— 04 Sep 20

Korjattu, kiitos!

— 11 Sep 20

Tapa 2: lyhyt ratkaisu gammafunktion avulla

Ominaisfunktio $\psi_0$ on normitettu, kun sen itseisarvon neliön integraali yli koko avaruuden $\R^3$ on eli [pallokoordinaateissa]https://tim.jyu.fi/view/kurssit/matematiikka/matikkapakki/koordinaatistot#pallokoordinaatit $\begin{align*} 1=\iiint_{\R^3}|\psi_0|^2\text dV&=\int_0^\pi\int_0^{2\pi}\int_0^\infty N^2e^{-2r/a_0}r^2\sin(\theta)\;\text dr\,\text d\varphi\,\text d\theta\\ &=N^2\red{\int_0^\pi\sin(\theta)\text d\theta}\blue{\int_0^{2\pi}\text d\varphi}\int_0^\infty e^{-2r/a_0}r^2\;\text dr\\ &=N^2\red 2\cdot\blue{2\pi}\violet{\int_0^\infty e^{-2r/a_0}r^2\;\text dr}. \end{align*}$ Tehdään viimeiseen integraaliin muuttujanvaihto u=2r/a_0, tällöin $\text dr=a_0/2\text du$ ja r^2=u^2a_0^2/4. Saadaan $\violet{\int_0^\infty e^{-2r/a_0}r^2\;\text dr}=\frac{a_0^3}{8}\int_0^\infty u^{3-1}e^{-u}\,\text du.$ Nyt integraali on gammafunktio $\Gamma(p)=\int_0^\infty x^{p-1}e^{-x}\,\text dx,$ kun p=3 . Kokonaisluvuilla n=1,2,3,... gammafunktion arvo on kertoma (n-1)!. Saadaan siis $\frac{a_0^3}{8}\int_0^\infty u^{3-1}e^{-u}\,\text du=\frac{a_0^3}{8}\;\Gamma(3)=\frac{a_0^3}{8}\;(3-1)!= \violet{\frac{a_0^3}{4}}.$ Nyt voimme viedä laskun loppuun ja ratkaista normitusvakion $N\text:$ $\begin{align*} 1&=4N^2 \pi\violet{\frac{a_0^3}{4}}=N^2\pi a_0^3,\\ N&=\frac{1}{\sqrt{\pi a_0^3}}. \end{align*}$