Sivun aiheet	Katso tarvittaessa
○ Sanastoa ○ Laskusääntöjä käyrille ○ Laskusääntöjä pinnoille	○ Integrointi ○ Vektorit ○ Derivointi
○ Parametrisointi ○ Tärkeitä tuloksia	○ Moniulotteinen derivointi ○ Koordinaatistot ○ Taso- ja tilavuusintegraalit

Tällä sivulla käsitellään moniulotteisen integroinnin käyräintegraali ja pintaintegraali sanastoineen. Myös joitain tärkeitä tuloksia on esitelty. Taso- ja tilavuusintegraalit käsitellään omalla sivullaan.

# pintajakayraintegraalit

Käyrä- ja pintaintegraalit

# sanastoa

Sanastoa ja määritelmiä

Vektorifunktio, vektorikenttä: $\ve{\red F}(\green x,\green y) =\left( \red P(\green x,\green y),\red Q(\green x,\green y)\right)$

Funktiota, jonka arvo on vektori, merkitään pienellä nuolella $\ve F(x,y).$ Tällaista funktiota kutsutaan vektorikentäksi, sillä se kuvaa jokaiseen pisteeseen (x,y) jonkin vektorin $\ve F.$

Lisää vektorifunktioista esimerkkien kera löytyy moniulotteisen derivoinnin sivulta.

Vektorifunktiolla (eli -kentällä) on komponentit, jotka ovat funktioita:

$\ve F(x,y)=\left( P(x,y),Q(x,y)\right).$
$\ve F(x,y,z)=\left( P(x,y,z),Q(x,y,z),R(x,y,z)\right).$

Funktio on kentän $x\text -$ komponentti ja ja ovat sen $y\text -$ ja $z\text-$ komponentit.

Konservatiivisuus

Konservatiivisuus on vektorikentän $\ve {\red F}(\green x,\green y)$ ominaisuus. Konservatiivisen kentän tekemä työ ei riipu kuljetusta polusta, vaan pelkästään polun alku- ja loppupisteistä.

Esimerkiksi Maan painovoimakentässä kappaleen nostamiseen vaadittava energia riippuu vain korkeuden muutoksesta.

Konservatiivinen kenttä on jonkin funktion gradientti, siis $\ve F(x,y)=\nabla \phi(x,y).$ Tällöin funktiota $\phi$ kutsutaan kentän $\ve F$ potentiaaliksi. Painovoimakenttä $\ve G(x,y,z)$ on gravitaatiopotentiaalienergian gradientti $\nabla U(x,y,z).$

Konservatiivinen vektorikenttä $\ve F$ on aina pyörteetön, eli kentän roottori on nolla: $\text{curl }(\ve F)=\nabla\times\ve F=\nabla\times(\nabla \phi)=0$ kaikissa pisteissä. Myös käänteinen pätee sopivilla lisäoletuksilla: "reiättömässä" alueessa pyörteetön vektorikenttä on konservatiivinen.

Polku $\blue \gamma,$ tasoalue $\blue D,$ pinta $\blue S$ ja kappale $\blue E$

Tässä materiaalissa käytetään seuraavia merkintöjä:

Polku $\gamma$ on jokin yksiulotteinen käyrä, jolla on parametrisaatio $\ve r(t)=\left( x(t),y(t)\right)$ tasossa tai $\ve r(t)=\left( x(t),y(t),z(t)\right)$ avaruudessa.
Tasoalue on $(x,y)\text-$ tason kaksiulotteinen osajoukko.
Pinta on $(x,y,z)\text-$ avaruuden kaksiuoltteinen osajoukko.
Kappale on $(x,y,z)\text-$ avaruuden kolmiulotteinen osajoukko. Kappaleella on jokin tilavuus, toisin kuin edellisillä joukoilla.

Tasoalue on ikään kuin tasainen pinta. Pinnan yksikkönormaalivektori on $\hat{\bold n},$ jonka pituus on ja suunta kohtisuoraan pinnasta poispäin.

Vektorin $\hat {\bold n}$ suunta riippuu sijainnista pinnalla sekä valinnasta pinnan "yläpuoleksi" eli pinnan suunnistuksesta.
Suljetun pinnan suunnistus valitaan aina siten, että $\hat {\bold n}$ osoittaa ulospäin pinnan sulkemasta alueesta.

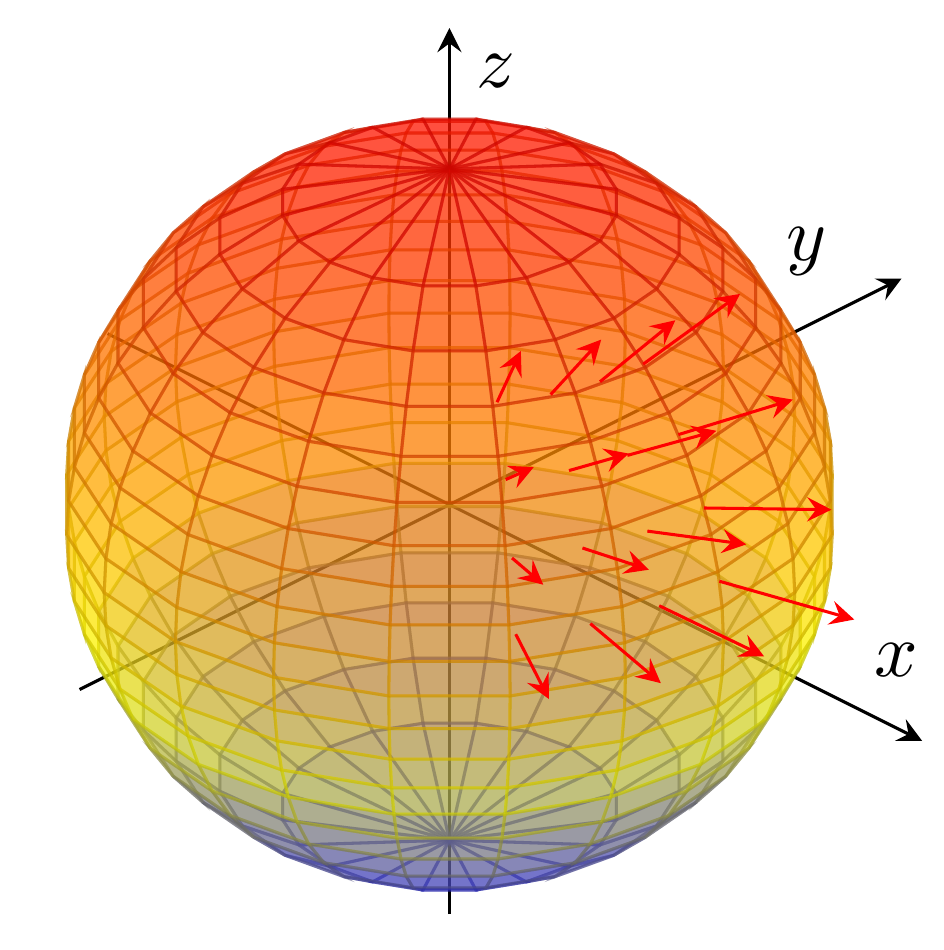
Esimerkiksi alla olevan kuvan pallokuori on eräs (suljettu) pinta ja nuolet kuvaavat joitakin pinnan normaalivektoreita $\hat{\bold n}.$ Kuoren sisään jäävä pallo on esimerkki kappaleesta Pallon pinnan pituus- ja leveyspiirit ovat esimerkkejä poluista $\gamma.$

Pallon jättämä varjo $(x,y)\text-$ tasolle on eräs tasoalue Pallokuori.

Polku/käyräintegraali: $\int_{\blue \gamma},$ $\oint_{\partial \blue D}$

$\gamma$ on polku ja $\ve r(t)$ polun parametrisaatio sopivalla välillä $a\le t\le b.$
- Polusta käytetään myös nimityksiä käyrä, tie ja viiva.
- $\ve r(t)$ on funktio, joka kuvaa jokaisen "ajanhetken" paikkavektoriksi $\left( x,y\right)$ tai $\left( x,y,z\right)$ .
Merkintä $\displaystyle \int_\gamma\text ds$ tai $\displaystyle \oint_\gamma\text ds$ tarkoittaa integraalia polun $\gamma$ yli.
Merkintä $\displaystyle \oint_\gamma$ korostaa, että integraalissa kuljetaan suljettu polku.
Merkintä $\displaystyle \oint_{\partial D}$ korostaa, että suljettu käyrä on alueen reuna.

Tasointegraali, pintaintegraali: $\iint_{\blue D},$ $\iint_{\blue S},$ $\oiint_{\partial\blue E}$

Sekä taso- että pintaintegraalit ovat tuplaintegraaleja, mutta tasointegraalilla tarkoitetaan kaksiulotteisen avaruuden osan (tällä sivulla ) yli integrointia ja pintaintegraalissa integroidaan kolmiulotteisessa avaruudessa olevan kaksiulotteisen pinnan yli.

Tuplaintegraalia merkitään $\iint\text-$ merkillä.

Merkintä $\displaystyle \oiint_S$ korostaa, että integroidaan suljetun pinnanSuljettu pinta rajaa sisälleen jonkin kolmiulotteisen kappaleen. yli. Merkintä $\displaystyle\oiint_{\partial E}$ korostaa, että integroidaan jonkin kappaleen reunan yli.

Usein kaksois- ja kolmoisintegraaleja merkitään vain yhdellä $\oint$ tai $\int\text-$ merkillä.

# laskusaantojakayrille

Hyödyllisiä määritelmiä ja laskusääntöjä käyrille

Määritelmä	Selitys
$\red{\ve r(t)=\left( x(t),y(t)\right)},\;t\in[a,b]$	Parametrisoitu käyrä.
$\blue{\ve r'(t)=\left( x'(t),y'(t)\right)} = \left(\frac{\dx}{\dt},\frac{\dy}{\dt}\right)$	Käyrän derivaatta eli nopeusvektori.
$\text ds=\|\blue{\ve r'(t)}\|\text dt\,$ ja $\,\text d\ve r=\blue{\ve r'(t)}\text dt$	Käyrän differentiaalit.
$\|\red{\ve r(t)}\|=\sqrt{x^2(t)+y^2(t)}$	Käyrän pisteen etäisyys origosta.
$l(\gamma)=\int_a^b\|\blue{\ve r'(t)}\|\;\text dt$	Käyrän $\gamma$ pituus.
$\int_\gamma \green f(x,y)\,\text ds=\int_a^b\green f(\red{\ve r(t)})\|\blue{\ve r'(t)}\|\,\text dt$	Funktion $\green f(x,y)$ integraali suunnistetun käyrän $\gamma$ yli.
$\int_\gamma \ve {\green F}(x,y)\cdot\text d \ve r=\int_a^b\ve {\green F}(\red{\ve r(t)})\cdot\blue{\ve r'(t)}\,\text dt$	Vektorikentän $\ve {\green F}(x,y)$ integraali käyrän $\gamma$ yli.
$\int_\gamma \ve F(x,y)\cdot\text d\ve r=\int_{\gamma}P\,\text dx+Q\,\text dy$	Vaihtoehtoinen laskutapa komponenttifunktioiden avulla, kun $\ve F(x,y) = \left( P(x,y),Q(x,y)\right).$

Käyräintegraali vektorikentässä

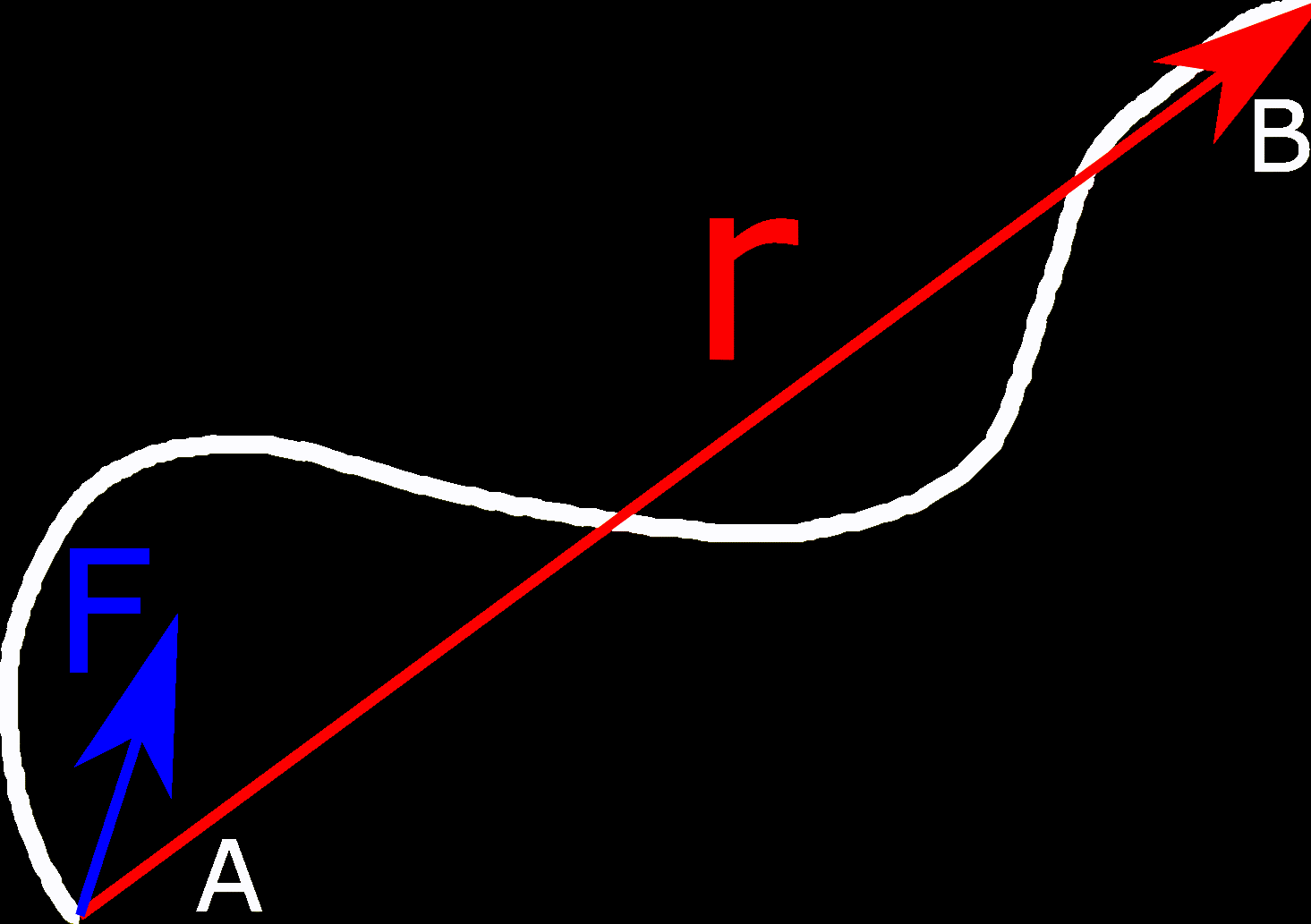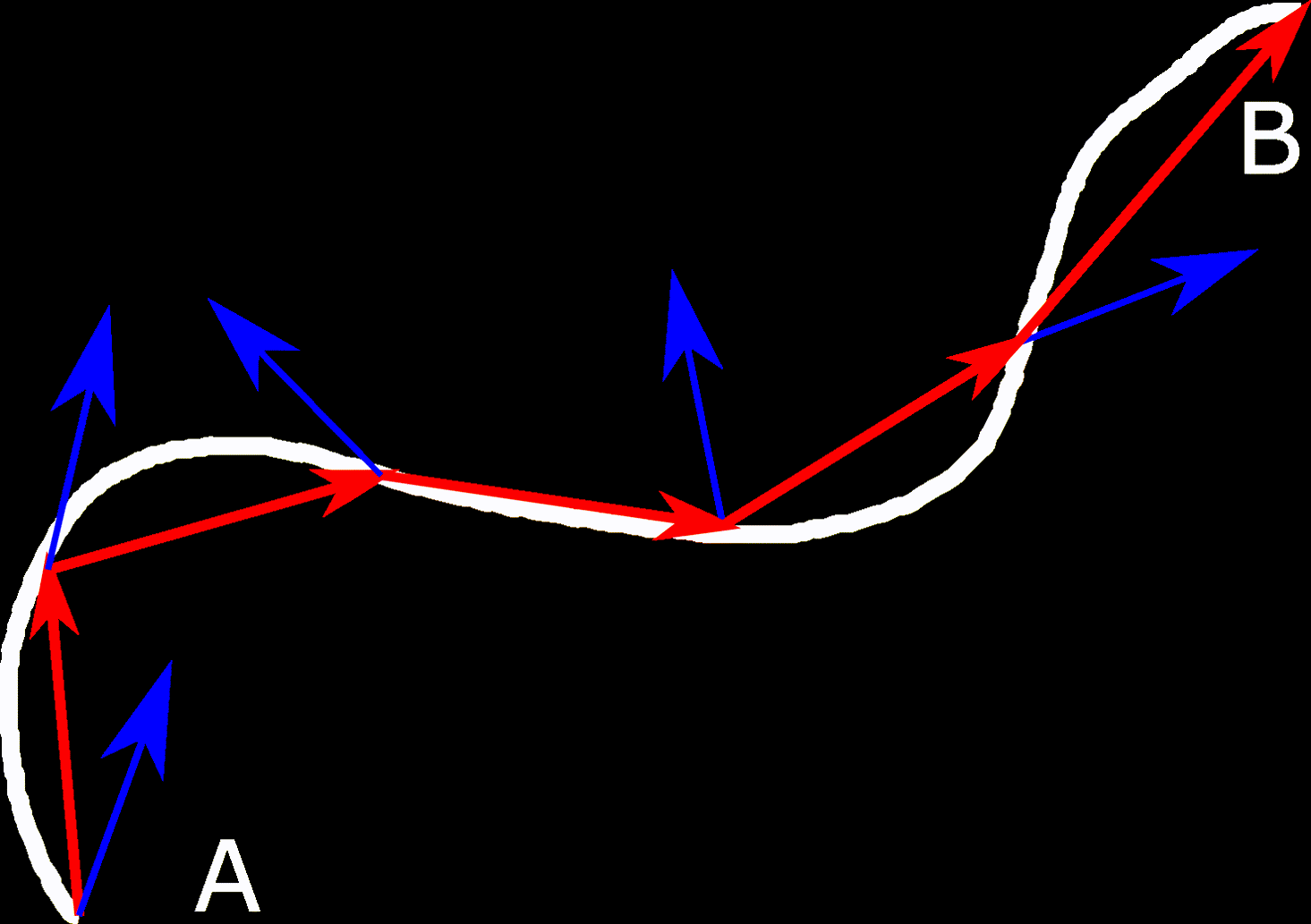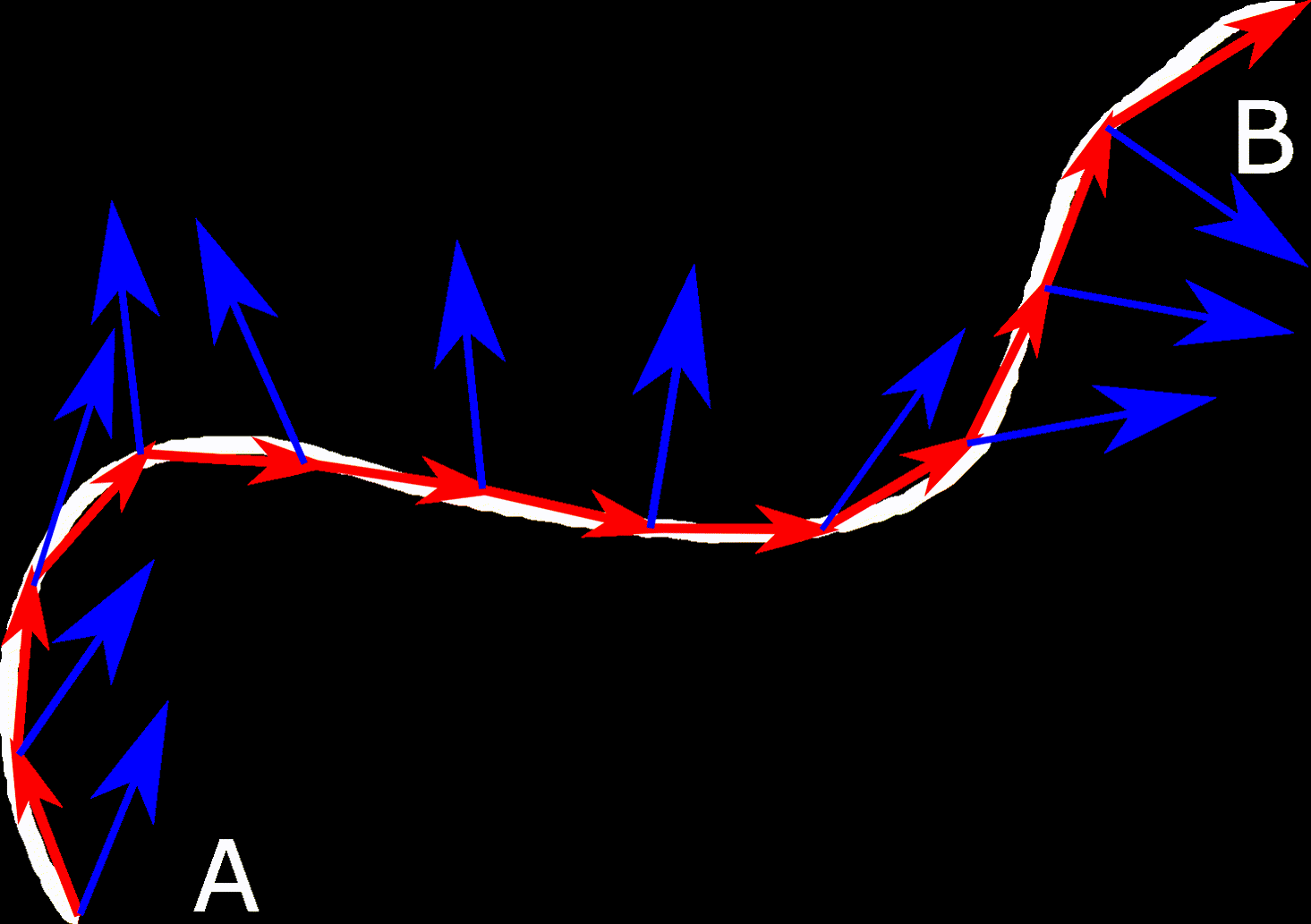
Käyräintegraalin idea on kulkea polku avaruudessa ja laskea esimerkiksi vektorikentän $\ve {\red F}$ tekemä työ. Polku pilkotaan pieniin osiin, joilla lasketaan pistetulojen $\ve{\red F}_i\cdot \ve{\red r}_i$ summa, kun vektorien $\ve{\red r}_i$ pituudet lähestyvät nollaa.

OpenStax Caclulus 3, Section 6.2, Figure 6.12 (CC BY-NC-SA 4.0)

# laskusaantojapinnoille

Hyödyllisiä määritelmiä ja laskusääntöjä pinnoille

Määritelmä	Selitys
$\ve {\red r}(\green u,\blue v)=\big( x(\green u,\blue v),y(\green u,\blue v),z(\green u,\blue v)\big)$	Pinnan parametrisaatio.
$\bold{\hat n}=\pm\dfrac{\ve {\green {r_u}}\times \ve {\blue {r_v}}}{\|\ve {\green {r_u}}\times \ve {\blue {r_v}}\|},\quad \ve {\green {r_u}}=\frac{\partial}{\partial \green u} \ve {\red r}(\green u,\blue v)$	Pinnan yksikkönormaalivektori. Suunnistus määrää etumerkin.
$\text dS = \|\ve {\green {r_u}} \times \ve {\blue {r_v}}\|\,\text dA$	Pinnan differentiaali.
$\ve {\red r}(x,y)=\left( x,y,f(x,y)\right)$	Parametrisaatio pinnalle, joka on funktion kuvaaja.
$\ve {\red r}_x \times \ve {\red r}_y=\left(-f_x,-f_y,1\right)$	Ristitulo antaa normaalivektorin funktion kuvaajalle.
$A(S)=\iint_S1\,\text dS=\iint_D\|\ve {\green {r_u}}\times \ve {\blue {r_v}}\|\,\text dA$	Pinnan pinta-ala.
$\iint_Sf(x,y,z)\,\text dS=\iint_Df(\ve {\red r}(\green u,\blue v))\|\ve {\green {r_u}}\times \ve {\blue {r_v}}\|\,\text dA$	Funktion integraali pinnan yli.
$\iint_S\ve F\cdot\underbrace{\bold{\hat n}\,\text dS}_{\text d{\ve S}}=\iint_D\ve F(\ve {\red r}(\green u,\blue v))\cdot(\ve {\green {r_u}}\times \ve {\blue {r_v}})\,\text dA$	Vektorikentän $\ve F$ vuo suunnistetun pinnan läpi.

Pintaintegraali vektorikentässä

Pintaintegraalin avulla voidaan laskea vektorikentän $\ve F$ vuo halutun pinnan läpi. Vuo on suure, joka kertoo vektorikentän virtauksen pinnan läpi per pinta-alayksikkö.

Esimerkiksi nesteen tai kaasun virtaukselle vuo voidaan ilmoittaa yksiköissä litroja sekunnissa per neliömetri: $l/(s\,m^2).$ Sähkökentän vuon yksikkö on SI-järjestelmässä volttimetri $V\.m.$

Differentiaalien muunnoskaavoista

Käyräintegraalissa integroidaan käyrän pituuden suhteen, eli otetaan pieniä pituusaskelia $\text ds$ pitkin käyrää $\ve{\red r}(\green t).$ Tämä ei kuitenkaan ole sama kuin pienten aika-askelten $\text dt$ ottaminen pitkin käyrän määrittelyväliä $\green t\in\blue{[a,b]}.$ Käyrän derivaatan itseisarvo $|\ve{\red r}'(\green t)|$ kertoo, kuinka kuvaus $\ve{\red r}(\green t)$ venyttää pisteen $\green t$ ympäristöä. Tästä syystä differentiaaleille saadaan yhteys $\text ds=|\ve{\red r}'(\green t)|\text dt.$

Vastaavalla tavalla osittaisderivaattojen ristitulo kertoo pienen tasoalueen ja sen kuvan suuruuden suhteesta, kun pinnan parametrisaatio on $\ve{\red r}(u,v)=\left( \green x(u,v),\green y(u,v),\green z(u,v)\right).$

Esimerkkejä

Laske kentän $\red{\ve F=\left(-x,y\right)}$ tekemä työ polun $\blue{y=x^2,}\; \blue{x\in[0,1]}$ yli.

Tehtävänä on laskea annetuilla arvoilla integraali $\int_{\blue\gamma} \red{\ve F}\cdot\text d\blue{\ve r}.$ Tälle on kaksi tapaa, joita merkitään $\int_{\blue\gamma} \red{\ve F(\ve r(t))}\cdot \blue{\ve r'(t)} \,\dt$ ja $\int_{\blue\gamma} \red P\,\dx + \red Q\,\dy.$

Molemmissa täytyy ensin parametrisoida polku $\blue \gamma$ , sillä integraalin laskemiseksi muuttujat ja täytyy esittää saman muuttujan suhteen. Tässä luonnollisin valinta on merkitä $\blue{x=t\in[0,1]},$ jolloin $\blue{y=t^2}.$ Saadaan siis parametrisaatio $\blue{\ve r(t) = (t,t^2)},$ missä $\blue {0\le t\le 1}.$ Polulla $\gamma$ vektorikenttä on $\red {\ve F = \left( -x,y\right) = \left( -t,t^2\right)}.$

Jatketaan tästä ensimmäisen kaavan mukaan. Nyt täytyy selvittää, mitä on nopeusvektori $\blue{\ve r'(t)}.$ Nopeusvektori on alkuperäisten muuttujien suhteen $\blue{\ve r'(x,y)}= \frac{\text d\ve r}{\dt}=\blue{\left( \frac{\dx}{\dt}, \frac{\dy}{\dt}\right)}.$ Parametrisoinnista saadaan differentiaalit $\dx = \dt$ ja $\dy = 2t\,\dt.$ Parametrisoitu nopeusvektori on siis $\blue{\ve r'(t)} = \left( \frac{\dt}{\dt}, \frac{2t\,\dt}{dt}\right) = \blue{\left( 1, 2t\right)}.$ Nyt integraali voidaan laskea sijoittamalla $\begin{aligned} \int_{\blue\gamma} \red{\ve F(r(t))} \cdot\blue{\ve r'(t)}\,\text dt &= \int_{\blue 0}^{\blue 1}\red{\left( -t,t^2\right)}\cdot\blue{\left(1, 2t\,\right)}\, \dt = \int_{\blue 0}^{\blue 1}-t +2t^3\,\dt \\ &=\intsub 0 1 -\frac1 2 t^2 + \frac{2}{4} t^4 = -\frac1 2 + \frac{2}{4} = 0. \end{aligned}$

Lopputulos nolla tarkoittaa, että kenttä ei tee työtä. Jos polku $\blue \gamma$ olisi varatun hiukkasen liikerata ja $\red {\ve F}$ sähkökenttä, tämä tarkoittaisi, että hiukkasen sähköinen potentiaalienergia on sama polun alku- ja loppupisteissä.

Toisessa tavassa parametrisoinnin jälkeen ratkaistaan differentiaalit $\dx=\dt$ ja $\dy=2t\,\dt,$ jonka jälkeen sijoitetaan $\red{\ve F(t) = \left( -t,t^2\right) = \left( P, Q\right)}$ . Saadaan $\int_{\blue\gamma} \red P\,\dx + \red Q\,\dy = \int_{\blue 0}^{\blue 1}\red{-t}\,\dt + \red{t^2}\,2t\,\dt = \int_{\blue 0}^{\blue 1}-t+2t^3\,\dt$ kuten edellä. Lopputulos on siis sama.

Laske kentän $\red{\ve F=\left( y,-x,z\right)}$ vuo läpi pinnan $\blue{S=\{(x,y,z):x^2+y^2+z^2=1,\;z>0\}}.$

Ratkaisemalla pinnan yhtälö muuttujan suhteen pinnalle saadaan parametrisaatio $\ve r(x,y)=\left( x,y,\sqrt{1-x^2-y^2}\right),$ missä $x^2+y^2\le1.$ Tämä on napakoordinaateissa $\ve r(r,\varphi)=\left( r\cos(\varphi),r\sin(\varphi),\sqrt{1-r^2}\right).$ Parametrisaatio on määritelty joukossa $\{(r,\varphi):0<r<1,\;0<\varphi<2\pi\}.$ Osittaisderivaattojen ristitulosta saadaan $\ve r_r\times \ve r_{\varphi}=\left(\frac{r^2\cos(\varphi)}{\sqrt{1-r^2}},\frac{r^2\sin(\varphi)}{\sqrt{1-r^2}},r\right).$ Integraalin arvo on $\begin{align*} \iint_SF\cdot\text dS&=\int_0^{2\pi}\int_0^1\left( r\sin(\varphi),-r\cos(\varphi),\sqrt{1-r^2}\right)\cdot\left(\frac{r^2\cos(\varphi)}{\sqrt{1-r^2}},\frac{r^2\sin(\varphi)}{\sqrt{1-r^2}},r\right)\; \text dr\text d\varphi\\ &=\int_0^{2\pi}\int_0^1r\sqrt{1-r^2}\; \text dr\text d\varphi\\ &=2\pi\intsub{0}{1}-\frac13(1-r^2)^{\frac32}\\ &=\frac23\pi. \end{align*}$

# parametrisointi

Käyrän ja pinnan parametrisaatio

Parametrisaation ideana on muuttaa käyrä- ja pintaintegraalit tavallisiksi $1\text-$ ja $2\text-$ ulotteisiksi integraaleiksi.

Reaaliarvoisien funktioiden integraali käyrän tai pinnan suhteen on riippumaton parametrisaatiosta, integraali tarkoittaa yksinkertaisesti funktion arvojen "summaa" kaikissa käyrän tai pinnan pisteissä.

Vektoriarvoisille funktioille käyrän tai pinnan suunnistus vaikuttaa lopputuloksen etumerkkiin: vastakkaisella suunnistuksella etumerkki vaihtuu. Polun yhteydessä suunnistuksella tarkoitetaan sitä, mihin suuntaan polkua kuljetaan. Pintojen suhteen tilannetta voi ajatella valintana siitä, kumpi on pinnan ylä- tai alapuoli.

Suljettu polku on silmukka, jolla on sama alku- ja loppupiste. Suljettu polku on jonkin pinnan reuna ja suunnistetaan vastapäivään. Toisin sanoen, jos kuvittelet kulkevasi polkua pitkin pinnan yläpuolella, polun sulkema alue on aina vasemmalla.

Suljettu pinta on jonkin kolmiulotteisen kappaleen reuna ja suunnistetaan ulospäin kappaleesta.

Esimerkkejä

Ympyrä- ja ellipsikäyrän parametrisaatio.

-säteisen origokeskisen ympyrän määrää yhtälö x^2+y^2=d^2. Tämän parametrisaatio kertaalleen vastapäivään kierrettynä saadaan trigonometriasta ja on $r(t)=\left( d\cos(t),d\sin(t)\right), \; t\in[0,2\pi].$

Ellipsin määrittää yhtälö $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$ Ellipsikäyrän parametrisaatio kertaalleen vastapäivään kierrettynä on $r(t)=\left( a\cos(t),b\sin(t)\right), \; t\in[0,2\pi].$

Tason $\green x+2\green y+3\green z=6$ ja koordinaattiakselien rajaaman tetraedrin pinta.

$\begin{tikzpicture}[domain=0:4] \draw[->] (0,0) -- (4,0) node[right] {$y$}; \draw[->] (0,0) -- (0,3) node[above] {$z$}; \draw[->] (0,0) -- (-3.5,-3.5) node[above] {$x$}; \node at (3.5,.3) {$(0,3,0)$}; \node at (0.6,2.3) {$(0,0,2)$}; \node at (-2.4,-3.2) {$(6,0,0)$}; \fill[fill=blue!33] (3,0) -- (0,2) -- (-3,-3); \draw[thick,blue] (3,0) -- (0,2); \draw[thick,blue] (0,2) -- (-3,-3); \draw[thick,blue] (-3,-3) -- (3,0); \draw[blue,dashed] (-3,-3) -- (0,0); \draw[blue,dashed] (3,0) -- (0,0); \draw[blue,dashed] (0,2) -- (0,0); \end{tikzpicture}$

Tetraedrin pinta voidaan jakaa neljään osaan, joista kolme on koordinaattiakselien muodostamilla tasoilla ja neljäs tasolla x+2y+3z=6.

xy- tasolla oleva pinnan osa on kolmio $\{(x,y,0):0<y<3,\;0<x<6-2y\}.$ Pinnan differentiaali on yksinkertaisesti $\text dS=\dx\,\dy.$ Lisäksi pinnan normaalivektori on $\left(0,0,\pm1\right)$ ja koska kyseessä on kappaleen reuna eli suljettu pinta valitaan suunnistus ulospäin, eli $\bold{\hat n}=\left(0,0,-1\right).$

yz- tasolla oleva osa on 0<y<3, $0<z<2-\frac23y$ ja normaalivektrori $\bold{\hat n}=\left(-1,0,0\right).$

xz- tasolla oleva osa on 0<z<2, 0<x<6-3z ja normaalivektori $\bold{\hat n}=\left(0,-1,0\right).$

Viimeisen osan parametrisaatio saadaan ratkaisemalla tason yhtälöstä ja ajattelemalla pintaa funktion f(x,y)=z kuvaajana -tasossa olevassa kolmiossa. Parametrisaatioksi saadaan $\ve r(x,y)=\left( x,y,\tfrac13(6-2y-x)\right),\text{ kun }\;0<y<3\text{ ja }\;0<x<6-2y.$ Differentiaalin muunnoskaava ja normaalivektori saadaan ristitulon avulla: $\begin{align*} \ve r_x\times\ve r_y&= \begin{vmatrix} \i &\j &\k \\ 1 &\ 0 &\ -\frac13 \\ 0 &\ 1 &\ -\frac23 \end{vmatrix} =\left(\frac13,\frac23,1\right)\\ \text dS=|\ve r_x\times\ve r_y|\text dA&=\sqrt{\left(\frac13\right)^2+\left(\frac23\right)^2+1^2}\;\text dA=\frac{\sqrt{14}}3\text dA\\ \bold{\hat n}&=\frac1{\sqrt{14}}\left(1,2,3\right). \end{align*}$

Vektorifunktion $\ve F(x,y,z)$ integraali tetraedrin pinnan yli on $\begin{align*} \oiint_S\ve F\cdot\bold{\hat n}\;\text dS&=\sum_{i=1}^4\iint_{S_i}\ve F\cdot\bold{\hat n_i}\;\text dS_i\\ &=\int_0^3\int_0^{6-2y}\ve F(x,y,0)\cdot\left(0,0,-1\right)\;\dx\,\dy\\ &+\int_0^3\int_0^{2-\frac23y}\ve F(0,y,z)\cdot\left(-1,0,0\right)\;\text dz\,\dy\\ &+\int_0^2\int_0^{6-3x}\ve F(x,0,z)\cdot\left(0,-1,0\right)\;\text dz\,\dx\\ &+\int_0^3\int_0^{6-2y}\ve F(x,y,\frac13(6-2y-x))\cdot\left(\frac13,\frac23,1\right)\;\dx\,\dy. \end{align*}$ Divergenssilauseen ja aiemmin näytetyn kyseisen tetraedrin rajaaman kappaleen esityksen avulla saadaan paljon yksinkertaisempi lasku, $\begin{align*} \oiint_S\ve F\cdot\bold{\hat n}\;\text dS&=\iiint_E\nabla\cdot\ve F\;\text dV\\ &=\int_0^6\int_0^{\frac12(6-x)}\int_0^{\frac13(6-2y-x)}\nabla\cdot\ve F\;\text dz\,\dy\,\dx. \end{align*}$

Napakoordinaatisto Funktion $\red f(\green x,\green y)=4-\green x^2-\green y^2$ määräämä pinta $xy\text-$ tason yläpuolella suunnistettuna ylöspäin.

Tämän tyylisen pinnan parametrisaatio $\ve p$ on yksinkertaisesti $\ve p(x,y)=\left( x,y,f(x,y)\right),$ kuitenkin symmetriasyistä kannattaa vaihtaa napakoordinaatteihin, jolloin saadaan $\ve p(r,\varphi)=\left( r\cos(\varphi),r\sin(\varphi),4-r^2\right).$ Parametrisaation rajat saadaan, kun huomataan että 4-x^2-y^2>0 jos ja vain jos x^2+y^2=r^2<4. Parametrisaatio on määrätty joukossa $\{(r,\varphi):0<\varphi<2\pi,\;0<r<2\}.$ Lasketaan parametrisaatiolle differentiaalin muunnoskaava ja normaalivektori ristitulon avulla: $\begin{align*} \ve p_r\times \ve p_\varphi&= \begin{vmatrix} \i &\ \j &\ \k \\ \cos(\varphi) &\ \sin(\varphi) &\ -2r \\ -r\sin(\varphi) &\ r\cos(\varphi) &\ 0 \end{vmatrix} =\left(2r^2\cos(\varphi),2r^2\sin(\varphi),r\right)\\ |\ve p_r\times \ve p_\varphi|&=\sqrt{4r^4+r^2}=r\sqrt{4r^2+1}\\ \text dS&=r\sqrt{4r^2+1}\;\text dr\text d\varphi\\ \bold{\hat n}&=\frac1{\sqrt{4r^2+1}}\left(2r\cos(\varphi),2r\sin(\varphi),1\right). \end{align*}$ $z\text-$ koordinaatti on aina positiivinen, joten suunnistus on ylöspäin kuten haluttiin.

# tarkeitatuloksia

Tärkeitä tuloksia

Analyysin peruslause $\int_a^b f'(x)\dx=f(b)-f(a)$ yhdistää integraalin ja derivaatan yhdessä ulottuvuudessa. Seuraavat lauseet ovat vastaavan kaltaisia tuloksia useammassa ulottuvuudessa.

Tulokset antavat matemaattisen pohjan esimerkiksi Maxwellin lakien eri esitysmuodoille.

Gradienttilause $\int_{\blue\gamma}\nabla\red\phi\cdot\text dr=\red\phi(\ve{\red r}(\green b))-\red\phi(\ve{\red r}(\green a)).$

KonservatiivisessaF on jonkin funktion gradientti $F=\nabla\phi.$ vektorikentässä käyräintegraalin arvo riippuu vain polun alku- ja loppupisteistä, erityisesti integraali suljetun käyrän yli on nolla.

Lauseen oletukset:

$\phi$ on sileä, eli jatkuvasti differentioituvaJatkuvasti differentioituvan funktion kaikki osittaisderivaatat ovat olemassa ja jatkuvia käyrän $\gamma$ sisältävässä avoimessa joukossa.
$\gamma$ on paloittain sileä käyrä, jonka parametrisaatio on $r(t),\;t\in[a,b].$

Mistä tietää onko vektorikenttä konservatiivinen? Vektorikenttä on konservatiivinen, jos sen roottori on nolla reiättömässäJoukossa on reikä, jos joukko ympäröi siihen kuulumattoman pisteen. alueessa. Tason vektorikentälle $F=\left( P,Q\right)$ saadaan vastaava ehto, $\osit{x}Q-\osit{y}P=0$ reiättömässä alueessa. Huomaa, kuinka Greenin lause sanoo tämän ehdon pohjalta, että polkuintegraali minkä tahansa suljetun polun yli on nolla. Myös tämä on yhtäpitävää konservatiivisuuden kanssa.

Vaihtoehtoisesti voi myös etsiä potentiaalifunktiota arvailun tai integroinnin avulla, jos potentiaalifunktio löytyy, on kenttä konservatiivinen.

Staattinen sähkökenttä ja gravitaatiokenttä ovat konservatiivisia, magneettikenttä taas ei. Tuulen voimakkuutta kuvaava vektorikenttä ei myöskään ole konservatiivinen, etenkään jos siinä on "pyörteitä".

Greenin lause tasossa $\oint_{\blue\gamma} \ve{\red F}\cdot \text d\ve r=\oint_{\blue\gamma} \red P\text d\green x+\red Q\text d\green y=\iint_{\blue D}\frac{\partial\red Q}{\partial\green x}-\frac{\partial\red P}{\partial\green y}\text dA.$

Greenin lause yhdistää polkuintegraalin integraaliin polun rajaaman joukon yli. Lause on erikoistapaus Stokesin lauseesta ja divergenssilauseesta.

Oletukset:

$\gamma$ on yksinkertainen ja paloittain sileä vastapäivään kierretty polku.
$F(x,y)=\left( P(x,y),Q(x,y)\right)$ on sileä vektorikenttä polun $\gamma$ sisältävässä avoimessa ja reiättömässäJoukossa on reikä, jos joukko ympäröi siihen kuulumattoman pisteen. joukossa.
on polun $\gamma$ rajaama alue.

Divergenssilause $\oiint_{\blue S}\ve{\red F}\cdot\text dS=\iiint_{\blue E}\nabla\cdot\ve{\red F}\;\text dV.$

Divergenssilause yhdistää vektorikentän integraalin kappaleen yli ja integraalin kappaleen reunan yli. Tulos pätee myös $\R^2$ :ssa ja vastaa siellä Greenin lausetta.

Lauseen oletukset:

Funktio $\ve F$ on sileä joukossa ja sen ympäristössä.
Kappaleella on paloittain sileä reuna

Sileän vektorikentän $\ve F(x,y,z)=\left( P(x,y,z), Q(x,y,z), R(x,y,z)\right)$ divergenssi on luku $\text{div}(\ve F)=\nabla\cdot \ve F=\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}.$

Tulos tunnetaan myös nimellä Gaussin laki.

# stokes

Stokesin lause $\oint_{\blue\gamma}\ve{\red F}\cdot\text d\ve r=\iint_{\blue S}\nabla\times\ve{\red F}\cdot\text dS.$

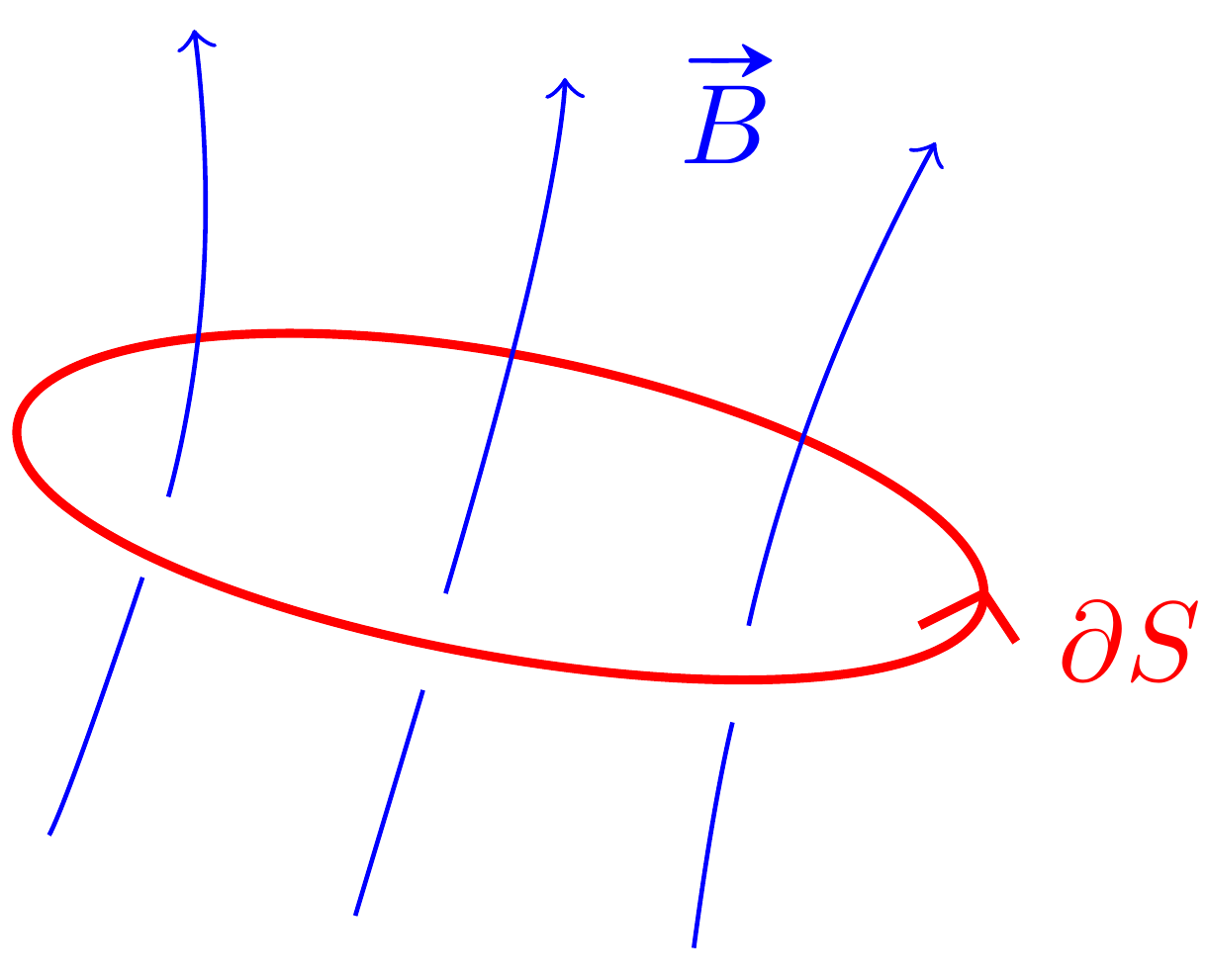
Stokesin lause yhdistää vektorikentän pintaintegraalin käyräintegraaliin pinnan reunan yli. Käyrä ja pinta suunnistetaan keskenään siten, että kuljettaessa käyrää pitkin pinnan "yläpuolella" pinta jää vasemmalle.

$\begin{tikzpicture}[domain=0:4] \draw[thick,->] (0,0) -- (3.5,0) node[right] {$x$}; \draw[thick,->] (0,0) -- (0,2.8) node[above] {$z$}; \draw[thick,->] (0,0) -- (-1,-1) node[above] {$y$}; \draw[thick] (0.5,1) to [bend left=65] (3.5,1); \draw[dashed,thick,->] (3.5,1) to [bend left=15] (2.5,1.3); \draw[dashed,thick,->] (2.5,1.3) to [bend right=10] (1.7,1.4); \draw[dashed,thick,->] (1.7,1.4) to [bend right=15] (0.5,1); \draw[thick,->] (2.5,0.7) to [bend right=15] (3.5,1); \draw[thick,->] (1.5,.5) to [bend right=10] (2.5,.7); \draw[thick,->] (.5,1) to [bend right=15] (1.5,.5); \node at (.5,.7) {$\gamma$}; \node at (2.4,2) {$S$}; \draw[thick,->] (2,1.8) -- (2,2.3); \end{tikzpicture}$

Suunnistuksen voi ajatella myös oikean käden säännöllä: jos oikean kätesi peukalo osoittaa samaan suuntaan kuin pinnan normaalivektori, näyttävät muut sormet pinnan reunan kiertosuunnan.

Lauseen oletukset:

on yksinkertainen ja (paloittain) sileä suunnistettu pinta.
$\partial S$ on (paloittain) sileä suljettu ja yksinkertainen käyrä.
$\ve F$ on sileä vektorikenttä pinnan ympäristössä.

Merkintä $\nabla\times\ve F$ tarkoittaa vektorikentän $\ve F=\left( P,Q,R\right)$ roottoria. Roottori on vektoriarvoinen funktio, joka lasketaan ristitulon avulla: $\begin{aligned} \text{curl}(\ve F)&=\nabla\times\ve F=\begin{vmatrix} \i & \j & \k\\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}\\ &=\left(\osit[R]{y}-\osit[Q]{z}\right)\i+\left(\osit[P]{z}-\osit[R]{x}\right)\j+\left(\osit[Q]{x}-\osit[P]{y}\right)\k. \end{aligned}$

Esimerkkilaskuja

Lasketaan vektorikentän $\ve{\red F}(\green x,\green y,\green z)=\left( 2\green {xy},\green x^2+2\green {yz},\green y^2\right)$ tekemä työ pitkin käyrää $\ve{\red r}(\green t)=\left( \green t,\green t^2,\green t^3\right), \;\green t\in\blue{[0,2]}.$

Koska $\text{curl}(F)= \begin{vmatrix} i &\ j &\ k \\ \osit{x} &\ \osit{y} &\ \osit{z} \\ \red{2xy} &\ x^2+2yz &\ \blue{y^2} \end{vmatrix} =\ve 0,$ kyseessä konservatiivinen vektorikenttä. Etsitään potentiaalifunktio $\phi(x,y,z),$ jolle $\nabla\phi=\left(\red{\osit{x}\phi},\osit{y}\phi,\blue{\osit{z}\phi}\right) =\left(\red{2xy},x^2+2yz,\blue{y^2}\right)=F.$ Koska $\red{\osit{x}\phi}=\red{2xy},$ saadaan integroimalla $\phi=\int\red{\osit{x}\phi}\;\text dx=\int \red{2xy}\;\dx=x^2y+C(y,z).$ Huomaa, että integrointivakio on vakio vain muuttujan suhteen, eli voi olla muuttujien ja funktio. Jatketaan muuttujan osittaisderivaatalla. Koska $\blue{\osit{z}\phi}=\osit{z}(x^2y+C(y,z))=\osit{z}C(y,z)=\blue{y^2},$ saadaan $\phi=x^2y+\int \blue{y^2}\;\text dz=x^2y+y^2z+C(y).$ Derivoimalla huomataan, että on etsitty potentiaalifunktio, joten voimme unohtaa integrointivakion C(y) . Yhdistämällä potentiaalifunktio käyrän parametrisaatioon saadaan $\begin{align*} \phi(x,y,z)&=x^2y+zy^2\\ \phi(r(t))&=t^2t^2+t^3(t^2)^2\\ &=t^4+t^7. \end{align*}$ Nyt saamme polkuintegraalin arvoksi gradienttilauseen avulla $\begin{align*} \int_{\gamma}F\cdot\text d\ve r&=\phi(r(2))-\phi(r(0))\\ &=2^4+2^7-0\\ &=144. \end{align*}$

Greenin lauseen sovellus: ellipsin pinta-ala.

Lasketaan ellipsin pinta-ala ellipsikäyrän parametrisaation $r(t)=\left( a\cos(t),b\sin(t)\right)$ ja Greenin lauseen avulla. Valitsemalla vektorikentäksi $F(x,y)=\left( P,Q\right)=\left(\frac{-y}2,\frac x2\right)$ saamme $\begin{align*} \iint_D1\;\text dA &= \iint_D \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\text dA\\ &=\oint_{\gamma}\ve F(r(t))\cdot r'(t)\;\text dt\\ &=\int_0^{2\pi}\frac12\left(-b\sin(t),a\cos(t)\right)\cdot\left( -a\sin(t),b\cos(t)\right)\;\text dt\\ &=\frac12\int_0^{2\pi}ab\;\text dt\\ &=\pi ab. \end{align*}$

Divergenssilauseen sovellus: pallon pinta-ala

Lasketaan divergenssilauseen avulla pallon pinta-ala, kun tiedetään, että pallon tilavuus on $\frac43\pi.$ Pinnan pinta-ala saadaan integraalista $\iint_{\partial E}1\;\text dS,$ joten tarvitsemme vektorikentän, jolle $F\cdot\bold{\hat n}=1.$ Tässä $\bold{\hat n}$ on pallopinnan ulospäin osoittava normaalivektori. Valitsemalla vektorikentäksi pinnan normaalivektorin, $F=\bold {\hat n}$ saadaan $F\cdot \bold {\hat n}=|\bold {\hat n}|^2=1.$ Yksikköpallon normaalivektori on $F=\bold {\hat n}=\left( x,y,z\right).$ Divergenssilauseella saadaan $\iint_{\partial E}1\;\text dS=\iiint_E\text{div}(F)\;\text dV=\iiint_E3\;\text dV.$ Yksikköpallon pinta-ala on siis kolme kertaa pallon tilavuus, eli $4\pi.$

-säteiselle pallolle normaalivektori on $\left( \frac xd,\frac yd,\frac zd\right)$ ja kuoren pinta-alaksi saadaan $\iint_{\partial E}1\;\text dS=\iiint_E\text{div}(F)\;\text dV=\iiint_E\frac3d\;\text dV.$ Koska -säteisen pallon tilavuus on $\frac43d^3\pi,$ saadaan sen pinta-alaksi $4\pi d^2.$

Stokesin lauseen sovellus: Maxwellin III yhtälö Faradayn induktiolaista.

Faradayn induktiolain mukaan muuttuva magneettikenttä indusoi sähkökentän. Tarkemmin ilmaistuna $\red{\oint_{\partial S}} \ve E\cdot\text d \ve r = - \frac{\text d}{\dt} \iint_S\blue{\ve B}\cdot \text d\ve s,$ missä $\blue{\ve B}$ on magneettikenttä ja $\ve E$ sähkökenttä.

Integroinnin ja derivoinnin järjestys voidaan vaihtaaLeibnizin integrointisääntö., eli $\frac{\text d}{\dt} \iint_S\blue{\ve B}\cdot \text d\ve s =\iint_S \frac{\partial \blue{\ve B}}{\partial t}\cdot \text d\ve s.$ Stokesin lauseesta saadaan $\red{\oint_{\partial S}} \ve E\cdot \text d \ve r = \iint_S\nabla\times\ve E\cdot \text d\ve s.$ Yhdistämällä nämä saadaan, että $\iint_S\nabla\times\ve E\cdot \text d\ve s = - \iint_S \frac{\partial \blue{\ve B}}{\partial t}\cdot \text d\ve s$ eli $\begin{aligned} &\iint_S\nabla\times\ve E\cdot \text d\ve s + \iint_S \frac{\partial \blue{\ve B}}{\partial t}\cdot \text d\ve s \\ &=\iint_S\left(\nabla\times\ve E+\frac{\partial \blue{\ve B}}{\partial t}\right)\cdot \text d\ve s = 0. \end{aligned}$ Tämä pätee kaikilla pinnoilla joten $\nabla \times \ve E = -\frac{\partial \blue{\ve B}}{\partial t}.$ Tämä tunnetaan Maxwellin kolmantena yhtälönä.

Lasketaan $\int_{\blue\gamma} \ve{\red F}\cdot\text d\ve r=\oint_{\blue\gamma}(\green x^2-\green y)\;\dx\;+(3\green x+e^{\green y}) \;\dy+(2\green x+\green y)\;\text dz,$ kun $\blue\gamma$ on yksikköpallon ja tason $\green x+\green y+\green z=1$ leikkausjoukko.

Lasketaan polkuintegraalin arvo Stokesin lauseella polun rajaaman ympyrän muotoisen pinnan yli.

Vektorikentän roottori on $\begin{align*} \begin{vmatrix} \i & \j & \k\\ \osit{x} & \osit{y} & \osit{z}\\ x^2-y & 3x+e^y & 2x+y \end{vmatrix} =\left( 1,-2,2\right). \end{align*}$ Pinnan normaalivektori saadaan tason yhtälön kertoimistatason ax+by+cz=d normaalivektori on (a,b,c). : $\bold{\hat n}=\frac1{\sqrt3}\left( 1,1,1\right).$ Tason pienin etäisyys origosta saadaan laskemalla piste, jossa origon kautta kulkeva normaalivektorin suuntainen jana leikkaa tasoa. Tason etäisyydeksi origosta saadaan $\frac{\sqrt 3}3.$ Pythagoraan lauseella saadaan polun rajaaman ympyrän säde , koska $\left(\frac{\sqrt 3}3\right)^2+d^2=1,$ eli $d=\frac{\sqrt{6}}3.$ Pintaintegraali ympyrän yli on sen pinta-ala, eli $\iint_S 1\;\text dS=\pi \left(\frac{\sqrt{6}}3\right)^2=\frac23\pi.$ Näillä tiedoilla saadaan: $\begin{align*} \int_\gamma \ve F\cdot\text d\ve r&=\iint_S\nabla\times\ve F\cdot\;\text dS\\ &=\iint_S\frac1{\sqrt 3}\left( 1,-2,2\right)\cdot\left( 1,1,1\right)\;\text dS\\ &=\iint_S \frac1{\sqrt 3}\;\text dS=\frac2{3\sqrt 3}\pi. \end{align*}$ Koska polun kiertosuuntaa ei määritelty, tulos voisi yhtä hyvin olla negatiivinen.