Integraalifunktio

# integraalifunktio

Integraalifunktion merkitys

Funktion integraalifunktio vastaa kysymykseen, "mitä on derivoitu, että on saatu ?"

Toisin sanoen, $F'(x) = \frac{d}{dx}F(x) = f(x).$ Funktio on vain eräs :n integraalifunktio. Kaikki integraalifunktiot saadaan lisäämällä reaalinen vakio . Tällöin kaikki funktion integraalifunktiot ovat muotoa F(x)+C.

Mutta miksi?

Kaikki funktion integraalifunktiot ovat muotoa F(x) + C , sillä derivoimissääntöjen nojalla vakion derivaatta on nolla: $\begin{aligned} \frac{d}{dx}\left(F(x) + C\right) &= \frac{d}{dx}F(x) \\ &= f(x) \end{aligned}$

Siispä funktiot F(x) + C toteuttavat integraalifunktion ehdon.

Integraalifunktiota käytetään erityisesti määrätyn integraalin arvon laskemiseen analyysin peruslauseen kanssa.

Integraalin merkinnöistä

Klikkaa merkintää tai käsitettä , josta haluat lisätietoja.

Integraalifunktio, integraali, määräämätön integraali, antiderivaatta: $\int f, \quad \int f(x) \, \text{d}x ,\quad \int f(t) \, \text{d}t$

Kaikki merkinnät tarkoittavat funktion integraalifunktiota, eli funktiota, jonka derivaatta on . Integraalifunktio saadaan yleensä integroimalla funktiota integrointisääntöjä käyttäen.

Merkinnässä $\dx$ kirjain kuvastaa sitä muuttujaa, jonka suhteen integroidaan. Esimerkiksi määritettäessä integraalia $\int f(t)\, \dt$ integroidaan muuttujan suhteen.

Katso esimerkkejä integroinnista.

Määrätty integraali: $\int_a^b{f}, \quad\mintegral{f(x)}{x}{a}{b}, \quad \mintegral{f(t)}{t}{a}{b}$

Merkinnöillä ilmaistaan funktion määrättyä integraalia yli välin [a,b] . Määrätty integraali on -akselin ja funktion kuvaajan väliin jäävä pinta-ala, mikäli funktio on välillä positiivinen. Katso määrätty integraali.

Jos funktion integraalifunktio tunnetaan, määrätty integraali voidaan laskea analyysin peruslausetta käyttäen. Myös määrätyn integraalin laskusäännöistä ja funktioiden integraalisäännöistä voi olla apua.

Epäoleellinen integraali: $\mintegral{f(x)}{x}{-\infty}{\infty}, \quad \mintegral{f(x)}{x}{-\infty}{b} ,\quad \mintegral{f(x)}{x}{a}{\infty}$

Merkinnöillä tarkoitetaan funktion epäoleellista integraalia. Katso epäoleellinen integraali.

Epäoleellinen integraali (improper integral) määritellään raja-arvon avulla:

$\dint_a^{\infty} f(x)\,\dx=\lim_{c\to\infty}\dint_a^c f(x)\,\dx$ ja vastaavasti $\dint_{-\infty}^a f(x)\,\dx=\lim_{c\to-\infty}\dint_c^a f(x)\,\dx.$ Epäoleellisten integraalien laskemiseen voidaan käyttää määrätyn integraalin ja raja-arvon laskusääntöjä.

# laskusäännöt

Integraalin laskusäännöt

Seuraavat säännöt liittyvät määräämättömään integraaliin:

Sääntö	Selitys tai nimi
$\dint 0\,\dx=C$	Nollan integraali on vakio.
$\dint a\,\dx=a\cdot x+C$	Vakion integraali.
$\dint a\cdot f(x)\,\dx=a\cdot\dint f(x)\,\dx$	Vakio voidaan ottaa ulos integroitaessa.
$\dint \left(f(x)+g(x)\right)\,\dx=\dint f(x)\,\dx+\dint g(x)\,\dx$	Summan integraali on integraalien summa.
$\dint \red{f'(x)}\cdot \left(f(x)\right)^a\,\dx=\frac{(f(x))^{a+1}}{a+1}+C\quad, a\neq-1$	Funktion potenssin integraali. Huomaa $\red{f'}$ .
$\dint \frac{f'(x)}{f(x)}\,\dx=\ln\|f(x)\|+C$	Funktion integraali.
$\dint f'(x)\cdot g(x)\,\dx=f(x)\cdot g(x)-\dint f(x)\cdot g'(x)\,\dx+C$	Osittaisintegrointi (integration by parts).
$\dint f'(x)\cdot g'(f(x))\,\dx=g(f(x))+C$	Yhdistetyn funktion integrointi.

Mutta miksi?

Osio työn alla.

Integrointikaavat saadaan yleisesti derivointikaavojen avulla.

Osittaisintegrointi: $\int f'(x)\cdot g(x)\,\dx=f(x)\cdot g(x)-\int f(x)\cdot g'(x)\,\dx+C$

Olkoon $f,g\colon [a,b]\to \R$ jatkuvasti derivoituvia, eli derivoituvia funktioita joiden derivaattafunktiot ovat myös jatkuvia. Merkitään $h(x)=f(x)\cdot g(x)$ . Tällöin h'(x)=f'(x) g(x)+f(x)g'(x) on myös jatkuva. Toisin sanoen $\frac{d}{dx}h=h',$ joten $\begin{align*} h(x)&=\integral{h'(x)}{x}\\ \iff f(x)g(x)&=\int\big(f'(x)g(x)+f(x)g'(x)\big)\,\dx &&\Big|\, \text{integraalien summa}\\ &=\int f'(x)g(x)\,\dx+\int f(x)g'(x)\,\dx. \end{align*}$ Tästä saadaan osittaisintegrointikaava, ratkaisemalla toinen edellisen rivin integraaleista $\int f'(x)g(x)\,\dx=f(x)g(x)-\int f(x)g'(x)\,\dx\,(+\, C).$

Yhdistetyn funktion integrointi: $\int f'(x)\cdot g'(f(x))\,\dx=g(f(x))+C$

Ketjusäännön mukaan $\frac{d}{dx}g(f(x)) = f'(x)g'(f(x))$ joten integraalin määritelmän nojalla $\dint f'(x) g'(f(x))\, \dx = g(f(x)) + C$

Funktion potenssin integraali: $\int {f'(x)}\cdot \left(f(x)\right)^a\,\dx=\frac{(f(x))^{a+1}}{a+1}+C\quad, a\neq-1$

Sääntö seuraa edellä osoitetusta yhdistetyn funktion integrointikaavasta valitsemalla kaavaan f(x) = x^a ja g(x) = f(x) .

Funktion integraali: $\int \frac{f'(x)}{f(x)}\,\dx=\ln|f(x)|+C$

Sääntö seuraa edellä osoitetusta yhdistetyn funktion integrointikaavasta valitsemalla kaavaan $f(x) = \frac{1}{x}$ ja g(x) = f(x) .

# funktioiden-integraaleja

Funktioiden integraaleja

Yleisimmille funktioille on voimassa seuraavat integrointisäännöt:

Sääntö	Funktio
$\dint 0\,\dx=C$	Nollan integraali on vakio.
$\dint a=a\cdot x+C$	Vakion integraali.
$\displaystyle\int x^a\,\dx=\frac{1}{a+1}\cdot x^{a+1}+C,\quad a\neq -1$	Potenssifunktio.
$\displaystyle\int x^{-1}\,\dx=\int\frac{1}{x}\,\dx=\ln\|x\|+C$	Potenssifunktio potenssilla -1.
$\displaystyle\int e^x\,\dx = e^x+C$	Luonnollinen eksponenttifunktio.
$\displaystyle\int f'(x)e^{f(x)}\,\dx = e^{f(x)}+C$	Yhdistetty luonnollinen eksponenttifunktio.
$\displaystyle\int a^x\,\dx=\frac{a^x}{\ln a}+C,\quad a>0,\, a\neq 1$	Eksponenttifunktio.
$\displaystyle\int \ln x\,\dx = x\cdot\ln x-x+C, \quad x > 0$	Luonnollinen logaritmifunktio.
$\displaystyle\int \log_{a}x\,\dx=\log_ae\cdot(x\cdot\ln x-x)+C, \quad x > 0$	-kantainen logaritmifunktio.
$\displaystyle\int \sin x\,\dx=-\cos x+C$	Sinifunktio.
$\displaystyle\int \cos x\,\dx=\sin x+C$	Kosinifunktio.
$\displaystyle\int\tan x\,\dx=-\ln\|\cos x \,\|+C$	Tangenttifunktio.

Mutta miksi?

Osio työn alla.

Integrointikaavat saadaan yleisesti derivointikaavojen avulla. Esimerkiksi $D(\sin x)=\cos x,$ joten $\int\cos x=\sin x +C.$

Joihinkin integrointikaavoihin kannattaa käyttää integaalin laskusääntöjä.

Luonnollinen logaritmi

Ideana on käyttää osittaisintegrointikaavaa. Tässä käytetään yleistä "kikkaa" matematiikassa, eli hyödynnetään sitä, että luvulla kertominen "ei tee mitään". Koska $\int \ln x\,\dx=\int 1\cdot \ln x\,\dx,$ niin valitaan osittaisintegrointikaavassa $f'(x)=1,\quad g(x)=\ln x,$ jolloin $f(x)=x,\quad g'(x)=\frac{1}{x}.$ Tällöin $\begin{align*} \int \ln x\,\dx&=\int 1\cdot \ln x\,\dx &&\Big|\,\text{osittaisintegroidaan}\\ &=x\cdot \ln x-\integral{x\cdot \frac{1}{x}}{x}\\ &=x\cdot \ln x-\integral{1}{x}\\ &=x\cdot \ln x-x+C. \end{align*}$

Trigonometrisia funktioita integroitaessa on hyvä pitää mielessä trigonometriset identiteetit, joilla trigonometrisia funktioita voi muokata.

Vähemmän käytettyjä integrointisääntöjä:

Muista näitä käyttäessäsi yhdistetyn funktion integrointisääntö!

Sääntö	Selitys tai nimi
$\integral{\sin^2 x}{x} = \frac{1}{2}\left(x-\frac{\sin{2x}}{2}\right) + C$	Sinin neliö.
$\integral{\cos^2 x}{x} = \frac{1}{2}\left(x+\frac{\sin{2x}}{2}\right) + C$	Kosinin neliö.
$\integral{\sin x \cos x}{x} = \frac{1}{2}\sin^2x + C$	Sinin ja kosinin tulo.
$\dint\frac{1}{1+x^2}\,\dx=\arctan x +C$	Arkustangentti integraalifunktiona.
$\dint\frac{1}{\sqrt{1-x^2}}=\arcsin x +C$	Arkussini integraalifunktiona.

Lisää vielä vähemmän käytettyjä integrointikaavoja löytyy wikipediasta.

Esimerkkejä määräämättömistä integraaleista ja integroinnista

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Potenssifunktion integrointi: Määritä $\dint f(t) \, \dt$ , kun $f(t) = 3t^5 - \frac{3}{2t}$ .

Lyhyesti:

Integrointisääntöjen mukaan $\begin{aligned} \int f(t) &= \int 3t^{5} - \frac{3}{{2}t} \, \dt\\ &= 3\cdot \frac{1}{{6}}t^{6}-{\frac{3}{2}}\cdot\ln|t| {+ \ C}\\ &= \frac{1}{2}t^6- \frac{3}{2}\ln|t| +C \end{aligned}$

Pitkästi:

Integraalin laskemiseksi tullaan tarvitsemaan potenssifunktion integroimissääntöjä.

Integrointisääntöjen mukaan: $\begin{aligned} \int f(t) &= \int 3t^{5} - \frac{3}{2t} \, \dt &&\Big| \ \text{summan integraali}\\ &= \int \green3t^{5} \, \dt + \int \green- \frac{\green3}{\green2t} \, \dt &&\Big| \ \text{\green{vakiot} ulos}\\ &= 3\int t^{\red5} \, \dt \,-{\frac{3}{2}}\cdot \int\frac{1}{t}\, \dt &&\Big| \ \text{integrointisäännöt}\\ &= 3\cdot\frac{1}{\red{5}+1}t^{\red5+1}- \frac{3}{2}\cdot\ln|t| \blue{+ \ C} &&\Big| \text{ \blue{integroimisvakio}}\\ &= \frac{3}{6}t^6- \frac{3}{2}\ln|t| +C \\ &= \frac{1}{2}t^6- \frac{3}{2}\ln|t| +C \\ \end{aligned}$

Integraalifunktion määrittäminen: Määritä se funktion g(x) =3^x integraalifunktio jolle G(2) = 0.

Integroidaan funktio : $\begin{aligned} \integral{g(x)}{x} &= \integral{3^x}{x}\\ &= \frac{3^x}{\ln 3} + C, \ \text{ jollakin } C \in \R. \end{aligned}$ Siispä $G(x) = \frac{3^x}{\ln 3} + C$ . Etsitään , jolla toteutuu G(2)=0 .

Jotta ehto toteutuu, on siis oltava $\begin{aligned} G(\red2) = 0 \\ \frac{3^{\red2}}{\ln 3} + C &= 0 \\ C &= -\frac{3^2}{\ln 3} \end{aligned}$

Haluttu integraalifunktio on siis $\begin{aligned} G(x) &= \frac{3^x}{\ln 3} -\frac{3^2}{\ln 3} &&\Big| \small\text{ voidaan sieventää halutessa} \\ &= \frac{1}{\ln 3}(3^x -9) \end{aligned}$

Yhdistetty funktio: Määritä $\integral{\cos(3x)}{x}.$

Lyhyesti: $\begin{align*} \integral{\cos(3x)}{x}&=\frac{1}{3}\integral{3\cos(3x)}{x}\\ &=\frac{1}{3}\sin(3x)+C \end{align*}$

Pitkästi:

Haluamme käyttää yhdistetyn funktion integrointikaavaa. Huomataan, että tällä hetkellä integraalissa ei ole sisäfunktion derivaattaa. Tässä tapauksessa voimme sen pakottaa näkymään, sillä $\cos(3x)=1\cdot\cos(3x)=\frac{1}{3}\cdot3\cdot\cos(3x).$ Tällä huomiolla integraali voidaan laskea $\begin{aligned} \integral{\cos(3x)}{x}&=\integral{\blue{\frac{1}{3}}\cdot3\cdot\cos(3x)}{x} &&\Big|\text{\blue{vakio ulos}}\\ &=\frac{1}{3}\integral{\red{3}\cdot\cos(3x)}{x} &&\Big|\textstyle\int\red{f'(x)}g'(f(x))\,\dx=g(f(x))+C\\ &=\frac{1}{3}\sin(3x)+C, \end{aligned}$ jollakin $C\in\R.$

Trigonometrisen funktion integraali: Osoita, että $\int \cos^2 x \, \dx = \frac{1}{2}\left(x+\frac{\sin 2x}{2}\right)+C$ .

Trigonometristen identiteettien listasta löydetään $\cos^2 x = \frac{1}{2}(1+\cos 2x)$ jolloin integraali saadaan laskettua tavallisella kosinin integrointikaavalla ja yhdistetyn funktion integrointisäännöllä:

$\begin{aligned} \dint \cos^2 x \, \dx &= \integral{\frac{1}{2}(1+\cos 2x)}{x}\\ &=\frac{1}{2}\left(\integral{1}{x}+\integral{\cos 2x}{x}\right)\\ &=\frac{1}{2}\left(\integral{1}{x}+\frac{1}{2}\integral{2\cos 2x}{x}\right)\\ &= \frac{1}{2}\left(x+\frac{\sin 2x}{2}\right)+C \end{aligned}$

Yhdistetyn eksponenttifunktion integrointi: Määritä $\integral{e^{-ax}}{x},$ kun a > 0 .

Integraali voidaan määrittää yhdistetyn funktion integroimiskaavalla. Yhdistetyn funktion integroimiskaavasta seuraa kuitenkin yhdistetyn luonnollisen eksponenttifunktion integroimiskaava, jota tässä ratkaisussa käytetään.

Lyhyesti:

Jotta voidaan käyttää integrointikaavaa

$\integral{f'(x)e^{f(x)}}{x}= e^{f(x)},$ on integraalin sisälle saatava sisäfunktion -ax derivaatta eli :

$\begin{aligned} \integral{e^{-ax}}{x} &= -\frac{1}{a}\integral{-ae^{-ax}}{x} &&\Big| -\frac{1}{a}\cdot(-a) = 1 \\ &= -\frac{1}{a}e^{-ax} + C \end{aligned}$ jollakin $C\in\R$ .

Pitkästi:

Integraali $\integral{e^{-ax}}{x}$ on muokattava muotoon $\integral{f'(x)e^{f(x)}}{x}$ , jotta voidaan käyttää integrointikaavaa

$\integral{f'(x)e^{f(x)}}{x}= e^{f(x)}.$

Tunnistetaan kaavassa käytettävät osat integraalista:

Integraali	Kaava	Havainto
$\integral{e^{\red{-ax}}}{x}$	$\integral{f'(x)e^{\red{f(x)}}}{x}= e^{f(x)}$	$\red{f(x)} = \red{-ax}$

Koska f(x) = -ax , niin oltava f'(x) = -a .

Jotta saadaan integraalin sisälle, on "kerrottava ykkösellä":

$\begin{aligned} \integral{e^{-ax}}{x} &= \integral{\red 1\cdot e^{-ax}}{x} &&\Big| \ \red 1 = -\frac{1}{a}\cdot(-a) \\ &= \integral{\green{(-\frac{1}{a})}\cdot(-a)e^{-ax}}{x} &&\Big| \text{ \green{vakio} ulos} \\ &= -\frac{1}{a}\integral{-ae^{-ax}}{x} &&\Big| \textstyle{ \int f'(x)e^{f(x)} \, \dx = e^{f(x)} }\\ &= -\frac{1}{a}e^{-ax}\ \blue{+ \ C} &&\Big| \text{ \blue{integroimisvakio}} \end{aligned}$ jollakin $C\in \R$ .

Yhdistetty funktio, rationaalifunktion integrointi: Määritä $\integral{\frac{x}{3x^2+1}}{x}$ .

Lyhyesti: $\begin{aligned} \integral{\frac{x}{3x^2+1}}{x} &= \frac{1}{6}\integral{\frac{\red{6x}}{3x^2+1}}{x} &&\Big| \ \textstyle\int \frac{\red{f'(x)}}{f(x)}\, \dx = \ln |f(x)| \\ &= \frac{1}{6}\ln|3x^2+1| + C &&\Big| \ 3x^2+1 > 0 \text{ aina } \\ &= \frac{1}{6}\ln(3x^2+1) + C \end{aligned}$ jollakin $C\in \R$ .

Pitkästi:

Integraali on muokattava muotoon $\integral{\frac{f'(x)}{f(x)}}{x}$ , jotta voidaan käyttää integrointikaavaa

$\int \frac{f'(x)}{f(x)}\, \dx = \ln |f(x)|.$

Integroitavan funktion nimittäjä on siis f(x) = 3x^2 +1 , joten f'(x) = 6x .

Integraali saadaan muokattua haluttuun muotoon "kertomalla ykkösellä": $\begin{aligned} \integral{\frac{x}{3x^2+1}}{x} &= \integral{\frac{\red{\frac{1}{6} \cdot 6 \cdot x}}{3x^2+1}}{x} &&\Big| \ \red{\frac{1}{6} \cdot 6 \cdot x} = x \\ &= \integral{\green{\frac{1}{6}}\cdot \frac{6x}{3x^2+1}}{x} &&\Big| \text{ \green{vakiot ulos}}\\ &= \frac{1}{6}\integral{\frac{\red{6x}}{3x^2+1}}{x} &&\Big| \ \textstyle\int \frac{\red{f'(x)}}{f(x)}\, \dx = \ln |f(x)|\\ &= \frac{1}{6}\ln|3x^2+1| + C &&\Big| \ 3x^2+1 > 0 \text{ aina }\\ &= \frac{1}{6}\ln(3x^2+1) + C \end{aligned}$ jollakin $C\in \R$ .

Osittaisintegrointi: Määritä $\dint x^2\sin x \, \dx.$

Määritetään integraali käyttämällä osittaisintegrointikaavaa

$\dint f'(x)\cdot g(x)\,\dx=f(x)\cdot g(x)-\dint f(x)\cdot g'(x)\,\dx$

Tehdään seuraavat valinnat kaavaan:

Integraali	Kaavassa	Havainto	Seuraus
$\dint \red{x^2}\blue{\sin x} \, \dx$	$\dint \blue{f'(x)}\cdot \red {g(x)}\,\dx$	$\blue{f'(x)} = \sin x$ $\red{g(x)} = x^2$	$f(x) = -\cos x$

Sijoitetaan valinnat kaavaan: $\dint f'(x)\cdot g(x)\,\dx=f(x)\cdot g(x)-\dint f(x)\cdot g'(x)\,\dx$ $\begin{aligned} \dint {x^2}{\sin x} \, \dx &= -x^2 \cos x - \dint -2x \cos x \, \dx\\ &= -x^2 \cos x +2\dint x \cos x \, \dx \end{aligned}$

Havaitaan, että jäljelle jäänyt integraali $\dint x \cos x \, \dx$ vaatii edelleen osittaisintegrointia. Tehdään seuraavat valinnat osittaisintegroinnin kaavaan:

Integraali	Kaavassa	Havainto	Seuraus
$\dint \red{x}\, \blue{\cos x} \, \dx$	$\dint\blue{f'(x)}\cdot \red {g(x)}\,\dx$	$\blue{f'(x)} = \cos x$ $\red{g(x)} = x$	$f(x) = \sin x$

Sijoitetaan valinnat kaavaan: $\begin{aligned} \dint x \cos x \, \dx &= x\sin x - \dint 1\cdot \sin x\, \dx\\ &= x\sin x + \cos x + C \end{aligned}$

Sijoitetaan saatu integraali alkuperäiseen integraalin lausekkeeseen: $\begin{aligned} \dint {x^2}{\sin x} \, \dx &= -x^2 \cos x +2\dint x \cos x \, \dx \\ &= -x^2 \cos x +2(x\sin x + \cos x + C) \\ &= -x^2\cos x + 2x\sin x + 2\cos x + 2C \\ &= 2x\sin x + (2-x^2)\cos x + D &&\Big| D = 2C,\text{ vakio } \end{aligned}$

# määrätty-integraali

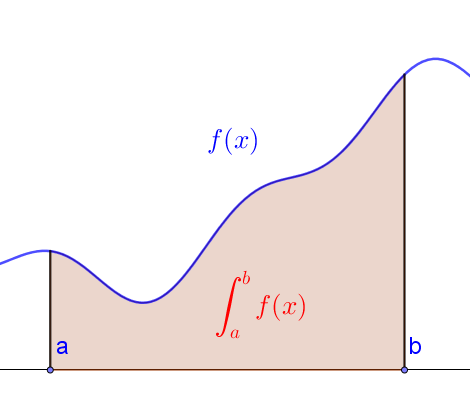
Määrätty integraali

Funktion määrätty integraali $\int_a^b f(x) \, \dx$ on funktion kuvaajan ja -akselin väliin jäävä pinta-ala välillä [a,b] .

Jos on -akselin alapuolella, on määrätty integraali $\int_a^b f(x) \, \dx$ negatiivinen.

Integraalin graafinen havainnollistus

Alla olevissa kuvassa esitellään, mitä määrätty integraali tarkoittaa graafisesti. Ensimmäisessä kuvassa kuvaaja on -akselin yläpuolella ja toisessa kuvaaja on -akselin alapuolella.

$\mintegral{f(x)}{x}{a}{b} > 0$	$\mintegral{f(x)}{x}{a}{b} < 0$
{wid	th=350}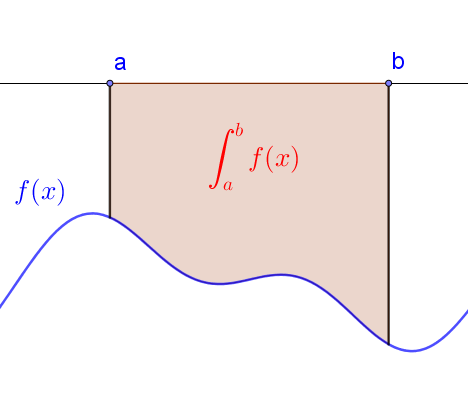

Määrätyn integraalin $\int_a^b f(x) \, \dx$ pinta-alan yksikkö on -akselin ja -akselin yksiköiden tulo eli

$\left[\int_a^b f(x) \, \dx\right] = [f] \cdot [x].$

Mutta miksi?

Summatessa saman mitattavan asian suureita yhteen yksikkö ei muutu. Esimerkiksi massoiltaan $m_1 = 5\text{ kg}$ ja $m_2 = 3\text{ kg}$ olevien punnusten yhteismassa on $m_1 + m_2 = 5 \text{ kg} + 3 \text{ kg} = 8 \text{ kg}.$

Määrätty integraali $\int_a^b f(x)\, \dx$ käyttäytyy kuten summa: integroiminen välin yli säilyttää yksiköt. Siispä

$\left[\dint f(x) \, \dx \right] = \left[f(x) \, \dx\right]$

Lauseke $f(x) \, \dx$ voidaan tulkita tuloksi. Koska tulon yksikkö on yksiköiden tulo, niin $[f(x) \, \dx] = [f(x)][\dx]$ Integraalista jäänyt $\dx$ voidaan ajatella hyvin pieneksi suureeksi. Suureen koko ei kuitenkaan vaikuta sen yksikköön. Siispä $[f(x)][\dx] = [f(x)][x].$ Yleensä jätetään merkitsemättä (x) funktion nimen jälkeen, sillä funktion yksikkö ei riipu muuttujasta.

# -määrätyn-integraalin-laskusääntöjä

Määrätyn integraalin laskusääntöjä

Alla olevassa taulukossa listataan yleisimpiä määrättyyn integraaliin liittyviä laskusääntöjä. Taulukossa $a,b\in\R$ ja F'(x)=f(x).

Sääntö	Selitys tai nimi
$\dint_a^b f(x)\,\dx=\intsub{a}{b}F(x)=F(b)-F(a)$	Analyysin peruslause, myös APL.
$\dint_a^bf(x)\,\dx=-\dint_b^af(x)\,\dx$	Integroimisvälin päätepisteiden vaihto.
$\dint_a^a f(x)\,\dx=0$	Yhden pisteen yli integrointi.
$\dint_a^bf(x)\,dx=\dint_a^cf(x)\,\dx+\dint_c^bf(x)\,\dx$	Integroimisvälin pilkkominen.
$\dint_a^b f(x)\,\dx\geq\dint_a^b g(x)\,\dx, \$ jos $\gray{f(x)\geq g(x)}$ kaikilla $\gray{x\in [a,b]}$	Järjestyksen säilyminen.
$\dint_a^b f'(x)\cdot g(x)\,\dx=\intsub{a}{b}f(x)\cdot g(x)-\dint_a^b f(x)\cdot g'(x)$	Osittaisintegrointi (integration by parts).
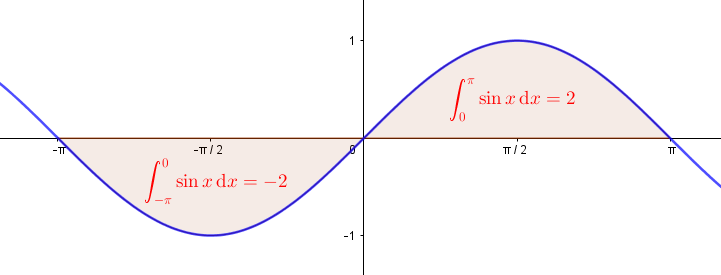
$\dint_{-a}^a f(x)\,\dx=2\cdot \dint_0^a f(x)\,\dx,$ jos on parillinen	Parillisen funktion integraali.
$\dint_{-a}^a f(x)\,\dx=0,$ jos on pariton	Parittoman funktion integraali.
$\dint_a^b 1 \, \dx = b-a$	Ykkösen integraali on välin pituus.

Määrättyjä integraaleja funktioista, joille ei ole olemassa perusfunktioiden avulla esitettävää integraalifunktiota, löytyy wikipediasta.

Esimerkkejä määrätyistä integraaleista ja integroinnista

Klikkaa esimerkkiä tarkastellaksesi vastausta.

Paikka nopeutta integroimalla: Kappaleen paikka s_f (metriä) ajanhetkellä t_f (sekuntia) voidaan määrittää integraalina $s_f = s_i + \dint_{t_i}^{t_f} v \, \dt.$ Kappale lähtee liikkeelle ajanhetkellä $t_i = 0\, \text{s}$ ja sen nopeus ajanhetkellä on $v = (10-3t)\frac{\text m}{\text s}$ . Mikä on kappaleen paikka ajanhetkellä $t_f = 5\,\text{s}$ ?

Tässä esimerkissä on siis merkitty:

$s_i = 0\, \text{m}$ kappaleen lähtöpaikka (initial position)
$t_i = 0\, \text{s}$ lähtötilanteen ajanhetki (initial time)
kappaleen loppupaikka (final position)
$t_f = 5\, \text{s}$ lopputilanteen ajanhetki (final time)

Sijoitetaan lausekkeeseen tiedot ilman yksiköitä: $\begin{aligned} s_f &= s_i + \mintegral{v}{t}{t_i}{t_f} \\ &= 0 + \mintegral{10-3t}{t}{0}{5} \\ &= \intsub{\blue0}{\red5}10t - \frac{3}{2}t^2 &&\Big| \ \text{APL}: F(\red5) - F(\blue0)\\ &= 10\cdot 5 - \frac{3}{2}\cdot 5^2 - (0 - 0) \\ &= 12{,}5 \, (\text{m}) \end{aligned}$

Siispä kappale liikkuu viidessä sekunnissa $12{,}5\,\text{m}$ .

Yksikkötarkastelu: Tarkistetaan, että integraalista todella tulee haluttua yksikköä, eli metrejä. Integraalissa $\mintegral{v}{t}{t_i}{t_f}$ -akselin yksikkönä on sekunti ( $\text{s}$ ) ja y-akselin yksikkönä on nopeus ( $\text{m/s}$ ). Siispä integraalista saadaan yksiköksi: $\begin{aligned} \left[\mintegral{v}{t}{t_i}{t_f}\right] = \text{m/s}\cdot \text{s} = \text m \end{aligned}$

Määrätty integraali: Määritä $\dint_1^2(at^{-1} + b + ct) \ \text{d}t$ .

Integraalissa a, b ja ovat vakioita. Integraalissa on merkitty $\dt$ , joten integraali tapahtuu muuttujan suhteen.

Lasketaan integraali käyttäen potenssifunktion ja vakion integrointisääntöjä ja analyysin peruslausetta.

$\begin{aligned} \mintegral{at^{-1}+b+ct}{t}{1}{2} &= \intsub{\green1}{\red2}\left( a\ln|t| + bt + c \, \frac{1}{2}t^2 \right) &&\Big | = F(\red2) - F(\green1) \\ &= a\ln|2| + 2b + c \, \frac{1}{2}2^2 - \left(a\ln|1| + b + c \, \frac{1}{2}\right) &&\Big| \ \ln(1) = 0 \\ &= a\ln(2) + 2b-b + 2c - \frac{c}{2} \\ &= a\ln(2)+b+\frac{3c}{2} \end{aligned}$

Määrätty integraali: Määritä $\dint_{-1}^1 \frac{\text{d}x}{2x+3}$ .

Integraalimerkintä, jossa $\dx$ on osoittajassa, voidaan kirjoittaa muodossa $\dint_{-1}^1 \frac{\text{d}x}{2x+3} = \mintegral{\frac{1}{2x+3}}{x}{-1}{1}.$

Integroitava funktio on yhdistetty funktio. Lasketaan määrätty integraali: $\begin{aligned} \mintegral{\frac{1}{2x+3}}{x}{-1}{1} &= \frac{1}{2}\mintegral{\frac{2}{2x+3}}{x}{-1}{1} &&\Bigg| \ \small{\int \frac{f'(x)}{f(x)}\, \dx = \ln |f(x)|} \\ &= \frac{1}{2}\intsub{\green{-1}}{\red1}\ln|2x+3| &&\Big| = F(\red1)-F(\green{-1})\\ &= \frac{1}{2}\left(\ln|2\cdot1+3|-\ln|2\cdot(-1)+3|\right) \\ &= \frac{1}{2}\left(\ln(5)-\ln(1)\right) \\ &= \frac{\ln(5)}{2} \end{aligned}$

Osittaisintegrointi: Määritä $\mintegral{e^xx}{x}{1}{2}$ .

Tämä määrätty integraali on helpoin laskea osittaisintegroimalla.

Lyhyesti:

Osittaisintegroidaan: $\begin{align*} \mintegral{e^xx}{x}{1}{2}&=\intsub{1}{2}e^xx-\mintegral{e^x\cdot 1}{x}{1}{2}\\ &=2e^2-e-\intsub{1}{2}e^x\\ &=2e^2-e-e^2+e\\ &=e^2 \end{align*}$

Pitkästi:

Osittaisintegrointikaavassa esiintyvien funktioiden ja valinta on tärkeässä osassa integraalin laskemisessa, sillä "väärällä" valinnalla integraalista tulee vain vaikeampi (ks. alla). Valitaan $\red{f'(x)=e^x},\quad \blue{g(x)=x},$ jolloin $\green{f(x)=e^x},\quad g'(x)=1.$ Näillä valinnoilla integraali saadaan muotoon $\begin{align*} \mintegral{\red{f'(x)}\blue{g(x)}}{x}{1}{2}&=\mintegral{\red{e^x}\blue{x}}{x}{1}{2}&&\Big|\,\text{osittaisintegrointi}\\ &=\intsub{1}{2}\green{e^x}\blue{x}-\mintegral{\green{e^x}\cdot 1}{x}{1}{2}&&\Big|\,\small\int_a^b \red{f'}\blue{g} = \intsub{a}{b}\green{f}\blue{g}-\int_a^b\green{f}g'\\ &=2e^2-e-\intsub{1}{2}e^x\\ &=2e^2-e-e^2+e\\ &=e^2. \end{align*}$

Varoittava esimerkki osittaisintegroinnista:

Jos tässä esimerkissä valitsee funktiot ja toisinpäin, eli $f'(x)=x,\quad g(x)=e^x,$ niin osittaisintegrointi ei auta ensimmäisen kerran jälkeen: $\begin{align*} \mintegral{e^xx}{x}{1}{2}&=\intsub{1}{2}\frac{1}{2}x^2e^x-\mintegral{\frac{1}{2}x^2e^x}{x}{1}{2}. \end{align*}$ Jälkimmäinen integraali on selvästi hankalampi kuin alkuperäinen. On tilanteita, joissa uusi osittaisintegroiminen auttaa, mutta tämä ei selvästi ole sellainen.

Epäoleellinen integraali kaavalla: Määritä $\dint_0^\infty ax^2e^{-bx} \, \text{d}x$ käyttämällä kaavaa $\int_0^\infty x^n e^{-ax}\, \text{d}x = \frac{n!}{a^{n+1}}$ .

Lyhyesti:

Käytetään integraalin laskemiseen annettua kaavaa

$\begin{aligned} \mintegral{ax^2e^{-bx}}{x}{0}{\infty}=\frac{2a}{b^3}. \end{aligned}$

Pitkästi:

Käytetään integraalin laskemiseen annettua kaavaa $\int_0^\infty x^{\blue{n}} e^{-\red{a}x}\, \text{d}x = \frac{\blue{n}!}{\red{a}^{\blue{n}+1}}.$ Tärkeintä on tunnistaa kaavassa olevat luvut oikein. Muokataan aluksi integraalia samaan muotoon kuin kaavassa, ottamalla vakio ulos $\mintegral{ax^2e^{-bx}}{x}{0}{\infty}=a\mintegral{x^{\blue{2}}e^{-\red{b}x}}{x}{0}{\infty}.$

Huomataan, että tässä tapauksessa $\blue{n}=\blue{2}$ ja $\red{a}=\red{b}.$ Tässä ei pidä sekoittaa tehtävän integraalin vakiota kaavassa esiintyvään eksponenttiin $\red{a}.$ Nyt voimme laskea integraalin

$\begin{aligned} \mintegral{ax^2e^{-bx}}{x}{0}{\infty}&=a\mintegral{x^{\blue{2}}e^{-\red{b}x}}{x}{0}{\infty}\\ &=a\cdot \frac{\blue{2}!}{\red{b}^{\blue{2}+1}}\\ &=\frac{a\cdot2\cdot1}{b^3}\\ &=\frac{2a}{b^3}. \end{aligned}$

Parittoman funktion integraali: Määritä $\dint_{-\pi}^{\pi} \sin x \, \dx$ .

Integraalin voi laskea tavanomaisin säännöin, mutta käytetään hyödyksi sinifunktion parittomuutta.

Koska sini on pariton integroimisvälillä $[-\pi, \pi]$ , niin $\dint_{-\pi}^{\pi}\sin x \, \dx = 0$ .