Funktioiden ominaisuuksista

Tälle sivulle on koottu erinäisiä funktioihin liittyviä työkaluja, joille ei ole löytynyt muuta paikkaa.

# injektiosurjektiobijektio

Injektio, surjektio ja bijektio

Tarkastellaan funktiota jonka lähtöjoukko on ja maalijoukko on Tällöin funktio voi olla injektio, surjektio tai bijektio, jos seuraavat ehdot täyttyvät:

Funktio on injektio, jos kaikille sen lähtöjoukon arvoille ja pätee $f(a)\ne f(b).$ Toisin sanoen eri parametrilla saadaan aina eri funktion arvo.
Funktio on surjektio, jos sen jokaiselle maalijoukon arvolle $y\in Y$ on olemassa lähtöjoukon arvo $x\in X$ siten, että Tällöin siis lähtöjoukon arvot "täyttävät" maalijoukon.
Funktio on bijektio, jos se on injektio ja surjektio.

Esimerkkejä injektioista, surjektioista ja bijektioista

Funktio $f:\R \rightarrow\R,$ f(x)=x+3 on injektio, koska millä tahansa $a,b\in\R$ pätee f(a)=a+3=b+3=f(3) jos ja vain jos a=b.

Funktio on myös surjektio, koska mikä tahansa maalijoukon arvo $y\in\R$ on jonkin lähtöjoukon alkion $x\in\R$ kuva. Tämä toteutuu, kun valitaan x=y-3, jolloin f(x)=x+3=(y-3)+3=y.

Tällöin on bijektio, koska se on injektio ja surjektio.

Funktio $g:\R\rightarrow\R,$ $g(x)=\cos(x)$ ei ole injektio, koska $g(0)=\cos(0)=1=\cos(2\pi)=g(2\pi).$

Funktio ei myöskään ole surjektio, koska ei ole olemassa $x\in\R$ siten, että $\cos(x)=2.$

Täten funktio ei varmasti ole bijektio, koska se ei ole injektio eikä surjektio.

# kaanteisfunktio

Käänteisfunktio

Bijektiivisen funktion käänteisfunktioksi sanotaan funktiota $f^{-1},$ joka peruuttaa funktion tekemät operaatiot :lle.

Esimerkiksi funktion f(x) = x^2 käänteisfunktio on $f^{-1}(x) = \sqrt{x}$ kun x > 0, sillä

$\begin{aligned} f(x) &= x^2 &&\Big| \ f^{-1}(\, \cdot\, ) \\ f^{-1}\big(f(x)\big) &= \sqrt{x^2} \\ f^{-1}\big(f(x)\big) &= x \end{aligned}$

Käänteisfunktion olemassaolo:

Funktiolla on käänteisfunktio vain, jos se on injektio eli jos kaikilla x_1, x_2 on voimassa $f(x_1)=f(x_2) \implies x_1=x_2.$

Lisäksi funktio on injektio, jos se on aidosti monotoninen (eli aidosti kasvava tai aidosti vähenevä).

Käänteisfunktion määrittäminen

Funktion käänteisfunktion voi selvittää ratkaisemalla yhtälön y = f(x) muuttujan suhteen, ja asettamalla $x = f^{-1}(x).$

Esimerkiksi funktion f(x) = x^3 käänteisfunktio: $\begin{aligned} y &= f(x) \\ y &= x^3 \\ x &= \sqrt[3]{y}\\ f^{-1}(y) &= \sqrt[3]{y} \end{aligned}$

Funktioita ja niiden käänteisfunktioita:

Funktion nimi		$f^{-1}$	Käänteisfunktion nimi
Potenssifunktio		$\sqrt[n]{x}$	Juurifunktio
Eksponenttifunktio		$\log_a x$	Logaritmifunktio
Luonnollinen eksponenttifunktio		$\ln x$	Luonnollinen logaritmifunktio
Sinifunktio	$\sin x$	$\arcsin x\;(=\sin^{-1}x)$	Arkussinifunktio
Kosinifunktio	$\cos x$	$\arccos x\;(=\cos^{-1}x)$	Arkuskosinifunktio
Tangenttifunktio	$\tan x$	$\arctan x\;(=tan^{-1}x)$	Arkustangenttifunktio

# parillisuus-parittomuus

Funktion parillisuus tai parittomuus

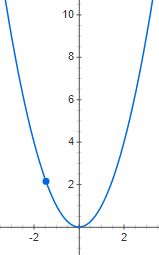
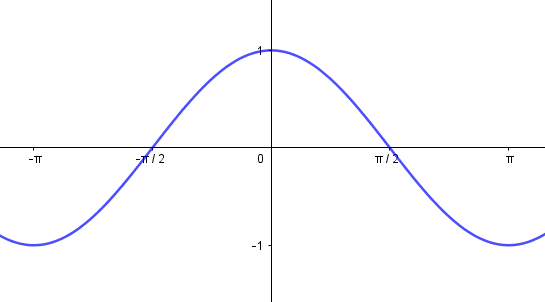
Funktio on parillinen, jos se saa yhtä kaukana origosta olevissa pisteissä arvoikseen sama luvut, toisin sanoen kaikilla :n arvoilla f(x) = f(-x) Parillinen funktio on siis y-akselin suhteen symmetrinen.

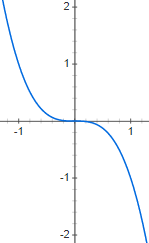
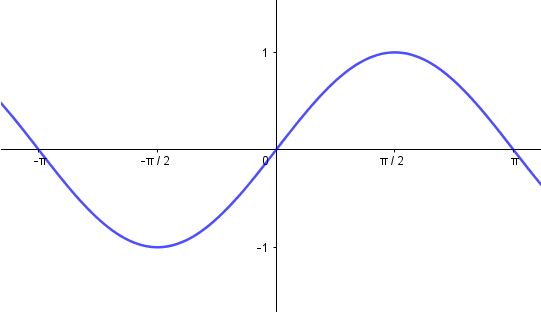
Funktio on pariton, jos se saa yhtä kaukana origosta olevissa pisteissä arvoikseen vastaluvut, toisin sanoen kaikilla :n arvoilla f(x) = -f(-x) Pariton funktio on siis origon suhteen symmetrinen.

Parillisia ja parittomia funktioita

Parillinen funktio		Pariton funktio

$\cos(x)$		$\sin(x)$

# fktjaksollisuus

Funktion jaksollisuus

Funktio f(x) on -jaksollinen, jos f(x+p) = f(x) kaikilla Jos f(x) on -jaksollinen, niin se on myös -jaksollinen, missä $n=2,3,\dots$ . Lukua sanotaan funktion f(x) perusjaksoksi.

Esimerkkejä jaksollisista funktioista

Esimerkiksi funkiot $\sin(x)$ ja $\cos(x)$ ovat jaksollisia ja niiden jakso on $2\pi$ eli kaikilla ja kokonaisluvuilla pätee $\begin{aligned} \sin(x)=\sin(2\pi n+x) \end{aligned}$ ja $\begin{aligned} \cos(x)=\cos(2\pi n+x). \end{aligned}$ Jaksoa voi tarkastella millä tahansa $2\pi$ -pituisella välillä. Alla olevassa kuvassa jaksoa tarkastellaan kohdissa $-3\pi, \, -\pi,\, \pi$ ja $3\pi.$

$\begin{tikzpicture} \begin{axis}[domain=-3.2*pi:3.2*pi, samples=100, %grid=major, % restrict y to domain=-1.25:1.25, legend pos = outer north east, axis lines= middle, xtick={-3*pi, -pi, pi, 3*pi}, xticklabel style = {xshift=-0.2cm}, xticklabels={$-3\pi$,$-\pi$,$\pi$,$3\pi$}, %ytick={-2, -1, 1,2}, %yticklabels={-2,-1, 1,2}, %yticklabel style = {yshift=0.2cm}, xlabel=$x$, ylabel=$y$] \addplot [color=blue, thick] {sin(deg(x))}; \addplot [color=red, thick] {cos(deg(x))}; %\addplot +[mark=none, color=black, loosely dashed,] coordinates {(0, -5) (0,5)}; \addplot +[mark=none, color=black!50!white, loosely dashed, ] coordinates {(pi, -5) (pi,5)}; \addplot +[mark=none, color=black!50!white, loosely dashed, ] coordinates {(-pi, -5) (-pi,5)}; \addplot +[mark=none, color=black!50!white, loosely dashed, ] coordinates {(-3*pi, -5) (-3*pi,5)}; \addplot +[mark=none, color=black!50!white, loosely dashed, ] coordinates {(3*pi, -5) (3*pi,5)}; \legend{$\sin (x)$, $\cos (x)$} \end{axis} \end{tikzpicture}$

Myös funktio $e^{ikx}$ on $2\pi$ -jaksollinen, sillä $\begin{aligned} e^{ik(x+2\pi)}&=e^{ikx}e^{i2k\pi}\\ &=(\cos(kx)+i\sin(kx))(\underbrace{\cos(2k\pi)}_{= \ 1} +i\underbrace{\sin(2k\pi)}_{= \ 0})\\ &= (\cos(kx)+i\sin(kx)) \\ &= e^{ikx}. \end{aligned}$