Tämä materiaali on tehty Tampereen yliopiston koordinoimassa hankkeessa “Matemaattisten aineiden verkkokurssit lukioon ja ammatilliseen koulutukseen”. Hankkeen ideana on toteuttaa kaikille avoimia verkkomateriaaleja toisen asteen koulutukseen. Hankkeen on rahoittanut Opetushallitus.

Materiaali sisältää lukion matematiikan MAY1 Luvut ja yhtälöt -kurssin teoriasisällön. Kirja on tehty noudattaen vuonna 2021 käyttöön otettavan lukion opetussuunnitelman perusteiden luonnosta. Kirja kokonaisuudessaan löytyy osoitteesta:

https://tim.jyu.fi/view/tau/toisen-asteen-materiaalit/matematiikka/algebra/may1-sisalto

Materiaali on tuotettu lisenssillä CC BY-SA 4.0.

1. Luvut ja laskutoimitukset

Ensimmäisessä kappaleessa käsitellään lukuja sekä niillä tehtäviä laskutoimituksia. Käymme läpi lukualueet sekä palautamme mieleen yläkoulusta tutut merkkisäännöt ja laskulait. Lisäksi kerrataan murtoluvuilla tehtävät laskutoimitukset. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

1.1 Lukualueet

Matematiikassa luvut muodostavat perustan laskutoimituksille. Nykyinen lukukäsite on pitkällisen, vuosituhansia kestäneen kehityksen tulosta, eikä pystytä sanomaan, onko tämä kehitys jo päättynyt.

Jo ensimmäisellä peruskoulun vuosiluokalla opimme lukumäärää ilmaisevat luonnolliset luvut. Miksi näitä on sitten lähdetty laajentamaan kohti reaalilukuja? Esimerkiksi Rene Descartesin (1596-1650) oli vaikea hyväksyä lukualueen laajennusta luonnollisista luvuista kokonaisluvuiksi ja hän kutsuikin negatiivisia lukuja "vääriksi luvuiksi". Yksi lähestymistapa lukulaajennuksille on yhtälöopillinen: Millainen yhtälö on ratkeamaton kyseisellä lukualueella, jota haluamme laajentaa? Esimerkiksi luonnollisten lukujen tapauksessa yhtälö x+1=0 on ratkeamaton, sillä x=-1 ei kuulu luonnollisiin lukuihin. Lisäämällä negatiiviset luvut $\mathbb{Z^-}=\{...,-3,-2,-1\}$ luonnollisten lukujen joukkoon saamme muun muassa edellä mainitun yhtälön ratkeavaksi.

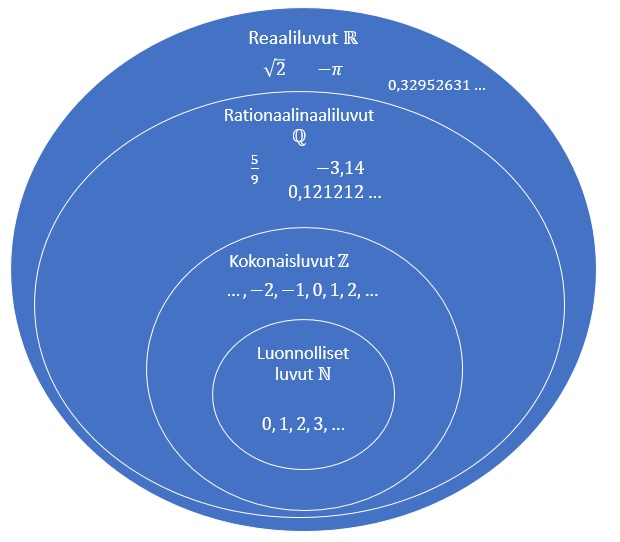
Lukualueen laajentaminen on näin edennyt luonnollisista luvuista aina reaalilukuihin asti. Uudet käyttöön otetut luvut on liitetty entisiin, jolloin uusi lukujoukko sisältää aikaisemmat lukujoukot.

Lukualueet

Luonnolliset luvut $\mathbb{N}=\{0,1,2,3,...\}$
Kokonaisluvut $\mathbb{Z}=\{...,-3,-2,-1,0,1,2,3,...\}$
Rationaaliluvut $\mathbb{Q}=\{\dfrac{m}{n}|m,n\in\mathbb{Z}, n\neq0\}$
Reaaliluvut $\mathbb{R}$ on rationaalilukujen lukulaajennus, joka saadaan lisäämällä irrationaalilukujen joukko rationaalilukuihin. Irrationaaliluvut ovat lukuja, joita ei voida esittää kahden kokonaisluvun osamääränä esim. $\sqrt{5}$ , $\pi$ ja jaksoton desimaaliluku . Käytännössä katsoen reaalilukuja ovat siis kaikki ne luvut, joita on peruskoulun matematiikassa käytetty.

1.1.1 Esimerkki: lukualueet

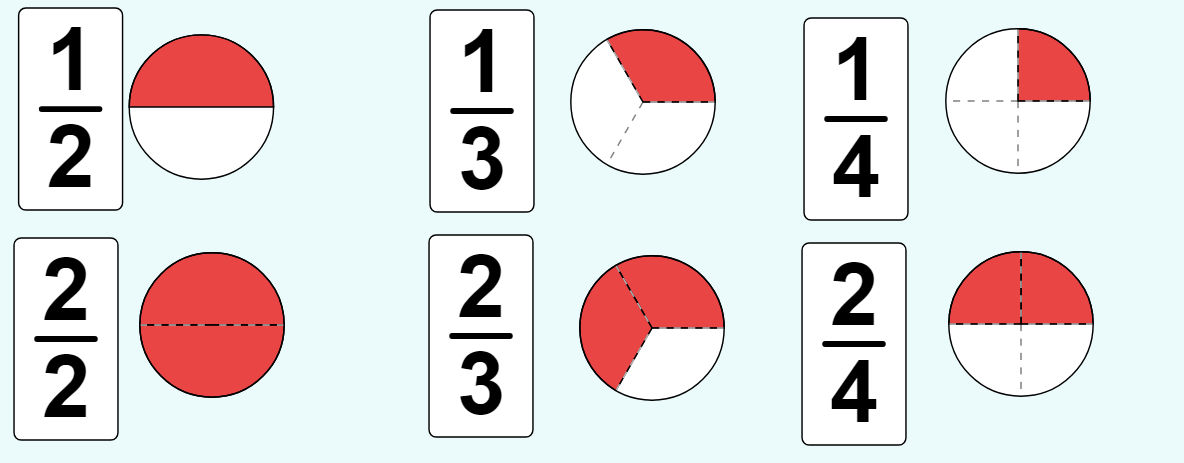
Mihin lukujoukkoihin luku kuuluu?

$\displaystyle\frac{3}{7}$

Ratkaisu:

Luonnollisiin lukuihin. Lisäksi, kokonais-, rationaali- sekä reaalilukuihin, koska nämä lukujoukot pitävät sisällään myös luonnolliset luvut.
Kokonaislukuihin. Lisäksi, rationaali- ja reaalilukuihin.
Rationaali- ja reaalilukuihin.
Rationaali- ja reaalilukuihin, sillä luku voidaan esittää murtolukuna $\displaystyle\frac{3}{5}$ .
Ainoastaan reaalilukuihin. Kyseessä on päättymätön ja jaksoton desimaaliluku, jonka vuoksi sitä ei voida esittää kahden kokonaisluvun osamääränä. Tämän vuoksi luku ei kuulu rationaalilukuihin, jolloin se ei myöskään kuulu kokonaislukuihin tai luonnollisiin lukuihin.

Lukualueet: tehtäviä

1.2 Laskulait

Palautetaan mieleen tutut merkkisäännöt ja laskulait. Kerto- ja jakolaskussa kahden samanmerkkisen luvun laskutoimitus on positiivinen ja kahden erimerkkisen negatiivinen. Tämän seurauksena kerto- ja jakolaskun tulos on positiviinen, kun negatiivisten tekijöiden lukumäärä on parillinen. Vastaavasti kerto- ja jakolaskun tulos on negatiivinen, kun negatiivisia tekijöitä on pariton määrä.

Merkkisäännöt

$a\cdot(-b)=-ab$ ja $\displaystyle\frac{a}{-b}=-\frac{a}{b}$
$(-a)\cdot(-b)=a\cdot b$ ja $\displaystyle\frac{-a}{-b}=\frac{a}{b}$

1.2.1 Esimerkki: merkkisäännöt

Laske.

$4\cdot(-2)$
$\displaystyle\frac{-3}{-6}$

Ratkaisu:

$4\cdot(-2)=-4\cdot2=-8$
$\displaystyle\frac{-3}{-6}=\displaystyle\frac{3}{6}=\frac{1}{2}$

Laskujärjestys noudattaa tuttua kaavaa.

Laskujärjestys

Lasketaan sulut
Lasketaan kerto- ja jakolaskut
Lasketaan yhteen- ja vähennyslaskut

1.2.2 Esimerkki: laskujärjestys

Laske.

$-2\cdot(-3)\cdot2$
$-4\cdot(-5)\cdot(-2)\cdot(-1)$
$5\cdot(-1)\cdot(-6):(-10)$
$3\cdot(2-8:2)\cdot(-2)+11$

Ratkaisu:

$\begin{align*} &-2\cdot(-3)\cdot2 && |\;\text{poistetaan sulut}\\ &=2\cdot3\cdot2 && |\;\text{lasketaan kertolaskut}\\ &=6\cdot2 \\ &=12 \end{align*}$

$\begin{align*} &-4\cdot(-5)\cdot(-2)\cdot(-1) && |\;\text{poistetaan ensimmäiset sulut}\\ &=4\cdot5\cdot(-2)\cdot(-1) && |\;\text{poistetaan toiset sulut}\\ &=4\cdot5\cdot2\cdot1 && |\;\text{lasketaan kertolaskut}\\ &=40 \end{align*}$

$\begin{align*} &5\cdot(-1)\cdot(-6):(-10) && |\;\text{poistetaan sulut}\\ &=-5\cdot1\cdot6:10 && |\;\text{lasketaan kertolaskut}\\ &=-30:10 && |\;\text{lasketaan jakolasku}\\ &=-3 \end{align*}$

$\begin{align*} &3\cdot(2-8:2)\cdot(-2)+11 && |\;\text{lasketaan jakolasku sulkujen sisältä}\\ &=3\cdot(2-4)\cdot(-2)+11 && |\;\text{lasketaan vähennyslasku sulkujen sisältä}\\ &=3\cdot(-2)\cdot(-2)+11 && |\;\text{poistetaan sulut}\\ &=3\cdot4+11 && |\;\text{lasketaan kertolasku}\\ &=12+11 && |\;\text{lasketaan yhteenlasku}\\ &=23 \end{align*}$

Oheiselta videolta löytyy tarvittaessa lisää esimerkkejä laskujärjestyksestä sekä negatiivisilla luvuilla laskemisesta.

Peruslaskutoimituksista yhteenlasku ja kertolasku noudattavat seuraavia laskulakeja.

Laskulait

Olkoon $a,b,c\in\mathbb{R}$ . Tällöin ovat voimassa seuraavat laskulait:

$\begin{equation*} \left.\begin{aligned} a + b &= b + a\\ ab &= ba \end{aligned}\right\} \text{vaihdantalait} \end{equation*}$

$\begin{equation*} \left.\begin{aligned} a + (b + c) &= (a + b) + c\\ a(bc) &= (ab)c \end{aligned}\right\} \text{liitäntälait} \end{equation*}$

$\begin{equation*} \left.\begin{aligned} a(b + c) = a b + ac\\ (a+b)c = ac + b c \end{aligned}\right\} \text{osittelulait} \end{equation*}$

Vaihdanta- ja liitäntälakien takia luvut voidaan laskea yhteen tai kertoa missä järjestyksessä tahansa. Sulkumerkit voidaan siis jättää pois ja merkitä vain a+b+c ja abc . Sopivalla ryhmittelyllä laskutehtävä saadaan usein yksinkertaistettua.

1.2.3 Esimerkki: laskulait

Laske käyttäen hyväksi laskulakeja.

$2\cdot8\cdot50$
$7\cdot46$

Ratkaisu:

Kertolasku voidaan laskea missä järjestyksessä tahansa, joten vaihdetaan lukujen ja paikkaa.

$2\cdot8\cdot50=2\cdot50\cdot8=100\cdot8=800$

Kirjoitetaan luku muodossa ja käytetään hyväksi osittelulakia.

$7\cdot46=7\cdot(40+6)=7\cdot40+7\cdot6=280+42=322$

Vastaluku ja käänteisluku

Kahta lukua, joiden summa on nolla, sanotaan toistensa vastaluvuiksi. Luvun vastaluku on -a, koska a+(-a)=0 . Jokaisella reaaliluvulla on vastaluku.

Kahta lukua, joiden tulo on yksi, sanotaan toistensa käänteisluvuiksi. Luvun käänteisluku on $\displaystyle\frac{1}{a},$ koska $a\cdot\displaystyle\frac{1}{a}=1$ . Kaikilla muilla reaaliluvuilla paitsi nollalla on käänteisluku.

1.2.4 Esimerkki: vasta- ja käänteisluku

Mikä on luvun vastaluku?
Mikä on luvun vastaluku?
Mikä on luvun käänteisluku?
Mikä on luvun käänteisluku?
Mikä on luvun vastaluvun käänteisluku?

Ratkaisu:

Luvun vastaluku on sillä

Luvun vastaluku on sillä

Luvun käänteisluku on $\displaystyle\frac{1}{2},$ sillä $2\cdot \displaystyle\frac{1}{2}=1.$

Luvun käänteisluku on $-\displaystyle\frac{1}{4},$ sillä $-4\cdot (-\displaystyle\frac{1}{4})=4\cdot \displaystyle\frac{1}{4}=\frac{4}{4}=1.$

Luvun vastaluku on sillä
Luvun käänteisluku on $-\displaystyle\frac{1}{11},$ sillä $-11\cdot (-\displaystyle\frac{1}{11})=11\cdot \frac{1}{11}=\frac{11}{11}=1.$
Siispä, luvun vastaluvun käänteisluku on $-\displaystyle\frac{1}{11}.$

Laskulait: tehtäviä

1.3 Itseisarvo

Reaaliluvun itseisarvo määritellään paloittain, erikseen ei-negatiivisille ja negatiivisille luvuille.

Itseisarvo

Reaaliluvun itseisarvo on

$|a|= \begin{cases} a,\;\;\;\;\;\ \text{kun}\;\;a\ge0 \\ -a,\;\;\;\; \text{kun}\;\;a<0 \end{cases}$

Positiivisen luvun ja nollan itseisarvo on siis luku itse. Esimerkiksi |2|=2 ja |0|=0.

Negatiivisen luvun itseisarvo on sen vastaluku. Esimerkiksi |-2|=-(-2)=2.

Geometrisesti tulkittuna itseisarvo kertoo sen etäisyyden lukusuoralla luvusta . Tätä on havainnollistettu oheisella appletilla. Liikuttamalla sinistä pistettä näet, kuinka mustalla palkilla kuvattu itseisarvo muuttuu. Koska kyseessä on etäisyys, niin $|a|\geq 0$ kaikilla :n arvoilla.

1.3.1 Esimerkki: luvun itseisarvo

Luvun itseisarvo koska

Luvun $\pi-2$ itseisarvo $|\pi-2|=\pi-2,$ koska $\pi-2>0.$

Luvun $1-\sqrt{2}$ itseisarvo $|1-\sqrt{2}|=-(1-\sqrt{2})=\sqrt{2}-1,$ koska $1-\sqrt{2}\approx-0,41<0.$

Itseisarvolle pätee seuraavat ominaisuudet.

Itseisarvon ominaisuuksia

$|a|\ge0$
$\Big|\displaystyle\frac{a}{b}\Big|=\frac{|a|}{|b|}$

1.3.2 Esimerkki: itseisarvolausekkeiden sieventämistä

Sievennä.

Ratkaisu:

$\begin{align*} &|4+(-5)|+(|4|+|-5|) &&|\;\text{lasketaan itseisarvot sulkujen sisältä} \\ &=\;|4-5|-(4+5) &&|\;\text{lasketaan vähennyslasku itseisarvon sisältä}\\ &=\;|-1|-9 \\ &=\;1-9\\&=\;-8 \end{align*}$

$\begin{align*} &|a-b|-|b-a| &&|b-a=-(a-b)\\ &=\;|a-b|-|-(a-b)| &&|\text{käytetään hyväksi itseisarvon 2. ominaisuutta} \\ &=\;|a-b|-|a-b| \\ &=\;0 \end{align*}$

Itseisarvo: tehtäviä

1.4 Murtoluvut

Kerrataan murtolukuihin liittyvät nimitykset ja laskutoimitukset.

Murtoluku on kahden kokonaisluvun osamäärä $\displaystyle\frac{m}{n}$ , missä jaettavaa (m) sanotaan osoittajaksi ja jakajaa (n) nimittäjäksi, ja osoittaja ei ole jaollinen jakajalla. Murtoluku on siis rationaaliluku, joka ei supistu kokonaisluvuksi.

Sekaluvut ovat murtoluvun vaihtoehtoinen esittämistapa. Jotta murtoluku voidaan esittää sekalukuna, nimittäjän tulee olla suurempi kuin osoittaja. Esimerkiksi murtoluku $\displaystyle\frac{7}{4}=\frac{4+3}{4}=\frac{4}{4}+\frac{3}{4}=1+\frac{3}{4}$ voidaan esittää sekalukuna $1\displaystyle\frac{3}{4}$ .

1.4.1 Esimerkki: murtolukujen suuruusjärjestys

Järjestä murtoluvut $\displaystyle\frac{3}{4}$ , $\displaystyle\frac{7}{8}$ ja $\displaystyle\frac{1}{2}$ suuruusjärjestykseen.

Ratkaisu:

Lavennetaan murtoluvut ensin samannimisiksi, jotta suuruusvertailu on helpompi tehdä.

$^{2)}\displaystyle\frac{3}{4}=\frac{2\cdot 3}{2\cdot 4}=\frac{6}{8}$

$^{4)}\displaystyle\frac{1}{2}=\frac{4\cdot 1}{4\cdot 2}=\frac{4}{8}$

Nyt $\displaystyle\frac{7}{8}>\frac{6}{8}>\frac{4}{8},\;$ joten $\;\displaystyle\frac{7}{8}>\frac{3}{4}>\frac{1}{2}.$

1.4.2 Esimerkki: sekaluvut

Muunna

$\displaystyle\frac{9}{2}$ sekaluvuksi.
$3\,\displaystyle\frac{4}{5}$ murtoluvuksi.

Ratkaisu:

Esitetään osoittaja nimittäjän tulona, jolloin jakojäännökseksi jää , ja sievennetään sekaluvuksi.

$\displaystyle\frac{9}{2}=\frac{4\cdot2 +1}{2}=\frac{4\cdot \cancel{2}}{\cancel{2}}+\frac{1}{2}=4+\frac{1}{2}=4\,\frac{1}{2}$

Lavennetaan kokonaisluku murtoluvuksi ja lasketaan murtoluvut yhteen.

$3\,\displaystyle\frac{4}{5}=3+\frac{4}{5}=^{5)}\!\frac{3}{1}+\frac{4}{5}=\frac{15}{5}+\frac{4}{5}=\frac{19}{5}$

Murtolukujen yhteen- ja vähennyslasku

$^{d)}\displaystyle\frac{a}{b}+\,^{b)\!}\frac{c}{d}=\frac{ad}{bd}+\frac{bc}{bd}=\frac{ad+bc}{bd}$

$^{d)}\displaystyle\frac{a}{b}-\,^{b)\!}\frac{c}{d}=\frac{ad}{bd}-\frac{bc}{bd}=\frac{ad-bc}{bd}$

1.4.3 Esimerkki: yhteen- ja vähennyslasku murtoluvuilla

Laske.

$\displaystyle\frac{1}{2} + \frac{3}{4}\;\;\;\;$ b. $\displaystyle\frac{9}{10} - \frac{7}{8}$

Ratkaisu:

$\begin{align*} &^{4)} \displaystyle\frac{1}{2} +\,^{2)}\frac{3}{4} &&|\;\text{lavennetaan murtoluvut samannimisiksi}\\ &=\frac{4\cdot 1}{4\cdot 2} + \frac{2\cdot 3}{2\cdot 4} \\ &=\frac{4}{8} + \frac{6}{8} &&|\;\text{lasketaan osoittajat yhteen, nimittäjä pysyy samana}\\ &=\frac{4+6}{8} \\ &=\displaystyle\frac{10}{8} ^{(2}=\frac{5}{4} &&|\;\text{sievennetään vastaus} \end{align*}$

$\begin{align*} &^{8)}\displaystyle\frac{9}{10} - \,^{10)} \frac{7}{8} &&|\;\text{lavennetaan murtoluvut samannimisiksi}\\ &=\frac{8\cdot 9}{8\cdot 10} - \frac{10\cdot7}{10\cdot8} \\ &=\frac{72}{80} - \frac{70}{80} &&|\;\text{vähennetään osoittajat toisistaan, nimittäjä pysyy samana}\\ &=\frac{72-70}{80} \\ &=\frac{2}{80}^{(2}=\frac{1}{40} &&|\;\text{sievennetään vastaus} \end{align*}$

Murtolukujen kertolasku

$\displaystyle\frac{a}{b}\cdot\frac{c}{d}=\frac{ac}{bd}$

1.4.4 Esimerkki: kertolasku murtoluvuilla

Laske.

$\displaystyle\frac{2}{3} \cdot \frac{5}{3}$
$-\displaystyle\frac{3}{4} \cdot \frac{5}{7}$
$5\cdot \displaystyle\frac{1}{3}$

Ratkaisu:

Kerrotaan osoittajat ja nimittäjät keskenään.

$\displaystyle\frac{2}{3} \cdot \frac{5}{3}=\frac{2\cdot5}{3\cdot3}=\frac{10}{9}$

Kerrotaan osoittajat ja nimittäjät keskenään. Kertolaskussa on pariton määrä negatiivisia tulontekijöitä, joten tulos on negatiivinen.

$-\displaystyle\frac{3}{4} \cdot \frac{5}{7}=-\frac{3\cdot5}{4\cdot7}=-\frac{15}{28}$

Muutetaan kokonaisluku murtoluvuksi ja kerrotaan osoittajat ja nimittäjät keskenään.

$5\cdot \displaystyle\frac{1}{3}=\frac{5}{1} \cdot \frac{1}{3}=\frac{5\cdot1}{1\cdot3}=\frac{5}{3}$

Murtolukujen jakolasku

$\displaystyle\frac{a}{b}:\frac{c}{d}=\displaystyle\frac{a}{b}\cdot\frac{d}{c}=\frac{ad}{bc}$

1.4.5 Esimerkki: jakolasku murtoluvuilla

Laske.

$\displaystyle\frac{2}{5} : \frac{1}{2}$
$\displaystyle\frac{3}{7} : \left(-\frac{2}{3}\right)$
$\displaystyle\frac{1}{3} : 11$

Ratkaisu:

Kerrotaan jaettava jakajan käänteisluvulla.

$\displaystyle\frac{2}{5} : \frac{1}{2}=\frac{2}{5} \cdot \frac{2}{1}=\frac{2\cdot2}{5\cdot1}=\frac{4}{5}$

Kerrotaan jaettava jakajan käänteisluvulla. Kertolaskussa on pariton määrä negatiivisia tulontekijöitä, joten tulos on negatiivinen.

$\displaystyle\frac{3}{7} : \left(-\frac{2}{3}\right)=\frac{3}{7} \cdot \left(-\frac{3}{2}\right)=-\frac{3\cdot3}{7\cdot2}=-\frac{9}{14}$

Muutetaan jakaja murtoluvuksi ja kerrotaan jaettava jakajan käänteisluvulla.

$\displaystyle\frac{1}{3} : 11=\frac{1}{3} : \frac{11}{1}=\frac{1}{3} \cdot \frac{1}{11}=\frac{1\cdot1}{3\cdot11}=\frac{1}{33}$

1.4.6 Esimerkki: pizzan jakaminen

Ystävykset Aada, Hilda, Iida ja Ville päättivät mennä syömään pizzeriaan. He tilasivat pepperoni- sekä vegepizzan, jotka he jakoivat seuraavasti:

Ville sanoi herrasmiehenä, että hän voi syödä jäljelle jäävät osuudet pizzoista viimeisenä. Aada leikkasi ensimmäisenä itselleen $\displaystyle\frac{1}{4}$ pepperonipizzaa ja $\displaystyle\frac{1}{8}$ vegepizzaa. Hilda leikkasi toisena jäljellä olevista pepperonipizzasta $\displaystyle\frac{4}{5}$ ja vegepizzasta $\displaystyle\frac{1}{4}$ . Iida leikkasi kolmentena jäljellä olevasta vegepizzasta puolet. Paljonko Villelle jäi pizzaa?

Ratkaisu:

Kun Aada leikkasi pepperonipizzaa, niin jäljelle jäi $^{4)}1-\displaystyle\frac{1}{4}=\frac{4}{4}-\frac{1}{4}=\frac{3}{4}$ .

Kun Aada leikkasi vegepizzaa, niin jäljelle jäi $^{8)}1-\displaystyle\frac{1}{8}=\frac{8}{8}-\frac{1}{8}=\frac{7}{8}$ .

Kun Hilda leikkasi pepperonipizzaa, niin jäljelle jäi $(1-\displaystyle\frac{4}{5})\cdot\frac{3}{4}=\frac{1}{5}\cdot\frac{3}{4}=\frac{3}{20}$ .

Kun Hilda leikkasi vegepizzaa, niin jäljelle jäi $(1-\displaystyle\frac{1}{4})\cdot\frac{7}{8}=\frac{3}{4}\cdot\frac{7}{8}=\frac{21}{32}$ .

Kun Iida leikkasi vegepizzaa, niin jäljelle jäi $(1-\displaystyle\frac{1}{2})\cdot\frac{21}{32}=\frac{1}{2}\cdot\frac{21}{32}=\frac{21}{64}$ .

Vastaus:

Villelle jäi siis $\displaystyle\frac{3}{20}$ pepperonipizzaa ja $\displaystyle\frac{21}{64}$ vegepizzaa.

Murtoluvut on tapana sieventää muotoon, jossa osoittajana ja nimittäjänä on mahdollisimman pienet kokonaisluvut. Tämän voi allekirjoittaneen mielestä tehdä helpoiten niin, että jakaa ensin osoittajan sekä nimittäjän alkutekijöihin, jonka jälkeen supistaa yhteiset tekijät pois.

Luvun jakamisella alkutekijöihinsä tarkoitetaan sen kirjoittamista alkulukujen tulona. Alkuluku on lukua suurempi luonnollinen luku, joka on jaollinen vain ja ainoastaan itsellään ja luvulla .

Esimerkiksi on alkuluku, koska se ei ole jaollinen muilla kokonaisluvuilla kuin ja , mutta $10=5\cdot2$ ei ole alkuluku, sillä se on jaollinen myös luvuilla ja .

1.4.7 Esimerkki: murtolukujen sieventäminen alkulukujen avulla

Sievennä murtoluvut muotoon, missä osoittajana ja nimittäjänä ovat mahdollisimman pienet kokonaisluvut.

$\displaystyle\frac{11}{77}\;\;\;$ b. $\displaystyle\frac{32}{64}\;\;\;$ c. $-\displaystyle\frac{36}{112}$

Ratkaisu:

Luku on alkuluku, mutta luku hajoaa alkutekijöihin seuraavasti $77=11\cdot7.$

Nyt voidaan sieventää: $\displaystyle\frac{11}{77}=\frac{\cancel{11}}{\cancel{11}\cdot 7 }=\frac{1}{7}$

Luku hajoaa alkutekijöihin seuraavasti $32=2^5=2\cdot2\cdot2\cdot2\cdot2$ ja luku seuraavasti $64=2^6=2\cdot2\cdot2\cdot2\cdot2\cdot2.$

Nyt voidaan sieventää: $\displaystyle\frac{32}{64}=\frac{\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}} {2\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}}=\frac{1}{2}$

Luku hajoaa alkutekijöihin seuraavasti $33=2\cdot2\cdot3\cdot3$ ja luku 112 seuraavasti $112=2\cdot2\cdot2\cdot2\cdot7.$

Nyt voidaan sieventää: $-\displaystyle\frac{36}{112}=-\frac{\cancel{2}\cdot\cancel{2}\cdot3\cdot3} {\cancel{2}\cdot\cancel{2}\cdot2\cdot2\cdot7}=-\frac{3\cdot3}{2\cdot2\cdot7}=-\frac{9}{28}$

HUOM! Samaan lopputulokseen olisi päästy supistamalla:

$-\displaystyle\frac{36}{112}^{(2}=-\frac{18}{56}^{(2}=-\frac{9}{28}$

Murtoluvut: tehtäviä

2. Yhtälö

Tässä kappaleessa käsitellään yhtälöitä. Keskitymme ensimmäisen asteen yhtälöiden sekä yhtälöparien ratkaisemiseen. Kappaleeseen liittyvät tehtävät omat omalla sivullaan.

Aluksi palautetaan mieleen yhtälön käsite alla olevan yhtälövaa'an avulla. Vie muuttujia kuvaavia laatikoita ja ilmapalloja vaa'alle ja pyri saamaan vaaka tasapainoon ohessa olevan yhtälön mukaan.

Kun vaa'an molempien puolien sisältö painaa yhtä paljon, vaaka on tasapainossa. Vaaka säilyttää tasapainonsa, jos sen molemmilta puolilta poistetaan tai molemmille puolille lisätään samanpainoiset kappaleet. Myös yhtälölle voidaan tehdä vastaavat toimenpiteet.

2.1 Peruskäsitteitä

Merkittyä laskutoimitusta tai pelkkää lukua kutsutaan lausekkeeksi. Lausekkeita ovat esimerkiksi

$x+3, a+b \; \text{ja} \; 8.$

Kun kaksi lauseketta merkitään yhtä suuriksi, muodostuu yhtälö. Yhtälöitä ovat esimerkiksi

$x+3=8 \; \text{ja} \; a+b=0.$

Yhtälöissä esiintyy yleensä yksi tai useampia muuttujia, joita merkitään kirjaimilla. Yllä olevissa yhtälöissä muuttujia ovat , ja . Niitä muuttujan arvoja, jotka toteuttavat yhtälön, sanotaan yhtälön ratkaisuiksi tai yhtälön juuriksi.

2.1.1 Esimerkki: onko kysytty luku yhtälön ratkaisu

Olkoon yhtälö 3x+2=-2x-8 . Onko luku

yhtälön ratkaisu?

Ratkaisu:

Tutkitaan, onko yhtälö tosi, kun sijoitetaan luku yhtälöön muuttujan paikalle.

Sijoitetaan , jolloin

$\begin{align*} 3\cdot 2 + 2 & = -2 \cdot 2 - 8 \\ 8 & = -12 \\ &\text{\bf{epätosi}} \end{align*}$

joten ei ole yhtälön 3x+2=-2x+-6 ratkaisu.

Sijoitetaan , jolloin

$\begin{align*} 3\cdot (-2) + 2 & = -2 \cdot (-2) - 8 \\ -4 & = -4 \\ \text{}&\text{\bf{tosi}} \end{align*}$

joten on yhtälön 3x+2=-2x+-6 ratkaisu.

Peruskäsitteitä: tehtäviä

2.2 Ensimmäisen asteen yhtälö

Ensimmäisen asteen yhtälö

Ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan saattaa muotoon

ax+b=0,

jossa $a\neq0$ .

Ensimmäisen asteen yhtälöllä on täsmälleen yksi ratkaisu.

2.2.1 Todistus: ensimmäisen asteen yhtälön ratkaisu

$\begin{align*} ax+b & = 0 && |-b \\ ax & = -b && |:a, a\neq0 \\ x & = -\frac{b}{a} \end{align*}$

Luku $-\displaystyle\frac{b}{a}$ on siis yhtälön ainoa ratkaisu. $\square$

2.2.2 Esimerkki: ensimmäisen asteen yhtälön ratkaiseminen

Ratkaise yhtälö 21x-3=0 .

Ratkaisu:

$\begin{align*} 21x-3 & = 0 && |+3 \\ 21x & = 3 && |:21 \\ x & = \frac{3}{21} \\ x & = \frac{1}{7} \end{align*}$

Vastaus: $x=\dfrac{1}{7}$

Jos ensimmäisen asteen yhtälö halutaan ratkaista graafisesti , piirretään suora y=ax+b ja katsotaan kuvaajasta kohta, jossa suora leikkaa akselin. Siinä kohdassa y=0.

2.2.3 Esimerkki: ensimmäisen asteen yhtälön ratkaiseminen graafisesti

Ratkaise graafisesti yhtälö -2x+2=5x-2.

Ratkaisu:

Sievennetään yhtälö ensin muotoon ax+b=0 yhdistämällä termit samalle puolelle.

$\begin{align*} -2x+2&=5x-2 \\ -2x+2-5x+2&=0 \\ -7x+4&=0 \end{align*}$

Piirretään nyt suora y=-7x+4 sopivalla ohjelmalla ja selvitetään suoran ja akselin leikkauskohta.

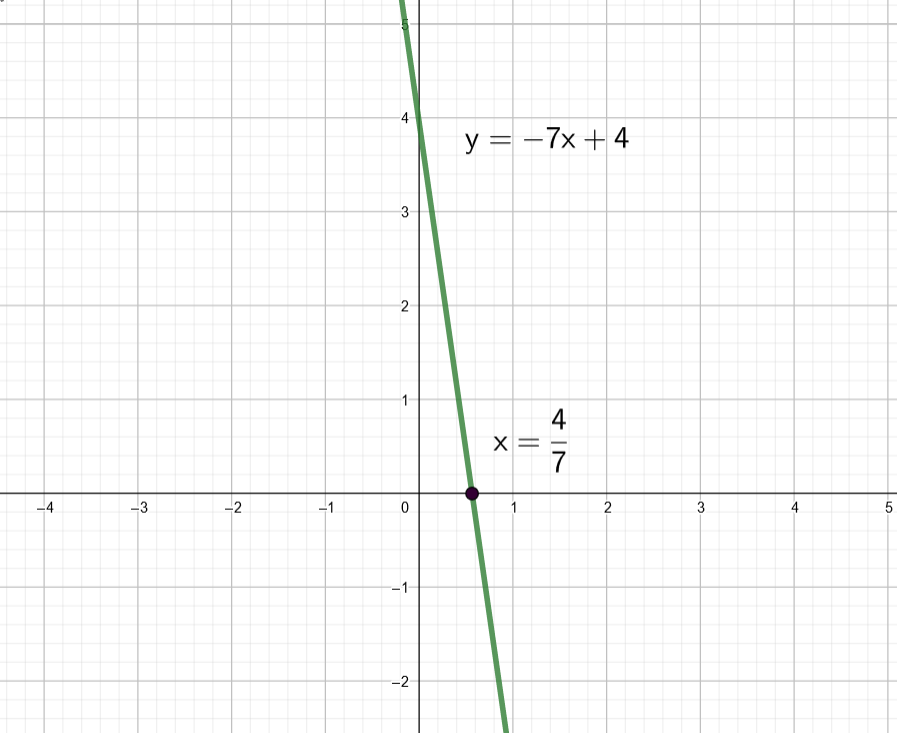
Suora leikkaa akselin, kun $x=\dfrac{4}{7}$ , joten tämä on yhtälön ratkaisu.

Vastaus: $x=\dfrac{4}{7}$

Yhtälön ratkaiseminen perustuu siihen, että yhtälölle tehtävät toimenpiteet pitävät yhtälön yhtäpitävänä eli yhtälön ratkaisut pysyvät samoina. Yllä olevissa esimerkeissä jo jaoimme ja vähensimme yhtälöä puolittain. Yleiset yhtälön ratkaisun toimenpiteet ovat esitelty kertauksen vuoksi alapuolella.

Yhtälön ratkaiseminen

1) Puolittain lisääminen tai vähentäminen

$\begin{align*} 1 & = 1 && |+3 \\ 4 & = 4 && | -2 \\ 2 & = 2 \end{align*}$

$\begin{align*} -4x+3 & = -4x+3 && |-3 \\ -4x & = -4x && | +4x \\ 0 & = 0 \end{align*}$

2) Puolittain kertominen ja jakaminen nollasta eroavalla luvulla

$\begin{align*} 4 & = 4 && | :2 \\ 2 & = 2 && | \cdot (-10) \\ -20 & = -20 \end{align*}$

$\begin{align*} 3x+9 & = 3x+9 && |:3 \\ x+3 & = x+3 && |\cdot (-1) \\ -x-3 & = -x-3 \end{align*}$

3) Yhtälön puolien vaihtaminen keskenään

$\begin{align*} 2x+1 & = 4x && \;\\ 4x & = 2x+1 && \end{align*}$

Näiden ominaisuuksien avulla voimme johtaa yhtälön ratkaistuun muotoon, missä yhtälön toisella puolella on ratkaistavissa oleva muuttuja ja toisella lukuarvo. Näin saadaan määritettyä yhtälön kaikki juuret.

Huom! Yhtäpitävyyttä merkitään ekvivalenssinuolella $\Leftrightarrow$ . Ekvivalenssinuolta tulee käyttää, jos keskenään yhtäpitävät yhtälöt kirjoitetaan rinnakkain. Tässä kirjassa yhtälöitä ratkaistaan pääsääntöisesti allekkain ja ekvivalenssinuolet jätetään merkitsemättä.

2.2.4 Esimerkki: yhtälön ratkaiseminen ja ratkaisun tarkistus

Ratkaise yhtälö 2x+1=-x+2 .

Ratkaisu:

$\begin{align*} 2x+1 & = -x+2 \;\;\;\;\;\;\;\;\,\;| +x \\ 3x+1 & = 2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; | -1 \\ 3x & = 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|:3 \\ x &= \frac{1}{3} \end{align*}$

Vastaus: $x = \displaystyle\frac{1}{3}$

Tarkistus:

Ratkaisun voi tarkistaa sijoittamalla vastaus $x=\dfrac{1}{3}$ yhtälöön:

$\begin{align*} 2\cdot\frac{1}{3}+1 &=-\frac{1}{3}+2 \\ \frac{2}{3}+\frac{3}{3} &=-\frac{1}{3}+\frac{6}{3} \\ \frac{5}{3}&=\frac{5}{3}\\ \text{}&{\bf{tosi}} \end{align*}$

Ratkaisun voi tarkistaa myös hyödyntämällä laskinohjelmistoja. Alla näytetään, miten se onnistuu Geogebran CAS-laskimella.

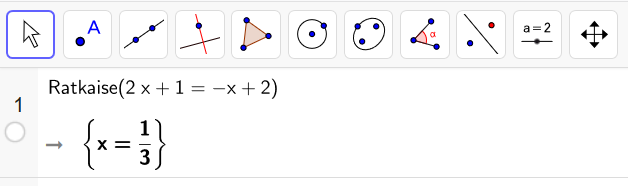
2.2.5 Esimerkki: ratkaisuja ei yhtään tai ääretön määrä

Ratkaise yhtälö.

$-5(2x-1)=-4x-2(3x-\dfrac{5}{2})$
$4x-\dfrac{2-3x}{3}=5x$

Ratkaisu:

$\begin{align*} -5(2x-1) & = -4x-2(3x-\dfrac{5}{2}) \\ -10x+5 & = -4x-6x+5 \\ -10x+5 & = -10x+5 && |-5 \\ -10x & = -10x &&|+10x \\ 0 & = 0 \\ \text{}&\text{\bf{tosi}} \end{align*}$

Yhtälö on tosi riippumatta muuttujan arvosta. Siispä yhtälöllä on äärettömän monta ratkaisua ja se toteutuu kaikilla $x \in\mathbb{R}$ (lue: " kuuluu reaalilukuihin").

$\begin{align*} 4x-\dfrac{2-3x}{3} & = 5x && |\cdot 3 \\ 12x-2+3x & = 15x \\ 15x-2 & = 15x && | -15x \\ -2 & = 0 \\ &\text{\bf{epätosi}} \end{align*}$

Yhtälö on epätosi riippumatta muuttujan arvosta, joten yhtälöllä ei ole ratkaisua.

Vastaus:

$x \in\mathbb{R}$
Yhtälöllä ei ole ratkaisua.

Huom! Esimerkin 3.2.3 yhtälöt eivät voi olla ensimmäisen asteen yhtälöitä, sillä ensimmäisen asteen yhtälöllä on aina täsmälleen yksi ratkaisu.

Ristiin kertominen

Olkoon $a,b,c,d\in\mathbb{R}$ ja $b,d\neq0$ . Tällöin voidaan sieventää

$\begin{align*} \frac{a}{b} & = \frac{c}{d} && | \cdot b \\ a & = b\cdot \frac{c}{d} && | \cdot d \\ ad & = bc \end{align*}$

Eli voidaan kertoa ristiin tällaista muotoa olevat yhtälöt.

2.2.6 Esimerkki: murtoyhtälöiden ratkaisemista

Ratkaise yhtälöt.

$\displaystyle\frac{2}{x}=\dfrac{3}{x}$
$\displaystyle\frac{2}{x+1}=\dfrac{3}{x-1}$

Ratkaisu:

Murtolauseke ei ole määritelty silloin, kun nimittäjässä on luku . Tämä tulee ottaa huomioon yhtälön ratkaisujen tarkastelussa. Saatu vastaus ei välttämättä kelpaa yhtälön ratkaisuksi.

$\begin{align*} \frac{2}{x} & = \frac{3}{x} && |\text{kerrotaan ristiin} \\ 2x & = 3x && | -2x\\ x & = 0 \end{align*}$

Murtolauseke on määritelty silloin, kun nimittäjät saavat nollasta poikkeavat arvot. Nyt tulee olla $x\neq0$ , jotta alkuperäisen yhtälön lausekkeet $\displaystyle\frac{2}{x}$ ja $\displaystyle\frac{3}{x}$ on määritelty. Siispä, yhtälöllä ei ole ratkaisua.

$\begin{align*} \frac{2}{x+1} &=\frac{3}{x-1} && |\text{kerrotaan ristiin} \\ 2(x-1) & = 3(x+1) \\ 2x-2 & = 3x+3 && |+2 \\ 2x & = 3x+5 && |-3x \\ -x & = 5 && |:(-1) \\ x & = -5 \end{align*}$

Nyt tulee olla $x\neq-1$ ja $x\neq1$ , jotta alkuperäisen yhtälön lausekkeet on määritelty. Siispä x=-5 on käypä ratkaisu.

Vastaus:

Yhtälöllä ei ole ratkaisua.

Ensimmäisen asteen yhtälö: tehtäviä

2.3 Yhtälö sovelluksissa

Usein matemaattisten ongelmien ratkaisemissa käytetään hyväksi yhtälöä. Nyt erona edellisiin esimerkkeihin yhtälö on laadittava itse. Ennen yhtälön laatimista täytyy vielä valita muuttuja. Muuttujaksi kannattaa yleensä valita tehtävänannossa kysytty seikka.

2.3.1 Esimerkki: ongelmanratkaisu yhtälön avulla

Kun kolme peräkkäistä kokonaislukua lasketaan yhteen saadaan 111 . Mitkä kolme lukua ovat kyseessä?

Ratkaisu:

Merkitään ensimmäistä lukua muuttujalla . Tällöin kaksi seuraavaa kokonaislukua ovat x+1 ja x+2 . Tästä saadaan muodostettua yhtälö.

$\begin{align*} x+(x+1)+(x+2)&=111 \\ 3x+3&=111 &&|-3\\ 3x&=108 &&|:3\\ x&=\frac{108}{3} \\ x&=36 \end{align*}$

Peräkkäiset luvut ovat siis , 36+1=37 ja 36+2=38 .

Vastaus: , ja

2.3.2 Esimerkki: kesätyöpalkan ratkaiseminen

Villen kesätöiden palkoista meni uuteen puhelimeen $\displaystyle\frac{1}{5}$ , festareihin $\displaystyle\frac{1}{7}$ ja vuokraan $\displaystyle\frac{2}{5}$ . Kuinka paljon Ville tienasi kesällä, kun edelläluettujen vähennysten jälkeen palkasta oli jäljellä $801\;\text{€}$ .

Ratkaisu:

Valitaan muuttujaksi Villen kesältä tienaama palkka. Palkka koostuu siis uudesta puhelimesta $\displaystyle\frac{x}{5}$ , festareista $\displaystyle\frac{x}{7}$ , vuokrasta $\displaystyle\frac{2x}{5}$ sekä jäljellä jäävästä osuudesta. Saadaan kirjoitettua yhtälö.

$\begin{align*} \displaystyle\frac{x}{5}+\frac{x}{7}+\frac{2x}{5}+801 &= x\;\;\;\;\;\;|\cdot35 \\ \displaystyle\frac{35x}{5}+\frac{35x}{7}+\frac{35\cdot2x}{5}+35\cdot800&=35x \\ 7x+5x+14x+28035&=35x \\ 35x-7x-5x-14x &=28035 \\ 9x &= 28035 \\ x &=\frac{28035}{9} \\ x &=3115 \end{align*}$

Vastaus: Ville tienasi kesällä $3115\;\text{€}$ .

Yhtälö sovelluksissa: tehtäviä

2.4 Yhtälöpari

Yhtälöpari

Yhtälöpari muodostuu kahdesta yhtälöstä, esimerkiksi

\[\begin{cases} 2x-y+3=0 \\ -4x+2y+1=0 \end{cases}\]

Yhtälöparin ratkaisu on lukupari (x,y) , joka toteuttaa molemmat yhtälöt. Muuttujia voidaan merkitä myös muilla kirjaimilla.

Yhtälöparin ratkaisemisessa käsin voidaan käyttää joko sijoitus- tai yhteenlaskukeinoa. Nämä menetelmät esitellään seuraavissa esimerkeissä.

2.4.1 Esimerkki: yhtälöparin ratkaiseminen sijoituskeinolla

Ratkaise yhtälöpari \[\begin{cases} 2x+y=6 \\ 3x+2y=2 \end{cases}\]

Ratkaisu:

\[\begin{cases} 2x+y=6 && (1)\\ 3x+2y=2 && (2) \end{cases}\]

Ratkaistaan esimerkiksi yhtälöstä (1) muuttuja muuttujan suhteen. Saadaan yhtälö

$y=-2x+6 \;\;\;\;\;\;(3)$

Sijoitetaan yhtälö (3) yhtälöön (2) , jolloin saadaan

$\begin{align*} 3x+2(-2x+6)&=2 \\ 3x-4x+12&=2 \\ -x&=-10 \\ x&=10 \end{align*}$

Muuttujan arvo saadaan sijoittamalla x=10 yhtälöön (3) .

$y=-2\cdot10+6=-20+6=-14$

Vastaus:

\[\begin{cases} x=10\\ y=-14 \end{cases}\]

2.4.2 Esimerkki: yhtälöparin ratkaiseminen yhteenlaskukeinolla

Ratkaise yhtälöpari \[\begin{cases} 2x+y=6 \\ 3x+2y=2 \end{cases}\]

Ratkaisu:

Kerrotaan ensin yhtälöt luvuilla, jotka tekevät muuttujan kertoimet toistensa vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.

$\begin{align*} &\begin{cases} 2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-3) \\ 3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot2\\ \end{cases}\\ + &\begin{cases} -6x-3y=-18\\ 6x+4y=4\\ \end{cases}\\ &\noindent\rule{3cm}{0.4pt}\\ &-3y+4y=-18+4\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;y=-14 \end{align*}$

Tämän jälkeen kerrotaan yhtälöt luvuilla, jotka tekevät muuttujan kertoimet toistensa vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.

$\begin{align*} &\begin{cases} 2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-2) \\ 3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot1\\ \end{cases}\\ + &\begin{cases} -4x-2y=-12\\ 3x+2y=2\\ \end{cases}\\ &\noindent\rule{3cm}{0.4pt}\\ &-4x+3x=-12+2\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=10 \end{align*}$

Vastaus:

\[\begin{cases} x=10\\ y=-14 \end{cases}\]

2.4.3 Esimerkki: yhtälöparin ratkaiseminen Geogebralla

Yhtälöparin ratkaiseminen Geogebran CAS-laskimella onnistuu syöttämällä aluksi yhtälöparin molemmat yhtälöt laskimeen. Yhtälöitä ei tarvitse välttämättä muokata muotoon y=ax+b .

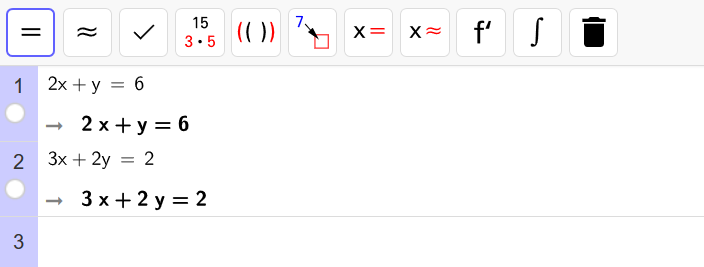
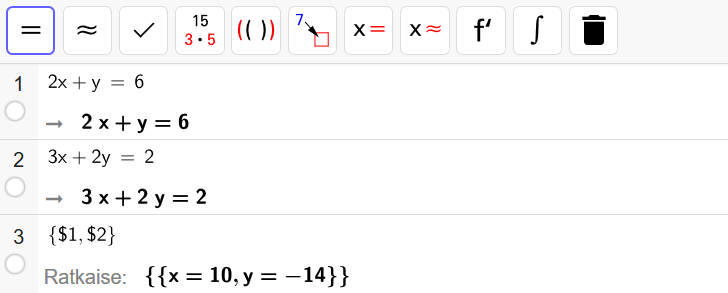
Kun yhtälöt on syötetty laskimeen, valitaan ne molemmat pitämällä ctrl- näppäintä pohjassa ja klikkaamalla vasemmasta palkista yhtälöiden vierestä. Kun yhtälöt on valittu, palkki muuttuu siniseksi. Lopuksi klikkaa yläpalkista -symbolia ja laskin kertoo yhtälöparin ratkaisun.

Yhtälöparin graafinen tarkastelu saattaa auttaa hahmottamaan paremmin tilanteen ja ratkaisujen lukumäärän. Yhtälöparin ratkaisuja ovat ne pisteet, jotka ovat kummankin yhtälön kuvaajalla.

# V7

Piirretään edellisten esimerkkien yhtälöpari koordinaatistoon. Yhtälöiden kuvaajat ovat suoria ja niiden piirtämisen helpottamiseksi ratkaistaan yhtälöt muuttujan suhteen.

$\begin{align*} 2x+y&=6 \\ y&=-2x+6 \end{align*}$

$\begin{align*} 3x+2y&=2 \\ 2y&=-3x+2 \\ y&=-\frac{3}{2}x+1 \end{align*}$

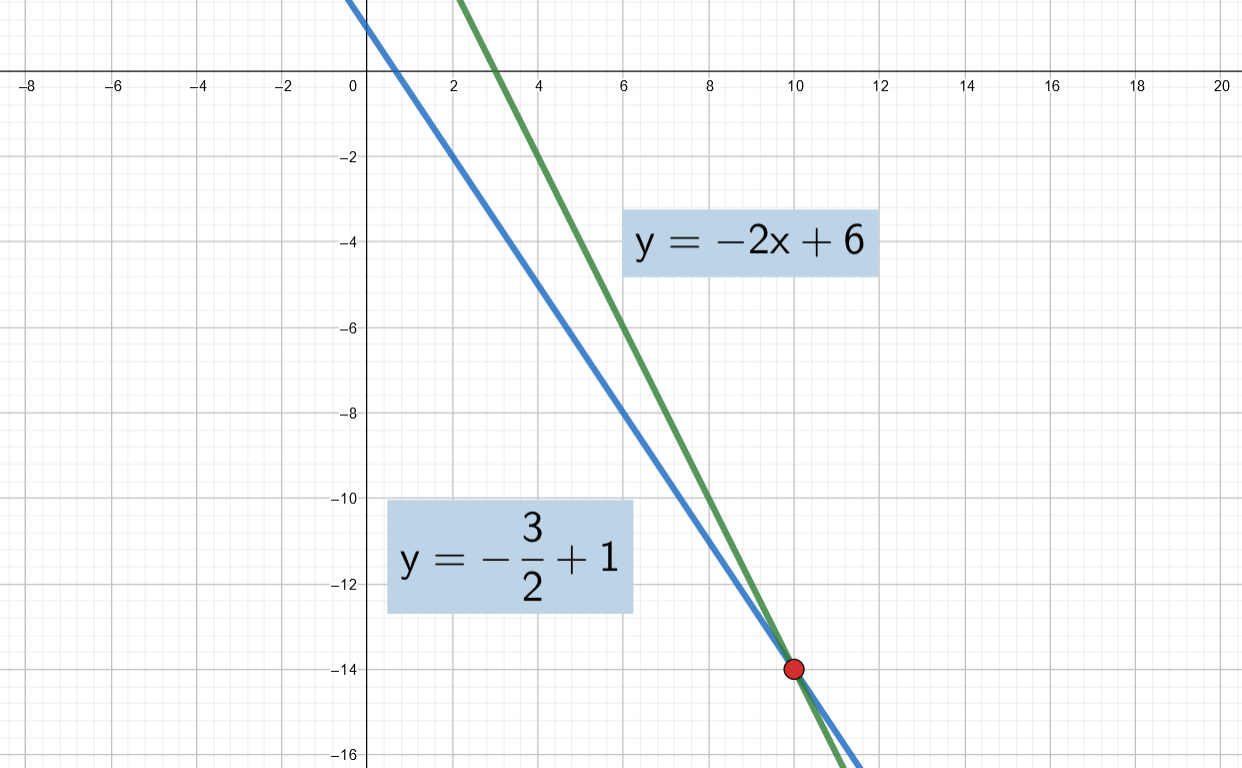
Suorien leikkauspiste (10,-14) on ainoa piste, joka toteuttaa molemmat yhtälöt, joten se on yhtälöparin ainoa ratkaisu.

2.4.4 Esimerkki: yhtälöparilla ei ratkaisua

Ratkaise yhtälöpari \[\begin{cases} 20x-15y=50 \\ 30y-40x=-30 \end{cases}\]

Ratkaisu:

Käytetään yhteenlaskukeinoa.

$\begin{align*} &\begin{cases} 20x-15y=50 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot2 \\ -40x+30y=-30 \;\;\;\;\;\;\;\,|\cdot1\\ \end{cases}\\ + &\begin{cases} 40x-30y=100\\ -40x+30y=-30 \\ \end{cases}\\ &\noindent\rule{3.2cm}{0.4pt}\\ &\;\;\;\;\,\,\,\;\;\;\;\;\;\;\;\;\;\;\;0=70\;\;\;\;\text{\bf{epätosi}}\\ \end{align*}$

Vastaus: Yhtälöparilla ei ole ratkaisua.

Tarkistus:

Ratkaistaan yhtälöt muuttujan suhteen.

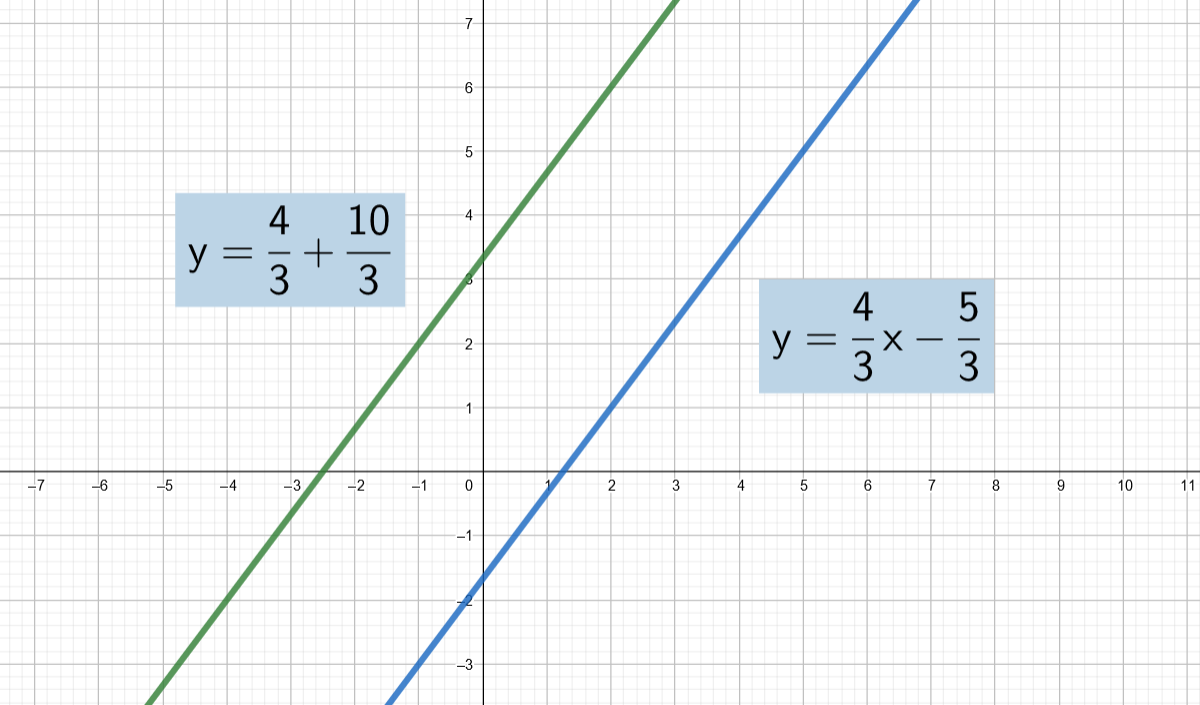
$\begin{align*} 20x-15y&=50 \\ 15y&=20x+50 \\ y&=\frac{4}{3}x+\frac{10}{3} \end{align*}$

$\begin{align*} 30y-40x&=-30 \\ 30y&=40x-50\\ y&=\frac{4}{3}x-\frac{5}{3} \end{align*}$

Suorat ovat yhdensuuntaiset (sama kulmakerroin), joten niillä ei ole yhteisiä pisteitä. Siksi yhtälöparilla ei ole ratkaisua.

2.4.5 Esimerkki: yhtälöparin ratkaisuna kaikki suoran pisteet

Ratkaise yhtälöpari \[\begin{cases} 4x-3y=-9 \\ -12x+9y=27 \end{cases}\]

Ratkaisu:

Käytetään yhteenlaskukeinoa.

$\begin{align*} &\begin{cases} 4x-3y=-9 \;\;\;\;\;\;\;\;\;\;\;|\cdot3 \\ -12x+9y=27 \;\;\;\;\;\;\;\,|\cdot1\\ \end{cases}\\ + &\begin{cases} 12x-9y=-27\\ -12x+9y=27 \\ \end{cases}\\ &\noindent\rule{3cm}{0.4pt}\\ &\;\;\;\;\,\,\,\;\;\;\;\;\;\;\;\;\;\;\;0=0\;\;\;\;\text{\bf{tosi}}\\ \end{align*}$

Koska päädyttiin yhtälöön, joka on aina tosi, yhtälöparin ratkaisuja ovat kaikki lukuparit (x,y) , joilla pätee

$\begin{align*} 4x-3y&=-9 \\ 3y&=4x+9 \\ y&=\frac{4}{3}x+3 \end{align*}$

Vastaus:

\[\begin{cases} x \in\mathbb{R} \\ y =\frac{4}{3}x+3 \end{cases}\]

Tarkistus:

Kun yhtälöt ratkaistaan muuttujan suhteen, saadaan molemmista ratkaisuksi

$y=\frac{4}{3}x+3$

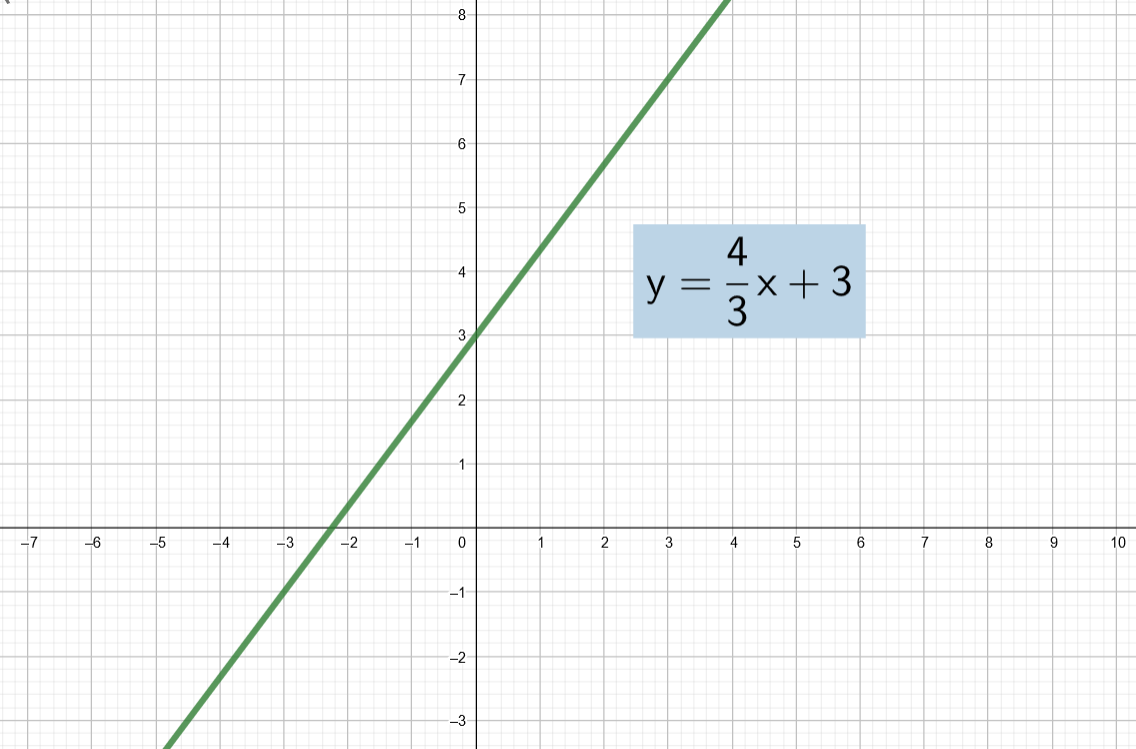
Yhtälöiden kuvaajana on siis sama suora, joten yhtälöparin ratkaisuna on kaikki suoran $y =\displaystyle\frac{4}{3}x+3$ pisteet.

2.4.6 Esimerkki: yhtälöpari sovelluksessa

Sonja haluaa suorakulmion muotoisen pöytäliinan, jonka pituus on $40\;\text{cm}$ suurempi kuin sen leveys. Sonja löysi kaupasta mieleistään kukallista kangasta ja siihen sopivaa reunanauhaa. Määritä pöytäliinaan tarvittavat mitat, kun reunanauhaa käytetään $6,0\;\text{m}$ .

Ratkaisu:

Valitaan muuttujaksi pöytäliinan leveys ja muuttujaksi pituus. Koska pituus on $40\;\text{cm}$ suurempi kuin leveys, saadaan ensimmäiseksi yhtälöksi y=x+40 . Reunanauhaa on $6,0\;\text{m}=600\;\text{cm}$ , joten toiseksi yhtälöksi saadaan 2x+2y=600 (suorakulmion piiri on $2\cdot\text{leveys}+2\cdot\text{pituus}$ ). Saadaan siis yhtälöpari

\[\begin{cases} y=x+40\\ 2x+2y=600 \end{cases}\]

Koska ensimmäinen yhtälö on ilmoitettu valmiiksi muuttujan suhteen, voidaan sijoittaa se suoraan toiseen yhtälöön.

$\begin{align*} 2x+2(x+40)=600 \\ 2x+2x+80=600 \\ 4x=520 \\ x=130 \end{align*}$
Muuttujan y arvo saadaan sijoittamalla x=130 ensimmäiseen yhtälöön.

y=130+40=170

Eli pöytäliinan kangaspalan leveys on $130\;\text{cm}$ ja pituus $170\;\text{cm}$ .

Vastaus: leveys $130\;\text{cm}$ ja pituus $170\;\text{cm}$

Yhtälöpari: tehtäviä

3. Verrannollisuus ja prosenttilaskenta

Tässä kappaleessa käsitellään verrannollisuutta sekä prosenttilaskentaa, jotka ovat matematiikan yleisiä sovelluskohteita. Verrannollisuudesta kerrataan suoraan sekä kääntäen verrannollisuus ja prosenttilaskennasta käydään läpi yleisimmät tehtävätyypit. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

3.1 Suoraan verrannollisuus

Kun työskennellään tuntipalkalla ansaitaan sitä enemmän, mitä useampi tunti työskennellään. Palkka ja tehtyjen tuntien määrä kasvavat siis samassa suhteessa. Kun esimerkiksi työtuntien määrä kasvaa kolminkertaiseksi, myös palkka kolminkertaistuu. Tällaisia suureita, joiden suhde on aina vakio, sanotaan suoraan verrannollisiksi.

Suoraan verrannollisuus

Suureet ja ovat suoraan verrannolliset, jos saadaan kertomalla vakiolla eli jos y=kx.

Vakio on nimeltään verrannollisuuskerroin.

Yhtälö y=kx saadaan muotoon $\dfrac{y}{x}=k,$ josta nähdään että suoraan verrannollisten suureiden suhde on vakio. On siis voimassa verranto $\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}$ eli $\dfrac{y_1}{y_2}=\dfrac{x_1}{x_2}.$

Suoraan verrannollisuutta kuvaa graafisesti origon kautta kulkeva suora.

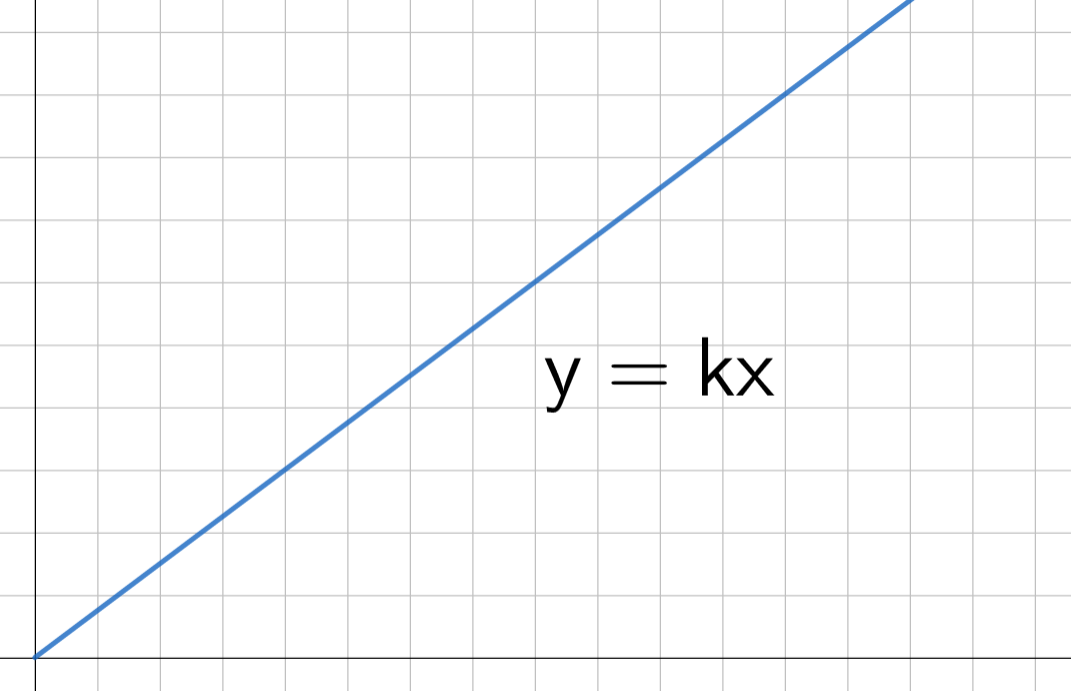
3.1.1 Esimerkki: hinnan riippuvuus määrästä Geogebralla

Tutkitaan esimerkkinä suoraan verrannollisuudesta hinnan riippuvuutta määrästä. Ostettujen tuotteiden hinta $(\text{€})$ on suoraan verrannollinen niiden määrään $(\text{kpl})$ eli

y=kx,

missä vakio kertoo yksittäisen tuotteen kappalehinnan.

Alla on Geogebralla taulukoituna toisiaan vastaavia suureiden arvoja sekä oheen piirretty arvoja vastaavat pisteet koordinaatistoon. Jos pisteiden kautta piirrettäisiin kuvaaja, se olisi muotoa y=kx oleva suora. Suoran kulmakertoimena on tuotteen kappalehinta, jota voi säätää liukusäätimestä.

3.1.2 Esimerkki: sovellus suoraan verrannollisuudesta

Vuotavasta vesihanasta tippuu tasatahtia pisaraa sekunnissa. Kuinka monta vesipisaraa hanasta tippuu minuutissa?

Ratkaisu:

Olkoon pisaramäärä ja aika . Koska pisaramäärä ja aika ovat suoraan verrannollisia suureita, niin

$\begin{align*} \frac{y_1}{x_1}=\frac{y_2}{x_2} \end{align*}$

Merkitään x_1=6, $y_1=10\;\text{(s)}$ ja $y_2=2\cdot 60=120\;\text{(s)}.$ Ratkaistaan x_2 , joka kuvaa kysyttyä pisaramäärää.

$\begin{align*} \frac{y_1}{x_1}&=\frac{y_2}{x_2} &&|\; \text{kerrotaan ristiin} \\ y_1x_2&=y_2x_1 &&|:y_1\\ x_2&=\frac{y_2 x_1}{y_1}&&|\;\text{sijoitetaan arvot}\\ x_2&=\frac{120\cdot6}{10} \\ x_2&=72 \end{align*}$

Vastaus: pisaraa

Suoraan verrannollisuus: tehtäviä

3.2 Kääntäen verrannollisuus

Kun ajetaan polkupyörällä, samaan matkaan menee lyhyempi aika, mitä kovempaa pyörällä polkee. Kun esimerkiksi nopeus kasvaa kaksinkertaiseksi, matka-aika lyhenee puoleen. Tällaisia suureita, joiden tulo on aina vakio, sanotaan kääntäen verrannollisiksi.

Kääntäen verrannollisuus

Suureet ja ovat kääntäen verrannolliset, jos saadaan jakamalla vakio suureella eli jos $y=\dfrac{k}{x}.$

Yhtälo $y=\dfrac{k}{x}$ saadaan muotoon xy=k, josta nähdään että kääntäen verrannollisten suureiden tulo on vakio. On siis voimassa myös yhtälö x_1y_1=x_2y_2 eli $\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}.$

Kääntäen verrannollisten suureiden kuvaaja on hyperbeli.

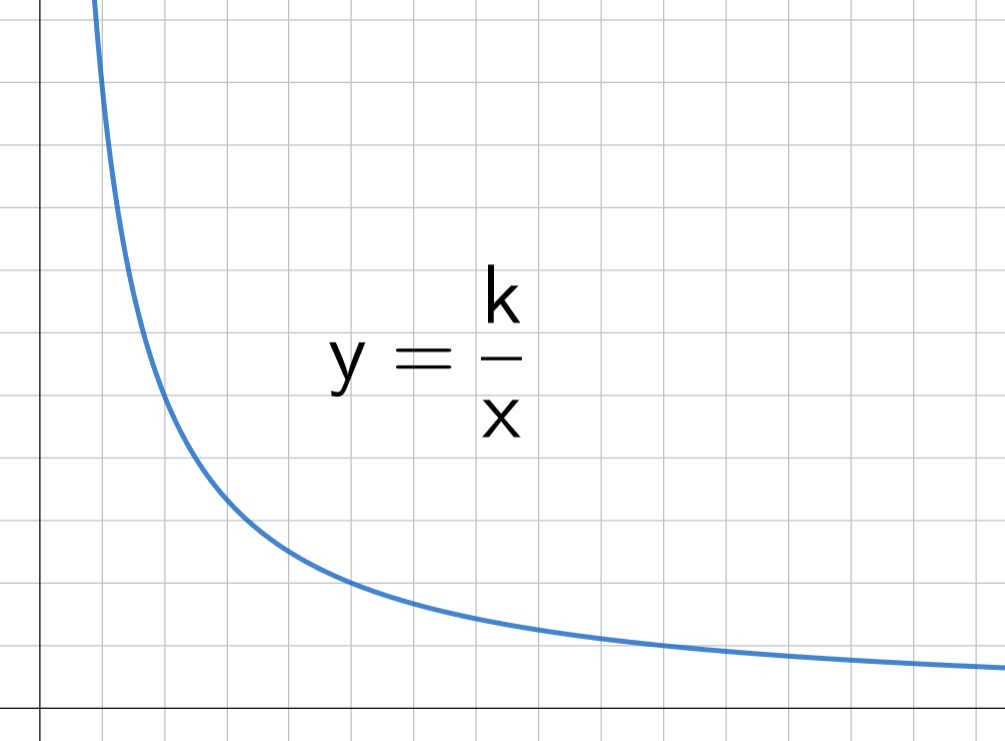
3.2.1 Esimerkki: sovellus kääntäen verrannollisuudesta

Kylpyhuoneen lattian kaakelointiin tarvitaan 360 kappaletta vaaleanpunaisia $10\;\text{cm}\times10\;\text{cm}$ -kokoisia laattoja. Kuinka paljon laattoja tarvittaisiin, jos niiden koko olisi $10\;\text{cm}\times10\;\text{cm}$ ?

Ratkaisu:

Olkoon laattojen määrä ja niiden koko. Laattojen määrä ja koko ovat kääntäen verrannollisia suureita, joten

$\begin{align*} x_1y_1=x_2y_2 \end{align*}$

Merkitään x_1=360, $y_1=10\cdot10=100\;(\text{cm}^2)$ ja $y_2=12\cdot12=144\;(\text{cm}^2)$ . Ratkaistaan x_2, joka kuvaa kysyttyä laattamäärää.

$\begin{align*} x_1y_1&=x_2y_2 && |:y_2\\ x_2&=\frac{x_1y_1}{y_2} &&|\;\text{sijoitetaan arvot}\\ x_2&=\frac{360\cdot100}{144} \\ x_2&=250 \end{align*}$

Vastaus: 250 laattaa

Kääntäen verrannollisuus: tehtäviä

3.3 Prosentti

Prosentin nimitys tulee latinan kielestä per centum, joka tarkoittaa yksi sadasta. Prosentti siis tarkoittaa sadasosaa, ja sen merkki on $\%$ . Prosenttia käytetään suhteellisen osuuden ilmoittamiseen.

Prosentti

$1\;\text{prosentti}=1\;\% =\frac{1}{100}=0,01$

3.3.1 Esimerkki: prosenttiluvun muuttaminen desimaaliluvuksi

Ilmaise sadasosina ja desimaalilukuna.

$3\;\%$
$15\;\%$
$-72\;\%$
$125,6\;\%$

Ratkaisu:

Kerrotaan prosenttiluku murtoluvulla $\dfrac{1}{100}.$ Tällöin saadaan murtoluku, jonka osoittaja kertoo suoraan desimaaliluvun sadasosat.

$3\;\%=3\cdot \displaystyle\frac{1}{100}=\displaystyle\frac{3}{100}=0,03$
$15\;\%=15\cdot \displaystyle\frac{1}{100}=\displaystyle\frac{15}{100}=0,15$
$-72\;\%=-72\cdot \displaystyle\frac{1}{100}=-\displaystyle\frac{72}{100}=-0,72$
$125,6\;\%=125,6\cdot \displaystyle\frac{1}{100}=\displaystyle\frac{125,6}{100}=1,256$

Prosenttiluvun muunnos desimaaliluvuksi vastaa siis käytännössä pilkun siirtämistä kahden numeron verran vasemmalle.

3.3.2 Esimerkki: luvun muuttaminen prosenttiluvuksi

Ilmaise prosentteina.

$\displaystyle\frac{4}{5}$

Ratkaisu:

Kerrotaan desimaaliluku sadalla, jolloin vastauksena saadaan suoraan prosenttiluku. Murtolukua muutettaessa prosenttiluvuksi, lavennetaan luku ensin muotoon, jossa nimittäjänä on luku 100.

$0,05=100\;\%\cdot 0,05=5\;\%$
$7,92=100\;\%\cdot 7,92=792\;\%$
$0,024=100\;\%\cdot 0,024=2,4\;\%$
$^{20)}\displaystyle\frac{4}{5}=\frac{80}{100}=80\;\%$

Desimaaliluvun muunnos prosenttiluvuksi vastaa siis käytännössä pilkun siirtämistä kahden numeron verran oikealle.

Seuraavaksi käydään läpi videollakin esiteltyjä, tyypillisimpiä prosenttilaskuihin liittyviä tehtävätyyppejä esimerkkien kanssa.

Kuinka paljon on prosenttia luvusta ?

Kun kysytään kuinka paljon prosenttia on luvusta , niin tällöin lasketaan tulo $p\cdot a$ Tulossa luku ilmaistaan sadasosina tai desimaalilukuna.

3.3.3 Esimerkki: prosenttia luvusta

Opiskelijaryhmän 32 opiskelijasta $62,5\;\%$ on tyttöjä. Tällöin tyttöjä on

$62,5\cdot\displaystyle\frac{1}{100}\cdot32=0,625\cdot32=20.$

3.3.4 Esimerkki: opintorahan verotus

Opintorahasta pidätettiin veroa $10\;\%$ ennen vuotta 2019 . Kuinka paljon opiskelija joutui vuodessa maksamaan veroa opintorahastaan, kun opintorahan suuruus oli $250,96\;\text{€/kk}$ ?

Ratkaisu:

Opiskelija saa vuodessa opintorahaa yhteensä $12\cdot250,96\;\text{€}$ . Tästä verotetaan $10\;\%$ , joten verotettava määrä on:

$10\;\%\cdot12\cdot250,96=\displaystyle\frac{10}{100}\cdot12\cdot250,96=301,152\approx30,15\;\text{(euroa)}.$

(Todellisuudessa opintoraha on verotonta, mutta siitä verotettiin tehtävänannon mukainen $10\;\%$ , jonka sai vuoden päätteeksi veronpalautuksina takaisin. Opintorahan pystyi halutessaan myös nostamaan suoraan verottomana.)

Vastaus: $30,15\;\text{€}$

Kuinka monta prosenttia luku on luvusta ?

Kun kysytään kuinka monta prosenttia on luvusta , niin kyseessä on suhdelasku $\frac{\displaystyle a}{\displaystyle b},$ joka muunnetaan prosenteiksi.

3.3.5 Esimerkki: montako prosenttia luku luvusta

Kuinka monta prosenttia luku on luvusta ?

$\displaystyle\frac{7}{30}\cdot100\;\%=\frac{70}{3}\;\%=23,33...\;\%\approx23,3\;\%$

3.3.6 Esimerkki: veroprosentin laskeminen

Edmonton Oilersin NHL-jääkiekkoilija Connor McDavidin bruttopalkka on $12\;500\;000$ dollaria ja tämän veronpidätys $5\;966\;250$ dollaria. Mikä on McDavidin veroprosentti?

Ratkaisu:

Lasketaan veronpidätyksen suhde bruttopalkkaan ja muutetaan tämä prosenteiksi:

$\displaystyle\frac{5\;966\;250}{12\;500\;000}=0,4797\approx0.48=48\;\%$

Vastaus: Veroprosentti on $48\;\%$ .

Prosenttilaskenta: tehtäviä

3.4 Muutos- ja vertailuprosentti

Prosenttiluvuilla kuvataan myös suureen muutosta alkuperäisestä arvosta.

Muutosprosentti

Kuinka monta prosenttia muutos on? $\displaystyle\frac{\text{muutos}}{\text{alkuperäinen arvo}}\cdot 100\;\%$

HUOM! Prosenttiyksikkö on absoluuttisen pronsenttimäärän yksikkö. Esimerkiksi koron noustessa 10 prosentista 11 prosenttiin:

korko kasvaa 10 prosenttia
korko kasvaa yhden prosenttiyksikön

3.4.1 Esimerkki: vuokran muutos prosentteina

Vuokra nousi 327 eurosta 333 euroon. Kuinka monta prosenttia vuokra nousi?

Ratkaisu:

Tapa 1:

Lasketaan vuokran muutoksen suuruus: $333-327=6\;\text{(euroa)}$

Lasketaan muutoksen suhde alkuperäiseen vuokraan: $\displaystyle\frac{6}{327}\approx0,018=1,8\;\%$

Tapa 2:

Lasketaan suoraan uuden vuokran suhde alkuperäiseen vuokraan:

$\displaystyle\frac{333}{327}\approx1,018=101,8\;\%$

Lasketaan suhteen ja alkuperäisen vuokran välinen ero, kun alkuperäistä vuokraa vastaava osuus on $100\;\%$ :

$101,8\;\%-100\;\%=1,8\;\%$

Vastaus: Vuokra nousi $1,8\;\%$ .

3.4.2 Esimerkki: prosentti vs. prosenttiyksikkö

Vuoden 2007 uusista ylioppilaista $57\;\%$ ei jatkanut tutkintoon johtavassa koulutuksessa valmistumisvuonnaan. Vuonna 2017 uusista ylioppilaista $72\;\%$ ei jatkanut tutkintoon johtavassa koulutuksessa valmistumisvuonnaan.

Kuinka monta prosenttiyksikköä tutkintoaan jatkamattomien määrä kasvoi vuodesta vuoteen ?
Kuinka monta prosenttia tutkintoaan jatkamattomien osuus kasvoi vuodesta vuoteen ?

Ratkaisu:

Lasketaan muutos prosenttiyksiköissä .

Tutkintoaan jatkamattomien määrä kasvoi prosenttiyksikköä.

Tutkintoaan jatkamattomien osuus kasvoi prosenttiyksikköä, jonka osuus alkuperäisestä osuudesta on:

$\displaystyle\frac{15}{57}\approx0,263=26,3\%.$

Tutkintoaan jatkamattomien osuus kasvoi $26,3\%$ .

Vastaus:

prosenttiyksikköä
$26,3\%$

Vertailuprosentti lasketaan samaan tyyliin kuin muutosprosentti.

Vertailuprosentti

Kuinka monta prosenttia on suurempi kuin ?

$\displaystyle\frac{a-b}{b}\cdot100\;\%$

Kuinka monta prosenttia on pienempi kuin ?

$\displaystyle\frac{a-b}{a}\cdot100\;\%$

3.4.3 Esimerkki: vertailuprosentit

Iltalehden tietojen mukaan Vaasalaisen jääkiekkoseura Sportin pelaajabudjetti kaudella 2018-2019 oli 1,5 miljoonan euron suuruinen, kun taas Helsinkiläisen HIFK:n budjetti oli 3,25 miljoonaa euroa.

Kuinka monta prosenttia Sportin pelaajabudjetti oli pienempi kuin HIFK:n?
Kuinka monta prosenttia HIFK:n pelaajabudjetti oli suurempi kuin Sportin?

Ratkaisu:

Lasketaan, kuinka monta prosenttia budjettien erotus on HIFK:in budjetista.

$\displaystyle\frac{3,25\;\text{milj. €}-1,5\;\text{milj. €}}{3,25\;\text{milj. €}} \approx 0,538=53,8\%$

Sportin pelaajabudjetti oli $53,8\;\%$ pienempi kuin HIFK:n.

Lasketaan, kuinka monta prosenttia budjettien erotus on Sportin budjetista.

$\displaystyle\frac{3,25\;\text{milj. €}-1,5\;\text{milj. €}}{1,5\;\text{milj. €}} \approx 1,167=116,7\%$

HIFK:n pelaajabudjetti oli $116,7\;\%$ suurempi kuin Sportin.

(Tehtävän olisi voinut ratkaista myös esimerkin 4.2.1 toisella tavalla)

Vastaus:

$53,8\;\%$
$116,7\;\%$

Muutos- ja vertailuprosentti: tehtäviä

3.5 Muuttuneen arvon laskeminen

Kun positiivinen luku kasvaa $p\;\%$ , saadaan

$a+\frac{p}{100}\;a=(1+\frac{p}{100})a$

Samoin kun pienenee $p\;\%$ , saadaan

$a-\frac{p}{100}\;a=(1-\frac{p}{100})a$

Näin saadaan laskettua muuttunut arvo.

Korotus

Mikä luku on $p\;\%$ suurempi kuin ?

$(1+\frac{p}{100})a$

Alennus

Mikä luku on $p\;\%$ pienempi kuin ?

$(1-\frac{p}{100})a$

3.5.1 Esimerkki: talletuksen arvo koron jälkeen

Pankki tarjoaa $2,5\%$ korkoa vuotuiselle talletuksella. Paljonko pankki antaa vuoden lopuksi takaisin

euron
$555\;555$ euron

talletuksesta?

Ratkaisu:

Pankki tarjoaa $2,5\;\%$ korkoa, joten vuoden lopuksi talletuksen suuruus on $100\%+2,5\%=102,5\%$ alkuperäisestä. Kerrotaan tällä alkuperäisen talletuksen suuruus:

$102,5\;\%\cdot1225=1,025\cdot1225=1255,625\approx1256\;\text{(euroa)}$

Pankki tarjoaa $2,5\;\%$ korkoa, joten vuoden lopuksi talletuksen suuruus on $100\;\%+2,5\;\%=102,5\;\%$ alkuperäisestä. Kerrotaan tällä alkuperäisen talletuksen suuruus:

$102,5\;\%\cdot555\;555=1,025\cdot555\;555=569\;443,8750\approx569\;444\;\text{(euroa)}$

Vastaus:

$1256\;\text{€}$
$569\;444\;\text{€}$

3.5.2 Esimerkki: osakkeiden hinta laskun jälkeen

Nokian osakkeet laskivat aamupäivällä $10,9\;\%$ . Kuinka paljon maksaa aiemmin

$1\;000\;\text{euroa}$
$12\;475\;\text{euroa}$

maksaneet osakkeet?

Ratkaisu:

Osakkeet laskivat $10,9\;\%$ , joten uusi osakkeiden hinta on $100\;\%-10,9\;\%=89,1\;\%$ alkuperäisestä. Kerrotaan tällä alkuperäinen hinta:

$89,1\;\%\cdot1000=0,891\cdot1000=891\;\text{(euroa)}$

Osakkeet laskivat $10,9\;\%$ , joten uusi osakkeiden hinta on $100\;\%-10,9\;\%=89,1\;\%$ alkuperäisestä. Kerrotaan tällä (desimaaliluku) alkuperäinen hinta:

$0,891\cdot12\;475=11\;115,22500\approx11\;115\;\text{(euroa)}$

Vastaus:

$891\;\text{€}$
$11\;115\;\text{€}$

3.5.3 Esimerkki: epäonnistunut myyntikikkailu

Viekas kaupistelija ajatteli, että jos hän nostaa ensin joulusuklaan hintaa $75\;\%$ ja tämän jälkeen ilmoittaa asiakkaillensa, että joulusuklaa on $60\;\%$ alennuksessa, niin hän saisi alennusmyynnin turvin myytyä suklaata alkuperäistä hintaa kalliimmalla.

Oliko kauppias oikeassa? Jos suklaan lähtöhinta oli $5,60\;\text{€}$ , kuinka paljon se maksoi myyntikikkailujen jälkeen?

Ratkaisu:

Kauppias korottaa hintaa $75\;\%$ , jonka jälkeen hinta on $1,75\cdot5,60\;\text{€}.$

Korotettua hintaa alennetaan $60\;\%$ , jonka jälkeen uusi hinta on $0,4\cdot1,75\cdot5,60\;\text{€}=0,7\cdot5,60\;\text{€}=3,92\;\text{€}.$

Kauppiaan myyntikikkailujen jälkeen uusi hinta on siis $70\%$ alkuperäisestä eli $3,92\;\text{€}.$ Kauppias myy nyt $100\%-70\%=30\%$ halvemalla joulusuklaataan.

Vastaus: Kauppias oli väärässä ja uusi hinta oli $3,92\;\text{€}$ .

Muuttuneen arvon laskeminen: tehtäviä

3.6 Prosenttilausekkeita ja -yhtälöitä

Katsotaan lopuksi esimerkkejä, joissa yhtälön ratkaisua käytetään hyväksi prosenttilaskennan tehtävissä.

3.6.1 Esimerkki: uusi arvo prosenttilausekkeena

Olkoon tietokoneen hinta. Ilmaise lausekkeena tietokoneen uusi arvo, kun

hinta nousee $30\;\%$
hinta laskee $15\;\%$

Ratkaisu:

Korotuskaavalla saadaan: $\displaystyle\frac{100+30}{100}x=\frac{130}{100}x=1,3x$

(Lausekkeen voisi muodostaa myös siten, että lisää alkuperäiseen osuuteen $30\;\%$ korotuksen eli $100\;\%+30\;\%=130\;\%=1,3$ ja kertoo tällä alkuperäisen hinnan.)

Alennuskaavalla saadaan: $\displaystyle\frac{100-15}{100}x=\frac{85}{100}x=0,85x$

(Lausekkeen voisi muodostaa myös siten, että vähentää alkuperäisestä osuudesta $15\;\%$ alennuksen eli $100\;\%-15\;\%=85\;\%=0,85$ ja kertoo tällä alkuperäisen hinnan.)

3.6.2 Esimerkki: alkuperäisen arvon laskeminen

Mikä oli edellisen esimerkin tietokoneen alkuperäinen arvo, kun sen hinta korotuksen jälkeen oli $907,40\;\text{€}$ ?

Ratkaisu:

Edellisen esimerkin lausekkeen avulla saadaan muodostettua yhtälö

$\begin{align*} 1,3x&=907,4 \\ x&=\displaystyle\frac{907,4}{1,3} \\ x&=698 \end{align*}$

Vastaus: Tietokoneen alkuperäinen hinta oli $698\;\text{€}$ .

3.6.3 Esimerkki: polttoainekustannusten muutos

Bensan hinta nousi viime viikon jälkeen $7,5\;\%$ , minkä vuoksi perhe päätti, että autolla ajetaan puolet vähemmän. Paljonko perheen tämän viikon polttoainekustannukset muuttuvat verrattuna viime viikon kustannuksiin?

Ratkaisu:

Merkitään muuttujalla polttoaineen hintaa viime viikolla.

Bensan hinta nousi $7,5\%$ , joten uusi bensan hinta on 1,075x .

Perhe ajaa autolla puolet vähemmän, joten polttoaineeseen kuluu rahaa $0,5\cdot1,075x=0,5375x$ .

Muutos viime viikon kustannuksiin on $\displaystyle\frac{x-0,5375x}{x}=\displaystyle\frac{0,4625x}{x}=0,4625\approx46,3\%$ .

Vastaus: Polttoainekustannukset vähenivät $46,3\;\%$ .

3.6.4 Esimerkki: hinnan korotus ja alennus alkuperäiseen

Hintaa korotetaan ensin $p\;\%$ . Kuinka monta prosenttia tulisi korotettua hinta alentaa, jotta hinta olisi alkuperäisen suuruinen?

Ratkaisu:

Merkitään muuttujalla alennusta prosentteina.

Hintaa korotetaan $p\;\%$ : $\displaystyle\frac{100+p}{100}h$

Korotettua hintaa alennetaan $x\;\%$ : $\displaystyle\frac{100-x}{100}\displaystyle\frac{100+p}{100}h$

Muodostetaan ja ratkaistaan yhtälö, kun uuden hinnan tulee olla yhtä suuri kuin alkuperäinen:

$\begin{align*} \frac{100-x}{100}\frac{100+p}{100}h & = h && |:h \\ \frac{100-x}{100}\frac{100+p}{100} & = 1 && | \cdot 100 \cdot 100 \\ (100-x)(100+p) &= 10000 \\ 10 000+100p-100x-xp&=10000 && |-10000 \\ 100p-100x-xp&=0 && |+100x+xp \\ 100x+xp&=100p \\ x(100+p)&=100p && |:(100+p) \\ x&=\frac{100p}{100+p} \end{align*}$

Vastaus: $\displaystyle\frac{100p}{100+p}\;\%$

Prosenttilausekkeita ja -yhtälöitä: tehtäviä

Hei

— 23 Nov 19

4. Potenssi ja juuri

Tässä kappaleessa käsitellään potenssilaskentaa sekä potenssille käänteistä laskutoimitusta juurta, keskittyen neliö- ja kuutiojuureen. Kappaleessa käydään läpi potenssien ja juurien laskusääntöjä, kymmenpotenssimuoto sekä lopuksi perehdytään potenssiyhtälöön. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

4.1 Potenssi

Potenssi on kertolaskun lyhennetty merkitsemistapa silloin, kun samaa lukua kerrotaan itsellään useamman kerran. Esimerkiksi merkintä 4^3 tarkoittaa tuloa $4\cdot4\cdot4$ ja se luetaan "neljä potenssiin kolme" tai "luvun 4 kolmas potenssi".

Potenssi

Olkoon positiivinen kokonaisluku ( n=1, 2, 3, ... ). Tällöin luvun :s potenssi on

$a^n=\underbrace{a\cdot a\cdot ... \cdot a}_{\text{$n$ kappaletta}}$

Erityisesti a^1=a.

Luku on potenssin kantaluku ja luku on eksponentti. Kantaluku on toisinaan tarpeen merkitä sulkeisiin. Esimerkiksi -3^2=-9, mutta (-3)^2=9. Samoin $\displaystyle\frac{2}{3}^2=\frac{4}{3},$ mutta $\left(\displaystyle\frac{2}{3}\right)^2=\displaystyle\frac{4}{9}.$

Potenssien sanotaan olevan samankantaisia, jos niillä on sama kantaluku.

Negatiivisen kantaluvun potenssi

Jos potenssin a^n kantaluku on negatiivinen ja eksponentti on

parillinen, niin potenssin arvo on positiivinen
pariton, niin potenssin arvo on negatiivinen

hei kiva määritelmä

— 09 Nov 19

4.1.1 Esimerkki: negatiivisen kantaluvun potenssi

Laske.

luvun toinen potenssi
luvun kolmas potenssi
luvun toisen potenssin vastaluku
luvun :s potenssi

Ratkaisu:

Negatiivinen kantaluku pitää merkitä sulkeisiin. Luvun toinen potenssi on

$(-3)^2=\underbrace{(-3)\cdot(-3)}_{2\text{ kpl, parillinen}}=9$

Luvun kolmas potenssi on

$(-2)^3=\underbrace{(-2)\cdot(-2)\cdot(-2)}_{3\text{ kpl, pariton}}=-8$

Luvun toinen potenssi on ja sen vastaluku

$-5^2=-5\cdot5=-25$

Luvun :s potenssi

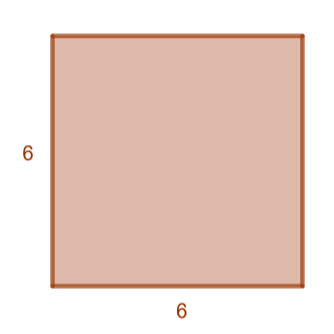
$(-1)^{2500}=\underbrace{(-1)\cdot(-1)\cdot ... \cdot(-1)}_{2500\text{ kpl, parillinen}}=1$

4.1.2 Esimerkki: neliö ja kuutio

Laske

neliön, jonka sivun pituus on pinta-ala.

kuution, jonka särmän pituus on tilavuus.

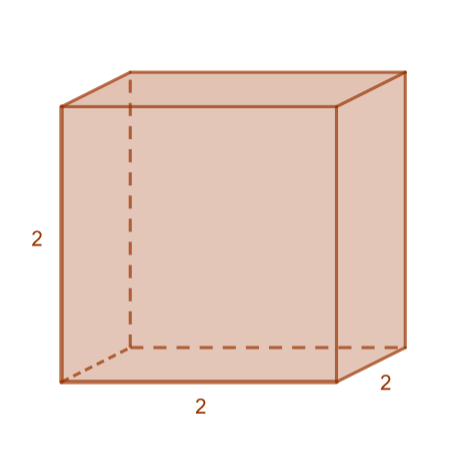
Ratkaisu:

Neliön pinta-ala saadaan kannan ja korkeuden tulona, joka voidaan ilmaista potenssin avulla.

$A=6^2=6\cdot6=36$

Kuution tilavuus saadaan särmien tulona, joka voidaan ilmaista potenssin avulla.

$V=2^3=2\cdot2\cdot2=8$

Potenssia a^2 sanotaan luvun neliöksi ja potenssia a^3 luvun kuutioksi.

4.1.3 Esimerkki: rahaston arvon kasvu

Eetu voitti veikkaamalla $6\,000$ euroa, jotka hän päätti sijoittaa indeksirahastoihin. Asiantuntija arvioi, että Eetu saisi $6,5\;\%$ :n vuotuisella korolla voittoa. Kuinka paljon Eetun rahaston arvo on vuoden kuluttua jos oletetaan, että vuotuinen korko säilyy?

Ratkaisu:

Indeksirahasto tuottaa vuodesa $6,5\;\%$ pääomasta, joten rahaston arvo kasvaa siis vuodessa 1,065 -kertaiseksi. Yhden vuoden kuluttua Eetun pääoman arvo on

$1,065\cdot6000\;\text{(euroa)}$

Korkoprosentti säilyy vakiona, joten vastaavasti myös seuraavan vuoden aikana rahaston arvo kasvaa 1,065 -kertaiseksi. Kahden vuoden kuluttua rahaston arvo on

$\underbrace{1,065\cdot 1,065}_{\text{$2$ kappaletta}}\cdot\;6000=1,065^2\cdot6000$

Vastaavasti kolmen vuoden kuluttua rahaston arvo on

$\underbrace{1,065\cdot 1,065\cdot1,065}_{\text{$3$ kappaletta}}\cdot\;6000=1,065^3\cdot6000$

20 vuoden kuluttua rahaston arvo on

$\underbrace{1,065\cdot 1,065\cdot ... \cdot 1,065}_{\text{20 kappaletta}}\cdot\;6000=1,065^{20}\cdot6000=21141,87038\approx21141,87$

Vastaus: vuoden kuluttua Eetun rahaston arvo on $21\;141,87$ euroa.

Rahalaskut pyöristetään aina sentin tarkkuudella ellei toisin mainita.

Potenssi: tehtäviä

4.2 Potenssin laskusääntöjä

Videolla esitellään viisi potenssien laskusääntöä, jotka käydään seuraavaksi läpi.

Potenssilauseke voidaan sieventää purkamalla sen potenssit tuloiksi. Tarkastellaan näin muutamia esimerkkejä ja yleistetään niiden perusteella potenssien laskusäännöt.

$a^2a^4=\underbrace{a\cdot a}_{\text{$2$ kpl}} \cdot \underbrace{a\cdot a\cdot a \cdot a}_{\text{$4$ kpl}}=a^{2+4}=a^6$

$\dfrac{a^7}{a^3}=\dfrac{a\cdot a\cdot a\cdot a\cdot \cancel{a}\cdot \cancel{a}\cdot \cancel{a}}{\cancel{a}\cdot \cancel{a}\cdot \cancel{a}}=a^{7-3}=a^4$

Samankantaisten potenssien tulossa eksponentit lasketaan yhteen ja samankantaisten potenssien osamäärässä eksponentit vähennetään toisistaan.

Samankantaisten potenssien tulo ja osamäärä

$a^ma^n=a^{m+n}$

$\frac{a^m}{a^n}=a^{m-n}$

$(ab)^3=ab\cdot ab \cdot ab=a\cdot a\cdot a\cdot b\cdot b\cdot b=a^3b^3$

$(\dfrac{a}{b})^3=\dfrac{a}{b}\cdot\dfrac{a}{b}\cdot\dfrac{a}{b}=\dfrac{a\cdot a\cdot a}{b\cdot b\cdot b}=\dfrac{a^3}{b^3}$

Tulon potenssissa tulon tekijät korotetaan erikseen potenssiin ja osamäärän potenssissa jakaja ja jaettava korotetaan erikseen potenssiin.

Tulon potenssi ja osamäärän potenssi

(ab)^n=a^nb^n

$\Big(\frac{a}{b}\Big)^n=\frac{a^n}{b^n}$

$(a^3)^2=\underbrace{a^3\cdot a^3}_{\text{$2$ kpl}}=a^{3\cdot2}=a^6$

Kun potenssi korotetaan potenssiin, niin eksponentiksi tulee eksponenttien tulo.

Potenssin potenssi $(a^{m})^n=a^{mn}$

4.2.1 Esimerkki: potenssin laskusääntöjä

Laske

$\left(\dfrac{12}{3}\right)^2$ b. c. $\dfrac{(-5)^7}{(-5)^5}$

Ratkaisu:

Osamäärän potenssissa sekä nimittäjä että osoittaja korotetaan potenssiin.

$\left(\dfrac{12}{3}\right)^2=\dfrac{12^2}{3^2}=\dfrac{144}{9}=16$

Potenssin potenssissa eksponentit kerrotaan keskenään.

$(3^2)^2=3^{2\cdot2}=3^4=81$

Samankantaisten potenssien osamäärässä eksponentit vähennetään toisistaan.

$\dfrac{(-5)^7}{(-5)^5}=(-5)^{7-5}=(-5)^2=25$

4.2.2 Esimerkki: potenssien sieventämistä

Sievennä.

$\dfrac{2d^7}{d^3}$ b. $3a^4\cdot(-2a^3)$ c.

Ratkaisu:

kantaisten potenssien eksponentit vähennetään toisistaan ja luku jää eteen kertoimeksi.

$\dfrac{2d^7}{d^3}=2d^{7-3}=2d^4$

kantaisten potenssien eksponentit lisätään yhteen ja luvut ja kerrotaan keskenään.

$3a^4\cdot(-2a^3)=-6a^{4+3}=-6a^7$

Jokainen termi korotetaan erikseen toiseen.

$(ax^3y)^2=a^2(x^3)^2y^2=a^2x^{3\cdot2}y^2=a^2x^{6}y^2$

Tutkitaan seuraavaksi, miten tulkitaan potenssi, missä eksponentti on tai negatiivinen kokonaisluku.

Samankantaisten potenssien osamäärän laskusäännön nojalla:

$\dfrac{a^n}{a^n}=a^{n-n}=a^0$

Toisaalta supistamalla saadaan:

$\dfrac{a^n}{a^n}=\dfrac{\overbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}^{n\;\text{ kpl}}}{\underbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}_{n\;\text{ kpl}}} =1$

On siis määriteltävä, että a^0=1, kun $a\neq0.$

Merkitään .

Samankantaisten potenssien osamäärän laskusäännön nojalla:

$\dfrac{a^m}{a^n}=a^{m-n}=a^{-(n-m)}=a^{-p}$

Toisaalta supistamalla saadaan ( $p=n-m \Leftrightarrow n=p+m$ ):

$\dfrac{a^m}{a^n}=\dfrac{\overbrace{a\cdot a\cdot ... \cdot a}^{m\;\text{kpl}}}{\underbrace{a\cdot a\cdot ... \cdot a}_{n\;\text{kpl}}} =\dfrac{\overbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}^{m\;\text{kpl}}}{\underbrace{a\cdot a\cdot ... \cdot a}_{p\;\text{kpl}}\cdot \underbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}_{m \;\text{kpl}}} =\dfrac{1}{\underbrace{a\cdot a\cdot ... \cdot a}_{p\;\text{kpl}}}=\dfrac{1}{a^{p}}$

On siis määriteltävä, että $a^{-p}=\dfrac{1}{a^p}.$

Eksponenttina nolla ja negatiivinen kokonaisluku

Olkoon $a\neq0$ ja positiivinen kokonaisluku.

${a^0}=1$

${a^{-n}}=\frac{1}{a^{n}}$

Erityisesti $a^{-1}=\dfrac{1}{a}$ . Eli luvun käänteislukua voidaan merkitä muodossa $a^{-1}$ .

Jos kantalukuna on murtomerkintä ja eksponentti negatiivinen, niin eksponentti voidaan vaihtaa positiiviseksi samalla, kun vaihdetaan kantaluku käänteisluvukseen.

$\left(\frac{k}{l}\right)^{-n}=\left(\frac{l}{k}\right)^{n}$

4.2.3 Esimerkki: negatiivinen eksponentti

Laske.

$4^{-3}$
$\dfrac{3^2}{3^4}$
$\left(\dfrac{2}{3}\right)^{-2}$
$(1,43\cdot10^{999})^0$

Ratkaisu:

Negatiivinen eksponentti hyppää kantaluvun käänteisluvun nimittäjään.

$4^{-3}=\dfrac{1}{4^3}=\dfrac{1}{64}$

Samankantaisten potenssien eksponentit vähennetään toisistaan ja saadaan negatiivinen eksponentti.

$\dfrac{3^2}{3^4}=3^{2-4}=3^{-2}=\dfrac{1}{3^2}=\dfrac{1}{9}$

Vaihdetaan eksponentti positiiviseksi ja kantaluku käänteisluvukseen.

$\left(\dfrac{2}{3}\right)^{-2}=\left(\dfrac{3}{2}\right)^{2}=\dfrac{3^2}{2^2}=\dfrac{9}{4}$

Jokaisen luvun nollas potenssi on luku . (Paitsi ei ole määritelty.)

$(1,43\cdot10^{999})^0=1$

Potenssin laskusääntöjä: tehtäviä

4.3 Kymmenpotenssimuoto

Suuria lukuja on tapana ilmaista kymmenpotenssimuodossa eli luvun potenssien avulla. Esimerkiksi, kun syötetään laskimeen luku $5^{16}$ , niin laskin antaa sen mitä todennäköisimmin muodossa $1,5\cdot10^{11},$ koska luku $5^{16}=152\;587\;890\;625\approx1 \underbrace{50\;000\;000\;000}_{11\text{kpl}}$ on liian suuri laskimen näytölle.

Kymmenpotenssimuoto (suuret luvut)

Suuri luku voidaan merkitä kymmenpotenssimuodossa $a\cdot10^n,$ missä $1 \leq a<10$ ja on positiivinen kokonaisluku.

4.3.1 Esimerkki: suuren luvun muuttaminen kymmenpotenssimuotoon

Ilmaise kolmen numeron tarkkuudella kymmenpotenssimuodossa

Suomen väkiluku $5\;518\;000$
maapallon ympärysmitta $40\;000\;\text{km}$
valon nopeus tyhjiössä $299\;792\;458\;\text{m/s}$

Ratkaisu:

$\begin{align*} &5 \underbrace{518\;000}_{6\text{kpl}} && \text{Siirretään pilkkua 6 numeroa vasemmalle} \\ &= 5,518\;000 \cdot 10^6\ && \text{Pyöristetään kolmen numeron tarkkuuteen}\\ &\approx 5,52 \cdot 10^6 && \\ \end{align*}$

$\begin{align*} &4 \underbrace{0\;000}_{4\text{kpl}} && \text{Siirretään pilkkua 4 numeroa vasemmalle} \\ &= 4,0000 \cdot 10^6\ && \text{Pyöristetään kolmen numeron tarkkuuteen}\\ &\approx 4,00 \cdot 10^4\;\text{(km)}&& \\ \end{align*}$

$\begin{align*} &2 \underbrace{99\;792\;458}_{8\text{kpl}} && \text{Siirretään pilkkua 8 numeroa vasemmalle} \\ &= 2,99792458 \cdot 10^8\ && \text{Pyöristetään kolmen numeron tarkkuuteen}\\ &\approx 3,00 \cdot 10^8\;\text{(m/s)} && \\ \end{align*}$

Erityisesti luonnontieteissä myös pieniä lukuja on tapana ilmaista kymmenpotenssimuodossa negatiivisen eksponentin avulla. Esimerkiksi:

$0,0003=3\cdot0,0001=3\cdot \dfrac{1}{10000}=3\cdot \dfrac{1}{10^4}=3\cdot10^{-4}$

Kymmenpotenssimuoto (pienet luvut)

Pieni luku voidaan merkitä kymmenpotenssimuodossa $a\cdot10^{-n},$

missä $1 \leq a<10$ ja on positiivinen kokonaisluku.

4.3.2 Esimerkki: pienen luvun muuttaminen standardimuotoon

Kirjoita standardimuodossa

protonin massa $1,672 621 64 \cdot 10^{-27}\;\text{kg}$
elektronin massa $9,109 382 15 \cdot 10^{-31}\;\text{kg}$

Ratkaisu:

Luvussa $10^{-27}=\dfrac{1}{10^{27}}$ on desimaalipilkun jälkeen nollaa ennen ykköstä.

$\begin{align*} &1,672\;621\;64\cdot 10^{-27}\;\text{kg}\\ =&\;1,672\;621\;64 \cdot 0,\underbrace{000\;000\;000\;000\;000\;000\;000\;000\;00}_{26\;\text{kpl}}1\;\text{kg} \\ =&\;0,\underbrace{000\;000\;000\;000\;000\;000\;000\;000\;00}_{26\;\text{kpl}}1\;672\;621\;64\;\text{kg} \end{align*}$

Luvussa $10^{-31}=\dfrac{1}{10^{31}}$ on desimaalipilkun jälkeen nollaa ennen ykköstä.

$\begin{align*} &9, 109\;382\;15 \cdot 10^{-31}\;\text{kg} \\ =&\;9, 109\;382\;15 \cdot 0,\underbrace{000\;000\;000\;000\;000\;000\;000\;000\;000\;000}_{30\;\text{kpl}}\;1\;\text{kg} \\ =& \;0,\underbrace{000 \;000\; 000\; 000\; 000\; 000\; 000\; 000\; 000\; 000}_{30\;\text{kpl}}\;910\;9 38\;2 15\;\text{kg} \end{align*}$

Kymmenpotenssimuoto: tehtäviä

4.4 Neliö- ja kuutiojuuri

Olkoon neliön pinta-ala A=9 . Mikä on neliön sivun pituus?

Neliön pinta-ala saadaan sivun neliönä, eli nyt tulee pohtia sitä, että mikä luku toteuttaa yhtälön x^2=9 .

Tiedämme, että 3^2=9 ja toisaalta (-3)^2=9 . Siispä x=3 tai x=-3 . Kuitenkin, sivun pituus ei voi olla negatiivinen luku, joten vain x=3 kelpaa nyt yhtälön ratkaisuksi. Neliön sivun pituus on siis x=3 .

Voidaan osoittaa, että yhtälöllä x^2=a on kaksi ratkaisua aina kun a>0. Positiivista ratkaisua sanotaan luvun neliöjuureksi ja merkitään $\sqrt{a}.$ Lukua sanotaan neliöjuuren juurrettavaksi.

Neliöjuuri

Luvun $a\geq 0$ neliöjuuri $\sqrt{a}$ toteuttaa ehdot

$\sqrt{a}\geq 0$
$(\sqrt{a})^2=a$

Miksi $a\geq0$ ?

Tiedämme, ettei minkään $^{*)}$ reaaliluvun parillinen potenssi voi olla negatiivinen luku. Neliöjuuren määrittelyehtona on siis, että juurrettavan tulee olla positiivinen tai nolla.

Miksi $\sqrt{a}\geq 0$ ?

Voisimme siis määritellä, että esimerkiksi $\sqrt{9}=3$ tai $\sqrt{9}=-3$ , sillä 3^2=(-3)^2=9 . Kuitenkin, neliöjuuren määritelmässä on tehty valinta, että neliöjuuri on vain ja ainoastaan ei-negatiivinen ratkaisu. Tämä valinta on tehty siksi, että neliöjuuri olisi yksikäsitteinen, eli voidaan sanoa yksikäsitteisesti esimerkiksi, että $\sqrt{9}=3$ .

$^{*)}$ Kompleksilukujen joukossa on määritelty $\textit{imaginääriyksikkö}$ i^2=-1 . Tällöin kompleksilukualueella yhtälön x^2=-4 ratkaisu olisi x=2i tai x=-2i . Kompleksiluvut eivät kuitenkaan kuulu lukion opetussuunnitelman perusteisiin, joten oletamme jatkossa lukujen olevan reaalilukuja.

4.4.1 Esimerkki: potenssiyhtälön ratkaisut

Ratkaise yhtälö.

Ratkaisu:

tai , sillä tai Ratkaisut voidaan esitää myös muodossa $x=\pm 4.$
Ei ratkaisua, sillä juurrettava on .
, sillä .

HUOM! Potenssiyhtälöä käsitellään lisää kappaleessa 5.5

4.4.2 Esimerkki: neliön sivun pituus

Neliön pinta-ala on $15\;\text{m}^2$ . Laske neliön sivun pituus.

Ratkaisu:

Mekitään muuttujalla neliön sivun pituutta metreinä. Tällöin voidaan suoraan neliöjuuren avulla laskea

$x=\sqrt{15}=3,872983\approx3,9\;\text{(m)}$

Vastaus: Neliön sivun pituus on noin $3,9\;\text{m}$ .

Neliöjuurilla laskettaessa käytetään seuraavia laskulakeja.

Neliöjuuren ominaisuuksia

$\sqrt{a}\sqrt{b}=\sqrt{ab}\;\;\;\;\;\;\;\;\text{tulon neliöjuuri}$

$\dfrac{\sqrt{a}}{{\sqrt{b}}}=\sqrt{\dfrac{a}{b}}\;\;\;\;\;\;\;\;\;\;\;\text{osamäärän neliöjuuri}$

$\sqrt{a^2}=|a|\;\;\;\;\;\;\;\;\;\;\;\;\;\text{neliön neliöjuuri}$

4.4.3 Todistus (1. kohta)

Olkoot $a\geq0$ ja $b\geq0$ . Tällöin tulon potenssin laskusäännön nojalla

$(\sqrt{a}\sqrt{b})^2=(\sqrt{a})^2(\sqrt{b})^2=ab.$

$\sqrt{a}$ ja $\sqrt{b}$ ovat ei-negatiivisiä, joten $\sqrt{a}\sqrt{b}$ on neliöjuuren määritelmän mukainen luku, joka korotettuna toiseen on $ab=(\sqrt{ab})^2.$ $_\square$

4.4.4 Todistus (2. kohta)

Olkoot $a\geq0$ ja b>0 . Tällöin osamäärän potenssin laskusäännön nojalla

$\Big(\dfrac{\sqrt{a}}{{\sqrt{b}}}\Big)^2=\dfrac{(\sqrt{a})^2}{(\sqrt{b})^2}=\dfrac{a}{b}.$

$\sqrt{a}$ ja $\sqrt{b}$ ovat ei-negatiivisiä, joten $\dfrac{\sqrt{a}}{\sqrt{b}}$ on neliöjuuren määritelmän mukainen luku, joka korotettuna toiseen on $\dfrac{a}{b}=\Big(\sqrt{\dfrac{a}{b}}\Big)^2.$ $_\square$

4.4.5 Todistus (3. kohta)

Koska $|a|\ge0,$ neliöjuuren määritelmän ensimmäinen ehto on voimassa.

Koska |a|^2=a^2 , myös toinen ehto toteutuu. $_\square$

4.4.6 Esimerkki: neliöjuuren laskusääntöjä

Sievennä.

$\sqrt{8}\sqrt{2}$
$\sqrt{\dfrac{4}{9}}$
$\sqrt{4\cdot2}$
$\sqrt{1000}$

Ratkaisu:

Neliöjuurten tulossa juurrettavat kerrotaan keskenään.

$\sqrt{8}\sqrt{2}=\sqrt{8\cdot2}=\sqrt{16}=4$

Osamäärän neliöjuuressa osoittajasta ja nimittäjästä otetaan molemmista erikseen neliöjuuri.

$\sqrt{\dfrac{4}{9}}=\dfrac{\sqrt{4}}{\sqrt{9}}=\dfrac{2}{3}$

Jos juuri on irrationaalinen (jaksoton ja päättymätön luku), niin neliöjuuri sievennetään muotoon, missä yksittäisenä juurrettavana on mahdollisimman pieni kokonaisluku.

$\sqrt{4\cdot2}=\sqrt{4}\sqrt{2}=2\sqrt{2}$

$\sqrt{1000}=\sqrt{100\cdot10}=\sqrt{100}\sqrt{10}=10\sqrt{10}$

4.4.7 Esimerkki: neliöjuurten sieventämistä

Sievennä.

$\sqrt{9}+\sqrt{16}$
$\sqrt{9+16}$
$\sqrt{\sqrt{25}+\sqrt{81}-5}$
$\sqrt{(x^2+1)^2}$

Ratkaisu:

Lasketaan ensin neliöjuuret.

$\sqrt{9}+\sqrt{16}=3+4=7$

Lasketaan ensin yhtenlasku.

$\sqrt{9+16}=\sqrt{25}=5$

Lasketaan ensin sisimmät neliöjuuret.

$\begin{align*} &\sqrt{\sqrt{25}+\sqrt{81}-5}\\ &=\sqrt{5+9-5}\\ &=\sqrt{9}=3 \end{align*}$

Käytetään neliöjuuren kolmatta ominaisuutta.

$\begin{align*} &\sqrt{(x^2+1)^2} \\ &=|x^2+1| \\ \text{(itseisarvot voidaan }&\text{poistaa, sillä aina}\;x^2+1>0) \\ &=x^2+1 \end{align*}$

Olkoon kuution tilavuus V=64 . Mikä on kuution särmän pituus?

Kuution tilavuus saadaan särmän kuutiona, eli nyt tulee pohtia sitä, että mikä luku toteuttaa yhtälön x^3=64 .

Tiedämme, että 4^3=64 . Siispä särmän pituus x=4 .

Voidaan osoittaa, että yhtälön x^3=a ratkaisu on $\sqrt[3]{a}$ . Tätä sanotaan luvun kuutiojuureksi.

Kuutiojuuri

Luvun kuutiojuuri $\sqrt[3]{a}$ toteuttaa ehdon

$(\sqrt[3]{a})^3=a$

Kuutiojuuren määritelmässä kelpaavat kaikki reaaliluvut eli voi olla myös negatiivinen luku. Tämä siksi, että kuutiojuuri on myös näin määriteltynä yksikäsitteinen, koska parittoman negatiivisen luvun kuutio on negatiivinen ja vastaavasti parittoman positiivisen luvun kuutio on positiivinen. Edellä johdetut neliöjuuren laskusäännöt pätevät myös kuutiojuurella ja lisäksi silloin, kun a<0 tai b<0 .

4.4.8 Esimerkki: kuutiojuurten laskemista

Laske

$\sqrt[3]{27}$
$\sqrt[3]{-8}$
$-\sqrt[3]{-216}$

Ratkaisu:

$\sqrt[3]{27}=3,$ sillä $3^3=3\cdot3\cdot3=27.$

$\sqrt[3]{-8}=-2,$ sillä $(-2)^2=(-2)\cdot(-2)\cdot(-2)=-8.$

$\sqrt[3]{-216}=-6,$ sillä $(-6)^3=(-6)\cdot(-6)\cdot(-6)=-216.$

Joten $-\sqrt[3]{-216}=-(-6)=6.$

Neliö- ja kuutiojuuri: tehtäviä

4.5 Potenssiyhtälö

Olemme käyneet läpi jo esimerkkejä muotoa x^2=a ja x^3=a olevien yhtälöiden ratkaisuista. Yleisesti muotoa x^n=a olevaa yhtälöä sanotaan potenssiyhtälöksi. Katsotaan vielä yleisesti, miten potenssiyhtälö ratkaistaan, kun n=2 tai n=3.

Neliöyhtälön ratkaiseminen (n=2)

Neliöyhtälön x^2=a juurten lukumäärä riippuu luvusta .

Jos , niin yhtälön ratkaisut ovat

$x=\sqrt{a} \text{ tai } x=-\sqrt{a}.$

Jos , niin yhtälön ratkaisu on

x=0.

Jos , niin yhtälöllä ei ole ratkaisua.

Jos $a \geq 0$ , niin neliöyhtälö voidaan ratkaista ottamalla puolittain neliöjuuri huomioiden ratkaisujen etumerkit.

4.5.1 Esimerkki: neliöyhtälön ratkaiseminen

Ratkaise yhtälö 2x^2+3=17

Ratkaisu:

Vastaavasti kuin ensimmäisen asteen yhtälöissä, muokataan yhtälö muotoon, jossa toisella puolella on muuttuja ja toisella vakio. Tämän jälkeen voidaan ottaa puolittain neliöjuuri, kun huomioidaan myös negatiivinen ratkaisu.

$\begin{align*} 2x^2+3 & = 17 && | -3 \\ 2x^2 & = 14 && | : 2 \\ x^2 & = 7 && | \sqrt{} \\ x &= \pm \sqrt{7} \end{align*}$

Vastaus: $x=\sqrt{7}$ tai $x=-\sqrt{7}$

4.5.2 Esimerkki: Coca-Cola -tölkin mitat

Amerikan standardimittaisen Coca-Cola -tölkin pohjaympyrän pinta-ala on noin cm. Laske tölkin pohjaympyrän säteen pituus.

Ratkaisu:

Ympyrän pinta-ala saadaan kaavalla $A=\pi r^2$ , missä $r=\text{ympyrän säteen pituus}$ . Muodostetaan tehtävänannon tiedoista yhtälö.

$\begin{align*} \pi r^2 & = 92 && | : \pi \\ r^2 & = \dfrac{92}{ \pi } && | \sqrt{} \\ r &= \pm \sqrt{\dfrac{92}{\pi}} \end{align*}$

Pituus ei voi olla negatiivinen, joten huomioimme vain positiivisen ratkaisun.

$r=\sqrt{\dfrac{92}{\pi}}=5,411516380\approx5,4\;\text{(cm)}.$

Vastaus: Pohjaympyrän säde on noin $5,4\;\text{cm}.$

Kuutioyhtälön ratkaiseminen (n=3)

Kuutioyhtälön x^3=a

ratkaisu on $x=(\sqrt[3]{a})$ .

Neliöjuuresta poiketen, kuutioyhtälön ratkaisu on yksikäsitteinen, sillä positiivisen luvun kuutio on positiivinen luku ja negatiivisen luvun kuutio on negatiivinen luku.

4.5.3 Esimerkki: kuutioyhtälön ratkaiseminen

Ratkaise yhtälö 3x^3+7=-4 .

Ratkaisu:

Vastaavasti kuin neliöyhtälössä, muokataan yhtälö muotoon, missä toisella puolella on muuttuja ja toisella vakio. Tämän jälkeen voidaan ottaa puolittain kuutiojuuri, mutta nyt ratkaisuja on vain yksi.

$\begin{align*} 3x^3+7 & = -4 && | -7 \\ 3x^3 & = -11 && | : 3 \\ x^3 & = -\dfrac{11}{3} && | \sqrt[3]{} \\ x &= \sqrt[3]{-\dfrac{11}{3}}=- \sqrt[3]{\dfrac{11}{3}} \end{align*}$

Vastaus: $x=- \sqrt[3]{\dfrac{11}{3}}$

4.5.4 Esimerkki: jalkapallon mitat

Vuoden 2018 jalkapallon mm-kisojen kisapallo oli Adidas Telstar. Telstarin tilavuus on noin 5,6 litraa. Mikä on Telstarin halkaisijan pituus senttimetreinä?

Ratkaisu:

Pallon tilavuus saadaan kaavalla $V=\dfrac{4\pi r^3}{3}$ , missä $r=\text{pallon säteen pituus}$ . Muodostetaan tehtävänannon tiedoista yhtälö ja ratkaistaan pallon säde.

$\begin{align*} \dfrac{4\pi r^3}{3} & = 5,6 && | \cdot 3 \\ 4\pi r^3 & = 3\cdot 5,6 && | : 4\pi \\ r^3 & = \dfrac{3\cdot 5,6}{4\pi} && | \sqrt[3]{} \\ r &= \sqrt[3]{\dfrac{3\cdot 5,6}{4\pi}} \text{ (dm)} \end{align*}$

Pallon halkaisija on kaksi kertaa säteen suuruinen, joten

$h=2\cdot\sqrt[3]{\dfrac{3\cdot 5,6}{4\pi}} \text{ dm } = 2,203246733 \text{ dm }\approx 22\;\text{cm}$ .

Vastaus: Pallon halkaisija on noin $22\;\text{cm}$ .

Potenssiyhtälö: tehtäviä

5. Funktio

Viimeisessä kappaleessa aiheena on funktio. Kappaleessa perehdytään siihen, mitä funktio tarkoittaa sekä käsitellään funktion kuvaajan piirtämistä ja tulkintaa. Lopuksi käydään läpi esimerkkejä funktion sovelluksista. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

Funktiota tarvitaan tutkittaessa muuttuvien suureiden välistä riippuvuutta. Usein suureen arvo riippuu siitä, mikä toisen suureen arvo on. Esimerkiksi ympyrän pinta-ala riippuu säteestä ja autolla ajettu matka riippuu nopeudesta.

5.1 Funktion määritelmä

# V2

Videossa on kone, joka tuottaa siihen syötetystä nimestä luvun. Sääntönä on, että koneen tuottama luku kertoo nimen pituuden. Tällainen yksikäsitteinen sääntö määrittelee funktion.

Funktio

Funktio on sääntö, joka ilmaisee, miten lähtöarvosta saadaan yksikäsitteisesti loppuarvo. Lähtöarvoa kutsutaan muuttujan arvoksi ja loppuarvoa funktion arvoksi.

Lähtöarvot eli luvut, jotka funktioon voidaan syöttää muodostavat funktion määrittelyjoukon. Loppuarvot eli luvut, jotka funktio tuottaa, muodostavat funktion arvojoukon.

Funktio nimetään tavallisesti kirjaimella , tai . Lähtöarvoa kuvaavana muuttujana käytetään yleensä kirjainta .

Usein funktion sääntö esitetään lausekkeena. Esimerkiksi sääntö "lukuun lisätään 4" voidaan esittää lausekkeena seuraavasti.

f(x)=x+4

Funktion lausekkeen avulla voidaan laskea funktion arvoja. Esimerkiksi "funktion arvo kohdassa 5" lasketaan sijoittamalla luku 5 muuttujan paikalle.

f(5)=5+4=9

5.1.1 Esimerkki: funktion arvon laskeminen

Funktion arvo lasketaan seuraavan säännön avulla:

Funktioon syötettyyn lukuun lisätään luku 8 ja summa jaetaan luvulla 2.

Muodosta funktion lauseke.
Laske funktion arvot ja .

Ratkaisu:

Merkitään funktioon syötettävää lukua eli muuttujaa kirjaimella . Kun muuttujaan lisätään luku 8, saadaan . Kun lauseke jaetaan luvulla 2, saadaan $\displaystyle \frac{x+8}{2}$ .

Funktion lauseke on $f(x)=\displaystyle \frac{x+8}{2}$ .
Funktion arvo kohdassa 5 merkitään ja lasketaan sijoittamalla lausekkeeseen muuttujan paikalle luku 5.

$f(5)=\displaystyle \frac{5+8}{2}=\displaystyle\frac{13}{2}$ .

Vastaavasti funktion arvo kohdassa -2 on

$f(-2)=\displaystyle \frac{-2+8}{2}=\displaystyle \frac{6}{2}=3$ .

5.1.2 Esimerkki: funktion määrittelyjoukko

Päättele funktion määrittelyjoukko.

$f(x)= \displaystyle \frac{3}{x-2}$
$g(x)= \sqrt{4-x}$

Ratkaisu:

Jakolasku $f(x)= \displaystyle \frac{3}{x-2}$ on määritelty vain, kun jakaja ei ole nolla.

Siten funktion määrittelyjoukon muodostavat luvut , jotka toteuttavat ehdon $x\neq2$ .
Neliöjuuri $\sqrt{4-x}$ on määritelty vain, kun luku on on suurempi tai yhtä suuri kuin nolla.

Siten funktion määrittelyjoukon muodostavat luvut , jotka toteuttavat ehdon $x\le4$ .

Funktion määritelmä: tehtäviä

5.2 Funktion nollakohta

Millä muuttujan arvolla funktio saa arvon nolla tai missä pisteessä kuvaaja leikkaa x-akselin? Kyse on samasta asiasta, funktion nollakohdan määrittämisestä.

Huom! "Funktion arvo kohdassa 0" ja "funktion nollakohta" tarkoittavat eri asiaa.

Funktion nollakohta

Niitä määrittelyjoukon lukuja, joilla funktion arvo on nolla, kutsutaan funktion nollakohdiksi. Funktion nollakohdat toteuttavat siis yhtälön f(x)=0 .

5.2.1 Esimerkki: funktion arvo kohdassa nolla ja funktion nollakohdat

Määritä funktion f(x)=5x+9 arvo kohdassa ja funktion nollakohdat.

Ratkaisu:

Funktion arvo kohdassa lasketaan sijoittamalla muuttujan paikalle luku .

$f(0)=5\cdot0+9=9$

Funktion nollakohdat löydetään ratkaisemalla yhtälö f(x)=0 .

$\begin{align*} f(x)=0 \\ 5x+9=0 \\ 5x=-9 \\ x=-\frac{9}{5} \end{align*}$

Funktion nollakohta on siis $x=- \displaystyle \frac{9}{5}$ .

Funktion nollakohta: tehtäviä

5.3 Funktion kuvaaja

# V1

Funktion kuvaaja xy-koordinaatistossa

Funktion kuvaaja muodostuu pisteistä (x, y) , joissa on muuttujan arvo ja funktion arvo kohdassa eli y=f(x) .

5.3.1 Esimerkki: funktion kuvaajan hahmottelu ilman ohjelmistoa

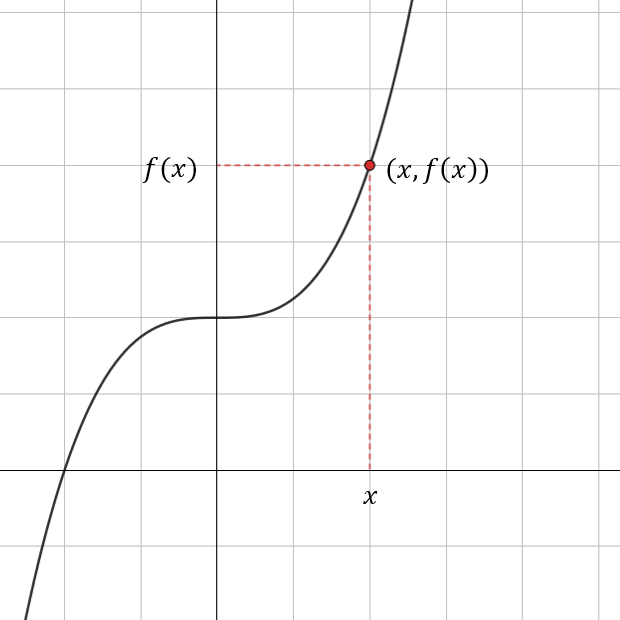
Funktion f(x)=3^x-2 kuvaaja muodostuu koordinaatiston pisteistä (x, y) , joissa on muuttujan arvo ja on funktion arvo kohdassa eli y=3^x-2 .

Taulukoidaan pisteitä, joiden kautta funktion kuvaaja esimerkiksi kulkee.

Alla olevaan koordinaatistoon on piirretty taulukoidut pisteet sekä niiden kautta kulkeva funktion kuvaaja.

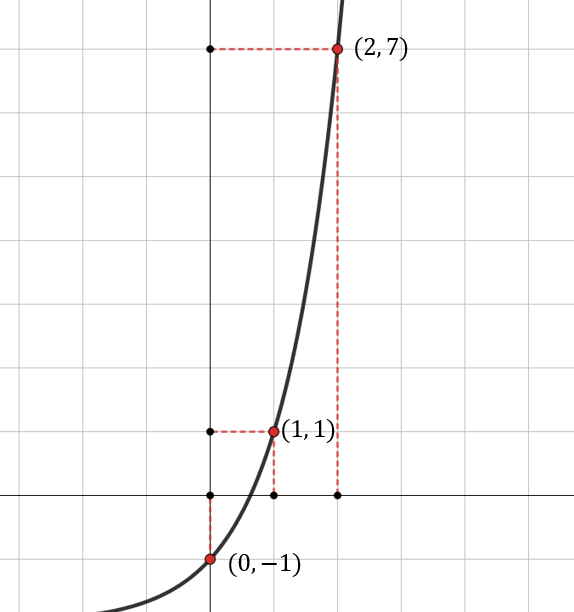
Funktion kuvaaja voidaan hahmotella saatujen pisteiden avulla vain karkeasti. Sopivan ohjelman avulla funktion kuvaaja saadaan piirrettyä täysin tarkasti.

Videolla näytetään kuvaajan piirtäminen TI-Nspire CAS -laskimella.

# V3

5.3.2 Esimerkki: funktion kuvaaja Geogebralla

Geogebran piirto-ohjelmalla funktioiden kuvaajien piirto tapahtuu helposti kirjoittamalla haluttu funktio syöttökenttään. Esimerkiksi funktio f(x)=x-2 piirrettäisiin seuraavasti.

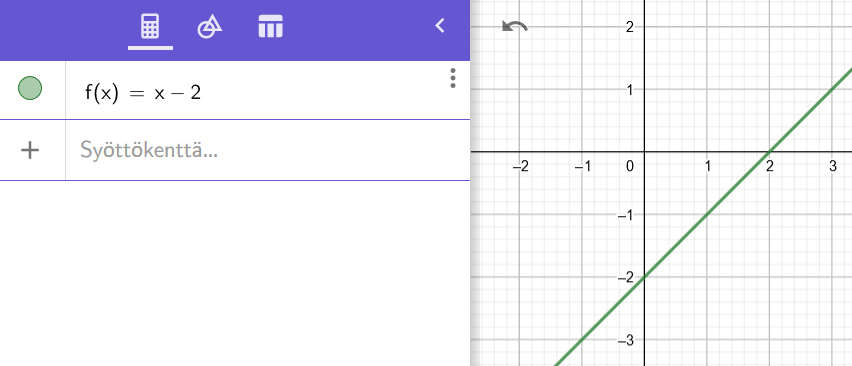
Alla olevalla Appletilla voi tutkia, mistä pisteistä funktion f(x)=x-2 kuvaaja koostuu liikuttelemalla keltaista pistettä kuvaajalla.

Huomataan, että funktion f(x)=x-2 kuvaaja muodostuu siis pisteistä (x, x-2) . Kuvaaja kulkee esimerkiksi pisteiden (3,3-2)=(3,1) ja (1,1-2)=(1,-1) kautta.

Funktion nollakohdassa funktio saa arvon nolla eli kuvaaja leikkaa x-akselin. Funktion f(x)=x-2 nollakohta on siten (2,0) .

Funktion kuvaaja: tehtäviä

5.4 Funktion kuvaajan tulkinta

Kuvaajan etuna on, että se havainnollistaa funktiota graafisesti, jolloin siitä on helpompi tehdä tulkintoja. Kuvaajasta nähdään monia funktion ominaisuuksia, kuten merkin vaihtuminen ja arvojen muuttuminen.

5.4.1 Esimerkki: funktion arvojen lukeminen kuvaajasta

Määritä kuvaajan perusteella

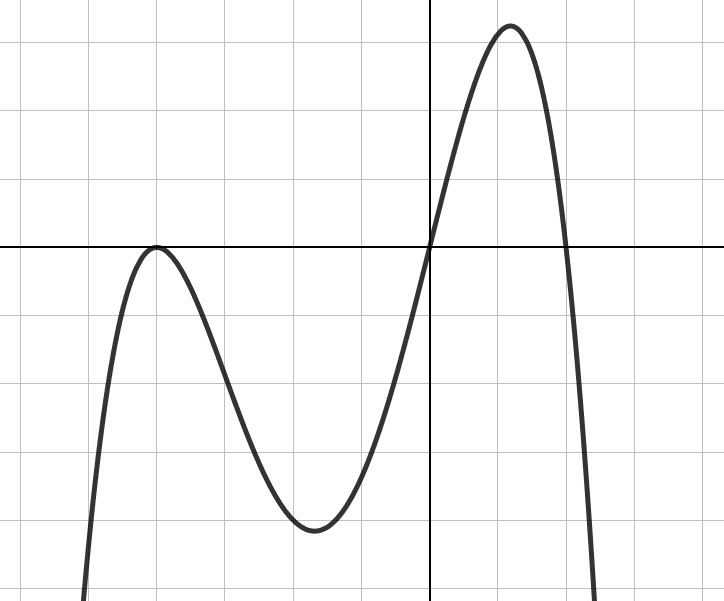
funktion nollakohdat
funktion arvo kohdassa
funktion arvot, joilla funktio saa arvon .

Ratkaisu

Nollakohdassa funktion arvo on nolla eli funktion kuvaaja leikkaa x-akselin. Kuvaajan perusteella funktion nollakohdat ovat $x\approx-4$ , $x\approx 0$ ja $x\approx2$ .

Kohdassa funktio näyttää kulkevan pisteen kautta, eli $f(-2)\approx-4$ .

Funktio saa arvon , kun kuvaajan pisteen y-koordinaatti on . Käyrällä on neljä pistettä, joissa . Tällöin $x\approx-5$ , $x\approx-2$ , $x\approx-1,3$ ja $x\approx2,3$ .

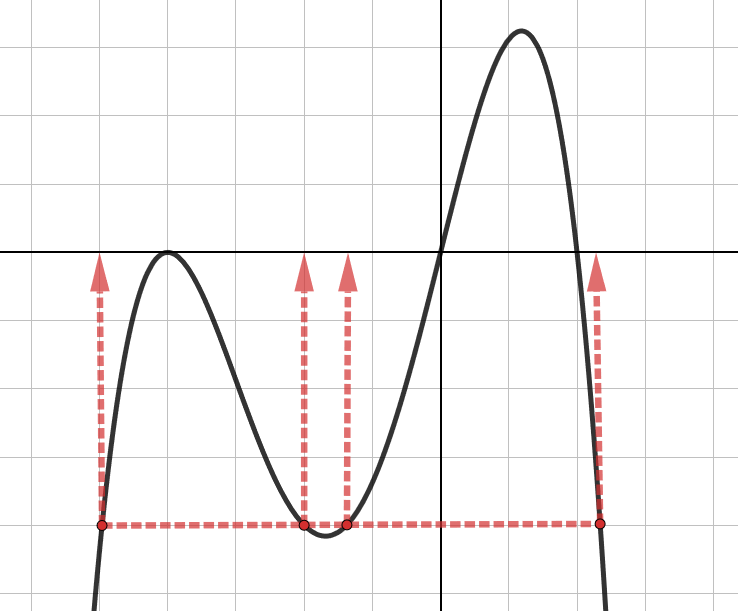
Funktion merkki

Funktion arvo on positiivinen, kun sen kuvaaja on x-akselin yläpuolella. Kuvan funktion arvot ovat siis positiivia, kun x<-2 tai x>2 .

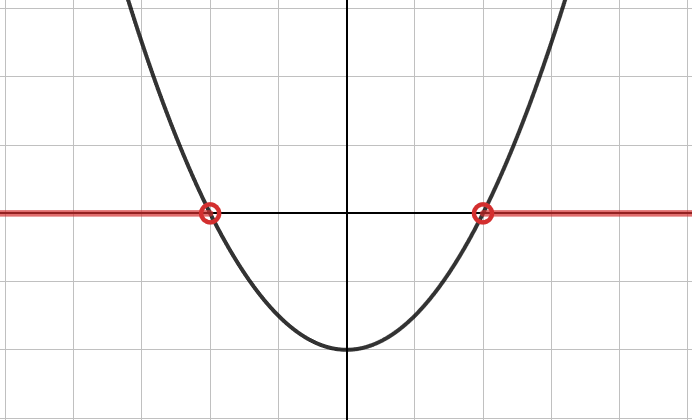
Funktion arvo on negatiivinen, kun sen kuvaaja on x-akselin alapuolella. Kuvan funktion arvot ovat siis negatiivisia, kun -2<x<2 .

5.4.2 Esimerkki: funktion merkin tutkimista Geogebralla

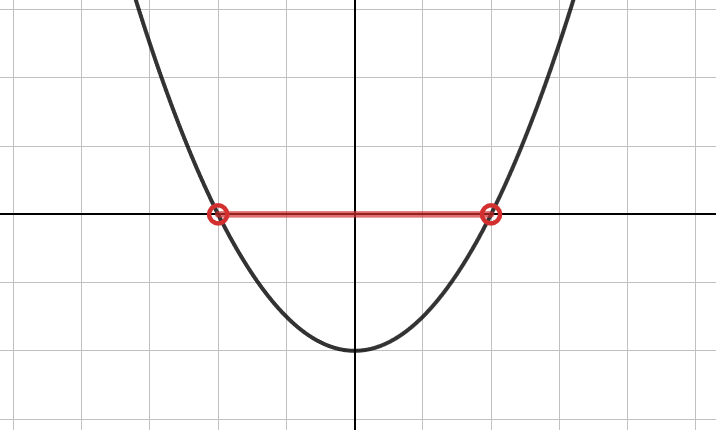
Syötä Applettiin haluamasi funktion lauseke ja tarkastele funktion kulkua. Koordinaatisto muuttuu vihreäksi kohdista, joissa funktion arvo on positiivinen ja punaiseksi kohdissa, joissa funktion arvo on negatiivinen. Funktio vaihtaa merkkinsä nollakohdissa, jotka on myös piirretty kuvaan.

5.4.3 Esimerkki: lämpötilakuvaajan tulkintaa

Kuvassa on esitetty Jyväskylän lentoaseman lämpötilahavainnot kahden vuorokauden ajalta. Tarkastellaan kuvaan merkattua aikaväliä 9.00-9.00 .

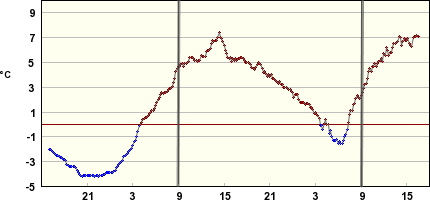
Milloin lämpötila on $4\;^{\circ}\text{C}$ ?
Onko lämpötila plussan vai miinuksen puolella keskiyöllä?
Milloin lämpötila on alle $0\;^{\circ}\text{C}$ ?

Ratkaisu:

Lämpötila saa arvon $4\;^{\circ}\text{C}$ vain kerran kysytyllä aikavälillä: noin kello .
Ajanhetkellä kuvaaja on punaisen viivan yläpuolella eli lämpötila on plussan puolella.
Lämpötila on alle $0\;^{\circ}\text{C}$ , kun kuvaaja on punaisen viivan alapuolella eli noin kellonaikojen ja välillä.

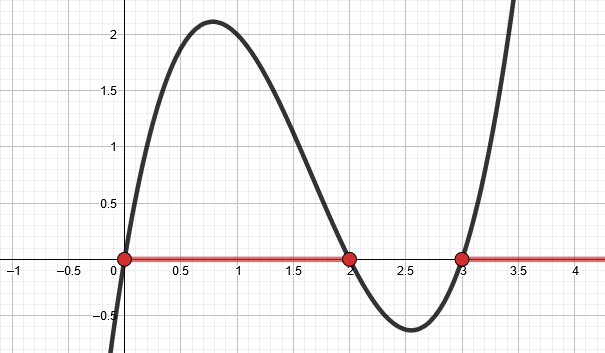
5.4.4 Esimerkki: funktion kuvaajan tulkintaa

Vastaa kuvan funktion kuvaajan perusteella.

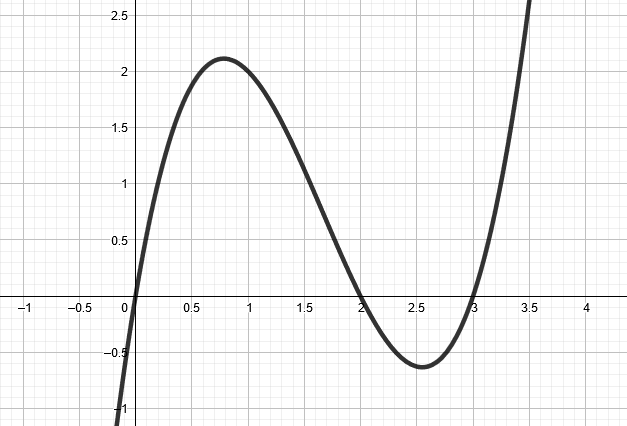
Minkä merkkinen funktion arvo on välillä ? Entä välillä ?
Milloin $f(x)\ge0$ ?

Ratkaisu:

Funktion kuvaaja kulkee välillä x-akselin yläpuolella. Funktion arvo on siis positiivinen, kun .

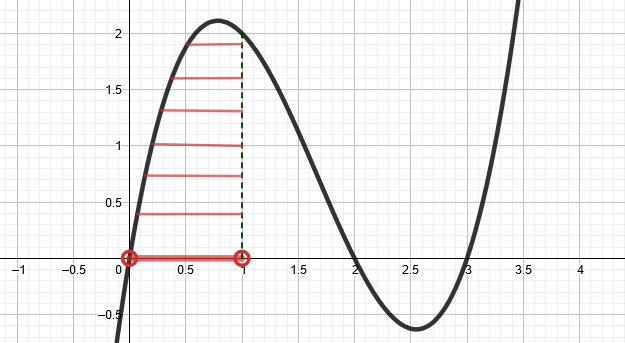
Funktion kuvaaja kulkee välillä 2,5<x<3 x-akselin alapuolella. Funktion arvo on siis negatiivinen, kun 2,5<x<3 .

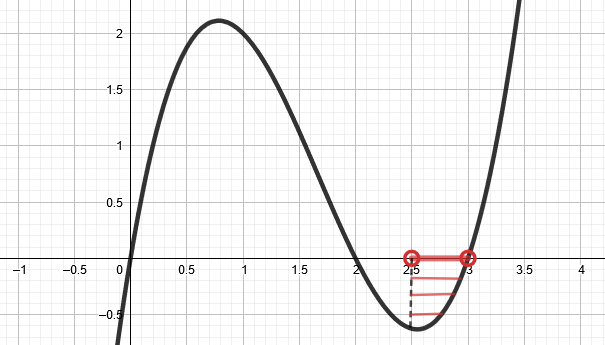
Tarkastellaan, milloin $f(x)\ge0$ eli funktion arvo on suurempi tai yhtä suuri kuin nolla. Funktion arvo on nolla x-akselin leikkauspisteissä ja positiivinen, kun funktion kuvaaja kulkee x-akselin yläpuolella.

Koska funktion arvo on negatiivinen kahdella eri välillä, annetaan vastaus kahdessa eri osassa.

$f(x)\ge0$ , kun $0\le x \le 2$ tai $x\le 3$ .

Huom! Nollakohdat kuuluvat välille, joten muista yhtäsuuruudet.

Funktion kuvaajan tulkinta: tehtäviä

5.5 Potenssifunktio

Kappaleessa 5 opimme, että muotoa x^n=a olevaa yhtälöä sanotaan potenssiyhtälöksi ja kävimme läpi potenssiyhtälön ratkaisut, kun n=2 tai n=3. Vastaavasti potenssifunktioksi sanotaan funktiota, jonka lauseke on potenssi ja muuttujana potenssin kantaluku.

Potenssifunktio

Potenssifunktio on funktio, joka on muotoa

f(x)=x^n,

missä on kokonaisluku.

Selvitetään seuraavaksi potenssifunktioiden tyypillisiä ominaisuuksia, joihin potenssiyhtälöiden ratkaisujen määrä ja olemassaolo perustuvat. Keskitytään taas tapauksiin, joissa n=2 tai n=3.

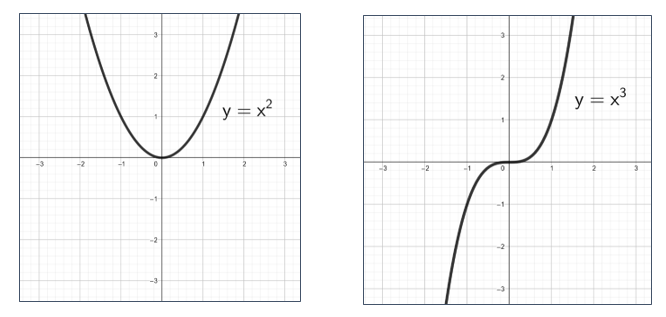
Funktion kuvaaja sijaitsee ensimmäisessä ja toisessa neljänneksessä ja se saa arvoja välillä $[0,\infty[$ .
Funktion kuvaaja sijaitsee ensimmäisessä ja kolmannessa neljänneksessä se saa arvoja koko reaalilukujoukossa $\mathbb{R}$ .
Molempien funktioiden määrittelyjoukko on $\mathbb{R}$ .

5.5.1 Esimerkki: ympyrän pinta-alan funktio

Ympyrän pinta-ala riippuu ympyrän säteestä eli pinta-ala on säteen funktio. Ympyrän pinta-alaa kuvaa funktio

$A(r)=\pi r^2$

Koska säteen arvot ovat positiivisia kokonaislukuja, määrittelyjoukkona ei ole koko reaalilukujoukko vaan positiiviset reaaliluvut. Määrittelyjoukko on siis $\mathbb{R}_+$ .

Piirretään funktion kuvaaja ja luetaan kuvaajalta ympyrän pinta-aloja eri säteen arvoilla.

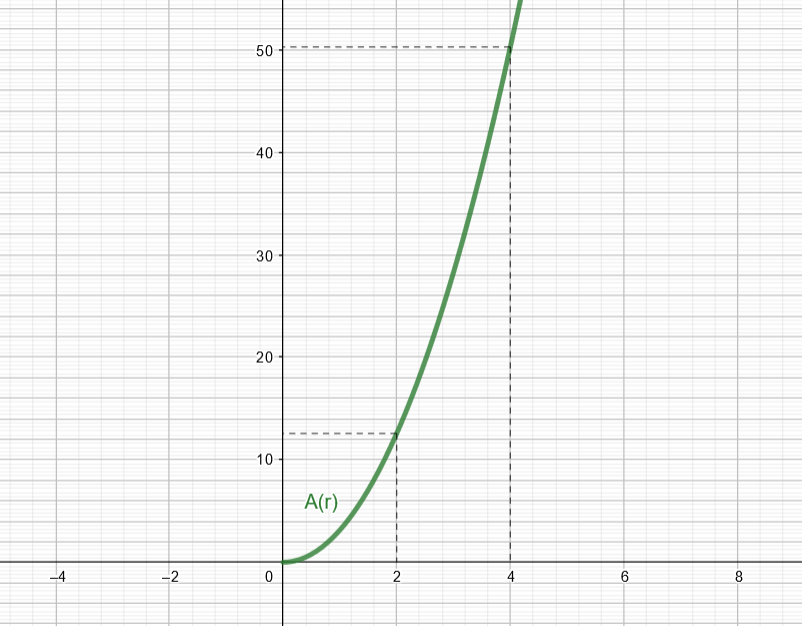
Funktion kuvaaja sijaitsee vain ensimmäisessä neljänneksessä määrittelyehdon vuoksi.

Kuvaajan perusteella voidaan päätellä, että kun ympyrän säde on , sen pinta-ala on 12,5 eli $A(2)\approx12,5$ .

Vastaavasti $A(r)\approx50$ kun r=4 , eli säteen arvolla ympyrän pinta-ala on noin 50.

Potenssifunktio: tehtäviä

5.6 Funktion sovelluksia

5.6.1 Esimerkki: bensatankillisen hinta

98E-bensiinin hinta on $1,638\;\text{€/l}$ . Muodosta tuotteen hintaa kuvaava funktio ja havainnollista hinnan muodostumista koordinaatistossa. Laske tai lue kuvaajasta kuinka paljon maksaa tankillinen bensaa, kun tankin tilavuus on litraa.

Ratkaisu:

Bensiinin hinta riippuu sen tilavuudesta. Merkitään tilavuutta litroina kirjaimella . Bensiinin hintaa kuvaa tällöin funktio g(x)=1,638x , jossa $x\ge0$ . (Hinta voidaan laskea vain silloin, kun bensiinin tilavuus ei ole negatiivinen.)

Piirretään funktion kuvaaja Geogebran avulla.

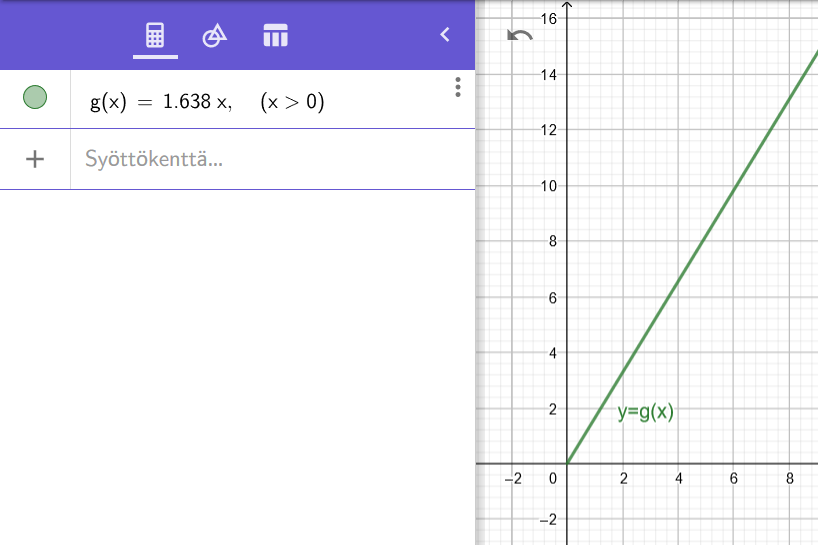
Selvitetään bensatankillisen hinta ensin kuvaajasta lukemalla. Muuttujan arvo on . Funktio saa kohdassa x=8 likimain arvon 13,5, joten bensatankillisen hinta olisi noin $13,5\;\text{€}$ .

Lasketaan bensatankillisen hinta myös funktion lausekkeen avulla. Kysytään siis funktion arvoa g(8) . $g(8)=1,688\cdot8=13,48\;(\text{euroa})$

Vastaus: Bensatankillisen hinta on 13,48 euroa.

5.6.2 Esimerkki: sähkönkulutuksen laskemista

Sähkön vuotuista kokonaiskulutusta gigawattitunteina (GWh) Suomessa vuosina 1970-2014 voidaan kuvata funktiolla f(x)=-1,3x^3+58,8x^2+1349,4x+21583, missä on kulunut aika (vuosina) vuodesta 1970 .

Laske sähkönkulutus vuonna ja vuonna .
Määritä kuvaajan avulla, minä vuonna sähkönkulutus kääntyi laskusuuntaan.

Ratkaisu:

Sähkönkulutus vuonna on funktion arvo kohdassa ja vuonna kohdassa . Lasketaan funktion arvot.

$f(0)=-1,3\cdot0+58,8\cdot0+1349,4\cdot0+21583=21583\approx21600$ $f(30)=-1,3\cdot30+58,8\cdot30+1349,4\cdot30+21583=79885\approx79900$

Vuonna 1970 sähköä kulutettiin noin $21\;600\;\text{GWh}$ ja vuonna 2000 noin $79\;900\;\text{GWh}$ .

Piirretään funktion kuvaaja välillä $0\le x \le44$ . Energiankulutus kääntyy laskuun siinä kohdassa, jossa funktion kuvaajan koordinaatti saa suurimman arvonsa. Geogebralla funktion suurimman arvon saa selville klikkaamalla valikosta Ääriarvot-komentoa ja sen jälkeen halutun funktion kuvaajaa.

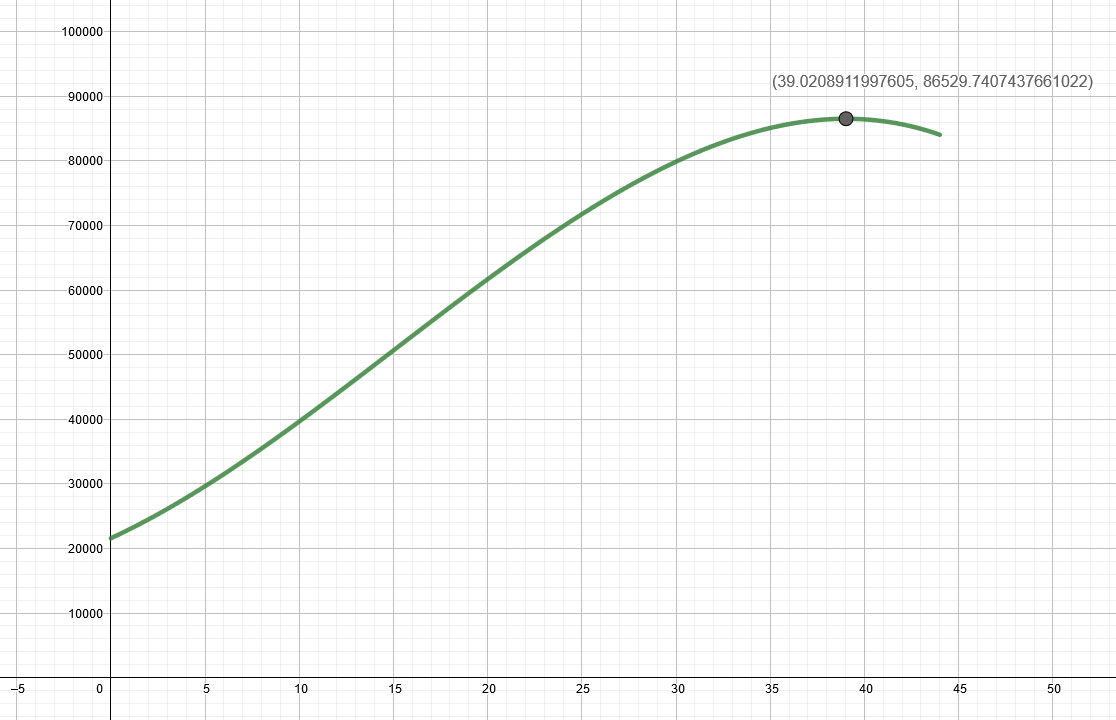
Kuvaajan perusteella funktio saa suurimman arvonsa kohdassa $x\approx39$ . Sähkönkulutus kääntyi laskuun siis vuonna 1970+39=2009 .

Funktion sovelluksia: tehtäviä