3. Verrannollisuus ja prosenttilaskenta: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Verrannollisuus ja prosenttilaskenta. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

3.1 Suoraan verrannollisuus: tehtäviä

Tämän kappaleen teoria.

3.1.1 Tehtävä

# Plugin1

3.1.2 Tehtävä

# p412

3.1.3 Tehtävä

Miisa on kutsunut kaveria grilli-iltaan. Miisa varaa ystävilleen $3,9\;\text{kg}$ makkaroita. Kolme Miisan kavereista ilmoittaa tuovansa oman kaverinsa mukanaan grilli-iltaan. Miisa ilahtuu tästä ja päättää hankkia makkaraa myös uusille tulokkaille.

# seq414

Vihje

Olkoon vieraat ja makkaramäärä $y\;\text{(kg)}$ . Vieraat ja makkaramäärä ovat suoraan verrannollisia suureita, joten

$\dfrac{y_1}{x_1}=\frac{y_2}{x_2}$

Merkitään x_1=9, x_2=9+3=12, y_1=3,9 ja ratkaistaan y_2 .

Huomaa, että kysytään, kuinka monta kiloa lisää $\dots$

3.1.4 Tehtävä

Kynttilä palaa tasaisella liekillä niin, että sydänlanka lyhenee $2\;\text{cm}$ minuutissa. Kello Violet sytyttää $27\;\text{cm}$ korkean kynttilän palamaan.

# seq413

Vihje

Olkoon sydänlangan lyhenemä $x\;\text{(cm)}$ ja aika $y\;\text{(min)}$ . Lyhenemä ja aika ovat suoraan verrannollisia suureita, joten

$\dfrac{y_1}{x_1}=\frac{y_2}{x_2}$

Merkitään x_1=2, x_2=27, y_1=20 ja ratkaistaan y_2 .

Koska kysytään kellon aikaa, täytyy miettiä paljonko kello on, kun 19.00 jälkeen kuluu y_2 verran minuutteja $\dots$

3.1.5 Tehtävä

Piirrä Geogebralla suora, jonka avulla voit muuttaa mailit kilometreiksi. Pituus maileina ja kilometreinä ovat suoraan verrannollisia suureita. Oletetaan, että $1\;\text{maili}=1,6\;\text{km}$ .

# funktio2

Määritä kuvaajasta montako

# seq414a

# seq414b

3.2 Kääntäen verrannollisuus: tehtäviä

Tämän kappaleen teoria.

3.2.1 Tehtävä

# pl421

3.2.2 Tehtävä

Vakiolämpötilassa kaasun paine on kääntäen verrannollinen kaasun tilavuuteen. Männällä varustetussa sylinterissä kaasun paine on $4,9\;\text{kPa}$ ja tilavuus $12\;\text{l}$ .

# seq422

Vihje

Suureet ja ovat kääntäen verrannollisia, joten niiden tulo $pV=\text{vakio}$ ja

p_1V_1=p_2V_2

Tästä saadaan ratkaistua tilavuus $V_2\dots$

3.2.3 Tehtävä

Suureiden ja välillä on voimassa verranto $\dfrac{a}{b}=\dfrac{c}{d}.$

# pl423a

# pl423b

3.2.4 Tehtävä

Suureet x>0 ja y>0 ovat kääntäen verrannollisia. Kun x=3, niin y=20. Muodosta suureiden välistä riippuvuutta kuvaava funktio ja piirrä Geogebralla kuvaaja suureesta suureen funktiona.

# funktio

Vihje

Koska suureet ovat kääntäen verrannollisia, niiden tulo on aina vakio eli $xy=3\cdot20=60$ . Yhtälö saadaan muotoon $y=\dots$

3.2.5 Tehtävä

Alkoholi poistuu elimistöstä pääasiassa maksan kautta. Aikuisen maksa polttaa alkoholia noin yhden gramman tunnissa henkilön kymmentä painokiloa kohden.

Veren alkoholipitoisuus promilleina (p) on suoraan verrannollinen juotuun puhtaan alkoholin määrään grammoina (A) ja kääntäen verrannollinen henkilön massaan kilogrammoina (m) . Sukupuolesta riippuvaa nestetilavuuskerrointa merkitään $k\;\text{:lla}$ .

# p424

3.3 Prosentti: tehtäviä

Tämän kappaleen teoria.

3.3.1 Tehtävä

Valitse prosenttilukua vastaava desimaaliluku.

# Plugin2

# Plugin3

# Plugin4

3.3.2 Tehtävä

# seq2_1

# seq2_2

# seq23

3.3.3 Tehtävä

# T56

3.3.4 Tehtävä

Vuonna 2019 Suomen eduskuntavaaleissa oli $3\;081\;916$ äänestäjää. Kolme suurinta puoluetta SDP, Perussuomalaiset ja Kokoomus saivat $17,7\;\%$ , $17,5\;\%$ ja $17,0\;\%$ äänestäneiden äänistä. Kuinka monta kansalaista äänesti

# p434a

# p434b

# p434c

# p434d

3.3.5 Tehtävä

Pankki tarjoaa $1\;000$ euron suuruisen lainan $3,45\;\%:$ n vuotuisella korolla. Pikavipin vuotuinen korko $1\;000$ euron lainasta on $475\;\%$ .

# seq415

3.3.6 Tehtävä

Vuoden 2018-2019 NHL:n playoffeissa Pekka Rinne torjui 162 laukausta ja päästi maalia.

# seq418

Vihje

Rinne torjui 162 laukausta ja päästi , joten häntä kohti lauottujen laukauksien lukumäärä on 162+17=179 . Nyt voidaan laskea Rinteen torjuntaprosentti: $\displaystyle\frac{162}{179}$

3.3.7 Tehtävä

400 gramman makeissekoitukseen, missä on $27,9\;\%$ salmiakkia, lisätään 200 grammaa hedelmämakeisia.

# seq4110

Vihje

Ensin selvitetään, kuinka paljon salmiakkia on: $0,279\cdot400\;\text{g}$

Uudessa sekoituksessa salmiakkien määrä pysyy ennallaan...

3.3.8 Tehtävä

1,5 kilogrammaan omenamehua, jonka sokeripitoisuus on $11\;\%$ , lisätään kilogramma kuusiprosenttista kevyt omenamehua. Saadaanko uuden omenamehuseoksen sokeripitoisuus alle $10\;\%$ ?

# Plugin6

Vihje

Ensin lasketaan molempien mehujen yhteissokerimäärä: $0,11\cdot1,5\;\text{kg}+0,06\cdot1\;\text{kg}$

Ja selvitetään tämän suhde koko mehusta...

3.3.9 Tehtävä: (k2019/A3)

Seychellien lipussa on viisi eri väriä kuvan mukaisesti. Kuinka monta prosenttia kukin väri peittää koko lipun pinta-alasta? (vastaa prosentin tarkkuudella)

# seq4311a

# seq4311b

# seq4311c

# seq4311d

# seq4311e

Vihje

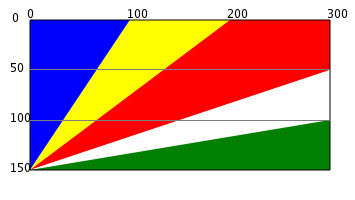
Jaetaan punainen alue kahtia lipun lävistäjän avulla.

Sinisen, keltaisen ja ylemmän punaisen kolmion korkeus on 150 ja kanta 100 . Eli kunkin pinta-ala $\displaystyle\frac{150\cdot100}{2}=7500$ .

Vihreän, valkoisen ja alemman punaisen kolmion korkeus on 300 ja kanta . Eli näidenkin kunkin pinta-ala 7500 .

Kun koko lipun pinta-ala on $300\cdot150=45\;000$ , saadaan laskettua värien suhteelliset osuudet.

3.4 Muutos- ja vertailuprosentti: tehtäviä

Tämän kappaleen teoria.

3.4.1 Tehtävä

Irtokarkkien kilohinta nousee 4,95 eurosta 5,75 euroon. Millä seuraavista kaavoista saadaan laskettua, kuinka monta prosenttia hinta nousi?

# plug421

3.4.2 Tehtävä

euron T-paidan sai alennuksesta 42,50 eurolla. Kuinka monta prosenttia oli alennus?

# tpaita

3.4.3 Tehtävä

Aarolla on euroa ja Sannilla euroa. Mitkä seuraavista väittämistä pitävät paikkansa?

# p423

Vihje

Kuinka paljon enemmän rahaa Sannilla on kuin Aarolla: $\displaystyle\frac{10-5}{5}=1,0=100\;\%$

Kuinka paljon vähemmän rahaa Aarolla on kuin Sannilla: $\displaystyle\frac{10-5}{10}=0,5=50\;\%$

3.4.4 Tehtävä

Vapun kunniaksi irtomakeisten kilohinta oli 4,99 euroa, mikä oli 2,50 euroa vähemmän kuin alkuperäinen hinta.

# seq424

3.4.5 Tehtävä

Vuonna 2018 Samsungin liikevaihto oli 211,2 miljardia ja Applen 265,6 miljardia (USD). (vastaukset prosentin kymmenesosan tarkkuudella)

# seq4_1

# seq4_2

3.4.6 Tehtävä

Puolen litran Jaffa maksaa Prismassa 2,01 euroa per pullo ja 1,5 litran pullojen -pack maksaa 3,97 euroa.

# seq426

Vihje

Puolen litran Jaffan litrahinta: $\displaystyle\frac{2,01}{0,5}=4,02\;\text{(€/l)}$

-packin litrahinta: $\displaystyle\frac{3,97}{2\cdot1,5}=1,32333...\;\text{(€/l)}$

3.4.7 Tehtävä

# seq427

Vihje

Suureet ja ovat kääntäen verrannollisia, joten $\dfrac{x_2}{x_1}=\dfrac{y_1}{y_2}.$

Tiedetään, että kasvaa $25\;\%$ eli uuden arvon suhde alkuperäiseen arvoon $\dfrac{x_2}{x_1}=1,25.$

Halutaan selvittää, paljonko pienenee, jolloin pitää selvittää suhde $\dfrac{y_2}{y_1}$ ja vähentää tämä
$100\;\%$ :sta $\dots$

Ratkaisu

$\begin{align*} 1,25&=\frac{y_1}{y_2} &&|\cdot y_2\\ 1,25\cdot y_2&=y_1 &&|: y_1\\ 1,25\cdot\frac{y_2}{y_1}&=1 &&|:1,25\\ \frac{y_2}{y_1}&=\frac{1}{1,25} \\ \frac{y_2}{y_1}&=0,8 \end{align*}$

Uuden arvon suhde alkuperäiseen arvoon on $0,8=80\;\%,$ joten kasvaa $100\;\%-80\;\%=20\;\%.$

3.4.8 Tehtävä

Vuonna 2009 Usain Bolt juoksi 100 metrin maailmanennätyksen aikaan 9,58 sekuntia virallisen mittauksen mukaan. Matin mukaan Boltin aika oli 9,99 sekuntia, kun taas Iida mittasi ajaksi 9,02 sekuntia. Oletetaan, että virallinen mittaus on oikeassa.

Suhteellinen virhe ilmaisee, kuinka monta prosenttia virheellinen arvo poikkeaa oikeasta arvosta. Positiivinen arvo kertoo, että poikkeama on ylöspäin ja negatiivinen arvo, että poikkeama on alaspäin. Vastaa yhden desimaalin tarkkuudella.

# bolt

# seq4111

3.5 Muuttuneen arvon laskeminen: tehtäviä

Tämän kappaleen teoria.

3.5.1 Tehtävä

Millä desimaaliluvulla hinta tulee kertoa, jos hintaa

# p431a

# p431b

# p431c

# p431d

3.5.2 Tehtävä

Hintoja korotetaan $22,5\;\%$ . Laske uusi hinta sentin tarkkuudella, kun alkuperäinen hinta on

# seq6_3

# seq6_4

3.5.3 Tehtävä

Hintoja alennetaan $17,5\;\%$ . Laske uusi hinta sentin tarkkuudella, kun alkuperäinen hinta on

# seq7_1

# seq7_4

3.5.4 Tehtävä

Hintaa nostetaan ensin $70\;\%$ ja lasketaan sen jälkeen $30\;\%$ . Monta prosenttia uusi hinta on alkuperäistä suurempi?

# p435

3.5.5 Tehtävä

# T59

3.625 pyöristys on 3.63 eikä 3.62

— 22 May 22

3.5.6 Tehtävä

# T58

31.465 pyöristys on 31.47 eikä 31.46

— 22 May 22

3.5.7 Tehtävä

Firman työntekijät olivat tyytymättömiä tämän hetken palkkaansa, jonka vuoksi työnantaja tiedotti:

"Minulla on teille tarjous, josta ette voi kieltäytyä! Ensi vuonna maksan teille kaikille $60\;\%$ ekstraa ensimmäiset kuukautta, jonka jälkeen alennan palkasta $50\;\%$ loppuvuodeksi."

# p438a

Vihje

Merkitään muuttujalla työntekijän kuukausipalkkaa.

$60\;\%$ palkankorotuksen jälkeen, työntekijä saa palkkaa 1,6x kuukaudessa.

Loppuvuodesta palkkaa alennetaan $50\;\%$ , jolloin palkkaa maksetaan $0,5\cdot1,6x=0,8x\dots$

# p438

Vihje

Merkitään muuttujalla työntekijän kuukausipalkkaa.

Tällöin alkuperäinen vuotuinen palkka oli suurudeltaan 12x .

$60\;\%$ palkankorotuksen jälkeen, työntekijä saa palkkaa 1,6x kuukaudessa, joten kuuden kuukauden palkka on $6\cdot1,6x=9,6x$ .

Loppuvuodesta palkkaa alennetaan $50\;\%$ , jolloin palkkaa maksetaan $0,5\cdot1,6x=0,8x$ , joten loppuvuoden palkka on $6\cdot0,8x=4,8x$ .

Nyt työntekijän vuotuinen palkka on 9,6x+4,8x=14,4x.

$\dots$

3.6 Prosenttilausekkeita ja -yhtälöitä: tehtäviä

3.6.1 Tehtävä

Laske alkuperäinen hinta, kun

# seq8_1

# seq8_2

3.6.2 Tehtävä

# seq419

Vihje

Merkitään muuttujalla Coca-Colan määrää kilogrammoissa. Tällöin voidaan muodostaa yhtälö:

$0,021\cdot x = 75$

3.6.3 Tehtävä

Tilastokeskuksen mukaan vuoden 2019 maaliskuussa työssäkäyvien lukumäärä oli $2\;538\;000$ ja työllisyysaste $71,8\;\%$ .

# seq420

Vihje

Merkitään muuttujalla työllisten (eli 15-64 vuotiaiden) lukumäärää. Tällöin työllisten lukumäärä voidaan ratkaista yhtälöstä:

$\begin{align*} 0,718\cdot x & = 2538000\;\;\;\;\;\;\;\; |:0,718 \\ x & = \frac{2538000}{0,718} \end{align*}$

Nyt työttömiä siis $100\;\%-71,8\;\%=28,2\;\%$ työllisten määrästä $x\dots$

3.6.4 Tehtävä

Elokuvalipun myyntihinta muodostuu perushinnasta ja $10\;\%$ arvonlisäverosta.

# p442a

# p442b

Vihje

Merkitään muuttujalla elokuvalipun perushintaa

Arvonlisävero hinnasta on
Lipun myyntihinta on

3.6.5 Tehtävä

# T66

3.6.6 Tehtävä

Jalkapalloseura korotti mestaruuskautensa jälkeen lippujen myyntihintoja. Seuraavalla kaudella joukkue ei menestynyt ja alensi lippujensa hintoja $15\%$ , jolloin ne olivat samanhintaiset kuin ennen mestaruutta.

# p448

Vihje

Merkitään muuttujalla lipun hintaa ennen mestaruutta ja muuttujalla korkoa.

Mestaruuden jälkeen lipun hinta on .

Tämän jälkeen lipun hintaa alennetaan $15\;\%$ , jolloin uusi hinta on 0,85kx . Tämän hinnan tulee olla yhtä suuri kuin lipun hinnan ennen mestaruutta, joten saadaan yhtälö:

0,85kx = x

3.6.7 Tehtävä

Kuten tehtävässä 4.1.5 yleinen tapa mitata humalatilaa on laskea kehon nesteiden alkoholipitoisuutta promilleina $(1\;\text{\textperthousand}=\displaystyle\frac{1}{1000})$ . Henkilö, jonka paino on kilogrammaa juo yhden keskioluen, jonka alkoholipitoisuus on $4,7\;\%$ ja tilavuus 0,33 litraa. Oletetaan, että litra olutta painaa kilogramman ja lisäksi, että henkilö juo juoman nopeasti, jolloin alkoholi ei ehdi poistumaan elimistöstä. Ylittyykö henkilöllä rattijuopumuksen eli $0,5\;\text{\textperthousand}$ :n raja, jos henkilön painosta $70\;\%$ on nesteitä?

# p447

Vihje

Henkilön massasta $70\;\%$ on nesteitä, joten nesteen massa on $0,7\cdot50\;\text{kg}=35\;\text{kg}.$

Koska litra olutta painaa kilogramman, niin yhdessä 0,33 litran $4,7\;\%$ :ssa oluessa on alkoholia $0,047\cdot0,33\;\text{kg}=0,01551\;\text{kg}$ .

Onko osuus henkilön nesteen massasta $<0,5\;\text{\textperthousand}=0,0005$ ?

3.6.8 Tehtävä

Lihassa on aluksi $70\;\%$ vettä. Lihasta halutaan tehdä kuivalihaa, jonka vesipitoisuus on $35\;\%$ .

# p446

Vihje

Merkitään muuttujalla lihan massaa alussa ja muuttujalla veden massaa lopussa.

Aluksi: Lihassa on 0,7x vettä ja 0,3x muuta.

Lopuksi: Lihassa on vettä ja edelleen 0,3x muuta.

Lihan vesipitoisuus on lopussa 0,35 , joten saamme yhtälön

$\frac{y}{y+0,3x} = 0,35$

Ratkaisu

Ratkaistaan yhtälö.

$\begin{align*} \frac{y}{y+0,3x} & = 0,35 && |\cdot (y+0,3x) \\ y & = 0,35y+0,105x && |-0,35y \\ 0,65y & = 0,105x && |:0,65 \\ y &= \frac{0,105}{0,65}x=0,16153846...x \end{align*}$

Nyt veden massan suhde alkuperäiseen veden määrään on $\dfrac{y}{0,7x}=\dfrac{0,16153846...x}{0,7x}\approx0,231=23,1\;\%$ .

Haihdutettava määrä on siis $100\;\%-23,1\;\%=76,9\;\%$ alkuperäisestä veden määrästä.

3. Verrannollisuus ja prosenttilaskenta: tehtäviä

3.1 Suoraan verrannollisuus: tehtäviä

3.1.1 Tehtävä

3.1.2 Tehtävä

3.1.3 Tehtävä

3.1.4 Tehtävä

3.1.5 Tehtävä

3.2 Kääntäen verrannollisuus: tehtäviä

3.2.1 Tehtävä

3.2.2 Tehtävä

3.2.3 Tehtävä

3.2.4 Tehtävä

3.2.5 Tehtävä

3.3 Prosentti: tehtäviä

3.3.1 Tehtävä

3.3.2 Tehtävä

3.3.3 Tehtävä

Tehtävän otsikko

3.3.4 Tehtävä

3.3.5 Tehtävä

3.3.6 Tehtävä

3.3.7 Tehtävä

3.3.8 Tehtävä

3.3.9 Tehtävä: (k2019/A3)

3.4 Muutos- ja vertailuprosentti: tehtäviä

3.4.1 Tehtävä

3.4.2 Tehtävä

3.4.3 Tehtävä

3.4.4 Tehtävä

3.4.5 Tehtävä

3.4.6 Tehtävä

3.4.7 Tehtävä

3.4.8 Tehtävä

3.5 Muuttuneen arvon laskeminen: tehtäviä

3.5.1 Tehtävä

3.5.2 Tehtävä

3.5.3 Tehtävä

3.5.4 Tehtävä

3.5.5 Tehtävä

Tehtävän otsikko

3.5.6 Tehtävä

Tehtävän otsikko

3.5.7 Tehtävä

3.6 Prosenttilausekkeita ja -yhtälöitä: tehtäviä

3.6.1 Tehtävä

3.6.2 Tehtävä

3.6.3 Tehtävä

3.6.4 Tehtävä

3.6.5 Tehtävä

Tehtävän otsikko

3.6.6 Tehtävä

3.6.7 Tehtävä

3.6.8 Tehtävä