3. Verrannollisuus ja prosenttilaskenta

Tässä kappaleessa käsitellään verrannollisuutta sekä prosenttilaskentaa, jotka ovat matematiikan yleisiä sovelluskohteita. Verrannollisuudesta kerrataan suoraan sekä kääntäen verrannollisuus ja prosenttilaskennasta käydään läpi yleisimmät tehtävätyypit. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

3.1 Suoraan verrannollisuus

Kun työskennellään tuntipalkalla ansaitaan sitä enemmän, mitä useampi tunti työskennellään. Palkka ja tehtyjen tuntien määrä kasvavat siis samassa suhteessa. Kun esimerkiksi työtuntien määrä kasvaa kolminkertaiseksi, myös palkka kolminkertaistuu. Tällaisia suureita, joiden suhde on aina vakio, sanotaan suoraan verrannollisiksi.

Suoraan verrannollisuus

Suureet ja ovat suoraan verrannolliset, jos saadaan kertomalla vakiolla eli jos y=kx.

Vakio on nimeltään verrannollisuuskerroin.

Yhtälö y=kx saadaan muotoon $\dfrac{y}{x}=k,$ josta nähdään että suoraan verrannollisten suureiden suhde on vakio. On siis voimassa verranto $\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}$ eli $\dfrac{y_1}{y_2}=\dfrac{x_1}{x_2}.$

Suoraan verrannollisuutta kuvaa graafisesti origon kautta kulkeva suora.

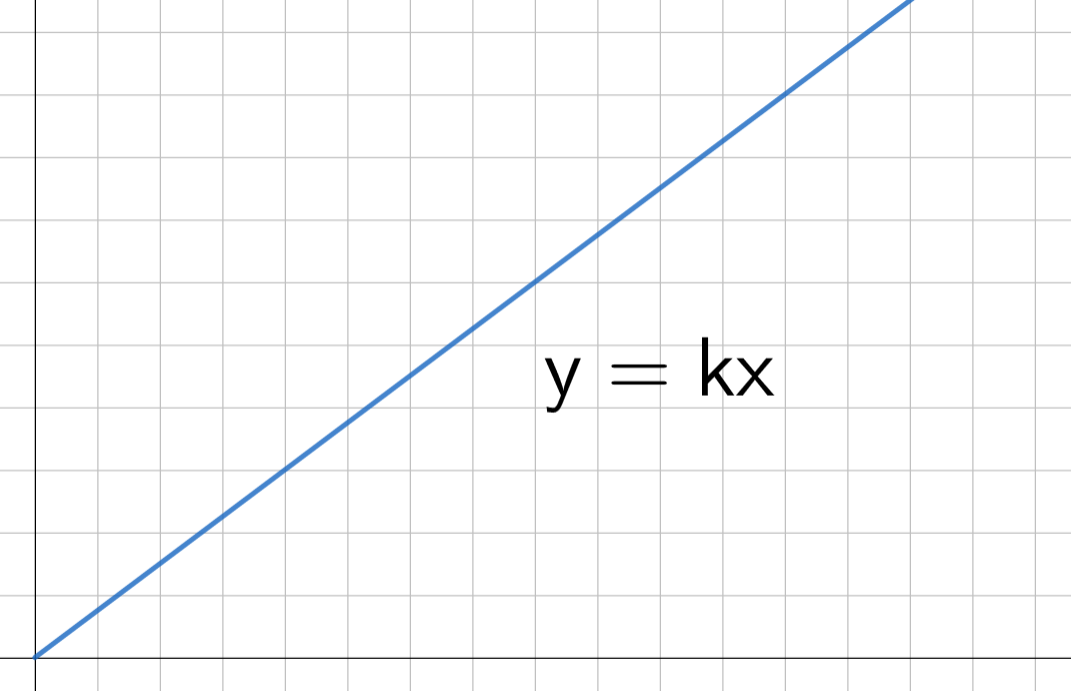
3.1.1 Esimerkki: hinnan riippuvuus määrästä Geogebralla

Tutkitaan esimerkkinä suoraan verrannollisuudesta hinnan riippuvuutta määrästä. Ostettujen tuotteiden hinta $(\text{€})$ on suoraan verrannollinen niiden määrään $(\text{kpl})$ eli

y=kx,

missä vakio kertoo yksittäisen tuotteen kappalehinnan.

Alla on Geogebralla taulukoituna toisiaan vastaavia suureiden arvoja sekä oheen piirretty arvoja vastaavat pisteet koordinaatistoon. Jos pisteiden kautta piirrettäisiin kuvaaja, se olisi muotoa y=kx oleva suora. Suoran kulmakertoimena on tuotteen kappalehinta, jota voi säätää liukusäätimestä.

3.1.2 Esimerkki: sovellus suoraan verrannollisuudesta

Vuotavasta vesihanasta tippuu tasatahtia pisaraa sekunnissa. Kuinka monta vesipisaraa hanasta tippuu minuutissa?

Ratkaisu:

Olkoon pisaramäärä ja aika . Koska pisaramäärä ja aika ovat suoraan verrannollisia suureita, niin

$\begin{align*} \frac{y_1}{x_1}=\frac{y_2}{x_2} \end{align*}$

Merkitään x_1=6, $y_1=10\;\text{(s)}$ ja $y_2=2\cdot 60=120\;\text{(s)}.$ Ratkaistaan x_2 , joka kuvaa kysyttyä pisaramäärää.

$\begin{align*} \frac{y_1}{x_1}&=\frac{y_2}{x_2} &&|\; \text{kerrotaan ristiin} \\ y_1x_2&=y_2x_1 &&|:y_1\\ x_2&=\frac{y_2 x_1}{y_1}&&|\;\text{sijoitetaan arvot}\\ x_2&=\frac{120\cdot6}{10} \\ x_2&=72 \end{align*}$

Vastaus: pisaraa

Suoraan verrannollisuus: tehtäviä

3.2 Kääntäen verrannollisuus

Kun ajetaan polkupyörällä, samaan matkaan menee lyhyempi aika, mitä kovempaa pyörällä polkee. Kun esimerkiksi nopeus kasvaa kaksinkertaiseksi, matka-aika lyhenee puoleen. Tällaisia suureita, joiden tulo on aina vakio, sanotaan kääntäen verrannollisiksi.

Kääntäen verrannollisuus

Suureet ja ovat kääntäen verrannolliset, jos saadaan jakamalla vakio suureella eli jos $y=\dfrac{k}{x}.$

Yhtälo $y=\dfrac{k}{x}$ saadaan muotoon xy=k, josta nähdään että kääntäen verrannollisten suureiden tulo on vakio. On siis voimassa myös yhtälö x_1y_1=x_2y_2 eli $\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}.$

Kääntäen verrannollisten suureiden kuvaaja on hyperbeli.

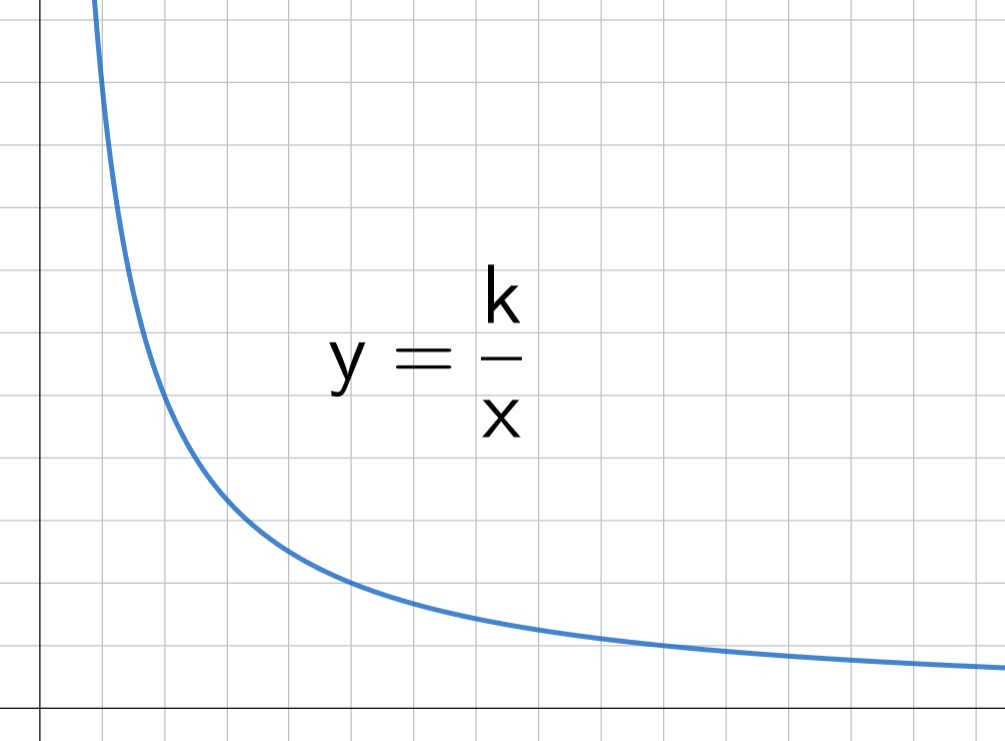
3.2.1 Esimerkki: sovellus kääntäen verrannollisuudesta

Kylpyhuoneen lattian kaakelointiin tarvitaan 360 kappaletta vaaleanpunaisia $10\;\text{cm}\times10\;\text{cm}$ -kokoisia laattoja. Kuinka paljon laattoja tarvittaisiin, jos niiden koko olisi $10\;\text{cm}\times10\;\text{cm}$ ?

Ratkaisu:

Olkoon laattojen määrä ja niiden koko. Laattojen määrä ja koko ovat kääntäen verrannollisia suureita, joten

$\begin{align*} x_1y_1=x_2y_2 \end{align*}$

Merkitään x_1=360, $y_1=10\cdot10=100\;(\text{cm}^2)$ ja $y_2=12\cdot12=144\;(\text{cm}^2)$ . Ratkaistaan x_2, joka kuvaa kysyttyä laattamäärää.

$\begin{align*} x_1y_1&=x_2y_2 && |:y_2\\ x_2&=\frac{x_1y_1}{y_2} &&|\;\text{sijoitetaan arvot}\\ x_2&=\frac{360\cdot100}{144} \\ x_2&=250 \end{align*}$

Vastaus: 250 laattaa

Kääntäen verrannollisuus: tehtäviä

3.3 Prosentti

Prosentin nimitys tulee latinan kielestä per centum, joka tarkoittaa yksi sadasta. Prosentti siis tarkoittaa sadasosaa, ja sen merkki on $\%$ . Prosenttia käytetään suhteellisen osuuden ilmoittamiseen.

Prosentti

$1\;\text{prosentti}=1\;\% =\frac{1}{100}=0,01$

3.3.1 Esimerkki: prosenttiluvun muuttaminen desimaaliluvuksi

Ilmaise sadasosina ja desimaalilukuna.

$3\;\%$
$15\;\%$
$-72\;\%$
$125,6\;\%$

Ratkaisu:

Kerrotaan prosenttiluku murtoluvulla $\dfrac{1}{100}.$ Tällöin saadaan murtoluku, jonka osoittaja kertoo suoraan desimaaliluvun sadasosat.

$3\;\%=3\cdot \displaystyle\frac{1}{100}=\displaystyle\frac{3}{100}=0,03$
$15\;\%=15\cdot \displaystyle\frac{1}{100}=\displaystyle\frac{15}{100}=0,15$
$-72\;\%=-72\cdot \displaystyle\frac{1}{100}=-\displaystyle\frac{72}{100}=-0,72$
$125,6\;\%=125,6\cdot \displaystyle\frac{1}{100}=\displaystyle\frac{125,6}{100}=1,256$

Prosenttiluvun muunnos desimaaliluvuksi vastaa siis käytännössä pilkun siirtämistä kahden numeron verran vasemmalle.

3.3.2 Esimerkki: luvun muuttaminen prosenttiluvuksi

Ilmaise prosentteina.

$\displaystyle\frac{4}{5}$

Ratkaisu:

Kerrotaan desimaaliluku sadalla, jolloin vastauksena saadaan suoraan prosenttiluku. Murtolukua muutettaessa prosenttiluvuksi, lavennetaan luku ensin muotoon, jossa nimittäjänä on luku 100.

$0,05=100\;\%\cdot 0,05=5\;\%$
$7,92=100\;\%\cdot 7,92=792\;\%$
$0,024=100\;\%\cdot 0,024=2,4\;\%$
$^{20)}\displaystyle\frac{4}{5}=\frac{80}{100}=80\;\%$

Desimaaliluvun muunnos prosenttiluvuksi vastaa siis käytännössä pilkun siirtämistä kahden numeron verran oikealle.

Seuraavaksi käydään läpi videollakin esiteltyjä, tyypillisimpiä prosenttilaskuihin liittyviä tehtävätyyppejä esimerkkien kanssa.

Kuinka paljon on prosenttia luvusta ?

Kun kysytään kuinka paljon prosenttia on luvusta , niin tällöin lasketaan tulo $p\cdot a$ Tulossa luku ilmaistaan sadasosina tai desimaalilukuna.

3.3.3 Esimerkki: prosenttia luvusta

Opiskelijaryhmän 32 opiskelijasta $62,5\;\%$ on tyttöjä. Tällöin tyttöjä on

$62,5\cdot\displaystyle\frac{1}{100}\cdot32=0,625\cdot32=20.$

3.3.4 Esimerkki: opintorahan verotus

Opintorahasta pidätettiin veroa $10\;\%$ ennen vuotta 2019 . Kuinka paljon opiskelija joutui vuodessa maksamaan veroa opintorahastaan, kun opintorahan suuruus oli $250,96\;\text{€/kk}$ ?

Ratkaisu:

Opiskelija saa vuodessa opintorahaa yhteensä $12\cdot250,96\;\text{€}$ . Tästä verotetaan $10\;\%$ , joten verotettava määrä on:

$10\;\%\cdot12\cdot250,96=\displaystyle\frac{10}{100}\cdot12\cdot250,96=301,152\approx30,15\;\text{(euroa)}.$

(Todellisuudessa opintoraha on verotonta, mutta siitä verotettiin tehtävänannon mukainen $10\;\%$ , jonka sai vuoden päätteeksi veronpalautuksina takaisin. Opintorahan pystyi halutessaan myös nostamaan suoraan verottomana.)

Vastaus: $30,15\;\text{€}$

Kuinka monta prosenttia luku on luvusta ?

Kun kysytään kuinka monta prosenttia on luvusta , niin kyseessä on suhdelasku $\frac{\displaystyle a}{\displaystyle b},$ joka muunnetaan prosenteiksi.

3.3.5 Esimerkki: montako prosenttia luku luvusta

Kuinka monta prosenttia luku on luvusta ?

$\displaystyle\frac{7}{30}\cdot100\;\%=\frac{70}{3}\;\%=23,33...\;\%\approx23,3\;\%$

3.3.6 Esimerkki: veroprosentin laskeminen

Edmonton Oilersin NHL-jääkiekkoilija Connor McDavidin bruttopalkka on $12\;500\;000$ dollaria ja tämän veronpidätys $5\;966\;250$ dollaria. Mikä on McDavidin veroprosentti?

Ratkaisu:

Lasketaan veronpidätyksen suhde bruttopalkkaan ja muutetaan tämä prosenteiksi:

$\displaystyle\frac{5\;966\;250}{12\;500\;000}=0,4797\approx0.48=48\;\%$

Vastaus: Veroprosentti on $48\;\%$ .

Prosenttilaskenta: tehtäviä

3.4 Muutos- ja vertailuprosentti

Prosenttiluvuilla kuvataan myös suureen muutosta alkuperäisestä arvosta.

Muutosprosentti

Kuinka monta prosenttia muutos on? $\displaystyle\frac{\text{muutos}}{\text{alkuperäinen arvo}}\cdot 100\;\%$

HUOM! Prosenttiyksikkö on absoluuttisen pronsenttimäärän yksikkö. Esimerkiksi koron noustessa 10 prosentista 11 prosenttiin:

korko kasvaa 10 prosenttia
korko kasvaa yhden prosenttiyksikön

3.4.1 Esimerkki: vuokran muutos prosentteina

Vuokra nousi 327 eurosta 333 euroon. Kuinka monta prosenttia vuokra nousi?

Ratkaisu:

Tapa 1:

Lasketaan vuokran muutoksen suuruus: $333-327=6\;\text{(euroa)}$

Lasketaan muutoksen suhde alkuperäiseen vuokraan: $\displaystyle\frac{6}{327}\approx0,018=1,8\;\%$

Tapa 2:

Lasketaan suoraan uuden vuokran suhde alkuperäiseen vuokraan:

$\displaystyle\frac{333}{327}\approx1,018=101,8\;\%$

Lasketaan suhteen ja alkuperäisen vuokran välinen ero, kun alkuperäistä vuokraa vastaava osuus on $100\;\%$ :

$101,8\;\%-100\;\%=1,8\;\%$

Vastaus: Vuokra nousi $1,8\;\%$ .

3.4.2 Esimerkki: prosentti vs. prosenttiyksikkö

Vuoden 2007 uusista ylioppilaista $57\;\%$ ei jatkanut tutkintoon johtavassa koulutuksessa valmistumisvuonnaan. Vuonna 2017 uusista ylioppilaista $72\;\%$ ei jatkanut tutkintoon johtavassa koulutuksessa valmistumisvuonnaan.

Kuinka monta prosenttiyksikköä tutkintoaan jatkamattomien määrä kasvoi vuodesta vuoteen ?
Kuinka monta prosenttia tutkintoaan jatkamattomien osuus kasvoi vuodesta vuoteen ?

Ratkaisu:

Lasketaan muutos prosenttiyksiköissä .

Tutkintoaan jatkamattomien määrä kasvoi prosenttiyksikköä.

Tutkintoaan jatkamattomien osuus kasvoi prosenttiyksikköä, jonka osuus alkuperäisestä osuudesta on:

$\displaystyle\frac{15}{57}\approx0,263=26,3\%.$

Tutkintoaan jatkamattomien osuus kasvoi $26,3\%$ .

Vastaus:

prosenttiyksikköä
$26,3\%$

Vertailuprosentti lasketaan samaan tyyliin kuin muutosprosentti.

Vertailuprosentti

Kuinka monta prosenttia on suurempi kuin ?

$\displaystyle\frac{a-b}{b}\cdot100\;\%$

Kuinka monta prosenttia on pienempi kuin ?

$\displaystyle\frac{a-b}{a}\cdot100\;\%$

3.4.3 Esimerkki: vertailuprosentit

Iltalehden tietojen mukaan Vaasalaisen jääkiekkoseura Sportin pelaajabudjetti kaudella 2018-2019 oli 1,5 miljoonan euron suuruinen, kun taas Helsinkiläisen HIFK:n budjetti oli 3,25 miljoonaa euroa.

Kuinka monta prosenttia Sportin pelaajabudjetti oli pienempi kuin HIFK:n?
Kuinka monta prosenttia HIFK:n pelaajabudjetti oli suurempi kuin Sportin?

Ratkaisu:

Lasketaan, kuinka monta prosenttia budjettien erotus on HIFK:in budjetista.

$\displaystyle\frac{3,25\;\text{milj. €}-1,5\;\text{milj. €}}{3,25\;\text{milj. €}} \approx 0,538=53,8\%$

Sportin pelaajabudjetti oli $53,8\;\%$ pienempi kuin HIFK:n.

Lasketaan, kuinka monta prosenttia budjettien erotus on Sportin budjetista.

$\displaystyle\frac{3,25\;\text{milj. €}-1,5\;\text{milj. €}}{1,5\;\text{milj. €}} \approx 1,167=116,7\%$

HIFK:n pelaajabudjetti oli $116,7\;\%$ suurempi kuin Sportin.

(Tehtävän olisi voinut ratkaista myös esimerkin 4.2.1 toisella tavalla)

Vastaus:

$53,8\;\%$
$116,7\;\%$

Muutos- ja vertailuprosentti: tehtäviä

3.5 Muuttuneen arvon laskeminen

Kun positiivinen luku kasvaa $p\;\%$ , saadaan

$a+\frac{p}{100}\;a=(1+\frac{p}{100})a$

Samoin kun pienenee $p\;\%$ , saadaan

$a-\frac{p}{100}\;a=(1-\frac{p}{100})a$

Näin saadaan laskettua muuttunut arvo.

Korotus

Mikä luku on $p\;\%$ suurempi kuin ?

$(1+\frac{p}{100})a$

Alennus

Mikä luku on $p\;\%$ pienempi kuin ?

$(1-\frac{p}{100})a$

3.5.1 Esimerkki: talletuksen arvo koron jälkeen

Pankki tarjoaa $2,5\%$ korkoa vuotuiselle talletuksella. Paljonko pankki antaa vuoden lopuksi takaisin

euron
$555\;555$ euron

talletuksesta?

Ratkaisu:

Pankki tarjoaa $2,5\;\%$ korkoa, joten vuoden lopuksi talletuksen suuruus on $100\%+2,5\%=102,5\%$ alkuperäisestä. Kerrotaan tällä alkuperäisen talletuksen suuruus:

$102,5\;\%\cdot1225=1,025\cdot1225=1255,625\approx1256\;\text{(euroa)}$

Pankki tarjoaa $2,5\;\%$ korkoa, joten vuoden lopuksi talletuksen suuruus on $100\;\%+2,5\;\%=102,5\;\%$ alkuperäisestä. Kerrotaan tällä alkuperäisen talletuksen suuruus:

$102,5\;\%\cdot555\;555=1,025\cdot555\;555=569\;443,8750\approx569\;444\;\text{(euroa)}$

Vastaus:

$1256\;\text{€}$
$569\;444\;\text{€}$

3.5.2 Esimerkki: osakkeiden hinta laskun jälkeen

Nokian osakkeet laskivat aamupäivällä $10,9\;\%$ . Kuinka paljon maksaa aiemmin

$1\;000\;\text{euroa}$
$12\;475\;\text{euroa}$

maksaneet osakkeet?

Ratkaisu:

Osakkeet laskivat $10,9\;\%$ , joten uusi osakkeiden hinta on $100\;\%-10,9\;\%=89,1\;\%$ alkuperäisestä. Kerrotaan tällä alkuperäinen hinta:

$89,1\;\%\cdot1000=0,891\cdot1000=891\;\text{(euroa)}$

Osakkeet laskivat $10,9\;\%$ , joten uusi osakkeiden hinta on $100\;\%-10,9\;\%=89,1\;\%$ alkuperäisestä. Kerrotaan tällä (desimaaliluku) alkuperäinen hinta:

$0,891\cdot12\;475=11\;115,22500\approx11\;115\;\text{(euroa)}$

Vastaus:

$891\;\text{€}$
$11\;115\;\text{€}$

3.5.3 Esimerkki: epäonnistunut myyntikikkailu

Viekas kaupistelija ajatteli, että jos hän nostaa ensin joulusuklaan hintaa $75\;\%$ ja tämän jälkeen ilmoittaa asiakkaillensa, että joulusuklaa on $60\;\%$ alennuksessa, niin hän saisi alennusmyynnin turvin myytyä suklaata alkuperäistä hintaa kalliimmalla.

Oliko kauppias oikeassa? Jos suklaan lähtöhinta oli $5,60\;\text{€}$ , kuinka paljon se maksoi myyntikikkailujen jälkeen?

Ratkaisu:

Kauppias korottaa hintaa $75\;\%$ , jonka jälkeen hinta on $1,75\cdot5,60\;\text{€}.$

Korotettua hintaa alennetaan $60\;\%$ , jonka jälkeen uusi hinta on $0,4\cdot1,75\cdot5,60\;\text{€}=0,7\cdot5,60\;\text{€}=3,92\;\text{€}.$

Kauppiaan myyntikikkailujen jälkeen uusi hinta on siis $70\%$ alkuperäisestä eli $3,92\;\text{€}.$ Kauppias myy nyt $100\%-70\%=30\%$ halvemalla joulusuklaataan.

Vastaus: Kauppias oli väärässä ja uusi hinta oli $3,92\;\text{€}$ .

Muuttuneen arvon laskeminen: tehtäviä

3.6 Prosenttilausekkeita ja -yhtälöitä

Katsotaan lopuksi esimerkkejä, joissa yhtälön ratkaisua käytetään hyväksi prosenttilaskennan tehtävissä.

3.6.1 Esimerkki: uusi arvo prosenttilausekkeena

Olkoon tietokoneen hinta. Ilmaise lausekkeena tietokoneen uusi arvo, kun

hinta nousee $30\;\%$
hinta laskee $15\;\%$

Ratkaisu:

Korotuskaavalla saadaan: $\displaystyle\frac{100+30}{100}x=\frac{130}{100}x=1,3x$

(Lausekkeen voisi muodostaa myös siten, että lisää alkuperäiseen osuuteen $30\;\%$ korotuksen eli $100\;\%+30\;\%=130\;\%=1,3$ ja kertoo tällä alkuperäisen hinnan.)

Alennuskaavalla saadaan: $\displaystyle\frac{100-15}{100}x=\frac{85}{100}x=0,85x$

(Lausekkeen voisi muodostaa myös siten, että vähentää alkuperäisestä osuudesta $15\;\%$ alennuksen eli $100\;\%-15\;\%=85\;\%=0,85$ ja kertoo tällä alkuperäisen hinnan.)

3.6.2 Esimerkki: alkuperäisen arvon laskeminen

Mikä oli edellisen esimerkin tietokoneen alkuperäinen arvo, kun sen hinta korotuksen jälkeen oli $907,40\;\text{€}$ ?

Ratkaisu:

Edellisen esimerkin lausekkeen avulla saadaan muodostettua yhtälö

$\begin{align*} 1,3x&=907,4 \\ x&=\displaystyle\frac{907,4}{1,3} \\ x&=698 \end{align*}$

Vastaus: Tietokoneen alkuperäinen hinta oli $698\;\text{€}$ .

3.6.3 Esimerkki: polttoainekustannusten muutos

Bensan hinta nousi viime viikon jälkeen $7,5\;\%$ , minkä vuoksi perhe päätti, että autolla ajetaan puolet vähemmän. Paljonko perheen tämän viikon polttoainekustannukset muuttuvat verrattuna viime viikon kustannuksiin?

Ratkaisu:

Merkitään muuttujalla polttoaineen hintaa viime viikolla.

Bensan hinta nousi $7,5\%$ , joten uusi bensan hinta on 1,075x .

Perhe ajaa autolla puolet vähemmän, joten polttoaineeseen kuluu rahaa $0,5\cdot1,075x=0,5375x$ .

Muutos viime viikon kustannuksiin on $\displaystyle\frac{x-0,5375x}{x}=\displaystyle\frac{0,4625x}{x}=0,4625\approx46,3\%$ .

Vastaus: Polttoainekustannukset vähenivät $46,3\;\%$ .

3.6.4 Esimerkki: hinnan korotus ja alennus alkuperäiseen

Hintaa korotetaan ensin $p\;\%$ . Kuinka monta prosenttia tulisi korotettua hinta alentaa, jotta hinta olisi alkuperäisen suuruinen?

Ratkaisu:

Merkitään muuttujalla alennusta prosentteina.

Hintaa korotetaan $p\;\%$ : $\displaystyle\frac{100+p}{100}h$

Korotettua hintaa alennetaan $x\;\%$ : $\displaystyle\frac{100-x}{100}\displaystyle\frac{100+p}{100}h$

Muodostetaan ja ratkaistaan yhtälö, kun uuden hinnan tulee olla yhtä suuri kuin alkuperäinen:

$\begin{align*} \frac{100-x}{100}\frac{100+p}{100}h & = h && |:h \\ \frac{100-x}{100}\frac{100+p}{100} & = 1 && | \cdot 100 \cdot 100 \\ (100-x)(100+p) &= 10000 \\ 10 000+100p-100x-xp&=10000 && |-10000 \\ 100p-100x-xp&=0 && |+100x+xp \\ 100x+xp&=100p \\ x(100+p)&=100p && |:(100+p) \\ x&=\frac{100p}{100+p} \end{align*}$

Vastaus: $\displaystyle\frac{100p}{100+p}\;\%$

Prosenttilausekkeita ja -yhtälöitä: tehtäviä