4. Potenssi ja juuri

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Potenssi ja juuri. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

4.1 Potenssi

Tämän kappaleen teoria.

4.1.1 Tehtävä

# Plugin1

4.1.2 Tehtävä

Laske ilman laskinta.

# seq9_3

# seq9_4

# seq9_5

# seq9_6

4.1.3 Tehtävä

Laske ilman laskinta.

# seq10_1

# seq10_2

# seq10_3

# seq10_4

4.1.4 Tehtävä

Eskon synnyttyä hänen vanhempansa tallettivat 5000 euroa säästötilille, jonka vuotuinen korko on $3,5\;\%$ .

# seq2_2

Vihje: Esimerkki 5.1.3

4.1.5 Tehtävä

Laske ilman laskinta.

# seq10_5

# seq10_6

# seq10_7

Mitä havaitset? Miten voit laskea ilman laskinta 1000^2-999^2 ?

# p515d

Ratkaisu

Perättäisten lukujen neliöiden erotus on yhtä suuri kuin samojen lukujen summa, joten 1000^2-999^2 = 1000 + 999 = 1999.

4.1.6 Tehtävä

Päättele, mikä luku sopii :n paikalle.

# seq11_1

# seq11_2

# seq11_3

4.1.7 Tehtävä

Venezuelan inflaation vuoksi kananlihan kilohinta on noussut $27\;\%$ viikossa ja on nyt 10.9 miljoonaa bolivaria. Oletetaan, että inflaatio on säilynyt vakiona kuukauden aikana.

# seq2_3

Vihje

Korkoprosentti on $27\;\%$ , joten korkokerroin on 1,27 . Neljän viikon aikana kilohinta on noussut 10,9 miljoonaan, mistä saamme yhtälön:

1,27^4x= 10,9

4.2 Potenssin laskusääntöjä

Tämän kappaleen teoria.

4.2.1 Tehtävä

# Potenssimonivalintaeka

Laske tehtävät 5.2.2-5.2.10 ilman laskinta. Voit hahmotella vastauksesi halutessasi ensin Abitti-editorilla, joka löytyy tehtävien alta.

4.2.2 Tehtävä

Sievennä käyttäen samankantaisten potenssien tulon kaavaa.

# seq12_9

# seq12_10

# seq12_11

Abitti-editori

# Plugin3

4.2.3 Tehtävä

Laske käyttäen samankantaisten potenssien osamäärän kaavaa.

# seq12_13

# seq12_14

# seq12_15

Abitti-editori

# pluginjoku

4.2.4 Tehtävä

Sievennä käyttäen potenssin potenssin kaavaa.

# seq12_17

# seq12_18

# seq12_19

Abitti-editori

# plugini

4.2.5 Tehtävä

Sievennä käyttäen tulon potenssin kaavaa.

# seq12_21

# seq12_22

# seq12_23

Abitti-editori

# pluginvaan

4.2.6 Tehtävä

Sievennä käyttäen osamäärän potenssin kaavaa.

# seq12_25

# seq12_26

# seq12_27

Abitti-editori

# plugin4

4.2.7 Tehtävä

# p524

4.2.8 Tehtävä

# T49

4.2.9 Tehtävä

Muodosta ja sievennä kuutioiden tilavuuksien lausekkeet.

# seq528a

# seq528b

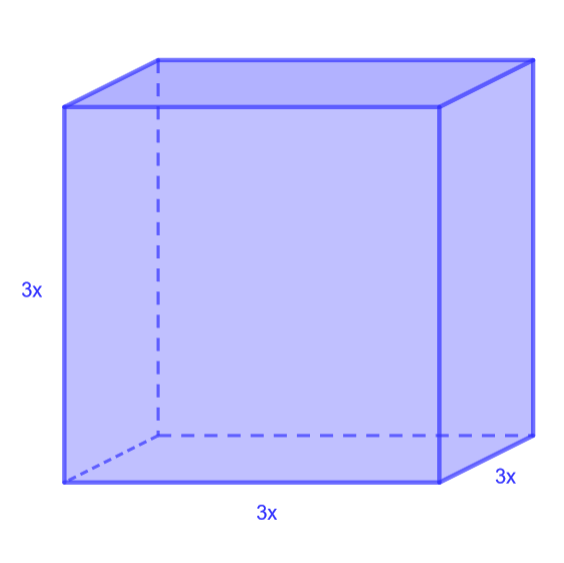
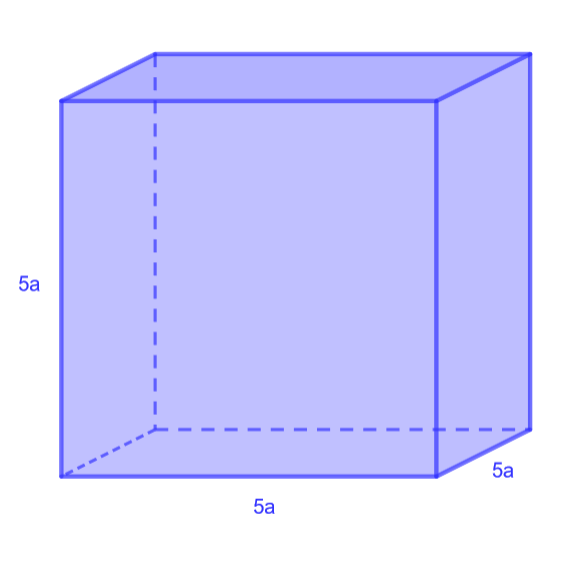
4.2.10 Tehtävä

Sievennä.

# seq12_24

Vihje

$\begin{align*} (x^4y)^2(x^2y^3)^4&=(x^4)^2y^2(x^2)^4(y^3)^4 \\ &=x^8y^2x^8y^{12} \\ &=\dots \end{align*}$

# seq12_12

# seq12_28

Vihje

$\begin{align*} \dfrac{9a^8b^6}{a^6b^9}\cdot\dfrac{a^6b^6}{9a^4b^2}&=\dfrac{\cancel{9}a^8b^6a^6b^6}{\cancel{9}a^6b^9a^4b^2} \\ &= \frac{a^{8+6}b^{6+6}}{a^{6+4}b^{9+2}} \\ &=\dots \end{align*}$

Abitti-editori

# Plugin5

4.2.11 Tehtävä

Suomi voitti vuoden 2019 jääkiekon maailmanmestaruuden. Mestaruuteen Suomi tarvitsi pudotuspeleissä puolivälierävoiton Ruotsista, välierävoiton Venäjästä sekä finaalivoiton Kanadasta. Oletetaan, että yksittäinen voitto vastaa kolikon heittoa eli toisin sanoen Suomen todennäköisyys voittaa yksittäinen ottelu on $\dfrac{1}{2}$ .

# seq5211

# seq5311b

Klassisessa todennäköisyyslaskennassa kahden toisistaan riippumattoman tapahtuman todennäköisyys voidaan laskea tuloperiaatteen avulla:

Jos tapahtuman todennäköisyys on ja tapahtuman todennäköisyys on , niin tällöin todennäköisyys sille, että tapahtuu ja voidaan laskea tulona .

Ratkaisu

Suomen tulee voittaa kolme kolikon heittoa putkeen, joten tuloperiaatteen mukaan saadaan todennäköisyys voittaa mestaruus:

$\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}=\Big(\dfrac{1}{2}\Big)^3=\dfrac{1}{8}$

$\Big(\dfrac{1}{2}\Big)^n$

4.2.12 Tehtävä

Katso oheinen video "suklaatempusta".

DailyBroccoli: Chocolate bar trick

Leikkaamalla suklaata kuten videossa, levystä poistuu aina pala per kierros, jonka jälkeen näyttää kuitenkin siltä, että levyssä olisi alkuperäinen määrä paloja. Kuvitellaan, että meillä on vastaavanlainen $9\times4$ suklaalevy. Toisin kuin videolla, leikkaamme jokaisella kierroksella levystä pois prosentuaalisesti saman verran suklaata kuin ensimmäisellä kierroksella. Siis vain ensimmäisellä kierroksella levystä poistuu tasan suklaapala. Kuinka paljon suklaata on jäljellä alkuperäiseen määrään verrattuna, kun leikkaamme levyä

# seq5212a

# seq5312b

Ratkaisu

Levyssä on $4\cdot9=36$ palaa, joista leikataan ensimmäisellä kierroksella pala pois ja jäljelle jää palaa. Tällöin ensimmäisen kierroksen jälkeen leikatun massa alkuperäisestä on $\dfrac{35}{36}$ .

Toisella kierroksella, leikkaamme suhteellisesti saman määrän, jolloin suklata jää jäljelle $\dfrac{35}{36}\cdot\dfrac{35}{36}=\left(\dfrac{35}{36}\right)^2$

Vastaavasti yhdeksännellä kierroksella suklaan suhde alkuperäiseen on $\left(\dfrac{35}{36}\right)^9\approx0,776=77,6\;\%$

$\left(\dfrac{35}{36}\right)^n$

4.2.13 Tehtävä

Osoita, että lausekkeen $\dfrac{2^n4^{n+3}}{8^{n+1}}$ arvo ei riipu positiivisen kokonaisluvun arvosta. Kirjoita vastauksesi haluamallasi ohjelmalla ja palauta tiedostona.

# p5213

Vihje

Ilmaistaan lausekkeet luvun potensseina, jolloin voidaan hyödyntää potenssin laskusääntöjä.

$\dfrac{2^n4^{n+3}}{8^{n+1}}=\dfrac{2^n(2^2)^{n+3}}{(2^3)^{n+1}}=\dfrac{2^n2^{2n+6}}{2^{3n+3}}=\dots$

Ratkaisu

$\dfrac{2^n4^{n+3}}{8^{n+1}}=\dfrac{2^n(2^2)^{n+3}}{(2^3)^{n+1}}=\dfrac{2^n2^{2n+6}}{2^{3n+3}}=\dfrac{2^{3n+6}}{2^{3n+3}} =\dfrac{2^{3n}}{2^{3n}}\cdot\dfrac{2^{6}}{2^3}=2^3$

Nyt lausekkeessa ei ole kokonaislukumuuttujaa , joten se ei siis riipu luvun arvosta.

4.2.14 Tehtävä

# T48

4.3 Kymmenpotenssimuoto

Tämän kappaleen teoria.

4.3.1 Tehtävä

Ilmaise kahden numeron tarkkuudella kymmenpotenssimuodossa.

# seq12_5

# seq12_6

# seq12_7

4.3.2 Tehtävä

Elektronin massa on noin $9,1\cdot10^{-31}\;\text{kg}$ ja protonin $1,7\cdot10^{-27}\;\text{kg}$ . Kuinka moninkertainen on

# seq12_29

# seq12_30

4.3.3 Tehtävä

Maan etäisyys toukokuussa Auringosta on noin 151,6 miljoonaa kilometriä ja valon nopeus on $2,998\cdot10^8\;\frac{\text{m}}{\text{s}}$ . Nopeudelle pätee yhtälö $v=\dfrac{s}{t}$ , missä matka ja =aika.

# seq533

Vihje

Maan etäisyys Auringosta pitää ensin muuttaa metreiksi kymmenpotenssimuotoon.

$151,6\;\text{milj.}\;\text{km}=151\;600\;000\;\text{km}=1,516\cdot10^8\;\text{km}=1,516\cdot10^{11}\;\text{m}$

Aika, joka valolla kestää Auringosta Maahan, saadaan laskettua kaavalla

$t=\dfrac{s}{v}=\frac{1,516\cdot10^{11}\;\text{m}}{2,998\cdot10^8\;\frac{\text{m}}{\text{s}}}=\dots$

4.3.4 Tehtävä

Vanhan tarinan mukaan shakkipeli keksittiin noin 2500 vuotta sitten Intiassa. Kun pelin keksijä oli esitellyt pelinsä kuninkaalleen, tämä ihastui peliin niin, että lupasi keksijälle palkinnoksi mitä tahansa. Keksijä ilmoitti tyytyvänsä vaatimattomaan palkkioon: hän pyysi ensimmäiselle ruudulle yhden vehnänjyvän, toiselle kaksi, kolmannelle neljä ja niin edelleen, aina seuraavalle ruudulle kaksi kertaa niin monta jyvää kuin edelliselle.

# seq534a

Vihje

ruutu:
ruutu: $2\cdot1$
ruutu: $2\cdot2\cdot1=2^2$
ruutu: $2\cdot2^2=2^3$ $\dots$

# seq534b

# seq534b2

4.3.5 Tehtävä

Luonnontieteissä pieniä lukuja on tapana ilmaista kymmenpotenssimuodossa negatiivisen eksponentin avulla. Taulukossa ovat näiden esitysmuotojen etuliitteet.

kymmenpotenssi	etuliite	lyhenne
$10^{-3}$	milli	$\text{m}$
$10^{-6}$	mikro	$\mu$
$10^{-9}$	nano	$\text{n}$
$10^{-12}$	piko	$\text{p}$
$10^{-15}$	femto	$\text{f}$
$10^{-18}$	atto	$\text{a}$

Valitse oikeat etuliitteet.

# p535a

# p535b

# p535c

# p535d

4.4 Neliö- ja kuutiojuuri

Tämän kappaleen teoria.

4.4.1 Tehtävä

# monivalintajuurieka

4.4.2 Tehtävä

Laske ilman laskinta.

# seq13_1

# seq13_2

# seq13_3

# seq13_4

4.4.3 Tehtävä

Laske ilman laskinta.

# seq543a

# seq14_5

# seq543c

# seq14_4

4.4.4 Tehtävä

Laske ilman laskinta. Käytä hyväksesi neliöjuuren ominaisuuksia. Hahmottele tarvittaessa Abitti-editorilla.

# seq15_1

# seq15_2

# seq15_3

# seq15_4

Abitti-editori

# Plugin6

4.4.5 Tehtävä

# Plugin28

# Plugin18

4.4.6 Tehtävä

Playstation-ohjaimen neliö-näppäimen kuvan pinta-ala on noin $42\;\text{mm}^2$ .

# seq545

4.4.7 Tehtävä

Jasminin isä valmistaa mokkapaloja Jasminin yo-juhliin. Hän arvioi, että keskimäärin yksi vieras syö mokkapalan, jonka pinta-ala on $50\;\text{mm}^2$ . Jasminin isä päättääkin tehdä juhliin yhden ison neliön muotoisen mokkapalan, josta vieraat voivat leikata haluamansa määrän.

# seq546

Vihje

Ison mokkapalan pinta-ala: $150\cdot50=7500\;\text{mm}^2$

4.4.8 Tehtävä (s1984/1)

Minkä positiivisen luvun neliöjuuri on luku $\sqrt{5}-2$ ?

# seq546a

# seq546b

Vihje

$\begin{align*} &(\sqrt{5}-2)^2 \\ &=(\sqrt{5}-2)(\sqrt{5}-2) \\ &=(\sqrt{5})^2-2\sqrt{5}-2\sqrt{5}+(-2)^2 \\ &=\dots \end{align*}$

Abitti-editori

# Plugin7

4.4.9 Tehtävä

Rationaalilauseke, missä nimittäjänä on neliöjuuri, voidaan sieventää laventamalla nimittäjällä. $^{\sqrt{b})}\dfrac{a}{\sqrt{b}}=\dfrac{a\sqrt{b}}{\sqrt{b}\sqrt{b}}=\dfrac{a\sqrt{b}}{b}$

Esimerkiksi: $^{\sqrt{5})}\dfrac{60}{\sqrt{5}}=\dfrac{60\sqrt{5}}{\sqrt{5}\sqrt{5}}=\dfrac{60\sqrt{5}}{5}=12\sqrt{5}$

Sievennä tätä käyttäen ilman laskinta seuraavat lausekkeet.

# seq549a

# seq549b

# seq549c

# seq549d

Abitti-editori

# Plugin8

4.4.10 Tehtävä

Standardimittaisen $3\times3$ Rubikin kuution tilavuus on noin $V=190\;\text{cm}^3$ .

# seq5410

Vihje

Rubiikin kuutiossa on paloja $3\cdot3\cdot3=27,$ joten yksittäisen palan tilavuus $\dfrac{190\;\text{cm}^2}{27}\dots$

4.4.11 Tehtävä

Laske lausekkeiden arvot, kun $a = 1, b = 6 \text{ ja } c = 8$ .

# seq5411a

# seq5411b

Sijoita lausekkeen arvot yhtälöön muuttujan paikalle.

# taskNimi

Vastaus

Molempien lausekkeiden arvot, x=-2 ja x=-4 , ovat yhtälön ratkaisuja.

Yleisesti yhtälö, joka on muotoa ax^2+bx+c=0 , voidaan ratkaista toisen asteen yhtälön ratkaisukaavaalla $x=\dfrac{-b \pm\sqrt{b^2-4ac}}{2a}.$ Tähän perehdytään lisää MAA2-kurssilla.

4.5 Potenssiyhtälö

Tämän kappaleen teoria.

4.5.1 Tehtävä

# Plugin68

Ratkaise tehtävät 5.5.2-5.5.3 ja 5.5.5 ilman laskinta. Hahmottele halutessasi ratkaisuja Abitti-editorilla, joka löytyy tehtävien alta.

4.5.2 Tehtävä

Ratkaise yhtälö.

# seq16_2

# seq16_3

# seq16_5

# seq16_6

Abitti-editori

# Plugin9

4.5.3 Tehtävä

Ratkaise yhtälö.

# seq17_1

# seq17_2

# seq17_3

# seq17_4

Abitti-editori

# Plugin10

4.5.4 Tehtävä

Kansainvälisen jääkiekkoliiton mukaan jääkiekkokaukalon aloitusympyröiden pinta-ala on yhteensä noin $320\;\text{m}^2$ .

# seq5411a2

Vihje

Kaukalossa on aloitusympyrää, joten yksittäisen ympyrän pinta-ala $A=\dfrac{320}{5}=64 \;(\text{m}^2)$ .

Ympyrän yhtälölle pätee $A=\pi r^2$ , josta voidaan ratkaista

$r=\sqrt{\dfrac{A}{\pi}}$ tai $r=-\sqrt{\dfrac{A}{\pi}}$

Negatiivinen ratkaisu ei kelpaa, siispä voidaan laskea halkaisija $h=2r=\dots$

4.5.5 Tehtävä

Ratkaise yhtälö.

# seq18_1

# seq18_2

# seq18_3

# seq18_4

Abitti-editori

# Plugin11

Ratkaisu

Muokataan yhtälöt muotoon, jossa toisella puolella on muuttuja ja toisella vakio ja otetaan puolittain neliö- tai kuutiojuuri.

$\begin{align*} -2x^2+1&=-2 \\ -2x^2&=-3 \\ x^2&=\frac{3}{2} \\ x=-\sqrt{\frac{3}{2}} \;\;&\text{tai}\;\; x=\sqrt{\frac{3}{2}} \end{align*}$

$\begin{align*} \frac{1}{9}x^2-1&=\frac{1}{7} \\ \frac{1}{9}x^2&=\frac{8}{7} &&|\cdot 9\\ x^2&=\frac{72}{7} \\ x=-\sqrt{\frac{72}{7}} \;\;&\text{tai}\;\; x=\sqrt{\frac{72}{7}} &&|\sqrt{72}=\sqrt{36}\cdot\sqrt{2}=6\sqrt{2}\\ x=-6\sqrt{\frac{2}{7}} \;\;&\text{tai}\;\; x=6\sqrt{\frac{2}{7}} \end{align*}$

$\begin{align*} -\frac{1}{9}x^3-1&=0 \\ -\frac{1}{9}x^3&=1 \\ x^3&=-9 \\ x&=\sqrt[3]{-9}=-\sqrt[3]{9} \end{align*}$

$\begin{align*} \frac{1}{9}x^3+\frac{1}{\pi}&=\pi \\ \frac{1}{9}x^3&=\pi-\frac{1}{\pi} &&|\cdot 9\\ x^3&=9\pi-\frac{9}{\pi} \\ x&=\sqrt[3]{9\pi-\frac{9}{\pi}} \end{align*}$

4.5.6 Tehtävä

Vuonna 2017 Suomessa hakattiin puuta ennätysmäärä, noin $7,2 \cdot 10^7\;\text{m}^3.$

Jos kaikki puu varastoidaan

# seq5411a3

Vihje

$\begin{align*} &x^3=V\\ &x=\sqrt[3]{V}\\ &\;\;\dots\\ \end{align*}$

# seq5411a4

Vihje

Pallon tilavuus saadaan kaavalla $V_{pallo}=\dfrac{4\pi r^3}{3}$ , joten puolipallon tilavuus $V_{puolipallo}=\dfrac{4\pi r^3}{3}\cdot\dfrac{1}{2}=\dfrac{2\pi r^3}{3}.$

Tästä voidaan ratkaista puolipallon säde $\dots$

# p556c

Vihje

Lasketaan molempien varastojen seinien pinta-alat. Kuution pinta-ala saadaan laskemalla viiden tahkon (pohja jätetään pois) pinta-alat yhteen.

$A_{kuutio}=5\cdot x^2=\dots$

Pallon pinta-ala saadaan kaavalla $4\pi r^2,$ joten puolipallon pinta-ala saadaan

$A_{puolipallo}=\dfrac{4\pi r^2}{2}=\dots$

4. Potenssi ja juuri

4.1 Potenssi

4.1.1 Tehtävä

4.1.2 Tehtävä

4.1.3 Tehtävä

4.1.4 Tehtävä

4.1.5 Tehtävä

4.1.6 Tehtävä

4.1.7 Tehtävä

4.2 Potenssin laskusääntöjä

4.2.1 Tehtävä

4.2.2 Tehtävä

Abitti-editori

4.2.3 Tehtävä

Abitti-editori

4.2.4 Tehtävä

Abitti-editori

4.2.5 Tehtävä

Abitti-editori

4.2.6 Tehtävä

Abitti-editori

4.2.7 Tehtävä

4.2.8 Tehtävä

Tehtävän otsikko

4.2.9 Tehtävä

4.2.10 Tehtävä

Abitti-editori

4.2.11 Tehtävä

4.2.12 Tehtävä

4.2.13 Tehtävä

4.2.14 Tehtävä

Tehtävän otsikko

4.3 Kymmenpotenssimuoto

4.3.1 Tehtävä

4.3.2 Tehtävä

4.3.3 Tehtävä

4.3.4 Tehtävä

4.3.5 Tehtävä

4.4 Neliö- ja kuutiojuuri

4.4.1 Tehtävä

4.4.2 Tehtävä

4.4.3 Tehtävä

4.4.4 Tehtävä

Abitti-editori

4.4.5 Tehtävä

Tehtävän otsikko

Tehtävän otsikko

4.4.6 Tehtävä

4.4.7 Tehtävä

4.4.8 Tehtävä (s1984/1)

Abitti-editori

4.4.9 Tehtävä

Abitti-editori

4.4.10 Tehtävä

4.4.11 Tehtävä

4.5 Potenssiyhtälö

4.5.1 Tehtävä

4.5.2 Tehtävä

Abitti-editori

4.5.3 Tehtävä

Abitti-editori

4.5.4 Tehtävä

4.5.5 Tehtävä

Abitti-editori

4.5.6 Tehtävä