Hei

— 23 Nov 19

4. Potenssi ja juuri

Tässä kappaleessa käsitellään potenssilaskentaa sekä potenssille käänteistä laskutoimitusta juurta, keskittyen neliö- ja kuutiojuureen. Kappaleessa käydään läpi potenssien ja juurien laskusääntöjä, kymmenpotenssimuoto sekä lopuksi perehdytään potenssiyhtälöön. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

4.1 Potenssi

Potenssi on kertolaskun lyhennetty merkitsemistapa silloin, kun samaa lukua kerrotaan itsellään useamman kerran. Esimerkiksi merkintä 4^3 tarkoittaa tuloa $4\cdot4\cdot4$ ja se luetaan "neljä potenssiin kolme" tai "luvun 4 kolmas potenssi".

Potenssi

Olkoon positiivinen kokonaisluku ( n=1, 2, 3, ... ). Tällöin luvun :s potenssi on

$a^n=\underbrace{a\cdot a\cdot ... \cdot a}_{\text{$n$ kappaletta}}$

Erityisesti a^1=a.

Luku on potenssin kantaluku ja luku on eksponentti. Kantaluku on toisinaan tarpeen merkitä sulkeisiin. Esimerkiksi -3^2=-9, mutta (-3)^2=9. Samoin $\displaystyle\frac{2}{3}^2=\frac{4}{3},$ mutta $\left(\displaystyle\frac{2}{3}\right)^2=\displaystyle\frac{4}{9}.$

Potenssien sanotaan olevan samankantaisia, jos niillä on sama kantaluku.

Negatiivisen kantaluvun potenssi

Jos potenssin a^n kantaluku on negatiivinen ja eksponentti on

parillinen, niin potenssin arvo on positiivinen
pariton, niin potenssin arvo on negatiivinen

hei kiva määritelmä

— 09 Nov 19

4.1.1 Esimerkki: negatiivisen kantaluvun potenssi

Laske.

luvun toinen potenssi
luvun kolmas potenssi
luvun toisen potenssin vastaluku
luvun :s potenssi

Ratkaisu:

Negatiivinen kantaluku pitää merkitä sulkeisiin. Luvun toinen potenssi on

$(-3)^2=\underbrace{(-3)\cdot(-3)}_{2\text{ kpl, parillinen}}=9$

Luvun kolmas potenssi on

$(-2)^3=\underbrace{(-2)\cdot(-2)\cdot(-2)}_{3\text{ kpl, pariton}}=-8$

Luvun toinen potenssi on ja sen vastaluku

$-5^2=-5\cdot5=-25$

Luvun :s potenssi

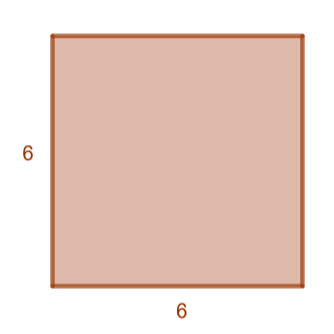
$(-1)^{2500}=\underbrace{(-1)\cdot(-1)\cdot ... \cdot(-1)}_{2500\text{ kpl, parillinen}}=1$

4.1.2 Esimerkki: neliö ja kuutio

Laske

neliön, jonka sivun pituus on pinta-ala.

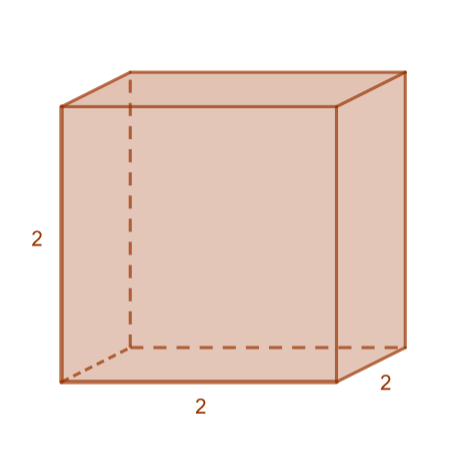
kuution, jonka särmän pituus on tilavuus.

Ratkaisu:

Neliön pinta-ala saadaan kannan ja korkeuden tulona, joka voidaan ilmaista potenssin avulla.

$A=6^2=6\cdot6=36$

Kuution tilavuus saadaan särmien tulona, joka voidaan ilmaista potenssin avulla.

$V=2^3=2\cdot2\cdot2=8$

Potenssia a^2 sanotaan luvun neliöksi ja potenssia a^3 luvun kuutioksi.

4.1.3 Esimerkki: rahaston arvon kasvu

Eetu voitti veikkaamalla $6\,000$ euroa, jotka hän päätti sijoittaa indeksirahastoihin. Asiantuntija arvioi, että Eetu saisi $6,5\;\%$ :n vuotuisella korolla voittoa. Kuinka paljon Eetun rahaston arvo on vuoden kuluttua jos oletetaan, että vuotuinen korko säilyy?

Ratkaisu:

Indeksirahasto tuottaa vuodesa $6,5\;\%$ pääomasta, joten rahaston arvo kasvaa siis vuodessa 1,065 -kertaiseksi. Yhden vuoden kuluttua Eetun pääoman arvo on

$1,065\cdot6000\;\text{(euroa)}$

Korkoprosentti säilyy vakiona, joten vastaavasti myös seuraavan vuoden aikana rahaston arvo kasvaa 1,065 -kertaiseksi. Kahden vuoden kuluttua rahaston arvo on

$\underbrace{1,065\cdot 1,065}_{\text{$2$ kappaletta}}\cdot\;6000=1,065^2\cdot6000$

Vastaavasti kolmen vuoden kuluttua rahaston arvo on

$\underbrace{1,065\cdot 1,065\cdot1,065}_{\text{$3$ kappaletta}}\cdot\;6000=1,065^3\cdot6000$

20 vuoden kuluttua rahaston arvo on

$\underbrace{1,065\cdot 1,065\cdot ... \cdot 1,065}_{\text{20 kappaletta}}\cdot\;6000=1,065^{20}\cdot6000=21141,87038\approx21141,87$

Vastaus: vuoden kuluttua Eetun rahaston arvo on $21\;141,87$ euroa.

Rahalaskut pyöristetään aina sentin tarkkuudella ellei toisin mainita.

Potenssi: tehtäviä

4.2 Potenssin laskusääntöjä

Videolla esitellään viisi potenssien laskusääntöä, jotka käydään seuraavaksi läpi.

Potenssilauseke voidaan sieventää purkamalla sen potenssit tuloiksi. Tarkastellaan näin muutamia esimerkkejä ja yleistetään niiden perusteella potenssien laskusäännöt.

$a^2a^4=\underbrace{a\cdot a}_{\text{$2$ kpl}} \cdot \underbrace{a\cdot a\cdot a \cdot a}_{\text{$4$ kpl}}=a^{2+4}=a^6$

$\dfrac{a^7}{a^3}=\dfrac{a\cdot a\cdot a\cdot a\cdot \cancel{a}\cdot \cancel{a}\cdot \cancel{a}}{\cancel{a}\cdot \cancel{a}\cdot \cancel{a}}=a^{7-3}=a^4$

Samankantaisten potenssien tulossa eksponentit lasketaan yhteen ja samankantaisten potenssien osamäärässä eksponentit vähennetään toisistaan.

Samankantaisten potenssien tulo ja osamäärä

$a^ma^n=a^{m+n}$

$\frac{a^m}{a^n}=a^{m-n}$

$(ab)^3=ab\cdot ab \cdot ab=a\cdot a\cdot a\cdot b\cdot b\cdot b=a^3b^3$

$(\dfrac{a}{b})^3=\dfrac{a}{b}\cdot\dfrac{a}{b}\cdot\dfrac{a}{b}=\dfrac{a\cdot a\cdot a}{b\cdot b\cdot b}=\dfrac{a^3}{b^3}$

Tulon potenssissa tulon tekijät korotetaan erikseen potenssiin ja osamäärän potenssissa jakaja ja jaettava korotetaan erikseen potenssiin.

Tulon potenssi ja osamäärän potenssi

(ab)^n=a^nb^n

$\Big(\frac{a}{b}\Big)^n=\frac{a^n}{b^n}$

$(a^3)^2=\underbrace{a^3\cdot a^3}_{\text{$2$ kpl}}=a^{3\cdot2}=a^6$

Kun potenssi korotetaan potenssiin, niin eksponentiksi tulee eksponenttien tulo.

Potenssin potenssi $(a^{m})^n=a^{mn}$

4.2.1 Esimerkki: potenssin laskusääntöjä

Laske

$\left(\dfrac{12}{3}\right)^2$ b. c. $\dfrac{(-5)^7}{(-5)^5}$

Ratkaisu:

Osamäärän potenssissa sekä nimittäjä että osoittaja korotetaan potenssiin.

$\left(\dfrac{12}{3}\right)^2=\dfrac{12^2}{3^2}=\dfrac{144}{9}=16$

Potenssin potenssissa eksponentit kerrotaan keskenään.

$(3^2)^2=3^{2\cdot2}=3^4=81$

Samankantaisten potenssien osamäärässä eksponentit vähennetään toisistaan.

$\dfrac{(-5)^7}{(-5)^5}=(-5)^{7-5}=(-5)^2=25$

4.2.2 Esimerkki: potenssien sieventämistä

Sievennä.

$\dfrac{2d^7}{d^3}$ b. $3a^4\cdot(-2a^3)$ c.

Ratkaisu:

kantaisten potenssien eksponentit vähennetään toisistaan ja luku jää eteen kertoimeksi.

$\dfrac{2d^7}{d^3}=2d^{7-3}=2d^4$

kantaisten potenssien eksponentit lisätään yhteen ja luvut ja kerrotaan keskenään.

$3a^4\cdot(-2a^3)=-6a^{4+3}=-6a^7$

Jokainen termi korotetaan erikseen toiseen.

$(ax^3y)^2=a^2(x^3)^2y^2=a^2x^{3\cdot2}y^2=a^2x^{6}y^2$

Tutkitaan seuraavaksi, miten tulkitaan potenssi, missä eksponentti on tai negatiivinen kokonaisluku.

Samankantaisten potenssien osamäärän laskusäännön nojalla:

$\dfrac{a^n}{a^n}=a^{n-n}=a^0$

Toisaalta supistamalla saadaan:

$\dfrac{a^n}{a^n}=\dfrac{\overbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}^{n\;\text{ kpl}}}{\underbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}_{n\;\text{ kpl}}} =1$

On siis määriteltävä, että a^0=1, kun $a\neq0.$

Merkitään .

Samankantaisten potenssien osamäärän laskusäännön nojalla:

$\dfrac{a^m}{a^n}=a^{m-n}=a^{-(n-m)}=a^{-p}$

Toisaalta supistamalla saadaan ( $p=n-m \Leftrightarrow n=p+m$ ):

$\dfrac{a^m}{a^n}=\dfrac{\overbrace{a\cdot a\cdot ... \cdot a}^{m\;\text{kpl}}}{\underbrace{a\cdot a\cdot ... \cdot a}_{n\;\text{kpl}}} =\dfrac{\overbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}^{m\;\text{kpl}}}{\underbrace{a\cdot a\cdot ... \cdot a}_{p\;\text{kpl}}\cdot \underbrace{\cancel{a}\cdot \cancel{a}\cdot ... \cdot \cancel{a}}_{m \;\text{kpl}}} =\dfrac{1}{\underbrace{a\cdot a\cdot ... \cdot a}_{p\;\text{kpl}}}=\dfrac{1}{a^{p}}$

On siis määriteltävä, että $a^{-p}=\dfrac{1}{a^p}.$

Eksponenttina nolla ja negatiivinen kokonaisluku

Olkoon $a\neq0$ ja positiivinen kokonaisluku.

${a^0}=1$

${a^{-n}}=\frac{1}{a^{n}}$

Erityisesti $a^{-1}=\dfrac{1}{a}$ . Eli luvun käänteislukua voidaan merkitä muodossa $a^{-1}$ .

Jos kantalukuna on murtomerkintä ja eksponentti negatiivinen, niin eksponentti voidaan vaihtaa positiiviseksi samalla, kun vaihdetaan kantaluku käänteisluvukseen.

$\left(\frac{k}{l}\right)^{-n}=\left(\frac{l}{k}\right)^{n}$

4.2.3 Esimerkki: negatiivinen eksponentti

Laske.

$4^{-3}$
$\dfrac{3^2}{3^4}$
$\left(\dfrac{2}{3}\right)^{-2}$
$(1,43\cdot10^{999})^0$

Ratkaisu:

Negatiivinen eksponentti hyppää kantaluvun käänteisluvun nimittäjään.

$4^{-3}=\dfrac{1}{4^3}=\dfrac{1}{64}$

Samankantaisten potenssien eksponentit vähennetään toisistaan ja saadaan negatiivinen eksponentti.

$\dfrac{3^2}{3^4}=3^{2-4}=3^{-2}=\dfrac{1}{3^2}=\dfrac{1}{9}$

Vaihdetaan eksponentti positiiviseksi ja kantaluku käänteisluvukseen.

$\left(\dfrac{2}{3}\right)^{-2}=\left(\dfrac{3}{2}\right)^{2}=\dfrac{3^2}{2^2}=\dfrac{9}{4}$

Jokaisen luvun nollas potenssi on luku . (Paitsi ei ole määritelty.)

$(1,43\cdot10^{999})^0=1$

Potenssin laskusääntöjä: tehtäviä

4.3 Kymmenpotenssimuoto

Suuria lukuja on tapana ilmaista kymmenpotenssimuodossa eli luvun potenssien avulla. Esimerkiksi, kun syötetään laskimeen luku $5^{16}$ , niin laskin antaa sen mitä todennäköisimmin muodossa $1,5\cdot10^{11},$ koska luku $5^{16}=152\;587\;890\;625\approx1 \underbrace{50\;000\;000\;000}_{11\text{kpl}}$ on liian suuri laskimen näytölle.

Kymmenpotenssimuoto (suuret luvut)

Suuri luku voidaan merkitä kymmenpotenssimuodossa $a\cdot10^n,$ missä $1 \leq a<10$ ja on positiivinen kokonaisluku.

4.3.1 Esimerkki: suuren luvun muuttaminen kymmenpotenssimuotoon

Ilmaise kolmen numeron tarkkuudella kymmenpotenssimuodossa

Suomen väkiluku $5\;518\;000$
maapallon ympärysmitta $40\;000\;\text{km}$
valon nopeus tyhjiössä $299\;792\;458\;\text{m/s}$

Ratkaisu:

$\begin{align*} &5 \underbrace{518\;000}_{6\text{kpl}} && \text{Siirretään pilkkua 6 numeroa vasemmalle} \\ &= 5,518\;000 \cdot 10^6\ && \text{Pyöristetään kolmen numeron tarkkuuteen}\\ &\approx 5,52 \cdot 10^6 && \\ \end{align*}$

$\begin{align*} &4 \underbrace{0\;000}_{4\text{kpl}} && \text{Siirretään pilkkua 4 numeroa vasemmalle} \\ &= 4,0000 \cdot 10^6\ && \text{Pyöristetään kolmen numeron tarkkuuteen}\\ &\approx 4,00 \cdot 10^4\;\text{(km)}&& \\ \end{align*}$

$\begin{align*} &2 \underbrace{99\;792\;458}_{8\text{kpl}} && \text{Siirretään pilkkua 8 numeroa vasemmalle} \\ &= 2,99792458 \cdot 10^8\ && \text{Pyöristetään kolmen numeron tarkkuuteen}\\ &\approx 3,00 \cdot 10^8\;\text{(m/s)} && \\ \end{align*}$

Erityisesti luonnontieteissä myös pieniä lukuja on tapana ilmaista kymmenpotenssimuodossa negatiivisen eksponentin avulla. Esimerkiksi:

$0,0003=3\cdot0,0001=3\cdot \dfrac{1}{10000}=3\cdot \dfrac{1}{10^4}=3\cdot10^{-4}$

Kymmenpotenssimuoto (pienet luvut)

Pieni luku voidaan merkitä kymmenpotenssimuodossa $a\cdot10^{-n},$

missä $1 \leq a<10$ ja on positiivinen kokonaisluku.

4.3.2 Esimerkki: pienen luvun muuttaminen standardimuotoon

Kirjoita standardimuodossa

protonin massa $1,672 621 64 \cdot 10^{-27}\;\text{kg}$
elektronin massa $9,109 382 15 \cdot 10^{-31}\;\text{kg}$

Ratkaisu:

Luvussa $10^{-27}=\dfrac{1}{10^{27}}$ on desimaalipilkun jälkeen nollaa ennen ykköstä.

$\begin{align*} &1,672\;621\;64\cdot 10^{-27}\;\text{kg}\\ =&\;1,672\;621\;64 \cdot 0,\underbrace{000\;000\;000\;000\;000\;000\;000\;000\;00}_{26\;\text{kpl}}1\;\text{kg} \\ =&\;0,\underbrace{000\;000\;000\;000\;000\;000\;000\;000\;00}_{26\;\text{kpl}}1\;672\;621\;64\;\text{kg} \end{align*}$

Luvussa $10^{-31}=\dfrac{1}{10^{31}}$ on desimaalipilkun jälkeen nollaa ennen ykköstä.

$\begin{align*} &9, 109\;382\;15 \cdot 10^{-31}\;\text{kg} \\ =&\;9, 109\;382\;15 \cdot 0,\underbrace{000\;000\;000\;000\;000\;000\;000\;000\;000\;000}_{30\;\text{kpl}}\;1\;\text{kg} \\ =& \;0,\underbrace{000 \;000\; 000\; 000\; 000\; 000\; 000\; 000\; 000\; 000}_{30\;\text{kpl}}\;910\;9 38\;2 15\;\text{kg} \end{align*}$

Kymmenpotenssimuoto: tehtäviä

4.4 Neliö- ja kuutiojuuri

Olkoon neliön pinta-ala A=9 . Mikä on neliön sivun pituus?

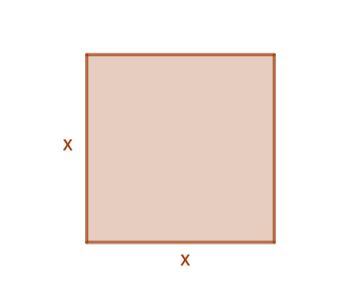
Neliön pinta-ala saadaan sivun neliönä, eli nyt tulee pohtia sitä, että mikä luku toteuttaa yhtälön x^2=9 .

Tiedämme, että 3^2=9 ja toisaalta (-3)^2=9 . Siispä x=3 tai x=-3 . Kuitenkin, sivun pituus ei voi olla negatiivinen luku, joten vain x=3 kelpaa nyt yhtälön ratkaisuksi. Neliön sivun pituus on siis x=3 .

Voidaan osoittaa, että yhtälöllä x^2=a on kaksi ratkaisua aina kun a>0. Positiivista ratkaisua sanotaan luvun neliöjuureksi ja merkitään $\sqrt{a}.$ Lukua sanotaan neliöjuuren juurrettavaksi.

Neliöjuuri

Luvun $a\geq 0$ neliöjuuri $\sqrt{a}$ toteuttaa ehdot

$\sqrt{a}\geq 0$
$(\sqrt{a})^2=a$

Miksi $a\geq0$ ?

Tiedämme, ettei minkään $^{*)}$ reaaliluvun parillinen potenssi voi olla negatiivinen luku. Neliöjuuren määrittelyehtona on siis, että juurrettavan tulee olla positiivinen tai nolla.

Miksi $\sqrt{a}\geq 0$ ?

Voisimme siis määritellä, että esimerkiksi $\sqrt{9}=3$ tai $\sqrt{9}=-3$ , sillä 3^2=(-3)^2=9 . Kuitenkin, neliöjuuren määritelmässä on tehty valinta, että neliöjuuri on vain ja ainoastaan ei-negatiivinen ratkaisu. Tämä valinta on tehty siksi, että neliöjuuri olisi yksikäsitteinen, eli voidaan sanoa yksikäsitteisesti esimerkiksi, että $\sqrt{9}=3$ .

$^{*)}$ Kompleksilukujen joukossa on määritelty $\textit{imaginääriyksikkö}$ i^2=-1 . Tällöin kompleksilukualueella yhtälön x^2=-4 ratkaisu olisi x=2i tai x=-2i . Kompleksiluvut eivät kuitenkaan kuulu lukion opetussuunnitelman perusteisiin, joten oletamme jatkossa lukujen olevan reaalilukuja.

4.4.1 Esimerkki: potenssiyhtälön ratkaisut

Ratkaise yhtälö.

Ratkaisu:

tai , sillä tai Ratkaisut voidaan esitää myös muodossa $x=\pm 4.$
Ei ratkaisua, sillä juurrettava on .
, sillä .

HUOM! Potenssiyhtälöä käsitellään lisää kappaleessa 5.5

4.4.2 Esimerkki: neliön sivun pituus

Neliön pinta-ala on $15\;\text{m}^2$ . Laske neliön sivun pituus.

Ratkaisu:

Mekitään muuttujalla neliön sivun pituutta metreinä. Tällöin voidaan suoraan neliöjuuren avulla laskea

$x=\sqrt{15}=3,872983\approx3,9\;\text{(m)}$

Vastaus: Neliön sivun pituus on noin $3,9\;\text{m}$ .

Neliöjuurilla laskettaessa käytetään seuraavia laskulakeja.

Neliöjuuren ominaisuuksia

$\sqrt{a}\sqrt{b}=\sqrt{ab}\;\;\;\;\;\;\;\;\text{tulon neliöjuuri}$

$\dfrac{\sqrt{a}}{{\sqrt{b}}}=\sqrt{\dfrac{a}{b}}\;\;\;\;\;\;\;\;\;\;\;\text{osamäärän neliöjuuri}$

$\sqrt{a^2}=|a|\;\;\;\;\;\;\;\;\;\;\;\;\;\text{neliön neliöjuuri}$

4.4.3 Todistus (1. kohta)

Olkoot $a\geq0$ ja $b\geq0$ . Tällöin tulon potenssin laskusäännön nojalla

$(\sqrt{a}\sqrt{b})^2=(\sqrt{a})^2(\sqrt{b})^2=ab.$

$\sqrt{a}$ ja $\sqrt{b}$ ovat ei-negatiivisiä, joten $\sqrt{a}\sqrt{b}$ on neliöjuuren määritelmän mukainen luku, joka korotettuna toiseen on $ab=(\sqrt{ab})^2.$ $_\square$

4.4.4 Todistus (2. kohta)

Olkoot $a\geq0$ ja b>0 . Tällöin osamäärän potenssin laskusäännön nojalla

$\Big(\dfrac{\sqrt{a}}{{\sqrt{b}}}\Big)^2=\dfrac{(\sqrt{a})^2}{(\sqrt{b})^2}=\dfrac{a}{b}.$

$\sqrt{a}$ ja $\sqrt{b}$ ovat ei-negatiivisiä, joten $\dfrac{\sqrt{a}}{\sqrt{b}}$ on neliöjuuren määritelmän mukainen luku, joka korotettuna toiseen on $\dfrac{a}{b}=\Big(\sqrt{\dfrac{a}{b}}\Big)^2.$ $_\square$

4.4.5 Todistus (3. kohta)

Koska $|a|\ge0,$ neliöjuuren määritelmän ensimmäinen ehto on voimassa.

Koska |a|^2=a^2 , myös toinen ehto toteutuu. $_\square$

4.4.6 Esimerkki: neliöjuuren laskusääntöjä

Sievennä.

$\sqrt{8}\sqrt{2}$
$\sqrt{\dfrac{4}{9}}$
$\sqrt{4\cdot2}$
$\sqrt{1000}$

Ratkaisu:

Neliöjuurten tulossa juurrettavat kerrotaan keskenään.

$\sqrt{8}\sqrt{2}=\sqrt{8\cdot2}=\sqrt{16}=4$

Osamäärän neliöjuuressa osoittajasta ja nimittäjästä otetaan molemmista erikseen neliöjuuri.

$\sqrt{\dfrac{4}{9}}=\dfrac{\sqrt{4}}{\sqrt{9}}=\dfrac{2}{3}$

Jos juuri on irrationaalinen (jaksoton ja päättymätön luku), niin neliöjuuri sievennetään muotoon, missä yksittäisenä juurrettavana on mahdollisimman pieni kokonaisluku.

$\sqrt{4\cdot2}=\sqrt{4}\sqrt{2}=2\sqrt{2}$

$\sqrt{1000}=\sqrt{100\cdot10}=\sqrt{100}\sqrt{10}=10\sqrt{10}$

4.4.7 Esimerkki: neliöjuurten sieventämistä

Sievennä.

$\sqrt{9}+\sqrt{16}$
$\sqrt{9+16}$
$\sqrt{\sqrt{25}+\sqrt{81}-5}$
$\sqrt{(x^2+1)^2}$

Ratkaisu:

Lasketaan ensin neliöjuuret.

$\sqrt{9}+\sqrt{16}=3+4=7$

Lasketaan ensin yhtenlasku.

$\sqrt{9+16}=\sqrt{25}=5$

Lasketaan ensin sisimmät neliöjuuret.

$\begin{align*} &\sqrt{\sqrt{25}+\sqrt{81}-5}\\ &=\sqrt{5+9-5}\\ &=\sqrt{9}=3 \end{align*}$

Käytetään neliöjuuren kolmatta ominaisuutta.

$\begin{align*} &\sqrt{(x^2+1)^2} \\ &=|x^2+1| \\ \text{(itseisarvot voidaan }&\text{poistaa, sillä aina}\;x^2+1>0) \\ &=x^2+1 \end{align*}$

Olkoon kuution tilavuus V=64 . Mikä on kuution särmän pituus?

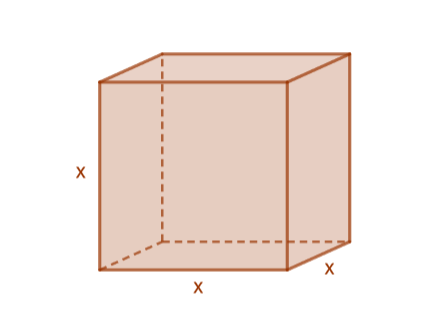
Kuution tilavuus saadaan särmän kuutiona, eli nyt tulee pohtia sitä, että mikä luku toteuttaa yhtälön x^3=64 .

Tiedämme, että 4^3=64 . Siispä särmän pituus x=4 .

Voidaan osoittaa, että yhtälön x^3=a ratkaisu on $\sqrt[3]{a}$ . Tätä sanotaan luvun kuutiojuureksi.

Kuutiojuuri

Luvun kuutiojuuri $\sqrt[3]{a}$ toteuttaa ehdon

$(\sqrt[3]{a})^3=a$

Kuutiojuuren määritelmässä kelpaavat kaikki reaaliluvut eli voi olla myös negatiivinen luku. Tämä siksi, että kuutiojuuri on myös näin määriteltynä yksikäsitteinen, koska parittoman negatiivisen luvun kuutio on negatiivinen ja vastaavasti parittoman positiivisen luvun kuutio on positiivinen. Edellä johdetut neliöjuuren laskusäännöt pätevät myös kuutiojuurella ja lisäksi silloin, kun a<0 tai b<0 .

4.4.8 Esimerkki: kuutiojuurten laskemista

Laske

$\sqrt[3]{27}$
$\sqrt[3]{-8}$
$-\sqrt[3]{-216}$

Ratkaisu:

$\sqrt[3]{27}=3,$ sillä $3^3=3\cdot3\cdot3=27.$

$\sqrt[3]{-8}=-2,$ sillä $(-2)^2=(-2)\cdot(-2)\cdot(-2)=-8.$

$\sqrt[3]{-216}=-6,$ sillä $(-6)^3=(-6)\cdot(-6)\cdot(-6)=-216.$

Joten $-\sqrt[3]{-216}=-(-6)=6.$

Neliö- ja kuutiojuuri: tehtäviä

4.5 Potenssiyhtälö

Olemme käyneet läpi jo esimerkkejä muotoa x^2=a ja x^3=a olevien yhtälöiden ratkaisuista. Yleisesti muotoa x^n=a olevaa yhtälöä sanotaan potenssiyhtälöksi. Katsotaan vielä yleisesti, miten potenssiyhtälö ratkaistaan, kun n=2 tai n=3.

Neliöyhtälön ratkaiseminen (n=2)

Neliöyhtälön x^2=a juurten lukumäärä riippuu luvusta .

Jos , niin yhtälön ratkaisut ovat

$x=\sqrt{a} \text{ tai } x=-\sqrt{a}.$

Jos , niin yhtälön ratkaisu on

x=0.

Jos , niin yhtälöllä ei ole ratkaisua.

Jos $a \geq 0$ , niin neliöyhtälö voidaan ratkaista ottamalla puolittain neliöjuuri huomioiden ratkaisujen etumerkit.

4.5.1 Esimerkki: neliöyhtälön ratkaiseminen

Ratkaise yhtälö 2x^2+3=17

Ratkaisu:

Vastaavasti kuin ensimmäisen asteen yhtälöissä, muokataan yhtälö muotoon, jossa toisella puolella on muuttuja ja toisella vakio. Tämän jälkeen voidaan ottaa puolittain neliöjuuri, kun huomioidaan myös negatiivinen ratkaisu.

$\begin{align*} 2x^2+3 & = 17 && | -3 \\ 2x^2 & = 14 && | : 2 \\ x^2 & = 7 && | \sqrt{} \\ x &= \pm \sqrt{7} \end{align*}$

Vastaus: $x=\sqrt{7}$ tai $x=-\sqrt{7}$

4.5.2 Esimerkki: Coca-Cola -tölkin mitat

Amerikan standardimittaisen Coca-Cola -tölkin pohjaympyrän pinta-ala on noin cm. Laske tölkin pohjaympyrän säteen pituus.

Ratkaisu:

Ympyrän pinta-ala saadaan kaavalla $A=\pi r^2$ , missä $r=\text{ympyrän säteen pituus}$ . Muodostetaan tehtävänannon tiedoista yhtälö.

$\begin{align*} \pi r^2 & = 92 && | : \pi \\ r^2 & = \dfrac{92}{ \pi } && | \sqrt{} \\ r &= \pm \sqrt{\dfrac{92}{\pi}} \end{align*}$

Pituus ei voi olla negatiivinen, joten huomioimme vain positiivisen ratkaisun.

$r=\sqrt{\dfrac{92}{\pi}}=5,411516380\approx5,4\;\text{(cm)}.$

Vastaus: Pohjaympyrän säde on noin $5,4\;\text{cm}.$

Kuutioyhtälön ratkaiseminen (n=3)

Kuutioyhtälön x^3=a

ratkaisu on $x=(\sqrt[3]{a})$ .

Neliöjuuresta poiketen, kuutioyhtälön ratkaisu on yksikäsitteinen, sillä positiivisen luvun kuutio on positiivinen luku ja negatiivisen luvun kuutio on negatiivinen luku.

4.5.3 Esimerkki: kuutioyhtälön ratkaiseminen

Ratkaise yhtälö 3x^3+7=-4 .

Ratkaisu:

Vastaavasti kuin neliöyhtälössä, muokataan yhtälö muotoon, missä toisella puolella on muuttuja ja toisella vakio. Tämän jälkeen voidaan ottaa puolittain kuutiojuuri, mutta nyt ratkaisuja on vain yksi.

$\begin{align*} 3x^3+7 & = -4 && | -7 \\ 3x^3 & = -11 && | : 3 \\ x^3 & = -\dfrac{11}{3} && | \sqrt[3]{} \\ x &= \sqrt[3]{-\dfrac{11}{3}}=- \sqrt[3]{\dfrac{11}{3}} \end{align*}$

Vastaus: $x=- \sqrt[3]{\dfrac{11}{3}}$

4.5.4 Esimerkki: jalkapallon mitat

Vuoden 2018 jalkapallon mm-kisojen kisapallo oli Adidas Telstar. Telstarin tilavuus on noin 5,6 litraa. Mikä on Telstarin halkaisijan pituus senttimetreinä?

Ratkaisu:

Pallon tilavuus saadaan kaavalla $V=\dfrac{4\pi r^3}{3}$ , missä $r=\text{pallon säteen pituus}$ . Muodostetaan tehtävänannon tiedoista yhtälö ja ratkaistaan pallon säde.

$\begin{align*} \dfrac{4\pi r^3}{3} & = 5,6 && | \cdot 3 \\ 4\pi r^3 & = 3\cdot 5,6 && | : 4\pi \\ r^3 & = \dfrac{3\cdot 5,6}{4\pi} && | \sqrt[3]{} \\ r &= \sqrt[3]{\dfrac{3\cdot 5,6}{4\pi}} \text{ (dm)} \end{align*}$

Pallon halkaisija on kaksi kertaa säteen suuruinen, joten

$h=2\cdot\sqrt[3]{\dfrac{3\cdot 5,6}{4\pi}} \text{ dm } = 2,203246733 \text{ dm }\approx 22\;\text{cm}$ .

Vastaus: Pallon halkaisija on noin $22\;\text{cm}$ .

Potenssiyhtälö: tehtäviä