2. Yhtälö: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Yhtälö. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

2.1 Peruskäsitteitä: tehtäviä

Tämän kappaleen teoria.

2.1.1 Tehtävä

# Plugin1

2.1.2 Tehtävä

# Plugin2

2.1.3 Tehtävä

Osoita, että x=1 on yhtälön 2(2x+1)=3(-4x+4)+6 ratkaisu. Tee osoitus valitsemallasi ohjelmistolla ja palauta alle.

# Plugin5

2.2 Ensimmäisen asteen yhtälö: tehtäviä

Tämän kappaleen teoria.

2.2.1 Tehtävä

# p321

Vihje

Voiko yhtälön esittää muodossa ax+b=0 , jossa $a\neq0$ ?

Ratkaise tehtävät 3.2.2-3.2.3 ja 3.2.6-3.2.9 ilman laskinta. Kirjoita ratkaisun välivaiheet näkyviin syöttökenttään.

2.2.2 Tehtävä

Ratkaise yhtälöt.

# p325

# p325b

# p325c

2.2.3 Tehtävä

Ratkaise yhtälöt.

# p325d

# p325e

# p325f

2.2.4 Tehtävä (s2017/2a)

Hannele on ratkaissut yhtälön 2(x^2+x+3)=8(x+1)+2x^2 , mutta välivaiheet ovat menneet sekaisin. Järjestä välivaiheet niin, että ne muodostavat yhtälön loogisesti etenevän ratkaisun.

$x=-\frac{1}{3}$

# plugin6

2.2.5 Tehtävä

# Plugin4

2.2.6 Tehtävä

# p328

Vihje

Sijoitetaan x=6 yhtälöön ja ratkaistaan muuttuja .

$\begin{align*} 3a \cdot 6^2-6\cdot6+18 & = 0 \\ 108a-18 & = 0 \\ \dots \end{align*}$

2.2.7 Tehtävä

Ratkaise yhtälöt.

# p329a

# p329b

2.2.8 Tehtävä

Ratkaise yhtälöt.

Vihje

Lavennetaan termien nimittäjät samannimisiksi tai kerrotaan yhtälö puolittain luvulla . Saadaan yhtälö muotoon

8x+4x-2x+x=55

Lavennetaan termien nimittäjät samannimisiksi tai kerrotaan yhtälö puolittain luvulla . Saadaan yhtälö muotoon

4x-9x=30

Lavennetaan termien nimittäjät samannimisiksi tai kerrotaan yhtälö puolittain luvulla . Saadaan yhtälö muotoon

3x-9(x-3)-14=0

# p3210a

# p3210b

# p3210c

2.2.9 Tehtävä

Millä vakion arvolla

# p3211a

Vihje

Kaikki luvut toteuttavat yhtälön, jos se sievenee muotoon '0=0' . Sievennetään yhtälöä

$\begin{align*} 3(a-3x) &=-5x-9x+7\\ 3a-9x &=-5a-9x+7\\ 3a+5a&=7\\ &\dots \end{align*}$

# p3211b

Vihje

Yhtälöllä ei ole ratkaisua, jos muuttujan sisältävä termi sievenee pois. Siis tulee olla $2ax=6x\dots$

2.2.10 Tehtävä

# yritystaaaa

Ratkaisu

Rivillä ( x(x-1)=0 ) jaetaan termillä x-1 . Koska x=1 , viidennellä rivillä siis jaetaan nollalla. Tässä tehdään virhe.

2.3 Yhtälö sovelluksissa: tehtäviä

Tämän kappaleen teoria.

2.3.1 Tehtävä

Ratkaise fysiikan kaavat kiihtyvyyttä kuvaavan muuttujan suhteen.

voima:

# p331a

matka: $s=\displaystyle\frac{1}{2}at^2$

# p331b

matka: $s=vt+\displaystyle\frac{1}{2}at^2$

# p331c

Vihje

$\begin{align*} s&=\frac{1}{2}at^2 \;\;\;\;\;|\cdot2\\ 2s&=at^2s\\ &\dots \end{align*}$

$\begin{align*} s&=v_0t+\frac{1}{2}at^2 \;\;\;\;\; |-v_0t\\ s-v_0t&=\frac{1}{2}at^2 \\ &\dots \end{align*}$

2.3.2 Tehtävä

Grillibileisiin kaikille vieraille varataan maissi, kanapihviä ja makkaraa. Yhteensä ruokatarvikkeita on 180 .

# p332

2.3.3 Tehtävä

Perheenjäsenten ikien summa on 148 vuotta. Isosisko on vuotta vanhempi kuin pikkuveljensä. Perheen äiti on iältään kaksi kertaa niin paljon kuin isosisko. Perheen isä on vuotta vanhempi kuin äiti. Kuinka vanha kukin on?

# p333a

# 333c

# p333c

# 333d

Vihje

Olkoon $x=\text{'isosiskon ikä (vuotta)'}$ . Tällöin saadaan lausekkeet kunkin iälle:

Veljen ikä: x-6
Äidin ikä:
Isän ikä: 2x+4

Näiden summan tulaa olla 148 , joten saadaan yhtälö:

x + x-6 + 2x + 2x+4 = 148

2.3.4 Tehtävä

League of Legends videopelissä erittäin keskeinen osa pelin voittamista on vastustajan mestarin vahingoittaminen, jota kuvaa yhtälö

V=kt,

missä on mestariin tehty vahingon määrä, vahinkokerroin ja on taitokerroin.

Pelissä on myös mahdollista suojautua vahingolta ostamalla suojuksia, joita kuvaa yhtälö

100k+kS=100,

missä on vahinkokerroin ja on vastustajan mestarin suojauksen arvo.

# vahinkokerroin1

Vihje

Ratkaise ensin vahinkokerroin yhtälöstä V=kt . Tämän jälkeen ratkaise suojauksen arvo yhtälöstä 100k+kS=100 .

2.3.5 Tehtävä

Elmeri tankkaa aina viikonloppuisin mopoautonsa tankkiin sen verran polttoainetta mitä viikkorahoilla sen hetkisellä hintatasolla saa. Tällä viikolla polttoaineen litrahinta oli laskenut senttiä, minkä vuoksi Elmeri sai tankattua viime viikon litran sijaan litraa. Elmeri sai saman verran viikkorahaa kuin viime viikollakin.

# seq334

Vihje

Olkoon $x=\text{'Polttoineen tämän viikon litrahinta (€/l)'}$ . Tällöin voidaan muodostaa lausekkeet Elmerin viikkorahoista:

Tällä viikolla: 15x
Viime viikolla: 13(x+0,22)

Muodostetaan yhtälö, kun tiedetään, että Elmerin viikkorahan suuruus säilyy:

15x = 13(x+0,22)

2.3.6 Tehtävä

Klassisessa voimanostossa on tapana verrata eri painoluokkien tuloksia niin sanotun Wilks-tuloksen avulla. Wilks tulos voidaan laskea kaavalla

W=ky,

missä on Wilks-kerroin ja on nostajan yhteistulos (penkkipunnerrus+kyykky+maastaveto) kilogrammoina. Kerroin saadaan kaavasta

$k=\dfrac{500}{a+bx+cx^2+dx^3+ex^4+fx^5}.$

Parametrit (miesten) a-f saadaan seuraavasta taulukosta:

parametri	arvo
a
b
c
d
e	$7,01863\cdot 10^{-6}$
f	$-1,291\cdot 10^{-8}$

Voimanostajan Wilks-tulos opiskelijoiden voimanoston avoimessa sarjassa oli W=414 ja massa $x=100\;\text{(kg)}$ .

# voimanostajatoka

Vihje

Ratkaise ensin sijoittamalla yhtälöön $k=\dfrac{500}{a+bx+cx^2+dx^3+ex^4+fx^5}$ taulukon arvot a-f sekä voimanostajan massa .

Tämän jälkeen ratkaistaan yhtälöstä W=ky ja voidaan sijoittaa ja ratkaistuun yhtälöön y=...

2.3.7 Tehtävä

Lil Pumpin kappaleessa Gucci gang toistetaan sanoja gucci gang ja ooh monia kertoja. Yhteensä kappaleen aikana toistetuissa gucci, gang ja ooh sanoissa on 513 kirjainta. Sanaparia gucci gang sanotaan -kertainen määrä verrattuna sanaan ooh. Kuinka monta kertaa kappaleessa sanotaan nämä sanat?

# seq335a

# seq335b

Vihje

Merkitään muuttujalla kappaleesta löytyvien ooh-sanojen määrää. Tällöin gucci gang-sanaparia toistuu kappaleessa kertaa. Tiedetään, että sanoissa gucci gang on kirjainta, sanassa ooh kirjainta ja kaikissa sanoissa on yhteensä 513 kirjainta, joten voidaan muodostaa yhtälö.

$3x+9\cdot6x=513$

2.4 Yhtälöpari: tehtäviä

Tämän kappaleen teoria.

Ratkaise tehtävät 3.4.1-3.4.4 ilman laskinta. Jos yhtälöparilla ei ole ratkaisua, vastaa syöttökenttiin ja tilalle $\text{FF}$ . Hahmottele halutessasi vastaukset Abitti-editorilla, joka löytyy tehtävien alta.

2.4.1 Tehtävä

Ratkaise yhtälöparit

\[\begin{cases} 4x-3y=9\\ x+3y=6 \end{cases}\]

# p341a1

# p341a2

\[\begin{cases} x-2y=-1\\ x+3y=2 \end{cases}\]

# p341b1

# p341b2

Abitti-editori

# pluginvaan

2.4.2 Tehtävä

\[\begin{cases} 7x-2y=25\\ 2x-y=8 \end{cases}\]

# p342a1

# p341b3

\[\begin{cases} 2a+3b=8\\ 6a+2b=-4 \end{cases}\]

# p342b1

# p342b2

Abitti-editori

# Plugin3

2.4.3 Tehtävä

Määritä kuvan perusteella yhtälöparin ratkaisu.

# 434a

# 434b

# 434b2

# 434c

# p343c

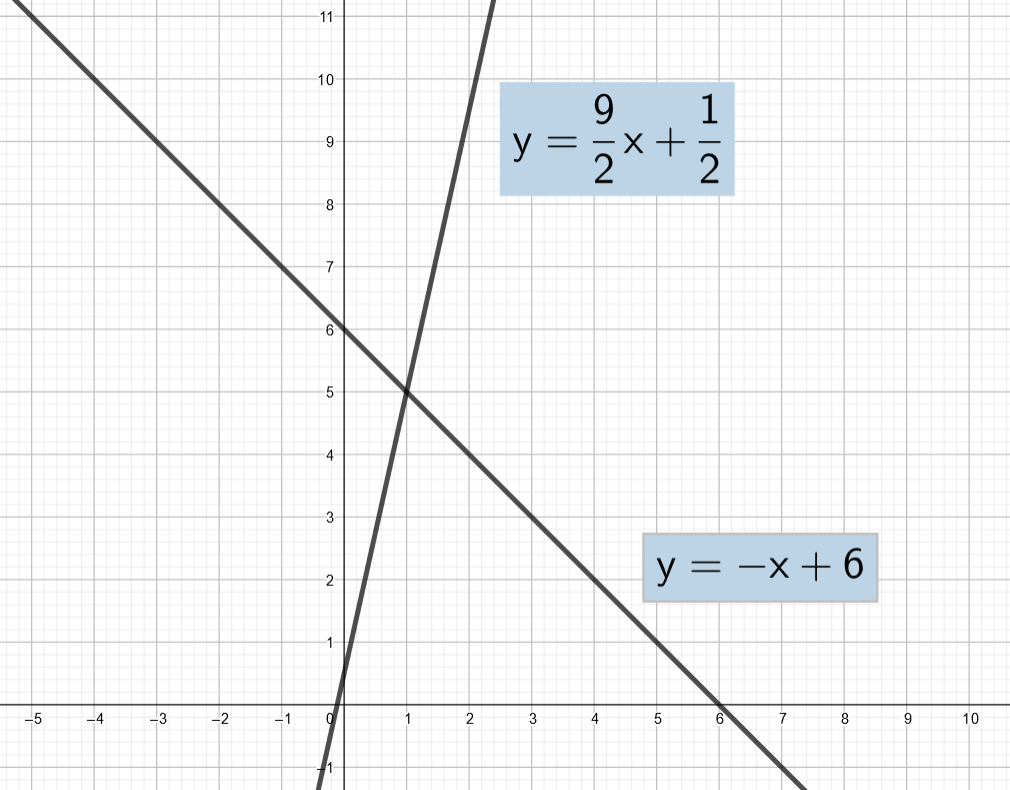
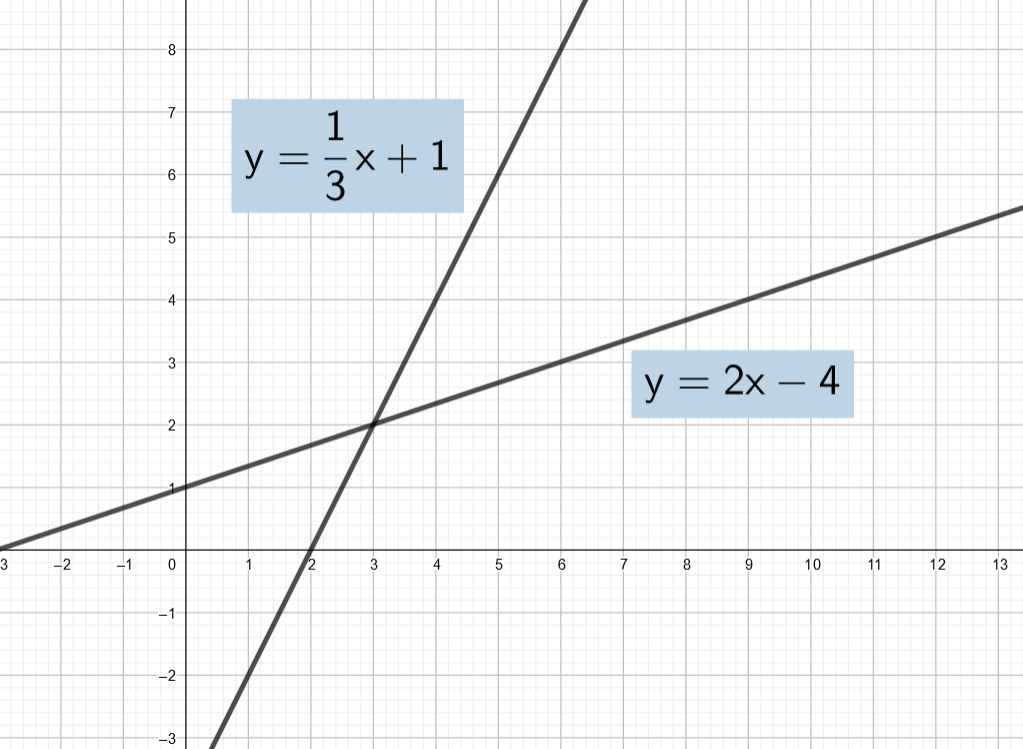
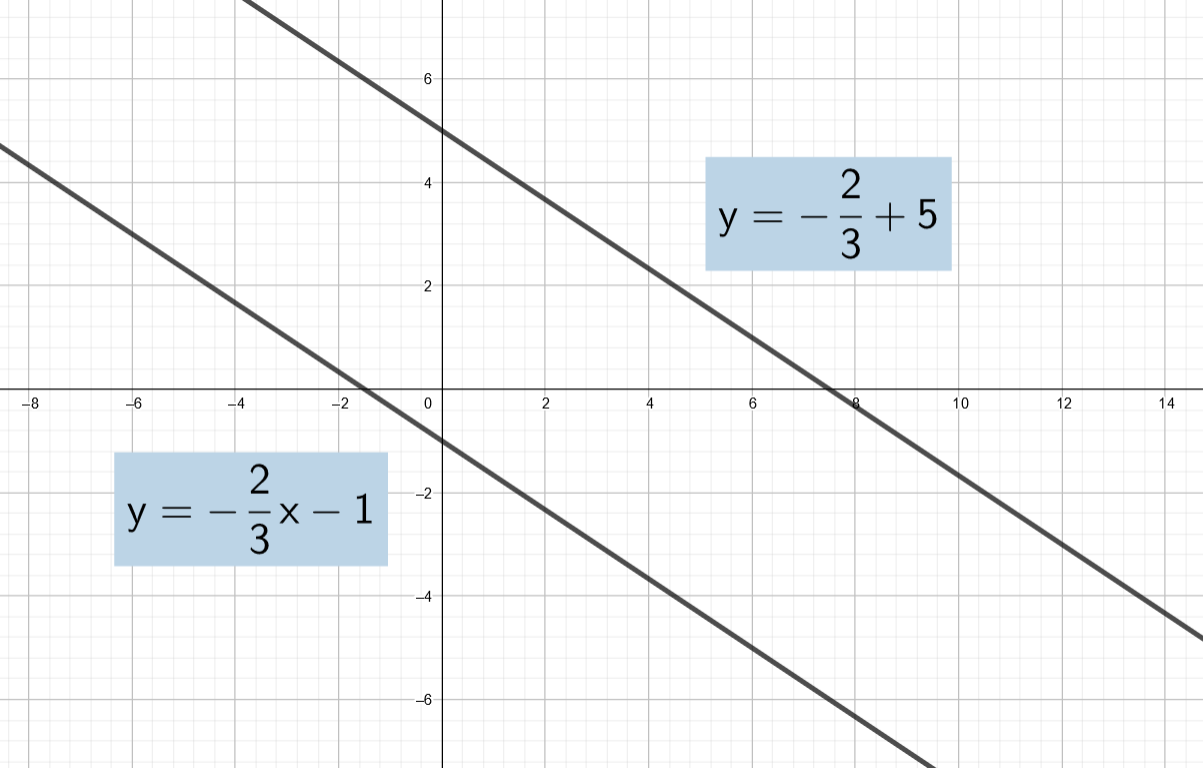
2.4.4 Tehtävä

Ratkaise yhtälöparit.

\[\begin{cases} 32x+8y-64=0 \\ 5y=-20x+40 \end{cases}\]

# seq244a

# seq244b

\[\begin{cases} 4x=3y+1 \\ \frac{1}{3}x=\frac{1}{4}y+1 \end{cases}\]

# seq244c

# seq244d

2.4.5 Tehtävä

Ratkaise yhtälöpari

\[\begin{cases} 2x+y=11 \\ 3y-4x=3 \end{cases}\]

graafisesti Geogebralla ja syötä vastaukset alapuolella oleviin vastauskenttiin.

Geogebra

Open plugin

# 435a

# 435b

2.4.6 Tehtävä

# PLUGINN

Vihje

Merkitään muuttujalla strutseja ja muuttujalla seeproja. Yhtälöpariksi saadaan

\[\begin{cases} x+y=17 \\ 2x+4y=60 \end{cases}\]

2.4.7 Tehtävä

Jalkapallopelin lipputulot olivat $19700\;\text{€}$ , kun aikuisten lippu maksoi $9\;\text{€}$ ja lasten lippu $5\;\text{€}$ . Kävijöitä oli yhteensä 2500 . Muodosta yhtälöpari ja laske, kuinka monta aikuista ja lasta tapahtumassa kävi?

# seq347a

# seq347b

Vihje

Merkitään muuttujalla aikusia ja muuttujalla lapsia. Tiedetään, että kävijöitä oli 2500 , joten tästä saadaan ensimmäinen yhtälö x+y=2500 . Lisäksi tiedetään, että lipputulot olivat $19700\;\text{€}$ , joten tästä saadaan toinen yhtälö 9x+5y=19700 . Ratkaistava yhtälöpari on siis

\[\begin{cases} x+y=2500\\ 9x+5y=19700 \end{cases}\]

2.4.8 Tehtävä

SM-liigan runkosarjassa kaudella 2018-2019 pelattiin ottelua. Voitetusta ottelusta joukkue saa kolme pistettä ja tasapelistä yhden pisteen. Tapparalla oli runkosarjan jälkeen pisteitä 105 . Tappara hävisi runkosarjan aikana ottelua.

# seq348

Vihje

Merkitään voitettuja pelejä muuttujalla ja tasapelejä muuttujalla .

Voitettuja pelejä ja tasapelejä oli yhteensä 60-19=41 , joten ensimmäinen yhtälö on x+y=41. Pisteitä joukkue sai 105 , joten toinen yhtälö on 3x+y=105.

2.4.9 *Tehtävä

Yhtälöryhmäksi kutsutaan ryhmää, jossa tarkasteltavia yhtälöitä on enemmän kuin kaksi. Vastaavasti kuin yhtälöparinkin tapauksessa, tulee yhtälöryhmän kohdalla varmistaa, että yksittäisen yhtälön toteuttava ratkaisu toteuttaa kaikki ryhmän yhtälöt. Ratkaise yhtälöryhmä

\[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1 \\ y+4=2x \end{cases}\]

algebrallisesti

Vihje

Ratkaise yhtälöpari

\[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1 \end{cases}\]

ja tutki toteuttaako ratkaisu yhtälöryhmän alimman yhtälön y+4=2x . Jos toteuttaa, niin kyseessä on yhtälöryhmän ratkaisu.

Ratkaisu

Yhtälöparin \[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1 \end{cases}\]

ratkaisuksi saadaan x=3 ja y=2 . Sijoitetaan piste (x,y)=(3,2) alimpaan yhtälöön, jolloin

$\begin{align*} y+4&=2x && |x=3, y=2 \\ 2+4&=2\cdot3 \\ 6&=6 \\ &\text{tosi} \end{align*}$

Näin ollen yhtälöryhmän \[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1\\ y+4=2x \end{cases}\]

ratkaisu on x=3 ja y=2 .

graafisesti

Ratkaisu

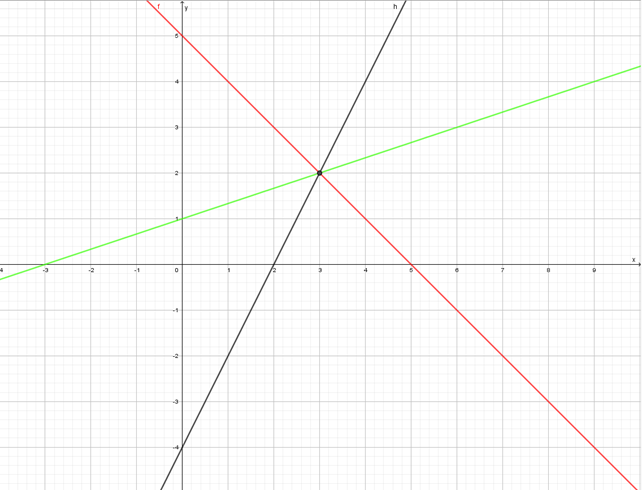
Punainen suora on y+x=5 , musta suora $\dfrac{1}{3}x+1$ ja vihreä suora y+4=2x . Suorat leikkaavat kuvan perusteella pisteessä (x,y)=(3,2) .

# yhtaloryhma1jokerix

# yhtaloryhma1jokeriy

2.4.10 *Tehtävä

Ratkaise kolmen muuttujan yhtälöryhmä

\[\begin{cases} -x+y+2z=-5 \\ 2x-y-z=3 \\ 3x+2y+z=4 \end{cases}\]

# yhtaloryhma2jokerix

# yhtaloryhma2jokeriy

# yhtaloryhma2jokeriz

Vihje

\[\begin{cases} \textcolor{red}{-x+y+2z=-5} && \textcolor{red}{1. \text{yhtälö}} \\ \textcolor{green}{2x-y-z=3} && \textcolor{green}{2. \text{yhtälö}} \\ \textcolor{blue}{3x+2y+z=4} && \textcolor{blue}{3. \text{yhtälö}} \end{cases}\]

Ratkaistaan 3.yhtälöstä , eli sievennetään vasemmalle ja muut termit yhtälön oikealle puolelle.
Tämän jälkeen sijoitetaan ratkaistu . ja yhtälöön, jolloin saamme kahden muuttujan yhtälöparin, josta voimme ratkaista :n ja :n.
Kyseisten :n ja :n arvojen tulee nyt toteuttaa myös . yhtälö, joten sijoittamalla nämä arvot . yhtälöön saamme lopulta myös :n ratkaistua.
Tuloksen voi vielä tarkistaa sijoittamalla ratkaistut , ja jokaiseen yhtälöryhmän yhtälöön ja toteamalla, että yhtälöistä tulee identtisesti todet!

Ratkaisu

Ratkaistaan ensin yhtälöryhmän yhtälö muuttujan suhteen.

$\begin{align*} 3x+2y+z=4 \\ z=-3x-2y+4 \end{align*}$

Tämän jälkeen voidaan sijoittaa ratkaistussa muodossa oleva kahteen yhtälöpariin, jonka muodostavat yhtälöt ja

\[\begin{cases} -x+y+2z=-5 && |z=-3x-2y+4\\ 2x-y-z=3 && |z=-3x-2y+4 \end{cases}\] \[\begin{cases} -x+y+2(-3x-2y+4)=-5 \\ 2x-y-(-3x-2y+4)=3 \end{cases}\] \[\begin{cases} -7x-3y=-13 \\ 5x+y=7 && |\cdot 3 \end{cases}\] \[\begin{cases} -7x-3y=-13 \\ 15x+3y=21 && |\text{lasketaan yhteen} \end{cases}\]

$\begin{align*} 8x=8\\ x=1 \end{align*}$

Sijoitetaan ratkaistu yhtälöparin ylempään yhtälöön.

$\begin{align*} -7x-3y=-13 && |x=1 \\ -7-3y=-13 \\ y=2 \end{align*}$

Sijoitetaan x=1 ja y=2 muuttujan suhteen ratkaistussa muodossa olevaan yhtälöön.

$\begin{align*} z=-3x-2y+4 && |x=1, y=2 \\ z=-3-4+4=-3 \end{align*}$

Näin ollen (x,y,z)=(1,2,-3) on yhtälöryhmän ratkaisu. Ratkaisun voi vielä tarkistaa sijoittamalla pisteen alkuperäiseen yhtälöryhmään.

\[\begin{cases} -x+y+2z=-5 &&|x=1,y=2,z=-3 \\ 2x-y-z=3 &&|x=1,y=2,z=-3 \\ 3x+2y+z=4 &&|x=1,y=2,z=-3 \end{cases}\] \[\begin{cases} -1+2-6=-5\\ 2-2+3=3 \\ 3+4-3=4 \end{cases}\] \[\begin{cases} -5=-5\\ 3=3 \\ 4=4 \\ \text{tosi} \end{cases}\]

Vastaus: x=1 , y=2 ja z=-3

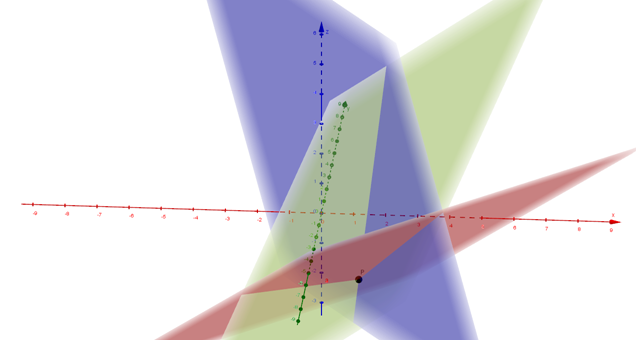
Geometrisesti tämä tarkoittaa yhtälöryhmän yhtälöiden leikkauspistettä. Kyseiset yhtälöt voidaan tulkita kolmiulotteisen avaruuden tasoina. Eli ratkaisu voidaan tulkita näiden tasojen leikkauspisteenä. Aiheeseen palataan lukion pitkän matematiikan vektorit -kurssilla, joten ei kannata todellakaan murehtia jos oheisen kuvan merkitys ei nyt aukea!