2. Yhtälö

Tässä kappaleessa käsitellään yhtälöitä. Keskitymme ensimmäisen asteen yhtälöiden sekä yhtälöparien ratkaisemiseen. Kappaleeseen liittyvät tehtävät omat omalla sivullaan.

Aluksi palautetaan mieleen yhtälön käsite alla olevan yhtälövaa'an avulla. Vie muuttujia kuvaavia laatikoita ja ilmapalloja vaa'alle ja pyri saamaan vaaka tasapainoon ohessa olevan yhtälön mukaan.

Kun vaa'an molempien puolien sisältö painaa yhtä paljon, vaaka on tasapainossa. Vaaka säilyttää tasapainonsa, jos sen molemmilta puolilta poistetaan tai molemmille puolille lisätään samanpainoiset kappaleet. Myös yhtälölle voidaan tehdä vastaavat toimenpiteet.

2.1 Peruskäsitteitä

Merkittyä laskutoimitusta tai pelkkää lukua kutsutaan lausekkeeksi. Lausekkeita ovat esimerkiksi

$x+3, a+b \; \text{ja} \; 8.$

Kun kaksi lauseketta merkitään yhtä suuriksi, muodostuu yhtälö. Yhtälöitä ovat esimerkiksi

$x+3=8 \; \text{ja} \; a+b=0.$

Yhtälöissä esiintyy yleensä yksi tai useampia muuttujia, joita merkitään kirjaimilla. Yllä olevissa yhtälöissä muuttujia ovat , ja . Niitä muuttujan arvoja, jotka toteuttavat yhtälön, sanotaan yhtälön ratkaisuiksi tai yhtälön juuriksi.

2.1.1 Esimerkki: onko kysytty luku yhtälön ratkaisu

Olkoon yhtälö 3x+2=-2x-8 . Onko luku

yhtälön ratkaisu?

Ratkaisu:

Tutkitaan, onko yhtälö tosi, kun sijoitetaan luku yhtälöön muuttujan paikalle.

Sijoitetaan , jolloin

$\begin{align*} 3\cdot 2 + 2 & = -2 \cdot 2 - 8 \\ 8 & = -12 \\ &\text{\bf{epätosi}} \end{align*}$

joten ei ole yhtälön 3x+2=-2x+-6 ratkaisu.

Sijoitetaan , jolloin

$\begin{align*} 3\cdot (-2) + 2 & = -2 \cdot (-2) - 8 \\ -4 & = -4 \\ \text{}&\text{\bf{tosi}} \end{align*}$

joten on yhtälön 3x+2=-2x+-6 ratkaisu.

Peruskäsitteitä: tehtäviä

2.2 Ensimmäisen asteen yhtälö

Ensimmäisen asteen yhtälö

Ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan saattaa muotoon

ax+b=0,

jossa $a\neq0$ .

Ensimmäisen asteen yhtälöllä on täsmälleen yksi ratkaisu.

2.2.1 Todistus: ensimmäisen asteen yhtälön ratkaisu

$\begin{align*} ax+b & = 0 && |-b \\ ax & = -b && |:a, a\neq0 \\ x & = -\frac{b}{a} \end{align*}$

Luku $-\displaystyle\frac{b}{a}$ on siis yhtälön ainoa ratkaisu. $\square$

2.2.2 Esimerkki: ensimmäisen asteen yhtälön ratkaiseminen

Ratkaise yhtälö 21x-3=0 .

Ratkaisu:

$\begin{align*} 21x-3 & = 0 && |+3 \\ 21x & = 3 && |:21 \\ x & = \frac{3}{21} \\ x & = \frac{1}{7} \end{align*}$

Vastaus: $x=\dfrac{1}{7}$

Jos ensimmäisen asteen yhtälö halutaan ratkaista graafisesti , piirretään suora y=ax+b ja katsotaan kuvaajasta kohta, jossa suora leikkaa akselin. Siinä kohdassa y=0.

2.2.3 Esimerkki: ensimmäisen asteen yhtälön ratkaiseminen graafisesti

Ratkaise graafisesti yhtälö -2x+2=5x-2.

Ratkaisu:

Sievennetään yhtälö ensin muotoon ax+b=0 yhdistämällä termit samalle puolelle.

$\begin{align*} -2x+2&=5x-2 \\ -2x+2-5x+2&=0 \\ -7x+4&=0 \end{align*}$

Piirretään nyt suora y=-7x+4 sopivalla ohjelmalla ja selvitetään suoran ja akselin leikkauskohta.

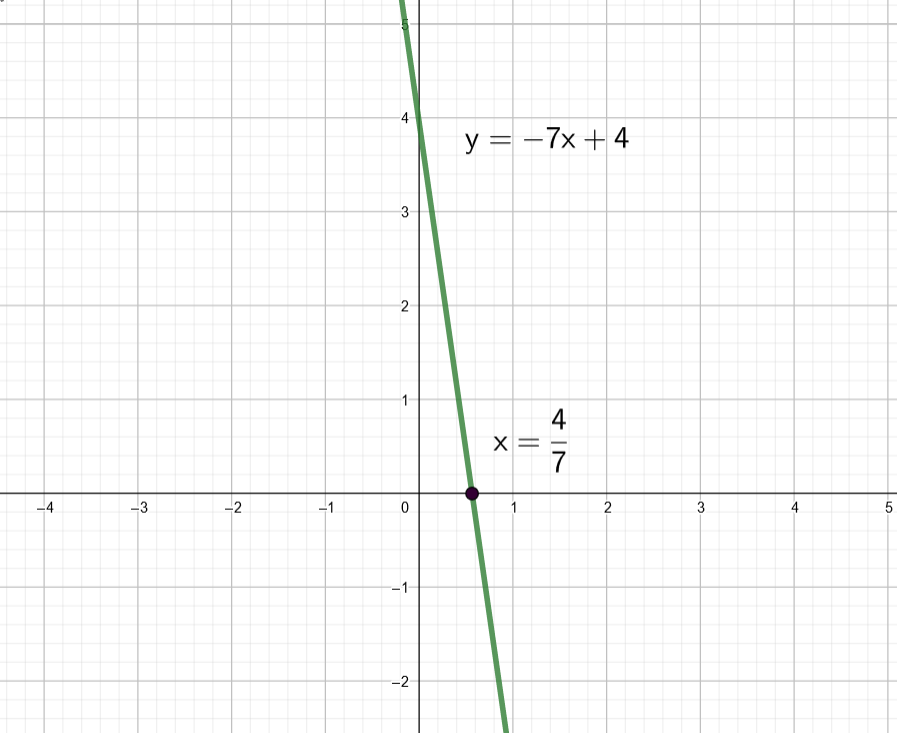
Suora leikkaa akselin, kun $x=\dfrac{4}{7}$ , joten tämä on yhtälön ratkaisu.

Vastaus: $x=\dfrac{4}{7}$

Yhtälön ratkaiseminen perustuu siihen, että yhtälölle tehtävät toimenpiteet pitävät yhtälön yhtäpitävänä eli yhtälön ratkaisut pysyvät samoina. Yllä olevissa esimerkeissä jo jaoimme ja vähensimme yhtälöä puolittain. Yleiset yhtälön ratkaisun toimenpiteet ovat esitelty kertauksen vuoksi alapuolella.

Yhtälön ratkaiseminen

1) Puolittain lisääminen tai vähentäminen

$\begin{align*} 1 & = 1 && |+3 \\ 4 & = 4 && | -2 \\ 2 & = 2 \end{align*}$

$\begin{align*} -4x+3 & = -4x+3 && |-3 \\ -4x & = -4x && | +4x \\ 0 & = 0 \end{align*}$

2) Puolittain kertominen ja jakaminen nollasta eroavalla luvulla

$\begin{align*} 4 & = 4 && | :2 \\ 2 & = 2 && | \cdot (-10) \\ -20 & = -20 \end{align*}$

$\begin{align*} 3x+9 & = 3x+9 && |:3 \\ x+3 & = x+3 && |\cdot (-1) \\ -x-3 & = -x-3 \end{align*}$

3) Yhtälön puolien vaihtaminen keskenään

$\begin{align*} 2x+1 & = 4x && \;\\ 4x & = 2x+1 && \end{align*}$

Näiden ominaisuuksien avulla voimme johtaa yhtälön ratkaistuun muotoon, missä yhtälön toisella puolella on ratkaistavissa oleva muuttuja ja toisella lukuarvo. Näin saadaan määritettyä yhtälön kaikki juuret.

Huom! Yhtäpitävyyttä merkitään ekvivalenssinuolella $\Leftrightarrow$ . Ekvivalenssinuolta tulee käyttää, jos keskenään yhtäpitävät yhtälöt kirjoitetaan rinnakkain. Tässä kirjassa yhtälöitä ratkaistaan pääsääntöisesti allekkain ja ekvivalenssinuolet jätetään merkitsemättä.

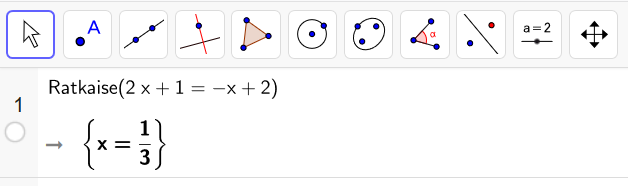
2.2.4 Esimerkki: yhtälön ratkaiseminen ja ratkaisun tarkistus

Ratkaise yhtälö 2x+1=-x+2 .

Ratkaisu:

$\begin{align*} 2x+1 & = -x+2 \;\;\;\;\;\;\;\;\,\;| +x \\ 3x+1 & = 2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; | -1 \\ 3x & = 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|:3 \\ x &= \frac{1}{3} \end{align*}$

Vastaus: $x = \displaystyle\frac{1}{3}$

Tarkistus:

Ratkaisun voi tarkistaa sijoittamalla vastaus $x=\dfrac{1}{3}$ yhtälöön:

$\begin{align*} 2\cdot\frac{1}{3}+1 &=-\frac{1}{3}+2 \\ \frac{2}{3}+\frac{3}{3} &=-\frac{1}{3}+\frac{6}{3} \\ \frac{5}{3}&=\frac{5}{3}\\ \text{}&{\bf{tosi}} \end{align*}$

Ratkaisun voi tarkistaa myös hyödyntämällä laskinohjelmistoja. Alla näytetään, miten se onnistuu Geogebran CAS-laskimella.

2.2.5 Esimerkki: ratkaisuja ei yhtään tai ääretön määrä

Ratkaise yhtälö.

$-5(2x-1)=-4x-2(3x-\dfrac{5}{2})$
$4x-\dfrac{2-3x}{3}=5x$

Ratkaisu:

$\begin{align*} -5(2x-1) & = -4x-2(3x-\dfrac{5}{2}) \\ -10x+5 & = -4x-6x+5 \\ -10x+5 & = -10x+5 && |-5 \\ -10x & = -10x &&|+10x \\ 0 & = 0 \\ \text{}&\text{\bf{tosi}} \end{align*}$

Yhtälö on tosi riippumatta muuttujan arvosta. Siispä yhtälöllä on äärettömän monta ratkaisua ja se toteutuu kaikilla $x \in\mathbb{R}$ (lue: " kuuluu reaalilukuihin").

$\begin{align*} 4x-\dfrac{2-3x}{3} & = 5x && |\cdot 3 \\ 12x-2+3x & = 15x \\ 15x-2 & = 15x && | -15x \\ -2 & = 0 \\ &\text{\bf{epätosi}} \end{align*}$

Yhtälö on epätosi riippumatta muuttujan arvosta, joten yhtälöllä ei ole ratkaisua.

Vastaus:

$x \in\mathbb{R}$
Yhtälöllä ei ole ratkaisua.

Huom! Esimerkin 3.2.3 yhtälöt eivät voi olla ensimmäisen asteen yhtälöitä, sillä ensimmäisen asteen yhtälöllä on aina täsmälleen yksi ratkaisu.

Ristiin kertominen

Olkoon $a,b,c,d\in\mathbb{R}$ ja $b,d\neq0$ . Tällöin voidaan sieventää

$\begin{align*} \frac{a}{b} & = \frac{c}{d} && | \cdot b \\ a & = b\cdot \frac{c}{d} && | \cdot d \\ ad & = bc \end{align*}$

Eli voidaan kertoa ristiin tällaista muotoa olevat yhtälöt.

2.2.6 Esimerkki: murtoyhtälöiden ratkaisemista

Ratkaise yhtälöt.

$\displaystyle\frac{2}{x}=\dfrac{3}{x}$
$\displaystyle\frac{2}{x+1}=\dfrac{3}{x-1}$

Ratkaisu:

Murtolauseke ei ole määritelty silloin, kun nimittäjässä on luku . Tämä tulee ottaa huomioon yhtälön ratkaisujen tarkastelussa. Saatu vastaus ei välttämättä kelpaa yhtälön ratkaisuksi.

$\begin{align*} \frac{2}{x} & = \frac{3}{x} && |\text{kerrotaan ristiin} \\ 2x & = 3x && | -2x\\ x & = 0 \end{align*}$

Murtolauseke on määritelty silloin, kun nimittäjät saavat nollasta poikkeavat arvot. Nyt tulee olla $x\neq0$ , jotta alkuperäisen yhtälön lausekkeet $\displaystyle\frac{2}{x}$ ja $\displaystyle\frac{3}{x}$ on määritelty. Siispä, yhtälöllä ei ole ratkaisua.

$\begin{align*} \frac{2}{x+1} &=\frac{3}{x-1} && |\text{kerrotaan ristiin} \\ 2(x-1) & = 3(x+1) \\ 2x-2 & = 3x+3 && |+2 \\ 2x & = 3x+5 && |-3x \\ -x & = 5 && |:(-1) \\ x & = -5 \end{align*}$

Nyt tulee olla $x\neq-1$ ja $x\neq1$ , jotta alkuperäisen yhtälön lausekkeet on määritelty. Siispä x=-5 on käypä ratkaisu.

Vastaus:

Yhtälöllä ei ole ratkaisua.

Ensimmäisen asteen yhtälö: tehtäviä

2.3 Yhtälö sovelluksissa

Usein matemaattisten ongelmien ratkaisemissa käytetään hyväksi yhtälöä. Nyt erona edellisiin esimerkkeihin yhtälö on laadittava itse. Ennen yhtälön laatimista täytyy vielä valita muuttuja. Muuttujaksi kannattaa yleensä valita tehtävänannossa kysytty seikka.

2.3.1 Esimerkki: ongelmanratkaisu yhtälön avulla

Kun kolme peräkkäistä kokonaislukua lasketaan yhteen saadaan 111 . Mitkä kolme lukua ovat kyseessä?

Ratkaisu:

Merkitään ensimmäistä lukua muuttujalla . Tällöin kaksi seuraavaa kokonaislukua ovat x+1 ja x+2 . Tästä saadaan muodostettua yhtälö.

$\begin{align*} x+(x+1)+(x+2)&=111 \\ 3x+3&=111 &&|-3\\ 3x&=108 &&|:3\\ x&=\frac{108}{3} \\ x&=36 \end{align*}$

Peräkkäiset luvut ovat siis , 36+1=37 ja 36+2=38 .

Vastaus: , ja

2.3.2 Esimerkki: kesätyöpalkan ratkaiseminen

Villen kesätöiden palkoista meni uuteen puhelimeen $\displaystyle\frac{1}{5}$ , festareihin $\displaystyle\frac{1}{7}$ ja vuokraan $\displaystyle\frac{2}{5}$ . Kuinka paljon Ville tienasi kesällä, kun edelläluettujen vähennysten jälkeen palkasta oli jäljellä $801\;\text{€}$ .

Ratkaisu:

Valitaan muuttujaksi Villen kesältä tienaama palkka. Palkka koostuu siis uudesta puhelimesta $\displaystyle\frac{x}{5}$ , festareista $\displaystyle\frac{x}{7}$ , vuokrasta $\displaystyle\frac{2x}{5}$ sekä jäljellä jäävästä osuudesta. Saadaan kirjoitettua yhtälö.

$\begin{align*} \displaystyle\frac{x}{5}+\frac{x}{7}+\frac{2x}{5}+801 &= x\;\;\;\;\;\;|\cdot35 \\ \displaystyle\frac{35x}{5}+\frac{35x}{7}+\frac{35\cdot2x}{5}+35\cdot800&=35x \\ 7x+5x+14x+28035&=35x \\ 35x-7x-5x-14x &=28035 \\ 9x &= 28035 \\ x &=\frac{28035}{9} \\ x &=3115 \end{align*}$

Vastaus: Ville tienasi kesällä $3115\;\text{€}$ .

Yhtälö sovelluksissa: tehtäviä

2.4 Yhtälöpari

Yhtälöpari

Yhtälöpari muodostuu kahdesta yhtälöstä, esimerkiksi

\[\begin{cases} 2x-y+3=0 \\ -4x+2y+1=0 \end{cases}\]

Yhtälöparin ratkaisu on lukupari (x,y) , joka toteuttaa molemmat yhtälöt. Muuttujia voidaan merkitä myös muilla kirjaimilla.

Yhtälöparin ratkaisemisessa käsin voidaan käyttää joko sijoitus- tai yhteenlaskukeinoa. Nämä menetelmät esitellään seuraavissa esimerkeissä.

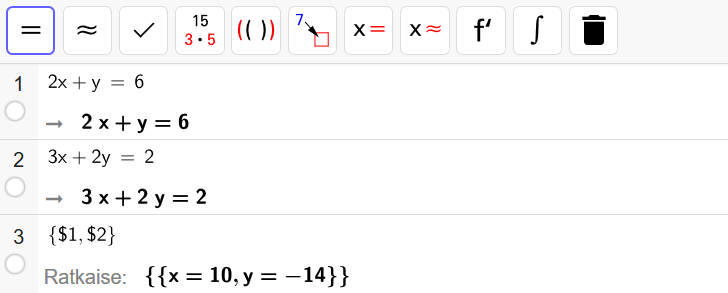
2.4.1 Esimerkki: yhtälöparin ratkaiseminen sijoituskeinolla

Ratkaise yhtälöpari \[\begin{cases} 2x+y=6 \\ 3x+2y=2 \end{cases}\]

Ratkaisu:

\[\begin{cases} 2x+y=6 && (1)\\ 3x+2y=2 && (2) \end{cases}\]

Ratkaistaan esimerkiksi yhtälöstä (1) muuttuja muuttujan suhteen. Saadaan yhtälö

$y=-2x+6 \;\;\;\;\;\;(3)$

Sijoitetaan yhtälö (3) yhtälöön (2) , jolloin saadaan

$\begin{align*} 3x+2(-2x+6)&=2 \\ 3x-4x+12&=2 \\ -x&=-10 \\ x&=10 \end{align*}$

Muuttujan arvo saadaan sijoittamalla x=10 yhtälöön (3) .

$y=-2\cdot10+6=-20+6=-14$

Vastaus:

\[\begin{cases} x=10\\ y=-14 \end{cases}\]

2.4.2 Esimerkki: yhtälöparin ratkaiseminen yhteenlaskukeinolla

Ratkaise yhtälöpari \[\begin{cases} 2x+y=6 \\ 3x+2y=2 \end{cases}\]

Ratkaisu:

Kerrotaan ensin yhtälöt luvuilla, jotka tekevät muuttujan kertoimet toistensa vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.

$\begin{align*} &\begin{cases} 2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-3) \\ 3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot2\\ \end{cases}\\ + &\begin{cases} -6x-3y=-18\\ 6x+4y=4\\ \end{cases}\\ &\noindent\rule{3cm}{0.4pt}\\ &-3y+4y=-18+4\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;y=-14 \end{align*}$

Tämän jälkeen kerrotaan yhtälöt luvuilla, jotka tekevät muuttujan kertoimet toistensa vastaluvuiksi, ja lasketaan saadut yhtälöt yhteen.

$\begin{align*} &\begin{cases} 2x+y=6 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot(-2) \\ 3x+2y=2 \;\;\;\;\;\;\;\;\;\,\,\;|\cdot1\\ \end{cases}\\ + &\begin{cases} -4x-2y=-12\\ 3x+2y=2\\ \end{cases}\\ &\noindent\rule{3cm}{0.4pt}\\ &-4x+3x=-12+2\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=10 \end{align*}$

Vastaus:

\[\begin{cases} x=10\\ y=-14 \end{cases}\]

2.4.3 Esimerkki: yhtälöparin ratkaiseminen Geogebralla

Yhtälöparin ratkaiseminen Geogebran CAS-laskimella onnistuu syöttämällä aluksi yhtälöparin molemmat yhtälöt laskimeen. Yhtälöitä ei tarvitse välttämättä muokata muotoon y=ax+b .

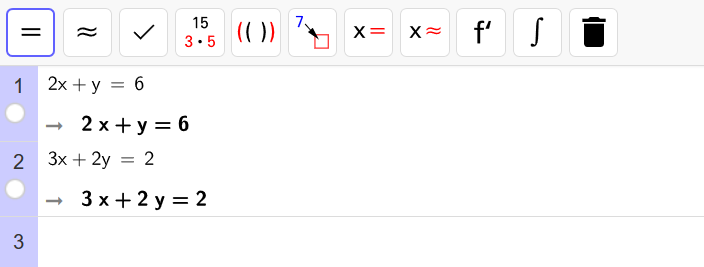
Kun yhtälöt on syötetty laskimeen, valitaan ne molemmat pitämällä ctrl- näppäintä pohjassa ja klikkaamalla vasemmasta palkista yhtälöiden vierestä. Kun yhtälöt on valittu, palkki muuttuu siniseksi. Lopuksi klikkaa yläpalkista -symbolia ja laskin kertoo yhtälöparin ratkaisun.

Yhtälöparin graafinen tarkastelu saattaa auttaa hahmottamaan paremmin tilanteen ja ratkaisujen lukumäärän. Yhtälöparin ratkaisuja ovat ne pisteet, jotka ovat kummankin yhtälön kuvaajalla.

# V7

Piirretään edellisten esimerkkien yhtälöpari koordinaatistoon. Yhtälöiden kuvaajat ovat suoria ja niiden piirtämisen helpottamiseksi ratkaistaan yhtälöt muuttujan suhteen.

$\begin{align*} 2x+y&=6 \\ y&=-2x+6 \end{align*}$

$\begin{align*} 3x+2y&=2 \\ 2y&=-3x+2 \\ y&=-\frac{3}{2}x+1 \end{align*}$

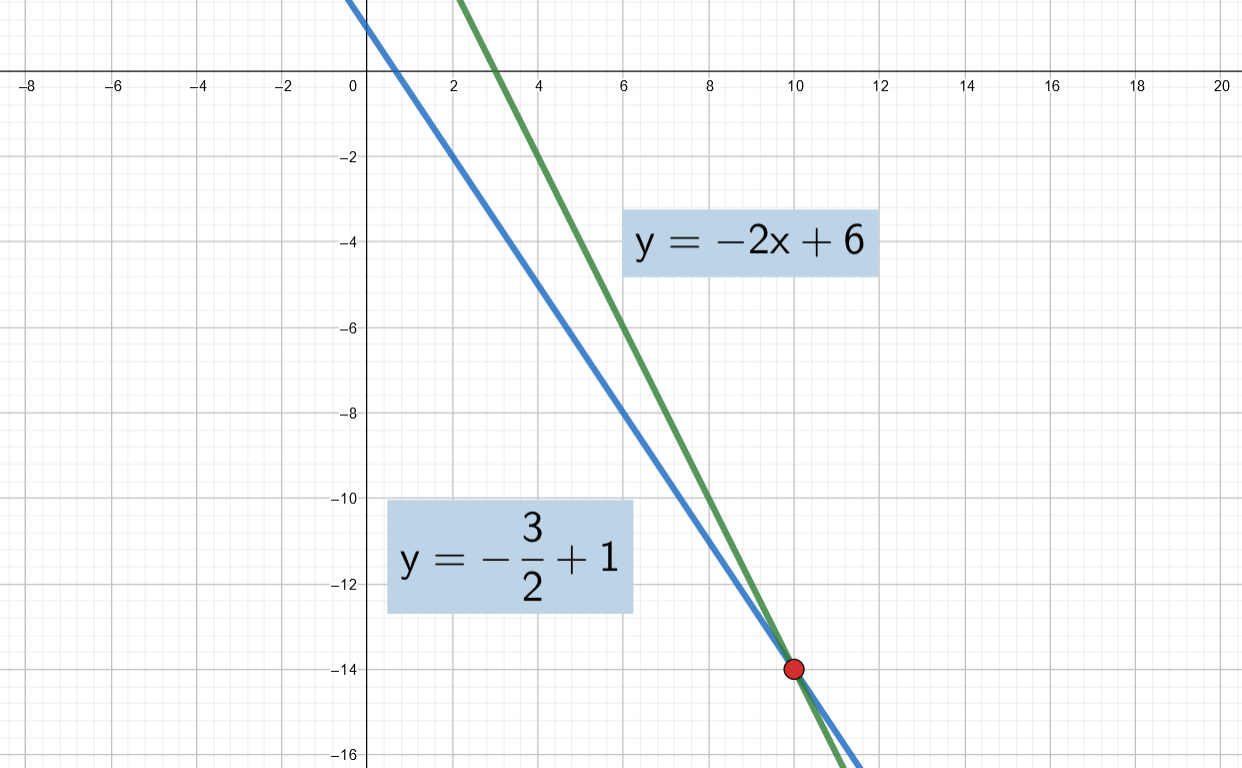
Suorien leikkauspiste (10,-14) on ainoa piste, joka toteuttaa molemmat yhtälöt, joten se on yhtälöparin ainoa ratkaisu.

2.4.4 Esimerkki: yhtälöparilla ei ratkaisua

Ratkaise yhtälöpari \[\begin{cases} 20x-15y=50 \\ 30y-40x=-30 \end{cases}\]

Ratkaisu:

Käytetään yhteenlaskukeinoa.

$\begin{align*} &\begin{cases} 20x-15y=50 \;\;\;\;\;\;\;\;\;\;\;\;\;|\cdot2 \\ -40x+30y=-30 \;\;\;\;\;\;\;\,|\cdot1\\ \end{cases}\\ + &\begin{cases} 40x-30y=100\\ -40x+30y=-30 \\ \end{cases}\\ &\noindent\rule{3.2cm}{0.4pt}\\ &\;\;\;\;\,\,\,\;\;\;\;\;\;\;\;\;\;\;\;0=70\;\;\;\;\text{\bf{epätosi}}\\ \end{align*}$

Vastaus: Yhtälöparilla ei ole ratkaisua.

Tarkistus:

Ratkaistaan yhtälöt muuttujan suhteen.

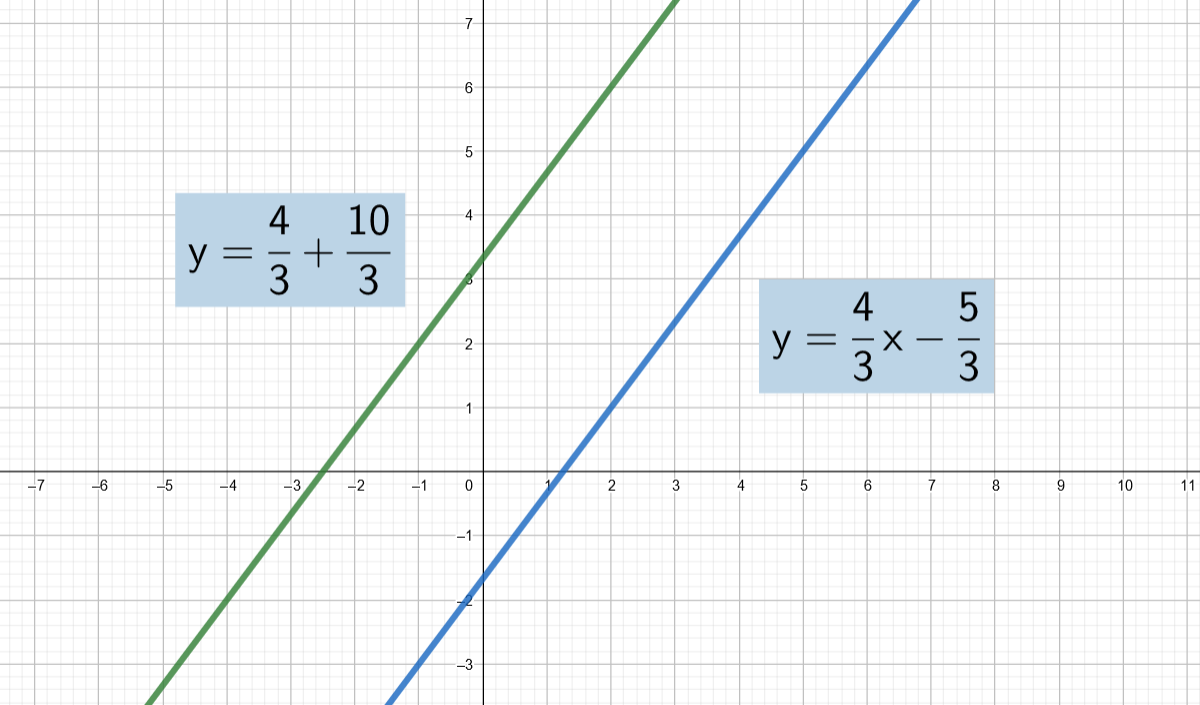
$\begin{align*} 20x-15y&=50 \\ 15y&=20x+50 \\ y&=\frac{4}{3}x+\frac{10}{3} \end{align*}$

$\begin{align*} 30y-40x&=-30 \\ 30y&=40x-50\\ y&=\frac{4}{3}x-\frac{5}{3} \end{align*}$

Suorat ovat yhdensuuntaiset (sama kulmakerroin), joten niillä ei ole yhteisiä pisteitä. Siksi yhtälöparilla ei ole ratkaisua.

2.4.5 Esimerkki: yhtälöparin ratkaisuna kaikki suoran pisteet

Ratkaise yhtälöpari \[\begin{cases} 4x-3y=-9 \\ -12x+9y=27 \end{cases}\]

Ratkaisu:

Käytetään yhteenlaskukeinoa.

$\begin{align*} &\begin{cases} 4x-3y=-9 \;\;\;\;\;\;\;\;\;\;\;|\cdot3 \\ -12x+9y=27 \;\;\;\;\;\;\;\,|\cdot1\\ \end{cases}\\ + &\begin{cases} 12x-9y=-27\\ -12x+9y=27 \\ \end{cases}\\ &\noindent\rule{3cm}{0.4pt}\\ &\;\;\;\;\,\,\,\;\;\;\;\;\;\;\;\;\;\;\;0=0\;\;\;\;\text{\bf{tosi}}\\ \end{align*}$

Koska päädyttiin yhtälöön, joka on aina tosi, yhtälöparin ratkaisuja ovat kaikki lukuparit (x,y) , joilla pätee

$\begin{align*} 4x-3y&=-9 \\ 3y&=4x+9 \\ y&=\frac{4}{3}x+3 \end{align*}$

Vastaus:

\[\begin{cases} x \in\mathbb{R} \\ y =\frac{4}{3}x+3 \end{cases}\]

Tarkistus:

Kun yhtälöt ratkaistaan muuttujan suhteen, saadaan molemmista ratkaisuksi

$y=\frac{4}{3}x+3$

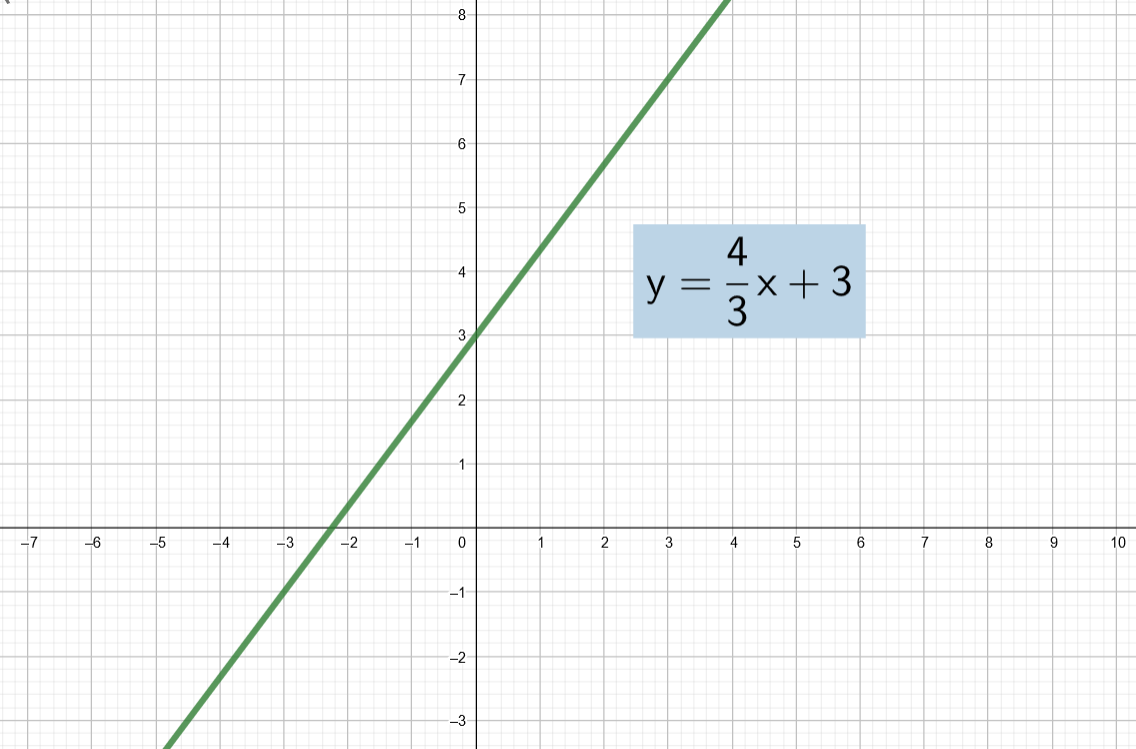
Yhtälöiden kuvaajana on siis sama suora, joten yhtälöparin ratkaisuna on kaikki suoran $y =\displaystyle\frac{4}{3}x+3$ pisteet.

2.4.6 Esimerkki: yhtälöpari sovelluksessa

Sonja haluaa suorakulmion muotoisen pöytäliinan, jonka pituus on $40\;\text{cm}$ suurempi kuin sen leveys. Sonja löysi kaupasta mieleistään kukallista kangasta ja siihen sopivaa reunanauhaa. Määritä pöytäliinaan tarvittavat mitat, kun reunanauhaa käytetään $6,0\;\text{m}$ .

Ratkaisu:

Valitaan muuttujaksi pöytäliinan leveys ja muuttujaksi pituus. Koska pituus on $40\;\text{cm}$ suurempi kuin leveys, saadaan ensimmäiseksi yhtälöksi y=x+40 . Reunanauhaa on $6,0\;\text{m}=600\;\text{cm}$ , joten toiseksi yhtälöksi saadaan 2x+2y=600 (suorakulmion piiri on $2\cdot\text{leveys}+2\cdot\text{pituus}$ ). Saadaan siis yhtälöpari

\[\begin{cases} y=x+40\\ 2x+2y=600 \end{cases}\]

Koska ensimmäinen yhtälö on ilmoitettu valmiiksi muuttujan suhteen, voidaan sijoittaa se suoraan toiseen yhtälöön.

$\begin{align*} 2x+2(x+40)=600 \\ 2x+2x+80=600 \\ 4x=520 \\ x=130 \end{align*}$
Muuttujan y arvo saadaan sijoittamalla x=130 ensimmäiseen yhtälöön.

y=130+40=170

Eli pöytäliinan kangaspalan leveys on $130\;\text{cm}$ ja pituus $170\;\text{cm}$ .

Vastaus: leveys $130\;\text{cm}$ ja pituus $170\;\text{cm}$

Yhtälöpari: tehtäviä