1. Luvut ja laskutoimitukset: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Luvut ja laskutoimitukset. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

1.1 Lukualueet: tehtäviä

Tämän kappaleen teoria.

1.1.1 Tehtävä

# p211a

# p211b

# p211c

# p212d2

1.1.2 Tehtävä

Mistä lukujoukoista luvut on otettu? Valitse suppein (pienin mahdollinen) joukko.

# p212a

# p212b

# p212c

# p212d

1.1.3 Tehtävä

Valitse kuvailuun sopiva yhtälö.

# p213a

# p213b

# p213c

1.2 Laskulait: tehtäviä

Tämän kappaleen teoria.

1.2.1 Tehtävä

Laske ilman laskinta.

# seq221a

# seq221b

# seq221c

1.2.2 Tehtävä

Laske ilman laskinta.

# seq222a

# seq222b

# seq222c

1.2.3 Tehtävä

Laske ilman laskinta. Käytä hyväksesi reaalilukujen laskulakeja.

# seq223a

Vihje

Osittelulaki:

$3,5\cdot178+6,5\cdot178=178\cdot(3,5+6,5)$

# seq223b

Vihje

Osittelulaki:

$38\cdot1,8-1,8\cdot28=1,8\cdot(38-28)$

# seq223c

Vihje

Liitäntälaki:

1,234+(5,766-8)=(1,234+5,766)-8=7-8

# seq223d

Vihje

Vaihdanta- ja liitäntälaki:

$\left(\displaystyle\frac{1}{9}\cdot2,222\right)\cdot180= \left(\displaystyle\frac{1}{9}\cdot180\right)\cdot2,222=20\cdot2,222$

1.2.4 Tehtävä

# T30

1.2.5 Tehtävä

# T33

1.2.6 Tehtävä

# T40

1.2.7 Tehtävä

Laske lukujen ja

# seq227a

# seq227b

# seq227c

# seq227d

Minkä yhteyden huomaat?

Vastaus

Lukujen summa on vastalukujen summan vastaluku. Vastaavasti lukujen erotus on vastalukujen erotuksen vastaluku.

Tulos pätee yleisestikin ottaen kaikilla $a,b\in\mathbb{R}$ , sillä a+b=-(-a+(-b)) ja a-b=-(-a-(-b)) .

1.2.8 Tehtävä

Merkitse lauseke ja laske, kun

# seq228a

# seq228b

Vihje

Lukujen ja summa on -19+3=-16 ja sen vastaluku

# seq228c

Vihje

$\displaystyle\frac{-77}{-11}\cdot(-10)=7\cdot(-10)$

# seq228d

Vihje

$\displaystyle\frac{-36}{-9}\cdot(1+(-5))=4\cdot(-4)$

1.3 Itseisarvo: tehtäviä

Tämän kappaleen teoria.

1.3.1 Tehtävä

Sievennä.

# seq23a

# seq23b

# seq23c

1.3.2 Tehtävä

Laske lukujen ja

# seq229a

# seq229b

# seq229c

1.3.3 Tehtävä

Lukujen ja erotuksen itseisarvo |a-b| ilmoittaa lukujen ja etäisyyden lukusuoralla.

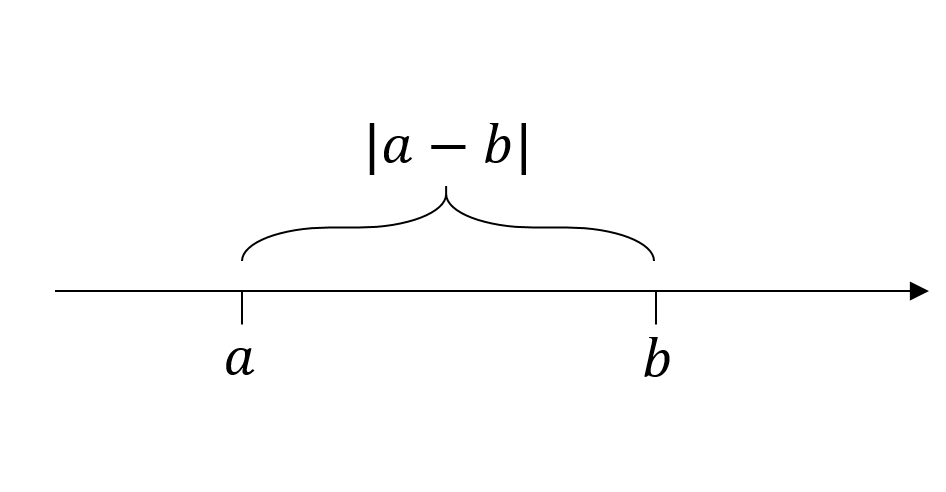
Määritä kaupunkien lämpötilaerot.

# seq231a

# seq231b

1.3.4 Tehtävä

# p234

1.3.5 Tehtävä

# p232

1.3.6 Tehtävä

Sievennä. Käytä hyväksesi itseisarvon ominaisuuksia.

# p235

# p235b

Vihje

|-2a|=|-2||a|=2|a|

Itseisarvomerkit saat komennolla abs().

1.4 Murtoluvut: tehtäviä

Tämän kappaleen teoria.

1.4.1 Tehtävä

Ilmaise sekalukumuodossa.

# 241a

# 241b

# 241c

# 241d

1.4.2 Tehtävä

Ilmaise murtolukuna.

# 242a

# 242b

# 242c

# p242d

1.4.3 Tehtävä

Supista murtoluvut siten, että osoittaja ja nimittäjä ovat mahdollisimman pieniä kokonaislukuja.

# 243a

# 243b

# 243c

# 243d

# 243e

1.4.4 Tehtävä

Lavenna murtoluvut samannimisiksi ja aseta luvut suuruusjärjestykseen pienimmästä suurimpaan.

# p244a

# p244b

1.4.5 Tehtävä

Laske lukujen $\displaystyle\frac{8}{9}$ ja $-\displaystyle\frac{4}{7}$

# 245a

# 245b

# 245c

# 245d

1.4.6 Tehtävä

# T34

1.4.7 Tehtävä

# T35

1.4.8 Tehtävä

Laske ja sievennä. Ilmoita vastaus kokonaisluku- tai murtolukumuodossa.

# 248a

# 248b

# 248c

1.4.9 Tehtävä

Sievennä.

# p2410a

# p2410b

# p2410c

# p2410d

1.4.10 Tehtävä

# seq2413

1.4.11 Tehtävä

# seq2411

1.4.12 Tehtävä

Pekka on tullut siihen lopputulokseen, että hänen kahvinsa on täydellistä, kun hän suodattaa kahvin kolmella eri suodatinpussilla. Ensimmäinen suodatinpussi suodattaa kahvipuruista neljäsosan, toinen kaksi viidesosaa ja kolmas neljä yhdeksäsosaa.

# seq2412

Vihje

Ensimmäinen suodatinpussi suodattaa neljäsosan puruista, joten jäljelle jää $1-\displaystyle\frac{1}{4}=\frac{3}{4}.$

Toinen suodatinpussi suodattaa kaksi viidesosaa jäljellä olevasta määrästä, joten sen jälkeen jäljelle jää $\left(1-\displaystyle\frac{2}{5}\right)\cdot\displaystyle\frac{3}{4} =\frac{3}{5}\cdot\frac{3}{4}=\frac{9}{20}.$

$\dots$

# p4211

1.4.13 Tehtävä

Jarkon osakesalkussa on 2232 osaketta. Osakkeista yksi kahdeksasosa on Vihreä energia -yhtiön osakkeita, viisi yhdeksäsosaa Puu ja sellu -yhtiön ja loput Ideatalo Oy:n osakkeita.

# seq2413a

# seq2413b

1.4.14 Tehtävä

Vilma, Virpi ja Visa istuttivat männyntaimia. Vilma istutti taimista kaksi viidesosaa, Virpi jäljelle jääneistä taimista kolmasosan ja Visa loput 960 tainta.

# seq2414a

Vihje

Vilman jälkeen taimia jäi jäljelle: $1-\dfrac{2}{5}=\dfrac{3}{5}.$

Virpin jälkeen taimia jäi jäljelle: $\left(1-\dfrac{1}{3}\right)\cdot\dfrac{3}{5}=\dots$

# seq2414b

Vihje

Kun merkitään muuttujalla taimien määrää, saadaan yhtälö

$\dfrac{2}{5}x=960,$

josta saadaan ratkaistua muuttujan arvo.

1.4.15 *Tehtävä

Saata murtolukumuotoon jaksollinen desimaaliluku

Vihje

Muodosta yhtälö , eli on se luku, jonka haluat muuttaa murtoluvuksi.
Kerro yhtälö puolittain luvulla sen mukaan kuinka monta numeroa jaksossa on. Esim. jos jaksossa on numeroa, kerrotaan luvulla :
Vähennä molemmilta puolilta :
Ratkaise .

# seq2415a

# seq2415b

# seq2415c

2. Yhtälö: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Yhtälö. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

2.1 Peruskäsitteitä: tehtäviä

Tämän kappaleen teoria.

2.1.1 Tehtävä

# Plugin1

2.1.2 Tehtävä

# Plugin2

2.1.3 Tehtävä

Osoita, että x=1 on yhtälön 2(2x+1)=3(-4x+4)+6 ratkaisu. Tee osoitus valitsemallasi ohjelmistolla ja palauta alle.

# Plugin5

2.2 Ensimmäisen asteen yhtälö: tehtäviä

Tämän kappaleen teoria.

2.2.1 Tehtävä

# p321

Vihje

Voiko yhtälön esittää muodossa ax+b=0 , jossa $a\neq0$ ?

Ratkaise tehtävät 3.2.2-3.2.3 ja 3.2.6-3.2.9 ilman laskinta. Kirjoita ratkaisun välivaiheet näkyviin syöttökenttään.

2.2.2 Tehtävä

Ratkaise yhtälöt.

# p325

# p325b

# p325c

2.2.3 Tehtävä

Ratkaise yhtälöt.

# p325d

# p325e

# p325f

2.2.4 Tehtävä (s2017/2a)

Hannele on ratkaissut yhtälön 2(x^2+x+3)=8(x+1)+2x^2 , mutta välivaiheet ovat menneet sekaisin. Järjestä välivaiheet niin, että ne muodostavat yhtälön loogisesti etenevän ratkaisun.

$x=-\frac{1}{3}$

# plugin6

2.2.5 Tehtävä

# Plugin4

2.2.6 Tehtävä

# p328

Vihje

Sijoitetaan x=6 yhtälöön ja ratkaistaan muuttuja .

$\begin{align*} 3a \cdot 6^2-6\cdot6+18 & = 0 \\ 108a-18 & = 0 \\ \dots \end{align*}$

2.2.7 Tehtävä

Ratkaise yhtälöt.

# p329a

# p329b

2.2.8 Tehtävä

Ratkaise yhtälöt.

Vihje

Lavennetaan termien nimittäjät samannimisiksi tai kerrotaan yhtälö puolittain luvulla . Saadaan yhtälö muotoon

8x+4x-2x+x=55

Lavennetaan termien nimittäjät samannimisiksi tai kerrotaan yhtälö puolittain luvulla . Saadaan yhtälö muotoon

4x-9x=30

Lavennetaan termien nimittäjät samannimisiksi tai kerrotaan yhtälö puolittain luvulla . Saadaan yhtälö muotoon

3x-9(x-3)-14=0

# p3210a

# p3210b

# p3210c

2.2.9 Tehtävä

Millä vakion arvolla

# p3211a

Vihje

Kaikki luvut toteuttavat yhtälön, jos se sievenee muotoon '0=0' . Sievennetään yhtälöä

$\begin{align*} 3(a-3x) &=-5x-9x+7\\ 3a-9x &=-5a-9x+7\\ 3a+5a&=7\\ &\dots \end{align*}$

# p3211b

Vihje

Yhtälöllä ei ole ratkaisua, jos muuttujan sisältävä termi sievenee pois. Siis tulee olla $2ax=6x\dots$

2.2.10 Tehtävä

# yritystaaaa

Ratkaisu

Rivillä ( x(x-1)=0 ) jaetaan termillä x-1 . Koska x=1 , viidennellä rivillä siis jaetaan nollalla. Tässä tehdään virhe.

2.3 Yhtälö sovelluksissa: tehtäviä

Tämän kappaleen teoria.

2.3.1 Tehtävä

Ratkaise fysiikan kaavat kiihtyvyyttä kuvaavan muuttujan suhteen.

voima:

# p331a

matka: $s=\displaystyle\frac{1}{2}at^2$

# p331b

matka: $s=vt+\displaystyle\frac{1}{2}at^2$

# p331c

Vihje

$\begin{align*} s&=\frac{1}{2}at^2 \;\;\;\;\;|\cdot2\\ 2s&=at^2s\\ &\dots \end{align*}$

$\begin{align*} s&=v_0t+\frac{1}{2}at^2 \;\;\;\;\; |-v_0t\\ s-v_0t&=\frac{1}{2}at^2 \\ &\dots \end{align*}$

2.3.2 Tehtävä

Grillibileisiin kaikille vieraille varataan maissi, kanapihviä ja makkaraa. Yhteensä ruokatarvikkeita on 180 .

# p332

2.3.3 Tehtävä

Perheenjäsenten ikien summa on 148 vuotta. Isosisko on vuotta vanhempi kuin pikkuveljensä. Perheen äiti on iältään kaksi kertaa niin paljon kuin isosisko. Perheen isä on vuotta vanhempi kuin äiti. Kuinka vanha kukin on?

# p333a

# 333c

# p333c

# 333d

Vihje

Olkoon $x=\text{'isosiskon ikä (vuotta)'}$ . Tällöin saadaan lausekkeet kunkin iälle:

Veljen ikä: x-6
Äidin ikä:
Isän ikä: 2x+4

Näiden summan tulaa olla 148 , joten saadaan yhtälö:

x + x-6 + 2x + 2x+4 = 148

2.3.4 Tehtävä

League of Legends videopelissä erittäin keskeinen osa pelin voittamista on vastustajan mestarin vahingoittaminen, jota kuvaa yhtälö

V=kt,

missä on mestariin tehty vahingon määrä, vahinkokerroin ja on taitokerroin.

Pelissä on myös mahdollista suojautua vahingolta ostamalla suojuksia, joita kuvaa yhtälö

100k+kS=100,

missä on vahinkokerroin ja on vastustajan mestarin suojauksen arvo.

# vahinkokerroin1

Vihje

Ratkaise ensin vahinkokerroin yhtälöstä V=kt . Tämän jälkeen ratkaise suojauksen arvo yhtälöstä 100k+kS=100 .

2.3.5 Tehtävä

Elmeri tankkaa aina viikonloppuisin mopoautonsa tankkiin sen verran polttoainetta mitä viikkorahoilla sen hetkisellä hintatasolla saa. Tällä viikolla polttoaineen litrahinta oli laskenut senttiä, minkä vuoksi Elmeri sai tankattua viime viikon litran sijaan litraa. Elmeri sai saman verran viikkorahaa kuin viime viikollakin.

# seq334

Vihje

Olkoon $x=\text{'Polttoineen tämän viikon litrahinta (€/l)'}$ . Tällöin voidaan muodostaa lausekkeet Elmerin viikkorahoista:

Tällä viikolla: 15x
Viime viikolla: 13(x+0,22)

Muodostetaan yhtälö, kun tiedetään, että Elmerin viikkorahan suuruus säilyy:

15x = 13(x+0,22)

2.3.6 Tehtävä

Klassisessa voimanostossa on tapana verrata eri painoluokkien tuloksia niin sanotun Wilks-tuloksen avulla. Wilks tulos voidaan laskea kaavalla

W=ky,

missä on Wilks-kerroin ja on nostajan yhteistulos (penkkipunnerrus+kyykky+maastaveto) kilogrammoina. Kerroin saadaan kaavasta

$k=\dfrac{500}{a+bx+cx^2+dx^3+ex^4+fx^5}.$

Parametrit (miesten) a-f saadaan seuraavasta taulukosta:

parametri	arvo
a
b
c
d
e	$7,01863\cdot 10^{-6}$
f	$-1,291\cdot 10^{-8}$

Voimanostajan Wilks-tulos opiskelijoiden voimanoston avoimessa sarjassa oli W=414 ja massa $x=100\;\text{(kg)}$ .

# voimanostajatoka

Vihje

Ratkaise ensin sijoittamalla yhtälöön $k=\dfrac{500}{a+bx+cx^2+dx^3+ex^4+fx^5}$ taulukon arvot a-f sekä voimanostajan massa .

Tämän jälkeen ratkaistaan yhtälöstä W=ky ja voidaan sijoittaa ja ratkaistuun yhtälöön y=...

2.3.7 Tehtävä

Lil Pumpin kappaleessa Gucci gang toistetaan sanoja gucci gang ja ooh monia kertoja. Yhteensä kappaleen aikana toistetuissa gucci, gang ja ooh sanoissa on 513 kirjainta. Sanaparia gucci gang sanotaan -kertainen määrä verrattuna sanaan ooh. Kuinka monta kertaa kappaleessa sanotaan nämä sanat?

# seq335a

# seq335b

Vihje

Merkitään muuttujalla kappaleesta löytyvien ooh-sanojen määrää. Tällöin gucci gang-sanaparia toistuu kappaleessa kertaa. Tiedetään, että sanoissa gucci gang on kirjainta, sanassa ooh kirjainta ja kaikissa sanoissa on yhteensä 513 kirjainta, joten voidaan muodostaa yhtälö.

$3x+9\cdot6x=513$

2.4 Yhtälöpari: tehtäviä

Tämän kappaleen teoria.

Ratkaise tehtävät 3.4.1-3.4.4 ilman laskinta. Jos yhtälöparilla ei ole ratkaisua, vastaa syöttökenttiin ja tilalle $\text{FF}$ . Hahmottele halutessasi vastaukset Abitti-editorilla, joka löytyy tehtävien alta.

2.4.1 Tehtävä

Ratkaise yhtälöparit

\[\begin{cases} 4x-3y=9\\ x+3y=6 \end{cases}\]

# p341a1

# p341a2

\[\begin{cases} x-2y=-1\\ x+3y=2 \end{cases}\]

# p341b1

# p341b2

Abitti-editori

# pluginvaan

2.4.2 Tehtävä

\[\begin{cases} 7x-2y=25\\ 2x-y=8 \end{cases}\]

# p342a1

# p341b3

\[\begin{cases} 2a+3b=8\\ 6a+2b=-4 \end{cases}\]

# p342b1

# p342b2

Abitti-editori

# Plugin3

2.4.3 Tehtävä

Määritä kuvan perusteella yhtälöparin ratkaisu.

# 434a

# 434b

# 434b2

# 434c

# p343c

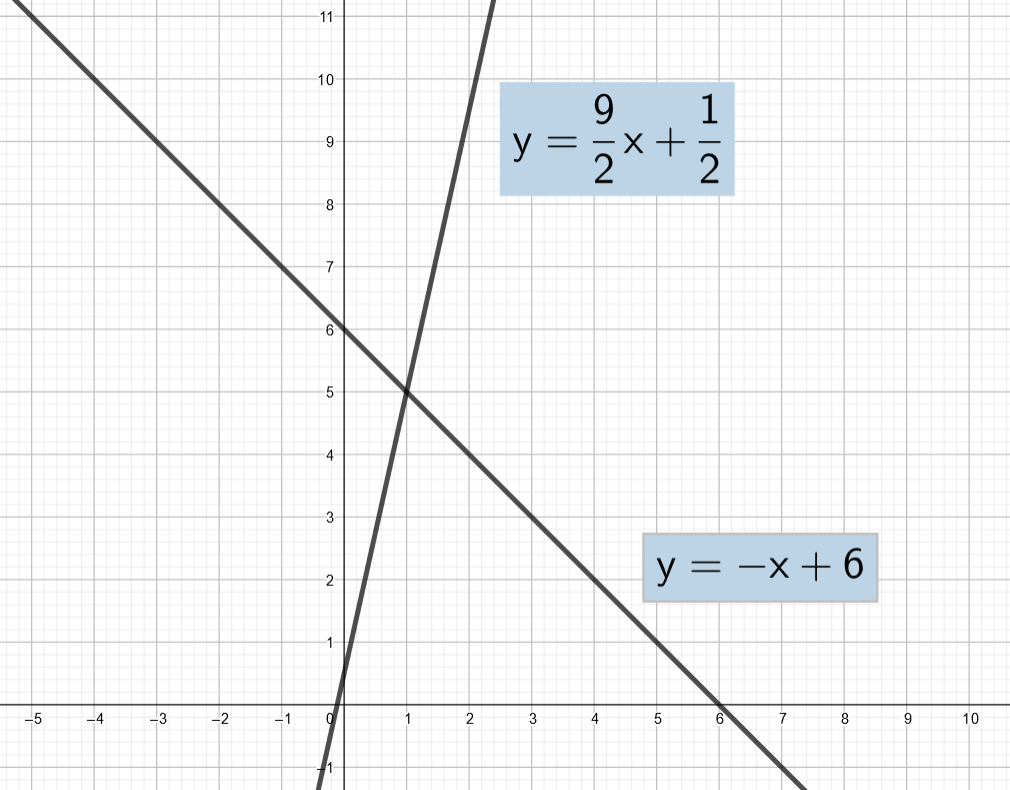
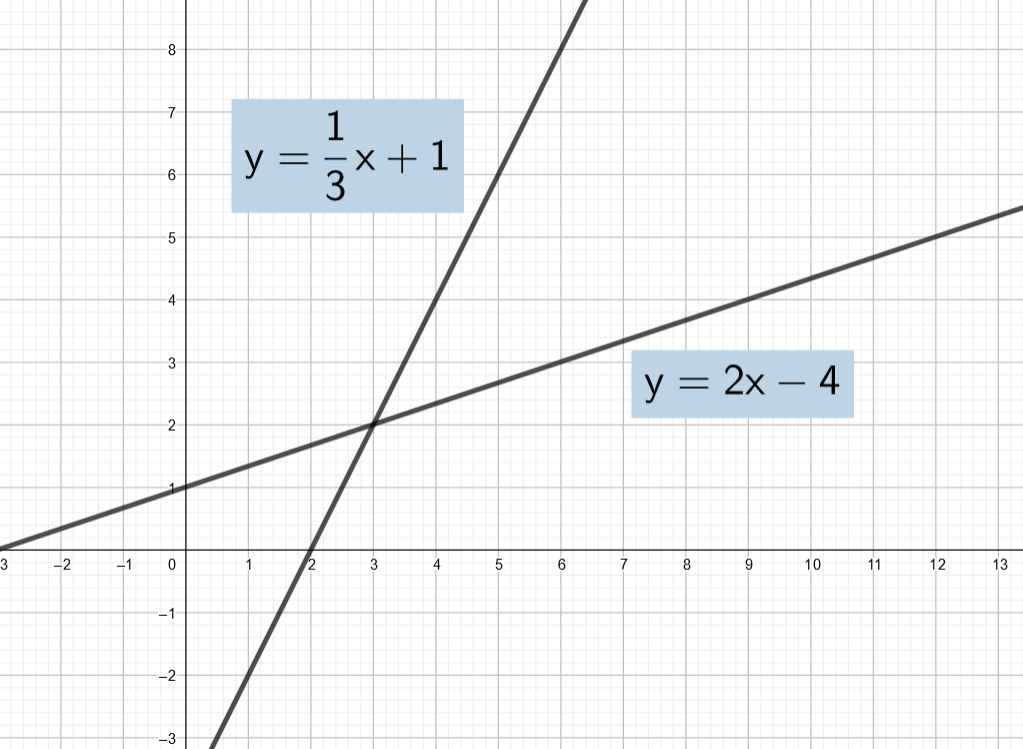
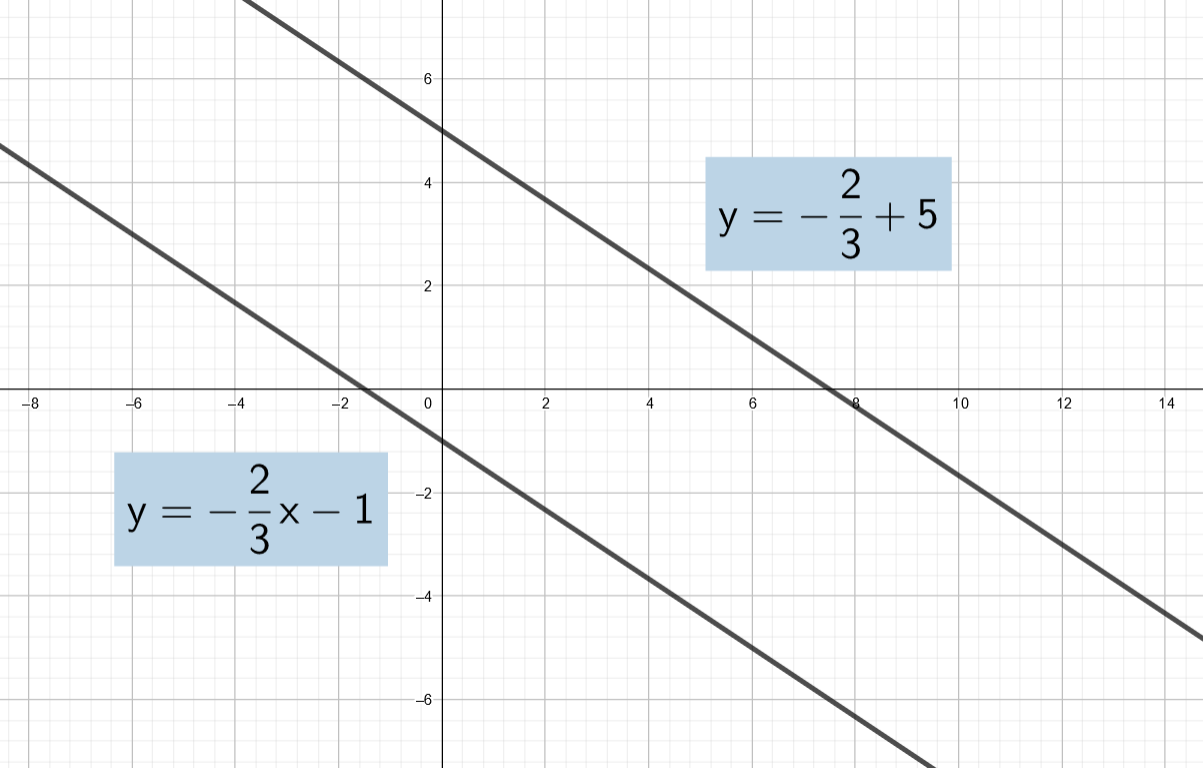
2.4.4 Tehtävä

Ratkaise yhtälöparit.

\[\begin{cases} 32x+8y-64=0 \\ 5y=-20x+40 \end{cases}\]

# seq244a

# seq244b

\[\begin{cases} 4x=3y+1 \\ \frac{1}{3}x=\frac{1}{4}y+1 \end{cases}\]

# seq244c

# seq244d

2.4.5 Tehtävä

Ratkaise yhtälöpari

\[\begin{cases} 2x+y=11 \\ 3y-4x=3 \end{cases}\]

graafisesti Geogebralla ja syötä vastaukset alapuolella oleviin vastauskenttiin.

Geogebra

Open plugin

# 435a

# 435b

2.4.6 Tehtävä

# PLUGINN

Vihje

Merkitään muuttujalla strutseja ja muuttujalla seeproja. Yhtälöpariksi saadaan

\[\begin{cases} x+y=17 \\ 2x+4y=60 \end{cases}\]

2.4.7 Tehtävä

Jalkapallopelin lipputulot olivat $19700\;\text{€}$ , kun aikuisten lippu maksoi $9\;\text{€}$ ja lasten lippu $5\;\text{€}$ . Kävijöitä oli yhteensä 2500 . Muodosta yhtälöpari ja laske, kuinka monta aikuista ja lasta tapahtumassa kävi?

# seq347a

# seq347b

Vihje

Merkitään muuttujalla aikusia ja muuttujalla lapsia. Tiedetään, että kävijöitä oli 2500 , joten tästä saadaan ensimmäinen yhtälö x+y=2500 . Lisäksi tiedetään, että lipputulot olivat $19700\;\text{€}$ , joten tästä saadaan toinen yhtälö 9x+5y=19700 . Ratkaistava yhtälöpari on siis

\[\begin{cases} x+y=2500\\ 9x+5y=19700 \end{cases}\]

2.4.8 Tehtävä

SM-liigan runkosarjassa kaudella 2018-2019 pelattiin ottelua. Voitetusta ottelusta joukkue saa kolme pistettä ja tasapelistä yhden pisteen. Tapparalla oli runkosarjan jälkeen pisteitä 105 . Tappara hävisi runkosarjan aikana ottelua.

# seq348

Vihje

Merkitään voitettuja pelejä muuttujalla ja tasapelejä muuttujalla .

Voitettuja pelejä ja tasapelejä oli yhteensä 60-19=41 , joten ensimmäinen yhtälö on x+y=41. Pisteitä joukkue sai 105 , joten toinen yhtälö on 3x+y=105.

2.4.9 *Tehtävä

Yhtälöryhmäksi kutsutaan ryhmää, jossa tarkasteltavia yhtälöitä on enemmän kuin kaksi. Vastaavasti kuin yhtälöparinkin tapauksessa, tulee yhtälöryhmän kohdalla varmistaa, että yksittäisen yhtälön toteuttava ratkaisu toteuttaa kaikki ryhmän yhtälöt. Ratkaise yhtälöryhmä

\[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1 \\ y+4=2x \end{cases}\]

algebrallisesti

Vihje

Ratkaise yhtälöpari

\[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1 \end{cases}\]

ja tutki toteuttaako ratkaisu yhtälöryhmän alimman yhtälön y+4=2x . Jos toteuttaa, niin kyseessä on yhtälöryhmän ratkaisu.

Ratkaisu

Yhtälöparin \[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1 \end{cases}\]

ratkaisuksi saadaan x=3 ja y=2 . Sijoitetaan piste (x,y)=(3,2) alimpaan yhtälöön, jolloin

$\begin{align*} y+4&=2x && |x=3, y=2 \\ 2+4&=2\cdot3 \\ 6&=6 \\ &\text{tosi} \end{align*}$

Näin ollen yhtälöryhmän \[\begin{cases} y+x=5 \\ y=\dfrac{1}{3}x+1\\ y+4=2x \end{cases}\]

ratkaisu on x=3 ja y=2 .

graafisesti

Ratkaisu

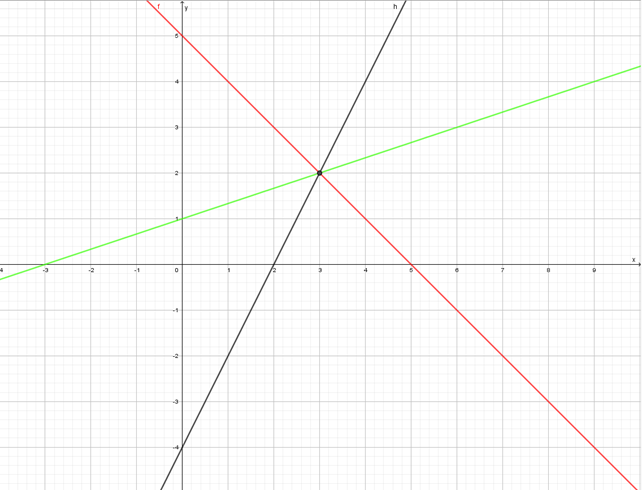
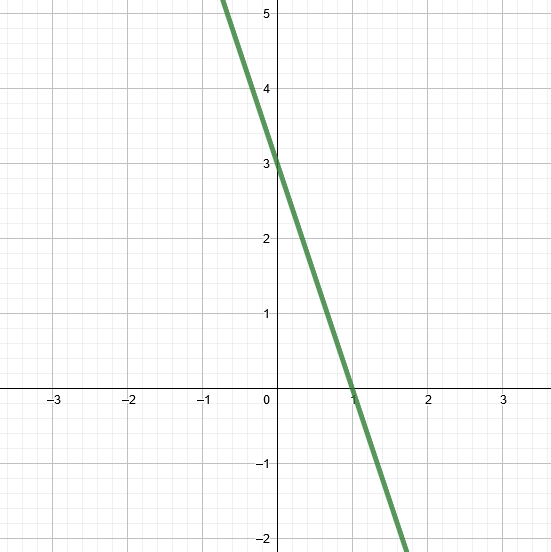
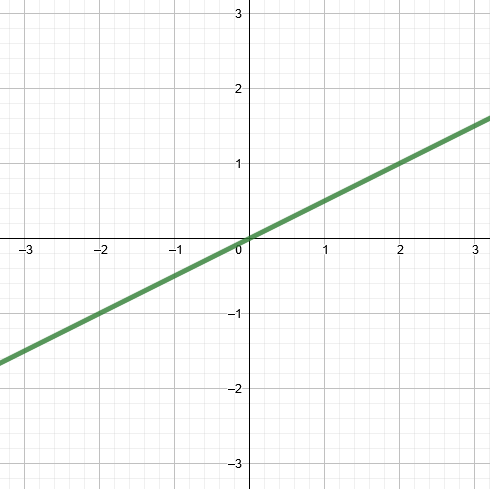
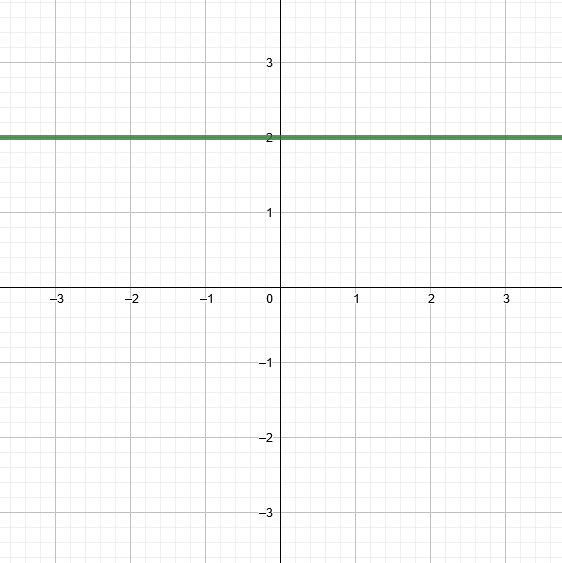
Punainen suora on y+x=5 , musta suora $\dfrac{1}{3}x+1$ ja vihreä suora y+4=2x . Suorat leikkaavat kuvan perusteella pisteessä (x,y)=(3,2) .

# yhtaloryhma1jokerix

# yhtaloryhma1jokeriy

2.4.10 *Tehtävä

Ratkaise kolmen muuttujan yhtälöryhmä

\[\begin{cases} -x+y+2z=-5 \\ 2x-y-z=3 \\ 3x+2y+z=4 \end{cases}\]

# yhtaloryhma2jokerix

# yhtaloryhma2jokeriy

# yhtaloryhma2jokeriz

Vihje

\[\begin{cases} \textcolor{red}{-x+y+2z=-5} && \textcolor{red}{1. \text{yhtälö}} \\ \textcolor{green}{2x-y-z=3} && \textcolor{green}{2. \text{yhtälö}} \\ \textcolor{blue}{3x+2y+z=4} && \textcolor{blue}{3. \text{yhtälö}} \end{cases}\]

Ratkaistaan 3.yhtälöstä , eli sievennetään vasemmalle ja muut termit yhtälön oikealle puolelle.
Tämän jälkeen sijoitetaan ratkaistu . ja yhtälöön, jolloin saamme kahden muuttujan yhtälöparin, josta voimme ratkaista :n ja :n.
Kyseisten :n ja :n arvojen tulee nyt toteuttaa myös . yhtälö, joten sijoittamalla nämä arvot . yhtälöön saamme lopulta myös :n ratkaistua.
Tuloksen voi vielä tarkistaa sijoittamalla ratkaistut , ja jokaiseen yhtälöryhmän yhtälöön ja toteamalla, että yhtälöistä tulee identtisesti todet!

Ratkaisu

Ratkaistaan ensin yhtälöryhmän yhtälö muuttujan suhteen.

$\begin{align*} 3x+2y+z=4 \\ z=-3x-2y+4 \end{align*}$

Tämän jälkeen voidaan sijoittaa ratkaistussa muodossa oleva kahteen yhtälöpariin, jonka muodostavat yhtälöt ja

\[\begin{cases} -x+y+2z=-5 && |z=-3x-2y+4\\ 2x-y-z=3 && |z=-3x-2y+4 \end{cases}\] \[\begin{cases} -x+y+2(-3x-2y+4)=-5 \\ 2x-y-(-3x-2y+4)=3 \end{cases}\] \[\begin{cases} -7x-3y=-13 \\ 5x+y=7 && |\cdot 3 \end{cases}\] \[\begin{cases} -7x-3y=-13 \\ 15x+3y=21 && |\text{lasketaan yhteen} \end{cases}\]

$\begin{align*} 8x=8\\ x=1 \end{align*}$

Sijoitetaan ratkaistu yhtälöparin ylempään yhtälöön.

$\begin{align*} -7x-3y=-13 && |x=1 \\ -7-3y=-13 \\ y=2 \end{align*}$

Sijoitetaan x=1 ja y=2 muuttujan suhteen ratkaistussa muodossa olevaan yhtälöön.

$\begin{align*} z=-3x-2y+4 && |x=1, y=2 \\ z=-3-4+4=-3 \end{align*}$

Näin ollen (x,y,z)=(1,2,-3) on yhtälöryhmän ratkaisu. Ratkaisun voi vielä tarkistaa sijoittamalla pisteen alkuperäiseen yhtälöryhmään.

\[\begin{cases} -x+y+2z=-5 &&|x=1,y=2,z=-3 \\ 2x-y-z=3 &&|x=1,y=2,z=-3 \\ 3x+2y+z=4 &&|x=1,y=2,z=-3 \end{cases}\] \[\begin{cases} -1+2-6=-5\\ 2-2+3=3 \\ 3+4-3=4 \end{cases}\] \[\begin{cases} -5=-5\\ 3=3 \\ 4=4 \\ \text{tosi} \end{cases}\]

Vastaus: x=1 , y=2 ja z=-3

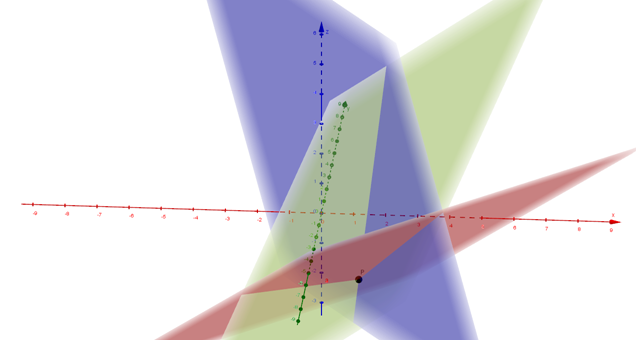
Geometrisesti tämä tarkoittaa yhtälöryhmän yhtälöiden leikkauspistettä. Kyseiset yhtälöt voidaan tulkita kolmiulotteisen avaruuden tasoina. Eli ratkaisu voidaan tulkita näiden tasojen leikkauspisteenä. Aiheeseen palataan lukion pitkän matematiikan vektorit -kurssilla, joten ei kannata todellakaan murehtia jos oheisen kuvan merkitys ei nyt aukea!

3. Verrannollisuus ja prosenttilaskenta: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Verrannollisuus ja prosenttilaskenta. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

3.1 Suoraan verrannollisuus: tehtäviä

Tämän kappaleen teoria.

3.1.1 Tehtävä

# Plugin1

3.1.2 Tehtävä

# p412

3.1.3 Tehtävä

Miisa on kutsunut kaveria grilli-iltaan. Miisa varaa ystävilleen $3,9\;\text{kg}$ makkaroita. Kolme Miisan kavereista ilmoittaa tuovansa oman kaverinsa mukanaan grilli-iltaan. Miisa ilahtuu tästä ja päättää hankkia makkaraa myös uusille tulokkaille.

# seq414

Vihje

Olkoon vieraat ja makkaramäärä $y\;\text{(kg)}$ . Vieraat ja makkaramäärä ovat suoraan verrannollisia suureita, joten

$\dfrac{y_1}{x_1}=\frac{y_2}{x_2}$

Merkitään x_1=9, x_2=9+3=12, y_1=3,9 ja ratkaistaan y_2 .

Huomaa, että kysytään, kuinka monta kiloa lisää $\dots$

3.1.4 Tehtävä

Kynttilä palaa tasaisella liekillä niin, että sydänlanka lyhenee $2\;\text{cm}$ minuutissa. Kello Violet sytyttää $27\;\text{cm}$ korkean kynttilän palamaan.

# seq413

Vihje

Olkoon sydänlangan lyhenemä $x\;\text{(cm)}$ ja aika $y\;\text{(min)}$ . Lyhenemä ja aika ovat suoraan verrannollisia suureita, joten

$\dfrac{y_1}{x_1}=\frac{y_2}{x_2}$

Merkitään x_1=2, x_2=27, y_1=20 ja ratkaistaan y_2 .

Koska kysytään kellon aikaa, täytyy miettiä paljonko kello on, kun 19.00 jälkeen kuluu y_2 verran minuutteja $\dots$

3.1.5 Tehtävä

Piirrä Geogebralla suora, jonka avulla voit muuttaa mailit kilometreiksi. Pituus maileina ja kilometreinä ovat suoraan verrannollisia suureita. Oletetaan, että $1\;\text{maili}=1,6\;\text{km}$ .

# funktio2

Määritä kuvaajasta montako

# seq414a

# seq414b

3.2 Kääntäen verrannollisuus: tehtäviä

Tämän kappaleen teoria.

3.2.1 Tehtävä

# pl421

3.2.2 Tehtävä

Vakiolämpötilassa kaasun paine on kääntäen verrannollinen kaasun tilavuuteen. Männällä varustetussa sylinterissä kaasun paine on $4,9\;\text{kPa}$ ja tilavuus $12\;\text{l}$ .

# seq422

Vihje

Suureet ja ovat kääntäen verrannollisia, joten niiden tulo $pV=\text{vakio}$ ja

p_1V_1=p_2V_2

Tästä saadaan ratkaistua tilavuus $V_2\dots$

3.2.3 Tehtävä

Suureiden ja välillä on voimassa verranto $\dfrac{a}{b}=\dfrac{c}{d}.$

# pl423a

# pl423b

3.2.4 Tehtävä

Suureet x>0 ja y>0 ovat kääntäen verrannollisia. Kun x=3, niin y=20. Muodosta suureiden välistä riippuvuutta kuvaava funktio ja piirrä Geogebralla kuvaaja suureesta suureen funktiona.

# funktio

Vihje

Koska suureet ovat kääntäen verrannollisia, niiden tulo on aina vakio eli $xy=3\cdot20=60$ . Yhtälö saadaan muotoon $y=\dots$

3.2.5 Tehtävä

Alkoholi poistuu elimistöstä pääasiassa maksan kautta. Aikuisen maksa polttaa alkoholia noin yhden gramman tunnissa henkilön kymmentä painokiloa kohden.

Veren alkoholipitoisuus promilleina (p) on suoraan verrannollinen juotuun puhtaan alkoholin määrään grammoina (A) ja kääntäen verrannollinen henkilön massaan kilogrammoina (m) . Sukupuolesta riippuvaa nestetilavuuskerrointa merkitään $k\;\text{:lla}$ .

# p424

3.3 Prosentti: tehtäviä

Tämän kappaleen teoria.

3.3.1 Tehtävä

Valitse prosenttilukua vastaava desimaaliluku.

# Plugin2

# Plugin3

# Plugin4

3.3.2 Tehtävä

# seq2_1

# seq2_2

# seq23

3.3.3 Tehtävä

# T56

3.3.4 Tehtävä

Vuonna 2019 Suomen eduskuntavaaleissa oli $3\;081\;916$ äänestäjää. Kolme suurinta puoluetta SDP, Perussuomalaiset ja Kokoomus saivat $17,7\;\%$ , $17,5\;\%$ ja $17,0\;\%$ äänestäneiden äänistä. Kuinka monta kansalaista äänesti

# p434a

# p434b

# p434c

# p434d

3.3.5 Tehtävä

Pankki tarjoaa $1\;000$ euron suuruisen lainan $3,45\;\%:$ n vuotuisella korolla. Pikavipin vuotuinen korko $1\;000$ euron lainasta on $475\;\%$ .

# seq415

3.3.6 Tehtävä

Vuoden 2018-2019 NHL:n playoffeissa Pekka Rinne torjui 162 laukausta ja päästi maalia.

# seq418

Vihje

Rinne torjui 162 laukausta ja päästi , joten häntä kohti lauottujen laukauksien lukumäärä on 162+17=179 . Nyt voidaan laskea Rinteen torjuntaprosentti: $\displaystyle\frac{162}{179}$

3.3.7 Tehtävä

400 gramman makeissekoitukseen, missä on $27,9\;\%$ salmiakkia, lisätään 200 grammaa hedelmämakeisia.

# seq4110

Vihje

Ensin selvitetään, kuinka paljon salmiakkia on: $0,279\cdot400\;\text{g}$

Uudessa sekoituksessa salmiakkien määrä pysyy ennallaan...

3.3.8 Tehtävä

1,5 kilogrammaan omenamehua, jonka sokeripitoisuus on $11\;\%$ , lisätään kilogramma kuusiprosenttista kevyt omenamehua. Saadaanko uuden omenamehuseoksen sokeripitoisuus alle $10\;\%$ ?

# Plugin6

Vihje

Ensin lasketaan molempien mehujen yhteissokerimäärä: $0,11\cdot1,5\;\text{kg}+0,06\cdot1\;\text{kg}$

Ja selvitetään tämän suhde koko mehusta...

3.3.9 Tehtävä: (k2019/A3)

Seychellien lipussa on viisi eri väriä kuvan mukaisesti. Kuinka monta prosenttia kukin väri peittää koko lipun pinta-alasta? (vastaa prosentin tarkkuudella)

# seq4311a

# seq4311b

# seq4311c

# seq4311d

# seq4311e

Vihje

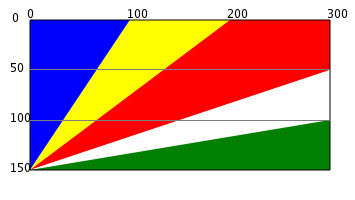
Jaetaan punainen alue kahtia lipun lävistäjän avulla.

Sinisen, keltaisen ja ylemmän punaisen kolmion korkeus on 150 ja kanta 100 . Eli kunkin pinta-ala $\displaystyle\frac{150\cdot100}{2}=7500$ .

Vihreän, valkoisen ja alemman punaisen kolmion korkeus on 300 ja kanta . Eli näidenkin kunkin pinta-ala 7500 .

Kun koko lipun pinta-ala on $300\cdot150=45\;000$ , saadaan laskettua värien suhteelliset osuudet.

3.4 Muutos- ja vertailuprosentti: tehtäviä

Tämän kappaleen teoria.

3.4.1 Tehtävä

Irtokarkkien kilohinta nousee 4,95 eurosta 5,75 euroon. Millä seuraavista kaavoista saadaan laskettua, kuinka monta prosenttia hinta nousi?

# plug421

3.4.2 Tehtävä

euron T-paidan sai alennuksesta 42,50 eurolla. Kuinka monta prosenttia oli alennus?

# tpaita

3.4.3 Tehtävä

Aarolla on euroa ja Sannilla euroa. Mitkä seuraavista väittämistä pitävät paikkansa?

# p423

Vihje

Kuinka paljon enemmän rahaa Sannilla on kuin Aarolla: $\displaystyle\frac{10-5}{5}=1,0=100\;\%$

Kuinka paljon vähemmän rahaa Aarolla on kuin Sannilla: $\displaystyle\frac{10-5}{10}=0,5=50\;\%$

3.4.4 Tehtävä

Vapun kunniaksi irtomakeisten kilohinta oli 4,99 euroa, mikä oli 2,50 euroa vähemmän kuin alkuperäinen hinta.

# seq424

3.4.5 Tehtävä

Vuonna 2018 Samsungin liikevaihto oli 211,2 miljardia ja Applen 265,6 miljardia (USD). (vastaukset prosentin kymmenesosan tarkkuudella)

# seq4_1

# seq4_2

3.4.6 Tehtävä

Puolen litran Jaffa maksaa Prismassa 2,01 euroa per pullo ja 1,5 litran pullojen -pack maksaa 3,97 euroa.

# seq426

Vihje

Puolen litran Jaffan litrahinta: $\displaystyle\frac{2,01}{0,5}=4,02\;\text{(€/l)}$

-packin litrahinta: $\displaystyle\frac{3,97}{2\cdot1,5}=1,32333...\;\text{(€/l)}$

3.4.7 Tehtävä

# seq427

Vihje

Suureet ja ovat kääntäen verrannollisia, joten $\dfrac{x_2}{x_1}=\dfrac{y_1}{y_2}.$

Tiedetään, että kasvaa $25\;\%$ eli uuden arvon suhde alkuperäiseen arvoon $\dfrac{x_2}{x_1}=1,25.$

Halutaan selvittää, paljonko pienenee, jolloin pitää selvittää suhde $\dfrac{y_2}{y_1}$ ja vähentää tämä
$100\;\%$ :sta $\dots$

Ratkaisu

$\begin{align*} 1,25&=\frac{y_1}{y_2} &&|\cdot y_2\\ 1,25\cdot y_2&=y_1 &&|: y_1\\ 1,25\cdot\frac{y_2}{y_1}&=1 &&|:1,25\\ \frac{y_2}{y_1}&=\frac{1}{1,25} \\ \frac{y_2}{y_1}&=0,8 \end{align*}$

Uuden arvon suhde alkuperäiseen arvoon on $0,8=80\;\%,$ joten kasvaa $100\;\%-80\;\%=20\;\%.$

3.4.8 Tehtävä

Vuonna 2009 Usain Bolt juoksi 100 metrin maailmanennätyksen aikaan 9,58 sekuntia virallisen mittauksen mukaan. Matin mukaan Boltin aika oli 9,99 sekuntia, kun taas Iida mittasi ajaksi 9,02 sekuntia. Oletetaan, että virallinen mittaus on oikeassa.

Suhteellinen virhe ilmaisee, kuinka monta prosenttia virheellinen arvo poikkeaa oikeasta arvosta. Positiivinen arvo kertoo, että poikkeama on ylöspäin ja negatiivinen arvo, että poikkeama on alaspäin. Vastaa yhden desimaalin tarkkuudella.

# bolt

# seq4111

3.5 Muuttuneen arvon laskeminen: tehtäviä

Tämän kappaleen teoria.

3.5.1 Tehtävä

Millä desimaaliluvulla hinta tulee kertoa, jos hintaa

# p431a

# p431b

# p431c

# p431d

3.5.2 Tehtävä

Hintoja korotetaan $22,5\;\%$ . Laske uusi hinta sentin tarkkuudella, kun alkuperäinen hinta on

# seq6_3

# seq6_4

3.5.3 Tehtävä

Hintoja alennetaan $17,5\;\%$ . Laske uusi hinta sentin tarkkuudella, kun alkuperäinen hinta on

# seq7_1

# seq7_4

3.5.4 Tehtävä

Hintaa nostetaan ensin $70\;\%$ ja lasketaan sen jälkeen $30\;\%$ . Monta prosenttia uusi hinta on alkuperäistä suurempi?

# p435

3.5.5 Tehtävä

# T59

3.625 pyöristys on 3.63 eikä 3.62

— 22 May 22

3.5.6 Tehtävä

# T58

31.465 pyöristys on 31.47 eikä 31.46

— 22 May 22

3.5.7 Tehtävä

Firman työntekijät olivat tyytymättömiä tämän hetken palkkaansa, jonka vuoksi työnantaja tiedotti:

"Minulla on teille tarjous, josta ette voi kieltäytyä! Ensi vuonna maksan teille kaikille $60\;\%$ ekstraa ensimmäiset kuukautta, jonka jälkeen alennan palkasta $50\;\%$ loppuvuodeksi."

# p438a

Vihje

Merkitään muuttujalla työntekijän kuukausipalkkaa.

$60\;\%$ palkankorotuksen jälkeen, työntekijä saa palkkaa 1,6x kuukaudessa.

Loppuvuodesta palkkaa alennetaan $50\;\%$ , jolloin palkkaa maksetaan $0,5\cdot1,6x=0,8x\dots$

# p438

Vihje

Merkitään muuttujalla työntekijän kuukausipalkkaa.

Tällöin alkuperäinen vuotuinen palkka oli suurudeltaan 12x .

$60\;\%$ palkankorotuksen jälkeen, työntekijä saa palkkaa 1,6x kuukaudessa, joten kuuden kuukauden palkka on $6\cdot1,6x=9,6x$ .

Loppuvuodesta palkkaa alennetaan $50\;\%$ , jolloin palkkaa maksetaan $0,5\cdot1,6x=0,8x$ , joten loppuvuoden palkka on $6\cdot0,8x=4,8x$ .

Nyt työntekijän vuotuinen palkka on 9,6x+4,8x=14,4x.

$\dots$

3.6 Prosenttilausekkeita ja -yhtälöitä: tehtäviä

3.6.1 Tehtävä

Laske alkuperäinen hinta, kun

# seq8_1

# seq8_2

3.6.2 Tehtävä

# seq419

Vihje

Merkitään muuttujalla Coca-Colan määrää kilogrammoissa. Tällöin voidaan muodostaa yhtälö:

$0,021\cdot x = 75$

3.6.3 Tehtävä

Tilastokeskuksen mukaan vuoden 2019 maaliskuussa työssäkäyvien lukumäärä oli $2\;538\;000$ ja työllisyysaste $71,8\;\%$ .

# seq420

Vihje

Merkitään muuttujalla työllisten (eli 15-64 vuotiaiden) lukumäärää. Tällöin työllisten lukumäärä voidaan ratkaista yhtälöstä:

$\begin{align*} 0,718\cdot x & = 2538000\;\;\;\;\;\;\;\; |:0,718 \\ x & = \frac{2538000}{0,718} \end{align*}$

Nyt työttömiä siis $100\;\%-71,8\;\%=28,2\;\%$ työllisten määrästä $x\dots$

3.6.4 Tehtävä

Elokuvalipun myyntihinta muodostuu perushinnasta ja $10\;\%$ arvonlisäverosta.

# p442a

# p442b

Vihje

Merkitään muuttujalla elokuvalipun perushintaa

Arvonlisävero hinnasta on
Lipun myyntihinta on

3.6.5 Tehtävä

# T66

3.6.6 Tehtävä

Jalkapalloseura korotti mestaruuskautensa jälkeen lippujen myyntihintoja. Seuraavalla kaudella joukkue ei menestynyt ja alensi lippujensa hintoja $15\%$ , jolloin ne olivat samanhintaiset kuin ennen mestaruutta.

# p448

Vihje

Merkitään muuttujalla lipun hintaa ennen mestaruutta ja muuttujalla korkoa.

Mestaruuden jälkeen lipun hinta on .

Tämän jälkeen lipun hintaa alennetaan $15\;\%$ , jolloin uusi hinta on 0,85kx . Tämän hinnan tulee olla yhtä suuri kuin lipun hinnan ennen mestaruutta, joten saadaan yhtälö:

0,85kx = x

3.6.7 Tehtävä

Kuten tehtävässä 4.1.5 yleinen tapa mitata humalatilaa on laskea kehon nesteiden alkoholipitoisuutta promilleina $(1\;\text{\textperthousand}=\displaystyle\frac{1}{1000})$ . Henkilö, jonka paino on kilogrammaa juo yhden keskioluen, jonka alkoholipitoisuus on $4,7\;\%$ ja tilavuus 0,33 litraa. Oletetaan, että litra olutta painaa kilogramman ja lisäksi, että henkilö juo juoman nopeasti, jolloin alkoholi ei ehdi poistumaan elimistöstä. Ylittyykö henkilöllä rattijuopumuksen eli $0,5\;\text{\textperthousand}$ :n raja, jos henkilön painosta $70\;\%$ on nesteitä?

# p447

Vihje

Henkilön massasta $70\;\%$ on nesteitä, joten nesteen massa on $0,7\cdot50\;\text{kg}=35\;\text{kg}.$

Koska litra olutta painaa kilogramman, niin yhdessä 0,33 litran $4,7\;\%$ :ssa oluessa on alkoholia $0,047\cdot0,33\;\text{kg}=0,01551\;\text{kg}$ .

Onko osuus henkilön nesteen massasta $<0,5\;\text{\textperthousand}=0,0005$ ?

3.6.8 Tehtävä

Lihassa on aluksi $70\;\%$ vettä. Lihasta halutaan tehdä kuivalihaa, jonka vesipitoisuus on $35\;\%$ .

# p446

Vihje

Merkitään muuttujalla lihan massaa alussa ja muuttujalla veden massaa lopussa.

Aluksi: Lihassa on 0,7x vettä ja 0,3x muuta.

Lopuksi: Lihassa on vettä ja edelleen 0,3x muuta.

Lihan vesipitoisuus on lopussa 0,35 , joten saamme yhtälön

$\frac{y}{y+0,3x} = 0,35$

Ratkaisu

Ratkaistaan yhtälö.

$\begin{align*} \frac{y}{y+0,3x} & = 0,35 && |\cdot (y+0,3x) \\ y & = 0,35y+0,105x && |-0,35y \\ 0,65y & = 0,105x && |:0,65 \\ y &= \frac{0,105}{0,65}x=0,16153846...x \end{align*}$

Nyt veden massan suhde alkuperäiseen veden määrään on $\dfrac{y}{0,7x}=\dfrac{0,16153846...x}{0,7x}\approx0,231=23,1\;\%$ .

Haihdutettava määrä on siis $100\;\%-23,1\;\%=76,9\;\%$ alkuperäisestä veden määrästä.

4. Potenssi ja juuri

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Potenssi ja juuri. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

4.1 Potenssi

Tämän kappaleen teoria.

4.1.1 Tehtävä

# Plugin1

4.1.2 Tehtävä

Laske ilman laskinta.

# seq9_3

# seq9_4

# seq9_5

# seq9_6

4.1.3 Tehtävä

Laske ilman laskinta.

# seq10_1

# seq10_2

# seq10_3

# seq10_4

4.1.4 Tehtävä

Eskon synnyttyä hänen vanhempansa tallettivat 5000 euroa säästötilille, jonka vuotuinen korko on $3,5\;\%$ .

# seq2_2

Vihje: Esimerkki 5.1.3

4.1.5 Tehtävä

Laske ilman laskinta.

# seq10_5

# seq10_6

# seq10_7

Mitä havaitset? Miten voit laskea ilman laskinta 1000^2-999^2 ?

# p515d

Ratkaisu

Perättäisten lukujen neliöiden erotus on yhtä suuri kuin samojen lukujen summa, joten 1000^2-999^2 = 1000 + 999 = 1999.

4.1.6 Tehtävä

Päättele, mikä luku sopii :n paikalle.

# seq11_1

# seq11_2

# seq11_3

4.1.7 Tehtävä

Venezuelan inflaation vuoksi kananlihan kilohinta on noussut $27\;\%$ viikossa ja on nyt 10.9 miljoonaa bolivaria. Oletetaan, että inflaatio on säilynyt vakiona kuukauden aikana.

# seq2_3

Vihje

Korkoprosentti on $27\;\%$ , joten korkokerroin on 1,27 . Neljän viikon aikana kilohinta on noussut 10,9 miljoonaan, mistä saamme yhtälön:

1,27^4x= 10,9

4.2 Potenssin laskusääntöjä

Tämän kappaleen teoria.

4.2.1 Tehtävä

# Potenssimonivalintaeka

Laske tehtävät 5.2.2-5.2.10 ilman laskinta. Voit hahmotella vastauksesi halutessasi ensin Abitti-editorilla, joka löytyy tehtävien alta.

4.2.2 Tehtävä

Sievennä käyttäen samankantaisten potenssien tulon kaavaa.

# seq12_9

# seq12_10

# seq12_11

Abitti-editori

# Plugin3

4.2.3 Tehtävä

Laske käyttäen samankantaisten potenssien osamäärän kaavaa.

# seq12_13

# seq12_14

# seq12_15

Abitti-editori

# pluginjoku

4.2.4 Tehtävä

Sievennä käyttäen potenssin potenssin kaavaa.

# seq12_17

# seq12_18

# seq12_19

Abitti-editori

# plugini

4.2.5 Tehtävä

Sievennä käyttäen tulon potenssin kaavaa.

# seq12_21

# seq12_22

# seq12_23

Abitti-editori

# pluginvaan

4.2.6 Tehtävä

Sievennä käyttäen osamäärän potenssin kaavaa.

# seq12_25

# seq12_26

# seq12_27

Abitti-editori

# plugin4

4.2.7 Tehtävä

# p524

4.2.8 Tehtävä

# T49

4.2.9 Tehtävä

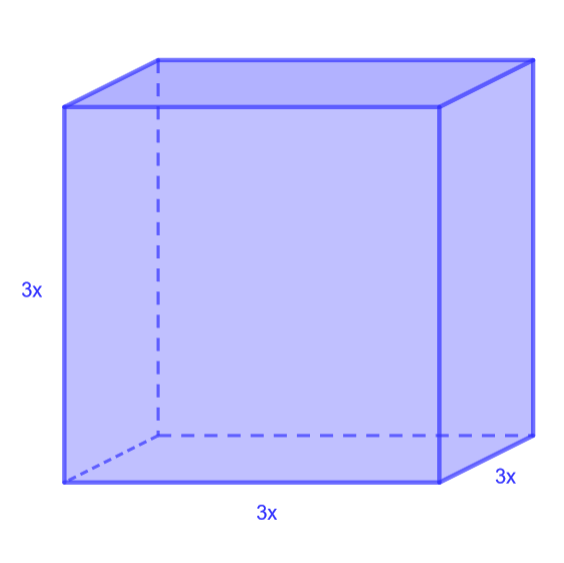
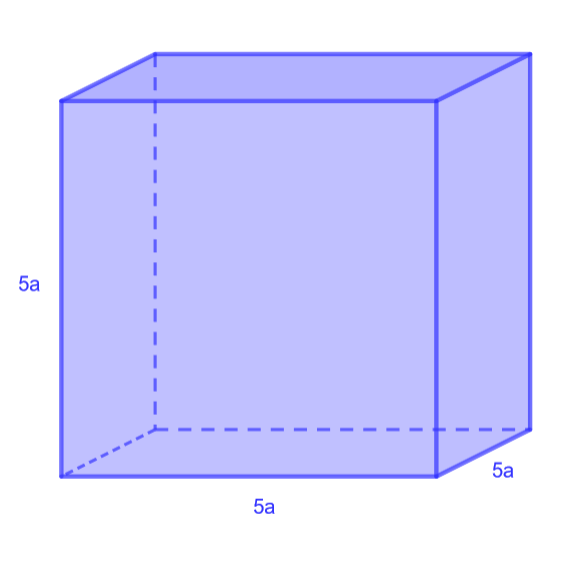
Muodosta ja sievennä kuutioiden tilavuuksien lausekkeet.

# seq528a

# seq528b

4.2.10 Tehtävä

Sievennä.

# seq12_24

Vihje

$\begin{align*} (x^4y)^2(x^2y^3)^4&=(x^4)^2y^2(x^2)^4(y^3)^4 \\ &=x^8y^2x^8y^{12} \\ &=\dots \end{align*}$

# seq12_12

# seq12_28

Vihje

$\begin{align*} \dfrac{9a^8b^6}{a^6b^9}\cdot\dfrac{a^6b^6}{9a^4b^2}&=\dfrac{\cancel{9}a^8b^6a^6b^6}{\cancel{9}a^6b^9a^4b^2} \\ &= \frac{a^{8+6}b^{6+6}}{a^{6+4}b^{9+2}} \\ &=\dots \end{align*}$

Abitti-editori

# Plugin5

4.2.11 Tehtävä

Suomi voitti vuoden 2019 jääkiekon maailmanmestaruuden. Mestaruuteen Suomi tarvitsi pudotuspeleissä puolivälierävoiton Ruotsista, välierävoiton Venäjästä sekä finaalivoiton Kanadasta. Oletetaan, että yksittäinen voitto vastaa kolikon heittoa eli toisin sanoen Suomen todennäköisyys voittaa yksittäinen ottelu on $\dfrac{1}{2}$ .

# seq5211

# seq5311b

Klassisessa todennäköisyyslaskennassa kahden toisistaan riippumattoman tapahtuman todennäköisyys voidaan laskea tuloperiaatteen avulla:

Jos tapahtuman todennäköisyys on ja tapahtuman todennäköisyys on , niin tällöin todennäköisyys sille, että tapahtuu ja voidaan laskea tulona .

Ratkaisu

Suomen tulee voittaa kolme kolikon heittoa putkeen, joten tuloperiaatteen mukaan saadaan todennäköisyys voittaa mestaruus:

$\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}=\Big(\dfrac{1}{2}\Big)^3=\dfrac{1}{8}$

$\Big(\dfrac{1}{2}\Big)^n$

4.2.12 Tehtävä

Katso oheinen video "suklaatempusta".

DailyBroccoli: Chocolate bar trick

Leikkaamalla suklaata kuten videossa, levystä poistuu aina pala per kierros, jonka jälkeen näyttää kuitenkin siltä, että levyssä olisi alkuperäinen määrä paloja. Kuvitellaan, että meillä on vastaavanlainen $9\times4$ suklaalevy. Toisin kuin videolla, leikkaamme jokaisella kierroksella levystä pois prosentuaalisesti saman verran suklaata kuin ensimmäisellä kierroksella. Siis vain ensimmäisellä kierroksella levystä poistuu tasan suklaapala. Kuinka paljon suklaata on jäljellä alkuperäiseen määrään verrattuna, kun leikkaamme levyä

# seq5212a

# seq5312b

Ratkaisu

Levyssä on $4\cdot9=36$ palaa, joista leikataan ensimmäisellä kierroksella pala pois ja jäljelle jää palaa. Tällöin ensimmäisen kierroksen jälkeen leikatun massa alkuperäisestä on $\dfrac{35}{36}$ .

Toisella kierroksella, leikkaamme suhteellisesti saman määrän, jolloin suklata jää jäljelle $\dfrac{35}{36}\cdot\dfrac{35}{36}=\left(\dfrac{35}{36}\right)^2$

Vastaavasti yhdeksännellä kierroksella suklaan suhde alkuperäiseen on $\left(\dfrac{35}{36}\right)^9\approx0,776=77,6\;\%$

$\left(\dfrac{35}{36}\right)^n$

4.2.13 Tehtävä

Osoita, että lausekkeen $\dfrac{2^n4^{n+3}}{8^{n+1}}$ arvo ei riipu positiivisen kokonaisluvun arvosta. Kirjoita vastauksesi haluamallasi ohjelmalla ja palauta tiedostona.

# p5213

Vihje

Ilmaistaan lausekkeet luvun potensseina, jolloin voidaan hyödyntää potenssin laskusääntöjä.

$\dfrac{2^n4^{n+3}}{8^{n+1}}=\dfrac{2^n(2^2)^{n+3}}{(2^3)^{n+1}}=\dfrac{2^n2^{2n+6}}{2^{3n+3}}=\dots$

Ratkaisu

$\dfrac{2^n4^{n+3}}{8^{n+1}}=\dfrac{2^n(2^2)^{n+3}}{(2^3)^{n+1}}=\dfrac{2^n2^{2n+6}}{2^{3n+3}}=\dfrac{2^{3n+6}}{2^{3n+3}} =\dfrac{2^{3n}}{2^{3n}}\cdot\dfrac{2^{6}}{2^3}=2^3$

Nyt lausekkeessa ei ole kokonaislukumuuttujaa , joten se ei siis riipu luvun arvosta.

4.2.14 Tehtävä

# T48

4.3 Kymmenpotenssimuoto

Tämän kappaleen teoria.

4.3.1 Tehtävä

Ilmaise kahden numeron tarkkuudella kymmenpotenssimuodossa.

# seq12_5

# seq12_6

# seq12_7

4.3.2 Tehtävä

Elektronin massa on noin $9,1\cdot10^{-31}\;\text{kg}$ ja protonin $1,7\cdot10^{-27}\;\text{kg}$ . Kuinka moninkertainen on

# seq12_29

# seq12_30

4.3.3 Tehtävä

Maan etäisyys toukokuussa Auringosta on noin 151,6 miljoonaa kilometriä ja valon nopeus on $2,998\cdot10^8\;\frac{\text{m}}{\text{s}}$ . Nopeudelle pätee yhtälö $v=\dfrac{s}{t}$ , missä matka ja =aika.

# seq533

Vihje

Maan etäisyys Auringosta pitää ensin muuttaa metreiksi kymmenpotenssimuotoon.

$151,6\;\text{milj.}\;\text{km}=151\;600\;000\;\text{km}=1,516\cdot10^8\;\text{km}=1,516\cdot10^{11}\;\text{m}$

Aika, joka valolla kestää Auringosta Maahan, saadaan laskettua kaavalla

$t=\dfrac{s}{v}=\frac{1,516\cdot10^{11}\;\text{m}}{2,998\cdot10^8\;\frac{\text{m}}{\text{s}}}=\dots$

4.3.4 Tehtävä

Vanhan tarinan mukaan shakkipeli keksittiin noin 2500 vuotta sitten Intiassa. Kun pelin keksijä oli esitellyt pelinsä kuninkaalleen, tämä ihastui peliin niin, että lupasi keksijälle palkinnoksi mitä tahansa. Keksijä ilmoitti tyytyvänsä vaatimattomaan palkkioon: hän pyysi ensimmäiselle ruudulle yhden vehnänjyvän, toiselle kaksi, kolmannelle neljä ja niin edelleen, aina seuraavalle ruudulle kaksi kertaa niin monta jyvää kuin edelliselle.

# seq534a

Vihje

ruutu:
ruutu: $2\cdot1$
ruutu: $2\cdot2\cdot1=2^2$
ruutu: $2\cdot2^2=2^3$ $\dots$

# seq534b

# seq534b2

4.3.5 Tehtävä

Luonnontieteissä pieniä lukuja on tapana ilmaista kymmenpotenssimuodossa negatiivisen eksponentin avulla. Taulukossa ovat näiden esitysmuotojen etuliitteet.

kymmenpotenssi	etuliite	lyhenne
$10^{-3}$	milli	$\text{m}$
$10^{-6}$	mikro	$\mu$
$10^{-9}$	nano	$\text{n}$
$10^{-12}$	piko	$\text{p}$
$10^{-15}$	femto	$\text{f}$
$10^{-18}$	atto	$\text{a}$

Valitse oikeat etuliitteet.

# p535a

# p535b

# p535c

# p535d

4.4 Neliö- ja kuutiojuuri

Tämän kappaleen teoria.

4.4.1 Tehtävä

# monivalintajuurieka

4.4.2 Tehtävä

Laske ilman laskinta.

# seq13_1

# seq13_2

# seq13_3

# seq13_4

4.4.3 Tehtävä

Laske ilman laskinta.

# seq543a

# seq14_5

# seq543c

# seq14_4

4.4.4 Tehtävä

Laske ilman laskinta. Käytä hyväksesi neliöjuuren ominaisuuksia. Hahmottele tarvittaessa Abitti-editorilla.

# seq15_1

# seq15_2

# seq15_3

# seq15_4

Abitti-editori

# Plugin6

4.4.5 Tehtävä

# Plugin28

# Plugin18

4.4.6 Tehtävä

Playstation-ohjaimen neliö-näppäimen kuvan pinta-ala on noin $42\;\text{mm}^2$ .

# seq545

4.4.7 Tehtävä

Jasminin isä valmistaa mokkapaloja Jasminin yo-juhliin. Hän arvioi, että keskimäärin yksi vieras syö mokkapalan, jonka pinta-ala on $50\;\text{mm}^2$ . Jasminin isä päättääkin tehdä juhliin yhden ison neliön muotoisen mokkapalan, josta vieraat voivat leikata haluamansa määrän.

# seq546

Vihje

Ison mokkapalan pinta-ala: $150\cdot50=7500\;\text{mm}^2$

4.4.8 Tehtävä (s1984/1)

Minkä positiivisen luvun neliöjuuri on luku $\sqrt{5}-2$ ?

# seq546a

# seq546b

Vihje

$\begin{align*} &(\sqrt{5}-2)^2 \\ &=(\sqrt{5}-2)(\sqrt{5}-2) \\ &=(\sqrt{5})^2-2\sqrt{5}-2\sqrt{5}+(-2)^2 \\ &=\dots \end{align*}$

Abitti-editori

# Plugin7

4.4.9 Tehtävä

Rationaalilauseke, missä nimittäjänä on neliöjuuri, voidaan sieventää laventamalla nimittäjällä. $^{\sqrt{b})}\dfrac{a}{\sqrt{b}}=\dfrac{a\sqrt{b}}{\sqrt{b}\sqrt{b}}=\dfrac{a\sqrt{b}}{b}$

Esimerkiksi: $^{\sqrt{5})}\dfrac{60}{\sqrt{5}}=\dfrac{60\sqrt{5}}{\sqrt{5}\sqrt{5}}=\dfrac{60\sqrt{5}}{5}=12\sqrt{5}$

Sievennä tätä käyttäen ilman laskinta seuraavat lausekkeet.

# seq549a

# seq549b

# seq549c

# seq549d

Abitti-editori

# Plugin8

4.4.10 Tehtävä

Standardimittaisen $3\times3$ Rubikin kuution tilavuus on noin $V=190\;\text{cm}^3$ .

# seq5410

Vihje

Rubiikin kuutiossa on paloja $3\cdot3\cdot3=27,$ joten yksittäisen palan tilavuus $\dfrac{190\;\text{cm}^2}{27}\dots$

4.4.11 Tehtävä

Laske lausekkeiden arvot, kun $a = 1, b = 6 \text{ ja } c = 8$ .

# seq5411a

# seq5411b

Sijoita lausekkeen arvot yhtälöön muuttujan paikalle.

# taskNimi

Vastaus

Molempien lausekkeiden arvot, x=-2 ja x=-4 , ovat yhtälön ratkaisuja.

Yleisesti yhtälö, joka on muotoa ax^2+bx+c=0 , voidaan ratkaista toisen asteen yhtälön ratkaisukaavaalla $x=\dfrac{-b \pm\sqrt{b^2-4ac}}{2a}.$ Tähän perehdytään lisää MAA2-kurssilla.

4.5 Potenssiyhtälö

Tämän kappaleen teoria.

4.5.1 Tehtävä

# Plugin68

Ratkaise tehtävät 5.5.2-5.5.3 ja 5.5.5 ilman laskinta. Hahmottele halutessasi ratkaisuja Abitti-editorilla, joka löytyy tehtävien alta.

4.5.2 Tehtävä

Ratkaise yhtälö.

# seq16_2

# seq16_3

# seq16_5

# seq16_6

Abitti-editori

# Plugin9

4.5.3 Tehtävä

Ratkaise yhtälö.

# seq17_1

# seq17_2

# seq17_3

# seq17_4

Abitti-editori

# Plugin10

4.5.4 Tehtävä

Kansainvälisen jääkiekkoliiton mukaan jääkiekkokaukalon aloitusympyröiden pinta-ala on yhteensä noin $320\;\text{m}^2$ .

# seq5411a2

Vihje

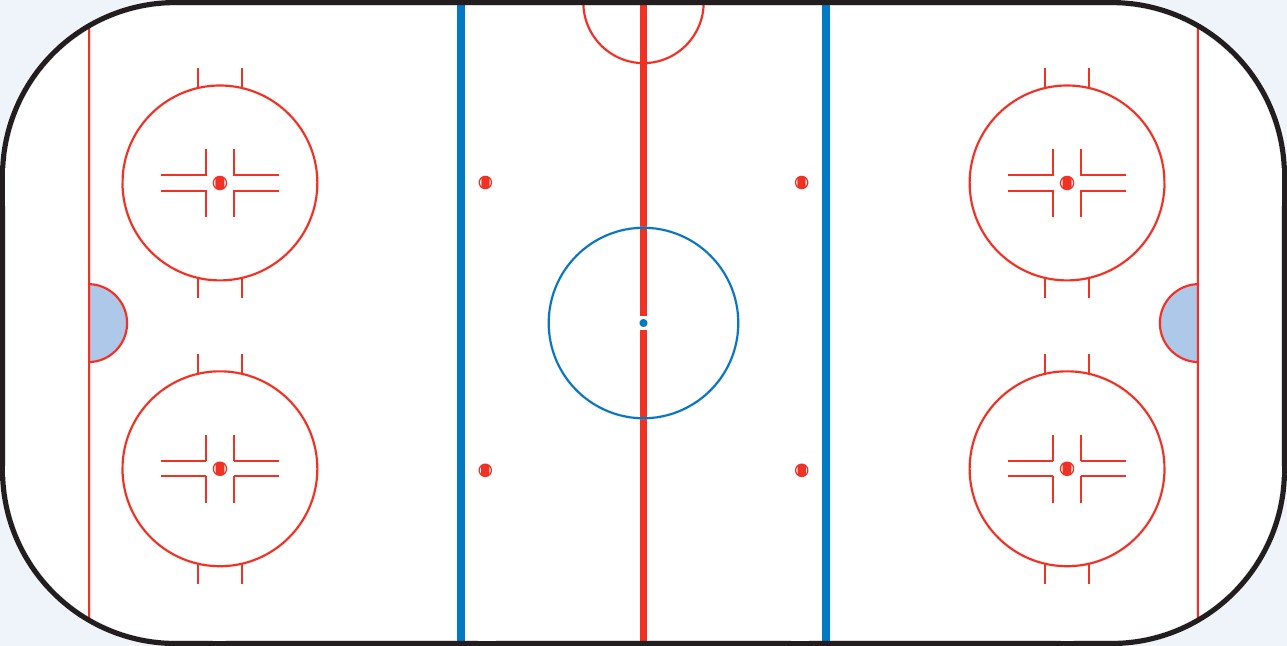
Kaukalossa on aloitusympyrää, joten yksittäisen ympyrän pinta-ala $A=\dfrac{320}{5}=64 \;(\text{m}^2)$ .

Ympyrän yhtälölle pätee $A=\pi r^2$ , josta voidaan ratkaista

$r=\sqrt{\dfrac{A}{\pi}}$ tai $r=-\sqrt{\dfrac{A}{\pi}}$

Negatiivinen ratkaisu ei kelpaa, siispä voidaan laskea halkaisija $h=2r=\dots$

4.5.5 Tehtävä

Ratkaise yhtälö.

# seq18_1

# seq18_2

# seq18_3

# seq18_4

Abitti-editori

# Plugin11

Ratkaisu

Muokataan yhtälöt muotoon, jossa toisella puolella on muuttuja ja toisella vakio ja otetaan puolittain neliö- tai kuutiojuuri.

$\begin{align*} -2x^2+1&=-2 \\ -2x^2&=-3 \\ x^2&=\frac{3}{2} \\ x=-\sqrt{\frac{3}{2}} \;\;&\text{tai}\;\; x=\sqrt{\frac{3}{2}} \end{align*}$

$\begin{align*} \frac{1}{9}x^2-1&=\frac{1}{7} \\ \frac{1}{9}x^2&=\frac{8}{7} &&|\cdot 9\\ x^2&=\frac{72}{7} \\ x=-\sqrt{\frac{72}{7}} \;\;&\text{tai}\;\; x=\sqrt{\frac{72}{7}} &&|\sqrt{72}=\sqrt{36}\cdot\sqrt{2}=6\sqrt{2}\\ x=-6\sqrt{\frac{2}{7}} \;\;&\text{tai}\;\; x=6\sqrt{\frac{2}{7}} \end{align*}$

$\begin{align*} -\frac{1}{9}x^3-1&=0 \\ -\frac{1}{9}x^3&=1 \\ x^3&=-9 \\ x&=\sqrt[3]{-9}=-\sqrt[3]{9} \end{align*}$

$\begin{align*} \frac{1}{9}x^3+\frac{1}{\pi}&=\pi \\ \frac{1}{9}x^3&=\pi-\frac{1}{\pi} &&|\cdot 9\\ x^3&=9\pi-\frac{9}{\pi} \\ x&=\sqrt[3]{9\pi-\frac{9}{\pi}} \end{align*}$

4.5.6 Tehtävä

Vuonna 2017 Suomessa hakattiin puuta ennätysmäärä, noin $7,2 \cdot 10^7\;\text{m}^3.$

Jos kaikki puu varastoidaan

# seq5411a3

Vihje

$\begin{align*} &x^3=V\\ &x=\sqrt[3]{V}\\ &\;\;\dots\\ \end{align*}$

# seq5411a4

Vihje

Pallon tilavuus saadaan kaavalla $V_{pallo}=\dfrac{4\pi r^3}{3}$ , joten puolipallon tilavuus $V_{puolipallo}=\dfrac{4\pi r^3}{3}\cdot\dfrac{1}{2}=\dfrac{2\pi r^3}{3}.$

Tästä voidaan ratkaista puolipallon säde $\dots$

# p556c

Vihje

Lasketaan molempien varastojen seinien pinta-alat. Kuution pinta-ala saadaan laskemalla viiden tahkon (pohja jätetään pois) pinta-alat yhteen.

$A_{kuutio}=5\cdot x^2=\dots$

Pallon pinta-ala saadaan kaavalla $4\pi r^2,$ joten puolipallon pinta-ala saadaan

$A_{puolipallo}=\dfrac{4\pi r^2}{2}=\dots$

5. Funktio: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Funktio. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

5.1 Funktion määritelmä: tehtäviä

Tämän kappaleen teoria.

5.1.1 Tehtävä

Funktion arvo lasketaan seuraavalla säännöllä: Funktioon syötetyn luvun neliöjuuresta vähennetään luku 4.

# p511

# p511b

# p511c

5.1.2 Tehtävä

Olkoon f(x)=x+5 . Laske

# p512a

# p512b

# p512c

5.1.3 Tehtävä

# MAA5_1b

5.1.4 Tehtävä

# plugin6

5.1.5 Tehtävä

Olkoon g(x)=2x^2-3x . Määritä seuraavat funktion arvot.

# p516b

# p616c

# p616d

5.1.6 Tehtävä

Millä muuttujan arvolla funktion arvoksi tulee ? (Jos useampia arvoja kirjoita väliin or.)

# p617a

# p617b

# p617c

# p617d

5.1.7 Tehtävä

# plugin4

5.1.8 Tehtävä

Mitkä ovat funktioiden määrittelyjoukot?

# p618a

# p618b

# p618c

5.1.9 Tehtävä

Taulukoissa on muuttujan arvoa vastaavat funktion arvot f(x) . Päättele funktion lauseke.

# p619a

# p619b

5.1.10 Tehtävä

# plugin8

5.1.11 Tehtävä

# p343c

Vihje

Laske funktion arvot välin päätepisteissä f(0) ja f(2) . Tiedetään, että funktion f(x) kuvaaja on nouseva suora (voit myös piirtää laskimella), joten funktio saa arvoja väliltä $f(0)\le f(x) \le f(2)\dots$

5.2 Funktion nollakohta: tehtäviä

Tämän kappaleen teoria.

5.2.1 Tehtävä

Määritä funktioiden nollakohdat.

# p621a

# p621b

# p621c

5.2.2 Tehtävä

Olkoon $g(x)=4^{2x+1}-16$ .

# p622a

# p622b

Vihje

$g(0)=4^{2\cdot0+1}-16$

$g(x)=0\Leftrightarrow4^{2x+1}-16=0\Leftrightarrow4^{2x+1}=16\Leftrightarrow4^{2x+1}=4^2\Leftrightarrow2x+1=2\dots$

5.2.3 Tehtävä

# p623

5.2.4 Tehtävä

# p624

Vihje

Funktion nollakohta on x=1 , kun $f(1)=4(a\cdot1 +2)+8=0\dots$

5.3 Funktion kuvaaja: tehtäviä

Tämän kappaleen teoria.

5.3.1 Tehtävä

Funktio liittää jokaiseen lähtöarvoon täsmälleen yhden loppuarvon eli jokaisella muuttujan arvolla funktio voi saada vain yhden arvon f(x) .

# moi

5.3.2 Tehtävä

Piirrä funktion f(x)=2x-6 kuvaaja Geogebralla.

# pl631b

Ratkaisu

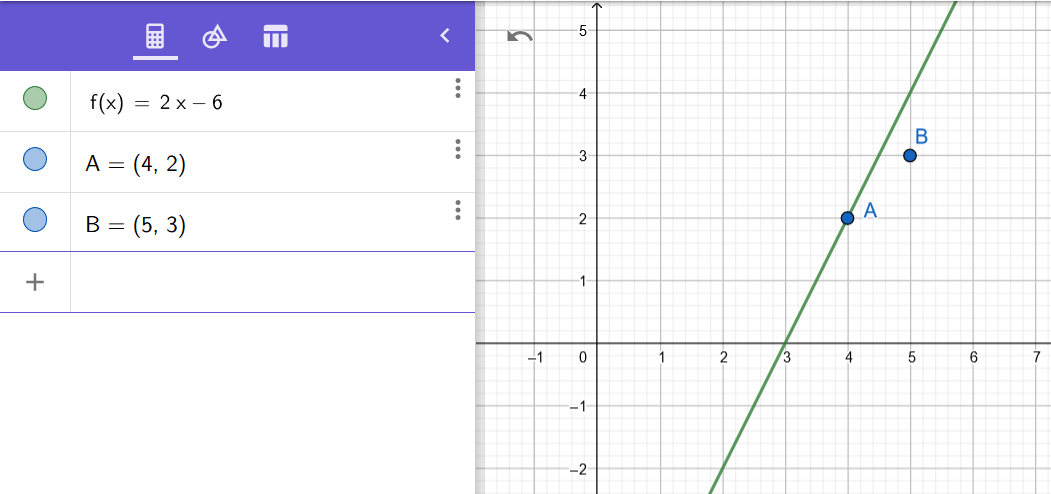
Tarkista a-kohdan tulokset laskemalla esimerkiksi alta löytyvällä Abitti-editorilla.

Abitti-editori

# Plugin3

Vihje

Syötä funktioon pisteen koordinaatin arvo ja laske tuleeko funktion arvoksi koordinaatin arvo.

$f(4)=2\cdot4-6=\dots$

5.3.3 Tehtävä

Appletissa on eräiden funktioiden kuvaajat. Päättele funktioiden lausekkeet muuttamalla muuttujan arvoja liikuttelemalla pistettä . Saat halutessasi vinkin ja funktion arvot näkyviin. Funktiota saat vaihdettua klikkaamalla vasemmasta reunasta.

# p632a

# p632b

# p632c

# p632d

5.3.4 Tehtävä

Täydennä taulukkoon funktion $f(x)=\dfrac{1}{4}x^2-4$ arvot kohdissa -8, -4, ja . Voit muokata taulukkoa tuplaklikkaamalla haluamaasi taulukon solua. Edit table-ikkunan, saa raahattua pois tieltä tarttumalla turkoosiin yläreunaan.

# taulukko1

Open plugin

Hahmottele taulukoiden pisteiden avulla ilman laskinta funktion f(x) kuvaaja. Alareunan Undo-napista saat peruttua viimeisimmän piirron ja Reset-napista saat aloitettua kuvaajan piirron alusta.

# Plugin4

5.4 Funktion kuvaajan tulkinta: tehtäviä

5.4.1 Tehtävä

Appletissa on kolmen funktion kuvaajat, joita saa vaihdeltua oikeasta alakulmasta. Nimetään funktiot:

funktio
funktio
funktio

Liikuttele punaista pistettä kuvaajalla ja vastaa alla oleviin kysymyksiin.

# pl641a

# pl641b

# pl641c

5.4.2 Tehtävä

Määritä kuvaajista funktioiden nollakohdat. Jos kuvaajalla ei ole nollakohtia, kirjoita x= tilalle FF.

# p641a

# p641b2

# seq8_5

5.4.3 Tehtävä

Lue kuvassa olevan funktion kuvaajalta

# p642a

# p642b

# p642c

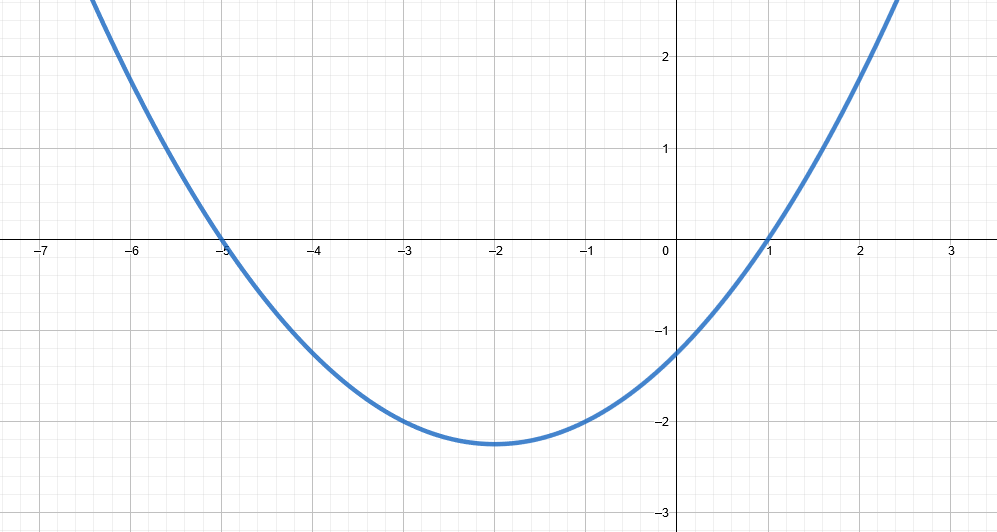
5.4.4 Tehtävä

# pl644

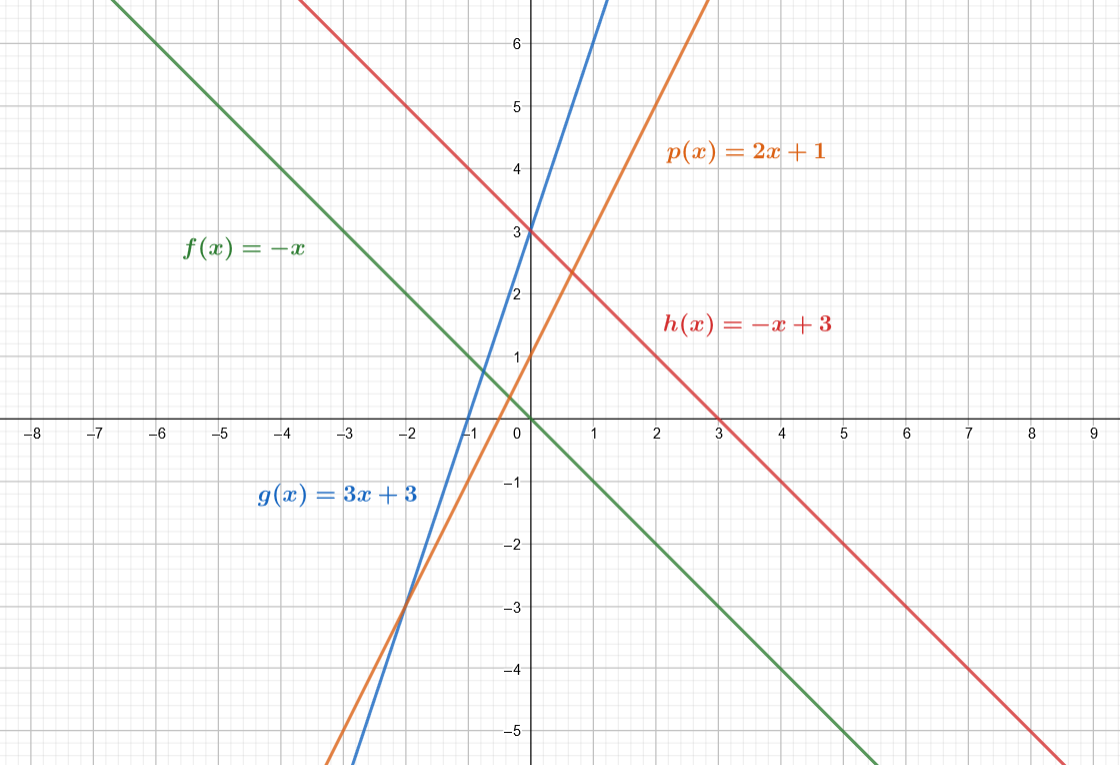
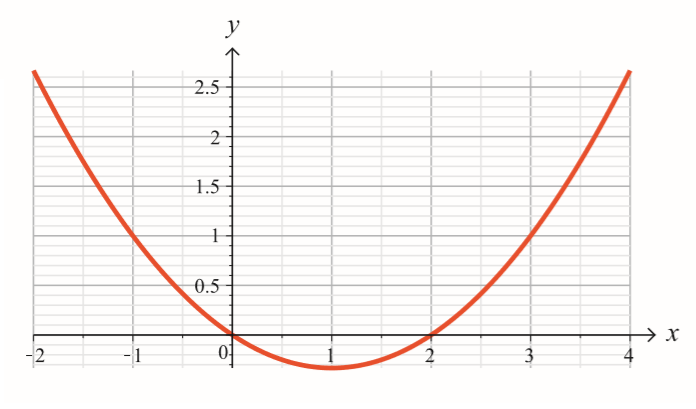
5.4.5 Tehtävä: s2015/3

Oheisessa kuvassa on erään funktion f(x) kuvaaja.

# p644

5.4.6 Tehtävä

# plugin9

5.4.7 Tehtävä

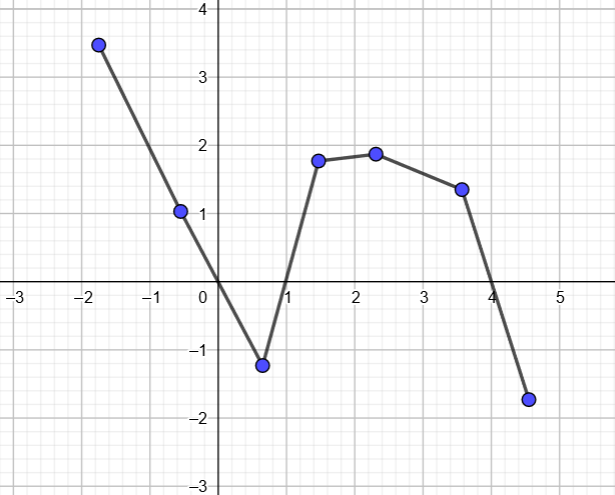
Siirrä oheisen appletin pisteitä siten, että funktiolle asetetut seuraavat ehdot toteutuvat:

Funktiolla on nollakohdat x=0 , x=1 ja x=4 , ja funktion arvo on negatiivinen välillä 0<x<1 ja positiivinen välillä 1<x<4 .

Tehtävästä ei tule pisteitä.

# kolmion_sivu

Ratkaisu

Esimerkiksi:

5.5 Potenssifunktio: tehtäviä

Tämän kappaleen teoria.

5.5.1 Tehtävä

Olkoon kuution sivun pituus ja A(x) kuution vaipan pinta-alaa kuvaava funktio. Vaipalla tarkoitetaan kuution pintaa pohjat pois lukien.

# pl651a2

# pll651b

# pll651c

5.5.2 Tehtävä

Kappaleessa olemme oppineet, että potenssiyhtälön ratkaisujen lukumäärä riippuu luvusta ja siitä, onko parillinen vai pariton.

# pl651a

# pl651b

Ratkaisu

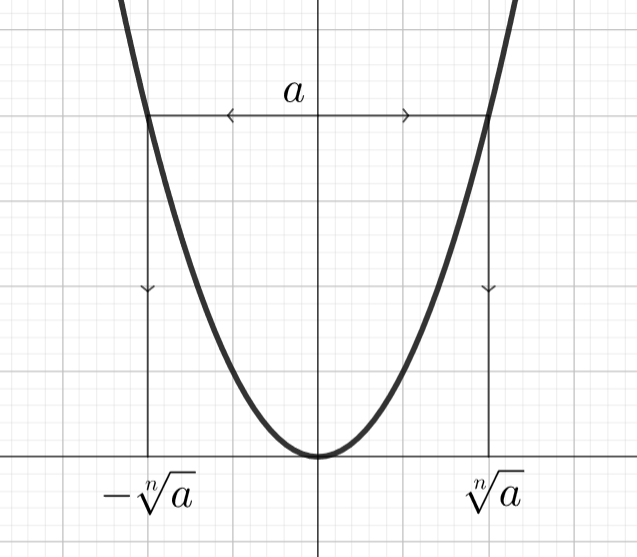
Yhtälön ratkaisut ovat $x=\pm \sqrt{a},$ kun . Koska funktion kuvaaja ei käy akselin alapuolella, yhtälöllä ei ole ratkaisuja, kun Tilanteessa kuvaaja käy origossa eli .

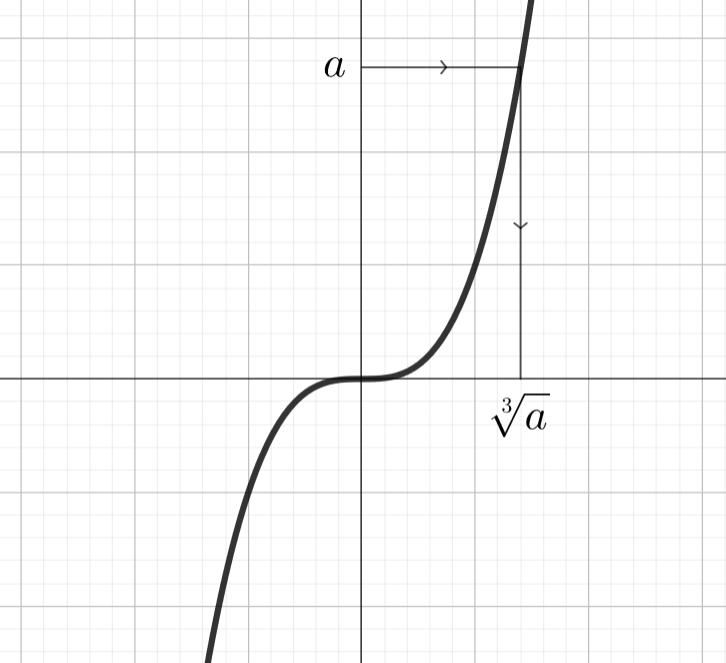
Yhtälöllä on kaikilla muuttujan arvoilla täsmälleen yksi ratkaisu $x=\sqrt[3]{a}.$

5.6 Funktion sovelluksia: tehtäviä

Tämän kappaleen teoria.

5.6.1 Tehtävä

# plugin14

# p651a

# p641b

5.6.2 Tehtävä

Funktio $f(c)=\displaystyle\frac{9}{5}c+32$ ilmaisee lämpötilan fahrenheitasteina, kun lämpötila celsiusasteina on . Floridassa lomaileva Kaisa sairastui. Sairaanhoitaja mittasi hänen ruumiinlämmökseen 98,6 fahrenheitastetta.

# Plugin1

Vihje

Asetetaan 98,6 funktion arvoksi $f(c)=\displaystyle\frac{9}{5}c+32=98,6$ ja ratkaistaan tästä muuttuja .

Jos $c\ge37,0$ , Kaisalla oli kuumetta.

5.6.3 Tehtävä

Kalle löi pesäpalloa asteen kulmassa alkunopeudella $125\;\text{km/h}$ . Tällöin pallon korkeus metreinä maan pinnasta noudattaa likimain funktiota h(t)=1,7+14,7t-4,9t^2 , missä on lyönnistä kulunut aika sekuntteina. Vastaa seuraaviin kysymyksiin metreinä.

# p653

# p653b

5.6.4 Tehtävä

Autovuokraamon hinnoittelu on seuraava:

Auto	Aloitusmaksu	Ajetut kilometrit
Kia Rio	$95\;\text{€}$	$0,4\;\text{€/km}$
Opel Astra	$145\;\text{€}$	$0,3\;\text{€/km}$

# Plugin2

Vihje

Merkitään ajettuja kilometrejä muuttujalla .

Kia: f(x)=95+0,4x

Opel: f(x)=145+0,3x

Sijoita funktioihin muuttujan paikalle 1200 , ja laske kumpi tulee halvemmaksi.

5.6.5 Tehtävä

Eijan puhelinlasku koostuu kiinteästä $11\;\text{€}$ kuukausimaksusta sekä neljän sentin suuruisesta veloituksesta per puhuttu minuutti. Elokuussa Eija puhui puhelimessa tuntia.

# Plugin5

Vihje

Merkitään muuttujalla Eijan puhelimessa puhumaa aikaa minuutteina. Tällöin voidaan muodostaa puhelinlaskua kuvaava funktio: f(x)=11+0.04x

Nyt pitää laskea, onko puhelinlasku enemmän kuin $25\;\text{€}$ kun Eija puhuu $8\;\text{h}=8\cdot60\;\text{min}=480\;\text{min}$ .

5.6.6 *Tehtävä: k2019/10

Vauvan painon voidaan arvioida kasvavan q^3 -kertaiseksi, kun vauvan pituus kasvaa -kertaiseksi. Tämä perustuu siihen, ettö vauva on kolmiulotteinen ja kasvua tapahtuu suurin piirtein yhtä paljon jokaiseen suuntaan. Oletetaan, että vauva on syntyessään cm pitkä ja painaa 4,0 kilogrammaa.

Arvioi vauvan painoa ( kilogramman tarkkuudella) tällä menetelmällä, kun vauvan pituus on

Vihje

Vauvan painoa kuvaa funktio m(x)=ax^3 , missä on vauvan pituus.

Tiedetään, että kun $x=0,52\;\text{cm}$ , niin $m=4,0\;\text{kg}$ eli $m(0,52)=a\cdot0,52^3=4.$ Tästä yhtälöstä saadaan ratkaistua vakion arvo.

Tämän jälkeen vauvan painoa voidaan arvioida sijoittamalla pituus muuttujan paikalle.

# p656a

# p656b

# p656c

# p656d

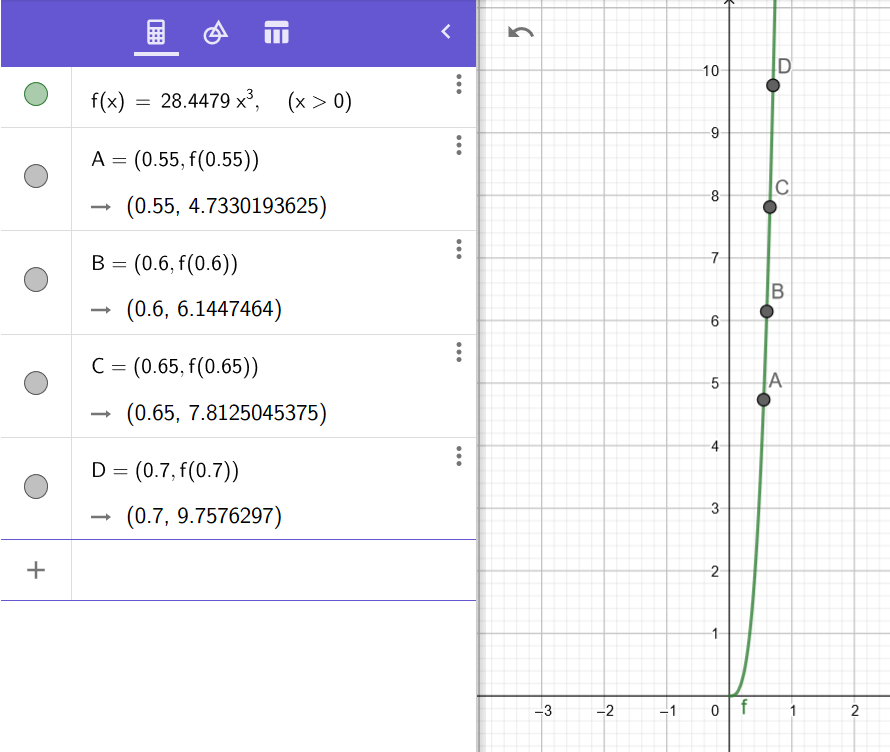
Piirrä kuvaaja, josta ilmenevät syntymämitat ja a-kohdassa lasketut tiedot.

Ratkaisu

1. Luvut ja laskutoimitukset: tehtäviä

1.1 Lukualueet: tehtäviä

1.1.1 Tehtävä

1.1.2 Tehtävä

1.1.3 Tehtävä

1.2 Laskulait: tehtäviä

1.2.1 Tehtävä

1.2.2 Tehtävä

1.2.3 Tehtävä

1.2.4 Tehtävä

Tehtävän otsikko

1.2.5 Tehtävä

Tehtävän otsikko

1.2.6 Tehtävä

Tehtävän otsikko

1.2.7 Tehtävä

1.2.8 Tehtävä

1.3 Itseisarvo: tehtäviä

1.3.1 Tehtävä

1.3.2 Tehtävä

1.3.3 Tehtävä

1.3.4 Tehtävä

1.3.5 Tehtävä

1.3.6 Tehtävä

1.4 Murtoluvut: tehtäviä

1.4.1 Tehtävä

1.4.2 Tehtävä

1.4.3 Tehtävä

1.4.4 Tehtävä

1.4.5 Tehtävä

1.4.6 Tehtävä

Tehtävän otsikko

1.4.7 Tehtävä

Tehtävän otsikko

1.4.8 Tehtävä

1.4.9 Tehtävä

1.4.10 Tehtävä

1.4.11 Tehtävä

1.4.12 Tehtävä

1.4.13 Tehtävä

1.4.14 Tehtävä

1.4.15 *Tehtävä

2. Yhtälö: tehtäviä

2.1 Peruskäsitteitä: tehtäviä

2.1.1 Tehtävä

2.1.2 Tehtävä

2.1.3 Tehtävä

2.2 Ensimmäisen asteen yhtälö: tehtäviä

2.2.1 Tehtävä

2.2.2 Tehtävä

2.2.3 Tehtävä

2.2.4 Tehtävä (s2017/2a)

2.2.5 Tehtävä

2.2.6 Tehtävä

2.2.7 Tehtävä

2.2.8 Tehtävä

2.2.9 Tehtävä

2.2.10 Tehtävä

2.3 Yhtälö sovelluksissa: tehtäviä

2.3.1 Tehtävä

2.3.2 Tehtävä

2.3.3 Tehtävä

2.3.4 Tehtävä

2.3.5 Tehtävä

2.3.6 Tehtävä

2.3.7 Tehtävä

2.4 Yhtälöpari: tehtäviä

2.4.1 Tehtävä

Abitti-editori

2.4.2 Tehtävä

Abitti-editori

2.4.3 Tehtävä

2.4.4 Tehtävä

2.4.5 Tehtävä

2.4.6 Tehtävä

2.4.7 Tehtävä

2.4.8 Tehtävä

2.4.9 *Tehtävä

2.4.10 *Tehtävä

3. Verrannollisuus ja prosenttilaskenta: tehtäviä