1. Luvut ja laskutoimitukset

Ensimmäisessä kappaleessa käsitellään lukuja sekä niillä tehtäviä laskutoimituksia. Käymme läpi lukualueet sekä palautamme mieleen yläkoulusta tutut merkkisäännöt ja laskulait. Lisäksi kerrataan murtoluvuilla tehtävät laskutoimitukset. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

1.1 Lukualueet

Matematiikassa luvut muodostavat perustan laskutoimituksille. Nykyinen lukukäsite on pitkällisen, vuosituhansia kestäneen kehityksen tulosta, eikä pystytä sanomaan, onko tämä kehitys jo päättynyt.

Jo ensimmäisellä peruskoulun vuosiluokalla opimme lukumäärää ilmaisevat luonnolliset luvut. Miksi näitä on sitten lähdetty laajentamaan kohti reaalilukuja? Esimerkiksi Rene Descartesin (1596-1650) oli vaikea hyväksyä lukualueen laajennusta luonnollisista luvuista kokonaisluvuiksi ja hän kutsuikin negatiivisia lukuja "vääriksi luvuiksi". Yksi lähestymistapa lukulaajennuksille on yhtälöopillinen: Millainen yhtälö on ratkeamaton kyseisellä lukualueella, jota haluamme laajentaa? Esimerkiksi luonnollisten lukujen tapauksessa yhtälö x+1=0 on ratkeamaton, sillä x=-1 ei kuulu luonnollisiin lukuihin. Lisäämällä negatiiviset luvut $\mathbb{Z^-}=\{...,-3,-2,-1\}$ luonnollisten lukujen joukkoon saamme muun muassa edellä mainitun yhtälön ratkeavaksi.

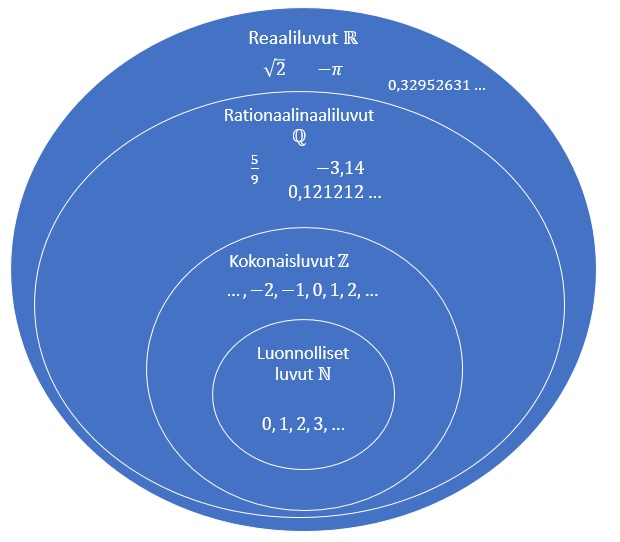
Lukualueen laajentaminen on näin edennyt luonnollisista luvuista aina reaalilukuihin asti. Uudet käyttöön otetut luvut on liitetty entisiin, jolloin uusi lukujoukko sisältää aikaisemmat lukujoukot.

Lukualueet

Luonnolliset luvut $\mathbb{N}=\{0,1,2,3,...\}$
Kokonaisluvut $\mathbb{Z}=\{...,-3,-2,-1,0,1,2,3,...\}$
Rationaaliluvut $\mathbb{Q}=\{\dfrac{m}{n}|m,n\in\mathbb{Z}, n\neq0\}$
Reaaliluvut $\mathbb{R}$ on rationaalilukujen lukulaajennus, joka saadaan lisäämällä irrationaalilukujen joukko rationaalilukuihin. Irrationaaliluvut ovat lukuja, joita ei voida esittää kahden kokonaisluvun osamääränä esim. $\sqrt{5}$ , $\pi$ ja jaksoton desimaaliluku . Käytännössä katsoen reaalilukuja ovat siis kaikki ne luvut, joita on peruskoulun matematiikassa käytetty.

1.1.1 Esimerkki: lukualueet

Mihin lukujoukkoihin luku kuuluu?

$\displaystyle\frac{3}{7}$

Ratkaisu:

Luonnollisiin lukuihin. Lisäksi, kokonais-, rationaali- sekä reaalilukuihin, koska nämä lukujoukot pitävät sisällään myös luonnolliset luvut.
Kokonaislukuihin. Lisäksi, rationaali- ja reaalilukuihin.
Rationaali- ja reaalilukuihin.
Rationaali- ja reaalilukuihin, sillä luku voidaan esittää murtolukuna $\displaystyle\frac{3}{5}$ .
Ainoastaan reaalilukuihin. Kyseessä on päättymätön ja jaksoton desimaaliluku, jonka vuoksi sitä ei voida esittää kahden kokonaisluvun osamääränä. Tämän vuoksi luku ei kuulu rationaalilukuihin, jolloin se ei myöskään kuulu kokonaislukuihin tai luonnollisiin lukuihin.

Lukualueet: tehtäviä

1.2 Laskulait

Palautetaan mieleen tutut merkkisäännöt ja laskulait. Kerto- ja jakolaskussa kahden samanmerkkisen luvun laskutoimitus on positiivinen ja kahden erimerkkisen negatiivinen. Tämän seurauksena kerto- ja jakolaskun tulos on positiviinen, kun negatiivisten tekijöiden lukumäärä on parillinen. Vastaavasti kerto- ja jakolaskun tulos on negatiivinen, kun negatiivisia tekijöitä on pariton määrä.

Merkkisäännöt

$a\cdot(-b)=-ab$ ja $\displaystyle\frac{a}{-b}=-\frac{a}{b}$
$(-a)\cdot(-b)=a\cdot b$ ja $\displaystyle\frac{-a}{-b}=\frac{a}{b}$

1.2.1 Esimerkki: merkkisäännöt

Laske.

$4\cdot(-2)$
$\displaystyle\frac{-3}{-6}$

Ratkaisu:

$4\cdot(-2)=-4\cdot2=-8$
$\displaystyle\frac{-3}{-6}=\displaystyle\frac{3}{6}=\frac{1}{2}$

Laskujärjestys noudattaa tuttua kaavaa.

Laskujärjestys

Lasketaan sulut
Lasketaan kerto- ja jakolaskut
Lasketaan yhteen- ja vähennyslaskut

1.2.2 Esimerkki: laskujärjestys

Laske.

$-2\cdot(-3)\cdot2$
$-4\cdot(-5)\cdot(-2)\cdot(-1)$
$5\cdot(-1)\cdot(-6):(-10)$
$3\cdot(2-8:2)\cdot(-2)+11$

Ratkaisu:

$\begin{align*} &-2\cdot(-3)\cdot2 && |\;\text{poistetaan sulut}\\ &=2\cdot3\cdot2 && |\;\text{lasketaan kertolaskut}\\ &=6\cdot2 \\ &=12 \end{align*}$

$\begin{align*} &-4\cdot(-5)\cdot(-2)\cdot(-1) && |\;\text{poistetaan ensimmäiset sulut}\\ &=4\cdot5\cdot(-2)\cdot(-1) && |\;\text{poistetaan toiset sulut}\\ &=4\cdot5\cdot2\cdot1 && |\;\text{lasketaan kertolaskut}\\ &=40 \end{align*}$

$\begin{align*} &5\cdot(-1)\cdot(-6):(-10) && |\;\text{poistetaan sulut}\\ &=-5\cdot1\cdot6:10 && |\;\text{lasketaan kertolaskut}\\ &=-30:10 && |\;\text{lasketaan jakolasku}\\ &=-3 \end{align*}$

$\begin{align*} &3\cdot(2-8:2)\cdot(-2)+11 && |\;\text{lasketaan jakolasku sulkujen sisältä}\\ &=3\cdot(2-4)\cdot(-2)+11 && |\;\text{lasketaan vähennyslasku sulkujen sisältä}\\ &=3\cdot(-2)\cdot(-2)+11 && |\;\text{poistetaan sulut}\\ &=3\cdot4+11 && |\;\text{lasketaan kertolasku}\\ &=12+11 && |\;\text{lasketaan yhteenlasku}\\ &=23 \end{align*}$

Oheiselta videolta löytyy tarvittaessa lisää esimerkkejä laskujärjestyksestä sekä negatiivisilla luvuilla laskemisesta.

Peruslaskutoimituksista yhteenlasku ja kertolasku noudattavat seuraavia laskulakeja.

Laskulait

Olkoon $a,b,c\in\mathbb{R}$ . Tällöin ovat voimassa seuraavat laskulait:

$\begin{equation*} \left.\begin{aligned} a + b &= b + a\\ ab &= ba \end{aligned}\right\} \text{vaihdantalait} \end{equation*}$

$\begin{equation*} \left.\begin{aligned} a + (b + c) &= (a + b) + c\\ a(bc) &= (ab)c \end{aligned}\right\} \text{liitäntälait} \end{equation*}$

$\begin{equation*} \left.\begin{aligned} a(b + c) = a b + ac\\ (a+b)c = ac + b c \end{aligned}\right\} \text{osittelulait} \end{equation*}$

Vaihdanta- ja liitäntälakien takia luvut voidaan laskea yhteen tai kertoa missä järjestyksessä tahansa. Sulkumerkit voidaan siis jättää pois ja merkitä vain a+b+c ja abc . Sopivalla ryhmittelyllä laskutehtävä saadaan usein yksinkertaistettua.

1.2.3 Esimerkki: laskulait

Laske käyttäen hyväksi laskulakeja.

$2\cdot8\cdot50$
$7\cdot46$

Ratkaisu:

Kertolasku voidaan laskea missä järjestyksessä tahansa, joten vaihdetaan lukujen ja paikkaa.

$2\cdot8\cdot50=2\cdot50\cdot8=100\cdot8=800$

Kirjoitetaan luku muodossa ja käytetään hyväksi osittelulakia.

$7\cdot46=7\cdot(40+6)=7\cdot40+7\cdot6=280+42=322$

Vastaluku ja käänteisluku

Kahta lukua, joiden summa on nolla, sanotaan toistensa vastaluvuiksi. Luvun vastaluku on -a, koska a+(-a)=0 . Jokaisella reaaliluvulla on vastaluku.

Kahta lukua, joiden tulo on yksi, sanotaan toistensa käänteisluvuiksi. Luvun käänteisluku on $\displaystyle\frac{1}{a},$ koska $a\cdot\displaystyle\frac{1}{a}=1$ . Kaikilla muilla reaaliluvuilla paitsi nollalla on käänteisluku.

1.2.4 Esimerkki: vasta- ja käänteisluku

Mikä on luvun vastaluku?
Mikä on luvun vastaluku?
Mikä on luvun käänteisluku?
Mikä on luvun käänteisluku?
Mikä on luvun vastaluvun käänteisluku?

Ratkaisu:

Luvun vastaluku on sillä

Luvun vastaluku on sillä

Luvun käänteisluku on $\displaystyle\frac{1}{2},$ sillä $2\cdot \displaystyle\frac{1}{2}=1.$

Luvun käänteisluku on $-\displaystyle\frac{1}{4},$ sillä $-4\cdot (-\displaystyle\frac{1}{4})=4\cdot \displaystyle\frac{1}{4}=\frac{4}{4}=1.$

Luvun vastaluku on sillä
Luvun käänteisluku on $-\displaystyle\frac{1}{11},$ sillä $-11\cdot (-\displaystyle\frac{1}{11})=11\cdot \frac{1}{11}=\frac{11}{11}=1.$
Siispä, luvun vastaluvun käänteisluku on $-\displaystyle\frac{1}{11}.$

Laskulait: tehtäviä

1.3 Itseisarvo

Reaaliluvun itseisarvo määritellään paloittain, erikseen ei-negatiivisille ja negatiivisille luvuille.

Itseisarvo

Reaaliluvun itseisarvo on

$|a|= \begin{cases} a,\;\;\;\;\;\ \text{kun}\;\;a\ge0 \\ -a,\;\;\;\; \text{kun}\;\;a<0 \end{cases}$

Positiivisen luvun ja nollan itseisarvo on siis luku itse. Esimerkiksi |2|=2 ja |0|=0.

Negatiivisen luvun itseisarvo on sen vastaluku. Esimerkiksi |-2|=-(-2)=2.

Geometrisesti tulkittuna itseisarvo kertoo sen etäisyyden lukusuoralla luvusta . Tätä on havainnollistettu oheisella appletilla. Liikuttamalla sinistä pistettä näet, kuinka mustalla palkilla kuvattu itseisarvo muuttuu. Koska kyseessä on etäisyys, niin $|a|\geq 0$ kaikilla :n arvoilla.

1.3.1 Esimerkki: luvun itseisarvo

Luvun itseisarvo koska

Luvun $\pi-2$ itseisarvo $|\pi-2|=\pi-2,$ koska $\pi-2>0.$

Luvun $1-\sqrt{2}$ itseisarvo $|1-\sqrt{2}|=-(1-\sqrt{2})=\sqrt{2}-1,$ koska $1-\sqrt{2}\approx-0,41<0.$

Itseisarvolle pätee seuraavat ominaisuudet.

Itseisarvon ominaisuuksia

$|a|\ge0$
$\Big|\displaystyle\frac{a}{b}\Big|=\frac{|a|}{|b|}$

1.3.2 Esimerkki: itseisarvolausekkeiden sieventämistä

Sievennä.

Ratkaisu:

$\begin{align*} &|4+(-5)|+(|4|+|-5|) &&|\;\text{lasketaan itseisarvot sulkujen sisältä} \\ &=\;|4-5|-(4+5) &&|\;\text{lasketaan vähennyslasku itseisarvon sisältä}\\ &=\;|-1|-9 \\ &=\;1-9\\&=\;-8 \end{align*}$

$\begin{align*} &|a-b|-|b-a| &&|b-a=-(a-b)\\ &=\;|a-b|-|-(a-b)| &&|\text{käytetään hyväksi itseisarvon 2. ominaisuutta} \\ &=\;|a-b|-|a-b| \\ &=\;0 \end{align*}$

Itseisarvo: tehtäviä

1.4 Murtoluvut

Kerrataan murtolukuihin liittyvät nimitykset ja laskutoimitukset.

Murtoluku on kahden kokonaisluvun osamäärä $\displaystyle\frac{m}{n}$ , missä jaettavaa (m) sanotaan osoittajaksi ja jakajaa (n) nimittäjäksi, ja osoittaja ei ole jaollinen jakajalla. Murtoluku on siis rationaaliluku, joka ei supistu kokonaisluvuksi.

Sekaluvut ovat murtoluvun vaihtoehtoinen esittämistapa. Jotta murtoluku voidaan esittää sekalukuna, nimittäjän tulee olla suurempi kuin osoittaja. Esimerkiksi murtoluku $\displaystyle\frac{7}{4}=\frac{4+3}{4}=\frac{4}{4}+\frac{3}{4}=1+\frac{3}{4}$ voidaan esittää sekalukuna $1\displaystyle\frac{3}{4}$ .

1.4.1 Esimerkki: murtolukujen suuruusjärjestys

Järjestä murtoluvut $\displaystyle\frac{3}{4}$ , $\displaystyle\frac{7}{8}$ ja $\displaystyle\frac{1}{2}$ suuruusjärjestykseen.

Ratkaisu:

Lavennetaan murtoluvut ensin samannimisiksi, jotta suuruusvertailu on helpompi tehdä.

$^{2)}\displaystyle\frac{3}{4}=\frac{2\cdot 3}{2\cdot 4}=\frac{6}{8}$

$^{4)}\displaystyle\frac{1}{2}=\frac{4\cdot 1}{4\cdot 2}=\frac{4}{8}$

Nyt $\displaystyle\frac{7}{8}>\frac{6}{8}>\frac{4}{8},\;$ joten $\;\displaystyle\frac{7}{8}>\frac{3}{4}>\frac{1}{2}.$

1.4.2 Esimerkki: sekaluvut

Muunna

$\displaystyle\frac{9}{2}$ sekaluvuksi.
$3\,\displaystyle\frac{4}{5}$ murtoluvuksi.

Ratkaisu:

Esitetään osoittaja nimittäjän tulona, jolloin jakojäännökseksi jää , ja sievennetään sekaluvuksi.

$\displaystyle\frac{9}{2}=\frac{4\cdot2 +1}{2}=\frac{4\cdot \cancel{2}}{\cancel{2}}+\frac{1}{2}=4+\frac{1}{2}=4\,\frac{1}{2}$

Lavennetaan kokonaisluku murtoluvuksi ja lasketaan murtoluvut yhteen.

$3\,\displaystyle\frac{4}{5}=3+\frac{4}{5}=^{5)}\!\frac{3}{1}+\frac{4}{5}=\frac{15}{5}+\frac{4}{5}=\frac{19}{5}$

Murtolukujen yhteen- ja vähennyslasku

$^{d)}\displaystyle\frac{a}{b}+\,^{b)\!}\frac{c}{d}=\frac{ad}{bd}+\frac{bc}{bd}=\frac{ad+bc}{bd}$

$^{d)}\displaystyle\frac{a}{b}-\,^{b)\!}\frac{c}{d}=\frac{ad}{bd}-\frac{bc}{bd}=\frac{ad-bc}{bd}$

1.4.3 Esimerkki: yhteen- ja vähennyslasku murtoluvuilla

Laske.

$\displaystyle\frac{1}{2} + \frac{3}{4}\;\;\;\;$ b. $\displaystyle\frac{9}{10} - \frac{7}{8}$

Ratkaisu:

$\begin{align*} &^{4)} \displaystyle\frac{1}{2} +\,^{2)}\frac{3}{4} &&|\;\text{lavennetaan murtoluvut samannimisiksi}\\ &=\frac{4\cdot 1}{4\cdot 2} + \frac{2\cdot 3}{2\cdot 4} \\ &=\frac{4}{8} + \frac{6}{8} &&|\;\text{lasketaan osoittajat yhteen, nimittäjä pysyy samana}\\ &=\frac{4+6}{8} \\ &=\displaystyle\frac{10}{8} ^{(2}=\frac{5}{4} &&|\;\text{sievennetään vastaus} \end{align*}$

$\begin{align*} &^{8)}\displaystyle\frac{9}{10} - \,^{10)} \frac{7}{8} &&|\;\text{lavennetaan murtoluvut samannimisiksi}\\ &=\frac{8\cdot 9}{8\cdot 10} - \frac{10\cdot7}{10\cdot8} \\ &=\frac{72}{80} - \frac{70}{80} &&|\;\text{vähennetään osoittajat toisistaan, nimittäjä pysyy samana}\\ &=\frac{72-70}{80} \\ &=\frac{2}{80}^{(2}=\frac{1}{40} &&|\;\text{sievennetään vastaus} \end{align*}$

Murtolukujen kertolasku

$\displaystyle\frac{a}{b}\cdot\frac{c}{d}=\frac{ac}{bd}$

1.4.4 Esimerkki: kertolasku murtoluvuilla

Laske.

$\displaystyle\frac{2}{3} \cdot \frac{5}{3}$
$-\displaystyle\frac{3}{4} \cdot \frac{5}{7}$
$5\cdot \displaystyle\frac{1}{3}$

Ratkaisu:

Kerrotaan osoittajat ja nimittäjät keskenään.

$\displaystyle\frac{2}{3} \cdot \frac{5}{3}=\frac{2\cdot5}{3\cdot3}=\frac{10}{9}$

Kerrotaan osoittajat ja nimittäjät keskenään. Kertolaskussa on pariton määrä negatiivisia tulontekijöitä, joten tulos on negatiivinen.

$-\displaystyle\frac{3}{4} \cdot \frac{5}{7}=-\frac{3\cdot5}{4\cdot7}=-\frac{15}{28}$

Muutetaan kokonaisluku murtoluvuksi ja kerrotaan osoittajat ja nimittäjät keskenään.

$5\cdot \displaystyle\frac{1}{3}=\frac{5}{1} \cdot \frac{1}{3}=\frac{5\cdot1}{1\cdot3}=\frac{5}{3}$

Murtolukujen jakolasku

$\displaystyle\frac{a}{b}:\frac{c}{d}=\displaystyle\frac{a}{b}\cdot\frac{d}{c}=\frac{ad}{bc}$

1.4.5 Esimerkki: jakolasku murtoluvuilla

Laske.

$\displaystyle\frac{2}{5} : \frac{1}{2}$
$\displaystyle\frac{3}{7} : \left(-\frac{2}{3}\right)$
$\displaystyle\frac{1}{3} : 11$

Ratkaisu:

Kerrotaan jaettava jakajan käänteisluvulla.

$\displaystyle\frac{2}{5} : \frac{1}{2}=\frac{2}{5} \cdot \frac{2}{1}=\frac{2\cdot2}{5\cdot1}=\frac{4}{5}$

Kerrotaan jaettava jakajan käänteisluvulla. Kertolaskussa on pariton määrä negatiivisia tulontekijöitä, joten tulos on negatiivinen.

$\displaystyle\frac{3}{7} : \left(-\frac{2}{3}\right)=\frac{3}{7} \cdot \left(-\frac{3}{2}\right)=-\frac{3\cdot3}{7\cdot2}=-\frac{9}{14}$

Muutetaan jakaja murtoluvuksi ja kerrotaan jaettava jakajan käänteisluvulla.

$\displaystyle\frac{1}{3} : 11=\frac{1}{3} : \frac{11}{1}=\frac{1}{3} \cdot \frac{1}{11}=\frac{1\cdot1}{3\cdot11}=\frac{1}{33}$

1.4.6 Esimerkki: pizzan jakaminen

Ystävykset Aada, Hilda, Iida ja Ville päättivät mennä syömään pizzeriaan. He tilasivat pepperoni- sekä vegepizzan, jotka he jakoivat seuraavasti:

Ville sanoi herrasmiehenä, että hän voi syödä jäljelle jäävät osuudet pizzoista viimeisenä. Aada leikkasi ensimmäisenä itselleen $\displaystyle\frac{1}{4}$ pepperonipizzaa ja $\displaystyle\frac{1}{8}$ vegepizzaa. Hilda leikkasi toisena jäljellä olevista pepperonipizzasta $\displaystyle\frac{4}{5}$ ja vegepizzasta $\displaystyle\frac{1}{4}$ . Iida leikkasi kolmentena jäljellä olevasta vegepizzasta puolet. Paljonko Villelle jäi pizzaa?

Ratkaisu:

Kun Aada leikkasi pepperonipizzaa, niin jäljelle jäi $^{4)}1-\displaystyle\frac{1}{4}=\frac{4}{4}-\frac{1}{4}=\frac{3}{4}$ .

Kun Aada leikkasi vegepizzaa, niin jäljelle jäi $^{8)}1-\displaystyle\frac{1}{8}=\frac{8}{8}-\frac{1}{8}=\frac{7}{8}$ .

Kun Hilda leikkasi pepperonipizzaa, niin jäljelle jäi $(1-\displaystyle\frac{4}{5})\cdot\frac{3}{4}=\frac{1}{5}\cdot\frac{3}{4}=\frac{3}{20}$ .

Kun Hilda leikkasi vegepizzaa, niin jäljelle jäi $(1-\displaystyle\frac{1}{4})\cdot\frac{7}{8}=\frac{3}{4}\cdot\frac{7}{8}=\frac{21}{32}$ .

Kun Iida leikkasi vegepizzaa, niin jäljelle jäi $(1-\displaystyle\frac{1}{2})\cdot\frac{21}{32}=\frac{1}{2}\cdot\frac{21}{32}=\frac{21}{64}$ .

Vastaus:

Villelle jäi siis $\displaystyle\frac{3}{20}$ pepperonipizzaa ja $\displaystyle\frac{21}{64}$ vegepizzaa.

Murtoluvut on tapana sieventää muotoon, jossa osoittajana ja nimittäjänä on mahdollisimman pienet kokonaisluvut. Tämän voi allekirjoittaneen mielestä tehdä helpoiten niin, että jakaa ensin osoittajan sekä nimittäjän alkutekijöihin, jonka jälkeen supistaa yhteiset tekijät pois.

Luvun jakamisella alkutekijöihinsä tarkoitetaan sen kirjoittamista alkulukujen tulona. Alkuluku on lukua suurempi luonnollinen luku, joka on jaollinen vain ja ainoastaan itsellään ja luvulla .

Esimerkiksi on alkuluku, koska se ei ole jaollinen muilla kokonaisluvuilla kuin ja , mutta $10=5\cdot2$ ei ole alkuluku, sillä se on jaollinen myös luvuilla ja .

1.4.7 Esimerkki: murtolukujen sieventäminen alkulukujen avulla

Sievennä murtoluvut muotoon, missä osoittajana ja nimittäjänä ovat mahdollisimman pienet kokonaisluvut.

$\displaystyle\frac{11}{77}\;\;\;$ b. $\displaystyle\frac{32}{64}\;\;\;$ c. $-\displaystyle\frac{36}{112}$

Ratkaisu:

Luku on alkuluku, mutta luku hajoaa alkutekijöihin seuraavasti $77=11\cdot7.$

Nyt voidaan sieventää: $\displaystyle\frac{11}{77}=\frac{\cancel{11}}{\cancel{11}\cdot 7 }=\frac{1}{7}$

Luku hajoaa alkutekijöihin seuraavasti $32=2^5=2\cdot2\cdot2\cdot2\cdot2$ ja luku seuraavasti $64=2^6=2\cdot2\cdot2\cdot2\cdot2\cdot2.$

Nyt voidaan sieventää: $\displaystyle\frac{32}{64}=\frac{\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}} {2\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}\cdot\cancel{2}}=\frac{1}{2}$

Luku hajoaa alkutekijöihin seuraavasti $33=2\cdot2\cdot3\cdot3$ ja luku 112 seuraavasti $112=2\cdot2\cdot2\cdot2\cdot7.$

Nyt voidaan sieventää: $-\displaystyle\frac{36}{112}=-\frac{\cancel{2}\cdot\cancel{2}\cdot3\cdot3} {\cancel{2}\cdot\cancel{2}\cdot2\cdot2\cdot7}=-\frac{3\cdot3}{2\cdot2\cdot7}=-\frac{9}{28}$

HUOM! Samaan lopputulokseen olisi päästy supistamalla:

$-\displaystyle\frac{36}{112}^{(2}=-\frac{18}{56}^{(2}=-\frac{9}{28}$

Murtoluvut: tehtäviä