5. Funktio

Viimeisessä kappaleessa aiheena on funktio. Kappaleessa perehdytään siihen, mitä funktio tarkoittaa sekä käsitellään funktion kuvaajan piirtämistä ja tulkintaa. Lopuksi käydään läpi esimerkkejä funktion sovelluksista. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

Funktiota tarvitaan tutkittaessa muuttuvien suureiden välistä riippuvuutta. Usein suureen arvo riippuu siitä, mikä toisen suureen arvo on. Esimerkiksi ympyrän pinta-ala riippuu säteestä ja autolla ajettu matka riippuu nopeudesta.

5.1 Funktion määritelmä

# V2

Videossa on kone, joka tuottaa siihen syötetystä nimestä luvun. Sääntönä on, että koneen tuottama luku kertoo nimen pituuden. Tällainen yksikäsitteinen sääntö määrittelee funktion.

Funktio

Funktio on sääntö, joka ilmaisee, miten lähtöarvosta saadaan yksikäsitteisesti loppuarvo. Lähtöarvoa kutsutaan muuttujan arvoksi ja loppuarvoa funktion arvoksi.

Lähtöarvot eli luvut, jotka funktioon voidaan syöttää muodostavat funktion määrittelyjoukon. Loppuarvot eli luvut, jotka funktio tuottaa, muodostavat funktion arvojoukon.

Funktio nimetään tavallisesti kirjaimella , tai . Lähtöarvoa kuvaavana muuttujana käytetään yleensä kirjainta .

Usein funktion sääntö esitetään lausekkeena. Esimerkiksi sääntö "lukuun lisätään 4" voidaan esittää lausekkeena seuraavasti.

f(x)=x+4

Funktion lausekkeen avulla voidaan laskea funktion arvoja. Esimerkiksi "funktion arvo kohdassa 5" lasketaan sijoittamalla luku 5 muuttujan paikalle.

f(5)=5+4=9

5.1.1 Esimerkki: funktion arvon laskeminen

Funktion arvo lasketaan seuraavan säännön avulla:

Funktioon syötettyyn lukuun lisätään luku 8 ja summa jaetaan luvulla 2.

Muodosta funktion lauseke.
Laske funktion arvot ja .

Ratkaisu:

Merkitään funktioon syötettävää lukua eli muuttujaa kirjaimella . Kun muuttujaan lisätään luku 8, saadaan . Kun lauseke jaetaan luvulla 2, saadaan $\displaystyle \frac{x+8}{2}$ .

Funktion lauseke on $f(x)=\displaystyle \frac{x+8}{2}$ .
Funktion arvo kohdassa 5 merkitään ja lasketaan sijoittamalla lausekkeeseen muuttujan paikalle luku 5.

$f(5)=\displaystyle \frac{5+8}{2}=\displaystyle\frac{13}{2}$ .

Vastaavasti funktion arvo kohdassa -2 on

$f(-2)=\displaystyle \frac{-2+8}{2}=\displaystyle \frac{6}{2}=3$ .

5.1.2 Esimerkki: funktion määrittelyjoukko

Päättele funktion määrittelyjoukko.

$f(x)= \displaystyle \frac{3}{x-2}$
$g(x)= \sqrt{4-x}$

Ratkaisu:

Jakolasku $f(x)= \displaystyle \frac{3}{x-2}$ on määritelty vain, kun jakaja ei ole nolla.

Siten funktion määrittelyjoukon muodostavat luvut , jotka toteuttavat ehdon $x\neq2$ .
Neliöjuuri $\sqrt{4-x}$ on määritelty vain, kun luku on on suurempi tai yhtä suuri kuin nolla.

Siten funktion määrittelyjoukon muodostavat luvut , jotka toteuttavat ehdon $x\le4$ .

Funktion määritelmä: tehtäviä

5.2 Funktion nollakohta

Millä muuttujan arvolla funktio saa arvon nolla tai missä pisteessä kuvaaja leikkaa x-akselin? Kyse on samasta asiasta, funktion nollakohdan määrittämisestä.

Huom! "Funktion arvo kohdassa 0" ja "funktion nollakohta" tarkoittavat eri asiaa.

Funktion nollakohta

Niitä määrittelyjoukon lukuja, joilla funktion arvo on nolla, kutsutaan funktion nollakohdiksi. Funktion nollakohdat toteuttavat siis yhtälön f(x)=0 .

5.2.1 Esimerkki: funktion arvo kohdassa nolla ja funktion nollakohdat

Määritä funktion f(x)=5x+9 arvo kohdassa ja funktion nollakohdat.

Ratkaisu:

Funktion arvo kohdassa lasketaan sijoittamalla muuttujan paikalle luku .

$f(0)=5\cdot0+9=9$

Funktion nollakohdat löydetään ratkaisemalla yhtälö f(x)=0 .

$\begin{align*} f(x)=0 \\ 5x+9=0 \\ 5x=-9 \\ x=-\frac{9}{5} \end{align*}$

Funktion nollakohta on siis $x=- \displaystyle \frac{9}{5}$ .

Funktion nollakohta: tehtäviä

5.3 Funktion kuvaaja

# V1

Funktion kuvaaja xy-koordinaatistossa

Funktion kuvaaja muodostuu pisteistä (x, y) , joissa on muuttujan arvo ja funktion arvo kohdassa eli y=f(x) .

5.3.1 Esimerkki: funktion kuvaajan hahmottelu ilman ohjelmistoa

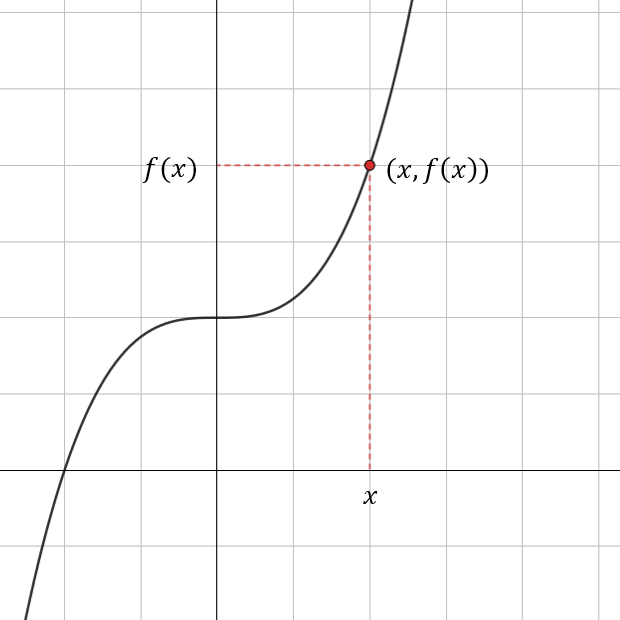
Funktion f(x)=3^x-2 kuvaaja muodostuu koordinaatiston pisteistä (x, y) , joissa on muuttujan arvo ja on funktion arvo kohdassa eli y=3^x-2 .

Taulukoidaan pisteitä, joiden kautta funktion kuvaaja esimerkiksi kulkee.

Alla olevaan koordinaatistoon on piirretty taulukoidut pisteet sekä niiden kautta kulkeva funktion kuvaaja.

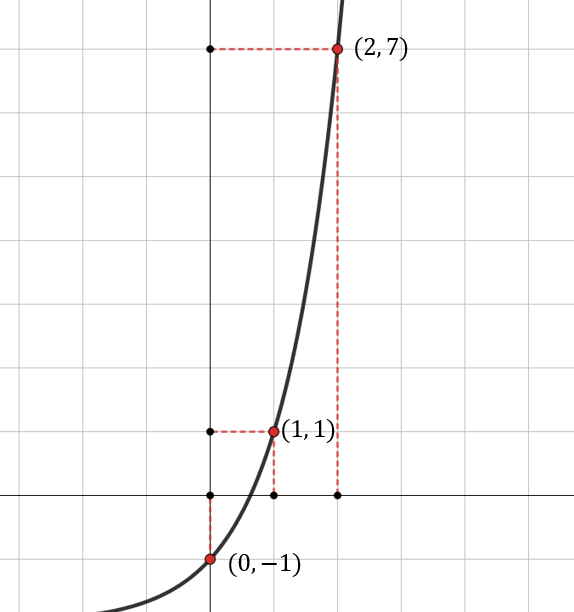
Funktion kuvaaja voidaan hahmotella saatujen pisteiden avulla vain karkeasti. Sopivan ohjelman avulla funktion kuvaaja saadaan piirrettyä täysin tarkasti.

Videolla näytetään kuvaajan piirtäminen TI-Nspire CAS -laskimella.

# V3

5.3.2 Esimerkki: funktion kuvaaja Geogebralla

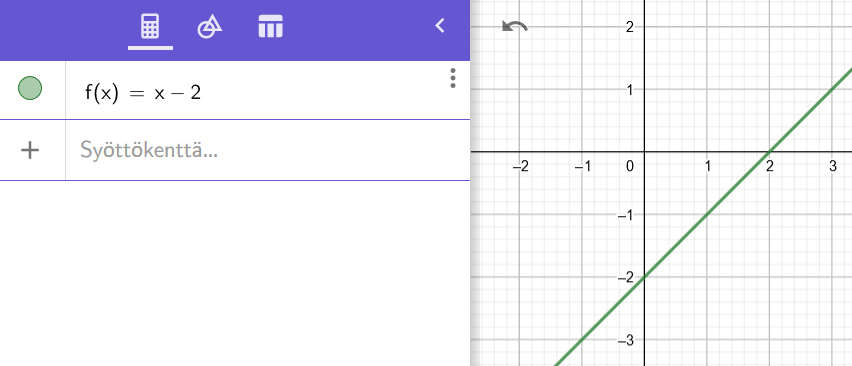
Geogebran piirto-ohjelmalla funktioiden kuvaajien piirto tapahtuu helposti kirjoittamalla haluttu funktio syöttökenttään. Esimerkiksi funktio f(x)=x-2 piirrettäisiin seuraavasti.

Alla olevalla Appletilla voi tutkia, mistä pisteistä funktion f(x)=x-2 kuvaaja koostuu liikuttelemalla keltaista pistettä kuvaajalla.

Huomataan, että funktion f(x)=x-2 kuvaaja muodostuu siis pisteistä (x, x-2) . Kuvaaja kulkee esimerkiksi pisteiden (3,3-2)=(3,1) ja (1,1-2)=(1,-1) kautta.

Funktion nollakohdassa funktio saa arvon nolla eli kuvaaja leikkaa x-akselin. Funktion f(x)=x-2 nollakohta on siten (2,0) .

Funktion kuvaaja: tehtäviä

5.4 Funktion kuvaajan tulkinta

Kuvaajan etuna on, että se havainnollistaa funktiota graafisesti, jolloin siitä on helpompi tehdä tulkintoja. Kuvaajasta nähdään monia funktion ominaisuuksia, kuten merkin vaihtuminen ja arvojen muuttuminen.

5.4.1 Esimerkki: funktion arvojen lukeminen kuvaajasta

Määritä kuvaajan perusteella

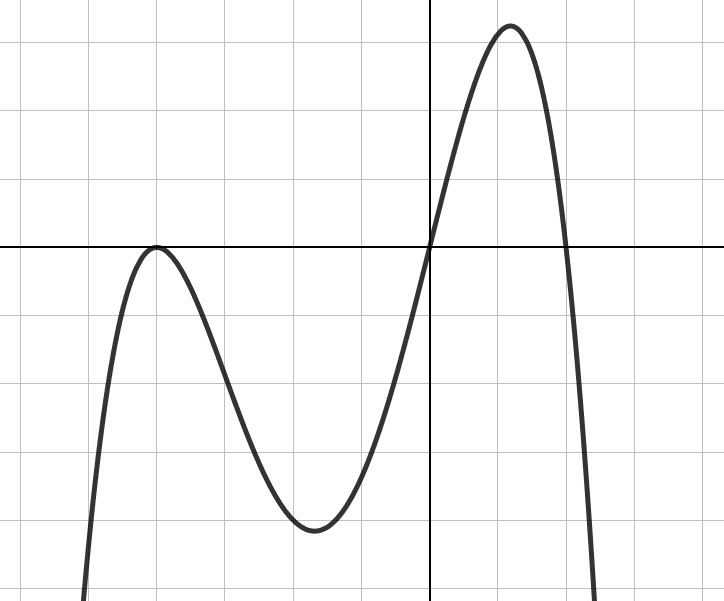
funktion nollakohdat
funktion arvo kohdassa
funktion arvot, joilla funktio saa arvon .

Ratkaisu

Nollakohdassa funktion arvo on nolla eli funktion kuvaaja leikkaa x-akselin. Kuvaajan perusteella funktion nollakohdat ovat $x\approx-4$ , $x\approx 0$ ja $x\approx2$ .

Kohdassa funktio näyttää kulkevan pisteen kautta, eli $f(-2)\approx-4$ .

Funktio saa arvon , kun kuvaajan pisteen y-koordinaatti on . Käyrällä on neljä pistettä, joissa . Tällöin $x\approx-5$ , $x\approx-2$ , $x\approx-1,3$ ja $x\approx2,3$ .

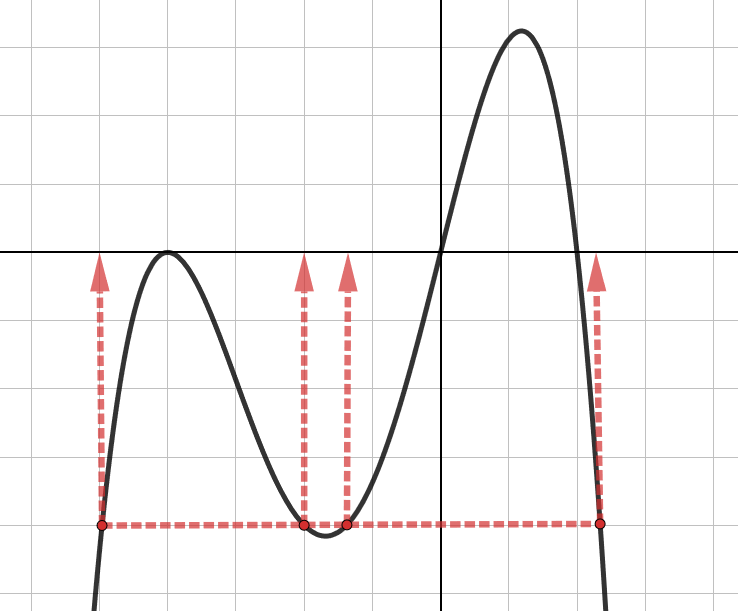
Funktion merkki

Funktion arvo on positiivinen, kun sen kuvaaja on x-akselin yläpuolella. Kuvan funktion arvot ovat siis positiivia, kun x<-2 tai x>2 .

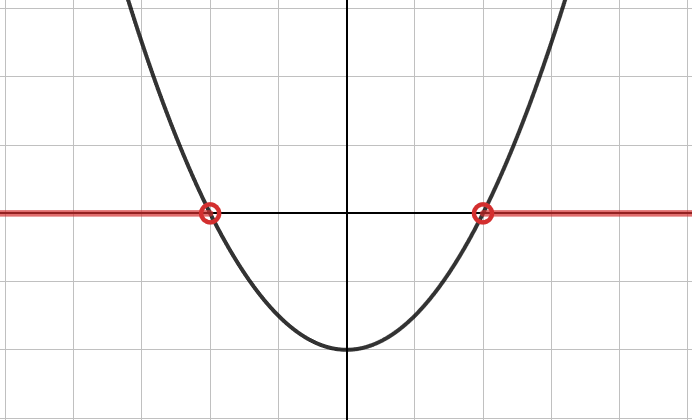
Funktion arvo on negatiivinen, kun sen kuvaaja on x-akselin alapuolella. Kuvan funktion arvot ovat siis negatiivisia, kun -2<x<2 .

5.4.2 Esimerkki: funktion merkin tutkimista Geogebralla

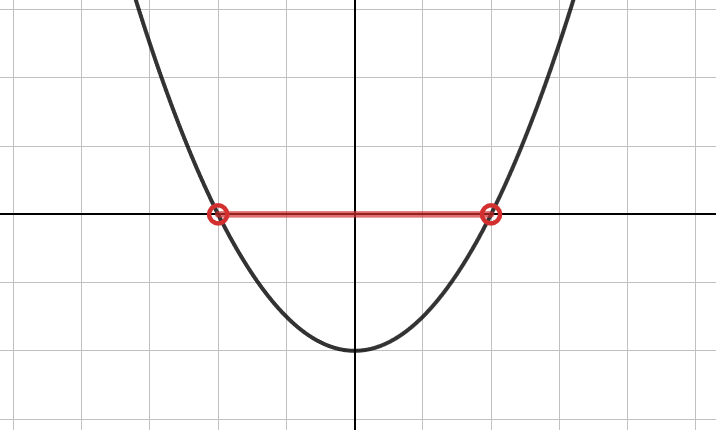
Syötä Applettiin haluamasi funktion lauseke ja tarkastele funktion kulkua. Koordinaatisto muuttuu vihreäksi kohdista, joissa funktion arvo on positiivinen ja punaiseksi kohdissa, joissa funktion arvo on negatiivinen. Funktio vaihtaa merkkinsä nollakohdissa, jotka on myös piirretty kuvaan.

5.4.3 Esimerkki: lämpötilakuvaajan tulkintaa

Kuvassa on esitetty Jyväskylän lentoaseman lämpötilahavainnot kahden vuorokauden ajalta. Tarkastellaan kuvaan merkattua aikaväliä 9.00-9.00 .

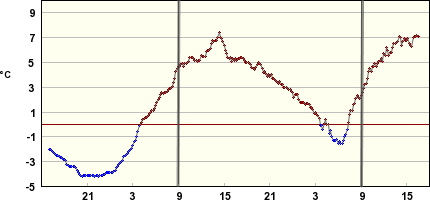
Milloin lämpötila on $4\;^{\circ}\text{C}$ ?
Onko lämpötila plussan vai miinuksen puolella keskiyöllä?
Milloin lämpötila on alle $0\;^{\circ}\text{C}$ ?

Ratkaisu:

Lämpötila saa arvon $4\;^{\circ}\text{C}$ vain kerran kysytyllä aikavälillä: noin kello .
Ajanhetkellä kuvaaja on punaisen viivan yläpuolella eli lämpötila on plussan puolella.
Lämpötila on alle $0\;^{\circ}\text{C}$ , kun kuvaaja on punaisen viivan alapuolella eli noin kellonaikojen ja välillä.

5.4.4 Esimerkki: funktion kuvaajan tulkintaa

Vastaa kuvan funktion kuvaajan perusteella.

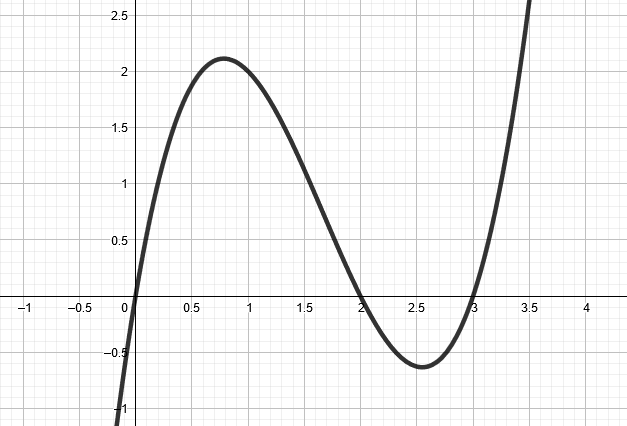
Minkä merkkinen funktion arvo on välillä ? Entä välillä ?
Milloin $f(x)\ge0$ ?

Ratkaisu:

Funktion kuvaaja kulkee välillä x-akselin yläpuolella. Funktion arvo on siis positiivinen, kun .

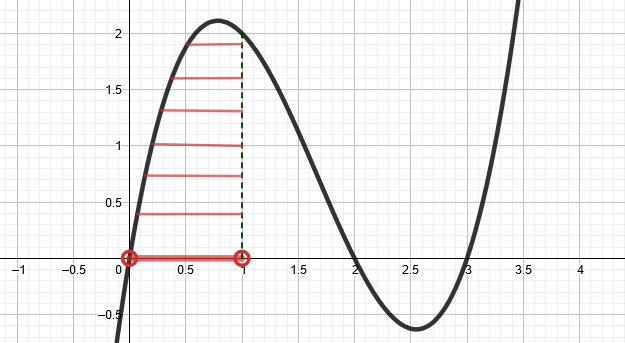
Funktion kuvaaja kulkee välillä 2,5<x<3 x-akselin alapuolella. Funktion arvo on siis negatiivinen, kun 2,5<x<3 .

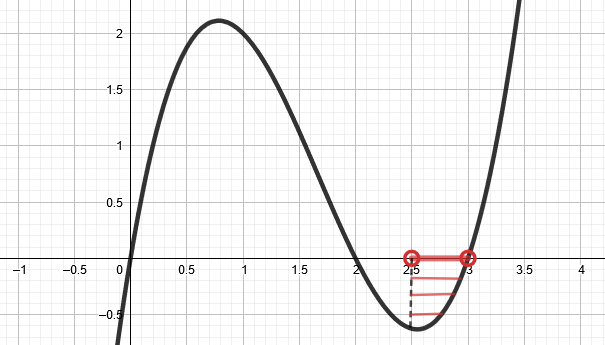
Tarkastellaan, milloin $f(x)\ge0$ eli funktion arvo on suurempi tai yhtä suuri kuin nolla. Funktion arvo on nolla x-akselin leikkauspisteissä ja positiivinen, kun funktion kuvaaja kulkee x-akselin yläpuolella.

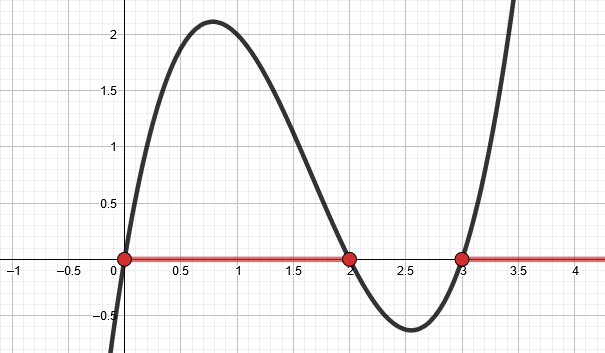
Koska funktion arvo on negatiivinen kahdella eri välillä, annetaan vastaus kahdessa eri osassa.

$f(x)\ge0$ , kun $0\le x \le 2$ tai $x\le 3$ .

Huom! Nollakohdat kuuluvat välille, joten muista yhtäsuuruudet.

Funktion kuvaajan tulkinta: tehtäviä

5.5 Potenssifunktio

Kappaleessa 5 opimme, että muotoa x^n=a olevaa yhtälöä sanotaan potenssiyhtälöksi ja kävimme läpi potenssiyhtälön ratkaisut, kun n=2 tai n=3. Vastaavasti potenssifunktioksi sanotaan funktiota, jonka lauseke on potenssi ja muuttujana potenssin kantaluku.

Potenssifunktio

Potenssifunktio on funktio, joka on muotoa

f(x)=x^n,

missä on kokonaisluku.

Selvitetään seuraavaksi potenssifunktioiden tyypillisiä ominaisuuksia, joihin potenssiyhtälöiden ratkaisujen määrä ja olemassaolo perustuvat. Keskitytään taas tapauksiin, joissa n=2 tai n=3.

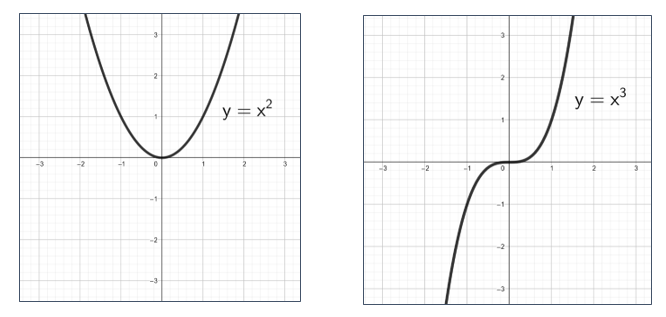
Funktion kuvaaja sijaitsee ensimmäisessä ja toisessa neljänneksessä ja se saa arvoja välillä $[0,\infty[$ .
Funktion kuvaaja sijaitsee ensimmäisessä ja kolmannessa neljänneksessä se saa arvoja koko reaalilukujoukossa $\mathbb{R}$ .
Molempien funktioiden määrittelyjoukko on $\mathbb{R}$ .

5.5.1 Esimerkki: ympyrän pinta-alan funktio

Ympyrän pinta-ala riippuu ympyrän säteestä eli pinta-ala on säteen funktio. Ympyrän pinta-alaa kuvaa funktio

$A(r)=\pi r^2$

Koska säteen arvot ovat positiivisia kokonaislukuja, määrittelyjoukkona ei ole koko reaalilukujoukko vaan positiiviset reaaliluvut. Määrittelyjoukko on siis $\mathbb{R}_+$ .

Piirretään funktion kuvaaja ja luetaan kuvaajalta ympyrän pinta-aloja eri säteen arvoilla.

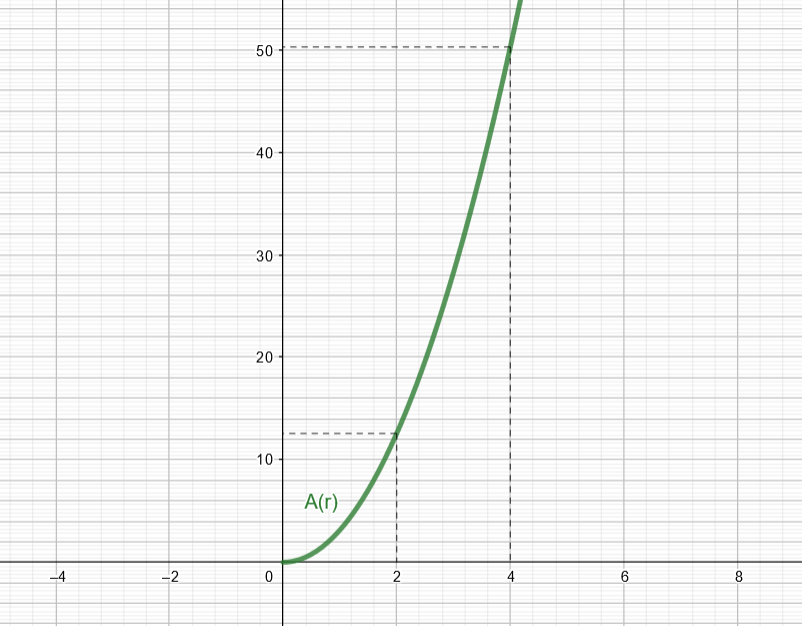
Funktion kuvaaja sijaitsee vain ensimmäisessä neljänneksessä määrittelyehdon vuoksi.

Kuvaajan perusteella voidaan päätellä, että kun ympyrän säde on , sen pinta-ala on 12,5 eli $A(2)\approx12,5$ .

Vastaavasti $A(r)\approx50$ kun r=4 , eli säteen arvolla ympyrän pinta-ala on noin 50.

Potenssifunktio: tehtäviä

5.6 Funktion sovelluksia

5.6.1 Esimerkki: bensatankillisen hinta

98E-bensiinin hinta on $1,638\;\text{€/l}$ . Muodosta tuotteen hintaa kuvaava funktio ja havainnollista hinnan muodostumista koordinaatistossa. Laske tai lue kuvaajasta kuinka paljon maksaa tankillinen bensaa, kun tankin tilavuus on litraa.

Ratkaisu:

Bensiinin hinta riippuu sen tilavuudesta. Merkitään tilavuutta litroina kirjaimella . Bensiinin hintaa kuvaa tällöin funktio g(x)=1,638x , jossa $x\ge0$ . (Hinta voidaan laskea vain silloin, kun bensiinin tilavuus ei ole negatiivinen.)

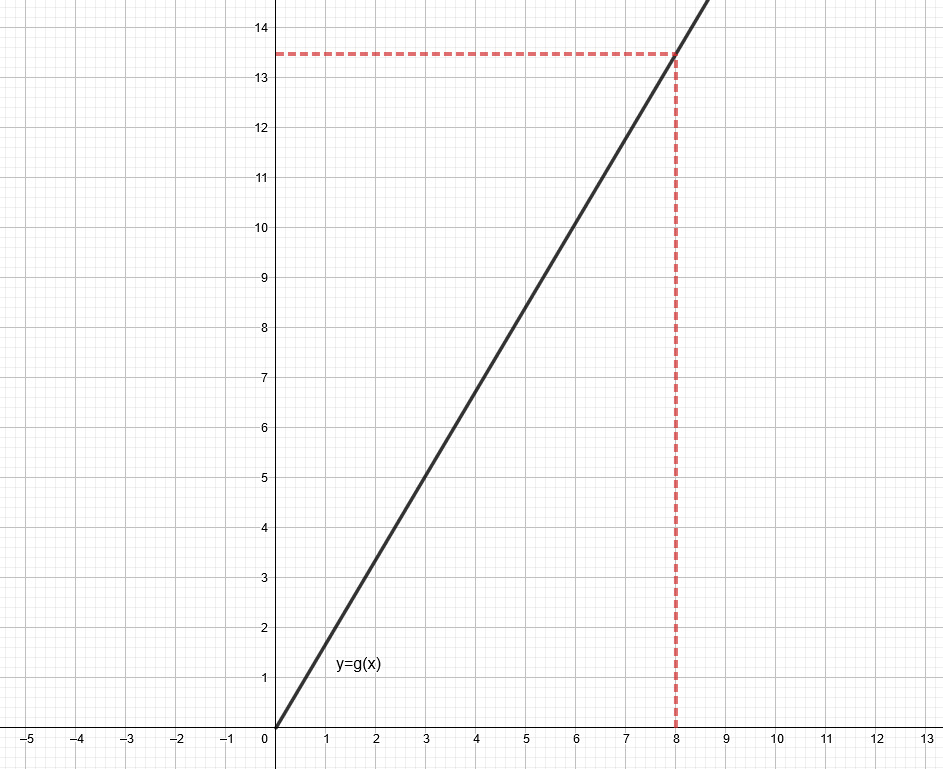
Piirretään funktion kuvaaja Geogebran avulla.

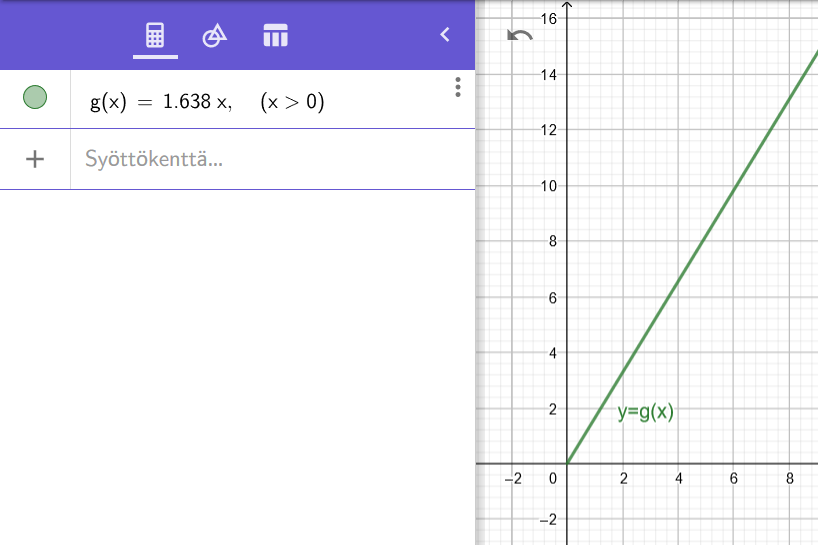
Selvitetään bensatankillisen hinta ensin kuvaajasta lukemalla. Muuttujan arvo on . Funktio saa kohdassa x=8 likimain arvon 13,5, joten bensatankillisen hinta olisi noin $13,5\;\text{€}$ .

Lasketaan bensatankillisen hinta myös funktion lausekkeen avulla. Kysytään siis funktion arvoa g(8) . $g(8)=1,688\cdot8=13,48\;(\text{euroa})$

Vastaus: Bensatankillisen hinta on 13,48 euroa.

5.6.2 Esimerkki: sähkönkulutuksen laskemista

Sähkön vuotuista kokonaiskulutusta gigawattitunteina (GWh) Suomessa vuosina 1970-2014 voidaan kuvata funktiolla f(x)=-1,3x^3+58,8x^2+1349,4x+21583, missä on kulunut aika (vuosina) vuodesta 1970 .

Laske sähkönkulutus vuonna ja vuonna .
Määritä kuvaajan avulla, minä vuonna sähkönkulutus kääntyi laskusuuntaan.

Ratkaisu:

Sähkönkulutus vuonna on funktion arvo kohdassa ja vuonna kohdassa . Lasketaan funktion arvot.

$f(0)=-1,3\cdot0+58,8\cdot0+1349,4\cdot0+21583=21583\approx21600$ $f(30)=-1,3\cdot30+58,8\cdot30+1349,4\cdot30+21583=79885\approx79900$

Vuonna 1970 sähköä kulutettiin noin $21\;600\;\text{GWh}$ ja vuonna 2000 noin $79\;900\;\text{GWh}$ .

Piirretään funktion kuvaaja välillä $0\le x \le44$ . Energiankulutus kääntyy laskuun siinä kohdassa, jossa funktion kuvaajan koordinaatti saa suurimman arvonsa. Geogebralla funktion suurimman arvon saa selville klikkaamalla valikosta Ääriarvot-komentoa ja sen jälkeen halutun funktion kuvaajaa.

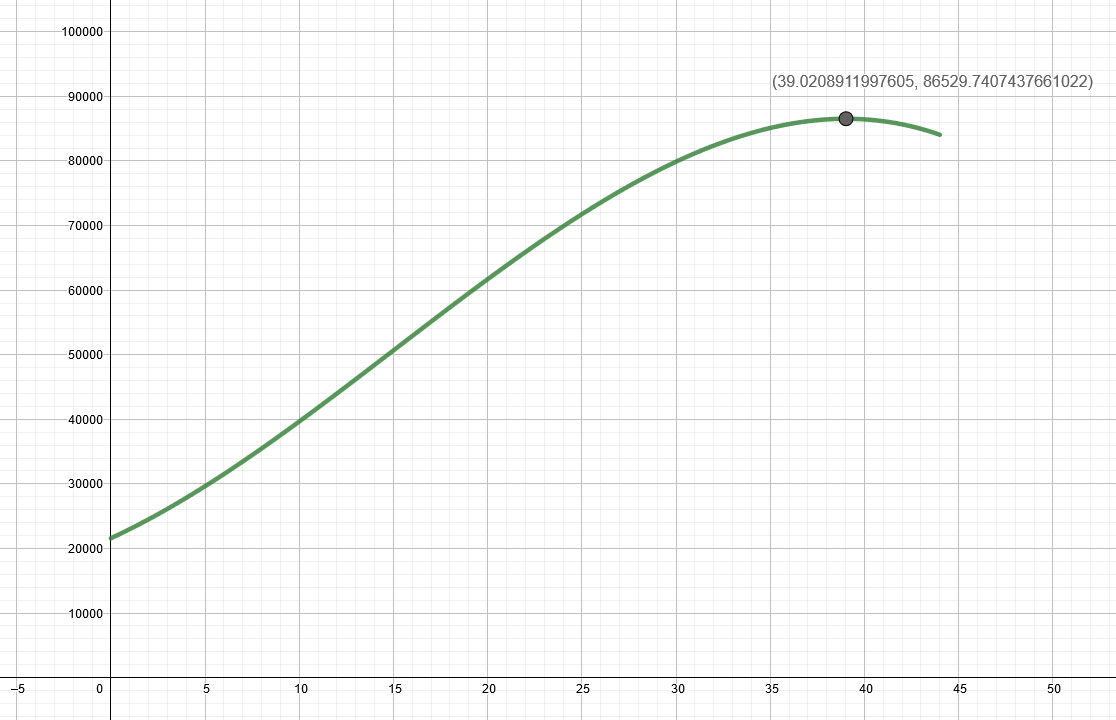
Kuvaajan perusteella funktio saa suurimman arvonsa kohdassa $x\approx39$ . Sähkönkulutus kääntyi laskuun siis vuonna 1970+39=2009 .

Funktion sovelluksia: tehtäviä