1. Geometrian perusteita
Tässä kappaleessa kerrataan tasokuvioiden ja avaruuskappaleiden ominaisuuksia. Kerrataan laskemaan erilaisten kappaleiden pinta-aloja sekä tilavuuksia. Lisäksi kappaleessa käsitellään mittasuhteita ja kuvioiden yhdenmuotoisuutta.
Yksikkömuunnokset liittyät kiinteästi geometriaan. Jos yksikkömuunnokset eivät vielä ole tuttuja, tai kaipaat kertailua, ohessa on Matikkamatskujen video yksikkömuunnoksista.
Harjoitustehtävät tähän kappaleeseen löydät täältä!
1.1 Kulmat
Kulmaan kuuluu kaksi kylkeä sekä kärki. Kulmat voidaan nimetä kolmella eri tavalla:
- Kärkipisteen mukaan
- Kolmen pisteen mukaan siten, että kirjoitetaan ensin oikean kyljen piste, sitten kärkipiste ja lopuksi vasemman kyljen piste
- Aukeaman avulla
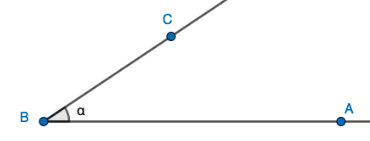Esimerkiksi ylläolevan kulman voi nimetä kolmella eri tavalla: \(\measuredangle B\), \(\measuredangle ABC\) ja \(\alpha\)
Kulmat voidaan luokitella niiden suuruuksien avulla seuraavasti:
| Kulman suuruus | Nimi | Piirros |
|---|---|---|
| \(0°\) | Nollakulma |  |
| \(0°<\alpha<90°\) | Teräväkulma |  |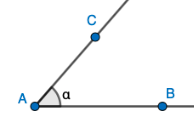
| \(90°\) | Suorakulma |  |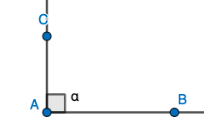
| \(90°<\alpha<180°\) | Tylppäkulma |  |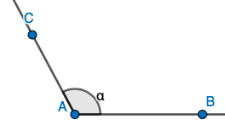
| \(180°\) | Oikokulma |  |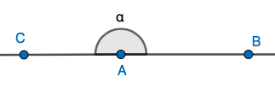
| \(360°\) | Täysikulma |  |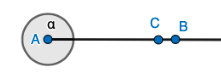
| \(0°<\alpha<180°\) | Kovera kulma |  |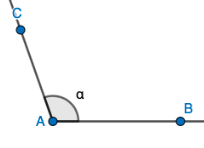
| \(180°<\alpha<360°\) | Kupera kulma |  |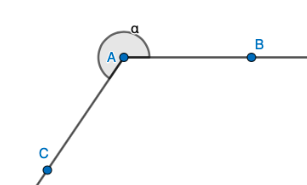
Kahden suoran leikkauksessa muodostuu neljä kulmaa. Näistä kulmista aina kaksi ovat yhtä suurta. Suorien välinen kulma tarkoittaa aina sitä pienempää kulmaa, joka suorien leikkauksessa muodostuu.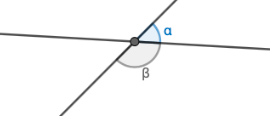 
Yllä olevassa kuvassa, kahden suoran leikkauksessa "suorien välinen kulma" on kulma \(\alpha\). Kulma \(\alpha\) on näistä kahdesta kulmasta terävämpi ja suuruudeltaan pienempi.
Vieruskulmat
Kun suora \(k\) ja \(l\) leikkaavat toisensa, vieruskulmat syntyvät leikkauspisteeseen vierekkäin. Vieruskulmien yhteenlaskettu kulma on \(180°\), eli ne muodostavat oikokulman.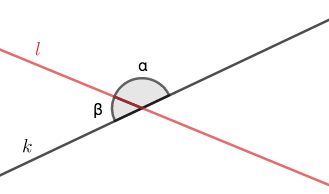 
Ristikulmat
Kun suorat \(k\) ja \(l\) leikkaavat toisensa, ristikulmat syntyvät leikkauspisteen vastakkaisille puolille. Nämä syntyneet ristikulmat ovat toistensa kanssa yhtä suuret.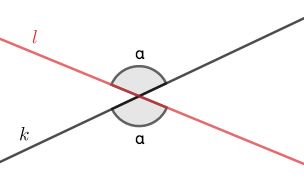 
Samankohtaiset kulmat
Kun yksi suora \(s\) leikkaa kaksi samansuuntaista suoraa \(k\) ja \(l\), leikkauspisteeseen muodostuvat kulmat ovat yhtä suuret.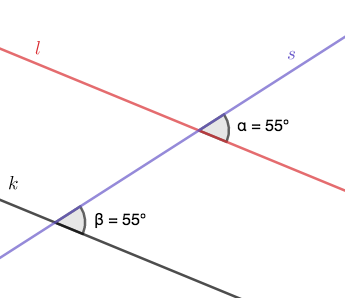 
Laske kulmien \(\alpha\) ja \(\beta\) suuruudet.
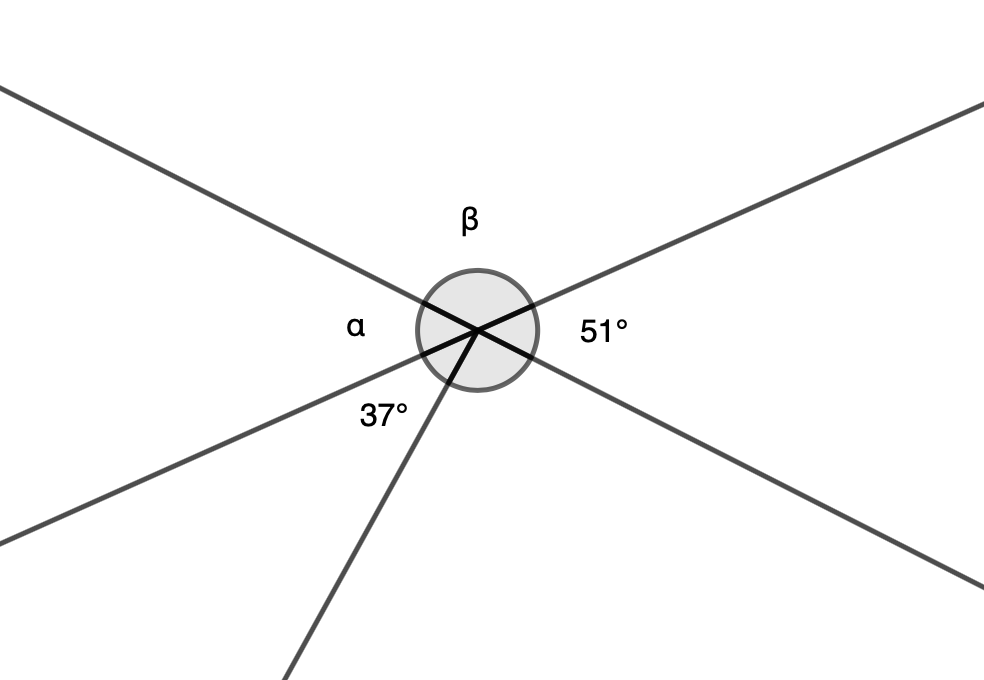
Ratkaisu
Huomataan, että kulma \(\alpha\) on \(51\) asteen kulman ristikulma, eli kulmat ovat yhtäsuuret.
\(\alpha = 51°\)
Kulma \(\beta\) saadaan kulman \(\alpha\) avulla, sillä ne ovat vieruskulmat. Vieruskulmien summa on \(180°\), joten
\[\begin{align} 51°+ \beta &= 180°& \quad &| -51° \\ \beta &= 180° - 51°& \quad &| \text{ suoritetaan vähennyslasku} \\ \beta &= 129 ° \end{align}\]
Suorat \(s\) ja \(t\) ovat yhdensuuntaiset. Laske kulmien \(\alpha\) ja \(\beta\) suuruudet.
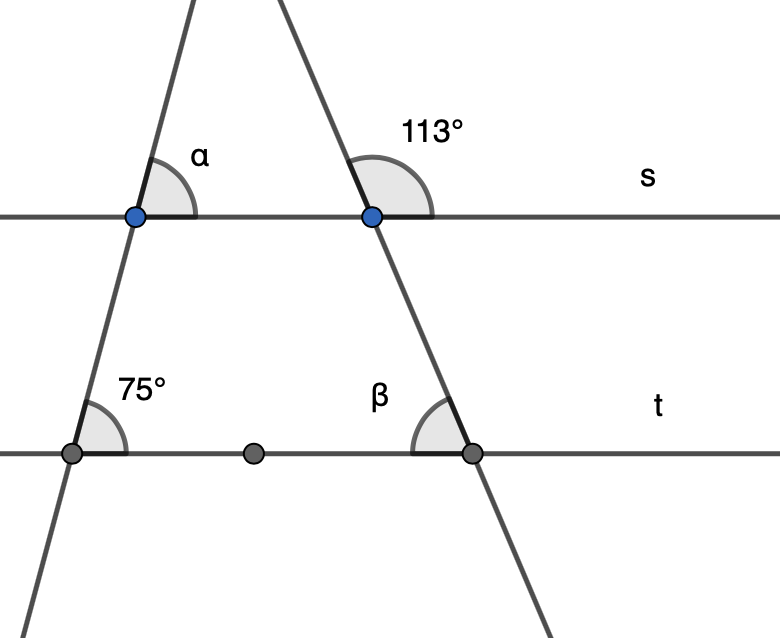
Ratkaisu
Koska suorat \(s\) ja \(t\) ovat yhdensuuntaiset, niin kulma \(\alpha\) ja 75 asteen kulma ovat samankohtaiset, jolloin ne ovat samat. Tällöin
\(\alpha = 75°.\)
Kulman 113° samankohtainen kulma muodostaa kulman \(\beta\) kanssa oikokulman, eli
\[\begin{align} 113° + \beta &= 180°& \quad &| -113° \\ \beta &= 180° - 113°& \quad &| \text{ suoritetaan vähennyslasku} \\ \beta &= 67°. \\ \end{align}\]
1.2 Yhdenmuotoisuus
Kaksi kuviota on yhdenmuotoisia, kun toinen kuvio saadaan siirtämällä, kiertämällä, peilaamalla, suurentamalla tai pienentämällä kuvio. Suurennoksessa kappale näyttää muuten samalta, mutta se on vain suurentunut.
Yhdenmuotoisuus
Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat samat riippumatta siitä, mitä sivuja tarkastellaan. Yhdenmuotoisissa kuvioissa vastinkulmat ovat aina yhtä suuret.
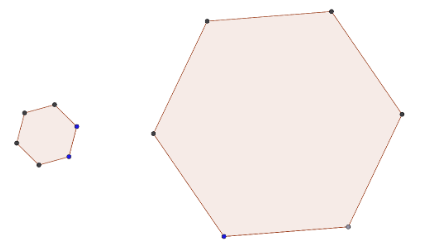
Yhdenmuotoisuutta voidaan merkitä lyhyesti symbolilla \(\sim\). Esimerkiksi \(K_1\sim K_{2}\) tarkoittaa, että kuvio \(K_1\) on yhdenmuotoinen kuvion \(K_2\) kanssa.
Jos kokoa ei muuteta ollenkaan, ja toinen kuvio saadaan toisesta kuviosta esimerkiksi kiertämällä tai peilaamalla, sanotaan, että kuviot ovat yhtenevät. Tälläiset kuviot ovat keskenään samankokoisia ja -muotoisia.
Yllä olevassa GeoGebra-appletissa oranssi nelikulmio on ns. vertailukuvio, joka pysyy koko ajan samana. Sen sijaan vihreää nelikulmiota pystyy muokkaamaan.
Kierrä vihreää nelikulmiota vetämällä “kierto”-liukusäädintä ja huomaa, että vihreä nelikulmio on silti yhdenmuotoinen oranssin nelikulmion kanssa.
Muuta seuraavaksi vihreän nelikulmion kokoa raahaamalla “koko”-liukusäädintä. Huomaa, että vihreän nelikulmion kulmien suuruudet pysyvät samoina kuin oranssissa nelikulmiossa, vaikka viheän nelikulmion koko muuttuisi.
Siirrä vihreää nelikulmiota eri suuntiin raahaamalla “siirto”-liukusäädintä. Vihreän nelikulmion muoto pysyy samana, vaikka se olisi eri paikassa. Se on siis edelleen yhdenmuotoinen oranssin nelikulmion kanssa.
Lopuksi lisää valinta kohtaan “peilaus”, jolloin vihreä nelikulmio peilataan pystysuoran akselin suhteen. Huomaa jälleen, että nelikulmioiden vastinkulmat pysyvät yhtä suurina, vaikka vihreä nelikulmio peilataan.
Näiden kohtien perusteella voidaan todeta, että jos kuviota kiertää, siirtää, peilaa tai sen kokoa muuttaa joka suunnassa, kuvio säilyy yhdenmuotoisena alkuperäisen kuvion kanssa.
Kokeile lopuksi muuttaa oranssin nelikulmion kärkipisteiden paikkoja raahamalla sinisiä kärkipisteitä eri paikkoihin. Huomaa, että vihreä ja oranssi nelikulmio pysyvät koko ajan yhdenmuotoisina.
Laske sivun x pituus, kun kolmiot \(ABC\) ja \(EDC\) ovat yhdenmuotoiset.
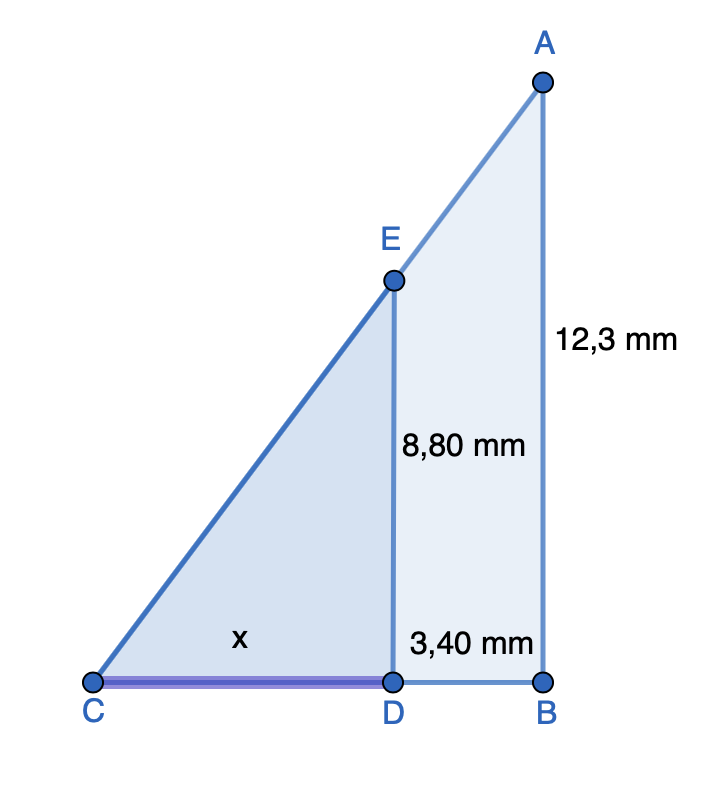
Ratkaisu
Sivun \(AB\) vastinjana pienemmässä kolmiossa on \(ED\) ja sivun \(CB\) vastinjana \(CD\).
Yhdenmuotoisilla kolmioilla vastinjanojen suhde on sama.
\[\begin{align} \frac{|AB|}{|ED|} &= \frac{|CB|}{|CD|} \\ \frac{12,3}{8,80} &= \frac{x+3,40}{x}& \quad &| \text{ kerrotaan ristiin}\\ 12,3x &= 8,80(x + 3,40)& \quad &| \text{ sievennetään} \\ 12,3x &= 8,80x + 29,92& \quad &| -8,80x \\ 3,5x &= 29,92& \quad &| :3,5 \\ x &= 8,5485... \text{ (mm)}& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x &≈ 8,55 \text{ (mm)} \end{align}\]
Sivun x pituus on 8,55 mm.
1.3 Kolmioiden yhdenmuotoisuus
Kolmioiden yhdenmuotoisuudesta voit lukea myös M niinkuin matematiikka -teoksesta, joka on lukiotason matematiikan tietosanakirja.
Kolmiot ovat yhdenmuotoisia, jos niillä on kaksi yhtä suurta kulmaa. Kahdesta yhtä suuresta kulmastahan seuraa myös, että kolmioiden kolmas kulma on yhtä suuri.
Kun siirrät yllä olevassa GeoGebra-appletissa kolmion ABC kärkipisteitä, huomaat, että kolmio DEF muuttuu samalla. Voit muuttaa kolmion DEF kokoa raahamalla pistettä E ja siirtää sitä raahaamalla pistettä D.
Koska kolmioiden vastinkulmat ovat koko ajan yhtä suuret, ovat kolmiot yhdenmuotoisia. Riittää, että kolmioissa on kaksi yhtä suurta vastinkulmaa, koska tällöin kolmioiden kolmannetkin vastinkulmat ovat välttämättä yhtä suuria.
Yhdenmuotoisuus
Kaksi tasokuviota \(K_1\) ja \(K_2\) ovat yhdenmuotoiset, kun
- kuvioiden vastinjanojen suhde on vakio
- kuvioiden vastinkulmat ovat yhtä suuret
Tällöin voidaan merkitä \(K_{1}\sim K_{2}\).
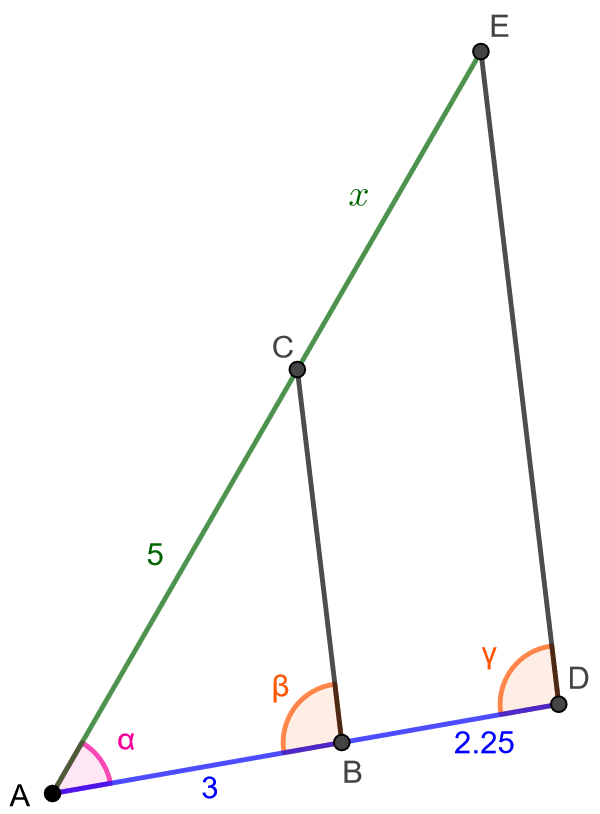
Määritä alla olevan kuvion janan \(CE\) pituus, joka on merkitty kuvioon kirjaimella \(x\). Janat \(BC\) ja \(DE\) ovat yhdensuuntaisia.
Ratkaisu
Huomataan, että kuviossa on oikeastaan kaksi päällekkäistä kolmiota: \(ABC\) ja \(ADE\). Kolmioilla on yksi yhteinen kulma \(\alpha\) joka on siis molemmissa kolmioissa yhtä suuri. Tarkastellaan seuraavaksi kulmia \(\beta\) ja \(\gamma\). Koska janat \(BC\) ja \(DE\) ovat yhdensuuntaisia, ja jana \(AD\) on molempien kulmien vasempana kylkenä, kulmat \(\beta\) ja \(\gamma\) ovat samankohtaisia. Tämä tarkoittaa, että kulmat \(\beta\) ja \(\gamma\) ovat yhtä suuria. Koska kolmioissa \(ABC\) ja \(ADE\) on kaksi yhtä suurta vastinkulmaparia, voidaan yhdenmuotoisuuslauseen KK perusteella sanoa, että kolmiot \(ABC\) ja \(ADE\) ovat yhdenmuotoiset.
Koska kolmiot ovat yhdenmuotoisia, sivun \(x\) pituuden määittämiseen voidaan käyttää yhdenmuotoisuussuhdetta. Vastinsivuparit ovat nyt \(AB\) ja \(AD\) sekä \(AC\) ja \(AE\). Näiden parien suhteet ovat yhtä suuret, joten saadaan yhtälö \[\frac{AD}{AB}=\frac{AE}{AC},\] johon sijoitetaan kunkin sivun pituus: \[\frac{3+2,25}{3}=\frac{5+x}{5}.\] Sievennetään yhtälöä, kerrotaan se ristiin ja ratkaistaan siitä \(x\): \[ \begin{aligned} \frac{5,25}{3} &= \frac{5+x}{5}& \quad &| \text{ kerrotaan ristiin} \\ 5,25 \cdot 5 &= 3 \cdot (5+x)& \quad &| \text{ sievennetään} \\ 26,25 &= 15 + 3x& \quad &| -15 \\ 11,25 &= 3x &\quad &| :3 \\ 3,75 &= x & \quad &| \text{ vaihdetaan yhtälön puolia} \\ x & = 3,75 \end{aligned} \]
Vastaukseksi saadaan, että janan \(CE\) pituus on \(3,75\).
Kk-lause
Kaksi kolmiota ovat yhdenmuotoiset, jos kolmioissa on kaksi yhtä suurta vastinkulmaparia.
Jos kolmion kulmien suuruuksia ei tiedetä, voidaan kolmioiden yhdenmuotoisuus päätellä myös niiden sivujen pituuksien avulla. Kuten aiemmin olet opiskellut, yhdenmuotoisissa kuvioissa niiden vastinsivujen suhteet ovat vakioita. Tätä ominaisuutta käytetään hyväksi yhdenmuotoisuuslauseessa SSS.
Kolmioiden yhdenmuotoisuuslause SSS
Jos kolmion kaikki sivut ovat verrannolliset vastinsivuihin toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.
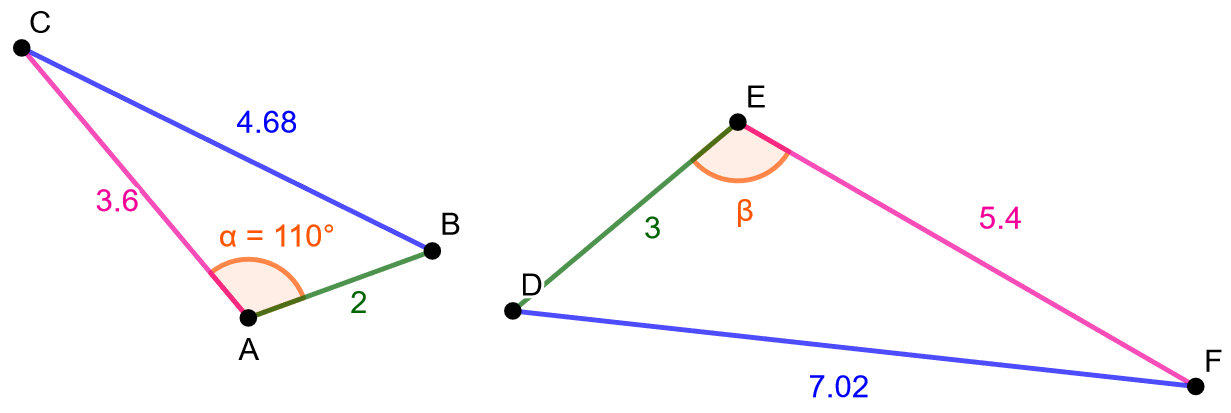
Määritä kuvaan merkityn kulman \(\beta\) suuruus.
Ratkaisu
Tutkitaan ensin, ovatko kolmiot yhdenmuotoisia. Koska molemmista kolmioista on tiedossa vain sivujen pituuksia, lasketaan kunkin vastinsivuparin suhde. Jos suhteet ovat samoja, voidaan käyttää kolmioiden yhdenmuotoisuuslausetta SSS. Sinisellä merkittyjen vastinsivujen suhde on \[\frac{7,02}{4,68}=1,5.\] Pinkillä merkittyjen vastinsivujen suhde on \[\frac{5,4}{3,6}=1,5.\] Vihreällä merkittyjen vastinsivujen suhde on \[\frac{3}{2}=1,5.\] Koska kaikkien vastisivuparien suhteet ovat samoja, yhdenmuotoisuuslauseen SSS mukaan kolmiot ovat yhdenmuotoisia. Koska kulmat \(\alpha\) ja \(\beta\) ovat vastinkulmia, ne ovat yhtä suuret. Kulma \(\beta\) on siis \(110^{\circ}\).
Jos kahdesta kolmiosta tiedetään, että vain kaksi vastinsivua on verrannollisia keskenään, ei vielä voida päätellä, ovatko kolmiot yhdenmuotoisia. Jos lisäksi tiedetään vielä, että kahden verrannollisen vastinsivun välissä olevat kulmat ovat molemmissa kolmioissa yhtä suuret, voidaan sanoa, että kolmiot ovat yhdenmuotoisia.
Kolmioiden yhdenmuotoisuuslause SKS
Jos kolmion kaksi sivua ovat verrannolliset vastinsivuihin toisessa kolmiossa ja niiden välinen kulma on yhtä suuri kuin vastinkulma toisessa kolmiossa, niin kolmiot ovat yhdenmuotoiset.
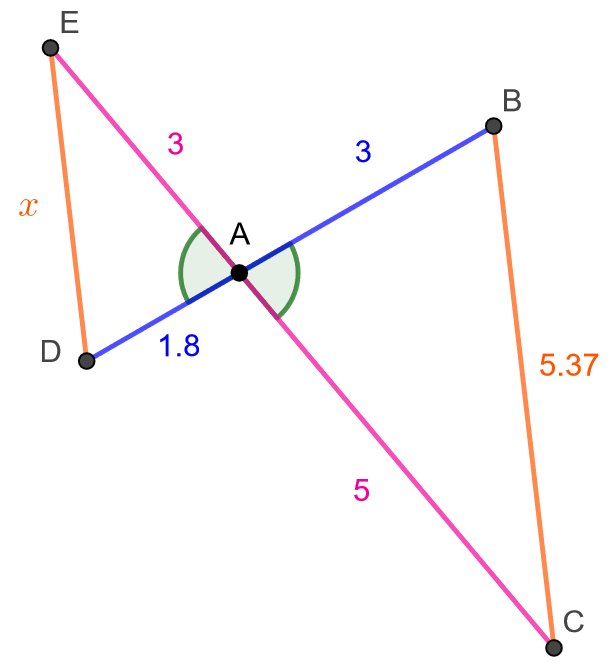
Määritä alla olevan kuvion sivun \(DE\) pituus, joka on merkitty kuvaan kirjaimella \(x\).
Ratkaisu
Sivun \(DE\) pituus saadaan helpoiten määritettyä, jos tiedetään, että kuviossa olevat kolmiot \(ABC\) ja \(ADE\) ovat yhdenmuotoiset. Kuvioon merkityt kulmat \(\angle EAD\) ja \(\angle CAB\) ovat toistensa ristikulmia ja siten yhtä suuria. Sinisellä mekittyjen vastinsivujen suhde on \[\frac{1,8}{3}=0,6\] ja pinkillä merkittyjen vastinsivujen suhde on \[\frac{3}{5}=0,6.\] Koska kahden vastinsivun suhteet ovat samat ja lisäksi näiden sivujen välinen kulma on kummassakin kolmiossa yhtä suuri, kolmiot ovat yhdenmuotoiset kolmioiden yhdenmuotoisuuslauseen SSS mukaan.
Oranssilla merkittyjen vastinsivujen suhteen tulee olla sama kuin muidenkin sivujen suhteet, joten saadaan seuraava yhtälö, joka ratkaistaan \[ \begin{aligned} \frac{x}{5,37}&=0,6 &\quad &|\cdot 5,37 \\ x &= 5,37 \cdot 0,6 &\quad &| \text{ sievennetään} \\ x &= 3,222 & \quad &| \text{ pyöristetään kahden desimaalin tarkkuudelle} \\ x &\approx 3,22 \end{aligned} \]
Kuvion sivun \(DE\) pituus on noin \(3,22\).
1.4 Mittakaava eli yhdenmuotoisuussuhde
Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat siis vakioita. Vastinsivut määritellään vastinpisteiden avulla. Alla olevassa kuvassa vastinpisteitä ovat \(A\) ja \(D\), \(E\) ja \(B\) sekä \(C\) ja \(F\). Näiden avulla voidaan määrittää vastisivut: \(a\) ja \(d\), \(b\) ja \(e\) sekä \(c\) ja \(f\). Lasketaan jokaisen vastisivuparin suhde, ja huomataan, että se on jokaisen vastinsivuparin tapauksessa \(1,5\).
Tätä suhdetta kutsutaan yhdenmuotoisuussuhteeksi ja se määritellään alla.
Yhdenmuotoisuussuhde eli mittakaava
Jos kuviot ovat yhdenmuotoiset, yhdenmuotoisuussuhde tarkoittaa suhdetta \[\frac{s_1}{s_2},\] missä \(s_1\) on sivun pituus ensimmäisessä kuviossa ja \(s_2\) sitä vastaavan sivun pituus toisessa kuviossa.
Yllä olevassa GeoGebra-appletissa on korostettu vastinpisteet ja vastinsivut samoilla väreillä. Lisäksi vasemmalla olevassa CAS-ikkunassa on laskettu kunkin vastinsivuparin suhde.
Kokeile siitää kolmioiden \(ABC\) ja \(DEF\) kärkipisteitä ja huomaa, että vastinsivujen suhteet pysyvät koko ajan samoina. Tuota suhdetta kutsutaan siis mittakaavaksi tai yhdenmuotoisuussuhteeksi.
Maratoonari harjoittelee kilpailuihin reitillä, jonka pituus on 50 km.
- Kuinka pitkä on lenkin reitti kartalla, jonka mittakaava on 1:400 000?
- Mikä on sellaisen kartan mittakaava, jossa maratoonarin reitti on 5,1 cm kartalla?
Ratkaisu
Pituus kastalla ilmoitetaan senttimetreinä, joten muunnetaan maratoonarin todellinen reitti myös senttimetreiksi.
\(50 \text{ km} = 50 000 \text{ m} = 5 000 000 \text{ cm}\)
Merkitään reitin pituutta kartalla kirjaimella x ja ratkaistaan pituus verrannolla kokoamalla tiedot taulukkoon. Pituus kartalla on suoraan verrannollinen pituuteen luonnossa.
Pituus kartalla (cm) Todellinen pituus (cm) x 5000000 1 400000 Suoraan verrannollisuuden avulla taulukosta saadaan
\[\begin{align} \frac{x}{1 \text{ cm}} &= \frac{5000000 \text{ cm}}{400000 \text{ cm}} \\ x &= 12,5 \text{ cm} \\ \end{align}\]
Koska tiedetään reitin pituus sekä kartalla (5,1 cm) että luonnossa (5 000 000 cm), niin mittakaava saadaan suoraan näiden kahden suhteena.
\(k = \frac{2,5\text{ cm}}{5 000 000 \text{ cm}}^{(2,5} = \frac{1}{2 000 000} =\) 1:2 000 000
1.5 Pinta-alan suhde
Aiemmin tarkastelit vain kuvioiden vastinkulmien suuruuksia (jotka olivat samoja) sekä vastisivujen pituuksien suhteita (jotka pysyivät vakioina riippumatta siitä mitä sivupareja tarkasteltiin). Yhdenmuotoisuuden avulla voidaan päätellä lisäksi myös kuvioiden pinta-aloihin liittyviä suhteita.
Yhdenmuotoisten kuvioiden pinta-alalause
Jos kuviot ovat yhdenmuotoiset yhdenmuotoisuussuhteessa \(s_1 : s_2\), niiden pinta-alojen suhde on \[\frac{A_1}{A_2} =\left(\frac{s_1}{s_2}\right)^2.\]
Tutki yllä olevaa GeoGebra-applettia siirtämällä suorakulmion \(ABCD\) kärkipisteitä sekä raahaamalla yhdenmuotoisuussuhde-liukusäädintä. Vasemmalla olevaan CAS-ikkunaan lasketaan vastinsivujen \(a\) ja \(e\) sekä \(b\) ja \(f\) väliset suhteet sekä suorakulmioiden pinta-alojen \(m1\) ja \(m2\) välinen suhde. Lisäksi lasketaan yhdenmuotoisuussuhteen neliön lukuarvo. Huomaa, että pinta-alojen suhde ja yhdenmuotoisuussuhteen neliö ovat koko ajan yhtä suuria.
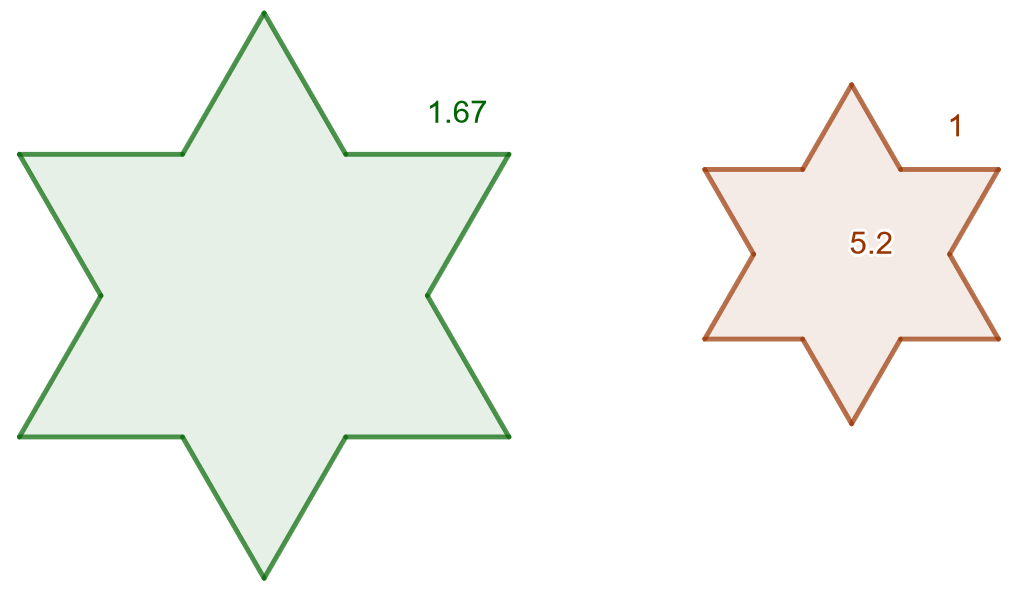
Laske alla olevan kuvan isomman tähden pinta-ala, kun tiedetään, että tähdet ovat yhdenmuotoiset.
Ratkaisu
Koska kuviot ovat yhdenmuotoisia, voidaan käyttää yhdenmuotoisten kuvioiden pinta-alalausetta. Kuvioiden yhdenmuotoisuussuhde on \[\frac{1,67}{1}=1,67.\] Merkitään kysyttyä isomman tähden pinta-alaa kirjaimella \(x\). Tehdään verranto yhdenmuotoisten kuvioiden pinta-alalauseen avulla ja ratkaistaan siitä \(x\): \[ \begin{aligned} \frac{x}{5,2}&=1,67^2 &\quad &| \cdot 5,2 \\ x &= 5,2 \cdot 1,67^2 &\quad &| \text{ sievennetään lauseke} \\ x &= 14,50228 &\quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x & \approx 14,5 \end{aligned} \] Isomman tähden pinta-ala on noin \(14,5\).
2. Monikulmioiden geometriaa
Tässä luvussa käsitellään monikulmioita, joista yksinkertaisin kulmio on kolmio. Tasogeometriassa kuviot sekä kappaleet piirretään yksiulotteisesti. Harjoittele kuvien piirtämistä käyttämälläsi laskimella tai vaikkapa Geogebralla!
Kappaleeseen liittyvät harjoitustehtävät löydät täältä!
Kolmioiden geometriaa
2.1 Kolmion rakenne
Kolmio on yksinkertaisin monikulmio, ja nimensä mukaisesti se koostuu kolmesta kulmasta ja kolmesta sivusta. Kolmion kulmat nimetään kreikkalaisin kirjaimin, \(\alpha\), \(\beta\) ja \(\gamma\).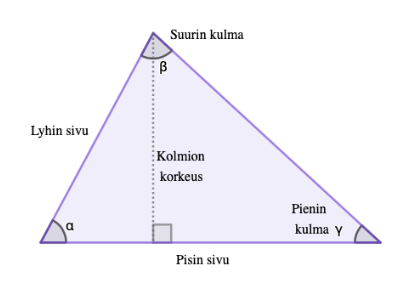 
Kolmion kaikkien kulmien yhteenlaskettu suuruun on aina \(180°\), eli \(\alpha+ \beta+\gamma=180°\) .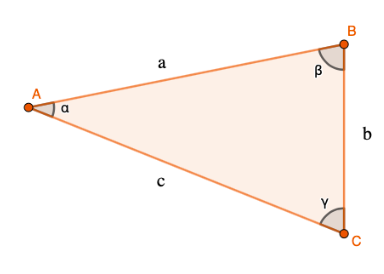 
Kaiken muotoisille kolmioille voidaan piirtää korkeusjana \(h\), joka kulkee kolmion huipusta kohtisuorasti kohti kolmion kantaa: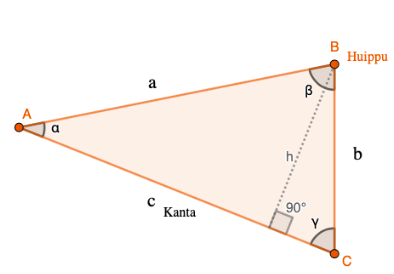 
Tämä korkeusjana \(h\) ilmoittaa kolmion korkeuden. Korkeusjanaa käytetään, kun tarkoituksena on määrittää kolmion pinta-ala.
Kolmion pinta-ala
\[\begin{align*} A=\frac{a\cdot h}{2}=\frac{1}{2}a\cdot h, \end{align*}\] missä \(a\) on kolmion kanta ja \(h\) kantaa kohtisuoraan piirretyn korkeusjanan pituus (eli kolmion korkeus).
Kolmiot voidaan jakaa ominaisuuksien avulla suorakulmaisiin kolmioihin, tasakylkisiin kolmioihin ja tasasivuisiin kolmioihin.
Suorakulmainen kolmio
Suorakulmaisessa kolmiossa on yksi \(90°\) kulma. Suorakulmainen kolmio koostuu kahdesta kateetista ja hypotenuusasta. Hypotenuusa on kolmion pisin sivu. Suoran kulman lisäksi kolmiossa on kaksi terävää kulmaa.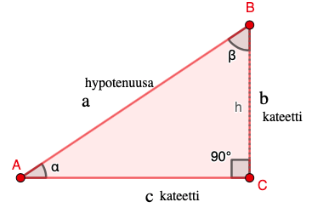 
Huomaa, että korkeusjana on nyt toinen kateeteista. Kuvassa kateetti \(b\).
Tasasivuinen kolmio
Tasasivuisen kolmion tilanteessa kolmion kaikki kulmat ovat suuruudeltaan \(60°\). Lisäksi kolmion kaikki sivut ovat keskenään yhtä pitkiä ja piirretty korkeusjana puolittaa kannan ja huippukulman.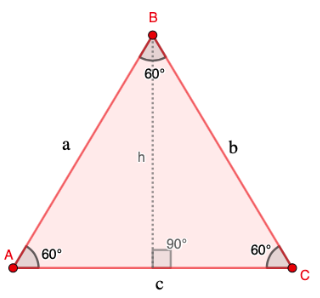 
Tasakylkinen kolmio
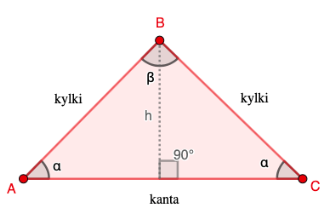
Tasakylkisessä kolmiossa kolmion kaksi sivua ovat yhtä pitkiä. Näitä yhtäpitkiä sivua kutsutaan kyljiksi. Tasakylkisen kantakulmat ovat yhtäsuuret, ja huipusta kantaan piirretty korkeusjana \(h\) puolittaa sekä huippukulman ja kannan.
2.2 Kolmion pinta-ala
Kolmion pinta-ala voidaan laskea tutulla tavalla, eli kerrotaan kolmion kanta ja korkeus keskenään ja jaetaan tulos kahdella. Joskus kolmion korkeus on kuitenkin vaikea määrittää. Yleisemmässä tapauksessa kolmion pinta-ala voidaan määrittää vain, kun tiedetään kahden kolmion sivun pituudet ja niiden sivujen välisen kulman suuruus.
Kolmion pinta-ala
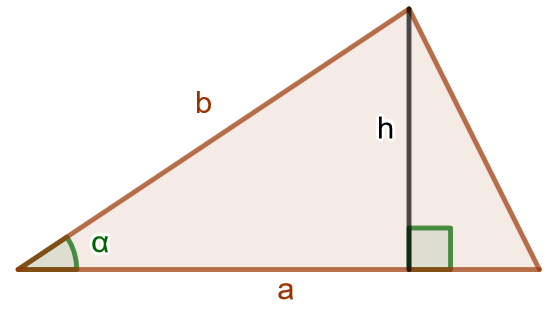
Jos kolmion kannan pituus on \(a\) ja korkeus \(h\), kolmion pinta-ala on \[A=\frac{1}{2} ah.\] Jos kolmion kahden sivun pituudet ovat \(a\) ja \(b\) ja näiden välisen kulman suuruus \(\alpha\), voidaan kolmion pinta-ala ilmaista lausekkeella \[A=\frac{1}{2} ab \sin \alpha.\]
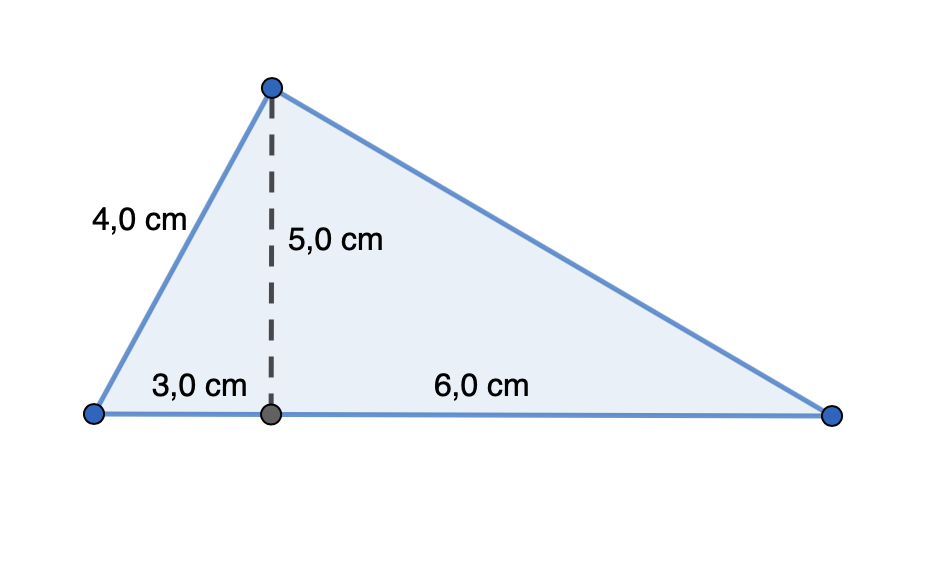
Laske kuvan kolmion pinta-ala
Ratkaisu
Kolmion korkeus \(h\) on \(5,0\) cm ja kanta \(a\) \(6,0 \text{ cm} + 3,0 \text{ cm} = 9,0 \text{ cm}\). Tällöin pinta-ala on
\(A_{kolmio} = \frac{ah}{2} = \frac{9,0 \text{ cm} \cdot 5,0 \text{ cm}}{2} = 22,5 \text{ cm}≈23 \text{ cm}\)
2.3 Suorakulmainen kolmio, Pythagoraan lause
Suorakulmainen kolmio on sellainen kolmio, jonka yksi kulma on suorakulma eli \(90^{\circ}\). Suoran kulman kylkinä olevia sivuja kutsutaan kateeteiksi ja suoran kulman vastaista sivua hypotenuusaksi.
Suorakulmaiseen kolmioon liittyy oleellisesti Pythagoraan lause, jonka mukaan suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin kolmion hypotenuusan neliö. Jos siis tiedetään kolmion kahden sivun pituudet, voidaan kolmannen sivun pituus ratkaista. Voit lukea lisää Pythagoaan lauseen historiasta.
Pythagoraan lause
Suorakulmaisen kolmion kateettien \(a\) ja \(b\) neliöiden summa on yhtä suuri kuin sen hypotenuusan \(c\) neliö, eli \[a^2+b^2=c^2.\]
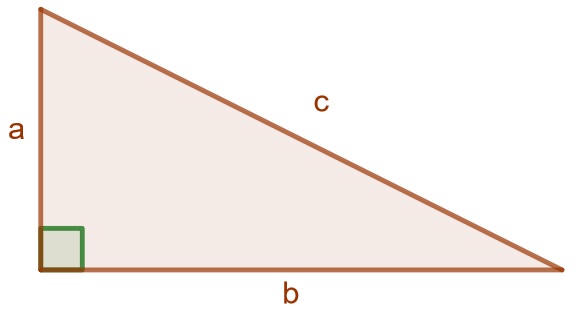
Suorakulmaisen kolmion lyhyemmän kateetin pituus on 8 m. Hypotenuusa on 3 m pidempi kuin pidempi kateetti. Selvitä kolmion sivujen pituudet.
Ratkaisu
Merkitään pidemmän kateetin sivun pituutta kirjaimella x. Tällöin hypotenuusan pituus on x + 3.
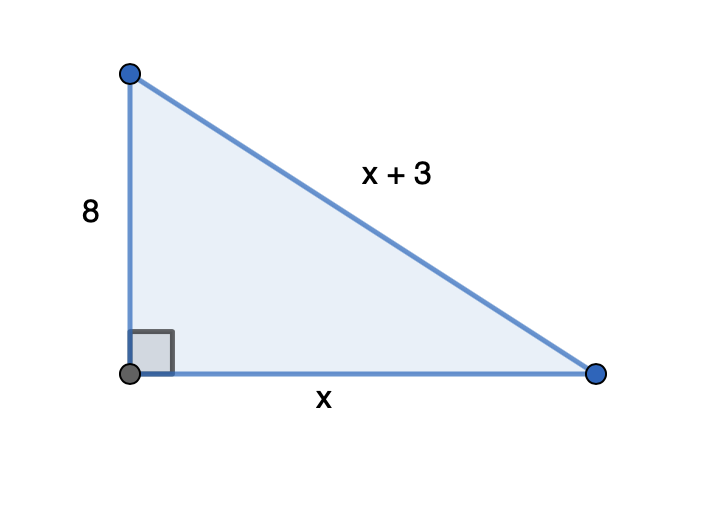
Ratkaistaan kateetin x pituus Pythagoraan lauseella.
\[\begin{align} 8^2 + x^2 &= (x + 3)^2& \quad &| \text{ kirjoitetaan potenssilauseke tulona} \\ 64 + x^2 &= (x + 3)(x + 3)& \quad &| \text{ lasketaan tulo} \\ 64 + x^2 &= x^2 + 3x + 3x + 9& \quad &| \text{ erotellaan muuttujat ja vakiot eri puolille yhtälöä} \\ x^2 - x^2 - 3x - 3x &= 9 - 64& \quad &| \text{ sievennetään} \\ -6x &= - 55& \quad & | :(-6) x &= 9,1666...& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ x &≈ 9 \\ \end{align}\]
Kolmion sivujen pituudet ovat siis \(8 \text{ m, } 9 \text{ m ja } (9 + 3) \text{ m}= 12 \text{ m}\).
2.4 Käänteinen Pythagoraan lause
Pythagoraan lauseen kohdalla todettiin, että se pätee vain suorakulmaisille kolmioille. Eli jos kolmio on suorakulmainen, sen kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö. Sama päättely voidaan kääntää toisinpäin. Jos kolmion kahden lyhyemmän sivun neliön summa on yhtä suuri kuin pisimmän sivun neliö, kyseessä on suorakulmainen kolmio. Jos suoraa kulmaa ei ole merkitty kuvaan tai sitä ei ole kerrottu erikseen, tulee aina tarkistaa, onko kolmio suorakulmainen, vaikka se saattaisi näyttää siltä.
Kolmion kahden lyhyemmän sivun pituudet ovat 3 ja 4. Pisin sivu on kaksi yksikköä lyhintä sivua pidempi. Onko kolmio suorakulmainen?
Ratkaisu
Jotta kolmio olisi suorakulmainen, sen sivujen pituuksien on toteutettava Pythagoraan lause. Pisimmän sivun pituus on 3 + 2 = 5. Tarkastetaan toteuttavatko luvut Pythagoraan lauseen, kun pisin sivu on hypotenuusa ja lyhyemmät sivut ovat kateetteja.
\[\begin{align} a^2 + b^2 &= c^2& \quad &| \text{ sijoitetaan sivujen pituuksien arvot} \\ 3^2 + 4^2 &= 5^2& \quad &| \text{ sievennetään} \\ 9 + 16 &= 25& \quad &| \text{ sievennetään} \\ 25 &= 25& \quad &| \text{ tosi} \\ \end{align}\]
Koska luvut toteuttevat Pythagoraan lauseen, on kyseessä suorakulmainen kolmio.
2.5 Trigonometriset funktiot
Suorakulmaisen kolmion terävien kulmien suuruudet voidaan ratkaista, jos tiedetään kolmion kateettien tai kateetin ja hypotenuusan pituudet. Tämä on mahdollista, sillä kolmion sivujen suhteet ovat tietyillä kulmilla aina vakioita. Näitä suhteita kutsutaan trigonometrisiksi funktioiksi.
Suorakulmaisen kolmion sini, kosini ja tangentti
Suorakulmaisessa kolmiossa kulman \(\alpha\) sini, kosini ja tangentti tarkoittavat seuraavia suhteita: \[\sin(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{hypotenuusa}}=\frac{a}{c}\] \[\cos(\alpha)=\frac{\text{kulman viereinen kateetti}}{\text{hypotenuusa}}=\frac{b}{c}\] \[\tan(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{kulman viereinen kateetti}}=\frac{a}{b}\]
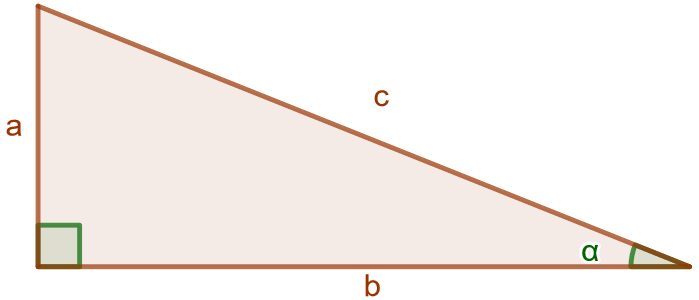
Kokeile laskea eri kulmien sini, kosini ja tangentti sekä sivujen suhteet vasemmalla olevassa cas-ikkunassa. Voit syöttää uuden komennon napauttamalla hiirellä rivinumeron 3 vieressä. Voit käyttää kuvassa näkyviä muuttujien nimiä. Kokeile myös raahata kolmion kärkipisteitä ja tutki, miten lukuarvot muuttuvat.
Muutama ohje cas-laskimen käyttöön:
- Jos haluat laskea kuvan \(\gamma\)-kulman sinin, kirjoita riville suoraan \(\sin(\gamma)\).
- Kreikkalaiset kirjaimet saat näppäimistöltä:
- Alt + a = \(\alpha\)
- Alt + b = \(\beta\)
- Alt + g = \(\gamma\)
- Jos laskin antaa vastauksen, kirjoita komento Lukuarvona(\(n)]{.red}, missä korvaat n-kirjaimen sen rivin numerolla, jonka likiarvon haluat näkyviin. Voit myös kirjoittaa suoraan [Lukuarvona(\)()$).
- Kokeile ensin laskea jonkin kulman sini ja sen jälkeen muuttaa pisteiden paikkaa kuvaajassa. Mitä sinin arvolle tapahtuu?
Määritä kuvan
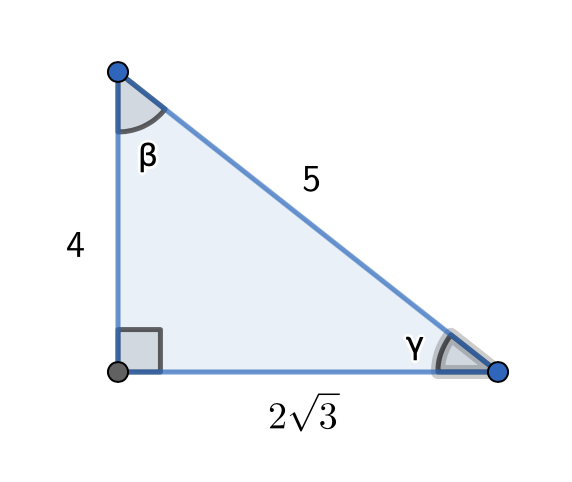
- kulman \(\beta\) tangentti ja sini.
- kulman \(\gamma\) kosini ja kulman \(\gamma\) suuruus.
Ratkaisu
Tangentti on vastaisen kateetin suhde viereiseen kateettiin. Kulman \(\beta\) vastaisen kateetin pituus on \(2\sqrt{3}\) ja viereisen kateetin pituus 4. Siis
\(\tan{\beta} = \frac{2\sqrt{3}}{4}\)
Sini on kulman vastaisen kateetin suhde hypotenuusaan. Hypotenuusan pituus on 5, joten kulman \(\beta\) sini on
\(\sin{\beta}=\frac{2\sqrt{3}}{5}\)
Kulman kosini on kulman viereisen kateetin suhde hypotenuusaan. Hypotenuusan pituus on edelleen 5. Nyt kulman \(\gamma\) viereisen kateetin pituus on \(2\sqrt{3}\), jolloin kulman \(\gamma\) kosini on
\[\begin{align} \cos{\gamma}&=\frac{2\sqrt{3}}{5}& \quad &| \text{ kulma }\gamma \text{ laskimella }\gamma=\cos^{-1}\left(\frac{2\sqrt{3}}{5}\right) \\ \gamma &= 46,1462...°& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ \gamma &≈ 46° \\ \end{align}\]
Kolmion trigonometristen funktioiden eli tangentin, sinin tai kosinin avulla voidaan siis määrittää suorakulmaisen kolmion kulmien suuruuksia.
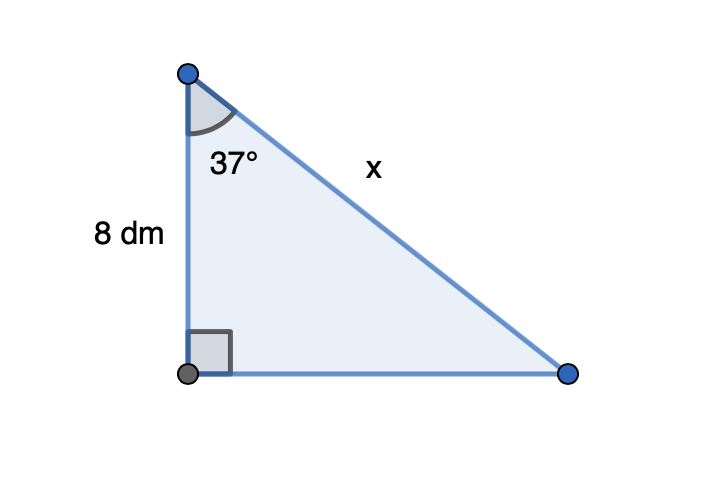
Laske kuvan kolmion sivun x pituus.
Ratkaisu
Kolmio on suorakulmainen, ja sen yhden terävän kulman suuruus on \(37°\). Terävän kulman viereisen kateetin pituus on 8 dm ja kolmion hypotenuusan pituus on x. Tällöin terävän kulman kosini on
\[\begin{align} \cos{37°} &= \frac{8}{x}& \quad &| \cdot x \\ x \cdot \cos{37°} &= 8& \quad &| : \cos{37°} \\ x &= \frac{8}{\cos{37°}}& \quad &| \text{ sievennetään} \\ x &= 10,0170...& \quad &| \text{ pyöritetään ykkösten tarkkuuteen} \\ x &≈ 10 \text{ (dm)} \\ \end{align}\]
Suorakulmaisen kolmion hypotenuusan pituus on 10 dm.
2.6 Nelikulmioiden rakenne
Nelikulmiot voidaan jakaa lävistäjän avulla kahdeksi kolmioksi. Koska kolmioiden kulmien summa on aina \(180°\), täytyy siis olla niin, että nelikulmioiden kulmien summa on \(2\cdot180°=360°\).
Alla olevassa kuvassa nelikulmio on jaettu kahdeksi kolmioksi piirtämällä jana pisteestä \(A\) pisteeseen \(C\). Nelikulmio voitaisiin myös jakaa kolmioiksi pisteiden \(B\) ja \(D\) avulla.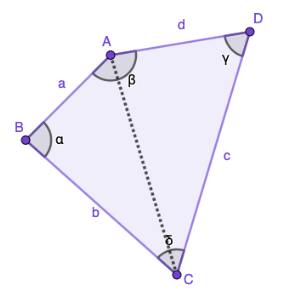 
Samoin kuin kolmionkin tapauksessa, nelikulmiot voidaan jaotella ominaisuuksiensa suhteen.
Suorakulmio
Kaikki nelikulmion kulmat ovat \(90°\). Tällöin myös nelikulmion vastakkaiset sivut ovat yhtäpitkiä.
Neliö on nelikulmion erikoistapaus, jossa nelikulmion kaikki sivut ovat yhtä pitkiä.
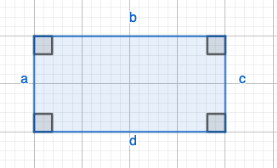
Suorakulmion pinta-ala on \(A=a\cdot b\)
Suunnikas
Suunnikas on vinossa oleva nelikulmio. Tällöin vastakkaiset sivut ovat yhtä pitkät ja yhdensuuntaiset, ja vastakkaiset kulmat ovat yhtä suuret.
Neljäkäs on suunnikas, jonka kaikki sivut ovat yhtä pitkiä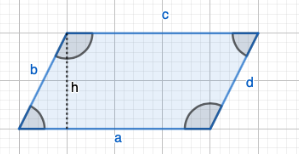 
Suunnikkaan pinta-ala on \(A=a\cdot h\)
Puolisuunnikas
Nimensä mukaisesti nelikulmio, jossa vain kaksi sivuista ovat yhdensuuntaisia, on puolisuunnikas. Tällöin kaikki sivut voivat olla eri pituisia ja kulmat eri suuruisia.
Tasakylkinen puolisuunnikas on puolisuunnikkaan erikoistapaus, jossa erisuuntaiset sivut ovat yhtäpiktiä. Tällöin puolisuunnikkaan kantakulmat ovat yhtä suuria.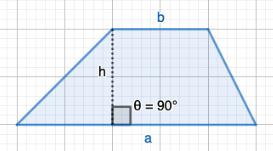 
Puolisuunnikkaan pinta-ala on \(A=\frac{a+b}{2}\cdot h\)
Laske kuvan suunnikkaan pinta-ala.
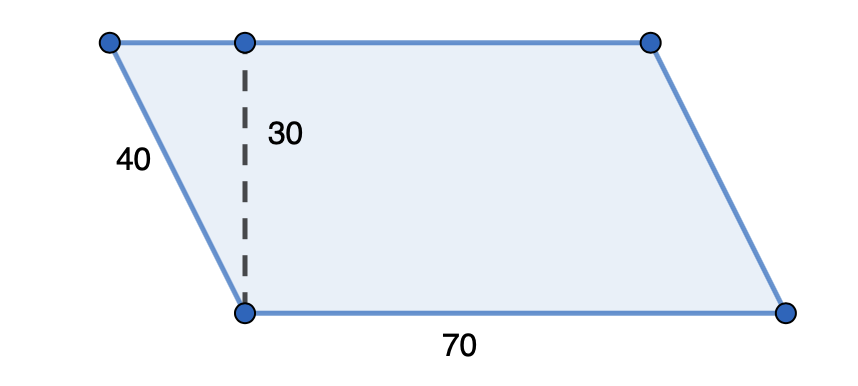
Ratkaisu
Suunnikkaan pinta-ala lasketaan kertomalla keskenään sen kanta ja korkeus. Kuvasta saadaan kannan pituudeksi 70. Koska korkeus on kohtisuora etäisyys kannasta, valitaan korkeuden pituudeksi 30. Tällöin koko suunnikkaan pinta-ala on
\(A_{suunnikas}= 70 \cdot 30 = 2100\)
Suunnikkaan pinta-ala on siis 2100.
Tasakylkisen puolisuunnikkaan muotisen terassin pinta-ala on 17 m\(^2\). Laske terassin piiri, kun yhdensuuntaisten sivujen pituudet ovat 4 m ja 12 m.
Ratkaisu
Koska puolisuunnikas on tasakylkinen, se muodostaa kaksi yhtenevää suorakulmaista kolmiota, joiden hypotenuusan pituus on x ja kateettien pituudet ovat h ja c.
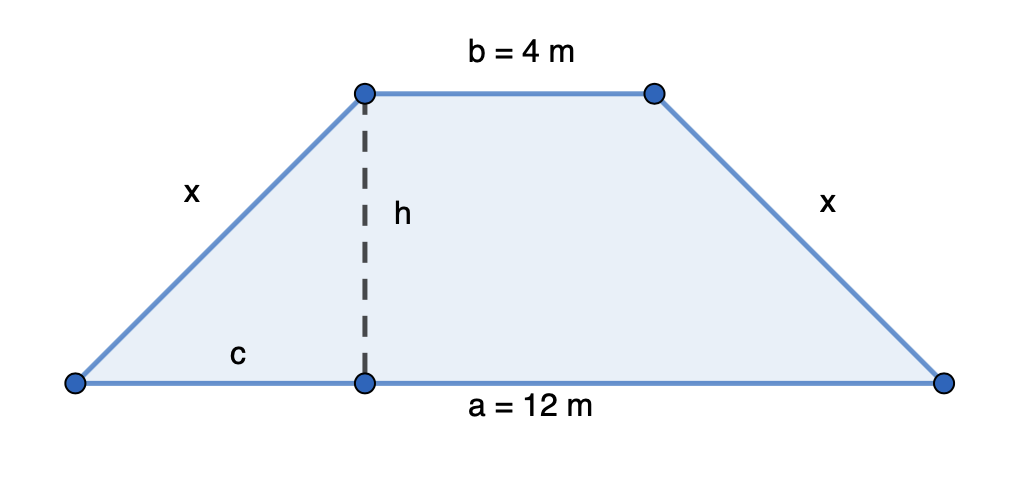
Sivun c pituus on \(\frac{12 \text{ m} - 4 \text{ m}}{2} = 4 \text{ m}\).
Selvitetään seuraavaksi puolisuunnikkaan korkeus h pinta-alan lausekkeesta.
\[\begin{align} A &= \frac{a + b}{2} \cdot h& \quad &| \text{ sijoitetaan arvot} \\ 17 \text{ m}^2 &= \frac{12 \text{ m} + 4 \text{ m}}{2} \cdot h& \quad &| \text{ vaihdetaan yhtälön puolia} \\ \frac{12 \text{ m} + 4 \text{ m}}{2} \cdot h &= 17 \text{ m}^2& \quad &| \text{ sievennetään} \\ 8 \text{ m} \cdot h &= 17 \text{ m}^2& \quad &| : 8 \text{ m} \\ h &= \frac{17 \text{ m}^2}{8 \text{ m}}& \quad &| \text{ sievennetään} \\ h &= 2,125 \text{ m} \end{align}\]
Seuraavaksi ratkaistaan suorakulmaisesta kolmiosta Pythagoraan lauseella hypotenuusan pituus x.
\[\begin{align} x^2 &= c^2 + h^2& \quad &| \text{ sijoitetaan arvot} \\ x^2 &= (4 \text{ m})^2 + (2,125 \text{ m})^2& \quad &| \text{ }\sqrt{\text{ }} \\ x &= \sqrt{(4 \text{ m})^2 + (2,125 \text{ m})^2}& \quad &| \text{ sievennetään} \\ x &= 4,5294... \text{ m}\\ \end{align}\]
Lasketaan vielä terassin piiri summaamalla kaikki sivut yhteen.
\(x+b+x+a = 2\cdot x + a + b= 2 \cdot 4,5294...\text{ m} + 4 \text{ m} + 12 \text{ m}=57,0588... \text{ m}≈ 57 \text{ m}\)
Terassin piirin pituus on 57 m.
Muut monikulmiot
2.7 Monikulmioiden rakenne
Kolmiot ja nelikulmiot ovat vain esimerkkejä monikulmioista. Monikulmioissa voi nimensä mukaisesti olla kuinka monta kulmaa tahansa. Alla olevassa kuvassa on mallinnettu säännöllistä kuusikulmiota ja kymmenkulmiota.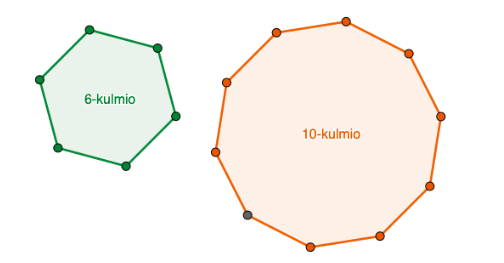 
Kulmien lukumäärästä huolimatta kuviot voidaan aina jakaa kolmioihin. Esimerkiksi yllä oleva kuusikulmio voidaan jakaa neljään kolmioon: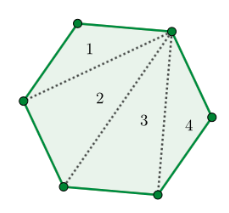 
Monikulmion kulmien summa
Jos monikulmiossa on \(n\) kärkeä tai kulmaa, tällöin kulmion kulmien summa on \[\begin{align*} (n-2)\cdot180° \end{align*}\]
Laske säännöllisen kuusikulmion
- kulmien summa
- pinta-ala,
kun sen sivun pituus on 15 cm.
Ratkaisu
Koska monikulmiossa on kuusi kulmaa, niin \(n = 6\) ja kuusikulmion kulmien summa voidaan laskea
\((n-2) \cdot 180° = (6-2) \cdot 180°= 4 \cdot 180°= 720°\)
Kuusikulmion kulmien summa on siis 720°.
Säännöllinen kuusikulmio koostuu kuudesta tasasivuisesta kolmiosta. Jokaisen kolmion sivun pituus on siis 15 cm. Kuusikulmion pinta-ala muodostuu kuuden kolmion pinta-alasta, joten lasketaan ensin yhden kolmion pinta-ala.
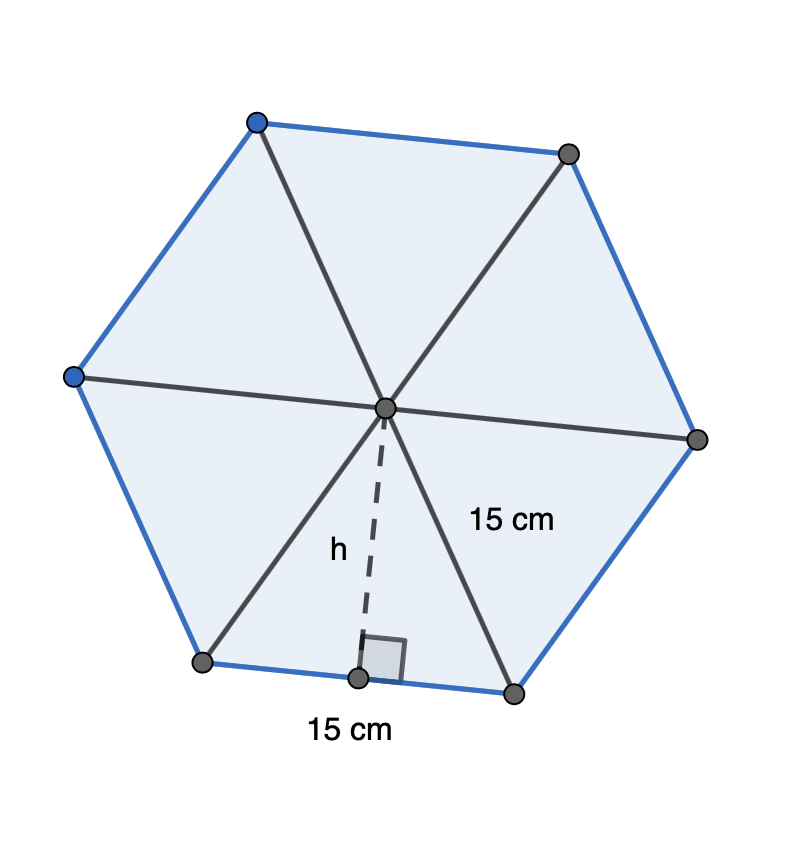
Selvitetään Pythagoraan lauseen avulla kolmion korkeus h, kun hypotenuusan pituus on 15 cm ja kateettien pituudet ovat h ja \(\frac{15 \text{ cm}}{2}= 7,5\) cm
\[\begin{align} h^2 + (7,5)^2 &= 15^2& \quad &| -(7,5)^2 \\ h^2 &= 15^2- (7,5)^2& \quad &| \text{ }\sqrt{\text{ }} \\ h &= \sqrt{15^2- (7,5)^2}& \quad &| \text{ sievennetään} \\ h &= 12,9903... \text{ (cm)} \end{align}\]
Lasketaan kolmion pinta-ala \(A_{kolmio}=\frac{15 \text{ cm} \cdot 12,9903... \text{ cm}}{2}=97,4278... \text{ cm}^2\).
Säännöllisen tasasivuisen kuusikulmion pinta-ala on tällöin
\(6 \cdot A_{kolmio}= 6 \cdot 97,4278... \text{ cm}^2= 584,5671... \text{ cm}^2 ≈ 580 \text{ cm}^2\).
Kuusikulmion pinta-ala on \(580 \text{ cm}^2\).
2.8 Monikulmiot koordinaatistossa
Usein geometrisia kuvioita tarkastellaan \(xy\)-koordinaatistossa.
\(xy\)-koordinaatisto
Koordinaatisto koostuu kahdesta akselista, jotka leikkaavat toisensa kohtisuorasti. Akselien leikkauspiste on nimeltään \(origo\) \(O\).
Usein akselit valitaan siten, että vaakasuora akseli on \(x\)-akseli ja pystysuora akseli on \(y\)-akseli.
Kolmiulotteisessa koordinaatistossa on myös \(z\)-akseli, joka on edelleen kohtisuorassa \(x\)- ja \(y\)-akseleihin. 
Monikulmioita piirrettäessä koordinaatistoon, monikulmion kärjet ovat joissain koordinaatiston pisteissä.
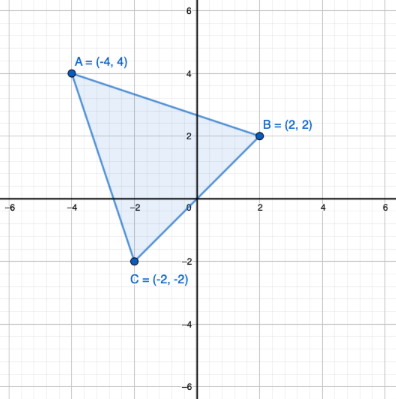
Yllä olevassa kuvassa on kolmio, jonka kärkipisteet on merkattu koordinaatistoon. Tekstissä kolmion kärkipisteet voitaisiin ilmoittaa esimerkiksi: "Kolmio, jonka kärjet ovat pisteet \(A(-4,4)\), \(B(2,2)\) ja \(C(-2,-2)\)."
Kolmion kateetin pituus pisteiden \(A\) ja \(B\) välillä voitaisiin laskea pisteiden koordinaattien avulla:
Pisteiden välinen etäisyys
Jos \(xy\)-koordinaatistossa on kaksi pistettä, joiden koordinaatit ovat \((x_1, y_1)\) ja \((x_2, y_2)\), niin näiden pisteiden välinen etäisyys on \[\begin{align*} |AB|=\sqrt{(x_1- x_2)^{2}+(y_1- y_2)^{2}} \end{align*}\]
Aiemmin esitetyn kolmion kateetin \(|AB|\) pituus olisi siis \[\begin{align*} |AB|=\sqrt{(2-(-4)^{2}+(2-4)^{2}}=\sqrt{6^2+(-2)^2}=\sqrt{36+4}=\sqrt{40}=2\cdot\sqrt{10}. \end{align*}\]
Janan päätepisteiden avulla voidaan laskea myös janan keskipisteen koordinaatit. Alla olevassa kuvassa piirretty kolmion sivujen keskipisteet.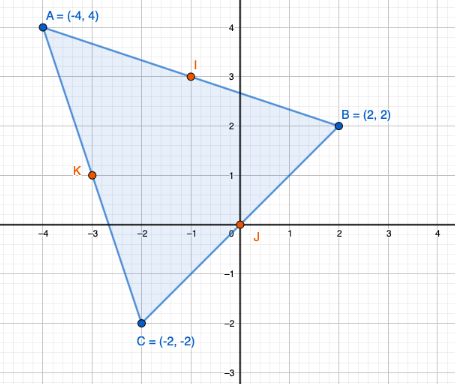 
Janan keskipisteen koordinaatit
Olkoon janan päätepisteiden koordinaatit \((x_1, y_1)\) ja \((y_1, y_2)\). Janan keskipisteen koordinaatit ovat päätepisteiden koordinaattien keskiarvo:
\[\begin{align*} (x_0,y_0)=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right) \end{align*}\]
Lasketaan nyt aiemmin esitetyn kolmion keskipiste \(I\) janalla \(AB\).
\[\begin{align*} (x_0,y_0)=\left(\dfrac{(-4)+2}{2},\;\dfrac{4+2}{2}\right)=\left(\dfrac{-2}{2},\;\dfrac{6}{2}\right)=(-1,3) \end{align*}\]
Kuvasta tarkistamalla huomataan, että piste \(I\) näyttäisi sijoittuvat koordinaatistossa pisteeseen \((-1,3)\) aivan kuten laskettiinkin.
Ratkaise kolmion \(ABC\) pinta-ala, kun kolmion kärkipisteet ovat \(A=(0,1)\), \(B=(2,2)\) ja \(C=(4,0)\).
Ratkaisu
Piirretään kolmion ympärille suorakulmio \(FDEC\) niin, että sen sivut ovat koordinaattiakselien suuntaiset. Suorakulmion pisteet saadaan kolmion pisteiden avulla. Esimerkiksi pisteen D x-koordinaatti on sama kuin pisteen A ja y-koordinaatti sama kuin pisteellä B.
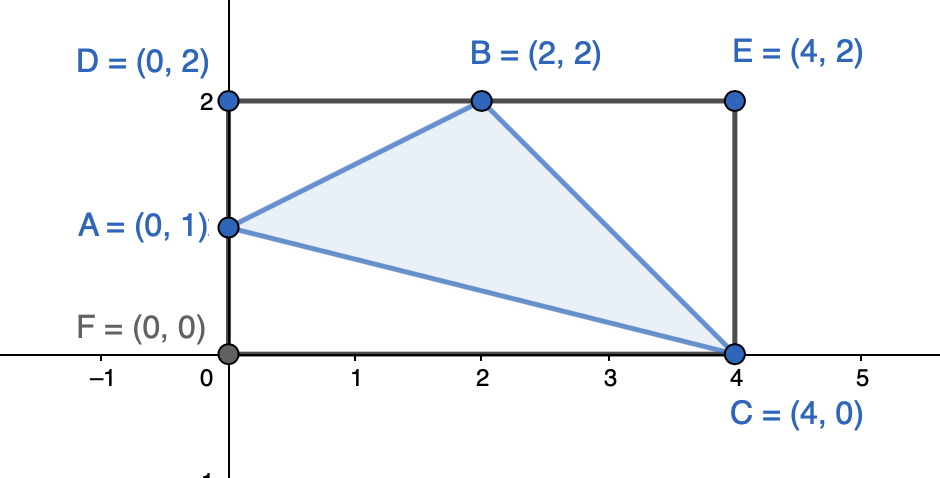
Lasketaan suorakulmion sivujen \(FD\) ja \(FC\) pituudet.
\(|FD| = 2 - 0 = 2 \\\) \(|FC| = 4 - 0 = 4 \\\)
Suorakulmion pinta-ala on siis \(A_{suorakulmio}=2 \cdot 4=8\).
Suorakulmion ja sen sisällä olevan kolmion rajaamat kolme kolmiota ovat suorakulmaisia, joten lasketaan kolmioiden kateettien pituudet ja pinta-alat.
Kolmio \(ADB\)
\(|DA|= 2-1=1 \\ |DB|=2-0=2 \\ A_{ADB}=\frac{2 \cdot 1}{2}=1\)
Kolmio \(AFC\)
\(|AF|= 1-0=1 \\ |FC|=4-0=4 \\ A_{ADB}=\frac{1 \cdot 4}{2}=2\)
Kolmio \(BEC\)
\(|BE|= 4-2=2 \\ |EC|=2-0=2 \\ A_{ADB}=\frac{2 \cdot 2}{2}=2\)
Vähennetään suorakulmiosta sen ja kolmion \(ABC\) rajaamien kolmioiden pinta-alat, saadaan kolmion \(ABC\) pinta-ala.
\[\begin{align} A_{ABC} &= A_{suorakulmio}-(A_{ADB}+A_{AFC}+A_{BEC})& \quad &| \text{ sijoitetaan arvot} \\ A_{ABC} &= 8-(1+2+2)& \quad &| \text{ sievennetään} \\ A_{ABC} &= 3 \\ \end{align}\]
Kolmion \(ABC\) pinta ala on 3.
3. Ympyrän geometriaa
- sekantti ja tangentti - pinta-ala - sektori - segmentti -
Tason pisteet, jotka ovat kiinteällä etäisyydellä pisteestä, muodostavat ympyrän eli ympyräviivan. Ympyröihin liittyy paljon mielenkiintoisia ominaisuuksia, laskuja ja lukuja, kuten irrationaaliluku pii \(\pi\). Lue myös luvun \(\pi\) historiasta.
Tähän kappaleeseen liittyvät harjoitustehtävät löydät täältä!
Alla olevalla videolla on esitelty ympyään liittyviä käsitteitä. Ne käydään myöhemmin läpi yksityiskohtaisemmin.
Käytä yllä olevaa GeoGebra-applettia tutkiaksesi videolla esiintyviä ympyrän osia. Muista kokeilla raahata kehällä olevia pisteitä.
3.1 Säde, halkaisija ja piiri
Ympyrän tärkein ja sen määrittävä ominaisuus on ympyrän säde, jota merkitään usein kirjaimella \(r\) (englannin kielen sanasta radius). Joskus puhutaan myös ympyrän halkaisijasta, jota merkitään kirjaimella \(d\) (englannin kielen sanasta diameter).
Ympyrän säde, halkaisija ja piiri
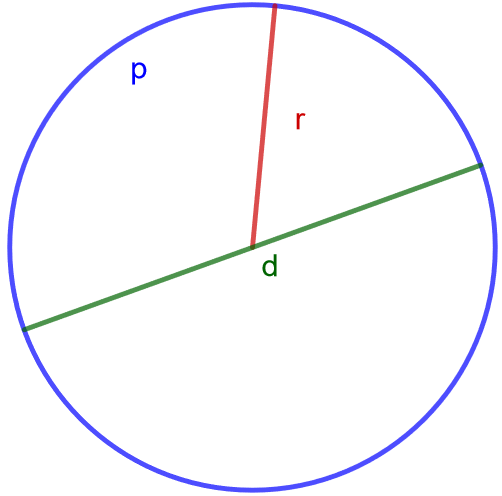
Ympyrän säde \(r\) on ympyrän keskipisteen etäisyys sen kehältä. Ympyrän halkaisija \(d\) on jana, joka kulkee ympyrän kehältä kehälle sen keskipisteen kautta. Halkaisijan pituus on \(d=2r\). Ympyrän piiri \(p\) on sen kehän pituus, ja se lasketaan \(p=2 \pi r = \pi d\).
Donitsin halkaisija on 9,5 cm ja reiän ympärys 6,1 cm.
Laske
- donitsin ulkoreunan ympärys.
- donitsin reiän säde.
Ratkaisu
Merkitään donitsin halkaisijaa kirjaimella \(d\). Donitsin ulkoreunan ympärys on \(p=2 \pi r= \pi d = \pi \cdot 9,5 \text{ cm}= 29.8451... \text{ cm}≈ 30 \text{ cm}\)
Merkitään donitsin reiän ympärystä eli piiriä kirjaimella \(p\), ja ratkaistaan sen säde
\[\begin{align} p&=2 \pi r& \quad &| :2\pi \text{ ja vaihdetaan yhtälön puolia} \\ r&= \frac{p}{2 \pi}& \quad &| \text{ sijoitetaan } p \\ &= \frac{6,1 \text{ cm}}{2 \pi}& \quad &| \text{ sievennetään} \\ &=0,9867... \text{ cm}& \quad &| \text{ pyöristetään yhden desimaalin tarkkuuteen} \\ &≈ 1,0 \text{ cm}. \\ \end{align}\]
3.2 Pinta-ala
Alla olevassa Opetus-tv:n videossa johdetaan ympyrän pinta-alan tuttu laskukaava. Videon täysi ymmärtäminen ei ole edellytys tehtävien osaamiselle, mutta se voi avata hieman paremmin, mistä ympyrän pinta-alan laskukaava tulee.
Ympyrän pinta-ala
Ympyrän pinta-ala lasketaan sen säteen \(r\) avulla seuraavasti \[A=\pi r^2.\]
Pihalle halutaan rakentaa ympyrän muotoinen uima-allas. Sille on varattu neliön muotoinen alue, jonka sivun pituus on \(2,5 \text{ m}\). Kuinka suuri on suurimman mahdollisen uima-altaan pinta-ala?
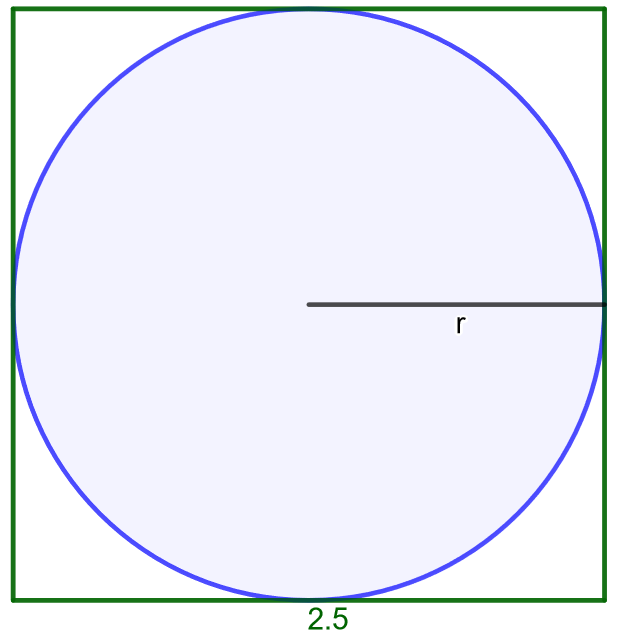
Ratkaisu
Yllä olevassa kuvassa on piirretty mallikuva tilanteesta. Jotta voitaisi laskea ympyrän pinta-ala, tulee selvittää neliöön mahtuvan ympyrän säde. Koska neliön sivun pituus on \(2,5 \text{ m}\), se on samalla ympyrän halkaisija. Ympyrän säde on puolet sen halkaisijasta, jolloin se on \(r=1,25 \text{ m}\).
Nyt ympyrän pinta-ala lasketaan \[ \begin{aligned} A&=\pi r^2& \quad &| \text{ sijoitetaan }r \\ A&= \pi \cdot 1,25^2& \quad &| \text{ sievennetään} \\ A&\approx 4,90874 \end{aligned} \] Vastausta annettaessa muistetaan lisätä tarvittava yksikkö. Eli alueelle mahtuvan suurimman mahdollisen uima-altaan pinta-ala on noin \(4,9 \text{ m}^2\).
3.3 Keskuskulma, kaaren pituus, sektorin pinta-ala
Käsitellään seuraavaksi ympyrään liittyviä käsitteitä. Jos ympyrä jaetaan osiin, muodostuu keskuskulmia, joita voidaan merkitä tutuilla merkinnöillä \(\alpha,\;\beta,\;\gamma...\). Muodostuva osa on nimeltään sektori, ja sen kaarella on jokin pituus \(b\). Lisäksi ympyrän sektorin pinta-ala on mahdollista määrittää.
Keskuskulma
Kulma, jonka kärki on ympyrän keskipisteessä, on keskuskulma.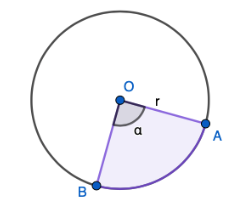 
Ympyrän kaaren pituus
Keskuskulman \(\alpha\) kyljet rajaavat ympyrän kehältä kaaren, jonka pituus \(b\) voidaan laskea seuraavasti \[b = \frac{\alpha}{360 ^{\circ}} 2\pi r.\]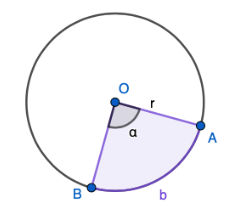 
Perustellaan ympyrän kaaren pituuden laskukaava \[b=\frac{\alpha}{360^{\circ}} 2 \pi r.\] Laskukaavan jälkimmäinen termi \(2 \pi r\) on sama kuin koko ympyrän piiri. Laskukaavan ensimmäinen termi \(\frac{\alpha}{360^{\circ}}\) kuvaa sitä, kuinka suuri osa kokonaisen ympyrän piiristä otetaan.
Jos kaarta vastaavan keskuskulman suuruus on esimerkiksi \(180^{\circ}\), on kyseisen kaaren pituus luonnollisesti puolet kokonaisen ympyrän kehän pituudesta, sillä \(\frac{180^{\circ}}{360^{\circ}}=\frac{1}{2}\).
Tarkastellaan alla olevan kuvan kaltaista sektoria.
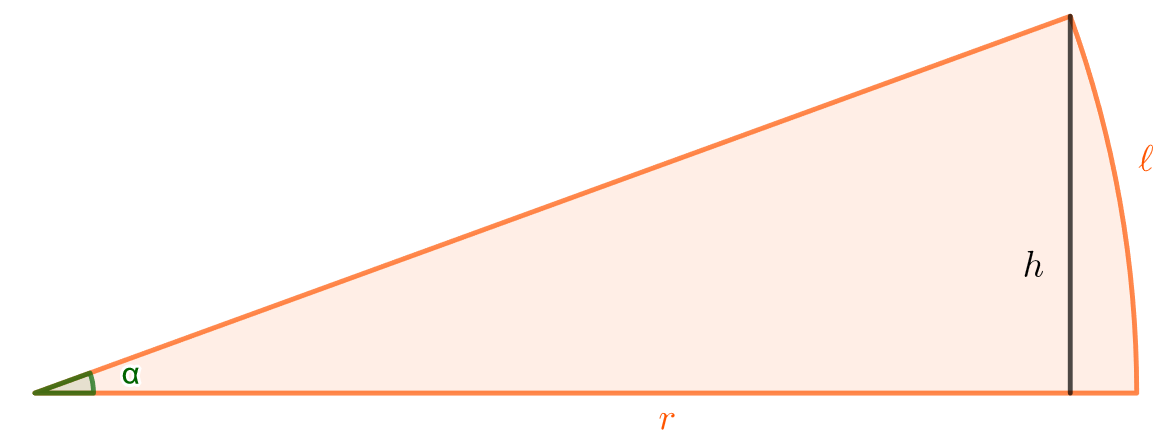
Ratkaistaan kaaren \(\ell\) pituus. Jos kulma \(\alpha\) on ilmaistu radiaaneissa, edellinen kaava muuttuu muotoon
\[b=\frac{\alpha}{2 \pi} 2 \pi r = \alpha r.\]
Nyt siis kaarelle \(\ell=\alpha r\). Pystysuoran pituuden \(h\) suuruus voidaan määrittää sinin avulla:
\[\sin \alpha= \frac{h}{r} \quad \Leftrightarrow \quad h = r \sin \alpha.\]
Kun kulmaa \(\alpha\) pienennetään, janan \(h\) ja kaaren \(\ell\) pituudet lähestyvät toisiaan. Voidaan siis merkitä, että kun \(\alpha\) on pieni,
\[ \begin{aligned} h & \approx \ell \\ r \sin \alpha & \approx \alpha r \quad |:r \\ \sin \alpha & \approx \alpha \end{aligned} \]
Eli kun kulma \(\alpha\) on pieni, sen siniä voidaan approksimoida kulman arvolla (radiaaneina).
Ympyrän sektorin pinta-ala
Keskuskulman \(\alpha\) kyljet rajaavat ympyrän sisältä sektorin, jonka pinta-ala \(A_{SEK}\) voidaan laskea seuraavasti: \[A_{SEK}= \frac{\alpha}{360 ^{\circ}} \pi r^2.\] Jos tiedetään keskuskulmaa vastaavan kaaren pituus \(b\), voidaan sektorin pinta-ala laskea myös kaavalla \[A_{SEK}=\frac{br}{2}.\]
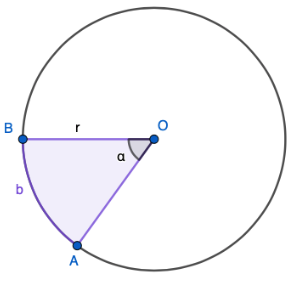
Sektorin pinta-alan ylempi kaava voidaan perustella samalla tavalla kuin ympyrän kaaren pituuden kaava perusteltiin aiemmin. Toinen kaava voidaan perustella sijoittamalla siihen \(b=\frac{\alpha}{360^{\circ}} 2 \pi r\), jolloin saadaan \[A_{SEK}=\frac{\alpha}{360^{\circ}} 2 \pi r \cdot \frac{r}{2}=\frac{\alpha}{360^{\circ}} \pi r^2\] joka on sama kuin sektorin pinta-alan ylempi kaava.
Laske alla olevan ympyräsektorin pinta-ala. Kuinka suuri keskuskulma \(\alpha\) on?
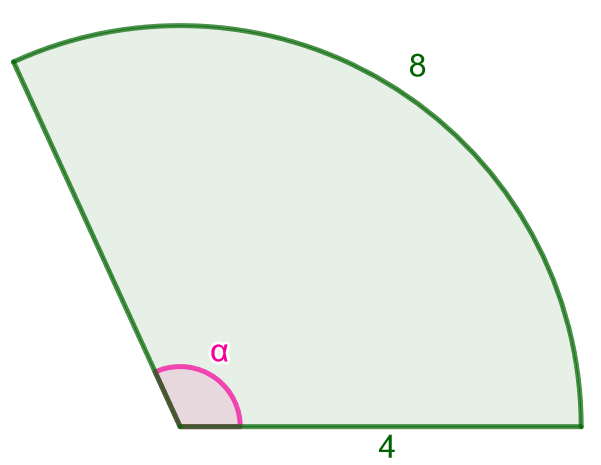
Ratkaisu
Nyt kaaren pituus on \(b=8\) ja säde \(r=4\). Sektorin pinta-ala saadaan laskettua näiden tietojen avulla: \[A=\frac{br}{2}=\frac{8 \cdot 4}{2}=16.\]
Nyt kysytyn keskuskulman suuruus voidaan ratkaista sektorin pinta-alan toisesta kaavasta tai kaaren pituuden kaavan avulla. Ratkaistaan tässä keskuskulma ensimmäisellä tavalla. Ratkaistaan \(\alpha\) sektorin pinta-alan kaavasta ja sijoitetaan arvot kaavaan \[ \begin{aligned} A&=\frac{\alpha}{360^{\circ}} \pi r^2 &\quad &|\cdot 360^{\circ} \\ 360 ^{\circ} A&= \alpha \pi r^2 &\quad &|:\pi r^2 \\ \alpha &= \frac{360^{\circ} A}{\pi r^2}& \quad &| \text{ sijoitetaan }A \text{ ja }r \\ \alpha &= \frac{360^{\circ} \cdot 16}{\pi \cdot 4^2}& \quad &| \text{ sievennetään} \\ \alpha &\approx 114,591559 ^{\circ}& \quad &| \text{ pyöristetään yhden desimaalin tarkkuuteen} \\ \alpha &\approx 114,6 ^{\circ} \end{aligned} \]
Sektorin pinta-ala on siis \(16\) ja sen keskuskulman suuruus on noin \(114,6^{\circ}\).
3.4 Jänne, segmentti
Ympyrä voidaan jakaa myös osiin, jotka eivät osu ympyrän keskipisteeseen \(O\). Tällaista janaa, joka piirretään kahden kehän pisteen välille kutsutaan jänteeksi, ja se rajaa ympyrästä kaksi segmenttiä.
Jänne
Ympyrän kehällä olevan kaaren päätepisteet yhdistää jänne.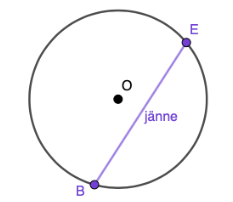 
Segmentin pinta-ala
Jänne jakaa ympyrän kahdeksi segmentiksi, joiden pinta-ala \(A_{SEG}\) saadaan laskettua kaavalla \[A_{SEG}=A_{SEK} \pm A_{keskuskolmio}.\] Kaavassa käytetään yhteenlaskua, jos keskuskulma \(\alpha\) on suurempi kuin \(180^{\circ}\), ja vähennyslaskua, jos keskuskulma \(\alpha\) on pienempi kuin \(180^{\circ}\).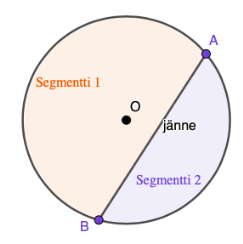 
Laske alla olevaan kuvaan sinisellä merkityn segmentin pinta-ala.
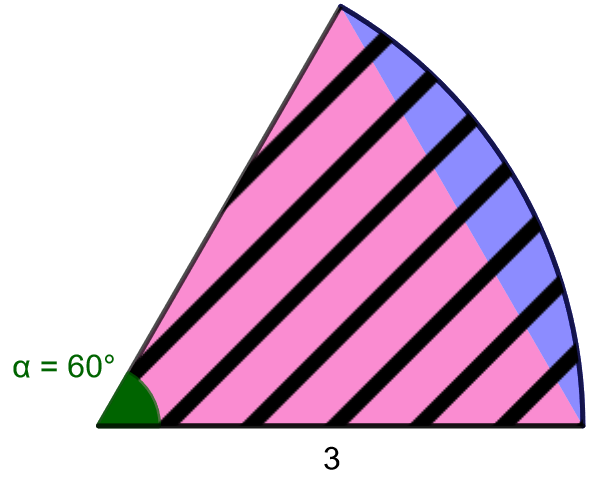
Ratkaisu
Koska keskuskulma \(\alpha\) on pienempi kuin \(180^{\circ}\), käytetään kaavaa \[A_{SEG}=A_{SEK}-A_{\text{keskuskolmio}}.\] Lasketaan ensin kuvaan mustalla vinoviivoituksella merkityn sektorin pinta-ala. Sektorin säde \(r=3\) ja keskuskulma \(\alpha=60^{\circ}\), joten sektorin pinta-ala on \[ \begin{aligned} A_{SEK}&=\frac{\alpha}{360^{\circ}} \pi r^2 & \quad &| \text{ sijoitetaan }\alpha \text{ ja }r \\ &=\frac{60^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2& \quad &| \text{ sievennetään} \\ &=\frac{3\pi}{2} \end{aligned} \] Lasketaan sitten kuvaan pinkillä merkityn keskuskolmion pinta-ala. Kolmion kahden sivun pituudet ovat säteen mittaiset eli \(3\), ja näiden sivujen välinen kulma on \(\alpha=60^{\circ}\). Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla, jossa \(a=b=r=3\). \[ \begin{aligned} A_{\text{keskuskolmio}}&=\frac{ab}{2} \sin(\alpha)& \quad &| \text{ sijoitetaan }ab=r^2 \\ &=\frac{r^2}{2} \sin(\alpha)& \quad &| \text{ sijoitetaan }r\text{ ja }\alpha \\ &=\frac{3^2}{2} \sin(60^{\circ})& \quad &| \text{ sievennetään} \\ &=\frac{9\sqrt{3}}{4} \end{aligned} \] Lopuksi lasketaan segmentin pinta-ala vähennyslaskulla \[ \begin{aligned} A_{SEG}&=A_{SEK}-A_{\text{keskuskolmio}}& \quad &| \text{ sijoitetaan }A_{SEK}\text{ ja }A_{keskuskolmio} \\ &= \frac{3 \pi}{2} - \frac{9 \sqrt{3}}{4}& \quad &| \text{ lavennetaan luku }\frac{3\pi}{2}\text{ luvulla 2} \\ &= \frac{6 \pi}{4} - \frac{9 \sqrt{3}}{4}& \quad &| \text{ sievennetään} \\ &= \frac{6 \pi - 9 \sqrt{3}}{4}& \quad &| \text{ sievennetään} \\ &\approx 0,81527& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ &\approx 0,82 \end{aligned} \] Kysytyn segmentin pinta-ala on siis noin \(0,82\).
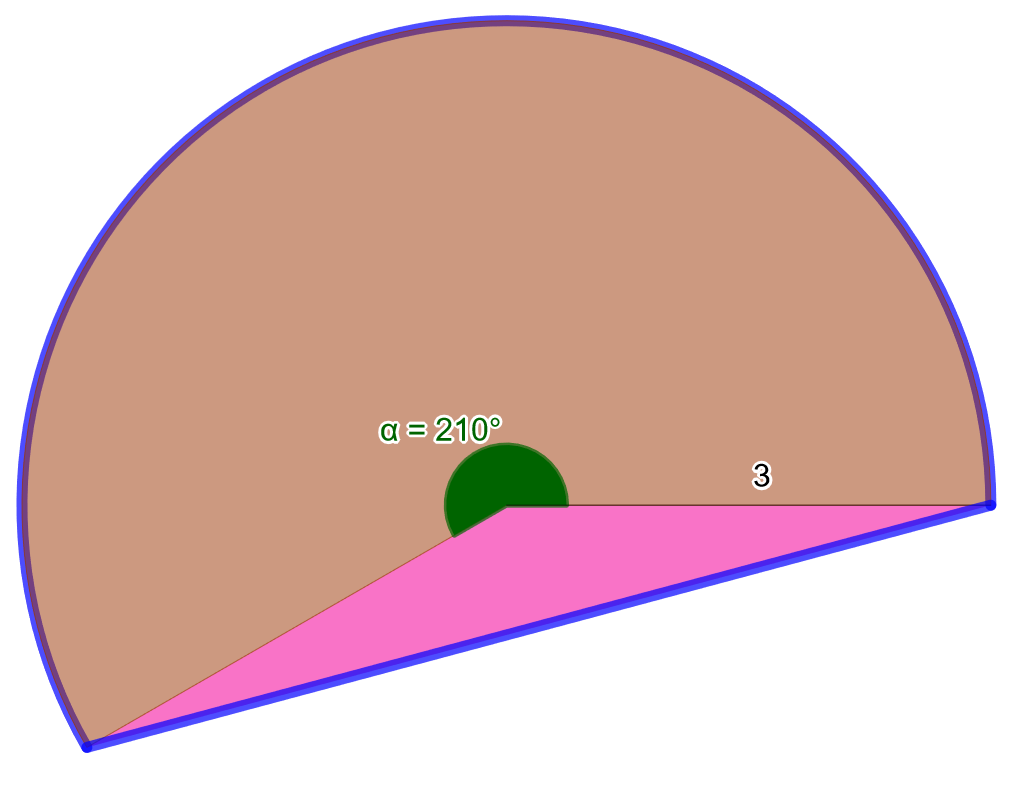
Ratkaise alla olevaan kuvaan sinisellä rajatun segmentin pinta-ala.
Ratkaisu
Koska keskuskulma \(\alpha=210^{\circ}\) on suurempi kuin \(180^{\circ}\), käytetään laskukaavaa \[A_{SEG}=A_{SEK}+A_{\text{keskuskolmio}}.\]
Lasketaan ensin kuvaan ruskealla merkityn sektorin pinta-ala. Nyt säde \(r=3\) ja keskuskulma \(\alpha=210^{\circ}\), joten sektorin pinta-ala on \[ \begin{aligned} A_{SEK} &= \frac{\alpha}{360^{\circ}}\pi r^2& \quad &| \text{ sijoitetaan }\alpha\text{ ja }r \\ &= \frac{210^{\circ}}{360^{\circ}} \pi \cdot 3^2& \quad &| \text{ sievennetään} \\ &= \frac{21 \pi}{4} \end{aligned} \] Seuraavaksi lasketaan keskuskolmion pinta-ala. Kolmion kahden sivun pituus on \(a=b=r=3\) ja näiden sivujen välisen kulman suuruus on \(\beta=360^{\circ}-210^{\circ}=150^{\circ}\). Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla. \[ \begin{aligned} A_{\text{keskuskolmio}}&= \frac{r^2}{2} \sin(\beta)& \quad &| \text{ sijoitetaan }r \text{ ja }\beta \\ &= \frac{3^2}{2} \sin(150^{\circ})& \quad &| \text{ sievennetään} \\ &= \frac{9}{4} \end{aligned} \] Lopuksi lasketaan segmentin pinta-ala yhteenlaskulla \[ \begin{aligned} A_{SEG} &= A_{SEK} + A_{\text{keskuskolmio}}& \quad &| \text{ sijoitetaan }A_{SEK}\text{ ja } A_{keskuskolmio} \\ &= \frac{21 \pi}{4} + \frac{9}{4}& \quad &| \text{ sievennetään} \\ &= \frac{21\pi +9}{4}& \quad &| \text{ sievennetään} \\ & \approx 18,7436& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ &\approx 18,74 \end{aligned} \]
Kuvaan sinisillä ääriviivoilla piirretyn segmentin pinta-ala on noin \(18,74\).
3.5 Tangentti, tangenttikulma
Sanalla tangentti voidaan matematiikassa tarkoittaa kahta asiaa, ja ne molemmat liittyvät geometriaan. Yleensä asiayhteydestä selviää, puhutaanko trigonometrisesta funktiosta nimeltä tangentti vai käyrää tasan yhdessä pisteessä sivuava suora. Tässä luvussa puhutaan tangentista sen jälkimmäisessä merkityksessä.
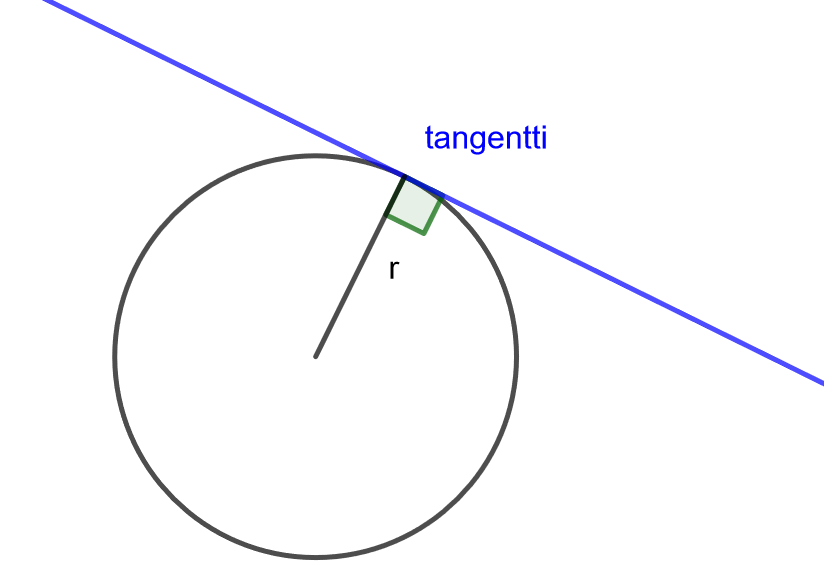
Tangentti
Tangentti on suora, joka kohtaa ympyrän vain yhdessä pisteessä. Ympyrän tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan.
Tangenttikulma
Tangenttikulma on kahden ympyrän tangentin leikkauspisteeseen muodostuva kulma, jonka aukeamassa ympyrä on. Tangenttikulman ja sitä vastaavan keskuskulman summa on aina \(180^{\circ}\).
Todistetaan tangenttikulmalause, jonka mukaan tangenttikulman ja sitä vastaavan keskuskulman summa on aina \(180^{\circ}\). Käytetään alla olevan kuvan merkintöjä.
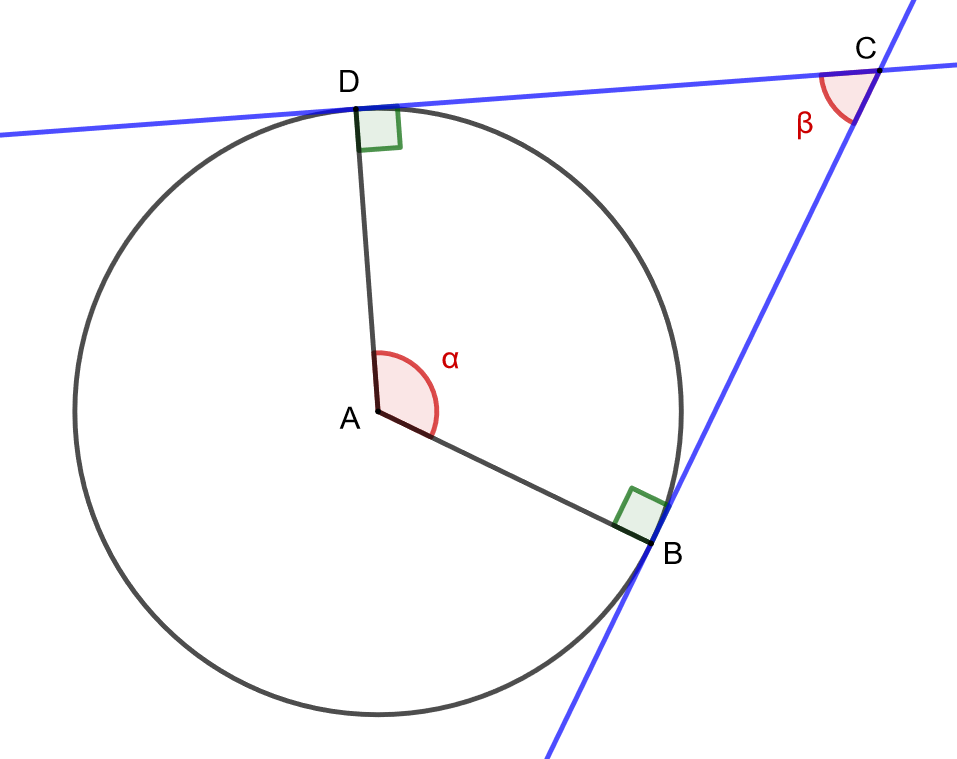
Ympyrän keskipiste \(A\), sen kehän pisteet \(B\) ja \(D\) sekä näiden kehän pisteiden kautta piirrettyjen tangenttien leikkauspiste \(C\) muodostavat nelikulmion \(ABCD\). Nelikulmion kulmien summa on aina \(360^{\circ}\). Ympyrän säteen \(AB\) sekä tangentin \(BC\) välinen kulma on aina suora. Samoin säteen \(AD\) ja tangentin \(CD\) välinen kulma on aina suora. Tästä saadaan, että on oltava \[\alpha + \beta = 360^{\circ} - 2 \cdot 90^{\circ} = 180^{\circ}.\] Toisin sanoen, tangenttikulman ja sitä vastaavan keskuskulman summan on oltava \(180^{\circ}\). Yllä olevalla GeoGebra-appletilla voit tutkia tangenttikulman ja sitä vastaavan keskuskulman suuruuksia. Huomaa, että tangenttien ja ympyrän säteiden väliset kulmat ovat koko ajan suoria kulmia, vaikka sinisiä pisteitä siirtäisikin.
Ympyrälle O on piirretty kaksi tangenttia, jotka molemmat kulkevat saman pisteen A kautta. Laske suuruus tangenttikulmalle \(\alpha\).
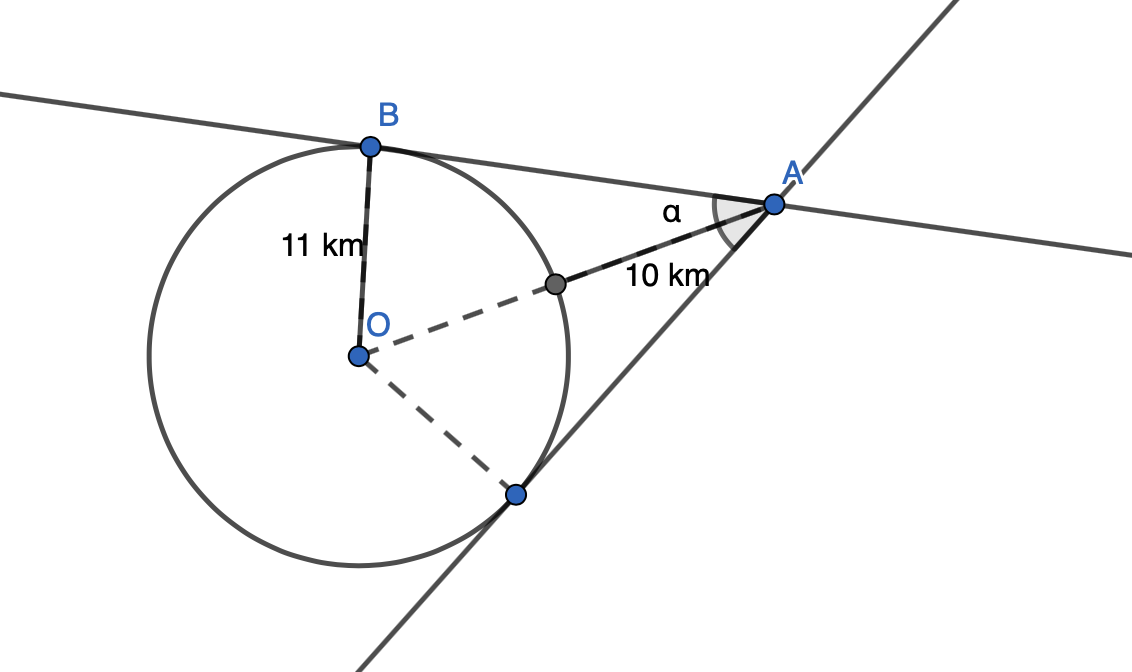
Ratkaisu
Nyt kolmio \(OAB\) on suorakulmainen, koska jana \(OB\) on kohtisuorassa janaa \(AB\) vastaan. Suorakulmaisen kolmion hypotenuusa on siis jana \(OA\).
Hypotenuusan pituus on
\(11 \text{ km} + 10 \text{ km} = 21 \text{ km}\)
Merkitään kirjaimella \(\beta\) kolmion kulmaa \(OAB\). Ratkaistaan kulma \(\beta\) sinin avulla.
\[\begin{align} \sin{\beta} &= \frac{11 \text{ km}}{21 \text{ km}}& \quad &| \text{ sievennetään ja otetaan }\sin^{-1} \\ \beta &= 31,5888...° \\ \end{align}\]
Kulma \(\beta\) on puolet halutun tangenttikulman suuruudesta. Tällöin \(\alpha= 2 \cdot 31,5888...°≈ 63°\)
Tangenttikulman suuruus on \(63°\).
Yllä olevalla GeoGebra-appletilla voit tutkia tangenttikulman ja sitä vastaavan keskuskulman suuruuksia. Huomaa, että tangenttien ja ympyrän säteiden väliset kulmat ovat koko ajan suoria kulmia, vaikka sinisiä pisteitä siirtäisikin.
Kehäkulma
Kehäkulma on kulma, jonka kärki on ympyrän kehällä ja jonka kylkinä on kaksi jännettä tai jänne ja tangentti. Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta. Samaa kaarta vastaavat kehäkulmat ovat aina yhtä suuria.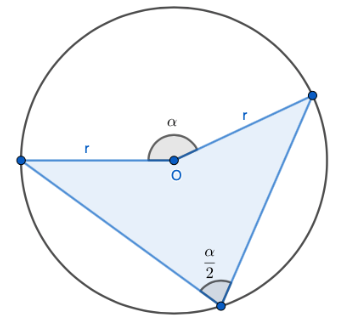 
Todistetaan kehäkulmalause eli lause "Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta". Tehdään todistus kolmessa vaiheessa:
- ympyrän keskipiste \(O\) on kehäkulman \(\beta\) kyljellä,
- ympyrän keskipiste \(O\) on kehäkulman \(\beta\) aukeamassa ja
- ympyrän keskipiste \(O\) ei ole kehäkulman \(\beta\) aukeamassa.
Tarkastellaan ensin tapausta, jossa jänne \(AC\) kulkee ympyrän keskisteen \(O\) kautta. Käytetään alla olevan kuvan merkintöjä.
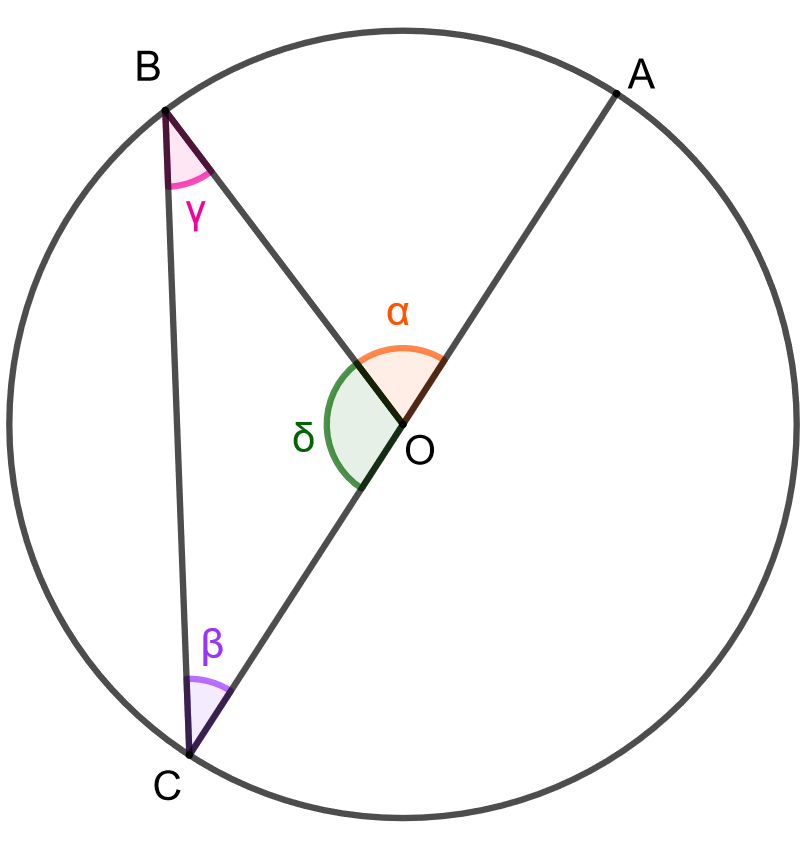
Huomataan, että pisteet \(O\), \(B\) ja \(C\) muodostavat tasakylkisen kolmion, jonka kantana on jänne \(BC\) ja kylkinä janat \(BO\) sekä \(CO\). Kyljet ovat keskenään yhtä pitkiä, koska molemmat ovat ympyrän säteitä. Tasakylkisen kolmion kantakulmat ovat keskenään yhtä suuria, joten \(\beta = \gamma\). Koska kolmion kulmien summa on \(180^{\circ}\), saadaan yhtälö \[\beta + \gamma + \delta = 180^{\circ}.\] Lisäksi huomataan, että kulmat \(\alpha\) ja \(\delta\) ovat vieruskulmia, jolloin niiden summa on \(180^{\circ}\) eli \(\alpha + \delta = 180^{\circ}\). Ratkaistaan tästä kulma \(\delta\), jolloin saadaan \(\delta = 180^{\circ} - \alpha\). Sijoitetaan tämä sekä \(\gamma = \beta\) kolmion kulmien summan lausekkeeseen, jolloin saadaan \[\beta + \beta + 180^{\circ} - \alpha = 180^{\circ} \Leftrightarrow \beta = \frac{\alpha}{2}.\] Eli kehäkulma on puolet vastaavasta keskuskulmasta. Tarkastellaan seuraavaksi tapausta, jossa ympyrän keskipiste \(O\) on kehäkulman \(\beta\) aukeamassa. Käytetään alla olevan kuvan merkintöjä.
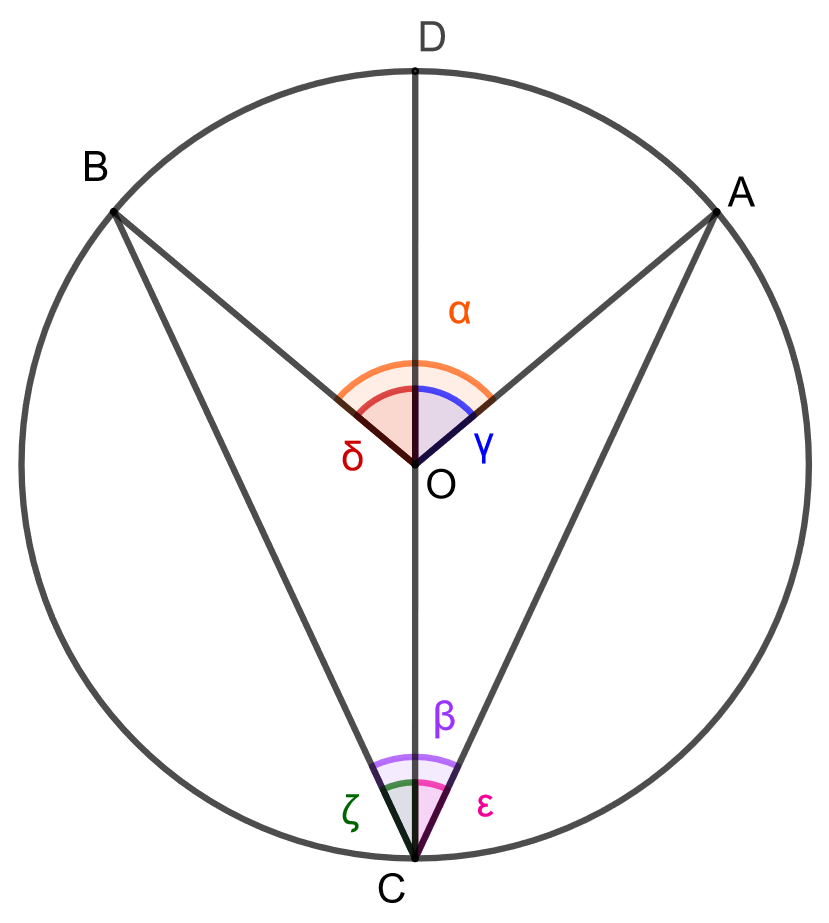
Jaetaan kulma \(\alpha\) kahdeksi kulmaksi \(\gamma\) ja \(\delta\) janalla \(CD\), joka kulkee ympyrän keskipisteen \(O\) kautta. Sama jana jakaa kehäkulman \(\beta\) kulmiksi \(\epsilon\) ja \(\zeta\). Voimme tarkastella ensin pelkästään janan \(CD\) oikealla puolella olevia kulmia ja sitten sen vasemmalla puolella olevia. Tällöin todistuksen edellisen kohdan perusteella saadaan \(\epsilon = \frac{\gamma}{2}\) ja \(\zeta=\frac{\delta}{2}\).
Tiedetään, että \(\alpha = \gamma + \delta\). Lisäksi tiedetään, että \(\beta = \epsilon + \zeta\). Sijoitetaan tähän aiemmat yhtälöt, jolloin saadaan \[\beta = \frac{\gamma}{2} + \frac{\delta}{2} = \frac{\gamma + \delta}{2} = \frac{\alpha}{2}.\] Eli kehäkulma \(\beta\) on puolet vastaavasta keskuskulmasta \(\alpha\).
Tarkastellaan lopuksi tapausta, jossa ympyrän keskipiste \(O\) ei ole kehäkulman \(\beta\) aukeamassa. Käytetään alla olevan kuvan merkintöjä.
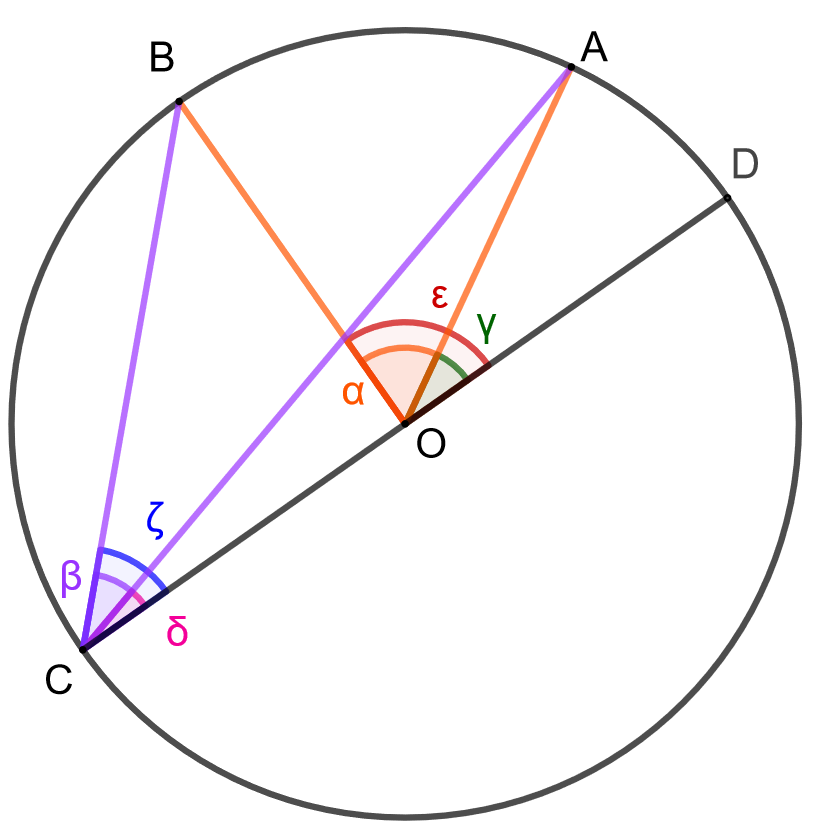
Huomataan, että \(\alpha = \epsilon - \gamma\) ja että \(\beta = \zeta - \delta\). Todistuksen ensimmäisen kohdan perusteella voidaan kirjoittaa \[\beta = \zeta - \delta = \frac{\epsilon}{2} - \frac{\gamma}{2} = \frac{\epsilon - \gamma}{2} = \frac{\alpha}{2}.\] Kehäkulma \(\beta\) on siis puolet keskuskulmasta \(\alpha\).
Yllä olevassa GeoGebra-appletissa on merkitty vihreällä keskuskulma ja pinkillä samoja pisteitä vastaava kehäkulma. Kokeile muuttaa kulmien suuruuksia, ja huomaa, että kehäkulma on aina puolet vastaavan keskuskulman suuruudesta.
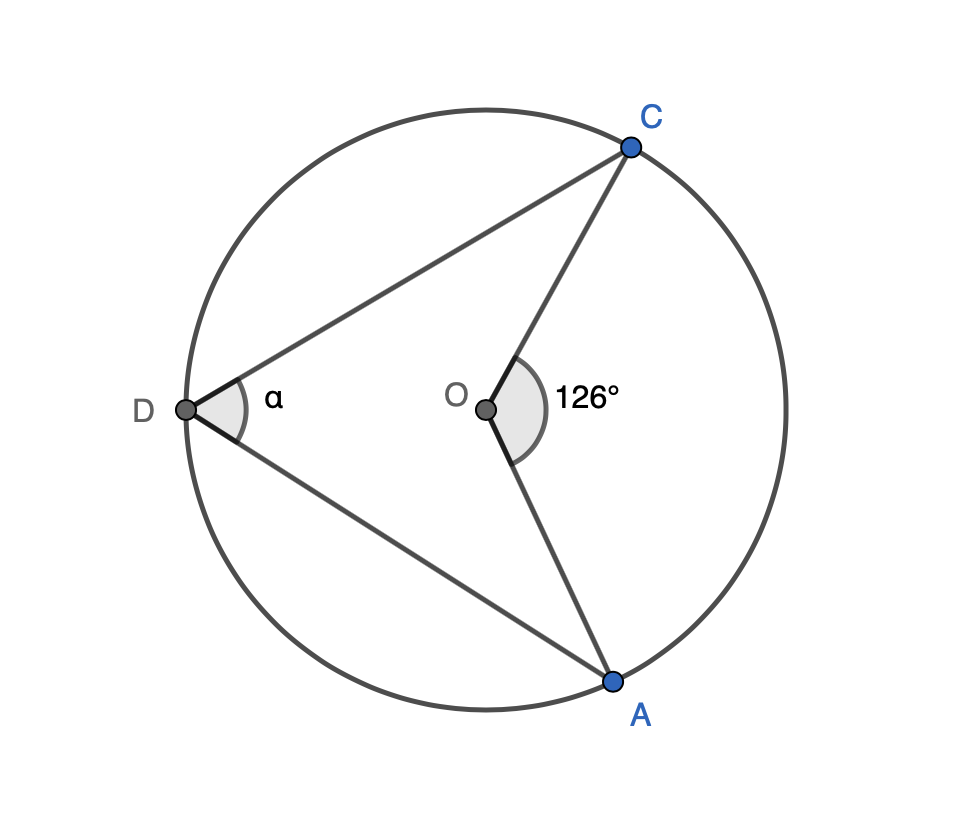
Laske kulman \(\alpha\) suuruus.
Ratkaisu
Ympyrän keskipiste on \(O\) ja pisteet \(A\), \(B\) ja \(C\) ovat ympyrän kehällä. Keskuskulma \(AOC\) ja kehäkulma \(ADC\), eli kulma \(\alpha\), vastaavat kaarta \(AC\). Kehäkulmalauseen nojalla kehäkulma on puolet vastaavan kaaren keskuskulmaan verrattuna, joten
\(\angle ADC = \alpha = \frac{126°}{2} = 63°\)
Yllä olevassa GeoGebra-appletissa on piirretty kaksi samaa ympyrän kaarta vastaavaa kehäkulmaa. Kokeile siirtää kuvion pisteitä ja huomaa, että kehäkulmat pysyvät koko ajan yhtä suurina keskenään.
3.7 Ympyrä koordinaatistossa
Samoin kuin monikulmioidenkin tilanteessa, ympyrä voidaan myös piirtää koordinaatistoon ja tutkia sen ominaisuuksia koordinaatiston avulla.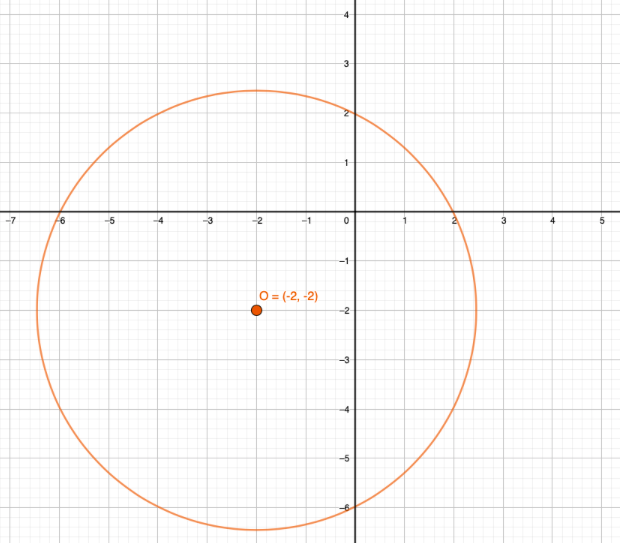 
Yllä olevassa kuvassa on piirretty ympyrä \(xy\)-koordinaatistoon. Ympyrän keskipiste \(O\) on kuvan mukaan pisteessä \((-2,-2)\).
Määritetään ympyrän säteen pituus. Hyödynnetään Monikulmiot koordinaatistossa -luvusta tuttuja lauseita janan pituudelle.
Ympyrän kehällä olevat pisteet ovat kaikki yhtä kaukana keskipisteestä. Tämä etäisyys on ympyrän säde \(r\). Valitaan nyt mikä tahansa piste kehältä, vaikkapa piste \(2,0\).
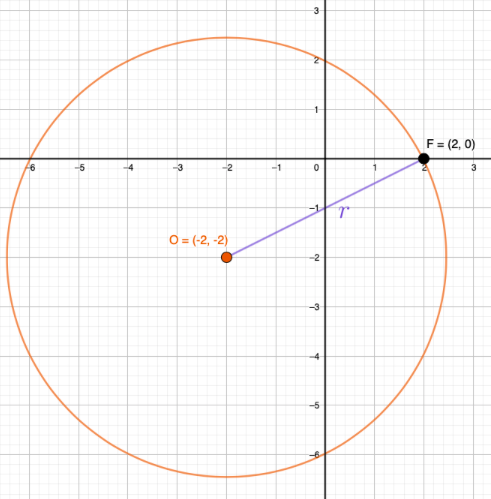
Lasketaan nyt siis janan \(OF\) pituus: \[\begin{align*} |OF|=\sqrt{(2-(-2))^{2}+(0-(-2))^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{20}=2\cdot\sqrt{5} \end{align*}\]
Ympyrän säde \(r=2\sqrt{5}\) ja keskipiste on pisteessä \((-2,-2)\).
Ympyrän keskipiste on \(O(-1,3)\) ja kehäpiste \(A(0,2)\). Ympyrälle piirretään kaksi tangenttia pisteen \(B(1,4)\) kautta. Tutki laskemalla, sivuaako toinen pisteen \(B\) kautta piirretyistä tangenteista ympyrää pisteessä \(A\).
Ratkaisu
Piirretään ensin kuvaan ympyrä ja tangentit.
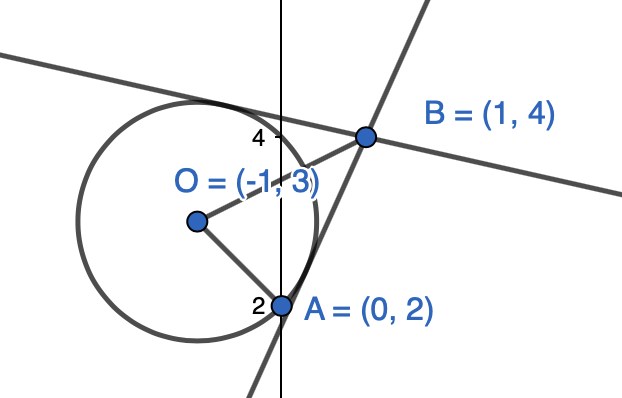
Tarkastellaan kolmiota \(OAB\). Jos piste \(A\) on sivuamispiste, tulisi kolmion olla suorakulmainen. Käytetään käänteistä Pythagoraan lausetta ja tutkitaan, toteuttavatko kolmion sivujen pituudet Pythagoraan lauseen.
Lasketaan ensin sivujen pituudet.
\(|OA|= \sqrt{(0- (-1))^2 + (2-3)^2} = \sqrt{2} \\ |OB|= \sqrt{(1-(-1))^2 + (4-3)^2} = \sqrt{5} \\ |BA|= \sqrt{(0-1)^2 + (2-4)^2} = \sqrt{5} \\\)
Tarkistetaan, toteuttavatko pituudet Pythagoraan lauseen.
\[\begin{align} |OB|^2 &= |OA|^2 + |BA|^2& \quad &| \text{ sijoitetaan arvot} \\ (\sqrt{5})^2 &= (\sqrt{2})^2 + (\sqrt{5})^2& \quad &| \text{ sievennetään} \\ 5 &= 2 + 5& \quad &| \text{ sievennetään} \\ 5 &≠ 7 \\ &\text{epätosi} \\ \end{align}\]
Koska sivujen pituudet eivät toteuttaneet Pythagoraan lausetta, ei kolmio \(OAB\) ole suorakulmainen eikä tangentti siis sivua ympyrää pisteessä \(A\).
4. Avaruusgeometriaa
- avaruuskappaleet - avaruuslävistäjä - pinta-alat ja tilavuudet
4.1 Avaruuskappaleita
Tässä luvussa siirrytään tasosta kolmiulotteiseen avaruuteen. Kuitenkin monia tasogeometriassa opittuja lauseita ja ominaisuuksia voi hyödyntää myös avaruusgeometriassa.
Tähän kappaleeseen liittyvät harjoitustehtävät löydät täältä!
Yllä olevassa GeoGebra-appletissa on käyty läpi monitahokkaan osia ja niiden nimityksiä. Monitahokas on mikä tahansa monikulmioista koostuva suljettu pinta. Jos kaikki monitahokkaan tahkot ovat samanlaisia säännöllisiä monikulmioita, kyseessä on säännöllinen monitahokas. Tällaisia ovat esimerkiksi kuutio, säännöllinen tetraedri ja oktaedri.
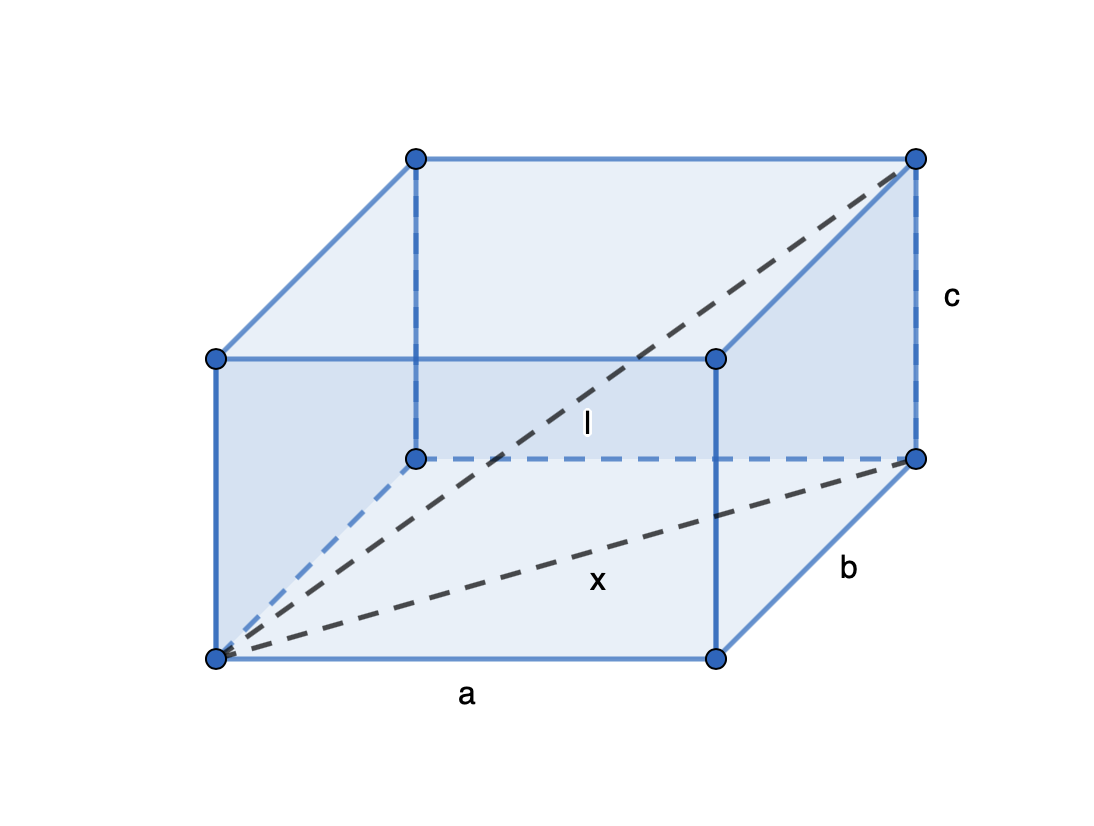
Sovelletaan kaksi kertaa Pythagoraan lausetta: avaruuslävistäjälle \(l\) ja pohjan lävistäjälle \(x\). Näin saadaan
\(x^2=a^2 +b^2\) ja \(l^2=x^2+c^2\),
ja sijoittamalla \(x^2\) yhtälö oikeanpuoleiseen yhtälöön saadaan voidaan ratkaista avaruuslävistäjä \(l\)
\(l=\sqrt{a^2+b^2+c^2}\).
Suorakulmaisen särmiön pohja on suorakulmio, jonka mitat ovat 20 cm ja 35 cm. Särmiön korkeus on 18 cm. Laske särmiön
- pohjan lävistäjän pituus
- avaruuslävistäjän pituus
- pohjan lävistäjän ja avaruuslävistäjän välinen kulma
Ratkaisu:
Merkitään pohjan lävistäjää kirjaimella x, ja ratkaistaan se Pythagoraan lauseella.
\[\begin{align} x^2 &={(20\text{ cm})}^2+{(35\text{ cm})}^2& \quad &| \sqrt{\text{ }} \\ x &=\sqrt{{(20\text{ cm})}^2+{(35\text{ cm})}^2}& \quad &| \text{ sievennetään} \\ x &= \pm 40,311... \text{ cm}& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ x &≈ \pm 40 \text{ cm}. \\ \end{align}\]
Koska \(x>0\), niin pohjan lävitäjän pituus on 40 cm.
Merkitään avaruuslävistäjää kirjaimella \(l\), ja ratkaistaan se Pythagoraan lauseella seuraavasti
\[\begin{align} l^2 &={(20\text{ cm})}^2+{(35\text{ cm})}^2+{(18\text{ cm})}^2& \quad &| \sqrt{\text{ }} \\ l &=\sqrt{{(20\text{ cm})}^2+{(35\text{ cm})}^2+{(18\text{ cm})}^2}& \quad &| \text{ sievennetään} \\ &=44,147...\text{ cm}& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈44\text{ cm}. \\ \end{align}\]
Avaruuslävistäjän pituus on siis 44 cm.
Merkitään pohjan lävistäjän ja avaruuslävistäjän välistä kulmaa kirjaimella \(\alpha\). Ratkaistaan kulma tangentin avulla.
\[\begin{align} \tan{\alpha} &=\frac{18\text{ cm}}{40.311...\text{ cm}}& \quad &| \text{ sievennetään ja otetaan} \tan^{-1}() \\ {\alpha} &= 24,062... °& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ {\alpha} &≈ 24 ° \end{align}\]
4.2 Pallo
Pallon pinta-ala ja tilavuus
Pallon muodostavat ne pisteet, jotka ovat säteen \(r\) etäisyydellä pallon keskipisteestä. Pallon pinta-ala ja tilavuus lasketaan sen säteen \(r\) avulla \[A=4 \pi r^2\] ja \[V=\frac{4\pi r^3}{3}.\]
Jalkapallon ympärysmitta on 68 cm.
- Laske jalkapallon pinta-ala yksikössä \(\text{dm}^2\).
- Laske jalkapallon tilavuus litroina.
Ratkaisu
Pallon säde voidaan selvittää ympärysmitan \(2\pi r\) avulla. Ympärysmitan kaavassa r on pallon säde.
\[\begin{align} 2\pi r& = 68& \quad &| :2\pi \\ r &= \frac{68}{2\pi}& \quad &| \text{ sievennetään} \\ r &= 10,8225... (\text{cm}) \\ \end{align}\] Nyt voidaan laskea pallon pinta-ala.
\[\begin{align} A &=4 \pi r^2& \quad &| \text{ sijoitetaan säde }r \\ &= 4 \cdot \pi \cdot (10,8225... \text{ cm})^2& \quad &| \text{ sievennetään} \\ &=1471,8550... \text{ cm}^2& \quad &| \text{ muunnetaan yksikköön dm}^2 \\ &=14,718550... \text{ dm}^2& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈ 15 \text{ dm}^2 \\ \end{align}\]
Jalkapallon pinta-ala on \(15 \text{ dm}^2\).
Lasketaan pallon tilavuus.
\[\begin{align} V &= \frac{4}{3} \pi r^3& \quad &| \text{ sijoitetaan säde }r \\ &= \frac{4}{3} \cdot \pi \cdot (10,8225... \text{ cm})^3& \quad &| \text{ sievennetään} \\ &= 5309,7172...\text{ cm}^3& \quad &| \text{ muunnetaan yksikköön dm}^3 = \text{l}\\ &= 5,3097172...\text{ dm}^3& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈ 5,3 \text{ l}\\ \end{align}\]
Jalkapallon tilavuus on \(5,3\) litraa.
4.3 Lieriö
Lieriön pinta-ala ja tilavuus
Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa, muodostuu lieriöpinta. Kun lieriöpinta leikataan kahdella tasolla, syntyy lieriö. Lieriön vaipan pinta-ala saadaan laskettua sen pohjan piirin \(p\) ja lieriön korkeuden \(h\) avulla \[A_v=ph.\] Lieriön tilavuus saadaan laskettua pohjan pinta-alan \(A_p\) ja lieriön korkeuden \(h\) avulla \[V=A_p h.\]
Erityistapaus lieriöstä on suora ympyrälieriö, jota kutsutaan myös sylinteriksi. Suoran ympyrälieriön pohja on ympyrän muotoinen ja sen korkeusjana sekä pohjan säde ovat kohtisuorassa toisiaan vastaan. Lieriö, jonka pohja on muodoltaan monikulmio, on särmiö. Erikoistapaus särmiöstä on esimerkiksi suorakulmainen särmiö.
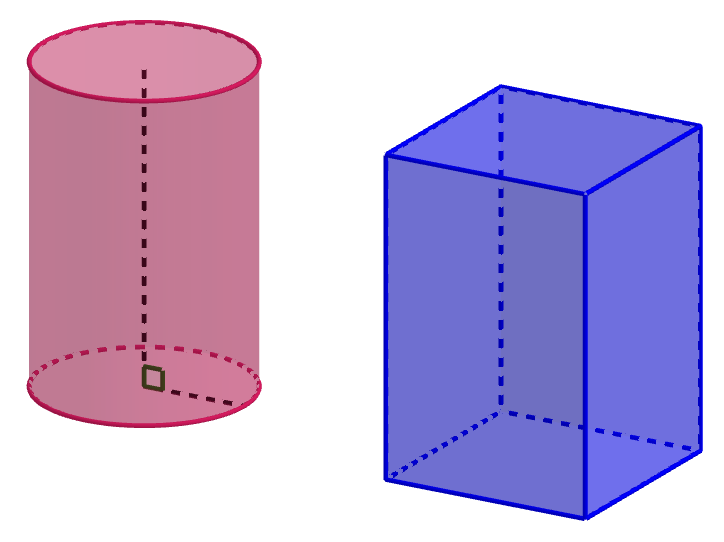
Laske suoran lieriön kokonaispinta-ala, kun sen
- korkeus on 23 cm ja pohjaympyrän halkaisija on 11 cm.
- korkeus on 55 cm ja pohja on neliö, jonka sivun pituus on 16 cm.
Ratkaisu
Ratkaistaan pohjan säde \(r\) jakamalla halkaisija kahdella.
\(r= \frac{11 \text{ cm}}{2}=5,5 \text{ cm}\)
Koska pohja on ympyrä, sen pinta-ala on
\(A_{pohja}=\pi r^2=\pi \cdot (5,5 \text{ cm})^2=95,0331... \text{ cm}^2\)
Lieriön vaippa on suorakulmio, jonka pinta-ala saadaan laskettua pohjaympyrän ympärysmitan ja lieriön korkeuden tulona.
\[\begin{align} A_{vaippa} &=2 \pi r \cdot h& \quad &| \text{ sijoitetaan säde }r \text{ ja korkeus }h \\ &= 2 \pi \cdot 5,5 \text{ cm} \cdot 23 \text{ cm}& \quad &| \text{ sievennetään} \\ &= 794,8229... \text{ cm}^2\\ \end{align}\]
Kokonaispinta-ala on
\[\begin{align} A_{lieriö} &=2 \cdot A_{pohja} + A_{vaippa}& \quad &| \text{ sijoitetaan }A_{pohja} \text{ ja }A_{vaippa} \\ &= 2 \cdot 95,0331... \text{ cm}^2 \\ &+ 794,8229... \text{ cm}^2& \quad &| \text{ sievennetään} \\ &= 984,8891... \text{ cm}^2& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈ 980 \text{ cm}^2. \\ \end{align}\]
Pohja on neliö, joten \(A_{pohja}=(16 \text{ cm})^2=256 \text{ cm}^2\)
Lasketaan vaipan pinta-alan laskemista varten pohjan ympärysmitta eli suorakulmion piiri \(p\).
\(p=4 \cdot 16 \text{ cm}= 64 \text{ cm}\)
Koska vaippa on suorakulmio, jonka korkeus on \(h=55\) cm ja kannan pituus pohjan piiri eli \(p=64\) cm.
\(A_{vaippa}=ph= 64 \text{ cm} \cdot 55 \text{ cm}=3520 \text{ cm}^2\)
Kokonaispinta-ala on
\[\begin{align} A_{lieriö} &= 2 \cdot A_{pohja}+ A_{vaippa}& \quad &| \text{ sijoitetaan }A_{pohja} \text{ ja }A_{vaippa} \\ &= 2 \cdot 256 \text{ cm}^2 + 3520 \text{ cm}^2& \quad &| \text{ sievennetään} \\ &=4032 \text{ cm}^2& \quad &| \text{ muunnetaan yksikköön dm}^2 \\ &=40,32 \text{ dm}^2& \quad &| \text{ pyöristetään yhden desimaalin tarkkuuteen} \\ &≈ 40,3 \text{ dm}^2.\\ \end{align}\]
4.4 Kartio
Kartion tilavuus
Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa ja lisäksi suora kulkee koko ajan saman pisteen kautta, syntyy kartiopinta. Kun kartiopinta leikataan tasolla, syntyy kartio. Kartion tilavuus lasketaan sen pohjan pinta-alan \(A_p\) ja korkeuden \(h\) avulla \[V = \frac{A_p h}{3}.\]
Erikoistapauksia kartiosta ovat ympyräkartio ja pyramidi eli särmäkartio. Ympyräkartion pohjana on ympyrä ja särmäkartion pohjana on monikulmio. Jos ympyräkartion kokeusjana on kohtisuorassa pohjaympyrän sädettä vastaan, kyseessä on suora ympyräkartio.
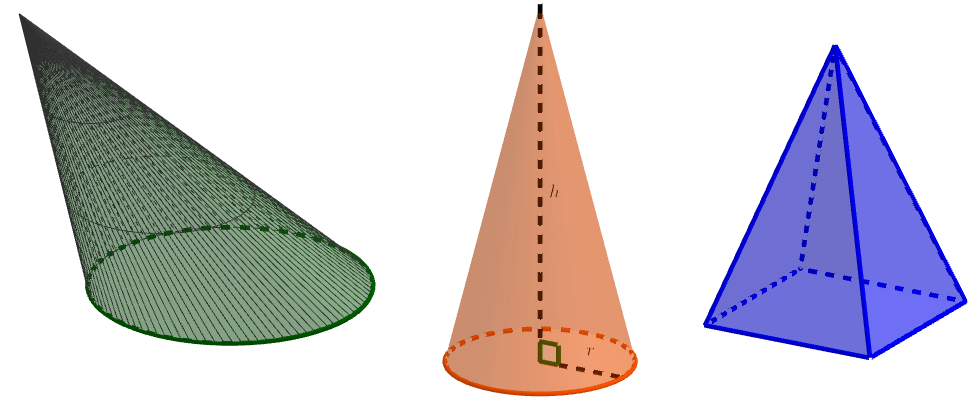
Laske suoran pyramidin kokonaispinta-ala ja tilavuus, kun pyramidin pohja on tasasivuinen kolmio, jonka piiri on 33,0 cm. Pyramidin vaippa koostuu tasakylkisistä kolmioista, joiden korkeus on 30,0 cm. Kartion korkeus on 18 cm. Ilmoita tilavuus desilitroina.
Ratkaisu
Koska pyramidin pohjana on tasasivuinen kolmio, pyramidin vaipan muodostaa kolme yhtä suurta tasakylkistä kolmiota. Vaipan pinta-ala on siis kolmen kolmion pinta-alojen summa.
Selvitetään ensin pohjakolmion sivun pituus, kun tiedetään sivujen pituuksien summa eli piiri. Sivun pituus pohjakolmiossa on siis \(\frac{33,0 \text{ cm}}{3}=11,0 \text{ cm}\)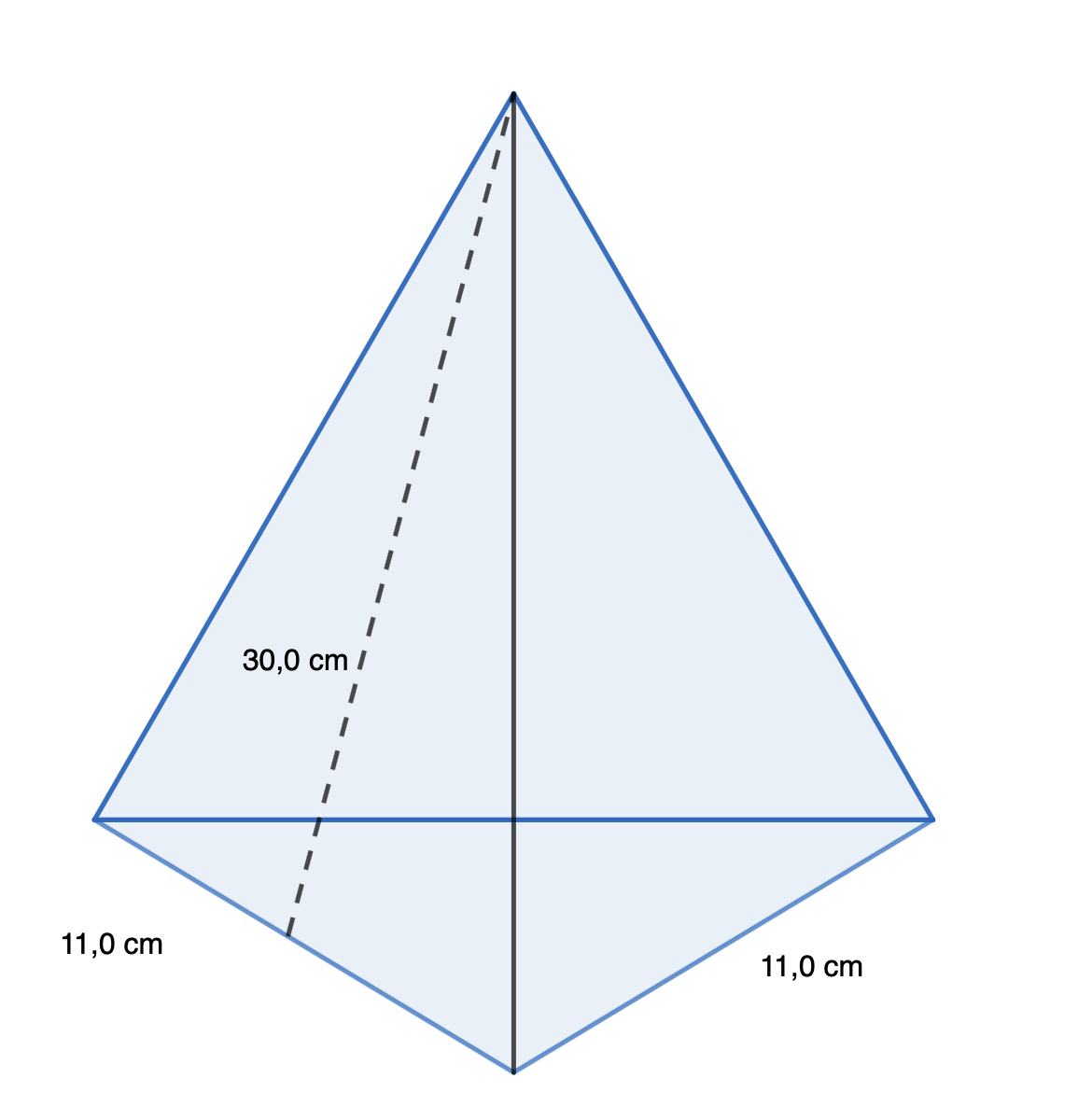 
Nyt voidaan siis laskea vaipan pinta-ala
\(A_{vaippa}= 3 \cdot \frac{1}{2} \cdot 11,0 \text{ cm} \cdot 30,0 \text{ cm} = 495 \text{ cm}^2\).
Jotta pohjan pinta-ala voitaisiin laskea, tulee laskea ensin pohjan korkeus x Pythagoraan lauseella.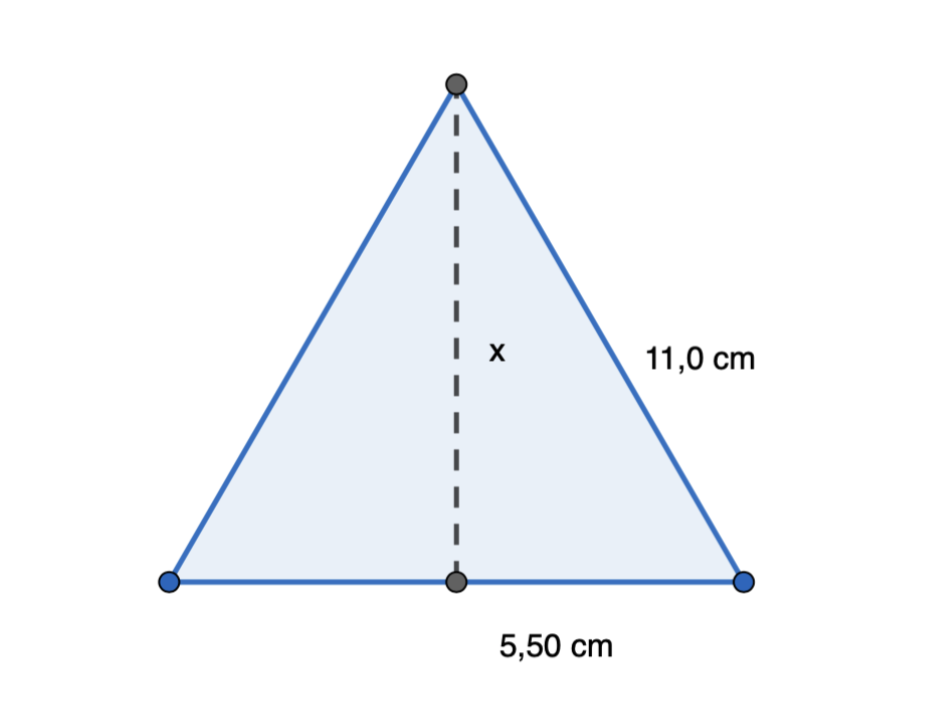 
\[\begin{align} x^2 + (5,50 \text{ cm})^2 &= (11,0 \text{ cm})^2& \quad &| -(5,50 \text{ cm})^2 \\ x^2 &= (11,0 \text{ cm})^2- (5,50 \text{ cm})^2& \quad &| \sqrt{\text{ }} \\ x &= \sqrt{(11,0 \text{ cm})^2- (5,50 \text{ cm})^2}& \quad &| \text{ sievennetään} \\ x &= 9.5262... \text{ cm} \\ \end{align}\]
Nyt voidaan laskea pohjan pinta-ala
\(A_{pohja}= \frac{1}{2} \cdot 11 \text{ cm} \cdot 9.5262... \text{ cm}= 52,3945... \text{ cm}^2\).
Kartion kokonaispinta-ala on siis
\[\begin{align} A_{kartio}&= A_{vaippa} + A_{pohja}& \quad &| \text{ sijoitetaan }A_{vaippa}\text{ ja }A_{pohja} \\ &= 495 \text{ cm}^2 + 52,3945... \text{ cm}^2& \quad &| \text{ sievennetään} \\ &= 547,3945... \text{ cm}^2& \quad &| \text{ pyöristetään kymmenten tarkkuuteen} \\ &≈ 550 \text{ cm}^2 \\ \end{align}\]
ja tilavuus on
\[\begin{align} V_{kartio} &= \frac{A_{pohja} \cdot h}{3}& \quad &| \text{ sijoitetaan }A_{pohja} \\ &= \pm \frac{52,3945... \text{ cm}^2 \cdot 18 \text{ cm}}{3}& \quad &| \text{ sievennetään} \\ &= \pm 314.367... \text{ cm}^3& \quad &| \text{ muunnetaan yksikköön dm}^3 \\ &= \pm 0,314367... \text{ dm}^3& \quad &| \text{ muunnetaan yksikköön dl} \\ &= \pm 3,14367... \text{ dl}& \quad &| \text{ ja pyöristetään kahden desimaalin tarkkuuteen} \\ &≈ \pm 3,10 \text{ dl} \\. \end{align}\]
Koska tilavuus on positiivinen arvo, \(V= 3,1\) dl.
Pyramidin kokonaispinta-ala on \(550 \text{ cm}^2\) ja tilavuus \(3,1 \text{ dl}\).
Suoran ympyräkartion vaipan pinta-ala on \(16,8 \text{ dm}^2\) ja pohjan säde 20,1 cm. Laske kartion korkeus.
Ratkaisu
Piirretään mallikuva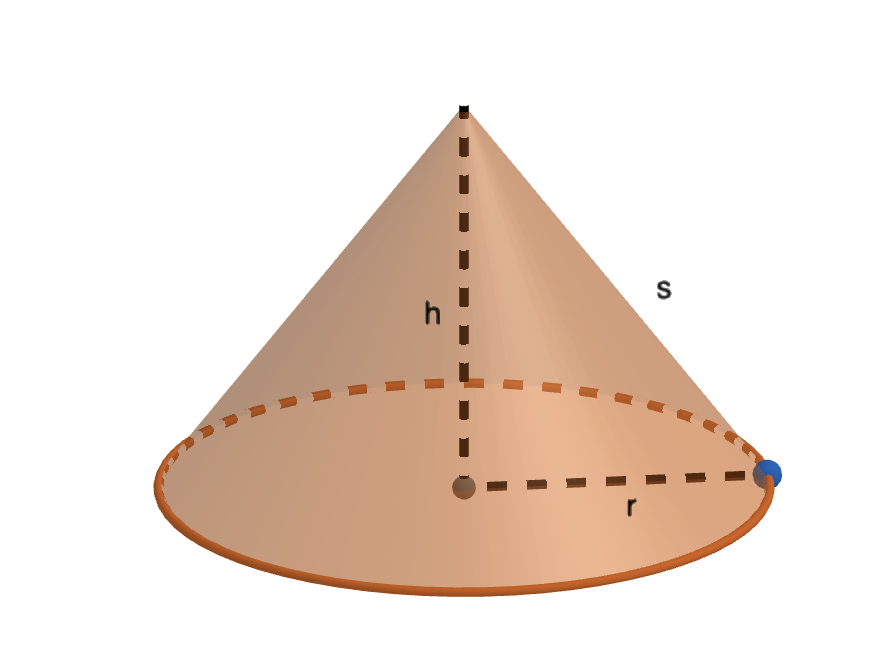 
Mitoista muodostuu suorakulmainen kolmio.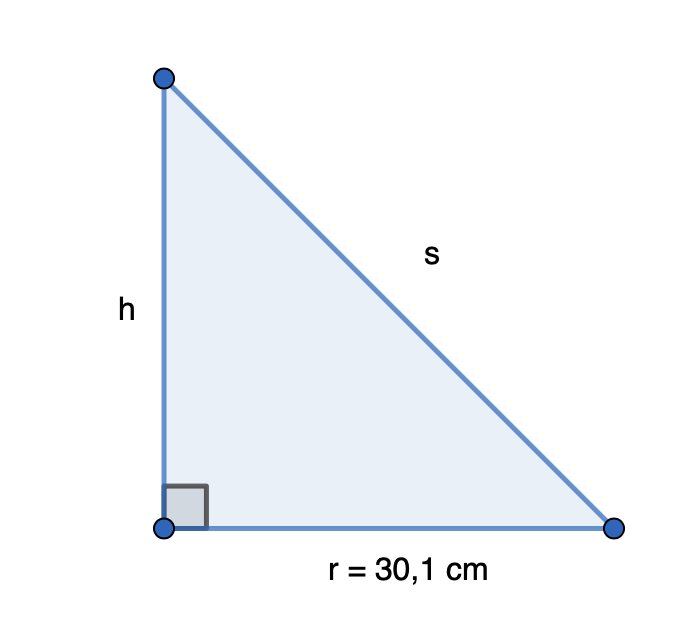 
Lasketaan ensin kartion sivujanan \(s\) pituus vaipan pinta-alan avulla.
\[\begin{align} \pi r s &= A_{vaippa}& \quad &| :\pi r \\ s &= \frac{A_{vaippa}}{\pi r}& \quad &| \text{ sijoitetaan }A_{vaippa}\text{ ja }r \\ s &= \frac{16,8 \text{ dm}^2}{\pi \cdot 2,01 \text{ dm}}& \quad &| \text{ sievennetään} \\ s &= 2,6605... \text{ dm} \\ \end{align}\]
Kartion korkeus saadaan Pythagoraan lauseella.
\[\begin{align} h^2 + (2,01 \text{ dm})^2 &= (2,6605... \text{ dm})^2& \quad &| -(2,01 \text{ dm})^2 \text{ ja }\sqrt{\text{ }} \\ h &= \pm{\sqrt{(2,6605... \text{ dm})^2 - (2,01 \text{ dm})^2}}& \quad &| \text{ sievennetään} \\ h &= \pm 1,7430... \text{ dm}& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ h &≈ \pm 1,74 \text{ dm}\\ \end{align}\]
Koska \(h > 0\), niin \(h = 1,74 \text{ dm}\).
4.5 Maapallo
Planeettamme Maa on likimain pallon muotoinen. Maapallo on jaettu leveys- ja pituuspiireihin, ja esimerkiksi pallon puolesta välistä kulkeva leveyspiiri on nimeltään päiväntasaaja. Pallon pohjoisnavalta etelänavalle kulkeva pituuspiiri, joka kulkee myös Lontoon läpi, on nimeltään nollameridiaani.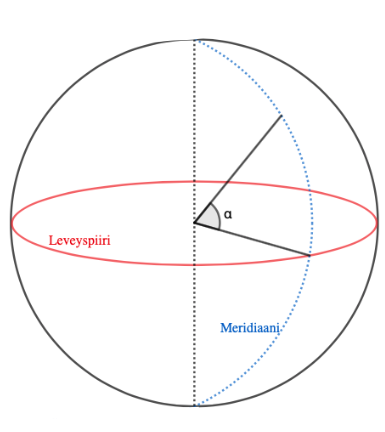 
Leveys- ja pituuspiirien avulla voidaan ilmoittaa koordinaatein esimerkiksi jonkin kaupungin sijainti maapallolla. Esimerkiksi Helsingin sijainti on \(60°N, 25°E\), eli \(60°\) pohjoista leveyttä (eli \(60°\) päiväntasaajalta kohti pohjoisnapaa) sekä \(25°\) itäistä pituutta (eli \(25°\) nollameridiaanista itään).
Tarkastele GeoGebra-appletilla leveys- ja pituuspiirejä raahaamalla pistettä \(P\)!
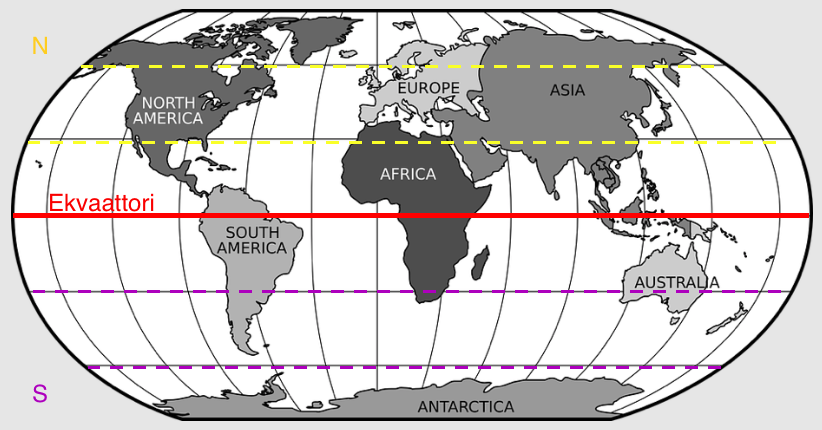
Leveyspiirit
Leveyspiirit jakavat maapallon itä-länsisuunnassa, eli leveyden suhteen. Leveyspiirit ovat ympyröitä, jotka eivät leikkaa toisiaan.
Pisin leveyspiiri jakaa maapallon kahteen yhtä suureen osaan ja tämä leveyspiiri on nimeltään päiväntasaaja eli ekvaattori.
Leveyspiirit voidaan jakaa pohjoisiin ja eteläisiin leveyspiireihin riippuen siitä, kummalla puolella päiväntasaajaa leveyspiirit sijaitsevat: päiväntasaajan eteläpuolella on eteläiset leveyspiirit.
Leveyspiirien kulmat ilmoitetaan astelukuina välillä \(0°-90°\).
Pituuspiirit
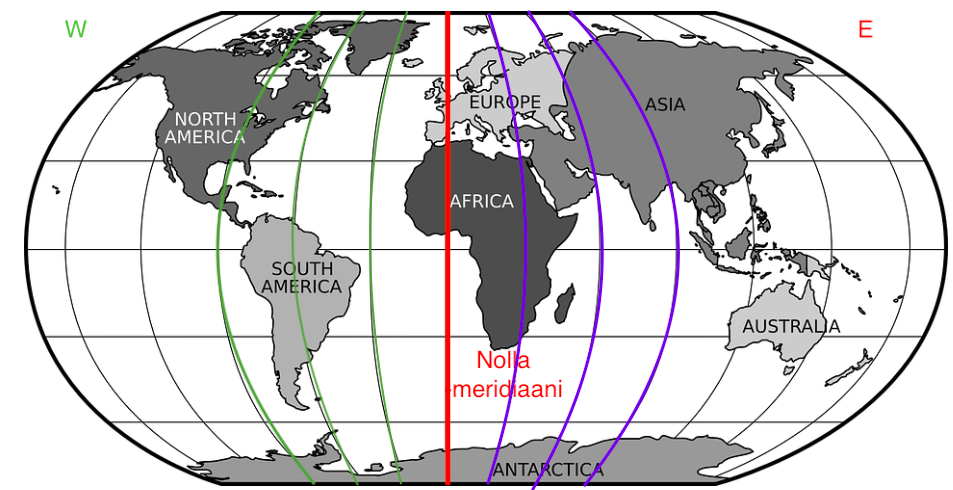
- Pituuspiirit kulkevat pohjoisnavalta etelänavalle ja jakavat maapallon osiin pituuden suhteen.
- Lontoon Greenwichin observatorion kautta kulkeva meridiaani on nimeltään nollameridiaani (0°).
- Pituuspiirit voidaan jakaa läntisiin ja itäisiin pituuspiireihin riippuen siitä, kummalla puolella pituuspiiri on nollameridiaaniin nähden.
- Pituuspiirien kulmat ilmoitetaan välillä \(0°-180°\).
Tampere ja Anchorage (USA, Alaska) sijaitsevat kutakuinkin samalla leveyspiirillä 61° pohjoista leveyttä. Laske Tampereen ja Anchoragen välinen etäisyys leveyspiiriä pitkin mitattuna, kun Anchoragen pituuspiiri on 149,85° ja Tampereen pituuspiiri on 23,78°. Maan säde on 6370 km.
Ratkaisu
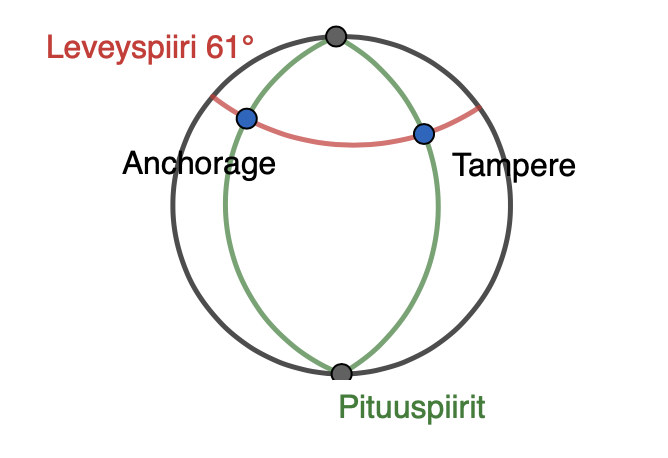
Kysytty etäisyys on leveyspiiriä pitkin kulkevan ympyrän kaaren pituus. Jotaa kaaren pituus saataisiin selville, tulee selvittää kaarta vastaava keskuskulma ja leveyspiiriä kuvaavan ympyrän säde.
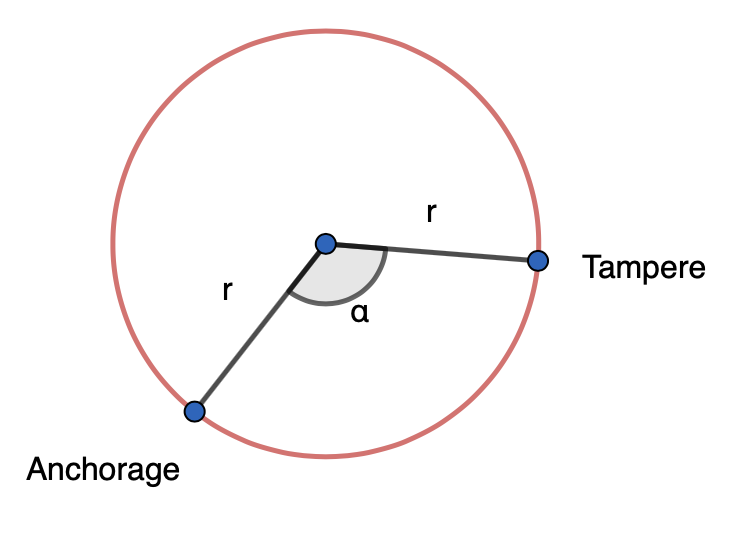Keskuskulma saadaan laskettua pituuspiirien avulla
\(\alpha=149,85°-23,78°=126,07°\)
Piirretään seuraavaksi poikkileikkaus maapallosta pystysuunnassa.
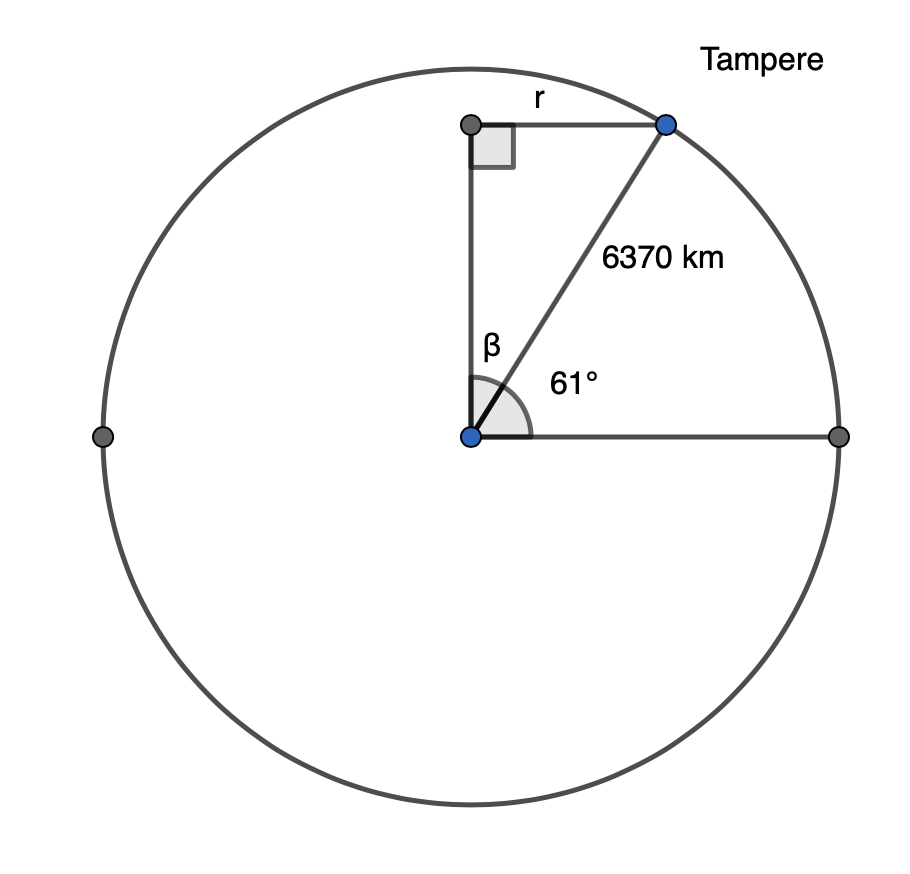
Kulma \(\beta\) saadaan leveyspiirin avulla \(\beta=90°-61°=29°\).
Leveyspiirin säde r saadaan ratkaistua poikkileikkausympyrään muodostuvan suorakulmaisen kolmion avulla käyttäen siniä.
\[\begin{align} \sin{29°} &= \frac{r}{6370}& \quad &| \cdot 6370 \\ r &= \sin{29°} \cdot 6370& \quad &| \text{ sievennetään} \\ r &= 3088,2372... \text{ (km)} \end{align}\]
Lasketaan Tampereen ja Anchoragen välistä matkaa kuvaavan kaaren pituus \(b\).
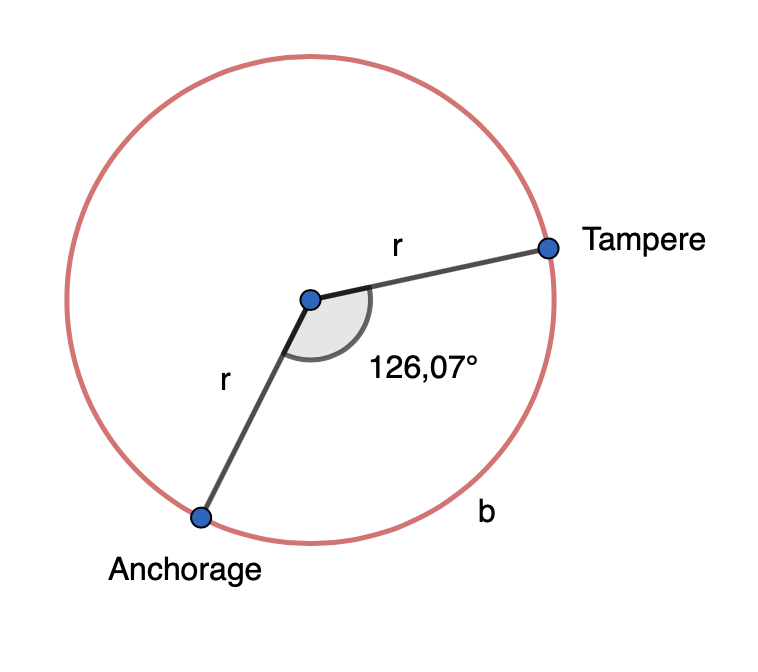
\[\begin{align} b &=\frac{\alpha}{360°}\cdot 2 \pi r& \quad &| \text{ sijoitetaan arvot} \\ b &=\frac{126,07°}{360°}\cdot 2 \pi \cdot 6370 \cdot\sin{29°}& \quad &| \text{ sievennetään} \\ b &= 6795,1614... \text{ km}& \quad &| \text{ pyöristetään satojen tarkkuuteen} \\ b &≈ 6800 \text{ km} \\ \end{align}\]
Tampereen ja Anchoragen etäisyys leveyspiiriä pitkin mitattuna on 6800 km.
4.6 Avaruuskappaleita koordinaatistossa
Luvussa Monikulmioita koordinaatistossa esiteltiin \(xy\)-koordinaatisto. Kyseiseen koordinaatistoon piirretyt kuviot ovat kaksiulotteisia.
Avaruuskappaleet ovat kolmiulotteisia, joten \(xy\)-koordinaatistoon pitää tehdä pieniä lisäyksiä.
\(xyz\)-koordinaatisto
\(xyz\)-koordinaatisto poikkeaa \(xy\)-koordinaatistosta siten, että akseleita on kahden sijaan kolme.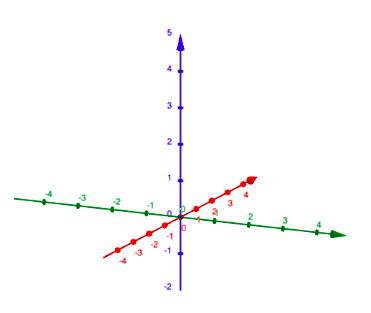 
Samoin kuin \(xy\)-koordinaatistossakin, pisteiden välinen etäisyys voidaan myös määrittää kolmiulotteisessa koordinaatistossa.
Pisteiden välinen etäisyys \(xyz\)-koordinaatistossa
Olkoon koordinaatistossa kaksi pistettä \(A\) ja \(B\), joiden koordinaatit ovat \((x_1,y_1,z_1)\) ja \((x_2,y_2,z_2)\). Nyt näiden pisteiden välinen etäisyys (eli janan pituus) on \[\begin{align*} |AB|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} \end{align*}\]
Vastaavalla tavalla laskukaavaa keskipisteen koordinaateille voidaan muuntaa sopivaksi \(xyz\)-koordinaatistoon.
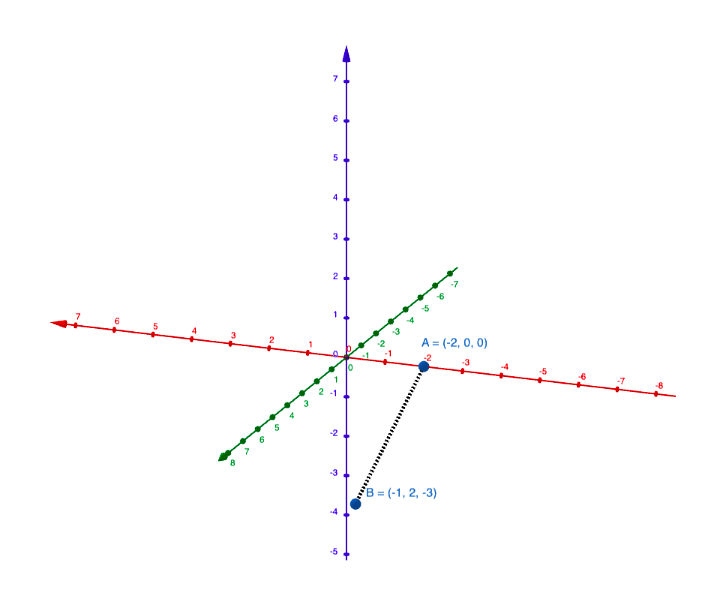
GeoGebralla voidaan piirtää siistejä avaruuskappaleita. Harjoittele erilaisten avaruuskappaleiden piirtämistä GeoGebralla tai omalla laskimellasi.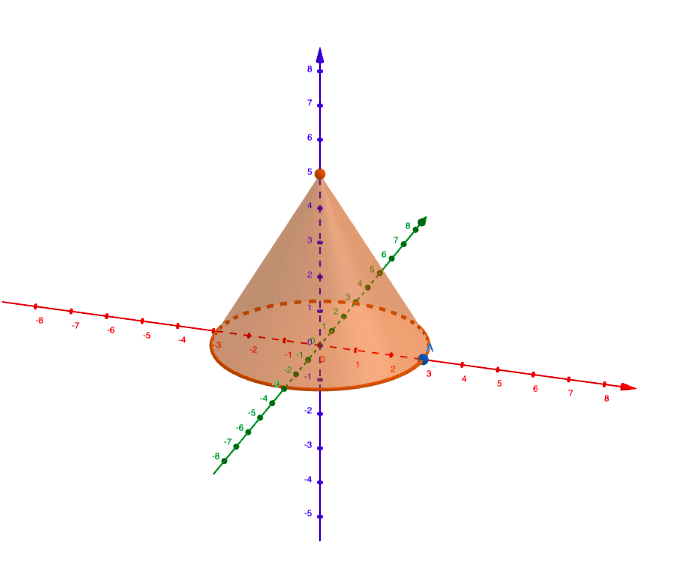 
Avaa alla oleva GeoGebra-appletti ja tutustu 
-ikonin takana oleviin 3D-työkaluihin.
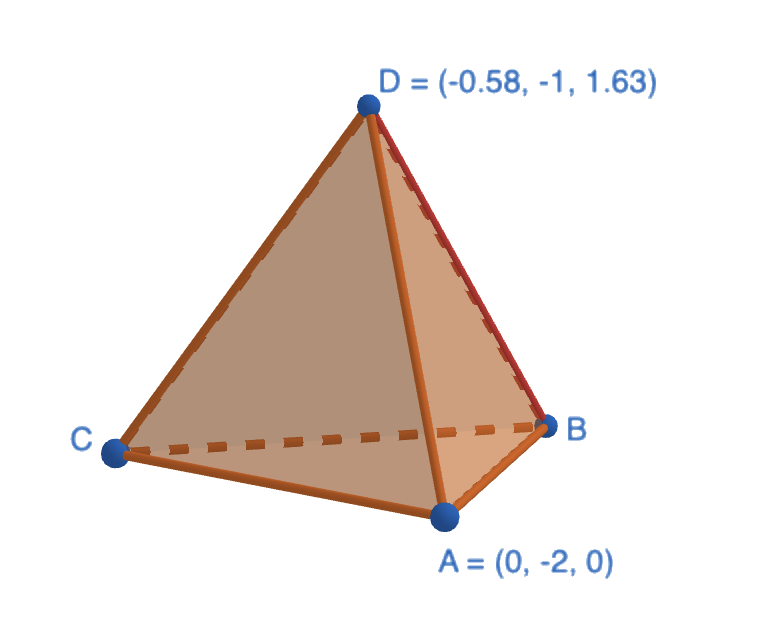
Laske tetraedrin pisteiden A ja D välinen etäisyys.
Ratkaisu
Lasketaan janan \(|AD|\) pituus, kun \(A=(0,-2,0)\) ja \(D=(-0,58;-1;-1,63)\).
\[\begin{align} |AD| &= \sqrt{(x_D-x_A)^2+(y_D-y_A)^2+(z_D-z_A)^2}& \quad &| \text{ sijoitetaan arvot} \\ |AD| &= \sqrt{(-0,58-0)^2+(-1-(-2))^2+(1,63-0)^2}& \quad &| \text{ sievennetään} \\ |AD| &= 1,9983...& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ |AD| &≈ 2 \\ \end{align}\]
Pisteiden A ja D välinen etäisyys on 2.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.