2. Monikulmioiden geometriaa: tehtäviä

Tehtäviä tehdessä harjoittele myös kuvioiden piirtämistä jollain sovelluksella: omalla laskimella tai vaikkapa Geogebralla!

Tähän tehtäväsivuun liittyvät teoriat löydät täältä!

Kolmioiden geometriaa

2.1 Kolmion rakenne

Tehtävä

# Kolmionrakenne

Onko väite totta vai tarua? Valitse oikea vaihtoehto.

2.2 Kolmion pinta-ala

Tehtävä

# kolmion_ala1

Kolmion kannan pituus on \(a=6\) ja korkeus on \(h=10\). Mikä on kolmion pinta-ala \(A\)?

<=> A=

 

Tehtävä

# kolmion_ala2

Kolmion kannan pituus on \(a=3\) ja pinta-ala on \(A=20\). Mikä on kolmion korkeus \(h\)?

<=> h=

 

Tehtävä

# kolmion_ala3

Kolmion korkeus on \(h=3\) ja pinta-ala on \(A=18\). Mikä on kolmion kannan pituus \(a\)?

<=> a=

 
# teht_kolmion_ala2

Tehtävä

MathCheck laskee kulmia aina radiaaneina. Jos haluat kirjoittaa sin(60°), sinun on kirjoitettava sen sijaan sin(60 * pi/180).

# kolmion_ala4

Kolmion kahden sivun pituudet ovat \(a=9\) ja \(b=10\), ja niiden välinen kulma on \(\alpha=60^{\circ}\). Mikä on kolmion pinta-ala \(A\)?

<=> A=

 
# teht_kolmion_ala3

Tehtävä

Kolmion kantasivun pituus on \(2 \sqrt{2}\) ja kolmion korkeus on \(\sqrt{2}\). Laske kolmion pinta-ala.

# kolmion_ala

Pinta-alan tarkka avo

=

 
# teht_tasasivuinen_ala

Tehtävä

Tasasivuisen kolmion sivun pituus on 3. Mikä on kolmion pinta-ala?

# tasasivuisen_kolmion_ala

Pinta-alan tarkka avo

=

 
# teht_lampi

Tehtävä

Maastossa olevan lammen pinta-ala on \(2,8 \text{ ha}\). Maastosta piirretään kartta, jonka mittakaava on \(1 : 20 \, 000\). Mikä on lammen pinta-ala kartalla?

# pintaala1

Lammen pinta-ala neliösentteinä yhden desimaalin tarkkuudella (ilman yksikköä)

=

 
# teht_pelto

Tehtävä

Kartan mittakaava on \(1 : 15 \, 000\). Kartalla olevan pellon pinta-ala on \(25 \text{ cm}^2\). Mikä on pellon pinta-ala hehtaareissa?

# pintaala2

Pellon pinta-ala hehtaareina yhden hehtaarin tarkkuudella (ilman yksikköä)

=

 
# teht_suorakulmainen_kolmio

Tehtävä

Kahden suorakulmaisen kolmion mittakaava on \(2 : 5\). Suuremman kolmion kannat ovat pituudeltaan \(8\) ja \(13\). Määritä pienemmän kolmion pinta-ala.

# pintaala3

Pienemmän kolmion pinta-ala kahden desimaalin tarkkuudella

=

 
# teht_kolmion_jako

Tehtävä

Kolmio \(ABC\) leikataan kahteen osaan kannan \(AB\) suuntaisella suoralla \(PQ\) siten, että \(AP:PC=2:3\). Missä suhteessa suora jakaa kolmion alan?

 
 
# pintaala4

Suhde jakolaskuna (esimerkiksi suhde \(3:4\) kirjoitetaan 3/4)

=

 

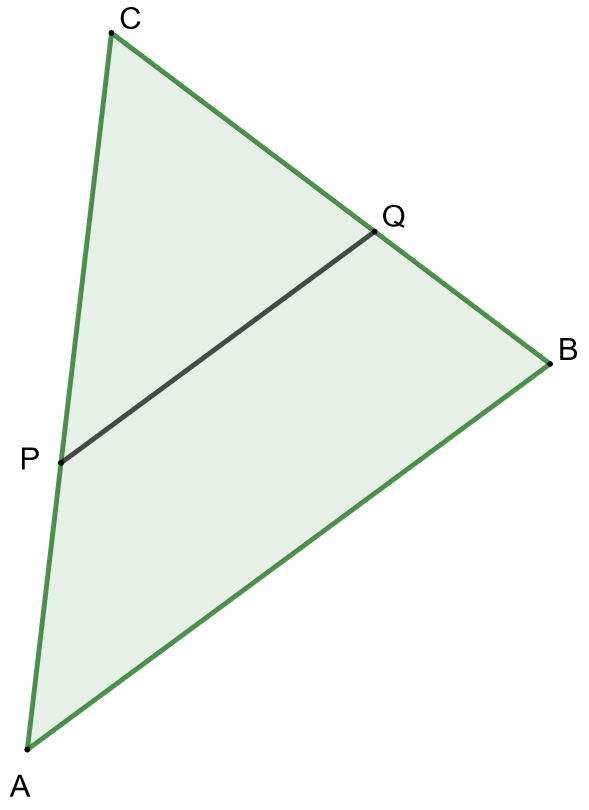
Vinkki

Osoita ensin, että kolmiot \(ABC\) ja \(CPQ\) ovat yhdenmuotoisia, minkä jälkeen voit ratkaista yhdenmuotoisuussuhteen.

2.3 Suorakulmainen kolmio ja Pythagoraan lause

Tehtävä

# pythagoras1

Jos suorakulmaisen kolmion kateettien pituudet ovat \(3\) ja \(2\), kuinka pitkä on kolmion hypotenuusa?

=

 
# teht_S11T1b

Tehtävä (S2011/1b)

Suorakulmaisen kolmion hypotenuusan pituus on \(5\) ja toisen kateetin pituus \(2\). Laske toisen kateetin pituus.

# pythagoras2 
=

 
# teht_geogebra_puu

Tehtävä

Seitsemän metriä korkea puu kasvaa kohtisuoraan maan pintaa vastaan. Puu taittuu kahden metrin korkeudelta niin, että puun latvaosa osuu maahan. Latva ja tyviosa eivät irtoa toisistaan. Piirrä tilanteesta mallikuva oikeanpuoleiselle piirtoalueelle (ei vaikuta tehtävän pisteytykseen) ja laske vasemmanpuoleiselle CAS-alueelle, kuinka suuri kulma on maanpinnan ja taittuneen latvan välillä.

Anna vastaus vasemmanpuoleisella CAS-alueella tallentamalla se muuttujaan nimeltä v. Pyöristä vastaus kokonaislukujen tarkkuudelle käyttämällä komentoa round.

# puu-kaatuu
Avaa GeoGebra tuomalla osoitin tähän

 

Vinkki GeoGebran käyttöön

  • Tekstin lisääminen

Monesti on hyödyllistä lisätä tehtävän ratkaisuun tekstiä, jossa selität, miten teit tehtävän. Valitse CAS-alueen oikeassa yläkulmassa oleva valikko ja valitse sieltä teksti . Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.

  • Muuttujan tallentaminen

Joskus on hyödyllistä tallentaa lukuarvo tai vastaus muuttujaan. Tällöin lukuarvon käyttäminen myöhemmin on kätevää. Jos haluat sijoittaa muuttujaan a arvon 4, kirjoita komento a := 4. Jos myöhemmin haluat laskea laskun \(5a\), kirjoita komento 5*a, jolloin saat vastaukseksi 20.

  • Yhtälön ratkaiseminen

Jos haluat ratkaista muuttujan \(a\) yhtälöstä \(a^2+3a-4=0\), syötä CAS-laskimeen komento Ratkaisut(a^2+3a-4,a). Vastaukseksi saat listan {-4,1}. Helpoiten ratkaisuihin pääsee käsiksi, kun tallentaa ne muuttujaan: vastaukset := Ratkaisut(a^2+3a-4,a). Tällöin komento vastaukset(1) tuottaa luvun -4, ja komento vastaukset(2) tuottaa luvun 1.

  • Lukuarvon näyttäminen

Joskus GeoGebra näyttää vastauksen hyvinkin monimutkaisessa muodossa. Käytä tällöin komentoa Lukuarvona(). Jos kirjoitat esimerkiksi komennon a:=sin^(-1)(1/2), GeoGebra tulostaa vastaukseksi saman eli a:=sin^(-1)(1/2). Jos haluat vastauksen lukuarvona, kirjoita komento Lukuarvona(a), jolloin GeoGebra tulostaa 60°.

Tehtävä

Suorakulmaisessa kolmiossa \(ABC\) kateetin \(AB\) pituus on \(4,4\) cm ja hypotenuusan \(AC\) pituus \(8,14\) cm.

  1. Laske kateetin \(BC\) pituus
# suorakulmaisenkateetinpituus

Anna vastauksesi senttimetrin kymmenesosan tarkkuudella ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 
  1. Laske kolmion pinta‐ala \(0,1\) neliösenttimetrin tarkkuudella. [4/K15]
# suorakulmaisenpinta-ala

Anna vastauksesi ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 

Tehtävä

Suorakulmaisen kolmion kummankin kateetin pituus on 5. Sen sisään on piirretty neliö kahdella eri tavalla kuvioiden mukaisesti. Kumman neliön pinta-ala on suurempi? [10/S14]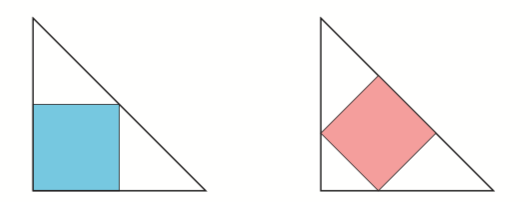

# punainensininennelio

+ question

2.4 Käänteinen Pythagoraan lause

# teht_onko_suorakulmainen1

Tehtävä

Kolmion sivujen pituudet ovat \(3\), \(5\) ja \(6\). Onko kolmio suorakulmainen?

# kaantpyhtagoras2

Open plugin
# teht_onko_suorakulmainen2

Tehtävä

Kolmion sivujen pituudet ovat \(3 \sqrt{2}\), \(4 \sqrt{2}\) ja \(5 \sqrt{2}\). Onko kolmio suorakulmainen?

# kaantpythagoras3

Open plugin

2.5 Trigonometriset funktiot

# teht_trig1

Tehtävä

Tehtävien 3.2.1-3.2.6 merkinnät vastaavat alla olevan kolmion merkintöjä.

 
 
# trig1

Jos \(a=1\), \(b=7\) ja \(c=5\), mitä on \(\sin\alpha\)?

=

 
# trig2

Jos \(a=10\), \(b=5\) ja \(c=7\), mitä on \(\cos\alpha\)?

=

 
# trig3

Jos \(a=2\), \(b=6\) ja \(c=9\), mitä on \(\cos\alpha\)?

=

 
# trig6

Jos \(a=2\), \(b=1\) ja \(c=6\), mitä on \(\tan\alpha\)?

=

 
# trig5

Jos \(a=9\), \(b=4\) ja \(c=4\), mitä on \(\sin\beta\)?

=

 
# trig4

Jos \(a=9\), \(b=4\) ja \(c=3\), mitä on \(\tan\alpha\)?

=

 
# teht_sin18

Tehtävä

Määritä lausekkeen \(\sin(18^{\circ})\) tarkka arvo käyttämällä alla olevaa tasakylkistä kolmiota.

!

— 10 Feb 21
# geo_sin18
Avaa GeoGebra tuomalla osoitin tähän

 

Vinkki 1

Ratkaise alkuperäisen kolmion kolmannen sivun pituus.

Vinkki 2

Lisää valinta kohtaan "vihje 1". Millainen kolmio muodostuu mustan janan oikealle puolelle? Voiko sitä verrata alkuperäiseen kolmioon? Saatko ratkaistua mustan janan pituuden?

Vinkki 3

Pidä edelleen valinta kohdassa "Vihje 1". Mustan janan oikealle puolelle muodostuu kolmio, joka on yhdenmuotoinen alkuperäisen kolmion kanssa (perustele tämä kulmien suuruuksien avulla). Käytä verrantoa ratkaistaksesi kolmion kolmannen sivun (ja samalla mustan janan) pituus.

Vinkki 4

Lisää valinta kohtaan "Vihje 2" ja huomaa, että \(\frac{36^{\circ}}{2}=18^{\circ}\).

# sin18

\(\sin (18^{\circ})\)

=

 

Nelikulmioiden geometriaa

2.6 Nelikulmioiden rakenne

Tehtävä

# Nelikulmiovalinta

Onko väite oikein vai väärin? Valitse oikea vaihtoehto.

Tehtävä

# Nelikulmiorakenne1

Yhdistä oikeat kulmiot oikeisiin alaotsikkoihin.

Tehtävä

Pöytäliinan alkuperäinen koko on 2 m kertaa 4 m. Se kutistuu pesussa 5 % sekä pituus- että leveyssuunnassa. Kuinka monella prosentilla pöytäliinan pinta-ala pienenee? [5/S16]

# mittakaava1a

Anna vastaus prosentin kymmenesosan tarkkuudella (ilman yksikköä).

=

 

Tehtävä

Peppi rakentaa oheisen kuvan mukaisista laudankappaleista linnunpöntön. Yksikkönä on senttimetri. [6/K16]

  1. Paljonko linnunpönttö painaa? Sisääntuloaukkoa ei tarvitse huomioida eikä käytettäviä nauloja. Laudan tiheys on \(550 \frac{kg}{m^3}\)ja paksuus \(2,0 cm\).
# Linnunpontto

Anna vastauksesi kilon sadasosan tarkkuudella ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 
  1. Mikä on linnunpöntön sisätilavuus?
# linnunpontontilavuus

Anna vastauksesi kuutiosenttimetrin tarkkuudella ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 

Tehtävä

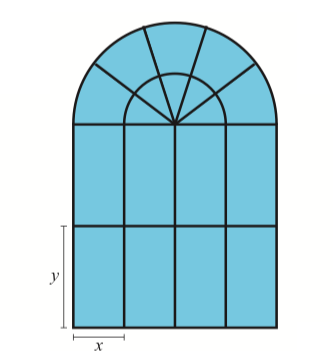
Kuvan kaari-ikkunassa on lasin tukena rimoja. Kuinka paljon rimaa tarvitaan kuvan mukaiseen kaari-ikkunaan, kun \(x=20\)cm ja \(y=40\) cm? Rimaa käytetään kaikkiin kuvion janoihin ja puoliympyröiden kaariin. [4/S13]

# kaarikkunat

Anna vastauksesi senttimetrin tarkkuudella ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 

Suorakulmio

# teht_suunnikkaan_osuus

Tehtävä

Määritä alla olevan kuvan suunnikkaan pinta-alan osuus suorakulmion pinta-alasta.

 
 
# suunnikas_suorakulmiossa

Suunnikkaan pinta-alan osuus suorakulmion pinta-alasta desimaalilukuna kahden desimaalin tarkkuudella

=

 
# teht_suorakulmio_kolmiossa

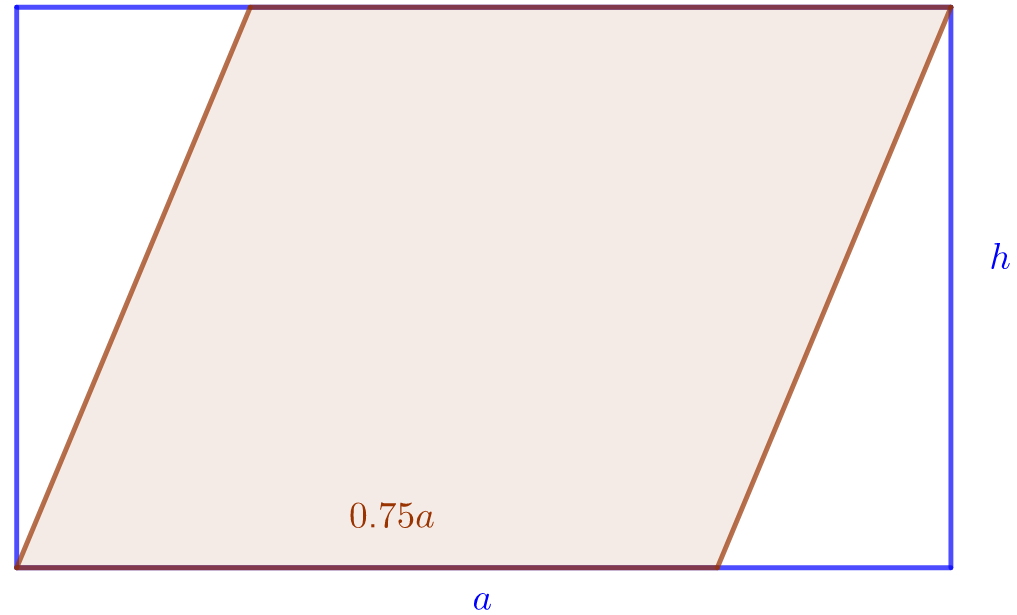
Tehtävä

Laske alla olevaan kuvaan sinisellä merkityn alueen pinta-ala.

 
 
# suorakulmio_kolmiossa

Sinisen alueen pinta-ala (ykkösten tarkkuudella)

=

 
# teht_suorakulmion_lavistajat

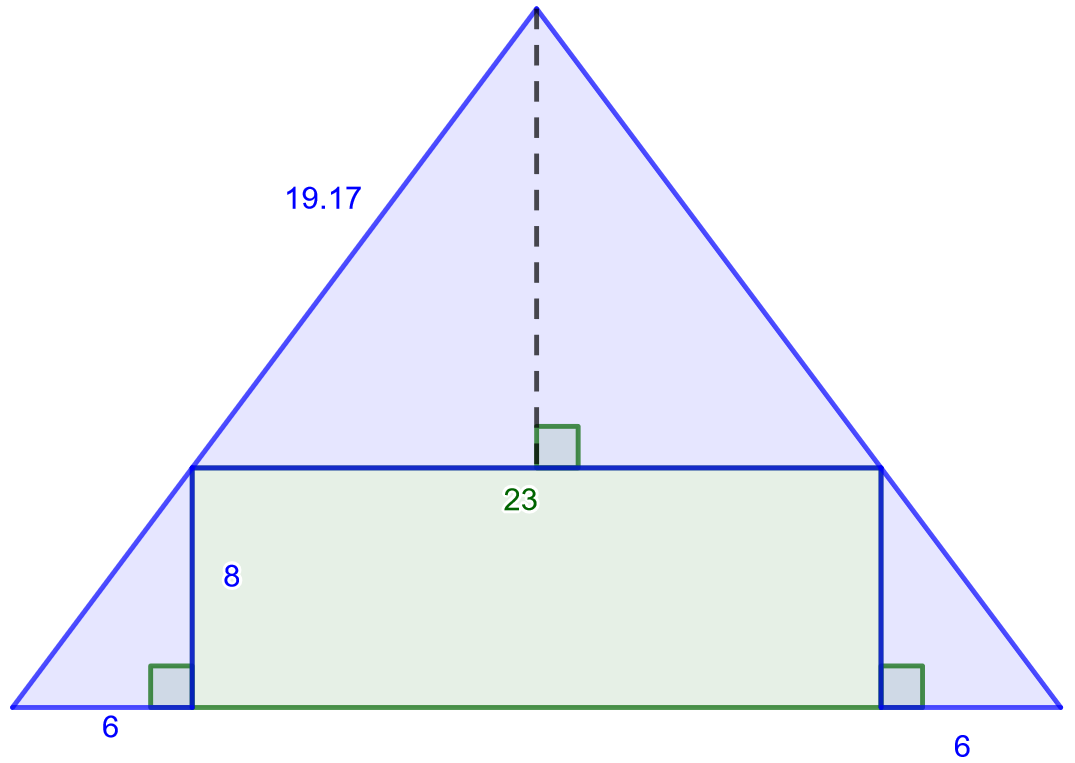
Tehtävä

Olkoot \(d_1\) ja \(d_2\) suorakulmion \(ABCD\) piirillä olevan pisteen \(P\) etäisyydet lävistäjistä \(AC\) ja \(BD\).

  1. Piirrä annettuja tietoja vastaava dynaaminen kuvio, jossa voit liikuttaa pistettä \(P\) suorakulmion ympäri pitkin suorakulmion piiriä.

  2. Mitä voit todeta summan \(d_1+d_2\) arvosta?

  3. Miten arvo riippuu suorakulmion koosta?

  4. Perustele havaintosi matemaattisesti.

Ratkaisu

# geo_suorakulmion_reunat
Avaa GeoGebra tuomalla osoitin tähän

 

  1. Tutkitaan yllä olevaa GeoGebra-applettia siirtämällä punaista pistettä \(P\) suorakulmion reunalla. Huomataan, että summa \(d_1+d_2\) pysyy koko ajan samana.

  2. Muutetaan suorakulmion kokoa raahaamalla pisteitä \(B\) ja \(C\). Huomataan, että summan \(d_1+d_2\) arvo muuttuu, mutta jos pistettä \(P\) liikuttaa, se pysyy edelleen samana. Summa on siis sitä suurempi, mitä suurempi suorakulmio on.

  3. Lisätään valinta GeoGebra-appletin kohtaan "Matemaattinen perustelu", jolloin kuvioon ilmestyy kulmia. (Huom! kulmat toimivat GeoGebrassa oikein vain, jos piste \(P\) on pisteiden \(A\) ja \(D\) välissä.) Merkitään kulmaa \(\angle BAC\) kirjaimella \(\alpha\) ja kulmaa \(\angle CAD\) kirjaimella \(\beta\). Koska suorakulmion kaikki kulmat ovat suoria, saadaan \(\alpha + \beta = 90^{\circ}\). Merkitään vihreää lävistäjää kirjaimella \(\ell\). Sen pituus voidaan ratkaista Pythagoraan lauseella: \[ \begin{aligned} \ell^2 &= a^2+b^2 \\ \ell &= \sqrt{a^2+b^2}. \end{aligned} \] Nyt voidaan merkitä \[ \cos \alpha = \frac{a}{\ell} = \frac{a}{\sqrt{a^2+b^2}}. \] Merkitään etäisyyttä \(DP\) kirjaimella \(x\), jolloin etäisyys \(AP\) on \(b-x\). Pienistä suorakulmaisista kolmioista saadaan \[ \cos \alpha = \frac{d_1}{b-x} \quad \Leftrightarrow \quad d_1 = (b-x) \cdot \cos \alpha \] ja \[ \cos \alpha = \frac{d_2}{x} \quad \Leftrightarrow \quad d_2 = x \cdot \cos \alpha \] jolloin summa saa arvon \[ \begin{aligned} d_1 + d_2 &= (b-x) \cdot \cos \alpha + x \cdot \cos \alpha \\ &= (b-x+x) \cdot \cos \alpha \\ &= b \cdot \frac{a}{\sqrt{a^2+b^2}} \\ &= \frac{ab}{\sqrt{a^2+b^2}}. \end{aligned} \] Tästä voidaan päätellä, että jos suorakulmion koko pysyy samana, summa \(d_1+d_2\) pysyy myös vakiona. Toisaalta jos suorakulmion koko kasvaa, myös summa kasvaa.

Tehtävä

Luomuviljelijä on hankkinut materiaalin 400 metrin pituiseen aitaan. Hän aikoo rajata sillä niitystä suorakulmion muotoisen alan, joka lisäksi jaetaan kuvion mukaisesti kolmeen yhtäsuureen osaan kahdella ulkoreunan suuntaisella sisäaidalla. Määritä aitauksen suurin mahdollinen kokonaispinta-ala [13/S18].

# Luomuviljelija

Aitauksen suurin mahdollinen pinta-ala (ykkösten tarkkuudella) ilman yksikköä

=

 

Neliö

# teht_nelio_suorakulmainen_kolmio

Tehtävä

Neliöllä ja suorakulmaisella kolmiolla on sama pinta-ala. Kumman piiri on pidempi?

# Plugin1

Open plugin
# teht_tahtinelikulmio

Tehtävä

Alla olevassa kuvassa on neliö, jonka pinta-ala on \(12\). Sen jokaiselle sivulle on piirretty tasasivuinen kolmio. Mikä on punaisella merkityn alueen pinta-ala?

 
 
# tahtinelikulmio

Punaisen alueen pinta-ala

=

 

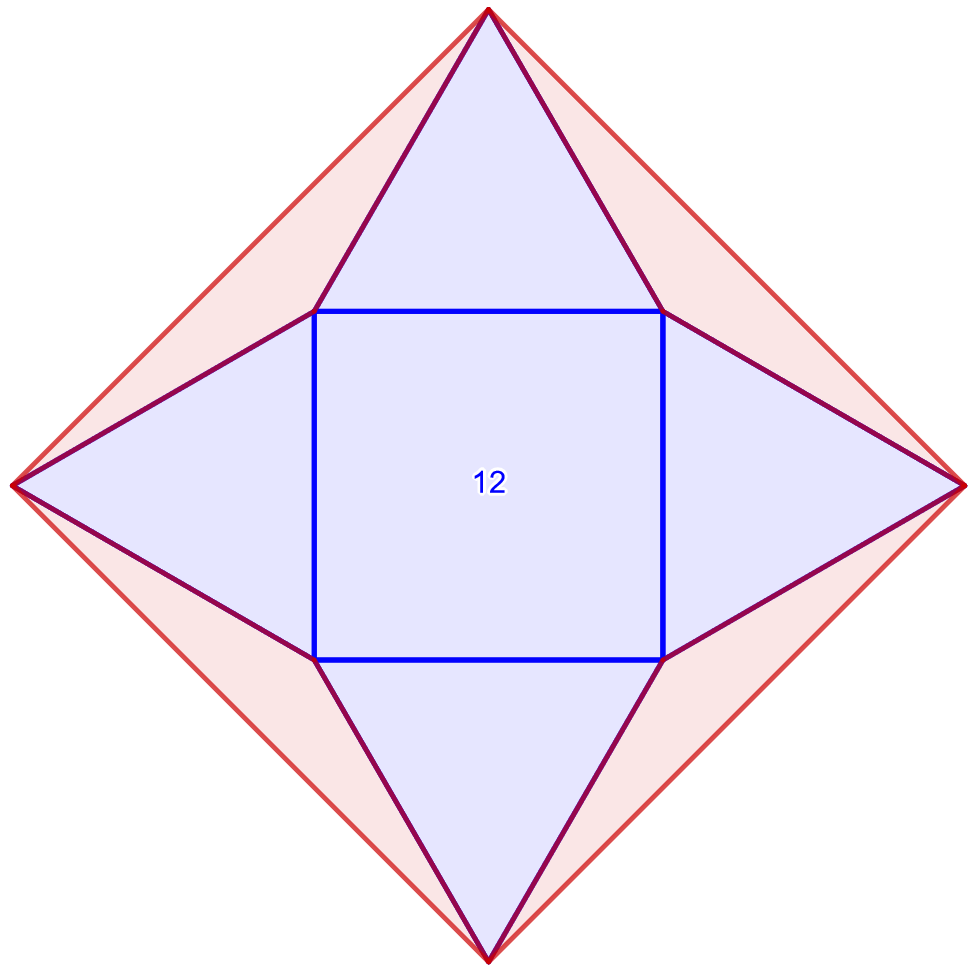
Suunnikas

Tehtävä

# suunnikas1

Suunnikkaan sivun pituus on \(10\) ja korkeus on \(3\). Mikä on suunnikkaan pinta-ala?

=

 

Tehtävä

# suunnikas2

Suunnikkaan sivujen pituudet ovat \(10\) ja \(9\) ja sivujen välinen kulma \(60 ^{\circ}\). Mikä on suunnikkaan pinta-ala?

=

 
# teht_suunnikkaan_kulma

Tehtävä

Suunnikkaan sivujen pituudet ovat \(3\) ja \(5\), ja sen pinta-ala on \(13\). Kuinka suuri kulma sivujen välissä on?

# suunnikas3

Sivujen välinen kulma asteen tarkkuudella (ilman astemerkkiä)

=

 
# teht_suunnikkaan_ala3

Tehtävä

Suunnikkaan sivujen välinen kulma on \(45^{\circ}\). Lyhyempi sivuista on pituudeltaan \(a\) ja pidempi \(4a\). Määritä suunnikkaan ala.

# s98T8a

Pinta-alan tarkka arvo (ilman kerrointa \(a^2\))

=

 
# aakkostehtava

Tehtävä

Aakkoskarkkien sivujen pituudet ovat \(2 \text{ cm}\) ja sen lyhyempi halkaisija on \(2,3 \text{ cm}\). Laske yhden karkin pinta-ala.

 
 
# aakkonen

Yhden aakkoskarkin pinta-ala yhden desimaalin tarkkuudella (neliösenttimetreinä, ilman yksikköä)

=

 

Tehtävä

Suunnikkaan sisälle piirretään pienempi suunnikas, jonka kärjet ovat alkuperäisen suunnikkaan sivujen keskipisteissä. Laske pienen suunnikkaan pinta‐ala käyttämällä kuvioon merkittyjä pituuksia.[2/S15]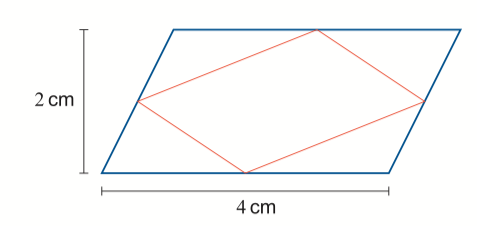

# Sisakkaisetsuunnikkaat

Pienemmän suunnikkaan pinta-ala yhden neliösenttimetrin tarkkuudella ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 

Puolisuunnikas

Tehtävä

# puolisuunnikas2

Puolisuunnikkaan kanta on \(6\), korkeus \(4\) ja pinta-ala \(32.0\). Mikä on puolisuunnikkaan toisen kannan pituus?

=

 

Tehtävä

# puolisuunnikas1

Jos puolisuunnikkaan kannat ovat \(10\) ja \(2\) ja korkeus \(4\), mikä on puolisuunnikkaan pinta-ala?

=

 

Tehtävä

# puolisuunnikas3

Puolisuunnikkaan kantojen pituudet ovat \(10\) ja \(5\) ja pinta-ala \(37.5\). Mikä on puolisuunnikkaan korkeus?

=

 

2.7 Muut monikulmiot

# teht_viisikulmion_pinta-ala

Tehtävä

Säännöllisen viisikulmion sivun pituus on \(3\). Laske viisikulmion pinta-ala.

# viisikulmion_ala

Vastaus yhden desimaalin tarkkuudella

=

 

2.8 Monikulmiot koordinaatistossa

Tehtävä

Kolmion kärjet ovat pisteissä \((-6,1)\), \((0,0)\) ja \((4,9)\).

  1. Laske kolmion kulmat asteen kymmenesosan tarkkuudella.
  2. Laske kolmion pinta-ala yhden desimaalin tarkkuudella. [9/K09]
# YO2009Kaisoin

  1. Anna kolmion suurin kulma. Anna vastaus kymmenesosan tarkkuudella ilman astemerkkiä.

=

 
# YO2009Kapienin

  1. Anna kolmion pienin kulma. Anna vastaus kymmenesosan tarkkuudella ilman astemerkkiä.

=

 
# YO2009Kakolmas

  1. Anna kolmion kolmas kulma. Anna vastaus kymmenesosan tarkkuudella ilman astemerkkiä.

=

 
# YO2009Kb

  1. Kolmion pinta-ala on

=

 

Tehtävä

  1. Suorakulmion kolme kärkeä ovat origossa, pisteessä \((2,1)\) ja pisteessä \((2,-4)\). Määritä neljännen kärjen koordinaatit.
  2. Määritä a-kohdan suorakulmion pinta-ala.
  3. Yhdysjanat origosta pisteisiin \((1,2,1)\), \((1,-1,1)\) ja \((2,0,-2)\) muodostavat suorakulmaisen särmiön kolme särmää. Mihin pisteeseen päättyy origosta alkava särmiön avaruuslävistäjä? [15/K15]
# YO2015ax

  1. Suorakulmion neljännen kärjen x-koordinaatti on

=

 
# YO2015ay

  1. Suorakulmion neljännen kärjen y-koordinaatti on.

=

 
# YO2015Kb

  1. Pinta-ala on

=

 
# YO2015Kcx

  1. Origon vastaisen kärjen x-koordinaatti on

=

 
# YO2015Kcy

  1. Origon vastaisen kärjen y-koordinaatti on

=

 
# YO2015Kcz

  1. Origon vastaisen kärjen z-koordinaatti on

=

 

Tehtävä

Havaintopisteessä \(A\) nähtiin trombi merellä suunnassa \(133,8°\) ja havaintopisteessä \(B\) sama trombi suunnassa \(205,0°\). Suunnat on ilmoitettu pohjoissuunnasta lähtien myötäpäivään. Pisteiden \(A\) ja \(B\) koordinaatit ovat \((6670801,2549572)\) ja \((6670015,2554955)\) koordinaatistossa, jonka x-akseli suuntautuu pohjoiseen ja y-akseli itään ja jonka yksikkönä on metri. Laske trombin sijainti. [12/K11]

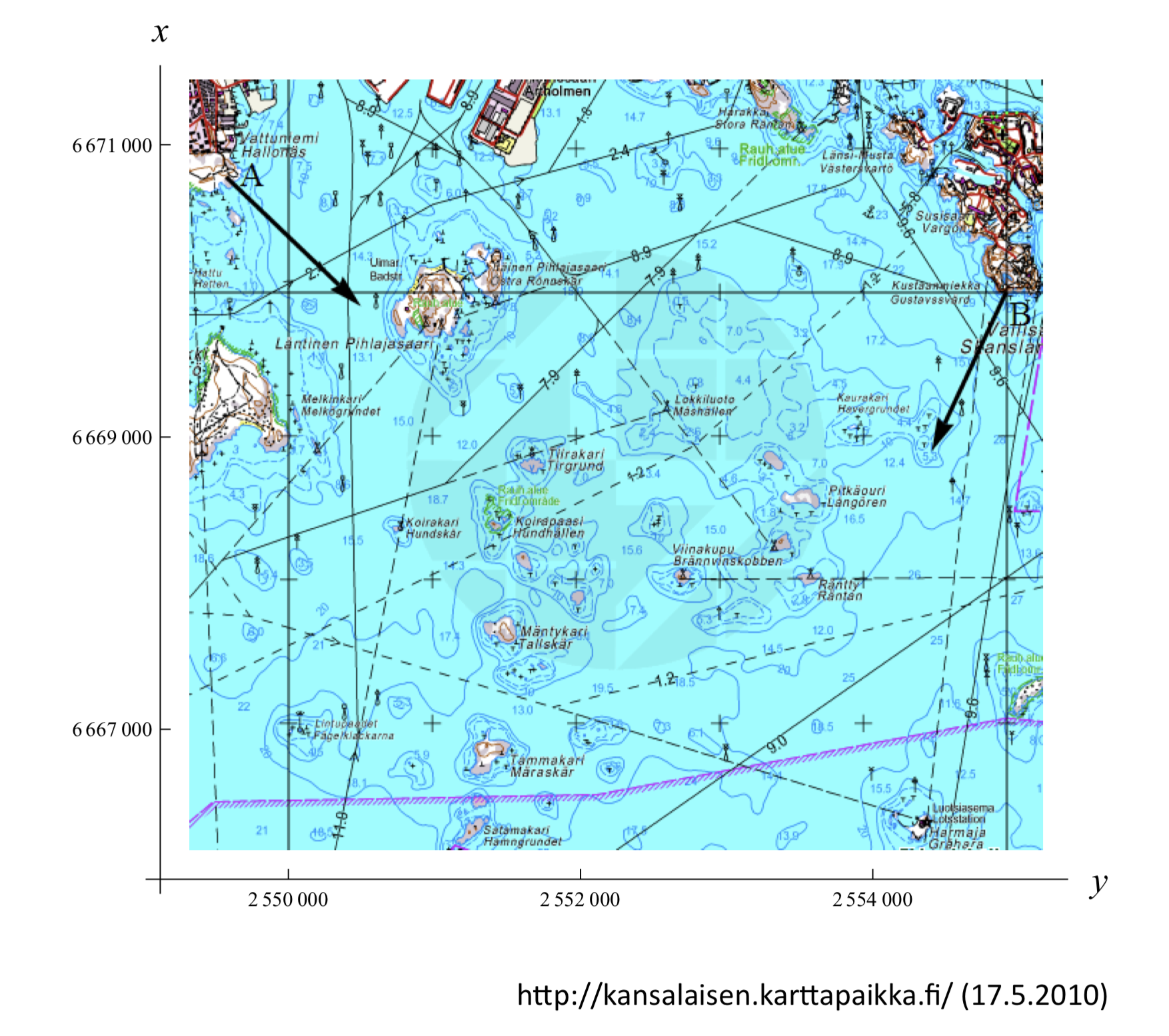
Vinkki

Vaihda laskua varten x- ja y-akselit keskenään ja vaihda lopuksi koordinaatit takaisin trombin alkuperäiseen koordinaatistoon vaihtamalla x- ja y-akselien koordinaatit päikseen.

# YO2011x

Trombin sijainnin x-koordinaatti on

=

 
# YO2011y

Trombin sijainnin y-koordinaatti on

=

 

These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.