4. Avaruusgeometriaa: tehtävät

4.1 Avaruuskappaleita ja kulmia

Tehtävä

# avaruuslavistaja

Mikä on suorakulmaisen särmiön avaruuslävistäjän pituus, jos sen sivujen pituudet ovat \(7\), \(9\) ja \(5\)?

=

 
# teht_avaruuskulma

Tehtävä

Suorakulmaisen särmiön muotoisen laatikon sivujen pituudet ovat \(x=10\), \(y=3\) ja \(z=8\). Laatikon sisään asetetaan lauta kuvan mukaisesti. Kuinka suuri on laatikon pohjan ja laudan välinen kulma?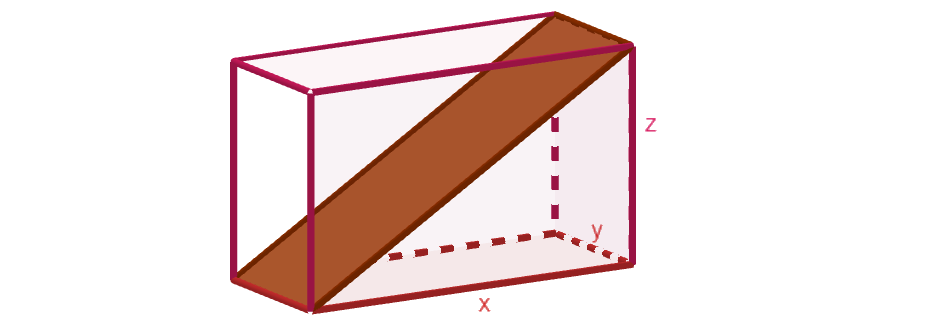

# avaruuslavistaja_kulma

Kulman suuruus asteen tarkkuudella (ilman astemerkkiä)

=

 
# teht_pahvikuutio

Tehtävä

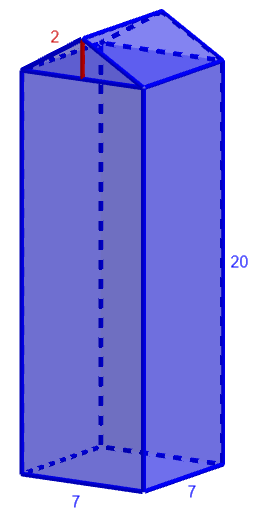
Matti valmistaa pahvista kuution, jonka sivun pituus on \(20 \text{ cm}\).

  1. Kuinka paljon pahvia tarvitaan kuution tekoon?
# pahvikuutio_1

Vastaus neliödesimetreinä ykkösten tarkkuudella (ilman yksikköä)

=

 
  1. Matti haluaa asettaa kuution sisään mahdollisimman pitkän ohuen riman. Kuinka pitkä rima kuutioon mahtuu?
# pahvikuutio_2

Riman pituus senttimetreinä ykkösten tarkkuudella (ilman yksikköä)

=

 

4.2 Pallo

# teht_auringonpimennys

Tehtävä

Täydellisessä auringonpimennyksessä kuu peittää maasta katsottuna auringon kokonaan. Jos auringon etäisyys maasta on \(387\)-kertainen kuun etäisyyteen maasta, kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna?

# auringonpimennys

Kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna

=

 
# teht_K16T6

Tehtävä (K2016/6)

Maapallon säde on \(6371 \text{ km}\), ja sen pohjoisen napapiirin leveysaste on \(66,5\). Pohjoiselta napapiiriltä valitaan pisteet \(A\) ja \(B\), joiden pituusasteiden erotus on \(90\) astetta.

  1. Määritä pisteiden \(A\) ja \(B\) välisen viivasuoran tunnelin pituus.
# K16T6a

Tunnelin pituus kilometrin tarkkuudella (ilman yksikköä)

=

 
  1. Määritä pisteiden \(A\) ja \(B\) välisen lyhimmän napapiirin kaaren pituus.
# K16T6b

Kaaren pituus kilometrin tarkkuudella (ilman yksikköä)

=

 
# teht_puolipallon_tilavuus

Tehtävä

Pallon pinta-ala on \(2,5 \text{ m}^2\). Pallo jaetaan kahteen yhtä suureen osaan. Laske muodostuvan puolipallon tilavuus.

# puolipallon_tilavuus

Tilavuus kuutiometreinä yhden desimaalin tarkkuudella (ilman yksikköä)

=

 
# teht_maapallon_vesi

Tehtävä

Vesi peittää noin \(70 \%\) maapallon pinnasta. Jos maapallon säde on noin \(6 370 \text{ km}\), kuinka suuren pinta-alan vesi peittää?

# veden_pinta_ala

Pinta-ala neliökilometreinä kymmenien miljoonien tarkkuudella (ilman yksikköä)

=

 
# teht_maapallon_vedet2

Tehtävä

Maapallon vesien yhteenlaskettu määrä on noin \(1,386 \cdot 10^9 \text{ km}^3\). Oletetaan, että maapallon säde on noin \(6370 \text{ km}\) ja että maapallo on täydellinen pallo. Jos kaikki vesi levittäytyisi maapallon pinnalle tasaisesti, kuinka syvä vesikerros olisi?

# maapallon_vedet2

Veden syvyys kilometreinä yhden desimaalin tarkkuudella (ilman yksikköä)

=

 

4.3 Lieriö

# teht_aakkoskarkki

Tehtävä

Palaa tehtävään, jossa laskettiin aakkoskarkin pinta-alaa. Jos aakkoskarkin paksuus on \(0,7 \text{ cm}\), mikä on yhden karkin tilavuus?

# aakkostilavuus

Karkin tilavuus kuutiosenttimetreinä yhden desimaalin tarkkuudella (ilman yksikköä)

=

 

Jos karkin tiheys on \(1,5 \text{ g/cm}^3\) ja yksi pussi painaa \(315 \text{ g}\), kuinka monta karkkia yhdessä pussissa on?

# aakkostilavuus2

Karkkien lukumäärä pussissa (pyöristettynä lähimpään kokonaislukuun)

=

 
# teht_vesitorni

Tehtävä

Vesitornin sylinterin muotoiseen säiliöön mahtuu vettä \(4000 \text{ m}^3\) ja säiliön korkeus on \(23\) metriä. Mikä on säiliön halkaisija?

# vesitorni

Säiliön halkaisija metreinä (ilman yksikköä)

=

 
# teht_maitotolkki

Tehtävä

Alla olevassa kuvassa on havainnekuva maitotölkistä sekä tölkin mitat (senttimetreinä). Laske koko tölkin tilavuus.

 
 
# maitotolkki

Koko maitotölkin tilavuus kuutiosenttimetreinä ykkösten tarkkuudella (ilman yksikköä)

=

 
# teht_muurahainen

Tehtävä

Muurahainen aloittaa kulkunsa kuution kulmasta. Kuution särmän pituus on \(1\). Mikä on lyhin matka, jonka kulkemalla muurahainen pääsee kuution vastakkaiseen kulmaan?

# muurahainen-geo
Avaa GeoGebra tuomalla osoitin tähän

 
# muurahaisen_matka

Muurahaisen kulkeman matkan tarkka arvo

=

 
# teht_kuutio_pallossa

Tehtävä

Jos pallon tilavuus on \(1\), mikä suurimman sen sisään mahtuvan kuution tilavuus?

# kuutio_pallossa

Kuution tilavuus kolmen desimaalin tarkkuudella

=

 
# teht_pallo_lieriossa

Tehtävä

Mahdollisimman pienen ympyräpohjaisen lieriön sisälle laitetaan mahdollisimman suuri pallo. Määritä pallon tilavuuden suhde lieriön tilavuuteen.

# pallo_lieriossa

Pallon tilavuuden suhde lieriön tilavuuteen prosentteina yhden desimaalin tarkkuudella (ilman prosenttimerkkiä)

=

 

4.4 Kartio

# teht_kartion_tilavuus

Tehtävä

# kartio1

Kartion pohjan pinta-ala on \(A_p=12\) ja sen korkeus \(h=7\). Mikä on kartion tilavuuden tarkka arvo?

=

 
# teht_suoran_ympyrakartion_tilavuus

Tehtävä

# kartio2

Suoran ympyräkartion pohjan säde on \(r=10\) ja sen korkeus \(h=4\). Mikä on kartion tilavuuden tarkka arvo?

=

 
# teht_katkaistu_kartio1

Tehtävä

Suoran ympyräkartion pohjan säde on \(4\) ja sen korkeus on \(12\). Kartion huipusta katkaistaan pienempi suora ympyräkartio. Tämän pienemmän kartion pohjan säde on \(1\). Kuinka korkea pienempi kartio on?

# katkaistu_kartio
Avaa GeoGebra tuomalla osoitin tähän

 
# kartio_yhdenmuotoisuus

Pienemmän kartion korkeus

=

 
# teht_katkaistu_kartio2

Tehtävä

Olkoon edelleen kartion pohjan säde \(4\) ja korkeus \(12\). Sen huipusta leikataan pois pienempi kartio, jonka pohjan säde on \(1\). Mikä on jäljelle jäävän osan tilavuus?

# katkaistu_kartio_tilavuus

Jäljelle jäävän osan tilavuus ykkösten tarkkuudella

=

 
# teht_suoran_ympyrakartion_tilavuus2

Tehtävä

Suoran ympyräkartion korkeus on \(h\) ja pohjan säde \(r\). Kartion huipulta katkaistaan pienempi kartio, jonka korkeus on \(\frac{1}{4}h\). Kuinka moninkertainen ison kartion tilavuus on verrattuna pienempään kartioon?

# katkaistu_kartio_tilavuus2

Jos merkitään pienemmän kartion tilavuutta \(V_p\) ja ison kartion tilavuutta \(V_i\), laske suhde \(\frac{V_i}{V_p}\).

=

 
# teht_suoran_ympyrakartion_vaippa

Tehtävä

# kartio_sivutahko

Suoran ympyräkartion pohjan säde on \(r=5\) ja sen sivujana on \(s=9\). Mikä on kartion vaipan pinta-alan tarkka arvo?

=

 
# teht_kheopsi

Tehtävä

Kheopsin pyramidin muoto on lähellä neliöpohjaista kartiota. Matti mittaa pyramidin pohjan sivun pituudeksi \(230 \text{ m}\) ja kuulee oppaalta pyramidin korkeuden olevan \(137 \text{ m}\). Laske annettujen tietojen avulla arvio pyramidin tilavuudelle.

# kheopsi

Pyramidin tilavuus kuutiometreinä satojen tuhansien tarkkuudella (ilman yksikköä)

=

 
# teht_kartion_pohja

Tehtävä

\(3,0 \text{ m}\) korkean kartion pohja muodostuu tasasivuisesta kolmiosta. Kartion tilavuus on \(150 \, \ell\). Määritä pohjakolmion sivun pituus.

# kartion_pohjan_sivun_pituus

Tasasivuisen kolmion sivun pituus desimetreinä yhden desimaalin tarkkuudella (ilman yksikköä)

=

 
# teht_jaatelotottero

Tehtävä

Kartion muotoisen jäätelötötterön sivun pituus on \(15 \text{ cm}\) ja sen suuaukon halkaisija on \(8 \text{ cm}\). Jäätelötötteröön asestetaan täsmälleen pallon muotoinen jäätelöpallo, jonka halkaisija on \(8 \text{ cm}\). Jos pallon annetaan sulaa kokonaan, mahtuuko se jäätelötötterön sisään?

# jaatelo

Open plugin

4.5 Maapallo

Avaa tästä GeoGebran havainnollistus leveys- ja pituuspiireistä!

Tehtävä

Merkitään Suomen kuntien koordinaatteja niin, että x-koordinaattina on pohjoinen leveys N ja y-koordinaattina itäinen pituus E. Merkitään esimerkiksi Helsingin koordinaatteja seuraavasti: \(60.2°\)N, \(24.9°\)E \(= (60.2, 24.9)\).

# Kaupunki

Valitse, onko väite tosi vai epätosi.

Tehtävä

Monet hallinnolliset rajat seuraavat luonnollisia maaston piirteitä, kuten jokia ja vuo- ristoja. Sen sijaan Yhdysvalloissa Coloradon osavaltion rajat määräytyvät Maapallon leveys- ja pituusasteiden avulla seuraavista ehdoista:

\[\begin{align*} 37° N ≤ \text{leveysaste} ≤ 41° N\\ 102° W ≤ \text{pituusaste} ≤ 109° W. \end{align*}\]

  1. Laske Coloradon osavaltion länsirajan pituus.
# leveysjapituuspiirit

Länsirajan pituus yhden kilometrin tarkkuudella (ilman yksikköä)

=

 
  1. Kumpi on pitempi, Coloradon osavaltion eteläraja vai pohjoisraja? Perustele.

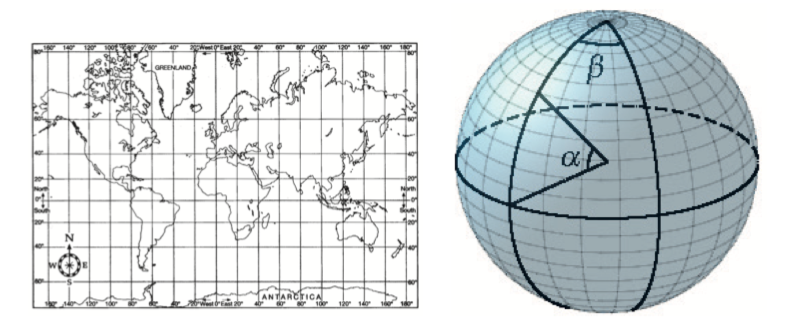
Tässä tehtäväassä Maa oletetaan palloksi, jonka säde on \(R=6 371\text{km}\). Tilanteen hahmottamisen helpottamiseksi on oikean puolen kuvaan merkitty päiväntasaajan suhteen mitattava leveysaste \(\alpha\) ja Greenwichin meridiaanin suhteen mitattava pituusaste \(\beta\). [8/S17]

# Perustelutpituudelle

Kumpi on pitempi etelä- vai pohjoisraja?



 

        

        





                
4.6 Avaruuskappaleita koordinaatistossa

        

        





                
Tehtävä

        

        





                
Suorakulmaisen kolmion kärkipisteet ovat \(A(-4,2)\), \(B(2,2)\) ja \(C(2,5)\). Kolmio pyörähtää sivun \(BC\) ympäri. Laske syntyvän pyörähdyskappaleen tilavuus desilitroina yhden desimaalin tarkkuudella, kun koordinaatiston yksikkönä on senttimetri.

        

        





                
Vinkki

        

        





                
Muodostuva pyörähdyskappale on ympyräpohjainen kartio.

        

        




                
                    #
                
                pyorahdyskpl
            

                
Pyörähdyskappaleen tilavuus desilitroina yhden desimaalin tarkkuudella on (ilman yksikköä)


=


 

        

        





                
Tehtävä

        

        





                
Pallon kuoren yksi piste on \(A(1,2,-2)\) ja sen keskipiste on \(O(0,1,0)\). Laske pallon pinta-ala yhden desimaalin tarkuudella.

        

        




                
                    #
                
                pallokoord
            

                
Pallon pinta-ala yhden desimaalin tarkkuudella on (ilman yksikköä)


=


 

        

        



                
            
Avaa tästä GeoGebran 3D-sovellus!

            
            
        

            
        

            
        

    

    
    
    


    
    
        
These are the current permissions for this document; please modify if needed.
            You can always modify these permissions from the manage page.