3. Ympyrän geometriaa: tehtävät

Tehtävä

# ympyramonivalinta

Onko väite totta vai tarua? Valitse oikea vaihtoehto.

3.1 Säde, halkaisija ja piiri

# teht_puhelinlinja

Tehtävä

Oleletaan, että maapallo on täysin pyöreä. Eräs puhelinyhtiö on vetänyt puhelinlinjan päiväntasaajaa pitkin maapallon ympäri. Kuinka paljon linjaa tarvitaan lisää, jos se halutaan nostaa \(10 \text{ m}\) korkeille tolpille. Anna vastaus metreinä ja yhden desimaalin tarkkuudella.

# puhelinlinja

# teht_polkupyora

Tehtävä

Polkupyörän renkaan koko on \(28"\) eli sen halkaisija on \(28\) tuumaa. Pyörään halutaan laittaa matkamittari, jota varten tarvitaan yhdellä renkaan pyörähdyksellä kuljettu matka. Laske pyörän yhden renkaan täydellä pyörähdyksellä kulkema matka ja ilmoita vastaus yhden desimaalin tarkkuudella senttimetreinä.

# polkupyörä

# teht_pyora

Tehtävä

Halkaisijaltaan \(60 \text{ cm}\) pyörä pyörähtää \(10\) kertaa. Kuinka pitkän matkan pyörä etenee?

# pyoriva_pyora_1

Kuinka monta pyörähdystä pyörä etenee \(200 \text{ m}\) matkalla?

# pyoriva_pyora_2

# teht_kukkaympyra

Tehtävä

Mari haluaa laittaa kukkia kasvamaan täsmälleen ympyrän muotoon. Hänellä on \(24\) kukkaa ja hän haluaa, että kukkien välinen etäisyys ympyrän kaarta pitkin mitattuna on tasan \(20 \text{ cm}\). Mikä on tällaisen ympyrän halkaisija?

# kukkaympyra

# teht_keskinormaali

Tehtävä

Osoita, että kahden leikkaavan ympyrän keskipisteiden välinen jana on ympyröiden leikkauspisteiden välisen janan keskinormaali.

Alla olevan kuvan merkinnöillä, sinun tulee osoittaa, että kuvaan punaisella merkittyjen janojen \(AB\) ja \(OO'\) välinen kulma on \(90^{\circ}\) ja että janat \(BC\) ja \(AC\) ovat keskenään yhtä pitkiä.

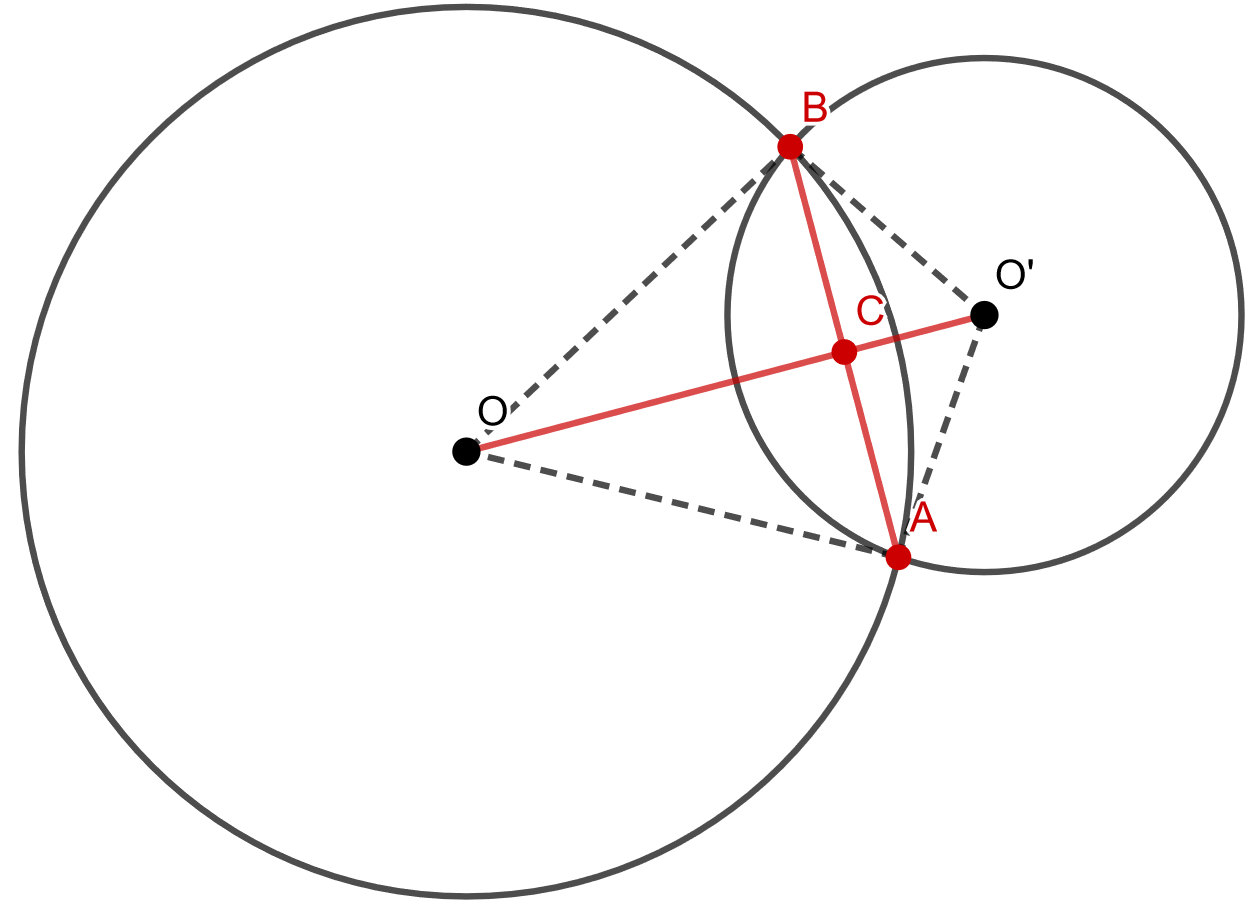
Ratkaisu

Tarkastellaan ensin kolmioita \(OO'B\) ja \(OO'A\). Kolmioiden sivut \(OB\) ja \(OA\) ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Samoin sivut \(O'B\) ja \(O'A\) ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Sivu \(OO'\) on molemmissa kolmioissa sama, joten kolmiot ovat yhteneviä (eli niiden kaikki mitat ovat yhtä suuria). Tällöin myös janat \(BC\) ja \(AC\) ovat keskenään yhtä pitkiä.

Kuvassa piste \(C\) on janojen \(AB\) ja \(OO'\) leikkauspiste, jolloin kulmat \(BCO\) ja \(OCA\) muodostavat oikokulman. Tarkastellaan seuraavaksi kolmioita \(BCO\) ja \(ACO\). Sivut \(OB\) ja \(OA\) ovat yhteneviä (kuten aiemmin todettiin). Lisäksi sivu \(OC\) on yhteinen kummallekin kolmiolle. Lisäksi kulmat \(COB\) ja \(AOC\) ovat yhteneviä, sillä kolmiot \(OO'B\) ja \(OO'A\) ovat yhteneviä (kuten aiemmin todettiin). Näin ollen kolmioiden \(BCO\) ja \(ACO\) on oltava yhtenevät ja kulmien \(BCO\) ja \(OCA\) on myös oltava yhtenevät. Tällöin \(BCO=OCA = \frac{180^{\circ}}{2}=90^{\circ}\).

3.2 Pinta-ala

# teht_koydella_rajataan_alue

Tehtävä

\(150\) metrin köydellä rajataan alue. Laske alueen pinta-ala, kun se on muodoltaan

neliön muotoinen.

# koysi_nelio

ympyrän muotoinen.

# koysi_ympyra

# teht_ympyra_arkilla

Tehtävä

Piirretään A4-arkille (\(210 \text{ mm} \times 297 \text{ mm}\)) mahdollisimman suuri ympyrä. Mikä on tämän ympyrän pinta-ala?

# a4

Tehtävä

Seitsemän mäntytukkia sidotaan vaijerilla alla olevan poikkileikkauskuvion mukaisesti. Kuinka paljon vaijeria tarvitaan yhteen kierrokseen? Jokaisen tukin halkaisija on 20 cm. Anna vastaus senttimetrin tarkkuudella. [7/K14]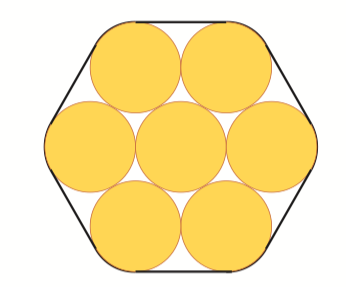

# Mantytukit

3.3 Keskuskulma, kaaren pituus, sektorin pinta-ala

Tehtävä

# sektori1

# teht_sektorin_keskuskulma

Tehtävä

Ympyräsektorin pinta-ala on \(52,9\) ja sen säde on \(5,4\). Kuinka suuri on sektorin keskuskulma?

# sektori2

# teht_pizzapalat

Tehtävä

Kumpi alla olevista pizzapaloista kannattaa ottaa, jos haluaa rahalleen eniten vastinetta?

# pizzapalat

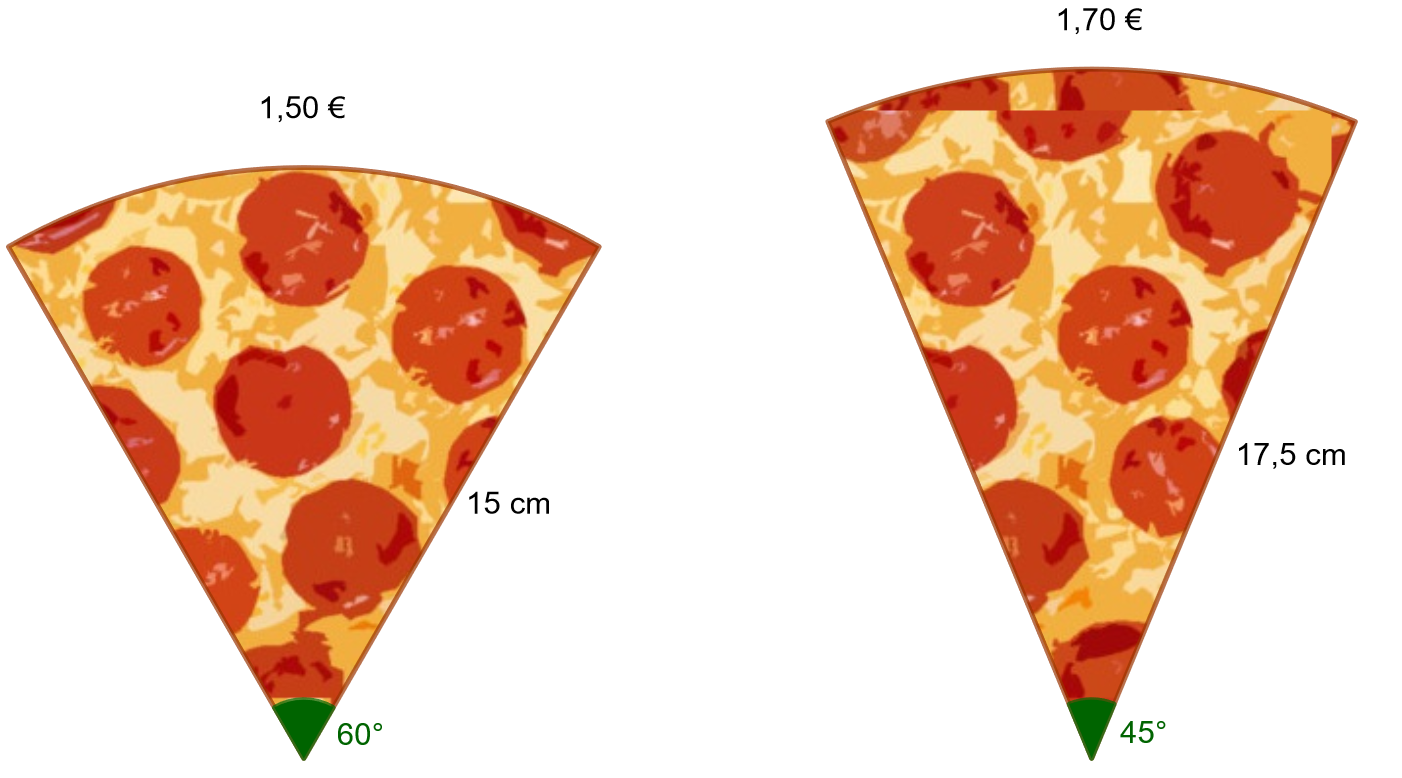
Open plugin

# teht_kuulantyonto

Tehtävä

Alla on kuva kuulantyöntöringistä ja -sektorista. Ringin halkaisija on \(7\) jalkaa eli \(2,135 \text{ m}\).

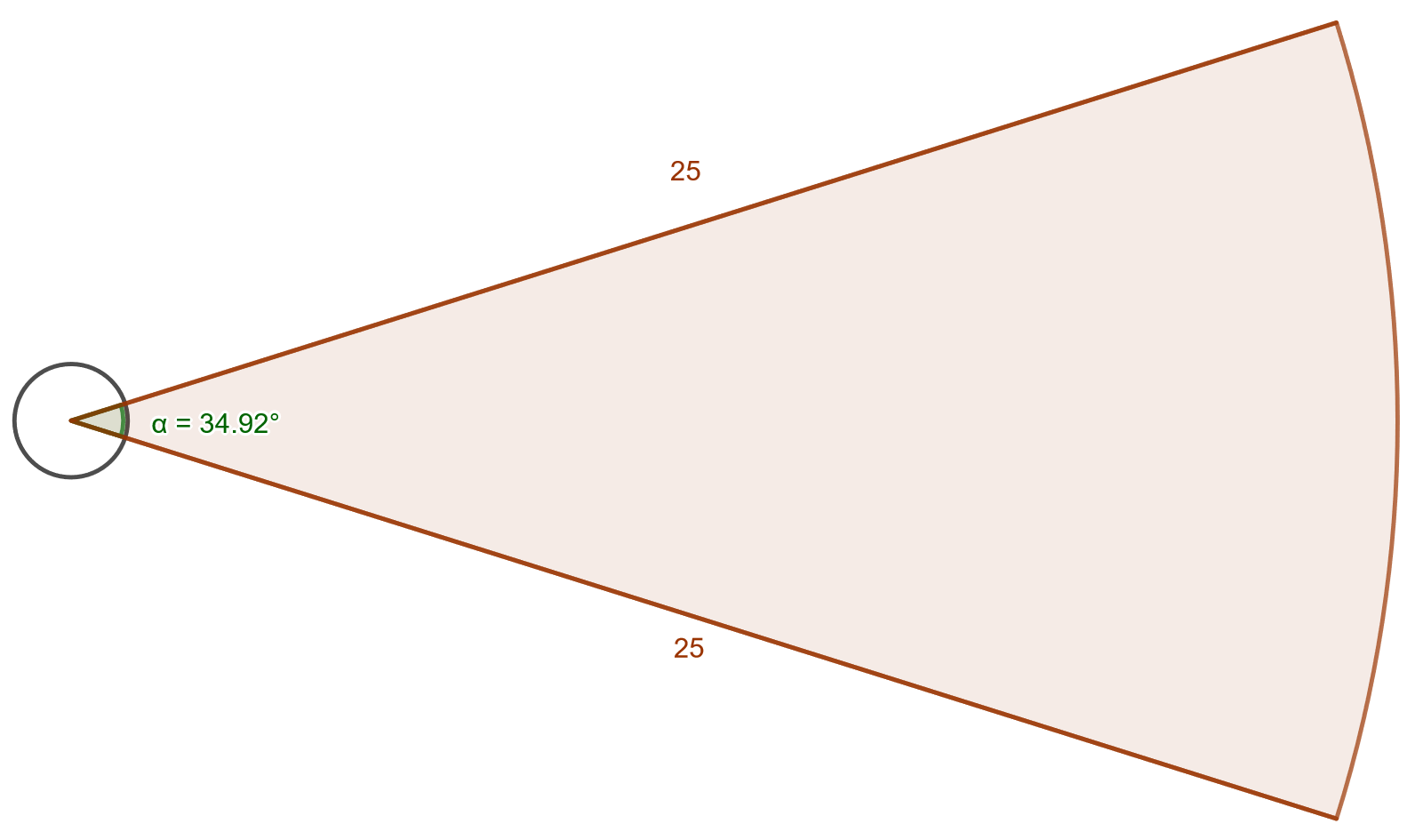
Kuulantyöntösektori peitetään hiekalla. Kuinka suuri pinta-ala peitetään? Rinkiin ei laiteta hiekkaa.

# kuulantyonto_a

Sektori ja rinki ympäröidään ulkoreunoja pitkin merkintänauhalla. Kuinka paljon nauhaa tarvitaan?

# kuulantyonto_b

# teht_lammas

Tehtävä

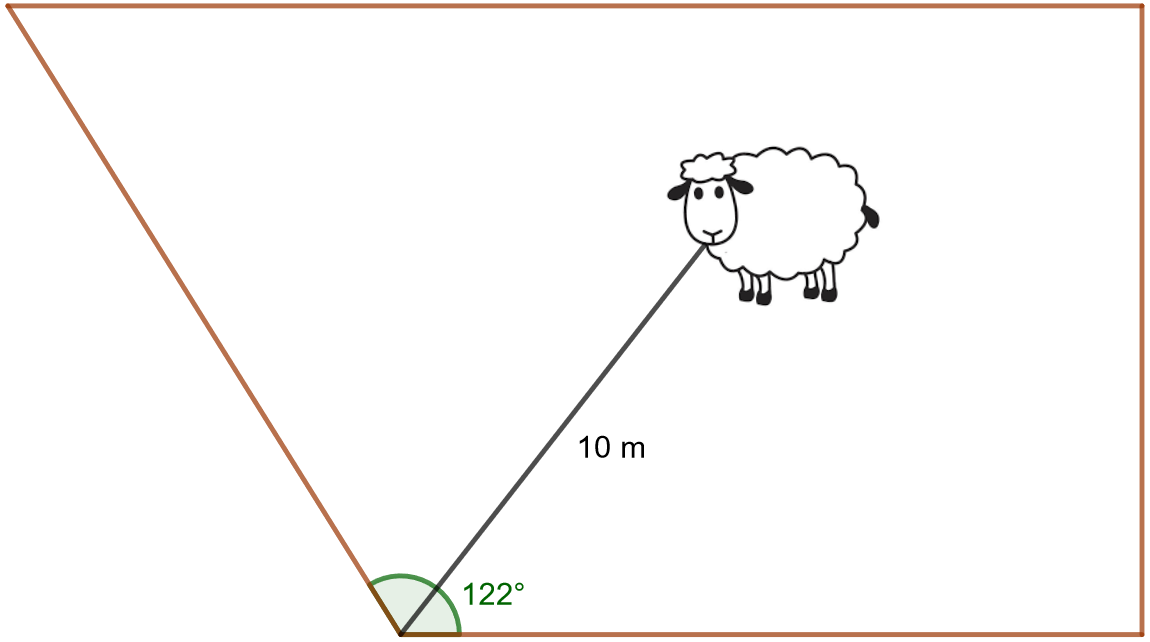
Lammas on kiinnitetty \(10 \text{ m}\) pitkällä hihnalla aidoitetun alueen kulmaan. Laske, kuinka suurelta alueelta lammas voi syödä ruohoa.

# lammas

3.4 Jänne, segmentti

# teht_segmentin_ala

Tehtävä

Ympyrän säde on \(2\) ja segmentin keskuskulman suuruus on \(138^{\circ}\). Mikä on pienemmän muodostuvan segmentin pinta-ala?

# segmentti1

# teht_suuremman_segmentin_ala

Tehtävä

Ympyrän säde on \(3\) ja segmentin keskuskulman suuruus on \(300^{\circ}\). Mikä on suuremman muodostuvan segmentin pinta-ala?

# segmentti2

# teht_segmentin_ala2

Tehtävä

Ympyrän halkaisija on \(14\). Ympyrään on piirretty segmentti, jota vastaavan kaaren pituus on \(17\). Kuinka suuri on pienemmän segmentin pinta-ala?

# segmentti3

# teht_ympyraneljannes

Tehtävä

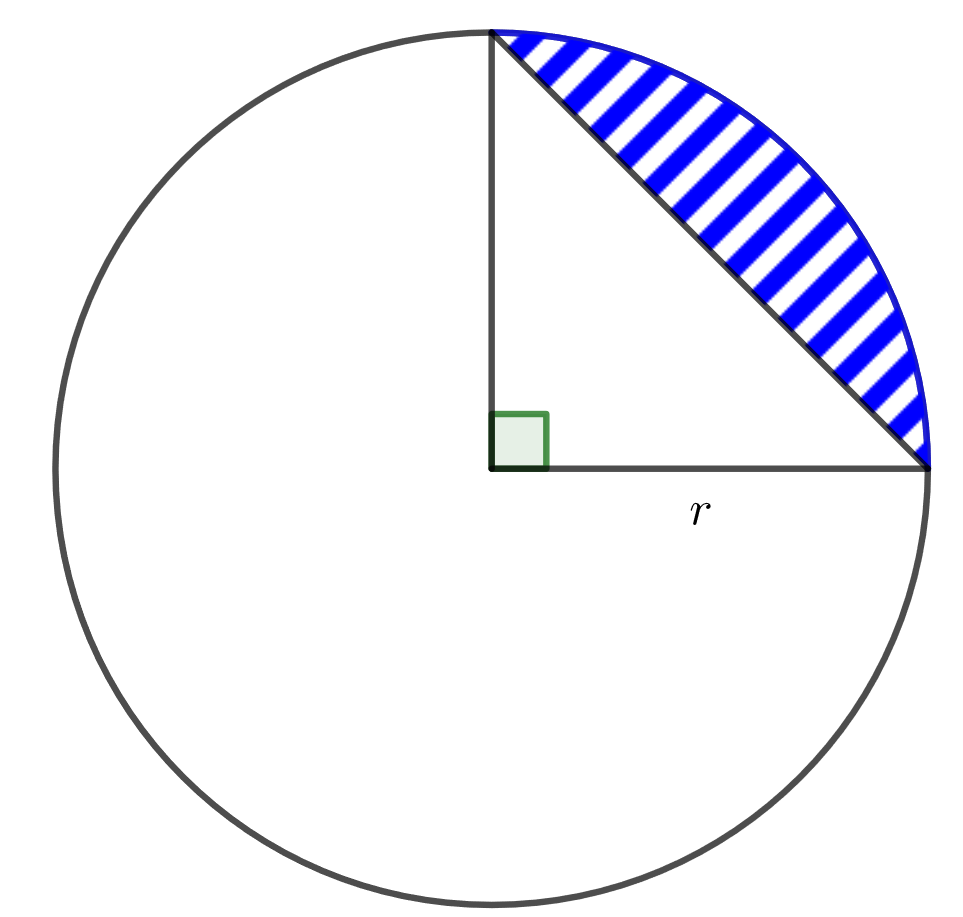
Kuinka monta prosenttia ympyräneljännekseen piirretyn segmentin pinta-ala on koko ympyrän pinta-alasta? Ympyrän säde on \(r\).

# ympyraneljannes

3.5 Tangentti, tangenttikulma

# teht_tangenttikulma1

Tehtävä

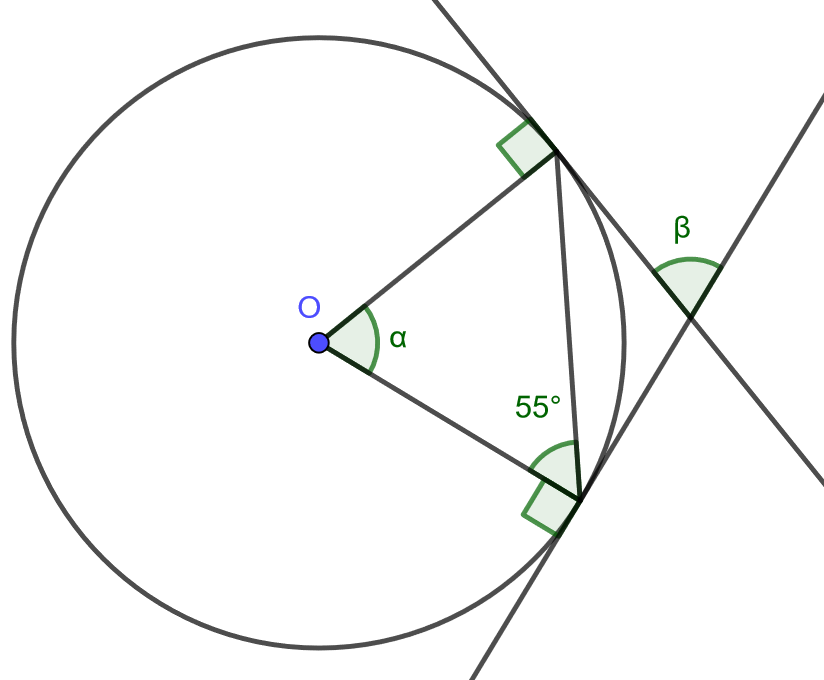
Ratkaise alla olevasta kuvasta \(\alpha\) ja \(\beta\).

# tangenttikulmat1

# tangenttikulmat2

# teht_vesitorni

Tehtävä

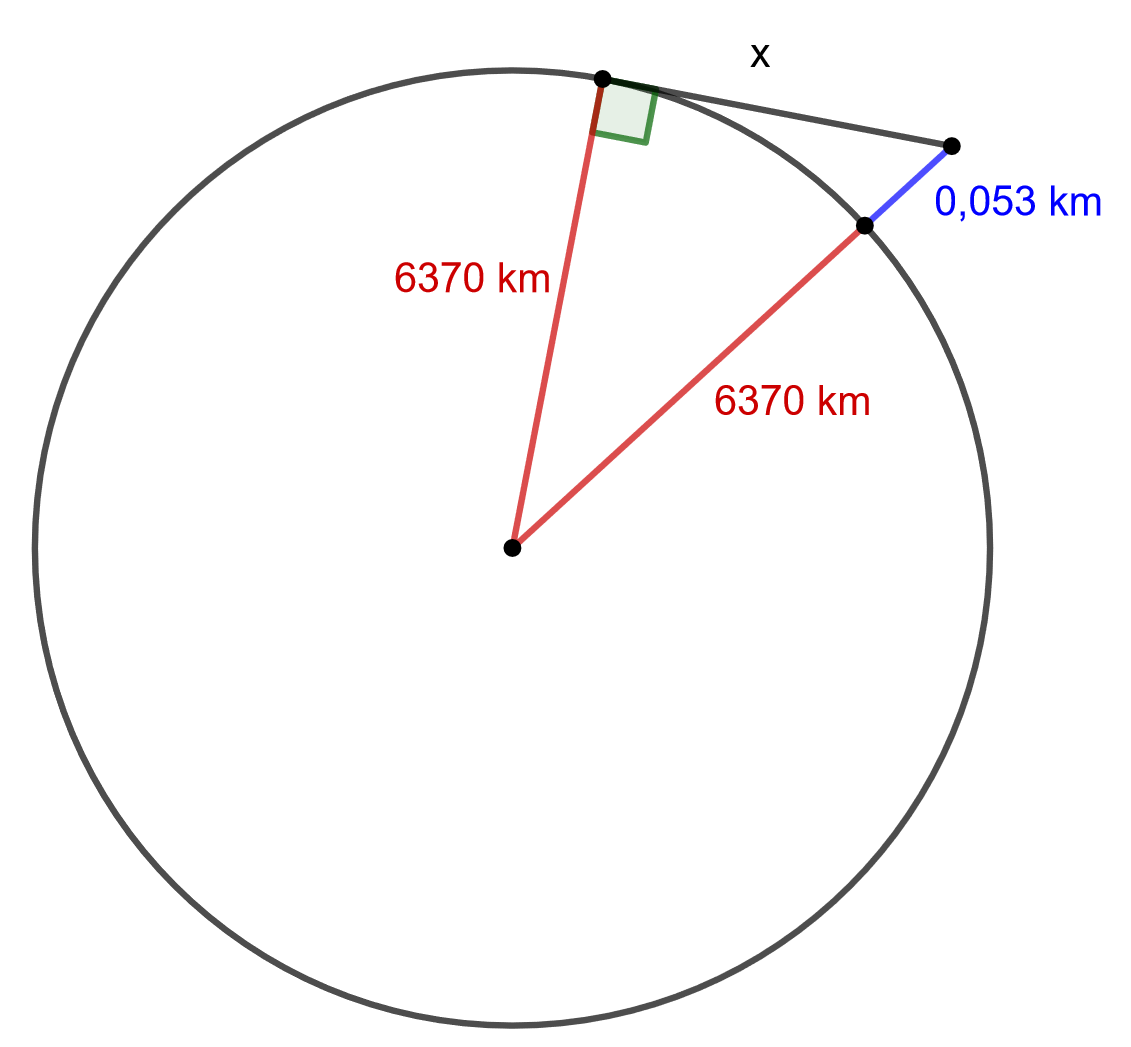
Kuinka pitkälle \(53 \text{ m}\) korkeasta vesitornista voi nähdä? Maapallon säde on \(6370 \text{ km}\). Oletetaan, että katsojan silmät ovat myös \(53 \text{ m}\) korkeudella maan pinnasta. Piirrä ensin mallikuva tilanteesta.

Huom! Mallikuva ei ole mittakaavassa!

Tehtävässä tulee ratkaista kuvaan merkitty pituus \(x\).

# vesitorni

# teht_tangenttikulma2

Tehtävä

Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä \(C\). Tangenttien sivuamispisteet \(E\) ja \(D\) ovat etäisyydellä \(10\) pisteestä \(C\). Piirretään ympyrälle vielä yksi tangentti pisteen \(F\) kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet \(A\) ja \(B\). Laske kolmion \(ABC\) piiri. [H]

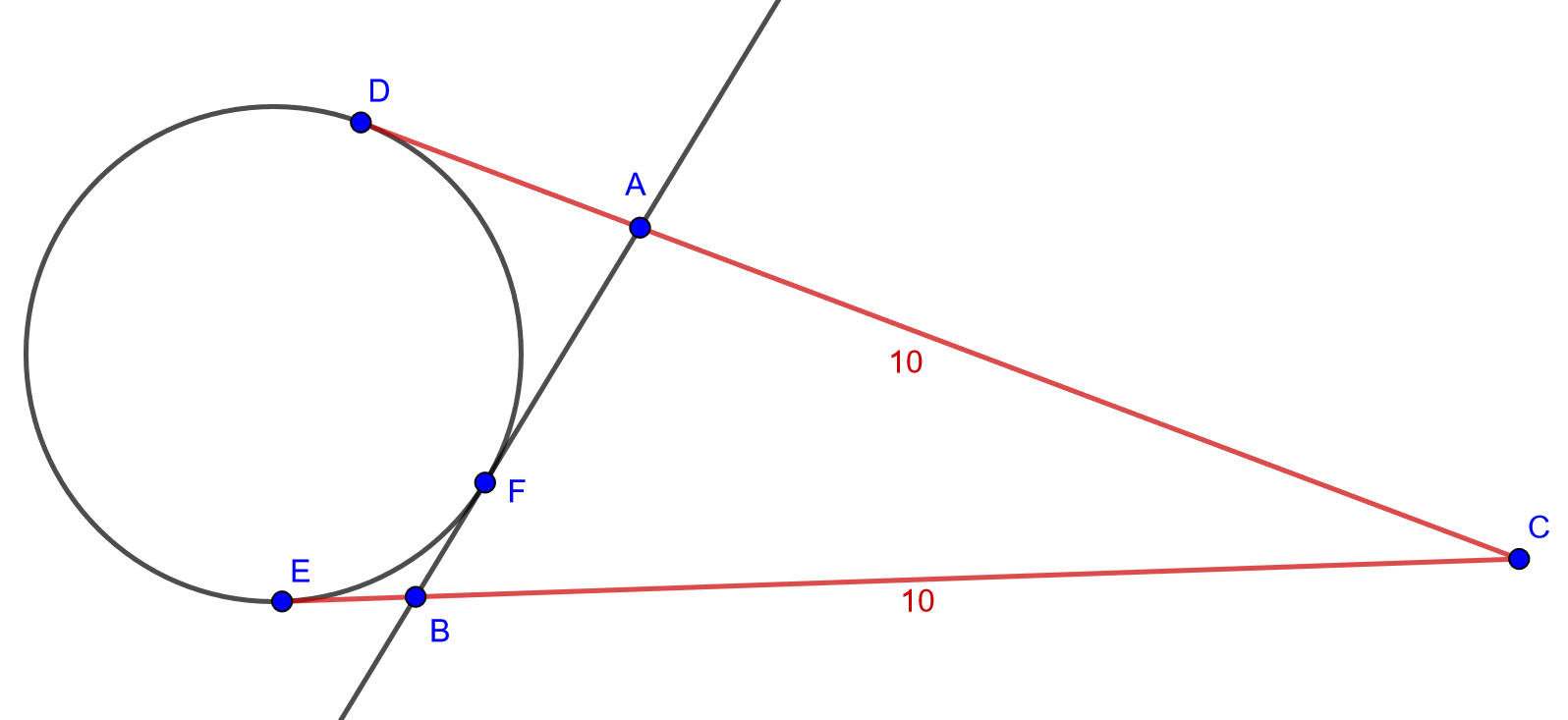
Vinkki

Pisteet A, B ja C ovat tangenttikulmien kärkiä, eli ne ovat yhtä etäällä molemmista tangenttipisteistään.

# tangenttikolmio

3.6 Keskuskulma, kehäkulma

# teht_kehakulma1

Tehtävä

Määritä kulman \(\alpha\) suuruus.

# kehakulma

# teht_kehakulma2

Tehtävä

Määritä kulman \(\alpha\) suuruus.

# kehakulma_2

# teht_kehakulma3

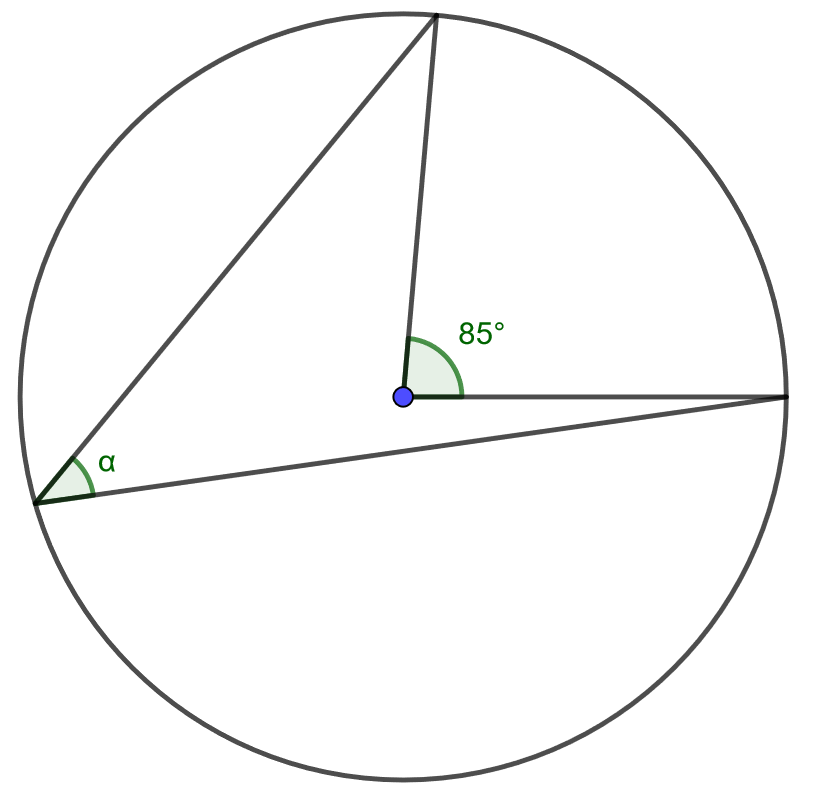
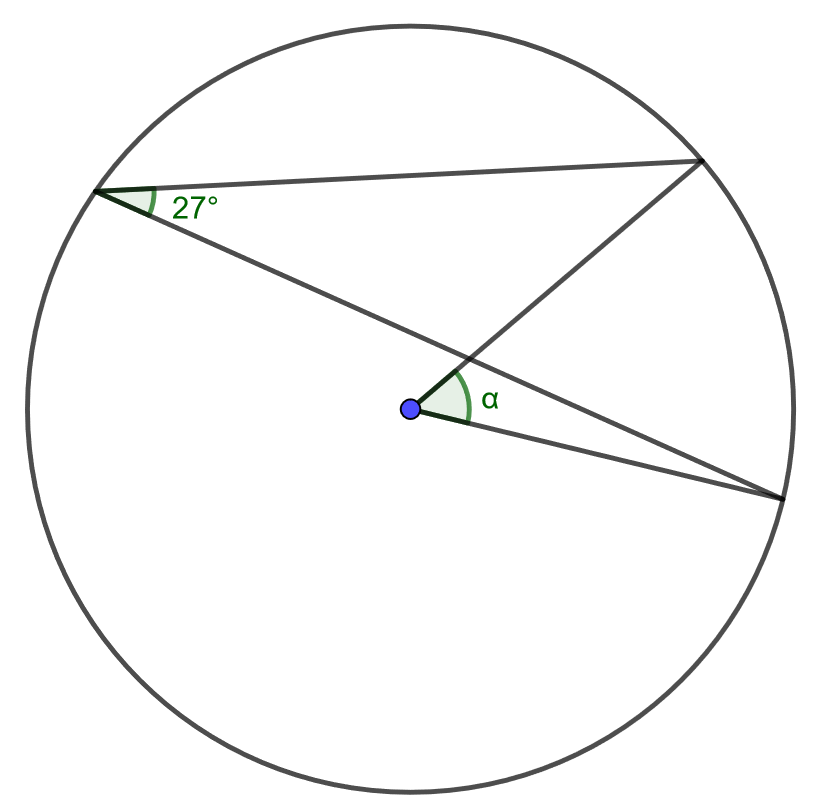
Tehtävä

Ratkaise alla olevasta kuvasta kulmat \(\alpha\) ja \(\beta\).

# kehakulma_3a

# kehakulma_3b

# teht_jannenelikulmio

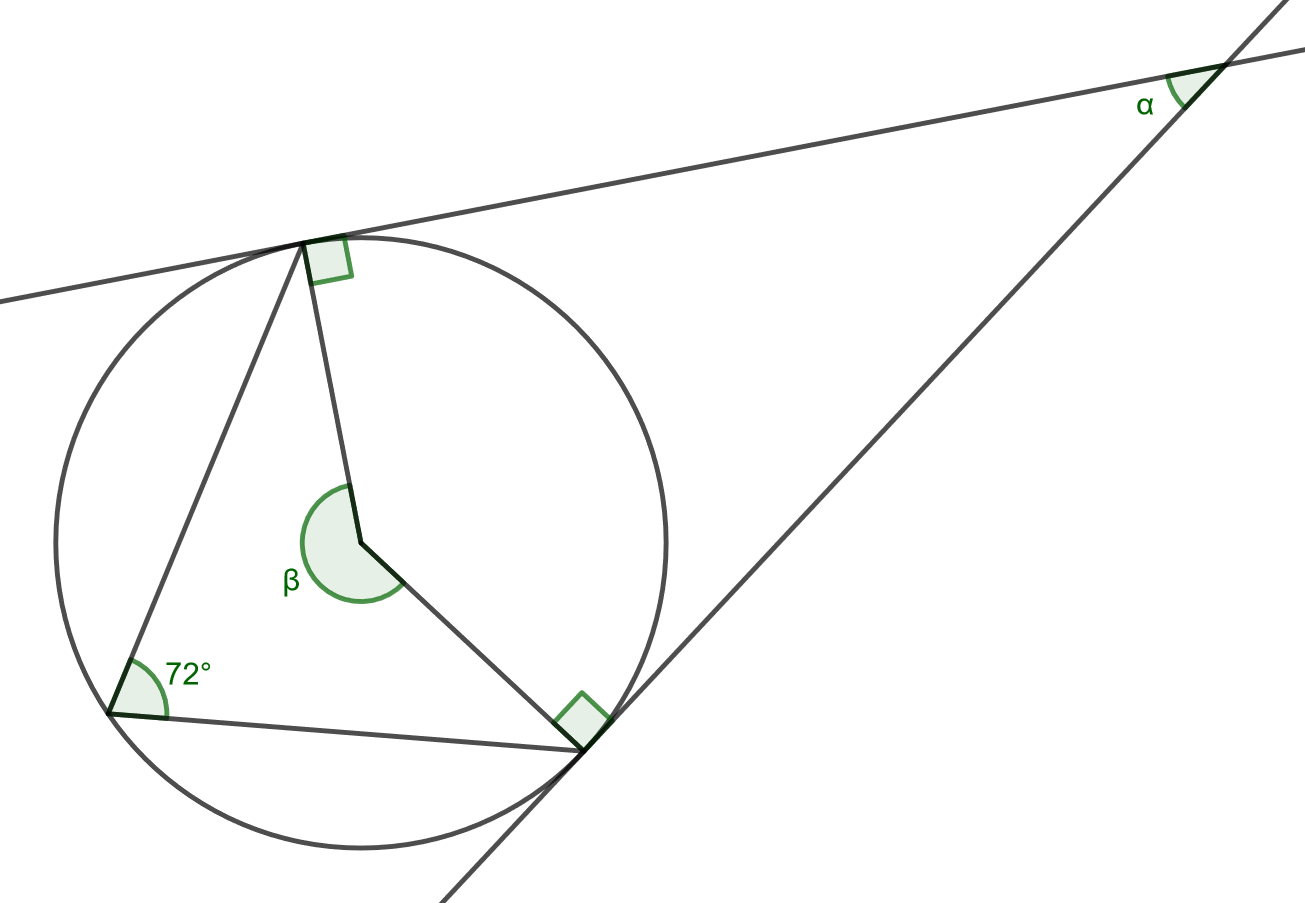
Tehtävä

Jos nelikulmion kaikki kulmat ovat saman ympyrän kaarella, nelikulmiota kutsutaan jännenelikulmioksi. Osoita, että jännenelikulmiossa vastakkaisten kulmien summa on aina \(180 ^{\circ}\).

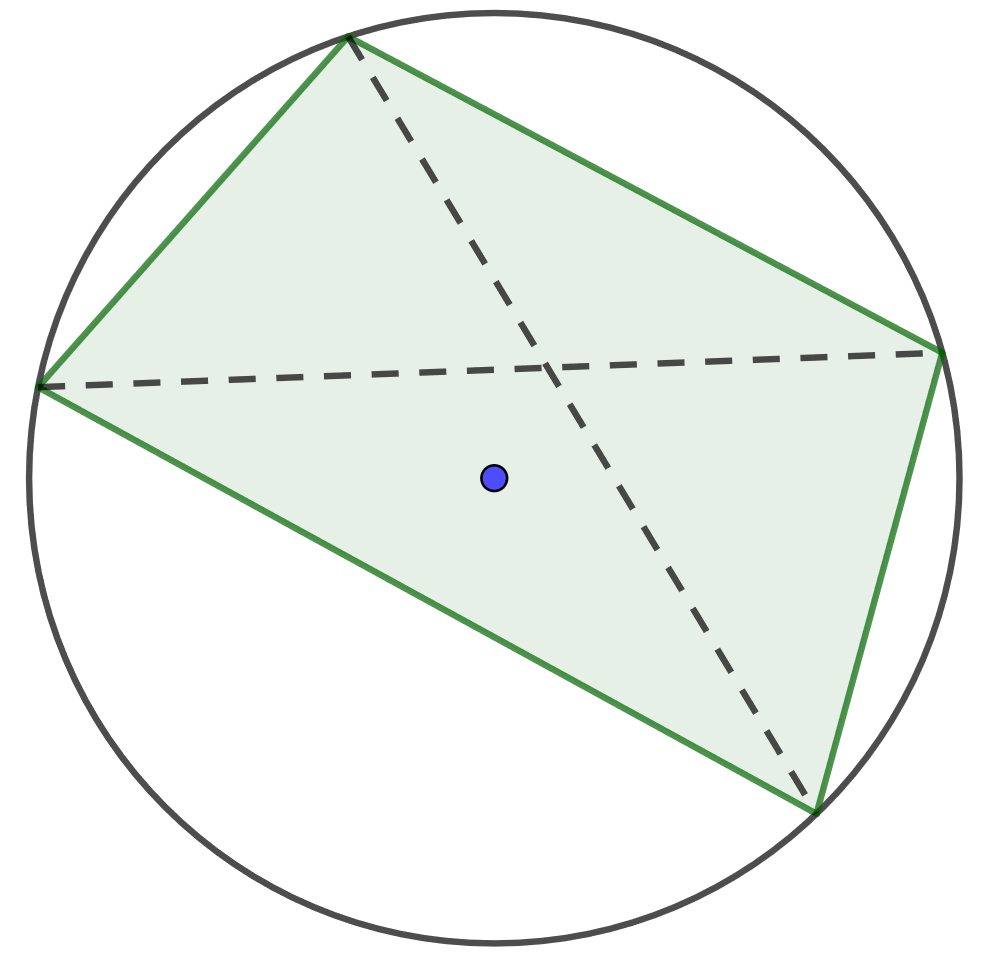
Vihje

Kokeile käyttää kehäkulmalausetta.

Ratkaisu

Käytetään alla olevan kuvan merkintöjä.

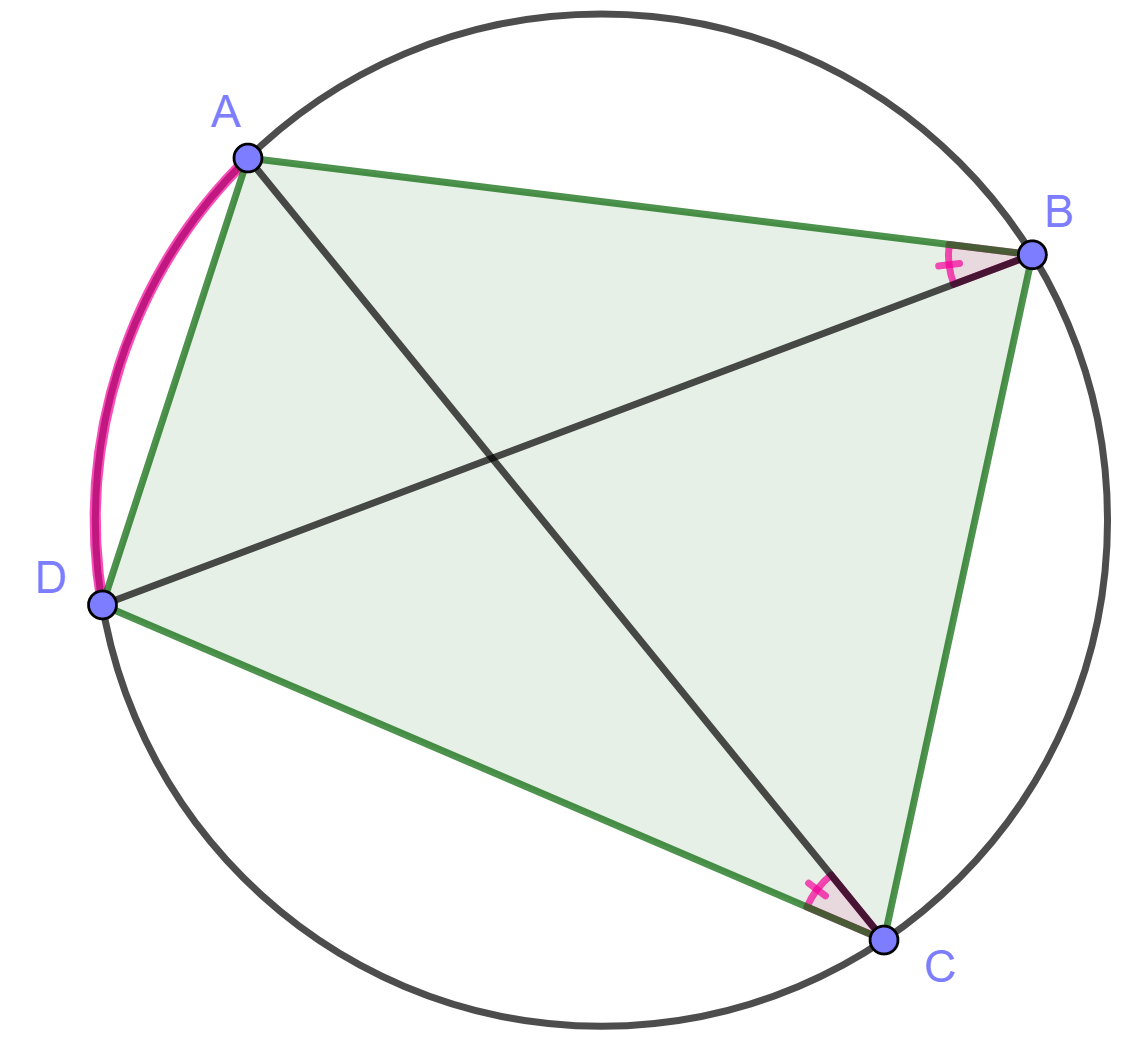
Kulmat \(ABD\) ja \(ACD\) ovat yhtä suuria, sillä ne ovat samaa kaarta \(AD\) vastaavia kehäkulmia.

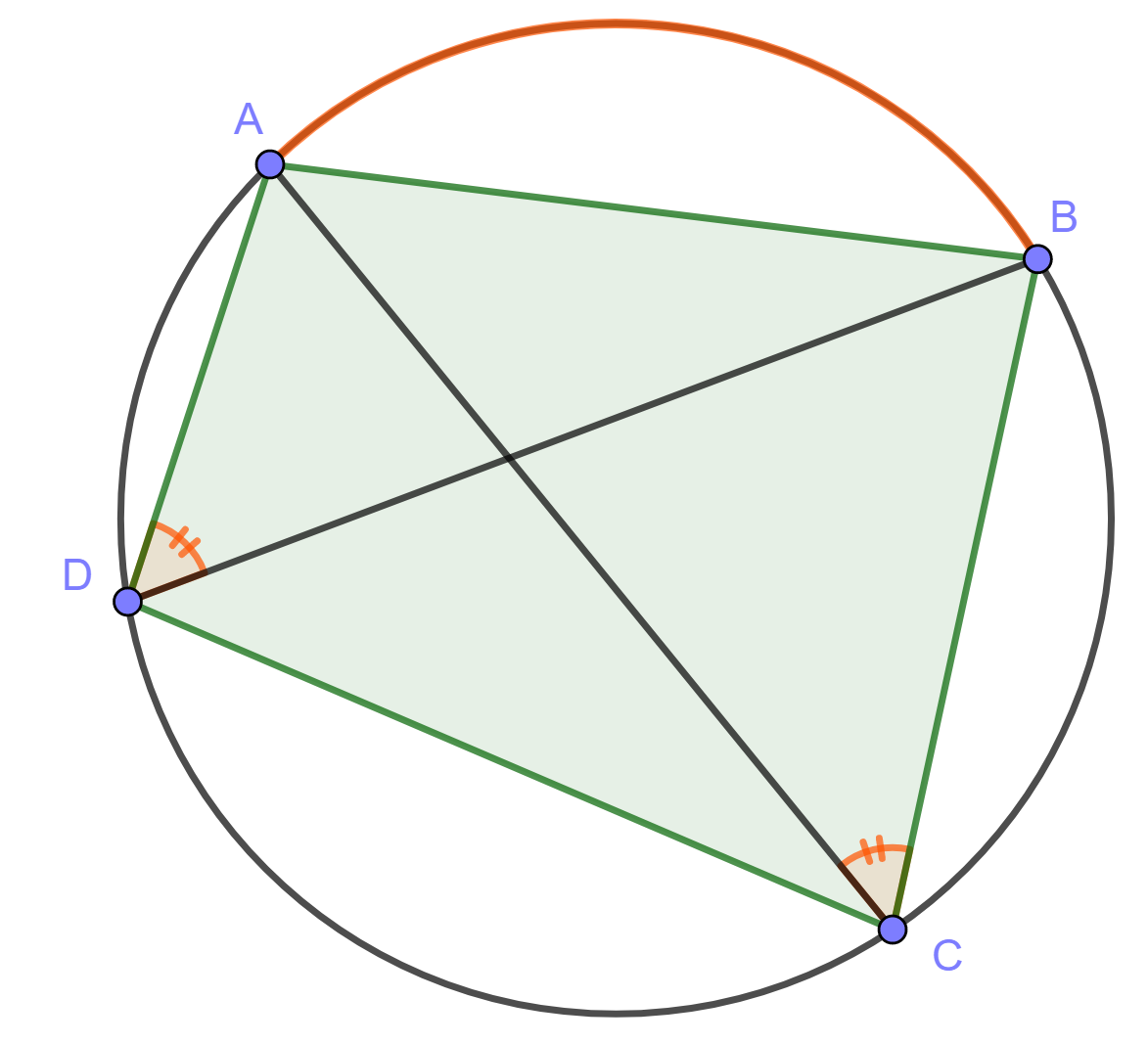
Vastaavasti kulmat \(BDA\) ja \(BCA\) ovat yhtä suuria, sillä ne ovat samaa kaarta \(AB\) vastaavia kehäkulmia.

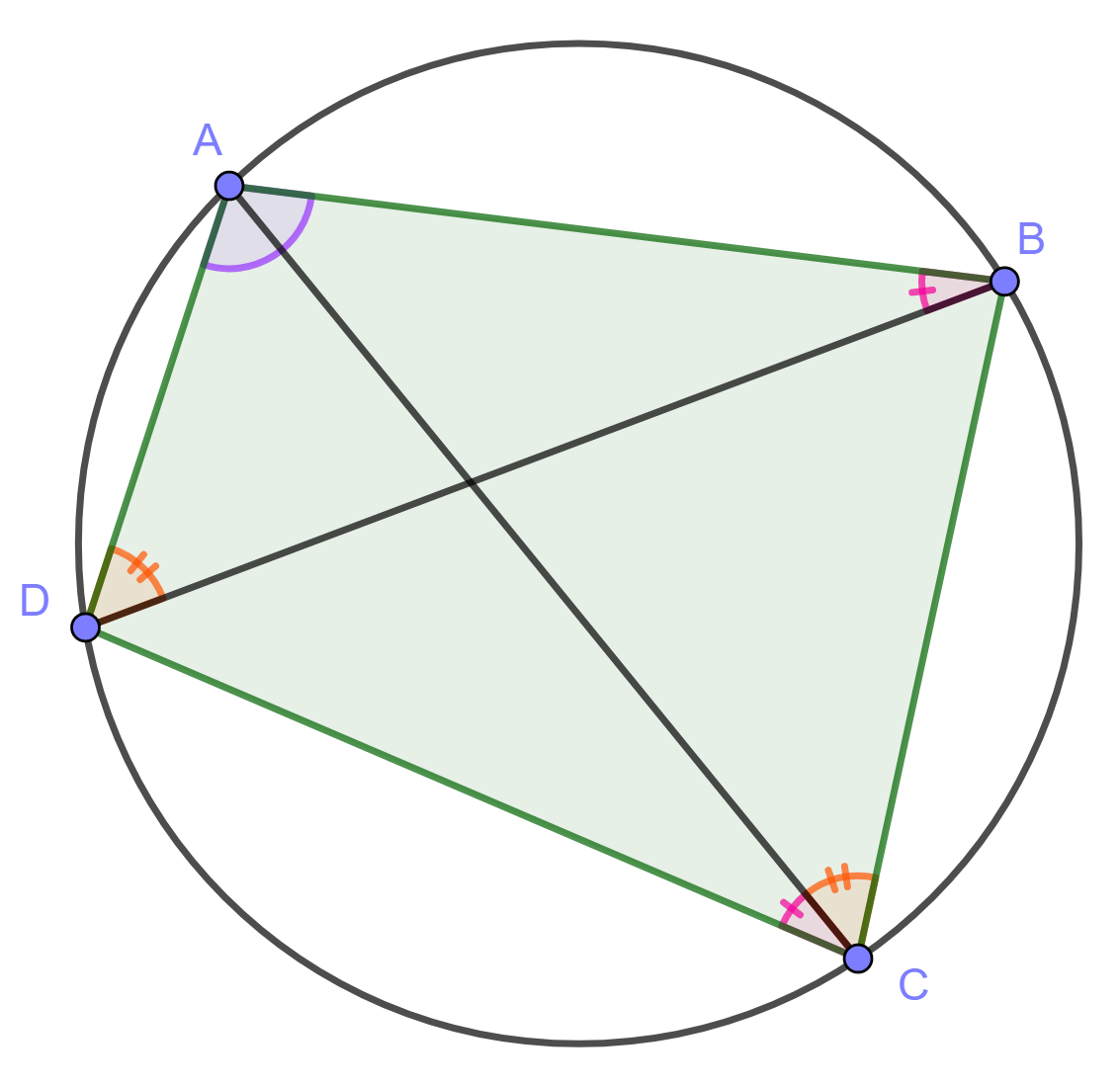
Kolmiosta \(ABD\) huomataan, että \(DAB=180^{\circ}-(BDA+ABD)\). Aiemmista kohdista tiedetään, että \(BCD=ACD+BCA=ABD+BDA\). Sijoitetaan tämä aiempaan yhtälöön, jolloin saadaan \(DAB = 180^{\circ} - BCD\) \(\Leftrightarrow DAB + BCD = 180^{\circ}\). Eli jännenelikulmion vastakkaisten kulmien summa on \(180^{\circ}\).

Sekalaisia tehtäviä

# teht_tukkikasa

Tehtävä

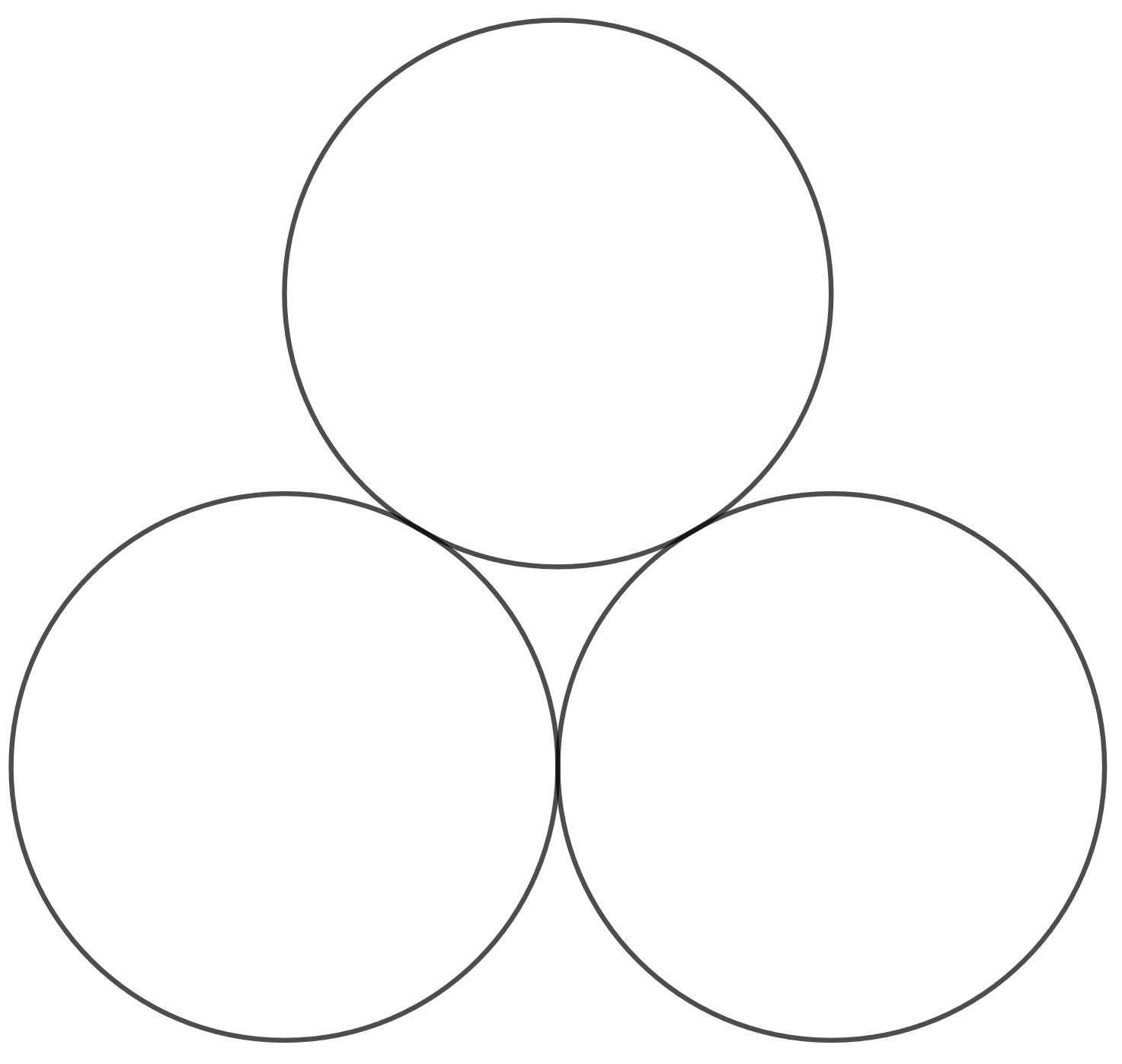
Laske tukkikasan korkeus, kun tukin säde on \(40,0 \text{ cm}\). Oletetaan tukkien poikkileikkaukset ympyröiksi. Ympyrät sivuavat toisiaan.

# tukkikasa

# teht_ympyrat_neliossa

Tehtävä

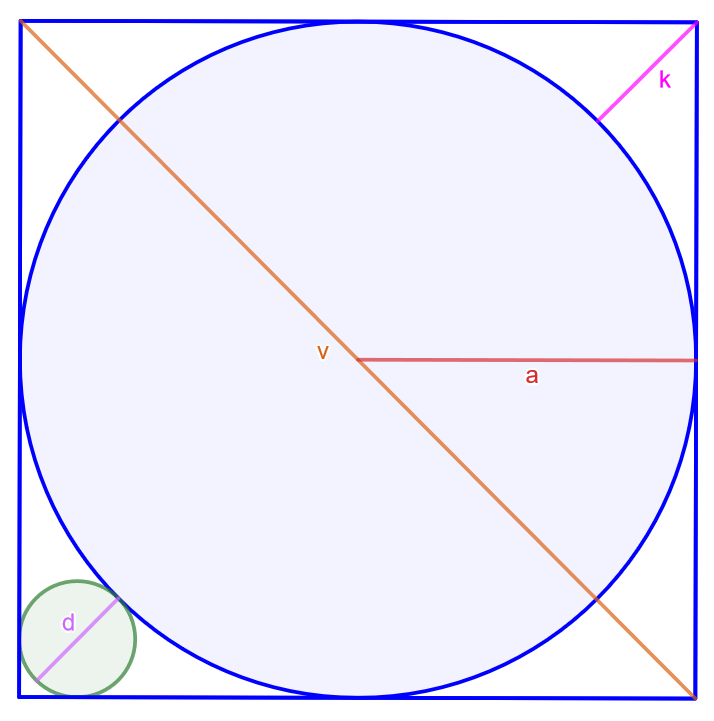
Ratkaise alla olevan kuvan pienemmän ympyrän halkaisija isomman ympyrän säteen \(a\) avulla.

Vinkki

Verranto: \(\dfrac{d}{k}=\dfrac{2a}{2a+k}\)

# iso_pieni_ympyra

# teht_kulma

Tehtävä

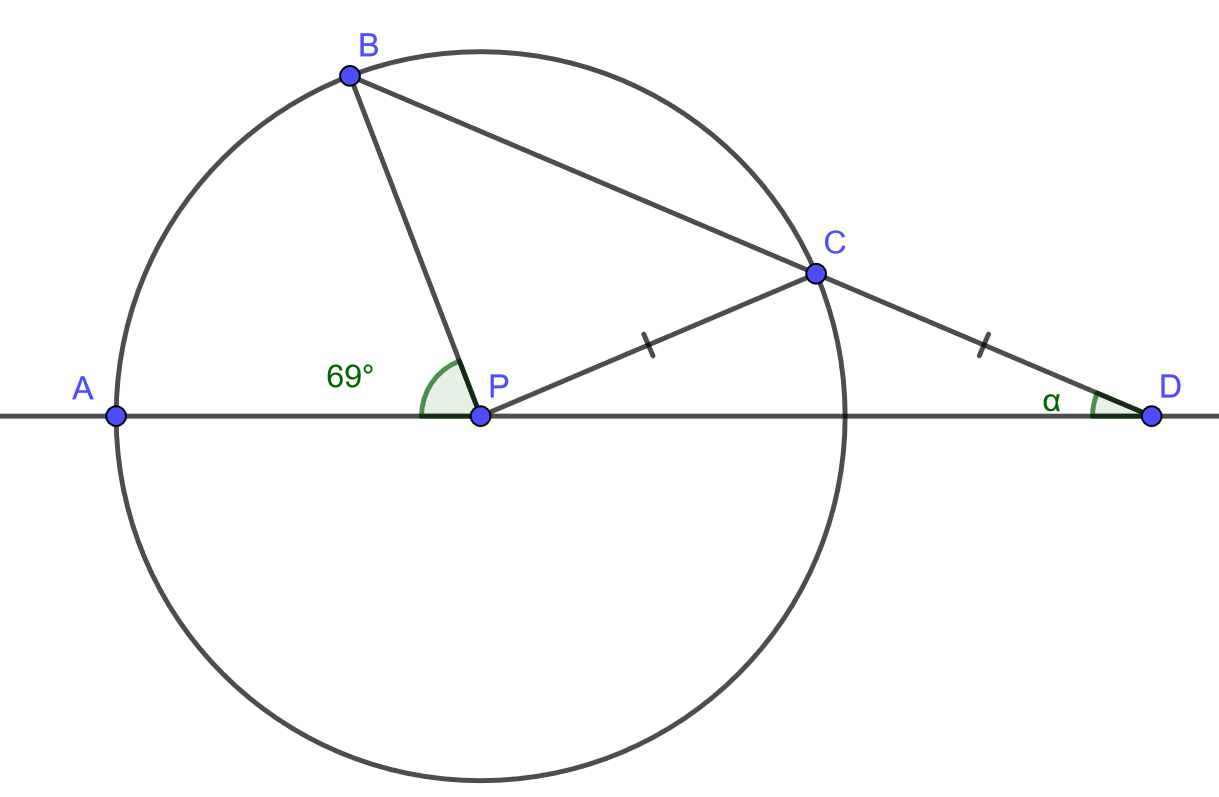
Alla olevassa kuvassa piste \(P\) on ympyrän keskipiste ja pisteet \(A\), \(B\) ja \(C\) ovat ympyrän kehän pisteitä. Piste \(D\) on suorien \(AP\) ja \(BC\) leikkauspiste ja janat \(PC\) ja \(CD\) ovat yhtä pitkät. Kulman \(\angle BPA\) suuruus on \(69^{\circ}\). Kuinka suuri on kulma \(\alpha\)? [H]

# vieruskulmat

# teht_suorakulmio_neljannesympyra

Tehtävä

Neliön sisään piirretään neljännesympyrä siten, että neliön ylänurkasta voidaan erottaa neljännesympyrää koskettava suorakulmio, jonka sivujen pituudet ovat \(1\) ja \(8\). Kuinka pitkä on neliön sivu?

# suorakaide-neljannesympyralla-geo

# suorakaide_neljannesympyralla

# teht_kaarien_rajaama_alue

Tehtävä

Ympyränkaaret, joiden säteet ovat \(2a\) ja \(a\), leikkaavat alla olevan GeoGebra-appletin mukaisesti. Mikä on kaarien rajaaman alueen pinta-ala? [T]

# kaarien-rajaama-ala-geo

Vinkki

Alue voidaan laskea kahden segmentin pinta-alojen summana.

# kaarien_rajaama_alue

# teht_suurempi_piiri

Tehtävä

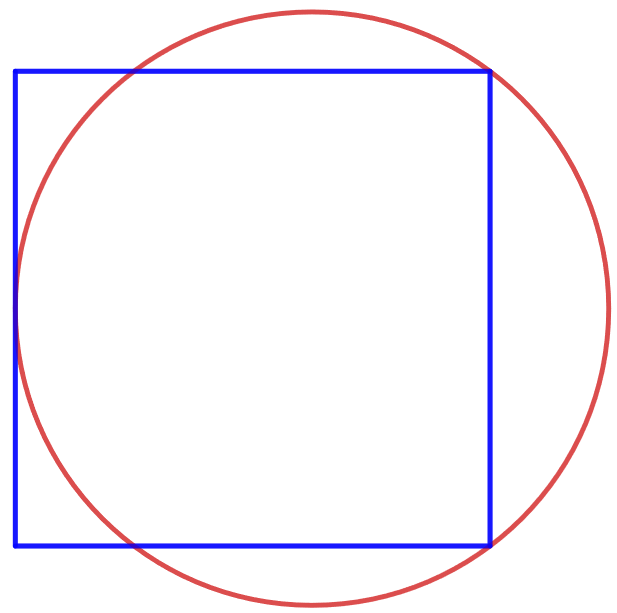
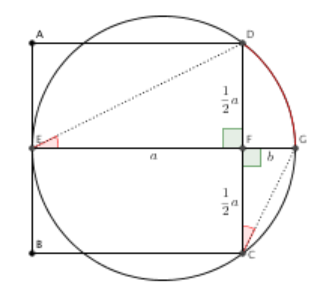
Neliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä.
Kummalla on suurempi piiri, neliöllä vai ympyrällä? [H]

Vinkki

# nelion-ja-ympyran-piirit

Open plugin

# teht_monikulmio_ympyrassa

Tehtävä

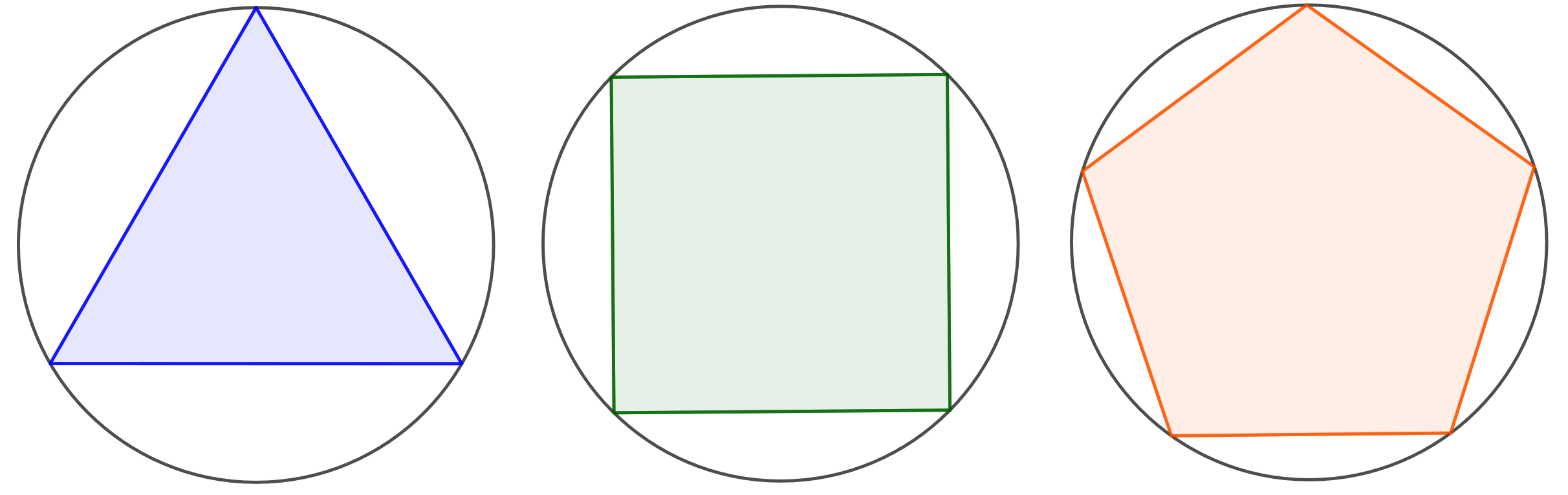
Mikä on suurimman mahdollisen \(r\)-säteisen ympyrän sisään mahtuvan säännöllisen \(n\)-kulmion pinta-ala?

Ratkaisu

Tehtävän voi ratkaista monilla eri tavoilla, joista tässä esitetään vain yksi. Käytetään hyväksi alla olevaa kuvaa.

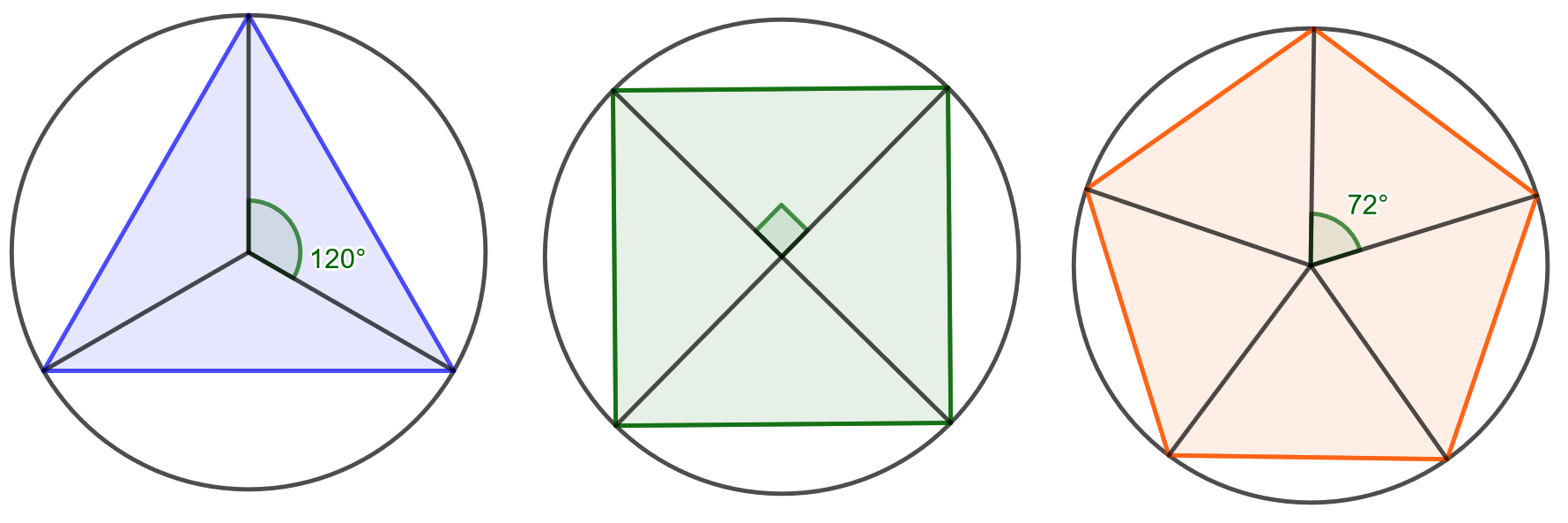
Jos monikulmiossa on \(n\) kulmaa, jaetaan monikulmio \(n\) kolmioon. Kolmiot muodostetaan piirtämällä janat ympyrän keskipisteestä monikulmion jokaiseen kulmaan. Kolmion kulma, jonka kärki on ympyrän keskipisteessä, on \(\frac{360^{\circ}}{n}\). Tämän kulman viereiset sivut ovat ympyrän säteen \(r\) mittaisia. Kolmion pinta-alan trigonometrisella kaavalla saadaan yhden kolmion alaksi \[A_k = \frac{r^2}{2} \cos \left( \frac{360^{\circ}}{n} \right).\] Koska kolmioita muodostuu monikulmion sisään \(n\) kappaletta, on koko monikulmion pinta-ala \[A=n \cdot A_k = \frac{r^2n}{2} \cos \left( \frac{360^{\circ}}{n} \right).\]

# teht_ympyrat_ympyrassa

Tehtävä

Alla olevassa GeoGebra-appletissa on isompi \(R\)-säteinen ympyrä, jonka sisällä on kolme pienempää \(r\)-säteistä ympyrää. Määritä pienempi säde \(r\) isomman säteen \(R\) avulla.

# kolme-ympyraa-ympyrassa-geo

# kolme-ympyraa-ympyrassa

# teht_viisikulmio_ympyrassa

Tehtävä

Ympyrän, jonka halkaisija on \(5,0 \text{ cm}\) sisälle piirretään mahdollisimman suuri viisikulmio. Määritä viisikulmion pinta-ala yhden desimaalin tarkkuudella.

# viisikulmio_ympyrassa

# teht_lehma

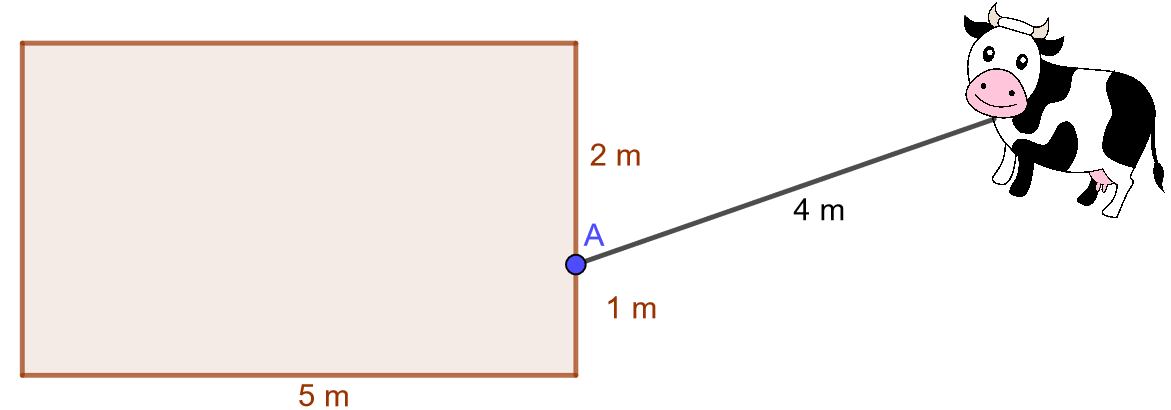
Tehtävä

Kuinka suurella alueella lehmä voi laiduntaa, kun sen kaulassa oleva köysi on kytketty kuvan mukaisesti ladon seinustalle pisteeseen \(A\) ja köyden pituus on \(4 \text{ m}\)?

# lehmalato