2. Monikulmioiden geometriaa
Tässä luvussa käsitellään monikulmioita, joista yksinkertaisin kulmio on kolmio. Tasogeometriassa kuviot sekä kappaleet piirretään yksiulotteisesti. Harjoittele kuvien piirtämistä käyttämälläsi laskimella tai vaikkapa Geogebralla!
Kappaleeseen liittyvät harjoitustehtävät löydät täältä!
Kolmioiden geometriaa
2.1 Kolmion rakenne
Kolmio on yksinkertaisin monikulmio, ja nimensä mukaisesti se koostuu kolmesta kulmasta ja kolmesta sivusta. Kolmion kulmat nimetään kreikkalaisin kirjaimin, \(\alpha\), \(\beta\) ja \(\gamma\).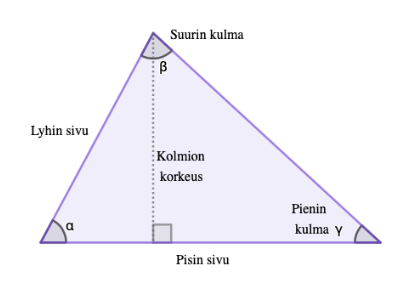 
Kolmion kaikkien kulmien yhteenlaskettu suuruun on aina \(180°\), eli \(\alpha+ \beta+\gamma=180°\) .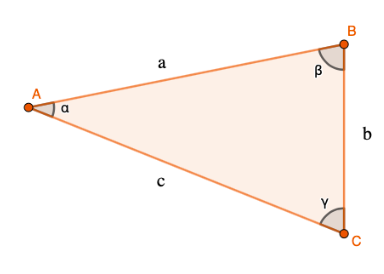 
Kaiken muotoisille kolmioille voidaan piirtää korkeusjana \(h\), joka kulkee kolmion huipusta kohtisuorasti kohti kolmion kantaa: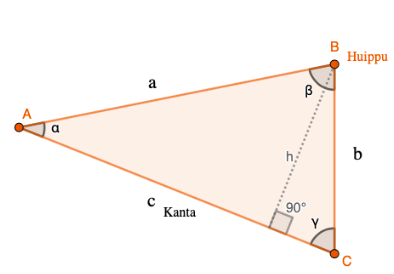 
Tämä korkeusjana \(h\) ilmoittaa kolmion korkeuden. Korkeusjanaa käytetään, kun tarkoituksena on määrittää kolmion pinta-ala.
Kolmion pinta-ala
\[\begin{align*} A=\frac{a\cdot h}{2}=\frac{1}{2}a\cdot h, \end{align*}\] missä \(a\) on kolmion kanta ja \(h\) kantaa kohtisuoraan piirretyn korkeusjanan pituus (eli kolmion korkeus).
Kolmiot voidaan jakaa ominaisuuksien avulla suorakulmaisiin kolmioihin, tasakylkisiin kolmioihin ja tasasivuisiin kolmioihin.
Suorakulmainen kolmio
Suorakulmaisessa kolmiossa on yksi \(90°\) kulma. Suorakulmainen kolmio koostuu kahdesta kateetista ja hypotenuusasta. Hypotenuusa on kolmion pisin sivu. Suoran kulman lisäksi kolmiossa on kaksi terävää kulmaa.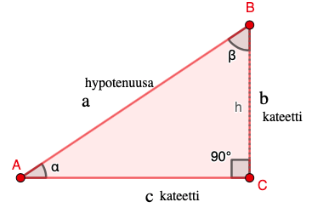 
Huomaa, että korkeusjana on nyt toinen kateeteista. Kuvassa kateetti \(b\).
Tasasivuinen kolmio
Tasasivuisen kolmion tilanteessa kolmion kaikki kulmat ovat suuruudeltaan \(60°\). Lisäksi kolmion kaikki sivut ovat keskenään yhtä pitkiä ja piirretty korkeusjana puolittaa kannan ja huippukulman.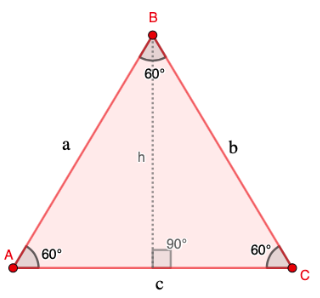 
Tasakylkinen kolmio
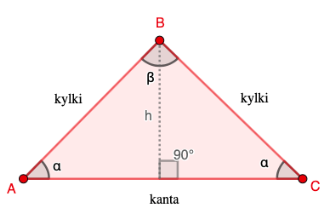
Tasakylkisessä kolmiossa kolmion kaksi sivua ovat yhtä pitkiä. Näitä yhtäpitkiä sivua kutsutaan kyljiksi. Tasakylkisen kantakulmat ovat yhtäsuuret, ja huipusta kantaan piirretty korkeusjana \(h\) puolittaa sekä huippukulman ja kannan.
2.2 Kolmion pinta-ala
Kolmion pinta-ala voidaan laskea tutulla tavalla, eli kerrotaan kolmion kanta ja korkeus keskenään ja jaetaan tulos kahdella. Joskus kolmion korkeus on kuitenkin vaikea määrittää. Yleisemmässä tapauksessa kolmion pinta-ala voidaan määrittää vain, kun tiedetään kahden kolmion sivun pituudet ja niiden sivujen välisen kulman suuruus.
Kolmion pinta-ala
Jos kolmion kannan pituus on \(a\) ja korkeus \(h\), kolmion pinta-ala on \[A=\frac{1}{2} ah.\] Jos kolmion kahden sivun pituudet ovat \(a\) ja \(b\) ja näiden välisen kulman suuruus \(\alpha\), voidaan kolmion pinta-ala ilmaista lausekkeella \[A=\frac{1}{2} ab \sin \alpha.\]
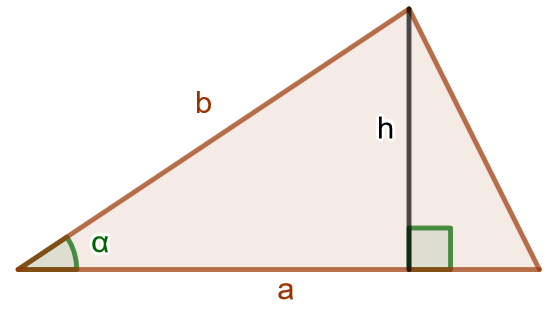
Laske kuvan kolmion pinta-ala
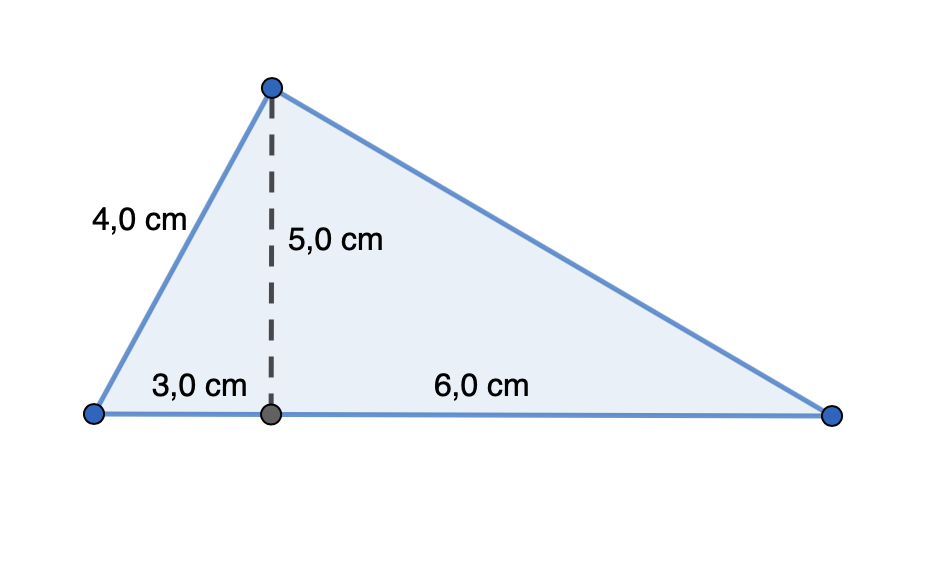
Ratkaisu
Kolmion korkeus \(h\) on \(5,0\) cm ja kanta \(a\) \(6,0 \text{ cm} + 3,0 \text{ cm} = 9,0 \text{ cm}\). Tällöin pinta-ala on
\(A_{kolmio} = \frac{ah}{2} = \frac{9,0 \text{ cm} \cdot 5,0 \text{ cm}}{2} = 22,5 \text{ cm}≈23 \text{ cm}\)
2.3 Suorakulmainen kolmio, Pythagoraan lause
Suorakulmainen kolmio on sellainen kolmio, jonka yksi kulma on suorakulma eli \(90^{\circ}\). Suoran kulman kylkinä olevia sivuja kutsutaan kateeteiksi ja suoran kulman vastaista sivua hypotenuusaksi.
Suorakulmaiseen kolmioon liittyy oleellisesti Pythagoraan lause, jonka mukaan suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin kolmion hypotenuusan neliö. Jos siis tiedetään kolmion kahden sivun pituudet, voidaan kolmannen sivun pituus ratkaista. Voit lukea lisää Pythagoaan lauseen historiasta.
Pythagoraan lause
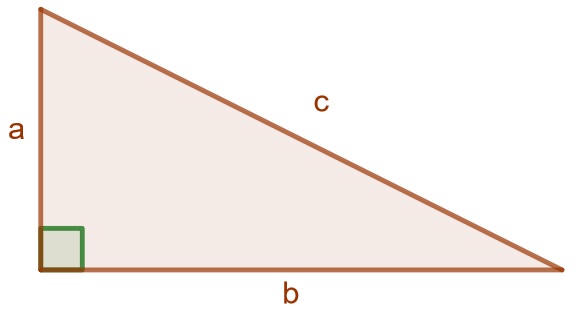
Suorakulmaisen kolmion kateettien \(a\) ja \(b\) neliöiden summa on yhtä suuri kuin sen hypotenuusan \(c\) neliö, eli \[a^2+b^2=c^2.\]
Suorakulmaisen kolmion lyhyemmän kateetin pituus on 8 m. Hypotenuusa on 3 m pidempi kuin pidempi kateetti. Selvitä kolmion sivujen pituudet.
Ratkaisu
Merkitään pidemmän kateetin sivun pituutta kirjaimella x. Tällöin hypotenuusan pituus on x + 3.
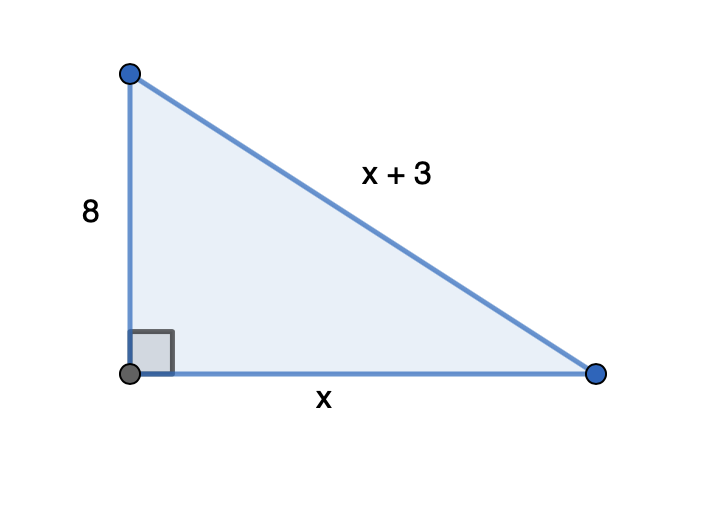
Ratkaistaan kateetin x pituus Pythagoraan lauseella.
\[\begin{align} 8^2 + x^2 &= (x + 3)^2& \quad &| \text{ kirjoitetaan potenssilauseke tulona} \\ 64 + x^2 &= (x + 3)(x + 3)& \quad &| \text{ lasketaan tulo} \\ 64 + x^2 &= x^2 + 3x + 3x + 9& \quad &| \text{ erotellaan muuttujat ja vakiot eri puolille yhtälöä} \\ x^2 - x^2 - 3x - 3x &= 9 - 64& \quad &| \text{ sievennetään} \\ -6x &= - 55& \quad & | :(-6) x &= 9,1666...& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ x &≈ 9 \\ \end{align}\]
Kolmion sivujen pituudet ovat siis \(8 \text{ m, } 9 \text{ m ja } (9 + 3) \text{ m}= 12 \text{ m}\).
2.4 Käänteinen Pythagoraan lause
Pythagoraan lauseen kohdalla todettiin, että se pätee vain suorakulmaisille kolmioille. Eli jos kolmio on suorakulmainen, sen kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö. Sama päättely voidaan kääntää toisinpäin. Jos kolmion kahden lyhyemmän sivun neliön summa on yhtä suuri kuin pisimmän sivun neliö, kyseessä on suorakulmainen kolmio. Jos suoraa kulmaa ei ole merkitty kuvaan tai sitä ei ole kerrottu erikseen, tulee aina tarkistaa, onko kolmio suorakulmainen, vaikka se saattaisi näyttää siltä.
Kolmion kahden lyhyemmän sivun pituudet ovat 3 ja 4. Pisin sivu on kaksi yksikköä lyhintä sivua pidempi. Onko kolmio suorakulmainen?
Ratkaisu
Jotta kolmio olisi suorakulmainen, sen sivujen pituuksien on toteutettava Pythagoraan lause. Pisimmän sivun pituus on 3 + 2 = 5. Tarkastetaan toteuttavatko luvut Pythagoraan lauseen, kun pisin sivu on hypotenuusa ja lyhyemmät sivut ovat kateetteja.
\[\begin{align} a^2 + b^2 &= c^2& \quad &| \text{ sijoitetaan sivujen pituuksien arvot} \\ 3^2 + 4^2 &= 5^2& \quad &| \text{ sievennetään} \\ 9 + 16 &= 25& \quad &| \text{ sievennetään} \\ 25 &= 25& \quad &| \text{ tosi} \\ \end{align}\]
Koska luvut toteuttevat Pythagoraan lauseen, on kyseessä suorakulmainen kolmio.
2.5 Trigonometriset funktiot
Suorakulmaisen kolmion terävien kulmien suuruudet voidaan ratkaista, jos tiedetään kolmion kateettien tai kateetin ja hypotenuusan pituudet. Tämä on mahdollista, sillä kolmion sivujen suhteet ovat tietyillä kulmilla aina vakioita. Näitä suhteita kutsutaan trigonometrisiksi funktioiksi.
Suorakulmaisen kolmion sini, kosini ja tangentti
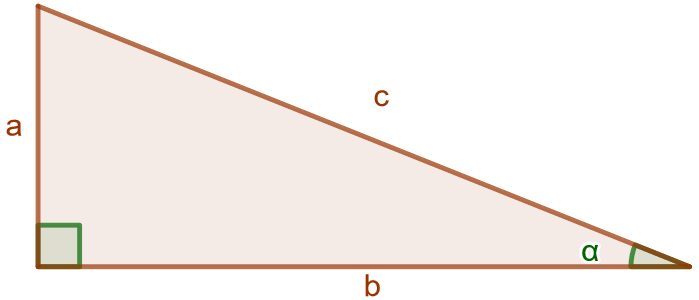
Suorakulmaisessa kolmiossa kulman \(\alpha\) sini, kosini ja tangentti tarkoittavat seuraavia suhteita: \[\sin(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{hypotenuusa}}=\frac{a}{c}\] \[\cos(\alpha)=\frac{\text{kulman viereinen kateetti}}{\text{hypotenuusa}}=\frac{b}{c}\] \[\tan(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{kulman viereinen kateetti}}=\frac{a}{b}\]
Kokeile laskea eri kulmien sini, kosini ja tangentti sekä sivujen suhteet vasemmalla olevassa cas-ikkunassa. Voit syöttää uuden komennon napauttamalla hiirellä rivinumeron 3 vieressä. Voit käyttää kuvassa näkyviä muuttujien nimiä. Kokeile myös raahata kolmion kärkipisteitä ja tutki, miten lukuarvot muuttuvat.
Muutama ohje cas-laskimen käyttöön:
- Jos haluat laskea kuvan \(\gamma\)-kulman sinin, kirjoita riville suoraan \(\sin(\gamma)\).
- Kreikkalaiset kirjaimet saat näppäimistöltä:
- Alt + a = \(\alpha\)
- Alt + b = \(\beta\)
- Alt + g = \(\gamma\)
- Jos laskin antaa vastauksen, kirjoita komento Lukuarvona(\(n)]{.red}, missä korvaat n-kirjaimen sen rivin numerolla, jonka likiarvon haluat näkyviin. Voit myös kirjoittaa suoraan [Lukuarvona(\)()$).
- Kokeile ensin laskea jonkin kulman sini ja sen jälkeen muuttaa pisteiden paikkaa kuvaajassa. Mitä sinin arvolle tapahtuu?
Määritä kuvan
- kulman \(\beta\) tangentti ja sini.
- kulman \(\gamma\) kosini ja kulman \(\gamma\) suuruus.
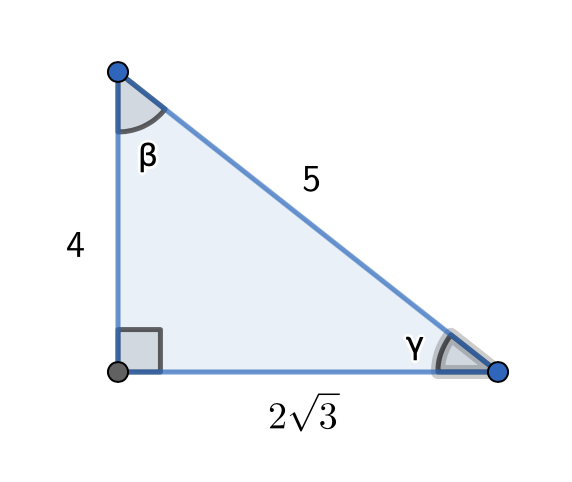
Ratkaisu
Tangentti on vastaisen kateetin suhde viereiseen kateettiin. Kulman \(\beta\) vastaisen kateetin pituus on \(2\sqrt{3}\) ja viereisen kateetin pituus 4. Siis
\(\tan{\beta} = \frac{2\sqrt{3}}{4}\)
Sini on kulman vastaisen kateetin suhde hypotenuusaan. Hypotenuusan pituus on 5, joten kulman \(\beta\) sini on
\(\sin{\beta}=\frac{2\sqrt{3}}{5}\)
Kulman kosini on kulman viereisen kateetin suhde hypotenuusaan. Hypotenuusan pituus on edelleen 5. Nyt kulman \(\gamma\) viereisen kateetin pituus on \(2\sqrt{3}\), jolloin kulman \(\gamma\) kosini on
\[\begin{align} \cos{\gamma}&=\frac{2\sqrt{3}}{5}& \quad &| \text{ kulma }\gamma \text{ laskimella }\gamma=\cos^{-1}\left(\frac{2\sqrt{3}}{5}\right) \\ \gamma &= 46,1462...°& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ \gamma &≈ 46° \\ \end{align}\]
Kolmion trigonometristen funktioiden eli tangentin, sinin tai kosinin avulla voidaan siis määrittää suorakulmaisen kolmion kulmien suuruuksia.
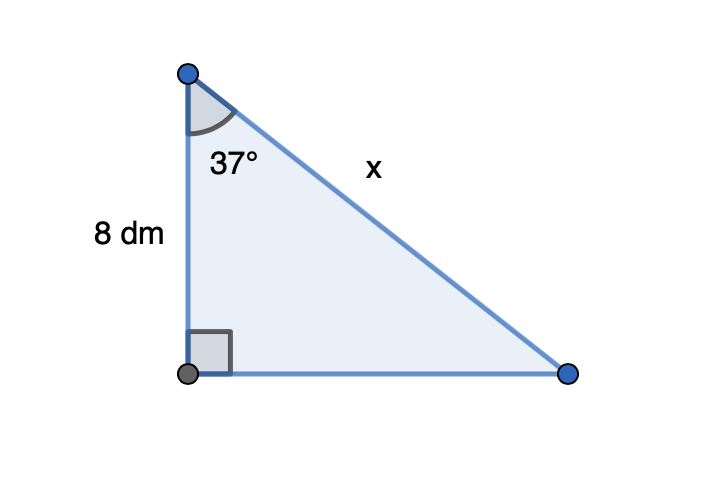
Laske kuvan kolmion sivun x pituus.
Ratkaisu
Kolmio on suorakulmainen, ja sen yhden terävän kulman suuruus on \(37°\). Terävän kulman viereisen kateetin pituus on 8 dm ja kolmion hypotenuusan pituus on x. Tällöin terävän kulman kosini on
\[\begin{align} \cos{37°} &= \frac{8}{x}& \quad &| \cdot x \\ x \cdot \cos{37°} &= 8& \quad &| : \cos{37°} \\ x &= \frac{8}{\cos{37°}}& \quad &| \text{ sievennetään} \\ x &= 10,0170...& \quad &| \text{ pyöritetään ykkösten tarkkuuteen} \\ x &≈ 10 \text{ (dm)} \\ \end{align}\]
Suorakulmaisen kolmion hypotenuusan pituus on 10 dm.
2.6 Nelikulmioiden rakenne
Nelikulmiot voidaan jakaa lävistäjän avulla kahdeksi kolmioksi. Koska kolmioiden kulmien summa on aina \(180°\), täytyy siis olla niin, että nelikulmioiden kulmien summa on \(2\cdot180°=360°\).
Alla olevassa kuvassa nelikulmio on jaettu kahdeksi kolmioksi piirtämällä jana pisteestä \(A\) pisteeseen \(C\). Nelikulmio voitaisiin myös jakaa kolmioiksi pisteiden \(B\) ja \(D\) avulla.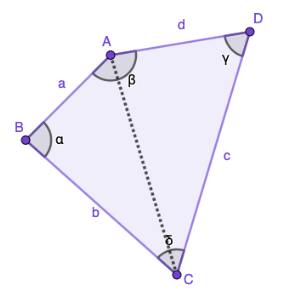 
Samoin kuin kolmionkin tapauksessa, nelikulmiot voidaan jaotella ominaisuuksiensa suhteen.
Suorakulmio
Kaikki nelikulmion kulmat ovat \(90°\). Tällöin myös nelikulmion vastakkaiset sivut ovat yhtäpitkiä.
Neliö on nelikulmion erikoistapaus, jossa nelikulmion kaikki sivut ovat yhtä pitkiä.
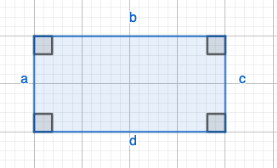
Suorakulmion pinta-ala on \(A=a\cdot b\)
Suunnikas
Suunnikas on vinossa oleva nelikulmio. Tällöin vastakkaiset sivut ovat yhtä pitkät ja yhdensuuntaiset, ja vastakkaiset kulmat ovat yhtä suuret.
Neljäkäs on suunnikas, jonka kaikki sivut ovat yhtä pitkiä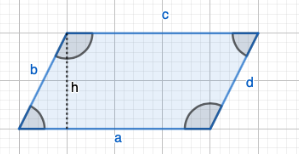 
Suunnikkaan pinta-ala on \(A=a\cdot h\)
Puolisuunnikas
Nimensä mukaisesti nelikulmio, jossa vain kaksi sivuista ovat yhdensuuntaisia, on puolisuunnikas. Tällöin kaikki sivut voivat olla eri pituisia ja kulmat eri suuruisia.
Tasakylkinen puolisuunnikas on puolisuunnikkaan erikoistapaus, jossa erisuuntaiset sivut ovat yhtäpiktiä. Tällöin puolisuunnikkaan kantakulmat ovat yhtä suuria.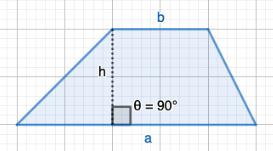 
Puolisuunnikkaan pinta-ala on \(A=\frac{a+b}{2}\cdot h\)
Laske kuvan suunnikkaan pinta-ala.
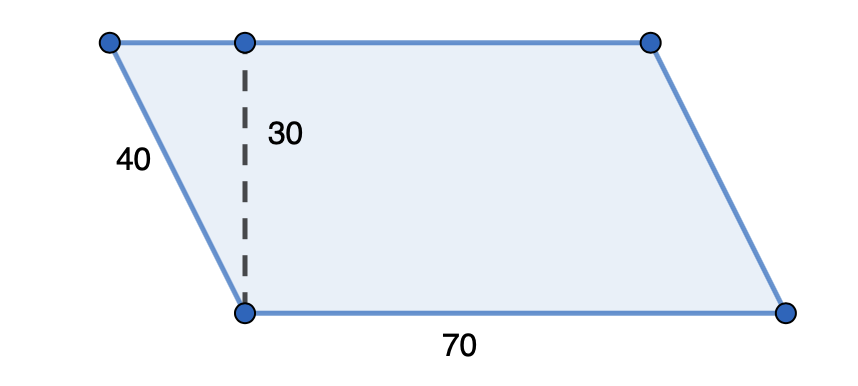
Ratkaisu
Suunnikkaan pinta-ala lasketaan kertomalla keskenään sen kanta ja korkeus. Kuvasta saadaan kannan pituudeksi 70. Koska korkeus on kohtisuora etäisyys kannasta, valitaan korkeuden pituudeksi 30. Tällöin koko suunnikkaan pinta-ala on
\(A_{suunnikas}= 70 \cdot 30 = 2100\)
Suunnikkaan pinta-ala on siis 2100.
Tasakylkisen puolisuunnikkaan muotisen terassin pinta-ala on 17 m\(^2\). Laske terassin piiri, kun yhdensuuntaisten sivujen pituudet ovat 4 m ja 12 m.
Ratkaisu
Koska puolisuunnikas on tasakylkinen, se muodostaa kaksi yhtenevää suorakulmaista kolmiota, joiden hypotenuusan pituus on x ja kateettien pituudet ovat h ja c.
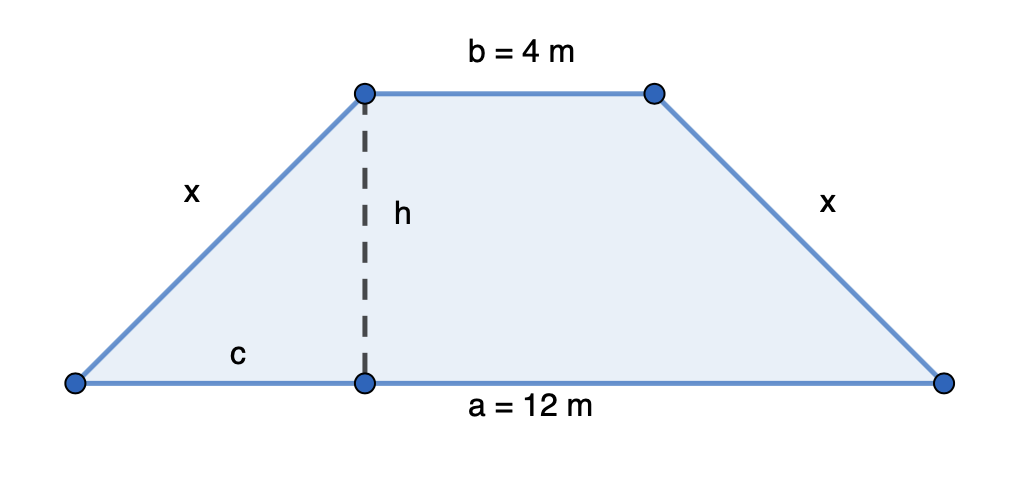
Sivun c pituus on \(\frac{12 \text{ m} - 4 \text{ m}}{2} = 4 \text{ m}\).
Selvitetään seuraavaksi puolisuunnikkaan korkeus h pinta-alan lausekkeesta.
\[\begin{align} A &= \frac{a + b}{2} \cdot h& \quad &| \text{ sijoitetaan arvot} \\ 17 \text{ m}^2 &= \frac{12 \text{ m} + 4 \text{ m}}{2} \cdot h& \quad &| \text{ vaihdetaan yhtälön puolia} \\ \frac{12 \text{ m} + 4 \text{ m}}{2} \cdot h &= 17 \text{ m}^2& \quad &| \text{ sievennetään} \\ 8 \text{ m} \cdot h &= 17 \text{ m}^2& \quad &| : 8 \text{ m} \\ h &= \frac{17 \text{ m}^2}{8 \text{ m}}& \quad &| \text{ sievennetään} \\ h &= 2,125 \text{ m} \end{align}\]
Seuraavaksi ratkaistaan suorakulmaisesta kolmiosta Pythagoraan lauseella hypotenuusan pituus x.
\[\begin{align} x^2 &= c^2 + h^2& \quad &| \text{ sijoitetaan arvot} \\ x^2 &= (4 \text{ m})^2 + (2,125 \text{ m})^2& \quad &| \text{ }\sqrt{\text{ }} \\ x &= \sqrt{(4 \text{ m})^2 + (2,125 \text{ m})^2}& \quad &| \text{ sievennetään} \\ x &= 4,5294... \text{ m}\\ \end{align}\]
Lasketaan vielä terassin piiri summaamalla kaikki sivut yhteen.
\(x+b+x+a = 2\cdot x + a + b= 2 \cdot 4,5294...\text{ m} + 4 \text{ m} + 12 \text{ m}=57,0588... \text{ m}≈ 57 \text{ m}\)
Terassin piirin pituus on 57 m.
Muut monikulmiot
2.7 Monikulmioiden rakenne
Kolmiot ja nelikulmiot ovat vain esimerkkejä monikulmioista. Monikulmioissa voi nimensä mukaisesti olla kuinka monta kulmaa tahansa. Alla olevassa kuvassa on mallinnettu säännöllistä kuusikulmiota ja kymmenkulmiota.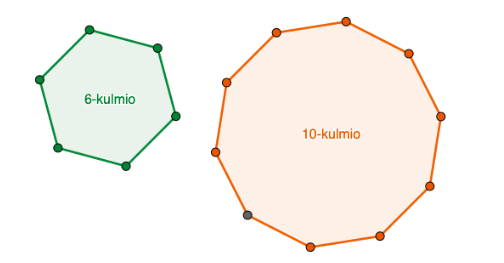 
Kulmien lukumäärästä huolimatta kuviot voidaan aina jakaa kolmioihin. Esimerkiksi yllä oleva kuusikulmio voidaan jakaa neljään kolmioon: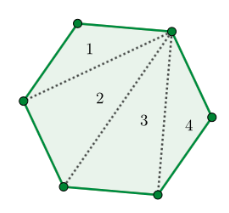 
Monikulmion kulmien summa
Jos monikulmiossa on \(n\) kärkeä tai kulmaa, tällöin kulmion kulmien summa on \[\begin{align*} (n-2)\cdot180° \end{align*}\]
Laske säännöllisen kuusikulmion
- kulmien summa
- pinta-ala,
kun sen sivun pituus on 15 cm.
Ratkaisu
Koska monikulmiossa on kuusi kulmaa, niin \(n = 6\) ja kuusikulmion kulmien summa voidaan laskea
\((n-2) \cdot 180° = (6-2) \cdot 180°= 4 \cdot 180°= 720°\)
Kuusikulmion kulmien summa on siis 720°.
Säännöllinen kuusikulmio koostuu kuudesta tasasivuisesta kolmiosta. Jokaisen kolmion sivun pituus on siis 15 cm. Kuusikulmion pinta-ala muodostuu kuuden kolmion pinta-alasta, joten lasketaan ensin yhden kolmion pinta-ala.
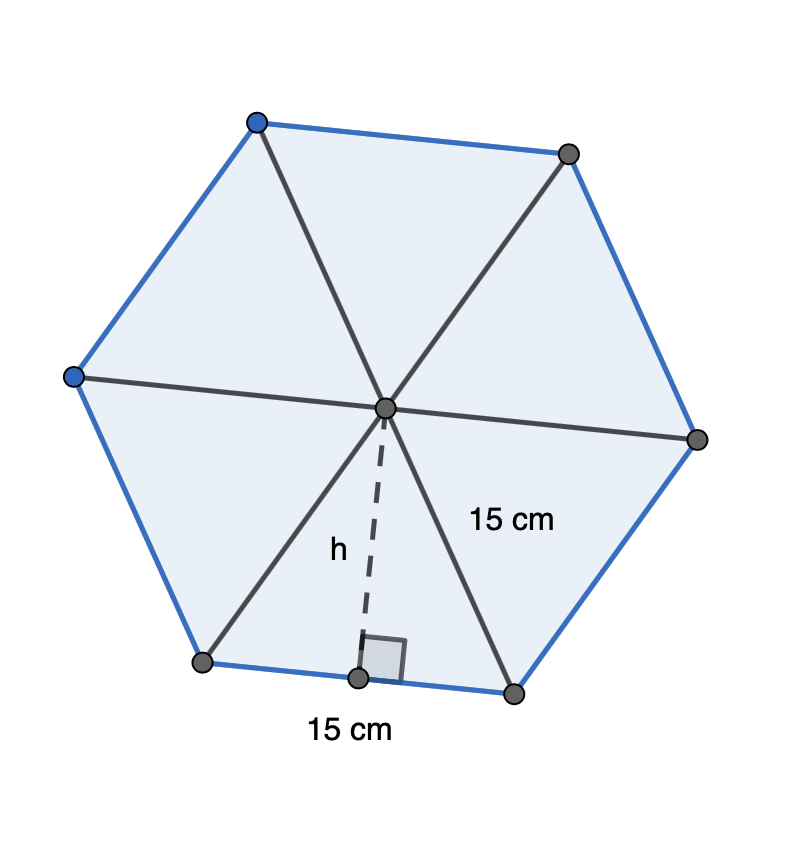
Selvitetään Pythagoraan lauseen avulla kolmion korkeus h, kun hypotenuusan pituus on 15 cm ja kateettien pituudet ovat h ja \(\frac{15 \text{ cm}}{2}= 7,5\) cm
\[\begin{align} h^2 + (7,5)^2 &= 15^2& \quad &| -(7,5)^2 \\ h^2 &= 15^2- (7,5)^2& \quad &| \text{ }\sqrt{\text{ }} \\ h &= \sqrt{15^2- (7,5)^2}& \quad &| \text{ sievennetään} \\ h &= 12,9903... \text{ (cm)} \end{align}\]
Lasketaan kolmion pinta-ala \(A_{kolmio}=\frac{15 \text{ cm} \cdot 12,9903... \text{ cm}}{2}=97,4278... \text{ cm}^2\).
Säännöllisen tasasivuisen kuusikulmion pinta-ala on tällöin
\(6 \cdot A_{kolmio}= 6 \cdot 97,4278... \text{ cm}^2= 584,5671... \text{ cm}^2 ≈ 580 \text{ cm}^2\).
Kuusikulmion pinta-ala on \(580 \text{ cm}^2\).
2.8 Monikulmiot koordinaatistossa
Usein geometrisia kuvioita tarkastellaan \(xy\)-koordinaatistossa.
\(xy\)-koordinaatisto
Koordinaatisto koostuu kahdesta akselista, jotka leikkaavat toisensa kohtisuorasti. Akselien leikkauspiste on nimeltään \(origo\) \(O\).
Usein akselit valitaan siten, että vaakasuora akseli on \(x\)-akseli ja pystysuora akseli on \(y\)-akseli.
Kolmiulotteisessa koordinaatistossa on myös \(z\)-akseli, joka on edelleen kohtisuorassa \(x\)- ja \(y\)-akseleihin. 
Monikulmioita piirrettäessä koordinaatistoon, monikulmion kärjet ovat joissain koordinaatiston pisteissä.
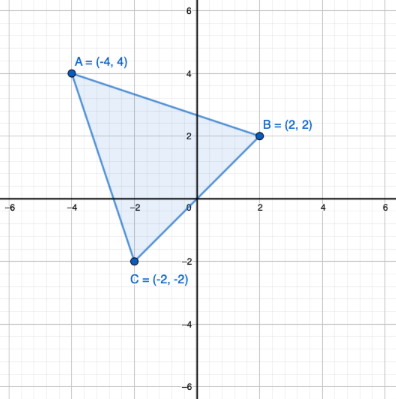
Yllä olevassa kuvassa on kolmio, jonka kärkipisteet on merkattu koordinaatistoon. Tekstissä kolmion kärkipisteet voitaisiin ilmoittaa esimerkiksi: "Kolmio, jonka kärjet ovat pisteet \(A(-4,4)\), \(B(2,2)\) ja \(C(-2,-2)\)."
Kolmion kateetin pituus pisteiden \(A\) ja \(B\) välillä voitaisiin laskea pisteiden koordinaattien avulla:
Pisteiden välinen etäisyys
Jos \(xy\)-koordinaatistossa on kaksi pistettä, joiden koordinaatit ovat \((x_1, y_1)\) ja \((x_2, y_2)\), niin näiden pisteiden välinen etäisyys on \[\begin{align*} |AB|=\sqrt{(x_1- x_2)^{2}+(y_1- y_2)^{2}} \end{align*}\]
Aiemmin esitetyn kolmion kateetin \(|AB|\) pituus olisi siis \[\begin{align*} |AB|=\sqrt{(2-(-4)^{2}+(2-4)^{2}}=\sqrt{6^2+(-2)^2}=\sqrt{36+4}=\sqrt{40}=2\cdot\sqrt{10}. \end{align*}\]
Janan päätepisteiden avulla voidaan laskea myös janan keskipisteen koordinaatit. Alla olevassa kuvassa piirretty kolmion sivujen keskipisteet.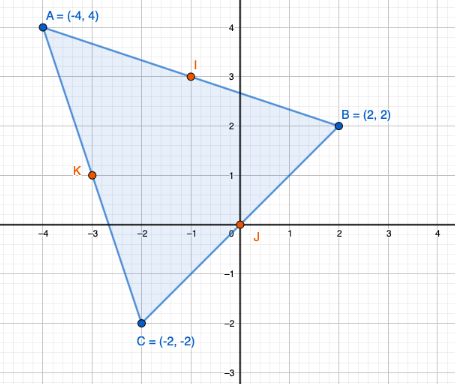 
Janan keskipisteen koordinaatit
Olkoon janan päätepisteiden koordinaatit \((x_1, y_1)\) ja \((y_1, y_2)\). Janan keskipisteen koordinaatit ovat päätepisteiden koordinaattien keskiarvo:
\[\begin{align*} (x_0,y_0)=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right) \end{align*}\]
Lasketaan nyt aiemmin esitetyn kolmion keskipiste \(I\) janalla \(AB\).
\[\begin{align*} (x_0,y_0)=\left(\dfrac{(-4)+2}{2},\;\dfrac{4+2}{2}\right)=\left(\dfrac{-2}{2},\;\dfrac{6}{2}\right)=(-1,3) \end{align*}\]
Kuvasta tarkistamalla huomataan, että piste \(I\) näyttäisi sijoittuvat koordinaatistossa pisteeseen \((-1,3)\) aivan kuten laskettiinkin.
Ratkaise kolmion \(ABC\) pinta-ala, kun kolmion kärkipisteet ovat \(A=(0,1)\), \(B=(2,2)\) ja \(C=(4,0)\).
Ratkaisu
Piirretään kolmion ympärille suorakulmio \(FDEC\) niin, että sen sivut ovat koordinaattiakselien suuntaiset. Suorakulmion pisteet saadaan kolmion pisteiden avulla. Esimerkiksi pisteen D x-koordinaatti on sama kuin pisteen A ja y-koordinaatti sama kuin pisteellä B.
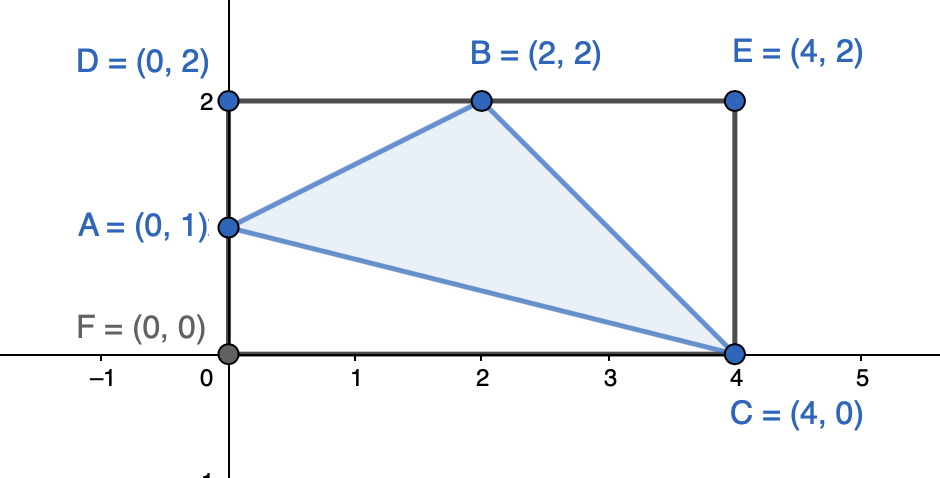
Lasketaan suorakulmion sivujen \(FD\) ja \(FC\) pituudet.
\(|FD| = 2 - 0 = 2 \\\) \(|FC| = 4 - 0 = 4 \\\)
Suorakulmion pinta-ala on siis \(A_{suorakulmio}=2 \cdot 4=8\).
Suorakulmion ja sen sisällä olevan kolmion rajaamat kolme kolmiota ovat suorakulmaisia, joten lasketaan kolmioiden kateettien pituudet ja pinta-alat.
Kolmio \(ADB\)
\(|DA|= 2-1=1 \\ |DB|=2-0=2 \\ A_{ADB}=\frac{2 \cdot 1}{2}=1\)
Kolmio \(AFC\)
\(|AF|= 1-0=1 \\ |FC|=4-0=4 \\ A_{ADB}=\frac{1 \cdot 4}{2}=2\)
Kolmio \(BEC\)
\(|BE|= 4-2=2 \\ |EC|=2-0=2 \\ A_{ADB}=\frac{2 \cdot 2}{2}=2\)
Vähennetään suorakulmiosta sen ja kolmion \(ABC\) rajaamien kolmioiden pinta-alat, saadaan kolmion \(ABC\) pinta-ala.
\[\begin{align} A_{ABC} &= A_{suorakulmio}-(A_{ADB}+A_{AFC}+A_{BEC})& \quad &| \text{ sijoitetaan arvot} \\ A_{ABC} &= 8-(1+2+2)& \quad &| \text{ sievennetään} \\ A_{ABC} &= 3 \\ \end{align}\]
Kolmion \(ABC\) pinta ala on 3.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.