2. Ensimmäisen asteen polynomifunktio ja -yhtälö

Tässä kappaleessa käsitellään ensimmäisen asteen polynomifunktiota sekä ensimmäisen asteen yhtälöä. Palautetaan mieleen ensimmäisen asteen polynomifunktion kuvaajan tulkitseminen sekä ensimmäisen asteen yhtälön ratkaisemisen keinot. Kappaleen asiat ovat pääosin yläkoulun matematiikan kertausta. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

Palauta halutessassi aluksi mieleen funktion määritelmä sekä funktion nollakohtien käsite MAY1-kurssilta täältä.

2.1 Ensimmäisen asteen polynomifunktio

Tämän kirjan ensimmäisessä luvussa opimme, että polynomin asteluku määräytyy sen muuttujan mukaan, jolla on suurin eksponentti. Näin ollen ensimmäisen asteen polynomi sisältää ensimmäisen asteen termin ja mahdollisesti vakiotermin. Esimerkiksi 3x-2 on ensimmäisen asteen polynomi.

Annetaan polynomille nimi jolloin voidaan merkitä f(x)=3x-2 . Tämä on esimerkiksi ensimmäisen asteen polynomifunktiosta.

Ensimmäisen asteen polynomifunktio

Ensimmäisen asteen polynomifunktioksi sanotaan funktiota, jonka lauseke on muotoa

f(x)=ax+b,

jossa ja ovat reaalilukuja ja $a\neq0$ .

2.1.1 Esimerkki: ensimmäisen asteen polynomifunktion kuvaajan tulkintaa

Kuvassa on esitetty ensimmäisen asteen polynomifunktion kuvaaja.

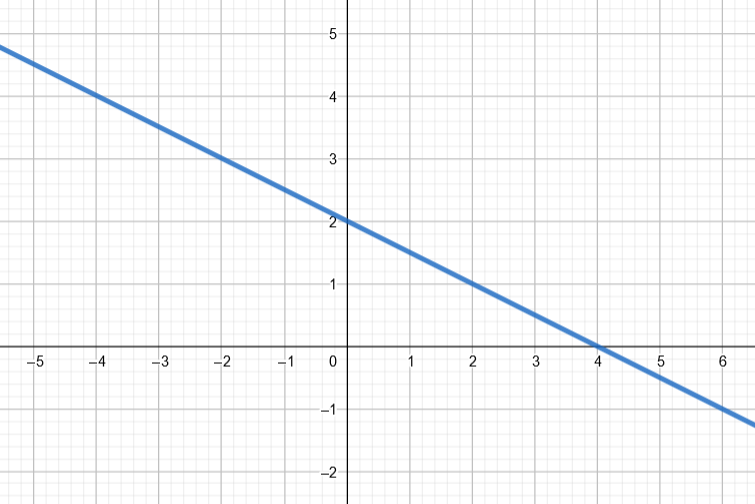
Päättele kuvaajan avulla

funktion arvo
yhtälön ratkaisu
epäyhtälön ratkaisu.

Ratkaisu:

Funktion arvo on muuttujan arvoa vastaavan kuvaajan pisteen koordinaatti.

f(-4)=4

Yhtälön ratkaisu on funktion nollakohta eli kohta, jossa funktion kuvaaja leikkaa akselin.

$f(x)=0,\;\text{kun}\;x=4$

Kun funktion arvot ovat positiivisia. Funktion kuvaaja kulkee akselin yläpuolella, kun

x<4

Ratkaisu:

Ensimmäisen asteen polynomifunktiota kutsutaan myös lineaariseksi funktioksi, sillä sen kuvaaja on aina suora. Lasketaan funktion f(x)=3x-2 lausekkeen arvoja muutamilla muuttujan arvoilla ja piirretään pisteiden kautta kulkeva suora.


	$y=3\cdot0-2=-2$
	$y=3\cdot1-2=1$
	$y=3\cdot2-2=4$

Muuttujan kerrointa kutsutaan kulmakertoimeksi. Kulmakerroin ilmoittaa suoran kaltevuuden ja sen, onko suora nouseva vai laskeva.

Kulmakerroin

Suoran yhtälössä y=ax+b esiintyvä kerrroin on kyseisen suoran kulmakerroin.

Jos kuvaaja on nouseva suora.
Jos kuvaaja on laskeva suora.

Jos funktiossa f(x)=ax+b kerroin a=0, kyseessä on nollannen asteen polynomifunktio eli vakiofunktio.

Vakiofunktio

Funktiota, joka on muotoa f(x)=b, missä on reaaliluku, sanotaan vakiofunktioksi.

Vakiofunktion kuvaaja on vaakasuora suora.

Funktion f(x)=ax+b vakiotermi ilmoittaa suoran y=ax+b ja akselin leikkauspisteen koordinaatti.

2.1.2 Esimerkki: kertoimien vaikutus suoran kuvaajaan GeoGebralla

Vaihtele liukusäätimillä kertoimien ja arvoja ja tarkkaile niiden vaikutusta suoran f(x)=ax+b kuvaajaan.

Voidaan tehdä seuraavat havainnot:

Kun kulmakerroin suora on laskeva.
Kun kulmakerroinkerron suora on askelin suuntainen.
Kun kulmakerroin suora on nouseva.
Kun vakiotermi muuttuu, paraabeli siirtyy pystysuunnassa.

Ensimmäisen asteen polynomifunktio: tehtäviä

2.2 Ensimmäisen asteen yhtälö

Ensimmäisen asteen yhtälön teorian voit kerrata MAY1-kirjasta täältä.

Seuraavalla videolla käydään läpi pari haastavampaa esimerkkiä ensimmäisen asteen yhtälöistä. Videolla esitellään myös, mitä yhtälön ratkaisu graafisesti tarkoittaa.

Ensimmäisen asteen yhtälö: tehtäviä

2.3 Ensimmäisen asteen polynomifunktio matemaattisena mallina

Monia ilmiöitä voidaan mallintaa ensimmäisen asteen polynomifunktioiden avulla. Tehtäviä ratkaistaessa aluksi kannattaa koota ja jäsentää kaikki ongelmaan liittyvät tiedot esimerkiksi taulukon muotoon.

2.3.1 Esimerkki: Berliinin matkan kulut

Sanna on lähdössä lomalle Berliiniin. Sannan lennot maksavat $140\;\text{€}$ ja hotellin vuorokausihinta on $92\;\text{€}$ .

Määritä funktion lauseke, joka kuvaa lentojen ja hotellin yhteishintaa, kun yöpymisia hotellissa on kappaletta.
Kuinka monta yötä Sanna on hotellissa, jos hän maksaa matkastaan $876\;\text{€}$ ?

Ratkaisu:

Merkitään hotellissa vietettyjen öiden lukumäärää muuttujalla . Kootaan matkan kulut taulukkoon.

Lentojen hinta ( $\text{€}$ )
Hotellin hinta ( $\text{€}$ )

Matkan yhteishinta koostuu siis hotellin ja lentojen hinnasta, joten hintaa kuvaa funktio

f(x)=140+92x

Ratkaistaan yhtälö .

$\begin{align*} 140+92x&=876 \\ 92x&=736 \\ x&=8 \end{align*}$

Jotta matkan hinnaksi tulee $876\;\text{€},$ pitää hotellissa yöpyä yötä.

Ratkaisu:

yötä

2.3.2 Esimerkki: Berliinin matkalle lähtö

Sanna on lähdössä Berliinin lomalleen ja lähtee ajamaan Tampereelta kohti Helsinki-Vantaan lentokenttää nopeudella $80\;\text{km/h}$ . Sanna huomaa passinsa unohtuneen kotiin, mutta ei ehdi kääntyä hakemaan passia, vaan hälyttää ystävänsä tuomaan sen. Ystävä lähtee ajamaan $15\;\text{min}$ kuluttua Sannan perään.

Kuinka kauan ystävän on ajettava nopeudella $100\;\text{km/h}$ ennen kuin hän saa Sannan kiinni? Sanna jatkaa nopeudella $80\;\text{km/h}$ .
Kuinka kaukana Tampereelta he silloin ovat?

Ratkaisu:

Täydennetään taulukkoon seuraavat tiedot:

	Sanna	Ystävä
Nopeus (km/h)
Etäisyys (km) Tampereelta, kun ystävä lähtee	$\dfrac{1}{4}\cdot80=20$
Etäisyys (km) Tampereelta, kun ystävä on ollut matkalla tuntia

Nyt halutaan selvittää muuttujan arvo, kun Sannan sekä ystävän etäisyys Tampereelta on yhtä suuri. Voidaan muodostaa ja ratkaista seuraava yhtälö.

$\begin{align*} 20+80x&=100x \\ 100x-80x&=20 \\ 20x&=20 \\ x&=1 \end{align*}$

Ystävä saa siis Sannan kiinni yhden tunnin kuluttua.

Kun ystävä on ollut matkalla tunnin, hänen etäisyytensä Tampereelle on

$100\;\text{km/h}\cdot1\;\text{h}=100\;\text{km}$

Vastaus:

$1\;\text{h}$
$100\;\text{km}$

2.3.3 Esimerkki: hiilidioksidipitoisuuden mallintaminen

Taulukossa on Havaijilla sijaitsevan Mauna Loan havaintoaseman mittaamia ilmakehän hiilidioksidipitoisuuksia vuosina 2008-2018 . Hiilidioksidin pitoisuus on ilmoitettu tilavuuden miljoonasosina (ppm). Määritä funktio, joka mallintaa hiilidioksipitoisuutta aikavälillä .

Vuosi	$\text{\bf{CO}}_2$

Ratkaisu:

Kun piirretään mittauspisteet koordinaatistoon, huomataan että ne ovat likimain suoralla. Tiedetään, että ensimmäisen asteen polynomifunktion kuvaaja on suora, joten haluttu funktio on mallia f(x)=ax+b . Tässä kuvaa vuotta, joka on menossa. Nyt täytyy selvittää kertoimet ja .

Funktion sovittaminen pistejoukkoon on tyypillinen ongelma matematiikassa ja sen ratkaiseminen onnistuu mukavasti ohjelmien avulla. GeoGebrassa on runsaasti erilaisia sovitus-komentoja eri funktioille. Ensimmäisen asteen polynomifunktion eli suoran sovittamisessa käytetään komentoa SovitaSuora.

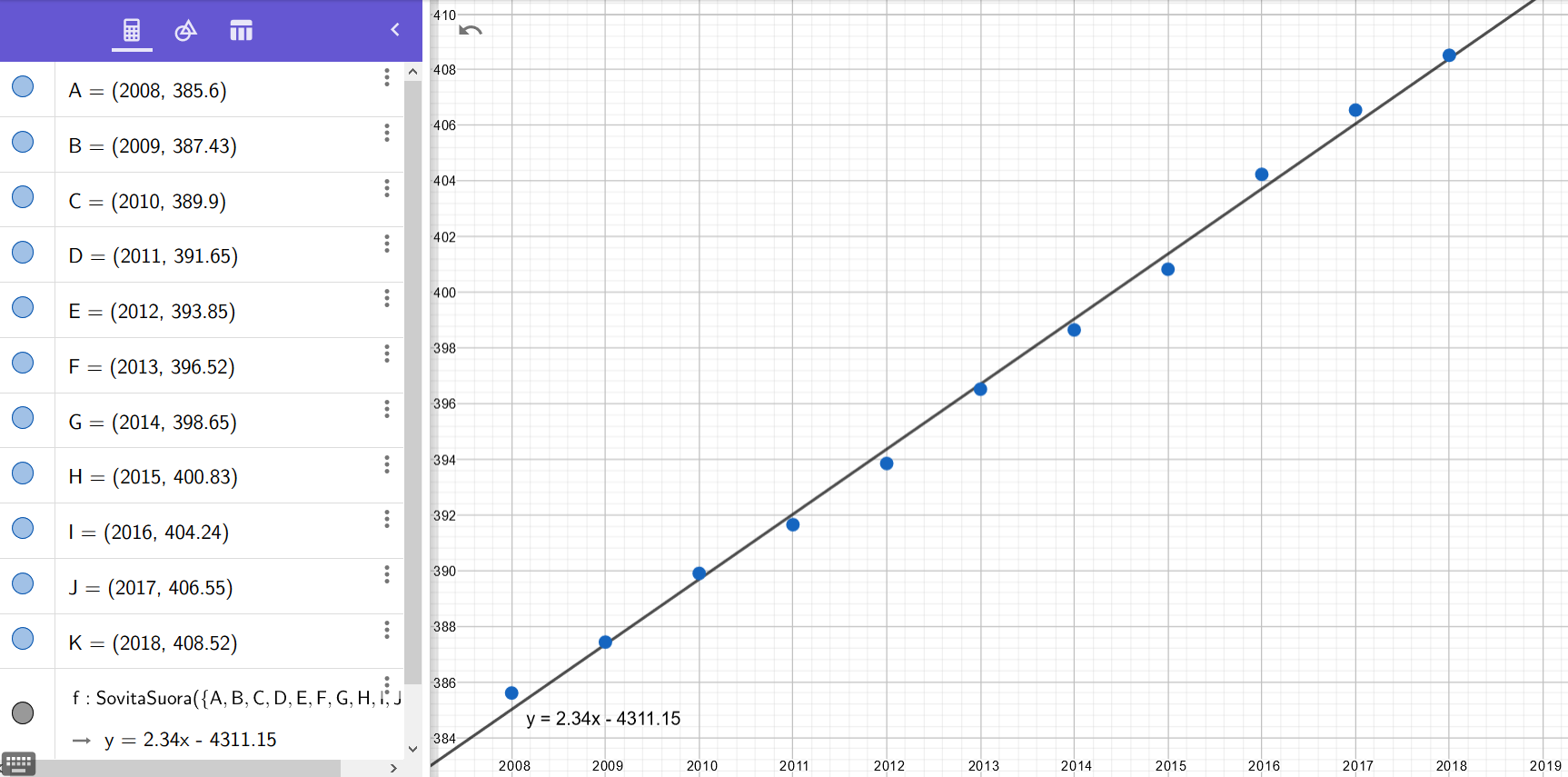
Funktioksi saadaan f(x)=2,34x-4311,15 . Kuvassa on siis pystyakselilla hiilidioksidin pitoisuus tilavuuden miljoonasosina (ppm) ja vaaka-akselilla aika vuosina.

Kulmakerroin ilmoittaa hiilidioksipitoisuuden keskimääräisen nousun vuotta kohden aikavälillä .
Vakio kuvaisi hiildioksidipitoisuutta ajanlaskun alkuhetkellä, jos ihmiskunnan tuottamat päästöt olisivat lisänneet hiilidioksidin määrää tasaisesti vuoden ajan. Näin ei tietenkään ole, sillä ilmakehän hiilidioksidipitoisuus on alkanut kasvaa vasta luvulla teollistumisen jälkeen.

Vastaus: f(x)=2,34x-4311,15

Ensimmäisen asteen polynomifunktio matemaattisena mallina: tehtäviä