2. Ensimmäisen asteen polynomifunktio ja -yhtälö: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Ensimmäisen asteen polynomifunktio ja -yhtälö. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

Ratkaise kappaleiden 2.1 ja 2.2 tehtävät ilman ohjelmistoja, jos tehtävänannossa ei toisin mainita. Kappaleen 2.3 tehtävissä voi käyttää apuna laskinta.

2.1 Ensimmäisen asteen polynomifunktio: tehtäviä

Tämän kappaleen teoria.

2.1.1 Tehtävä

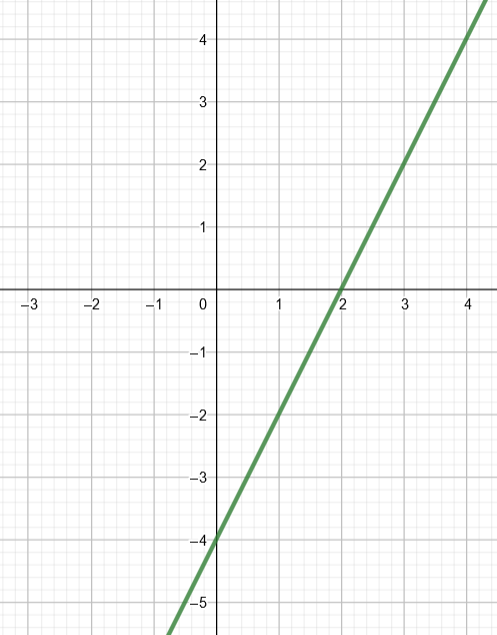
Tutki polynomifunktion kuvaajaa ja päättele kuvaajan avulla

# p211a

# p211b

# p211c

# p211d

2.1.2 Tehtävä

# p211

2.1.3 Tehtävä

# p213

2.1.4 Tehtävä

Täydennä taulukkoon suoran kulmakerroin ja vakiotermi. Tehtävässä ei ole automaattitarkistusta.

# t111

Open plugin

2.1.5 Tehtävä

Yhdistä funktiot oikeisiin kuvaajiin. Tehtävästä saa pisteet, kun funktion lausekkeen sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

# p215

2.1.6 Tehtävä

Määritä ensimmäisen asteen polynomifunktion lauseke, kun sen kuvaaja kulkee

pisteen kautta ja sen kulmakerroin on .

# p215a

pisteen kautta ja sen kulmakerroin on .

# p215b

pisteiden ja kautta.

# p215c

Vihje

Kun akselilla siirrytään yksi askel vasemmalle kuvaaja nousee yhden askeleen ylöspäin, joten kuvaajan kulmakerroin on .

pisteiden ja kautta.

# p215d

Vihje

Kun akselilla siirrytään vasemmalle, kuvaaja pysyy samalla korkeudella, joten sen kulmakerroin on . Funktion kuvaaja on vaakasuora suora, joka saa aina arvon .

2.1.7 Tehtävä

Valitse, millä muuttujan arvoilla funktion arvot ovat negatiivisia. Piirrä halutessasi ensin funktion kuvaaja GeoGebralla ja päättele kuvaajan perusteella vastaus.

# p217a

# p217b

# p217c

# p217d

2.1.8 Tehtävä

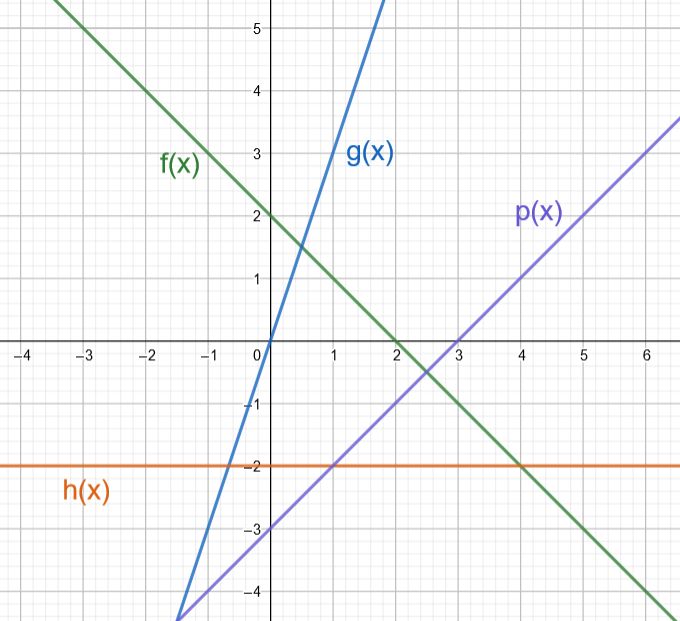
Määritä kuvan funktioiden lausekkeet.

# p216a

# p216b

# p216c

# p216d

2.2 Ensimmäisen asteen yhtälö: tehtäviä

Tämän kappaleen teoria.

2.2.1 Tehtävä

# p221

2.2.2 Tehtävä

Yhdistä yhtälöihin oikeat ratkaisut. Tehtävästä saa pisteet, kun ratkaisun sininen pallo osuu oikean yhtälön edessä olevaan ruutuun.

# p222

Kirjoita ratkiasun välivaiheet syöttökenttään tai halutessasi hahmottele ratkaisu ensin paperilla ja syötä lopuksi vastaus syöttökenttään. Jos yhtälöllä ei ole ratkaisua, vastaa kenttään FF.

2.2.3 Tehtävä

Ratkaise yhtälöt.

# p223a

# p223b

2.2.4 Tehtävä

Ratkaise yhtälöt.

# p224a

# p224b

2.2.5 Tehtävä

# p225

2.2.6 Tehtävä

Ratkaise yhtälöt.

# p226a

Vihje

$\begin{align*} \frac{x}{4}+\frac{x}{2}&=6 &&|\cdot4 \\ \frac{4x}{4}+\frac{4x}{2}&=4\cdot6 \\ x+2x&=24 \\ &\dots \end{align*}$

# p226b

Vihje

$\begin{align*} 3x-\frac{x-2}{2}&=\frac{1}{6} &&|\cdot2\\ 6x-(x-2)&=\frac{1}{3} \\ &\dots \end{align*}$

2.2.7 Tehtävä

Ratkaise yhtälöt.

# seq227a

Vihje

(x+1)^2=(x+1)(x+1)=x^2+x+x+1^2=x^2+2x+1

Sijoitetaan tämä yhtälöön, niin saadaan

$\begin{align*} 4x+x^2+2x+1-2&=x^2+5 \\ x^2-x^2+4x+2x&=5-1+2 \\ &\dots \end{align*}$

# seq227b

Vihje

$\begin{align*} -\frac{1}{2}(x+4)&=\frac{6-2x}{4} &&|\cdot4\\ -\frac{4}{2}(x+4)&=\frac{4(6-2x)}{4} \\ -2(x+4)&=6-2x \\ &\dots \end{align*}$

2.2.8 Tehtävä

Yhdistä yhtälöt niiden graafisiin ratkaisuihin. Tehtävästä saa pisteet, kun yhtälön sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

# p228

2.2.9 Tehtävä

Jaa luku kahteen osaan siten, että suurempi osa on $\dfrac{1}{4}$ suurempi kuin pienempi osa. Mikä luku on

# p229a

# p229b

Vihje

Merkitään pienempää osaa muuttujalla . Suurempi osa on $\dfrac{1}{4}$ suurempi kuin pienempi osa eli suurempi osa saadaan kertomalla luvulla $\dfrac{5}{4}$ . Saadaan yhtälö

$\begin{align*} x+\frac{5}{4}x=54. \end{align*}$

Yhtälöstä voidaan ratkaista pienempi osa ja sen jälkeen suurempi osa.

2.2.10 Tehtävä

# seq229

Vihje

$\begin{align*} k+\dfrac{k}{3}+\dfrac{k}{6}&=2 &&|\cdot6 \\ 6k+\frac{6k}{3}+\frac{6k}{6}&=6\cdot2 \\ 6k+2k+k&=12 \\ &\dots \end{align*}$

2.2.11 Tehtävä (yo lyhyt s1993/2)

Murtolukuja ei pidä laskea yhteen seuraavasti: $\dfrac{3}{2}+\dfrac{a}{4}=\dfrac{3+a}{2+4}$ .

# seq2211

Vihje

Oikea tulos saadaan muuttujan arvolla, jolla kaava pätee. Ratkaistaan siis yhtälö

$\begin{align*} \frac{3}{2}+\frac{a}{4}&=\frac{3+a}{2+4} \\ \frac{3}{2}+\frac{a}{4}&=\frac{3+a}{6} &&|\cdot6 \\ 6\cdot\frac{3}{2}+6\cdot\frac{a}{4}&=6\cdot\frac{3+a}{6} \\ 9+\frac{3}{2}a&=3+a \\ &\dots \end{align*}$

2.3 Ensimmäisen asteen polynomifunktio matemaattisena mallina: tehtäviä

Tämän kappaleen teoria.

2.3.1 Tehtävä

Seuraavat kuvaajat esittävät sähköpotkulaudan hinnan riippuvuutta ajetun matkan kestosta, kun potkulaudalla ajetaan minuuttia. Eri firmat hinnoittelevat matkan eri tavalla. Valitse kuvaajiin sopivat hinnoittelut.

# p231b

# p231c

# p231a

2.3.2 Tehtävä

Sähköpotkulaudalla ajetaan $4\;\text{km}$ matka keskinopeudella $16\;\text{km/h}$ . Paljon matka maksaa yhteensä, kun käytetään edellisen tehtävän c-kohdan hinnoittelua (aloitusmaksu $1\;\text{€}$ , matkataksa $0,25\;\text{€/min}$ )?

# p232

Vihje

Matkan hintaa euroina siis kuvaa edellisen tehtävän perusteella ensimmäisen asteen polynomifuntkio, joka on muotoa f(x)=1+0,25x . Funktiossa muuttuja on matkaan kulunut aika minuutteina.

Ensin täytyy siis selvittää, kuinka kauan nopeudella $16\;\text{km/h}$ ajettu kilometrin matka kestää. Sen jälkeen voidaan sijoittaa tämä arvo funktioon f(x) ja laskea funktion arvo.

2.3.3 Tehtävä

Matematiikan kokeesta saa arvosanan nollalla pisteellä. Opettaja tekee kokeeseen löysän arvostelun ja päättää, että jokainen kokeesta saatu piste nostaa arvosanaa puoli askelta ylöspäin.

a) Määritä funktion lauseke, joka kuvaa matematiikan kokeen arvosanaa, kun oppilas on saanut kokeesta pistettä.

# p233a

# p233b

# p233c

2.3.4 Tehtävä

Kuvaajat esittää kahden kävelijän etenemistä.

# p234

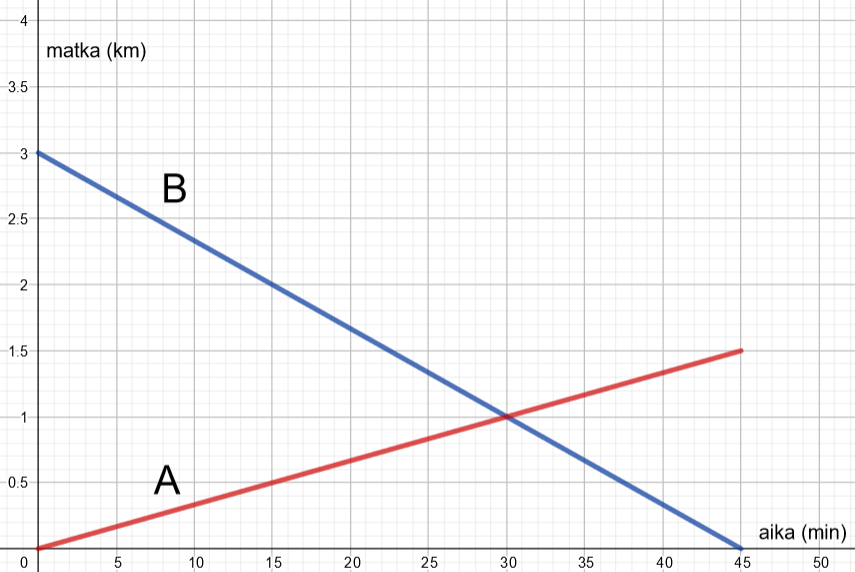
2.3.5 Tehtävä

Sandra on kesätöissä maataloustyöntekijänä. Hän saa palkkaa $9\;\text{€/h}$ . Sandra yöpyy myös maatilalla ja joutuu maksamaan yöpymisestä ja ruuasta $7\;\text{€}$ vuorokaudelta. Sandralle ehdotetaan, ettei hänen tarvitse maksaa yöpymisestä ja ruuasta, jos hänen tuntipalkkaansa alennettaisiin eurolla.

# p233

Vihje

Olkoon työtuntien määrä. Muodostetaan funktiot, jotka kuvaavat Sandran vuorokauden käteenjäävää palkkaa yöpymis- ja ruokakulujen jälkeen.

Ennen muutosta Sandran vuorokaudesta käteenjäävä palkka

f_1(x)=9x-7

ja muutoksen jälkeen

f_2(x)=8x

Halutaan selvittää, monta tuntia Sandran pitäisi työskennellä vähintään, että muutoksen jälkeinen palkka f_2(x) olisi suurempi kuin palkka ennen muutosta $f_1(x)\dots$

2.3.6 Tehtävä

Leijona ja antilooppi ottavat juoksukilpailun. Leijonan huippunopeus on $80\;\text{km/h}\approx22\;\text{m/s}$ ja antiloopin $40\;\text{km/h}\approx11\;\text{m/s}$ . Oletetaan, että eläimet juoksevat koko matkan tasaisesti huippunopeudella. Antilooppi saa etumatkaa $100\;\text{m}$ .

# leijona

Vihje

Esimerkki 2.3.2

2.3.7 Tehtävä

Taskulampun valo on suunnattu maahan 1,4 metrin korkeudelta. Valokiilan yläreuna laskee metrin matkalla $40\;\text{cm}$ .

# p237b

# p237c

2.3.8 Tehtävä (yo lyhyt s2012/11)

Aikuisen ihmisen sääriluun pituus riippuu henkilön pituudesta kaavojen

$\begin{align*} y&=0,43x-27\;\text{(nainen)} \\ y&=0,45x-31\;\text{(mies)} \end{align*}$

mukaisesti, kun yksikkönä on senttimetri.

# p238a

# p238b2

2.3.9 Tehtävä

Taulukossa on pikajuoksija Usain Boltin 100 metrin maailmanennätysjuoksun väliajat Berliinin MM-kilpailuista vuodelta 2009 . (Kuvan lähde: Independent)

$x\;\text{(m)}$	$y\;\text{(s)}$

Sovita GeoGebralla suora, joka mallintaa Boltin juoksumatkaan kulunutta aikaa . Käytä komentoa SovitaSuora.

# funktio

# p232b

Vihje

Esimerkki 2.3.3

2.3.10 Tehtävä

Martti saa ilmaiseksi mopon, joka kuluttaa $6\;\text{l}/100\;\text{km}$ . Jonna taas maksaa 900 euroa skootteristaan, joka kuluttaa $3\;\text{l}/100\;\text{km}$ .

# p134b

Vihje

Merkataan muuttujalla ajettuja sataa kilometriä. Muodostetaan funktiot, jotka kuvaavat Martin ja Jonnan ajamiseen käyttämää rahaa.

Sadan kilometrin jälkeen Martin mopo on kuluttanut bensaa $6x\;\text{(l)}$ ja rahaa ajamiseen on kulunut $1,6\cdot6x=9,6x\;\text{(€)}$ . Martin rahanmenoa sadan kilometrin jälkeen kuvaa siis funktio

f_1(x)=9,6x

Sadan kilometrin jälkeen Jonnan skootteri on kuluttanut bensaa $3x\;\text{(l)}$ ja rahaa ajamiseen on kulunut $1,6\cdot3x=4,8x\;\text{(€)}$ . Lisäksi Jonna on käyttänyt rahaa $900\;\text{€}$ skootterin ostamiseen, joten Jonnan rahanmenoa sadan kilometrin jälkeen kuvaa funktio

f_2(x)=900+4,8x

Jonnan sijoituksesta tulee kannattava, kun Martin ja Jonnan kuluttama raha on yhtä suuri eli funktiot f_1(x) ja f_2(x) saavat saman arvon.

Saadaan siis yhtälö 9,6x=900+4,8x

Muista, että tehtävässä kysytään ajettuja kilometrejä, joten muuttujan arvo ei kelpaa suoraan vastaukseksi...