3. Ympyrän geometriaa
 - sekantti ja tangentti - pinta-ala - sektori - segmentti -
- sekantti ja tangentti - pinta-ala - sektori - segmentti -
Tason pisteet, jotka ovat kiinteällä etäisyydellä pisteestä, muodostavat ympyrän eli ympyräviivan. Ympyröihin liittyy paljon mielenkiintoisia ominaisuuksia, laskuja ja lukuja, kuten irrationaaliluku pii \(\pi\). Lue myös luvun \(\pi\) historiasta.
Tähän kappaleeseen liittyvät harjoitustehtävät löydät täältä!
Alla olevalla videolla on esitelty ympyään liittyviä käsitteitä. Ne käydään myöhemmin läpi yksityiskohtaisemmin.
Käytä yllä olevaa GeoGebra-applettia tutkiaksesi videolla esiintyviä ympyrän osia. Muista kokeilla raahata kehällä olevia pisteitä.
3.1 Säde, halkaisija ja piiri
Ympyrän tärkein ja sen määrittävä ominaisuus on ympyrän säde, jota merkitään usein kirjaimella \(r\) (englannin kielen sanasta radius). Joskus puhutaan myös ympyrän halkaisijasta, jota merkitään kirjaimella \(d\) (englannin kielen sanasta diameter).
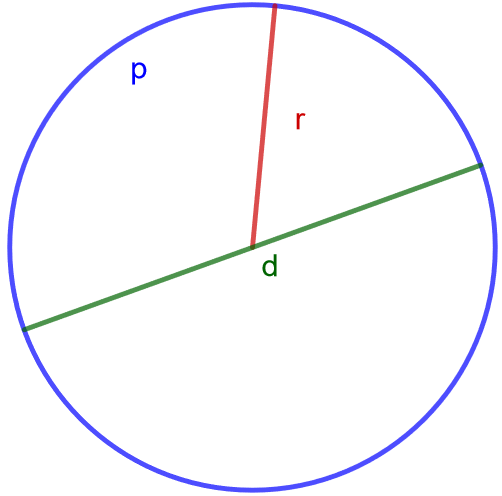
Ympyrän säde, halkaisija ja piiri
Ympyrän säde \(r\) on ympyrän keskipisteen etäisyys sen kehältä. Ympyrän halkaisija \(d\) on jana, joka kulkee ympyrän kehältä kehälle sen keskipisteen kautta. Halkaisijan pituus on \(d=2r\). Ympyrän piiri \(p\) on sen kehän pituus, ja se lasketaan \(p=2 \pi r = \pi d\).

Donitsin halkaisija on 9,5 cm ja reiän ympärys 6,1 cm.
Laske
- donitsin ulkoreunan ympärys.
- donitsin reiän säde.
Ratkaisu
Merkitään donitsin halkaisijaa kirjaimella \(d\). Donitsin ulkoreunan ympärys on \(p=2 \pi r= \pi d = \pi \cdot 9,5 \text{ cm}= 29.8451... \text{ cm}≈ 30 \text{ cm}\)
Merkitään donitsin reiän ympärystä eli piiriä kirjaimella \(p\), ja ratkaistaan sen säde
\[\begin{align} p&=2 \pi r& \quad &| :2\pi \text{ ja vaihdetaan yhtälön puolia} \\ r&= \frac{p}{2 \pi}& \quad &| \text{ sijoitetaan} p \\ &= \frac{6,1 \text{ cm}}{2 \pi}& \quad &| \text{ sievennetään} \\ &=0,9867... \text{ cm}& \quad &| \text{ pyöristetään yhden desimaalin tarkkuuteen} \\ &≈ 1,0 \text{ cm}. \\ \end{align}\]
3.2 Pinta-ala
Alla olevassa Opetus-tv:n videossa johdetaan ympyrän pinta-alan tuttu laskukaava. Videon täysi ymmärtäminen ei ole edellytys tehtävien osaamiselle, mutta se voi avata hieman paremmin, mistä ympyrän pinta-alan laskukaava tulee.
Ympyrän pinta-ala
Ympyrän pinta-ala lasketaan sen säteen \(r\) avulla seuraavasti \[A=\pi r^2.\]
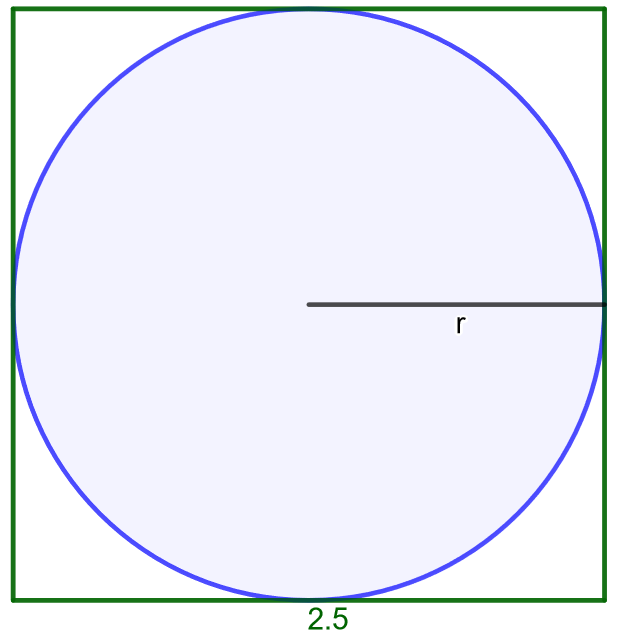
Pihalle halutaan rakentaa ympyrän muotoinen uima-allas. Sille on varattu neliön muotoinen alue, jonka sivun pituus on \(2,5 \text{ m}\). Kuinka suuri on suurimman mahdollisen uima-altaan pinta-ala?
Ratkaisu
Yllä olevassa kuvassa on piirretty mallikuva tilanteesta. Jotta voitaisi laskea ympyrän pinta-ala, tulee selvittää neliöön mahtuvan ympyrän säde. Koska neliön sivun pituus on \(2,5 \text{ m}\), se on samalla ympyrän halkaisija. Ympyrän säde on puolet sen halkaisijasta, jolloin se on \(r=1,25 \text{ m}\).
Nyt ympyrän pinta-ala lasketaan \[ \begin{aligned} A&=\pi r^2& \quad &| \text{ sijoitetaan }r \\ A&= \pi \cdot 1,25^2& \quad &| \text{ sievennetään} \\ A&\approx 4,90874 \end{aligned} \] Vastausta annettaessa muistetaan lisätä tarvittava yksikkö. Eli alueelle mahtuvan suurimman mahdollisen uima-altaan pinta-ala on noin \(4,9 \text{ m}^2\).
3.3 Keskuskulma, kaaren pituus, sektorin pinta-ala
Käsitellään seuraavaksi ympyrään liittyviä käsitteitä. Jos ympyrä jaetaan osiin, muodostuu keskuskulmia, joita voidaan merkitä tutuilla merkinnöillä \(\alpha,\;\beta,\;\gamma...\). Muodostuva osa on nimeltään sektori, ja sen kaarella on jokin pituus \(b\). Lisäksi ympyrän sektorin pinta-ala on mahdollista määrittää.
Keskuskulma
Kulma, jonka kärki on ympyrän keskipisteessä, on keskuskulma. 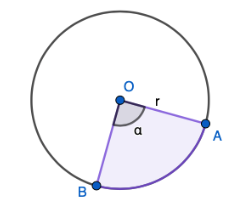
Ympyrän kaaren pituus
Keskuskulman \(\alpha\) kyljet rajaavat ympyrän kehältä kaaren, jonka pituus \(b\) voidaan laskea seuraavasti \[b = \frac{\alpha}{360 ^{\circ}} 2\pi r.\] 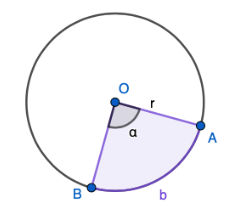
Perustellaan ympyrän kaaren pituuden laskukaava \[b=\frac{\alpha}{360^{\circ}} 2 \pi r.\] Laskukaavan jälkimmäinen termi \(2 \pi r\) on sama kuin koko ympyrän piiri. Laskukaavan ensimmäinen termi \(\frac{\alpha}{360^{\circ}}\) kuvaa sitä, kuinka suuri osa kokonaisen ympyrän piiristä otetaan.
Jos kaarta vastaavan keskuskulman suuruus on esimerkiksi \(180^{\circ}\), on kyseisen kaaren pituus luonnollisesti puolet kokonaisen ympyrän kehän pituudesta, sillä \(\frac{180^{\circ}}{360^{\circ}}=\frac{1}{2}\).
Tarkastellaan alla olevan kuvan kaltaista sektoria.
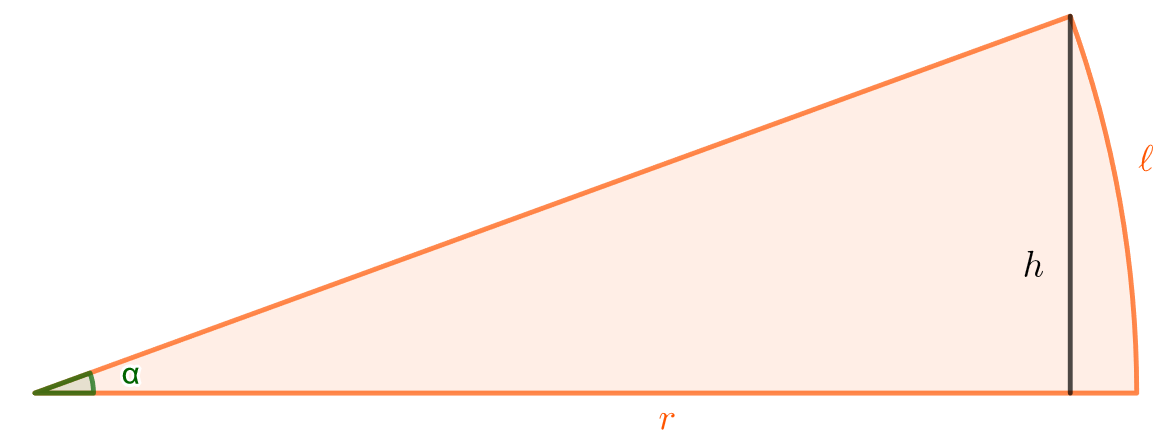
Ratkaistaan kaaren \(\ell\) pituus. Jos kulma \(\alpha\) on ilmaistu radiaaneissa, edellinen kaava muuttuu muotoon
\[b=\frac{\alpha}{2 \pi} 2 \pi r = \alpha r.\]
Nyt siis kaarelle \(\ell=\alpha r\). Pystysuoran pituuden \(h\) suuruus voidaan määrittää sinin avulla:
\[\sin \alpha= \frac{h}{r} \quad \Leftrightarrow \quad h = r \sin \alpha.\]
Kun kulmaa \(\alpha\) pienennetään, janan \(h\) ja kaaren \(\ell\) pituudet lähestyvät toisiaan. Voidaan siis merkitä, että kun \(\alpha\) on pieni,
\[ \begin{aligned} h & \approx \ell \\ r \sin \alpha & \approx \alpha r \quad |:r \\ \sin \alpha & \approx \alpha \end{aligned} \]
Eli kun kulma \(\alpha\) on pieni, sen siniä voidaan approksimoida kulman arvolla (radiaaneina).
Ympyrän sektorin pinta-ala
Keskuskulman \(\alpha\) kyljet rajaavat ympyrän sisältä sektorin, jonka pinta-ala \(A_{SEK}\) voidaan laskea seuraavasti: \[A_{SEK}= \frac{\alpha}{360 ^{\circ}} \pi r^2.\] Jos tiedetään keskuskulmaa vastaavan kaaren pituus \(b\), voidaan sektorin pinta-ala laskea myös kaavalla \[A_{SEK}=\frac{br}{2}.\]
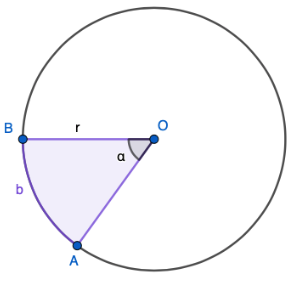
Sektorin pinta-alan ylempi kaava voidaan perustella samalla tavalla kuin ympyrän kaaren pituuden kaava perusteltiin aiemmin. Toinen kaava voidaan perustella sijoittamalla siihen \(b=\frac{\alpha}{360^{\circ}} 2 \pi r\), jolloin saadaan \[A_{SEK}=\frac{\alpha}{360^{\circ}} 2 \pi r \cdot \frac{r}{2}=\frac{\alpha}{360^{\circ}} \pi r^2\] joka on sama kuin sektorin pinta-alan ylempi kaava.
Laske alla olevan ympyräsektorin pinta-ala. Kuinka suuri keskuskulma \(\alpha\) on?
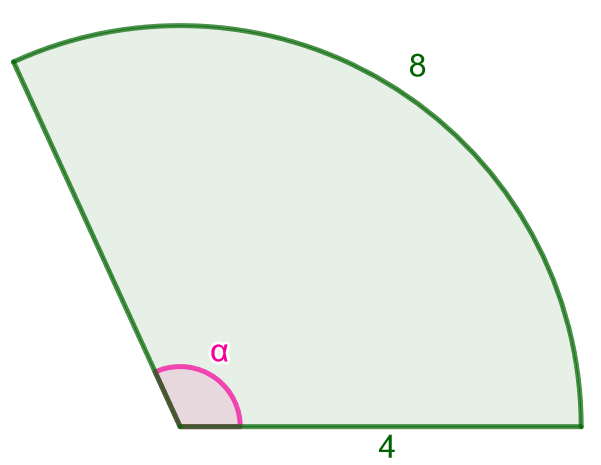
Ratkaisu
Nyt kaaren pituus on \(b=8\) ja säde \(r=4\). Sektorin pinta-ala saadaan laskettua näiden tietojen avulla: \[A=\frac{br}{2}=\frac{8 \cdot 4}{2}=16.\]
Nyt kysytyn keskuskulman suuruus voidaan ratkaista sektorin pinta-alan toisesta kaavasta tai kaaren pituuden kaavan avulla. Ratkaistaan tässä keskuskulma ensimmäisellä tavalla. Ratkaistaan \(\alpha\) sektorin pinta-alan kaavasta ja sijoitetaan arvot kaavaan \[ \begin{aligned} A&=\frac{\alpha}{360^{\circ}} \pi r^2 &\quad &|\cdot 360^{\circ} \\ 360 ^{\circ} A&= \alpha \pi r^2 &\quad &|:\pi r^2 \\ \alpha &= \frac{360^{\circ} A}{\pi r^2}& \quad &| \text{ sijoitetaan }A \text{ ja }r \\ \alpha &= \frac{360^{\circ} \cdot 16}{\pi \cdot 4^2}& \quad &| \text{ sievennetään} \\ \alpha &\approx 114,591559 ^{\circ}& \quad &| \text{ pyöristetään yhden desimaalin tarkkuuteen} \\ \alpha &\approx 114,6 ^{\circ} \end{aligned} \]
Sektorin pinta-ala on siis \(16\) ja sen keskuskulman suuruus on noin \(114,6^{\circ}\).
3.4 Jänne, segmentti
Ympyrä voidaan jakaa myös osiin, jotka eivät osu ympyrän keskipisteeseen \(O\). Tällaista janaa, joka piirretään kahden kehän pisteen välille kutsutaan jänteeksi, ja se rajaa ympyrästä kaksi segmenttiä.
Jänne
Ympyrän kehällä olevan kaaren päätepisteet yhdistää jänne. 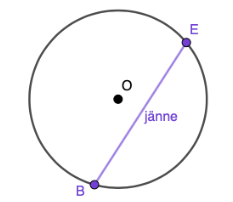
Segmentin pinta-ala
Jänne jakaa ympyrän kahdeksi segmentiksi, joiden pinta-ala \(A_{SEG}\) saadaan laskettua kaavalla \[A_{SEG}=A_{SEK} \pm A_{keskuskolmio}.\] Kaavassa käytetään yhteenlaskua, jos keskuskulma \(\alpha\) on suurempi kuin \(180^{\circ}\), ja vähennyslaskua, jos keskuskulma \(\alpha\) on pienempi kuin \(180^{\circ}\). 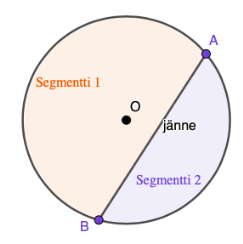
Laske alla olevaan kuvaan sinisellä merkityn segmentin pinta-ala.
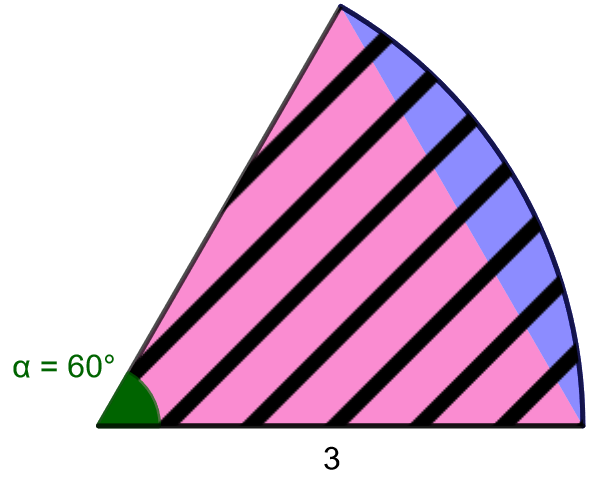
Ratkaisu
Koska keskuskulma \(\alpha\) on pienempi kuin \(180^{\circ}\), käytetään kaavaa \[A_{SEG}=A_{SEK}-A_{\text{keskuskolmio}}.\] Lasketaan ensin kuvaan mustalla vinoviivoituksella merkityn sektorin pinta-ala. Sektorin säde \(r=3\) ja keskuskulma \(\alpha=60^{\circ}\), joten sektorin pinta-ala on \[ \begin{aligned} A_{SEK}&=\frac{\alpha}{360^{\circ}} \pi r^2 & \quad &| \text{ sijoitetaan }\alpha \text{ ja }r \\ &=\frac{60^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2& \quad &| \text{ sievennetään} \\ &=\frac{3\pi}{2} \end{aligned} \] Lasketaan sitten kuvaan pinkillä merkityn keskuskolmion pinta-ala. Kolmion kahden sivun pituudet ovat säteen mittaiset eli \(3\), ja näiden sivujen välinen kulma on \(\alpha=60^{\circ}\). Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla, jossa \(a=b=r=3\). \[ \begin{aligned} A_{\text{keskuskolmio}}&=\frac{ab}{2} \sin(\alpha)& \quad &| \text{ sijoitetaan }ab=r^2 \\ &=\frac{r^2}{2} \sin(\alpha)& \quad &| \text{ sijoitetaan }r\text{ ja }\alpha \\ &=\frac{3^2}{2} \sin(60^{\circ})& \quad &| \text{ sievennetään} \\ &=\frac{9\sqrt{3}}{4} \end{aligned} \] Lopuksi lasketaan segmentin pinta-ala vähennyslaskulla \[ \begin{aligned} A_{SEG}&=A_{SEK}-A_{\text{keskuskolmio}}& \quad &| \text{ sijoitetaan }A_{SEK}\text{ ja }A_{keskuskolmio} \\ &= \frac{3 \pi}{2} - \frac{9 \sqrt{3}}{4}& \quad &| \text{ lavennetaan luku }\frac{3\pi}{2}\text{ luvulla 2} \\ &= \frac{6 \pi}{4} - \frac{9 \sqrt{3}}{4}& \quad &| \text{ sievennetään} \\ &= \frac{6 \pi - 9 \sqrt{3}}{4}& \quad &| \text{ sievennetään} \\ &\approx 0,81527& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ &\approx 0,82 \end{aligned} \] Kysytyn segmentin pinta-ala on siis noin \(0,82\).
Ratkaise alla olevaan kuvaan sinisellä rajatun segmentin pinta-ala.
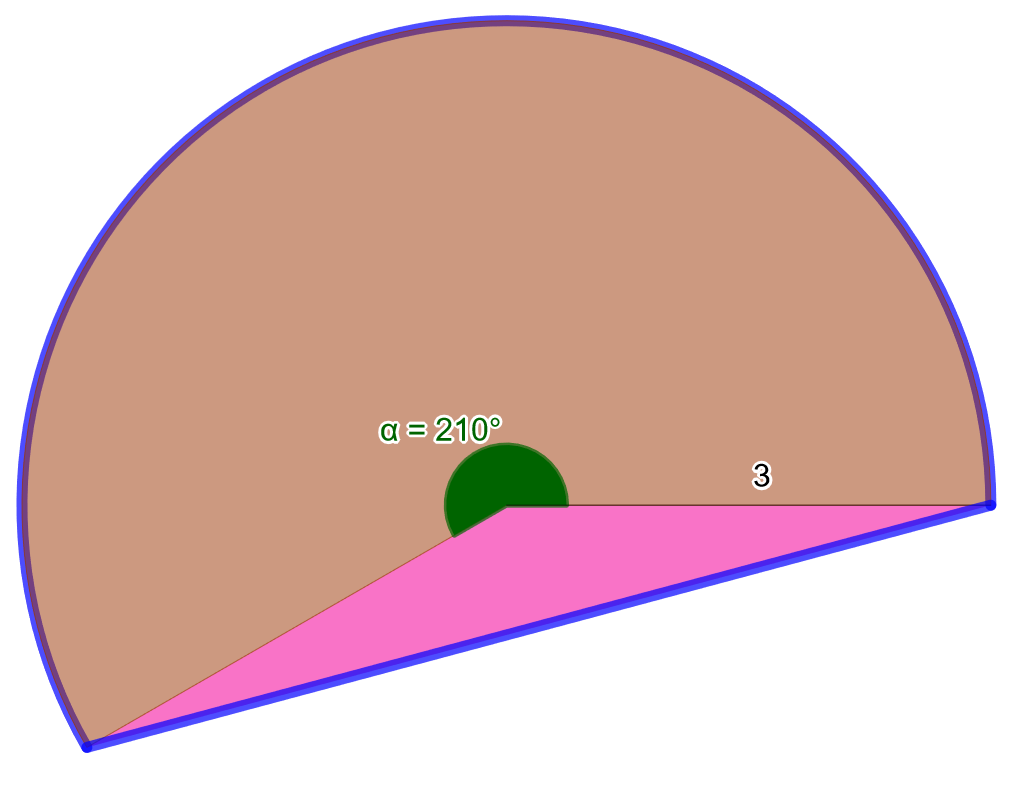
Ratkaisu
Koska keskuskulma \(\alpha=210^{\circ}\) on suurempi kuin \(180^{\circ}\), käytetään laskukaavaa \[A_{SEG}=A_{SEK}+A_{\text{keskuskolmio}}.\]
Lasketaan ensin kuvaan ruskealla merkityn sektorin pinta-ala. Nyt säde \(r=3\) ja keskuskulma \(\alpha=210^{\circ}\), joten sektorin pinta-ala on \[ \begin{aligned} A_{SEK} &= \frac{\alpha}{360^{\circ}}\pi r^2& \quad &| \text{ sijoitetaan }\alpha\text{ ja }r \\ &= \frac{210^{\circ}}{360^{\circ}} \pi \cdot 3^2& \quad &| \text{ sievennetään} \\ &= \frac{21 \pi}{4} \end{aligned} \] Seuraavaksi lasketaan keskuskolmion pinta-ala. Kolmion kahden sivun pituus on \(a=b=r=3\) ja näiden sivujen välisen kulman suuruus on \(\beta=360^{\circ}-210^{\circ}=150^{\circ}\). Lasketaan kolmion pinta-ala trigonometrisen laskukaavan avulla. \[ \begin{aligned} A_{\text{keskuskolmio}}&= \frac{r^2}{2} \sin(\beta)& \quad &| \text{ sijoitetaan }r \text{ ja }\beta \\ &= \frac{3^2}{2} \sin(150^{\circ})& \quad &| \text{ sievennetään} \\ &= \frac{9}{4} \end{aligned} \] Lopuksi lasketaan segmentin pinta-ala yhteenlaskulla \[ \begin{aligned} A_{SEG} &= A_{SEK} + A_{\text{keskuskolmio}}& \quad &| \text{ sijoitetaan }A_{SEK}\text{ ja } A_{keskuskolmio} \\ &= \frac{21 \pi}{4} + \frac{9}{4}& \quad &| \text{ sievennetään} \\ &= \frac{21\pi +9}{4}& \quad &| \text{ sievennetään} \\ & \approx 18,7436& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ &\approx 18,74 \end{aligned} \]
Kuvaan sinisillä ääriviivoilla piirretyn segmentin pinta-ala on noin \(18,74\).
3.5 Tangentti, tangenttikulma
Sanalla tangentti voidaan matematiikassa tarkoittaa kahta asiaa, ja ne molemmat liittyvät geometriaan. Yleensä asiayhteydestä selviää, puhutaanko trigonometrisesta funktiosta nimeltä tangentti vai käyrää tasan yhdessä pisteessä sivuava suora. Tässä luvussa puhutaan tangentista sen jälkimmäisessä merkityksessä.
Tangentti
Tangentti on suora, joka kohtaa ympyrän vain yhdessä pisteessä. Ympyrän tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan.
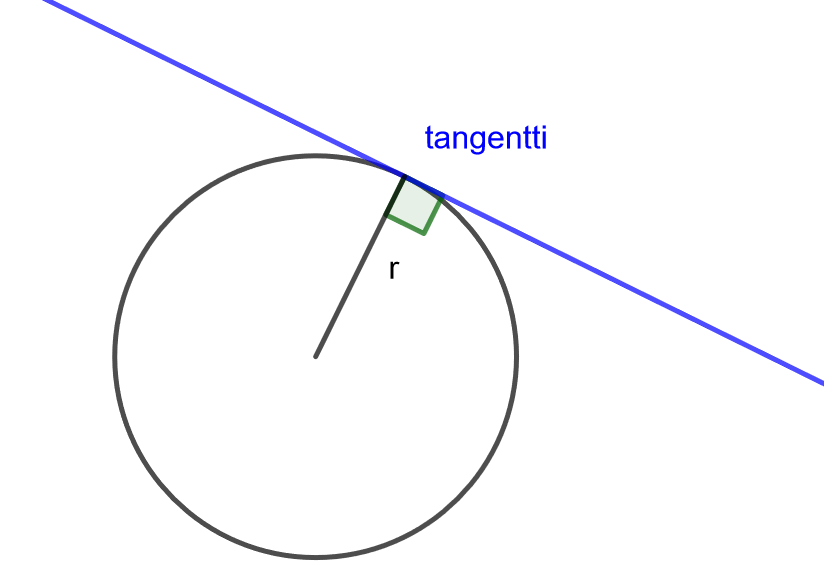
Tangenttikulma
Tangenttikulma on kahden ympyrän tangentin leikkauspisteeseen muodostuva kulma, jonka aukeamassa ympyrä on. Tangenttikulman ja sitä vastaavan keskuskulman summa on aina \(180^{\circ}\).
Todistetaan tangenttikulmalause, jonka mukaan tangenttikulman ja sitä vastaavan keskuskulman summa on aina \(180^{\circ}\). Käytetään alla olevan kuvan merkintöjä.
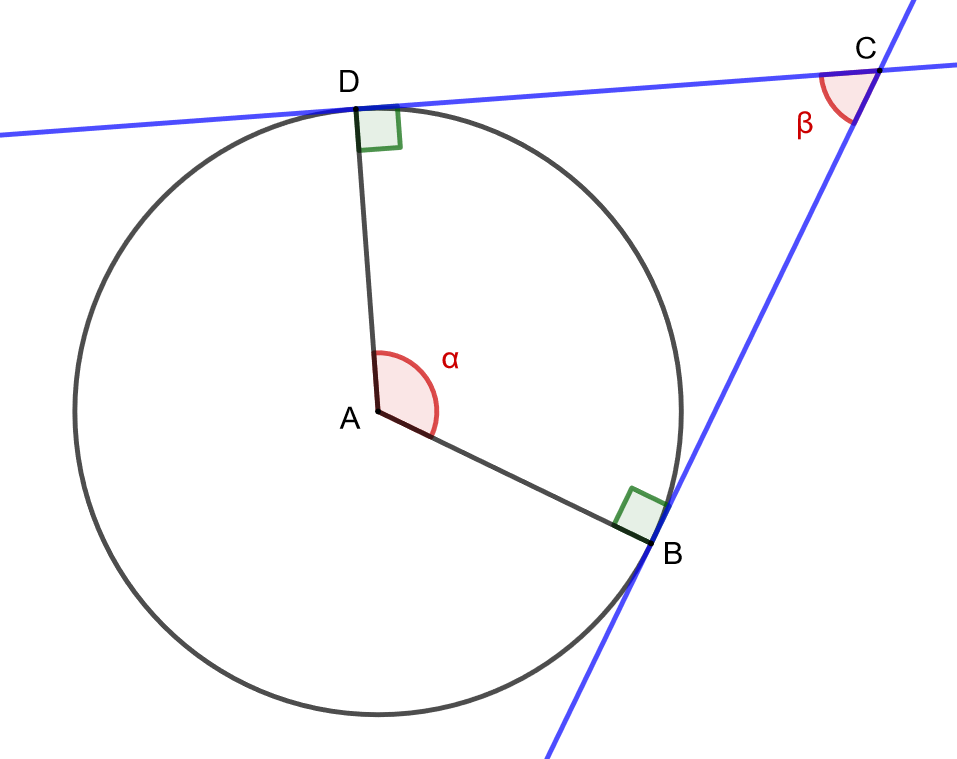
Ympyrän keskipiste \(A\), sen kehän pisteet \(B\) ja \(D\) sekä näiden kehän pisteiden kautta piirrettyjen tangenttien leikkauspiste \(C\) muodostavat nelikulmion \(ABCD\). Nelikulmion kulmien summa on aina \(360^{\circ}\). Ympyrän säteen \(AB\) sekä tangentin \(BC\) välinen kulma on aina suora. Samoin säteen \(AD\) ja tangentin \(CD\) välinen kulma on aina suora. Tästä saadaan, että on oltava \[\alpha + \beta = 360^{\circ} - 2 \cdot 90^{\circ} = 180^{\circ}.\] Toisin sanoen, tangenttikulman ja sitä vastaavan keskuskulman summan on oltava \(180^{\circ}\). Yllä olevalla GeoGebra-appletilla voit tutkia tangenttikulman ja sitä vastaavan keskuskulman suuruuksia. Huomaa, että tangenttien ja ympyrän säteiden väliset kulmat ovat koko ajan suoria kulmia, vaikka sinisiä pisteitä siirtäisikin.
Ympyrälle O on piirretty kaksi tangenttia, jotka molemmat kulkevat saman pisteen A kautta. Laske suuruus tangenttikulmalle \(\alpha\).
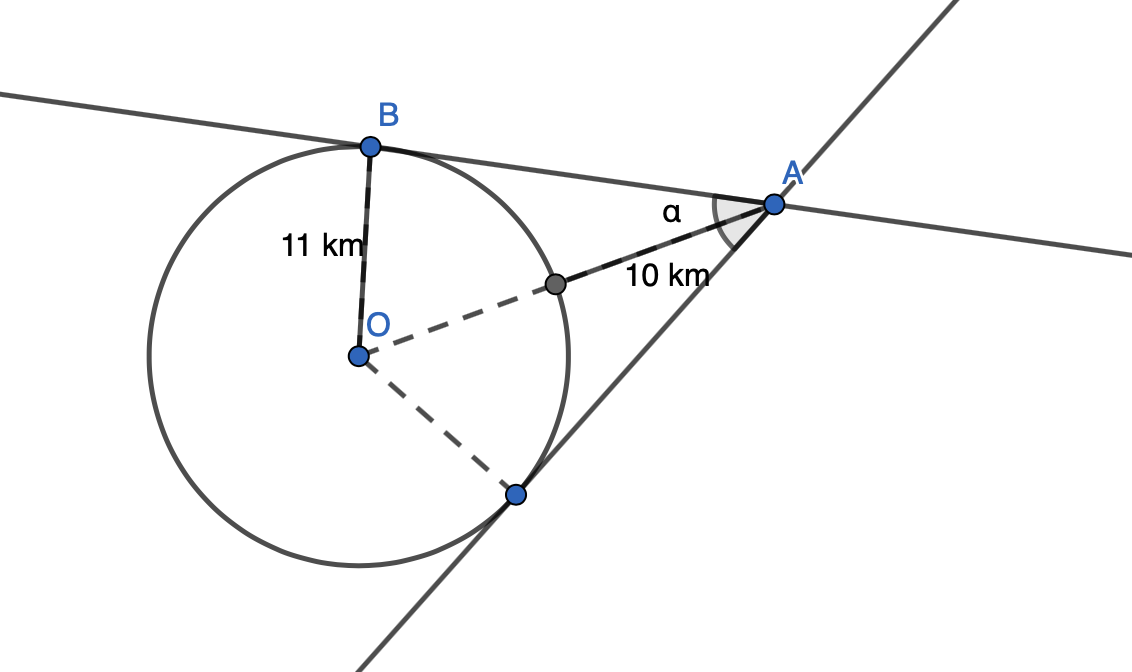
Ratkaisu
Nyt kolmio \(OAB\) on suorakulmainen, koska jana \(OB\) on kohtisuorassa janaa \(AB\) vastaan. Suorakulmaisen kolmion hypotenuusa on siis jana \(OA\).
Hypotenuusan pituus on
\(11 \text{ km} + 10 \text{ km} = 21 \text{ km}\)
Merkitään kirjaimella \(\beta\) kolmion kulmaa \(OAB\). Ratkaistaan kulma \(\beta\) sinin avulla.
\[\begin{align} \sin{\beta} &= \frac{11 \text{ km}}{21 \text{ km}}& \quad &| \text{ sievennetään ja otetaan }\tan^{-1} \\ \beta &= 31,5888...° \\ \end{align}\]
Kulma \(\beta\) on puolet halutun tangenttikulman suuruudesta. Tällöin \(\alpha= 2 \cdot 31,5888...°≈ 63°\)
Tangenttikulman suuruus on \(63°\).
Yllä olevalla GeoGebra-appletilla voit tutkia tangenttikulman ja sitä vastaavan keskuskulman suuruuksia. Huomaa, että tangenttien ja ympyrän säteiden väliset kulmat ovat koko ajan suoria kulmia, vaikka sinisiä pisteitä siirtäisikin.
3.6 Keskuskulma, kehäkulma
Kehäkulma
Kehäkulma on kulma, jonka kärki on ympyrän kehällä ja jonka kylkinä on kaksi jännettä tai jänne ja tangentti. Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta. Samaa kaarta vastaavat kehäkulmat ovat aina yhtä suuria. 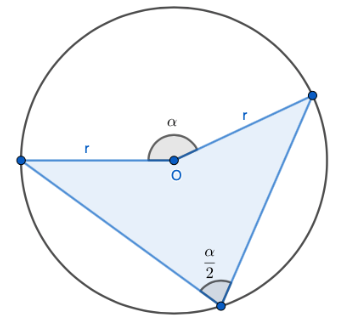
Todistetaan kehäkulmalause eli lause "Kehäkulman suuruus on puolet sitä vastaavan keskuskulman suuruudesta". Tehdään todistus kolmessa vaiheessa:
- ympyrän keskipiste \(O\) on kehäkulman \(\beta\) kyljellä,
- ympyrän keskipiste \(O\) on kehäkulman \(\beta\) aukeamassa ja
- ympyrän keskipiste \(O\) ei ole kehäkulman \(\beta\) aukeamassa.
Tarkastellaan ensin tapausta, jossa jänne \(AC\) kulkee ympyrän keskisteen \(O\) kautta. Käytetään alla olevan kuvan merkintöjä.
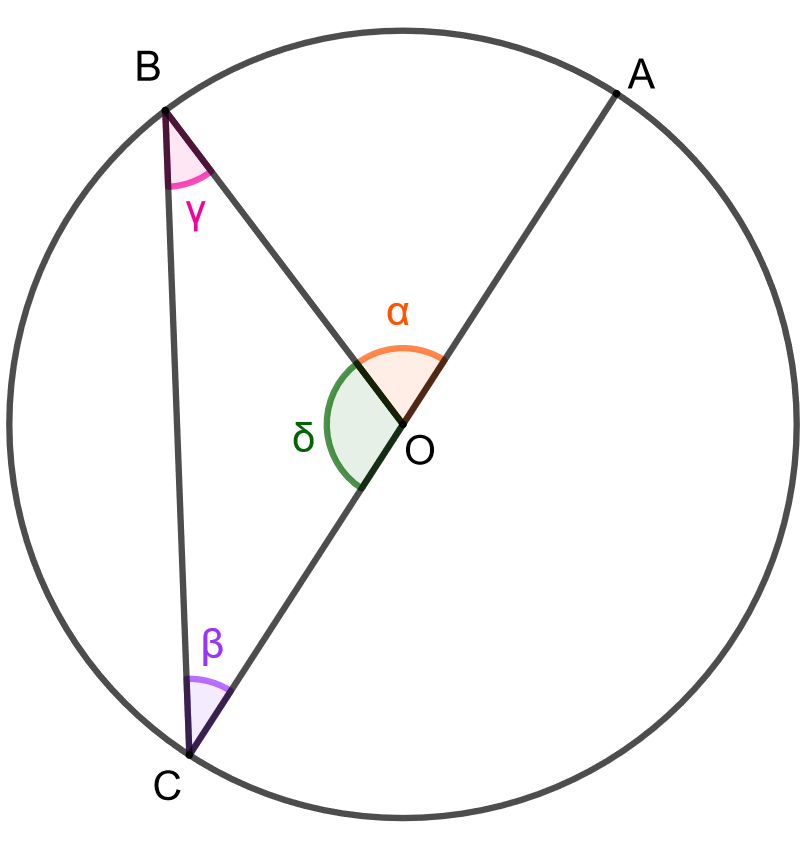
Huomataan, että pisteet \(O\), \(B\) ja \(C\) muodostavat tasakylkisen kolmion, jonka kantana on jänne \(BC\) ja kylkinä janat \(BO\) sekä \(CO\). Kyljet ovat keskenään yhtä pitkiä, koska molemmat ovat ympyrän säteitä. Tasakylkisen kolmion kantakulmat ovat keskenään yhtä suuria, joten \(\beta = \gamma\). Koska kolmion kulmien summa on \(180^{\circ}\), saadaan yhtälö \[\beta + \gamma + \delta = 180^{\circ}.\] Lisäksi huomataan, että kulmat \(\alpha\) ja \(\delta\) ovat vieruskulmia, jolloin niiden summa on \(180^{\circ}\) eli \(\alpha + \delta = 180^{\circ}\). Ratkaistaan tästä kulma \(\delta\), jolloin saadaan \(\delta = 180^{\circ} - \alpha\). Sijoitetaan tämä sekä \(\gamma = \beta\) kolmion kulmien summan lausekkeeseen, jolloin saadaan \[\beta + \beta + 180^{\circ} - \alpha = 180^{\circ} \Leftrightarrow \beta = \frac{\alpha}{2}.\] Eli kehäkulma on puolet vastaavasta keskuskulmasta. Tarkastellaan seuraavaksi tapausta, jossa ympyrän keskipiste \(O\) on kehäkulman \(\beta\) aukeamassa. Käytetään alla olevan kuvan merkintöjä.
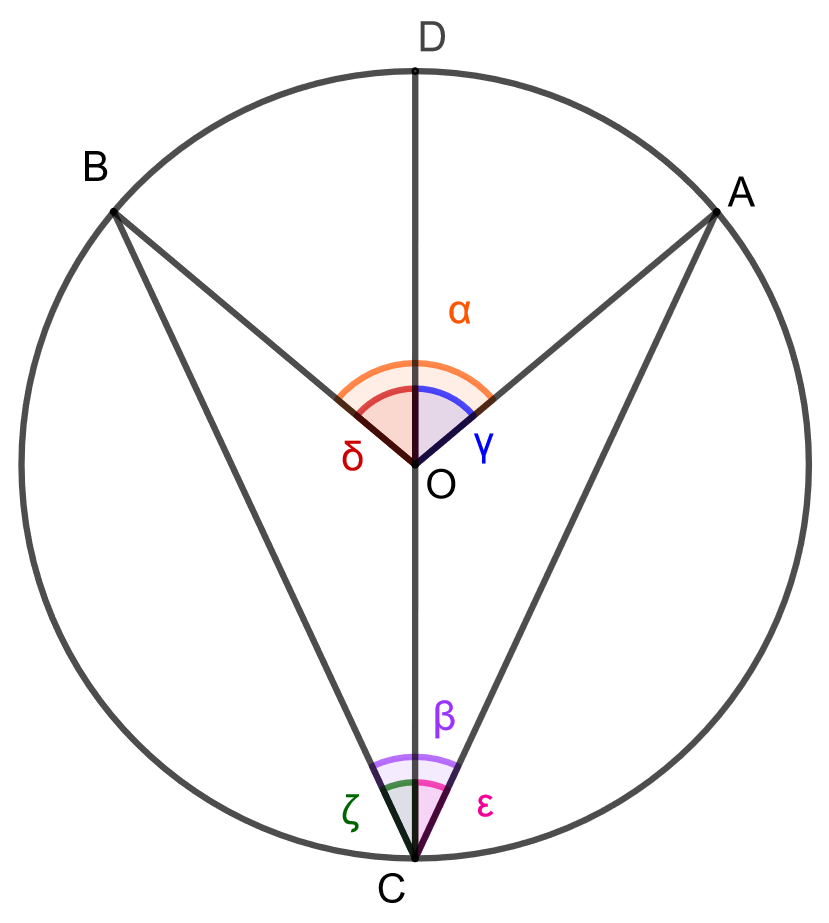
Jaetaan kulma \(\alpha\) kahdeksi kulmaksi \(\gamma\) ja \(\delta\) janalla \(CD\), joka kulkee ympyrän keskipisteen \(O\) kautta. Sama jana jakaa kehäkulman \(\beta\) kulmiksi \(\epsilon\) ja \(\zeta\). Voimme tarkastella ensin pelkästään janan \(CD\) oikealla puolella olevia kulmia ja sitten sen vasemmalla puolella olevia. Tällöin todistuksen edellisen kohdan perusteella saadaan \(\epsilon = \frac{\gamma}{2}\) ja \(\zeta=\frac{\delta}{2}\).
Tiedetään, että \(\alpha = \gamma + \delta\). Lisäksi tiedetään, että \(\beta = \epsilon + \zeta\). Sijoitetaan tähän aiemmat yhtälöt, jolloin saadaan \[\beta = \frac{\gamma}{2} + \frac{\delta}{2} = \frac{\gamma + \delta}{2} = \frac{\alpha}{2}.\] Eli kehäkulma \(\beta\) on puolet vastaavasta keskuskulmasta \(\alpha\).
Tarkastellaan lopuksi tapausta, jossa ympyrän keskipiste \(O\) ei ole kehäkulman \(\beta\) aukeamassa. Käytetään alla olevan kuvan merkintöjä.
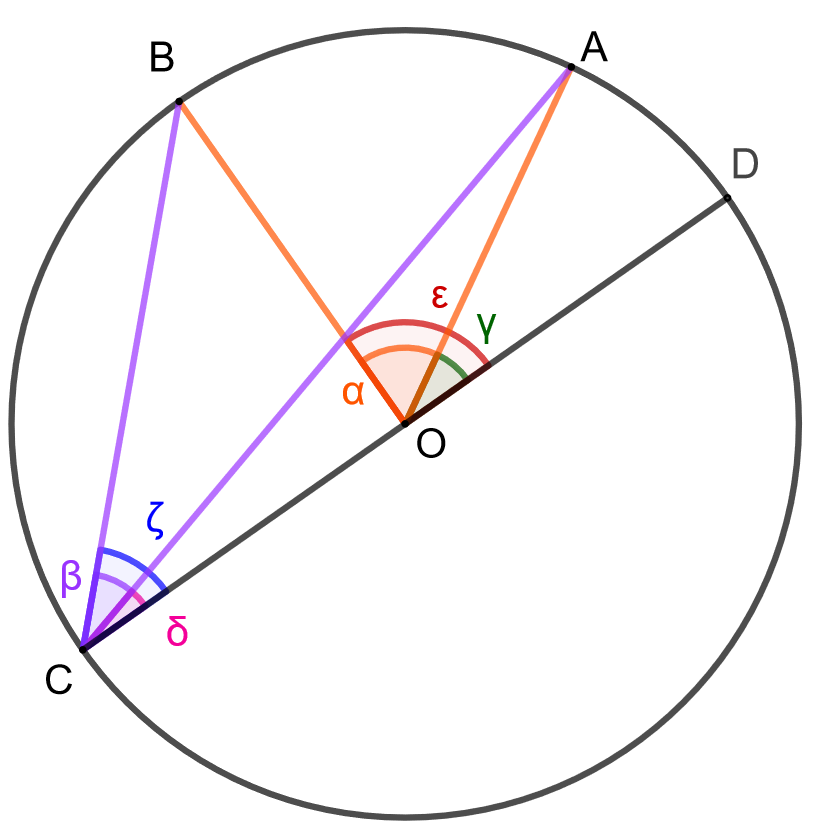
Huomataan, että \(\alpha = \epsilon - \gamma\) ja että \(\beta = \zeta - \delta\). Todistuksen ensimmäisen kohdan perusteella voidaan kirjoittaa \[\beta = \zeta - \delta = \frac{\epsilon}{2} - \frac{\gamma}{2} = \frac{\epsilon - \gamma}{2} = \frac{\alpha}{2}.\] Kehäkulma \(\beta\) on siis puolet keskuskulmasta \(\alpha\).
Yllä olevassa GeoGebra-appletissa on merkitty vihreällä keskuskulma ja pinkillä samoja pisteitä vastaava kehäkulma. Kokeile muuttaa kulmien suuruuksia, ja huomaa, että kehäkulma on aina puolet vastaavan keskuskulman suuruudesta.
Laske kulman \(\alpha\) suuruus.
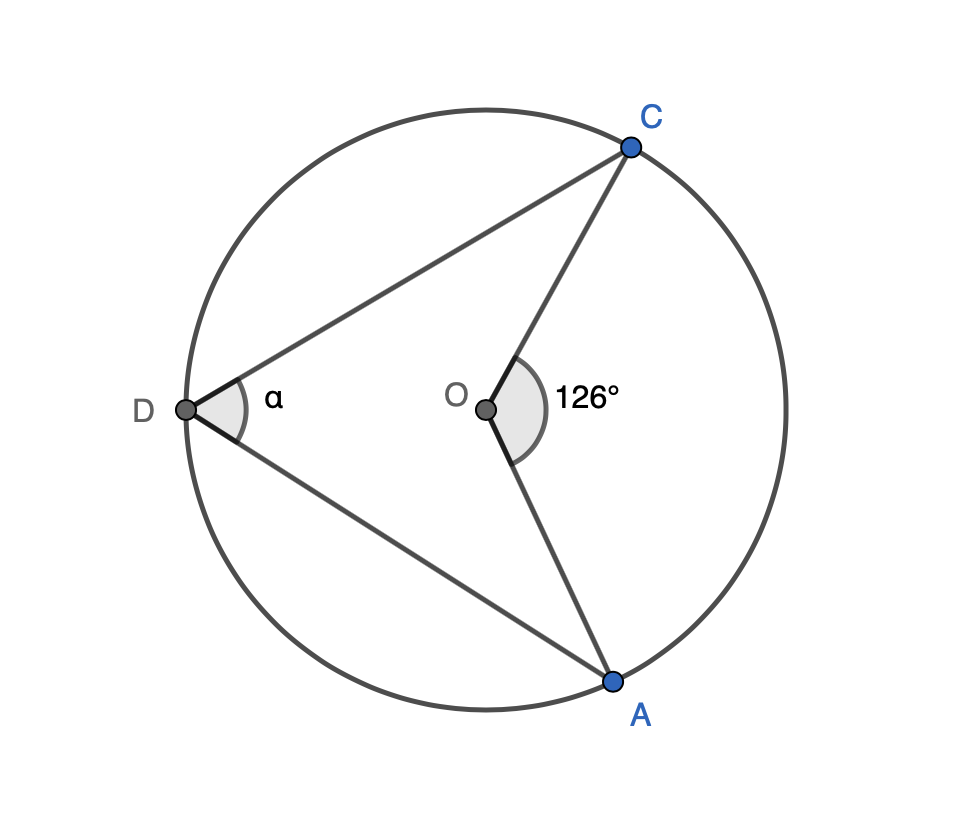
Ratkaisu
Ympyrän keskipiste on \(O\) ja pisteet \(A\), \(B\) ja \(C\) ovat ympyrän kehällä. Keskuskulma \(AOC\) ja kehäkulma \(ADC\), eli kulma \(\alpha\), vastaavat kaarta \(AC\). Kehäkulmalauseen nojalla kehäkulma on puolet vastaavan kaaren keskuskulmaan verrattuna, joten
\(\angle ADC = \alpha = \frac{126°}{2} = 63°\)
Yllä olevassa GeoGebra-appletissa on piirretty kaksi samaa ympyrän kaarta vastaavaa kehäkulmaa. Kokeile siirtää kuvion pisteitä ja huomaa, että kehäkulmat pysyvät koko ajan yhtä suurina keskenään.
3.7 Ympyrä koordinaatistossa
Samoin kuin monikulmioidenkin tilanteessa, ympyrä voidaan myös piirtää koordinaatistoon ja tutkia sen ominaisuuksia koordinaatiston avulla. 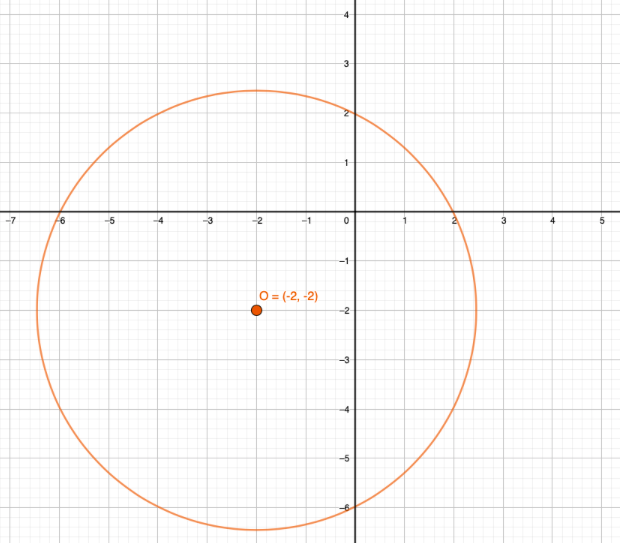
Yllä olevassa kuvassa on piirretty ympyrä \(xy\)-koordinaatistoon. Ympyrän keskipiste \(O\) on kuvan mukaan pisteessä \((-2,-2)\).
Määritetään ympyrän säteen pituus. Hyödynnetään Monikulmiot koordinaatistossa -luvusta tuttuja lauseita janan pituudelle.
Ympyrän kehällä olevat pisteet ovat kaikki yhtä kaukana keskipisteestä. Tämä etäisyys on ympyrän säde \(r\). Valitaan nyt mikä tahansa piste kehältä, vaikkapa piste \(2,0\).
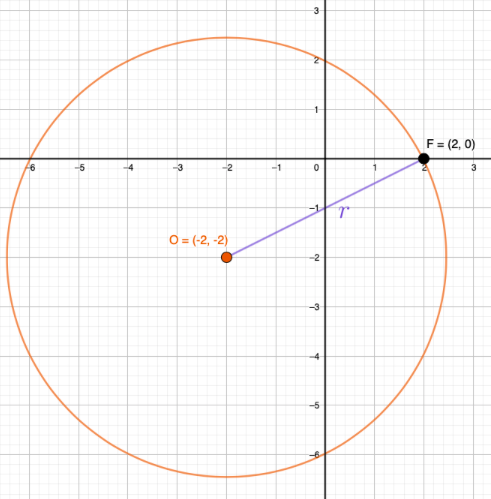
Lasketaan nyt siis janan \(OF\) pituus: \[\begin{align*} |OF|=\sqrt{(2-(-2))^{2}+(0-(-2))^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{20}=2\cdot\sqrt{5} \end{align*}\]
Ympyrän säde \(r=2\sqrt{5}\) ja keskipiste on pisteessä \((-2,-2)\).
Ympyrän keskipiste on \(O(-1,3)\) ja kehäpiste \(A(0,2)\). Ympyrälle piirretään kaksi tangenttia pisteen \(B(1,4)\) kautta. Tutki laskemalla, sivuaako toinen pisteen \(B\) kautta piirretyistä tangenteista ympyrää pisteessä \(A\).
Ratkaisu
Piirretään ensin kuvaan ympyrä ja tangentit.
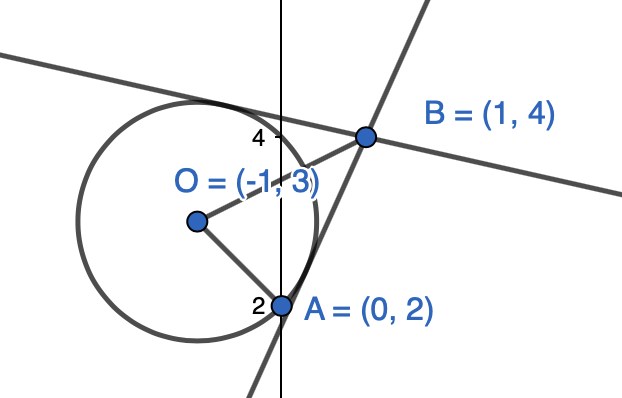
Tarkastellaan kolmiota \(OAB\). Jos piste \(A\) on sivuamispiste, tulisi kolmion olla suorakulmainen. Käytetään käänteistä Pythagoraan lausetta ja tutkitaan, toteuttavatko kolmion sivujen pituudet Pythagoraan lauseen.
Lasketaan ensin sivujen pituudet.
\(|OA|= \sqrt{(0- (-1))^2 + (2-3)^2} = \sqrt{2} \\ |OB|= \sqrt{(1-(-1))^2 + (4-3)^2} = \sqrt{5} \\ |BA|= \sqrt{(0-1)^2 + (2-4)^2} = \sqrt{5} \\\)
Tarkistetaan, toteuttavatko pituudet Pythagoraan lauseen.
\[\begin{align} |OB|^2 &= |OA|^2 + |BA|^2& \quad &| \text{ sijoitetaan arvot} \\ (\sqrt{5})^2 &= (\sqrt{2})^2 + (\sqrt{5})^2& \quad &| \text{ sievennetään} \\ 5 &= 2 + 5& \quad &| \text{ sievennetään} \\ 5 &≠ 7 \\ &\text{epätosi} \\ \end{align}\]
Koska sivujen pituudet eivät toteuttaneet Pythagoraan lausetta, ei kolmio \(OAB\) ole suorakulmainen eikä tangentti siis sivua ympyrää pisteessä \(A\).
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.