4. Avaruusgeometriaa
- avaruuskappaleet - avaruuslävistäjä - pinta-alat ja tilavuudet
4.1 Avaruuskappaleita
Tässä luvussa siirrytään tasosta kolmiulotteiseen avaruuteen. Kuitenkin monia tasogeometriassa opittuja lauseita ja ominaisuuksia voi hyödyntää myös avaruusgeometriassa.
Tähän kappaleeseen liittyvät harjoitustehtävät löydät täältä!
Yllä olevassa GeoGebra-appletissa on käyty läpi monitahokkaan osia ja niiden nimityksiä. Monitahokas on mikä tahansa monikulmioista koostuva suljettu pinta. Jos kaikki monitahokkaan tahkot ovat samanlaisia säännöllisiä monikulmioita, kyseessä on säännöllinen monitahokas. Tällaisia ovat esimerkiksi kuutio, säännöllinen tetraedri ja oktaedri.
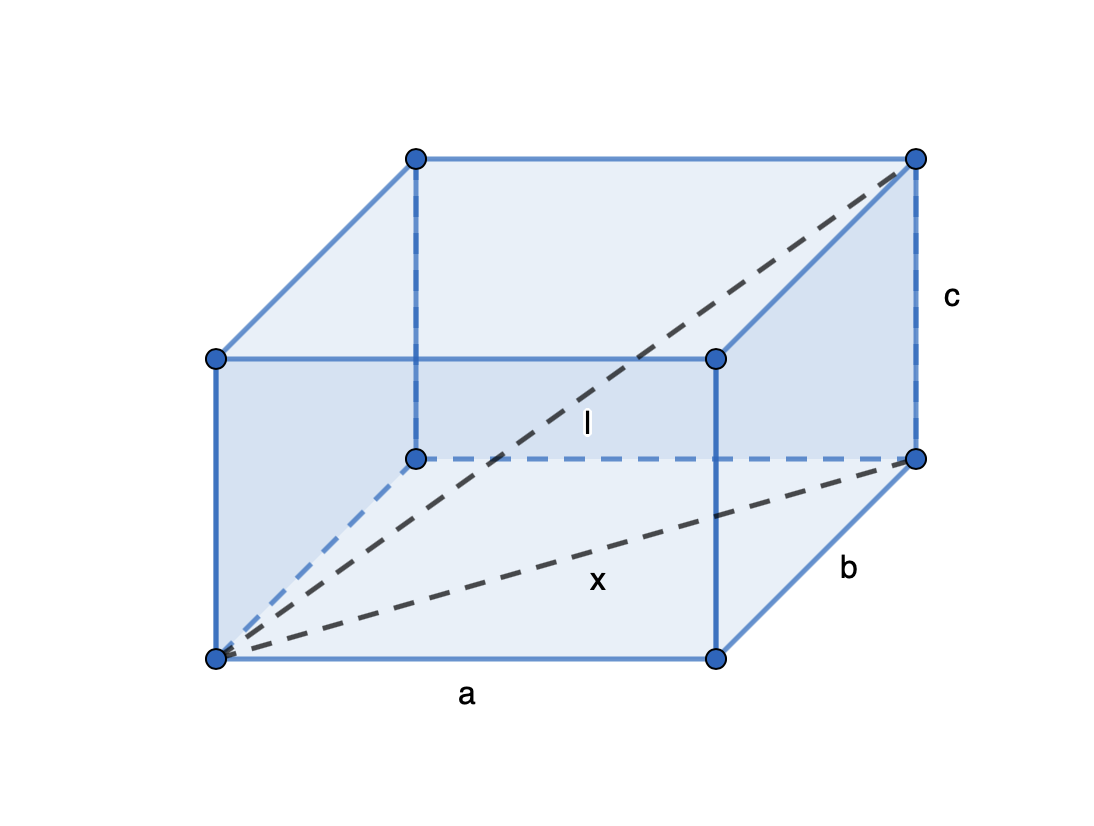
Sovelletaan kaksi kertaa Pythagoraan lausetta: avaruuslävistäjälle \(l\) ja pohjan lävistäjälle \(x\). Näin saadaan
\(x^2=a^2 +b^2\) ja \(l^2=x^2+c^2\),
ja sijoittamalla \(x^2\) yhtälö oikeanpuoleiseen yhtälöön saadaan voidaan ratkaista avaruuslävistäjä \(l\)
\(l=\sqrt{a^2+b^2+c^2}\).
Suorakulmaisen särmiön pohja on suorakulmio, jonka mitat ovat 20 cm ja 35 cm. Särmiön korkeus on 18 cm. Laske särmiön
- pohjan lävistäjän pituus
- avaruuslävistäjän pituus
- pohjan lävistäjän ja avaruuslävistäjän välinen kulma
Ratkaisu:
Merkitään pohjan lävistäjää kirjaimella x, ja ratkaistaan se Pythagoraan lauseella.
\[\begin{align} x^2 &={(20\text{ cm})}^2+{(35\text{ cm})}^2& \quad &| \sqrt{\text{ }} \\ x &=\sqrt{{(20\text{ cm})}^2+{(35\text{ cm})}^2}& \quad &| \text{ sievennetään} \\ x &= \pm 40,311... \text{ cm}& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ x &≈ \pm 40 \text{ cm}. \\ \end{align}\]
Koska \(x>0\), niin pohjan lävitäjän pituus on 40 cm.
Merkitään avaruuslävistäjää kirjaimella \(l\), ja ratkaistaan se Pythagoraan lauseella seuraavasti
\[\begin{align} l^2 &={(20\text{ cm})}^2+{(35\text{ cm})}^2+{(18\text{ cm})}^2& \quad &| \sqrt{\text{ }} \\ l &=\sqrt{{(20\text{ cm})}^2+{(35\text{ cm})}^2+{(18\text{ cm})}^2}& \quad &| \text{ sievennetään} \\ &=44,147...\text{ cm}& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈44\text{ cm}. \\ \end{align}\]
Avaruuslävistäjän pituus on siis 44 cm.
Merkitään pohjan lävistäjän ja avaruuslävistäjän välistä kulmaa kirjaimella \(\alpha\). Ratkaistaan kulma tangentin avulla.
\[\begin{align} \tan{\alpha} &=\frac{18\text{ cm}}{40.311...\text{ cm}}& \quad &| \text{ sievennetään ja otetaan} \tan^{-1}() \\ {\alpha} &= 24,062... °& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ {\alpha} &≈ 24 ° \end{align}\]
4.2 Pallo
Pallon pinta-ala ja tilavuus
Pallon muodostavat ne pisteet, jotka ovat säteen \(r\) etäisyydellä pallon keskipisteestä. Pallon pinta-ala ja tilavuus lasketaan sen säteen \(r\) avulla \[A=4 \pi r^2\] ja \[V=\frac{4\pi r^3}{3}.\]
Jalkapallon ympärysmitta on 68 cm.
- Laske jalkapallon pinta-ala yksikössä \(\text{dm}^2\).
- Laske jalkapallon tilavuus litroina.
Ratkaisu
Pallon säde voidaan selvittää ympärysmitan \(2\pi r\) avulla. Ympärysmitan kaavassa r on pallon säde.
\[\begin{align} 2\pi r& = 68& \quad &| :2\pi \\ r &= \frac{68}{2\pi}& \quad &| \text{ sievennetään} \\ r &= 10,8225... (\text{cm}) \\ \end{align}\] Nyt voidaan laskea pallon pinta-ala.
\[\begin{align} A &=4 \pi r^2& \quad &| \text{ sijoitetaan säde }r \\ &= 4 \cdot \pi \cdot (10,8225... \text{ cm})^2& \quad &| \text{ sievennetään} \\ &=1471,8550... \text{ cm}^2& \quad &| \text{ muunnetaan yksikköön dm}^2 \\ &=14,718550... \text{ dm}^2& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈ 15 \text{ dm}^2 \\ \end{align}\]
Jalkapallon pinta-ala on \(15 \text{ dm}^2\).
Lasketaan pallon tilavuus.
\[\begin{align} V &= \frac{4}{3} \pi r^3& \quad &| \text{ sijoitetaan säde }r \\ &= \frac{4}{3} \cdot \pi \cdot (10,8225... \text{ cm})^3& \quad &| \text{ sievennetään} \\ &= 5309,7172...\text{ cm}^3& \quad &| \text{ muunnetaan yksikköön dm}^3 = \text{l}\\ &= 5,3097172...\text{ dm}^3& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈ 5,3 \text{ l}\\ \end{align}\]
Jalkapallon tilavuus on \(5,3\) litraa.
4.3 Lieriö
Lieriön pinta-ala ja tilavuus
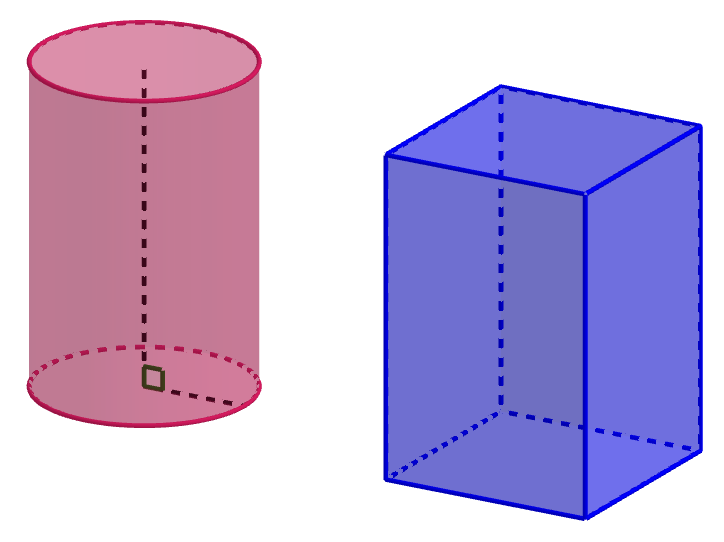
Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa, muodostuu lieriöpinta. Kun lieriöpinta leikataan kahdella tasolla, syntyy lieriö. Lieriön vaipan pinta-ala saadaan laskettua sen pohjan piirin \(p\) ja lieriön korkeuden \(h\) avulla \[A_v=ph.\] Lieriön tilavuus saadaan laskettua pohjan pinta-alan \(A_p\) ja lieriön korkeuden \(h\) avulla \[V=A_p h.\]
Erityistapaus lieriöstä on suora ympyrälieriö, jota kutsutaan myös sylinteriksi. Suoran ympyrälieriön pohja on ympyrän muotoinen ja sen korkeusjana sekä pohjan säde ovat kohtisuorassa toisiaan vastaan. Lieriö, jonka pohja on muodoltaan monikulmio, on särmiö. Erikoistapaus särmiöstä on esimerkiksi suorakulmainen särmiö.
Laske suoran lieriön kokonaispinta-ala, kun sen
- korkeus on 23 cm ja pohjaympyrän halkaisija on 11 cm.
- korkeus on 55 cm ja pohja on neliö, jonka sivun pituus on 16 cm.
Ratkaisu
Ratkaistaan pohjan säde \(r\) jakamalla halkaisija kahdella.
\(r= \frac{11 \text{ cm}}{2}=5,5 \text{ cm}\)
Koska pohja on ympyrä, sen pinta-ala on
\(A_{pohja}=\pi r^2=\pi \cdot (5,5 \text{ cm})^2=95,0331... \text{ cm}^2\)
Lieriön vaippa on suorakulmio, jonka pinta-ala saadaan laskettua pohjaympyrän ympärysmitan ja lieriön korkeuden tulona.
\[\begin{align} A_{vaippa} &=2 \pi r \cdot h& \quad &| \text{ sijoitetaan säde }r \text{ ja korkeus }h \\ &= 2 \pi \cdot 5,5 \text{ cm} \cdot 23 \text{ cm}& \quad &| \text{ sievennetään} \\ &= 794,8229... \text{ cm}^2\\ \end{align}\]
Kokonaispinta-ala on
\[\begin{align} A_{lieriö} &=2 \cdot A_{pohja} + A_{vaippa}& \quad &| \text{ sijoitetaan }A_{pohja} \text{ ja }A_{vaippa} \\ &= 2 \cdot 95,0331... \text{ cm}^2 \\ &+ 794,8229... \text{ cm}^2& \quad &| \text{ sievennetään} \\ &= 984,8891... \text{ cm}^2& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ &≈ 980 \text{ cm}^2. \\ \end{align}\]
Pohja on neliö, joten \(A_{pohja}=(16 \text{ cm})^2=256 \text{ cm}^2\)
Lasketaan vaipan pinta-alan laskemista varten pohjan ympärysmitta eli suorakulmion piiri \(p\).
\(p=4 \cdot 16 \text{ cm}= 64 \text{ cm}\)
Koska vaippa on suorakulmio, jonka korkeus on \(h=55\) cm ja kannan pituus pohjan piiri eli \(p=64\) cm.
\(A_{vaippa}=ph= 64 \text{ cm} \cdot 55 \text{ cm}=3520 \text{ cm}^2\)
Kokonaispinta-ala on
\[\begin{align} A_{lieriö} &= 2 \cdot A_{pohja}+ A_{vaippa}& \quad &| \text{ sijoitetaan }A_{pohja} \text{ ja }A_{vaippa} \\ &= 2 \cdot 256 \text{ cm}^2 + 3520 \text{ cm}^2& \quad &| \text{ sievennetään} \\ &=4032 \text{ cm}^2& \quad &| \text{ muunnetaan yksikköön dm}^2 \\ &=40,32 \text{ dm}^2& \quad &| \text{ pyöristetään yhden desimaalin tarkkuuteen} \\ &≈ 40,3 \text{ dm}^2.\\ \end{align}\]
4.4 Kartio
Kartion tilavuus
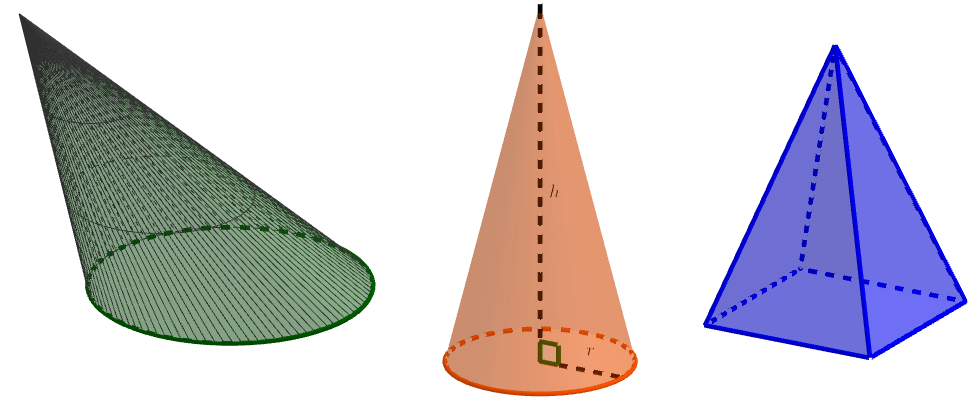
Jos suora kulkee pitkin itseään leikkaamatonta umpinaista suoraa ja lisäksi suora kulkee koko ajan saman pisteen kautta, syntyy kartiopinta. Kun kartiopinta leikataan tasolla, syntyy kartio. Kartion tilavuus lasketaan sen pohjan pinta-alan \(A_p\) ja korkeuden \(h\) avulla \[V = \frac{A_p h}{3}.\]
Erikoistapauksia kartiosta ovat ympyräkartio ja pyramidi eli särmäkartio. Ympyräkartion pohjana on ympyrä ja särmäkartion pohjana on monikulmio. Jos ympyräkartion kokeusjana on kohtisuorassa pohjaympyrän sädettä vastaan, kyseessä on suora ympyräkartio.
Laske suoran pyramidin kokonaispinta-ala ja tilavuus, kun pyramidin pohja on tasasivuinen kolmio, jonka piiri on 33,0 cm. Pyramidin vaippa koostuu tasakylkisistä kolmioista, joiden korkeus on 30,0 cm. Kartion korkeus on 18 cm. Ilmoita tilavuus desilitroina.
Ratkaisu
Koska pyramidin pohjana on tasasivuinen kolmio, pyramidin vaipan muodostaa kolme yhtä suurta tasakylkistä kolmiota. Vaipan pinta-ala on siis kolmen kolmion pinta-alojen summa.
Selvitetään ensin pohjakolmion sivun pituus, kun tiedetään sivujen pituuksien summa eli piiri. Sivun pituus pohjakolmiossa on siis \(\frac{33,0 \text{ cm}}{3}=11,0 \text{ cm}\)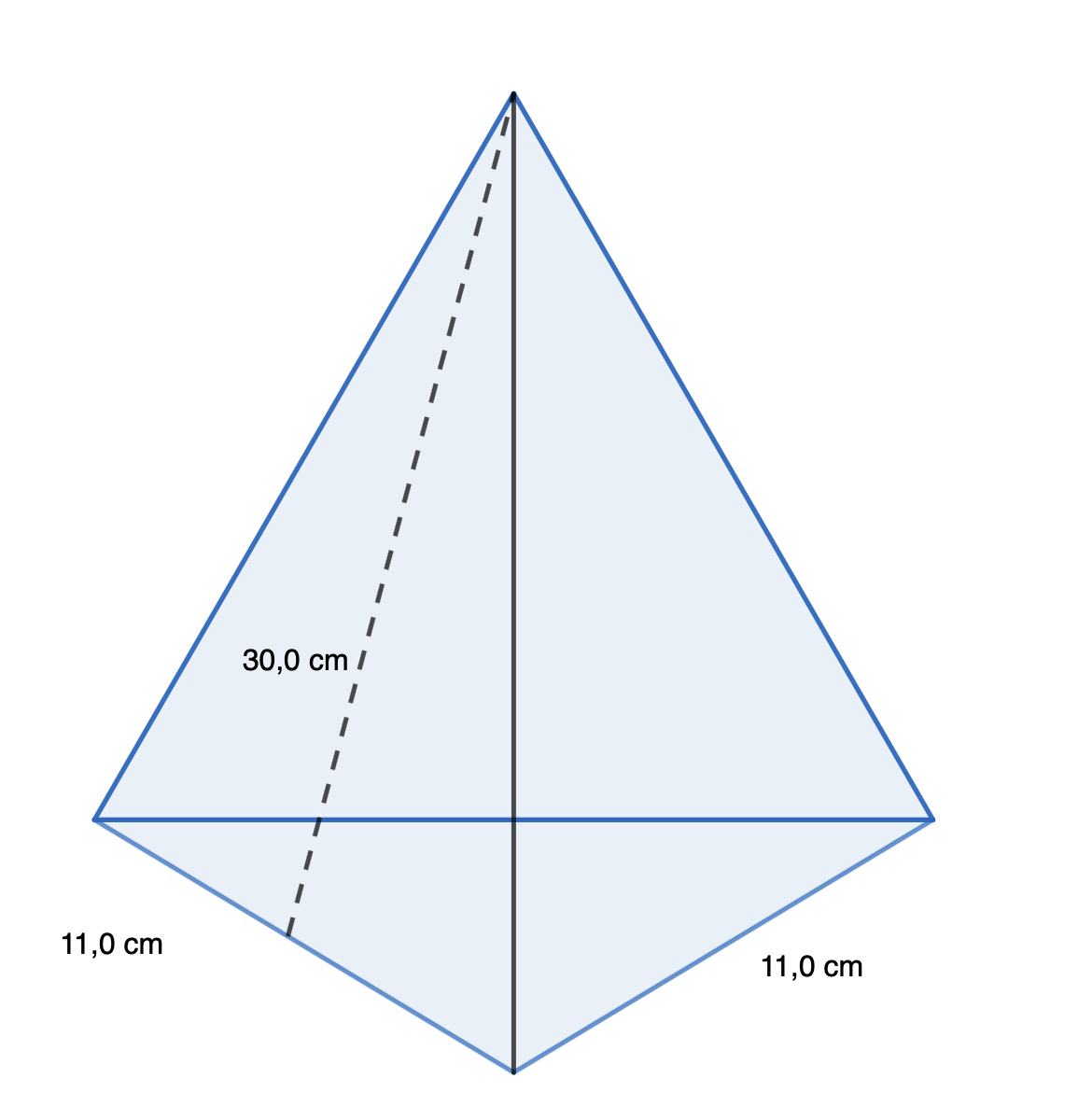 
Nyt voidaan siis laskea vaipan pinta-ala
\(A_{vaippa}= 3 \cdot \frac{1}{2} \cdot 11,0 \text{ cm} \cdot 30,0 \text{ cm} = 495 \text{ cm}^2\).
Jotta pohjan pinta-ala voitaisiin laskea, tulee laskea ensin pohjan korkeus x Pythagoraan lauseella.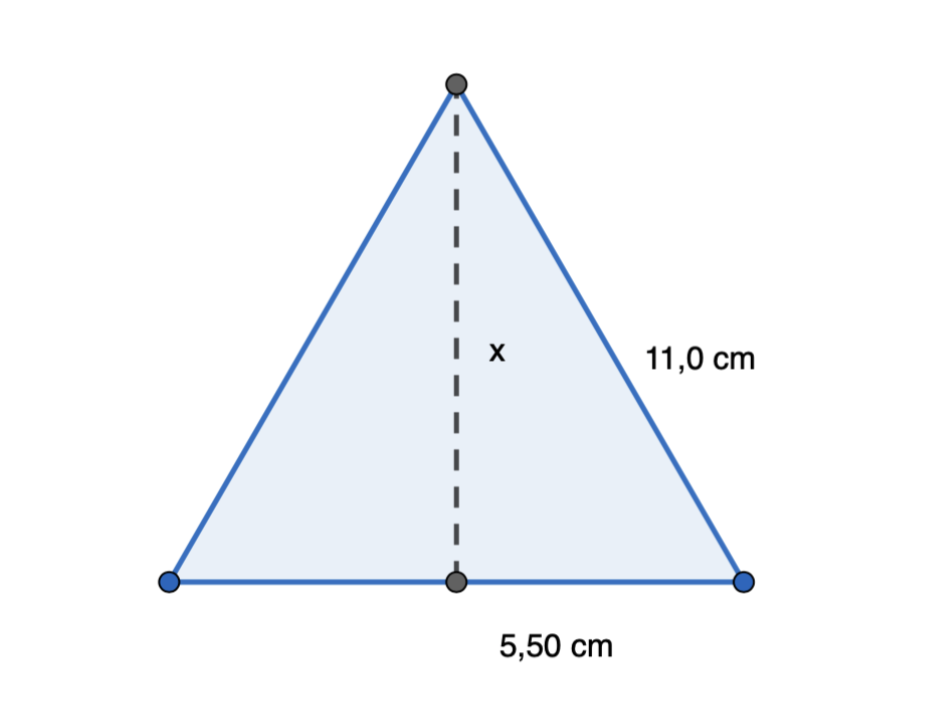 
\[\begin{align} x^2 + (5,50 \text{ cm})^2 &= (11,0 \text{ cm})^2& \quad &| -(5,50 \text{ cm})^2 \\ x^2 &= (11,0 \text{ cm})^2- (5,50 \text{ cm})^2& \quad &| \sqrt{\text{ }} \\ x &= \sqrt{(11,0 \text{ cm})^2- (5,50 \text{ cm})^2}& \quad &| \text{ sievennetään} \\ x &= 9.5262... \text{ cm} \\ \end{align}\]
Nyt voidaan laskea pohjan pinta-ala
\(A_{pohja}= \frac{1}{2} \cdot 11 \text{ cm} \cdot 9.5262... \text{ cm}= 52,3945... \text{ cm}^2\).
Kartion kokonaispinta-ala on siis
\[\begin{align} A_{kartio}&= A_{vaippa} + A_{pohja}& \quad &| \text{ sijoitetaan }A_{vaippa}\text{ ja }A_{pohja} \\ &= 495 \text{ cm}^2 + 52,3945... \text{ cm}^2& \quad &| \text{ sievennetään} \\ &= 547,3945... \text{ cm}^2& \quad &| \text{ pyöristetään kymmenten tarkkuuteen} \\ &≈ 550 \text{ cm}^2 \\ \end{align}\]
ja tilavuus on
\[\begin{align} V_{kartio} &= \frac{A_{pohja} \cdot h}{3}& \quad &| \text{ sijoitetaan }A_{pohja} \\ &= \pm \frac{52,3945... \text{ cm}^2 \cdot 18 \text{ cm}}{3}& \quad &| \text{ sievennetään} \\ &= \pm 314.367... \text{ cm}^3& \quad &| \text{ muunnetaan yksikköön dm}^3 \\ &= \pm 0,314367... \text{ dm}^3& \quad &| \text{ muunnetaan yksikköön dl} \\ &= \pm 3,14367... \text{ dl}& \quad &| \text{ ja pyöristetään kahden desimaalin tarkkuuteen} \\ &≈ \pm 3,10 \text{ dl} \\. \end{align}\]
Koska tilavuus on positiivinen arvo, \(V= 3,1\) dl.
Pyramidin kokonaispinta-ala on \(550 \text{ cm}^2\) ja tilavuus \(3,1 \text{ dl}\).
Suoran ympyräkartion vaipan pinta-ala on \(16,8 \text{ dm}^2\) ja pohjan säde 20,1 cm. Laske kartion korkeus.
Ratkaisu
Piirretään mallikuva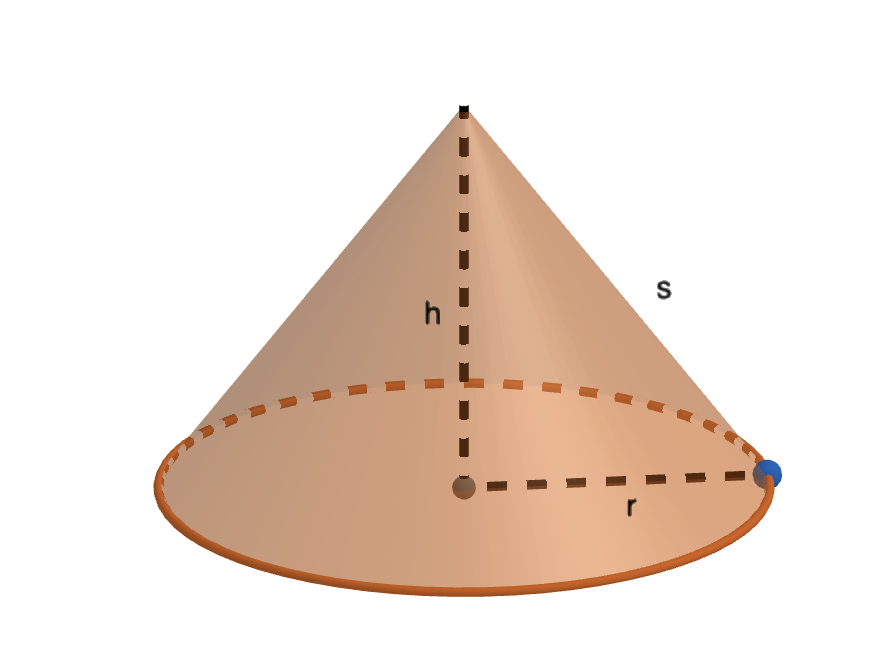 
Mitoista muodostuu suorakulmainen kolmio.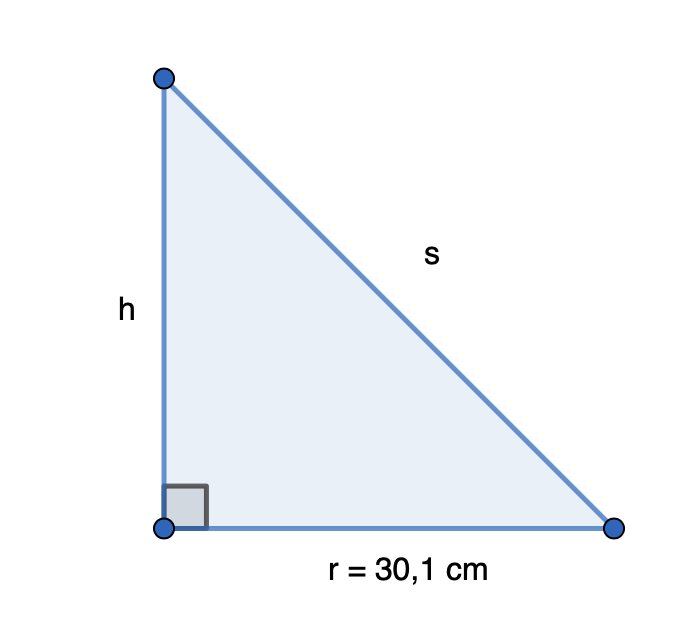 
Lasketaan ensin kartion sivujanan \(s\) pituus vaipan pinta-alan avulla.
\[\begin{align} \pi r s &= A_{vaippa}& \quad &| :\pi r \\ s &= \frac{A_{vaippa}}{\pi r}& \quad &| \text{ sijoitetaan }A_{vaippa}\text{ ja }r \\ s &= \frac{16,8 \text{ dm}^2}{\pi \cdot 2,01 \text{ dm}}& \quad &| \text{ sievennetään} \\ s &= 2,6605... \text{ dm} \\ \end{align}\]
Kartion korkeus saadaan Pythagoraan lauseella.
\[\begin{align} h^2 + (2,01 \text{ dm})^2 &= (2,6605... \text{ dm})^2& \quad &| -(2,01 \text{ dm})^2 \text{ ja }\sqrt{\text{ }} \\ h &= \pm{\sqrt{(2,6605... \text{ dm})^2 - (2,01 \text{ dm})^2}}& \quad &| \text{ sievennetään} \\ h &= \pm 1,7430... \text{ dm}& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ h &≈ \pm 1,74 \text{ dm}\\ \end{align}\]
Koska \(h > 0\), niin \(h = 1,74 \text{ dm}\).
4.5 Maapallo
Planeettamme Maa on likimain pallon muotoinen. Maapallo on jaettu leveys- ja pituuspiireihin, ja esimerkiksi pallon puolesta välistä kulkeva leveyspiiri on nimeltään päiväntasaaja. Pallon pohjoisnavalta etelänavalle kulkeva pituuspiiri, joka kulkee myös Lontoon läpi, on nimeltään nollameridiaani.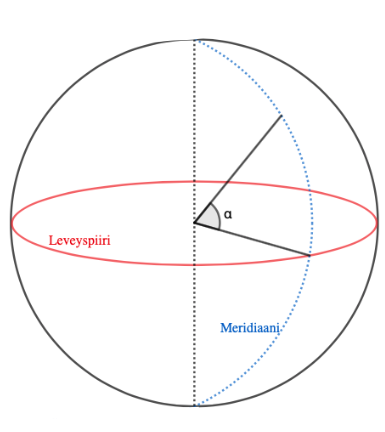 
Leveys- ja pituuspiirien avulla voidaan ilmoittaa koordinaatein esimerkiksi jonkin kaupungin sijainti maapallolla. Esimerkiksi Helsingin sijainti on \(60°N, 25°E\), eli \(60°\) pohjoista leveyttä (eli \(60°\) päiväntasaajalta kohti pohjoisnapaa) sekä \(25°\) itäistä pituutta (eli \(25°\) nollameridiaanista itään).
Tarkastele GeoGebra-appletilla leveys- ja pituuspiirejä raahaamalla pistettä \(P\)!
Leveyspiirit
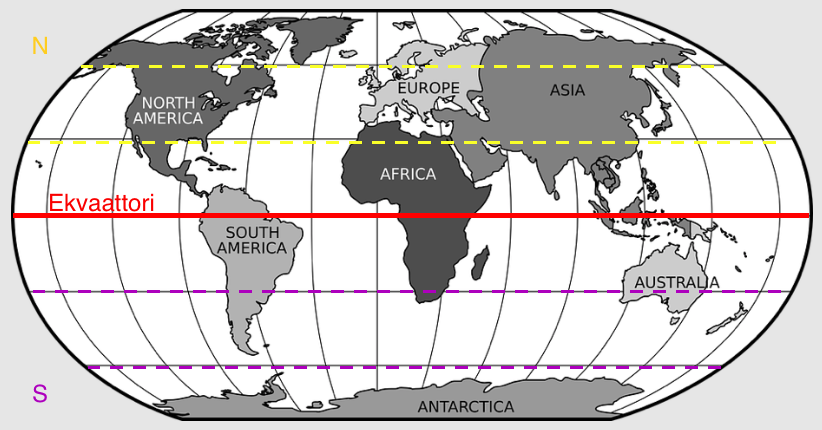
Leveyspiirit jakavat maapallon itä-länsisuunnassa, eli leveyden suhteen. Leveyspiirit ovat ympyröitä, jotka eivät leikkaa toisiaan.
Pisin leveyspiiri jakaa maapallon kahteen yhtä suureen osaan ja tämä leveyspiiri on nimeltään päiväntasaaja eli ekvaattori.
Leveyspiirit voidaan jakaa pohjoisiin ja eteläisiin leveyspiireihin riippuen siitä, kummalla puolella päiväntasaajaa leveyspiirit sijaitsevat: päiväntasaajan eteläpuolella on eteläiset leveyspiirit.
Leveyspiirien kulmat ilmoitetaan astelukuina välillä \(0°-90°\).
Pituuspiirit
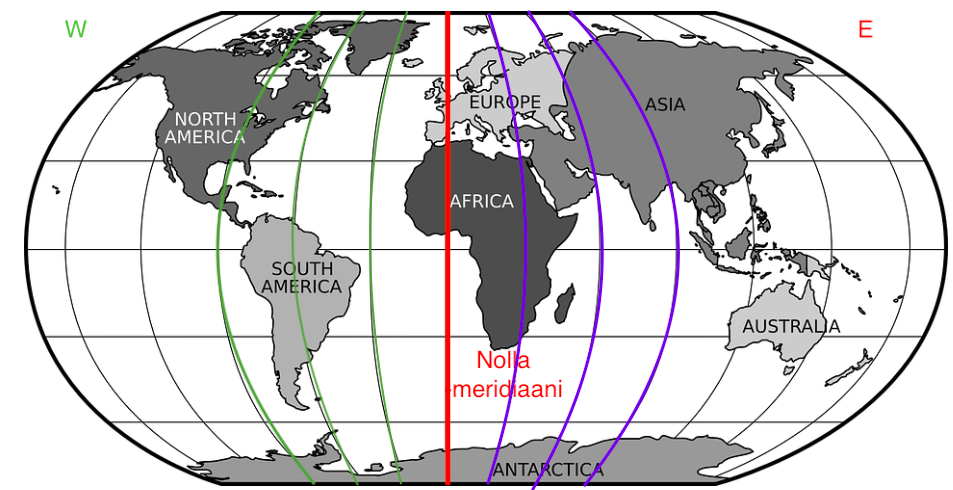
- Pituuspiirit kulkevat pohjoisnavalta etelänavalle ja jakavat maapallon osiin pituuden suhteen.
- Lontoon Greenwichin observatorion kautta kulkeva meridiaani on nimeltään nollameridiaani (0°).
- Pituuspiirit voidaan jakaa läntisiin ja itäisiin pituuspiireihin riippuen siitä, kummalla puolella pituuspiiri on nollameridiaaniin nähden.
- Pituuspiirien kulmat ilmoitetaan välillä \(0°-180°\).
Tampere ja Anchorage (USA, Alaska) sijaitsevat kutakuinkin samalla leveyspiirillä 61° pohjoista leveyttä. Laske Tampereen ja Anchoragen välinen etäisyys leveyspiiriä pitkin mitattuna, kun Anchoragen pituuspiiri on 149,85° ja Tampereen pituuspiiri on 23,78°. Maan säde on 6370 km.
Ratkaisu
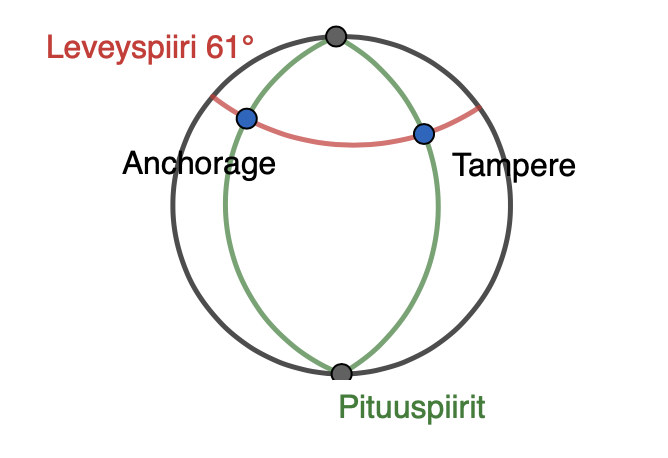
Kysytty etäisyys on leveyspiiriä pitkin kulkevan ympyrän kaaren pituus. Jotaa kaaren pituus saataisiin selville, tulee selvittää kaarta vastaava keskuskulma ja leveyspiiriä kuvaavan ympyrän säde.
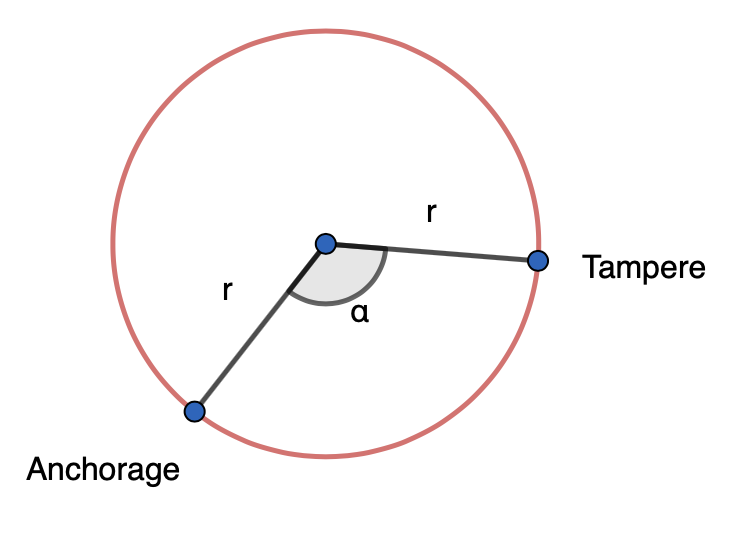Keskuskulma saadaan laskettua pituuspiirien avulla
\(\alpha=149,85°-23,78°=126,07°\)
Piirretään seuraavaksi poikkileikkaus maapallosta pystysuunnassa.
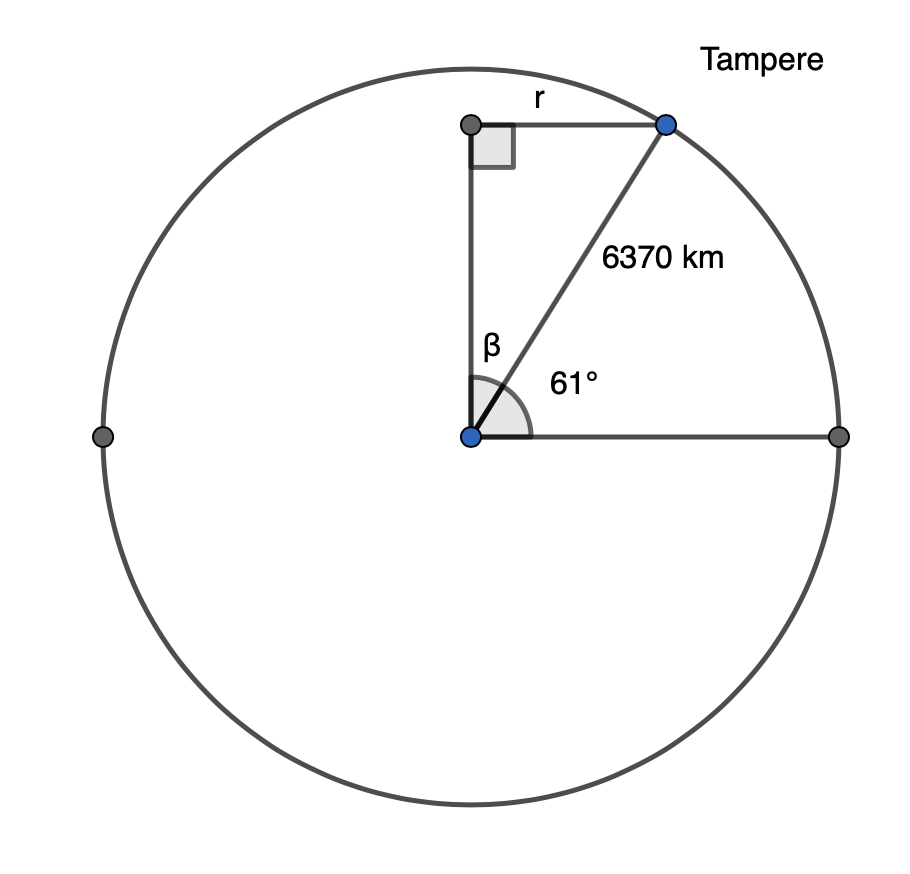
Kulma \(\beta\) saadaan leveyspiirin avulla \(\beta=90°-61°=29°\).
Leveyspiirin säde r saadaan ratkaistua poikkileikkausympyrään muodostuvan suorakulmaisen kolmion avulla käyttäen siniä.
\[\begin{align} \sin{29°} &= \frac{r}{6370}& \quad &| \cdot 6370 \\ r &= \sin{29°} \cdot 6370& \quad &| \text{ sievennetään} \\ r &= 3088,2372... \text{ (km)} \end{align}\]
Lasketaan Tampereen ja Anchoragen välistä matkaa kuvaavan kaaren pituus \(b\).
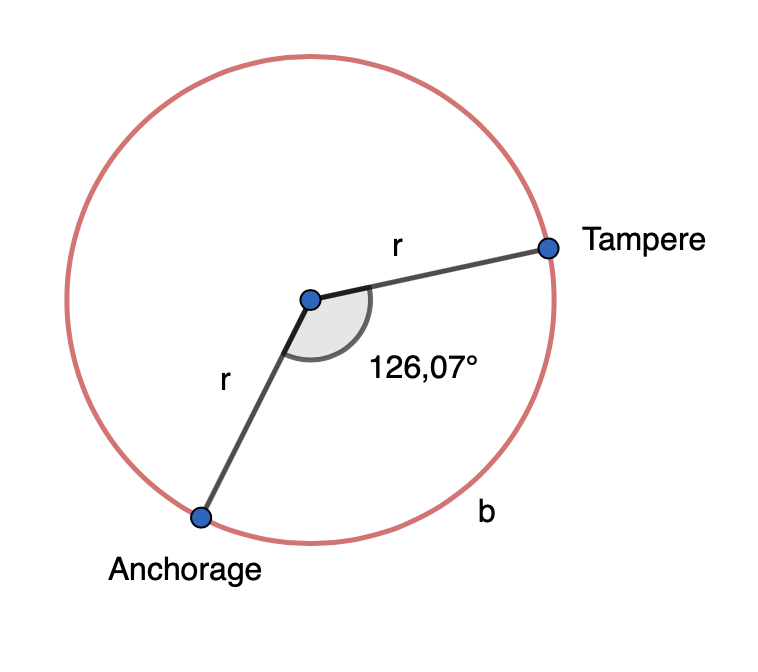
\[\begin{align} b &=\frac{\alpha}{360°}\cdot 2 \pi r& \quad &| \text{ sijoitetaan arvot} \\ b &=\frac{126,07°}{360°}\cdot 2 \pi \cdot 6370 \cdot\sin{29°}& \quad &| \text{ sievennetään} \\ b &= 6795,1614... \text{ km}& \quad &| \text{ pyöristetään satojen tarkkuuteen} \\ b &≈ 6800 \text{ km} \\ \end{align}\]
Tampereen ja Anchoragen etäisyys leveyspiiriä pitkin mitattuna on 6800 km.
4.6 Avaruuskappaleita koordinaatistossa
Luvussa Monikulmioita koordinaatistossa esiteltiin \(xy\)-koordinaatisto. Kyseiseen koordinaatistoon piirretyt kuviot ovat kaksiulotteisia.
Avaruuskappaleet ovat kolmiulotteisia, joten \(xy\)-koordinaatistoon pitää tehdä pieniä lisäyksiä.
\(xyz\)-koordinaatisto
\(xyz\)-koordinaatisto poikkeaa \(xy\)-koordinaatistosta siten, että akseleita on kahden sijaan kolme.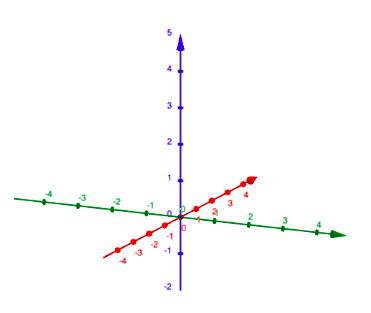 
Samoin kuin \(xy\)-koordinaatistossakin, pisteiden välinen etäisyys voidaan myös määrittää kolmiulotteisessa koordinaatistossa.
Pisteiden välinen etäisyys \(xyz\)-koordinaatistossa
Olkoon koordinaatistossa kaksi pistettä \(A\) ja \(B\), joiden koordinaatit ovat \((x_1,y_1,z_1)\) ja \((x_2,y_2,z_2)\). Nyt näiden pisteiden välinen etäisyys (eli janan pituus) on \[\begin{align*} |AB|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} \end{align*}\]
Vastaavalla tavalla laskukaavaa keskipisteen koordinaateille voidaan muuntaa sopivaksi \(xyz\)-koordinaatistoon.
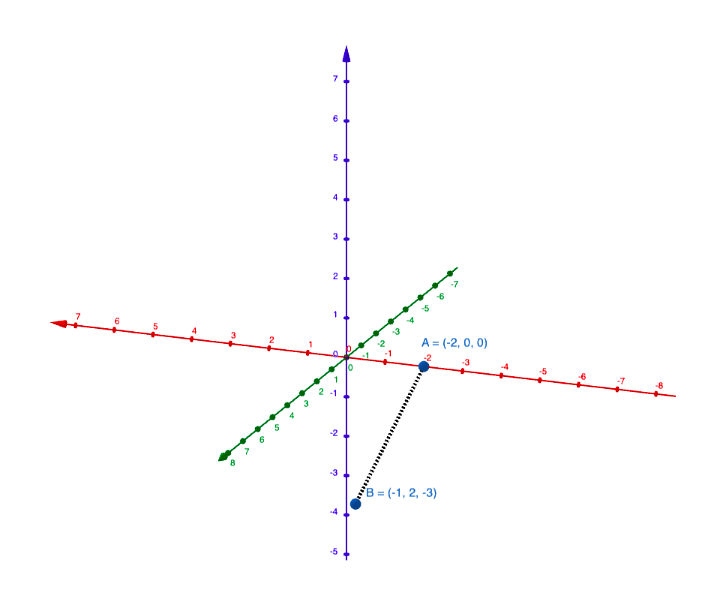
GeoGebralla voidaan piirtää siistejä avaruuskappaleita. Harjoittele erilaisten avaruuskappaleiden piirtämistä GeoGebralla tai omalla laskimellasi.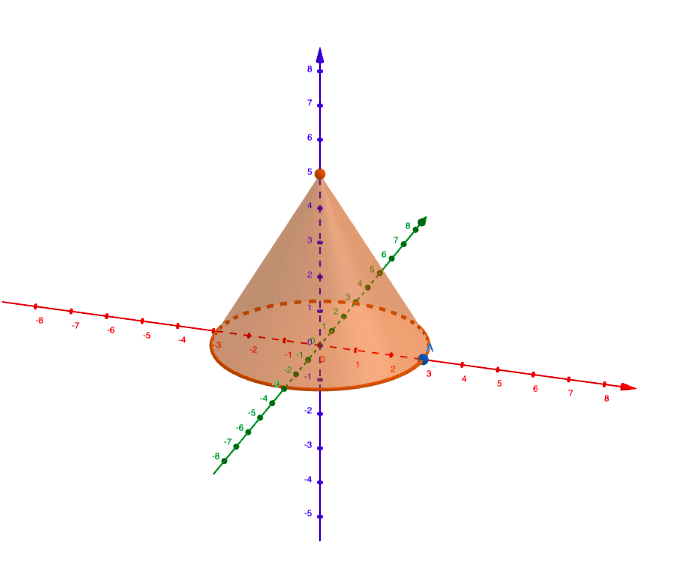 
Avaa alla oleva GeoGebra-appletti ja tutustu 
-ikonin takana oleviin 3D-työkaluihin.
Laske tetraedrin pisteiden A ja D välinen etäisyys.
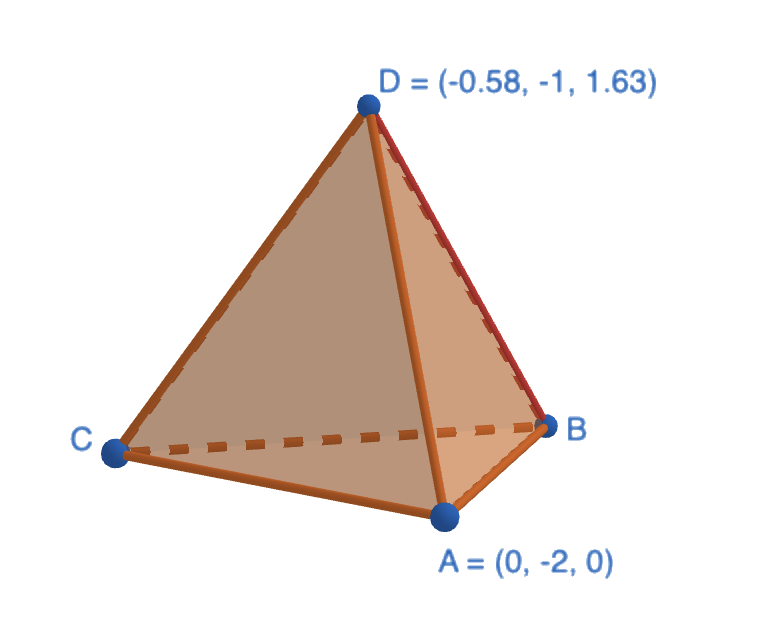
Ratkaisu
Lasketaan janan \(|AD|\) pituus, kun \(A=(0,-2,0)\) ja \(D=(-0,58;-1;-1,63)\).
\[\begin{align} |AD| &= \sqrt{(x_D-x_A)^2+(y_D-y_A)^2+(z_D-z_A)^2}& \quad &| \text{ sijoitetaan arvot} \\ |AD| &= \sqrt{(-0,58-0)^2+(-1-(-2))^2+(1,63-0)^2}& \quad &| \text{ sievennetään} \\ |AD| &= 1,9983...& \quad &| \text{ pyöristetään ykkösten tarkkuuteen} \\ |AD| &≈ 2 \\ \end{align}\]
Pisteiden A ja D välinen etäisyys on 2.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.