2. Potenssi ja juuri

Tässä kappaleessa laajennetaan neliöjuuren käsite yleisempään nteen juureen. Lisäksi, aiemmin potenssi ja neliöjuuri käytiin yhtälöopillisesti, mutta nyt tarkoitus on tutkia myös näihin liittyviä funktioita. Potenssin ja neliöjuuren voit tarvittaessa kerrata täältä. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

2.1 Potenssifunktio ja -yhtälö

Luvun :s potenssi a^n on merkintä tulolle $a\cdot a\cdot ... \cdot a,$ jossa on tekijää ( n=2,3,... ). Erityisesti on sovittu, että a^1=a . Luku on potenssin kantaluku ja potenssin eksponentti.

Potenssifunktio

Potenssifunktioksi sanotaan funktiota, jonka määrittelevä lauseke on potenssi ja kantalukuna on muuttuja . Siis potenssifunktiot ovat muotoa f(x)=x^n, missä $n\in\mathbb{N}$ .

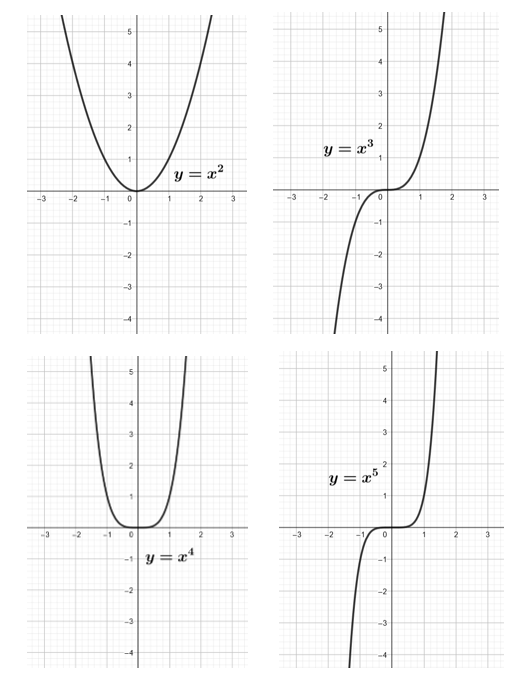
Kun on parillinen, potenssifunktion kuvaaja on ja neljänneksessä ja kun pariton niin kuvaaja on ja neljänneksessä.

Potenssiyhtälö

Potenssiyhtälö on muotoa tai voidaan saattaa muotoon

x^n=a,

missä $n\in\mathbb{N}$ ja $a\in\mathbb{R}$ .

Potenssiyhtälön ratkaisujen lukumäärä riippuu siitä, onko potenssi parillinen vai pariton.

Muistamme edelliseltä kurssilta, että jos n=2 , niin yksittäisen ratkaisun lisäksi myös sen vastaluku toteuttaa potenssiyhtälön. Esimerkiksi

$\begin{align*} x^2&=4 \\ x &= \pm \sqrt{4} \\ x &= \pm 2, \end{align*}$ sillä 2^2=4 tai (-2)^2=4 .

Jos n=3 , niin ratkaisuja on täsmälleen yksi. Esimerkiksi

$\begin{align*} x^3&=8 \\ x &= \sqrt[3]{8} \\ x &= 2, \end{align*}$ sillä 2^3=8 . Parittoman potenssin tapauksessa vastaluku ei ole ratkaisu, sillä pariton potenssi säilyttää merkkinsä. Nyt siis x=-2 ei ole ratkaisu, sillä (-2)^3=-8 .

Vastaavanlainen ideologia yleistyy myös korkeamman asteen potenssiyhtälöille: Jos on pariton positiivinen kokonaisluku, niin ratkaisuja on vain yksi johtuen merkin säilymisestä. Jos on parillinen positiivinen kokonaisluku, niin myös ratkaisun vastaluku kuuluu ratkaisujoukkoon, sillä x^n=(-x)^n .

Potenssiyhtälön ratkaisut

Kun on parillinen positiivinen kokonaisluku ja $a\geq 0$ , niin yhtälön x^n=a ratkaisut ovat

$x=\pm\sqrt[n]{a}.$

Kun on pariton positiivinen kokonaisluku ja $a \in \mathbb{R}$ , niin yhtälön x^n=a ratkaisu on

$x=\sqrt[n]{a}.$

2.1.1 Esimerkki: kuutioyhtälön ratkaiseminen graafisesti

Ratkaise funktion f(x)=x^3 kuvaajan perusteella yhtälö

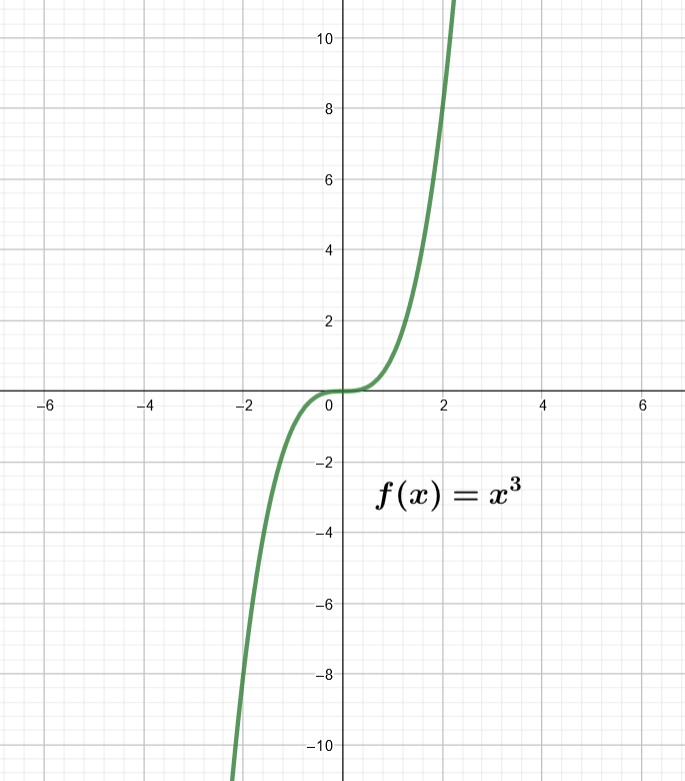
Ratkaisu:

Positiivisen kantaluvun pariton potenssi on aina positiivinen luku ja vastaavasti negatiivisen kantaluvun pariton potenssi on aina negatiivinen luku. Näin ollen yhtälön ratkaisun eli kantaluvun täytyy olla positiivinen luku, minkä kuutio saa arvon . Kuvaajan perusteella , kun , joten on yhtälön ratkaisu.

Ratkaisun voi vielä tarkistaa sijoittamalla x=2 yhtälöön x^3=8 .

$\begin{align*} 2^3&=8 \\ 8 &= 8 \\ \end{align*}$

Tiedetään, että jos luvun kuutio on negatiivinen luku, niin myös luvun täytyy olla negatiivinen luku. Näin ollen yhtälön ratkaisun täytyy olla akselin negatiivisella puolella. Kuvaajasta huomataan, että , kun . Näin ollen on yhtälön ratkaisu.

Tämän voisi myös päätellä a)-kohdan perusteella, sillä x^3 on symmetrinen origon suhteen, jolloin jos funktiolla on piste (2,8) , niin sillä on myös origon suhteen symmetrinen piste -(2,8)=(-2,-8) .

Tarkistetaan ratkaisu vielä sijoittamalla x=-2 yhtälöön x^3=-8 .

$\begin{align*} (-2)^3&=-8 \\ -8 &= -8 \\ \end{align*}$

Vastaus:

2.1.2 Esimerkki: :s juuri laskimella

Laske laskimella ja tarkista

luvun neljäs juuri
luvun kuudes juuri
luvun $-\dfrac{1}{279936}$ seitsemäs juuri
luvun kahdestoista juuri
luvun $-\pi$ kolmastoista juuri.

Ratkaisu:

Geogebran CAS-laskimesta löytyy :s juuri klikkaamalla ensin vasemmasta alakulmasta auki valikon ja sieltä kuvan osoittamista symboleista.

Luvun neljäs juuri merkitään $\sqrt[4]{81}$ ja laskimella saadaan

$\sqrt[4]{81}=3.$

Tuloksen voi vielä tarkistaa laskemalla luvun neljännen potenssin: 3^4=81

Negatiivisen luvun :s juurta ei ole määritelty (reaaliluvuilla), kun on parillinen, johtuen siitä, että luvun parillinen potenssi on aina ei-negatiivinen luku. Näin ollen, jos CAS-laskimeen syöttää $\sqrt[6]{-729},$ niin saa kompleksiluvun $3\sqrt[6]{-1}=3i$ . Tavanomaisella funktiolaskimella tyypillisin ilmoitus lienee "undefined".
Luvun $-\dfrac{1}{279936}$ seitsemäs juuri merkitään $\sqrt[7]{-\dfrac{1}{279936}}$ ja laskimesta saadaan

$\sqrt[7]{-\dfrac{1}{279936}}=-\dfrac{1}{6}.$

Luvun kahdestoista juuri ei ole määritelty reaaliluvuilla samoin perustein kuin b)-kohdassakin.
Luvun $-\pi$ kolmastoista juuri merkitään $\sqrt[13]{-\pi}$ ja laskimesta saadaan:

$\sqrt[13]{-\pi}\approx -1,09.$

Vastaus:

$\sqrt[4]{81}=3$
$\sqrt[6]{-729}$ ei ole määritelty reaalikualueella.
$\sqrt[7]{-\dfrac{1}{279936}}=-\dfrac{1}{6}$
Luvun kahdestoista juuri ei ole määritelty reaalilukualueella.
$\sqrt[13]{-\pi}\approx -1,09$

2.1.3 Esimerkki: potenssiyhtälön ratkaiseminen algebrallisesti

Ratkaise potenssiyhtälöt.

$11x^8-\pi=\dfrac{1}{2}$ .

Ratkaisu:

Yhtälöllä on täsmälleen yksi ratkaisu, sillä on pariton.

$\begin{align*} x^5 &= 32 && |\sqrt[5]{}\\ x &= \sqrt[5]{32} \\ x &= 2 \end{align*}$

Yhtälöllä on kaksi ratkaisua, luvun kuudes juuri ja sen vastaluku, sillä on parillinen.

$\begin{align*} x^6 &= 4096 && |\sqrt[6]{}\\ x &=\pm\sqrt[6]{4096} \\ x &=\pm4 \end{align*}$

Yhtälöllä on täsmälleen yksi ratkaisu, sillä on pariton.

$\begin{align*} -2x^7 &= 4 && |:(-2)\\ x^7 &= -2 && |\sqrt[7]{} \\ x &= \sqrt[7]{-2} \\ x &= -\sqrt[7]{2} \end{align*}$

Muokataan potenssiyhtälö ensin muotoon Yhtälöllä on kaksi ratkaisua, sillä on parillinen.

$\begin{align*} 11x^8-\pi&=\dfrac{1}{2} &&|+\pi\\ 11x^8 &= \pi+\dfrac{1}{2} && |:11 \\ x^8 &=\dfrac{\pi+\dfrac{1}{2}}{11} \\ x^8 &= \dfrac{2\pi+1}{22} && |\sqrt[8]{} \text{ } \\ x&=\pm\sqrt[8]{\dfrac{2\pi+1}{22}} \end{align*}$

2.1.4 Esimerkki: säästötilin talletuskoron laskeminen

Annin vanhemmat tallettavat säästötilille $100\;000$ euroa. :n vuoden kuluttua talletus on kasvanut miljoonan euron suuruiseksi. Kuinka suuri on säästötilin talletuskorko prosentin kymmenysosan tarkkuudella?

Ratkaisu:

Olkoon $x=\text{''korkokerroin''}$ .

Talletuksen arvo kasvaa vuodessa -kertaiseksi, joten talletuksen arvo yhden vuoden kuluttua on

$100\;000 \;x.$

Kahden vuoden kuluttua talletus kasvaa edelleen -kertaiseksi, jolloin tilillä on

$x\cdot 100\;000 \;x=100\;000 \;x^2.$

Koska korko pysyy vakiona, niin vuoden kuluttua tilillä on

$100\;000 \;x^{40}.$

Tehtävänannossa todettiin, että tämä talletus on kasvanut miljoonan suuruiseksi, joten muodostetaan ja ratkaistaan yhtälö

$\begin{align*} 100\;000 \;x^{40} &= 1\;000\;000 && |:100\;000 \\ x^{40} &= 10 && |\sqrt[40]{} \\ x &= \pm \sqrt[40]{10} \\ x &= \pm 1,059253725 \\ x &= \pm \approx 1,059. \end{align*}$

Parillisella potenssiyhtälöllä on kaksi ratkaisua, mutta negatiivinen kerroin ei kelpaa, koska kyseessä on korko. Näin ollen säästötilin korko on $1,059-1=0,059=5,9\%.$

Vastaus: Säästötilin korko on $5,9\%$ .

Potenssifunktio ja -yhtälö: tehtäviä

2.2 Juurifunktio ja -yhtälö

Seuraavaksi laajennetaan neliö- ja kuutiojuuren käsitteet yleiseen juureen. Yleinen juuri $\sqrt[n]{a}$ eli
:s juuri :sta määritellään neliöjuuren ja kuutiojuuren tapaan. Määritelmässä pitää ottaa huomioon, onko juuren indeksi parillinen vai pariton.

Yleinen juuri

$\sqrt[n]{a}$ tarkoittaa lukua, jonka :s potenssi on .

Jos on parillinen ja $a\ge0$ , $\sqrt[n]{a}$ on ei-negatiivinen.

Nyt voidaan määritellä juurifunktio.

Juurifunktio

Juurifunktio on muotoa

$f(x)=\sqrt[n]{x},$

missä $n=2,3,4,\dots$

2.2.1 Esimerkki: juurifunktion kuvaajan tarkastelu GeoGebralla

Vaihtele juuren indeksin arvoja liukusäätimestä ja tarkkaile juurifunktion kuvaajaa eri indeksin arvoilla.

Kun on parillinen

Funktio on määritelty, kun $x\ge0$ .
Funktio on jatkuva ja kasvava ja saa kaikki positiiviset arvot ja arvon nolla.

Kun on pariton

Funktio on määritelty kaikilla reaaliluvuilla.
Funktio on jatkuva ja kasvava ja saa kaikki reaalilukuarvot.

Juuriyhtälö

Juuriyhtälö on muotoa tai voidaan saattaa muotoon

$\sqrt[n]{x}=a,$

missä $n\in\mathbb{N}$ ja $a\in\mathbb{R}$ .

Juuriyhtälön ratkaisut

Kun on parillinen positiivinen kokonaisluku ja $a\geq 0$ , niin yhtälön $\sqrt[n]{x}=a$ ratkaisu on x=a^n .

Kun on pariton positiivinen kokonaisluku ja $a \in \mathbb{R}$ , niin yhtälön $\sqrt[n]{x}=a$ ratkaisu on x=a^n .

Yhtälö $\sqrt[n]{x}=a$ on ratkeamaton, jos on parillinen ja a<0 . Muussa tapauksessa yhtälöllä on olemassa yksikäsitteinen ratkaisu . Yksikäsitteisyys on tärkeä huomata, sillä potenssiyhtälöistä poiketen, parillisella juuri yhtälöllä ei ole ratkaisun lisäksi ratkaisun vastaluku ratkaisua.

2.2.2 Esimerkki: neliöjuuriyhtälön ratkaiseminen graafisesti

Ratkaise funktion $f(x)=\sqrt{x}$ kuvaajan perusteella yhtälö

$\sqrt{x}=2$
$\sqrt{x}=3$
$\sqrt{x}=-3$ .

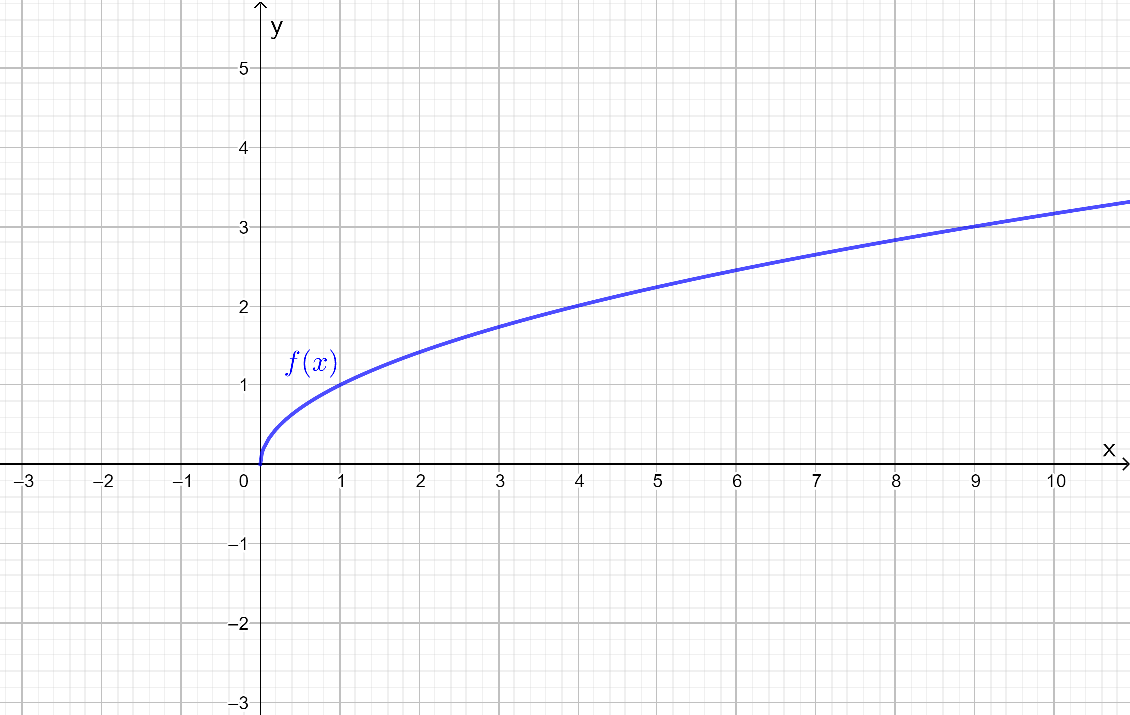
Ratkaisu:

Kun on parillinen positiivinen kokonaisluku ja $x\geq 0$ , niin luvun :s juuri $\sqrt[n]{x}$ on se ei-negatiivinen luku, jonka :s potenssi on luku . Nyt kyseessä on neliöjuuri eli , joten tiedämme, että yhtälön ratkaisun täytyy olla -akselin positiivisella puolella, sillä negatiivisen luvun neliöjuurta ei ole määritelty.

Nyt tulee etsiä kuvaajasta se luvun arvo, millä $f(x)=\sqrt[]{x}$ saa arvokseen y=2 .

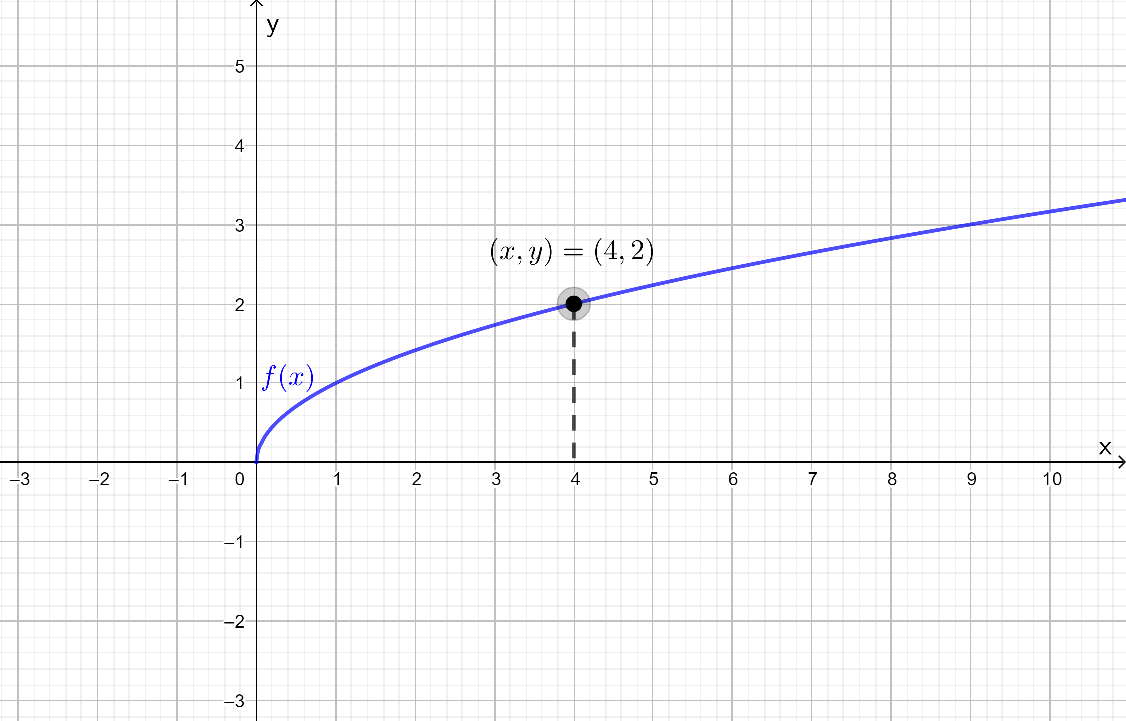
Kuvaajan perusteella $f(4)=\sqrt[]{4}=2$ . Tuloksen voi myös tarkistaa sijoittamalla alkuperäiseen yhtälöön x=4 .

$\begin{align*} \sqrt[]{4}&=2 \\ 2&=2 \\ \end{align*}$

Vastaavasti kuin a.-kohdassakin, etsitään kuvaajasta se muuttujan arvo, millä funktio $f(x)=\sqrt[]{x}$ saa arvokseen .

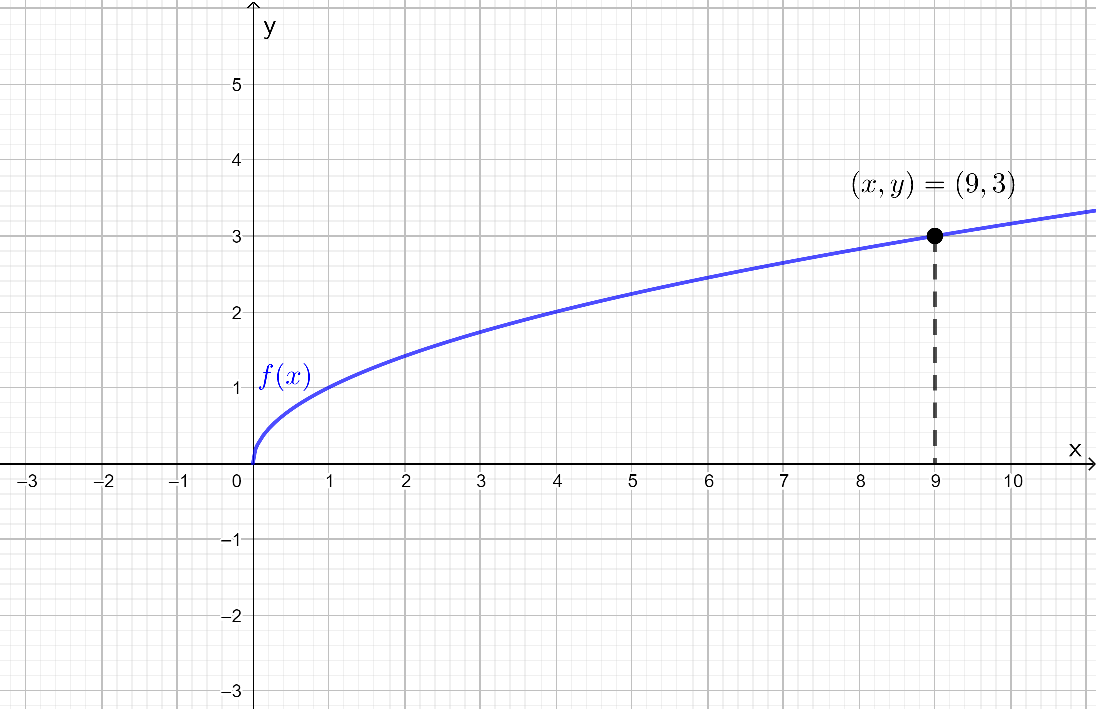
Kuvaajan perusteella $f(9)=\sqrt[]{9}=3$ . Tarkistetaan.

$\begin{align*} \sqrt[]{9}&=3 \\ 3&=3 \\ \end{align*}$

Neliöjuuren määritelmän nojalla, yhtälöllä $\sqrt{x}=-3$ ei ole ratkaisua, sillä neliöjuurifunktio saa arvokseen vain ja ainoastaan positiivisia lukuja.

Vastaus:

Yhtälöllä ei ole olemassa reaalilukuratkaisua.

2.2.3 Esimerkki: juuriyhtälön ratkaiseminen algebrallisesti

Ratkaise yhtälö.

$\sqrt[5]{x}=2$
$\sqrt[6]{x}=4$
$-2\sqrt[7]{x} = 4$
$11\sqrt[8]{x}+\pi=\dfrac{1}{2}$ .

Ratkaisu:

Yhtälöllä on olemassa ratkaisu, sillä on pariton.

$\begin{align*} \sqrt[5]{x}&=2 && |()^5\\ (\sqrt[5]{x})^5 &= 2^5 \\ x &= 32 \end{align*}$

Nyt juuriyhtälön on parillinen, joten täytyy olla $a\geq0$ . , joten yhtälöllä on olemassa ratkaisu ja voidaan korottaa puolittain kuudenteen potenssiin.

$\begin{align*} \sqrt[6]{x}&=4 && |()^6\\ (\sqrt[6]{x})^6 &=4^6\\ x &=4096 \end{align*}$

Parittomalla juuriyhtälöllä on aina olemassa ratkaisu, joten ratkaistaan yhtälö.

$\begin{align*} -2\sqrt[7]{x} &= 4 && |:(-2)\\ \sqrt[7]{x} &= -\dfrac{1}{2} &&|()^7 \\ (\sqrt[7]{x})^7 &= (-\dfrac{1}{2})^7 \\ x &= -\dfrac{1}{128} \end{align*}$

Sievennetään ensin juuriyhtälö standardimuotoon $\sqrt[n]{x}=a$ .

$\begin{align*} 11\sqrt[8]{x}+\pi&=\dfrac{1}{2} && |-\pi\\ 11\sqrt[8]{x} &= \dfrac{1}{2}-^{2)}\pi &&| \\ 11\sqrt[8]{x} &= \dfrac{1}{2}-\dfrac{2\pi}{2} \\ 11\sqrt[8]{x} &= \dfrac{1-2\pi}{2} && |\cdot \dfrac{1}{11}\\ \sqrt[8]{x} &= \dfrac{1-2\pi}{2} \cdot \dfrac{1}{11} \\ \sqrt[8]{x} &= \dfrac{1-2\pi}{22} \end{align*}$

Tässä kohtaa on hyvä huomata, että nyt on parillinen ja $\dfrac{1-2\pi}{22}\approx-0,24<0$ . Emme voi korottaa puolittain kahdeksaan, joten yhtälöllä ei ole ratkaisua.

2.2.4 Esimerkki: sanallinen juuriyhtälöongelma

Mikä reaaliluku on kyseessä, kun luvun ja sitä yhtä isomman luvun osamäärän kuutiojuuri on ?

Ratkaisu:

Olkoon $x="\text{kysytty luku}"$ . Muodostetaan ja ratkaistaan tehtävänannon mukainen yhtälö.

$\begin{align*} \sqrt[3]{\dfrac{x}{x+1}}&= 2 && |()^3 \\ \dfrac{x}{x+1}&= 8 && |\cdot(x+1), \text{ missä } x+1\neq0 \\ x &= 8x + 8 && |-x-8 \\ 7x &= -8 && |:7 \\ x &= -\dfrac{8}{7} \end{align*}$

Alkuperäisen yhtälön nimittäjän x+1 tulee olla nollasta poikkeava, koska nollalla jakoa ei ole määritelty. Näin ollen saadaan ehto

$\begin{align*} x+1 \neq 0 && |-1 \\ x \neq -1, \end{align*}$

jonka ratkaisumme $x = -\dfrac{8}{7}$ toteuttaa.

Vastaus: Kyseessä on luku $-\dfrac{8}{7}$ .

Juurifunktio ja -yhtälö: tehtäviä

2.3 Murtopotenssi

2.3.1 Esimerkki: johdanto murtopotenssiin $a^{\frac{1}{n}}$

MAY1 -kurssin kappaleessa Potenssi ja juuri esiteltiin potenssin potenssin laskusääntö

$({a^m})^n=a^{mn}.$

Laske potenssin potenssin laskusäännöllä luvun $3^{\frac{1}{2}}$ neliö.
Ilmaise ilman potenssimerkintää luku $3^{\frac{1}{2}}$ .
Laske potenssin potenssin laskusäännöllä luvun $5^{\frac{1}{3}}$ kuutio.
Ilmaise ilman potenssimerkintää luku $5^{\frac{1}{3}}$ .
Laske potenssin potenssin laskusäännöllä luvun $a^{\frac{1}{n}}$ :s potenssi, missä ja on positiivinen kokonaisluku.
Ilmaise ilman potenssimerkintää luku $a^{\frac{1}{n}}$ .

Ratkaisu:

Lasketaan potenssin potenssin laskusäännön avulla luvun $3^{\frac{1}{2}}$ toinen potenssi.

$\begin{align*} (3^{\frac{1}{2}})^2 &= 3^{\frac{1}{2}\cdot 2} \\ &= 3^{1} \\ &= 3 \end{align*}$

Luvun neliöjuuri $\sqrt{a}$ on sellainen ei-negatiivinen reaaliluku, jonka neliö on luku . a.-kohdan perusteella luvun $3^{\frac{1}{2}}$ neliö on luku . Näin ollen, koska luvun $3^{\frac{1}{2}}$ toinen potenssi on luku , niin

$3^{\frac{1}{2}}=\sqrt{3}.$

Lasketaan potenssin potenssin laskusäännön avulla luvun $5^{\frac{1}{3}}$ kolmas potenssi.

$\begin{align*} (5^{\frac{1}{3}})^3 &= 5^{\frac{1}{3}\cdot 3} \\ &= 5^{1} \\ &= 5 \end{align*}$

Luvun kuutiojuuri $\sqrt[3]{a}$ on sellainen reaaliluku, jonka kuutio on luku . Edellisen kohdan perusteella luvun $5^{\frac{1}{3}}$ kolmas potenssi on luku . Myös luvun $\sqrt[3]{5}$ kolmas potenssi on luku , joten

$5^{\frac{1}{3}}=\sqrt[3]{5}.$

Lasketaan potenssin potenssin laskusäännöllä luvun $a^{\frac{1}{n}}$ :s potenssi.

$\begin{align*} (a^{\frac{1}{n}})^n &= a^{\frac{1}{n}\cdot n} \\ &= a^{1} \\ &= a \end{align*}$

Edellisen perusteella $(a^{\frac{1}{n}})^n=a$ . Koska , niin myös $(\sqrt[n]{a})^n=a$ , riippumatta siitä, onko kokonaisluku parillinen vai pariton. Näin ollen

$a^{\frac{1}{n}}=\sqrt[n]{a}.$

Edellisen esimerkin havaintojen perusteella voidaan määritellä ensin murtopotenssi $a^{\frac{1}{n}}$ .

Murtopotenssi $(a^\frac{1}{n})$

Olkoon a>0 ja positiivinen kokonaisluku. Tällöin luku korotettuna murtopotenssiin $\frac{1}{n}$ on luvun :s juuri.

$a^{\frac{1}{n}}=\sqrt[n]{a}$

2.3.2 Esimerkki: murtopotenssin $a^{\frac{1}{n}}$ ja juuren $\sqrt[n]{a}$ välinen yhteys

Ilmaise juurina potenssit.

$11^{\frac{1}{2}}$
$13^{\frac{1}{3}}$
$(-17)^{\frac{1}{5}}$

Ratkaisu:

$11^{\frac{1}{2}}=\sqrt{11}$
$13^{\frac{1}{3}}=\sqrt[3]{13}$
Negatiivisesta luvusta voidaan ottaa :s juuri, kun on pariton. Nyt , joten

$(-17)^{\frac{1}{5}}=\sqrt[5]{-17}=-\sqrt[5]{17.}$

2.3.3 Esimerkki: johdanto murtopotenssiin $a^{\frac{m}{n}}$

Ilmaise :s juuren ja potenssin potenssin laskusäännön avulla

$3^{\frac{5}{7}}$
$a^{\frac{m}{n}}$ , missä sekä ja ovat positiivisia kokonaislukuja.

Ratkaisu:

Murtoluku $\frac{5}{7}$ voidaan ilmoittaa myös muodossa $\frac{5}{7}=5\cdot\frac{1}{7}$ . Sievennetään

$\begin{align*} 3^{\frac{5}{7}} &= 3^{5\cdot\frac{1}{7}} && |\text{ potenssin potenssi } a^{m\cdot n}=(a^m)^n\\ &= (3^5)^{\frac{1}{7}} && |\text{ murtopotenssi } a^{\frac{1}{n}}=\sqrt[n]{a} \\ &= \sqrt[7]{3^5}. \end{align*}$

Murtoluku $\frac{m}{n}$ voidaan ilmoittaa myös muodossa $\frac{m}{n}=m\cdot\frac{1}{n}$ . Sievennetään

$\begin{align*} a^{\frac{m}{n}} &= a^{m\cdot\frac{1}{n}} && |\text{ potenssin potenssi } \\ &= (a^m)^{\frac{1}{n}} && |\text{ murtopotenssi } \\ &= \sqrt[n]{a^m} \end{align*}$

Nyt edellisen esimerkin perusteella voidaan määritellä murtopotenssi $a^{\frac{n}{m}}$ .

Murtopotenssi $(a^{\frac{m}{n}})$

Olkoon a>0 sekä ja positiivisia kokonaislukuja. Tällöin luku korotettuna murtopotenssiin $\frac{m}{n}$ on luvun a^m :s juuri.

$a^{\frac{m}{n}}=\sqrt[n]{a^m}$

2.3.4 Esimerkki: murtopotenssin $a^{\frac{m}{n}}$ ja juuren $\sqrt[n]{a^m}$ välinen yhteys

Ilmaise juurina potenssit.

$3^{\frac{5}{7}}$
$5^{\frac{143}{121}}$

Ratkaisu:

Murtopotenssin $a^{\frac{m}{n}}$ määritelmän mukaan

$3^{\frac{5}{7}}=\sqrt[7]{3^5}=\sqrt[7]{243}.$

Vastaavasti

$5^{\frac{143}{121}}=\sqrt[121]{5^{143}}$

2.3.5 Esimerkki: johdanto murtopotenssiin $a^{-\frac{m}{n}}$

Olkoon a>0 ja $n\neq 0$ . Ilmaise $a^{-\frac{m}{n}}$

:s juuren avulla
potenssimuodossa ilman negatiivistä eksponenttia.

Ratkaisu:

Ilmoitetaan kuten aiemminkin murtoluku $-\frac{m}{n}$ tulomuodossa $-m\cdot\frac{1}{n}$ . Sievennetään

$\begin{align*} a^{-\frac{m}{n}} &= a^{-m\cdot\frac{1}{n}} && | \text{ potenssin potenssi} \\ &= (a^{-m})^{\frac{1}{n}} && | \text{ murtopotenssi} \\ &= \sqrt[n]{a^{-m}} \\ \end{align*}$

Negatiivisen eksponentin laskusäännöllä saadaan

$\begin{align*} a^{-\frac{m}{n}} &= \dfrac{1}{a^\frac{m}{n}}. \end{align*}$

Vimeiseksi määritellään murtopotenssi $a^{-\frac{m}{n}}$ .

Murtopotenssi $(a^{-\frac{m}{n}})$

Olkoon a>0 sekä ja kokonaislukuja, missä $n\neq 0$ . Tällöin luku korotettuna murtopotenssiin $-\frac{m}{n}$ on luvun $a^\frac{m}{n}$ käänteisluku.

$a^{-\frac{m}{n}}=\dfrac{1}{a^\frac{m}{n}}=\sqrt[n]{a^{-m}}$

Huom! Murtopotenssin määritelmässä voisi periaattessa hyväksyä myös $a\geq 0$ , mutta tämä aiheuttaa ongelman negatiivisen eksponentin määritelmässä, sillä nollalla jakoa ei ole määritelty reaaliluvuilla. Esimerkiksi

$0^{-\frac{1}{2}}=\frac{1}{0^{\frac{1}{2}}}=\frac{1}{\sqrt{0}}=\frac{1}{0} \text{ ei ole määritelty.}$

2.3.6 murtopotenssin $a^{-\frac{m}{n}}$ ja juuren $\sqrt[n]{a^{-m}}$ välinen yhteys

Ilmaise juurina potenssit.

$3^{-\frac{5}{7}}$
$5^{-\frac{143}{121}}$

Ratkaisu:

Murtopotenssin $a^{-\frac{m}{n}}$ määritelmän mukaan

$3^{-\frac{5}{7}}=\sqrt[7]{3^{-5}}=\sqrt[7]{\frac{1}{243}}.$

Vastaavasti

$5^{-\frac{143}{121}}=\sqrt[121]{5^{-143}}=\sqrt[121]{\frac{1}{5^{143}}}.$

Nyt olemme siis määrittäneet yleisen rationaalisen eksponentin a^r , missä $r=\frac{m}{n}$ on rationaaliluku ja a>0 . Lisäksi huomasimme, että potenssilla ja juurella on yhteys. Tämän vuoksi, voimme yleistää aiemmin opitut (MAY1) potenssien laskusäännöt murtopotensseille sekä myös yleisille juurille.

Potenssin laskusääntöjä

Olkoon a,b>0 sekä ja rationaalilukuja. Tällöin ovat voimassa seuraavat laskusäännöt.

Samankantaisten potenssien tulo

$a^ra^s=a^{r+s}$

Samankantaisten potenssien osamäärä

$\dfrac{a^r}{a^s}=a^{r-s}$

Tulon potenssi

(ab)^r=a^rb^r

Osamäärän potenssi

$\Big(\dfrac{a}{b}\Big)^r=\dfrac{a^r}{b^r}$

Potenssin potenssi

$(a^r)^s=a^{rs}$

2.3.7 Esimerkki: murtopotenssin laskusääntöjä

Sievennä lauseke.

$(\sqrt[3]{5})^6$
$\dfrac{3}{\sqrt[3]{9}}$
$x^{0,5}(\sqrt[3]{x})^{1,5}$ ,

Ratkaisu:

Muunnetaan lauseke $(\sqrt[3]{5})^6$ potenssimuotoon ja hyödynnetään potenssin potenssin laskusääntöä.

$\begin{align*} (\sqrt[3]{5})^6 &= (5^{\frac{1}{3}})^6 && |\text{ potenssin potenssi} \\ &= 5^{\frac{1}{3}\cdot6} \\ &= 5^2 \\ &= 25 \end{align*}$

Muunnetaan lauseke $\dfrac{3}{\sqrt[3]{9}}$ potenssimuotoon ja hyödynnetään murtopotenssin laskusääntöjä.

$\begin{align*} \dfrac{3}{\sqrt[3]{9}} &= \dfrac{3}{9^{\frac{1}{3}}} && |\text {negatiivinen eksponentti} \\ &= 3\cdot 9^{-\frac{1}{3}} && | 9=3^2 \\ &= 3\cdot (3^2)^{-\frac{1}{3}} && |\text{ potenssin potenssi}\\ &= 3\cdot3^{2\cdot(-\frac{1}{3})} \\ &= 3\cdot 3^{-\frac{2}{3}} && |\text{ samankantaisten potenssien tulo} \\ &= 3^{1-\frac{2}{3}} \\ &= 3^{\frac{1}{3}} \\ &= \sqrt[3]{3} \end{align*}$

Toimitaan vastaavasti kuin edelläkin.

$\begin{align*} x^{0,5}(\sqrt[3]{x})^{1,5} &= x^{0,5} \cdot (x^{\frac{1}{3}})^{1,5} && |\text{ potenssin potenssi} \\ &= x^{0,5} \cdot x^{\frac{1}{3}\cdot 1,5} \\ &= x^{0,5} \cdot x^{0,5} && |\text{ samankantaisten potenssien tulo}\\ &= x^{0,5+0,5} \\ &= x \end{align*}$

(Huomaa, että luvut $0,5=\dfrac{1}{2}$ ja $1,5=\dfrac{3}{2}$ ovat murtolukuja.)

2.3.8 Perustelu: miksi

Syy sille, miksi emme määrittele murtopotenssia negatiivisilla luvuilla a<0 johtuu siitä, että haluamme luvun a^r olevan yksikäsitteinen. Tutkitaan tätä seuraavaksi.

Olkoon a<0 ja pariton kokonaisluku. Tällöin

$a^{\frac{1}{p}}=\sqrt[p]{a}<0.$

Toisaalta, jos lavennamme eksponenttia $\frac{1}{p}$ parillisella luvulla , niin saamme

$a^{^{q)}\frac{1}{p}}=a^{\frac{q}{qp}}=\sqrt[qp]{a^q}.$

Koska a<0 ja on parillinen, niin a^q>0 . Näin ollen

$a^{\frac{1}{p}}=\sqrt[qp]{a^q}>0.$

Laventamisen jälkeen murtopotenssilausekkeemme $a^{\frac{1}{p}}$ vaihtoi siis etumerkkiään negatiivisesta positiviiseksi, minkä vuoksi $a^{\frac{1}{p}}$ ei ole yksikäsittäinen.

Lisäksi, ei ole myöskään olemassa lukua, joka on pienempi kuin ja suurempi kuin .

Pitäydytään siis jatkossakin siinä, että reaalinen murtopotenssi voidaan määritellä yksikäsitteisesti, kun . Todetaan kuitenkin aiheesta kiinnostuneille, että kompleksiluvuilla voidaan määritellä murtopotenssi myös silloin, kun a<0 . Kompleksinen murtopotenssi (kompleksinen juuri) ei kuitenkaan ole yksikäsitteinen.

2.3.9 Esimerkki: entä jos ?

Laske

$(-1)^{\frac{1}{3}}$
$(-1)^{\frac{2}{6}}$
Mitä huomaat?

Ratkaisu:

$(-1)^{\frac{1}{3}}=\sqrt[3]{-1}=-1.$

$(-1)^{\frac{2}{6}}=\sqrt[6]{(-1)^2}=\sqrt[6]{1}=1.$

Koska $\dfrac{1}{3}=\dfrac{2}{6}$ , niin täytyy olla

$(-1)^{\frac{1}{3}}=(-1)^{\frac{2}{6}}.$

Näin ei kuitenkaan ole a.- ja b.-kohdan perusteella, sillä $-1\neq 1$ .

Siispä (-1)^r , missä on rationaaliluku, ei ole yksikäsitteinen.

Murtopotenssi: tehtäviä

2. Potenssi ja juuri

2.1 Potenssifunktio ja -yhtälö

2.1.1 Esimerkki: kuutioyhtälön ratkaiseminen graafisesti

2.1.2 Esimerkki: :s juuri laskimella

2.1.3 Esimerkki: potenssiyhtälön ratkaiseminen algebrallisesti

2.1.4 Esimerkki: säästötilin talletuskoron laskeminen

2.2 Juurifunktio ja -yhtälö

2.2.1 Esimerkki: juurifunktion kuvaajan tarkastelu GeoGebralla

2.2.2 Esimerkki: neliöjuuriyhtälön ratkaiseminen graafisesti

2.2.3 Esimerkki: juuriyhtälön ratkaiseminen algebrallisesti

2.2.4 Esimerkki: sanallinen juuriyhtälöongelma

2.3 Murtopotenssi

2.3.1 Esimerkki: johdanto murtopotenssiin

2.3.2 Esimerkki: murtopotenssin ja juuren välinen yhteys

2.3.3 Esimerkki: johdanto murtopotenssiin

2.3.4 Esimerkki: murtopotenssin ja juuren välinen yhteys

2.3.5 Esimerkki: johdanto murtopotenssiin

2.3.6 murtopotenssin ja juuren välinen yhteys

2.3.7 Esimerkki: murtopotenssin laskusääntöjä

2.3.8 Perustelu: miksi

2.3.9 Esimerkki: entä jos ?

2.3.1 Esimerkki: johdanto murtopotenssiin $a^{\frac{1}{n}}$

2.3.2 Esimerkki: murtopotenssin $a^{\frac{1}{n}}$ ja juuren $\sqrt[n]{a}$ välinen yhteys

2.3.3 Esimerkki: johdanto murtopotenssiin $a^{\frac{m}{n}}$

2.3.4 Esimerkki: murtopotenssin $a^{\frac{m}{n}}$ ja juuren $\sqrt[n]{a^m}$ välinen yhteys

2.3.5 Esimerkki: johdanto murtopotenssiin $a^{-\frac{m}{n}}$

2.3.6 murtopotenssin $a^{-\frac{m}{n}}$ ja juuren $\sqrt[n]{a^{-m}}$ välinen yhteys